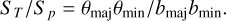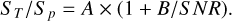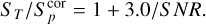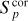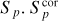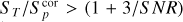| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A179 | |
| Number of page(s) | 12 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202348333 | |
| Published online | 18 March 2024 | |
LOFAR HBA observations of the Euclid Deep Field North (EDFN)
1
INAF – Istituto di Radioastronomia,
Via Gobetti 101,
40129
Bologna,
Italy
e-mail: marco.bondi@inaf.it
2
INFN – Sezione di Roma, Piazzale Aldo Moro,
2 – c/o Dipartimento di Fisica, Edificio G. Marconi,
00185
Roma,
Italy
3
INAF – Osservatorio Astronomico di Roma,
Via Frascati 33,
00078
Monteporzio Catone,
Italy
4
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna,
Via Gobetti 93/3,
40129
Bologna,
Italy
5
INAF – Osservatorio Astrofisico di Catania,
Via Santa Sofia 78,
95123
Catania,
Italy
6
Leiden Observatory, Leiden University,
PO Box 9513,
2300
RA Leiden,
The Netherlands
7
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill,
Edinburgh,
EH9 3HJ,
UK
8
Dipartimento di Fisica e Astronomia, Università di Bologna,
Via P. Gobetti 93/2,
40129
Bologna,
Italy
9
Centre for Astrophysics Research, University of Hertfordshire, College Lane,
Hatfield
AL10 9AB,
UK
10
INAF – IAPS,
Via Fosso del Cavaliere 100,
00133
Rome,
Italy
11
Dipartimento di Fisica, Universitá degli Studi di Torino,
Via Pietro Giuria 1,
10125
Torino,
Italy
12
Centre for Extragalactic Astronomy, Department of Physics, Durham University,
Durham
DH1 3LE,
UK
13
Institute for Computational Cosmology, Department of Physics, University of Durham,
South Road,
Durham
DH1 3LE,
UK
14
ASTRON, Netherlands Institute for Radio Astronomy,
Oude Hoogeveensedijk 4,
7991
PD Dwingeloo,
The Netherlands
15
GEPI & ORN, Observatoire de Paris, Université PSL, CNRS,
5 Place Jules Janssen,
92190
Meudon,
France
16
Department of Physics & Electronics, Rhodes University,
PO Box 94,
Grahamstown,
6140,
South Africa
17
School of Physical Sciences, The Open University, Walton Hall,
Milton Keynes,
MK7 6AA,
UK
18
RAL Space, STFC Rutherford Appleton Laboratory,
Chilton, Didcot, Oxfordshire,
OX11 0QX,
UK
Received:
20
October
2023
Accepted:
9
December
2024
We present the first deep (72 h of observations) radio image of the Euclid Deep Field North (EDFN) obtained with the LOw-Frequency ARray (LOFAR) High Band Antenna (HBA) at 144 MHz. The EDFN is the latest addition to the LOFAR Two-Metre Sky Survey (LoTSS) Deep Fields, and these observations represent the first data release for this field. The observations produced a 6″ resolution image with a central rms noise of 32 μJy beam−1. A catalogue of ~23 000 radio sources above a signal-to-noise ratio threshold of five is extracted from the inner circular 10 deg2 region. We discuss the data analysis, and we provide a detailed description of how we derived the catalogue of radio sources, the issues related to direction-dependent calibration, and their effects on the final products. Finally, we derive the radio source counts at 144 MHz in the EDFN using catalogues of mock radio sources to derive the completeness correction factors. The source counts in the EDFN are consistent with those obtained from the first data release of the other LoTSS Deep Fields (ELAIS-N1, Lockman Hole and Bootes), despite the different method adopted to construct the final catalogue and to assess its completeness.
Key words: catalogs / surveys / radio continuum: galaxies / radio continuum: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In the last 20 yr, it has been demonstrated that panchromatic surveys (from X-rays to radio wavelengths) of selected regions of the sky (e.g. Le Fèvre et al. 2005; Scoville et al. 2007; Driver et al. 2011; Grogin et al. 2011; Chen et al. 2016; Franco et al. 2018; Pentericci et al. 2018; Weaver et al. 2022; Treu et al. 2022; Finkelstein et al. 2023) are fundamental to providing the database on which to build a consensus on galaxy formation and evolution (e.g. Conselice 2014; Somerville & Davé 2015; Förster Schreiber & Wuyts 2020). Observations at different wavelengths can reveal different aspects of the structure and properties of the galaxies, such as the distribution of stars, gas, and dust, as well as the presence of active galactic nuclei (AGNs). For example, optical and infrared observations can provide information on the stars within a galaxy, while radio and X-ray observations can reveal the presence of AGNs and the energetic processes associated with them. By combining data at multiple wavelengths, astronomers can hence obtain a comprehensive picture of how galaxies form and evolve over time.
Observations in the radio waveband are extremely important to the study of the physical processes connected to star formation, the properties of supermassive black holes, and the interplay between star formation and AGNs across cosmic time. The radio continuum emission is not affected by dust extinction and therefore provides a dust-unbiased star formation tracer (e.g. Condon 1992; Haarsma et al. 2000; Seymour et al. 2008; Smolčić et al. 2009; Novak et al. 2017; van der Vlugt et al. 2022; Cochrane et al. 2023). Moreover, only at radio frequencies can one reliably identify and probe low-luminosity jet-mode AGNs hosted by the most massive galaxies and therefore investigate the effects of feedback on their growth (e.g. Croton et al. 2006; Best et al. 2006; Hardcastle et al. 2007; Smolčić 2009; Best & Heckman 2012; Heckman & Best 2014; Smolčić et al. 2017b; Kondapally et al. 2022; Mingo et al. 2022). Present and future radio surveys can reach the depth needed to detect star-forming galaxies as well as quasar-mode AGNs, which are typically faint in the radio band (Bonzini et al. 2012; Padovani 2016; Best et al. 2023). However, most of the existing deep radio observations required to study these source populations at high redshifts are usually limited to small regions of the sky, ranging from tens of square arcminutes to a few square degrees (e.g. Hopkins et al. 1998, 2003; Ciliegi et al. 1999; Prandoni et al. 2000, 2018; Bondi et al. 2003, 2007; Huynh et al. 2005; Schinnerer et al. 2007, 2010; Tasse et al. 2007; Owen & Morrison 2008; Miller et al. 2008, 2013; Morrison et al. 2010; Smolčić et al. 2017a; Murphy et al. 2017; Owen 2018; Muxlow et al. 2020; van der Vlugt et al. 2022; Algera et al. 2022; Heywood et al. 2022; D'Amato et al. 2022; Hale et al. 2023). In this context, large area (e.g. tens of degrees) surveys down to unprecedented depths are planned with new and upgraded facilities (e.g. Jarvis et al. 2016). The LOw-Frequency ARray (LOFAR; van Haarlem et al. 2013) plays a key role in this framework by combining a wide field of view with high sensitivity and angular resolution. The recently published second data release of the LOFAR Two-Metre Sky Survey (LoTSS; Shimwell et al. 2017, 2019, Shimwell et al. 2022) publicly released images covering 5700 square degrees in the northern sky centred at approximately 12 h 45 m +44°30′ and 1 h 00 m +28°00′ and spanning 4178 and 1457 square degrees, respectively. The observations are carried out at the central frequency of 144 MHz and each pointing is observed for ~8 h. The images have a median 1σ rms sensitivity of 83 μJy beam−1 at 6″ resolution. When completed, the LoTSS observations will cover the whole northern sky. To complement the LoTSS observations, deeper pointings (the LoTSS Deep Fields; Best et al. 2023) in regions already covered by extensive and deep multi-wavelength ancillary observations are being carried out with LOFAR with the aim to reach an rms noise of ≃10 μJy beam−1 over a sky area of ≃50 deg2. The LoTSS Deep Fields data release 1 (DR1) accounts for about 1/3 of the integration time for three deep fields (Lockman Hole, Bootes and ELAIS-N1) and provides radio images and catalogues (Tasse et al. 2021; Sabater et al. 2021), near-infrared (NIR) and optical identifications (Kondapally et al. 2021), photometric redshifts (Duncan et al. 2021), and host galaxies' classification and properties (Best et al. 2023).
The North Ecliptic Pole (NEP) region is the fourth field of the LoTSS Deep Fields project (Best et al. 2023), but it was not included in the first LoTSS-Deep data release as the data were obtained later. This field was chosen because the NEP is the location of the Euclid Deep Field North (EDFN), one of the deep fields observed by the Euclid mission (Euclid Collaboration 2022) and the only one in the northern sky. Euclid observations will provide sub-arcsecond NIR imaging down to H = 26 mag over a 20 deg2 field centred at RA = 269.73 deg and Dec = +66.02 deg. This paper complements the LoTSS Deep Fields DR1 presenting the LOFAR 6″ resolution image at 144 MHz and the radio source catalogue obtained from the first 72 h in the EDFN. Other publications in preparation will present the NIR-optical identifications of the radio sources and will focus on the results obtained with the inclusion of the LOFAR International Stations that allow improvement of the angular resolution. The LOFAR observations of the EDFN were completed in May 2023, totalling around 400 h of observations (expected final noise ~12 μJy beam−1), and this complete dataset is now being processed and analysed.
This paper is organised as follows. In Sects. 2 and 3 we describe the 72 h of LOFAR observations and summarise the data calibration and imaging procedures, respectively. Section 4 contains a detailed description of the methods used to test the reliability of the LOFAR data products, including the refinement of the amplitude calibration, the compilation of the final radio source catalogue, and an analysis of the properties of the radio sources at different distances from the field centre. The generation of mock samples of realistic radio sources used to derive the completeness factors to be applied to the source counts is described in Sect. 5. Finally, Sect. 6 presents the radio source counts obtained in the EDFN and a brief comparison with those obtained from the other LoTSS Deep Fields. Throughout this paper, we adopt the spectral index convention Sν ∝ ν−α.
2 LOFAR observations
LOFAR observed the EDFN for 72 h at 144 MHz during cycle 12 (proposal LC12_027, PI: van Weeren). The proposal combined EDFN observations with those of the galaxy cluster Abell 2255 (Botteon et al. 2022). This was possible because the targets, EDFN and Abell 2255, are about five degrees apart on the sky (resulting in minimal sensitivity losses due to the LOFAR HBA tile beam), and with the adopted setup we were able to split the LOFAR beam to observe both targets. The observations presented in this paper were obtained using a single pointing centre, shifted by ≃30″ with respect to the EDFN positions.
The 72 h were split over nine nights in the period from June to November, 2019 (see Table 1). The observations were carried out with the high-frequency band antennas in HBA_DUAL_INNER configuration, which provides a uniform shape of the primary beam over the whole of the LOFAR Dutch stations (i.e. only using the inner 24 tiles of the 48 tiles on the remote stations). All data sets were recorded with an integration time of 1s, a 48 MHz bandwidth centred at 144 MHz, and a channel width of 3.05 kHz. The data were then passed through the standard LOFAR pre-processing pipeline (Heald et al. 2010), which performed the Dysco compression to reduce the data size (Offringa 2016), the RFI flagging using the AOflagger tool (Offringa et al. 2012), and averaged down the data to a channel width of 12.2 kHz. Time resolution remains unchanged.
All the observations were preceded and followed by an ~15 min run on the calibrators 3C295 and 3C48, respectively. The latter source was selected as the primary amplitude calibrator for the data sets. During the nine epochs of observations, the number of observing stations, including the international stations, varied from 47 to 51; two nights had one international station missing and one night had four stations (two international and two core stations) missing. In the standard LOFAR data analysis aimed at producing an ~6″ angular resolution image, only the data from the 38 Dutch stations (with baseline lengths in the 0.15-100 km range) are processed. The international stations are flagged out at an early stage of processing to reduce the sizes of intermediate data products since they are not used.
3 Data calibration and imaging
The data calibration and imaging were performed using the OCCAM infrastructure for high performance computing (HPC) run by the Competence Centre for Scientific Computing (C3S), a joint interdepartmental advanced research centre of Turin University and the Italian National Institute for Nuclear Physics (INFN; Aldinucci et al. 2017).
The data were downloaded from the LOFAR Long Term Archive and copied over to the OCCAM system. The data are stored using the Dysco data compression format (Offringa 2016) that makes it possible to reduce the data volume by roughly a factor of four. Each night of observation amounts to ~4.2 TB, including the calibrator scans. For the data reduction we used one OCCAM Fat Node, running 48 cores with 768 GB of RAM available.
For the calibration and imaging, we followed the same steps used for the Bootes and Lockman Hole deep fields explained in detail in Tasse et al. (2021). Here, we briefly summarise these steps. Direction-independent calibration was performed using the PREFACTOR version 3 pipeline (de Gasperin et al. 2019; van Weeren et al. 2016; Williams et al. 2016)1 using 3C48 as amplitude calibrator. The PREFACTOR calibrator pipeline was run individually for each of the nine nights, and the resulting bandpasses were checked for possible antenna malfunctions. Then, the PREFACTOR target pipeline was run for each night, producing the calibration tables to be applied in the next data reduction step. Direction-dependent calibration was performed using the DDF-pipeline (Shimwell et al. 2019; Tasse et al. 2021)2, which combines the solver KillMS3 (Tasse 2014b,a; Smirnov & Tasse 2015) and the imager DDFacet4 (Tasse et al. 2018). First, each night was processed to an early stage of reduction, that stopped after the direction-independent corrected image was produced. These images were checked for evident issues, such as poor ionospheric conditions and processing failures. Seven nights produced images with very similar rms noise values, with the remaining two having slightly higher but still acceptable values (the noise values are reported in Table 1). The night with the best noise (15 November 2019) was fully processed with DDF-pipeline to produce the sky model and, finally, the DDF-pipeline was run combining all the nine nights together using this sky model as a starting model for the self-calibration direction-dependent stage.
After the completion of the DDF-pipeline we obtained the deep (72 h), full-resolution (6 arcsec) Stokes I radio image centred on the EDFN. The size of the image is an input parameter for the pipeline and is usually set to 20 000 × 20 000 pixels (1 pixel = 1.5 arcsec). In processing the EDFN data sets, we set this size to a slightly larger value (21 500 × 21 500 pixels, ~9 × 9 deg2) to mitigate artefacts associated with a few bright sources at the edges of the field. A lower resolution Stokes I image (20 arcsec) was also produced by the pipeline, but this image was not used as part of the analysis presented here. The final image (before the refinement of the amplitude scale, see Sect. 4.2) has a central r.m.s noise of 36 μJy beam−1. A ~0.6 × 0.3 deg2 inset of the final image is shown in Fig. 1.
A preliminary catalogue of the whole field was produced from the full-resolution image using PyBDSF (Mohan & Rafferty 2015). PyBDSF fits individual Gaussian components in regions selected on the basis of the local noise, extracting sources that can either be composed of a single or multiple components. Very extended radio sources or sources whose brightness spatial distribution cannot be properly modelled by Gaussian components are effectively recovered using wavelets. The parameters used to run PyBDSF on the EDFN are the same as those used for the other Deep Fields and listed in Table C.1 in Sabater et al. (2021). PyBDSF found almost 50 000 sources above a signal-to-noise ratio (SNR = Sρ/σ where Sp is the peak brightness and σ is the local rms noise) threshold of five over the whole imaged area.
EDFN observations.
4 Data analysis
In this section, we describe the methods adopted to test the reliability of the data products, refining the amplitude calibration, producing the final catalogue of radio sources, and classifying all the sources as resolved or unresolved.
4.1 Direction-dependent effects
We decided to investigate the possible effects on the catalogued source parameters introduced by the choice of a different field faceting geometry and of a different sky model during the direction-dependent calibration. For this reason the EDFN datasets were independently reduced in Leiden using a different computer infrastructure. During this procedure the image obtained from the observation carried out on 7 June 2019 was adopted as the sky model along with a different faceting geometry. The two final images, the one obtained by us and the one obtained in Leiden, were then compared. For each image we measured the median noise in annular regions at increasing distances from the centre and found that the median values were consistent to within 1% (corresponding to ~0.3 μJy beam−1) up to a radius of 2.5 deg from the field centre. Beyond this distance the difference in the median noise increases, reaching 4% at 4 deg from the field centre. Then, we used the same version of PyBDSF with the same set of parameters on the two images obtaining two catalogues. The two catalogues (hereafter dubbed as Leiden catalogue and Turin catalogue) were cross-matched using a matching radius of 3 arcsec, and only the 2918 matched sources with SNR > 50 in both catalogues were selected. These sources were then split according to their distance r from the field centre in four annular regions: r < 1 deg, 1 < r < 2 deg, 2 < r < 3 deg, and 3 < r < 4 deg. For each group of matched sources we calculated the ratio between the total (peak) fluxes obtained in the Turin and Leiden catalogues, and we derived the median and the scaled median absolute deviation (MAD) in each of the four distance intervals.
The main results obtained from this comparison are shown in Fig. 2 and can be summarised as follows. The median values of the peak brightness ratios and total flux density ratios do not significantly change with increasing distance from the field centre and are consistent with a value of 1, meaning there is no systematic scale offset in the amplitudes of the two images. Furthermore, the MAD associated with each median value increases with r. Within r < 2 deg the MAD is <0.05 for both the peak brightness ratios and total flux ratios. Beyond this distance, the peak brightness ratios show a larger dispersion up to a MAD = 0.16 in the range 3 < r < 4 deg compared to a MAD = 0.09 for the total flux density ratios in the same distance range. Finally, we also checked whether the position of the radio sources in the Leiden and Turin catalogues could depend on r. The right panel in Fig. 2 shows the median separation in arcseconds as a function of distance r. We remind the reader that the two catalogues were matched using a maximum distance r = 3 arcsec, half the size of the restoring beam. There is a trend of larger differences in the source positions between the two catalogues with increasing distance from the field centre, but the median shifts are small, ≲0.2 arcsec for r < 2 deg and even at the largest distance probed by this test the median shift is ~0.6 arcsec, less than half of the pixel size.
In summary, the peak brightness and flux density ratios are consistent to ≤5% within a radius of r = 2 deg from the field centre. However, it should be noted that at larger distances from the field centre these uncertainties increase significantly, reaching values of about 16 and 9% at distance r ≃ 4 deg for the peak brightness and total flux density, respectively. The two images have been obtained using the same pipeline but on different computer infrastructures, slightly different singularity images, different starting sky models and faceting geometry. We note that we cannot exclude that the differences between the two images might be caused, at least to some extent, by different software versions or different computer hardware used to run the pipeline by us and in Leiden, but this is rather unlikely. The larger dispersion observed in the measured peak brightness ratios with respect to the total flux density ratios, and the general trend for the dispersion to be larger at larger distances suggest that the differences between the two images are likely caused by residual smearing and uncertainties in the direction-dependent calibration derived using different faceting patterns and starting sky models in the two images (see also the discussion in Sect. 4.4).
 |
Fig. 1 LOFAR image of Euclid Deep Field North; the image shows only a sub-region ~0.6 × 0.3 deg2 centred at RA = 270.3086 deg and Dec = 65.882 deg. |
 |
Fig. 2 Median peak brightness ratio (left panel), median total flux density ratio (middle panel), and median absolute value separation (right panel) in the four annular regions at increasing distance r from the pointing centre for matched sources in the Turin and Leiden catalogues with SNR > 50. The error bars are the scaled median absolute deviation (MAD) values. |
4.2 Absolute flux density calibration
We followed the method described in Sabater et al. (2021) to adjust the absolute flux density scale using the external radio catalogues available from the literature. We compared the flux density of sources in common between our catalogue and the external catalogues using only sources with distance r < 3 deg from the field centre and adopting the constraints listed in Sect. 3.5 from Sabater et al. (2021) to avoid the introduction of biases due to the different depths and angular resolution of the external catalogues. The external catalogues we used are the VLASSr at 74 MHz (Lane et al. 2014), the TGSS at 150 MHz (Intema et al. 2017), the 6C at 151 MHz (Hales et al. 1990), the WENSS at 350 MHz (Rengelink et al. 1997), the NVSS at 1.4 GHz (Condon et al. 1998), and a WSRT pointed observation at 1.4 GHz (White et al. 2010).
The result is shown in Fig. 3. Each point is the median of the flux density ratios obtained from the LOFAR sources matched with each of the other external catalogues, and the red dashed line is the linear best fit to these points. Assuming perfect a priori calibration of the LOFAR array after the direction-dependent corrections, and of all other surveys plotted in Fig. 3, and that a simple power-law spectral index is appropriate, the line should pass through the ratio value of 1 at 144 MHz. As can be seen from the inset in Fig. 3, the best-fit line has a value of 0.88 ± 0.04. This is the scale factor that needs to be applied to the final image to correct the absolute amplitude scale. The value we obtained for the EDFN is similar to those previously derived for other deep fields that are in the 0.80-0.92 range (Sabater et al. 2021). We scaled the radio image by a factor of 0.88 to set the final LOFAR image of the EDFN to the correct amplitude scale.
 |
Fig. 3 Calibration of EDFN flux density scale. The flux density scale after DDF-pipeline is set to unity and shown as a blue cross. The flux density ratios with respect to the external catalogues from the literature and their errors are shown in different colours. The red dashed line is the linear fit to the data. The inset shows a zoomed-in view close to the LOFAR HBA central frequency. |
4.3 The final catalogue of the Euclid Deep Field North
Due to the intrinsic nature of the cleaning process, radio images can be contaminated by spurious sources in the proximity of real bright radio objects. Furthermore, radio sources can have morphologies too complex or extended to be properly recovered by source-finding algorithms, which only provide a catalogue of radio components. Moving from a catalogue of radio components to a catalogue of radio sources requires some additional steps, which we discuss below.
With the final radio image set to the correct flux scale, we ran PyBDSF again to obtain a new catalogue of radio sources, using the same parameters as before. Then, we selected only the sources within a 10 deg2 circular area (r = 1.784 deg) centred on the Euclid Deep Field North position (RA = 17:58:55.9 Dec = 66:01:03.7), and throughout the rest of the paper we only consider this area. This is the region that was originally selected for the EDFN when the observations presented in this paper were planned, and only more recently was the area extended to 20 deg2. It is worth saying that producing a catalogue from these observations covering the whole 20 deg2 of the EDFN is not convenient, considering that the noise increases with the distance from the pointing centre and the effects discussed in Sect. 4.1. The more recent observations of the EDFN adopted a different pointing strategy that will increase sensitivity and accuracy over a larger area allowing us to properly investigate the full 20 deg2 field. In the final rescaled image the central rms noise is 32 μJy beam−1, increasing to ~45 μJy beam−1 at r ≃ 1.8 deg due to the primary beam correction.
PyBDSF is a tool designed to decompose a radio image in islands and extract the components as a set of Gaussians, shapelets, or wavelets above a given SNR threshold (Mohan & Rafferty 2015). Two or more radio components found inside the same island can be grouped together to form a single radio source on the basis of the distance between the components and the brightness distribution along the line joining the centre of the components. The outcome of this procedure is recorded in the output catalogue by the S_Code parameter that is used to define the source structure: S_Code = S for a single-Gaussian source that is the only component in the island, S_Code = C for a single-Gaussian source in an island with other sources, S_Code = M for a multi-Gaussian source. The raw catalogue produced by PyBDSF needs to be checked against known issues that can affect it, and we briefly discuss them below together with the solutions we adopted. We supported our analysis by using the unWISE catalogue in the overlapping 10 deg2 region (Lang 2014; Meisner et al. 2017b,a). The unWISE Catalogue is derived from the unWISE coadds of the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) images and includes two billion sources over the entire sky at 3.4 and 4.6 microns. We used the catalogue produced after five years of WISE imaging (Schlafly et al. 2019). The unWISE catalogue has two advantages over the existing WISE catalogue (AllWISE); first, it is based on significantly deeper imaging, and second, it features improved modelling of crowded regions using the crowdsource5 analysis pipeline to simultaneously determine the positions and fluxes of all sources in the unWISE coadds.
Firstly, we checked for spurious sources. Bright sources, in particular those where the direction-dependent calibration did not perform well, can produce artefacts associated with calibration uncertainties that can exceed the local SNR threshold. PyBDSF can generally deal with this issue by adapting the window size over which to calculate the local rms around bright sources, but in some cases this is not effective. These calibration artefacts produce a typical pattern with spikes irradiating from the bright source. We visually checked the region within a radius of 90 arcsec around the sources with total flux ST > 15 mJy looking for sources with 5 < SNR < 10 and without a counterpart in the unWISE catalogue (within a matching radius of 3 arcsec). When such a source was found to be located along one of the spikes, it was considered a spurious source and it was removed from the catalogue. According to this criterion, we removed 110 sources (~0.5%).
As said above, when more than one Gaussian component is found within an island and a set of conditions are fulfilled, PyBDSF attempts to group together the components into a single radio source. This process cannot be perfect. For instance, two or more distinct radio sources can be grouped into a single multi-component source due to the limited resolution of the LOFAR observations. For this reason, we visually inspected all the catalogued radio sources classified as ‘M’ or ‘C’ by PyBDSF, again using the unWISE catalogue to support our analysis. Figure 4 shows the three typical cases we encountered. In each panel, the radio image is shown in colours, the cyan circles are centred at the positions of the different radio Gaussian components, the black cross is the final position of the radio source derived from a brightness weighted average of the position of the individual components, and the green small circles indicate the positions of the unWISE sources in the area. In the left panel, the three Gaussian components are grouped to form a single radio source by PyBDSF, but the comparison of the radio and unWISE source positions strongly suggests that we have three different radio sources. There were around 550 such cases where sources originally classified as a single source had to be split in two or more individual sources, in these cases we replace the single source in the radio catalogue with the individual Gaussian components that have SNR > 5. Deblended sources with SNR < 5 were not included in the radio catalogue. In the example shown in Fig. 4 all the three Gaussian components have SNR > 5 and therefore the single entry is replaced by three entries with appropriate parameters in the final radio catalogue. The middle panel shows an example where there is an unWISE source close to the radio source position and no unWISE sources near the peak of the individual components; in all these cases we considered the PyBDSF outcome reliable. In the right panel, unWISE sources are found both at the radio source position and close to the peak of the individual components. Such cases are uncertain, and we decided not to change the PyBDSF output.
Another typical case of PyBDSF failure, in combining the appropriate components into a single radio source, is when components that belong to the same radio source are catalogued as distinct sources. This can happen when the lobes of a very extended radio galaxy are separated by tens of arcseconds or even arcminutes. Each of the two lobes (and a radio core, if present) can be classified as a distinct source by PyBDSF, with each lobe usually classified as a multi-component source. We visually inspected all the sources classified with S_Code = M or S_Code = C, and we identified the lobe components of extended radio galaxies. Whenever necessary we grouped together the lobe components into a single source in the catalogue. We also searched for a possible radio core previously identified as a separate source and we assigned it to the extended radio source. The total flux of the source was assumed to be the sum of the fluxes of all grouped components and its position the one of the radio core. When no radio core is detected, the radio position is set as equal to the flux density weighted average of the position of the lobes. For these 131 sources (~0.6% of the total) the size parameters in the catalogue are set to −1 and the error associated with the total flux density is derived combining the errors of the individual components. As a result of this process we obtain a final catalogue6 over the 10 deg2 field centred on the EDFN containing 23 333 sources (93% classified as S_Code = S) with an SNR > 5.
It is worth mentioning that the errors given in the catalogue are only those derived by PyBDSF from the fitting procedure. In particular, as far as the peak brightness and total flux density values are concerned, these errors do not include the effects investigated in Sects. 4.1 and 4.2. Combining the error associated with the linear fit in Sect. 4.2 with the error on peak brightness or total flux density for sources within two degrees of the field centre we have a likely uncertainty of around 6% in the flux density scale, a value consistent with that quoted for other deep fields (Sabater et al. 2021).
 |
Fig. 4 LOFAR radio images at 144 MHz of three multi-component sources each originally classified as a single radio source by PyBDSF. Large cyan circles identify the individual Gaussian components, the black cross is the derived radio position of the source, and the green circles mark the position of unWISE sources inside the region. The left panel shows a case where deblending is necessary as all the three components are very likely distinct radio sources. The middle panel gives an example of correct association of different components to a single radio source, while the right panel gives an uncertain case. |
4.4 Resolved and unresolved sources
The ratio between measured total and peak fluxes (ST/Sp) is a proxy for the extension of a radio source since it is equivalent to the ratio between the fitted source full width at half maximum (FWHM) axes, θmaj and θmin, and the restoring beam FWHM axes, bmaj and bmin:
In Fig. 5 (upper panel) we plot ST/Sp versus the SNR for all the sources in the final catalogue. Values of ST/Sp < 1 are due to statistical errors affecting the flux density measurements, and these errors should equally affect the ST/Sp > 1 region. In the following we use ST/Sp to classify the sources as resolved or unresolved. It is also clear that high SNR sources systematically lie above the ST/Sp = 1 line (shown in black in Fig. 5). This is a clear indication that the distribution of ST/Sp is affected by an offset that artificially increases the derived ratios. Such an offset was previously found, for instance, in measurements derived from images affected by bandwidth smearing (e.g. Bondi et al. 2008) and in the LOFAR observations of the Lockman Hole and ELAIS-N1, where it has been interpreted as due to a combination of residual facet-dependent calibration errors and PSF modelling (Mandal et al. 2021).
Mandal et al. (2021) accounted for the statistical errors in ST/Sp by defining a lower envelope of the ST/Sp distribution shown in Fig. 5 as
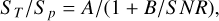 (2)
(2)
where the parameter A represents the aforementioned offset. The lower envelope can then be mirrored around the ST/Sp = A axis to obtain the upper envelope:
All the sources above the upper envelope are classified as resolved, while those below are considered unresolved. Mandal et al. (2021) derived single A and Β values for each of the LoTSS Deep Fields.
We decided to use a slightly different approach. To investigate and quantify the offset A we split all the sources with SNR > 40 in the final catalogue according to their distance from the field centre (r) into five different sub-samples: r < 0.7 deg, 0.7 < r < 1.0 deg, 1.0 < r < 1.25 deg, 1.25 < r < 1.6 deg, and r > 1.6 deg. For each sub-sample, we plot the distribution of the ratio ST/Sp inFig. 6. Theplots are truncated at ST/Sp = 1.5, but the tail of extended sources continues up to value of ~50. Each distribution shows a Gaussian-like region at low ST/Sp values that we fit with a Gaussian (the black curves in Fig. 6).
We found that the Gaussian region of the ST/Sp distribution has an offset with respect to the ST/Sp value and that this offset changes for sources at different distances from the field centre. More distant sources show a higher value (A ~ 1.12) than the sources closer to the field centre (A ~ 1.03). For each sub-sample, we list the range in r, the number of sources in that distance range, and the A values derived from the Gaussian region of the ST/Sp distributions in Table 2.
The radio catalogue lists sources in a 10 deg2 circular region (r < 1.784 deg) and, given the spectral (97.6 kHz) and time (8 s) averaging of the data, we can expect bandwidth and time smearing up to 20% at the edges of the field and around 8% at 1 deg from the field centre (Bridle & Schwab 1999). DDFacet, the imaging code within DDF-pipeline is specifically designed to minimise the decorrelation and smearing effects using facet-dependent corrections during the deconvolution (Tasse et al. 2018). Such a radially dependent residual smearing was already noted by Shimwell et al. (2019) in the LoTSS images (see Fig. 10 in their paper). DDFacet derives, for each facet, its own PSF to be used during deconvolution, but large facets (spanning a significant range in r) can still produce smearing at the levels we observe. Moreover, it is worth noting that facets at larger distances tend to be larger. As discussed in Sect. 4.1, the accuracy of the flux measurements decreases with increasing distance from the field centre, and this effect is stronger for peak fluxes compared to total fluxes, as expected in the case of smearing. Mandal et al. (2021) arrived at the same conclusion, with the only difference being that they used a single A value, averaged over distance. We conclude that the observed total-to-peak flux ratio offset is caused by a residual smearing effect, which is not totally corrected by DDFacet.
In order to separate resolved from unresolved sources, we first corrected the source peak fluxes in the final catalogue using the A values listed in Table 2 according to the distance of the source from the field centre. The values in Table 2 are reasonably well fitted by a parabola given by A(r) = 1.025 + (r2/35), where r is the distance from the field centre in degree, and we used this expression to interpolate the corrected peak fluxes (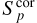 ) at each distance. The lower panel in Fig. 5 shows the new
) at each distance. The lower panel in Fig. 5 shows the new 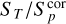 versus SNR plot. The
versus SNR plot. The 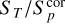 distribution, for the sources at high SNR, has a Gaussian region centred at
distribution, for the sources at high SNR, has a Gaussian region centred at 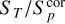 = 1. Then, we assumed
= 1. Then, we assumed
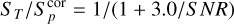 (4)
(4)
for the lower envelope, where B = 3.0 was chosen to be comparable with the equivalent functions in Mandal et al. (2021) and satisfying the criterion that only ≃ 1 % of the points are outliers (i.e. sources below the lower envelope). Mirroring Eq. (4), we obtained the selection function for the resolved sources:
Adopting this relation, ≃24% of the sources were classified as resolved. This value is consistent with the values of resolved sources derived in other LOFAR Deep Fields such as Lockman Hole and Elais-N1 (Mandal et al. 2021). This is also consistent with the fraction of 24% of resolved sources found in the VLA-VIRMOS VLT Deep Survey (Bondi et al. 2003), a survey made with the VLA at 1.4 GHz, but with the same angular resolution (6 arcsec) of LOFAR HBA images. For the purposes of deriving the radio number counts (see Sect. 6), we used the total flux density (ST) for the ~5500 resolved sources and the corrected peak flux (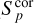 ) for the ~ 17 800 unresolved sources. Needless to say that the method adopted to classify a source as resolved or unresolved is an approximation. One limitation is that we assume that all the sources below the upper envelope of Fig. 5 but with
) for the ~ 17 800 unresolved sources. Needless to say that the method adopted to classify a source as resolved or unresolved is an approximation. One limitation is that we assume that all the sources below the upper envelope of Fig. 5 but with 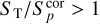 are unresolved, and this is likely not entirely true. Another one is how to fit the lower envelope. For all these reasons the classification as resolved or unresolved was used only on a statistical basis and the total flux density derived from the classification was used only to calculate the source counts and not listed in the catalogue. The fluxes in the catalogue are those derived by fitting and assembling Gaussian components by PyBDSF or manually for the very extended sources. Having said that, we note that using samples of mock sources to derive the source counts corrections allows to correct, if not entirely, at least for part of these limitations as we explain in the next section.
are unresolved, and this is likely not entirely true. Another one is how to fit the lower envelope. For all these reasons the classification as resolved or unresolved was used only on a statistical basis and the total flux density derived from the classification was used only to calculate the source counts and not listed in the catalogue. The fluxes in the catalogue are those derived by fitting and assembling Gaussian components by PyBDSF or manually for the very extended sources. Having said that, we note that using samples of mock sources to derive the source counts corrections allows to correct, if not entirely, at least for part of these limitations as we explain in the next section.
 |
Fig. 5 Total-to-peak flux ratio versus signal-to-noise ratio plot for all the sources in the catalogue. The upper panel shows the ratio derived using the Sp values derived by PyBDSF. The lower panel shows the same plot using |
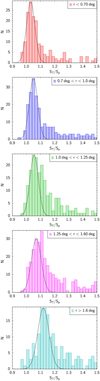 |
Fig. 6 Distribution of ST/Sp values for sources in different bins of distance from field centre. Only sources with SNR > 40 are considered. The plots are truncated at ST/Sp = 1.5 for a better visualisation. For each distance bin, we fit a Gaussian function to the region of low ST/Sp values. |
ST/Sp offset values.
5 Radio source count corrections
The observed number counts of radio sources must be corrected for several effects. These are the following. Firstly, we have to take into account the varying noise distribution in the radio image due to the presence of bright sources and the effect of the primary beam correction. Secondly, systematic errors in the source extraction procedure could affect the measured peak brightness and total flux density. Thirdly, the number counts are derived in bins of total flux density from samples of radio sources that are selected on the basis of their peak brightness. For this reason, the completeness of the radio sample depends also on the intrinsic angular size distribution. This issue is known as the resolution bias. Fourthly, we have to correct for the Eddington bias (Eddington 1913), also referred to as noise bias. Finally, the contribution of spurious sources needs to be estimated.
In order to take into account the combined effects of the first four effects, we used mock samples of radio sources as described below (see Sect. 5.2). The contamination by spurious sources is not modelled by the simulations, since the mock samples are inserted in the same residual image obtained after subtraction of all the components. The fraction of spurious sources is derived in the next sub-section.
5.1 False detection rate
The false detection rate is associated with spurious sources that are detected above the SNR threshold value. To derive an estimate of the fraction of spurious sources still present in the catalogue, we ran PyBDSF on the inverted (i.e. multiplied by -1) LOFAR image with the same settings used to produce the catalogue. Since there is no negative emission in the radio continuum emission of the sky, every detection above 5σ in the inverted image is due to a noise peak. Therefore, assuming the noise distribution is symmetric around zero we expect a similar number of noise peaks above 5σ (false detection rate) in the positive image as well. This assumption may not be valid near the bright sources due to the combination of residual calibration errors and the shape of the side lobes of the beam (i.e. the peak of the positive side lobes is higher than the absolute value of the peak of the negative side lobes). Therefore, the number of negative peaks has to be considered as a lower limit for the number of spurious sources. For this reason, in Sect. 4.3 we describe how we removed spurious radio sources with an S NR > 5 produced or contaminated by the secondary lobes of nearby bright objects (ST > 15 mJy). PyBDSF returned 236 negative peaks above 5σ within the 10 deg2 region. Among these 236 negative peaks, 101 are found within a distance of 90″ from a bright source in the positive image. This number is close to the number of sources (110) that were excluded as spurious in Sect. 4.3. We derived the fraction of false detections using both the 135 sources far from bright sources (as a lower limit) and the whole sample of 236 sources. The sources were binned in SNR groupings alongside true detections, and the false detection rates, defined as the number of false detections divided by the number of recovered sources in each SNR bin, are reported in Table 3. In general, the false detection rate values derived are rather small. We expect ~3% of false detection rate for sources in the range 5.0 ≤ SNR < 5.5 and about ~1.5% in the range 5.5 ≤ SNR < 6.0. For sources with an SNR > 10 the false detection rate is < 0. 5%, so practically negligible. We applied a correction due to the false detection rate to the differential source counts listed in Table 4 and Fig. 7 using all the 236 false detections split into the appropriate total flux density bins. We note that the differences in the source counts deriving from using 135 or 236 false detections are much smaller than the error bars.
False detection rates.
5.2 Completeness and noise bias corrections
To derive the completeness and noise bias corrections affecting the EDFN radio catalogue, we followed the same approach used, for instance, for the COSMOS-3GHz catalogue (Smolčić et al. 2017a). This procedure requires generating samples of mock radio sources to be added to a radio image with the same noise properties of the real one. Then, the new image containing the mock sources is processed with the same algorithm that yielded the radio source catalogue. Sources in the input and recovered catalogues are then split into bins of total flux density, and the numbers of injected versus recovered sources in each total flux density bin are compared. The image on which the mock sources are injected is the residual image produced by PyBDSF after the real sources have been extracted. To limit the effects of confusion and blending of different radio sources (the effect we partially corrected for using the UnWISE images as described in Sect. 4.3 for the real sources), we set a minimum distance of 12 arcsec between two mock sources. We used samples of mock sources that follows a flux density and angular size distribution as close as possible to those of real radio sources as described in the next sub-sections.
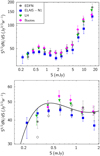 |
Fig. 7 Euclidean normalised radio source counts at 144 MHz, obtained for Euclid Deep Field North plotted together with those obtained from other LOFAR Deep Fields (see symbols) from Mandal et al. (2021). The black line is the seventh-order polynomial fit from Mandal et al. (2021). The lower panel is a zoomed-in view of the region between 0.2 and 2 mJy also showing the uncorrected normalised source counts for the EDFN with empty circles. |
5.2.1 Mock radio source catalogue: Flux density distribution
To simulate the flux density distribution we used a seventh-order polynomial function fitting the differential source counts derived from the other LoTSS Deep Fields and the TGSS-ADR1 (Intema et al. 2017) to better constrain the bright end of the counts (Eq. (13) and Table 4 in Mandal et al. 2021). The mock catalogue was generated down to a flux density of 90 μJy (roughly 3σ) well below the 5σ detection threshold used to produce our radio catalogue. We generated three different realisations of the mock source catalogue that were individually processed and compared. Each mock catalogue contains ≃55 000 sources in the 10 deg2 area.
5.2.2 Mock radio source catalogue: Angular size distribution
The most challenging aspect in generating mock samples of radio sources is to assign to each source its own angular size. This is because the intrinsic source angular size distribution of sub-milli-Jansky radio sources is still not well known. The modelling of the intrinsic angular size distribution of the radio sources is necessary to correct for the resolution bias, which can severely affect the radio source counts, since these are a function of the total flux density, while the completeness of a radio catalogue is typically based on the signal-to-noise ratio and, therefore, on the peak brightness. Clearly, such an effect is more severe for catalogues derived from observations with an angular resolution θ ≲ 1″, but it needs to be taken into account in the lower resolution (θ ≃ 6″) LOFAR observations as well. For a more detailed description of the methods used to overcome this issue, we refer the reader to Bondi et al. (2008) and Smolčić et al. (2017a).
To allow for an easier comparison with the results obtained in the other LoTSS Deep Fields, we adopted the radio source angular size distribution modelled by Eqs. (7) and (9) in Mandal et al. (2021) with m = 0.3. Using this distribution, we assigned to each source its own angular size, and we modelled the mock sources as circular Gaussians. It is worth noting that real radio sources are not usually circular Gaussians. The effects on the radio source counts produced by a parent source population with more realistic source morphologies were recently investigated by Hale et al. (2023). Using rather low resolution (≃8″) images, Hale et al. (2023) find that the source counts are not strongly affected by different source models. This is not surprising given the low resolution, which is comparable to that of our LOFAR image. At these resolutions the bulk of the radio sources detected in a deep field are unresolved or slightly resolved, and the circular Gaussian approximation is appropriate. Such an approximation is no longer valid for catalogues of radio sources derived from images at higher resolution, and in such a case a more detailed source modelling is necessary (e.g. Smolčić et al. 2017a).
Differential source counts in the EDFN.
5.2.3 Mock radio source catalogue: Injection and recovering
We generated three different catalogues of mock radio sources using the flux density and angular size distributions as described above. The mock sources were inserted, as circular Gaussian components, in the residual image, and PyBDSF was run with the same parameters used for the real image to recover the mock sources. The catalogues of retrieved mock sources with SNR ≥ 5 were cross-matched with their respective input catalogues producing the recovered mock sources matched catalogues (simply referred to as matched catalogues in the following). We then used the method discussed in Sect. 4.4 to classify the mock sources in the matched catalogues as resolved or unresolved. The mock sources are not affected by residual calibration errors or bandwidth smearing and, therefore, the ST/Sp versus SNR diagram shows no systematic offset. This means A = 1 in Eqs. (2) and (3). For the B parameter in Eqs. (2) and (3), we used B = 3.0, the same value adopted for the real sources. In summary, for the matched catalogues we used the same selection function used for the real sources (after the correction for the radially dependent offset). The percentage of resolved mock sources in the matched catalogue is 23%, which is entirely consistent with the 24% we found for the real sources.
Finally, the mock sources were split into different bins of flux density. For the input catalogues, the flux density is that generated using the input flux density distribution, whilst for the matched catalogue the flux density is the measured flux density for the mock sources classified as resolved or the peak flux density for the unresolved ones. The ratio (for each flux density bin) between the number of input sources and the number of retrieved sources in the same flux density bin is the correction factor that needs to be applied to the source number counts. We find good consistency, within 1σ, in the values of the correction factors among the three different catalogues of mock sources, and therefore we adopted an average correction factor for each flux density bin. The final values of the correction factors are reported in Table 4.
As discussed in Sect. 4.4, the method adopted to classify a source as resolved or unresolved is an approximation and somewhat arbitrary. Therefore, we also used slightly different B values and shapes of the selection function (Eq. (2)) to derive alternative versions of the matched catalogues for the mock radio sources. Then, we compared the correction factors we obtained for these catalogues with those originally derived. The differences in the correction factors obtained from different selection functions are taken into account in an additional fractional error quantified as ~5%.
6 Differential source counts
The Euclidean normalised source counts at 144 MHz obtained for the EDFN are presented in Fig. 7 and listed in Table 4. The errors associated with the number counts contain the term due to the Poisson statistics for the number of sources in each flux density bin, plus the fixed term of 5% as discussed above. For the purposes of this paper it is useful to compare the source counts derived from the EDFN with those derived from the other LoTSS Deep Fields (Mandal et al. 2021), also shown in Fig. 7, since we used a different method to assemble the final source catalogue and to derive the counts' corrections. A more comprehensive analysis on the source counts is postponed until the full set of observations of the EDFN is completed and processed. The lower panel of Fig. 7 gives a zoomed-in view of the region between 0.2 and 2 mJy at 144 MHz (corresponding to about 0.04 mJy and 0.4 mJy at 1.4 GHz assuming a spectral index α = 0.7), where it is quite common to find significant differences in the source counts from different surveys at the depths we are achieving. Such differences are usually interpreted as a mixing of cosmic variance and uncertainty in the derived correction factors. In this panel, for comparison, we also show the uncorrected normalized source counts (empty circles with no errors).
The source counts obtained for the EDFN are in good agreement with those derived from the other LoTSS Deep Fields and this is reassuring considering the differences in obtaining them. One major difference between the source counts derived from the EDFN and the other LoTSS Deep Fields is the method applied to derive the correction factors for completeness. For the EDFN we produced mock catalogues of radio sources that were added to the residual radio image and then retrieved with the same procedure adopted for the real ones, while for the other LoTSS Deep Fields Mandal et al. (2021) derived the correction factors using a more theoretical approach.
In addition, the counts for Elais N-1, Lockman Hole, and Bootes were obtained using a sample of optically identified and fully deblended radio sources, while for the EDFN only a firstorder deblending was performed using the unWISE catalogue. Most of the sources that went through deblending had fluxes around ~ 1–2 mJy, and the higher value of the source counts in this flux density range suggests that it is possible that not all the sources (that needed to be deblended) were actually deblended. It is worth noting that the number of these potentially not deblended sources is rather small; about 50 sources that were not deblended can explain the somewhat higher value of the counts in the EDFN around ~1–2 mJy. Clearly, the same effect would lead to an underestimation of the source counts at fluxes ≲1 mJy producing a sort of discontinuity in the shape of the EDFN source counts around 1 mJy. This effect was indeed noted in Mandal et al. (2021) when comparing source counts obtained from raw catalogues (containing radio sources that were not optically identified and not checked and corrected for deblending) and final catalogues (containing only optically identified radio sources with source deblending when needed). In summary, the EDFN source counts are generally between those derived from the ELAIS-N1 field, which are systematically slightly lower than the other two deep fields, and those from the Lockman Hole and Bootes fields. The observed field-to-field differences in the source counts at sub-mJy levels are typically around a few percent, and these can be justified both by the different methods adopted to derive the source counts (e.g. EDFN with respect to other LoTSS Deep Fields) and the expectations from sample variance for surveys covering areas ≲ 10 deg2 (Heywood et al. 2013; Prandoni et al. 2018).
Once the LoTSS Deep Field project is completed and fully analysed, it will deliver images and catalogues of radio sources down to ~60 μJy beam−1 (5σ) at 144 MHz (corresponding to ~10 μJy beam−1 at 1.4 GHz) over a region of ~50 deg2. Considering the range of angular resolutions that LOFAR can probe with the international stations, as well as the multi-wavelengts ancillary observations already available or that will be soon available for these fields, in the next few years it is reasonable to assume that the LoTSS Deep Fields will allow us to make a major leap in our comprehension of the processes related to galaxy and black-hole formation and co-evolution over cosmic time from a radio perspective.
7 Summary
In this paper, we present the image and catalogue derived from the first 72 h of LOFAR observations at 144 MHz covering the central 10 deg2 region of the Euclid Deep Field North. The image has an angular resolution of 6″ and a central rms sensitivity of 32 μJy beam−1. The main results presented in this paper can be summarised as follows.
We compared images obtained from the same data sets but produced with different faceting geometry and starting sky models in the direction-dependent calibration pipeline (DDF-pipeline). We found that for sources within r < 2 deg of the field centre, the peak or total flux density are usually consistent within ≲ 5%, while sources at r > 2 deg can have larger differences up to ~ 10−15% for sources at r > 3 deg. Whilst the two images were obtained running DDF-pipeline on different computers with different individual software package versions, the radial dependency of the dispersion of the measured flux ratios in the two images suggests that a different faceting geometry could be responsible for the observed trend.
From the inner 10 deg2 circular region (r < 1.784 deg) we derived a 5σ catalogue listing about 23 000 radio sources. We used the unWISE five-year catalogue to check for possible blended sources in all the objects that were classified as multiple or complex components by PyBDSF. We also visually inspected the extended sources to properly assign radio lobes and diffuse components to the correct radio source.
We performed a detailed analysis of the properties of the derived catalogue of radio sources, finding a radially dependent effect on the ST/Sp ratio. We interpreted this as an underestimate of the peak brightness with increasing distance from the field centre as due to residual direction-dependent calibration errors. For the purpose of deriving the radio source counts, we corrected the peak brightness of the sources classified as unresolved.
Samples of mock sources following realistic flux density and angular size distributions were used to derive the completeness correction factors to be applied to the observed source counts. An estimate of the source's false detection rate was obtained as well. We found a fraction of false detections of ~3% for sources in the 5.0 ≤ SNR ≤ 5.5 range, and of ~1.5% in the 5.5 ≤ SNR < 6.0 range. For sources with an SNR > 10, the false detection rate is <0.5% and practically negligible.
The final source counts obtained in the EDFN are consistent with those obtained for the other LoTSS Deep Fields (ELAIS-N1, Lockman Hole and Bootes) and, in particular, they lie between those derived from ELAIS-N1 and those obtained for the other two fields. In our analysis, we also explored the contribution to the errors associated with the source counts produced by slightly different selection functions to separate resolved from unresolved sources. Such differences can be quantified in a 5% additional noise factor that we factored into the final errors shown in Fig. 7 and listed in Table 4.
Acknowledgements
M.Bond., I.P., M.Bona., M.Br., M.M., L.P., and R.S. acknowledge support from INAF under the Large Grant 2022 funding scheme (project “MeerKAT and LOFAR Team up: a Unique Radio Window on Galaxy/AGN co-Evolution”). P.N.B. is grateful for support from the UK STFC via grant ST/V000594/1. M.Bri. acknowledges support from the ERC-Stg “DRANOEL”, no. 714245, from the agreement ASI-INAF n. 2017-14-H.O and from the PRIN MIUR 2017PH3WAT “Blackout”. M.A. acknowledges support from the VENI research programme with project number 202.143, which is financed by the Netherlands Organisation for Scientific Research (NWO). L.K.M. is grateful for support from the Medical Research Council [MR/T042842/1]. R.Jv.W. acknowledges support from the ERC Starting Grant ClusterWeb 804208. G.J.W. gratefully acknowledges an Emeritus Fellowship from The Leverhulme Trust. This paper is based on data obtained with the International LOFAR Telescope (ILT) under project codes LC12_027. A.B. acknowledges financial support from the European Union - Next Generation EU. LOFAR is the Low-Frequency ARray, designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources), and which are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d'Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland; The Istituto Nazionale di Astrofisica (INAF), Italy. This research made use of the OCCAM supercomputing facility run by the Competence Centre for Scientific Computing an interdepartmental advanced research centre, that specializes in High Performance Computing (HPC). The unWISE coadded images and catalogue are based on data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, and NEOWISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology. WISE and NEOWISE are funded by the National Aeronautics and Space Administration.
References
- Aldinucci, M., Bagnasco, S., Lusso, S., et. al. 2017, J. Phys. Conf. Ser., 898, 082039 [NASA ADS] [CrossRef] [Google Scholar]
- Algera, H. S. B., Hodge, J. A., Riechers, D. A., et. al. 2022, ApJ, 924, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kaiser, C. R., Heckman, T. M., & Kauffmann, G. 2006, MNRAS, 368, L67 [NASA ADS] [Google Scholar]
- Best, P. N., Kondapally, R., Williams, W. L., et. al. 2023, MNRAS, 523, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, M., Ciliegi, P., Zamorani, G., et. al. 2003, A & A, 403, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, M., Ciliegi, P., Venturi, T., et. al. 2007, A & A, 463, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, M., Ciliegi, P., Schinnerer, E., et. al. 2008, ApJ, 681, 1129 [Google Scholar]
- Bonzini, M., Mainieri, V., Padovani, P., et. al. 2012, ApJS, 203, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Botteon, A., van Weeren, R. J., Brunetti, G., et. al. 2022, Sci. Adv., 8, eabq7623 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, A. H., & Schwab, F. R. 1999, ASP Conf. Ser., 180, 371 [NASA ADS] [Google Scholar]
- Chen, C.-C., Smail, I., Ivison, R. J., et. al. 2016, ApJ, 820, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Ciliegi, P., McMahon, R. G., Miley, G., et. al. 1999, MNRAS, 302, 222 [Google Scholar]
- Cochrane, R. K., Kondapally, R., Best, P. N., et. al. 2023, MNRAS, 523, 6082 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA & A, 30, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et. al. 1998, AJ, 115, 1693 [Google Scholar]
- Conselice, C. J. 2014, ARA & A, 52, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et. al. 2006, MNRAS, 365, 11 [Google Scholar]
- D'Amato, Q., Prandoni, I., Gilli, R., et. al. 2022, A & A, 668, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Gasperin, F., Dijkema, T. J., Drabent, A., et. al. 2019, A & A, 622, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et. al. 2011, MNRAS, 413, 971 [Google Scholar]
- Duncan, K. J., Kondapally, R., Brown, M. J. I., et. al. 2021, A & A, 648, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Euclid Collaboration, (Scaramella, R., et al.) 2022, A & A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkelstein, S. L., Bagley, M. B., Ferguson, H. C., et. al. 2023, ApJ 946, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., & Wuyts, S. 2020, ARA & A, 58, 661 [CrossRef] [Google Scholar]
- Franco, M., Elbaz, D., Béthermin, M., et. al. 2018, A & A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et. al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Haarsma, D. B., Partridge, R. B., Windhorst, R. A., & Richards, E. A. 2000, ApJ, 544, 641 [Google Scholar]
- Hale, C. L., Whittam, I. H., Jarvis, M. J., et. al. 2023, MNRAS, 520, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, S. E. G., Masson, C. R., Warner, P. J., & Baldwin, J. E. 1990, MNRAS, 246, 256 [NASA ADS] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., McKean, J., Pizzo, R., et. al. 2010, arXiv e-prints [arXiv:1008.4693] [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA & A, 52, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Heywood, I., Jarvis, M. J., & Condon, J. J. 2013, MNRAS, 432, 2625 [Google Scholar]
- Heywood, I., Jarvis, M. J., Hale, C. L., et. al. 2022, MNRAS, 509, 2150 [Google Scholar]
- Hopkins, A. M., Mobasher, B., Cram, L., & Rowan-Robinson, M. 1998, MNRAS, 296, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Afonso, J., Chan, B., et. al. 2003, AJ, 125, 465 [Google Scholar]
- Huynh, M. T., Jackson, C. A., Norris, R. P., & Prandoni, I. 2005, AJ, 130, 1373 [Google Scholar]
- Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A & A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarvis, M., Taylor, R., Agudo, I., et. al. 2016, in MeerKAT Science: On the Pathway to the SKA (MeerKAT Science: South Africa), 6 [Google Scholar]
- Kondapally, R., Best, P. N., Hardcastle, M. J., et. al. 2021, A & A, 648, A3 [CrossRef] [EDP Sciences] [Google Scholar]
- Kondapally, R., Best, P. N., Cochrane, R. K., et. al. 2022, MNRAS, 513, 3742 [NASA ADS] [CrossRef] [Google Scholar]
- Lane, W. M., Cotton, W. D., van Velzen, S., et. al. 2014, MNRAS, 440, 327 [Google Scholar]
- Lang, D. 2014, AJ, 147, 108 [Google Scholar]
- Le Fèvre, O., Vettolani, G., Bottini, D., et. al. 2005, The Messenger, 119, 30 [Google Scholar]
- Mandal, S., Prandoni, I., Hardcastle, M. J., et. al. 2021, A & A, 648, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meisner, A. M., Lang, D., & Schlegel, D. J. 2017a, AJ, 154, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Meisner, A. M., Lang, D., & Schlegel, D. J. 2017b, AJ, 153, 38 [Google Scholar]
- Miller, N. A., Fomalont, E. B., Kellermann, K. I., et. al. 2008, ApJS, 179, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N. A., Bonzini, M., Fomalont, E. B., et. al. 2013, ApJS, 205, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Mingo, B., Croston, J. H., Best, P. N., et. al. 2022, MNRAS, 511, 3250 [NASA ADS] [CrossRef] [Google Scholar]
- Mohan, N., & Rafferty, D. 2015, Astrophysics Source Code Library [record ascl:1502.007] [Google Scholar]
- Morrison, G. E., Owen, F. N., Dickinson, M., Ivison, R. J., & Ibar, E. 2010, ApJS, 188, 178 [Google Scholar]
- Murphy, E. J., Momjian, E., Condon, J. J., et. al. 2017, ApJ, 839, 35 [Google Scholar]
- Muxlow, T. W. B., Thomson, A. P., Radcliffe, J. F., et. al. 2020, MNRAS, 495, 1188 [Google Scholar]
- Novak, M., Smolčić, V., Delhaize, J., et. al. 2017, A & A, 602, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R. 2016, A & A, 595, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R., van de Gronde, J. J., & Roerdink, J. B. T. M. 2012, A & A, 539, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, F. N. 2018, ApJS, 235, 34 [Google Scholar]
- Owen, F. N., & Morrison, G. E. 2008, AJ, 136, 1889 [Google Scholar]
- Padovani, P. 2016, A & A Rev., 24, 13 [NASA ADS] [Google Scholar]
- Pentericci, L., McLure, R. J., Garilli, B., et. al. 2018, A & A, 616, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prandoni, I., Gregorini, L., Parma, P., et. al. 2000, A & AS, 146, 41 [NASA ADS] [Google Scholar]
- Prandoni, I., Guglielmino, G., Morganti, R., et. al. 2018, MNRAS, 481, 4548 [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et. al. 1997, A & AS, 124, 259 [NASA ADS] [Google Scholar]
- Sabater, J., Best, P. N., Tasse, C., et. al. 2021, A & A, 648, A2 [CrossRef] [EDP Sciences] [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et. al. 2007, ApJS, 172, 46 [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et. al. 2010, ApJS, 188, 384 [Google Scholar]
- Schlafly, E. F., Meisner, A. M., & Green, G. M. 2019, ApJS, 240, 30 [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et. al. 2007, ApJS, 172, 1 [Google Scholar]
- Seymour, N., Dwelly, T., Moss, D., et. al. 2008, MNRAS, 386, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et. al. 2017, A & A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et. al. 2019, A & A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Hardcastle, M. J., Tasse, C., et. al. 2022, A & A, 659, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnov, O. M., & Tasse, C. 2015, MNRAS, 449, 2668 [Google Scholar]
- Smolčić, V. 2009, ApJ, 699, L43 [Google Scholar]
- Smolčić, V., Schinnerer, E., Zamorani, G., et. al. 2009, ApJ, 690, 610 [CrossRef] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et. al. 2017a, A & A, 602, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Novak, M., Delvecchio, I., et. al. 2017b, A & A, 602, A6 [CrossRef] [EDP Sciences] [Google Scholar]
- Somerville, R. S., & Davé, R. 2015, ARA & A, 53, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Tasse, C. 2014a, arXiv e-prints [arXiv:1418.8786] [Google Scholar]
- Tasse, C. 2014b, A & A, 566, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., Röttgering, H. J. A., Best, P. N., et. al. 2007, A & A, 471, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., Hugo, B., Mirmont, M., et. al. 2018, A & A, 611, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., Shimwell, T., Hardcastle, M. J., et. al. 2021, A & A, 648, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., Roberts-Borsani, G., Bradac, M., et. al. 2022, ApJ, 935, 110 [NASA ADS] [CrossRef] [Google Scholar]
- van der Vlugt, D., Hodge, J. A., Algera, H. S. B., et. al. 2022, ApJ, 941, 10 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et. al. 2013, A & A, 556, A2 [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Williams, W. L., Hardcastle, M. J., et. al. 2016, ApJS, 223, 2 [Google Scholar]
- Weaver, J. R., Kauffmann, O. B., Ilbert, O., et. al. 2022, ApJS, 258, 11 [NASA ADS] [CrossRef] [Google Scholar]
- White, G. J., Pearson, C., Braun, R., et. al. 2010, A & A, 517, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, W. L., van Weeren, R. J., Röttgering, H. J. A., et. al. 2016, MNRAS, 460, 2385 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et. al. 2010, AJ, 140, 1868 [Google Scholar]
The data associated with this article are released at https://lofar-surveys.org
All Tables
All Figures
 |
Fig. 1 LOFAR image of Euclid Deep Field North; the image shows only a sub-region ~0.6 × 0.3 deg2 centred at RA = 270.3086 deg and Dec = 65.882 deg. |
| In the text | |
 |
Fig. 2 Median peak brightness ratio (left panel), median total flux density ratio (middle panel), and median absolute value separation (right panel) in the four annular regions at increasing distance r from the pointing centre for matched sources in the Turin and Leiden catalogues with SNR > 50. The error bars are the scaled median absolute deviation (MAD) values. |
| In the text | |
 |
Fig. 3 Calibration of EDFN flux density scale. The flux density scale after DDF-pipeline is set to unity and shown as a blue cross. The flux density ratios with respect to the external catalogues from the literature and their errors are shown in different colours. The red dashed line is the linear fit to the data. The inset shows a zoomed-in view close to the LOFAR HBA central frequency. |
| In the text | |
 |
Fig. 4 LOFAR radio images at 144 MHz of three multi-component sources each originally classified as a single radio source by PyBDSF. Large cyan circles identify the individual Gaussian components, the black cross is the derived radio position of the source, and the green circles mark the position of unWISE sources inside the region. The left panel shows a case where deblending is necessary as all the three components are very likely distinct radio sources. The middle panel gives an example of correct association of different components to a single radio source, while the right panel gives an uncertain case. |
| In the text | |
 |
Fig. 5 Total-to-peak flux ratio versus signal-to-noise ratio plot for all the sources in the catalogue. The upper panel shows the ratio derived using the Sp values derived by PyBDSF. The lower panel shows the same plot using |
| In the text | |
 |
Fig. 6 Distribution of ST/Sp values for sources in different bins of distance from field centre. Only sources with SNR > 40 are considered. The plots are truncated at ST/Sp = 1.5 for a better visualisation. For each distance bin, we fit a Gaussian function to the region of low ST/Sp values. |
| In the text | |
 |
Fig. 7 Euclidean normalised radio source counts at 144 MHz, obtained for Euclid Deep Field North plotted together with those obtained from other LOFAR Deep Fields (see symbols) from Mandal et al. (2021). The black line is the seventh-order polynomial fit from Mandal et al. (2021). The lower panel is a zoomed-in view of the region between 0.2 and 2 mJy also showing the uncorrected normalised source counts for the EDFN with empty circles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.