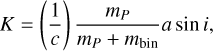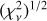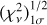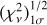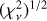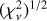EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A129 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A129
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202347030
Published online 15 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The formation and evolution of main sequence (MS) binary star systems imply substantial changes in the shape and size of the orbit, and in the physical properties of the stellar components. However, the formation of stellar multiples is complex (van den Berk et al. 2007). Following a recent review by Tokovinin (2021), three main ingredients are necessary for the formation of stellar systems: fragmentation, accretion, and dynamical processes. This involves the initial collapse of a molecular cloud of gas, and dust. The frequent gravitational interactions and the subsequent dynamical capture of nearby stars naturally leads to a high fraction of stellar multiplicity (Larson 1972; van den Berk et al. 2007; Bate 2018). Surprisingly, the formation of isolated binary systems is the exception and the majority of stars are found in hierarchical multiple stellar systems. In this context, post-common-envelope binaries (PCEBs) constitute a particular class of binaries with periods of the order of hours. Remarkably, some of them are believed to harbor one or more massive companion. The literature lists several systems where authors have claimed the discovery of one or two high-mass circumbinary companions of planetary nature with a semi-major axis of greater than 1 au (see e.g., Marsh 2018, and references therein).

To date, over 5000 confirmed planets have been discov-ered1, with the majority found in orbit around a single host star. Approximately 5% of these planets are known to orbit binary star systems2 (Schwarz et al. 2016; Bonavita & Desidera 2020). In the case of PCEBs, the presence of low-mass stellar objects is indirectly detected through the effect of eclipse timing variation (Woltjer 1922, ETV) caused by the light-travel time (Irwin 1952, LTT) effect, also known as the Rømer effect. Several other mechanisms that cause ETVs are known and we refer to Southworth et al. (2019) for a review. According to Zorotovic & Schreiber (2013), nearly 90% of PCEBs exhibit an ETV signal amplitude compatible with a substellar high-mass interpretation, although alternative period variation mechanisms have been suggested. One such mechanism that may account for the observed timing variation is the Applegate mechanism (Applegate 1992; Völschow et al. 2018).

Additional physical mechanisms, such as mass transfer, apsi-dal precession, chromospheric spots, solar-like cycles in one of the stars, or angular momentum-loss due to magnetic breaking, may cause period variations (see e.g., Lanza 2020; Pulley et al. 2022; Lee et al. 2009). In terms of magnitude, the largest contribution to period variation is from a bound massive companion. The effect of smaller period-variation contributions are usually accounted for by considering a quadratic term that describes secular changes in the binary eclipse period (Southworth et al. 2019).

In the present work, we revisit the QS Vir system (Stobie et al. 1997) and present a time-series analysis for the determination of orbital fits based on the LTT model. The QS Vir binary system (V ≃ 11.8, O’Donoghue et al. 2003; Zacharias et al. 2013) is composed of a white dwarf (WD) and a low-mass M-dwarf that nearly fills its Roche lobe (see Fig. 1) with an orbital period of around 3.5 h (O’Donoghue et al. 2003). This binary system is classified according to its evolutionary phase as a PCEB, although it can also be associated with the precataclysmic variable (CV) classification (Parsons et al. 2011, 2016). This latter association is based on the fact that it is on its way to becoming a semi-detached cataclysmic variable through a greater loss of angular momentum and a reduction of the orbit due to gravitational waves or magnetic braking (Paczyński 1967; O’Donoghue et al. 2003).

A schematic representation of QS Vir is shown in Fig. 1, where we collect some of the main physical parameters of the stars that compose the binary. Among them are the mass and radius determined by O’Donoghue et al. (2003) with values of 0.78 ± 0.04 M⊙ and 0.01 ± 0.01 R⊙ for the WD star, and values 0.43 ± 0.04 M⊙ and 0.42 ± 0.02 R⊙ for the M-class MS dwarf star. On the other hand, we calculated the luminosity of both stars using the temperature provided by O’Donoghue et al. (2003) and their respective radii, finding approximately 0.004 L⊙ and 0.01 L⊙ for the two stars, respectively.

Parsons et al. (2016) find certain prominences in their spectra that are maintained over time. These arise from the M-dwarf and appear to be locked in stable configurations within the binary system; their manifestations are found to last for more than a year. Besides the WD eclipse, the binary’s light curve shows a small reflection effect at blue wavelengths, and ellipsoidal modulation at redder wavelengths (Parsons et al. 2010).

Several attempts have been made to elucidate the underlying cause of the substantial and erratic period variations observed in the binary eclipses of QS Vir. The energy available in the secondary star was calculated by Qian et al. (2010), who determined that it was insufficient to account for the observed large-amplitude O – C variations3 through Applegate’s mechanism. Instead, these authors proposed a combination of a significant continuous reduction in the binary’s orbital period and the presence of a circumbinary planet with a mass of approximately 7 MJup. However, Parsons et al. (2010) obtained new eclipse data that suggest a broader and more eccentric orbit for the solitary companion, as documented in Table 1. Almeida & Jablonski (2011) subsequently presented an alternative data fit, which incorporated two circumbinary objects: a giant planet (approximately 0.009 M⊙) and a brown dwarf (approximately 0.056 M⊙) in orbit around QS Vir. Nevertheless, the significant deviation occurring near cycle number 30 000 requires at least one unseen massive companion being in a highly eccentric orbit, resulting in an orbital-crossing architecture.

Horner et al. (2013) showed that the two circumbinary companions proposed to orbit QS Vir are dynamically unstable on timescales of less than 1000 yr. This applies across the entire range of orbital elements that provide a plausible fit to the observational data of Almeida & Jablonski (2011). Therefore, the proposed planetary system with two planets orbiting QS Vir is unlikely to exist.

interpretation of the observed ETVs in QS Vir remains remarkably challenging. According to Bours et al. (2016), there are 86 published mid-eclipse times, and they added an additional 24 previously unpublished measurements as part of the eclipse timing programme presented in their work. In addition, from the latest eclipse times, the authors report another local or absolute maximum in the O – C residuals, similar to the O – C variations observed around cycle numbers 5000 and 20000.

In the present work, we revisit the orbital fits for QS Vir using an existing dataset from previous research. We examine a total of 105 mid-eclipse times for QS Vir, comprising 86 that have been publicly reported, and 19 additional ones that have not been analyzed before (Bours 2015, see their Table A.41). This dataset provides the cycle number, mid-time transits in Barycentric Julian Date (BJD) with the corresponding errors, and the corresponding reference for the data. In total, the dataset considered here contains 105 observations covering 22.9 yr of observations. The effect and contribution to the O – C amplitude due to various other effects are hard to estimate, and in the following we assume that the observed O – C variations are due to a single companion.

This paper is structured as follows. In Sect. 2, we describe the procedure to obtain the named O – C curves from mid-transit times, and the procedure applied to obtain orbital fits. In Sect. 3, we analyze the errors considering different approaches, paying attention to the robustness of the solutions over the years and discuss the sensitivity of the fits as a function of the number of timing measurements. Finally, in Sect. 4, we present our conclusions.

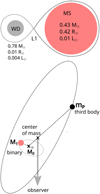thumbnail Fig. 1

Schematic representation of QS Vir with its physical parameters. Top: physical parameters, Lagrangian point L1, and equipotential surface in QS Vir. The parameter values of the binary system were obtained by O’Donoghue et al. (2003) and we calculated the luminosity using temperature and radius. Bottom: schematic configuration in the case where a third body modifies the binary barycentric position with respect to the observer. The movement of the binary can be modeled to infer the mass and the orbital parameters of the third body.
Table 1

Parameters for the planets proposed for QS Vir.

2 Methods

In this section, we present the method used to construct the named O – C signal, which consists in calculating the difference between the observed mid-eclipsing time with either linear or quadratic time dependence.

2.1 Linear ephemeris versus quadratic ephemeris

An isolated binary star without considering additional effects (such as tides, pericentric movement, and angular momentum exchange) has a constant orbital period. The presence of an additional perturbing body introduces period changes in the binary orbit.

The models that predict the mid-transit times of the observed eclipses Tobs are the linear, sinusoidal LTT, and quadratic ephemeris (although, more sophisticated models can be considered according to Hilditch 2001). We consider a combination of these three effects to build the O – C signal, which is the difference between the observed times (Tobs) and the calculated times (Tcalc)4: 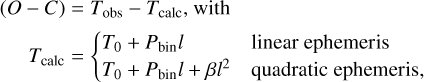(O−C)=Tobs −Tcalc , with Tcalc ={ T0+Pbin l linear ephemeris T0+Pbin l+βl2 quadratic ephemeris,  $\eqalign{ & (O - C) = {T_{{\rm{obs }}}} - {T_{{\rm{calc }}}},{\rm{ with }} \cr & {T_{{\rm{calc }}}} = \left\{ {\matrix{ {{T_0} + {P_{{\rm{bin }}}}l} \hfill & {{\rm{ linear ephemeris }}} \hfill \cr {{T_0} + {P_{{\rm{bin }}}}l + \beta {l^2}} \hfill & {{\rm{ quadratic ephemeris, }}} \hfill \cr } } \right. \cr} $(1)

where T0, Pbin, and l are the initial epoch (or mid-eclipse at cycle l = 0), the orbital period of the binary, and the cycle number (l = 0, 1, 2,..). The factor ß in the quadratic ephemeris models a secular change in the binary orbital period and can be thought of as a factor that describes the damping (change) of the binary period due to mass transfer, magnetic braking, and gravitational radiation (Goździewski et al. 2012). We used 105 mid-eclipsing times of QS Vir published by Bours (2015), because this latter is the most updated publicly available dataset that can constrain the signal. For mid-eclipsing times, we used Barycentric modified Julian Dates, with Barycentric Dynamical Time, BMJD (TDB), which according to Bours et al. (2016) are corrected for the motion of the Sun around the Barycentre of the Solar System5. 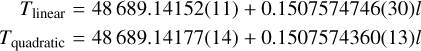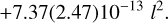The results of the fits with both models Tcalc are Tlinear =48 689.14152(11)+0.1507574746(30)l${T_{{\rm{linear }}}} = 48689.14152(11) + 0.1507574746(30)l$(2) Tquadratic=48 689.14177(14)+0.1507574360(13)l+7.37(2.47)10−13l2.$\matrix{ {{T_{{\rm{quadratic}}}} = } & {48689.14177(14) + 0.1507574360(13)l} \cr {} & { + 7.37(2.47){{10}^{ - 13}}{l^2}.} \cr } $(3)

Depending on which ephemeris is considered, the shape of the O – C curve drastically changes (see different symbols in the top panel of Fig. 2).

Qian et al. (2010) were the initial proponents of modeling an unseen companion to QS Vir. These authors used a limited dataset consisting of 36 timing measurements collected over a period of 17 yr to describe the orbital behavior of QS Vir. The addition by Parsons et al. (2010) of 16 new mid-time eclipse observations led to significant changes in the O – C binary period, and in O – C shapes. Consequently, best-fit orbital parameters and masses changed between authors (see our Table 1). More importantly, we note that for each dataset considered, the binary period needs to be redetermined, therefore producing slightly different O – C signals. This could explain the discrepancies observed in the O – C signals published in previous works. To illustrate this, Fig. 3 presents four O – C signals constructed using the first 45, 65, 85, and 105 mid-time eclipses in chronological order. Each signal is depicted in a distinct color, revealing variations in the shape, maximum, and minimum of the O – C. These changes indicate different orbital parameters for each corresponding fit.

To test the robustness of the underlying model, one could successively remove the last measured timing and measure the resulting best-fit parameter from linear ephemerids. Furthermore, successive fitting of linear ephemeris shows that the period of the binary changes constantly as a function of data points, as can be seen in the bottom panel of Fig. 3. Interestingly, the two values for the binary period widely used for QS Vir are Pbin = 0.150757475 (O’Donoghue et al. 2003) and Pbin = 0.150757467717 (Bours 2015), which are consistent with the dataset presented in this work.

thumbnail Fig. 2

Best orbital fits and residuals. Upper panel: O – C diagram of QS Vir. The crosses and plus symbols represent the O – C values built with the linear and quadratic ephemeris, respectively (O – C = Tcalc-Eq. (2)). The solid line and the dashed line represent the models fitted using the two models as described in the text. Lower panel: residuals using the same symbol and color coding as the top panel.
thumbnail Fig. 3

Dependence of the shape of the O – C and the period of the binary on the dataset considered. Top panel: O – C signal produced using four different datasets that mimic available observational data. Data point colors correspond to different datasets and horizontal lines at the top help to identify the corresponding observational baseline (ΔT). Bottom panel: determination of the binary period from the linear ephemeris as a function of the dataset. The horizontal solid and dashed lines represent the values of Pbin given by Bours (2015) and O’Donoghue et al. (2003), respectively. Pbin changes depending on the dataset selected.

2.2 Best orbital fits

The presence of a third body produces a signal that can be modeled in the O – C diagram, minimizing the residuals. The signal τ is obtained from the subtraction of mid-time transits with either the linear or quadratic fit, which can be modeled with a Keplerian orbit. The signal τ depends on K, P, e, ω, t0, and Z, which represent the semi-amplitude, period, eccentricity, argument of periapsis, time of passage at periapsis, and the origin value for the movement of the baricenter, respectively (we refer to the original formulation of Woltjer 1922, for an explanation of the meaning of Z). Thus, as derived in Goździewski et al. (2012), τ can be written as 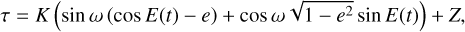τ=K(sinω(cosE(t)−e)+cosω1−e2 sinE(t))+Z$\tau = K\left( {\sin \omega (\cos E(t) - e) + \cos \omega \sqrt {1 - {e^2}} \sin E(t)} \right) + Z$(4)

with K=(1c)mPmP+mbinasini,$K = \left( {{1 \over c}} \right){{{m_P}} \over {{m_P} + {m_{{\rm{bin}}}}}}a\sin i$(5)

where mP is the companion mass, a the companion semi-major axis, i the companion inclination, E(t) the eccentric anomaly, and mbin is the mass of the binary. For a best-fit parameter of K, there exists a set of values of {mP, a sin i, mbin} that produces the same amplitude of the signal.

To calculate the best-fit parameters, we minimize a certain function of the residuals, which is defined as a statistical measure of the goodness of the fit. Assuming a Gaussian distribution for the errors, the goodness-of-fit statistics usually used is 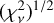(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$. This quantity is defined as follows: 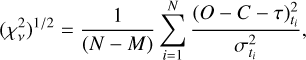(χv2)1/2=1(N−M)∑i=1N(O−C−τ)ti2σti2${\left( {\chi _v^2} \right)^{1/2}} = {1 \over {(N - M)}}\sum\limits_{i = 1}^N {{{(O - C - \tau )_{{t_i}}^2} \over {\sigma _{{t_i}}^2}}} $(6)

which depends on 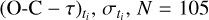(O−C−τ)ti,σti,N=105${({\rm{O}} - {\rm{C}} - \tau )_{{t_i}}},{\sigma _{{t_i}}},N = 105$, and M = 6, which are the difference between the observer O – C signal with respect to the modeled τ; the uncertainties for the time of eclipsing ti; the number of observations; and the parameters to be determined, respectively. The quantities 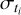σti${\sigma _{{t_i}}}$ are usually referred to as weights of the observations.

The strategy of fitting the O – C signal using a global exploration of the parameter space with a genetic algorithm followed by a local search for the minimum has already been shown to be successful in modeling the ETV in many works (see e.g., Beuermann et al. 2012; Almeida et al. 2013, 2020; Brown-Sevilla et al. 2021; Er et al. 2021). Here, we employ the same strategy, with particular attention to the robustness of the fit. We used two different and sequential subroutines to calculate the best Keplerian fit. First, we used a genetic algorithm with a population of 150 members (with random initial conditions in the parameter space), which evolved over approximately 1000 generations. We explored the hyper-parameter options and found optimal values for a mutation rate dithering based on the generation number of (0.025, 0.5), a relative tolerance for convergence of (0.001), and a strategy to evolve the population, retaining the best solution among new generations. We ran the algorithm and found the global minimum, although for other systems and/or datasets, these numbers could change depending on the coverage periods of the dataset (see e.g, Beaugé et al. 2008; Giuppone et al. 2011, for radial velocity applications). As genetic algorithms are only exploratory tools, they only guarantee a certain proximity to the global minimum of the fitness function, and not a precise value. Finally, we used a simplex subroutine to improve the result (Nelder-Mead algorithm, Press et al. 1992) with a tolerance of 10−5 to assure the convergence of the goodness-of-fit evaluation. We find a global minimum with parameters, 𝒜BF. Our code relies on the algorithms scipy differential evolution6 and scipy optimize.minimize7 from the SciPy Python packages (Virtanen et al. 2020).

Our best-fit values are shown in Table 2. With these parameter values, we reconstruct the τ signal using lines in the top panel of Fig. 2. The lower panel in the same figure shows the distribution of the residuals. The points obtained with the quadratic ephemeris fit (in red) produce a signal O – C that covers more than one period, although the maximum values (~100 s) observed at T ~ 53 000 are not similar to those observed at T ~ 57 000 (~50 s). This asymmetry prevents us from finding a good solution with a single frequency. Consequently, the values of the goodness-of-fit statistic are downgraded 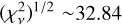(χv2)1/2~32.84${\left( {\chi _v^2} \right)^{1/2}}\~32.84$ (see the values in Table 2). The residuals for the linear ephemeris show a sinusoidal behavior with a lower value of 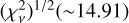(χv2)1/2(~14.91)${\left( {\chi _v^2} \right)^{1/2}}(\~14.91)$. This solution corresponds to a mass of the unseen additional body of equal to mP = 57.71 Mjup. We conducted a Lomb-Scargle (Lomb 1976; Scargle 1982) periodogram analysis to assess the significance of periodic signals. The Lomb-Scargle algorithm is suitable for unevenly spaced data and has been applied in a similar context in the literature (Cortés-Zuleta et al. 2020; Burt 2016). Initially, the Lomb-Scargle analysis was applied to the O – C values derived from the linear ephemeris, revealing a single periodic signal at approximately 16.43 yr with a signal-to-noise ratio (S/N) of around 3.5 – a result consistent with our best-fit period of 16.69 yr. Subsequently, following our best-fit analysis, the Lomb-Scargle periodogram applied to the new O – C data identified two periods with peaks at approximately 4.98 and 7.34 yr, each associated with a lower S/N of approximately 1.5. We obtain our results by running the Lomb-Scargle implementation within the ASTROPY v6.0 package (Astropy Collaboration 2022).

For the remainder of this work, we only consider the described O – C signal model for a linear ephemeris. We also explore the solutions given by the quadratic ephemerids but do not show them here as they provide less accurate fits to the observed data.

Table 2

Best Keplerian orbital fits for a circumbinary companion around QS Vir.

2.3 Orbital stability of solutions

In order to analyze the stability of the best-fit solutions described in the following sections, we performed long-term N-body integrations of each solution. The simulations were performed with a Bulirsch-Stoer integrator with adaptive step size, which was modified to independently monitor the error in each variable; this imposes a relative precision of better than 10−12. The computations are stopped when the distance from the planet to any star is less than two times the sum of their radii, or when the planet is ejected from the system after scattering between bodies (>10au). We use Jacobi elements for our initial conditions. For each simulation, we calculate the averaged MEGNO (〈Y〉) chaos indicator (see Cincotta & Simó 2000, for details). As the value of this indicator may be sensitive to the integration time span (Cincotta et al. 2003; Hinse et al. 2010), we verified its value for 103 and 104 yr. We study only coplanar orbits, and initial angular orbital elements for the binary were set equal to zero. We have previously examined stability and chaos for planets around binaries (Gianuzzi et al. 2023). However, it is worth noting that the present work is considered an extreme case due to the high eccentricity of the third body (e > 0.8).

3 Strategy to determine errors in orbital fits

In the following, we briefly outline and follow two methods for the computation of parameter uncertainties. This approach provides a critical evaluation of the robustness of the uncertainties. If the same confidence interval is reproduced from two different methods, we lend trust to the derived uncertainties. Otherwise, we consider that there is little or no consensus at all between the two methods, and the more conservative confidence interval is then adopted. Namely, we use the Markov chain Monte Carlo (MCMC) algorithm and other proven alternative strategies that help to understand the errors in this kind of minimization (Beaugé et al. 2008).

3.1 Parameter uncertainties from MCMC

MCMC methods are designed to sample the errors from the posterior probability density function (PDF) by utilizing the likelihood function, even in parameter spaces with high dimensionality (see Foreman-Mackey et al. 2013, for in-deep discussion). In simpler terms, this method estimates errors by sampling regions near the best-fit solution using the posterior distribution. To determine uncertainties, we obtain the 1σ interval of the 1D projections of the sampling onto the parameter sub-space (𝒜 = K, e, ω, Z, t0, P). We used the emcee implementation described in Foreman-Mackey et al. (2013), configuring the number of MCMC steps as NMCMC, the number of chains (or walkers) as 𝒲, and the initial distribution of walkers, βMCMC. The best-fit parameters obtained from the linear fit model (see Table 2) served as priors in the MCMC.

Following the recommendations of Foreman-Mackey et al. (2013), we employed an ensemble of 64 walkers (𝒲 = 32−64) and ran the chain for NMCMC = 100 000 steps. The initial distribution of walkers was set as βMCMC = 0.01 (except for t0, where ß = 0.0001). We discarded the first 7000 steps as part of the burn-in stage and estimated uncertainties using the posterior distribution. The dispersion point panels shown in Fig. 4 depict parameter correlations, while the histograms represent posterior probability density functions for the selected parameters. The uncertainties are calculated as the range of values encompassing 66% of the mean (indicated on each histogram). This figure offers valuable insights into parameter space exploration, facilitating a comprehensive understanding of uncertainties and correlations among model parameters. Notably, strong correlations are observed between (ω, K), (e, K), (e, ω), (Z, K), (Z, e), and (Z, ω). Visualizing these pairwise relationships helps in identifying optimal parameter combinations, thereby enhancing the robustness of our analysis. Despite the absence of multimodal posteriors, the O – C signal models exhibit significant parameter correlations, making the application of the MCMC method to explore the entire parameter space particularly challenging (Foreman-Mackey et al. 2013; Marsh et al. 2014).

We conducted a thorough evaluation of the MCMC analysis to ensure convergence and reliability of the results. This involved carefully examining convergence diagnostics, increasing the number of iterations, and adjusting the burn-in period to ensure it was of sufficient length. Despite these efforts, the obtained results remained unchanged. It is important to note that the accuracy of uncertainty estimates from MCMC chains relies on the assumption that the model being fitted to the data accurately captures the underlying complexities of the observed phenomena.

We note that MCMC is the most commonly method adopted by observers when reporting orbital fits for regularly sampled data. Therefore, as these errors appear to be underestimated according to the orbital fits reported by different authors, in the following we present a complementary approach that allows us to better estimate these errors.

thumbnail Fig. 4

Results of MCMC chains selecting pairs of parameters. We estimate the uncertainties using the posterior distribution of MCMC chains. Mean values, i.e., best-fit solutions, are plotted with black crosses. Level curves indicate 1σ (dark red) and 2σ (light blue) levels of posterior distributions. We note that for 2D histograms, these values correspond to roughly 39 and 86% confidence levels of the mean. In the top panels, we show the posterior distributions with their quantile levels at 0.14, 0.5, and 0.84. Here, t0 is given as a BMJD.

3.2 Stability of MCMC solutions

To analyze the stability of the results of MCMC chains, we first calculated the Mahalanobis distance r of each solution. This quantity represents the distance between each point x and the mean µ, and is defined as 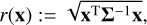r(x):=xTΣ−1x,$r({\bf{x}}): = \sqrt {{{\bf{x}}^{\rm{T}}}{{\bf{\Sigma }}^{ - 1}}{\bf{X}}} $(7)

where Σ is the symmetric covariance matrix. In the 1D case, this quantity reduces to the absolute value of the standard score (σ), and the distribution reduces to a univariate normal distribution.

We generated a random sample of 1000 solutions out of the r-closest 67 200 solutions (30% of the total), and integrated them for 5000 yr. Figure 5 shows the averaged MEGNO value (〈Y〉) of each integrated solution as a function of the Mahalanobis distance. All solutions have |〈Y〉 − 2.0| < 0.005, which means that all the orbits are regular. We do not find a correlation between 〈Y〉 and r.

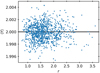thumbnail Fig. 5

Averaged MEGNO as a function of Mahalanobis distance. The horizontal line denotes 〈Y〉 = 2.

3.3 Parameter uncertainties from a grid search around the best fit

Starting from the best-fit solution 𝒜BF, we selected each parameter individually and evaluated the change in 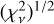(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$, calculating a new 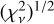(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ , where we only fixed the new value of a selected parameter, leaving the others the possibility to change. For example, in top left panel of Fig. 6, we show subsequent fits from the best-fit solution (red cross) in the amplitude K. Every new Ki is calculated in a grid of values of Ki = K + δ, K + 2δ,.., K + nδ, where δ is a small parameter. We repeated the procedure for positive and negative values of δ, and plot the values of 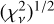(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ with respect to Ki. We note that the remaining parameters from A are fitted and this is a projection in the plane 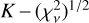K−(χv2)1/2$K - {\left( {\chi _v^2} \right)^{1/2}}$. We observe a depth minimum starting at 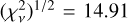(χv2)1/2=14.91${\left( {\chi _v^2} \right)^{1/2}} = 14.91$ and increasing as we depart from the best fit. We repeated the procedure for the remaining five parameters of 𝒜 and plot the results in the panels of Fig. 6.

To estimate the uncertainties, we employed a method based on the 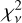χv2$\chi _v^2$ statistic and calculated the 1σ confidence levels. Due to the nonlinearity of the fitness function, conventional confidence ellipsoids cannot be directly applied in this case. Following the approach described in Beaugé et al. (2008), we set v = N − M, where N is the number of data points and M is the number of model parameters. By determining the mean (v) and variance (2v) of 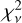χv2$\chi _v^2$, we can approximate the 1σ confidence level value using the formula: 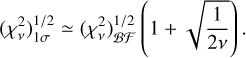(χv2)1σ1/2≃(χv2)ℬℱ1/2(1+12v).$\left( {\chi _v^2} \right)_{1\sigma }^{1/2} \simeq \left( {\chi _v^2} \right)_{{\cal B}{\cal F}}^{1/2}\left( {1 + \sqrt {{1 \over {2v}}} } \right)$(8)

We reiterate that our 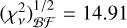(χv2)ℬℱ1/2=14.91$\left( {\chi _v^2} \right)_{{\cal B}{\cal F}}^{1/2} = 14.91$ (see Table 2). To obtain the 1 σ value for each parameter 𝒜i, we perform a numerical analysis to identify the intersection of 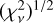(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ with the 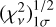(χv2)1σ1/2$\left( {\chi _v^2} \right)_{1\sigma }^{1/2}$ (~ 15.98) at each panel of the 𝒜i best fits. The resulting estimation of the uncertainties in 𝒜i is given in Table 2. This approach allows a quantitative assessment of the range of 𝒜i values consistent with the dataset and provides insight into the reliability and confidence associated with the parameter estimation.

Additionally, we show the results obtained from the dynamical study of our solutions in Fig. 6. We identify regular and chaotic orbits with different symbols. However, chaotic and regular orbits are stable in long-term integrations for 1 × 106 yr (i.e., ~6 × 105 periods of the unseen companion). The orbits neither escape from the system nor have a close encounter between involved bodies. Remarkably, we observe that the systems with the highest values of K or eccentricity (or lowest w or Z values) have chaotic orbits.

Combining the period of the unseen companion and K, we obtain the mass of the companion (see Eq. (5)). At this stage, it is relevant to evaluate the stability of these solutions. Figure 7 shows 〈Y〉 as a function of the companion mass for each best fit obtained by varying K in Fig. 6 (top-left panel). Despite a drop at mP ~ 80 MJ, we generally see that larger mP values result in larger 〈Y〉 values. We define 〈Y〉c = 2.1 as the averaged MEGNO cutoff value to differentiate chaotic from regular orbits during our integration of 50 000 yr. Given this value, most of the solutions with 〈Y〉 > 〈Y〉c (orange crosses in Figs. 6 and 7) have mP > 90 MJ.

In Fig. 8, we show the long-term evolution of two example orbits with MEGNO values of 〈Y〉 ~ 2.00 and 〈Y〉 ~ 17.31 at 50 000 yr. The initial conditions of both orbits are a = (7.0758786, 7.0008565) au, e = (0.93139948, 0.99), and mp = (63.8105, 273.2768) MJ for the regular and chaotic orbits, respectively. We choose to show the evolution of the semi-major axis of the best-fit solution and MEGNO in the panels. The orange orbit, although flagged as stable, shows recurrent and irregular variations in semi-major axis (also in eccentricity, but not shown here). In the presence of an additional body, this orbit could lead to a dynamically unstable system.

3.4 Dependence of the best fit on the choice of observational dataset

In this section, we lower the number of observations in the dataset and analyze the resulting variations in the orbital fits. We progressively consider different orbital fits obtained from a reduced dataset where the last point has been removed. In other words, we first perform the linear fit to obtain the O − C and the best fit on the full dataset with 105 data points. We then carry out different linear fits to get the O − C with only 104 points (removing the last one, chronologically speaking) and we repeat this procedure until we are left with around 50 points.

We can plot the variation of the parameters 𝒜 of each orbit fit as a function of the observation time interval (or the number of data points). If the current solution is robust, we should expect only small and smooth changes in the parameters as a function of the dataset considered. If the solutions do not change, we can expect that the future addition of observations will not significantly change our knowledge of the system. Again, we refer to Beaugé et al. (2008) for a discussion of this method and its application to the radial velocity technique. The results for Kep-lerian fits are shown in Fig. 9, where the central eclipse values are ordered chronologically. We recall that for every new dataset, we need to recalculate the new linear ephemeris (a new Pbin value is determined), mimicking the dataset for a given epoch. The best orbital fit was calculated using the simplex algorithm with the starting point using the previous fit in order to speed up the minimization algorithm without considering a global exploration of space parameter.

We note an abrupt change in some parameters when fewer data points are eliminated. For instance, the semi-amplitude of the signal K suddenly increases from 140 to 150 s at around ~96 observations. This jump is also observed in the panels of Fig. 9 showing e, Z, and ω. The argument of periapsis ω changes by only about 10%, while eccentricity is higher as we consider less mid-time transits. This could explain the higher e values reported in the solutions by former authors. We reiterate that each dataset has its own binary period determined, and that the shape of the O − C curve to be adjusted also changes (see Fig. 3).

Figure 10 shows the companion’s mass and semi-major axis derived from the fitted parameters as a function of dataset size. We observe a decrease in mass, from ~90 MJup to ~50 MJup, with increasing dataset size. In addition, there is an almost linear increase in the companion’s semi-major axis from ~6.4 to ~7.05 au. The binary semi-major axis remains approximately constant at a ~ 5.907279 × 10−3 au, with small increments of the order of 10−10 au.

Successive fitting gives different values of 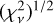(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$, as shown in Fig. 11. When the dataset size is around 88 observations, there is a sudden increase in 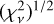(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$. For smaller datasets, there is a smooth change that leads to a decrease in the goodness-of-fit as we consider additional points, starting from 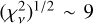(χv2)1/2~9${\left( {\chi _v^2} \right)^{1/2}}\~9$ for 50 points until reaching 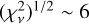(χv2)1/2~6${\left( {\chi _v^2} \right)^{1/2}}\~6$ for 88 points (see the denominator in Eq. (6) to understand the behavior of 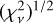(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ as we increase N). For datasets with more than 88 points, the 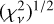(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ increases drastically and presents values around 14. Therefore, we conclude for the most recent mid-time observations that solutions are scarcely distributed and are unable to restrict the possible orbits to a unique solution. In order to comprehend the discrepancy observed in 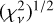(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ for a dataset size of approximately 88, Fig. 12 illustrates the uncertainties associated with each observation. Notably, we observe that the uncertainties in mid-time eclipse times, denoted σi, are potentially underestimated for mid-time transits, particularly when N > 88. This discrepancy leads to greater weight being assigned to the new data and has the potential to alter the absolute minimum of orbital fits.

In conclusion, using the data from Parsons et al. (2010) (58 data points, covering approximately 17.85 yr of observations), we note that the orbital fit for determining the hidden companion of QS-Virginis yields completely different results compared to those obtained using 105 data points (spanning nearly 22.9 yr). Our findings support the idea that poorly sampled eclipse times, insufficient sampling over long time periods, and/or incomplete coverage of the unseen companion’s orbital period can lead to incorrect characterization of the third body. In the specific case of QS-Virginis, acquiring additional data would be desirable in order to establish orbital parameters with greater confidence.

We integrated the solutions shown in Fig. 9 performing N-body simulations. All the solutions considered are stable over 104 yr and exhibit log∣〈Y〉 − 2.0| < −1.8, implying regular orbits. Furthermore, our findings are validated by extensive long-term simulations, where each initial condition was tracked over a span of 106 yr (~2 × 109 Pbin ~ 6 × 104 Ppl).

Figure 13 shows the total amplitude of the evolution of orbital elements during the integration, named the Δa = (amax − amin) and Δe = (emax − emin) indicators, for the binary orbit and the planet orbit, respectively. The low values obtained indicate stability for these orbits. We generally observe that Δa and Δe values are the lowest for the largest dataset. In particular, the results obtained for the fits using all the data points (105) appear to have converged to a steady value. Furthermore, we note that simulations with a dataset of larger than 73 (discontinuity point) exhibit milder variations in orbital elements, suggesting more regular orbits (compared to simulations with smaller datasets).

For each integration, a rough estimation of the lowest peri-center distance (qpl) of the planet orbit in a Jacobi reference frame can be computed as: 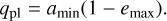qpl=amin(1−emax).${q_{{\rm{pl}}}} = {a_{\min }}\left( {1 - {e_{\max }}} \right).$(9)

Given that δa and δe of the binary are almost constant, we can estimate the companion’s pericentric distance for each simulation when both Δa and Δe are maximum as 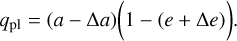qpl=(a−Δa)(1−(e+Δe))${q_{{\rm{pl}}}} = (a - \Delta a)(1 - (e + \Delta e))$(10)

In Fig. 14, we observe that for dataset sizes ∈ [45−73], we obtain a nearly constant value of qpl ~ 49 R⊙. This is also the lowest value for all the simulations. For dataset sizes of ∈ [74–92], we reach another nearly constant value of qpl ~ 73 R⊙. For dataset sizes ≥92, qpl is always greater than 80 R⊙, which avoids close encounters with the binary.

thumbnail Fig. 6

Goodness-of-fit (χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ as a function of a fixed parameter 𝒜i, while letting the remaining parameters vary freely. The red circle marks the best-fit value (𝒜BF as determined from the genetic-simplex method). The dashed line marks the value of (χv2)1σ1/2$\left( {\chi _v^2} \right)_{1\sigma }^{1/2}$ defined in Eq. (8). The intersection of (χv2)1σ1/2$\left( {\chi _v^2} \right)_{1\sigma }^{1/2}$ with the blue points defines the 1σ confidence interval for the parameter 𝒜i (see the results in Table 2). Orange circles correspond to chaotic orbits, with 〈Y〉 ≳ 2.1 (see the text).
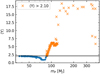thumbnail Fig. 7

Averaged MEGNO as a function of the planet mass in logarithmic scale for integrations over 5 × 104 yr. The horizontal line denotes the critical value 〈Y〉c = 2.1, and orange crosses represent integrations with 〈Y〉 > 〈Y〉c.
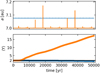thumbnail Fig. 8

Semi-major axis (top) and averaged MEGNO (bottom) as a function of time for a chaotic (orange) and a nonchaotic (blue) system.
thumbnail Fig. 9

Evolution of the parameters fitted as a function of the number of data points used. In the different panels, the value of the best-fit parameter for the third body is shown.
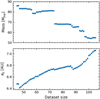thumbnail Fig. 10

Mass (top) and semi-major axis (bottom) of the planet as functions dataset size.
thumbnail Fig. 11

Dependence of (χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ on the choice of dataset. (χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ calculated using the different datasets, with solutions given in Fig. 9.
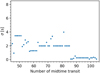thumbnail Fig. 12

Representation of error weights for each mid-time transit as collected bv Bonrs (2015)
thumbnail Fig. 13

Δa (top) and Δe (bottom) stability indicators of the binary (left) and the modeled companion (right panels) integrated orbits, as a function of dataset size.
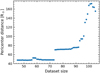thumbnail Fig. 14

Estimated minimum planet pericenter distance as a function of dataset size.

4 Discussion and conclusions

We explored different strategies to model the O – C signal present in some of the evolved binary stars. To do so, we designed an algorithm that produces the O – C signals starting from the linear or quadratic ephemeris. We also built an algorithm that models the O – C diagram and obtains the best-fit Keplerian parameters of a third body orbiting the binary.

We tested our methods on QS Vir because of the intriguing dispersion of best-fit values found in the literature, as well as the availability of an extended baseline of observations spanning approximately 22.9 yr. In the case of QS Vir, we reach the following conclusions:

  • The residuals from a linear ephemeris provide a more suitable model for capturing the O – C signal, while a quadratic ephemeris results in a modulated signal that cannot be adequately modeled with an isolated body around the binary system.

  • The binary period is found to be modified as a function of the observational data. These modified values roughly agree with those reported by previous authors (see Fig. 3, bottom panel).

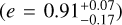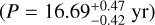  • The best-fit values for the unseen companion indicate the presence of a low-mass stellar companion (57.71 Mjup) on an eccentric orbit (e=0.91−0.17+0.07),$\left( {e = 0.91_{ - 0.17}^{ + 0.07}} \right),$, with a range of compatible periods (P=16.69−0.42+0.47 yr)$\left( {P = 16.69_{ - 0.42}^{ + 0.47}{\rm{yr}}} \right)$.

  • Parameters such as the companion’s period and its argument of periapsis (ω) exhibit significant variations depending on the size of the observational dataset used.

It is important to note that the best-fit values obtained are not statistically robust without a proper error analysis. We successfully tested different strategies for determining the uncertainties of best-fit parameters, and evaluated their variations as a function of the observational data (this allowed us to mimic the observational dataset according to the publication epoch). In our analysis, we took great care to ensure the suitability of the model and the fidelity of the MCMC methodology in capturing the relevant data features. We thoroughly evaluated the performance of the model and scrutinized the MCMC convergence to ensure both robustness and reliability. The parameter space in these optimization problems is usually a forest of many local minima, and once a solution is found the uncertainties with MCMC are calculated within that particular narrow pit. This is not a failure of the algorithm, but is connected to the intrinsic nature of this problem.

To further strengthen our error analysis, we introduced an alternative approach known as grid search. This method allows us to systematically search for errors in each parameter 𝓐i that exhibits statistical significance. Specifically, we identified parameters for which their best fits gave 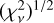(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ values lower than the 1σ value of 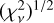(χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$. By identifying the interval of possible values of 𝓐i, we provide additional insights into the reliability of the parameter estimates. Our dynamical study of best-fit solutions does not show unstable orbits. However, we find some regions of chaotic solutions, which could shrink the possible solutions of an additional body in the system. However, our study indicates that the current available observations are insufficient to confidently confirm or rule out the presence of such an additional body.

At face value, and based on the available data, we cannot exclude the presence of a hypothetical fourth body in the outer regions of the QS Vir system. It is worth highlighting that the methodology proposed here is robust enough to tackle the analysis of challenging ETV signals in a more general context. For the enigmatic case of QS Vir, future high-precision measurements will be crucial to reveal its elusive orbital architecture.

Acknowledgements

We thank the anonymous reviewer who, through a rigorous examination of the manuscript, suggested substantial improvements to this final version. T.C.H. acknowledges Dr. Jennifer Burt for valuable discussion on the computation of Lomb-Scargle power spectra within PYTHON. N-body computations were performed at Clemente Cluster from IATE, Argentina and at the Mulatona Cluster from the CCAD-UNC, which is part of SNCAD-MinCyT, Argentina. This project has received funding from the European Research Council (ERC) under the European Union Horizon Europe programme (grant agreement No. 101042275, project Stellar-MADE).

References

  1. Almeida, L. A., & Jablonski, F. 2011, IAU Symp., 276, 495 [NASA ADS] [Google Scholar]
  2. Almeida, L. A., Jablonski, F., & Rodrigues, C. V. 2013, ApJ, 766, 11 [Google Scholar]
  3. Almeida, L. A., Pereira, E. S., Borges, G. M., et al. 2020, MNRAS, 497, 4022 [Google Scholar]
  4. Applegate, J. H. 1992, ApJ, 385, 621 [Google Scholar]
  5. Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bate, M. R. 2018, MNRAS, 475, 5618 [Google Scholar]
  7. Beaugé, C., Giuppone, C. A., Ferraz-Mello, S., & Michtchenko, T. A. 2008, MNRAS, 385, 2151 [CrossRef] [Google Scholar]
  8. Beuermann, K., Dreizler, S., Hessman, F. V., & Deller, J. 2012, A&A, 543, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bonavita, M., & Desidera, S. 2020, Galaxies, 8, 16 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bours, M. C. P. 2015, PhD thesis, University of Warwick, UK [Google Scholar]
  11. Bours, M. C. P., Marsh, T. R., Parsons, S. G., et al. 2016, MNRAS, 460, 3873 [Google Scholar]
  12. Brown-Sevilla, S. B., Nascimbeni, V., Borsato, L., et al. 2021, MNRAS, 506, 2122 [NASA ADS] [CrossRef] [Google Scholar]
  13. Burt, J. 2016, PhD thesis, University of California, Santa Cruz, USA [Google Scholar]
  14. Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Cincotta, P. M., Giordano, C. M., & Simó, C. 2003, Phys. D Nonlinear Phenom., 182, 151 [Google Scholar]
  16. Cortés-Zuleta, P., Rojo, P., Wang, S., et al. 2020, A&A, 636, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Er, H., Özdönmez, A., & Nasiroglu, I. 2021, MNRAS, 507, 809 [NASA ADS] [CrossRef] [Google Scholar]
  18. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  19. Gianuzzi, E., Giuppone, C., & Cuello, N. 2023, A&A, 669, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Giuppone, C. A., Leiva, A. M., Correa-Otto, J., & Beaugé, C. 2011, A&A, 530, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Gozdziewski, K., Nasiroglu, I., Slowikowska, A., et al. 2012, MNRAS, 425, 930 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hilditch, R. W. 2001, An Introduction to Close Binary Stars (Cambridge: Cambridge University Press) [Google Scholar]
  23. Hinse, T. C., Christou, A. A., Alvarellos, J. L. A., & Gozdziewski, K. 2010, MNRAS, 404, 837 [NASA ADS] [CrossRef] [Google Scholar]
  24. Horner, J., Wittenmyer, R. A., Hinse, T. C., et al. 2013, MNRAS, 435, 2033 [CrossRef] [Google Scholar]
  25. Irwin, J. B. 1952, ApJ, 116, 211 [Google Scholar]
  26. Lanza, A. F. 2020, MNRAS, 491, 1820 [NASA ADS] [Google Scholar]
  27. Larson, R. B. 1972, MNRAS, 156, 437 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lee, J. W., Kim, S.-L., Kim, C.-H., et al. 2009, AJ, 137, 3181 [Google Scholar]
  29. Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
  30. Marsh, T. R. 2018, Circumbinary Planets Around Evolved Stars (Berlin: Springer International Publishing), 96 [Google Scholar]
  31. Marsh, T. R., Parsons, S. G., Bours, M. C. P., et al. 2014, MNRAS, 437, 475 [NASA ADS] [CrossRef] [Google Scholar]
  32. O’Donoghue, D., Koen, C., Kilkenny, D., et al. 2003, MNRAS, 345, 506 [CrossRef] [Google Scholar]
  33. Paczynski, B. 1967, Acta Astron., 17, 287 [Google Scholar]
  34. Parsons, S. G., Marsh, T. R., Copperwheat, C. M., et al. 2010, MNRAS, 407, 2362 [NASA ADS] [CrossRef] [Google Scholar]
  35. Parsons, S. G., Marsh, T. R., Gänsicke, B. T., Drake, A. J., & Koester, D. 2011, ApJ, 735, L30 [NASA ADS] [CrossRef] [Google Scholar]
  36. Parsons, S. G., Hill, C. A., Marsh, T. R., et al. 2016, MNRAS, 458, 2793 [NASA ADS] [CrossRef] [Google Scholar]
  37. Pereira, E. S., & Almeida, L. A. 2018, Boletim da Sociedade Astronómica Brasileira, 30, 54 [Google Scholar]
  38. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
  39. Pulley, D., Sharp, I. D., Mallett, J., & von Harrach, S. 2022, MNRAS, 514, 5725 [NASA ADS] [CrossRef] [Google Scholar]
  40. Qian, S. B., Liao, W. P., Zhu, L. Y., et al. 2010, MNRAS, 401, L34 [NASA ADS] [CrossRef] [Google Scholar]
  41. Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
  42. Schwarz, R., Funk, B., Zechner, R., & Bazsó, Á. 2016, MNRAS, 460, 3598 [Google Scholar]
  43. Southworth, J., Dominik, M., Jørgensen, U. G., et al. 2019, MNRAS, 490, 4230 [CrossRef] [Google Scholar]
  44. Stobie, R. S., Kilkenny, D., O'Donoghue, D., et al. 1997, MNRAS, 287, 848 [NASA ADS] [CrossRef] [Google Scholar]
  45. Tokovinin, A. 2021, Universe, 7, 352 [NASA ADS] [CrossRef] [Google Scholar]
  46. van den Berk, J., Portegies Zwart, S. F., & McMillan, S. L. W. 2007, MNRAS, 379, 111 [NASA ADS] [CrossRef] [Google Scholar]
  47. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  48. Völschow, M., Schleicher, D. R. G., Banerjee, R., & Schmitt, J. H. M. M. 2018, A&A, 620, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Woltjer, J., J. 1922, Bull. Astron. Inst. Netherlands, 1, 93 [NASA ADS] [Google Scholar]
  50. Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [Google Scholar]
  51. Zorotovic, M., & Schreiber, M. R. 2013, A&A, 549, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
3

Residuals between the calculated (C) and observed (O) mid-eclipse times.

4

A word of caution: in the case of poor sampling of mid-eclipse times, the analysis can result in erroneous results. We here assume that we are working on a sufficiently sampled signal.

5

Equivalent to (BJD-2 450 000.0), but for sake of simplicity we use BMJD.

All Tables

Table 1

Parameters for the planets proposed for QS Vir.

In the text
Table 2

Best Keplerian orbital fits for a circumbinary companion around QS Vir.

In the text

All Figures

thumbnail Fig. 1

Schematic representation of QS Vir with its physical parameters. Top: physical parameters, Lagrangian point L1, and equipotential surface in QS Vir. The parameter values of the binary system were obtained by O’Donoghue et al. (2003) and we calculated the luminosity using temperature and radius. Bottom: schematic configuration in the case where a third body modifies the binary barycentric position with respect to the observer. The movement of the binary can be modeled to infer the mass and the orbital parameters of the third body.
In the text
thumbnail Fig. 2

Best orbital fits and residuals. Upper panel: O – C diagram of QS Vir. The crosses and plus symbols represent the O – C values built with the linear and quadratic ephemeris, respectively (O – C = Tcalc-Eq. (2)). The solid line and the dashed line represent the models fitted using the two models as described in the text. Lower panel: residuals using the same symbol and color coding as the top panel.
In the text
thumbnail Fig. 3

Dependence of the shape of the O – C and the period of the binary on the dataset considered. Top panel: O – C signal produced using four different datasets that mimic available observational data. Data point colors correspond to different datasets and horizontal lines at the top help to identify the corresponding observational baseline (ΔT). Bottom panel: determination of the binary period from the linear ephemeris as a function of the dataset. The horizontal solid and dashed lines represent the values of Pbin given by Bours (2015) and O’Donoghue et al. (2003), respectively. Pbin changes depending on the dataset selected.
In the text
thumbnail Fig. 4

Results of MCMC chains selecting pairs of parameters. We estimate the uncertainties using the posterior distribution of MCMC chains. Mean values, i.e., best-fit solutions, are plotted with black crosses. Level curves indicate 1σ (dark red) and 2σ (light blue) levels of posterior distributions. We note that for 2D histograms, these values correspond to roughly 39 and 86% confidence levels of the mean. In the top panels, we show the posterior distributions with their quantile levels at 0.14, 0.5, and 0.84. Here, t0 is given as a BMJD.
In the text
thumbnail Fig. 5

Averaged MEGNO as a function of Mahalanobis distance. The horizontal line denotes 〈Y〉 = 2.
In the text
thumbnail Fig. 6

Goodness-of-fit (χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ as a function of a fixed parameter 𝒜i, while letting the remaining parameters vary freely. The red circle marks the best-fit value (𝒜BF as determined from the genetic-simplex method). The dashed line marks the value of (χv2)1σ1/2$\left( {\chi _v^2} \right)_{1\sigma }^{1/2}$ defined in Eq. (8). The intersection of (χv2)1σ1/2$\left( {\chi _v^2} \right)_{1\sigma }^{1/2}$ with the blue points defines the 1σ confidence interval for the parameter 𝒜i (see the results in Table 2). Orange circles correspond to chaotic orbits, with 〈Y〉 ≳ 2.1 (see the text).
In the text
thumbnail Fig. 7

Averaged MEGNO as a function of the planet mass in logarithmic scale for integrations over 5 × 104 yr. The horizontal line denotes the critical value 〈Y〉c = 2.1, and orange crosses represent integrations with 〈Y〉 > 〈Y〉c.
In the text
thumbnail Fig. 8

Semi-major axis (top) and averaged MEGNO (bottom) as a function of time for a chaotic (orange) and a nonchaotic (blue) system.
In the text
thumbnail Fig. 9

Evolution of the parameters fitted as a function of the number of data points used. In the different panels, the value of the best-fit parameter for the third body is shown.
In the text
thumbnail Fig. 10

Mass (top) and semi-major axis (bottom) of the planet as functions dataset size.
In the text
thumbnail Fig. 11

Dependence of (χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ on the choice of dataset. (χv2)1/2${\left( {\chi _v^2} \right)^{1/2}}$ calculated using the different datasets, with solutions given in Fig. 9.
In the text
thumbnail Fig. 12

Representation of error weights for each mid-time transit as collected bv Bonrs (2015)
In the text
thumbnail Fig. 13

Δa (top) and Δe (bottom) stability indicators of the binary (left) and the modeled companion (right panels) integrated orbits, as a function of dataset size.
In the text
thumbnail Fig. 14

Estimated minimum planet pericenter distance as a function of dataset size.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.