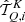| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A207 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202346399 | |
| Published online | 20 March 2024 | |
Modeling the scattering polarization in the solar Ca I 4227Å line with angle-dependent PRD effects and bulk velocities
1
Istituto ricerche solari Aldo e Cele Daccò (IRSOL), Faculty of Informatics, Università della Svizzera italiana (USI), Locarno, Switzerland
e-mail: nuno.guerreiro@irsol.usi.ch
2
Euler Institute, Università della Svizzera italiana (USI), Lugano, Switzerland
3
Simula Research Laboratory, Oslo, Norway
4
Leibniz-Institut für Sonnenphysik (KIS), Freiburg i. Br., Germany
Received:
10
March
2023
Accepted:
13
November
2023
Context. Modeling the scattering polarization signals of strong chromospheric lines requires solving the radiative transfer problem for polarized radiation, out of local thermodynamic equilibrium, taking partial frequency redistribution (PRD) effects into account. This problem is extremely challenging from a computational standpoint and, so far, most studies have been carried out by either modeling PRD effects under the angle-average approximation or by considering academic models of the solar atmosphere. Thanks to a new solution strategy, applicable to atomic systems that allow for a linearization of the problem, accurate solutions can now be routinely obtained in realistic 1D models, taking angle-dependent (AD) PRD effects into account.
Aims. This work is aimed at assessing the suitability and performance of this new approach to handling dynamic scenarios. At the same time, it aims to explore the joint impact of magnetic fields and bulk velocities on the scattering polarization profiles of strong resonance lines, accounting for AD PRD effects and considering more realistic atmospheric models than in previous investigations.
Methods. By using a two-level atomic model for neutral calcium, we synthesized the intensity and polarization profiles of the Ca I 4227 Å line. Our calculations were performed in 1D atmospheric models, both semi-empirical and extracted from 3D magnetohydrodynamic simulations, including vertical bulk velocities and magnetic fields of arbitrary strength and orientation, both constant and varying with height.
Results. We obtained accurate solutions after only a few iterations across all considered scenarios. Even when formulating the problem in the observer’s reference frame, the frequency and angular grids required for accurate results were easily manageable. The calculated profiles showed the expected signatures of bulk velocities: wavelength shifts, enhancement of the line-core polarization amplitude, and prominent asymmetries in the wing signals. The results obtained in atmospheric models with complex thermal, dynamic, and magnetic structures unveiled the broad diversity of features in the emergent radiation that can be expected from realistic scenarios.
Conclusions. The presented results assess the suitability of the proposed solution strategy and its parallel implementation, thus supporting its generalization to the 3D case. Our applications in increasingly realistic atmospheric models showed the difficulty related to precisely establishing the individual weight of bulk velocities and magnetic fields in the shape of the emergent profiles. This highlights the need to account for both these physical ingredients to perform reliable inversions of observed scattering polarization profiles.
Key words: polarization / radiative transfer / scattering / Sun: atmosphere
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Despite significant progress in recent years with respect to observing and modeling the solar atmosphere at increasingly smaller scales, we still lack a deep understanding of its structure and physical properties (Thompson 2014). Thanks to the improving computational power of our day, numerical modeling is poised to probe beyond the observational horizon, allowing us to explore scales inaccessible by current instrumentation (Solanki et al. 2017; Rimmele et al. 2020; Müller et al. 2020; Guo et al. 2021).
A number of numerical codes to model the solar atmosphere with focus on different physical processes are presently available, each with its own merit. Just to provide a few examples, we refer the reader to Bifrost (Gudiksen et al. 2011) and COBOLD (Freytag et al. 2012) for magnetohydrodynamic (MHD) simulations, RH (Uitenbroek 2001) and PORTA (Štěpán & Trujillo Bueno 2013) for radiative transfer forward modeling, and NICOLE (Socas-Navarro et al. 2015) and TIC (Li et al. 2022) for inversions, with no prejudice to those not cited. These computational tools have provided insights that were unthinkable just a few decades ago.
It is broadly accepted that magnetic fields are the driving force behind the activity in the solar atmosphere and play a critical role in determining its structure (Priest 2014). Despite ubiquitous and fundamental to our understanding, measuring the magnetic field in the upper layers of the solar atmosphere remains a challenging task. Crucially, information on the magnetic fields is encoded in the polarization profiles of spectral lines (e.g., Stenflo 1994; Landi Degl’Innocenti & Landolfi 2004; Harvey 2006). The Zeeman effect dominates circular polarization and plays a fundamental role in magnetic field diagnostics of the photosphere. On the other hand, scattering polarization dominates the linear polarization signals that can be observed in the quiet Sun, especially close to the edge of the solar disk (limb). Its magnetic sensitivity via the Hanle and magneto-optical effects allows for the investigation of small-scale unresolved fields in the photosphere (e.g., Trujillo Bueno et al. 2004), as well as the ever elusive fields in the chromosphere and transition region (e.g., Manso Sainz & Trujillo Bueno 2010; Štěpán & Trujillo Bueno 2016; Trujillo Bueno et al. 2017). However, scattering polarization is not only modified by the magnetic field, but it is also significantly impacted by the presence of bulk velocities in the solar plasma. In particular, bulk velocity gradients can enhance the anisotropy of the radiation field that illuminates the atoms, thus increasing the amount of atomic polarization that is induced in the atomic system and, consequently, the amplitude of scattering polarization signals (e.g., Carlin et al. 2012). Such enhancements, as well as the asymmetries and shifts that bulk velocities produce on scattering polarization must therefore be carefully accounted for in order to correctly extract the information on the magnetic field through the Hanle effect (e.g., Carlin et al. 2012; Štěpán et al. 2015; Štěpán & Trujillo Bueno 2016; Nagendra et al. 2019; Jaume Bestard et al. 2021).
We have developed a new code that solves the radiative transfer (RT) problem out of local thermodynamic equilibrium (LTE) in 1D atmospheric models, considering scattering polarization and angle-dependent (AD) PRD effects, in the presence of arbitrary magnetic and bulk velocity fields (Benedusi et al. 2022). By considering the Ca I 4227 Å line as a benchmark, we aim to better understand the impact of plasma bulk velocities on the scattering polarization profiles of strong chromospheric lines. Such profiles are characterized by extended wing lobes produced by partially coherent scattering processes and they can thus only be modeled by including PRD effects. Additionally, this investigation aims to assess the performing capabilities of the aforementioned 1D code in non-static scenarios, which, in turn, will facilitate the ongoing development of a 3D code encompassing equivalent physical properties. Beside building on a well understood semi-empirical model (i.e., model C of Fontenla et al. 1993), we also explore more complex atmospheric models with origin in the 3D magnetohydrodynamic (MHD) simulation of Carlsson et al. (2016).
The paper is organized as follows. Section 2 presents the RT problem for polarized radiation, while Sect. 3 tackles the solution strategy used to handle the numerical challenges inherent to modeling scattering polarization with AD PRD effects and bulk velocities. In Sect. 4, we present the results of the numerical modeling of the Ca I 4227 Å line in the presence of both magnetic fields and bulk velocities in different atmospheric models. Finally, our conclusions are given in Sect. 5.
2. RT problem for polarized radiation
A complete description of the polarization state of the radiation field is provided by the four Stokes parameters I, Q, U, and  . These quantities are often treated as the four components of the Stokes vector,
. These quantities are often treated as the four components of the Stokes vector, 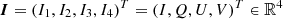 . Assuming steady-state conditions, the Stokes vector, as well as the other physical quantities entering the RT problem are generally functions of the frequency,
. Assuming steady-state conditions, the Stokes vector, as well as the other physical quantities entering the RT problem are generally functions of the frequency, ![$ \nu \in [\nu_{\min}, \nu_{\max}] \subset \mathbb R_+ $](/articles/aa/full_html/2024/03/aa46399-23/aa46399-23-eq3.gif) , and propagation direction, Ω = (θ, χ)∈[0, π]×[0, 2π), of the considered radiation beam1, and of the spatial point
, and propagation direction, Ω = (θ, χ)∈[0, π]×[0, 2π), of the considered radiation beam1, and of the spatial point 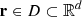 , with d ∈ {1, 2, 3} the dimensionality of the spatial domain, D.
, with d ∈ {1, 2, 3} the dimensionality of the spatial domain, D.
The transfer of partially polarized light along the direction Ω at frequency ν is described by the system of coupled first-order inhomogeneous ordinary differential equations, given by
where K ∈ ℝ4 × 4 is the so-called propagation matrix:
with ηi and ρi being the dichroism and anomalous dispersion coefficients, respectively, while ε ∈ ℝ4 is the emission vector (i.e., a vector whose components are the emission coefficients in the four Stokes parameters).
The elements of the propagation matrix and the emission vector (often referred as a whole to as RT coefficients) receive contributions from two types of physical processes characterizing the matter-radiation interaction: line processes (i.e., transitions between bound states of a given atom or molecule) and continuum processes (i.e., transitions between bound and free states or between free states). The line and continuum contributions to the RT coefficients (hereafter labeled with the superscripts ℓ and c, respectively) simply add to one another. The line contribution to RT coefficient depends on the state of the considered atomic system, which is determined by solving a set of rate equations (statistical equilibrium, SE, equations). In this work, we consider a two-level atomic model with an unpolarized and infinitely sharp lower level. In the solar atmosphere, the impact of stimulated emission in the spectral range of the Ca I line is very small and thus ends up neglected.
2.1. Propagation matrix
For the considered atomic model, the line contributions to the elements of the propagation matrix (2) are given by (see, e.g., Alsina Ballester et al. 2017)
where the factor kL is the frequency-integrated absorption coefficient. This quantity depends on the population of the lower level, obtained from the solution of the SE equations. The quantity 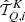 is the polarization tensor (e.g., Chapter 5 of Landi Degl’Innocenti & Landolfi 2004), evaluated in the magnetic reference system2. The quantities
is the polarization tensor (e.g., Chapter 5 of Landi Degl’Innocenti & Landolfi 2004), evaluated in the magnetic reference system2. The quantities 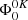 and
and 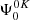 are particular components of the generalized profile and generalized dispersion profile, respectively, which are comprehensively described in Appendix 13 of Landi Degl’Innocenti & Landolfi (2004). In the visible part of the solar spectrum, continuum processes only effectively contribute (isotropically) to the diagonal element of the propagation matrix, namely,
are particular components of the generalized profile and generalized dispersion profile, respectively, which are comprehensively described in Appendix 13 of Landi Degl’Innocenti & Landolfi (2004). In the visible part of the solar spectrum, continuum processes only effectively contribute (isotropically) to the diagonal element of the propagation matrix, namely,
where δij is the Kronecker delta.
2.2. Emission vector
The line contribution to the emission vector can be decomposed into two terms
where the term labeled “th” describes the contribution by atoms that are collisionally excited (collisional or thermal term), while the term labeled “sc” describes the contribution brought by radiatively excited atoms (scattering term).
Assuming that inelastic collisions are isotropic, the line thermal term is (see Alsina Ballester et al. 2017):
where ϵ is the photon destruction probability and WT is the Planck function in the Wien limit at the line-center frequency.
For a two-level atomic model with an unpolarized lower level, an analytical solution of the SE equations is available and the line scattering contribution to the emissivity can be expressed through the redistribution matrix formalism, which is particularly suitable for describing PRD phenomena (Hummer 1962; Bommier 1997a,b). In this formalism, the εℓ,sc term is given by the following integral operator:
where 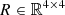 is the so-called redistribution matrix, which encodes the physics of the scattering process, coupling all Stokes parameters, all directions, and all frequencies at each spatial point. We follow the convention that primed and unprimed quantities refer to the incident and scattered radiation, respectively. Following Bommier (1997b), the redistribution matrix for the considered atomic model is given by the sum of two terms, namely,
is the so-called redistribution matrix, which encodes the physics of the scattering process, coupling all Stokes parameters, all directions, and all frequencies at each spatial point. We follow the convention that primed and unprimed quantities refer to the incident and scattered radiation, respectively. Following Bommier (1997b), the redistribution matrix for the considered atomic model is given by the sum of two terms, namely,
where RII describes scattering processes that are coherent in frequency in the atomic frame and RIII describes scattering processes that are totally incoherent in the same frame. The evaluation of εℓ,sc in the observer’s frame, accounting for Doppler redistribution, requires complex algorithmic formulations, which in themselves are computationally expensive. This aspect is usually tackled by applying approximate expressions of the redistribution matrices which simplify the evaluation of the integrals in Eq. (6) and significantly reduce the computational cost of the whole problem.
In this work, the exact AD expression of the RII redistribution matrix in the observer’s frame is considered. By contrast, the assumption of complete frequency redistribution (CRD) in the observer’s frame is made for the RIII matrix. This approximation has already been extensively used in the modeling of strong chromospheric lines (e.g., Alsina Ballester et al. 2017; Janett et al. 2021a). Its suitability has been accurately verified by Riva et al. (2023), also confirming the results of Sampoorna et al. (2017).
Continuum processes also contribute to the emissivity with a thermal and a scattering term. In the solar atmosphere, it is a good approximation to assume the continuum thermal contribution to be unpolarized and isotropic, namely,
Under the assumption that continuum scattering processes are coherent in the observer’s frame, their contribution to the emissivity is given by (see Alsina Ballester et al. 2017):
where σ is the continuum opacity for scattering, and 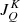 is the radiation field tensor, defined as
is the radiation field tensor, defined as
where 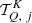 is the polarization tensor evaluated in the reference system of the problem (see footnote 1).
is the polarization tensor evaluated in the reference system of the problem (see footnote 1).
2.3. Bulk velocity impact
The numerical solution of RT problems in dynamic atmospheres is more complex than its static counterpart. According to the classical Doppler effect formula, given a beam of radiation of frequency, ν, and propagation direction, Ω, and an atom moving with non-relativistic velocity, v, the frequency 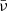 in the atomic frame is given by:
in the atomic frame is given by:
with c as the speed of light. In the presence of a bulk velocity field, vb, the Doppler effect, which depends on the projection, vb ⋅ Ω, therefore adds angular- and spatial-dependent frequency shifts to the propagation matrix elements (3) and (4), to the line thermal emissivity (5), and doubly affects the redistribution matrices by shifting both incident and emitted radiation. We must note that this inherent coupling between angles and frequencies is already present in the exact AD expression of the RII redistribution matrix.
As far as continuum processes are concerned, the Doppler shifts due to a bulk velocity field can be neglected in the evaluation of kc, 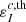 , and σ, considering that these quantities are nearly constant over the frequency interval of a spectral line. However, Doppler shifts must be considered when evaluating the radiation field tensor
, and σ, considering that these quantities are nearly constant over the frequency interval of a spectral line. However, Doppler shifts must be considered when evaluating the radiation field tensor 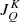 in Eq. (8).
in Eq. (8).
2.4. Boundary conditions
In this work, we assume that no radiation is entering the spatial domain D from the top boundary at zmax, while we consider an isotropic, spectrally-flat, and unpolarized Planckian incident radiation from the bottom boundary at zmin. Boundary conditions are thus given by:
where BT is the Planck function at the line-center frequency for the temperature at zmin.
3. Numerical solution strategy
The solution of the RT problem in dynamic environments is notoriously expensive from a computational standpoint, as a consequence of the wide and fine frequency grids needed in order to accurately include the Doppler shifts introduced by macroscopic velocities (see Sect. 2.3). Moreover, fine angular grids are also required to obtain accurate results in the presence of bulk velocities, especially if PRD effects are included, as they introduce a complex coupling between frequencies and directions (e.g., Sampoorna & Nagendra 2015).
Approaches tailored for treating highly dynamic scenarios have been proposed, such as the comoving frame method (CFM; e.g., Mihalas 1978), and fine compromises have been found over time to balance scientific ambitions and computational challenges. In fact, most investigations into the impact of bulk velocity fields on scattering polarization have been carried out by considering the limit of CRD, in both 1D (e.g., Carlin et al. 2012, 2013; Milić & Faurobert 2014; Carlin & Bianda 2017) and 3D (e.g., Štěpán & Trujillo Bueno 2016; del Pino Alemán et al. 2018; Jaume Bestard et al. 2021) geometries.
The RT modeling of scattering polarization in moving atmospheres, including PRD effects, was pioneered by Nagendra (1996), applying the CFM to this problem and comparing it to the observer’s frame method. Later, Sampoorna & Nagendra (2015) broadened that work by including weak magnetic fields and additionally confirmed the very good competitive performance of the CFM. The aforementioned studies were carried out considering a two-level atom in 1D isothermal atmospheric models, including PRD effects both under the angle-averaged (AA) approximation and in the general AD formulation. Applying the CFM, Sampoorna & Nagendra (2016) solved the same problem in semi-empirical 1D models of the solar atmosphere with non-monotonic vertical velocity gradients, including PRD effects under the AA approximation in the comoving frame. Recently, del Pino Alemán et al. (2020) solved the RT problem for a two-term atom in realistic 1D atmospheric models, including vertical bulk velocities and magnetic fields of arbitrary strength and orientation, accounting for AD PRD effects in the standard observer’s frame. Finally, worth mentioning are the works of Megha et al. (2019, 2020), who applied the CFM to model scattering polarization with AA PRD effects in spherically symmetric moving atmospheres.
In this work, we model scattering polarization accounting for AD PRD effects and bulk velocities by applying the solution strategy recently developed by Benedusi et al. (2022). The suitability of this approach to handle velocity fields is tested in dynamic 1D models of the solar atmosphere of increasing complexity. The problem is solved without applying the CFM: our computations show that for the typical bulk velocities of the solar chromosphere, the frequency and angular grids needed to obtain accurate results remain manageable also in the observer’s frame. The increased computational complexity due to the slightly larger number of grid points, in comparison to those needed in the CFM scenario, is fully compensated by the very high convergence rate of the solution method. The application of the latter together with the CFM goes beyond the scope of this paper and is left for a future investigation.
In this section, we first present the considered discretization of the problem and its corresponding algebraic formulation in terms of transfer and scattering operators. We then present our linearization strategy and we provide some details on the numerical methods used within our effective iterative solution approach.
3.1. Discretization
In 1D geometries, the considered discrete atmospheric model usually provides the discretization of the spatial domain 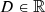 with an unevenly spaced grid with Nr nodes, namely:
with an unevenly spaced grid with Nr nodes, namely:
For the angular discretization of Ω = (θ,χ), we use a tensor product quadrature with NΩ = NθNχ nodes. For the inclination μ = cos(θ)∈[−1, 1], we consider two Gauss-Legendre grids (and corresponding weights), one for μ ∈ ( − 1, 0) and one for μ ∈ (0, 1). Each grid has Nθ/2 = 6 nodes, ordered as:
These nodes correspond to the angles θj = arccos(μj) ∈ (0, π) with j = 1, …, 12. For the azimuth χ ∈ (0, 2π], we consider an equidistant grid (and corresponding trapezoidal weights) with Nχ = 8 nodes, namely:
Extensive experimentation with different combinations of inclinations and azimuthal nodes showed that this spherical grid, with a total of NΩ = 96 directions, adequately balances the need for accuracy and computational affordability in the AD PRD modeling of Ca I 4227, also in the presence of complex velocity profiles. This grid is thus used across all modeling instances shown in Sect. 4.
The considered spectral interval around the Ca I 4227 Å line,
is discretized in frequency with Nν = 299 unevenly spaced nodes, namely:
These frequency nodes are equally spaced in the line core and logarithmically distributed over the wings. It must be observed that in order to adequately model the line core and near wings, we need to consider a total number of frequency grid points larger than in the static case, where Nν ≈ 100 is sufficient to get accurate results. Additionally, in order to account for the Doppler shifts in a more precise way, the spectral region where the points are equally spaced was increased in comparison to the static setting.
3.2. Algebraic formulation
Hereafter, we use the notation that vectors and matrices are represented by bold and uppercase letters, respectively. Collecting the discretized Stokes parameters in the vector 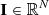 , with N = 4NrNνNΩ the total number of degrees of freedom, the above-mentioned RT problem can be then expressed in the following compact matrix form (see, e.g., Janett et al. 2021a; Benedusi et al. 2022)
, with N = 4NrNνNΩ the total number of degrees of freedom, the above-mentioned RT problem can be then expressed in the following compact matrix form (see, e.g., Janett et al. 2021a; Benedusi et al. 2022)
where 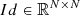 is the identity matrix. The transfer operator,
is the identity matrix. The transfer operator,
encodes the numerical solution of the set of initial value problems (IVPs) arising from (1), that is, the formal solution described in Sect. 3.4. The scattering operator,
encodes the evaluation of the scattering contribution to emissivity given by (6). The vector 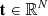 represents the radiation transmitted from the boundaries, while the vector
represents the radiation transmitted from the boundaries, while the vector 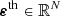 represents the thermal contributions to the emissivity.
represents the thermal contributions to the emissivity.
3.3. Linearization
The RT problem described in Sect. 2 and formulated in the compact form expressed in Eq. (9) is generally nonlinear. This is because the coefficient kL in Eqs. (3), (4), and (6) is proportional to the population of the lower level, which, in turn, depends on the radiation field through the SE equations in a nonlinear way. The problem can be reframed as a set of linear systems if the population of the lower level is known a priori and is kept unchanged. (see, e.g., Belluzzi & Trujillo Bueno 2014; Sampoorna et al. 2017; Alsina Ballester et al. 2017; Janett et al. 2021a; Benedusi et al. 2022). By so doing, the propagation matrix K and the thermal emissivity εℓ,th become independent of the radiation field, I, whereas εℓ,sc and εc,sc depend on it linearly through scattering terms3. Thus, the whole problem becomes linear in I, since it consists of the set of linear IVPs (1) linearly coupled through a scattering term of the form of Eq. (6).
The population of the lower level can be taken either from the atmospheric model (if provided), or from independent RT calculations. Noticing that polarization is expected to have a marginal impact on the population of ground or metastable levels, such calculations can be performed with available RT codes that possibly neglect the polarization, but do consider realistic multi-level atomic models. In this way, accurate values of the lower level population can be used and reliable results can be obtained, in spite of the simplicity of the considered two-level atomic model.
In this work, the population of the lower level (i.e., the population of the ground level of neutral calcium) is calculated with the RH code (Uitenbroek 2001), using an atomic model for calcium composed of 25 levels, including five levels of Ca II and the ground level of Ca III. The output of RH also provides the rates for elastic and inelastic collisions, as well as continuum quantities, which are necessary inputs for our code. Given that the presence of bulk velocities has a non-negligible impact on the population of the ground level of neutral calcium, the latter is re-calculated each time a different setting for the velocity is considered. Since the 1D module of RH allows for only vertical bulk velocities to be considered, we limited this investigation to such velocities, although our code can generally handle bulk velocities with an arbitrary orientation.
3.4. Numerical methods
The numerical solution of the set of IVPs arising from (1), known as the “formal solution”, is performed with a suitable numerical solver for ODEs. For reasons of stability, we adopt the L-stable DELO-linear formal solver (see Rees et al. 1989; Janett et al. 2017a,b, 2018; Janett & Paganini 2018).
The calculation of the scattering integral in Eq. (6) for the RII redistribution matrix in its AD form is by far the most time-consuming step of the whole problem (see, e.g., del Pino Alemán et al. 2020; Benedusi et al. 2022). The complexity of this operation is very high (e.g., ∼108 entries at each spatial node) because the RII matrix locally couples all frequencies and directions of the discretized problem. Additional difficulties are due to the highly complex behavior of RII, which imposes the use of dedicated frequency grids to obtain reliable and fast computations of the scattering integral in Eq. (6). More details on the algorithm for calculating the contribution of RII to the emissivity can be found in Benedusi et al. (2023). In order to speed up the calculation of the emissivity, the scattering integral is evaluated in the comoving reference frame (i.e. the reference frame in which the bulk velocity is zero). The advantage of this choice is that the dedicated frequency grid for calculating Eq. (6) becomes independent of the Doppler shifts, and the number of evaluations of RII is significantly reduced. This strategy implies to first evaluate the incident radiation field on the nodes of the dedicated frequency grid, defined in the comoving frame. This is performed by means of interpolations, taking into account the Doppler shifts associated to the change of the reference system. Once the scattering integral has been evaluated, the ensuing emission coefficient is transformed from the comoving frame into the observer’s frame through a new interpolation on the frequency axis. High-order interpolations (e.g., cubic splines) are performed. We note that possible numerical instabilities (e.g., oscillations) in the computed Stokes profiles may indicate that the frequency grid of the problem is not sufficiently dense (or wide) for the considered bulk velocities.
For the iterative solution of the linearized system (9), we apply a preconditioned Krylov solver, namely the generalized minimal residual (GMRES) method preconditoned in the lightweight CRD limit (Janett et al. 2021b, 2024; Benedusi et al. 2021, 2022), setting a tolerance of 10−8. The iterative method converges in a few iterations (between 10 and 20), with no need of a suitable initial guess. When combined with a suitable parallelization strategy and high-performance computing tools, this approach leads to competitive run times, providing accurate solutions in a few minutes (approximately 5 minutes, with the presented discretization settings). For more details on the convergence properties of this iterative method and timings, we refer the reader to Benedusi et al. (2022). The calculations have been performed on the Cray XC40 nodes of the Piz Daint supercomputer of the Swiss national supercomputing centre (CSCS)4. The applied partition features computing nodes with two 18-core Intel Xeon E5-2695v4 (2.10 GHz) processors.
4. Numerical results
We elected to evaluate our results obtained with different atmospheric models for the Ca I 4227 Å line. This line is particularly appealing as a baseline as it is well understood observationally, it is adequately modeled with a two-level atom approach, and its large and broad scattering polarization signal is produced by coherent scattering processes with PRD effects.
The Ca I 4227 Å line has indeed been intensively observed, particularly in the context of scattering polarization (e.g., Brückner 1963; Stenflo 1974; Wiehr 1975, 1978; Stenflo et al. 1980; Bianda et al. 1998; Capozzi et al. 2020). Its RT numerical modeling has been instrumental in a variety of contexts, both as a diagnostic tool, and as a test-bench of significant value to novel approaches to the modeling of scattering polarization (e.g., Dumont et al. 1973; Faurobert-Scholl 1992; Frisch 1996; Anusha et al. 2011; Supriya et al. 2014; Carlin & Bianda 2017; Alsina Ballester et al. 2018; Jaume Bestard et al. 2021; Janett et al. 2021a; Capozzi et al. 2022).
4.1. Modeling Ca I 4227 Å in the FAL-C atmospheric model
The Ca I 4227 Å line is initially modeled in the semi-empirical atmospheric model C of Fontenla et al. (1993), hereafter, FAL-C, representing the quiet Sun. This spans about 2000 km of the solar atmosphere, from the photosphere to the bottom of the transition region, discretized in Nr = 70 spatial nodes. Using this model, we explored the impact of vertical bulk velocities that are either constant with height or that vary with a constant gradient. Throughout this work, bulk velocities directed outwards are conventionally taken as positive. Without loss of generality, we consider the radiation emergent from the atmosphere with azimuth χ = 0. The line of sight (LOS) towards the observer is then fully defined by μ = cos θ.
Figure 1 displays the fractional polarization Q/I and U/I emergent profiles at μ = 0.38, obtained in the static case (solid lines) and including a constant bulk velocity of −10 km s−1 (dashed lines). We show the calculations for the unmagnetized case (black lines) and including horizontal magnetic fields of different strengths (red lines). As expected, the impact of a constant bulk velocity is to simply introduce a wavelength shift of the profiles, as can be seen by comparing the black solid and dashed lines. When a magnetic field is included, the typical signatures of the Hanle and magneto-optical effects, which operate in the core and wings, respectively, can be clearly observed (compare black and red profiles). The impact of bulk velocities in the magnetized case is exactly the same as in the unmagnetized one. Although this result is of limited physical interest, it benchmarks the capability and accuracy of the code in taking bulk velocities into account.
 |
Fig. 1. Fractional polarization Q/I (upper panels) and U/I (lower panels) profiles for the Ca I 4227 Å line calculated at μ = 0.38 in the absence (solid lines) and in the presence (dashed lines) of a height-independent vertical bulk velocity of −10 km s−1. The profiles are obtained both neglecting (black lines) and taking into account (red lines) the impact of a height-independent horizontal magnetic field (θB = π/2, χB = 0) with strength B = 10 G (left column) and B = 30 G (right column). The calculations are performed in the FAL-C atmospheric model. The reference direction for positive Stokes Q is the parallel to the limb. |
In order to analyze the impact of vertical bulk velocities that vary with height with a constant gradient, we considered the two velocity profiles shown in Fig. 2. The other curves plotted in the same figure display the formation height of the line, here defined as the height at which the optical depth is unity, for two different LOSs. Both velocity models have vb = 0 km s−1 at the height corresponding to 0 km. The first model (blue line) has a slope α = 0.009 s−1; at the formation height of the line core, vb ≃ 7.5 km s−1 for μ = 0.96, and vb ≃ 10 km s−1 for μ = 0.03. The second one (red line) has instead a slope equal to 2α; at any height, the corresponding velocities are therefore twice as large as for the previous model.
 |
Fig. 2. Bulk velocity profiles with constant vertical gradients α (blue line) and 2α (red line), with α = 0.009 s−1. The black and grey curves display the height at which the optical depth, as a function of frequency, is unity, for μ = 0.96 and μ = 0.03, respectively. |
The panels of Fig. 3 display a comparison of the Q/I and U/I emergent profiles at μ = 0.38 obtained both in the reference static unmagnetized case and considering different combinations of the bulk velocities of Fig. 2 and height-independent horizontal magnetic fields of different strengths. Confirming the conclusions of previous CRD investigations (see, e.g., Carlin et al. 2012; Štěpán et al. 2015; Štěpán & Trujillo Bueno 2016; Jaume Bestard et al. 2021), our results show that in addition to causing a wavelength shift of the profiles, the bulk velocity gradients also produce a significant enhancement of the line-core scattering polarization signal. The profiles calculated including a magnetic field highlight that such enhancement, which is larger for a larger velocity gradient, mixes up with the modification of the same signal produced by the Hanle effect. This further highlights the need of taking the dynamics of the solar plasma carefully into account in order to perform reliable Hanle diagnostics of chromospheric magnetic fields. Our AD PRD computations also provide accurate results for the line-wing scattering polarization signals. In agreement with previous results (e.g., Sampoorna & Nagendra 2015, 2016), we find that in this spectral region, velocity gradients give rise to clear asymmetries between the linear polarization signals in the blue and red wing of the line.
 |
Fig. 3. Fractional polarization Q/I (upper panels) and U/I (lower panels) profiles for the Ca I 4227 Å line calculated at μ = 0.38 in the static case (solid lines, label v0) and in the presence of vertical bulk velocities with constant gradients (dashed lines). The velocity profiles of Fig. 2, with gradients α (label vα) and 2α (label v2α) are considered. The calculations are performed both for the unmagnetized case (black lines, label B0) and including a height-independent horizontal (θB = π/2, χB = 0) magnetic field (red lines) with strength B = 10 G (label B1) and B = 30 G (label B2). The calculations are performed in the FAL-C atmospheric model. The reference direction for positive Stokes Q is the parallel to the limb. |
4.2. MHD atmospheric models
In this section, we analyze the impact of vertical bulk velocities, considering 1D models extracted from a snapshot of a 3D MHD simulation of the solar atmosphere (Carlsson et al. 2016) obtained with the Bifrost5 code (Gudiksen et al. 2011). This simulation of an enhanced network region is characterized by an average unsigned magnetic field strength in the photosphere of 50 G with two dominant opposite polarity regions set 8 Mm apart. Additionally, non-equilibrium hydrogen ionization is included. The cube encompasses 24 × 24 × 17 Mm3 and is discretized with 504 × 504 × 496 grid points. The horizontal resolution is therefore 48 km and the vertical one ranges between 19 and 100 km. The considered 1D atmospheric models are vertical columns chosen to analyze the impact of velocity fields of different strength and with different gradients in the formation region of the Ca I 4227 Å line. These columns, discretized in Nr = 118 grid points, are clipped to account for the height interval:
which fully includes the formation region of the line (see Fig. 4). These atmospheric models provide temperature, electron and proton number density, vertical bulk velocity, magnetic field vector, and the hydrogen populations at each height node. We also included microturbulence, which was adopted from Fontenla et al. (1991) and interpolated to fit the grid of the models.
 |
Fig. 4. Temperature (left panel), vertical component of the bulk velocity (central panel), and magnetic field strength (right panel) as a function of height for the four considered atmospheric models (see legend). The vertical dashed lines indicate the height where the optical depth at the line center wavelength is unity for μ = 0.03. The models are vertical columns extracted from a 3D snapshot of an MHD simulation performed with the Bifrost code. |
Figure 4 displays the temperature (left panel), vertical bulk velocity (middle panel), and the magnetic field strength (right panel) as a function of height for the four considered models, labeled A, B, C, and D. The vertical dashed lines signal the formation height for the line center wavelength at μ = 0.036.
The left panel of Fig. 4 shows that for a LOS with μ = 0.03, the line core forms between 900 km and 1020 km in models A, B, and C. At the corresponding heights, the temperature is lowest in model A (3758 K) and higher in model B (4857 K) and C (5330 K). The temperature structure of model D is clearly different from the other models. Here, for the same LOS, the line core forms at about 680 km at a temperature of 7637 K. In the line core formation region, the bulk velocity is positive (≈2.80 km s−1) and with a positive gradient in model A, negative and nearly constant (≈ − 0.35 km s−1) in model B, and negative (≈ − 1.88 km s−1) with a clear negative gradient in model C. Model D was specifically chosen because it shows a quite steep negative gradient in the line formation region, with velocities in the order of −9.00 km s−1. In the line formation region, model A is characterized by a nearly constant and low value of the magnetic field strength (≈8 G), while all the other models show positive gradients and values ranging between approximately 50 G and 65 G (see right panel of Fig. 4).
Figures 5–8 show the emergent intensity I (top panels), Q/I (middle panels), and U/I (bottom panels) profiles for three different LOS corresponding to (left to right) μ = 0.03, μ = 0.38, and μ = 0.996. Each figure corresponds to one of the atmospheric models labeled A, B, C, or D in Fig. 4. In each panel, we compare three different scenarios: the benchmark case with no magnetic field and no bulk velocities, the case with a height-dependent magnetic field and no bulk velocities, and the case with both height-dependent magnetic field and bulk velocities. In the absence of magnetic and bulk velocity fields (black lines), all cases present symmetrical I and Q/I profiles, while U/I (and V/I) signals are zero. The typical triplet peak structure of the Q/I profile, which is commonly observed in quite regions close to the limb, is accurately reproduced. The relative amplitude of the central peak relative to the wing lobes varies with the atmospheric models due to their inherent thermodynamic structure. As expected, the Q/I amplitudes decrease from the limb to the disk center. In the presence of magnetic fields (red lines), the I profiles remain substantially unaltered, while the Q/I and U/I signals are impacted. In particular, the Hanle effect is responsible for the magnetic sensitivity of Q/I and U/I in the line core, while the magneto-optical effects impact the wing lobes. It is worth observing that at μ = 0.996 the Hanle effect leads to an enhancement of the polarization degree. This mechanism is commonly known as forward scattering Hanle effect (Trujillo Bueno 2001). All Stokes profiles remain symmetric in the presence of magnetic fields. The presence of vertical bulk velocities (see green lines) leads to shifts in all profiles, which, as expected, are larger at the disk center and smaller close to the limb. Additionally, the Q/I and U/I profiles show clear enhancements in the line core, as well as asymmetries which increase from the limb to the disk center. These effects result from the presence of velocity gradients and become more pronounced the steeper the gradients in the line formation region (see Fig. 8 for Model D). Our work highlights that bulk velocities and magnetic fields have a combined action on the amplitude of scattering polarization signals and in general their individual contributions cannot be easily distinguished.
 |
Fig. 5. Results for model A: Emergent intensity I (upper row), Q/I (middle row) and U/I (lower row) profiles for the Ca I 4227 Å line, at μ = 0.03 (left column), μ = 0.38 (middle column), and μ = 0.96 (right column). Each panel shows the results obtained in the absence of magnetic fields and bulk velocities (black lines), including the model’s height-dependent magnetic field (red lines), and including the model’s height-dependent magnetic and bulk velocity fields (green lines). The reference direction for positive Stokes Q is the parallel to the closest limb. |
Figure 7 presents an interesting and rather counter-intuitive feature particular to Model C, which is the enhancement of the amplitude of the line-core Q/I peak induced by the magnetic field at μ = 0.03. This behavior, which may appear surprising given that the Hanle effect typically produces a depolarization at the limb, is probably due to the particular variation of the magnetic field intensity and orientation with height in this specific model. An additional feature in this atmospheric model is the sharp peak on the blue side of the U/I profile for μ = 0.03 (see bottom left panel in Fig. 7). The origin of this feature has been carefully analysed and numerical instabilities were excluded. Similar analyses were carried out to assess the reliability of other small spectral features in the polarization profiles. Figure 8 presents a remarkable aspect particular to Model D. When the velocity field of this model (which has a very steep gradient in the line formation region) is included, the I profile at μ = 0.03 shows an inverted trough at the core. An in-depth study of these findings is ongoing and will be presented in the future.
5. Conclusions
Considering the benchmark case of the Ca I 4227 Å line, we applied a new numerical approach for modeling the intensity and polarization profiles of strong resonance lines taking AD PRD effects into account. The presented work, formulated for the case of a two-level atom, has the double aim of proving the suitability of the approach to handle dynamic scenarios of increasing complexity and of investigating the impact of plasma bulk velocities on the broad scattering polarization signals of chromospheric lines. A number of valuable contributions have already addressed the important role of the dynamics of the solar plasma on scattering polarization, but most of them either consider the limit of CRD or included AD PRD effects in simplified atmospheric models (e.g., isothermal or with cylindrical symmetry). In this investigation, we considered non-homogeneous 1D atmospheric models (both semi-empirical and extracted from 3D MHD simulations) that include vertical bulk velocities and inclined magnetic fields, which break the cylindrical symmetry of the problem.
The results of this study confirm the strong impact of the dynamics of the solar plasma on the emergent spectral line radiation. In particular, scattering polarization signals are heavily affected by the presence of bulk velocity gradients in the line formation region, as pointed out in previous works. The calculated Q/I and U/I profiles actually show all the expected traits of the presence of bulk motions, namely, wavelength shifts, enhancements of the line-core polarization, and prominent asymmetries in the wing signals. The possibility of considering atmospheric models with increasingly complex thermal, dynamic, and magnetic structures allowed us to further unveil the diversity of features that can appear in the emergent radiation. Interesting examples are the substructure in the core of the intensity profile obtained at μ = 0.03 in Model D, which is characterized by a very steep velocity gradient in the line formation region, and the increased amplitude of the line-core Q/I signal found in Model C when a magnetic field is included. Overall, our study emphasizes the complexity of disentangling the signatures of bulk velocities and magnetic fields in the emergent scattering polarization profiles. All these physical mechanisms thus need to be taken into account when trying to infer information from the inversion of spectropolarimetric observations (e.g., Li et al. 2022).
Finally, this investigation has allowed us to assess the suitability of the solution strategy and implementation for dynamic scenarios. This facilitates the ongoing development of a software framework for solving the non-LTE RT problem for polarized radiation in realistic 3D models of the solar atmosphere, while taking AD PRD effects into account (Benedusi et al. 2023).
The problem is formulated in a right-handed Cartesian reference system with the z-axis directed along the vertical. Any vector is specified through its modulus and polar angles (inclination and azimuth). The inclination θ is measured with respect to the vertical. The azimuth χ is measured counterclockwise in the x − y plane from the x-axis for an observer standing in the positive range of the z-axis.
Acknowledgments
The financial support by the Swiss National Science Foundation (SNSF) through grant CRSII5_180238 is gratefully acknowledged as well as the invaluable comments of Han Uitenbroek.
References
- Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2017, ApJ, 836, 6 [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2018, ApJ, 854, 150 [Google Scholar]
- Anusha, L. S., Nagendra, K. N., Bianda, M., et al. 2011, ApJ, 737, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Belluzzi, L., & Trujillo Bueno, J. 2014, A&A, 564, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedusi, P., Janett, G., Belluzzi, L., & Krause, R. 2021, A&A, 655, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedusi, P., Janett, G., Riva, G., Belluzzi, L., & Krause, R. 2022, A&A, 664, A197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedusi, P., Riva, S., Zulian, P., et al. 2023, J. Comput. Phys., 112013 [NASA ADS] [CrossRef] [Google Scholar]
- Bianda, M., Solanki, S. K., & Stenflo, J. O. 1998, A&A, 331, 760 [NASA ADS] [Google Scholar]
- Bommier, V. 1997a, A&A, 328, 706 [NASA ADS] [Google Scholar]
- Bommier, V. 1997b, A&A, 328, 726 [NASA ADS] [Google Scholar]
- Brückner, G. 1963, Z. Astrophys., 58, 73 [Google Scholar]
- Capozzi, E., Ballester, E. A., Belluzzi, L., et al. 2020, A&A, 641, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capozzi, E., Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2022, A&A, 657, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlin, E. S., & Bianda, M. 2017, ApJ, 843, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, E. S., Manso Sainz, R., Asensio Ramos, A., & Trujillo Bueno, J. 2012, ApJ, 751, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, E. S., Asensio Ramos, A., & Trujillo Bueno, J. 2013, ApJ, 764, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- del Pino Alemán, T., Trujillo Bueno, J., Štěpán, J., & Shchukina, N. 2018, ApJ, 863, 164 [CrossRef] [Google Scholar]
- del Pino Alemán, T., Trujillo Bueno, J., Casini, R., & Manso Sainz, R. 2020, ApJ, 891, 91 [CrossRef] [Google Scholar]
- Dumont, S., Pecker, J.-C., & Omont, A. 1973, Sol. Phys., 28, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Faurobert-Scholl, M. 1992, A&A, 258, 521 [NASA ADS] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1991, ApJ, 377, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H. G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Frisch, H. 1996, Sol. Phys., 164, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Y., Thompson, P., Wirzburger, J., et al. 2021, Acta Astronaut., 179, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. W. 2006, in Solar Polarization 4, eds. R. Casini, & B. W. Lites, ASP Conf. Ser., 358, 419 [NASA ADS] [Google Scholar]
- Hummer, D. G. 1962, MNRAS, 125, 21 [Google Scholar]
- Janett, G., & Paganini, A. 2018, ApJ, 857, 91 [Google Scholar]
- Janett, G., Carlin, E. S., Steiner, O., & Belluzzi, L. 2017a, ApJ, 840, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Janett, G., Steiner, O., & Belluzzi, L. 2017b, ApJ, 845, 104 [Google Scholar]
- Janett, G., Steiner, O., & Belluzzi, L. 2018, ApJ, 865, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Janett, G., Alsina Ballester, E., Guerreiro, N., et al. 2021a, A&A, 655, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janett, G., Benedusi, P., Belluzzi, L., & Krause, R. 2021b, A&A, 655, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janett, G., Benedusi, P., & Riva, F. 2024, A&A, 682, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaume Bestard, J., Trujillo Bueno, J., Štěpán, J., & del Pino Alemán, T. 2021, ApJ, 909, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, in Polarization in Spectral Lines, (Dordrecht: Kluwer Academic Publishers), Astrophys. Space Sci. Lib., 307 [Google Scholar]
- Li, H., del Pino Alemán, T., Trujillo Bueno, J., & Casini, R. 2022, ApJ, 933, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Manso Sainz, R., & Trujillo Bueno, J. 2010, ApJ, 722, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Megha, A., Sampoorna, M., Nagendra, K. N., Anusha, L. S., & Sankarasubramanian, K. 2019, ApJ, 879, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Megha, A., Sampoorna, M., Nagendra, K. N., Anusha, L. S., & Sankarasubramanian, K. 2020, ApJ, 903, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres (W.H: Freeman) [Google Scholar]
- Milić, I., & Faurobert, M. 2014, A&A, 571, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Nagendra, K. N. 1996, Sol. Phys., 164, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Nagendra, K. N. 2019, ASP Conf. Ser., 526, 99 [Google Scholar]
- Priest, E. 2014, Magnetohydrodynamics of the Sun (Cambridge University Press) [Google Scholar]
- Rees, D. E., Murphy, G. A., & Durrant, C. J. 1989, ApJ, 339, 1093 [Google Scholar]
- Rimmele, T. R., Warner, M., Keil, S. L., et al. 2020, Sol. Phys., 295, 172 [Google Scholar]
- Riva, S., Guerreiro, N., Janett, G., et al. 2023, A&A, 679, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sampoorna, M., & Nagendra, K. N. 2015, IAU Symp., 305, 387 [NASA ADS] [Google Scholar]
- Sampoorna, M., & Nagendra, K. N. 2016, ApJ, 833, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Sampoorna, M., Nagendra, K. N., & Stenflo, J. O. 2017, ApJ, 844, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., de la Cruz Rodríguez, J., Asensio Ramos, A., Trujillo Bueno, J., & Ruiz Cobo, B. 2015, A&A, 577, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K., Riethmüller, T. L., Barthol, P., et al. 2017, ApJS, 229, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1974, Sol. Phys., 37, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. 1994, in Solar Magnetic Fields: Polarized Radiation Diagnostics, (Berlin: Springer), Astrophys. Space Sci. Lib., 189 [CrossRef] [Google Scholar]
- Stenflo, J. O., Baur, T. G., & Elmore, D. F. 1980, A&A, 84, 60 [NASA ADS] [Google Scholar]
- Supriya, H. D., Smitha, H. N., Nagendra, K. N., et al. 2014, ApJ, 793, 42 [Google Scholar]
- Thompson, M. 2014, Front. Astron. Space Sci., 1, 1 [CrossRef] [Google Scholar]
- Trujillo Bueno, J. 2001, ASP Conf. Ser., 236, 161 [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Trujillo Bueno, J., Landi Degl’Innocenti, E., & Belluzzi, L. 2017, Space Sci. Rev., 210, 183 [CrossRef] [Google Scholar]
- Uitenbroek, H. 2001, ApJ, 557, 389 [Google Scholar]
- Štěpán, J., & Trujillo Bueno, J. 2013, A&A, 557, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Štěpán, J., & Trujillo Bueno, J. 2016, ApJ, 826, L10 [Google Scholar]
- Štěpán, J., Trujillo Bueno, J., Leenaarts, J., & Carlsson, M. 2015, ApJ, 803, 65 [CrossRef] [Google Scholar]
- Wiehr, E. 1975, A&A, 38, 303 [NASA ADS] [Google Scholar]
- Wiehr, E. 1978, A&A, 67, 257 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1. Fractional polarization Q/I (upper panels) and U/I (lower panels) profiles for the Ca I 4227 Å line calculated at μ = 0.38 in the absence (solid lines) and in the presence (dashed lines) of a height-independent vertical bulk velocity of −10 km s−1. The profiles are obtained both neglecting (black lines) and taking into account (red lines) the impact of a height-independent horizontal magnetic field (θB = π/2, χB = 0) with strength B = 10 G (left column) and B = 30 G (right column). The calculations are performed in the FAL-C atmospheric model. The reference direction for positive Stokes Q is the parallel to the limb. |
| In the text | |
 |
Fig. 2. Bulk velocity profiles with constant vertical gradients α (blue line) and 2α (red line), with α = 0.009 s−1. The black and grey curves display the height at which the optical depth, as a function of frequency, is unity, for μ = 0.96 and μ = 0.03, respectively. |
| In the text | |
 |
Fig. 3. Fractional polarization Q/I (upper panels) and U/I (lower panels) profiles for the Ca I 4227 Å line calculated at μ = 0.38 in the static case (solid lines, label v0) and in the presence of vertical bulk velocities with constant gradients (dashed lines). The velocity profiles of Fig. 2, with gradients α (label vα) and 2α (label v2α) are considered. The calculations are performed both for the unmagnetized case (black lines, label B0) and including a height-independent horizontal (θB = π/2, χB = 0) magnetic field (red lines) with strength B = 10 G (label B1) and B = 30 G (label B2). The calculations are performed in the FAL-C atmospheric model. The reference direction for positive Stokes Q is the parallel to the limb. |
| In the text | |
 |
Fig. 4. Temperature (left panel), vertical component of the bulk velocity (central panel), and magnetic field strength (right panel) as a function of height for the four considered atmospheric models (see legend). The vertical dashed lines indicate the height where the optical depth at the line center wavelength is unity for μ = 0.03. The models are vertical columns extracted from a 3D snapshot of an MHD simulation performed with the Bifrost code. |
| In the text | |
 |
Fig. 5. Results for model A: Emergent intensity I (upper row), Q/I (middle row) and U/I (lower row) profiles for the Ca I 4227 Å line, at μ = 0.03 (left column), μ = 0.38 (middle column), and μ = 0.96 (right column). Each panel shows the results obtained in the absence of magnetic fields and bulk velocities (black lines), including the model’s height-dependent magnetic field (red lines), and including the model’s height-dependent magnetic and bulk velocity fields (green lines). The reference direction for positive Stokes Q is the parallel to the closest limb. |
| In the text | |
 |
Fig. 6. Same as Fig. 5, but for Model B. |
| In the text | |
 |
Fig. 7. Same as Fig. 5, but for Model C. |
| In the text | |
 |
Fig. 8. Same as Fig. 5, but for Model D. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



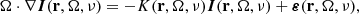
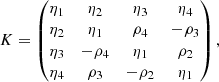
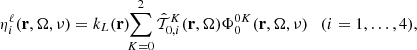
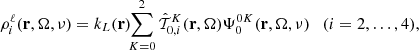
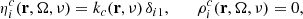
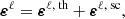
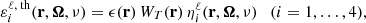
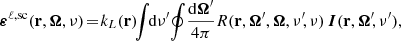
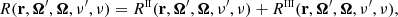
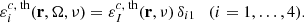
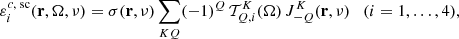
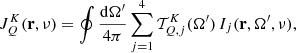
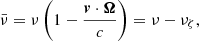
![$$ \begin{aligned}&I(z_{\min },\theta ,\chi ,\nu ) = B_T,\quad \text{ for} \ \theta \in [0, \pi /2), \forall \chi , \forall \nu ,\\&I(z_{\max },\theta ,\chi ,\nu ) = 0,\quad \ \ \text{ for} \ \theta \in (\pi /2, \pi ], \forall \chi , \forall \nu , \end{aligned} $$](/articles/aa/full_html/2024/03/aa46399-23/aa46399-23-eq27.gif)
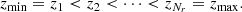
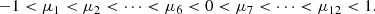
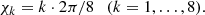
![$$ \begin{aligned}=[4224{\,\AA },4230{\,\AA }]\end{aligned} $$](/articles/aa/full_html/2024/03/aa46399-23/aa46399-23-eq32.gif)
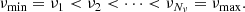
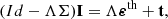
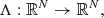
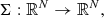
![$$ \begin{aligned}\approx [-100\,\mathrm{km},2200\,\mathrm{km}],\end{aligned} $$](/articles/aa/full_html/2024/03/aa46399-23/aa46399-23-eq41.gif)