| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 16 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348471 | |
| Published online | 06 February 2024 | |
Examining the nature of the ultraluminous X-ray source Holmberg II X-1
1
Università degli Studi di Palermo, Dipartimento di Fisica e Chimica, Via Archirafi 36, 90123 Palermo, Italy
e-mail: francesco.barra@unipa.it
2
INAF/IASF Palermo, Via Ugo La Malfa 153, 90146 Palermo, Italy
3
Department of Physics & Astronomy, University of Southampton, Southampton SO17 1BJ, UK
4
Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
5
Centre for Extragalactic Astronomy & Dept of Physics, Durham University, South Road, Durham DH1 3LE, UK
Received:
2
November
2023
Accepted:
22
November
2023
We present a comprehensive spectral analysis of the ultraluminous X-ray source Holmberg II X-1 using broadband and high-resolution X-ray spectra taken with the XMM-Newton satellite over a period of 19 yr, taking advantage of data from a recent campaign. We tested several models for the broadband spectra, including a double thermal component provided a reasonable description for the continuum between 0.3 and 10 keV and enabled us to constrain the properties of the accretion disc. The luminosity–temperature trends of the inner and outer disc components broadly agree with the expectations for a thin disc, although the exact values of the slopes are slightly sensitive to the adopted model. However, all tested models show L − T trends that deviate from a power law above a bolometric luminosity of about 5 × 1039 erg s−1, particularly for the hot thermal component associated with the inner accretion flow. Assuming that such deviations are due to the accretion rate exceeding its Eddington limit or, most likely, the super-critical rate, a compact object with a mass of 16–36 M⊙ was inferred, specifically, a stellar-mass black hole. The time-averaged (2021) high-resolution spectra present narrow emission lines at 1 keV primarily from Ne IX-X and a very strong at 0.5 keV from N VII, which indicate Ne–N-rich gas with non-solar abundances. This favours a nitrogen-rich donor star, such as a blue or red supergiant, which has escaped from its native stellar cluster characterised by a low-metallicity environment.
Key words: accretion / accretion disks / X-rays: binaries / X-rays: individuals: Holmberg II X-1
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Ultraluminous X-ray sources (ULXs) are off-nucleus, point-like extragalactic sources with X-ray luminosities above LX > 1039 erg s−1 (for recent reviews, see Pinto & Walton 2023; King et al. 2023), brighter than the Eddington limit for a black hole of 10 M⊙, resulting from accretion onto a compact object. The luminosity of a ULX can reach 1041 erg s−1 in the X-ray band (0.3–10 keV) alone has led to many conjectures on the nature of the compact object. In fact, ULXs, have been theorized to be black holes (BHs) with a mass greater than 10 and up to 105 M⊙ (intermediate mass black hole, IMBH, Miller et al. 2004), with ESO 243-49 HLX-1 as the best candidate (Webb et al. 2012). However, the discovery of X-ray pulsations in a fraction of the population of ULXs revealed that at least some ULXs are powered by neutron stars (NSs). Notable examples are M 82 X-2 (Bachetti et al. 2014), NGC 5907 ULX-1 (Fürst et al. 2016) and NGC 7793 P13 (Israel et al. 2017). The number of persistent ULXs which exhibit pulsations is currently six, with another six transient pulsars whose X-ray luminosity has exceeded 1039 erg s−1 for a short period (see Table 2 in King et al. 2023). Given the fact that about 30 systems have sufficiently good statistics to detect pulsations, the fraction of NS-powered ULXs might be around 30% or above (Rodríguez Castillo et al. 2020, see also Middleton & King 2017; King & Lasota 2020).
Overall, ULX spectra are marked out by a curvature in the range 2–10 keV and a soft excess below 2 keV (the ‘ultraluminous state’, Gladstone et al. 2009) and can typically be classified into three different regimes, according to their spectral slope Γ in the 0.3–10 keV energy range: the soft ultraluminous (SUL) regime for Γ > 2, hard ultraluminous regime (HUL) for Γ < 2 and broadened disc (BD), the latter where the X-ray spectrum presents a single peak and is dominated by a blackbody-like component in the 2–5 keV band (Sutton et al. 2013). Several ULXs sometimes show spectra switching between these regimes (Middleton et al. 2015a; Gúrpide et al. 2021b). If the ULX spectrum is dominated by a cool blackbody-like component with kT ≲ 0.1 keV, with a bolometric luminosity LBOL > 1039 erg s−1, and little detected emission above 1 keV, the source can also be defined as an ultraluminous supersoft source (ULS or SSUL). The presence of a weak hard tail in the X-ray band in ULSs suggests they are accreting in a super-Eddington regime, but seen at high inclinations through the wind cone obscuring the innermost part of the disc (Middleton et al. 2015a; Gúrpide et al. 2021b). This is confirmed by the presence of sharp drops in flux or dips in light curves, followed by spectral softening (e.g., Stobbart et al. 2004; Urquhart & Soria 2016; Alston et al. 2021). These winds were suggested in several ULXs due to the presence of unresolved and intense features in CCD spectra, typically at lower energies (< 2 keV; Stobbart et al. 2006; Sutton et al. 2015; Middleton et al. 2014, 2015b, although this was recently detected in two cases above 6 keV: Walton et al. 2016; Brightman et al. 2023). Critically, they have since been unambiguously resolved in several ULXs with the XMM-Newton Reflection Grating Spectrometers (RGS, hereafter, e.g., Pinto et al. 2016, 2017; Kosec et al. 2018a,b). The Doppler blueshift of the absorption lines unveiled the long-sought relativistic (0.1 − 0.2 c) winds predicted by theoretical simulations of super-Eddington accretion discs (Takeuchi et al. 2013); for a recent review on ULX winds, we refer to Pinto & Walton (2023).
1.1. HOLMBERG II X-1
Holmberg II X-1 (hereafter, Ho II X-1), located at a distance of 3.05 Mpc1 in the Holmberg II dwarf galaxy, is characterized by a luminosity in the X-ray band (0.3–10 keV) LX ≥ 1039 erg s−1 and up to 1040 erg s−1 (Gúrpide et al. 2021b). It is possible to see from Fig. 1 that the X-ray spectrum of Ho II X-1 tends to fit in between the spectra of bright SUL and the hardest ULXs.
 |
Fig. 1. Comparison of some ULX XMM-Newton/EPIC-PN spectra from the harder to softer (top to bottom). Ho II X-1 spectrum is the brightest below 1 keV. Adapted from Barra et al. (2022). |
Importantly, observations of Ho II X-1 in the radio reveals collimated jets, which are at least partially responsible for inflating the surrounding nebula, carrying a kinetic luminosity of > 1039 erg s−1 (Cseh et al. 2014). In this sense, Ho II X-1 is expected to be analogous to the extreme Galactic source, SS433 (Fabrika 2004), the latter considered to be an edge-on ULX (Begelman et al. 2006; Middleton et al. 2021) and proposed to harbour a fairly massive black hole of ≥25 M⊙ (Cseh et al. 2014), in agreement with previous X-ray spectral analysis (Goad et al. 2006). In fact, by comparing the spectral modelling of the microquasar GRS 1915+105 at very high state (e.g, the χ class) with that of Ho II X-1, a compact object of few tens of Solar masses radiating at or above its Eddington limit was forecasted for the latter case and, however, no more massive of 100 M⊙ (Goad et al. 2006).
A relative uncrowded field around Ho II X-1 permitted the identification of an optical counterpart. In fact, the presence of a He IIλ4686 nebula, with a luminosity of L ∼ 1036 erg s−1, and a point-like young companion star consistent with a spectral type O4V or B3 Ib were reported (Pakull & Mirioni 2002; Kaaret et al. 2004; Kaaret 2005; however, see Tao et al. 2012).
The unknown demographic of ULXs, and difficulty to separate them spectrally (see Walton et al. 2018; Mills et al. 2023, although several alternatives have been suggested, e.g., Middleton et al. 2019, 2023; Song et al. 2020), makes Ho II X-1 an important target given its probable black hole nature. Specifically, we can learn about the nature of the accretion flow by comparing the properties of the wind and evolution of the spectrum to other ULXs and sub-Eddington sources.
This paper is structured as follows. In Sect. 2, we report on the observations of the source and the spectral modelling in Sect. 3. In Sect. 4, we present results on the lines seen by RGS. In Sect. 5, we discuss our results and give our conclusions in Sect. 6. All uncertainties are at 1σ (68% level).
2. Observations and data reduction
Ho II X-1 was observed by XMM-Newton 20 times over a period of 19 yr (see Table 1), benefiting from a recent 250 ks campain (PI: Middleton). This high quality data-set spread over time has allowed us to probe both short-term (hours-to-days) and long-term (months-to-years) variability. The raw data were obtained from the XMM-Newton Science Archive (XSA)2 and were reduced with the Science Analysis System (SAS) version 18.0.03. In the observations with ID 0112522201 and 0112522301, the satellite’s filters were closed and the observation ID 0843840201 was in timing mode and badly calibrated, which leaves 17 well-exposed observations. We used recent calibration files (October 2022).
XMM-Newton observations of Holmberg II X-1.
The events files of the EPIC camera were generated through the epproc and emproc tasks and filtered thereafter for the flaring particle background at the recommended threshold above 10 keV (count rate < 0.5 ct s−1 for EPIC-PN and < 0.35 ct s−1 for EPIC-MOS 1 and 2). We selected the counts in the source and background regions using the evselect task and corrected the light curves with the epiclccor task. We chose a circular region for the source of 30 arcsec radius centered on the Chandra X-ray position (RA: 08h 19m 28.99s, Dec: +70d 42m 19.37s); whilst for the background, we selected a larger circular region a few arc minutes away from the source, but still on the same chip, avoiding contamination from the copper ring and away from chip gaps. The rmfgen and arfgen tasks were used to generate response matrices and effective area files. For illustration, the concatenated 0.3–10 keV EPIC-PN light curves of the individual observations are shown in Fig. 2. The XMM-Newton light curves confirm that the source brightness changed by a factor of 2–3 within the observations and up to a factor of 6–7 between observations. Defining the hardness ratio (HR) as the ratio between the counts in the 1.5–10 keV and the 0.3–10 keV energy bands, we see that the HR is generally higher (i.e., the spectrum is harder) when the source is brighter and lower in proximity of the dips (Fig. 2 lower-left and right panels), which is typical in ULXs (e.g., Weng & Feng 2018). The EPIC-PN spectra of all the observations are shown in Fig. 3, divided by the instrument response but without any spectral model.
 |
Fig. 2. Concatenated XMM-Newton EPIC-PN light curves for the 17 well-exposed observations of Ho II X-1 and the hardness ratio below (here defined as the (1.5–10 keV/0.3–10 keV counts ratio) from 2002 to 2021 with time bins of 1 ks (left)). The vertical dotted lines were included in order to separate each of the individual XMM observations. Hardness-intensity diagram where the points belonging to the same observation have the same colour (right). |
 |
Fig. 3. EPIC-PN spectra for the 17 well-exposed observations of Ho II X-1. MOS 1,2 spectra are not shown for clarity purposes. |
The archival RGS spectra were already thoroughly studied in a previous work (Kosec et al. 2018a, 2021); we therefore focused on the new data from the 2021 campaign. The RGS data of all observations were reduced according to the standard procedure with the rgsproc pipeline in SAS. We filtered out periods of high background by selecting intervals in the light curves of the RGS 1,2 CCD 9 with a count rate below 0.2 ct s−1.
We extracted the 1st-order RGS spectra in a cross-dispersion region of 0.8 arcmin width, centred on the same source coordinates used for extracting the EPIC spectra. The background regions were chosen by selecting photons outside of 98% of the source point-spread-function. ULX RGS spectra typically require at least 100 ks exposure time to achieve the number of counts necessary to detect narrow lines (ideally ∼10 000 counts, e.g., Pinto et al. 2016). We stacked the 1st-order RGS 1 and 2 spectra from the 2021 observations with rgscombine for a total exposure time of 210 ks and about 25 900 net source counts. This is amongst the 10 deepest RGS spectra available for a ULX (for a comparison see Fig. 5 in Kosec et al. 2021). RGS operates in the 0.33–2.5 keV band, but the source is above the background (and the instrumental foreground) between 0.4 and 2.0 keV and we use this band for the analysis. The search for spectral features requires accurate knowledge of the continuum shape; therefore, we also stacked the 2021 MOS 1, MOS 2, and pn spectra to cover the 2–10 keV band. In the end, we produced four time-averaged 2021 spectra: one for each camera (RGS, MOS1, MOS2, and pn).
3. Broadband X-ray spectroscopy
For the purpose of studying the behaviour of the source, we initially proceed to analyse the data collected by the CCDs. The spectra were modelled with the SPEX fitting package v3.07.03 (Kaastra et al. 1996). EPIC PN and MOS 1,2 spectra were rebinned to at least 1/3 of the spectral resolution and with at least 25 counts per bin using the task SPECGROUP. All the models take into account the absorption from the circumstellar and interstellar medium by using the hot model (with a gas temperature of 10−4 keV, which yields a quasi-neutral gas phase in SPEX). All spectral models also account for the source redshift (z = 0.000524). EPIC MOS/PN for each observation spectra were fitted simultaneously as they overlap in the 0.3–10 keV band including a multiplicative constant to account for the well known ≲5% cross-calibration uncertainties.
3.1. Testing different spectral models for Obs. 02004710101
In order to describe Ho II X-1 spectrum, we proceed to test several models on the longest observation (obs. ID 0200470101), which provides the largest number of counts, with double thermal models, as common procedure in ULX spectra modelling (Gúrpide et al. 2021a; Pintore et al. 2015; Stobbart et al. 2006; Walton et al. 2018). In particular we want to compare our results with those obtained by Walton et al. (2015) and Gúrpide et al. (2021a).
The spectral models that we used to describe the data were different combinations of the following components: blackbody emission (bb) and blackbody modified by coherent Compton scattering (mbb) often used for super-Eddington discs (Pinto et al. 2017; Barra et al. 2022), multi-temperature disc blackbody (dbb) and inverse comptonisation of soft photons in a hot plasma (comt), typically used for Eddington-limited Galactic XRBs but sometimes also for ULXs (Done et al. 2007; Middleton et al. 2015a). In order to fit emission and absorption lines we used Gaussian lines. A summary of the models tested is below. All models are corrected for the redshift and neutral interstellar absorption:
-
RHB(B): single or multiple blackbody emission;
-
RHBD: cool blackbody emission and a warmer disc blackbody;
-
RHDD: a double disc- blackbody model;
-
RHBM: a modified single blackbody model;
-
RHMM: a modified double blackbody model;
-
RHBCom: blackbody plus comptonisation;
-
RHDCom: disc blackbody plus comptonisation;
-
RHBDP: a powerlaw with a cutoff (etau) added to the RHBD model;
-
RHMMG(G): one or more Gaussian lines included to the blackbody fit to account for emission or absorption lines.
Fits to the data with continuum-only models (i.e., without Gaussians) show residuals around 1 keV, 0.75 keV, and 0.5 keV (as previously reported in several ULXs including Ho II X-1: Middleton et al. 2015b). These lines are resolved with the high-resolution RGS spectrometers, as explained below.
The spectral fits of Obs. ID 0200470101 are reported in Figs. 4 and 5. In particular, the double thermal component bb+mbb (RHBM model, top panel) does not give a good description of the data above 6 keV. For the power law in the bb+dbb+pow model (RHBDP), we adopted a cutoff (etau) at 7.9 keV and a spectral index of 0.59 (Walton et al. 2020). Although the RHDCom and RHBDP models provide a slightly better fit, we prefer to continue with the mbb+mbb model (RHMM model, Fig. 5, top panel), with temperatures of ∼0.37 keV and ∼1.6 keV for the cool and hot component respectively, in order to study the behaviour of the thermal components with the bolometric luminosity (Fig. 10) and the radii. The latter model provides also a lower χ2 with respect to the dbb+dbb model (RHDD model, Fig. 5, bottom panel). The cool (hot) thermal component accounts for the mainly soft (hard) X-ray emission, coming from the wind and the outer (inner) part of the disc.
 |
Fig. 4. Spectral fits to the EPIC PN and MOS 1,2 data using the RHBM model (top panel), the RHDCom (middle panel), and the RHBDP models (bottom panel) for the Obs. ID 0200470101. The dashed dotted lines indicate the background spectra. |
 |
Fig. 5. Spectral fits to the EPIC PN and MOS 1,2 data using the RHMM model (top panel) and RHDD model (bottom panel) for Obs. ID 0200470101. |
The results from our fits of observation ID 02004710101 are shown in Table 2. We also test the other models mentioned in the Table 2, but we were unable to constrain the parameters of the hard tail of the comptonisation (see Sect. 3.2). This is likely due to the lack of high-energy coverage (E > 10 keV) during this epoch. By adding, in fact, NuSTAR data, an additional component (comt or pow) is needed to describe the spectrum at high energies (see Sect. 5.1). The total column density in several models assumes values, particularly for the RHBDP model (see Table A.1, perhaps due to the emission lines at 0.5 keV), smaller than the Galactic value (see Table 2). Thus, we decided to restrict the column density to have a minimum value of 5 × 1020 cm−2.
Results from the modelling of the XMM-Newton spectra of Holmberg II X-1 with the data of Obs. ID 0200470101.
3.2. Spectral modelling of individual observations
We show in Fig. 3 the EPIC PN spectra of the 17 observations analysed. As with the longest observation, we fit the EPIC PN and MOS 1,2 spectra of all observations with all models described before. The primary goal is to understand the trends of the spectral components with the time and, then, to check for systematic effects on the results from the model choice. In particular, testing several models, we obtained NH values ranging from (0.5 to 0.8)×1021 cm−2. This was likely due to some dependence with the model applied (i.e., the curvature adopted in the soft band). For clarity and comparison with other sources, we focus on the best-fit RHMM model in the main text. The first fits with NH left free yielded values consistent within 2–3σ. We therefore rerun them by fixing the column density at the average value of 7 × 1020 cm−2. The results are shown in Table 3 for all the observations. The best-fit RHMM model provided a good representation of the data with the exception of the well known residuals at 0.5 keV, 0.75 keV, and 1 keV. However, we stress that these residuals do not dramatically vary using the models with comptonisation (see e.g., Fig. 4) and are later fitted by adding three Gaussian lines to the RHMM model (see Sect. 3.3).
Results of the best fit RHMM model for all observations.
3.3. Variability of the wind features
The strength of the spectral features and their variability in Holmberg II X-1 were studied by using the mbb + mbb model by adding three Gaussian lines (RHMMGGG model). We fixed the line width to 1 eV for all three Gaussian lines since EPIC spectra lack the necessary spectral resolution around 1 keV. The energy centroids were left free to vary and they agreed within the error bars with 0.75 for the absorption line, 0.5 and 1.0 keV for the emission lines between the various observations. The normalisations of the Gaussian lines for the seventeen spectra are shown in Fig. 6. They do not show significant variability within the uncertainties; the 0.5 keV emission line weakly brightens, whilst the 0.75 keV feature is undetected at the highest luminosities.
 |
Fig. 6. Normalisation of the Gaussian lines vs bolometric luminosity for the three-Gaussian model (RHMMGGG) fits. The negative normalisations refer to absorption lines. The red dotted lines in each panel refer to the average value of the Gaussian normalization. |
We preferred to use the simplified RHMM(GGG) model in order to avoid complicating the continuum model by adding the powerlaw component for the hard X-ray tail because for such a model and the one with the Comptonisation several parameters remain unconstrained. However, we have tested the addition of three Gaussian lines to the RHBDP model over the 17 spectra and obtained results consistent with those of the RHMMGGG.
4. High-resolution X-ray spectroscopy
In order to search for and identify narrow lines, we regrouped the 2021 time-averaged EPIC PN, MOS1, MOS2, and RGS spectra according to the optimal binning discussed in Kaastra & Bleeker (2016), which adopts energy bins of at least 1/3 of the spectral resolutions and a minimal, positive, number of counts per bin. Therefore, in the current analysis, we fit the data by reducing the Cash statistic (C-stat; Cash 1979). Our binning choice smooths the background spectra in the energy range with low statistics and removes narrow spurious features. However, we notice that both the RGS and EPIC stacked spectra have high statistics and, as a result, the regrouping turns out to be similar to the standard 1/3 of the spectral resolution in the region of interest for the narrow lines (0.4–2 keV). Moreover, further tests that were performed by rebinning to at least 25 counts per bin, using the SAS task specgroup showed consistent results.
The RGS and EPIC time-averaged spectra are shown in Fig. 7; they exhibit a very strong, narrow emission feature around 24 Å close to the dominant 1s-2p transition of the N VII. There are additional features between 12 and 13 Å compatible with Ne IX-X transitions and a drop below 12 Å similar to that detected in the ULXs NGC 1313 X-1 and NGC 5408 X-1 (Pinto et al. 2016).
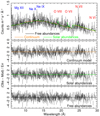 |
Fig. 7. 2021 time-averaged RGS spectrum and residuals for fits with the RHMM continuum-only model, the photoionised wind with Solar abundances, and with free abundances (shown from top to bottom). Rest-frame centroids of the typical, dominant H-/He-like transitions are labelled and colour-coded according to the contribution from the hot (blue) and cool (red) phases. Note: there is a drop below 12 Å and the strong N VII line. |
In a previous work, the EPIC data in the 0.4–1.77 keV band were ignored to avoid smearing the narrow features and unnecessarily boosting model degeneracy owing to worse energy resolution for the EPIC (see e.g., Pinto et al. 2021). We adopted the same approach and fitted the EPIC and RGS stacked spectra with the RHMM model. In all fits, the parameters of the spectral components and the ISM absorber were coupled among the EPIC and RGS models. However, we left the overall normalisations of the MOS 1,2 and RGS models free to vary with respect to the PN to account for the typical ≲5% cross-calibration uncertainties. The RGS + EPIC continuum model provides an overall C-stat of 844 (and a comparable χ2) for 725 deg of freedom (the detailed RGS spectrum is shown in Fig. 7).
4.1. Gaussian line scan
In order to search for and identify the strongest lines, we performed a standard scan of the spectra with a moving Gaussian line following the approach used in Pinto et al. (2016). We adopted a logarithmic grid of 1000 points with energies between 0.4 (30 Å) and 10 keV (1.24 Å). This provided an energy step that is comparable to the RGS and EPIC resolving power in their energy range. We tested line widths ranging from 100 to 10 000 km s−1. At each energy we recorded the ΔC improvement to the best-fit continuum model and measured the single-trial significance as the square root of the ΔC. To easily distinguish between emission and absorption lines, we multiplied the 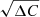 by the sign of the Gaussian normalisation.
by the sign of the Gaussian normalisation.
The results of the line scan obtained for the 2021 time-averaged stacked RGS + EPIC spectra are shown in Fig. 8. We highlight that in the 0.4 − 2 keV energy band (7 − 30 Å) only the RGS data is considered. The line scan picked out the strong emission-like feature near 0.5 keV (N VII) and a weaker one at 0.9 keV (Ne IX), as well as some faint absorption-like features between 0.6 and 0.8 keV and above 1 keV. This shows a very good agreement with the CCD-quality EPIC spectra and supports our former approach of using three Gaussian lines (see Fig. 4 and Table 2). The results of the Gaussian line scan are very similar to those obtained for NGC 1313 X-1 (Pinto et al. 2016) but the striking, close to rest-frame, N VII emission line would indicate a nitrogen-rich material, which we discuss later.
 |
Fig. 8. Gaussian line scan for the 2021 time-averaged RGS (0.4–2 keV) and EPIC (2–10 keV) spectra and different line widths. |
The single-trial line significance of the strongest feature from N VII is around 5σ, which is very high. Accounting for the look-elsewhere effect and multiplying for the number of free bins within the whole 6–30 Å band (which would however not apply here since the line is close to rest) we can exclude at 3.5σ that the feature is due to the noise (Pinto et al. 2016). The absorption features, if real, are offset from the dominant 1s-2p transitions and, therefore, have weaker significance as previously reported for the archival data (Kosec et al. 2018a, 2021; Pinto et al. 2020a).
4.2. Grids of the photoionisation model
Previous works have performed multi-dimensional scans of plasma models to fit multiple lines simultaneously, combining their individual improvements with respect to the continuum model (see, e.g., Kosec et al. 2018a; Pinto et al. 2020b). This technique has the advantage of (a) preventing the fits from getting stuck in local minima and (b) searching for multiple components or phases. Here, we tried the same approach with the aim of locating velocity shifts in the emission and absorption lines. In order to avoid strong degeneracy in the plasma models, we adopted Solar abundances. This will have an impact on the overall spectral improvement due to the obvious nitrogen over-abundance; however, we address this when directly fitting the RGS spectra (see Sect. 4.3).
The broadband spectral energy distribution (SED) was estimated by extrapolating the best-fit continuum model between 0.001 and 100 keV. We then computed the (photo-) ionisation balance with the SPEX component pion parameterised by the standard ionisation parameter, ξ = Lion/(nH R2). Here, Lion is the ionising luminosity (measured between 13.6 eV and 13.6 keV), nH is the hydrogen number density and R is the distance from the ionising source. We also computed the stability (or S) curve, namely, the relationship between the temperature and the ratio between the radiation and the thermal pressure, Ξ = F/(nHckT) = 19 222 ξ/T. The SED, ionisation balance T − ξ and S curves are shown in Fig. A.1. The branches of the S curve with a positive (negative) gradient are characterised by thermally stable (unstable) gas. Further technical details are provided in Fig. A.1.
Following Pinto et al. (2021), we created grids of emission and absorption models using pion and xabs components in SPEX, respectively. For the line-emitting gas, we performed a multi-dimensional scan by adopting a logarithmic grid of ionisation parameters (log ξ between 0 and 5 with steps of 0.1) and line-of-sight velocities, vLOS, between −0.1c (blueshift) and +0.1c (redshift, with steps of 500 km s−1). We adopted a velocity dispersion, vσ, of 1000 km s−1 which is the typical width of the features found in the Gaussian line scan (see Fig. 8). As mentioned above, abundances were chosen to be Solar which saves a great deal of computing time. For the grids of absorption line models, we chose a vLOS range up to −0.3c as done in previous work. The only free parameter for the pion and xabs components is the column density, NH.
We applied the automated routine scanning through the emission and absorption model grids fitting the Ho II X-1 2021 time-averaged EPIC and RGS spectra, again using the RGS only in the 0.4−1.77 keV band. The results are shown in Fig. A.2 in the 2D parameter space of line-of-sight velocity and ionisation parameter. The colour is coded according to the improvement relative to the continuum-only fit. Negative velocities refer to blueshifts or motion towards the observer. The emission model grids hint at a multi-phase gas. The solution with log ξ = 0 and vLOS = −0.018c is likely an artefact as it would require very low ionisation species moving at high velocities. The solutions that yield quasi-rest-frame emission lines are more feasible and would indicate the presence of cool (O VII–N VII) and hot (O VIII – Ne IX) gas describing the emission-like features shown in Fig. 8. The absorption model grids favour a solution of plasma outflowing at 0.03c with a high ionisation state (log ξ = 3.2), which is similar to the hotter solution for the emission lines. An alternative solution for the absorption lines yields parameters very similar to NGC 1313 X-1 (log ξ = 2.8 and vLOS = −0.19c) and a former tentative detection shown in Pinto et al. (2020a) for Holmberg II X-1 archival data (log ξ = 3.3 and vLOS = −0.20c). As expected, the changes in the C-stat are not very large, most likely because all the emission grids underpredict the N VII emission line. Instead, for the absorption features, the low C-stat is likely due to both adopted abundances and the spectral stacking between different observations which smears out the wind features in the LOS. The latter would smooth the lines because they are expected to be variable over timescales of days (Kosec et al. 2018a, 2021; Pinto et al. 2020b). All observations were taken between three and five days apart, which prevented us from building two to three large stacks ad hoc, and the signal-to-noise ratio (S/N) of each spectrum is not sufficient to search for lines.
4.3. Photoionised and hybrid plasma modelling
In order to obtain tighter constraints on the plasma models, we proceeded to model the RGS + EPIC spectra by adding absorption and emission components of plasma in photoionisation equilibrium with spectral parameters starting from the solutions found in the scans (Fig. A.2), at first keeping Solar abundances.
The addition of a single photoionised absorbing xabs component onto the continuum model confirmed the results from the scan with vLOS = −0.033 ± 0.003c, log ξ [erg s−1 cm] = 3.3 ± 0.1, vσ = 1500 ± 1000 km s−1 and NH = (1.1 ± 0.4)×1022 cm−2. The fit improvement is still rather small (ΔC = 16) for it to be a significant detection.
The addition of a photoionised emitting pion component also provides results consistent with the model scan. In particular, vLOS = +0.006 ± 0.002c and log ξ [erg s−1 cm] = 1.15 ± 0.15. However, the fit with Solar abundances was poor (ΔC = 13) since it over-predicted the O VIII 19 Å line and under-predicted the N VII 24.8 Å. A single pion component is also not able to fit all features, particularly those from higher ionic species such as Ne IX-X around 12–13 Å. A better description of these features are achieved by adding another pion component with log ξ [erg s−1 cm] = 2.9 ± 0.2 at the same velocities. This fit with two emitting and one absorbing components with Solar abundances is shown in Fig. 7 and corresponds to an overall ΔC = 34 improvement with respect to the continuum model for 10 deg of freedom, which is a rather small improvement (C/d.o.f. = 811/715).
4.3.1. Non-solar abundances and alternative plasma models
Finally, we attempted at fitting again the RGS and EPIC spectra by releasing some of the abundances of the photoionised gas but keeping them coupled among the emission and absorption components. However, due to the weakness of most spectral features, we couple some of the elemental abundances. In the Gaussian line scan (and visually in the RGS spectrum), the N VII, Ne IX-X, and Mg XII lines appear significantly stronger than those from O VII-VIII. We therefore fitted the spectra by coupling the N, Ne, and Mg abundances and releasing the iron (which follows different evolutionary scenarios than the other three). Oxygen is kept fixed to Solar as hydrogen does not produce any lines in the 0.3–10 keV energy range. This provided a best fit with a final C/d.o.f. = 784/713 (see Fig. 7, top and bottom panel). This corresponds to a large improvement with respect to the continuum, ΔC = 60 (with ΔC = 22, 11, and 27 from the xabs, the hot and cool pion components, respectively). The contribution of each component is therefore increased over the continuum when releasing the abundances despite being coupled with each other. There is substantial co-dependence between the xabs (stronger) and the pion (weaker) components. We obtained the following abundance ratios: O/H = 1 (fixed), Fe/H = 3, C–N–Ne–Mg/H = 14 with uncertainties of ∼50%.
In principle, the emission lines could be produced by plasmas in different conditions such as shocks within the ULX wind (especially for the higher ionisation component which may be supersonic) or photoionisation balance. The features can indeed be described with nearly indistinguishable fits and comparable C-stat values by substituting the two pion components with two collisionally-ionised emission components (cie in SPEX, with temperatures kTcool ∼ 0.17 and kThot ∼ 1.2 keV and the abundance ratios being consistent with those obtained with the two pion components).
5. Discussion
This paper focuses on the physical processes that might cause spectral transitions in Ho II X-1 and in general in ULXs. We first discuss the broadband properties of the XMM-Newton and NuSTAR spectra, as well as the possible presence of a hard tail above 10 keV. Then we search for a correlation between the total luminosity, the temperature, and the radius of the thermal components. Finally, we compare our results with those obtained for different sources and discuss the properties of the wind.
5.1. Broadband spectral properties
Ho II X-1 shows a flux variability of a factor of 2–3 within a given observation and a factor of up to 6–7 in different observations, as shown in Fig. 2 (left-top panel). In addition there are a few flux drops (the phenomenon is more evident in long-term monitoring with Swift/XRT, see e.g., Gúrpide et al. 2021b) of the order of few ks due probably to wind optically-thick clumps that briefly obscure the innermost part of the disc, with a reduction of the spectral hardness (Fig. 2, lower-left panel). This can be caused either by an increase in the accretion rate or by the precession of the disc, although the lack of periodicity in the phenomenon would favour the former one. Our results showed that the spectrum is well described with a double thermal model (two mbb components), in agreement with the general properties of intermediate-soft ULX spectra (Sutton et al. 2013). Alternative models using comptonisation for the hotter component provides comparably good fits but the parameters are unconstrained for low-statistics short observations and, therefore, we focussed primarily on the double thermal model.
We also tested a model with a third component (a cutoff powerlaw) describing the hard tail in the fashion of a NS magnetosphere and obtained similar results. However, we note that it mainly affects the band beyond 10 keV (see, e.g., Walton et al. 2015); therefore, the powerlaw parameters could not be well constrained. In order to determine the role of such third component, we also fit the XMM-Newton data (Obs. ID 0724810101-301) with the simultaneous NuSTAR data (Obs. ID 30001031002/3, 30001031005; see Fig. A.3), which were retrieved from Walton et al. (2015). These data were fitted with the RHMM model with a cutoff powerlaw (Ecutoff = 7.9 keV and Γ = 0.59; see Walton et al. 2020). The cool and hot component are characterized by a temperature ∼0.3 keV and ∼1.8 keV, respectively. As expected, the addition of a third component (pow+etau), does not dramatically influence the constraints of the two mbb components.
The data collected by NuSTAR above 7 keV are overwhelmed by the background when the source is at low flux. Constraints on the hard energy tail above 10 keV are very hard to set. A constraint on the properties of such hard X-ray component in the low-flux regime is necessary to understand its nature and help distinguish between a magnetosphere typical of a NS and a small corona around a BH. In order to study this, we proceeded to perform a low-flux simulations of Ho II X-1 spectra with the HEX-P satellite (see Fig. 9, response matrices from July 2023; Stern et al. 2023). HEX-P will be able to detect the source at 10 keV and above, which is necessary to place constraints on the tail and the inner part of the disc. This may unveil the presence of an accretion column and the nature of the compact object.
 |
Fig. 9. HEX-P simulation with an exposure time of 500 ks. The simulated spectra were generated using the RHBDP model (with the parameters obtained from the best fit of the low-flux Obs. ID 0864550201). The spectra were then fitted with the disc blackbody + comptonisation components (RHDCom model, χ2/d.o.f. = 485/356). The disc blackbody and the comptonisation components are represented in orange and blue, respectively. The residuals show that a third component is necessary to describe the simulated spectra above 8 keV. |
The thermal components appear hotter at higher luminosity (see Table 3) maybe due to an increase of the accretion rate Ṁ or a better view of the inner accretion flow (wind photosphere less dense due to a precessing disc, although this should not be the case for the cooler, outer, component).
5.2. Luminosity–temperature relations
In order to unveil any of the disc’s structural changes over time, we examined the luminosity vs. temperature (L − T) behaviour for both thermal components of the best fit RHMM model. In particular, it is useful to compare the L − T trends with the theoretical expectations for a thin disc model with a constant emitting area (L∝ T4; Shakura & Sunyaev 1973) and advection dominated model (L ∝ T2; Watarai & Mineshige 2001). For each thermal component we estimate the bolometric luminosity extrapolating down to 0.001 and up 1000 keV from the best-fit models. There is a small uncertainty in the total luminosity owing to our ignorance of the UV flux, but we only expect those to make a minor contribution for such a bright intermediate-hardness ULX (see discussion on the spectral energy distribution in Pinto & Walton 2023). The luminosity–temperature results are reported in Fig. 10 and Table 4, which clearly show positive correlations between luminosity and temperature for both components. In addition to the RHMM model, we also explore the results for the RHBDP model in Appendix A. We find a general agreement although there are some deviations with respect to the RHMM model for the hot thermal component at high luminosities.
 |
Fig. 10. Luminosity–temperature plot for the RHMM model. Bolometric luminosity (0.001–1000 keV) versus temperature for the cool (in blue) and hot (in orange) components. The black solid, the black-dotted, and the red dashed lines represent the regression line and the two theoretical models of the slim disc and thin disc models, respectively. |
Pearsons–Spearman coefficients and slope from the regression least square for the L − T trends, for both cool and hot components, by using the best fit values of the RHMM model.
The L − T plot confirms that the source becomes spectrally harder when brighter as seen in Fig. 2 (lower-left panel). In both plots and for each thermal component we compute the regression lines of the L − T points. We also quantify the L − T trends by computing the Pearsons and Sperman correlation coefficients by using scipy.stats.pearsonsr and scipy.stats.spearmanr routines in PYTHON. These are reported in Table 4: for both thermal components, a strong correlation is suggested. At low luminosities, the L − T trends of all models broadly agree with a L ∝ T4 relationship as predicted for Eddington-limited thin discs (Shakura & Sunyaev 1973). There are significant deviations at high luminosities, especially for the hot component which exhibit a large scatter from a regression line (see Fig. 10). The exact trend depends on the model adopted. For the RHBDP model (Fig. A.4, middle panel), the temperatures are lower than predicted for a thin disc with constant emitting area, suggesting a possible expansion of the disc and/or a contribution to the emission from the wind. Instead, for the RHMM model, the scatter is less clear although it seems to saturate (see Fig. 10). These deviations appear for a total bolometric luminosity greater than 5 × 1039 erg s−1. As seen for NGC 55 ULX-1 (Barra et al. 2022), deviations from sub-Eddington behaviour could potentially be used to place rough constraints on the mass of the compact object. If we assume the deviations are due to the fact the source is exceeding the Eddington limit 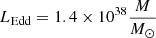 erg s−1 or the critical luminosity
erg s−1 or the critical luminosity 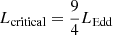 (Poutanen et al. 2007), we estimated a mass for the compact object ranging between 16 and 36 M⊙. This would suggest a stellar mass black hole in agreement with estimates inferred from the powerful radio jets from this source (see Cseh et al. 2014). However, deviations were found in Galactic XRBs when the source exceeded 30% of the Eddington luminosity (e.g., Steiner et al. 2009; Lančová et al. 2019), which might indicate a slightly more massive BH. Given that Holmberg II X-1 always shows the typical characteristics of a ULX (soft spectra, turnover, high luminosity and lines) it is more likely that the accretion rate is around Eddington and it exceeds the critical value during these deviations, altering the structure of the accretion disc.
(Poutanen et al. 2007), we estimated a mass for the compact object ranging between 16 and 36 M⊙. This would suggest a stellar mass black hole in agreement with estimates inferred from the powerful radio jets from this source (see Cseh et al. 2014). However, deviations were found in Galactic XRBs when the source exceeded 30% of the Eddington luminosity (e.g., Steiner et al. 2009; Lančová et al. 2019), which might indicate a slightly more massive BH. Given that Holmberg II X-1 always shows the typical characteristics of a ULX (soft spectra, turnover, high luminosity and lines) it is more likely that the accretion rate is around Eddington and it exceeds the critical value during these deviations, altering the structure of the accretion disc.
5.3. Radius–temperature relation
We show the radius–temperature (R − T) plots for the RHMM model in Fig. 11; however, we do not present the results for the other models because they are consistent within the uncertainties. The radii are estimated from the relation between the luminosity and the temperature of a blackbody. In all cases, there is no clear trend between radii of the two thermal components and their temperatures. The radii would appear constant at confidence levels within 90–95%. The radius of the hot component has a value ranging between 50 and 90 km; instead, the radius of the cold component is ranging in the range 1500 and 2200 km. The tests performed with the alternative models yield a similar order of magnitude for such radii. By assuming an average value of the mass of the compact object of 25 M⊙ (from the range obtained through the luminosity–temperature relation), these correspond to 2 RG and 80 RG, respectively. The values found might refer to the inner and the outer part of the disc, respectively. Indeed, for Ṁ ∼ ṀCritical = 9/4 ṀEdd, we would obtain a spherisation radius of 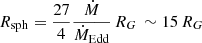 .
.
 |
Fig. 11. Radius–temperature plot for the thermal components of the RHMM model. The coloured circles scale with the luminosity of the source in each specific observation. |
We note that in the case of a NS or very small BH accretor (up to a few times M⊙) the rate would be highly super-Eddington, Rsph would be larger by a factor of a few, and the models might fail to reproduce the exact values of disc radii and temperature, although our L − T trends would disfavour it.
5.4. Comparison with other ULXs
A similar study was performed for the soft ultraluminous X-ray source NGC 55 ULX-1 (Barra et al. 2022). Also, in this case, the regression line in the L − T plot agreed with the thin disc and the deviations implied a 6–14 M⊙ stellar-mass black hole and smaller Ṁ. In the case of NGC 1313 X-1, deviations from a single L − T track are present for the hot component linked to an obscuring wind or a change of the disc scale height; whereas there is no L − T correlation for the cool component, perhaps due to the modelling of hotter part of the accretion disc (see, e.g., Walton et al. 2020; Miller et al. 2013; although see Gúrpide et al. 2021a for the caveats and related to the modelling and the associated trends).
Ho II X-1 is similar to NGC 5204 X-1 regarding repeated transitions between the three classical ULXs regimes (HUL, SUL and SSUL/ULS; Gúrpide et al. 2021b). However, according to their long-term Swift/XRT light curves, Ho II X-1 remains around a 0.3–10 keV count rate of 0.15–0.20 c s−1 for most of the time with an isolated long episode with the count rate switching between 0.05 and 0.30 c s−1, which correspond to SUL and SSUL regimes, respectively.
These transitions may be driven by geometrical effects (the funnel structure) and wind due to a varying accretion rate and/or precession, as well as a line of sight grazing the wind allowing for a rapid transition between the SUL-SSUL regimes. These transitions were also found during the epochs of highest flux of the ULXs NGC 55 ULX-1 and NGC 247 ULX-1 (see e.g., Stobbart et al. 2004; D’Aí et al. 2021), although for these two ULXs, and especially the latter, the flux drops are more prominent. This would therefore suggest a lower inclination angle in Ho II X-1 (for a comparable Ṁ) or a lower accretion rate and, therefore, a thinner wind along the line of sight.
5.5. Wind properties
X-ray spectra from CCD / imaging detectors such as EPIC have lower spectral resolution than gratings, but they provide a far greater number of counts and may therefore yield important results provided that there are some dominant and reasonably well-isolated lines. This is the case for the feature at 0.5 keV from N VII (which is well resolved in the RGS stacked spectrum, see Fig. 7). Its flux weakly correlates with the source bolometric luminosity, see Fig. 6. This line is produced along with others by a cool plasma (see Fig. 7), which is perhaps associated with the cool thermal component. If such trend were to be confirmed with deep flux-resolved RGS spectra, it would suggest an increase of the accretion rate (as the L − T trends indicate) because a changing viewing angle or ionisation would produce an opposite trend. A parallel paper will also make use of NICER and Swift X-ray observations and data from other energy bands to investigate the variability of the dominant spectral features on timescales from a few days to several weeks.
The physical modelling of the spectral lines present in the RGS data indicate evidence for a multiphase plasma. The phase responsible for the strong N VII emission line (log ξ ∼ 1) appears to be distinct from the two hotter absorption and emitting components (log ξ ∼ 3). Although the T − Ξ curve appears generally stable to thermal perturbations, there is evidence for some possible points of instability which would indeed split the plasma into multiple phases (see Fig. A.1). The two hot components are not independent of each other due to the low velocity of the absorbing gas; in other words, the inclusion of one weakens the significance of the other although the absorption is clearly stronger. This may also be due to the detailed shapes of the features which resemble those of P Cygni profiles, especially that of Mg XII and Ne X at 8.4 and 12.1 Å, respectively (see Fig. 7). However, the statistics are not strong enough to make actual claims of P-Cygni profiles although the physical modelling would confirm them through weakly-redshifted emission and blue-shifted absorption (see Fig. A.2). Due to this mutual dependence, the fit of the abundances (but also the strength of the N VII line) makes performing Monte Carlo simulations for the physical models (as done in previous work, e.g., Kosec et al. 2021; Pinto et al. 2021) challenging because degeneracy prevents a meaningful parameter space exploration. The fact that the spectral improvement of each component is boosted when releasing the abundances despite being coupled with each other would suggest that they are all present. Indeed, Goad et al. (2006) first report on the presence of a possible emission excess from the O VII triplet around 22 Å in the deepest, individual, RGS spectrum of Ho II X-1 from the archival observation taken in 2004. Moreover, Kosec et al. (2018a) and (later) Kosec et al. (2021) studied these data as well as the 2002–2013 time average RGS spectrum (137 ks) and found features consistent with those reported in this work. The 2021 time averaged RGS spectrum seems to show variability with respect to the archival data (Kosec et al. 2018a, 2021), in which the dominant feature was the O VI line due probably to a variation in the ionisation parameter and so in the luminosity.
The line-emitting plasma components are consistent with being at rest within 2–3σ, each with a velocity dispersion of about 1000–3000 km s−1 which is very similar (albeit cooler or with lower ionisation parameters) to that observed in the ubiquitous winds of Eddington-limited Galactic X-ray binaries (for a review, see Neilsen & Degenaar 2023). This might suggest a common mechanism such as thermal driving (Middleton et al. 2022). From simultaneous fits of the He-like triplets of Mg XI, Ne IX, and (especially) O VII, we obtained a 2σ upper limit on the gas density of about 1.5 × 1011 cm−3 (with the most probable value of 1010 cm−3) in agreement with results by Pinto et al. (2020a) for the ULX NGC 1313 X-1 and for line-emitting plasma of Galactic XRBs (Psaradaki et al. 2018), which reinforces our hypothesis for a common mechanism. This was expected given the very weak, undetected, O VII forbidden line at 22.1 Å, with respect to the unresolved resonance and intercombination line complex at 21.6–21.8 Å seen both in the spectrum and the line scan (Figs. 7 and 8). Of course, the wind in Ho II X-1 is more extreme than in XRBs, given that each line-emitting components has an X-ray luminosity, L[0.3 − 10 keV], of about 1038 erg s−1, namely, orders of magnitude higher than in Galactic XRB winds.
The super-solar abundance of nitrogen in the wind of Holmberg II X-1 is most likely a signature of the abundance pattern of the donor companion star. This could provide alternative means for constraining its nature because previous work has shown that the optical and infrared fluxes are strongly affected by the irradiated outer disc and the surrounding nebula, making it difficult to retrieve information on the companion star (Tao et al. 2012; Heida et al. 2016; Lau et al. 2019). N-rich stars with a super-Solar N/Fe ratio are found in low-metallicity environments, with some examples being B-type giant and supergiant stars, as reported for Ho II X-1, where the optical counterpart is consistent with a O/B type companion star (Kaaret et al. 2004), or Wolf-Rayet stars in young star clusters of the Magellanic clouds and similar dwarf galaxies (Lennon et al. 2003; Yarovova et al. 2023). In some cases they might be luminous evolved stars on the asymptotic giant branch (AGB) and more regular red giant stars in the LMC. The latter have been interpreted as the observational evidence of the result of tidally shredded stellar clusters (see Fernández-Trincado et al. 2020). This is supported in the case of Holmberg II X-1 by the discovery of a bow shock, which indicates that the ULX binary system was likely ejected from the nearby young star cluster (Egorov et al. 2017). These results suggest that Holmberg II X-1 system was born into a low-metallicity environment, rich in young and massive stars, later escaping from the native stellar cluster.
6. Conclusions
In this work, we carry out an X-ray spectral analysis to understand the nature of the ultraluminous X-ray source Holmberg II X-1. Two thermal components provide a good description of the 0.3–10 keV spectra with the hotter component broadened perhaps by Compton scattering. Both thermal components become hotter at higher luminosities indicating an increase in the accretion rate (most likely) or a clearer view of the inner part of the accretion flow due to a disc precession. The trends between the bolometric luminosity and temperature of each component broadly agree, at low luminosities, with the L ∝ T4 relationship expected from Eddington-limited thin disc. Deviations are seen above 5 × 1039 erg s−1 which are likely due to the accretion rate exceeding the supercritical rate; this would imply a black hole with a mass ranging between 16 and 36 M⊙ as the compact object. Our results suggest that the two thermal components unveil the portions of the disc inside (hotter) and outside (cooler) the spherisation radius where the wind is launched, in agreement with the super-Eddington scenario. The wind abundance pattern strongly favours a nitrogen-rich donor star, likely a supergiant, which has escaped from its native stellar cluster characterised by a low-metallicity environment.
Acknowledgments
This work is based on observations obtained with XMM-Newton an ESA science mission funded by ESA Member States and the USA (NASA). C.P. acknowledges support for PRIN MUR 2022 SEAWIND 2022Y2T94C and INAF LG 2023 BLOSSOM. T.D.S. acknowledges support from PRIN-INAF 2019 with the project “Probing the geometry of accretion: from theory to observations” (PI: Belloni). T.P.R. acknowledges funding from STFC as part of the consolidated grants ST/T000244/1 and ST/X001075/1. All the data and software used in this work are publicly available from ESA’s XMM-Newton science Archive (XSA, https://www.cosmos.esa.int/web/XMM-Newton/xsa) and NASA’s HEASARC archive (https://heasarc.gsfc.nasa.gov/). Our spectral codes and automated scanning routines are publicly available and can be found on GitHub (https://github.com/ciropinto1982).
References
- Alston, W. N., Pinto, C., Barret, D., et al. 2021, MNRAS, 505, 3722 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Barra, F., Pinto, C., Walton, D. J., et al. 2022, MNRAS, 516, 3972 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [Google Scholar]
- Brightman, M., Kosec, P., Fuerst, F., et al. 2023, Am. Astron. Soc. Meet. Abstr., 55, 214.04 [NASA ADS] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Cseh, D., Kaaret, P., Corbel, S., et al. 2014, MNRAS, 439, L1 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aí, A., Pinto, C., Pintore, F., et al. 2021, MNRAS, 507, 5567 [CrossRef] [Google Scholar]
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [Google Scholar]
- Egorov, O. V., Lozinskaya, T. A., & Moiseev, A. V. 2017, MNRAS, 467, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrika, S. 2004, Astrophys. Space Phys. Rev., 12, 1 [NASA ADS] [Google Scholar]
- Fernández-Trincado, J. G., Beers, T. C., Minniti, D., et al. 2020, ApJ, 903, L17 [Google Scholar]
- Fürst, F., Walton, D. J., Harrison, F. A., et al. 2016, ApJ, 831, L14 [Google Scholar]
- Gladstone, J. C., Roberts, T. P., & Done, C. 2009, MNRAS, 397, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Goad, M. R., Roberts, T. P., Reeves, J. N., & Uttley, P. 2006, MNRAS, 365, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Gúrpide, A., Godet, O., Koliopanos, F., Webb, N., & Olive, J. F. 2021a, A&A, 649, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gúrpide, A., Godet, O., Vasilopoulos, G., Webb, N. A., & Olive, J. F. 2021b, A&A, 654, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heida, M., Jonker, P. G., Torres, M. A. P., et al. 2016, MNRAS, 459, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belfiore, A., Stella, L., et al. 2017, Science, 355, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P. 2005, Chin. J. Astron. Astrophys., 5, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Ward, M. J., & Zezas, A. 2004, MNRAS, 351, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, eds. K. Yamashita, & T. Watanabe (Tokyo: Universal Academy Press, Inc.), 411 [Google Scholar]
- King, A., & Lasota, J.-P. 2020, MNRAS, 494, 3611 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96, 101672P [CrossRef] [Google Scholar]
- Kosec, P., Pinto, C., Fabian, A. C., & Walton, D. J. 2018a, MNRAS, 473, 5680 [NASA ADS] [CrossRef] [Google Scholar]
- Kosec, P., Pinto, C., Walton, D. J., et al. 2018b, MNRAS, 479, 3978 [NASA ADS] [Google Scholar]
- Kosec, P., Pinto, C., Reynolds, C. S., et al. 2021, MNRAS, 508, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- Lančová, D., Abarca, D., Kluźniak, W., et al. 2019, ApJ, 884, L37 [CrossRef] [Google Scholar]
- Lau, R. M., Heida, M., Walton, D. J., et al. 2019, ApJ, 878, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Lennon, D. J., Dufton, P. L., & Crowley, C. 2003, A&A, 398, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middleton, M. J., & King, A. 2017, MNRAS, 470, L69 [Google Scholar]
- Middleton, M. J., Walton, D. J., Roberts, T. P., & Heil, L. 2014, MNRAS, 438, L51 [Google Scholar]
- Middleton, M. J., Heil, L., Pintore, F., Walton, D. J., & Roberts, T. P. 2015a, MNRAS, 447, 3243 [Google Scholar]
- Middleton, M. J., Walton, D. J., Fabian, A., et al. 2015b, MNRAS, 454, 3134 [Google Scholar]
- Middleton, M. J., Fragile, P. C., Ingram, A., & Roberts, T. P. 2019, MNRAS, 489, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M. J., Walton, D. J., Alston, W., et al. 2021, MNRAS, 506, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M. J., Higginbottom, N., Knigge, C., Khan, N., & Wiktorowicz, G. 2022, MNRAS, 509, 1119 [Google Scholar]
- Middleton, M., Gúrpide, A., & Walton, D. J. 2023, MNRAS, 519, 2224 [Google Scholar]
- Miller, J. M., Fabian, A. C., & Miller, M. C. 2004, ApJ, 607, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Walton, D. J., King, A. L., et al. 2013, ApJ, 776, L36 [Google Scholar]
- Mills, B. S., Davis, S. W., Jiang, Y. F., & Middleton, M. J. 2023, ApJ, submitted [arXiv:2304.07977] [Google Scholar]
- Neilsen, J., & Degenaar, N. 2023, arXiv e-prints [arXiv:2304.05412] [Google Scholar]
- Pakull, M. W., & Mirioni, L. 2002, arXiv e-prints [arXiv:astro-ph/0202488] [Google Scholar]
- Pinto, C., & Walton, D. J. 2023, arXiv e-prints [arXiv:2302.00006] [Google Scholar]
- Pinto, C., Middleton, M. J., & Fabian, A. C. 2016, Nature, 533, 64 [Google Scholar]
- Pinto, C., Alston, W., Soria, R., et al. 2017, MNRAS, 468, 2865 [Google Scholar]
- Pinto, C., Mehdipour, M., Walton, D. J., et al. 2020a, MNRAS, 491, 5702 [Google Scholar]
- Pinto, C., Walton, D. J., Kara, E., et al. 2020b, MNRAS, 492, 4646 [Google Scholar]
- Pinto, C., Soria, R., Walton, D. J., et al. 2021, MNRAS, 505, 5058 [NASA ADS] [CrossRef] [Google Scholar]
- Pintore, F., Esposito, P., Zampieri, L., Motta, S., & Wolter, A. 2015, MNRAS, 448, 1153 [Google Scholar]
- Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Psaradaki, I., Costantini, E., Mehdipour, M., & Díaz Trigo, M. 2018, A&A, 620, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez Castillo, G. A., Israel, G. L., Belfiore, A., et al. 2020, ApJ, 895, 60 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Song, X., Walton, D. J., Lansbury, G. B., et al. 2020, MNRAS, 491, 1260 [Google Scholar]
- Steiner, J. F., McClintock, J. E., Remillard, R. A., Narayan, R., & Gou, L. 2009, ApJ, 701, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Madsen, K., & Garcia, J. 2023, BAAS, 55, 4 [NASA ADS] [Google Scholar]
- Stobbart, A. M., Roberts, T. P., & Warwick, R. S. 2004, MNRAS, 351, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Stobbart, A. M., Roberts, T. P., & Warwick, R. S. 2006, MNRAS, 370, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, A. D., Roberts, T. P., & Middleton, M. J. 2013, MNRAS, 435, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, A. D., Roberts, T. P., & Middleton, M. J. 2015, ApJ, 814, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Takeuchi, S., Ohsuga, K., & Mineshige, S. 2013, PASJ, 65, 88 [Google Scholar]
- Tao, L., Kaaret, P., Feng, H., & Grisé, F. 2012, ApJ, 750, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, R., & Soria, R. 2016, MNRAS, 456, 1859 [Google Scholar]
- Walton, D. J., Middleton, M. J., Rana, V., et al. 2015, ApJ, 806, 65 [Google Scholar]
- Walton, D. J., Middleton, M. J., Pinto, C., et al. 2016, ApJ, 826, L26 [Google Scholar]
- Walton, D. J., Fürst, F., Heida, M., et al. 2018, ApJ, 856, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Pinto, C., Nowak, M., et al. 2020, MNRAS, 494, 6012 [Google Scholar]
- Watarai, K.-Y., & Mineshige, S. 2001, PASJ, 53, 915 [NASA ADS] [Google Scholar]
- Webb, N., Cseh, D., Lenc, E., et al. 2012, Science, 337, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Weng, S.-S., & Feng, H. 2018, ApJ, 853, 115 [Google Scholar]
- Yarovova, A. D., Egorov, O. V., Moiseev, A. V., & Maryeva, O. V. 2023, MNRAS, 518, 2256 [Google Scholar]
Appendix A: Additional figures and tables
Fig. A.1 shows the spectral energy distribution (SED, top panel), photo-ionisation balance (middle panel), and log T − Ξ stability curves (bottom panel).
 |
Fig. A.1. Spectral energy distribution (SED, top panel), photo-ionisation balance (middle panel), and log T − Ξ stability curves (bottom panel). The plasma is expected to be generally stable. Solid segments show the best-fit solutions for photoionised absorption (xabs) and hot/cool emission (pion) components. |
Fig. A.2 shows the photoionised emission (top panel) and absorption (bottom panel) model scan.
 |
Fig. A.2. Top (bottom) panel: photoionised emission (absorption) model scan, right panel. These scans adopted a line-broadening of 1,000 km/s and Solar abundances. This of course decreased the chance of fake detections but, on the other hand, decreased the improvement to the spectral continuum as some elements, such as nitrogen, are clearly super-Solar with respect to e.g. oxygen (see Fig. 7). |
Fig. A.3 shows the spectral modelling of the XMM-Newton & NuSTAR simultaneous data with the RHMM model plus a cutoff powerlaw.
 |
Fig. A.3. XMM-Newton (obsid: 0724810301) + NuSTAR simultaneous data (2013). The spectra were fitted with a RHMM model plus a cutoff powerlaw. For the description of NuSTAR data is necessary the addition of a third component for the high-energy tail. |
Fig. A.4 shows the luminosity-temperature trends with the following models: RHBM (top panel), RHDD model (middle panel) and RHBDP (bottom panel) model.
 |
Fig. A.4. L-T plots for the RHBM model (top panel), RHDD model (middle panel) and RHBDP model (bottom panel). Labels are the same as in Fig. 10. |
Table A.1 reports the spectral fits results with RHBPD model for all observations.
Results of the RHBDP model for all observations.
Table A.2 reports the slopes of the regression least square and the Pearsons/Spearman coefficients for the L-T trends with the following models: RHBM, RHBDP, and RHDD model.
Pearsons/Spearman coefficients and slope from the regression least square for the L-T trends, for both cool and hot components, by using the best fit values of the RHBM, RHBDP, and RHDD models.
All Tables
Results from the modelling of the XMM-Newton spectra of Holmberg II X-1 with the data of Obs. ID 0200470101.
Pearsons–Spearman coefficients and slope from the regression least square for the L − T trends, for both cool and hot components, by using the best fit values of the RHMM model.
Pearsons/Spearman coefficients and slope from the regression least square for the L-T trends, for both cool and hot components, by using the best fit values of the RHBM, RHBDP, and RHDD models.
All Figures
 |
Fig. 1. Comparison of some ULX XMM-Newton/EPIC-PN spectra from the harder to softer (top to bottom). Ho II X-1 spectrum is the brightest below 1 keV. Adapted from Barra et al. (2022). |
| In the text | |
 |
Fig. 2. Concatenated XMM-Newton EPIC-PN light curves for the 17 well-exposed observations of Ho II X-1 and the hardness ratio below (here defined as the (1.5–10 keV/0.3–10 keV counts ratio) from 2002 to 2021 with time bins of 1 ks (left)). The vertical dotted lines were included in order to separate each of the individual XMM observations. Hardness-intensity diagram where the points belonging to the same observation have the same colour (right). |
| In the text | |
 |
Fig. 3. EPIC-PN spectra for the 17 well-exposed observations of Ho II X-1. MOS 1,2 spectra are not shown for clarity purposes. |
| In the text | |
 |
Fig. 4. Spectral fits to the EPIC PN and MOS 1,2 data using the RHBM model (top panel), the RHDCom (middle panel), and the RHBDP models (bottom panel) for the Obs. ID 0200470101. The dashed dotted lines indicate the background spectra. |
| In the text | |
 |
Fig. 5. Spectral fits to the EPIC PN and MOS 1,2 data using the RHMM model (top panel) and RHDD model (bottom panel) for Obs. ID 0200470101. |
| In the text | |
 |
Fig. 6. Normalisation of the Gaussian lines vs bolometric luminosity for the three-Gaussian model (RHMMGGG) fits. The negative normalisations refer to absorption lines. The red dotted lines in each panel refer to the average value of the Gaussian normalization. |
| In the text | |
 |
Fig. 7. 2021 time-averaged RGS spectrum and residuals for fits with the RHMM continuum-only model, the photoionised wind with Solar abundances, and with free abundances (shown from top to bottom). Rest-frame centroids of the typical, dominant H-/He-like transitions are labelled and colour-coded according to the contribution from the hot (blue) and cool (red) phases. Note: there is a drop below 12 Å and the strong N VII line. |
| In the text | |
 |
Fig. 8. Gaussian line scan for the 2021 time-averaged RGS (0.4–2 keV) and EPIC (2–10 keV) spectra and different line widths. |
| In the text | |
 |
Fig. 9. HEX-P simulation with an exposure time of 500 ks. The simulated spectra were generated using the RHBDP model (with the parameters obtained from the best fit of the low-flux Obs. ID 0864550201). The spectra were then fitted with the disc blackbody + comptonisation components (RHDCom model, χ2/d.o.f. = 485/356). The disc blackbody and the comptonisation components are represented in orange and blue, respectively. The residuals show that a third component is necessary to describe the simulated spectra above 8 keV. |
| In the text | |
 |
Fig. 10. Luminosity–temperature plot for the RHMM model. Bolometric luminosity (0.001–1000 keV) versus temperature for the cool (in blue) and hot (in orange) components. The black solid, the black-dotted, and the red dashed lines represent the regression line and the two theoretical models of the slim disc and thin disc models, respectively. |
| In the text | |
 |
Fig. 11. Radius–temperature plot for the thermal components of the RHMM model. The coloured circles scale with the luminosity of the source in each specific observation. |
| In the text | |
 |
Fig. A.1. Spectral energy distribution (SED, top panel), photo-ionisation balance (middle panel), and log T − Ξ stability curves (bottom panel). The plasma is expected to be generally stable. Solid segments show the best-fit solutions for photoionised absorption (xabs) and hot/cool emission (pion) components. |
| In the text | |
 |
Fig. A.2. Top (bottom) panel: photoionised emission (absorption) model scan, right panel. These scans adopted a line-broadening of 1,000 km/s and Solar abundances. This of course decreased the chance of fake detections but, on the other hand, decreased the improvement to the spectral continuum as some elements, such as nitrogen, are clearly super-Solar with respect to e.g. oxygen (see Fig. 7). |
| In the text | |
 |
Fig. A.3. XMM-Newton (obsid: 0724810301) + NuSTAR simultaneous data (2013). The spectra were fitted with a RHMM model plus a cutoff powerlaw. For the description of NuSTAR data is necessary the addition of a third component for the high-energy tail. |
| In the text | |
 |
Fig. A.4. L-T plots for the RHBM model (top panel), RHDD model (middle panel) and RHBDP model (bottom panel). Labels are the same as in Fig. 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


