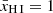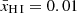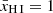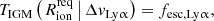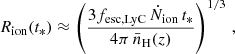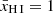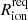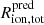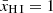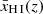| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347176 | |
| Published online | 31 January 2024 | |
Inside the bubble: exploring the environments of reionisation-era Lyman-α emitting galaxies with JADES and FRESCO⋆
1
Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
e-mail: jnw30@cam.ac.uk
2
Cavendish Laboratory, University of Cambridge, 19 JJ Thomson Avenue, Cambridge CB3 0HE, UK
3
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
4
Department of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
5
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
6
Steward Observatory, University of Arizona, 933 N. Cherry Ave., Tucson, AZ 85721, USA
7
AURA for European Space Agency, Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21210, USA
8
Centro de Astrobiología (CAB), CSIC–INTA, Cra. de Ajalvir Km. 4, 28850 Torrejón de Ardoz, Madrid, Spain
9
European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
10
European Space Agency, ESA/ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
11
School of Physics, University of Melbourne, Parkville, 3010 VIC, Australia
12
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Australia
13
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126 Pisa, Italy
14
Sorbonne Université, CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98 bis bd Arago, 75014 Paris, France
15
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
16
Centre for Astrophysics Research, Department of Physics, Astronomy and Mathematics, University of Hertfordshire, Hatfield AL10 9AB, UK
17
Center for Astrophysics | Harvard & Smithsonian, 60 Garden St., Cambridge, MA 02138, USA
18
Department of Astronomy, University of Texas, Austin, TX 78712, USA
19
Department for Astrophysical and Planetary Science, University of Colorado, Boulder, CO 80309, USA
20
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
21
Department of Astronomy and Astrophysics University of California, Santa Cruz, 1156 High Street, Santa Cruz, CA 96054, USA
22
NSF’s National Optical-Infrared Astronomy Research Laboratory, 950 North Cherry Avenue, Tucson, AZ 85719, USA
23
NRC Herzberg, 5071 West Saanich Rd, Victoria, BC V9E 2E7, Canada
Received:
13
June
2023
Accepted:
26
October
2023
We present a study of the environments of 17 Lyman-α emitting galaxies (LAEs) in the reionisation-era (5.8 < z < 8) identified by JWST/NIRSpec as part of the JWST Advanced Deep Extragalactic Survey (JADES). Unless situated in sufficiently (re)ionised regions, Lyman-α emission from these galaxies would be strongly absorbed by neutral gas in the intergalactic medium (IGM). We conservatively estimate sizes of the ionised regions required to reconcile the relatively low Lyman-α velocity offsets (ΔvLyα < 300 km s−1) with moderately high Lyman-α escape fractions (fesc, Lyα > 5%) observed in our sample of LAEs, suggesting the presence of ionised hydrogen along the line of sight towards at least eight out of 17 LAEs. We find minimum physical ‘bubble’ sizes of the order of Rion ∼ 0.1–1 pMpc are required in a patchy reionisation scenario where ionised bubbles containing the LAEs are embedded in a fully neutral IGM. Around half of the LAEs in our sample are found to coincide with large-scale galaxy overdensities seen in FRESCO at z ∼ 5.8–5.9 and z ∼ 7.3, suggesting Lyman-α transmission is strongly enhanced in such overdense regions, and underlining the importance of LAEs as tracers of the first large-scale ionised bubbles. Considering only spectroscopically confirmed galaxies, we find our sample of UV-faint LAEs (MUV ≳ −20 mag) and their direct neighbours are generally not able to produce the required ionised regions based on the Lyman-α transmission properties, suggesting lower-luminosity sources likely play an important role in carving out these bubbles. These observations demonstrate the combined power of JWST multi-object and slitless spectroscopy in acquiring a unique view of the early Universe during cosmic reionisation via the most distant LAEs.
Key words: dark ages / reionization / first stars / large-scale structure of Universe / galaxies: high-redshift
The main data underlying this study are publicly available on https://archive.stsci.edu/hlsp/jades
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Cosmic Dawn marked the formation of the first astrophysical objects a few hundred million years after the Big Bang (z ≳ 15), bringing the Dark Ages to an end and, importantly, setting in motion the process of cosmic reionisation (Dayal & Ferrara 2018). Optical-depth measurements of the cosmic microwave background indicate reionisation reached a midpoint at approximately z ∼ 8, suggesting that this momentous phase transition transpired broadly in the first billion years of cosmic time (e.g. Planck Collaboration VI 2020). In the past decade, various independent methods tracing the neutrality of the intergalactic medium (IGM) have started to further elucidate the timeline and origin of reionisation, indicating the bulk of neutral hydrogen in the Universe was reionised at 6 ≲ z ≲ 10, likely driven by the ionising radiation of star-forming galaxies (Robertson et al. 2015; Finkelstein et al. 2019; Naidu et al. 2020). One powerful probe of the ionising capabilities of reionisation-era galaxies is Lyman-α (Lyα), one of the most prominent electronic transitions of hydrogen (Partridge & Peebles 1967).
Unless the IGM is highly ionised, photons escaping a galaxy at a rest-frame wavelength of λemit ≲ λLyα = 1215.67 Å are nearly entirely scattered out of the line of sight before they redshift away from resonance (Gunn & Peterson 1965). If there is little to no significant evolution in the intrinsic Lyα properties of galaxies, reionisation should therefore be characterised by a rapid decline towards higher redshift of the fraction of galaxies observed to have Lyman-α emission (Furlanetto et al. 2004; Dijkstra 2014; Ouchi et al. 2020). Indeed, a plummeting fraction of Lyman-α emitting galaxies (LAEs) has been interpreted as evidence of a rapidly evolving neutral hydrogen fraction between z ∼ 6 and z ∼ 8 (Stark et al. 2010, 2017; Pentericci et al. 2011; Ono et al. 2012; Caruana et al. 2012, 2014; Treu et al. 2013; Schenker et al. 2014; Tilvi et al. 2014, 2020; Mason et al. 2018b, 2019; Whitler et al. 2020).
Beyond providing global IGM constraints, however, LAEs can be exploited to trace the detailed progression of reionisation. Reionisation has been shown to be an inhomogeneous process (e.g. Pentericci et al. 2014; Becker et al. 2018; Kulkarni et al. 2019; Keating et al. 2020; Bosman et al. 2022), suggesting that galaxies in overdense regions are expected to carve out the first ionised ‘bubbles’ that preferentially allow Lyα emission to be observed when they have grown sufficiently large (e.g. Weinberger et al. 2018; Mason et al. 2018a; Endsley et al. 2021, 2022; Qin et al. 2022; Jung et al. 2022a, 2022b; Leonova et al. 2022). The most distant LAEs therefore form a crucial observational frontier in mapping the reionisation process, providing unique signposts of the first large-scale, ionised patches of the Universe (Hu et al. 2021; Endsley & Stark 2022; Larson et al. 2022; Lu et al. 2023; Trapp et al. 2023; Whitler et al. 2023b).
Building on the legacy of the Hubble Space Telescope (HST), the successful commissioning of JWST (McElwain et al. 2023; Rigby et al. 2023), specifically designed for finding and characterising the first generation of galaxies (Robertson 2022; Gardner et al. 2023), now places us in prime position to address several fundamental questions surrounding reionisation. In particular, with spectroscopic coverage of the rest-frame UV and optical, JWST allows for the unprecedented characterisation of LAEs throughout the epoch of reionisation (EoR) for the first time (Tang et al. 2023; Jung et al. 2023; Witten et al. 2023; Whitler et al. 2023b). Crucially, the JWST/Near-Infrared Spectrograph (NIRSpec; Jakobsen et al. 2022; Böker et al. 2023) possesses the required sensitivity, and particularly the multiplexing capabilities (via its micro-shutter assembly or MSA; Ferruit et al. 2022), to extend pioneering ground-based efforts that were restricted to the few brightest sources (e.g. Ono et al. 2012; Finkelstein et al. 2013; Zitrin et al. 2015; Oesch et al. 2015; Roberts-Borsani et al. 2016). Reaching absolute AB magnitudes in the UV of MUV ∼ −17 mag even without gravitational lensing, JWST finally enables an extensive investigation of the faint-end of the luminosity function to reveal which sources are the dominant drivers of cosmic reionisation (e.g. Saxena et al. 2023b).
Here, we aim to investigate the environments, including potential ionised bubbles, of such faint (MUV ≳ −20 mag) reionisation-era galaxies which have been observed to exhibit Lyα emission in recent JWST measurements (Jones et al. 2023). We restrict this current study to redshifts of z ≳ 5.8, considering the global neutral hydrogen fraction approaches 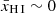 at later times even in ‘late’ reionisation scenarios (e.g. Weinberger et al. 2018, 2019; Zhu et al. 2022). The outline of this work is as follows: in Sect. 2, we discuss the data set considered in this work. Section 3 presents our findings on the potential ionised bubbles surrounding these galaxies and discusses these findings in context of previous works, while Sect. 4 summarises our results. We consistently use a flat ΛCDM cosmology based on the latest results of the Planck Collaboration (i.e. H0 = 67.4 km s−1 Mpc−1, Ωm = 0.315, Ωb = 0.0492; Planck Collaboration VI 2020) and a cosmic hydrogen fraction of fH = 0.76 throughout. On-sky separations of 1″ and 1′ at z = 7 hence correspond to 5.34 physicalkpc (pkpc) and 0.32 physicalMpc (pMpc), respectively. Quoted magnitudes are in the AB system (Oke & Gunn 1983).
at later times even in ‘late’ reionisation scenarios (e.g. Weinberger et al. 2018, 2019; Zhu et al. 2022). The outline of this work is as follows: in Sect. 2, we discuss the data set considered in this work. Section 3 presents our findings on the potential ionised bubbles surrounding these galaxies and discusses these findings in context of previous works, while Sect. 4 summarises our results. We consistently use a flat ΛCDM cosmology based on the latest results of the Planck Collaboration (i.e. H0 = 67.4 km s−1 Mpc−1, Ωm = 0.315, Ωb = 0.0492; Planck Collaboration VI 2020) and a cosmic hydrogen fraction of fH = 0.76 throughout. On-sky separations of 1″ and 1′ at z = 7 hence correspond to 5.34 physicalkpc (pkpc) and 0.32 physicalMpc (pMpc), respectively. Quoted magnitudes are in the AB system (Oke & Gunn 1983).
2. Observations
In the following sections, we discuss several spectroscopic data sets containing both the main LAEs considered in this work as well as the reference sample of galaxies used to characterise their environments. We show their redshift histograms in Fig. 1, while Fig. 2 shows their distribution on the sky.
 |
Fig. 1. Redshift histogram of spectroscopically confirmed galaxies over GOODS-S. Sources confirmed in JADES NIRSpec observations (Sect. 2.1) are shown by the black histogram (Bunker et al. 2023b), while the red distribution is of those identified in FRESCO data (Oesch et al. 2023), discussed in Sect. 2.3. EoR (z ≳ 5.8) LAEs identified in JADES (Jones et al. 2023; Saxena et al. 2023a) are marked by vertical solid-dashed lines, coloured by Lyα rest-frame EW according to the scale on the right. Additional LAEs found at z > 5.5 in the MUSE HUDF surveys (Bacon et al. 2023), discussed in Sect. 2.2, are shown by the light blue distribution. |
 |
Fig. 2. On-sky distribution of spectroscopically confirmed galaxies in the vicinity of z ≳ 5.8 LAEs identified in JADES NIRSpec observations over GOODS-S. Sources found in the JADES, FRESCO, and MUSE HUDF surveys are respectively shown by hexagons, squares, and circles; larger grey squares indicate LAEs. Each panel shows a different redshift slice, approximately corresponding to a distance along the line of sight between 2 pMpc ≲ Δl ≲ 6 pMpc. The JADES footprint is indicated by the black rectangles, FRESCO is highlighted in red, and the total (MOSAIC) extent of the MUSE HUDF surveys is shown by the light blue rectangle. Projected sizes of the ionised bubbles centred on each LAE, inferred based on the observed Lyα properties (with |
2.1. JADES
2.1.1. Data and sample selection
The data presented in this work were obtained as part of the DEEP and MEDIUM tiers of the JWST Advanced Deep Extragalactic Survey (JADES; Eisenstein et al. 2023), a joint survey conducted by the guaranteed time observations (GTO) instrument science teams of the JWST/Near-Infrared Camera (NIRCam; Rieke et al. 2023a) and JWST/NIRSpec. Specifically, deep NIRCam imaging was taken over the Great Observatories Origins Deep Survey – South (GOODS-S; Giavalisco et al. 2004), containing the Hubble Ultra Deep Field (HUDF; e.g. Beckwith et al. 2006) previous JADES works (e.g. Robertson et al. 2023). The imaging (JWST programme 1180; PI: Eisenstein) spans 65 arcmin2 over a wavelength range of λobs ≃ 0.8 μm to 5 μm and reaches mF200W ∼ 30 mag (Rieke et al. 2023b). This is complemented by public medium-band imaging from the JWST Extragalactic Medium-band Survey (JEMS) in the HUDF (JWST programme 1963, PI: Williams; Williams et al. 2023) and from the First Reionization Epoch Spectroscopic COmplete Survey (FRESCO; JWST programme 1895, PI: Oesch; Oesch et al. 2023).
Multi-object spectroscopy in GOODS-S was subsequently obtained in the NIRSpec MSA mode (Ferruit et al. 2022), primarily targeting high-redshift galaxy candidates selected in a combination of NIRCam and publicly available HST imaging (Bunker et al. 2023a). Under JWST programme 1210 (PI: LützGendorf), targets were observed both in the PRISM/CLEAR spectral configuration (simply PRISM hereafter; spectral range 0.6 μm to 5.3 μm, resolving power R ∼ 100) and ‘R1000’ medium-resolution gratings (in grating-filter combinations G140M/F070LP, G235M/F170LP, and G395M/F290LP; resolving power R ∼ 1000; e.g. Cameron et al. 2023; Curti et al. 2023). Total exposure times in the DEEP tier ranged from 9.3 to 28 h (depending on slit placement across three visits; e.g. Curtis-Lake et al. 2023) in the PRISM configuration, with the R1000 gratings each receiving a third of the PRISM integration time, whereas the MEDIUM tier targeted a larger number of sources at shallower depth (between 1 and 2 h for both PRISM and R1000 configurations; Jones et al. 2023).
2.1.2. Data reduction
The data reduction procedure of the NIRSpec observations have been outlined in preceding JADES works (e.g. Curtis-Lake et al. 2023; Eisenstein et al. 2023) and will be described in detail in a forthcoming paper (Carniani & NIRSpec GTO Collaboration, in prep.). Briefly, flux-calibrated spectra were extracted with pipelines developed by the ESA NIRSpec Science Operations Team and the NIRSpec GTO team, generally adopting the same algorithms as the STScI pipeline. Path-loss corrections were performed assuming point-like sources located at the position of the target object within the micro-shutter. In the DEEP tier, the one-dimensional PRISM spectra extracted over a shutter-size aperture reach a continuum sensitivity (3σ) of ∼6–40 × 10−22 erg s−1 cm−2 Å−1 (apparent magnitude of m ∼ 27.2–29.1) per spectral pixel at ∼2 μm (Witstok et al. 2023).
2.1.3. Data analysis
Having performed an automated spectral fitting routine with BAGPIPES (Bayesian Analysis of Galaxies for Physical Inference and Parameter EStimation; Carnall et al. 2018) on the PRISM spectra within the DEEP tier, spectroscopic redshift estimates were confirmed by visual inspection independently by at least two team members. The results of consolidated spectroscopic redshift confirmation are described in Bunker et al. (2023b). Using the inferred redshifts as a strict prior, the NIRSpec PRISM and R1000 spectra were fitted independently using the PPXF software (Cappellari 2017) to obtain emission-line fluxes and accurate redshifts (e.g. Curti et al. 2023).
Lyα emission in reionisation-era galaxies (z > 5.8) was identified during visual inspection, resulting in a sample of eight galaxies in the DEEP tier with secure detections in both the PRISM and R1000 spectra, and one additional galaxy where Lyα is only detected in the PRISM. We complement our sample with seven LAEs identified in one of the MEDIUM tiers (Jones et al. 2023)1. This sample notably includes the extreme z = 7.276 LAE JADES-GS-z7-LA (ID 10013682; Saxena et al. 2023b), while the intrinsically UV-brightest source in our sample (ID 12637 at z = 7.66) was previously identified as the LAE z7-GSD-3811 by Song et al. (2016).
The spectral properties, including those of Lyα, were obtained using a custom fitting routine of the PRISM and R1000 spectra. Specifically, these properties include the Lyα flux (measured from the R1000 spectra) and EW (measured in the PRISM spectra), the velocity offset (ΔvLyα; measured in the R1000 spectra), and finally the escape fraction (fesc, Lyα). The details of these measurements, and related empirical diagnostics derived from the measured line fluxes, are described in a companion paper (Saxena et al. 2023a). Briefly, systemic redshifts were established from a SNR-weighted combination of Gaussian functions individually fitted to detected strong rest-frame optical emission lines in the R1000 spectra, specifically the [O II] λ 3727,3730 Å doublet ([O II] hereafter), Hβ, the [O III] λ 4960,5800 Å lines ([O III]), and Hα. Integrated line fluxes of these strong lines were determined from the fitted Gaussian profiles, taking into account the continuum level as measured in adjacent spectral regions; we turned to the PRISM spectra for lines that remained undetected in the R1000 spectra. The Lyα flux was similarly determined by fitting a Gaussian profile to the R1000 measurements, which benefit from a higher sensitivity for emission lines.
We considered different methods of determining the Lyα velocity offset; however, given the asymmetry of several Lyα spectral profiles, which introduced systematic offsets between the peak of the best-fit Gaussian profile and the observed line profile, we opted to measure the velocity offset from the centre of the observed peak pixel of the line. The uncertainty of this measurement is conservatively estimated to be the width of a single spectral pixel, translating to ∼100 km s−1. Lyα escape fractions are inferred by dividing the observed, dust-corrected Lyα/Hα ratio (or Lyα/Hβ if Hα is not available) by the intrinsic luminosity ratio of LLyα/LHα = 8.2 under Case-B recombination, ne = 100 cm−3, and Te = 10 000 K (Osterbrock 1989). Here, we report the main properties of the 17 LAEs in Table 1.
Observed LAE properties.
Spectroscopically confirmed NIRSpec targets were matched to NIRCam photometric candidates (Rieke et al. 2023b) where possible, noting that several sources fall outside the NIRCam footprint (including the LAE IDs 12637, 15362, and 10056849). For consistency with the samples from the FRESCO and MUSE surveys (Sects. 2.2 and 2.3), we adopted absolute UV magnitudes MUV derived from NIRCam photometry probing a rest-frame wavelength of ∼ 1500 Å (F115W at 5.7 < z ≲ 7.2 or F150W at 7.2 ≲ z < 10) for all sources. We measured UV slopes (βUV) of all LAEs from the PRISM spectra (see Saxena et al. 2023a), verifying that their normalisation at 1500 Å shows good agreement (∼20%) with the NIRCam UV magnitudes (adopting the NIRSpec value if NIRCam data was not available). As detailed in Witstok et al. (2023), UV slopes of galaxies other than the 17 LAEs were measured directly from the PRISM spectra for the sample of galaxies with median SNR higher than 3 on the continuum (per spectral pixel, whose sizes are chosen adaptively such that the full width at half maximum (FWHM) is covered by 3.5 pixels; e.g. Bunker et al. 2023a); otherwise, they were derived from the NIRCam photometry.
2.2. MUSE HUDF surveys
Since the JADES coverage of GOODS-S fully incorporates the HUDF, we further supplement our sample of spectroscopically confirmed galaxies with sources identified in the publicly available MUSE HUDF surveys (Bacon et al. 2017). From the DR2 catalogue presented in Bacon et al. (2023), we selected galaxies with a confident spectroscopic redshift (ZCONF of either 2 or 3; e.g. Simmonds et al. 2023) at z > 5.5, which are all spectroscopically confirmed solely via Lyα as a result of the wavelength range covered by MUSE (e.g. Bacon et al. 2017). Since this prohibits us from obtaining a Lyα velocity offset, we do not include these LAEs in our main sample, only considering them in the environmental analysis of other LAEs instead (Sect. 3.2). As for the JADES galaxies, we measured UV magnitudes and UV slopes based on the NIRCam photometric catalogue (Sect. 2.1.3).
Having performed a cross-matching procedure, however, we find that all five JADES LAEs observable with MUSE (i.e. within its footprint and at z ≲ 6.7) are contained as robustly confirmed galaxies (ZCONF ≥ 2) in the MUSE HUDF DR2 catalogue. Specifically, IDs 19606, 9365, 19342, 14123, and 16625 in Table 1 are matched to the respective MUSE IDs 3203, 3089, 547, 6231, and 852 in Bacon et al. (2023); these sources were removed from the MUSE sample to avoid double counting. One of these sources is the z = 5.889 LAE (ID 19606) where Lyα emission is only seen in the PRISM spectrum; in this case, we adopt the offset of the Lyα line observed by MUSE from the systemic redshift measured by NIRSpec, Δv ≈ 50 km s−1, as the Lyα velocity offset. In the other four cases, the Lyα offset as observed by NIRSpec is further redshifted by between 50 km s−1 and 200 km s−1 compared to what was reported in Bacon et al. (2023). While unlikely to be affected by the underlying continuum which remains undetected in the medium-resolution R1000 spectra (Saxena et al. 2023a), this systematic difference may be due to potential calibration issues. Alternatively, it could suggest the Lyα emission is spatially extended with the two instruments probing different spatial regions with mildly varying peak wavelength as a result of the spatial variation in the column density of neutral hydrogen (e.g. Leclercq et al. 2020).
2.3. FRESCO
In addition to the JADES imaging and spectroscopy, we made use of NIRCam wide-field slitless spectroscopy (WFSS) taken over GOODS-S as part of FRESCO (JWST programme 1895, PI: Oesch; Oesch et al. 2023). For the public FRESCO data, we follow the NIRCam WFSS data reduction routine outlined in Sun et al. (2023) and emission-line identification algorithms presented in Helton et al. (2023a). After a careful visual inspection of extracted slitless spectra of galaxies with NIRCam photometric redshifts of z > 5, we spectroscopically confirmed hundreds of galaxies within the JADES footprint via Hα emission at 4.9 < z < 6.5 or [O II] λ 5800 Å emission at 6.8 < z < 8.9 Sun et al.; in prep.. A future work will present detailed descriptions of the WFSS data reduction and catalogues of these spectroscopically confirmed galaxies. Cross matching the MUSE and FRESCO samples resulted in ten LAEs originally identified in the MUSE HUDF surveys for which a new systemic redshift is found in FRESCO, resulting in implied Lyα velocity offsets ranging from ΔvLyα ∼ 100 km s−1 to 400 km s−1 (we note that NIRCam WFSS redshifts may be subject to a calibration uncertainty of 40–80 km s−1). We removed these objects from the FRESCO sample and updated the systemic redshift of the corresponding sources in the MUSE sample. Finally, we confirm the spectroscopic redshift z = 7.955 of GSDY-2209651370, which was previously identified as an LAE by Roberts-Borsani et al. (2023). The systemic redshift found in FRESCO implies a Lyα velocity offset of ΔvLyα ≈ 230 km s−1.
2.4. Combined spectroscopically confirmed galaxy samples
In summary, our main sample comprises 17 LAEs at 5.8 ≲ z ≲ 8 observed as part of JADES, five of which have previously been identified as part of the MUSE HUDF surveys. To study their environments, we further consider 88 LAEs at 5.5 ≲ z ≲ 6.7 from the MUSE HUDF surveys, as well as spectroscopically confirmed galaxies (without confirmed Lyα emission) from JADES and FRESCO data, totalling respectively 22 and 243 sources in the same redshift range.
3. Results and discussion
3.1. Ionised bubble sizes
In a patchy reionisation scenario, where a galaxy embedded in a neutral IGM emits Lyα at a velocity offset2 of ΔvLyα ≲ 300 km s−1 (as is typical for our sample; Table 1), the photons experience substantial absorption unless the galaxy is situated in a highly ionised region with radius of the order of Rion ≳ 0.1 pMpc (e.g. Mason & Gronke 2020; Umeda et al. 2023). Transmission of Lyα photons in a fully neutral IGM, on the other hand, is possible even without such an ionised bubble, as long as they are sufficiently redshifted (cf. Bunker et al. 2023b). This is illustrated in Fig. 3, which shows the IGM transmission as a function of the ionised bubble size, following the modelling prescription in Mason & Gronke (2020). Specifically, the transmission was calculated using a two-zone model, first considering the trajectory of a photon through an ionised bubble3 of size Rion before encountering the neutral IGM (see also Cen & Haiman 2000; Mesinger et al. 2004). Following Mason & Gronke (2020), the gas in the ionised bubble was assumed to have a temperature of T = 104 K while the neutral IGM has T = 1 K; both are considered to have mean cosmic density and be at rest with respect to the central source. We assumed the bubble to be highly ionised, where the residual neutral fraction is either constant with radius (fixed at xH I = 10−8), corresponding to homogeneous reionisation of the bubble, or scales as xH I ∝ r2 with normalisation xH I(r = 0.1 pMpc) = 10−8, as would be expected with a central source of ionisation. The implications of these assumptions will be discussed further below.
 |
Fig. 3. IGM transmission TIGM for a Lyα emitting source at z = 6 for a given Lyα velocity offset ΔvLyα (coloured according to the scale shown on the top) as a function of the size of the ionised bubble, Rion. Results are shown both for a residual neutral fraction within the bubble scaling as xH I ∝ r2 (solid lines) and where it is constant with radius (dashed lines). Transmission curves in the top panel assume a global neutral hydrogen fraction of |
Here, we aim to infer a first-order estimate in the form of a lower limit on the size of the ionised region that allows each observed Lyα line in our sample to be observed close to the systemic redshift. We note that this framework is expected to become inaccurate towards the end of reionisation, where ionised bubbles start to overlap and the neutral fraction of the IGM uniformly approaches 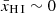 (Lu et al. 2023), such that the distinction between ionised bubbles and neutral IGM breaks down. This is illustrated in the top panel of Fig. 3, showing that in our model (assuming a static IGM) even without a large ionised region, a low neutral fraction of the IGM accommodates significant transmission of redshifted Lyα (ΔvLyα ≳ 0). We note, however, that a bulk infalling motion of the IGM lowers such transmission: in the rest frame of the IGM, having a peculiar velocity directed towards the central emitter, light will appear blueshifted thus ‘resetting’ any redshift the Lyα photons may have. This effectively shrinks the size of a potential ionised bubble, requiring a larger physical size for Lyα to escape. Patches of residual neutral hydrogen within ionised bubbles, as predicted by cosmological hydrodynamical simulations of the reionisation process, would similarly cause an additional suppression of transmitted Lyα photons on the red side (ΔvLyα > 0), though minimally as this mainly affects transmission on the blue side (ΔvLyα ≲ 0; Keating et al. 2023). Instead, our approach is designed to give an insight into the minimum sizes of local ionised regions of the highest-redshift (z ≳ 6) LAEs while being agnostic to the evolution of the global neutral fraction, which instead will be discussed in a different work (Jones et al. 2023).
(Lu et al. 2023), such that the distinction between ionised bubbles and neutral IGM breaks down. This is illustrated in the top panel of Fig. 3, showing that in our model (assuming a static IGM) even without a large ionised region, a low neutral fraction of the IGM accommodates significant transmission of redshifted Lyα (ΔvLyα ≳ 0). We note, however, that a bulk infalling motion of the IGM lowers such transmission: in the rest frame of the IGM, having a peculiar velocity directed towards the central emitter, light will appear blueshifted thus ‘resetting’ any redshift the Lyα photons may have. This effectively shrinks the size of a potential ionised bubble, requiring a larger physical size for Lyα to escape. Patches of residual neutral hydrogen within ionised bubbles, as predicted by cosmological hydrodynamical simulations of the reionisation process, would similarly cause an additional suppression of transmitted Lyα photons on the red side (ΔvLyα > 0), though minimally as this mainly affects transmission on the blue side (ΔvLyα ≲ 0; Keating et al. 2023). Instead, our approach is designed to give an insight into the minimum sizes of local ionised regions of the highest-redshift (z ≳ 6) LAEs while being agnostic to the evolution of the global neutral fraction, which instead will be discussed in a different work (Jones et al. 2023).
For this reason, we calculated ionised bubble sizes under two opposite extremes. The first method simply assumes the IGM (i.e. all gas outside an ionised bubble), has a residual global neutral hydrogen fraction of 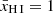 (as in Mason & Gronke 2020). The second method instead assumes the global neutral fraction follows a smooth redshift evolution,
(as in Mason & Gronke 2020). The second method instead assumes the global neutral fraction follows a smooth redshift evolution, 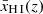 . This scenario of a homogeneously ionised Universe is likely appropriate for the end stages of reionisation and afterwards (z < 6; e.g. Bosman et al. 2022). Noting recent evidence points towards a (very) late cosmic reionisation history where this global neutral fraction could still be non-negligible at the redshift range considered here (e.g.
. This scenario of a homogeneously ionised Universe is likely appropriate for the end stages of reionisation and afterwards (z < 6; e.g. Bosman et al. 2022). Noting recent evidence points towards a (very) late cosmic reionisation history where this global neutral fraction could still be non-negligible at the redshift range considered here (e.g. 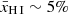 at z ∼ 5.6; Zhu et al. 2022), we adopted the rapid and late reionisation presented as ‘Model II’ in Naidu et al. (2020) as a fiducial model for the evolution of
at z ∼ 5.6; Zhu et al. 2022), we adopted the rapid and late reionisation presented as ‘Model II’ in Naidu et al. (2020) as a fiducial model for the evolution of 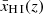 .
.
Using this model of IGM absorption, we estimate how large the ionised region needs to be in the conservative case where all Lyα escapes the galaxy in the first place: that is, we infer the minimum required bubble size 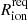 for which
for which
where fesc, Lyα is inferred from the Lyα/Hα ratio and represents the observed fraction of Lyα photons intrinsically produced in H II regions (Saxena et al. 2023a). We thus approximate all Lyα flux has the same velocity whereas in reality, the line is broadened. We expect this approximation to be reasonably accurate, however, as additional absorption of photons bluewards of the peak wavelength is balanced by enhanced transmission of their red counterparts, particularly when the intrinsic line profile (i.e. before, or in the absence of, IGM attenuation) has a dominant, asymmetric redshifted peak (as seen at lower redshift; Appendix A). We note that current observations prevent an accurate measurement of the intrinsic line width: our observed line profiles are only marginally resolved at a resolution of R ∼ 1000, typically spanning only a few spectral channels in the first place (see Saxena et al. 2023a), while the exact spectral resolution of the NIRSpec micro-shutters is dependent on the (unknown) morphology of the Lyα emission (de Graaff et al. 2023).
This method effectively provides a lower limit to the ionised bubble size, since the number of Lyα photons that travel through the IGM towards our line of sight is further lowered by any additional absorption or loss of photons that can be attributed to (i) dust within the interstellar medium, (ii) an IGM infall velocity (discussed above), (iii) a higher residual neutral fraction within the bubble, or (iv) resonant scattering on the scales of the circumgalactic medium (CGM) that extend outside the NIRSpec micro-shutter. Each of these effects would require an even larger ionised region to reconcile the observed Lyα flux with the intrinsic Lyα production via recombinations probed by the Hα flux, the two components that enter into the Lyα escape fraction estimated via the Lyα/Hα ratio. We note, however, the impact of dust in the sample of LAEs considered here is expected to be minimal, as measured by the effectively non-existent Balmer decrement (consistent with E(B − V) = 0 within uncertainties) indicating that nebular dust attenuation in these galaxies is negligible (Saxena et al. 2023a; Sandles et al. 2023). Moreover, while Lyα emission around star-forming galaxies at 2 ≲ z ≲ 6 has been shown to extend to scales of ∼5 kpc (e.g. Rauch et al. 2008; Leclercq et al. 2020) which roughly corresponds to the extent of a NIRSpec MSA shutter at z ∼ 7 (Ferruit et al. 2022), it is unclear whether this Lyα emission can actually be directly tied to the central galaxy. Indeed, there are indications that such extended emission may be largely produced in situ (e.g. by collisional excitation or faint, unresolved neighbouring LAEs; Witstok et al. 2021a; Bacon et al. 2021), while the central component is expected to predominantly originate in recombinations traced by Balmer emission (e.g. Byrohl et al. 2021; Runnholm et al. 2023).
We opted for the quadratic radial profile of the residual neutral fraction within the ionised bubble (i.e. xH I ∝ r2), noting the results do not strongly depend on this assumption for all but the most blueshifted Lyα emission (cf. Fig. 3). The resulting ionised bubble sizes, if required, are reported in Fig. 2 for both assumptions on the global neutral hydrogen fraction discussed above. In case Eq. (1) has no solution for all Rion > 10−3 pMpc (which is the case for most z < 6.5 LAEs in the evolving 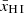 scenario), we conclude a bubble does not need to be invoked for the model to reconcile the observations: in this case, the minimum IGM transmission (i.e. that without a bubble) is already higher than the Lyα escape fraction, indicating that given the modelled IGM transmission our conservative assumption on the IGM accounting for all absorption is no longer valid. The sizes inferred in the case where
scenario), we conclude a bubble does not need to be invoked for the model to reconcile the observations: in this case, the minimum IGM transmission (i.e. that without a bubble) is already higher than the Lyα escape fraction, indicating that given the modelled IGM transmission our conservative assumption on the IGM accounting for all absorption is no longer valid. The sizes inferred in the case where 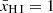 are furthermore shown in Fig. 2. The conservatively estimated uncertainty on the measured Lyα velocity offsets of ∼100 km s−1 (Sect. 2.1.3) translates to a ∼0.1–0.15 pMpc uncertainty on the required sizes, significantly smaller than the estimated bubble sizes in the majority of cases.
are furthermore shown in Fig. 2. The conservatively estimated uncertainty on the measured Lyα velocity offsets of ∼100 km s−1 (Sect. 2.1.3) translates to a ∼0.1–0.15 pMpc uncertainty on the required sizes, significantly smaller than the estimated bubble sizes in the majority of cases.
Inferred minimum ionised bubble sizes.
In a patchy reionisation scenario where all LAEs are still surrounded by a fully neutral IGM (i.e. under the assumption that 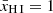 ), we find ionised bubble sizes of the order of
), we find ionised bubble sizes of the order of 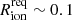 –1 pMpc, except for the extreme z = 7.276 LAE JADES-GS-z7-LA (ID 10013682), for which we find Rion ≈ 2.4 pMpc (in agreement with Saxena et al. 2023b). The largest ionised bubbles are generally inferred for the highest equivalent width LAEs: for instance, the two largest bubble sizes after JADES-GS-z7-LA are those around the z ∼ 5.889 and z ∼ 6.204 LAEs, both having EWLyα ∼ 90 Å. Given our sample does not have a large variation in Lyα velocity offsets, this can be explained by the strong correlation between EWLyα and Lyα escape fraction (Saxena et al. 2023a) that can be interpreted as the LAEs being characterised by a similar ξion (implying a similar ratio between the strength of Hα and the UV continuum) such that the ratio of Lyα to the UV continuum (i.e. the Lyα EW) tightly follows the ratio between Lyα and Hα. In the case where the global neutral hydrogen fraction evolves with redshift (
–1 pMpc, except for the extreme z = 7.276 LAE JADES-GS-z7-LA (ID 10013682), for which we find Rion ≈ 2.4 pMpc (in agreement with Saxena et al. 2023b). The largest ionised bubbles are generally inferred for the highest equivalent width LAEs: for instance, the two largest bubble sizes after JADES-GS-z7-LA are those around the z ∼ 5.889 and z ∼ 6.204 LAEs, both having EWLyα ∼ 90 Å. Given our sample does not have a large variation in Lyα velocity offsets, this can be explained by the strong correlation between EWLyα and Lyα escape fraction (Saxena et al. 2023a) that can be interpreted as the LAEs being characterised by a similar ξion (implying a similar ratio between the strength of Hα and the UV continuum) such that the ratio of Lyα to the UV continuum (i.e. the Lyα EW) tightly follows the ratio between Lyα and Hα. In the case where the global neutral hydrogen fraction evolves with redshift (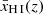 ), the Lyα transmission of many of the lower-redshift LAEs is found to be consistent with not having a bubble, while for sources at z ≳ 6.5 we still find minimum bubble sizes of
), the Lyα transmission of many of the lower-redshift LAEs is found to be consistent with not having a bubble, while for sources at z ≳ 6.5 we still find minimum bubble sizes of 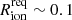 –0.5 pMpc.
–0.5 pMpc.
3.2. Ionised bubble growth
The expected connection between LAEs and ionised bubbles is corroborated by the expectation that the physical conditions necessary for an efficient production and escape of Lyman-continuum (LyC) photons required to create these bubbles – at least if the LyC escape fraction is less than unity – should be accompanied by intrinsically (i.e. before IGM attenuation) luminous Lyα lines, both from a theoretical perspective as well as empirical evidence at z ∼ 2 (Matthee et al. 2022; Naidu et al. 2022). On the other hand, galaxies observed to have bright Lyα emission do not necessarily have to be efficient LyC leakers themselves (Choustikov et al. 2023). This degeneracy can be broken by measuring the sizes of ionised regions required to explain the observed Lyα properties and testing whether these agree with their predicted ionised output of the LAE and any potential neighbouring galaxies. The immediate environments of reionisation-era LAEs inside ionised bubbles therefore provide a unique laboratory in which we can start to establish which sources are the dominant ionising agents.
We therefore proceed by obtaining first-order estimates for the sizes of local, ionised bubbles that are expected to be in place for our sample of LAEs. Following Saxena et al. (2023b), we calculate the bubble growth as a function of time t* since a central source started producing LyC photons using a simplified solution of the equation describing ionisation-front propagation with a central ionising source (cf. Cen & Haiman 2000). We assumed this source has a given production rate of ionising photons Ṅion and escape fraction fesc, LyC. Neglecting the accelerated bubble expansion due to the Hubble flow and under the assumption of a subdominant recombination rate, which at redshift z ≲ 8 is a good approximation4, the size evolution is given by Eq. (6) in Mason & Gronke (2020),
where 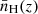 is the mean hydrogen number density at redshift z.
is the mean hydrogen number density at redshift z.
Assuming star formation as the dominant source of ionising photons, bubble sizes that can be produced by the LAE on its own (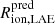 ) or by the LAE and its direct neighbours (
) or by the LAE and its direct neighbours (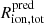 ) are reported in Table 2. For the latter calculation, we simply used a combined ionising photon production rate for all spectroscopically confirmed sources contained within the bubble whose minimum size required for Lyα to escape was inferred in Sect. 3.1 (i.e. Ṅion,tot = ∑ Ṅion,i with i iterating over each neighbour). In calculating Ṅion for the LAEs, we converted the UV magnitude MUV using the ionising photon production efficiency ξion that was directly measured (with median ξion ≈ 1025.59 Hz erg−1; Saxena et al. 2023a). For neighbouring sources, lacking a direct measurement of ξion, we took their UV magnitude MUV and UV slope βUV to estimate Ṅion under the assumption that the ionising spectrum assumes a double power-law shape, as described by Eqs. (7) to (9) in Mason & Gronke (2020). We assumed an ionising-continuum slope α = 2 (Saxena et al. 2023b), noting that for a typical βUV = −2 this corresponds to assuming ξion ≈ 1025.58 Hz erg−1 for the ionising photon production efficiency, comparable to what is directly measured for LAEs (e.g. Saxena et al. 2023a; see also Tang et al. 2023; Simmonds et al. 2023).
) are reported in Table 2. For the latter calculation, we simply used a combined ionising photon production rate for all spectroscopically confirmed sources contained within the bubble whose minimum size required for Lyα to escape was inferred in Sect. 3.1 (i.e. Ṅion,tot = ∑ Ṅion,i with i iterating over each neighbour). In calculating Ṅion for the LAEs, we converted the UV magnitude MUV using the ionising photon production efficiency ξion that was directly measured (with median ξion ≈ 1025.59 Hz erg−1; Saxena et al. 2023a). For neighbouring sources, lacking a direct measurement of ξion, we took their UV magnitude MUV and UV slope βUV to estimate Ṅion under the assumption that the ionising spectrum assumes a double power-law shape, as described by Eqs. (7) to (9) in Mason & Gronke (2020). We assumed an ionising-continuum slope α = 2 (Saxena et al. 2023b), noting that for a typical βUV = −2 this corresponds to assuming ξion ≈ 1025.58 Hz erg−1 for the ionising photon production efficiency, comparable to what is directly measured for LAEs (e.g. Saxena et al. 2023a; see also Tang et al. 2023; Simmonds et al. 2023).
For these estimates, we assumed fiducial values of fesc, LyC = 5% (as should be appropriate for these LAEs; Saxena et al. 2023a) and an age of t* = 50 Myr, noting the inferred bubble size does not strongly depend on small deviations in LyC escape fraction and age. In this simple framework that only counts the total number of ionising photons, there is a degeneracy between the two parameters: for instance, fesc, LyC = 5% and t* = 50 Myr are equivalent to having a LyC escape fraction of 10% (50%) for 25 Myr (5 Myr). Finally, we note these parameters are fundamentally bounded: the ionising photon production efficiency is unlikely to exceed ξion = 1026 Hz erg−1 (e.g. Tang et al. 2023; Seeyave et al. 2023), the escape fraction is limited to a maximum of 100%, and periods of constant star formation are generally not expected to significantly exceed 200 Myr at this early epoch (Tacchella et al. 2018; Whitler et al. 2023a). We again consider both assumptions on the global neutral hydrogen fraction discussed in Sect. 3.1, though this only impacts the number of neighbours and thus the inferred 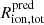 , since the LAE itself is always contained within its own bubble. The resulting predicted sizes of ionised bubbles are presented in Table 2; we will discuss how these compare with the minimum sizes required based on the Lyα transmission in the next section, first briefly discussing the environments of the LAEs in our sample.
, since the LAE itself is always contained within its own bubble. The resulting predicted sizes of ionised bubbles are presented in Table 2; we will discuss how these compare with the minimum sizes required based on the Lyα transmission in the next section, first briefly discussing the environments of the LAEs in our sample.
3.3. Reionisation-era LAEs and their environments
To illustrate the potential importance of environment in our sample of LAEs, we show examples of the 3D distributions of spectroscopically confirmed galaxies in Figs. 4 and 5. In these cases, as also seen in Fig. 1, LAEs coincide with a large number of galaxies identified spectroscopically in FRESCO data (Helton et al. 2023b), which for the z ∼ 7.3 case is supported by photometric selection of galaxies (Endsley et al. 2023). We further note the association of LAEs shown in Fig. 4 is relatively close (within ∼10 pMpc) to the z ∼ 5.78 LAE overdensity already reported by Bacon et al. (2021); indeed, both the z ∼ 5.78 and z ∼ 5.93 associations coincide with several of the first LAEs found in GOODS-S (Bunker et al. 2003; Stanway et al. 2004, 2007). The FRESCO data additionally confirms the presence of more than ten galaxies in small redshift slices around z ∼ 5.78, z ∼ 5.93, and z ∼ 7.25, rendering each of them significant overdensities compared to the average field. Details of the clustering properties of these galaxy associations are discussed in Helton et al. (2023b). In addition, close to the z ∼ 5.93 overdensity there is another densely packed group of z ∼ 5.89 LAEs in a ‘filament’, in which the IGM is likely highly ionised leading to enhanced transmission of Lyα.
 |
Fig. 4. Three-dimensional visualisation of the complex of spectroscopically confirmed z ∼ 5.9 galaxies situated along the line of sight. JADES sources are shown by hexagons, FRESCO sources by squares, and MUSE sources by circles. Many of the objects in JADES and MUSE are observed to be LAEs (indicated by large grey squares). For the six LAEs observed in JADES, ionised bubbles whose sizes were inferred under the assumption that |
 |
Fig. 5. Similar to Fig. 4, but for spectroscopically confirmed galaxies around JADES-GS-z7-LA, the extreme z = 7.276 LAE (Saxena et al. 2023b). |
For the main LAEs shown in Figs. 4 and 5, even when considering all detected sources located within the minimum required bubble size for Lyα escape, the ionising photon budget appears to fall short of explaining the inferred bubble size (reconciliation requires all sources to leak LyC radiation at fesc, LyC = 20% for t* ∼ 50 Myr). In the case of the z ∼ 5.9 LAE complex (Fig. 4), this likely indicates that the neutral hydrogen fraction outside the ionised bubble is lower than the assumed 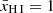 , at least for these overdense patches of the Universe: the fact that many LAEs are observed closely together (in particular the dense cluster around z ∼ 5.889) shows that the ionised bubbles, required as a minimum around each LAE individually, together make up a significant volume fraction of (nearly) fully ionised hydrogen. This likely represents the stage of reionisation where individual bubbles have started to overlap and thus form larger ionised regions in which the simplified approach of isolated bubbles within a fully neutral IGM is no longer valid, as discussed in Sect. 3.1. Indeed, independent methods indicate ionised bubble sizes of the order of 5 pMpc at this redshift regime (5.7 < z < 6.1; Meyer et al. 2020; Kashino et al. 2023), in agreement with expectations from simulations which further show galaxy overdensities are more likely to reside in large bubbles (e.g Qin et al. 2022; Lu et al. 2023). While representing lower limits, our ionised bubble size estimates are considerably smaller than Rion ∼ 100 pMpc recently inferred by Umeda et al. (2023) for brighter systems (typically MUV ≲ −20 mag; note however that Keating et al. 2023 show the blue flux transmission at z ∼ 7 implied by such large ionised regions is not measured in the Lyα forest of quasars until z ≲ 3). In the case with a smoothly evolving global neutral hydrogen fraction (where
, at least for these overdense patches of the Universe: the fact that many LAEs are observed closely together (in particular the dense cluster around z ∼ 5.889) shows that the ionised bubbles, required as a minimum around each LAE individually, together make up a significant volume fraction of (nearly) fully ionised hydrogen. This likely represents the stage of reionisation where individual bubbles have started to overlap and thus form larger ionised regions in which the simplified approach of isolated bubbles within a fully neutral IGM is no longer valid, as discussed in Sect. 3.1. Indeed, independent methods indicate ionised bubble sizes of the order of 5 pMpc at this redshift regime (5.7 < z < 6.1; Meyer et al. 2020; Kashino et al. 2023), in agreement with expectations from simulations which further show galaxy overdensities are more likely to reside in large bubbles (e.g Qin et al. 2022; Lu et al. 2023). While representing lower limits, our ionised bubble size estimates are considerably smaller than Rion ∼ 100 pMpc recently inferred by Umeda et al. (2023) for brighter systems (typically MUV ≲ −20 mag; note however that Keating et al. 2023 show the blue flux transmission at z ∼ 7 implied by such large ionised regions is not measured in the Lyα forest of quasars until z ≲ 3). In the case with a smoothly evolving global neutral hydrogen fraction (where 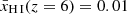 ; Naidu et al. 2020) we infer ionised bubbles are not necessarily required to explain the observed Lyα transmission properties for any of these sources (Table 2).
; Naidu et al. 2020) we infer ionised bubbles are not necessarily required to explain the observed Lyα transmission properties for any of these sources (Table 2).
Conversely, the extreme z = 7.276 LAE (ID 10013682 or JADES-GS-z7-LA) shown in Fig. 5, requires a large ionised bubble (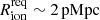 even with a smoothly evolving global neutral fraction; Table 2), as discussed in Saxena et al. (2023b). Such a bubble is difficult to attribute to the relatively UV-faint galaxies identified in its environment (the FRESCO data being able to identify sources with MUV ≲ −18 mag; Fig. 5), let alone to the LAE itself, suggesting in this case significant ionising photon escape is required from a number of sources that are not included in our (incomplete) spectroscopically confirmed sample, or from fainter sources still. Indeed, an independent photometric selection of galaxy candidates points out a highly overdense region located to the east of JADES-GS-z7-LA (Endsley et al. 2023).
even with a smoothly evolving global neutral fraction; Table 2), as discussed in Saxena et al. (2023b). Such a bubble is difficult to attribute to the relatively UV-faint galaxies identified in its environment (the FRESCO data being able to identify sources with MUV ≲ −18 mag; Fig. 5), let alone to the LAE itself, suggesting in this case significant ionising photon escape is required from a number of sources that are not included in our (incomplete) spectroscopically confirmed sample, or from fainter sources still. Indeed, an independent photometric selection of galaxy candidates points out a highly overdense region located to the east of JADES-GS-z7-LA (Endsley et al. 2023).
Additionally, we note this LAE, among the cluster of z ∼ 7.3 spectroscopically confirmed galaxies, is situated as one of the furthest along the line of sight (from the perspective of an observer at z = 0). When considering the next simplest geometry from a single bubble centred on the LAE, two overlapping ionised spheres of equal size coincidentally aligned towards the observer (e.g. Mesinger & Furlanetto 2007), the required volume of the ionised region (and hence the number of ionising photons) may be ∼5× reduced5. In the specific case of JADES-GS-z7-LA, where there are indications for such chance alignment based on the distribution of nearby galaxies (Fig. 5), this could be a viable explanation for the apparent disproportionately large required ionised bubble size 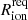 compared to the estimated ionising photon production rate of neighbouring sources.
compared to the estimated ionising photon production rate of neighbouring sources.
In the redshift regime of 6 < z < 7, we do not find a large number of FRESCO sources surrounding any of the LAEs in our sample. This is perhaps not that surprising: galaxies at z ∼ 6.6 fall in the ‘redshift desert’ of FRESCO, where Hα is redshifted out of the F444W grism wavelength coverage (approximately ranging from 3 μm to 5 μm, depending on the location on the detector), while the strong [O III] λ 4960,5800 Å and Hβ lines are not yet contained within it (Oesch et al. 2023). Additionally, the decreasing sensitivity past a wavelength of ∼4 μm and reduced effective survey area of the NIRCam grism imply it is more challenging to find galaxies around a redshift of z ∼ 6.2–6.3. Finally, since FRESCO relies on strong emission-line signatures for spectroscopic confirmation, it is by construction only sensitive to galaxies undergoing bursts of star formation, implying that a significant fraction of sources may be missed if star formation histories are bursty (as suggested by recent findings; e.g. Looser et al. 2023a,b; Endsley et al. 2023). However, if all LAEs are located in extreme overdensities we would still expect to observe a higher number of FRESCO sources.
To more systematically investigate whether LAEs can plausibly create their own bubbles, or whether the contribution of additional (fainter) sources is required, we present a comparison of predicted to minimum required bubble sizes in Fig. 6. Notably, even in the scenario with a smoothly evolving global neutral hydrogren fraction, we infer local ionised bubbles are required to explain the observed Lyα properties for eight out of the 17 LAEs considered here. This provides strong evidence for the presence of ionised bubbles at z > 6, complementary to the fact that these sources exhibit Lyα escape fractions comparable to low-redshift LAEs (where IGM absorption does not play a significant role), while having similar rest-frame optical properties (e.g. the [O III] to [O II] line ratio; see Saxena et al. 2023a).
 |
Fig. 6. Comparison of the inferred bubble sizes ( |
Several of these faint high-redshift LAEs (z > 6), with the notable exceptions of ID 4297 and JADES-GS-z7-LA, require relatively small ionised bubbles (≲0.3 pMpc). Particularly considering they represent lower limits, however, the required minimum ionised bubble sizes are still larger than what we estimate the LAEs and their direct neighbours to be able to assemble, assuming the IGM is still fully neutral outside these bubbles (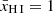 ). The opposite scenario with a smoothly evolving global neutral hydrogen fraction (
). The opposite scenario with a smoothly evolving global neutral hydrogen fraction (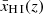 ) improves the agreement for most of the sources, except for the two highest-redshift LAEs and JADES-GS-z7-LA. We have moreover verified that including photometric galaxy candidates (with limiting magnitude MUV ∼ −18 mag) only marginally increases the number of sources contained within the bubbles, therefore not drastically impacting the predicted bubble size estimates. While it may seem trivial that our incomplete sample of galaxies fails to explain the required sizes of ionised bubbles, this does have important implications: crucially, in either case this implies that the relatively UV-faint LAEs considered here are not solely responsible for carving out their ionised bubbles, unless they are extremely efficient LyC leakers (e.g. if they are able to sustain fesc, LyC ∼ 50% for t* ∼ 50 Myr, which is at odds with expectations; see Saxena et al. 2023a). We note there are indications the same holds true for UV-bright LAEs (e.g. Jung et al. 2023). Instead, our results therefore suggest there is still a significant population of undetected, and thus likely ultra-faint (MUV ≳ −18 mag), sources contributing to or even dominating the reionisation of the environments of LAEs in our sample.
) improves the agreement for most of the sources, except for the two highest-redshift LAEs and JADES-GS-z7-LA. We have moreover verified that including photometric galaxy candidates (with limiting magnitude MUV ∼ −18 mag) only marginally increases the number of sources contained within the bubbles, therefore not drastically impacting the predicted bubble size estimates. While it may seem trivial that our incomplete sample of galaxies fails to explain the required sizes of ionised bubbles, this does have important implications: crucially, in either case this implies that the relatively UV-faint LAEs considered here are not solely responsible for carving out their ionised bubbles, unless they are extremely efficient LyC leakers (e.g. if they are able to sustain fesc, LyC ∼ 50% for t* ∼ 50 Myr, which is at odds with expectations; see Saxena et al. 2023a). We note there are indications the same holds true for UV-bright LAEs (e.g. Jung et al. 2023). Instead, our results therefore suggest there is still a significant population of undetected, and thus likely ultra-faint (MUV ≳ −18 mag), sources contributing to or even dominating the reionisation of the environments of LAEs in our sample.
4. Summary and conclusions
We have investigated the environments of 17 reionisation-era LAEs identified by JWST/NIRSpec as part of JADES observations over GOODS-S (Jones et al. 2023). We conservatively estimate sizes of ionised bubbles required to reconcile the measured Lyα velocity offset with the Lyα escape fraction (Saxena et al. 2023a). We summarise our main findings as follows:
-
The relatively low Lyα velocity offsets (ΔvLyα ≲ 300 km s−1) combined with moderately high Lyα escape fractions (fesc, Lyα > 5%) observed in our sample of LAEs suggest the presence of ionised bubbles of the order of
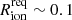 –1 pMpc in a patchy reionisation scenario where the bubbles are still surrounded by a fully neutral IGM. At the highest-redshift regime (z ≳ 6.5), we find such bubbles are necessitated even if the rest of the IGM is homogeneously (but moderately) reionised.
–1 pMpc in a patchy reionisation scenario where the bubbles are still surrounded by a fully neutral IGM. At the highest-redshift regime (z ≳ 6.5), we find such bubbles are necessitated even if the rest of the IGM is homogeneously (but moderately) reionised. -
Around half of the LAEs in our sample are found to coincide with large-scale galaxy overdensities at z ∼ 5.8–5.9 and z ∼ 7.3 (Endsley et al. 2023; Helton et al. 2023b), suggesting Lyα transmission is strongly enhanced in such regions, and underlining the importance of LAEs as tracers of the first large-scales ionised regions.
-
Considering only spectroscopically confirmed galaxies, we find our sample of z > 7 LAEs and their direct neighbours are generally not able to produce the required ionised bubbles based on the Lyα transmission properties (assuming ionising radiation escapes from these sources at fesc, LyC = 5% for t* = 50 Myr), suggesting fainter sources (MUV ≳ −18 mag) likely play an important role in carving out these bubbles.
We conclude that our findings support the case for faint, numerous star-forming galaxies as the main drivers of cosmic reionization. Harnessing the combined power of NIRSpec multi-slit and NIRCam slitless spectroscopy in acquiring a unique view of the early Universe during cosmic reionisation, these results demonstrate the potential of the most distant LAEs as probes of the reionization. Future observational campaigns with JWST, pushing to fainter magnitudes and larger galaxy samples, will therefore undoubtedly help us converge on a more detailed understanding of reionization.
We note Jones et al. (2023) report four additional LAEs in which the signal-to-noise ratio (S/N) was insufficient to be included in the current sample.
It is expected that as a result of complex radiative transfer in the interstellar and circumgalactic medium, the Lyα emission of a galaxy (before IGM processing) typically has a line profile dominated by a redshifted peak with respect to its rest frame (Mitchell et al. 2021; Blaizot et al. 2023), as seen in observations (e.g. Hayes et al. 2021; Witstok et al. 2021b).
For simplicity, we work under the assumption that radiation from a central ionising source is emitted isotropically, resulting in a spherical geometry of ionised bubbles. We will further discuss the implications of this assumption in Sect. 3.3.
Within this framework of a central ionising source at z = 6 (z = 8), the recombination rate within its ionised bubble (the rightmost term of Eq. (3) in Cen & Haiman 2000) becomes comparable to the ionisation rate only when t* ≳ 600 Myr (300 Myr) assuming a clumping factor of CH II = 3 (e.g. Pawlik et al. 2009).
Acknowledgments
We thank the anonymous referee for their constructive feedback that helped to improve this work. We further thank Callum Witten for helpful suggestions. This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope (JWST). The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with programmes 1180, 1210, 1895, and 1963. The authors acknowledge the FRESCO team led by PI Pascal Oesch for developing their observing program with a zero-exclusive-access period. J.W., R.M., W.M.B., M.C., T.J.L., L.S., and J.S. acknowledge support by the Science and Technology Facilities Council (STFC), by the European Research Council (ERC) through Advanced Grant 695671, ‘QUENCH’, and by the UK Research and Innovation (UKRI) Frontier Research grant RISEandFALL. J.W. further gratefully acknowledges support from the Fondation MERAC. R.S. acknowledges support from an STFC Ernest Rutherford Fellowship (ST/S004831/1). A.S., G.C.J., A.J.B., A.J.C., and J.C. acknowledge funding from the ‘FirstGalaxies’ Advanced Grant from the ERC under the European Union’s Horizon 2020 research and innovation programme (Grant agreement No. 789056). J.M.H., D.J.E., B.D.J., B.E.R., and C.N.A.W. acknowledge a JWST/NIRCam contract to the University of Arizona (NAS5-02015). R.M. also acknowledges support by the STFC and funding from a research professorship from the Royal Society. S.A. and M.P. acknowledge support from Grant PID2021-127718NB-I00 funded by the Spanish Ministry of Science and Innovation/State Agency of Research (MICIN/AEI/10.13039/501100011033). This research is supported in part by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. S.C. acknowledges support by European Union’s HE ERC Starting Grant 101040227, ‘WINGS’. E.C.L. acknowledges support of an STFC Webb Fellowship (ST/W001438/1). D.J.E. is supported as a Simons Investigator. M.P. also acknowledges support from the Programa Atracción de Talento de la Comunidad de Madrid via grant 2018-T2/TIC-11715. H.Ü. gratefully acknowledges support by the Isaac Newton Trust and by the Kavli Foundation through a Newton-Kavli Junior Fellowship. The research of C.C.W. is supported by NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. This work has also used the following packages in PYTHON: the SCIPY library (Jones et al. 2001), its packages NUMPY (van der Walt et al. 2011) and MATPLOTLIB (Hunter 2007), the ASTROPY package (Astropy Collaboration 2013, 2018).
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Mary, D., Garel, T., et al. 2021, A&A, 647, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Brinchmann, J., Conseil, S., et al. 2023, A&A, 670, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, G. D., Davies, F. B., Furlanetto, S. R., et al. 2018, ApJ, 863, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Stiavelli, M., Koekemoer, A. M., et al. 2006, AJ, 132, 1729 [Google Scholar]
- Blaizot, J., Garel, T., Verhamme, A., et al. 2023, MNRAS, 523, 3749 [NASA ADS] [CrossRef] [Google Scholar]
- Böker, T., Beck, T. L., Birkmann, S. M., et al. 2023, PASP, 135, 038001 [CrossRef] [Google Scholar]
- Bosman, S. E. I., Davies, F. B., Becker, G. D., et al. 2022, MNRAS, 514, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Stanway, E. R., Ellis, R. S., McMahon, R. G., & McCarthy, P. J. 2003, MNRAS, 342, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Cameron, A. J., Curtis-Lake, E., et al. 2023a, A&A, submitted [arXiv:2306.02467] [Google Scholar]
- Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023b, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Byrohl, C., Nelson, D., Behrens, C., et al. 2021, MNRAS, 506, 5129 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. J., Saxena, A., Bunker, A. J., et al. 2023, A&A, 677, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Carnall, A. C., McLure, R. J., Dunlop, J. S., & Davé, R. 2018, MNRAS, 480, 4379 [Google Scholar]
- Caruana, J., Bunker, A. J., Wilkins, S. M., et al. 2012, MNRAS, 427, 3055 [NASA ADS] [CrossRef] [Google Scholar]
- Caruana, J., Bunker, A. J., Wilkins, S. M., et al. 2014, MNRAS, 443, 2831 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Haiman, Z. 2000, ApJ, 542, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Choustikov, N., Katz, H., Saxena, A., et al. 2023, MNRAS, submitted [arXiv:2304.08526] [Google Scholar]
- Curti, M., Maiolino, R., Curtis-Lake, E., et al. 2023, A&A, submitted [arXiv:2304.08516] [Google Scholar]
- Curtis-Lake, E., Carniani, S., Cameron, A., et al. 2023, Nat. Astron., 7, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., & Ferrara, A. 2018, Phys. Rep., 780, 1 [Google Scholar]
- de Graaff, A., Rix, H. W., Carniani, S., et al. 2023, ArXiv e-prints [arXiv:2308.09742] [Google Scholar]
- Dijkstra, M. 2014, PASA, 31, e040 [Google Scholar]
- Eisenstein, D. J., Willott, C., Alberts, S., et al. 2023, ApJS, submitted [arXiv:2306.02465] [Google Scholar]
- Endsley, R., & Stark, D. P. 2022, MNRAS, 511, 6042 [NASA ADS] [CrossRef] [Google Scholar]
- Endsley, R., Stark, D. P., Charlot, S., et al. 2021, MNRAS, 502, 6044 [NASA ADS] [CrossRef] [Google Scholar]
- Endsley, R., Stark, D. P., Bouwens, R. J., et al. 2022, MNRAS, 517, 5642 [NASA ADS] [CrossRef] [Google Scholar]
- Endsley, R., Stark, D. P., Whitler, L., et al. 2023, MNRAS, submitted [arXiv:2306.05295] [Google Scholar]
- Erb, D. K., Steidel, C. C., & Chen, Y. 2018, ApJ, 862, L10 [Google Scholar]
- Ferruit, P., Jakobsen, P., Giardino, G., et al. 2022, A&A, 661, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finkelstein, S. L., Papovich, C., Dickinson, M., et al. 2013, Nature, 502, 524 [CrossRef] [Google Scholar]
- Finkelstein, S. L., D’Aloisio, A., Paardekooper, J.-P., et al. 2019, ApJ, 879, 36 [Google Scholar]
- Furlanetto, S. R., Hernquist, L., & Zaldarriaga, M. 2004, MNRAS, 354, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, J. P., Mather, J. C., Abbott, R., et al. 2023, PASP, 135, 068001 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Peterson, B. A. 1965, ApJ, 142, 1633 [Google Scholar]
- Hayes, M. J., & Scarlata, C. 2023, ApJ, 954, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M. J., Runnholm, A., Gronke, M., & Scarlata, C. 2021, ApJ, 908, 36 [Google Scholar]
- Helton, J. M., Sun, F., Woodrum, C., et al. 2023a, ApJ, submitted [arXiv:2302.10217] [Google Scholar]
- Helton, J. M., Sun, F., Woodrum, C., et al. 2023b, ApJ, submitted [arXiv:2311.04270] [Google Scholar]
- Hu, W., Wang, J., Infante, L., et al. 2021, Nat. Astron., 5, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsen, P., Ferruit, P., Alves de Oliveira, C., et al. 2022, A&A, 661, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., & Peterson, P. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
- Jones, G. C., Bunker, A. J., Saxena, A., et al. 2023, A&A, submitted [arXiv:2306.02471] [Google Scholar]
- Jung, I., Finkelstein, S. L., Larson, R. L., et al. 2022a, ApJ, submitted [arXiv:2212.09850] [Google Scholar]
- Jung, I., Papovich, C., Finkelstein, S. L., et al. 2022b, ApJ, 933, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Jung, I., Finkelstein, S. L., Arrabal Haro, P., et al. 2023, ApJ, submitted [arXiv:2304.05385] [Google Scholar]
- Kashino, D., Lilly, S. J., Matthee, J., et al. 2023, ApJ, 950, 66 [CrossRef] [Google Scholar]
- Keating, L. C., Weinberger, L. H., Kulkarni, G., et al. 2020, MNRAS, 491, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Keating, L. C., Bolton, J. S., Cullen, F., et al. 2023, MNRAS, submitted [arXiv:2308.05800] [Google Scholar]
- Kulkarni, G., Keating, L. C., Haehnelt, M. G., et al. 2019, MNRAS, 485, L24 [Google Scholar]
- Larson, R. L., Finkelstein, S. L., Hutchison, T. A., et al. 2022, ApJ, 930, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Leclercq, F., Bacon, R., Verhamme, A., et al. 2020, A&A, 635, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leonova, E., Oesch, P. A., Qin, Y., et al. 2022, MNRAS, 515, 5790 [NASA ADS] [CrossRef] [Google Scholar]
- Looser, T. J., D’Eugenio, F., Maiolino, R., et al. 2023a, A&A, submitted [arXiv:2306.02470] [Google Scholar]
- Looser, T. J., D’Eugenio, F., Maiolino, R., et al. 2023b, ArXiv e-prints [arXiv:2302.14155] [Google Scholar]
- Lu, T. Y., Mason, C., Hutter, A., et al. 2023, MNRAS, submitted [arXiv:2304.11192] [Google Scholar]
- Mason, C. A., & Gronke, M. 2020, MNRAS, 499, 1395 [Google Scholar]
- Mason, C. A., Treu, T., de Barros, S., et al. 2018a, ApJ, 857, L11 [Google Scholar]
- Mason, C. A., Treu, T., Dijkstra, M., et al. 2018b, ApJ, 856, 2 [Google Scholar]
- Mason, C. A., Fontana, A., Treu, T., et al. 2019, MNRAS, 485, 3947 [NASA ADS] [CrossRef] [Google Scholar]
- Matthee, J., Naidu, R. P., Pezzulli, G., et al. 2022, MNRAS, 512, 5960 [NASA ADS] [CrossRef] [Google Scholar]
- McElwain, M. W., Feinberg, L. D., Perrin, M. D., et al. 2023, PASP, 135, 058001 [NASA ADS] [CrossRef] [Google Scholar]
- Mesinger, A., & Furlanetto, S. 2007, ApJ, 669, 663 [Google Scholar]
- Mesinger, A., Haiman, Z., & Cen, R. 2004, ApJ, 613, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, R. A., Kakiichi, K., Bosman, S. E. I., et al. 2020, MNRAS, 494, 1560 [Google Scholar]
- Mitchell, P. D., Blaizot, J., Cadiou, C., et al. 2021, MNRAS, 501, 5757 [Google Scholar]
- Naidu, R. P., Tacchella, S., Mason, C. A., et al. 2020, ApJ, 892, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Matthee, J., Oesch, P. A., et al. 2022, MNRAS, 510, 4582 [CrossRef] [Google Scholar]
- Oesch, P. A., van Dokkum, P. G., Illingworth, G. D., et al. 2015, ApJ, 804, L30 [Google Scholar]
- Oesch, P. A., Brammer, G., Naidu, R. P., et al. 2023, MNRAS, 525, 2864 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Ouchi, M., Mobasher, B., et al. 2012, ApJ, 744, 83 [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito, California: University Science Books) [Google Scholar]
- Ouchi, M., Ono, Y., & Shibuya, T. 2020, ARA&A, 58, 617 [Google Scholar]
- Partridge, R. B., & Peebles, P. J. E. 1967, ApJ, 147, 868 [Google Scholar]
- Pawlik, A. H., Schaye, J., & van Scherpenzeel, E. 2009, MNRAS, 394, 1812 [Google Scholar]
- Pentericci, L., Fontana, A., Vanzella, E., et al. 2011, ApJ, 743, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Vanzella, E., Fontana, A., et al. 2014, ApJ, 793, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qin, Y., Wyithe, J. S. B., Oesch, P. A., et al. 2022, MNRAS, 510, 3858 [CrossRef] [Google Scholar]
- Rauch, M., Haehnelt, M., Bunker, A., et al. 2008, ApJ, 681, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, M. J., Kelly, D. M., Misselt, K., et al. 2023a, PASP, 135 [Google Scholar]
- Rieke, M. J., Robertson, B., Tacchella, S., et al. 2023b, ApJS, 269, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Rigby, J., Perrin, M., McElwain, M., et al. 2023, PASP, 135, 048001 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts-Borsani, G. W., Bouwens, R. J., Oesch, P. A., et al. 2016, ApJ, 823, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts-Borsani, G., Treu, T., Mason, C., et al. 2023, ApJ, 948, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E. 2022, ARA&A, 60, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Ellis, R. S., Furlanetto, S. R., & Dunlop, J. S. 2015, ApJ, 802, L19 [Google Scholar]
- Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, Nat. Astron., 7, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Runnholm, A., Hayes, M. J., Lin, Y.-H., et al. 2023, MNRAS, 522, 4275 [NASA ADS] [CrossRef] [Google Scholar]
- Sandles, L., D’Eugenio, F., Maiolino, R., et al. 2023, A&A, submitted [arXiv:2306.03931] [Google Scholar]
- Saxena, A., Bunker, A. J., Jones, G. C., et al. 2023a, A&A, submitted [arXiv:2306.04536] [Google Scholar]
- Saxena, A., Robertson, B. E., Bunker, A. J., et al. 2023b, A&A, 678, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schenker, M. A., Ellis, R. S., Konidaris, N. P., & Stark, D. P. 2014, ApJ, 795, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Seeyave, L. T. C., Wilkins, S. M., Kuusisto, J. K., et al. 2023, MNRAS, 525, 2422 [NASA ADS] [CrossRef] [Google Scholar]
- Shibuya, T., Ouchi, M., Nakajima, K., et al. 2014, ApJ, 788, 74 [Google Scholar]
- Simmonds, C., Tacchella, S., Maseda, M., et al. 2023, MNRAS, 523, 5468 [NASA ADS] [CrossRef] [Google Scholar]
- Song, M., Finkelstein, S. L., Livermore, R. C., et al. 2016, ApJ, 826, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Glazebrook, K., Bunker, A. J., et al. 2004, ApJ, 604, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Bunker, A. J., Glazebrook, K., et al. 2007, MNRAS, 376, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Chiu, K., Ouchi, M., & Bunker, A. 2010, MNRAS, 408, 1628 [Google Scholar]
- Stark, D. P., Ellis, R. S., Charlot, S., et al. 2017, MNRAS, 464, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, F., Egami, E., Pirzkal, N., et al. 2023, ApJ, 953, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Bose, S., Conroy, C., Eisenstein, D. J., & Johnson, B. D. 2018, ApJ, 868, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, M., Stark, D. P., Chen, Z., et al. 2023, MNRAS, 526, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Tilvi, V., Papovich, C., Finkelstein, S. L., et al. 2014, ApJ, 794, 5 [Google Scholar]
- Tilvi, V., Malhotra, S., Rhoads, J. E., et al. 2020, ApJ, 891, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Trapp, A. C., Furlanetto, S. R., & Davies, F. B. 2023, MNRAS, 524, 5891 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Schmidt, K. B., Trenti, M., Bradley, L. D., & Stiavelli, M. 2013, ApJ, 775, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., Ouchi, M., Nakajima, K., et al. 2023, ArXiv e-prints [arXiv:2306.00487] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Weinberger, L. H., Kulkarni, G., Haehnelt, M. G., Choudhury, T. R., & Puchwein, E. 2018, MNRAS, 479, 2564 [Google Scholar]
- Weinberger, L. H., Haehnelt, M. G., & Kulkarni, G. 2019, MNRAS, 485, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Whitler, L. R., Mason, C. A., Ren, K., et al. 2020, MNRAS, 495, 3602 [Google Scholar]
- Whitler, L., Endsley, R., Stark, D. P., et al. 2023a, MNRAS, 519, 157 [Google Scholar]
- Whitler, L., Stark, D. P., Endsley, R., et al. 2023b, MNRAS, submitted [arXiv:2305.16670] [Google Scholar]
- Williams, C. C., Tacchella, S., Maseda, M. V., et al. 2023, ApJS, 268, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Witstok, J., Puchwein, E., Kulkarni, G., Smit, R., & Haehnelt, M. G. 2021a, A&A, 650, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witstok, J., Smit, R., Maiolino, R., et al. 2021b, MNRAS, 508, 1686 [NASA ADS] [CrossRef] [Google Scholar]
- Witstok, J., Shivaei, I., Smit, R., et al. 2023, Nature, 621, 267 [CrossRef] [Google Scholar]
- Witten, C., Laporte, N., Martin-Alvarez, S., et al. 2023, Nature, submitted [arXiv:2303.16225] [Google Scholar]
- Zhu, Y., Becker, G. D., Bosman, S. E. I., et al. 2022, ApJ, 932, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Labbé, I., Belli, S., et al. 2015, ApJ, 810, L12 [Google Scholar]
Appendix A: Detailed Lyα line profile radiative transfer
In this appendix, we consider the effects of broadened line profiles on the net absorption of Lyα photons by the IGM. This requires us to assume the full Lyα spectral profile as it emerges from a galaxy6, which we are prevented from directly observing in the reionisation era. While observations at lower redshift can provide some clues to the expected intrinsic line profiles, the evolving physical properties of galaxies (e.g. specific star formation rate and dust content) may cause them to change as a function of cosmic time (Hayes et al. 2021).
Here, we considered several cases to gain insight into the impact of varying the intrinsic Lyα spectral profile. As a first category, we examined regular Gaussian profiles. Secondly, we considered an empirical asymmetric Gaussian profile (Shibuya et al. 2014). Motivated by the observed line profile of a galaxy with similar properties as those studied in this work (MUV = −19.6 mag; EWLyα ≈ 100 Å) at z ≃ 4.88 (Witstok et al. 2021a), we choose a fiducial asymmetry parameter of aasym = 0.3 (see also e.g. Leclercq et al. 2020). For both categories we considered lines with a given velocity offset consisting either of a single component, or of two components each containing a set fraction of the total flux but at opposite velocity offset). For double-peaked lines, we choose the blue peak to contain a fiducial 30% of the total flux, a conservatively high value based on studies of low-redshift LAEs (e.g. Hayes et al. 2021).
We obtained mock observations by attenuating each Lyα spectral profile as it is assumed to emerge from a galaxy – a single or double (a)symmetric Gaussian – by a representative IGM absorption curve. This curve corresponds to the galaxy being centred in an ionised bubble at z = 6 with radius Rion = 0.5 pMpc and residual neutral fraction of xH I = 10−8. Finally, we convolved the spectrum to a fiducial spectral resolution of R = 1000. In Fig. A.1, the case of single asymmetric line profiles is shown as an example, including a comparison between the ratio of observed flux to the intrinsic flux (the ‘true’ transmission) and the transmission at the peak of the observed line profile (which provides our estimate of IGM transmission; Sect. 3.1). This shows that for the assumed intrinsic line profile, the estimates are consistent with the true transmission, if mildly underestimated. In this case, the size of the ionised bubble would therefore be underestimated by our method.
 |
Fig. A.1. Examples of the wavelength-dependent IGM processing for a source at z = 6 situated in an ionised bubble with Rion = 0.5 pMpc and xH I = 10−8. Intrinsic Lyα line profiles (dashed coloured lines) are asymmetric Gaussian profiles with varying velocity offsets ΔvLyα and an intrinsic FWHM of 100 km s−1 (top panel) and 300 km s−1 (bottom panel). Observed line profiles (solid coloured lines) are convolved to a fiducial spectral resolution of R = 1000. Above the peak of each observed profile (indicated by vertical dotted lines), the true transmission fractions (total flux of the observed line profile divided by the total intrinsic flux) are annotated, while those estimated based on the transmission curve at this wavelength are shown below. |
A more complete assessment of the systematic effects for each assumed intrinsic profile, with varying velocity offset and line width, is shown in Fig. A.2. Given the uncertainty in the precise spectral resolution of our NIRSpec measurements (Sect. 3.1), we show the convolved line widths of JADES LAEs as upper limits to compare with the mock observations described above. While each simulated line profile is systematically shifted to redder wavelengths due to IGM absorption, the transmission characteristics are entirely dependent on the intrinsic line profile. Since the blue peak experiences near-complete absorption, transmission estimates for the double-peaked profiles are up to a factor ∼2 higher than the true values, although this only occurs at large velocity offsets (ΔvLyα ≳ 200 km s−1). On the other hand, a single asymmetric red peak consistently has a higher transmission fraction than estimated.
 |
Fig. A.2. Systematic effects involved in estimating the IGM transmission for different Lyα line profiles. The intrinsic profiles considered (shown in the grey inset panels) are composed of a single (left columns) or double (with a fraction of 30% and 70% of the total flux contained by the blue and red peaks respectively, which have an equal but opposite velocity offset; right columns) Gaussian profile, either regular (top row) or asymmetric (Shibuya et al. 2014; bottom row). For each intrinsic line profile with a given FWHM and velocity offset ΔvLyα (indicated by open circles), the corresponding observed velocity offset and convolved line width (filled circles) are connected by grey lines. The colour of each point shows the ratio between the estimated and true transmission, Test/Ttrue. A horizontal dashed black line indicates the fiducial spectral resolution of R = 1000. Black hexagons show the JADES LAEs (upper limits indicating the line widths have not been deconvolved) considered in this work. |
We conclude that the true transmission is highly dependent on the intrinsic line profile. However, it is well approximated by the transmission at the observed peak wavelength for an asymmetric, red-dominated line profile, as commonly seen in low-redshift observations where IGM absorption does not play a major role (e.g. Erb et al. 2018; Hayes et al. 2021; Hayes & Scarlata 2023). In this case, the transmission may even be systematically underestimated by up to ∼20%, which again results in effective lower limits on the estimated sizes of ionised bubbles.
All Tables
All Figures
 |
Fig. 1. Redshift histogram of spectroscopically confirmed galaxies over GOODS-S. Sources confirmed in JADES NIRSpec observations (Sect. 2.1) are shown by the black histogram (Bunker et al. 2023b), while the red distribution is of those identified in FRESCO data (Oesch et al. 2023), discussed in Sect. 2.3. EoR (z ≳ 5.8) LAEs identified in JADES (Jones et al. 2023; Saxena et al. 2023a) are marked by vertical solid-dashed lines, coloured by Lyα rest-frame EW according to the scale on the right. Additional LAEs found at z > 5.5 in the MUSE HUDF surveys (Bacon et al. 2023), discussed in Sect. 2.2, are shown by the light blue distribution. |
| In the text | |
 |
Fig. 2. On-sky distribution of spectroscopically confirmed galaxies in the vicinity of z ≳ 5.8 LAEs identified in JADES NIRSpec observations over GOODS-S. Sources found in the JADES, FRESCO, and MUSE HUDF surveys are respectively shown by hexagons, squares, and circles; larger grey squares indicate LAEs. Each panel shows a different redshift slice, approximately corresponding to a distance along the line of sight between 2 pMpc ≲ Δl ≲ 6 pMpc. The JADES footprint is indicated by the black rectangles, FRESCO is highlighted in red, and the total (MOSAIC) extent of the MUSE HUDF surveys is shown by the light blue rectangle. Projected sizes of the ionised bubbles centred on each LAE, inferred based on the observed Lyα properties (with |
| In the text | |
 |
Fig. 3. IGM transmission TIGM for a Lyα emitting source at z = 6 for a given Lyα velocity offset ΔvLyα (coloured according to the scale shown on the top) as a function of the size of the ionised bubble, Rion. Results are shown both for a residual neutral fraction within the bubble scaling as xH I ∝ r2 (solid lines) and where it is constant with radius (dashed lines). Transmission curves in the top panel assume a global neutral hydrogen fraction of |
| In the text | |
 |
Fig. 4. Three-dimensional visualisation of the complex of spectroscopically confirmed z ∼ 5.9 galaxies situated along the line of sight. JADES sources are shown by hexagons, FRESCO sources by squares, and MUSE sources by circles. Many of the objects in JADES and MUSE are observed to be LAEs (indicated by large grey squares). For the six LAEs observed in JADES, ionised bubbles whose sizes were inferred under the assumption that |
| In the text | |
 |
Fig. 5. Similar to Fig. 4, but for spectroscopically confirmed galaxies around JADES-GS-z7-LA, the extreme z = 7.276 LAE (Saxena et al. 2023b). |
| In the text | |
 |
Fig. 6. Comparison of the inferred bubble sizes ( |
| In the text | |
 |
Fig. A.1. Examples of the wavelength-dependent IGM processing for a source at z = 6 situated in an ionised bubble with Rion = 0.5 pMpc and xH I = 10−8. Intrinsic Lyα line profiles (dashed coloured lines) are asymmetric Gaussian profiles with varying velocity offsets ΔvLyα and an intrinsic FWHM of 100 km s−1 (top panel) and 300 km s−1 (bottom panel). Observed line profiles (solid coloured lines) are convolved to a fiducial spectral resolution of R = 1000. Above the peak of each observed profile (indicated by vertical dotted lines), the true transmission fractions (total flux of the observed line profile divided by the total intrinsic flux) are annotated, while those estimated based on the transmission curve at this wavelength are shown below. |
| In the text | |
 |
Fig. A.2. Systematic effects involved in estimating the IGM transmission for different Lyα line profiles. The intrinsic profiles considered (shown in the grey inset panels) are composed of a single (left columns) or double (with a fraction of 30% and 70% of the total flux contained by the blue and red peaks respectively, which have an equal but opposite velocity offset; right columns) Gaussian profile, either regular (top row) or asymmetric (Shibuya et al. 2014; bottom row). For each intrinsic line profile with a given FWHM and velocity offset ΔvLyα (indicated by open circles), the corresponding observed velocity offset and convolved line width (filled circles) are connected by grey lines. The colour of each point shows the ratio between the estimated and true transmission, Test/Ttrue. A horizontal dashed black line indicates the fiducial spectral resolution of R = 1000. Black hexagons show the JADES LAEs (upper limits indicating the line widths have not been deconvolved) considered in this work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.