The UMIST Database for Astrochemistry 2022

T. J. Millar; C. Walsh; M. Van de Sande; A. J. Markwick

doi:10.1051/0004-6361/202346908

Home

All issues

Volume 682 (February 2024)

A&A, 682 (2024) A109

Full HTML

Highlight

Open Access

Issue		A&A Volume 682, February 2024


Article Number		A109
Number of page(s)		26
Section		Atomic, molecular, and nuclear data
DOI		https://doi.org/10.1051/0004-6361/202346908
Published online		09 February 2024

A&A, 682, A109 (2024)

The UMIST Database for Astrochemistry 2022

T. J. Millar¹, C. Walsh², M. Van de Sande²^,3 and A. J. Markwick¹^,4

¹ Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, University Road, Belfast BT7 1NN, UK
e-mail: tom.millar@qub.ac.uk
² Department of Physics and Astronomy, University of Leeds, Leeds LS2 9JT, UK
³ Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
⁴ Department of Physics and Astronomy, School of Natural Sciences, The University of Manchester, Manchester M13 9PL, UK

Received: 15 May 2023
Accepted: 27 October 2023

Abstract

Context. Detailed astrochemical models are a key component to interpret the observations of interstellar and circumstellar molecules since they allow important physical properties of the gas and its evolutionary history to be deduced.

Aims. We update one of the most widely used astrochemical databases to reflect advances in experimental and theoretical estimates of rate coefficients and to respond to the large increase in the number of molecules detected in space since our last release in 2013.

Methods. We present the sixth release of the UMIST Database for Astrochemistry (UDfA), a major expansion of the gas-phase chemistry that describes the synthesis of interstellar and circumstellar molecules. Since our last release, we have undertaken a major review of the literature which has increased the number of reactions by over 40% to a total of 8767 and increased the number of species by over 55% to 737. We have made a particular attempt to include many of the new species detected in space over the past decade, including those from the QUIJOTE and GOTHAM surveys, as well as providing references to the original data sources.

Results. We use the database to investigate the gas-phase chemistries appropriate to both O-rich and C-rich conditions in TMC-1 and to the circumstellar envelope of the C-rich AGB star IRC+10216 and identify successes and failures of gas-phase only models.

Conclusions. This update is a significant improvement to the UDfA database. For both the dark cloud and C-rich circumstellar envelope models, calculations match around 60% of the abundances of observed species to within an order of magnitude. There are a number of detected species, however, that are not included in the model either because their gas-phase chemistry is unknown or because they are likely formed via surface reactions on icy grains. Future laboratory and theoretical work is needed to include such species in reaction networks.

Key words: astrochemistry / molecular data / molecular processes / ISM: molecules / circumstellar matter

© The Authors 2024

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The first release of the UMIST Database for Astrochemistry (UDfA) was made public in 1991 (Millar et al. 1991). It was, in main part, motivated by the various astrophysical applications – dark clouds, hot cores, circumstellar clouds, novae, and super-novae – that were being studied by the UMIST (University of Manchester Institute of Science and Technology) Astrochemistry Group and the recognition that members of the group should have access to one set of reactions and rate coefficients that encompassed their various needs. Once we had done this, it became clear that releasing it to the wider community would encourage the spread of astrochemical modelling as a tool both to interpret and to understand and make predictions for observations of molecules in space.

It has been known for some time that gas-phase synthesis dominates the formation of many important interstellar molecules, such as CO, N₂, HCO⁺, N₂H⁺, H₂D⁺, and the unsaturated hydrocarbon chains. For others, however, a detailed description of interstellar chemistry has to be augmented through reactions within and on the icy mantles of interstellar dust grains. Gas-phase reactions do remain, however, the foundation on which such ice chemistry rests. It provides the feedstock for the grain mantle and can chemically process material that is removed from ices. The detections of around 100 new molecules in space in the last few years have led to the addition of many new reactions and species to gas-phase networks and reflects the importance of chemical networks in the interpretation of molecular line observations. This is particularly true in the current paradigm in which 'bottom-up' synthesis determines the abundances of larger species. Readers wishing to keep abreast of the latest detections of molecules in space should consult the Cologne Database for Molecular Spectroscopy¹ (Endres et al. 2016) or the Astrochemyst website² managed by David Woon.

It is in this context that we present the sixth release of the UDfA, RATE22 (previous releases: RATE91 – Millar et al. 1991; RATE95 – Millar et al. 1997; RATE99 – Le Teuff et al. 2000; RATE06 – Woodall et al. 2007; RATE 12 – McElroy et al. 2013). The year suffix refers to the date at which we stopped collecting new data. Thus, RATE22 contains data published or in press up to the end of 2022. Our fifth release (McElroy et al. 2013) contained 6173 reactions among 467 species and 13 elements and was developed in the context of the astronomical identification of around 150 molecular species at that time³ and has proven a very popular source of astrochemical data with over 600 references to date. Applications of the data occur to sources as diverse as protoplanetary disks (Walsh et al. 2015), infrared dark clouds (Entekhabi et al. 2022), brown dwarf disks (Greenwood et al. 2017), the dynamical and chemical evolution of prestellar cores (Priestley et al. 2023), photo dissociation regions (Röllig & Ossenkopf-Okada 2022), external galaxies (Shimonishi et al. 2020), and cometary comae (Heritier et al. 2017). Its data have also been used in non-astrophysical applications, most commonly in plasma physics.

Table 1

Code, reaction type, and the number of each reaction type in RATE12 and RATE22.

2 The Rate22 database

2.1 Description of the data

Our basic gas-phase ratefile, RATE22⁴, now contains some 8767 individual rate coefficients. These correspond to 737 species involving 17 elements, increases of over 40% and 55% in reactions and species, respectively, from Rate12. The additional elements are Al, Ar, Ca, and Ti. The basic format is that each line of data consists of 18 colon-separated entries: the first two are the reaction number and reaction type, defined in Table 1, followed by two reactants and up to four products. The ninth entry denotes the number of temperature ranges, NTR, over which the rate coefficient is defined, while entries 10–12 give the values of α, β and γ used to calculate the rate coefficients. Entries 13–14 give the temperature range over which the rate coefficient is defined, entry 15 provides the method by which the rate coefficient has been determined (M: measured; C: calculated; E: estimated; L: literature). Literature values have generally been harvested from reaction networks published within papers or in their supplementary materials. It also refers to rate coefficients for which we have no information on the method by which they have been determined. In some cases, it describes data taken from ratefiles sent to us on request by their authors. An example of the latter is the OSU high-temperature network (Harada et al. 2010). We note, however, that the difference between estimated and literature values has been rather eroded over time. Of those reactions labelled 'E', some 1501 are mutual neutralisation reactions, all of which are given the same rate coefficient (Harada & Herbst 2008; Loomis et al. 2016). Entry 16 is an estimate of accuracy, entry 17 gives, where available, some 7464 Digital Object Identifiers (DOI) or web page (URL) links that will take the user to the original data source. As part of this update, we have calculated the rate coefficients of 788 ion-dipole reactions using the approach described in Sect. 3. Of these, 601 currently contain no reference label; we shall update these DOI’s upon publication of this paper which is the source of these rate coefficients. Entry 18 lists additional notes in which 'Millar i-d' identifies these 788 ion-dipole reactions. A further 78 reactions identified by 'Millar' refer to rate coefficients calculated or estimated by us. Of our total set of reactions, only 325 lack both a reference and an associated note. Further details on the file format are given in McElroy et al. (2013). Table 1 lists the different reaction types and compares the numbers of each in the RATE12 and RATE22 databases. In addition, it gives data on the origin and methodology by which the rate coefficients have been determined.

2.2 Calculation of rate coefficients

A specific rate coefficient is calculated from α, β, and γ according to its reaction type. For binary reactions, this corresponds to the de Kooij-Arrhenius (KA), or modified Arrhenius, formula: 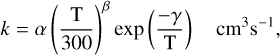$k = α {(\frac{T}{300})}^{β} \exp (\frac{- γ}{T}) {cm}^{3} s^{- 1},$ $k = \alpha {\left( {{{\rm{T}} \over {300}}} \right)^\beta }\exp \left( {{{ - \gamma } \over {\rm{T}}}} \right)\quad {\rm{c}}{{\rm{m}}^3}{{\rm{s}}^{ - 1}},$ (1)

where T(K) is the gas temperature. For cases in which a single rate coefficient is fit by different formulae over several contiguous temperature ranges (NTR > 1), the entry is extended by including the appropriate data as additional colon-separated entries that have the same format as entries 10–18. For example, the rate coefficient of the ion-neutral reaction between H⁻ and CH₂, with NTR = 3, has been fitted to three KA formulae, one each for the temperature ranges 30–100 K, 100–300 K and 300–1000 K (Yurtsever et al. 2020). In some complex cases, the rate coefficient of a particular reaction is best fitted by a sum of KA formulae over the same temperature range. In such cases we list the reaction as a series of independent rate coefficients each with its specific parameters. An example is the reaction between CN and HC₃N to form NC₄N. A combined experimental and theoretical study of this reaction over the temperature range 5–400 K by Cheikh Sid Ely et al. (2013) shows that the rate coefficient is better fit as the sum of two KA formulae each of which is included as a separate line in the ratefile. In total, 10 reactions have complex rate coefficients described as the sum of two or more Arrhenius formulae so that the number of fully independent reactions in RATE22 is 8757.

For one-body reactions, that is those involving photons or cosmic ray particles. For cosmic-ray ionisation (CP), the formula for evaluation of the rate coefficients becomes 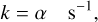$k = α s^{- 1},$ $k = \alpha \quad {{\rm{s}}^{ - 1}},$ (2)

where α is the cosmic-ray ionisation rate, while for those involving UV continuum photons (PH) the formula is: 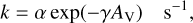$k = α \exp (- γ A_{V}) s^{- 1},$ $k = \alpha \exp \left( { - \gamma {A_{\rm{V}}}} \right)\quad {{\rm{s}}^{ - 1}},$ (3)

where α represents the rate coefficient in the unshielded interstellar ultraviolet radiation field, A_V is the dust extinction at visible wavelengths, and γ is the parameter used to take into account the increased dust extinction at ultraviolet wavelengths. We have not explicitly included the effects of self-shielding in the database. Such a process can occur in situations in which dissociating photons are absorbed through line rather than continuum processes and acts in addition to the extinction caused by dust grains. It can be important for molecules including H₂, CO, N₂, OH, and H₂O and depends on the column density of the molecule with these species showing almost complete shielding once a column density of around 10¹⁵ cm⁻² is reached (Heays et al. 2017). Numerical approaches often involve the use of look-up tables. Details on the self-shielding of H₂, CO, and N₂ are discussed by Sternberg et al. (2014), Visser et al. (2009), Li et al. (2013) and Heays et al. (2014). The inclusion of self-shielding is particularly important in the atomic to molecular transition regions in molecular clouds, in photon-dominated regions (PDRs) circumstellar envelopes, and in certain regions of protoplanetary disks.

For cosmic ray-induced photoreactions (CR) the rate coefficient becomes: 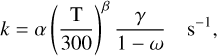$k = α {(\frac{T}{300})}^{β} \frac{γ}{1 - ω} s^{- 1},$ $k = \alpha {\left( {{{\rm{T}} \over {300}}} \right)^\beta }{\gamma \over {1 - \omega }}\quad {{\rm{s}}^{ - 1}},$ (4)

where α is the cosmic-ray ionisation rate, γ is the efficiency factor as defined in Eq. (8) of Gredel et al. (1989), and ω is the dust-grain albedo in the far ultraviolet, typically 0.4–0.6 at 150 nm for particles large compared to the wavelength and close to zero for very small grains (Jones et al. 2013). We choose ω = 0.5 in our model calculations. The particular value of γ depends on the Lyman band photons emitted by H₂ following collisional excitation by the energetic electrons released in cosmic-ray ion-isation. Thus the intensity and wavelength dependence of the cosmic ray-induced UV flux is very different from interstellar photons. Note that our γ values are relative to the H₂ density and are different by a factor of two from those listed by Heays et al. (2017) to account for the factor 1/(1 – ω) in Eq. (4). The cosmicray ionisation rates listed here are normalised to a total rate for electron production from cosmic ray ionisation (primarily from H₂ and He in dark clouds) of ζ₀ = 1.36 × 10⁻¹⁷ s⁻¹ (Prasad & Huntress 1980). Rates for both direct cosmic ray ionisation and cosmic ray-induced photoreactions can be scaled to other choices of the ionisation rate, ζ, by multiplying the appropriate rate coefficients by ζ/ζ₀.

While the absolute rates for CR reactions are different from those of PH reactions for reasons mentioned above, we note that the number of CR reactions is significantly less than those of PH. We have looked in detail at the reasons for this. Three factors emerge: (i) ionisation by cosmic-ray photons is negligible for some species that readily ionised by the interstellar radiation field (see Heays et al. 2017 for examples); (ii) CR destruction of molecular ions, particularly where these react rapidly with H₂, is ignored; (iii) our literature searches showed that many hydrocarbon chain species have several product channels when subject to interstellar photodissociation but only one when cosmic-ray-induced photons are involved. If we consider photorates for the species C_n H_m, n = 6−11, m = 0−2, there are 61 PH channels compared to 21 CR channels (Bettens & Herbst 1995; Wakelam et al. 2010; Harada et al. 2010). Since it is not clear how the branching ratios might differ between PH and CR reactions, we have decided to retain, rather than augment, the original data.

2.3 Caveats and limitations

Very recently, Tinacci et al. (2023) used quantum chemistry to investigate the thermochemistry of some 5768 reactions and the electronic energies of over 500 species contained in the KIDA database⁵ (Wakelam et al. 2015a) identifying 306 that are endothermic. We have searched for each of these in our database finding that 53 overlap in terms of reactants and products with our list and should be removed. The fact that our number is so much smaller than in the KIDA database is due to a number of reasons: over 170 of the endothermic reactions identified in KIDA, particularly those involving large hydrocarbon chains, are not in RATE22; RATE22 does not differentiate between certain isomers, for example between l-C₃H and c-C₃H nor between the cumulene H₂C₄ and diacetylene HC₄H, whereas KIDA does; energy barriers are already present in the RATE22 reactions; and the fact that RATE22 uses lower energy isomers where KIDA does not, for example SiOH⁺, HOSO⁺, HSCO⁺, and H₂CSH⁺ in RATE22 versus HSiO⁺, HSO₂⁺, HOCS⁺, and H₃CS⁺ in KIDA.

We note too that many of the reactions excluded by Tinacci et al. (2023) are ion-neutral reactions with rate coefficients measured in low-pressure experiments to be a significant fraction of the collisional rate coefficients. In these cases ionic products are normally identified by mass spectrometry so that a mis-identification of an ionic product may simply be due to the fact that the structures identified in the KIDA database are not the lowest energy isomer. This is likely to be the case where independent measurements give similar products and rate coefficients. In other cases, particularly where the branching ratio of a channel is small at room temperature, an energy barrier may indeed be present.

As discussed in Sect. 4, the removal of these reactions does not make a significant difference to the comparison between observed and calculated abundances in both TMC-1 and IRC+10216. Both the full and the reduced ratefiles are made available to the community.

In addition to the differences between KIDA and RATE22 discussed above, and noting that there are significant overlaps in reactions and rate coefficients, there remain other important differences. The KIDA database includes several networks that incorporate both gas-phase and grain-surface reactions as well as several that describe chemistry in planetary atmospheres. Our new database includes reactions involving many of the complex organic molecules detected in recent years. It can also be applied to the circumstellar chemistries around both C-rich and O-rich AGB stars and will, no doubt, continue to be used in the range of applications listed in Sect. 1.

As mentioned in Sect. 1, many situations in astrochemistry need to involve surface or bulk chemistry on ice-mantled dust grains. The most important surface reaction is the association of two H atoms to form H₂ on a grain surface. This reaction is not included explicitly in the RATE22 database. Our software does, however, include a term for this process in the ODEs describing the formation and destruction of H atoms. That is, it contains a term, HLOSS, which accounts for the loss of H atoms through the surface formation of H₂, the abundance of which is calculated, like that of electrons, by a conservation equation. The formation of H₂ on grains has been the subject of many studies including the pioneering paper by Hollenbach & Salpeter (1971). For example, Cazaux & Tielens (2004) described the process by which both physisorption and chemisorption contributed to H₂ formation on bare silicate and carbonaceous surfaces (see the correction in Cazaux & Tielens 2010), while Le Bourlot et al. (2012) discussed production in PDRs through both the Langmuir-Hinshelwood and Eley-Rideal mechanisms and Foley et al. (2018) investigated H₂ formation on PAH particles. When using the database in other codes (that is, not the codes provided by us), care must to be taken to include grain-surface formation of H₂ (either implicitly or explicitly).

Other than H₂ formation, grain surface chemistry is neglected here. It is an essential part of many astrochemical applications, particularly in the description of hot cores, hot corinos and protoplanetary disks. Many current models do incorporate such reactions but their networks have been developed mostly in isolation, that is, specific networks have been designed by individuals or groups for a particular purpose; there is no central source of 'agreed' data. In particular, a quantitative description of surface chemistry needs to include parameters such as binding energies, diffusion barriers, reaction products and branching ratios, thermal and non-thermal desorption mechanisms, and the nature and composition of the ice, amongst others. The method of solving the grain chemistry ODEs is also a matter of choice, ranging from the computationally fast, but not always applicable, rate equation approach, to slower but more accurate Monte Carlo methods. Cuppen et al. (2017) discuss these issues in an extensive review article. Experimental and theoretical approaches that minimise uncertainties are underway but the lack of systematic results has prevented implementation of more general rules that might allow surface chemistry to be better described. We note, however, that the binding energies of some 133 molecules has been published by Ligterink & Minissale (2023). Nonetheless, it has long been known experimentally that binding energies are dependent on the specific site at which a molecule sits within the ice (Collings et al. 2004). More recent calculations by Bovolenta et al. (2022) and Tinacci et al. (2022) have provided the binding energies of over 20 molecules on model water ice clusters and show that all have a broad distribution of binding energies rather than a unique value.

As discussed above, values of the α, β, and γ parameters used to calculate rate coefficients are defined over specific temperature ranges. In many cases, these are fits to experimental data and it is appropriate to give a note of caution to their use at temperatures outside these ranges. Röllig (2011) noted that the extrapolation to low temperatures of rate coefficients in the RATE06 release could led to divergent and unphysical behaviour due to the incorporation of large negative γ values. We corrected this and other issues noted by Röllig (2011) in our RATE12 release and have been careful to ensure that our current rate coefficients are not divergent. The choice of whether or not to extrapolate a given rate coefficient outside of its given temperature range, particularly when determined experimentally, is not straightforward and it is unlikely that any one prescription works for all reactions. It is known, for example, that the quantum tunnelling of H atoms in reactions involving OH can increase rate coefficients substantially at low temperatures (Heard 2018). Choices also have to be made where rate coefficients are defined over two non-contiguous temperature ranges. For this situation we recommend that the rate coefficient is interpolated over the intermediate range, a solution that has the advantage that it does not allow a discontinuity in the value of the rate coefficient. Röllig (2011) provides an excellent summary of the issues involved in such cases.

It is also possible that certain rate coefficients with large positive values of β can diverge and be unphysical when extrapolated to temperatures much above the upper limit, T_u, of the range over which the fit is made (see Shaw et al. 2023 for a discussion of this issue in RATE12). This occurs only for NN reactions and we have identified 10 such reactions. There is no unique way to choose a formulation of these rate coefficients above T_u and indeed, given the large values of β involved in some, it can be dangerous to extrapolate to higher temperatures. We therefore adopt a simple approach. For these reactions, we set NTR = 2, k(T > T_u) = k(T_u) and noted this fact in the individual entries.

Finally, it is worth recalling that the number of reactions that describe the chemistry of individual species varies enormously from several hundred in some cases, for example CO, H₂O, C₂H, and C₄H amongst others, to a handful, particularly for many of the complex organic molecules and the large, newly detected, hydrocarbons. In the former case, one may expect that calculated abundances will be less sensitive to the values of rate coefficients. Particular circumstances can make this expectation fail. An example is diffuse cloud chemistry in which photodissoci-ation dominates the loss of neutral species. In this case, their abundances should be inversely proportional to their unshielded photodissociation rates. In the latter case, the formation routes of large molecules are often unknown and have allocated rate coefficients that may be highly uncertain. The abundances of these species are likely to be almost directly proportional to the adopted rate coefficients although complex re-formation pathways may mitigate this behaviour to some extent. We plan a full sensitivity analysis of the RATE22 network for both dark clouds and circumstellar envelopes in order to identify critical reactions for further study.

3 New and updated reactions and species

Here we present brief summaries of the chemistry associated with new species included since the RATE12 release as well as important updates to reaction rate coefficients. We have made a comprehensive literature search for species detected in space since our last release, identifying around 100 new molecules. We have searched for their formation routes in the literature and added destruction through a set of standard loss mechanisms: proton transfer reactions with species such as H⁺, H₃O⁺, HCO⁺, and N₂H⁺, and reactions with He⁺ and C⁺ which tend either to break molecular bonds or to build complexity. Charge exchange (CE) reactions with H⁺, and to a lesser extent C⁺, can also play an important role in chemistry. To help augment the formation routes of complex species, we have also added some mutual neutralisation (MN) reactions between common anions observed in IRC+10216 and TMC-1 − C₃N⁻, C₅N⁻, C₇N⁻, C₄H⁻, C₆H⁻, and C₈H⁻ – and molecular cations (see Millar et al. 2007, Cordiner & Millar 2009 and Walsh et al. 2009). For these, we have adopted the rate coefficients suggested by Harada & Herbst (2008). Calculated abundances are particularly sensitive when a species has only one or a few known formation routes. Since this applies to many of the new molecules, we have allowed the dissociative recombination (DR) of their protonated forms to produce smaller fragments as well as the parent neutral. This approach is needed in dark clouds to prevent unphysical cycling of a species, that is, it prevents the effective loss rate of a molecule from being zero. In photon-dominated regions, photodissociation prevents such recycling. We have included neutral-neutral (NN) reactions where we have evidence for these and destruction by interstellar and cosmic ray-induced photons. We have searched for permanent electric dipole moments and provide a list of over 270 values on our website. We then used these in an approximation of the Su-Chesnovich formula (Su & Chesnavich 1982) to calculate ion-neutral (IN) rate coefficients: 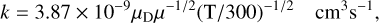$k = 3.87 \times 10^{- 9} μ_{D} μ^{- 1 / 2} {(T / 300)}^{- 1 / 2} {cm}^{3} s^{- 1},$ $k = 3.87 \times {10^{ - 9}}{\mu _{\rm{D}}}{\mu ^{ - 1/2}}{({\rm{T}}/300)^{ - 1/2}}\quad {\rm{c}}{{\rm{m}}^3}{{\rm{s}}^{ - 1}},$ (5)

where μ_D is the electric dipole moment of the neutral molecule in Debye and μ is the reduced mass of the reactants in atomic mass units. This approximation is likely correct to within 20% for species with dipole moments greater than 1 Debye and is well within the uncertainties of astrochemical model calculations. Where a specific rate coefficient has been measured at 300 K, we have used the measured rather than the calculated value to scale to other temperatures.

We have also taken the opportunity to relabel a small number of species in RATE 12. These are mostly protonated ions and have been relabelled to make clear their structural form. Table 2 lists these.

In the following, all fractional abundances are given relative to H₂ unless otherwise stated. Within each sub-section, the discussion of the chemistry is ordered by the mass of the molecule.

Table 2

Relabelled species in RATE22.

3.1 HCCNC, HCCNCH⁺, HC₄NC, HC₅NH⁺, C₇N⁻ and HC₁₁N

HCCNC and HCCNCH⁺ were first detected in TMC-1 by Kawaguchi et al. (1992) and Agúndez et al. (2022a), respectively, at fractional abundances of 3 × 10⁻¹⁰ (Cernicharo et al. 2020a) and 3 × 10⁻¹² (Agúndez et al. 2022a) and an abundance ratio HCCNC/HNC₃ = 5.8 (Cernicharo et al. 2020a). We note that Vastel et al. (2018) have detected both HCCNC and HNC₃ in L1544 with an abundance ratio around 10.

The formation of HCCNC is thought to be due to the DR of protonated HC₃N. We include five DR channels with rate coefficients taken from Wakelam et al. (2010) and adopt the same branching ratios for HCCNC and HNC₃. Unfortunately, the experimental studies of the DR products of DC₃ND⁺ do not distinguish between the DC₃N isomers (Vigren et al. 2012). We include proton transfer reactions to form HCCNCH⁺ with rate coefficients calculated using Eq. (5) as well as destruction involving reactions with C⁺ and He⁺.

Isocyanodiacetylene, HC₄NC, has been detected in TMC-1 by Xue et al. (2020) and Cernicharo et al. (2020a) with the latter authors determining a fractional abundance of 3 × 10⁻¹¹, much less than the value of 1.8 × 10⁻⁸ found for HC₅N. Protonated cyanodiacetylene, HC₅NH⁺, has been tentatively detected in TMC-1 with a fractional abundance of 7.5 × 10⁻¹¹ by Marcelino et al. (2020). The basic chemistry is taken from Cernicharo et al. and, following these authors, we assume that the dissociative recombination of HC₅NH⁺ produces HC₄NC with 1% efficiency. We have also included formation of HC₄NC through MN between HC₄NC⁺ and the anions listed above. These particular processes may be important in both interstellar clouds and C-rich AGB outflows such as that around IRC+10216.

Cernicharo et al. (2023) have detected several transitions of the anion C₇N⁻ in both TMC-1 and IRC+10216 allowing for accurate abundance estimates in both sources. It is a new species in RATE22 and we have included its formation through the reaction of H⁻ with HC₇N with a rate coefficient calculated by Gianturco et al. (2017) as well as through the radiative electron attachment between C₇N and e⁻ (Cordiner & Millar 2009). Loss occurs through photodetachment of the electron, reactions with H and O atoms as well as in several MN reactions with cations.

HC₁₁N is the largest cyanopolyyne detected to date and was identified in TMC-1 by Loomis et al. (2021) with an abundance of 1.0 × 10⁻¹⁰. It was not included in RATE 12. Loomis et al. (2016) provide a detailed chemical model for the synthesis of HC₁₁N as well as several other large carbon-chain molecules, including HC₇N and HC₉N, CH₃C₇N, and CH₃C₉N, and radicals such as C₁₀N and C₁₁N. We have included close to 100 of their reactions in the database to enhance the formation of these large species.

3.2 NC₄NH⁺

Following the detection in TMC-1 of NCCNH⁺, which is a tracer of the unobservable – at least through its rotational line emission – cyanogen molecule NCCN, with an abundance 8.6 × 10⁻¹² by Agúndez et al. (2015a), a related ion, protonated dicyanoacety-lene, NC₄NH⁺, has been detected in the same source with a slightly smaller abundance 1.1 × 10⁻¹² by Agúndez et al. (2023a). The chemistry of cyanogen and its related ions has been well studied in the laboratory and is described in detail in RATE12. Its larger counterpart NC₄N is likely to form through exothermic NN reactions involving C₃N and both HCN and HNC, studied in detail by Petrie & Osamura (2004). A more efficient route though is the reaction of CN with HC₃N which has been studied experimentally over the temperature range 22-296 K by Cheikh Sid Ely et al. (2013). These authors also fit their data to higher temperature measurements and fit a double Arrhenius form from 5–400 K to the rate coefficient which has a value in excess of 10⁻¹⁰ cm³ s⁻¹ at 10 K.

3.3 Propargyl and related species: CH₂CCH and CH₂C₃N

Propargyl, CH₂CCH, has been detected in TMC-1 with a fractional abundance of 10⁻⁸ by Agúndez et al. (2021a, 2022b) making it one of the most abundant hydrocarbon radicals yet detected. It was included in RATE12 but its ion-neutral reactions were erroneously given a T^−1/2 dependence. Since its dipole moment is small, 0.15 D, this dependence has been removed.

3-cyanopropargyl, CH₂C₃N, has been detected in TMC-1 by Cabezas et al. (2021b) with a fractional abundance of 1.6 × 10⁻¹¹. This molecule is newly included in the RATE22 database and we follow the approach discussed by Cabezas et al. 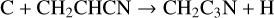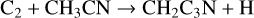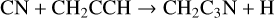with formation driven by four NN reactions: $C + {CH}_{2} CHCN \to {CH}_{2} C_{3} N + H$ ${\rm{C}} + {\rm{C}}{{\rm{H}}_2}{\rm{CHCN}} \to {\rm{C}}{{\rm{H}}_2}{{\rm{C}}_3}{\rm{N}} + {\rm{H}}$ (6) $C_{2} + {CH}_{3} CN \to {CH}_{2} C_{3} N + H$ ${{\rm{C}}_2} + {\rm{C}}{{\rm{H}}_3}{\rm{CN}} \to {\rm{C}}{{\rm{H}}_2}{{\rm{C}}_3}{\rm{N}} + {\rm{H}}$ (7) $CN + {CH}_{2} CCH \to {CH}_{2} C_{3} N + H$ ${\rm{CN}} + {\rm{C}}{{\rm{H}}_2}{\rm{CCH}} \to {\rm{C}}{{\rm{H}}_2}{{\rm{C}}_3}{\rm{N}} + {\rm{H}}$ (8) ${CH}_{3} + C_{3} N \to {CH}_{2} C_{3} N + H,$ ${\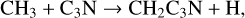rm{C}}{{\rm{H}}_3} + {{\rm{C}}_3}{\rm{N}} \to {\rm{C}}{{\rm{H}}_2}{{\rm{C}}_3}{\rm{N}} + {\rm{H}},$ (9)

with rate coefficients as suggested by Cabezas et al. Loss is assumed to be via the standard set of ion-neutral reactions with the DR of protonated CH₂C₃N assumed to be divided equally between the product channels CH₂C₃N + H and CH₂ + HC₃N.

3.4 Methyl cyanopolyynes and their isomers

3.4.1 CH₃C₃N, HCCCH₂CN and H₂CCCHCN

Two isomers of methyl cyanoacetylene, CH₃C₃N, propargyl cyanide, HCCCH₂CN, and cyanoallene, H₂CCCHCN, have been detected in TMC-1 by Marcelino et al. (2021). All three species have very large dipole moments and we have calculated ion-neutral rate coefficients for new chemistry involving these species using Eq. (5). We have, in the absence of evidence, assumed that the DR of the protonated forms of both propar-gyl cyanide and cyanoallene results in their parent neutral and propargyl, CH₂CCH, with a 50:50 branching ratio. Formation of all three species occurs primarily through neutral-neutral reactions involving CN: with propyne, CH₃CCH, and allene, CH₂CCH₂, to form CH₃C₃N (Abeysekera et al. 2015; Carty et al. 2001); with allene to form propargyl cyanide at a branching ratio of 0.1 (Balucani et al. 2002), and with both propyne and allene to form cyanoallene, with branching ratios again taken from Balucani et al. (2002).

3.4.2 CH₃C₅N and H₂CCCHC₃N

CH₃C₅N was detected in TMC-1 by Snyder et al. (2006). Fuentetaja et al. (2022b) used their most recent data to calculate its fractional abundance as 9.5 × 10⁻¹², about 8 times smaller than the value given by Snyder et al. (2006), arguing that their analysis fits better to the high-J transitions that they observe. Its isomer, cyanoacetyleneallene H₂CCCHC₃N, was detected in TMC-1 via the line stacking method by Shingledecker et al. (2021) who derive a preferred value of its abundance as 2 × 10⁻¹¹. Fuentetaja et al. (2022b) subsequently confirmed this identification through the detection of 20 rotational transitions and derived an abundance of 1.2 × 10⁻¹¹.

Rate 12 assumed that the radiative association between CH₃⁺ and HC₅N leads to CH₃C₅NH⁺ followed by DR to form CH₃C₅N (Herbst & Leung 1989). For its formation, we add the detailed pathways and rate coefficients suggested by Shingledecker et al. (2021) and based on the laboratory study by Fournier (2014) who studied the reaction of C₃N with allene and propyne down to 24 K. The allene reactions are assumed to produce H₂CCCHC₃N with 50% efficiency. Shingledecker et al. assume that there are five product channels, with equal branching ratios, of the propyne reaction, including the formation of both CH₃C₅N and H₂CCCHC₃N. Two of these, however, are species not contained in the database, namely CH₃CC and HCCCH₂C₃N. We thus substitute these species as their equivalents, propargyl CH₂CCH, and H₂CCCHC₃N. In addition to these two reactions involving C₃N, we include another neutral-neutral formation reaction, that between CN and acetylene allene, H₂CCCHCCH. Since the dipole moment of H₂CCCHC₃N is large, 5.15 D (Cabezas, priv. comm.), we have also included the usual ion-neutral reactions with enhanced rate coefficients.

3.4.3 CH₃C₇N and CH₃C₉N

CH₃C₇N was discovered in TMC-1 by Siebert et al. (2022a) who determined an abundance of 8.6 × 10⁻¹². Its chemistry in Rate 12 is parallel to that of CH₃C₅N but with the radiative association now involving HC₇N rather than HC₅N (Herbst & Leung 1989).

CH₃C₉N is newly included in the database and is as yet undetected in TMC-1. Its formation is assumed to be through the radiative association of CH₃⁺ and HC₉N with a rate coefficient assumed to be equal to that of the RA forming CH₃C₇NH⁺. It has a large dipole moment, 6.5 D, and we included the usual set of ion-neutral reactions with rate coefficients determined from Eq. (5). CH₃C₉NH⁺ is formed in proton transfer reactions as well as in the reaction of N with C₁₀H₅⁺ and is lost via DR and by reaction with C atoms to form H₂C₁₁NH⁺ (Loomis et al. 2016). For both species we have added some new ion-neutral loss reactions and calculated their rate coefficients using Eq. (5).

3.5 CH₂CHCCH

Vinyl acetylene was included in the Rate 12 release but its chemistry was extremely limited with destruction only via interstellar and cosmic-ray-induced photons. Here, we have added formation through the measured C₂H + C₂H₄ reaction (Bouwman et al. 2012), destruction through IN and NN reactions involving C₂H to form ortho-benzyne, c-C₆H₄ (Zhang et al. 2011), and CN to form, as suggested by Lee et al. (2021b), the more complex and newly-detected interstellar species vinylcyanoacetylene, H₂CCHC₃N, and cyanovinylacety-lene, HCCCHCHCN, the chemistry of which are discussed further in Sect. 3.18.

3.6 Methyl polyacetylenes and their isomers

3.6.1 CH₃C₄H and H₂CCCHCCH

Allenyl acetylene, H₂CCCHCCH, was detected in TMC-1 by Cernicharo et al. (2021f) with a fractional abundance of 1.2 × 10⁻⁹, essentially identical to that of its isomer methyl diacetylene, CH₃C₄H. Here we adopt the formation reactions suggested by Cernicharo et al., namely reactions of C₂H with CH₂CCH₂ and CH₃CCH, and of C₂ with CH₃CHCH₂ which have been measured at low temperatures (Carty et al. 2001; Daugey et al. 2008). Product branching ratios for these two reactions have been determined by Goulay et al. (2007). The dipole moment of allenyl acetylene is small, 0.63 D, so its ion-neutral reactions do not have a T^−1/2 dependence.

3.6.2 CH₃C₆H and H₂CCCHC₄H

Allenyl diacetylene, H₂CCCHC₄H, an isomer of CH₃C₆H, has been detected in TMC-1 with an abundance 2.2 × 10⁻¹⁰ by Fuentetaja et al. (2022b) who also determine the abundance of CH₃C₆H to be 7 × 10⁻¹¹. We adopt the same neutral-neutral formation routes as Fuentetaja et al. which are based on the low-temperature experiments of Berteloite et al. (2010). The Rate 12 database contains many measured ion-neutral reactions that produce the C₇H₅⁺ ion. Unfortunately, information on the isomeric forms of this ion produced in the experiments is unknown. Here we assume that the isomeric forms are split equally between CH₃C₆H₂⁺ and H₂CCCHC₄H₂⁺. Note that in Rate 12 protonated CH₃C₆H was labelled as C₇H₅⁺. We explicitly differentiate between the protonated forms of the two isomers in RATE22.

3.6.3 CH₃C₈H

Siebert et al. (2022a) searched unsuccessfully for CH₃C₈H in TMC-1 deriving an upper limit to its abundance of 9.8 × 10⁻¹⁰. We have included it in RATE22 assuming that it is one of the products of the dissociative recombination of C₉H₅⁺ formed in the radiative association of C₅H₃⁺ and C₄H₂ (Herbst & Leung 1989). The DR rate coefficient and its branching ratios are set equal to those of C₇H₅⁺. The C₉H₅⁺ ion is also lost through reaction with N atoms, leading eventually to HC₉N (Loomis et al. 2016).

3.7 Molecules containing the C–S bond

3.7.1 HCS and HSC

The first detections of the HCS radical and its metastable isomer HSC were made by Agúndez et al. (2018b) in the dark cloud L483. Cernicharo et al. (2021g), in their survey of S-bearing molecules in TMC-1, give an abundance of 5.5 × 10⁻¹⁰ for HCS and an upper limit of 1.3 × 10⁻¹¹ for HSC.

We have added formation of HCS via the fast reactions C + H₂S (Deeyamulla & Husain 2006) and S with propargyl as well as some DR channels in the recombination of larger S-bearing ions. We note that RATE12 included photoionisation but not photodissociation of HCS. We now include dissociation from both interstellar and cosmic ray-induced photons, setting the rates for these equal to those for HCO. The gas-phase synthesis of HSC is essentially unknown (see Agúndez et al. 2018b) and we do not include it here.

3.7.2 HCCS, HC₂S⁺, H₂CCS, HC₃S, H₂CCCS, C₄S, HC₄S and C₅S

A number of new S-bearing hydrocarbons were discovered in TMC-1 by Cernicharo et al. (2021g), who discuss their chemistry in detail. We have adopted their approach to the chemistry, taking many of the reactions and their rate coefficients from Vidal et al. (2017) in their pioneering study of complex S-chemistry. Since all species have dipole moments greater than 1 D, we have recalculated all ion-neutral reactions using Eq. (5), adding proton transfer and IN reactions involving abundant ions where these are missing.

HC₂S⁺ has been detected in TMC-1 by Cabezas et al. (2022b) at an abundance of 1.1 × 10⁻¹⁰. It appears in the RATE 12 database but we have added a small number of reactions here. As C₂S has a very large proton affinity, 869.6 kJ mol⁻¹, larger than that of NH₃ and smaller than that of C₃S, we have added some additional proton transfer reactions for the formation of HC₂S⁺ and included proton transfer to C₃S as a loss mechanism.

The HC₄S molecule has been detected in TMC-1 with an abundance of 9.5 × 10⁻¹² by Fuentetaja et al. (2022a). We include the primary formation routes suggested by them, notably the reactions of S and S⁺ with C₄H₃⁺ and C₄H₃, respectively, and C with H₂CCCS. To these we have added formation through S and C₄H₂. Loss reactions include those with N atoms and charge exchange and proton transfer reactions with rate coefficients calculated using Eq. (5).

The thio-carbon chains, C₄S and C₅S, which have been detected in TMC-1 with fractional abundances of 3.8 × 10⁻¹² for C₄S and 5.0 × 10⁻¹² for C₅S by Cernicharo et al. (2021g), have large dipole moments and therefore the IN reactions involving both species have a T^−1/2 dependence at low temperature. C₄S was included in RATE12 with its formation dominated by MN reactions between anions and C₄S⁺. We have recalculated all IN rate coefficients using Eq. (5) and added some neutral-neutral formation routes including the reactions between S and C₄H and between C and HC₃S (Vidal et al. 2017) as well as C and H₂CCCS. C₅S is a new species in the database and we have followed closely the approach for its formation and destruction suggested by Cernicharo et al. and Vidal et al., although we have again calculated IN rate coefficients using the ion-dipole approach.

3.7.3 NCS, HNCS and HSCN

Isothiocyanic acid, HNCS, and its metastable isomer thiocyanic acid, HSCN, were detected first in the Sgr B2 molecular cloud by Frerking et al. (1979) and Halfen et al. (2009), respectively. Subsequently, Adande et al. (2010) detected both species in TMC-1 while Cernicharo et al. (2021g) detected NCS in the same object and gave abundances for all three species, 7.8 × 10⁻¹¹, 3.8 × 10⁻¹¹ and 5.8 × 10⁻¹¹, respectively. The chemistry of these three molecules are heavily interlinked and has been discussed in some detail by Gronowski & Kolos (2014), who focused primarily on the routes forming HNCSH⁺ and H₂NCS⁺, and Vidal et al. (2017). We adopt their pathways but for consistency recalculate IN rate coefficients using Eq. (5).

3.7.4 HCSC₂H and HCSCN

Propynethial, HCSC₂H, and cyanothioformaldehyde, HCSCN, have been detected in TMC-1 by Cernicharo et al. (2021i) with abundances of 3.2 × 10⁻¹¹ and 1.3 × 10⁻¹⁰, respectively. For HCSC₂H we have included the formation reactions suggested by Cernicharo et al., namely S with CH₂CCH and C₂H with H₂CS, with rate coefficients of 10⁻¹⁰ cm³ s⁻¹. We have included ion-neutral destruction with He⁺ and C⁺ as well as proton transfer reactions with the main proton carriers in dark clouds, H₃⁺, HCO⁺, N₂H⁺, and H₃O⁺, followed by dissociative recombination with two equal product channels to HCSC₂H + H and C₂H₂ + HCS. To enhance its formation, we have also included a number of MN reactions as discussed in Sect. 1.

The formation of HCSCN is treated in a similar manner to that of HCSC₂H, that is, we adopt two formation reactions S + CH₂CN and CN + H₂CS. These reactions, and those mentioned above for HCSC₂H, are analogues of the O and H₂CO reactions that produce the interstellar molecules HCCCHO and HCOCN (see Sect. 3.9).

3.7.5 CH₃SH and C₂H₅SH

Methyl mercaptan or methanethiol, CH₃SH, was first detected in the interstellar medium by Linke et al. (1979) and has been seen in a wide variety of massive star-forming regions as well as in the low-mass star-forming system IRAS 16293-2422 (Majumdar et al. 2016). It has not been detected in the classical cold dark clouds TMC-1 and L483. Two recent papers (el Akel et al. 2022; Bouscasse et al. 2022) have performed extensive line surveys of two complex sources containing both hot and cold gas to unravel sulphur chemistry. Bouscasse at el. find CH₃SH only in hot gas surrounding G328.2551-0.5321 while el Akal et al. find it in the cold envelope of Cyg X-N12 as well as in the hot gas. The formation of CH₃SH in the gas-phase appears to be difficult with no efficient routes identified that involve either ion-neutral or neutral-neutral reactions, leading to the conclusion that its chemistry is dominated by grain surface reactions (see, for example, Majumdar et al. 2016).

One measured ion-neutral reaction that forms the C-S bond is: 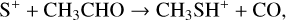$S^{+} + {CH}_{3} CHO \to {CH}_{3} {SH}^{+} + CO,$ ${{\rm{S}}^ + } + {\rm{C}}{{\rm{H}}_3}{\rm{CHO}} \to {\rm{C}}{{\rm{H}}_3}{\rm{S}}{{\rm{H}}^ + } + {\rm{CO}},$ (10)

although the branching ratio to this channel is only 0.2 (Decker et al. 2000). We assume that the CH₃SH⁺ ion is converted to CH₃SH through a series of MN reactions with anions. Loss of CH₃SH occurs in ion-neutral reactions. Where there is no experimental evidence, we have adopted the branching ratios suggested by Majumdar et al. although we have been more conservative in including reactions and products that are analogous to reactions involving CH₃OH.

Ethyl mercaptan, C₂H₅SH, has been detected in its gauche (lowest energy) form toward the galactic centre by Rodriguez-Almeida et al. (2021a) who discuss its formation via possible grain-surface reactions (see also Lamberts 2018). Due to the lack of feasible gas-phase formation routes, we have not included this species in the database.

3.8 The hydrocarbon chains – C₅H⁺, C₅H₂, C₆H₂, HCCCHCCC, C₁₀H and C₁₀H⁻

C₅H⁺ was detected in TMC-1 by Cernicharo et al. (2022a) at an abundance of 8.8 × 10⁻¹². C₅H⁺ has many formation routes but relatively few destruction reactions in RATE12. We have added proton transfer reactions involving C₅ with N₂H⁺ and H₃O⁺ to the former and included MN loss reactions with anions to the latter.

The linear cumulene pentatetraenylidene, C₅H₂, has been detected with one of the lowest abundances seen in TMC-1, of 1.35 × 10⁻¹² (Cabezas et al. 2021d). Its chemistry was covered extensively in RATE12 but, as its dipole moment is 5.9 D, we have updated all IN rate coefficients involving this species using Eq. (5).

Cabezas et al. (2021d) also reported the abundances of the ortho- and para-cumulene forms of C₆H₂ with an ortho-para ratio of 3 and a total abundance equal to 8 × 10⁻¹² in TMC-1 while Fuentetaja et al. (2022a) identified several emission lines in the same source from its isomer HCCCHCCC with an abundance of 1.3 × 10⁻¹¹. We do not include the latter species in the network.

The largest pure hydrocarbon chains detected to date are C₁₀H and C₁₀H⁻ both of which have been observed, the former a tentative detection, by Remijan et al. (2023) in TMC-1 with abundances of 2.0 × 10⁻¹¹ and 4.0 × 10⁻¹¹, respectively. As noted by Remijan et al. (2023), this is the first neutral-anion pair in which the anion has a larger abundance than the neutral, a result difficult to explain with our current, and still limited, understanding of anion chemistry. These two species were already included in RATE12 but their chemistry was incomplete since, unlike smaller hydrocarbon chains, we did not allow their formation from larger chains. We have rectified this by including C₁₁H and C₁₁H⁻ in our species set and including the reaction O + C₁₁H⁻ to form C₁₀H⁻ + CO. The formation of a smaller hydrocarbon anion has been found in the measurements of O with C₂H⁻, C₄H⁻, and C₆H⁻ by Eichelberger et al. (2007) who also note that the reactions become more exothermic as the chain length increases. Although we fit the observed abundance of C₁₀H well, we find, in common with Remijan et al. (2023), that we underproduce C₁₀H⁻ (see Sect. 4.1.1).

3.9 HCCCHO, c-C₃H₂O, H₂CCCO, HCOCN and CH₂CHCHO

Propynal, HCCCHO, was detected in TMC-1 by Irvine et al. (1988) and subsequently observed by Cernicharo et al. (2021i) who derived a fractional abundance of 1.5 × 10⁻¹⁰. The chemistry of its isomers, c-C₃H₂O (cyclopropenone), with an abundance of 5.4 × 10⁻¹² (Loison et al. 2016), and H₂CCCO (propadienone), which has an upper limit of 1.1 × 10⁻¹¹ (Cernicharo et al. 2020b) have been discussed in some detail by Loison et al. Here, we include only the chemistry of HCCCHO and, in particular, the two reactions considered by Cernicharo et al. 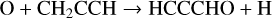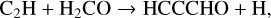(2021i): $O + {CH}_{2} CCH \to HCCCHO + H$ ${\rm{O}} + {\rm{C}}{{\rm{H}}_2}{\rm{CCH}} \to {\rm{HCCCHO}} + {\rm{H}}$ (11) $C_{2} H + H_{2} CO \to HCCCHO + H,$ ${{\rm{C}}_2}{\rm{H}} + {{\rm{H}}_2}{\rm{CO}} \to {\rm{HCCCHO}} + {\rm{H}},$ (12)

with rate coefficients of 10⁻³ cm³ s⁻¹. Ion-neutral rate coefficients are calculated using Eq. (5) since the dipole moment of propynal is 2.78 D.

Remijan et al. (2008) made the first detection of formyl cyanide (or cyanoformaldehyde), HCOCN, in Sgr B2(N) and suggested that it was formed through the reaction of CN with H₂CO, a suggestion strengthened by the quantum theoretical study of Tonolo et al. (2020). More recently, however, West et al. (2023) studied the reaction experimentally over the range 32–103 K and performed high-level quantum calculations to find that the dominant product channel is HCN + HCO. They found that the pathway to HCOCN formation is hindered by a submerged energy barrier. Based on a combination of experimental and theoretical approaches, they produced a fit to the rate coefficient over the temperature range 6–1500 K. 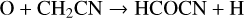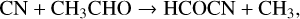In RATE22, the synthesis of HCOCN is dominated by two NN reactions: $O + {CH}_{2} CN \to HCOCN + H$ ${\rm{O}} + {\rm{C}}{{\rm{H}}_2}{\rm{CN}} \to {\rm{HCOCN}} + {\rm{H}}$ (13) $CN + {CH}_{3} CHO \to HCOCN + {CH}_{3},$ ${\rm{CN}} + {\rm{C}}{{\rm{H}}_3}{\rm{CHO}} \to {\rm{HCOCN}} + {\rm{C}}{{\rm{H}}_3},$ (14)

with rate coefficients equal to 10⁻¹⁰ (Cernicharo et al. 2021i) and 6.5 × 10⁻¹⁰ cm³ s⁻¹ (Tonolo et al. 2020). In TMC-1, Cernicharo et al. find the fractional abundance of HCOCN is 3.5 × 10⁻¹¹.

The lowest energy conformer of propenal, CH₂CHCHO, was originally discovered by Hollis et al. (2004) in the giant molecular cloud Sgr B2(N) and subsequently detected in TMC-1 by Agúndez et al. (2021b) with an abundance of 2.2 × 10⁻¹¹. It is formed through NN reactions (Tsang 1991; Goulay et al. 2012; Xie et al. 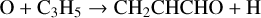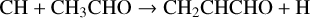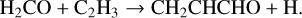2005): $O + C_{3} H_{5} \to {CH}_{2} CHCHO + H$ ${\rm{O}} + {{\rm{C}}_3}{{\rm{H}}_5} \to {\rm{C}}{{\rm{H}}_2}{\rm{CHCHO}} + {\rm{H}}$ (15) $CH + {CH}_{3} CHO \to {CH}_{2} CHCHO + H.$ ${\rm{CH}} + {\rm{C}}{{\rm{H}}_3}{\rm{CHO}} \to {\rm{C}}{{\rm{H}}_2}{\rm{CHCHO}} + {\rm{H}}$ (16) $H_{2} CO + C_{2} H_{3} \to {CH}_{2} CHCHO + H .$ ${{\rm{H}}_2}{\rm{CO}} + {{\rm{C}}_2}{{\rm{H}}_3} \to {\rm{C}}{{\rm{H}}_2}{\rm{CHCHO}} + {\rm{H}}.$ (17)

We also include its formation through MN between the common anions and CH₂CHCHO⁺, formed in charge exchange with H⁺ and C⁺.

3.10 H₂NC and H₂CN

H₂CN was included in RATE 12 but its chemistry was limited and dominated by neutral-neutral reactions taken from Smith et al. (2004). Since its dipole moment is 2.54 D, we have added our usual suite of ion-neutral reactions with rate coefficients calculated by Eq. (5). H₂NC, the highest energy isomer of H₂CN, was discovered in the dark clouds L483 and B1-b by Cabezas et al. (2021a) although they did not detect it nor H₂CN in TMC-1, with upper limits to their fractional abundances of 3.2 × 10⁻¹¹ and 4.8 × 10⁻¹¹, respectively. Although the energy difference is 29.9 kJ mol⁻¹, the abundance ratio of these two molecules is close to 1 in both cold clouds. We have adopted a similar chemistry for H₂NC, adding the measured reaction between C and NH₃ (Bourgalais et al. 2015) to form both isomers with equal efficiency. Neutral atom destruction of H₂NC is assumed to proceed at the same rate as that of H₂CN.

3.11 C_n O and HC_n O, n = 4−9

In recent years, there has been a number of successful (and unsuccessful) observational searches in TMC-1 for long carbon-chain molecules terminated by an oxygen atom (McGuire et al. 2017a; Cordiner et al. 2017; Cernicharo et al. 2021b). Between them, these papers give fractional abundances for species C₂O to C₇O and HCO to HC₇O.

Two major mechanisms have been suggested to form these molecules. The first is based on experimental work on the ternary association reactions between CO and unsaturated hydrocarbon ions from which are deduced two-body radiative association rate coefficients at 10 K to form HC_n+1O⁺, HC_n+1OH⁺ ,and H₂C_n+1OH⁺ ions, n = 2−6 (Adams et al. 1989). We have adjusted their pre-exponential factor and adopted a (T/300)⁻²⁵ dependence so that the rates can be used at other temperatures. Such a dependence is based on the modified thermal approach (Harada et al. 2010) where the exponent depends on the sum of the rotational degrees of freedom of the reactants. In this case we assume that the hydrocarbon ions are non-linear. If instead, the dominant collisional ion is linear, then the dependence should be (T/300)^−2.0. This would mean that we overestimate the rate constant at 10 K by a factor of 5.5. In addition, we have extended the set of reactions to include the C₉O species. Since the 10 K rates are already close to their collisional values for n = 5, we assume that the radiative association rates for these larger species are equal to that for the C₅H⁺ + CO association.

Once formed these ions can then undergo DR to form the range of neutrals observed. It should be clear, however, that the actual abundances of the (H)C_nO species are particularly sensitive to the branching ratios for these DR processes. In the absence of any evidence, we have chosen a procedure that is easy to implement (and to change in the light of future information) – each ion formed through radiative association dissociates into two channels with equal branching ratios. 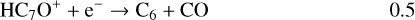Using C₇O as an example: ${HC}_{7} O^{+} + e^{-} \to C_{6} + CO 0.5$ ${\rm{H}}{{\rm{C}}_7}{{\rm{O}}^ + } + {{\rm{e}}^ - } \to {{\rm{C}}_6} + {\rm{CO}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(0}}{\rm{.5)}}$ (18) ${HC}_{7} O^{+} + e^{-} \to C_{7} O + H 0.5$ ${\rm{H}}{{\rm{C}}_7}{{\rm{O}}^ + } + {{\rm{e}}^ - } \to {{\rm{C}}_7}{\rm{O}} + {\rm{H}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(0}}{\rm{.5)}}$ (19) ${HC}_{7} {OH}^{+} + e^{-} \to C_{7} O + H_{2} 0.5$ ${\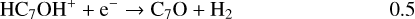rm{H}}{{\rm{C}}_7}{\rm{O}}{{\rm{H}}^ + } + {{\rm{e}}^ - } \to {{\rm{C}}_7}{\rm{O}} + {{\rm{H}}_2}\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(0}}{\rm{.5)}}$ (20) ${HC}_{7} {OH}^{+} + e^{-} \to {HC}_{7} O + H 0.5$ ${\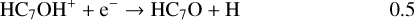rm{H}}{{\rm{C}}_7}{\rm{O}}{{\rm{H}}^ + } + {{\rm{e}}^ - } \to {\rm{H}}{{\rm{C}}_7}{\rm{O}} + {\rm{H}}\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(0}}{\rm{.5)}}$ (21) $H_{2} C_{7} {OH}^{+} + e^{-} \to C_{7} O + H_{2} + H 0.5$ ${{\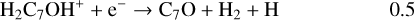rm{H}}_2}{{\rm{C}}_7}{\rm{O}}{{\rm{H}}^ + } + {{\rm{e}}^ - } \to {{\rm{C}}_7}{\rm{O}} + {{\rm{H}}_2} + {\rm{H}}\,\,\,\,\,\,\,\,\,\,\,{\rm{(0}}{\rm{.5)}}$ (22) $H_{2} C_{7} {OH}^{+} + e^{-} \to {HC}_{7} O + H_{2} 0.5.$ ${{\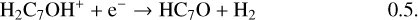rm{H}}_2}{{\rm{C}}_7}{\rm{O}}{{\rm{H}}^ + } + {{\rm{e}}^ - } \to {\rm{H}}{{\rm{C}}_7}{\rm{O}} + {{\rm{H}}_2}\,\,\,\,\,\,\,\,\,\,{\rm{(0}}{\rm{.5)}}$ (23)

The second route to these long chain molecules has been proposed by Cordiner & Charnley (2012) and is based on the laboratory measurements of Eichelberger et al. (2007). 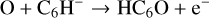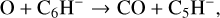These form the chain species through reactions involving O atoms and hydrocarbon anions, such as: $O + C_{6} H^{-} \to {HC}_{6} O + e^{-}$ ${\rm{O}} + {{\rm{C}}_6}{{\rm{H}}^ - } \to {\rm{H}}{{\rm{C}}_6}{\rm{O}} + {{\rm{e}}^ - }$ (24) $O + C_{6} H^{-} \to CO + C_{5} H^{-},$ ${\rm{O}} + {{\rm{C}}_6}{{\rm{H}}^ - } \to {\rm{CO}} + {{\rm{C}}_5}{{\rm{H}}^ - },$ (25)

again with equal branching ratios.

In both of these scenarios, a certain simplicity of implementation is adopted. The real situation is likely to be more complex with other possible product channels and branching ratios so our approach, in the absence of further investigation, likely overestimates the gas-phase formation of these neutral chain molecules.

The C_nO species all have large dipole moments (Moazzen-Ahmadi & Zebretto 1995); those of HC_nO are smaller (Mohamed et al. 2005) but still larger than 1 D. We use Eq. (5) to generate the rate coefficients for ion-neutral reactions.

3.12 CH₃CHCHCN

The trans- and cis- forms of crotononitrile, CH₃CHCHCN, are two of five cyano derivatives of propene discovered in TMC-1 by Cernicharo et al. (2022c), the others being methacry-lonitrile, CH₂CH(CH₃)CN, and gauche- and cis-allyl cyanide, CH₂CHCH₂CN. All species have very similar abundances, ~10⁻¹¹, indicating that they are likely to form in the same manner. Cernicharo et al. note that the reaction of CN with propene, CH₃CHCH₂, has been measured to be fast down to 23 K (Morales et al. 2010) with products that could include the above species as well as vinyl cyanide, CH₂CHCN, with a branching ratio that greatly favours vinyl cyanide.

Since the detailed chemistry of these cyano derivatives and the interplay between them is not understood, here we only include crotononitrile as a proxy for the others and allocate it a branching ratio of 30%, with vinyl cyanide allocated 70% in the CN-CH₃CHCH₂ reaction. In addition to photodissociation, we include the usual ion-neutral loss reactions. As noted by Cernicharo et al., this formation route is now a very inefficient mechanism for forming these cyano derivatives. This is a result of a very much decreased production rate of propene following the study by Lin et al. (2013) who showed that the radiative associations of both C₃H₃⁺ and C₃H₅⁺ with H₂ possess energy barriers and do not proceed at low temperatures. The result is a precipitous decrease in the abundance of C₃H₇⁺ and hence of propene calculated under dark cloud conditions, well below that observed, and as a result, leads to very low abundances for these cyano derivatives (see Sect. 4.1.1).

3.13 Cyanates, their isomers and related species

3.13.1 HNCO and its isomers

Isocyanic acid, HNCO, has three metastable isomers whose chemistry has been discussed in detail by Quan et al. (2010). Here we updated ion-neutral rate coefficients using Eq. (5) and added proton transfer reactions with HCO⁺, N₂H⁺, and H₃O⁺.

3.13.2 OCN, H₂NCO⁺ and H₂OCN⁺

These molecules have not been observed as yet in TMC-1 but the first two were detected in L483 by Marcelino et al. (2018). OCN has a fairly extensive chemistry in the RATE12 database but the only proton transfer reaction included was with H₃⁺ which erroneously had a T^−1/2 dependence. We have corrected this and included a wider range of such reactions. We have also added a new formation reaction CN + O₂ for which Sims et al. (1992) measured the rate coefficient from 26 to 295 K. At higher temperatures we adopt the rate coefficient recommended by Baulch et al. (1994).

The chemistry of H₂NCO⁺ and H₂OCN⁺ is very limited in RATE12 where they are formed only by proton transfer of H₃⁺ with HNCO and HOCN respectively, and by the reactions of H₂ with HCNO⁺ and HOCN⁺, respectively. Marcelino et al. have shown that the H₂ reactions are, however, endothermic. We have therefore removed the H₂ reactions and added additional proton transfer reactions. Furthermore, the only loss routes for the two ions in RATE12 are via DR; we have added MN reactions as a result.

3.13.3 CH₃NCO, HOCH₂CN and C₂H₅NCO

The first detection of interstellar methyl isocyanate, CH₃NCO, was made in Sgr B2(N) by Halfen et al. (2015).

Majumdar et al. (2018) have discussed its gas and grain chemistry. Their list of reactions contains only one gas-phase formation pathway, the reaction of HNCO and CH₃. Their calculation of the rate coefficient, however, has an energy barrier of 8040 K making it unimportant in most interstellar sources, with the possible exception of shocked gas. Their modelled abundance of CH₃NCO therefore depends completely on grain surface reactions. Subsequently, Gorai et al. (2020) revised the value of the rate coefficient to a temperature-independent value of 1.0 × 10⁻¹² cm³ s⁻¹, whereas Quénard et al. (2018) adopt a value of 5.0 × 10⁻¹¹ cm³ s⁻¹. Since this is the single gas-phase production reaction for CH₃NCO, its calculated abundance is directly proportional to the value of the rate coefficient. Here we adopt the value of Quénard et al. to maximise its abundance but note that this will be overestimated by a factor of 50 if Gorai et al.’s value is correct. We have taken the bulk of our additional gas-phase reactions from Majumdar et al., updating them using Eq. (5) where appropriate.

Glycolonitrile, HOCH₂CN, an isomer of CH₃NCO, has been detected in two interstellar sources IRAS 16293-2422B (Zeng et al. 2019) and Serpens SMM1 (Ligterink et al. 2021). There are, however, no gas-phase routes identified to form this molecule and we do not include it in the ratefile.

Finally, we note in passing that ethyl isocyanate, C₂H₅NCO, has been detected in the galactic centre cloud G+0.693-0.027 by Rodríguez-Almeida et al. (2021b). There is no gas-phase chemistry available for the formation of this molecule and it is not included in the database.

3.14 NH₂CHO

Formamide, NH₂CHO, is observed in many interstellar clouds although not in TMC-1, where its upper limit is 5 × 10⁻¹² (Cernicharo et al. 2020b), and was not included in Rate 12, consistent with the subsequent findings by Redondo et al. (2014b,a) that potential gas-phase ion-neutral syntheses had energy barriers despite being exothermic. The molecule was added to the current database following the calculation by Barone et al. (2015) that the reaction between NH₂ and H₂CO was efficient in making NH₂CHO. However, a very recent experimental and theoretical study of this reaction down to 34 K shows that the channel producing NH₂CHO has an energy barrier of over 1800 K and therefore cannot act as a production route in interstellar clouds (Douglas et al. 2022). There appears to be no route to NH₂CHO⁺ thereby ruling out MN as a low-temperature route to formamide. We do, however, leave this species in the database since the high temperatures that need to be reached to overcome the energy barrier can be realised in hot, inner circumstellar envelopes (CSEs) and in post-shock gas.

3.15 HCOOCH₃, CH₃COOH, HOCH₂CHO and (CHOH)₂

Acetic acid, CH₃COOH, glycolaldehyde HOCH₂CHO, and 1,2-ethenediol, (CHOH)₂, hereafter AA, GA, and ED, respectively, are isomers of the common interstellar molecule methyl formate, HCOOCH₃, hereafter MF, the only one of the four included in Rate 12. Its formation there, though, is very inefficient, essentially due to one slow ion-neutral reaction, that between CH₃OH₂⁺ and H₂CO to produce protonated MF. The Rate 12 model produces a maximum abundance of less than 10⁻¹⁶ under TMC-1 conditions (Sect. 4.1.1). MF is the only one of these four species to be detected in TMC-1 with an abundance of 1.1 × 10⁻¹⁰ (Agúndez et al. 2021b). The others are observed in molecular clouds associated with star forming regions.

Ascenzi et al. (2019) have measured the rate coefficient of He⁺ with MF and re-evaluated other proton transfer reactions. We have followed their suggestions but used Eq. (5) to calculate total rate coefficients except where measured values are available.

Gas-phase formation of AA and GA, as currently understood, is an inefficient process and most models that attempt to reproduce their abundances in interstellar clouds tend to rely on grain surface chemistry. Skouteris et al. (2018) discuss this in some detail. 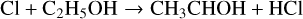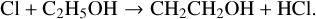Their gas-phase scheme begins with the hydrogen abstraction reactions of Cl and OH with ethanol: $Cl + C_{2} H_{5} OH \to {CH}_{3} CHOH + HCl$ ${\rm{Cl}} + {{\rm{C}}_2}{{\rm{H}}_5}{\rm{OH}} \to {\rm{C}}{{\rm{H}}_2}{\rm{C}}{{\rm{H}}_2}{\rm{OH}} + {\rm{HCl}}.$ (26) $Cl + C_{2} H_{5} OH \to {CH}_{2} {CH}_{2} OH + HCl .$ ${{\rm{H}}_2}{\rm{CO}} + {\rm{C}}{{\rm{H}}_2}{\rm{OH}} \to {\rm{HOCHCHOH}} + {\rm{H}}$ (27)

These radicals then react with O atoms – CH₃CHOH to form AA and CH₂CH₂OH to form GA, amongst other products. Skouteris et al. calculate rate coefficients and branching ratios for all these reactions which we adopt here. As usual, we have used Eq. (5) to calculate the rate coefficients of the ion-neutral loss reactions. We have taken DR rate coefficients for both ionised and protonated AA and GA from Walsh (priv. comm.) with some adjustments to branching ratios for channels involving products CH₃CO and COOH that are not contained in this release.

(Z)-1,2-ethenediol, which we write in the database as HOCHCHOH, has recently been detected in the Galactic Centre cloud G+0.693-0.027 by Rivilla et al. (2022). They find a low rotational excitation temperature of about 8.6 K, and an abundance ratio with respect to glycolaldehyde of 0.19. 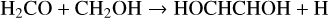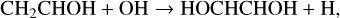We include the two gas-phase routes suggested by Rivilla et al.: $H_{2} CO + {CH}_{2} OH \to HOCHCHOH + H$ ${\rm{C}}{{\rm{H}}_2}{\rm{CHOH}} + {\rm{OH}} \to {\rm{HOCHCHOH}} + {\rm{H}},$ (28) ${CH}_{2} CHOH + OH \to HOCHCHOH + H,$ ${{\rm{C}}_2}{\rm{H}}_5^ + + {\rm{C}}{{\rm{H}}_3}{\rm{C}}{{\rm{H}}_3} \to {{\rm{C}}_3}{\rm{H}}_7^ + + {\rm{C}}{{\rm{H}}_4}$ (29)

with temperature-independent rate coefficients 2 × 10⁻¹⁰ cm³ s⁻¹.

3.16 CH₃NH, CH₂NH₂ and CH₃NH₂

Methylamine, CH₃NH₂, was one of the earliest detected interstellar molecules having been observed in the Giant Molecular Clouds Sgr B2 and Orion A by Kaifu et al. (1974) and Fourikis et al. (1974), respectively. It was not included in earlier versions of the database. Its gas-phase formation is highly uncertain with the dominant pathway initiated by the radiative association of CH₃⁺ and NH₃ to form CH₃NH₃⁺ (Herbst 1985) followed by dissociative recombination. It has recently been shown experimentally that it has a fast loss reaction with OH at 22 K in which the radicals CH₂NH₂ and CH₃NH are produced (González et al. 2022) with a rate coefficient some 20 times larger than that at 300 K. Puzzarini et al. (2020) have made a theoretical study of the H-atom abstraction reaction of CH₃NH₂ with CN and we adopt their rate coefficients and branching ratios to CH₂NH₂ and CH₃NH. These two radicals have also been added to RATE22. We note that Schmid et al. (2022) have recently obtained a laboratory rotational spectrum of protonated methylamine and searched for it in several cores in Sgr B2, determining an upper limit of ~10⁻¹⁰. Finally, we note that Wlodek & Bohme (1988) have studied the reaction of Si⁺ with CH₃NH₂ showing that it forms SiNH⁺ and hence SiN following DR.

3.17 Cyclic hydrocarbons - c-C₅H, c-C₃HCCH, c-C₅H₆, c-C₆H₄, c-C₆H₅, c-C₅H₄CCH₂, c-C₅H₅CCH, c-C₅H₅CN, C₆H₅CCH, c-C₆H₅CN, c-C₉H₈ and c-C₉H₇CN

c-C₅H, written as C₃CCH to distinguish it from linear C₅H in the database, has been detected with an abundance of 9 × 10⁻¹² in TMC-1 (Cabezas et al. 2022a). They suggest two formation reactions, one the reaction of C₂H with c-C₃H, which retains the triangular C₃ structure in c-C₅H. The second is the reaction of C atoms with diacetylene, a reaction they suggest may produce both linear and cyclic C₅H, although they note that production of the latter is close to thermo-neutral and may not proceed at low temperatures. We have therefore adopted their suggestion and taken a branching ratio of 10% for c-C₅H. In addition to destruction by N, C and O atoms, we have added our usual suite of dipole-enhanced IN reactions.

Ethynyl cyclopropenylidenene, c-C₃HCCH, written simply as C₃HCCH in the database, and cyclopentadiene, c-C₅H₆, and written C₅H₆, were detected in TMC-1 with fractional abundances of 3.1 × 10⁻¹¹ and 1.2 × 10⁻⁹, respectively, by Cernicharo et al. (2021e,c). Since the basic structure of the former species is a C₃-triangle, its chemistry is thought to be dominated by the reaction of C₂H with cyclopropenylidene, c-C₃H₂, given that both reactants are abundant in TMC-1 and that other reactions between C₂H and hydrocarbon radicals are known to be fast at low temperature. c-C₃HCCH has a large dipole moment, 3.54 D, so again we have used Eq. (5) to calculate ion-neutral rate coefficients. Theoretical and/or experimental studies on reactions that might lead to this molecule are clearly needed.

The gas-phase chemistry of cyclopentadiene, c-C₅H₆, is also likely to be incomplete. Its neutral-neutral formation is entirely dependent on one reaction between CH and butadiene, CH₂CHCHCH₂ (Cernicharo et al. 2021c). The dissociative recombination of C₅H₇⁺ can also produce it but, other than proton transfer reactions of c-C₅H₆ forming C₅H₇⁺, which are cyclic in nature and not therefore true formation routes to C₅H₆, this ion is only produced in slow ion-molecule reactions involving C₃H₄⁺ and C₃H₅⁺. In general, the unreactivity of large carbon-bearing species with H₂ makes the synthesis of such molecules with more than 3–4 hydrogen atoms, and in particular C₅H₇⁺, inefficient.

Cernicharo et al. (2021d) detected ortho-benzyne, hereafter C₆H₄, with a fractional abundance of 5.0 × 10⁻¹¹ in TMC-1. They provide an exhaustive discussion of a total of 14 possible formation routes, many of which possess energy barriers. Here, we include the four major neutral-neutral routes identified by Cernicharo et al. The exothermic, barrierless reaction between C₂H and vinyl acetylene, CH₂CHCCH, has been measured by Zhang et al. (2011) with an estimated rate coefficient of 8 × 10⁻¹¹ cm³ s⁻¹. The other three syntheses involve the reactions of C₂H₄, C₃H, and C₃H₂ with C₄H, CH₃CCH, and CH₂CCH, respectively. We have also included the reaction between C₃H and CH₂CCH₂ with all rate coefficients set to 10⁻¹⁰ cm³ s⁻¹. Loss reactions include charge exchange with H⁺ and C⁺ and proton transfer reactions. The phenyl radical, hereafter C₆H₅, has not yet been detected in the interstellar medium but plays an important role in the chemistry of the benzene-like ring molecules.

Fulvenallene, C₅H₄CCH₂, was detected with an abundance of 2.7 × 10⁻¹⁰ in TMC-1 by Cernicharo et al. (2022b). They suggested that it was formed as one of the products in the reaction of C₂H with cyclopentadiene, c-C₅H₆, the other two channels producing 1- and 2-ethynyl cyclopentadiene, c-C₅H₅CCH. Since both propene and c-C₅H₆ play an important role in the synthesis of fulvenallene we have added a number of ion-molecule reactions, taken from the compilations by Anicich & Huntress (1986) and Anicich (1993), aimed at increasing the abundances of these species. 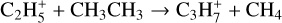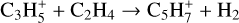These include: $C_{2} H_{5}^{+} + {CH}_{3} {CH}_{3} \to C_{3} H_{7}^{+} + {CH}_{4}$ ${{\rm{C}}_3}{\rm{H}}_5^ + + {{\rm{C}}_2}{{\rm{H}}_4} \to {{\rm{C}}_5}{\rm{H}}_7^ + + {{\rm{H}}_2}$ (30) $C_{3} H_{5}^{+} + C_{2} H_{4} \to C_{5} H_{7}^{+} + H_{2}$ ${\rm{C}}{{\rm{H}}_2}{\rm{CC}}{{\rm{H}}^ + } + {{\rm{C}}_2}{{\rm{H}}_4} \to {{\rm{C}}_5}{\rm{H}}_5^ + + {{\rm{H}}_2}.$ (31) ${CH}_{2} {CCH}^{+} + C_{2} H_{4} \to C_{5} H_{5}^{+} + H_{2} .$ ${\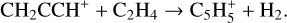rm{CH}} + {\rm{HCN}} \to {\rm{HCCN}} + {\rm{H}}$ (32)

Cernicharo et al. (2022b) suggest that the radiative association reaction between l-C₃H₃⁺, denoted CH₂CCH⁺ in the database, and C₂H₄ forms C₅H₇⁺ with a very large rate coefficient. Although this product ion was detected in the laboratory, the measurement was performed under the relatively high pressure conditions within an ion cyclotron resonance experiment, so that the rate coefficient determined is more likely to be the two-body equivalent of a three-body process rather than that of radiative association.

The two isomers 1- and 2-ethynyl cyclopentadiene, C₅H₅CCH, have been detected in TMC-1 by Cernicharo et al. (2021e) with abundances of 1.4 × 10⁻¹⁰ and 2.0 × 10⁻¹⁰, respectively. We do not differentiate between these two forms in the network. In addition to the reaction between C₂H and c-C₅H₆ mentioned above, we have also included formation via the dissociative recombination of the C₇H₇⁺ ion which forms primarily from the reaction of CH₂CCH⁺ with benzene (Smyth et al. 1982) as well as in ion-neutral reactions between c-C₆H₅⁺ and various hydrocarbons (Ausloos et al. 1989).

The detection of 1-cyanocyclopentadiene, C₅H₅CN, in TMC-1 by McCarthy et al. (2021) was followed quickly by the identification of 2-cyanocyclopentadiene (Lee et al. 2021a). Lee et al. analysed their velocity-stacked spectra and used MCMC modelling to derive total fractional abundances of 8.3 × 10⁻¹¹ and 1.9 × 10⁻¹¹, respectively. We ignore the difference in structure between these two isomers in the database. Lee et al. suggest that the molecule is formed by the reaction of CN with cyclopen-tadiene, c-C₅H₆, in analogy with the formation of benzonitrile from benzene, while Cernicharo et al. (2021e) suggest formation via the reaction between C₂N and CH₂CHCHCH₂. Here we take the rate coefficient for the former reaction to be the same as that for benzonitrile formation. Given their large dipole moments (Lee et al. 2021a), proton transfer reactions and other ion-neutral rate coefficients are calculated using Eq. (5).

Cernicharo et al. (2021e) tentatively detected ethynyl benzene, c-C₆H₅CCH, in TMC-1 at an abundance 2.5 × 10⁻¹⁰. They suggested two formation routes, reactions of C₂H with C₆H₆ and C₆H₅CN, where the first of these has been measured to have a fast reaction down to 103 K (Goulay & Leone 2006). Although not applicable in the case of dark clouds, we have added the measured high-temperature formation reaction between C₂H₂ and C₆H₅ to the network and adopted temperature-independent rate coefficients for its destruction.

Benzonitrile, C₆H₅CN was first detected in TMC-1 by McGuire et al. (2018). Subsequently, Burkhardt et al. (2021b) detected it in four other cold sources and derived a total abundance of 1.6 × 10⁻¹⁰ in TMC-1, using an MCMC analysis to fit their data to four components in their line-of-sight. Burkhardt et al. present a model for its interstellar synthesis. It is readily formed in the reaction of CN with benzene, C₆H₆, a reaction that is measured to be fast down to 15 K (Cooke et al. 2020). Both its proton affinity and dipole moment are relatively large and we therefore allow proton-transfer reactions with H₃⁺, N₂H⁺, HCO⁺, and H₃O⁺ to produce C₆H₅CNH⁺ with rate coefficients calculated using Eq. (5). We note that proton transfer reactions, and therefore C₆H₅CNH⁺, are not included in the Burkhardt et al. chemical model. We assume that its DR leads to benzonitrile and phenyl, C₆H₅, with equal branching ratios.

Indene, c-C₉H₈, was detected in TMC-1 by both Cernicharo et al. (2021c) and Burkhardt et al. (2021a). The latter authors have described a pathway to indene based on the work of Doddipatla et al. (2021) and involving the reaction of CH with styrene, c-C₆H₅C₂H₃. Their calculated abundances fall several orders of magnitude below that observed. We have not included indene in the database.

Sita et al. (2022) have recently searched for the isomers of cyanoindene, C₉H₇CN in TMC-1, detecting 2-cyanoindene at a fractional abundance of 2.1 × 10⁻¹¹. The formation of this molecule likely occurs in a manner similar to that of benzonitrile, that is, through a fast reaction between CN and indene. Such a reaction results in an abundance ratio of cyanoindene to indene close to that observed but gas-phase synthesis, as currently understood, is not able to reproduce the observed abundance by several orders of magnitude. Cyanoindene is not included here.

The model failure to reproduce the large observed abundances of the benzene-related cyclic hydrocarbons is ultimately due to a lack of efficient, barrierless pathways to C₆H₆, mainly due to the fact that the fast pathway to propene formation is no longer feasible as discussed in Sect. 3.12 (Lin et al. 2013). The identification of such pathways, or alternative routes to benzene, is a key issue for astrochemistry research.

3.18 H₂CCHC₃N and HCCCHCHCN

Vinylcyanoacetylene, H₂CCHC₃N, and its isomer cyanoviny-lacetylene, HCCCHCHCN, the latter in its trans-(E) conformer, have been detected in TMC-1 by Lee et al. (2021b). They calculate abundances of 2 × 10⁻¹¹ for the former and 3 × 10⁻¹¹ for the latter as well as an upper limit of 2 × 10⁻¹¹ for the trans-(Z) conformer of cyanovinylacetylene. The neutral-neutral reactions that form these species are taken from Lee et al. to which we add our usual suite of ion-neutral and photoreactions.

3.19 CH₂CHOH

Vinyl alcohol, CH₂CHOH, an isomer of acetaldehyde, CH₃CHO, has been detected in TMC-1 at an abundance of 2.5 × 10⁻¹⁰ by Agúndez et al. (2021b), very close to the abundance, 3.5 × 10⁻¹⁰, of acetaldehyde (Cernicharo et al. 2020b). In general, experimental studies of neutral-neutral reactions cannot differentiate between isomeric products. As a result, it is possible that those NN reactions that are thought to produce CH₃CHO could also produce CH₂CHOH. The essential equality of the isomeric abundances suggests that both form by the same processes. RATE12 already contains several neutral-neutral reactions that form CH₃CHO so here we make the simple assumption that both isomers are produced by these reactions with equal branching ratios. We have made the same assumption for the DR of the protonated forms of both CH₂CHOH and CH₃CHO.

3.20 HCCN, HCCO and HC₄N

Thirty years separate the discovery of HCCN in the outer envelope of IRC+10216 (Guélin & Cernicharo 1991) and in TMC-1 (Cernicharo et al. 2021a). Its synthesis has been discussed by Osamura & Petrie (2004) and, with particular reference to Titan chemistry, by Loison et al. (2015). 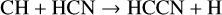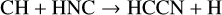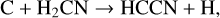Its formation is via neutral-neutral reactions: $CH + HCN \to HCCN + H$ ${\rm{CH}} + {\rm{HNC}} \to {\rm{HCCN}} + {\rm{H}}$ (33) $CH + HNC \to HCCN + H$ ${\rm{C}} + {{\rm{H}}_2}{\rm{CN}} \to {\rm{HCCN}} + {\rm{H}},$ (34) $C + H_{2} CN \to HCCN + H,$ ${\rm{CH}} + {\rm{H}}{{\rm{C}}_3}{\rm{N}} \to {\rm{H}}{{\rm{C}}_4}{\rm{N}} + {\rm{H}}$ (35)

with loss through reactions with H, N and CH₃ and with ions.

HCCO was first detected in dark clouds by Agúndez et al.(2015b) and reported in TMC-1 by Cernicharo al. (2020b, 2021b) with a fractional abundance of 7.7 × 10⁻¹¹. Its chemistry was discussed by Wakelam et al. (2015b) who proposed both gas-phase and grain-surface syntheses. In the gas phase its major formation reactions are those of C₂H with OH and O₂. For the former, we adopt the rate coefficient suggested by Wakelam et al. For the latter, we include the four product channels in the compilation by Baulch et al. (2005) with that to HCCO given a branching ratio of 20%. Loss occurs through H and O atoms (Baulch et al. 2005) together with ion-neutral reactions. We follow the recommendation by Wakelam et al. (2015b) for the products and branching ratios for the dissociative recombination of H₂CCO⁺, replacing those contained in RATE12 which were taken from Prasad & Huntress (1980). HCCO was not contained in RATE12 but its protonated form, CH₂CO⁺, was included. For consistency, we have relabelled CH₂CO⁺ as H₂CCO⁺ in RATE22.

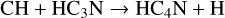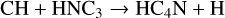HC₄N was detected in TMC-1 by Cernicharo et al. (2021a) with an abundance of 3.7 × 10⁻¹¹. We assume that it is formed in a similar fashion to HCCN, that is through reactions of CH and both HC₃N and its isomer HNC₃. 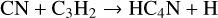$CH + {HC}_{3} N \to {HC}_{4} N + H$ ${\rm{CH}} + {\rm{HN}}{{\rm{C}}_3} \to {\rm{H}}{{\rm{C}}_4}{\rm{N}} + {\rm{H}}$ (36) $CH + {HNC}_{3} \to {HC}_{4} N + H$ ${\rm{CN}} + {{\rm{C}}_3}{{\rm{H}}_2} \to {\rm{H}}{{\rm{C}}_4}{\rm{N}} + {\rm{H}}$ (37) $CN + C_{3} H_{2} \to {HC}_{4} N + H$ ${\rm{CN}} + {{\rm{H}}_2}{\rm{CCC}} \to {\rm{H}}{{\rm{C}}_4}{\rm{N}} + {\rm{H}}$ (38) $CN + H_{2} CCC \to {HC}_{4} N + H$ ${\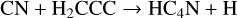rm{CN}} + {{\rm{H}}_2}{\rm{CCC}} \to {\rm{H}}{{\rm{C}}_4}{\rm{N}} + {\rm{H}}$ (39) $C_{2} N + C_{2} H_{2} \to {HC}_{4} N + H,$ ${{\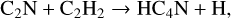rm{C}}_2}{\rm{N}} + {{\rm{C}}_2}{{\rm{H}}_2} \to {\rm{H}}{{\rm{C}}_4}{\rm{N}} + {\rm{H}},$ (40)

with rate coefficients taken from Loison et al. (2015). We calculate loss rates in IN reactions with common ions and also include loss with N atoms.

3.21 CH₃Cl

Methyl chloride was detected in the proto-binary source IRAS 16293-2422B by Fayolle et al. (2017). The chemistry of this molecule and related species has been discussed in detail by Acharyya & Herbst (2017) and we adopt their scheme for RATE22.

3.22 PH₃

Phosphine was not included in the RATE12 release as no route to PH₄⁺ could be found. As the 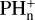${PH}_{n}^{+}$ ${\rm{PH}}_{\rm{n}}^ +$ reactions with H₂ are endother-mic, formation of the P-H bond proceeds via the RA of P⁺ and PH⁺ with H₂. However, PH₃⁺ does not react with H₂ to form PH₄⁺. Here we circumvent this issue by incorporating MN reactions of PH₃⁺ with anions to form PH₃ directly. Its loss via ion-neutral reactions is taken from Charnley & Millar (1994) with its photodissociation rate from Sil et al. (2021).

3.23 ArH⁺

ArH⁺ was detected by Barlow et al. (2013) in the Crab Nebula and subsequently in absorption toward several Galactic molecular clouds by Schilke et al. (2014). Argon has an unusual interstellar chemistry in that its proton affinity is lower than that of H₂ while its ionisation potential is larger than that of atomic hydrogen meaning that Ar cannot be ionised by the interstellar UV field nor can ArH⁺ be formed through the proton transfer between Ar and H₃⁺. Instead, ArH⁺ is formed by the reaction of Ar⁺ with H₂ where the ion is the result of cosmic ray ion-isation of Ar and charge exchange between He⁺ and Ar (Babb & McLaughlin 2018). We have adopted the chemistry and rate coefficients proposed by Schilke et al. augmented by the laboratory measurements of the rate coefficients of ArH⁺ with H₂ and CO (Villinger et al. 1982). Its DR rate coefficient has been calculated by Abdoulanziz et al. (2018) who show that it is van-ishingly small for vibrationally cold ArH⁺ and we neglect it here. Schilke et al. show that that ArH⁺ is a tracer of gas with a low H₂ fraction.

3.24 Circumstellar chemistry

In the following, we describe the chemistries of elements that, due to their large depletion in interstellar clouds, are predominantly found in molecular form in the circumstellar environments.

3.24.1 MgO and MgOH

MgO and MgOH are formed through NN reactions in either the hot inner winds of O-rich AGB stars or following grain disruption in post-shock gas, rate coefficients taken from the theoretical calculations by Decin et al. (2018). In general these reactions have large energy barriers. MgO also forms in the radiative association of Mg and O (Bai et al. 2021a) but the rate coefficient is too small to produce it in any significant amount. Its photodissociation rate is taken from Bai et al. (2021b).

3.24.2 MgNC, MgCN and HMgNC

These Mg-bearing species have all been detected in the outer envelope of the carbon-rich AGB star, IRC+10216 - MgNC (Guélin et al. 1993), MgCN (Ziurys et al. 1995), and HMgNC (Cabezas et al. 2013) - indicating that a relatively low-temperature chemistry produces these species. Cabezas et al. calculate column densities of 1.3 × 10¹³ (MgNC), 7.4 × 10¹¹ (MgCN), and 6 × 10¹¹ (HMgNC) cm⁻² to show their abundance ratios scale roughly as MgNC:MgCN:HMgNC = 15:1:0.8. The first two are likely formed in the dissociative recombination of MgNCH⁺ formed by the radiative association of Mg⁺ and HCN (Petrie & Dunbar 2000). We used the Levenberg-Marquardt algorithm to fit their tabulated data over the temperature range 10–100 K by the expression 1.96 × 10⁻¹⁷(T/300)⁻¹⁴⁹ cm³ s⁻¹ and added the association of Mg⁺ with HNC which is slightly faster than that with HCN. Cabezas et al. also suggest that some HMgNC could be formed with a branching ratio of about 1% in the dissociative recombination of larger Mg-cyanopolyyne ions and we include this possibility (see Sect. 3.24.3). Mutual neutralisation between the protonated versions of these molecules with the observed anions, listed in Sect. 1, are also included. For MN reactions involving MgNCH⁺ we have assumed a 50:50 branching ratio to MgNC and MgCN.

We have included the standard set of IN reactions and ion-dipole rate coefficients for the loss of these species. For the case of IRC+10216, however, photodissociation is likely to be a more important loss process in the external envelope and one that can determine both column densities and the radial extent of these species. We have allocated uniform (and highly uncertain) rates of 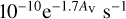$10^{- 10} e^{- 1.7 A} s^{- 1}$ ${10^{ - 10}}{{\rm{e}}^{ - 1.7A}}{{\rm{s}}^{ - 1}}$ for all these species.

Table 3

Fit parameters for the radiative association of Mg⁺ with cyanopolyynes over the range 10–300 K.

3.24.3 MgC₃N, HMgC₃N, MgC₅N and MgC₇N

The magnesium cyanopolyynes, MgC₃N and MgC₅N have both been detected in the outer envelope of IRC+10216 with column densities of 9.3 ×10¹² and 4.7 ×10¹² cm⁻², respectively (Cernicharo et al. 2019; Pardo et al. 2021). The formation of these species is thought to proceed from the radiative association of Mg⁺ with the HC_2n+1N cyanopolyynes. Their rate coefficients have been tabulated by Dunbar & Petrie (2002) over the range 10–00 K. Our fits to these are shown in Table 3. For completeness, we include the rate coefficient for HC₉N in this table although MgC₉N is not included in the ratefile. On the other hand, MgC₇N, which is not yet detected, is included here.

The large ions created via radiative association will disso-ciatively recombine with electrons and could, in principle, have several product channels. Here, we have followed the scaling procedures adopted by Pardo et al. (2021) with a total rate coefficient of 3 ×10⁻⁷ (T/300)^−1/2 cm³ s⁻¹. As an example, the dissociative recombination of MgC₅NH⁺ leads to MgNC, MgC₅N, and HMgNC with values of the rate coefficients at 300 K of 7.80 ×10⁻⁸, 2.22 ×10⁻⁷, and 2.22 ×10⁻⁹ cm³ s⁻¹, respectively. In addition, we have included MN reactions between the observed anions and Mg-bearing cations. The Mg-carbon chain molecules have very large dipole moments, in excess of 6 D, and therefore very large rate coefficients for ion-neutral reactions at low temperature. As for the smaller Mg-CN species, their abundance and extent in the outer envelope is likely to be determined by photodissociation; we adopt the same photodissociation rates as those for the smaller Mg-bearing species. In all cases we assume that the product is Mg and the appropriate C_2n+1 N radical.

Recently Cabezas et al. (2023) detected HMgC₃N in IRC+10216 with a column density of 3 × 10¹² cm⁻². Its formation is uncertain but may occur as a product channel in the DR of the larger Mg-cyanopolyyne ions. It is not included in RATE22.

3.24.4 MgC₂, MgC₂H, MgC₄H, MgC₆H and MgC₈H

The magnesium acetylide chains MgC₂H, MgC₄H, and MgC₆H have all been detected in the outer envelope of IRC+10216 (Agúndez et al. 2014; Cernicharo et al. 2019; Pardo et al. 2021) with column densities of 2 × 10¹², 2.2 × 10¹³, and 2 × 10¹³ cm⁻², respectively, and abundance ratios of 1:11:10 in order of increasing size (Pardo et al. 2021). More recently, MgC₂ has been detected in the same region with a column density of 10¹² cm⁻² (Changala et al. 2022). Their formation routes are, as for the magnesium cyanopolyynes, thought to be dominated by radiative association, in this case between Mg⁺ and the polyacetylenes. These rate coefficients are tabulated by Petrie & Dunbar (2000) and Dunbar & Petrie (2002) and we have again found a best fit to them (Table 4). The ions so produced are assumed to recombine in a manner in which 80% of the recombinations lose either a hydrogen or a magnesium atom, for example, dissociative recombination of MgC₄H₂⁺ leads to either Mg + C₄H₂ or MgC₄H + H with equal branching ratios, with the remaining 20% divided equally between MgC₂ and MgC₂H. Of these species, the most difficult to match calculated and observed column densities is MgC₄H for which the value of the RA rate coefficient is more than three orders of magnitude smaller than those for the larger hydrocarbons.

In common with the magnesium cyanopolyynes, photodis-sociation plays an important role in setting the abundance and radial extent of these molecules. We assume the same rate coefficients as in Sect. 3.24.2 and assume that the sole product is Mg and the appropriate C_2nH radical.

Table 4

Fit parameters for the radiative association of Mg⁺ with polyynes over the range 10–300 K.

3.24.5 Aluminium chemistry

Seventeen Al-bearing molecules, including AlO, AlOH, AlF, and AlCl which are detected in AGB stars (Decin et al. 2017; Danilovich et al. 2021), are included in this release. Given the fact that along with Ti and Ca, aluminium is one of the most depleted elements in interstellar clouds, our primary purpose is to include a network that describes as best as possible the synthesis of observed Al-bearing molecules in hot gas in the inner circumstellar envelopes of these stars. As such, it is dominated by nearly 100 neutral–neutral reactions and contains molecules in size up to 5 atoms (Al₂O₃) and in mass up to 132 amu (AlCl₃). Some of these, particularly the oxides, have measured rate coefficients but the majority are theoretical estimates which, because of the high-temperature environment in which these species are found, have both forward and backward determinations of rate coefficients. The main sources of information on these reactions comes are from Swihart et al. (2003) and Gobrecht et al. (2022). We note that the latter authors, who are interested in how Al-O clusters can grow to dust grains, describe routes to molecules much larger than included in the database.

There is no gas-phase formation for AlH₃ included in RATE22. We retain it for those occasions in which it may be chosen as a parent molecule in the calculation of Al chemistry in the inner regions of O-rich AGB stars. If not included as a parent, its abundance is always calculated to be zero.

3.24.6 Calcium chemistry

Eleven NN reactions are used to describe CaO and CaOH formation at high temperature, appropriate for conditions in the inner envelopes of O-rich AGB stars. Rate coefficients are a mix of theoretical, taken mainly from Decin et al. (2018), and experimental values.

Table 5

Fit parameters for the radiative association of Na⁺ with cyanopolyynes over the range 10–300 K.

3.24.7 Titanium chemistry

TiO and TiO₂ are detected species in the circumstellar envelopes of O-rich AGB stars (Decin et al. 2020; Wallström et al. 2024). Laboratory data exists for the synthesis of both through a mixture of IN and NN chemistry. Rate coefficients for the latter are mostly experimental and taken from Campbell & McClean (1993) and Plane (2013). Ti is reactive with several common interstellar and circumstellar oxides to form TiO which can be converted to TiO₂ through reaction with OH and O₂. Some of these reactions are known to be efficient at room temperature and, since both have large dipole moments, we have included proton transfer with rate coefficients calculated using Eq. (5) which, following DR, lead to loss mechanisms for both. A low-temperature interstellar synthesis of these species is therefore possible though this will be limited in effect since Ti is one of the most heavily depleted elements in interstellar gas.

3.24.8 Sodium chemistry

Petrie & Dunbar (2000) and Dunbar & Petrie (2002) give rate coefficients for the RA of Na⁺ with HCN and the cyanopolyynes up to HC₉N for temperatures up to 100 K and 300 K, respectively. As for the corresponding data for Mg⁺, we have fitted their tabulated values to the usual modified Arrhenius formula. NaCN is a T-shaped molecule and has been observed in IRC+10216, originally by Turner et al. (1994) and mapped with ALMA by Quintana-Lacaci et al. (2017) who show that, in common with CH₃CN (Agúndez et al. 2015c) and HC₃N (Siebert et al. 2022b), it has emission close to the star and extends out to a distance of a few times 10¹⁵ cm.

To estimate the abundance of NaCN, which has a dipole moment of 8.85 D, we have included the usual set of ion-dipole rate coefficients and adopted an unshielded photodissociation rate of 10^-10 s^-1. The branching ratios of the DR reactions of the NaC_2n+1NH⁺ ions (n = 0–4) are unknown; here we adopt a 50:50 ratio between the Na and NaCN channels.

Cabezas et al. (2023) detected NaC3N in the outer envelope of IRC+10216 with a column density of 1.2 × 10¹¹ cm^-2, about a factor of eight less than that of MgC3N and a detection aided by its extremely large dipole moment, 12.9 D. Its formation routes are unknown but, as with the Mg cyanopolyynes, they are likely to involve the dissociative recombination of the products of the radiative association between Na⁺ and the cyanopolyynes. Table 5 shows our fits to the rate coefficients calculated by Dunbar & Petrie (2002) for the radiative associations of Na⁺ with the cyanopolyynes. Below 30 K, the rate coefficients for Na⁺ are, however, more than an order of magnitude smaller than those of Mg⁺ with HC₃N and HC₅N indicating that efficient formation of NaC3N may depend on either a larger branching ratio or rate coefficent in the DR of NaC₃NH⁺, or on preferential production via DR of the larger RA products. We note that NaC₃N is not yet included in the database.

Sodium chloride has been detected most frequently in the CSEs of both C-rich and O-rich AGB stars (Cernicharo & Guélin 1987; Decin et al. 2016), in the post-AGB object CRL 2688 (Highberger et al. 2003) and in one early-type region, the protostellar disk around Orion Srcl (Ginsburg et al. 2019). The formation of NaCl is very poorly understood. Šimsová-Zámecníková et al. (2022) have calculated the rate coefficient of the direct formation through the RA between Na and Cl over the temperature range 30–750 K. We have also included formation via the reaction of Na and HCl for which we adopt a fit over 591–966 K to the two experimental data sets in the NIST database. Petrie (1996) has suggested that NaCl can react with CN to produce NaCN and we have included this reaction with a (very uncertain) rate coefficient of 10^-10 cm³ s^-1. NaCl has a large dipole moment, 9.0 D, so ion-dipole rate coefficients are adopted, with photodissociation and cosmic ray-induced photodissociation rates taken from Heays et al. (2017).

Finally, it is worth pointing out that Na has a very low ionization potential. However, Na⁺ is unreactive with many common neutral species which makes it an important source of free electrons in dark clouds.

Table 6

Detected species, listed by number of atoms, missing from the Rate22 database.

3.25 Other detected molecules

As noted previously, there are a number of molecules detected in recent years that are not included in RATE22. The main reasons for such exclusion are: (i) that gas-phase formation routes have not yet been identified for them; (ii) their formation, while known, depends on the presence of another species whose origin is unknown; and (iii) grain surface chemistry likely dominates their syntheses. In addition to those molecules mentioned previously, these include ethylene oxide, also known as oxirane, c-C₂H₄O, isocyanogen, CNCN, detected in TMC-1 by Agúndez et al. (2018a), nitrous acid, HONO, 3-hydroxypropenal, HOCHCHCHO, also known as malonalde-hyde, detected in IRAS 16293-2422B (Coutens et al. 2019, 2022), and methoxymethanol, CH₃OCH₂OH, discovered in NGC6334I MM1 (McGuire et al. 2017b). Missing species, ignoring conformers and the fullerene molecules, are shown in Table 6.

4 Model results

In this section, we describe our model calculations for conditions appropriate to the dark cloud TMC-1 and to the circumstellar envelope of the carbon-rich AGB star IRC+10216. In both cases, we discuss the results for two ratefiles – our standard file and the reduced file in which the 53 endothermic reactions identified by Tinacci et al. (2023) are excluded (Sect. 2.3) and compare these to the extensive observational data for both objects.

4.1 Dark cloud TMC-1

We choose typical dark cloud parameters; n(H₂) = 10⁴ cm^-3, a kinetic temperature T = 104 K, a visual extinction of 10 mag., and a cosmic-ray ionisation rate of 1.3 × 10^-17 s^-1.

4.1.1 O-rich TMC-1 model

We have calculated a time-dependent model using the ‘low metal’ initial elemental abundances given in Table 7. These O-rich (C/O less than 1) abundances are the same as those in McElroy et al. (2013) with the exception of S for which we adopt the value of 1.5 × 10^-6 as suggested by Fuente et al. (2023) in their recent modelling of the chemistry of dark clouds in Taurus and Perseus.

Figures 1 and 2 show the time evolution of various N-bearing molecules in the O-rich, Rate22 and Rate 12 models. There are significant differences between the results that are, in major part, driven by the inclusion of the reaction of C + NH₃ in RATE22. This reaction was studied experimentally from 50 K to 300 K by Hickson et al. (2015) and shown to be fast at low temperatures. Since atomic carbon is the dominant form of this element before it is processed into CO, the abundance of NH₃ is depressed at times up to about 5 × 10⁵ yr. For the cyanopolyynes, the situation is somewhat different. Here, their peak abundances in RATE 22 are reached at slightly earlier times than in RATE12 but the peak abundances are fairly similar. The major differences now occur at long times, greater than 10⁶ yr.

We have searched for a ‘best time’ fit between calculated, f_c, and observed, f₀, fractional abundances for those 134 species for which we have ‘retrieved’ abundances, that is, we neglect those species for which only upper limits are available. To do so, we calculate the average modulus of the difference, D, in the logarithms of these between these two abundances: $D = \frac{1}{N_{obs}} Σ {({[\log f_{c} - \log f_{o}]}^{2})}^{1 / 2} .$ $D = {1 \over {{N_{{\rm{obs}}}}}}\Sigma {\left( {{{\left[ {\log {f_{\rm{c}}} - \log {f_{\rm{o}}}} \right]}^2}} \right)^{1/2}}.$ (41)

Since we know that gas-phase chemistry is not appropriate for certain species – CH₃OH is a well-known example – we also calculated a ‘reduced’ difference, D_red, in which we remove species with D > 4, that is, those whose calculated abundance differs by more than 4 orders of magnitude from that observed. Figure 3 shows values of D, D_red and the number of excluded species, NR, as a function of time in the chemical evolution. A ‘best-fit’ solution would be one in which D is a minimum and N, the number of species whose abundances are within an order of magnitude of those observed, a maximum. This occurs in the range of (1– 2) × 10⁵ yr with the formal ‘best fit’ time at 1.6 × 10⁵ yr at which NR = 9 and 55 of the 134 species have calculated abundances that fall within an order of magnitude of their observed values (see Table 8). A better fit, in the sense of a lower D_red, can be found at earlier time but at the expense of removing a significant number of species. If we seek to mimimise the number excluded, we again find that a time of 1.6 × 10⁵ yr is the preferred time. At times longer than 3 × 10⁵ yr, NR increases and Ν decreases so that at 10⁶ yr, D = 3.34, NR = 39 and Ν = 20, an extremely poor fit. This table also includes values in parentheses when the reduced reaction ratefile is used. One sees that the exclusion of reactions makes the fit slightly worse although the overall differences are marginal at 1.6 × 10⁵ yr.

Table A.1 compares the model results for the full ratefile with the observed fractional abundances, including upper limits, of 149 species in TMC-1 at a time of 1.6 × 10⁵ yr. It is clear from this table that the model, which has an initial C/O abundance = 0.44, fails to reproduce the abundances of many species by several orders of magnitude, as indeed was the case for the Rate 12 models. These include species that are thought, from observations of massive star-forming regions, to be either formed on icy grains or from the evaporation products of such surface reactions, species such as methanol, methyl formate, and dimethyl ether.

In general, the C_nO abundances are well fit for η = 2, 3 but are severely over-produced for larger values as are the related species, HC_nO. This may be due to an overestimate of the RA rate coefficients for the CO-hydrocarbon ion reactions since these are estimated from three-body experimental measurements (Adams et al. 1989).

One of the major changes between these results and Rate 12 is the huge decrease in the calculated abundance of propene, CH₃CHCH₂, by ten orders of magnitude, contrary to the fact that its observed value in TMC-1 is 4.0 × 10⁻⁹ (Marcelino et al. 2007). Previously, it was formed by the DR of C₃H₇⁺ formed in successive radiative association reactions of H₂ with C₃H₃⁺ and C₃H₅⁺. These reactions, included in RATE 12, were subsequently determined to have barriers in their entrance channels and therefore not to proceed (Lin et al. 2013). The large decrease in the propene abundance has significant implications for larger hydrocarbons since it is a reactive species with large rate coefficients measured in NN reactions at low temperatures. For example, in terms of observed molecules in TMC-1, laboratory studies have shown that reactions of propene with C₂ form CH₃C₄H and its isomer allenyl acetylene, H₂CCCHCCH, those with C₂H form propyne, CH₃CCH, those with C₄H form CH₃C₆H, those with CN form vinyl cyanide, CH₂CHCN, crotononi-trile, CH₃CHCHCN, methacrylonitrile, CH₂C(CH₃)CN, and allyl cyanide, CH₂CHCH₂CN (Cernicharo et al. 2022c), and those with CH form cyclopentadiene, c-C₅H₆, and butadiene, CH₂CHCHCH₂. These newly formed species can then react to form other organic species. For example, c-C₅H₆ can react with CN to form cyanocyclopentadiene, C₅H₅CN, with C₂H to form both fulvenallene, C₅H₄CCH₂, and ethynyl cyclopentadiene, C₅H₅CCH, and with C to form phenyl, C-C₆H₅ (Cernicharo et al. 2022b). Similarly, allenyl acetylene, H₂CCCHCCH, can react with CN to form cyanoacetyleneallene, H₂CCCHC₃N, an isomer of CH₃C₅N (Shingledecker et al. 2021). All of these species are calculated to have abundances at least three orders of magnitude less than their observed values in TMC-1. Very few of these large hydrocarbons are included in the RATE 12 ratefile but, as an example of the different predictions of the RATE22 models, we compare in Fig. 4 the abundances of four molecules in common, including those of propene and butadiene, CH₂CHCHCH₂. One sees clearly that this catastrophic decrease in the calculated propene abundance has a severe effect on those of the larger hydrocarbons.

Table 7

Initial abundances relative to total Η nuclei, n_H.

Fig. 1

Time evolution of various N-bearing molecules in the dark cloud, O-rich model for both Rate22 (solid lines) and Rate12 (dashed lines).

Fig. 2

Time evolution of various cyanopolyynes in the dark cloud, O-rich model for both Rate22 (solid lines) and Rate12 (dashed lines).

Fig. 3

Best-fit, D, and reduced best-fit, Dred, average difference between observed and calculated species for the full ratefile and O-rich initial conditions. The curve labelled ‘NR’ indicates the number of species removed in calculating the global average, Dred, and Ν is the number of species whose abundances lie within an order of magnitude of those observed.

Table 8

Fitting information on the comparison between observed and calculated abundances for the O-rich case.

4.1.2 C-rich TMC-1 model

One possible mechanism to enhance the formation rate of complex hydrocarbons is to adopt a model with an elemental C/O ratio greater than 1, simulating an environment, say, where Ο is removed from the gas in the form of H₂0 ice. We note that a selective depletion process for oxygen can also occur on warm dust in PDRs due to the high binding energy of Ο atoms (Esplugues et al. 2019; Röllig & Ossenkopf-Okada 2022). Here we adopt the values for the fractional abundance of C and Ο relative to H₂ of 2.8 × 10⁻⁴ and 2.0 × 10⁻⁴, respectively, values taken from Agúndez & Wakelam (2013). Figure 5 shows the results and Table 9 provides global information on the fit at various times. In general the D and D_red values are reduced for the C-rich model compared to the O-rich model. For these conditions, the abundances of many of the complex hydrocarbons discussed above now agree with observation to within an order of magnitude at 10⁶ yr. In addition to propene, only CH₃C₄H, c-C₅H₆, CH₃CHCHCN, and C₅H₅CN show differences with observation of more than an order of magnitude.

In this case the number of species whose abundances agree to within an order of magnitude of those observed ranges from 50 at 1.6 × 10⁵ yr to a maximum of 79 at 10⁶ yr. In the latter case, only 10 species are different by more than four orders of magnitude and when these are removed, the average difference between observed and calculated values is less than a factor of 10. If one considers the additional 15 upper limits in Table A.2, a further 7 species agree, that is the model gives agreement for 86 out of a total of 149 species, or 58%. Many species showing the largest differences are the same in both models but in the C-rich case, there is a tendency to over-produce the large hydrocarbon chains, including C₅H₂, C₆H₂, C_BO (n = 4–7), HC_BO (n = 4–7) C_nS (n = 4,5), and the cyanopolyynes with η > 7.

Other values of C/O are used in the literature and to see the effect of these, we have also considered a model in which C/O =1.1, with an Ο abundance of 3.1 × 10⁻⁴ (Barnum et al. 2022). The models show an improvement with respect to the C/O = 1.4 models (see Table 9) and in particular at a time of 5.0 × 10⁵ yr, when D_red is about 15% smaller and Ν about 19% larger than the values for C/O = 1.4. In part, the improved fit is a result of a reduction in the over-production of large hydrocarbon chains discussed in the previous paragraph. As was also found for the O-rich case, the removal of the 53 endothermic reactions makes only a slight change in the results presented here for the full ratefile.

Fig. 4

Time evolution of propene and species formed from it in the dark cloud, O-rich model for both Rate22 (solid lines) and Rate 12 (dashed lines).

Fig. 5

Best-fit, D, and reduced best-fit, Dred, average difference between observed and calculated species for the full ratefile and C/O = 1.4. The curve labelled ‘NR’ indicates the number of species removed in calculating the global average, Dred, and Ν is the number of species whose abundances lie within an order of magnitude of those observed.

Table 9

Fitting information on the comparison between observed and calculated abundances for the C-rich model with C/O = 1.4.

Table 10

Initial fractional abundances, f, relative to H₂ for the CSE model.

4.2 IRC+10216

We have also investigated the application of the ratenle to a model of the circumstellar envelope surrounding IRC+10216 in which the external interstellar UV field drives the chemistry. We assume standard physical parameters for the outflow. Motivated by the revised, and larger, distance to IRC+10216 suggested by Andriantsaralaza et al. (2022), we adopt a uniform mass-loss rate, Ṁ, of 3.0 × 10⁻⁵ M_⊙ yr⁻¹. We choose an expansion velocity, v_e, of 14.5 km s⁻¹, and a power-law temperature distribution, T(r) = T*(r/R_*)^−0.7, with a stellar temperature T_* = 2330 Κ and stellar radius R_*= 5.0 × 10¹³ cm. With a constant mass-loss rate and expansion velocity, the number density of H₂, which is proportional to Ṁ/v_e, follows an r⁻² power law while the visual extinction to interstellar UV radiation follows an r⁻¹ distribution. | We have adopted input parent abundances from Agúndez et al. (2020) and Van de Sande et al. (2021) augmented by metal atom abundances (Table 10). We calculate the chemistry from an initial radius of 10¹⁴ cm out to 10¹⁸ cm. At 10¹⁴ cm, n(H₂) = 2.33 × lO⁹ cm⁻³, Τ = 1424 Κ, and A_v = 1160 mag.

Figures 6 and 7 show the fractional abundances of the cyanopolyynes and the Mg-terminated cyanopolyynes as a function of radial distance. We compare calculated column densities with those of 61 observed daughter species, that is, species which are not parents, in IRC+10216 for a mass-loss rate of 3.0 × 10⁻⁵Μ_⊙ yr⁻¹ in Table 11. We note, however, that observationally-derived column densities of the same molecule can differ by more than an order of magnitude as they are often dependent on a variety of factors: the particular excitation properties associated with observed transitions; the angular resolution of the telescope; whether or not the column density calculation includes an estimation of the size of the emitting region, often taken to be the photodissociation radius; and whether or not a beam-averaged column density is given. Thus our comparison is at best only indicative of how the model behaves.

We find that only one species, MgC₄H, has a column density more than 4 orders of magnitude different (less) than that observed. For our power-law temperature distribution, we find D = 1.00(0.99), D_red = 0.95(0.94), and that 37(38) of the 61 species have calculated and observed column densities that differ by less than an order of magnitude, where the values in parentheses are from the reduced ratefile. One sees that the reduction in the number of reactions has a negligible effect on our overall fit, with negligible differences also on column densities (though not shown here).

Eight species have column densities that fall more than a factor of 100 less than those observed: the anions CN^-, C₄H^-, and C₇N^-; the Mg-species MgC₄H and MgC₃N, CH₂NH, CH₂CN, and CCP. No species has a column density more than 100 times larger than observed.

Figure 8 shows the radial distribution of the magnesium polyacetylides for a mass-loss rate of 3.0 × 10^-5 M_⊙,yr^-1.

The abundance of the longest chain MgC₈H is larger than the others primarily because the rate coefficient of the RA between Mg⁺ and C₈H₂ is larger than those of Mg⁺ with the smaller cumulenes (see Sect. 3.24.4).

The reason for the large discrepancy between model and observed abundances for MgC₄H could be due to the fact that we do not differentiate between diacetylene, HC₄H, and the cumu-lene H₂C₄. As a result, we do not include either of these as a parent molecule whereas in fact Fonfría et al. (2018) have found that diacetylene has a column density of around 1.9 × 10¹⁶ cm^-2 close to the star. We thus investigated a model in which we included diacetylene as a parent species with an initial abundance of 1.6 × 10^-6 but found that the column density of MgC₄H increased only by an order of magnitude, still far too low. The reason appears to be that the RA rate coefficient (see Table 4) is simply too low. It also may be possible to synthesise the correct abundance if the larger protonated Mg-acetylide chains formed it via DR. That is, MgC₆H₂+/MgC₈H₂⁺ + e^- → MgC₄H as well as other products. This would imply substantial rearrangement in the DR process and should be the subject of theoretical or experimental investigation.

Fig. 6

Fractional abundances of the cyanopolyynes for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr⁻¹ as a function of radial distance from the central star.

Fig. 7

Fractional abundances of the Mg-terminated cyanopolyynes for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr⁻¹ as a function of radial distance from the central star.

Table 11

Observed and calculated column densities (cm⁻²) in IRC+10216 for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr ¹.

Fig. 8

Fractional abundances of the Mg-terminated polyacetylides for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr⁻¹ as a function of radial distance from the central star.

5 Summary

We have outlined the major differences between our new release of the UMIST Database for Astrochemistry, RATE22, and the previous version RATE 12. The numbers of species and reactions have increased substantially in large part driven by the substantial number of new detections made over the past decade. Many observed species are, however, excluded from the database due to the lack of identified gas-phase mechanisms.

We have calculated time-dependent chemical kinetic models for a dark cloud with physical conditions similar to those in TMC-1 for both O-rich and C-rich initial conditions. As expected, the C-rich models give a much better agreement with observations with 70–80 having abundances within an order of magnitude of the 134 observed. Our results, at least in terms of our ‘reduced least squares’ fit, are not affected significantly by the choice of C/O ratio although the lower value of 1.1 reduces the degree of over-production of hydrocarbon chain molecules. We discuss reasons for the largest discrepancies and conclude that while grain surface formation is indicated for some species, the inefficient production of C₃H₇⁺ and hence of propene, CH₃CHCH₂, is a key inhibitor of the production of larger hydrocarbons. We have also applied our network to the case of an outflow from a carbon-rich AGB star, finding agreement to within an order of magnitude between calculated and observed column densities for about 60% of the daughter species included in chemistry.

In several cases, abundances are either greatly over- or underproduced. For dark clouds, these include species affected by the ‘propene catastrophe’ as discussed in Sect. 4.1.1. Other examples include the C_nO and the HC_nO species also discussed in Sect. 4.1.1, and the Mg-bearing molecules observed in IRC+10216 (Sect. 4.2). The chemistry of all these species rely on two processes, radiative association and dissociative recombination, and their calculated abundances are therefore very sensitive to the rate coefficients adopted for both and to branching ratios of the DR reactions.

We have also considered the removal of the endothermic reactions identified in the KIDA database by Tinacci et al. (2023). We find that these make only a minor change to our global fits for all models considered here.

We have not attempted to produce isotopic versions of RATE22, the most important of which would include ¹³C and D. Both would need significant effort if multiply-substituted species were to be included. Even if one considers single isotopic substitutions, there are severe uncertainties in the choice of additional reactions and rate coefficients. For example, during a formation process that involves reactants containing multiple carbon atoms, there is almost no information on where a ¹³C atom might replace a ¹²C atom, nor where ¹³C might be retained in the DR of a complex hydrocarbon ion. Nearly 200 species in RATE22 contain 5 or more C atoms. With the exception of HC₅N and HC₇N, (Burkhardt et al. 2018), there is little observational data available on ¹³C/¹²C ratios in larger molecules. Molecules with large numbers of carbon atoms are more likely to contain a ¹³C atom simply from a statistical viewpoint (Burkhardt et al. 2018), further confusing an understanding of the impact of ¹³C chemistry.

For deuterium, the situation is complicated by the need to include the spin chemistry of H₂, its ions and deuterated counterparts, as well as those of multiply-deuterated species given that many such species are detected in interstellar clouds. Majumdar et al. (2017) published such a model based on a KIDA network that incorporated 7509 gas-phase reactions. The ratefile contained 111 000 reactions when deuterated. A similar multiplicative factor might be expected for the Rate22 ratefile.

In addition to the gas-phase chemistry discussed here, we have produced a website that will include the codes needed to generate chemical models for both interstellar clouds and circumstellar envelopes. Previously, Van de Sande & Millar extended the Rate 12 CSE models to include the effects of porosity, clumpy outflows and irradiation by internal UV photons from the AGB star (Van de Sande & Millar 2019) and from an nearby companion star (Van de Sande & Millar 2022). We shall extend the capability of our CSE models by calculating these photorates for use with the RATE22 network. Finally, we note that, although there has been a decade between this and the previous release of the UDfA, we plan to issue updates to the database on an annual basis.

Acknowledgements

We are extremely grateful to the anonymous reviewer whose close, careful reading and expert comments greatly improved the original manuscript. This work could not have been completed without the support of the Leverhulme Trust through the award of an Emeritus Fellowship to TJ.M. He also acknowledges support from the STFC through grants ST/P000312/1 and ST/T000287/1. M.V.d.S. acknowledges support from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 882991. C.W. acknowledges financial support from the University of Leeds, the Science and Technology Facilities Council, and UK Research and Innovation (grant numbers ST/T000287/1 and MR/T040726/1).

Appendix A Comparison of observed and calculated abundances in TMC-1

We compare observed fractional abundances in TMC-1 with calculated abundances for two models, the first for the O-rich conditions described in Sect. 4.1.1 (Table A.1), the second for the C-rich conditions described in Sect. 4.1.2 (Table A.2).

Table A.1

Observed fractional abundances, relative to H₂, in TMC-1(CP) and corresponding calculated ‘best fit’ values at 1.6 × 10⁵ years for the O-rich model.

Table A.2

Observed fractional abundances, relative to H₂, in TMC-1(CP) and corresponding calculated ‘best fit’ values at 1.0 × 10⁶ years for the C-rich (C/O = 1.4) model.

References

Abdoulanziz, A., Colboc, F., Little, D. A., et al. 2018, MNRAS, 479, 2415 [NASA ADS] [CrossRef] [Google Scholar]
Abeysekera, C, Joalland, B., Ariyasingha, N., et al. 2015, J. Phys. Chem. Letts., 6, 1599 [CrossRef] [Google Scholar]
Acharyya, K., & Herbst, E. 2017, ApJ, 850, 105 [NASA ADS] [CrossRef] [Google Scholar]
Adams, N. G., Smith, D., Giles, K., & Herbst, E. 1989, A&A, 220, 269 [Google Scholar]
Adande, G. R., Halfen, D. T., Ziurys, L. M., Quan, D., & Herbst, E. 2010, ApJ, 725, 561 [NASA ADS] [CrossRef] [Google Scholar]
Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
Agúndez, M., Fonfría, J. P., Cernicharo, J., Pardo, J. R., & Guélin, M. 2008, A&A, 479, 493 [Google Scholar]
Agúndez, M., Cernicharo, J., Guélin, M., et al. 2010, A&A, 517, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agúndez, M., Cernicharo, J., & Guélin, M. 2014, A&A, 570, A45 [Google Scholar]
Agúndez, M., Cernicharo, J., de Vicente, P., et al. 2015a, A&A, 579, A10 [Google Scholar]
Agúndez, M., Cernicharo, J., & Guélin, M. 2015b, A&A, 577, A5 [Google Scholar]
Agúndez, M., Cernicharo, J., Quintana-Lacaci, G., et al. 2015c, ApJ, 814, 143 [Google Scholar]
Agúndez, M., Marcelino, N., & Cernicharo, J. 2018a, ApJ, 861, L22 [Google Scholar]
Agúndez, M., Marcelino, N., Cernicharo, J., & Tafalla, M. 2018b, A&A, 611, Al [Google Scholar]
Agúndez, M., Martínez, J. I., de Andres, P. L., Cernicharo, J., & Martín-Gago, J. A. 2020, A&A, 637, A59 [Google Scholar]
Agúndez, M., Cabezas, C., Tercero, B., et al. 2021a, A&A, 647, A10 [Google Scholar]
Agúndez, M., Marcelino, N., Tercero, B., et al. 2021b, A&A, 649, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agúndez, M., Cabezas, C., Marcelino, N., et al. 2022a, A&A, 659, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agúndez, M., Marcelino, N., Cabezas, C., et al. 2022b, A&A, 657, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agúndez, M., Cabezas, C., Marcelino, N., et al. 2023a, A&A, 669, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agúndez, M., Loison, J. C., Hickson, K. M., et al. 2023b, A&A, 673, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Agúndez, M., Marcelino, N., Tercero, B., Jiménez-Serra, I., & Cernicharo, J. 2023c, A&A, 677, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Andriantsaralaza, M., Ramstedt, S., Vlemmings, W. H. T., & De Beck, E. 2022, A&A, 667, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Anicich, V. G. 1993, ApJS, 84, 215 [NASA ADS] [CrossRef] [Google Scholar]
Anicich, V. G., & Huntress, W. T., J. 1986, ApJS, 62, 553 [NASA ADS] [CrossRef] [Google Scholar]
Apponi, A. J., McCarthy, M. C., Gottlieb, C. A., & Thaddeus, P. 1999, ApJ, 516, L103 [Google Scholar]
Ascenzi, D., Cernuto, A., Balucani, N., et al. 2019, A&A, 625, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ausloos, P., Lias, S. G., Buckley, T. J., & Rogers, E. E. 1989, Int. J. Mass Spectrom. Ion Processes, 92, 65 [NASA ADS] [CrossRef] [Google Scholar]
Babb, J. F., & McLaughlin, B. M. 2018, ApJ, 860, 151 [Google Scholar]
Bai, T., Qin, Z., & Liu, L. 2021a, MNRAS, 500, 2496 [Google Scholar]
Bai, T., Qin, Z., & Liu, L. 2021b, MNRAS, 505, 2177 [NASA ADS] [CrossRef] [Google Scholar]
Bakker, E. J., van Dishoeck, E. F., Waters, L. B. F. M., & Schoenmaker, T. 1997, A&A, 323, 469 [NASA ADS] [Google Scholar]
Balucani, N., Asvany, O., Kaiser, R., & Osamura, Y. 2002, J. Phys. Chem. A, 106, 4301 [NASA ADS] [CrossRef] [Google Scholar]
Barlow, M. J., Swinyard, B. M., Owen, P. J., et al. 2013, Science, 342, 1343 [NASA ADS] [CrossRef] [Google Scholar]
Barnum, T. J., Siebert, M. A., Lee, K. L. K., et al. 2022, J. Phys. Chem. A, 126, 2716 [NASA ADS] [CrossRef] [Google Scholar]
Barone, V., Latouche, C., Skouteris, D., et al. 2015, MNRAS, 453, L31 [Google Scholar]
Baulch, D. L., Cobos, C. J., Cox, R. A., et al. 1994, J. Phys. Chem. Ref. Data, 23, 847 [CrossRef] [Google Scholar]
Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [Google Scholar]
Bell, M. B., Avery, L. W., & Feldman, P. A. 1993, ApJ, 417, L37 [Google Scholar]
Berteloite, C., Le Picard, S. D., Balucani, N., Canosa, A., & Sims, I. R. 2010, PCCP, 12, 3677 [NASA ADS] [CrossRef] [Google Scholar]
Bettens, R. P. A., & Herbst, E. 1995, Int. J. Mass Spectrom. Ion Processes, 149, 321 [CrossRef] [Google Scholar]
Bourgalais, J., Capron, M., Abhinavam Kailasanathan, R. K., et al. 2015, ApJ, 812, 106 [NASA ADS] [CrossRef] [Google Scholar]
Bouscasse, L., Csengeri, T., Belloche, A., et al. 2022, A&A, 662, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bouwman, J., Goulay, F., Leone, S. R., & Wilson, K. R. 2012, J. Phys. Chem. A, 116, 3907 [Google Scholar]
Bovolenta, G. M., Vogt-Geisse, S., Bovino, S., & Grassi, T. 2022, ApJS, 262, 17 [NASA ADS] [CrossRef] [Google Scholar]
Brünken, S., Gupta, H., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2007, ApJ, 664, L43 [CrossRef] [Google Scholar]
Burkhardt, A. M., Herbst, E., Kalenskii, S. V., et al. 2018, MNRAS, 474, 5068 [NASA ADS] [CrossRef] [Google Scholar]
Burkhardt, A. M., Long Kelvin Lee, K., Bryan Changala, P., et al. 2021a, ApJ, 913, L18 [NASA ADS] [CrossRef] [Google Scholar]
Burkhardt, A. M., Loomis, R. A., Shingledecker, C. N., et al. 2021b, Nat. Astron., 5, 181 [Google Scholar]
Cabezas, C., Cernicharo, J., Alonso, J. L., et al. 2013, ApJ, 775, 133 [NASA ADS] [CrossRef] [Google Scholar]
Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021a, A&A, 654, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021b, A&A, 654, A9 [Google Scholar]
Cabezas, C., Endo, Y., Roueff, E., et al. 2021c, A&A, 646, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cabezas, C., Tercero, B., Agúndez, M., et al. 2021d, A&A, 650, A9 [Google Scholar]
Cabezas, C., Agúndez, M., Fuentetaja, R., et al. 2022a, A&A, 663, A2 [Google Scholar]
Cabezas, C., Agúndez, M., Marcelino, N., et al. 2022b, A&A, 657, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cabezas, C., Agúndez, M., Marcelino, N., et al. 2022c, A&A, 659, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cabezas, C., Pardo, J. R., Agúndez, M., et al. 2023, A&A, 672, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Campbell, M., & McClean, R. 1993, J. Phys. Chem., 97, 7942 [CrossRef] [Google Scholar]
Carty, D., Le Page, V., Sims, I., & Smith, I. 2001, CPL, 344, 310 [NASA ADS] [CrossRef] [Google Scholar]
Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
Cazaux, S., & Tielens, A. G. G. M. 2010, ApJ, 715, 698 [NASA ADS] [CrossRef] [Google Scholar]
Cernicharo, J., & Guélin, M. 1987, A&A, 183, L10 [NASA ADS] [Google Scholar]
Cernicharo, J., Guélin, M., Hein, H., & Kahane, C. 1987, A&A, 181, L9 [Google Scholar]
Cernicharo, J., Gottlieb, C. A., Guelin, M., Thaddeus, P., & Vrtilek, J. M. 1989, ApJ, 341, L25 [NASA ADS] [CrossRef] [Google Scholar]
Cernicharo, J., Gottlieb, C. A., Guelin, M., et al. 1991a, ApJ, 368, L39 [NASA ADS] [CrossRef] [Google Scholar]
Cernicharo, J., Gottlieb, C. A., Guélin, M., et al. 1991b, ApJ, 368, L43 [NASA ADS] [CrossRef] [Google Scholar]
Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Guélin, M., & Pardo, J. R. 2004, ApJ, 615, L145 [Google Scholar]
Cernicharo, J., Guélin, M., Agúndez, M., et al. 2007, A&A, 467, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Guélin, M., Agúndez, M., McCarthy, M. C., & Thaddeus, P. 2008, ApJ, 688, L83 [NASA ADS] [CrossRef] [Google Scholar]
Cernicharo, J., Spielfiedel, A., Balanca, C., et al. 2011, A&A, 531, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Lefloch, B., Agúndez, M., et al. 2018, ApJ, 853, L22 [CrossRef] [Google Scholar]
Cernicharo, J., Cabezas, C., Pardo, J. R., et al. 2019, A&A, 630, A2 [Google Scholar]
Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020a, A&A, 642, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020b, A&A, 642, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Marcelino, N., Pardo, J. R., et al. 2020c, A&A, 641, A9 [Google Scholar]
Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021a, A&A, 647, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021b, A&A, 656, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021c, A&A, 649, A15 [Google Scholar]
Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021d, A&A, 652, A9 [Google Scholar]
Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021e, A&A, 655, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021f, A&A, 647, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021g, A&A, 648, A3 [Google Scholar]
Cernicharo, J., Cabezas, C., Bailleux, S., et al. 2021h, A&A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021i, A&A, 650, A14 [Google Scholar]
Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021j, A&A, 646, A3 [Google Scholar]
Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2022a, A&A, 657, A16 [Google Scholar]
Cernicharo, J., Fuentetaja, R., Agúndez, M., et al. 2022b, A&A, 663, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Fuentetaja, R., Cabezas, C., et al. 2022c, A&A, 663, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cernicharo, J., Pardo, J. R., Cabezas, C., et al. 2023, A&A, 670, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Changala, P. B., Gupta, H., Cernicharo, J., et al. 2022, ApJ, 940, L42 [NASA ADS] [CrossRef] [Google Scholar]
Charnley, S. B., & Millar, T. J. 1994, MNRAS, 270, 570 [NASA ADS] [CrossRef] [Google Scholar]
Cheikh Sid Ely, S., Morales, S. B., Guillemin, J.-C., Klippenstein, S. J., & Sims, I. R. 2013, J. Phys. Chem. A, 117, 12155 [NASA ADS] [CrossRef] [Google Scholar]
Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
Cooke, I. R., Gupta, D., Messinger, J. P., & Sims, I. R. 2020, ApJ, 891, L41 [Google Scholar]
Cordiner, M. A., & Charnley, S. B. 2012, ApJ, 749, 120 [NASA ADS] [CrossRef] [Google Scholar]
Cordiner, M. A., & Millar, T. J. 2009, ApJ, 697, 68 [NASA ADS] [CrossRef] [Google Scholar]
Cordiner, M. A., Charnley, S. B., Kisiel, Z., McGuire, B. A., & Kuan, Y. J. 2017, ApJ, 850, 187 [NASA ADS] [CrossRef] [Google Scholar]
Coutens, A., Ligterink, N. F. W., Loison, J. C., et al. 2019, A&A, 623, A13 [Google Scholar]
Coutens, A., Loison, J. C., Boulanger, A., et al. 2022, A&A, 660, A6 [Google Scholar]
Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [Google Scholar]
Danilovich, T., Van de Sande, M., Plane, J. M. C., et al. 2021, A&A, 655, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Daugey, N., Caubet, P., Bergeat, A., Costes, M., & Hickson, K. M. 2008, PCCP, 10, 729 [NASA ADS] [CrossRef] [Google Scholar]
Decin, L., Richards, A. M. S., Millar, T. J., et al. 2016, A&A, 592, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Decin, L., Richards, A. M. S., Waters, L. B. F. M., et al. 2017, A&A, 608, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Decin, L., Danilovich, T., Gobrecht, D., et al. 2018, ApJ, 855, 113 [NASA ADS] [CrossRef] [Google Scholar]
Decin, L., Montarges, M., Richards, A. M. S., et al. 2020, Science, 369, 1497 [NASA ADS] [CrossRef] [Google Scholar]
Decker, B. K., Babcock, L. M., & Adams, N. G. 2000, J. Phys. Chem. A, 104, 801 [NASA ADS] [CrossRef] [Google Scholar]
Deeyamulla, M. P., & Husain, D. 2006, J. Photochem. Photobiol. A-Chem., 184, 347 [CrossRef] [Google Scholar]
Doddipatla, S., Galimova, G. R., Wei, H., et al. 2021, Sci. Adv., 7, eabd4044 [Google Scholar]
Douglas, K. M., Lucas, D. I., Walsh, C., et al. 2022, ApJ, 937, L16 [CrossRef] [Google Scholar]
Dunbar, R. C., & Petrie, S. 2002, ApJ, 564, 792 [NASA ADS] [CrossRef] [Google Scholar]
Eichelberger, B., Snow, T. P., Barckholtz, C., & Bierbaum, V. M. 2007, ApJ, 667, 1283 [NASA ADS] [CrossRef] [Google Scholar]
el Akel, M., Kristensen, L. E., Le Gal, R., et al. 2022, A&A, 659, A100 [CrossRef] [EDP Sciences] [Google Scholar]
Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Miller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
Entekhabi, N., Tan, J. C., Cosentino, G., et al. 2022, A&A, 662, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Esplugues, G., Cazaux, S., Caselli, P., Hocuk, S., & Spaans, M. 2019, MNRAS, 486, 1853 [NASA ADS] [Google Scholar]
Fayolle, E. C., Öberg, K. I., Jørgensen, J. K., et al. 2017, Nat. Astron., 1, 703 [NASA ADS] [CrossRef] [Google Scholar]
Foley, N., Cazaux, S., Egorov, D., et al. 2018, MNRAS, 479, 649 [NASA ADS] [Google Scholar]
Fonfría, J. P., Agúndez, M., Cernicharo, J., Richter, M. J., & Lacy, J. H. 2018, ApJ, 852, 80 [Google Scholar]
Ford, K. E. S., Neufeld, D. A., Schilke, P., & Melnick, G. J. 2004, ApJ, 614, 990 [NASA ADS] [CrossRef] [Google Scholar]
Fourikis, N., Takagi, K., & Morimoto, M. 1974, ApJ, 191, L139 [Google Scholar]
Fournier, M. 2014, PhD thesis, Universite de Rennes I, France [Google Scholar]
Frerking, M. A., Linke, R. A., & Thaddeus, P. 1979, ApJ, 234, L143 [NASA ADS] [CrossRef] [Google Scholar]
Fuente, A., Rivière-Marichalar, P., Beitia-Antero, L., et al. 2023, A&A, 670, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fuentetaja, R., Agúndez, M., Cabezas, C., et al. 2022a, A&A, 667, A4 [Google Scholar]
Fuentetaja, R., Cabezas, C., Agúndez, M., et al. 2022b, A&A, 663, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gianturco, F. A., Satta, M., Yurtsever, E., & Wester, R. 2017, ApJ, 850, 42 [Google Scholar]
Ginsburg, A., McGuire, B., Plambeck, R., et al. 2019, ApJ, 872, 54 [NASA ADS] [CrossRef] [Google Scholar]
Gobrecht, D., Plane, J. M. C., Bromley, S. T., et al. 2022, A&A, 658, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
González, D., Ballesteros, B., Canosa, A., Albaladejo, J., & Jiménez, E. 2022, Front. Astron. Space Sci., 8, 239 [CrossRef] [Google Scholar]
Gorai, P., Bhat, B., Sil, M., et al. 2020, ApJ, 895, 86 [Google Scholar]
Goulay, F., & Leone, S. 2006, J. Phys. Chem. A, 110, 1875 [NASA ADS] [CrossRef] [Google Scholar]
Goulay, F., Osborn, D. L., Taatjes, C. A., et al. 2007, PCCP, 9, 4291 [CrossRef] [Google Scholar]
Goulay, F., Trevitt, A. J., Savee, J. D., et al. 2012, J. Phys. Chem. A, 116, 6091 [Google Scholar]
Gratier, P., Majumdar, L., Ohishi, M., et al. 2016, ApJS, 225, 25 [Google Scholar]
Gredel, R., Lepp, S., Dalgarno, A., & Herbst, E. 1989, ApJ, 347, 289 [Google Scholar]
Greenwood, A. J., Kamp, I., Waters, L. B. F. M., et al. 2017, A&A, 601, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gronowski, M., & Kolos, R. 2014, ApJ, 792, 89 [NASA ADS] [CrossRef] [Google Scholar]
Guélin, M., & Cernicharo, J. 1991, A&A, 244, L21 [NASA ADS] [Google Scholar]
Guélin, M., Lucas, R., & Cernicharo, J. 1993, A&A, 280, L19 [NASA ADS] [Google Scholar]
Guélin, M., Muller, S., Cernicharo, J., McCarthy, M. C., & Thaddeus, P. 2004, A&A, 426, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Halfen, D. T., Clouthier, D. J., & Ziurys, L. M. 2008, ApJ, 677, L101 [NASA ADS] [CrossRef] [Google Scholar]
Halfen, D. T., Ziurys, L. M., Brünken, S., et al. 2009, ApJ, 702, L124 [NASA ADS] [CrossRef] [Google Scholar]
Halfen, D. T., Ilyushin, V. V., & Ziurys, L. M. 2015, ApJ, 812, L5 [Google Scholar]
Harada, N., & Herbst, E. 2008, ApJ, 685, 272 [NASA ADS] [CrossRef] [Google Scholar]
Harada, N., Herbst, E., & Wakelam, V. 2010, ApJ, 721, 1570 [NASA ADS] [CrossRef] [Google Scholar]
Heard, D. E. 2018, Acc. Chem. Res., 51, 2620 [CrossRef] [Google Scholar]
Heays, A. N., Visser, R., Gredel, R., et al. 2014, A&A, 562, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Herbst, E. 1985, ApJ, 292, 484 [Google Scholar]
Herbst, E., & Leung, C. M. 1989, ApJS, 69, 271 [Google Scholar]
Heritier, K. L., Altwegg, K., Balsiger, H., et al. 2017, MNRAS, 469, S427 [Google Scholar]
Hickson, K. M., Loison, J.-C., Bourgalais, J., et al. 2015, ApJ, 812, 107 [NASA ADS] [CrossRef] [Google Scholar]
Highberger, J. L., Thomson, K. J., Young, P. A., Arnett, D., & Ziurys, L. M. 2003, ApJ, 593, 393 [NASA ADS] [CrossRef] [Google Scholar]
Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Mollendal, H. 2004, ApJ, 610, L21 [NASA ADS] [CrossRef] [Google Scholar]
Irvine, W. M., Brown, R. D., Cragg, D. M., et al. 1988, ApJ, 335, L89 [Google Scholar]
Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Kaifu, N., Morimoto, M., Nagane, K., et al. 1974, ApJ, 191, L135 [Google Scholar]
Kalenskii, S. V., Slysh, V. I., Goldsmith, P. F., & Johansson, L. E. B. 2004, ApJ, 610, 329 [NASA ADS] [CrossRef] [Google Scholar]
Kawaguchi, K., Ohishi, M., Ishikawa, S.-I., & Kaifu, N. 1992, ApJ, 386, L51 [NASA ADS] [CrossRef] [Google Scholar]
Lamberts, T. 2018, A&A, 615, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lee, K. L. K., Changala, P. B., Loomis, R. A., et al. 2021a, ApJ, 910, L2 [NASA ADS] [CrossRef] [Google Scholar]
Lee, K. L. K., Loomis, R. A., Burkhardt, A. M., et al. 2021b, ApJ, 908, L11 [CrossRef] [Google Scholar]
Le Teuff, Y. H., Millar, T. J., & Markwick, A. J. 2000, A&A, 146, 157 [NASA ADS] [Google Scholar]
Li, X., Heays, A. N., Visser, R., et al. 2013, A&A, 555, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ligterink, N. F. W., & Minissale, M. 2023, A&A, 676, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ligterink, N. F. W., Ahmadi, A., Coutens, A., et al. 2021, A&A, 647, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lin, Z., Talbi, D., Roueff, E., et al. 2013, ApJ, 765, 80 [NASA ADS] [CrossRef] [Google Scholar]
Linke, R. A., Frerking, M. A., & Thaddeus, P. 1979, ApJ, 234, L139 [NASA ADS] [CrossRef] [Google Scholar]
Loison, J. C., Hébrard, E., Dobrijevic, M., et al. 2015, Icarus, 247, 218 [CrossRef] [Google Scholar]
Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]
Loomis, R. A., Shingledecker, C. N., Langston, G., et al. 2016, MNRAS, 463, 4175 [NASA ADS] [CrossRef] [Google Scholar]
Loomis, R. A., Burkhardt, A. M., Shingledecker, C. N., et al. 2021, Nat. Astron., 5, 188 [NASA ADS] [CrossRef] [Google Scholar]
Majumdar, L., Gratier, P., Vidal, T., et al. 2016, MNRAS, 458, 1859 [NASA ADS] [CrossRef] [Google Scholar]
Majumdar, L., Gratier, P., Ruaud, M., et al. 2017, MNRAS, 466, 4470 [Google Scholar]
Majumdar, L., Loison, J. C., Ruaud, M., et al. 2018, MNRAS, 473, L59 [NASA ADS] [CrossRef] [Google Scholar]
Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [Google Scholar]
Marcelino, N., Agúndez, M., Cernicharo, J., Roueff, E., & Tafalla, M. 2018, A&A, 612, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marcelino, N., Agúndez, M., Tercero, B., et al. 2020, A&A, 643, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marcelino, N., Tercero, B., Agúndez, M., & Cernicharo, J. 2021, A&A, 646, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
McCarthy, M. C., Lee, K. L. K., Loomis, R. A., et al. 2021, Nat. Astron., 5, 176 [Google Scholar]
McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
McGuire, B. A., Burkhardt, A. M., Shingledecker, C. N., et al. 2017a, ApJ, 843, L28 [NASA ADS] [CrossRef] [Google Scholar]
McGuire, B. A., Shingledecker, C. N., Willis, E. R., et al. 2017b, ApJ, 851, L46 [Google Scholar]
McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [Google Scholar]
Milam, S. N., Halfen, D. T., Tenenbaum, E. D., et al. 2008, ApJ, 684, 618 [NASA ADS] [CrossRef] [Google Scholar]
Millar, T. J., Bennett, A., Rawlings, J. M. C., Brown, P. D., & Charnley, S. B. 1991, A&AS, 87, 585 [NASA ADS] [Google Scholar]
Millar, T. J., Farquhar, P. R. A., & Willacy, K. 1997, A&AS, 121, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Millar, T. J., Herbst, E., & Bettens, R. P. A. 2000, MNRAS, 316, 195 [NASA ADS] [CrossRef] [Google Scholar]
Millar, T. J., Walsh, C., Cordiner, M. A., Ní Chuimín, R., & Herbst, E. 2007, ApJ, 662, L87 [NASA ADS] [CrossRef] [Google Scholar]
Moazzen-Ahmadi, N., & Zebretto, F. 1995, J. Chem. Phys., 103, 6343 [NASA ADS] [CrossRef] [Google Scholar]
Mohamed, S., McCarthy, M. C., Cooksy, A. L., Hinton, C., & Thaddeus, P. 2005, J. Chem. Phys., 123, 234301 [NASA ADS] [CrossRef] [Google Scholar]
Morales, S. B., Le Picard, S. D., Canosa, A., & Sims, I. R. 2010, Farad. Disc., 147, 155 [NASA ADS] [CrossRef] [Google Scholar]
Ohishi, M., Kaifu, N., Kawaguchi, K., et al. 1989, ApJ, 345, L83 [CrossRef] [Google Scholar]
Osamura, Y., & Petrie, S. 2004, J. Phys. Chem. A, 108, 3615 [NASA ADS] [CrossRef] [Google Scholar]
Pardo, J. R., Cabezas, C., Fonfría, J. P., et al. 2021, A&A, 652, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Petrie, S. 1996, MNRAS, 282, 807 [NASA ADS] [CrossRef] [Google Scholar]
Petrie, S., & Dunbar, R. C. 2000, J. Phys. Chem. A, 104, 4480 [CrossRef] [Google Scholar]
Petrie, S., & Osamura, Y. 2004, J. Phys. Chem. A, 108, 3623 [NASA ADS] [CrossRef] [Google Scholar]
Plane, J. M. C. 2013, Philos. Trans. R. Soc. A, 371, 20120335 [NASA ADS] [CrossRef] [Google Scholar]
Prasad, S. S., & Huntress, W. T., J. 1980, ApJS, 43, 1 [NASA ADS] [CrossRef] [Google Scholar]
Pratap, P., Dickens, J. E., Snell, R. L., et al. 1997, ApJ, 486, 862 [Google Scholar]
Priestley, F. D., Whitworth, A. P., & Fogerty, E. 2023, MNRAS, 518, 4839 [Google Scholar]
Pulliam, R. L., Edwards, J. L., & Ziurys, L. M. 2011, ApJ, 743, 36 [NASA ADS] [CrossRef] [Google Scholar]
Puzzarini, C., Salta, Z., Tasinato, N., et al. 2020, MNRAS, 496, 4298 [CrossRef] [Google Scholar]
Quénard, D., Jiménez-Serra, I., Viti, S., Holdship, J., & Coutens, A. 2018, MNRAS, 474, 2796 [Google Scholar]
Quan, D., Herbst, E., Osamura, Y., & Roueff, E. 2010, ApJ, 725, 2101 [NASA ADS] [CrossRef] [Google Scholar]
Quintana-Lacaci, G., Cernicharo, J., Velilla Prieto, L., et al. 2017, A&A, 607, A5 [Google Scholar]
Redondo, P., Barrientos, C., & Largo, A. 2014a, ApJ, 793, 32 [NASA ADS] [CrossRef] [Google Scholar]
Redondo, P., Barrientos, C., & Largo, A. 2014b, ApJ, 780, 181 [Google Scholar]
Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2007, ApJ, 664, L47 [NASA ADS] [CrossRef] [Google Scholar]
Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [Google Scholar]
Remijan, A., Scolati, H. N., Burkhardt, A. M., et al. 2023, ApJ, 944, L45 [NASA ADS] [CrossRef] [Google Scholar]
Rivilla, V. M., Colzi, L., Jiménez-Serra, I., et al. 2022, ApJ, 929, L11 [NASA ADS] [CrossRef] [Google Scholar]
Rodríguez-Almeida, L. F., Jiménez-Serra, I., Rivilla, V. M., et al. 2021a, ApJ, 912, L11 [Google Scholar]
Rodríguez-Almeida, L. F., Rivilla, V. M., Jiménez-Serra, I., et al. 2021b, A&A, 654, A1 [Google Scholar]
Röllig, M. 2011, A&A, 530, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Röllig, M., & Ossenkopf-Okada, V. 2022, A&A, 664, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schilke, P., Neufeld, D. A., Müller, H. S. P., et al. 2014, A&A, 566, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schmid, P. C., Thorwirth, S., Endres, C. P., et al. 2022, Front. Astron. Space Sci., 8, 257 [NASA ADS] [CrossRef] [Google Scholar]
Shaw, G., Ferland, G., & Chatzikos, M. 2023, RNAAS, 7, 153 [NASA ADS] [Google Scholar]
Shimonishi, T., Das, A., Sakai, N., et al. 2020, ApJ, 891, 164 [NASA ADS] [CrossRef] [Google Scholar]
Shingledecker, C. N., Lee, K. L. K., Wandishin, J. T., et al. 2021, A&A, 652, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Siebert, M. A., Lee, K. L. K., Remijan, A. J., et al. 2022a, ApJ, 924, 21 [CrossRef] [Google Scholar]
Siebert, M. A., Van de Sande, M., Millar, T. J., & Remijan, A. J. 2022b, ApJ, 941, 90 [NASA ADS] [CrossRef] [Google Scholar]
Sil, M., Srivastav, S., Bhat, B., et al. 2021, AJ, 162, 119 [NASA ADS] [CrossRef] [Google Scholar]
Silva, W. G. D. P., Cernicharo, J., Schlemmer, S., et al. 2023, A&A, 676, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sims, I. R., Queffelec, J. L., Defrance, A., et al. 1992, J. Chem. Phys., 97, 8798 [NASA ADS] [CrossRef] [Google Scholar]
Šimsová-Zámecníková, M., Soldán, P., & Gustafsson, M. 2022, A&A, 664, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sita, M. L., Changala, P. B., Xue, C., et al. 2022, ApJ, 938, L12 [NASA ADS] [CrossRef] [Google Scholar]
Skouteris, D., Balucani, N., Ceccarelli, C., et al. 2018, ApJ, 854, 135 [NASA ADS] [CrossRef] [Google Scholar]
Smith, I. W. M., Herbst, E., & Chang, Q. 2004, MNRAS, 350, 323 [Google Scholar]
Smyth, K. C., Lias, S. G., & Ausloos, P. 1982, Combust. Sci. Technol., 28, 147 [CrossRef] [Google Scholar]
Snyder, L. E., Hollis, J. M., Jewell, P. R., Lovas, F. J., & Remijan, A. 2006, ApJ, 647, 412 [NASA ADS] [CrossRef] [Google Scholar]
Sternberg, A., Le Petit, F., Roueff, E., & Le Bourlot, J. 2014, ApJ, 790, 10 [CrossRef] [Google Scholar]
Su, T., & Chesnavich, W. J. 1982, J. Chem. Phys., 76, 5183 [NASA ADS] [CrossRef] [Google Scholar]
Swihart, M., Catoire, L., Legrand, B., Gokalp, I., & Paillard, C. 2003, Combust. Flame, 132, 91 [Google Scholar]
Tenenbaum, E. D., Apponi, A. J., Ziurys, L. M., et al. 2006, ApJ, 649, L17 [CrossRef] [Google Scholar]
Tenenbaum, E. D., Dodd, J. L., Milam, S. N., Woolf, N. J., & Ziurys, L. M. 2010, ApJS, 190, 348 [NASA ADS] [CrossRef] [Google Scholar]
Thaddeus, P., Gottlieb, C. A., Gupta, H., et al. 2008, ApJ, 677, 1132 [NASA ADS] [CrossRef] [Google Scholar]
Tinacci, L., Germain, A., Pantaleone, S., et al. 2022, ACS Earth Space Chem., 6, 1514 [NASA ADS] [CrossRef] [Google Scholar]
Tinacci, L., Ferrada-Chamorro, S., Ceccarelli, C., et al. 2023, ApJS, 266, 38 [NASA ADS] [CrossRef] [Google Scholar]
Tonolo, F., Lupi, J., Puzzarini, C., & Barone, V. 2020, ApJ, 900, 85 [Google Scholar]
Tsang, W. 1991, J. Phys. Chem. Ref. Data, 20, 221 [NASA ADS] [CrossRef] [Google Scholar]
Turner, B. E. 1992, ApJ, 388, L35 [NASA ADS] [CrossRef] [Google Scholar]
Turner, B. E., Steimle, T. C., & Meerts, L. 1994, ApJ, 426, L97 [NASA ADS] [CrossRef] [Google Scholar]
Van de Sande, M., & Millar, T. J. 2019, ApJ, 873, 36 [CrossRef] [Google Scholar]
Van de Sande, M., & Millar, T. J. 2022, MNRAS, 510, 1204 [Google Scholar]
Van de Sande, M., Walsh, C., & Millar, T. J. 2021, MNRAS, 501, 491 [Google Scholar]
Vastel, C., Kawaguchi, K., Quénard, D., et al. 2018, MNRAS, 474, L76 [NASA ADS] [CrossRef] [Google Scholar]
Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [Google Scholar]
Vigren, E., Semaniak, J., Hamberg, M., et al. 2012, Planet. Space Sci., 60, 102 [NASA ADS] [CrossRef] [Google Scholar]
Villinger, H., Futrell, J. H., Howorka, F., Duric, N., & Lindinger, W. 1982, J. Chem. Phys., 76, 3529 [NASA ADS] [CrossRef] [Google Scholar]
Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Wakelam, V., Herbst, E., Le Bourlot, J., et al. 2010, A&A, 517, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Wakelam, V., Loison, J. C., Herbst, E., et al. 2015a, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
Wakelam, V., Loison, J. C., Hickson, K. M., & Ruaud, M. 2015b, MNRAS, 453, L48 [CrossRef] [Google Scholar]
Wallström, S. H. J., Danilovich, T., Müller, H. S. P., et al. 2024, A&A, 681, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Walsh, C., Harada, N., Herbst, E., & Millar, T. J. 2009, ApJ, 700, 752 [NASA ADS] [CrossRef] [Google Scholar]
Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
West, N. A., Li, L. H. D., Millar, T. J., et al. 2023, PCCP, 25, 7719 [NASA ADS] [CrossRef] [Google Scholar]
Wlodek, S., & Bohme, D. 1988, JACS, 110, 2396 [CrossRef] [Google Scholar]
Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [CrossRef] [EDP Sciences] [Google Scholar]
Xie, H., Ding, Y., & Sun, C. 2005, J. Phys. Chem. A, 109, 8419 [NASA ADS] [CrossRef] [Google Scholar]
Xue, C., Willis, E. R., Loomis, R. A., et al. 2020, ApJ, 900, L9 [Google Scholar]
Yurtsever, E., Satta, M., Wester, R., & Gianturco, F. A. 2020, J. Phys. Chem. A, 124, 5098 [NASA ADS] [CrossRef] [Google Scholar]
Zeng, S., Quénard, D., Jiménez-Serra, I., et al. 2019, MNRAS, 484, L43 [Google Scholar]
Zhang, F., Parker, D., Kim, Y. S., Kaiser, R. I., & Mebel, A. M. 2011, ApJ, 728, 141 [NASA ADS] [CrossRef] [Google Scholar]
Ziurys, L. M., Apponi, A. J., Guélin, M., & Cernicharo, J. 1995, ApJ, 445, L47 [NASA ADS] [CrossRef] [Google Scholar]

¹

https://cdms.astro.uni-koeln.de/

²

https://www.astrochymist.org/

³

http://udfa.net/

⁴

https://umistdatabase.net

⁵

https://kida.astrochem-tools.org/

All Tables

Table 1

Code, reaction type, and the number of each reaction type in RATE12 and RATE22.

In the text

Table 2

Relabelled species in RATE22.

In the text

Table 3

Fit parameters for the radiative association of Mg⁺ with cyanopolyynes over the range 10–300 K.

In the text

Table 4

Fit parameters for the radiative association of Mg⁺ with polyynes over the range 10–300 K.

In the text

Table 5

Fit parameters for the radiative association of Na⁺ with cyanopolyynes over the range 10–300 K.

In the text

Table 6

Detected species, listed by number of atoms, missing from the Rate22 database.

In the text

Table 7

Initial abundances relative to total Η nuclei, n_H.

In the text

Table 8

Fitting information on the comparison between observed and calculated abundances for the O-rich case.

In the text

Table 9

Fitting information on the comparison between observed and calculated abundances for the C-rich model with C/O = 1.4.

In the text

Table 10

Initial fractional abundances, f, relative to H₂ for the CSE model.

In the text

Table 11

Observed and calculated column densities (cm⁻²) in IRC+10216 for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr ¹.

In the text

Table A.1

Observed fractional abundances, relative to H₂, in TMC-1(CP) and corresponding calculated ‘best fit’ values at 1.6 × 10⁵ years for the O-rich model.

In the text

Table A.2

Observed fractional abundances, relative to H₂, in TMC-1(CP) and corresponding calculated ‘best fit’ values at 1.0 × 10⁶ years for the C-rich (C/O = 1.4) model.

In the text

All Figures

	Fig. 1 Time evolution of various N-bearing molecules in the dark cloud, O-rich model for both Rate22 (solid lines) and Rate12 (dashed lines).
In the text

	Fig. 2 Time evolution of various cyanopolyynes in the dark cloud, O-rich model for both Rate22 (solid lines) and Rate12 (dashed lines).
In the text

	Fig. 3 Best-fit, D, and reduced best-fit, Dred, average difference between observed and calculated species for the full ratefile and O-rich initial conditions. The curve labelled ‘NR’ indicates the number of species removed in calculating the global average, Dred, and Ν is the number of species whose abundances lie within an order of magnitude of those observed.
In the text

	Fig. 4 Time evolution of propene and species formed from it in the dark cloud, O-rich model for both Rate22 (solid lines) and Rate 12 (dashed lines).
In the text

	Fig. 5 Best-fit, D, and reduced best-fit, Dred, average difference between observed and calculated species for the full ratefile and C/O = 1.4. The curve labelled ‘NR’ indicates the number of species removed in calculating the global average, Dred, and Ν is the number of species whose abundances lie within an order of magnitude of those observed.
In the text

	Fig. 6 Fractional abundances of the cyanopolyynes for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr⁻¹ as a function of radial distance from the central star.
In the text

	Fig. 7 Fractional abundances of the Mg-terminated cyanopolyynes for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr⁻¹ as a function of radial distance from the central star.
In the text

	Fig. 8 Fractional abundances of the Mg-terminated polyacetylides for a mass-loss rate of 3.0 × 10⁻⁵ M_⊙ yr⁻¹ as a function of radial distance from the central star.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Abdoulanziz, A., Colboc, F., Little, D. A., et al. 2018, MNRAS, 479, 2415 [NASA ADS] [CrossRef] [Google Scholar]

[2] Abeysekera, C, Joalland, B., Ariyasingha, N., et al. 2015, J. Phys. Chem. Letts., 6, 1599 [CrossRef] [Google Scholar]

[3] Acharyya, K., & Herbst, E. 2017, ApJ, 850, 105 [NASA ADS] [CrossRef] [Google Scholar]

[4] Adams, N. G., Smith, D., Giles, K., & Herbst, E. 1989, A&A, 220, 269 [Google Scholar]

[5] Adande, G. R., Halfen, D. T., Ziurys, L. M., Quan, D., & Herbst, E. 2010, ApJ, 725, 561 [NASA ADS] [CrossRef] [Google Scholar]

[6] Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]

[7] Agúndez, M., Fonfría, J. P., Cernicharo, J., Pardo, J. R., & Guélin, M. 2008, A&A, 479, 493 [Google Scholar]

[8] Agúndez, M., Cernicharo, J., Guélin, M., et al. 2010, A&A, 517, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[9] Agúndez, M., Cernicharo, J., & Guélin, M. 2014, A&A, 570, A45 [Google Scholar]

[10] Agúndez, M., Cernicharo, J., de Vicente, P., et al. 2015a, A&A, 579, A10 [Google Scholar]

[11] Agúndez, M., Cernicharo, J., & Guélin, M. 2015b, A&A, 577, A5 [Google Scholar]

[12] Agúndez, M., Cernicharo, J., Quintana-Lacaci, G., et al. 2015c, ApJ, 814, 143 [Google Scholar]

[13] Agúndez, M., Marcelino, N., & Cernicharo, J. 2018a, ApJ, 861, L22 [Google Scholar]

[14] Agúndez, M., Marcelino, N., Cernicharo, J., & Tafalla, M. 2018b, A&A, 611, Al [Google Scholar]

[15] Agúndez, M., Martínez, J. I., de Andres, P. L., Cernicharo, J., & Martín-Gago, J. A. 2020, A&A, 637, A59 [Google Scholar]

[16] Agúndez, M., Cabezas, C., Tercero, B., et al. 2021a, A&A, 647, A10 [Google Scholar]

[17] Agúndez, M., Marcelino, N., Tercero, B., et al. 2021b, A&A, 649, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Agúndez, M., Cabezas, C., Marcelino, N., et al. 2022a, A&A, 659, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[19] Agúndez, M., Marcelino, N., Cabezas, C., et al. 2022b, A&A, 657, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[20] Agúndez, M., Cabezas, C., Marcelino, N., et al. 2023a, A&A, 669, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[21] Agúndez, M., Loison, J. C., Hickson, K. M., et al. 2023b, A&A, 673, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[22] Agúndez, M., Marcelino, N., Tercero, B., Jiménez-Serra, I., & Cernicharo, J. 2023c, A&A, 677, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[23] Andriantsaralaza, M., Ramstedt, S., Vlemmings, W. H. T., & De Beck, E. 2022, A&A, 667, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[24] Anicich, V. G. 1993, ApJS, 84, 215 [NASA ADS] [CrossRef] [Google Scholar]

[25] Anicich, V. G., & Huntress, W. T., J. 1986, ApJS, 62, 553 [NASA ADS] [CrossRef] [Google Scholar]

[26] Apponi, A. J., McCarthy, M. C., Gottlieb, C. A., & Thaddeus, P. 1999, ApJ, 516, L103 [Google Scholar]

[27] Ascenzi, D., Cernuto, A., Balucani, N., et al. 2019, A&A, 625, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[28] Ausloos, P., Lias, S. G., Buckley, T. J., & Rogers, E. E. 1989, Int. J. Mass Spectrom. Ion Processes, 92, 65 [NASA ADS] [CrossRef] [Google Scholar]

[29] Babb, J. F., & McLaughlin, B. M. 2018, ApJ, 860, 151 [Google Scholar]

[30] Bai, T., Qin, Z., & Liu, L. 2021a, MNRAS, 500, 2496 [Google Scholar]

[31] Bai, T., Qin, Z., & Liu, L. 2021b, MNRAS, 505, 2177 [NASA ADS] [CrossRef] [Google Scholar]

[32] Bakker, E. J., van Dishoeck, E. F., Waters, L. B. F. M., & Schoenmaker, T. 1997, A&A, 323, 469 [NASA ADS] [Google Scholar]

[33] Balucani, N., Asvany, O., Kaiser, R., & Osamura, Y. 2002, J. Phys. Chem. A, 106, 4301 [NASA ADS] [CrossRef] [Google Scholar]

[34] Barlow, M. J., Swinyard, B. M., Owen, P. J., et al. 2013, Science, 342, 1343 [NASA ADS] [CrossRef] [Google Scholar]

[35] Barnum, T. J., Siebert, M. A., Lee, K. L. K., et al. 2022, J. Phys. Chem. A, 126, 2716 [NASA ADS] [CrossRef] [Google Scholar]

[36] Barone, V., Latouche, C., Skouteris, D., et al. 2015, MNRAS, 453, L31 [Google Scholar]

[37] Baulch, D. L., Cobos, C. J., Cox, R. A., et al. 1994, J. Phys. Chem. Ref. Data, 23, 847 [CrossRef] [Google Scholar]

[38] Baulch, D. L., Bowman, C. T., Cobos, C. J., et al. 2005, J. Phys. Chem. Ref. Data, 34, 757 [Google Scholar]

[39] Bell, M. B., Avery, L. W., & Feldman, P. A. 1993, ApJ, 417, L37 [Google Scholar]

[40] Berteloite, C., Le Picard, S. D., Balucani, N., Canosa, A., & Sims, I. R. 2010, PCCP, 12, 3677 [NASA ADS] [CrossRef] [Google Scholar]

[41] Bettens, R. P. A., & Herbst, E. 1995, Int. J. Mass Spectrom. Ion Processes, 149, 321 [CrossRef] [Google Scholar]

[42] Bourgalais, J., Capron, M., Abhinavam Kailasanathan, R. K., et al. 2015, ApJ, 812, 106 [NASA ADS] [CrossRef] [Google Scholar]

[43] Bouscasse, L., Csengeri, T., Belloche, A., et al. 2022, A&A, 662, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[44] Bouwman, J., Goulay, F., Leone, S. R., & Wilson, K. R. 2012, J. Phys. Chem. A, 116, 3907 [Google Scholar]

[45] Bovolenta, G. M., Vogt-Geisse, S., Bovino, S., & Grassi, T. 2022, ApJS, 262, 17 [NASA ADS] [CrossRef] [Google Scholar]

[46] Brünken, S., Gupta, H., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2007, ApJ, 664, L43 [CrossRef] [Google Scholar]

[47] Burkhardt, A. M., Herbst, E., Kalenskii, S. V., et al. 2018, MNRAS, 474, 5068 [NASA ADS] [CrossRef] [Google Scholar]

[48] Burkhardt, A. M., Long Kelvin Lee, K., Bryan Changala, P., et al. 2021a, ApJ, 913, L18 [NASA ADS] [CrossRef] [Google Scholar]

[49] Burkhardt, A. M., Loomis, R. A., Shingledecker, C. N., et al. 2021b, Nat. Astron., 5, 181 [Google Scholar]

[50] Cabezas, C., Cernicharo, J., Alonso, J. L., et al. 2013, ApJ, 775, 133 [NASA ADS] [CrossRef] [Google Scholar]

[51] Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021a, A&A, 654, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[52] Cabezas, C., Agúndez, M., Marcelino, N., et al. 2021b, A&A, 654, A9 [Google Scholar]

[53] Cabezas, C., Endo, Y., Roueff, E., et al. 2021c, A&A, 646, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[54] Cabezas, C., Tercero, B., Agúndez, M., et al. 2021d, A&A, 650, A9 [Google Scholar]

[55] Cabezas, C., Agúndez, M., Fuentetaja, R., et al. 2022a, A&A, 663, A2 [Google Scholar]

[56] Cabezas, C., Agúndez, M., Marcelino, N., et al. 2022b, A&A, 657, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[57] Cabezas, C., Agúndez, M., Marcelino, N., et al. 2022c, A&A, 659, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[58] Cabezas, C., Pardo, J. R., Agúndez, M., et al. 2023, A&A, 672, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[59] Campbell, M., & McClean, R. 1993, J. Phys. Chem., 97, 7942 [CrossRef] [Google Scholar]

[60] Carty, D., Le Page, V., Sims, I., & Smith, I. 2001, CPL, 344, 310 [NASA ADS] [CrossRef] [Google Scholar]

[61] Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]

[62] Cazaux, S., & Tielens, A. G. G. M. 2010, ApJ, 715, 698 [NASA ADS] [CrossRef] [Google Scholar]

[63] Cernicharo, J., & Guélin, M. 1987, A&A, 183, L10 [NASA ADS] [Google Scholar]

[64] Cernicharo, J., Guélin, M., Hein, H., & Kahane, C. 1987, A&A, 181, L9 [Google Scholar]

[65] Cernicharo, J., Gottlieb, C. A., Guelin, M., Thaddeus, P., & Vrtilek, J. M. 1989, ApJ, 341, L25 [NASA ADS] [CrossRef] [Google Scholar]

[66] Cernicharo, J., Gottlieb, C. A., Guelin, M., et al. 1991a, ApJ, 368, L39 [NASA ADS] [CrossRef] [Google Scholar]

[67] Cernicharo, J., Gottlieb, C. A., Guélin, M., et al. 1991b, ApJ, 368, L43 [NASA ADS] [CrossRef] [Google Scholar]

[68] Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[69] Cernicharo, J., Guélin, M., & Pardo, J. R. 2004, ApJ, 615, L145 [Google Scholar]

[70] Cernicharo, J., Guélin, M., Agúndez, M., et al. 2007, A&A, 467, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[71] Cernicharo, J., Guélin, M., Agúndez, M., McCarthy, M. C., & Thaddeus, P. 2008, ApJ, 688, L83 [NASA ADS] [CrossRef] [Google Scholar]

[72] Cernicharo, J., Spielfiedel, A., Balanca, C., et al. 2011, A&A, 531, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[73] Cernicharo, J., Lefloch, B., Agúndez, M., et al. 2018, ApJ, 853, L22 [CrossRef] [Google Scholar]

[74] Cernicharo, J., Cabezas, C., Pardo, J. R., et al. 2019, A&A, 630, A2 [Google Scholar]

[75] Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020a, A&A, 642, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[76] Cernicharo, J., Marcelino, N., Agúndez, M., et al. 2020b, A&A, 642, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[77] Cernicharo, J., Marcelino, N., Pardo, J. R., et al. 2020c, A&A, 641, A9 [Google Scholar]

[78] Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021a, A&A, 647, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[79] Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021b, A&A, 656, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[80] Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021c, A&A, 649, A15 [Google Scholar]

[81] Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021d, A&A, 652, A9 [Google Scholar]

[82] Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021e, A&A, 655, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[83] Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021f, A&A, 647, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[84] Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021g, A&A, 648, A3 [Google Scholar]

[85] Cernicharo, J., Cabezas, C., Bailleux, S., et al. 2021h, A&A, 646, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[86] Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021i, A&A, 650, A14 [Google Scholar]

[87] Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021j, A&A, 646, A3 [Google Scholar]

[88] Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2022a, A&A, 657, A16 [Google Scholar]

[89] Cernicharo, J., Fuentetaja, R., Agúndez, M., et al. 2022b, A&A, 663, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[90] Cernicharo, J., Fuentetaja, R., Cabezas, C., et al. 2022c, A&A, 663, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[91] Cernicharo, J., Pardo, J. R., Cabezas, C., et al. 2023, A&A, 670, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[92] Changala, P. B., Gupta, H., Cernicharo, J., et al. 2022, ApJ, 940, L42 [NASA ADS] [CrossRef] [Google Scholar]

[93] Charnley, S. B., & Millar, T. J. 1994, MNRAS, 270, 570 [NASA ADS] [CrossRef] [Google Scholar]

[94] Cheikh Sid Ely, S., Morales, S. B., Guillemin, J.-C., Klippenstein, S. J., & Sims, I. R. 2013, J. Phys. Chem. A, 117, 12155 [NASA ADS] [CrossRef] [Google Scholar]

[95] Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]

[96] Cooke, I. R., Gupta, D., Messinger, J. P., & Sims, I. R. 2020, ApJ, 891, L41 [Google Scholar]

[97] Cordiner, M. A., & Charnley, S. B. 2012, ApJ, 749, 120 [NASA ADS] [CrossRef] [Google Scholar]

[98] Cordiner, M. A., & Millar, T. J. 2009, ApJ, 697, 68 [NASA ADS] [CrossRef] [Google Scholar]

[99] Cordiner, M. A., Charnley, S. B., Kisiel, Z., McGuire, B. A., & Kuan, Y. J. 2017, ApJ, 850, 187 [NASA ADS] [CrossRef] [Google Scholar]

[100] Coutens, A., Ligterink, N. F. W., Loison, J. C., et al. 2019, A&A, 623, A13 [Google Scholar]

[101] Coutens, A., Loison, J. C., Boulanger, A., et al. 2022, A&A, 660, A6 [Google Scholar]

[102] Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [Google Scholar]

[103] Danilovich, T., Van de Sande, M., Plane, J. M. C., et al. 2021, A&A, 655, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[104] Daugey, N., Caubet, P., Bergeat, A., Costes, M., & Hickson, K. M. 2008, PCCP, 10, 729 [NASA ADS] [CrossRef] [Google Scholar]

[105] Decin, L., Richards, A. M. S., Millar, T. J., et al. 2016, A&A, 592, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[106] Decin, L., Richards, A. M. S., Waters, L. B. F. M., et al. 2017, A&A, 608, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[107] Decin, L., Danilovich, T., Gobrecht, D., et al. 2018, ApJ, 855, 113 [NASA ADS] [CrossRef] [Google Scholar]

[108] Decin, L., Montarges, M., Richards, A. M. S., et al. 2020, Science, 369, 1497 [NASA ADS] [CrossRef] [Google Scholar]

[109] Decker, B. K., Babcock, L. M., & Adams, N. G. 2000, J. Phys. Chem. A, 104, 801 [NASA ADS] [CrossRef] [Google Scholar]

[110] Deeyamulla, M. P., & Husain, D. 2006, J. Photochem. Photobiol. A-Chem., 184, 347 [CrossRef] [Google Scholar]

[111] Doddipatla, S., Galimova, G. R., Wei, H., et al. 2021, Sci. Adv., 7, eabd4044 [Google Scholar]

[112] Douglas, K. M., Lucas, D. I., Walsh, C., et al. 2022, ApJ, 937, L16 [CrossRef] [Google Scholar]

[113] Dunbar, R. C., & Petrie, S. 2002, ApJ, 564, 792 [NASA ADS] [CrossRef] [Google Scholar]

[114] Eichelberger, B., Snow, T. P., Barckholtz, C., & Bierbaum, V. M. 2007, ApJ, 667, 1283 [NASA ADS] [CrossRef] [Google Scholar]

[115] el Akel, M., Kristensen, L. E., Le Gal, R., et al. 2022, A&A, 659, A100 [CrossRef] [EDP Sciences] [Google Scholar]

[116] Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Miller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]

[117] Entekhabi, N., Tan, J. C., Cosentino, G., et al. 2022, A&A, 662, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[118] Esplugues, G., Cazaux, S., Caselli, P., Hocuk, S., & Spaans, M. 2019, MNRAS, 486, 1853 [NASA ADS] [Google Scholar]

[119] Fayolle, E. C., Öberg, K. I., Jørgensen, J. K., et al. 2017, Nat. Astron., 1, 703 [NASA ADS] [CrossRef] [Google Scholar]

[120] Foley, N., Cazaux, S., Egorov, D., et al. 2018, MNRAS, 479, 649 [NASA ADS] [Google Scholar]

[121] Fonfría, J. P., Agúndez, M., Cernicharo, J., Richter, M. J., & Lacy, J. H. 2018, ApJ, 852, 80 [Google Scholar]

[122] Ford, K. E. S., Neufeld, D. A., Schilke, P., & Melnick, G. J. 2004, ApJ, 614, 990 [NASA ADS] [CrossRef] [Google Scholar]

[123] Fourikis, N., Takagi, K., & Morimoto, M. 1974, ApJ, 191, L139 [Google Scholar]

[124] Fournier, M. 2014, PhD thesis, Universite de Rennes I, France [Google Scholar]

[125] Frerking, M. A., Linke, R. A., & Thaddeus, P. 1979, ApJ, 234, L143 [NASA ADS] [CrossRef] [Google Scholar]

[126] Fuente, A., Rivière-Marichalar, P., Beitia-Antero, L., et al. 2023, A&A, 670, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[127] Fuentetaja, R., Agúndez, M., Cabezas, C., et al. 2022a, A&A, 667, A4 [Google Scholar]

[128] Fuentetaja, R., Cabezas, C., Agúndez, M., et al. 2022b, A&A, 663, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[129] Gianturco, F. A., Satta, M., Yurtsever, E., & Wester, R. 2017, ApJ, 850, 42 [Google Scholar]

[130] Ginsburg, A., McGuire, B., Plambeck, R., et al. 2019, ApJ, 872, 54 [NASA ADS] [CrossRef] [Google Scholar]

[131] Gobrecht, D., Plane, J. M. C., Bromley, S. T., et al. 2022, A&A, 658, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[132] González, D., Ballesteros, B., Canosa, A., Albaladejo, J., & Jiménez, E. 2022, Front. Astron. Space Sci., 8, 239 [CrossRef] [Google Scholar]

[133] Gorai, P., Bhat, B., Sil, M., et al. 2020, ApJ, 895, 86 [Google Scholar]

[134] Goulay, F., & Leone, S. 2006, J. Phys. Chem. A, 110, 1875 [NASA ADS] [CrossRef] [Google Scholar]

[135] Goulay, F., Osborn, D. L., Taatjes, C. A., et al. 2007, PCCP, 9, 4291 [CrossRef] [Google Scholar]

[136] Goulay, F., Trevitt, A. J., Savee, J. D., et al. 2012, J. Phys. Chem. A, 116, 6091 [Google Scholar]

[137] Gratier, P., Majumdar, L., Ohishi, M., et al. 2016, ApJS, 225, 25 [Google Scholar]

[138] Gredel, R., Lepp, S., Dalgarno, A., & Herbst, E. 1989, ApJ, 347, 289 [Google Scholar]

[139] Greenwood, A. J., Kamp, I., Waters, L. B. F. M., et al. 2017, A&A, 601, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[140] Gronowski, M., & Kolos, R. 2014, ApJ, 792, 89 [NASA ADS] [CrossRef] [Google Scholar]

[141] Guélin, M., & Cernicharo, J. 1991, A&A, 244, L21 [NASA ADS] [Google Scholar]

[142] Guélin, M., Lucas, R., & Cernicharo, J. 1993, A&A, 280, L19 [NASA ADS] [Google Scholar]

[143] Guélin, M., Muller, S., Cernicharo, J., McCarthy, M. C., & Thaddeus, P. 2004, A&A, 426, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[144] Halfen, D. T., Clouthier, D. J., & Ziurys, L. M. 2008, ApJ, 677, L101 [NASA ADS] [CrossRef] [Google Scholar]

[145] Halfen, D. T., Ziurys, L. M., Brünken, S., et al. 2009, ApJ, 702, L124 [NASA ADS] [CrossRef] [Google Scholar]

[146] Halfen, D. T., Ilyushin, V. V., & Ziurys, L. M. 2015, ApJ, 812, L5 [Google Scholar]

[147] Harada, N., & Herbst, E. 2008, ApJ, 685, 272 [NASA ADS] [CrossRef] [Google Scholar]

[148] Harada, N., Herbst, E., & Wakelam, V. 2010, ApJ, 721, 1570 [NASA ADS] [CrossRef] [Google Scholar]

[149] Heard, D. E. 2018, Acc. Chem. Res., 51, 2620 [CrossRef] [Google Scholar]

[150] Heays, A. N., Visser, R., Gredel, R., et al. 2014, A&A, 562, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[151] Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[152] Herbst, E. 1985, ApJ, 292, 484 [Google Scholar]

[153] Herbst, E., & Leung, C. M. 1989, ApJS, 69, 271 [Google Scholar]

[154] Heritier, K. L., Altwegg, K., Balsiger, H., et al. 2017, MNRAS, 469, S427 [Google Scholar]

[155] Hickson, K. M., Loison, J.-C., Bourgalais, J., et al. 2015, ApJ, 812, 107 [NASA ADS] [CrossRef] [Google Scholar]

[156] Highberger, J. L., Thomson, K. J., Young, P. A., Arnett, D., & Ziurys, L. M. 2003, ApJ, 593, 393 [NASA ADS] [CrossRef] [Google Scholar]

[157] Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]

[158] Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Mollendal, H. 2004, ApJ, 610, L21 [NASA ADS] [CrossRef] [Google Scholar]

[159] Irvine, W. M., Brown, R. D., Cragg, D. M., et al. 1988, ApJ, 335, L89 [Google Scholar]

[160] Jones, A. P., Fanciullo, L., Köhler, M., et al. 2013, A&A, 558, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[161] Kaifu, N., Morimoto, M., Nagane, K., et al. 1974, ApJ, 191, L135 [Google Scholar]

[162] Kalenskii, S. V., Slysh, V. I., Goldsmith, P. F., & Johansson, L. E. B. 2004, ApJ, 610, 329 [NASA ADS] [CrossRef] [Google Scholar]

[163] Kawaguchi, K., Ohishi, M., Ishikawa, S.-I., & Kaifu, N. 1992, ApJ, 386, L51 [NASA ADS] [CrossRef] [Google Scholar]

[164] Lamberts, T. 2018, A&A, 615, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[165] Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[166] Lee, K. L. K., Changala, P. B., Loomis, R. A., et al. 2021a, ApJ, 910, L2 [NASA ADS] [CrossRef] [Google Scholar]

[167] Lee, K. L. K., Loomis, R. A., Burkhardt, A. M., et al. 2021b, ApJ, 908, L11 [CrossRef] [Google Scholar]

[168] Le Teuff, Y. H., Millar, T. J., & Markwick, A. J. 2000, A&A, 146, 157 [NASA ADS] [Google Scholar]

[169] Li, X., Heays, A. N., Visser, R., et al. 2013, A&A, 555, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[170] Ligterink, N. F. W., & Minissale, M. 2023, A&A, 676, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[171] Ligterink, N. F. W., Ahmadi, A., Coutens, A., et al. 2021, A&A, 647, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[172] Lin, Z., Talbi, D., Roueff, E., et al. 2013, ApJ, 765, 80 [NASA ADS] [CrossRef] [Google Scholar]

[173] Linke, R. A., Frerking, M. A., & Thaddeus, P. 1979, ApJ, 234, L139 [NASA ADS] [CrossRef] [Google Scholar]

[174] Loison, J. C., Hébrard, E., Dobrijevic, M., et al. 2015, Icarus, 247, 218 [CrossRef] [Google Scholar]

[175] Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]

[176] Loomis, R. A., Shingledecker, C. N., Langston, G., et al. 2016, MNRAS, 463, 4175 [NASA ADS] [CrossRef] [Google Scholar]

[177] Loomis, R. A., Burkhardt, A. M., Shingledecker, C. N., et al. 2021, Nat. Astron., 5, 188 [NASA ADS] [CrossRef] [Google Scholar]

[178] Majumdar, L., Gratier, P., Vidal, T., et al. 2016, MNRAS, 458, 1859 [NASA ADS] [CrossRef] [Google Scholar]

[179] Majumdar, L., Gratier, P., Ruaud, M., et al. 2017, MNRAS, 466, 4470 [Google Scholar]

[180] Majumdar, L., Loison, J. C., Ruaud, M., et al. 2018, MNRAS, 473, L59 [NASA ADS] [CrossRef] [Google Scholar]

[181] Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [Google Scholar]

[182] Marcelino, N., Agúndez, M., Cernicharo, J., Roueff, E., & Tafalla, M. 2018, A&A, 612, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[183] Marcelino, N., Agúndez, M., Tercero, B., et al. 2020, A&A, 643, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[184] Marcelino, N., Tercero, B., Agúndez, M., & Cernicharo, J. 2021, A&A, 646, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[185] McCarthy, M. C., Lee, K. L. K., Loomis, R. A., et al. 2021, Nat. Astron., 5, 176 [Google Scholar]

[186] McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[187] McGuire, B. A., Burkhardt, A. M., Shingledecker, C. N., et al. 2017a, ApJ, 843, L28 [NASA ADS] [CrossRef] [Google Scholar]

[188] McGuire, B. A., Shingledecker, C. N., Willis, E. R., et al. 2017b, ApJ, 851, L46 [Google Scholar]

[189] McGuire, B. A., Burkhardt, A. M., Kalenskii, S., et al. 2018, Science, 359, 202 [Google Scholar]

[190] Milam, S. N., Halfen, D. T., Tenenbaum, E. D., et al. 2008, ApJ, 684, 618 [NASA ADS] [CrossRef] [Google Scholar]

[191] Millar, T. J., Bennett, A., Rawlings, J. M. C., Brown, P. D., & Charnley, S. B. 1991, A&AS, 87, 585 [NASA ADS] [Google Scholar]

[192] Millar, T. J., Farquhar, P. R. A., & Willacy, K. 1997, A&AS, 121, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[193] Millar, T. J., Herbst, E., & Bettens, R. P. A. 2000, MNRAS, 316, 195 [NASA ADS] [CrossRef] [Google Scholar]

[194] Millar, T. J., Walsh, C., Cordiner, M. A., Ní Chuimín, R., & Herbst, E. 2007, ApJ, 662, L87 [NASA ADS] [CrossRef] [Google Scholar]

[195] Moazzen-Ahmadi, N., & Zebretto, F. 1995, J. Chem. Phys., 103, 6343 [NASA ADS] [CrossRef] [Google Scholar]

[196] Mohamed, S., McCarthy, M. C., Cooksy, A. L., Hinton, C., & Thaddeus, P. 2005, J. Chem. Phys., 123, 234301 [NASA ADS] [CrossRef] [Google Scholar]

[197] Morales, S. B., Le Picard, S. D., Canosa, A., & Sims, I. R. 2010, Farad. Disc., 147, 155 [NASA ADS] [CrossRef] [Google Scholar]

[198] Ohishi, M., Kaifu, N., Kawaguchi, K., et al. 1989, ApJ, 345, L83 [CrossRef] [Google Scholar]

[199] Osamura, Y., & Petrie, S. 2004, J. Phys. Chem. A, 108, 3615 [NASA ADS] [CrossRef] [Google Scholar]

[200] Pardo, J. R., Cabezas, C., Fonfría, J. P., et al. 2021, A&A, 652, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[201] Petrie, S. 1996, MNRAS, 282, 807 [NASA ADS] [CrossRef] [Google Scholar]

[202] Petrie, S., & Dunbar, R. C. 2000, J. Phys. Chem. A, 104, 4480 [CrossRef] [Google Scholar]

[203] Petrie, S., & Osamura, Y. 2004, J. Phys. Chem. A, 108, 3623 [NASA ADS] [CrossRef] [Google Scholar]

[204] Plane, J. M. C. 2013, Philos. Trans. R. Soc. A, 371, 20120335 [NASA ADS] [CrossRef] [Google Scholar]

[205] Prasad, S. S., & Huntress, W. T., J. 1980, ApJS, 43, 1 [NASA ADS] [CrossRef] [Google Scholar]

[206] Pratap, P., Dickens, J. E., Snell, R. L., et al. 1997, ApJ, 486, 862 [Google Scholar]

[207] Priestley, F. D., Whitworth, A. P., & Fogerty, E. 2023, MNRAS, 518, 4839 [Google Scholar]

[208] Pulliam, R. L., Edwards, J. L., & Ziurys, L. M. 2011, ApJ, 743, 36 [NASA ADS] [CrossRef] [Google Scholar]

[209] Puzzarini, C., Salta, Z., Tasinato, N., et al. 2020, MNRAS, 496, 4298 [CrossRef] [Google Scholar]

[210] Quénard, D., Jiménez-Serra, I., Viti, S., Holdship, J., & Coutens, A. 2018, MNRAS, 474, 2796 [Google Scholar]

[211] Quan, D., Herbst, E., Osamura, Y., & Roueff, E. 2010, ApJ, 725, 2101 [NASA ADS] [CrossRef] [Google Scholar]

[212] Quintana-Lacaci, G., Cernicharo, J., Velilla Prieto, L., et al. 2017, A&A, 607, A5 [Google Scholar]

[213] Redondo, P., Barrientos, C., & Largo, A. 2014a, ApJ, 793, 32 [NASA ADS] [CrossRef] [Google Scholar]

[214] Redondo, P., Barrientos, C., & Largo, A. 2014b, ApJ, 780, 181 [Google Scholar]

[215] Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2007, ApJ, 664, L47 [NASA ADS] [CrossRef] [Google Scholar]

[216] Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [Google Scholar]

[217] Remijan, A., Scolati, H. N., Burkhardt, A. M., et al. 2023, ApJ, 944, L45 [NASA ADS] [CrossRef] [Google Scholar]

[218] Rivilla, V. M., Colzi, L., Jiménez-Serra, I., et al. 2022, ApJ, 929, L11 [NASA ADS] [CrossRef] [Google Scholar]

[219] Rodríguez-Almeida, L. F., Jiménez-Serra, I., Rivilla, V. M., et al. 2021a, ApJ, 912, L11 [Google Scholar]

[220] Rodríguez-Almeida, L. F., Rivilla, V. M., Jiménez-Serra, I., et al. 2021b, A&A, 654, A1 [Google Scholar]

[221] Röllig, M. 2011, A&A, 530, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[222] Röllig, M., & Ossenkopf-Okada, V. 2022, A&A, 664, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[223] Schilke, P., Neufeld, D. A., Müller, H. S. P., et al. 2014, A&A, 566, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[224] Schmid, P. C., Thorwirth, S., Endres, C. P., et al. 2022, Front. Astron. Space Sci., 8, 257 [NASA ADS] [CrossRef] [Google Scholar]

[225] Shaw, G., Ferland, G., & Chatzikos, M. 2023, RNAAS, 7, 153 [NASA ADS] [Google Scholar]

[226] Shimonishi, T., Das, A., Sakai, N., et al. 2020, ApJ, 891, 164 [NASA ADS] [CrossRef] [Google Scholar]

[227] Shingledecker, C. N., Lee, K. L. K., Wandishin, J. T., et al. 2021, A&A, 652, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[228] Siebert, M. A., Lee, K. L. K., Remijan, A. J., et al. 2022a, ApJ, 924, 21 [CrossRef] [Google Scholar]

[229] Siebert, M. A., Van de Sande, M., Millar, T. J., & Remijan, A. J. 2022b, ApJ, 941, 90 [NASA ADS] [CrossRef] [Google Scholar]

[230] Sil, M., Srivastav, S., Bhat, B., et al. 2021, AJ, 162, 119 [NASA ADS] [CrossRef] [Google Scholar]

[231] Silva, W. G. D. P., Cernicharo, J., Schlemmer, S., et al. 2023, A&A, 676, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[232] Sims, I. R., Queffelec, J. L., Defrance, A., et al. 1992, J. Chem. Phys., 97, 8798 [NASA ADS] [CrossRef] [Google Scholar]

[233] Šimsová-Zámecníková, M., Soldán, P., & Gustafsson, M. 2022, A&A, 664, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[234] Sita, M. L., Changala, P. B., Xue, C., et al. 2022, ApJ, 938, L12 [NASA ADS] [CrossRef] [Google Scholar]

[235] Skouteris, D., Balucani, N., Ceccarelli, C., et al. 2018, ApJ, 854, 135 [NASA ADS] [CrossRef] [Google Scholar]

[236] Smith, I. W. M., Herbst, E., & Chang, Q. 2004, MNRAS, 350, 323 [Google Scholar]

[237] Smyth, K. C., Lias, S. G., & Ausloos, P. 1982, Combust. Sci. Technol., 28, 147 [CrossRef] [Google Scholar]

[238] Snyder, L. E., Hollis, J. M., Jewell, P. R., Lovas, F. J., & Remijan, A. 2006, ApJ, 647, 412 [NASA ADS] [CrossRef] [Google Scholar]

[239] Sternberg, A., Le Petit, F., Roueff, E., & Le Bourlot, J. 2014, ApJ, 790, 10 [CrossRef] [Google Scholar]

[240] Su, T., & Chesnavich, W. J. 1982, J. Chem. Phys., 76, 5183 [NASA ADS] [CrossRef] [Google Scholar]

[241] Swihart, M., Catoire, L., Legrand, B., Gokalp, I., & Paillard, C. 2003, Combust. Flame, 132, 91 [Google Scholar]

[242] Tenenbaum, E. D., Apponi, A. J., Ziurys, L. M., et al. 2006, ApJ, 649, L17 [CrossRef] [Google Scholar]

[243] Tenenbaum, E. D., Dodd, J. L., Milam, S. N., Woolf, N. J., & Ziurys, L. M. 2010, ApJS, 190, 348 [NASA ADS] [CrossRef] [Google Scholar]

[244] Thaddeus, P., Gottlieb, C. A., Gupta, H., et al. 2008, ApJ, 677, 1132 [NASA ADS] [CrossRef] [Google Scholar]

[245] Tinacci, L., Germain, A., Pantaleone, S., et al. 2022, ACS Earth Space Chem., 6, 1514 [NASA ADS] [CrossRef] [Google Scholar]

[246] Tinacci, L., Ferrada-Chamorro, S., Ceccarelli, C., et al. 2023, ApJS, 266, 38 [NASA ADS] [CrossRef] [Google Scholar]

[247] Tonolo, F., Lupi, J., Puzzarini, C., & Barone, V. 2020, ApJ, 900, 85 [Google Scholar]

[248] Tsang, W. 1991, J. Phys. Chem. Ref. Data, 20, 221 [NASA ADS] [CrossRef] [Google Scholar]

[249] Turner, B. E. 1992, ApJ, 388, L35 [NASA ADS] [CrossRef] [Google Scholar]

[250] Turner, B. E., Steimle, T. C., & Meerts, L. 1994, ApJ, 426, L97 [NASA ADS] [CrossRef] [Google Scholar]

[251] Van de Sande, M., & Millar, T. J. 2019, ApJ, 873, 36 [CrossRef] [Google Scholar]

[252] Van de Sande, M., & Millar, T. J. 2022, MNRAS, 510, 1204 [Google Scholar]

[253] Van de Sande, M., Walsh, C., & Millar, T. J. 2021, MNRAS, 501, 491 [Google Scholar]

[254] Vastel, C., Kawaguchi, K., Quénard, D., et al. 2018, MNRAS, 474, L76 [NASA ADS] [CrossRef] [Google Scholar]

[255] Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [Google Scholar]

[256] Vigren, E., Semaniak, J., Hamberg, M., et al. 2012, Planet. Space Sci., 60, 102 [NASA ADS] [CrossRef] [Google Scholar]

[257] Villinger, H., Futrell, J. H., Howorka, F., Duric, N., & Lindinger, W. 1982, J. Chem. Phys., 76, 3529 [NASA ADS] [CrossRef] [Google Scholar]

[258] Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[259] Wakelam, V., Herbst, E., Le Bourlot, J., et al. 2010, A&A, 517, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[260] Wakelam, V., Loison, J. C., Herbst, E., et al. 2015a, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]

[261] Wakelam, V., Loison, J. C., Hickson, K. M., & Ruaud, M. 2015b, MNRAS, 453, L48 [CrossRef] [Google Scholar]

[262] Wallström, S. H. J., Danilovich, T., Müller, H. S. P., et al. 2024, A&A, 681, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[263] Walsh, C., Harada, N., Herbst, E., & Millar, T. J. 2009, ApJ, 700, 752 [NASA ADS] [CrossRef] [Google Scholar]

[264] Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[265] West, N. A., Li, L. H. D., Millar, T. J., et al. 2023, PCCP, 25, 7719 [NASA ADS] [CrossRef] [Google Scholar]

[266] Wlodek, S., & Bohme, D. 1988, JACS, 110, 2396 [CrossRef] [Google Scholar]

[267] Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [CrossRef] [EDP Sciences] [Google Scholar]

[268] Xie, H., Ding, Y., & Sun, C. 2005, J. Phys. Chem. A, 109, 8419 [NASA ADS] [CrossRef] [Google Scholar]

[269] Xue, C., Willis, E. R., Loomis, R. A., et al. 2020, ApJ, 900, L9 [Google Scholar]

[270] Yurtsever, E., Satta, M., Wester, R., & Gianturco, F. A. 2020, J. Phys. Chem. A, 124, 5098 [NASA ADS] [CrossRef] [Google Scholar]

[271] Zeng, S., Quénard, D., Jiménez-Serra, I., et al. 2019, MNRAS, 484, L43 [Google Scholar]

[272] Zhang, F., Parker, D., Kim, Y. S., Kaiser, R. I., & Mebel, A. M. 2011, ApJ, 728, 141 [NASA ADS] [CrossRef] [Google Scholar]

[273] Ziurys, L. M., Apponi, A. J., Guélin, M., & Cernicharo, J. 1995, ApJ, 445, L47 [NASA ADS] [CrossRef] [Google Scholar]

The UMIST Database for Astrochemistry 2022

1 Introduction

2 The Rate22 database

2.1 Description of the data

2.2 Calculation of rate coefficients

2.3 Caveats and limitations

3 New and updated reactions and species

3.1 HCCNC, HCCNCH+, HC4NC, HC5NH+, C7N− and HC11N

3.2 NC4NH+

3.3 Propargyl and related species: CH2CCH and CH2C3N

3.4 Methyl cyanopolyynes and their isomers

3.4.1 CH3C3N, HCCCH2CN and H2CCCHCN

3.4.2 CH3C5N and H2CCCHC3N

3.4.3 CH3C7N and CH3C9N

3.5 CH2CHCCH

3.6 Methyl polyacetylenes and their isomers

3.6.1 CH3C4H and H2CCCHCCH

3.6.2 CH3C6H and H2CCCHC4H

3.6.3 CH3C8H

3.7 Molecules containing the C–S bond

3.7.1 HCS and HSC

3.7.2 HCCS, HC2S+, H2CCS, HC3S, H2CCCS, C4S, HC4S and C5S

3.7.3 NCS, HNCS and HSCN

3.7.4 HCSC2H and HCSCN

3.7.5 CH3SH and C2H5SH

3.8 The hydrocarbon chains – C5H+, C5H2, C6H2, HCCCHCCC, C10H and C10H−

3.9 HCCCHO, c-C3H2O, H2CCCO, HCOCN and CH2CHCHO

3.10 H2NC and H2CN

3.11 Cn O and HCn O, n = 4−9

3.12 CH3CHCHCN

3.13 Cyanates, their isomers and related species

3.13.1 HNCO and its isomers

3.13.2 OCN, H2NCO+ and H2OCN+

3.13.3 CH3NCO, HOCH2CN and C2H5NCO

3.14 NH2CHO

3.15 HCOOCH3, CH3COOH, HOCH2CHO and (CHOH)2

3.16 CH3NH, CH2NH2 and CH3NH2

3.17 Cyclic hydrocarbons - c-C5H, c-C3HCCH, c-C5H6, c-C6H4, c-C6H5, c-C5H4CCH2, c-C5H5CCH, c-C5H5CN, C6H5CCH, c-C6H5CN, c-C9H8 and c-C9H7CN

3.18 H2CCHC3N and HCCCHCHCN

3.19 CH2CHOH

3.20 HCCN, HCCO and HC4N

3.21 CH3Cl

3.22 PH3

3.23 ArH+

3.24 Circumstellar chemistry

3.24.1 MgO and MgOH

3.24.2 MgNC, MgCN and HMgNC

3.24.3 MgC3N, HMgC3N, MgC5N and MgC7N

3.24.4 MgC2, MgC2H, MgC4H, MgC6H and MgC8H

3.24.5 Aluminium chemistry

3.24.6 Calcium chemistry

3.24.7 Titanium chemistry

3.24.8 Sodium chemistry

3.25 Other detected molecules

4 Model results

4.1 Dark cloud TMC-1

4.1.1 O-rich TMC-1 model

4.1.2 C-rich TMC-1 model

4.2 IRC+10216

5 Summary

Acknowledgements

Appendix A Comparison of observed and calculated abundances in TMC-1

References

All Tables

All Figures

3.1 HCCNC, HCCNCH⁺, HC₄NC, HC₅NH⁺, C₇N⁻ and HC₁₁N

3.2 NC₄NH⁺

3.3 Propargyl and related species: CH₂CCH and CH₂C₃N

3.4.1 CH₃C₃N, HCCCH₂CN and H₂CCCHCN

3.4.2 CH₃C₅N and H₂CCCHC₃N

3.4.3 CH₃C₇N and CH₃C₉N

3.5 CH₂CHCCH

3.6.1 CH₃C₄H and H₂CCCHCCH

3.6.2 CH₃C₆H and H₂CCCHC₄H

3.6.3 CH₃C₈H

3.7.2 HCCS, HC₂S⁺, H₂CCS, HC₃S, H₂CCCS, C₄S, HC₄S and C₅S

3.7.4 HCSC₂H and HCSCN

3.7.5 CH₃SH and C₂H₅SH

3.8 The hydrocarbon chains – C₅H⁺, C₅H₂, C₆H₂, HCCCHCCC, C₁₀H and C₁₀H⁻

3.9 HCCCHO, c-C₃H₂O, H₂CCCO, HCOCN and CH₂CHCHO

3.10 H₂NC and H₂CN

3.11 C_n O and HC_n O, n = 4−9

3.12 CH₃CHCHCN

3.13.2 OCN, H₂NCO⁺ and H₂OCN⁺

3.13.3 CH₃NCO, HOCH₂CN and C₂H₅NCO

3.14 NH₂CHO

3.15 HCOOCH₃, CH₃COOH, HOCH₂CHO and (CHOH)₂

3.16 CH₃NH, CH₂NH₂ and CH₃NH₂

3.17 Cyclic hydrocarbons - c-C₅H, c-C₃HCCH, c-C₅H₆, c-C₆H₄, c-C₆H₅, c-C₅H₄CCH₂, c-C₅H₅CCH, c-C₅H₅CN, C₆H₅CCH, c-C₆H₅CN, c-C₉H₈ and c-C₉H₇CN

3.18 H₂CCHC₃N and HCCCHCHCN

3.19 CH₂CHOH

3.20 HCCN, HCCO and HC₄N

3.21 CH₃Cl

3.22 PH₃

3.23 ArH⁺

3.24.3 MgC₃N, HMgC₃N, MgC₅N and MgC₇N

3.24.4 MgC₂, MgC₂H, MgC₄H, MgC₆H and MgC₈H