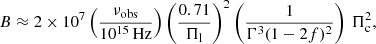EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 680 (December 2023) A&A, 680 (2023) L11 Full HTML
Open Access
Issue
A&A
Volume 680, December 2023
Article Number L11
Number of page(s) 4
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202348214
Published online 15 December 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The origin of the high-energy (keV – TeV) emission in blazar jets is a highly debated open question since the discovery of these jets (Blandford et al. 2019; Hovatta & Lindfors 2019). In the past few years, this debate has intensified since the potential association of TXS 0506+06 with a high-energy neutrino (IceCube Collaboration 2018). The standard approach to the problem has been to model the (quasi-)simultaneous spectral energy distribution (SED) of flaring blazars (e.g., Raiteri et al. 2017; Acciari et al. 2022; MAGIC Collaboration 2023). However, the incomplete wavelength coverage, the complexity of even the simplest models, and the uncertainty introduced by relativistic effects and degenerate parameters leads to multiple and often drastically different models to provide equally good fits to the data.

X-ray polarization has recently provided a new path forward with the launch of the Imaging X-ray Polarimetry Explorer (IXPE; Weisskopf et al. 2022). The first observations of IXPE clearly demonstrated two things. First, the most commonly used single-zone models to describe the SEDs are not consistent with the observed behavior (Liodakis et al. 2022b; Di Gesu et al. 2023; Middei et al. 2023b). Second, the X-ray polarization observations of low-synchrotron peaked sources (LSP; i.e., sources in which the X-ray emission is dominated by the high-energy emission component) favor a scenario in which inverse-Compton scattering from relativistic electrons likely causes at least the keV emission in LSP blazars (Middei et al. 2023a; Peirson et al. 2023). However, LSPs are typically at or below the detection capabilities of IXPE, and it is therefore likely that future missions such as e-XTP are required to solve this puzzle (Peirson et al. 2022).

All of the above demonstrates that new and complementary approaches are necessary. Optical circular polarization (OCP) offers such a complementary pathway, but it remains unexplored to this day because fewer optical polarimeters are available with CP capabilities. There are only a handful of OCP measurements for blazars and for quasars in general (Valtaoja et al. 1993; Wagner & Mannheim 2001; Hutsemékers et al. 2010; Liodakis et al. 2022a), all of which are ≤1%. While the vast majority are upper limits, three sources (3C 279, Wagner & Mannheim 2001; PKS 1256−229, PKS 2155−152, Hutsemékers et al. 2010) have a > 3σ detection. However, it is still unclear whether the reported OCP values are due to instrumental effects (Bagnulo et al. 2011), and if the origin of OCP is intrinsic to the sources (for a discussion of alternative models, see Wagner & Mannheim 2001; Rieger & Mannheim 2005).

We report the first OCP observations of the LSP1 BL Lac-type object S4 0954+65. It is located at RA = 09h58m47.24s, Dec = +65°33′54.81″, and z = 0.367. It is one of the few LSP blazars that has been detected in TeV γ-rays (MAGIC Collaboration 2018), often showing a very high degree (> 30%) of optical linear polarization (OLP; e.g., Blinov et al. 2021; Raiteri et al. 2021). In Sect. 2 we discuss the OCP observations and attempt to constrain the magnetic field strength and particle composition of the jet. In Sect. 3 we discuss our findings.

2. Optical circular polarization observations and modeling

The OCP observations were performed with the SCORPIO-2 focal reducer (Afanasiev & Moiseev 2011) with a thick CCD E2V 261-84 (Afanasieva et al. 2023) at the 6 m BTA telescope of the special astrophysical observatory in highly polarized OLP states found by the St. Petersburg State University’s monitoring program2. In OCP mode, we observed S4 0954+65 twice, in June 2022 and in May 2023. In both cases, we used a z-SDSS broadband filter (Δλ ∼ 830 − 1000 nm). The double Wollaston prism was used as a polarization analyzer, with the λ/4 phase plate used in fixed positions of 0° and 90°. The observations were conducted under cloudy weather conditions with cirrus clouds and a seeing of ∼2″ and ∼1.2″ in the first and second epoch, respectively. Nevertheless, the signal-to-noise ratio (S/N) obtained from each frame with 20 s exposure was S/N ∼ 500 in 2022 and 400 in 2023. The total integration time was 1.06 h and 1.39 h, respectively. The data were reduced following the standard steps of bias and flat-field subtraction, as well as the correction of the polarization channel transmission performed using two stars in 3′ field of view (FoV) around the source. The processing of the SCORPIO-2 polarimetric data is described in detail in Afanasiev & Amirkhanyan (2012). Table 1 summarizes the OCP and OLP observations.

Table 1.

Summary of the observations for S4 0954+65.

Following Liodakis et al. (2022a), we constrained the magnetic field strength and positron fraction using

B ≈ 2 × 10 7 ( ν obs 10 15 Hz ) ( 0.71 Π l ) 2 ( 1 Γ 3 ( 1 − 2 f ) 2 ) Π c 2 , $$ \begin{aligned} B \approx 2\times 10^7 \left( \frac{\nu _{\rm obs}}{10^{15}\,\mathrm{Hz}}\right) \left( \frac{0.71}{\Pi _{\rm l}}\right)^{2} \left( \frac{1}{\Gamma ^3(1-2f)^2}\right) \, \Pi _{\rm c}^2, \end{aligned} $$(1)

where Πl and Πc are the OLP and OCP, respectively, f is the fraction of positrons, νobs is the observing frequency set to the central wavelength of the z-SDSS band (3.28 × 1014 Hz), and B is the intrinsic magnetic field strength in Gauss (Rieger & Mannheim 2005). f is defined as the fraction of positrons to the total number of leptons, that is, f = Ne+/(Ne+ + Ne−). Hence, f = 0 is for a pure proton-electron plasma (or normal plasma), and f = 0.5 is for a pure electron-positron plasma (or pair plasma). The model assumes a power-law distribution of emitting particles, an intrinsic magnetic field perpendicular to the jet axis, and that the jet is viewed at the critical angle (θobs ≈ 1/Γ), which implies that the Lorentz factor (Γ) is approximately equal to the Doppler factor (Γ ≈ δ). We estimated the Doppler factor of the source following Liodakis et al. (2018) and using the most recent data release from the Owens Valley Radio Observatory (up to August 2023; Richards et al. 2011). In brief, we used the Bayesian hierarchical models implemented in Magnetron3 (Huppenkothen et al. 2015) to model the radio light curve at 15 GHz as a series of flares superimposed on stochastic backgrounds. We used the results of Magnetron to compute the maximum observed brightness temperature distribution, which we compared to the intrinsic maximum brightness temperature of Tint, max = 2.78 × 1011 K (Liodakis et al. 2018). We find a Doppler factor of 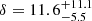δ = 11 . 6 − 5.5 + 11.1 $ \delta=11.6^{+11.1}_{-5.5} $, which is consistent with previous estimates in the literature (Liodakis et al. 2017, 2021). The uncertainties on δ are not statistical, but rather express the range of possible values over the ∼15 years of radio observations. In addition, the imperfectly ordered magnetic field will reduce OCP and OLP similarly from the maximum polarization (Jones & O’Dell 1977; hence the [0.71/Πl] term). The OLP observations are made in the R band, but the polarization degree of S4 0954+65 is fairly achromatic (e.g., Raiteri et al. 2021), with any differences far below the observational uncertainties, which we have taken into account in our simulations below.

With this model, we explored a parameter space for f = [0, 0.5] and for B = [0.1, 20] Gauss. For each pair of (B,  f), we drew a random value for the Doppler factor and the OLP given the uncertainties. We marginalized over all potential values by repeating the process 20 000 times. For each simulation, we evaluated whether the produced OCP was below the observed 3σ upper limit. Figure 1 shows the results of the simulations. It is evident for both observations that models with magnetic field strengths B > 10 Gauss and a low positron fraction (f < 0.2) are disfavored. It is also evident that the observation on JD 2459738.3737 provides more stringent constraints on [B,  f].

thumbnail Fig. 1.

Constraints on the magnetic field strength and positron fraction for the two observations of S4 0954+65. The left panel shows JD 2459738.3737, and the right panel shows JD 2460084.4184. The color bar shows the fraction of successful simulations for each (B,  f) pair. The contours have been added to guide the eye.

3. Discussion

We presented the first optical circular polarization observations of S4 0954+65 in high linear polarized states. Our observations provide strict upper limits below < 0.5% at the 3σ level. The nondetection of the OCP at this low level is consistent with our previous observations of 3C 279 and PKS 1510−089 (Liodakis et al. 2022a), as well as with other past blazar observations (Valtaoja et al. 1993; Wagner & Mannheim 2001; Hutsemékers et al. 2010). We re-estimated the Doppler factor for the source using ∼15 years of radio observations at 15 GHz from OVRO, which we used to constrain its magnetic field strength and jet composition. Throughout our modeling, we assumed that the optical and radio emission regions have the same Doppler factor and that the entire potential OCP signal is intrinsic to the source. If the interstellar dust contributes to the OCP, then our limits will decrease, tightening the constraints on (B,  f). Similarly, if the optical emission region has a higher Doppler factor, as is typically assumed to resolve the Doppler crisis in high-synchrotron peak blazars4 (e.g., Georganopoulos & Kazanas 2003), our constraints would tighten further. Our model considers a scenario in which the intrinsic magnetic field is perpendicular to the jet axis, as is expected in shock-in jet scenarios, for instance Marscher & Gear (1985). In this case, the intrinsic CP is maximized. Our scenario would suggest that the polarization angle is roughly parallel to the jet. This has been found to be true in individual source studies and small sample analyses (e.g., Hovatta et al. 2016). Recent X-ray polarization results for high-peaked blazars (analogous to optical polarization for low-peaked blazars) have also found that the X-ray polarization angle is about the jet axis (Liodakis et al. 2022b; Di Gesu et al. 2022). However, the position angle of the jet can vary over time (e.g., Lico et al. 2020), the optical polarization angle is often highly variable (Kiehlmann et al. 2021), and to our knowledge, there is no population study of the connection between the magnetic field orientation and the jet direction. The radio polarization angle in S4 0954+65 has been found to be parallel to the jet axis (O’Sullivan & Gabuzda 2008; Hodge et al. 2018). The position angle of the jet is 166.3 ± 2.1° (Weaver et al. 2022), but it varies from 129° to 174° (e.g., MAGIC Collaboration 2018). Near in time to our observations, the innermost jet direction changed from 168 ± 3° (5 June 2022) to 129 ± 3° (21 May 2023; S. Jorstad, priv. comm.). According to our OLP angle measurements (Table 1), the magnetic field was roughly parallel to the jet during the first observation and perpendicular during the second. The OLP angle traces the integrated magnetic field direction along the line of sight, and the inner jet direction is estimated using the brightest knot that is well resolved from the radio core (i.e., the brightest feature in the radio image). Hence, our estimates might not be representative of the true direction of the magnetic field with respect to the jet axis. While our quantitative estimates might be affected because our observations encompass different conditions, it is unlikely that our conclusions will be altered.

We find that high magnetic field values (> 10 Gauss) and predominately proton-electron jets overproduce the observed level of OCP. This is important in the context of leptonic versus hadronic models because the latter typically require much larger magnetic field strengths (> 30 Gauss; e.g., Cerruti 2020). Liodakis & Petropoulou (2020) estimated the minimum magnetic field strength required for proton synchrotron models to produce the observed SED for 145 blazars. While S4 0954+65 was not included in their sample, we can use the distribution of the population. For all subclasses of blazars, we find a median of 238 Gauss, and the lowest estimate is 2.85 Gauss. When the sample is restricted to the LSP sources (the subclass of S4 0954+65), the median and lowest value are 243.2 Gauss and 5.34 Gauss, respectively. For high values close to the median, we can exclude the pure electron–proton models at > 4σ significance. For any value above 70 Gauss, we can exclude the pure electron–proton models at > 3σ significance. At 5.34 Gauss, as the minimum found for LSPs, only 3% of the simulations can produce consistent OCP values. For 2.85 Gauss, 4.4% of the simulations are consistent with the observations.

Estimates of the magnetic field strength of S4 0954+65 through leptonic SED modeling (Tanaka et al. 2016; MAGIC Collaboration 2018) suggest values at 1 Gauss or lower. In this case, > 9% of the simulations can produce consistent OCP values. Therefore, we cannot exclude a significant fraction of relativistic protons. However, at such low magnetic field strengths, protons are no longer efficient in producing radiation (Sikora et al. 2009). We note that these B-field estimates are based on single-zone models, which are strongly disfavored by recent X-ray polarization observations (e.g., Liodakis et al. 2022b), but are in fact typically found independently in radio observations (e.g., Pushkarev et al. 2012). If this is the case, then it would suggest that proton emission, and the potential high-energy neutrino emission, is rare or takes place under certain conditions, for example, compression from a shock that would amplify the magnetic field strength, shock–shock interactions, or rotations of the polarization angle (e.g., Liodakis et al. 2020; Novikova et al. 2023). This is in line with the small fraction of observed orphan γ-ray flares (Liodakis et al. 2019; de Jaeger et al. 2023) and the predictions for neutrino emission from X-ray/γ-ray flares (Oikonomou et al. 2019; Stathopoulos et al. 2022), and it might explain why the neutrino-blazar connection remains uncertain even after significant effort (e.g., Plavin et al. 2020; Hovatta et al. 2021; Kovalev et al. 2023).

1

S4 0954+65 has a synchrotron peak frequency of νsyn = 1.1 × 1013 Hz (Ajello et al. 2020)

4

I.e., blazars with νsyn > 1015 Hz

Acknowledgments

We thank the anonymous referee for comments that helped improve this work. We also thank Svetlana Jorstad for providing the estimates of the inner jet position angles at the time of our observations through the BEAM-ME program. I. Liodakis was supported by the NASA Postdoctoral Program at the Marshall Space Flight Center, administered by Oak Ridge Associated Universities under contract with NASA. This research has made use of data from the OVRO 40-m monitoring program (Richards et al. 2011), supported by private funding from the California Institute of Technology and the Max Planck Institute for Radio Astronomy, and by NASA grants NNX08AW31G, NNX11A043G, and NNX14AQ89G and NSF grants AST-0808050 and AST-1109911. S. Kiehlmann acknowledges support from the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme under grant agreement No. 771282. E.S. Shablovinskaya acknowledges support from ANID BASAL project FB210003 and Gemini ANID ASTRO21-0003. Observations with the SAO RAS telescopes are supported by the Ministry of Science and Higher Education of the Russian Federation. The renovation of telescope equipment is currently provided within the national project “Science and Universities”. E. S. Shablovinskaya, E. A. Malygin and S. S. Kotov obtained observational data on the unique scientific facility “Big Telescope Alt-azimuthal” of SAO RAS as well as made data processing with the financial support of grant No 075-15-2022-262 (13.MNPMU.21.0003) of the Ministry of Science and Higher Education of the Russian Federation. This study makes use of VLBA data from the VLBA-BU Blazar Monitoring Program (BEAM-ME and VLBA-BU-BLAZAR; http://www.bu.edu/blazars/BEAM-ME.html), funded by NASA through the Fermi Guest Investigator Program. The VLBA is an instrument of the National Radio Astronomy Observatory. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated by Associated Universities, Inc.

References

  1. Acciari, V. A., Aniello, T., Ansoldi, S., et al. 2022, ApJ, 927, 197 [NASA ADS] [CrossRef] [Google Scholar]
  2. Afanasiev, V. L., & Amirkhanyan, V. R. 2012, Astrophys. Bull., 67, 438 [Google Scholar]
  3. Afanasiev, V. L., & Moiseev, A. V. 2011, Baltic Astron., 20, 363 [NASA ADS] [Google Scholar]
  4. Afanasieva, I., Murzin, V., Ardilanov, V., et al. 2023, Photonics for Solar Energy Systems IX, 10, 774 [NASA ADS] [Google Scholar]
  5. Ajello, M., Angioni, R., Axelsson, M., et al. 2020, ApJ, 892, 105 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bagnulo, S., Sterzik, M., & Fossati, L. 2011, in Astronomical Polarimetry 2008: Science from Small to Large Telescopes, eds. P. Bastien, N. Manset, D. P. Clemens, & N. St-Louis, ASP Conf. Ser., 449, 76 [Google Scholar]
  7. Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
  8. Blinov, D., Kiehlmann, S., Pavlidou, V., et al. 2021, MNRAS, 501, 3715 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cerruti, M. 2020, Galaxies, 8, 72 [NASA ADS] [CrossRef] [Google Scholar]
  10. de Jaeger, T., Shappee, B. J., Kochanek, C. S., et al. 2023, MNRAS, 519, 6349 [NASA ADS] [CrossRef] [Google Scholar]
  11. Di Gesu, L., Donnarumma, I., Tavecchio, F., et al. 2022, ApJ, 938, L7 [CrossRef] [Google Scholar]
  12. Di Gesu, L., Marshall, H. L., Ehlert, S. R., et al. 2023, Nat. Astron., 7, 1245 [NASA ADS] [CrossRef] [Google Scholar]
  13. Georganopoulos, M., & Kazanas, D. 2003, ApJ, 594, L27 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hodge, M. A., Lister, M. L., Aller, M. F., et al. 2018, ApJ, 862, 151 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hovatta, T., & Lindfors, E. 2019, New Astron. Rev., 87, 101541 [CrossRef] [Google Scholar]
  16. Hovatta, T., Lindfors, E., Blinov, D., et al. 2016, A&A, 596, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Hovatta, T., Lindfors, E., Kiehlmann, S., et al. 2021, A&A, 650, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Huppenkothen, D., Brewer, B. J., Hogg, D. W., et al. 2015, ApJ, 810, 66 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hutsemékers, D., Borguet, B., Sluse, D., Cabanac, R., & Lamy, H. 2010, A&A, 520, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. IceCube Collaboration (Aartsen, M. G., et al.) 2018, Science, 361, 147 [NASA ADS] [Google Scholar]
  21. Jones, T. W., & O’Dell, S. L. 1977, ApJ, 214, 522 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kiehlmann, S., Blinov, D., Liodakis, I., et al. 2021, MNRAS, 507, 225 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kovalev, Y. Y., Plavin, A. V., Pushkarev, A. B., & Troitsky, S. V. 2023, Galaxies, 11, 84 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lico, R., Liu, J., Giroletti, M., et al. 2020, A&A, 634, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Liodakis, I., & Petropoulou, M. 2020, ApJ, 893, L20 [Google Scholar]
  26. Liodakis, I., Marchili, N., Angelakis, E., et al. 2017, MNRAS, 466, 4625 [NASA ADS] [CrossRef] [Google Scholar]
  27. Liodakis, I., Hovatta, T., Huppenkothen, D., et al. 2018, ApJ, 866, 137 [Google Scholar]
  28. Liodakis, I., Romani, R. W., Filippenko, A. V., Kocevski, D., & Zheng, W. 2019, ApJ, 880, 32 [NASA ADS] [CrossRef] [Google Scholar]
  29. Liodakis, I., Blinov, D., Jorstad, S. G., et al. 2020, ApJ, 902, 61 [NASA ADS] [CrossRef] [Google Scholar]
  30. Liodakis, I., Hovatta, T., Aller, M. F., et al. 2021, A&A, 654, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Liodakis, I., Blinov, D., Potter, S. B., & Rieger, F. M. 2022a, MNRAS, 509, L21 [Google Scholar]
  32. Liodakis, I., Marscher, A. P., Agudo, I., et al. 2022b, Nature, 611, 677 [CrossRef] [Google Scholar]
  33. MAGIC Collaboration (Ahnen, M. L., et al.) 2018, A&A, 617, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. MAGIC Collaboration (Acciari, V. A., et al.) 2023, A&A, 670, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [Google Scholar]
  36. Middei, R., Liodakis, I., Perri, M., et al. 2023a, ApJ, 942, L10 [NASA ADS] [CrossRef] [Google Scholar]
  37. Middei, R., Perri, M., Puccetti, S., et al. 2023b, ApJ, 953, L28 [NASA ADS] [CrossRef] [Google Scholar]
  38. Novikova, P., Shishkina, E., & Blinov, D. 2023, MNRAS, 526, 347 [NASA ADS] [CrossRef] [Google Scholar]
  39. Oikonomou, F., Murase, K., Padovani, P., Resconi, E., & Mészáros, P. 2019, MNRAS, 489, 4347 [Google Scholar]
  40. O’Sullivan, S. P., & Gabuzda, D. C. 2008, in Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, eds. T. A. Rector, & D. S. De Young, ASP Conf. Ser., 386, 284 [Google Scholar]
  41. Peirson, A. L., Liodakis, I., & Romani, R. W. 2022, ApJ, 931, 59 [CrossRef] [Google Scholar]
  42. Peirson, A. L., Negro, M., Liodakis, I., et al. 2023, ApJ, 948, L25 [NASA ADS] [CrossRef] [Google Scholar]
  43. Plavin, A., Kovalev, Y. Y., Kovalev, Y. A., & Troitsky, S. 2020, ApJ, 894, 101 [Google Scholar]
  44. Pushkarev, A. B., Hovatta, T., Kovalev, Y. Y., et al. 2012, A&A, 545, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Raiteri, C. M., Nicastro, F., Stamerra, A., et al. 2017, MNRAS, 466, 3762 [NASA ADS] [CrossRef] [Google Scholar]
  46. Raiteri, C. M., Villata, M., Larionov, V. M., et al. 2021, MNRAS, 504, 5629 [NASA ADS] [CrossRef] [Google Scholar]
  47. Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [Google Scholar]
  48. Rieger, F. M., & Mannheim, K. 2005, Chin. J. Astron. Astrophys. Suppl., 5, 311 [NASA ADS] [CrossRef] [Google Scholar]
  49. Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [CrossRef] [Google Scholar]
  50. Stathopoulos, S. I., Petropoulou, M., Giommi, P., et al. 2022, MNRAS, 510, 4063 [CrossRef] [Google Scholar]
  51. Tanaka, Y. T., Becerra Gonzalez, J., Itoh, R., et al. 2016, PASJ, 68, 51 [NASA ADS] [CrossRef] [Google Scholar]
  52. Valtaoja, L., Karttunen, H., Valtaoja, E., Shakhovskoy, N. M., & Efimov, Y. S. 1993, A&A, 273, 393 [NASA ADS] [Google Scholar]
  53. Wagner, S. J., & Mannheim, K. 2001, in Particles and Fields in Radio Galaxies Conference, eds. R. A. Laing, & K. M. Blundell, ASP Conf. Ser., 250, 142 [NASA ADS] [Google Scholar]
  54. Weaver, Z. R., Jorstad, S. G., Marscher, A. P., et al. 2022, ApJS, 260, 12 [NASA ADS] [CrossRef] [Google Scholar]
  55. Weisskopf, M. C., Soffitta, P., Baldini, L., et al. 2022, J. Astron. Telesc. Instrum. Syst., 8, 026002 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Summary of the observations for S4 0954+65.

In the text

All Figures

thumbnail Fig. 1.

Constraints on the magnetic field strength and positron fraction for the two observations of S4 0954+65. The left panel shows JD 2459738.3737, and the right panel shows JD 2460084.4184. The color bar shows the fraction of successful simulations for each (B,  f) pair. The contours have been added to guide the eye.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.