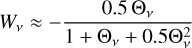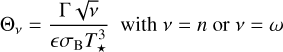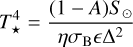EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 680 (December 2023) A&A, 680 (2023) A77 Full HTML
Open Access
Issue
A&A
Volume 680, December 2023
Article Number A77
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202347342
Published online 12 December 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The Yarkovsky effect is the change in the semi-major axis, caused by anisotropic thermal radiation from the surface of the asteroid (Bottke et al. 2006). It can be divided into diurnal and seasonal components (Vokrouhlický et al. 2015a). The first component relates to a delay between the absorption and re-emission of thermal radiation on a rotating body having some thermal inertia. Generally, the diurnal Yarkovsky effect increases the semimajor axis of prograde rotators and decreases for retrograde rotating asteroids. The seasonal effect is related to the seasonal heating and cooling of the asteroid’s hemispheres during its yearly orbital motion. The seasonal effect always leads to an decrease in the semi-major axis. For asteroids larger than 100 m in diameter, the diurnal effect dominates (Farinella et al. 1998).

The diurnal effect depends on the physical and dynamic properties of the asteroid. The typical diameter for which the diurnal effect is the strongest is considered to be on the order of centimetres to meters. Larger objects will be less affected, and the effect is negligible for bodies with d ≳40 km (Bottke et al. 2006). Contrary to the seasonal effect, the diurnal effect is maximum for obliquity γ = 0° or 180° and null for γ = 90°. Moreover, the overall Yarkovsky effect depends on the surface conductivity, density, shape, and heliocentric distance of the object (see Bottke et al. 2006; Vokrouhlicky et al. 2015a, for a full description).

The Yarkovsky effect was first detected for the LAGEOS (Rubincam 1988) artificial Earth satellite as an explanation of the residuals in its orbital elements. The semimajor axis exhibited a decrease at a rate of approximately 1.1 mm day−1. Considering LAGEOS’ rapid rotation and its high surface thermal inertia, this specific rate of change aligned with the seasonal component of the Yarkovsky effect (Rubincam 1988). Later, the Yarkovsky effect was detected for the asteroid (6489) Golevka (Chesley et al. 2003), thanks to radar observations during Golevka’s close approaches in 1991, 1995, and 2003.

As of today, a few objects have a precisely (signal to noise S /N > 100) determined Yarkovsky effect (Farnocchia et al. 2021; Pérez-Hernández & Benet 2022; Vokrouhlický et al. 2015b). Thanks to the NASA OSIRIS-REx mission Lauretta et al. (2017), the asteroid with the most accurately determined Yarkosvy drift is (101955) Bennu. The latest research has led to the result of da/dt = −284.6 ± 0.2 m yr−1, which corresponds to a large S/N of ~1400 (Farnocchia et al. 2021).

The Yarkovsky effect also plays a significant role in the long-term assessment and mitigation strategies of Earth’s impact risk (Farnocchia et al. 2015). For example, (99942) Apophis was on the top of the Risk lists1 for about 17 yr (Chesley 2005). Due to accurate astrometry from new radar and stellar occultation observations, made during its close approach in 2021, the impact could now be ruled out (at least for the next 100 yr)2. This was possible due to the precise Yarkovsky drift determination (da/dt = −199.0 ± 1.5 m yr−1; Pérez-Hernández & Benet 2022). Improvement of the Yarkovsky effect will lead to a better estimate of collision probability, because it has been found to be the most significant non-gravitational acceleration affecting asteroid orbits (Chesley et al. 2014).

Estimations of the Yarkovsky effect can also be used to constrain asteroid densities. Since its determination is agnostic about the physical parameters of the object, the only assumption to make is that the non-gravitational acceleration is dominated by the Yarkovsky effect (Chesley et al. 2014). Solving the approximate analytical expression of the Yarkovsky effect allows for the determination of the bulk density (Golubov et al. 2016; Nugent et al. 2012). Using this method, the bulk density of (101955) Bennu was accurately determined at 1260 ± 70 kg m−3 (Chesley et al. 2014), prior to the OSIRIS-REx mission’s encounter with the asteroid (Goossens et al. 2021). This was later confirmed to be 1191.57 ± 1.74 kg m−3 using data collected during the mission (Goossens et al. 2021). Furthermore, seven additional asteroids have undergone density determinations utilizing this approach: (3200) Phaethon, with a reported density of ρ = 1.67 ± 0.47 g cm−3 (Hanuš et al. 2018), (6489) Golevka, with a density of 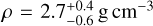ρ=2.7−0.6+0.4g cm−3$\rho = 2.7_{ - 0.6}^{ + 0.4}{\rm{g}}\,{\rm{c}}{{\rm{m}}^{ - 3}}$ (Chesley et al. 2003), (1862) Apollo with a density of 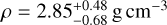ρ=2.85−0.68+0.48g cm−3$\rho = 2.85_{ - 0.68}^{ + 0.48}{\rm{g}}\,{\rm{c}}{{\rm{m}}^{ - 3}}$ (Rozitis et al. 2013), (1620) Geographos with a density of 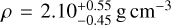ρ=2.10−0.45+0.55g cm−3$\rho = 2.10_{ - 0.45}^{ + 0.55}{\rm{g}}\,{\rm{c}}{{\rm{m}}^{ - 3}}$ (Rozitis & Green 2014) and asteroids with bulk density functions presented in Farnocchia et al. (2013).

The Yarkovsky effect plays a crucial role in understanding the dynamical evolution of individual asteroids, asteroid families, and the overall asteroid population (Bottke et al. 2001; Nesvorny & Bottke 2004). It also contributes to our understanding of meteorite delivery to Earth (Bottke et al. 2006), aids in determining the ages of asteroid families (Spoto et al. 2015), and impact monitoring (Farnocchia et al. 2015). So far the effect has been directly detected for about a few hundred asteroids, all of them being NEOs (Greenberg et al. 2020; Del Vigna et al. 2018; Farnocchia et al. 2013; Nugent et al. 2012; Chesley et al. 2008).

Orbital inversion (without the Yarkovsky effect) is performed routinely in the Gaia development units DU456 and DU457 (Coordination Unit CU4 object processing) of the Gaia Data Processing and Analysis Consortium (DPAC). The methods implemented in the short-term processing pipeline are derived from the work of Muinonen et al. (2016), Oszkiewicz et al. (2009), Virtanen et al. (2001; DU456). The long-term data processing (DU457) of astrometry involves the traditional least-squares method with the differential correction algorithm (Gaia Collaboration 2018; Tanga et al. 2023; Spoto et al. 2018; Milani & Gronchi 2010).

Prior to the start of the Gaia mission, the expectation was that the high precision of astrometry from the ESA’s Gaia space mission will allow for the detection of the effect for a large number of asteroids, including Main Belt objects (Mignard et al. 2007; Mouret & Mignard 2011; Mouret 2011; Spoto et al. 2018). In Dziadura et al. (2022) we determined the effect for 42 asteroids from the Gaia DR2 catalog. Here, we significantly extended our sample and used the latest release of the Gaia catalog. Gaia DR3 was published on 13 June 2022 and contains astrometry for over 150 000 Solar System Objects (SSOs). Moreover, compared to DR2, this data release not only contains more objects and observations but also provides a longer observational arc (22 vs 63 months) which is critical for precise orbit determination (Tanga et al. 2023).

The present study focuses on the determination of the non-gravitational transverse acceleration (the Yarkovsky effect – A2 or da/dt) with the use of Gaia DR3 asteroid astrometry, similar to Dziadura et al. (2022). We process the DR3 astrometry of all near-Earth asteroids (NEAs) and asteroids in the inner main belt in combination with all the available observations from the MPC and radar measurements from Jet Propulsion Laboratory (JPL). In Sect. 2, we describe the data used in this work. In Sect. 3, we describe the methodology used for the orbit determination and the density determination process. In Sect. 4, we present the results of the A2 and densities. We summarize our results in Sect. 5.

2 Data and selection of asteroids

Gaia is a space observatory orbiting at the Lagrangian point L2 of the Sun-Earth system. On 13 June 2022, it had the third complete data release (Gaia DR3). The DR3 catalog contains a large number of stellar data and a large number of asteroid observations. In particular, there are 23 336 467 astrometric measurements that represent 3 214 776 focal CCD plane transits (Tanga et al. 2023). The DR3 along scan astrometric uncertainty is at a sub-milliarcsecond level for objects of magnitude G < 18. For the purpose of this study, we used the astrometry of selected Solar System objects from DR3.

Gaia mission was designed for stellar astrometry; therefore, moving objects (such as asteroids) will drift during observation on the focal plane. Due to this effect, its signal can be cut at the scanning window. Moreover, the information across the scan of the object comes only from the sky mapper field of the CCD. Thus, the accuracy of the across scan is around one arcsecond while for the along scan information comes from the astrometric field of Gaia and reaches the milliarcsecond level. For this reason, the Gaia astrometry data points are highly correlated, and it is crucial to use both error components (systematic and random) of the astrometry (Spoto et al. 2018; Tanga et al. 2023; Dziadura et al. 2022).

Generally, the detection of the Yarkovsky effect depends on the formal uncertainty of the orbital elements, especially the semi-major axis (Del Vigna et al. 2018). Asteroids with longer observational arcs have typically been observed in more oppositions; thus, uncertainties of the orbital parameters are usually smaller. Gaia mission observes numbered asteroids with relatively long observational arcs. Therefore, we selected all objects from Gaia DR3 without additional requirements for the length of the observing arc.

From the Gaia DR3 catalog, we selected all available NEA (446), including 93 Potentially Hazardous Asteroids (PHAs), and all Inner Main Belt Asteroids (IMBAs) and Mars Crossers (semi-major axes a < 2.5 au) which accounts for 54 094 asteroids. The total number of Gaia observations used for this study is 7 323 333. For these objects, we also downloaded all available optical data (ground-based and satellite) from Minor Planet Center (2022) and radar observations from JPL Solar System Dynamics (2022b). The number of optical and radar observations incorporated in this research is 70858 247 and 681, respectively.

We present a summary of the data used for this study in Table 1. For each population, we indicate the number of total observations used and the number of optical, radar, and DR3 data. Furthermore, in Table 2 we present a more detailed breakdown of the data, we indicate the date of the first and last observations, and the number of each type of observation (MPC, radar, Gaia DR3) used in this study, diameters, and the dynamical group. All available diameters and their uncertainties were retrieved from the SsODNet service (Berthier et al. 2023) using its rocks python package3. Most of the diameters come from the NEOWISE mission (Masiero et al. 2011; Masiero et al. 2012, Masiero et al. 2014; Nugent et al. 2016). If the uncertainty was not available, we assumed it to be 1/3 of the diameter (as in Greenberg et al. 2020) and if the diameter was not available, we estimated it from the absolute magnitude and albedo.

Astrometric data were corrected for biases arising from the use of various stellar catalogs (Farnocchia et al. 2015; Eggl et al. 2020). We use a modified version of the OrbFit software developed at the Minor Planet Center that accounts for corrections of the biases arising from the use of various stellar catalogs (Farnocchia et al. 2015; Eggl et al. 2020) and the weighting scheme (Farnocchia et al. 2015; Vereš et al. 2017).

Table 1

Number of objects and observations.

3 Methodology

3.1 Detection of the Yarkovsky effect

We used the standard linearized least-squares orbit computation method with differential corrections described, for example, in Milani & Gronchi (2010), Milani et al. (2005), Farnocchia et al. (2015). We follow the procedure outlined in our previous work (Dziadura et al. 2022) that we summarize here.

The general idea of orbit determination is to minimize the linearized target function (Eq. (1)) and the vectors of residuals. 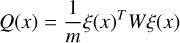Q(x)=1mξ(x)TWξ(x)$Q\left( x \right) = {1 \over m}\xi {\left( x \right)^T}W\xi \left( x \right)$(1)

where Q(x) is the target function, m is the number of observations, ξ(x) are residuals and W is the weight matrix. To find the best fit (minimum residual), we search for stationary points of the target function. In each iteration, an orbit improvement is made, and the solution is given by the differential corrections algorithm.

Different observations from various telescopes have different weights, which are included in the weighing scheme that is used during the orbiting computation. Outliers are automatically removed from the fit using a threshold value of χ2. The rejected observation can be recovered for the fit in a further iteration if it provides a smaller χ2 (Carpino et al. 2003; Milani & Gronchi 2010).

In the N-body problem, we included the masses of all planets, the Moon, Pluto and the 16 most massive asteroids in accordance with the precision of the astrometric observations and because they have a significant gravitational effect (Milani & Gronchi 2010). The list of the 16 most massive asteroids used in this work can be found in Del Vigna et al. (2018; Table 1).

3.2 Density estimation

The daily and annual components of the Yarkovsky effect can be written, using the formalism adapted from Farinella et al. (1998) and Vokrouhlický et al. (2015a): dadt=6(1−A)S⊙9nDρcΔ2[ Wnsin2γ−2Wωcosγ ]${{da} \over {dt}} = {{6\left( {1 - A} \right){S_ \odot }} \over {9nD\rho c{\Delta ^2}}}\left[ {{W_n}{{\sin }^2}{\rm{\gamma }} - 2{W_\omega }\cos {\rm{\gamma }}} \right]$(2)

with : Wv≈−0.5 Θv1+Θv+0.5Θv2${W_v} \approx - {{0.5\,{\Theta _v}} \over {1 + {\Theta _v} + 0.5\Theta _v^2}}$ Θv=Γv∈σBT∗3 with v=n or v=ω${\Theta _v} = {{\Gamma \sqrt v } \over { \in {\sigma _{\rm{B}}}T_ * ^3}}\,{\rm{with}}\,v = n\,{\rm{or}}\,v = \omega $ T*4=(1−A)S⊙ησB∈Δ2$T_*^4 = {{\left( {1 - A} \right){S_ \odot }} \over {\eta {\sigma _{\rm{B}}} \in {\Delta ^2}}}$

where n is the orbital mean motion (rad s−1) dictating the annual component Wn sin2 γ, ω is the asteroid angular rotation frequency (rad s−1) responsible for the daily component Wω cos γ, D is the asteroid diameter (m), A its Bond albedo ((0.29 + 0.684G)pV, with G the phase slope and pV the geometric albedo in V band), ρ its density (kg m−3), Γ its thermal inertia (J m−2 s−1/2 K−1), γ its obliquity (the angle between its orbital and rotational angular momenta, in rad), Δ is the distance to the Sun (au), S⊙ is the solar constant at 1 au (W m−2), T⋆ is the subsolar point temperature (K) and the other parameters are constants: (c the speed of light, ϵ the emissivity, σB the Stefan-Boltzmann constant, and η the beaming parameter). The Eq. (2) derives from the solution of the linearized heat diffusion in a spherical body orbiting the Sun on a circular trajectory. Depending on the specific shape, the Yarkovsky effect value can deviate by several tens of percent from the true value (Vokrouhlicky 1998) Those factors introduce an element of uncertainty.

From the knowledge of the semi-major axis drift (da/dt) derived from the astrometry (Sect. 3.1) and of the other parameters in Eq. (2), one can determine the density ρ of the asteroid (e.g., Chesley et al. 2014). We thus compiled the best estimates for these parameters for each asteroid in our sample, using the ssoCard of SsODNet4 through its rocks5 interface (Berthier et al. 2023). This service contains all parameters from all available literature. If there are multiple measurements of one parameter present in the literature, it provides the one obtained using the most accurate technique or computes a statistically weighted average of the parameter. Many parameters are, however, unknown for many targets, such as their thermal inertia or their obliquity. We thus build a reference probability density function (PDF) of each parameter based on all asteroids (using the BFT, see Berthier et al. 2023). To determine the density and its uncertainty, we use a Monte-Carlo approach, drawing 20 000 random samples for each parameter (either from its known estimate or from the reference PDFs).

Table 2

Summary of the data used for this study.

4 Results

We computed orbits for 54,633 asteroids using a modified version OrbFit software6 (Milani & Gronchi 2010) developed at the Minor Planet Center. For each object, we estimated the six usual orbital parameters along with A2, the non-gravitational transverse acceleration.

To verify the reliability of the detection, we computed the theoretically expected values of the Yarkovsky effect for all of the studied objects and compared them to our empirical estimates. We used the same approach as in Spoto et al. (2015); Del Vigna et al. (2018); Dziadura et al. (2022, Eq. (2)) with one exception. All the previous works have used the asteroid (101955) Bennu as a benchmark to validate the detected Yarkovsky accelerations. Recent results from the OSIRIS-REx mission (Farnocchia et al. 2021; Hergenrother et al. 2019) proved that modelling the Yarkovsky effect for Bennu requires more attention than just fitting the available optical and radar astrometry. Therefore, we have decided to adopt another asteroid as our benchmark, namely (99942) Apophis. Thanks to its close approach to Earth in 2021, Apophis has now the second best-known value of the Yarkovsky effect (Sect. 1). The orbital parameters of (101955) Bennu are better known; however, its semimajor axis undergoes variations influenced by its intrinsic activity Consequently, we computed the expected values A2expected of the Yarkovsky effect using the physical and orbital parameters of the studied objects and scalling it to the Apophis elements provided in Table 3.

Next, we determined the parameter S, which is the ratio between the estimated A2 based on astrometry (empirical approach) and the expected value (theoretical approach) S = A2empirical / A2expected. Detection is considered accepted when the S parameter <2 (the determined value is less than twice the theoretically expected A2) and the signal-to-noise ratio (S / NA2) >3. The marginal results are those with S < 2 and 2.5 < S / NA2 < 3. The remaining supposed detections are rejected. Objects with S / N > 3 but S > 2 have much higher A2 values than predicted and the reason for that may be related to other effects (e.g. cometary-like activity) or wrong estimation of physical properties for which we determine the theoretical effect. However, we are not able to tell if it is just a systematic bias in astrometry therefore further studies for these objects are needed and here we categorise them as rejected. Using a different approach for computing the expected value yield more accepted objects. Nevertheless, we selected the most stringent and accurate method to ensure the validity of our results and avoid any potential false claims.

First, we determined A2 for all NEAs without using Gaia DR3 data. The results are presented in Fig. 1 top panel. There are 41 accepted (green circles), 2 marginal (blue diamonds), and 403 rejected (red pentagons) asteroids. Next, we repeat the computation by adding Gaia DR3 observations. The results are presented in Fig. 1 bottom panel. We obtained 49 accepted asteroids, 8 marginal asteroids, and 389 rejected asteroids. As a result of adding Gaia DR3 observations, there are 10 new accepted results for asteroids. Two of the asteroids that were accepted without using Gaia DR3, due to the reduction of both the A2 value and the uncertainty, fell into marginal cases. For most objects, adding the Gaia data resulted in the reduction of the orbital element uncertainties and global Root Mean Square (RMS) of the observations. In Table A.1 we list the results and other parameters of all accepted NEAs when using Gaia DR3. There are 20 PHAs and 3 binary objects in this data set.

We compared the results of A2 presented in this work with the value of A2 from the literature. We show the comparison in Fig. 2. Generally, the results agree well. Most objects are consistent with the literature. However, there are two objects, 7782 and 7822, with opposite signs. Any other minor discrepancies in values are likely attributed to the utilization of distinct data sets for orbit determination, particularly the inclusion of Gaia DR3 in our study. Furthermore, for all asteroids, the uncertainty of A2 is smaller in this work than in the literature. In the figure, we also present the S value as a colour bar.

We introduced an additional verification method for the accepted results. This method involved calculating the orbit using the most recent 5 yr of observations, and then progressively including older observations in two-year intervals. This approach allowed us to assess the behaviour of the A2 parameter and determine if its value or signal-to-noise ratio (S/N) was significantly influenced by the oldest observations. In most cases, we observed a distinct pattern of decreasing the absolute value of A2 and decreasing uncertainty. A notable example of this behaviour can be seen in the case of (3200) Phaethon (see Fig. 3). However, we obtained a different result for asteroid (433) Eros (Fig. 4). If we had considered only the last observation in 1952 for the fit, the result would have been positive with considerably high uncertainty. We refrain from claiming accepted results if they are only based on old observations. Additionally, the obliquity of (433) Eros, which suggested the A2 to be positive, further supported the decision to exclude it from the accepted group. As a result, (433) Eros was not used for further computations, and it was removed from Fig. 1.

The theoretical equation of the drift of the Yarkovsky effect predicts a diameter dependence <da/dt> ∝ D−1.0 (Greenberg et al. 2020). We compute the empirical value of A2 based on astrometric measurements independent of the physical properties of the asteroids. Therefore, we can determine the dependence of the Yarkovsky effect on the diameter. To compare the results, we derived the value da/dt from A2 as in Farnocchia et al. (2013). In Fig. 5, we present a comparison of the magnitude of the Yarkovsky effect and the diameter of the object. We used an Orthogonal Distance Regression (Jones et al. 2001) and fit a power law. The best fit <da/dt> ∝ D−1.09±0.15, similar to Greenberg et al. (2020). In Fig. 5, there is an exceptional green object located at the top right. This object corresponds to (3200) Phaethon. The reason for this behaviour is its high eccentricity, with a value of e ~0.89 and the A2 value is inversely proportional to (1 − e2).

Among the accepted A2 values for NEA, there are 39 negative and 10 positive results. This corresponds to 39 retrograde rotators Nr and 10 prograde rotators Np. It leads to the preponderance of retrograde rotators (Nr) over prograde rotators (Np), the ratio is Nr/Np = 3.9. Similar to the Farnocchia et al. (2013) Nr/Np = 4 and higher than in Greenberg et al. (2020) Nr/Np = 2.7, La Spina et al. (2004) 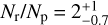Nr/Np=2−0.7+1${N_{\rm{r}}}/{N_{\rm{p}}} = 2_{ - 0.7}^{ + 1}$, Greenberg et al. (2017) Nr/Np = 2.9 ± 0.7 and Nugent et al. (2012) Nr/Np = 2.5 ± 0.1. The excess in retrograde rotators was to be expected, considering that all the objects examined are small NEAs primarily injected into their current orbits by the v6 resonance (Ďurech et al. 2018; La Spina et al. 2004; Granvik et al. 2018). This resonance is located in the Inner Main Belt area therefore, only objects evolve towards the Sun (retrograde rotators). Other resonances (like 3:1 resonance) that are injecting NEAs from the Main Belt are affecting both types of asteroids (prograde and retrograde). Therefore, the presence of retrograde axes in NEAs is important not only for their rotational characteristics but also for understanding their dynamical evolution and the implications of the Yarkovsky effect on these objects.

Furthermore, we analyzed the dependence of formal semi-major axis uncertainties on the detectability of the Yarkovsky effect for NEAs. The theoretical Yarkovsky drift for a 1 km asteroid is in order of 3 × 10−10 au y−1, therefore it causes an orbit change of 3 × 10−9 au in 10 yr (Farnocchia et al. 2013). For this reason, the theoretical uncertainty of the semimajor axis, for ~1 km object, should be lower than σ(a) < 3 × 10−9 au, so we could detect the effect (Del Vigna et al. 2018). Among the accepted NEAs, the formal uncertainty was σ(a) < 3 × 10−9 au with the exception of one small object (141531) with σ(a) < 3.7 × 10−9 and diameter = 303 ± 14 m (Nugent et al. 2016). Overall, including Gaia DR3 in the fit resulted in a decrease in the orbital parameters uncertainties.

We have computed the density values for all accepted and marginally accepted results. An example of physical properties presented as a function of density can be found in Fig. 6. Ten results were excluded from the list due to physically implausible values. A histogram showing the distribution of these results, grouped according to taxonomic class, is presented in Fig. 7. The values are presented in Table A.1. There were three results available in the literature for comparison. For (1862) Apollo ρ ~ 2050 ± 350 kg m−3 in Ford et al. (2014) and 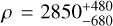ρ=2850−680+480$\rho = 2850_{ - 680}^{ + 480}$ kg m−3 (Rozitis et al. 2013), while our work yielded a value of 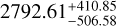2792.61−506.58+410.85$2792.61_{ - 506.58}^{ + 410.85}$ kg m−3. For (66391) Moshup ρ ~ 1267.9 ± 627.16 kg m−3 (Scheirich & Pravec 2009; Scheirich et al. 2021) and here we obtained 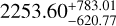2253.60−620.77+783.01$2253.60_{ - 620.77}^{ + 783.01}$ kg m−3. For (88710) ρ ~ 1800.0± 1500.0 kg m−3 (Scheirich et al. 2021), whereas our result was 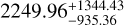2249.96−935.36+1344.43$2249.96_{ - 935.36}^{ + 1344.43}$ kg m−3. These consistent findings further support the reliability of our measurements.

Moreover, we computed orbits including A2, for all IMBAs and Mars-crossing asteroids in Gaia DR3 (54,094 objects). We used the same approach to determine the S value as we used for NEAs. Results are presented in Fig. 8, where we present the S/NA2 versus S for all IMBAs and Mars-crossing asteroids. We are yet not ready to claim the first detections for Non-NEA objects. However, when we used a less restrictive approach –just comparing the A2 to Bennu diameter only – there were 3 accepted and 18 marginal results and 54 073 rejected. Nevertheless, this indicates that we are really close to detecting the A2 for the non-NEA object. Further investigation of these objects is necessary using Gaia DR4 or maybe even the focus product release (October 2023), which will provide a 5-yr observational arc.

Table 3

Apophis orbital and physical parameters.

thumbnail Fig. 1

Parameter S as a function of S / NA2 for all NEA without using Gaia DR3 – top panel, using Gaia DR3 – bottom panel. Green circles represent accepted values (S / NA2 > 3 and S < 2) – consistent with the expected value scaled to the (99942) Apophis A2 value, blue circles are marginal cases with 2.5 < S / NA2 < 3 and S < 2 and red are values with S / NA2 > 3 or S > 2.5. The horizontal line represents S =2. The vertical line represents S / NA2 = 3.
thumbnail Fig. 2

Comparison of the A2 value determined in this work with the literature Greenberg et al. (2020), Ďurech et al. (2018), Del Vigna et al. (2018), Farnocchia et al. (2013), Nugent et al. (2012). S value computed for the A2 parameter determined in this work.
thumbnail Fig. 3

A2 value of (3200) Phaethon, depicted as a function of the observational arc utilized for orbit determination, with the cut-off date representing the date of the last observation included in the fit. The colorbar indicates the number of observations used for the determination of A2. The horizontal line is set at the value 0.
thumbnail Fig. 4

A2 value of (433) Eros as a function of observational arc. Axes, colours, horizontal line as in Fig. 3. The inside panel is zoomed in on the years 1893–1974.
thumbnail Fig. 5

Non-gravitational transverse acceleration as a function of the object diameter, D, for accepted and marginal NEA. Our analysis yields a diameter dependence of D−1.09±0.15, consistent with the theoretical expectation for the Yarkovsky effect of D−1.0 and the one estimated in Greenberg et al. (2020), D−1.06±0.05.

5 Conclusions

We have computed orbits for 54 094 objects in the Main Belt and Mars Crosser groups and 446 NEAs with the goal of estimating the Yarkovsky effect. We obtained 41 accepted A2 results without using Gaia DR3 data and 49 accepted A2 results when using Gaia DR3 data. None of the previous studies used Gaia Data Release 3 (DR3) for orbit determination. Our results prove that adding a small number of ultraprecise astrometry allows better detections of the Yarkovsky effect.

Based on the results of the Yarkovsky effect for accepted NEAs, we determined the retrograde to prograde rotation ratio as Nr/Np = 3.9 and the diameter dependence <da/dt> ∝ D−1.09±0.15. Furthermore, in this study, we introduced an additional validation method. Firstly, we employed the A2 dependence of the observational arc utilized for orbit determination, resulting in the exclusion of (433) Eros from the accepted list. Secondly, we used the Yarkovsky effect to determine the density by considering the A2 values of all accepted and marginal detections and verifying the physicality of the obtained results. Additionally, we provided density measurements for all of these objects.

In this study, we have made significant progress towards the detection of the Yarkovsky effect in non-NEA objects. We are nearing the threshold of detecting a reliable A2 measurement for these objects. However, it is important to note that further investigation is required to establish the discovery of this effect, using an empirical approach, in Main Belt asteroids. Our current methodology is limited in its ability to consider all potential close approaches of other Solar System objects, thereby making it challenging to disentangle non-gravitational effects from small gravitational perturbations. Our gravitational force calculations encompass the influence of all planets, the moon, the 16 most massive asteroids, and Pluto. Consequently, there exists a possibility of ambiguity in our findings.

Moreover, through our analysis, we have identified a set of 11 069 objects with S /N > 2, providing a valuable catalogue of promising Main Belt asteroids that warrant additional scrutiny. These objects represent the initial targets for future investigations into the Yarkovsky effect among MBAs. As we move forward, it is imperative to incorporate data from a more comprehensive ensemble of perturbing asteroids, in conjunction with forthcoming Gaia focus product release and Gaia DR4 data, to enhance our understanding of this phenomenon.

thumbnail Fig. 6

Example of density determination for (1566) Icarus. The cross indicates the best solution, and the dashed line the variation for each parameter. The reported density and uncertainties (Table A.1) are computed by fitting a two-sided Gaussian on the distribution of density.
thumbnail Fig. 7

Histogram displaying the density results, categorized by the taxonomic type of the asteroids.
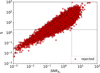thumbnail Fig. 8

Parameter S as a function of S / NA2 for all IMBAs and Mars-crossing asteroids using Gaia DR3. Axes, colours, horizontal and vertical lines as in Fig. 1.

Acknowledgements

We thank the referee David Vokrouhlicky for insightful comments. The research leading to these results has received funding from the National Science Center, Poland, grant number 2022/45/N/ST9/01403 in the years 2023/2024 and Ministry of Science and Higher Education of Poland in the years 2018/2021, as a research project under the “Diamond Grant” program, grant number 0062/DIA/2018/47. D.O. was supported by the National Science Center, Poland, grant number 2017/26/D/ST9/00267. P.B. was supported by grant no. 2022/45/ST9/00267 and through the Spanish Government retraining plan “María Zambrano 2021–2023” at the University of Alicante (ZAMBRANO22-04). This work has used data from the European Space Agency (ESA) Gaia mission (https://www.cosmos.esa.int/gaia). This work presents results from the European Space Agency (ESA) Gaia space mission. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular, the institutions participating in the Gaia Multilateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia and was possible thanks to the open source OrbFit software (http://adams.dm.unipi.it/orbfit/). This research has used data and/or services provided by the International Astronomical Union Minor Planet Center, The JPL Horizons On-Line Ephemeris System, and the Gaia Collaboration. We thank all observers who submitted data to the Minor Planet Center. We did an extensive use of the VO tools TOPCAT (Taylor 2005) and SsODNet (Berthier et al. 2023). Thanks to all the developers and maintainers.

Appendix A Results of the Yarkovsky effect and densities

Table A.1

Estimated Yarkovsky effect for all accepted cases, orbital and physical parameters including determined densities.

References

  1. Alí-Lagoa, V., Müller, T. G., Usui, F., & Hasegawa, S. 2018, A&A, 612, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Benner, L. A. M., Hudson, R. S., Ostro, S. J., et al. 1999, Icarus, 139, 309 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benner, L. A. M., Ostro, S. J., Hudson, R. S., et al. 2002, Icarus, 158, 379 [NASA ADS] [CrossRef] [Google Scholar]
  4. Berthier, J., Carry, B., Mahlke, M., & Normand, J. 2023, A&A, 671, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Binzel, R. P., DeMeo, F. E., Turtelboom, E. V., et al. 2019, Icarus, 324, 41 [Google Scholar]
  6. Bottke, W. F., Vokrouhlický, D., Broz, M., Nesvorný, D., & Morbidelli, A. 2001, Science, 294, 1693 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [CrossRef] [Google Scholar]
  8. Brozovic, M., Benner, L. A., McMichael, J. G., et al. 2018, Icarus, 300, 115 [CrossRef] [Google Scholar]
  9. Busch, M. W., Giorgini, J. D., Ostro, S. J., et al. 2007, Icarus, 190, 608 [NASA ADS] [CrossRef] [Google Scholar]
  10. Busch, M. W., Benner, L. A. M., Ostro, S. J., et al. 2008, Icarus, 195, 614 [NASA ADS] [CrossRef] [Google Scholar]
  11. Carpino, M., Milani, A., & Chesley, S. R. 2003, Icarus, 166, 248 [NASA ADS] [CrossRef] [Google Scholar]
  12. Carry, B. 2012, Planet. Space Sci., 73, 98 [CrossRef] [Google Scholar]
  13. Carry, B., Solano, E., Eggl, S., & DeMeo, F. E. 2016, Icarus, 268, 340 [CrossRef] [Google Scholar]
  14. Chesley, S. R. 2005, Proc. Int. Astron. Union, 1, 215 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chesley, S. R., Ostro, S. J., Vokrouhlicky, D., et al. 2003, Science, 302, 1739 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chesley, S., Vokrouhlický, D., Ostro, S., et al. 2008, LPI Contrib., 1405, 37 [Google Scholar]
  17. Chesley, S. R., Farnocchia, D., Nolan, M. C., et al. 2014, Icarus, 235, 5 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dandy, C. L., Fitzsimmons, A., & Collander-Brown, S. J. 2003, Icarus, 163, 363 [NASA ADS] [CrossRef] [Google Scholar]
  19. Delbo, M. 2004, PhD thesis, Free University of Berlin, Germany [Google Scholar]
  20. Delbó, M., Harris, A. W., Binzel, R. P., Pravec, P., & Davies, J. K. 2003, Icarus, 166, 116 [CrossRef] [Google Scholar]
  21. Del Vigna, A., Faggioli, L., Milani, A., et al. 2018, A&A, 617, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Ďurech, J., Vokrouhlický, D., Kaasalainen, M., et al. 2008, A&A, 488, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Ďurech, J., Vokrouhlický, D., Baransky, A., et al. 2012, A&A, 547, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Ďurech, J., Vokrouhlický, D., Pravec, P., et al. 2018, A&A, 609, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dziadura, K., Oszkiewicz, D., & Bartczak, P. 2022, Icarus, 383, 115040 [NASA ADS] [CrossRef] [Google Scholar]
  26. Eggl, S., Farnocchia, D., Chamberlin, A. B., & Chesley, S. R. 2020, Icarus, 339, 113596 [NASA ADS] [CrossRef] [Google Scholar]
  27. Farinella, P., Vokrouhlický, D., & Hartmann, W. K. 1998, Icarus, 132, 378 [NASA ADS] [CrossRef] [Google Scholar]
  28. Farnocchia, D., Chesley, S., Vokrouhlický, D., et al. 2013, Icarus, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
  29. Farnocchia, D., Chesley, S., Chamberlin, A., & Tholen, D. 2015, Icarus, 245, 94 [NASA ADS] [CrossRef] [Google Scholar]
  30. Farnocchia, D., Chesley, S. R., Milani, A., Gronchi, G. F., & Chodas, P. W. 2015, Orbits, Long-Term Predictions, Impact Monitoring, 815 [Google Scholar]
  31. Farnocchia, D., Chesley, S. R., Takahashi, Y., et al. 2021, Icarus, 369, 114594 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ford, T. F., Benner, L. A., Brozovic, M., et al. 2014, in AAS/Division for Planetary Sciences Meeting Abstracts, 46, 213 [Google Scholar]
  33. Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Golubov, O., Kravets, Y., Krugly, Y. N., & Scheeres, D. 2016, MNRAS, 458, 3977 [NASA ADS] [CrossRef] [Google Scholar]
  35. Goossens, S., Rowlands, D. D., Mazarico, E., et al. 2021, Planet. Sci. J., 2, 219 [NASA ADS] [CrossRef] [Google Scholar]
  36. Granvik, M., Morbidelli, A., Jedicke, R., et al. 2018, Icarus, 312, 181 [CrossRef] [Google Scholar]
  37. Greenberg, A. H., Margot, J.-L., Verma, A. K., Taylor, P. A., & Hodge, S. E. 2017, Yarkovsky Drift Detections for 159 Near-Earth Asteroids (eScholarship, University of California) [Google Scholar]
  38. Greenberg, A. H., Margot, J.-L., Verma, A. K., Taylor, P. A., & Hodge, S. E. 2020, AJ, 159, 92 [NASA ADS] [CrossRef] [Google Scholar]
  39. Grott, M., Knollenberg, J., Hamm, M., et al. 2019, Nat. Astron., 3, 971 [Google Scholar]
  40. Hanuš, J., Delbo’, M., Durech, J., & Alí-Lagoa, V. 2015, Icarus, 256, 101 [CrossRef] [Google Scholar]
  41. Hanuš, J., Delbo’, M., Vokrouhlický, D., et al. 2016, A&A, 592, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Hanuš, J., Vokrouhlický, D., Delbo’, M., et al. 2018, A&A, 620, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Hergenrother, C., Maleszewski, C., Nolan, M., et al. 2019, Nat. Commun., 10, 1 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hromakina, T., Birlan, M., Barucci, M. A., et al. 2021, A&A, 656, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Huang, J., Ji, J., Ye, P., et al. 2013, Sci. Rep., 3, 3411 [NASA ADS] [CrossRef] [Google Scholar]
  46. Hudson, R. S., Ostro, S. J., & Harris, A. W. 1997, Icarus, 130, 165 [NASA ADS] [CrossRef] [Google Scholar]
  47. Hung, D., Hanuš, J., Masiero, J. R., & Tholen, D. J. 2022, Planet. Sci. J., 3, 56 [CrossRef] [Google Scholar]
  48. Jackson, S. L., Rozitis, B., Dover, L. R., et al. 2022, MNRAS, 513, 3076 [NASA ADS] [CrossRef] [Google Scholar]
  49. Jones, E., Oliphant, T., & Peterson, P. 2001, SciPy: Open Source Scientific Tools for Python, http://www.scipy.org [Google Scholar]
  50. JPL Solar System Dynamics 2022a, JPL Small-Body Database Lookup, https://ssd.jpl.nasa.gov/sbdb.cgi [Google Scholar]
  51. JPL Solar System Dynamics 2022b, JPL Small-Body Radar Astrometry, https://ssd.jpl.nasa.gov/?radar [Google Scholar]
  52. Kaasalainen, M., Durech, J., Warner, B. D., Krugly, Y. N., & Gaftonyuk, N. M. 2007, Nature, 446, 420 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kim, M. J., Lee, H. J., Lee, S. M., et al. 2018, A&A, 619, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. La Spina, A., Paolicchi, P., Kryszczynska, A., & Pravec, P. 2004, Nature, 428, 400 [NASA ADS] [CrossRef] [Google Scholar]
  55. Lauretta, D., Balram-Knutson, S., Beshore, E., et al. 2017, Space Sci. Rev., 212, 925 [CrossRef] [Google Scholar]
  56. Mahlke, M., Carry, B., & Mattei, P. A. 2022, A&A, 665, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Mainzer, A., Grav, T., Bauer, J., et al. 2011, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
  58. Mainzer, A., Grav, T., Masiero, J., et al. 2012, ApJ, 760, L12 [NASA ADS] [CrossRef] [Google Scholar]
  59. Mainzer, A., Bauer, J., Grav, T., et al. 2014, ApJ, 784, 110 [Google Scholar]
  60. Marchis, F., Enriquez, J. E., Emery, J. P., et al. 2012, Icarus, 221, 1130 [NASA ADS] [CrossRef] [Google Scholar]
  61. Masiero, J. R., Mainzer, A. K., Grav, T., et al. 2011, ApJ, 741, 68 [Google Scholar]
  62. Masiero, J. R., Mainzer, A., Grav, T., et al. 2012, ApJ, 759, L8 [NASA ADS] [CrossRef] [Google Scholar]
  63. Masiero, J. R., Grav, T., Mainzer, A., et al. 2014, ApJ, 791, 121 [NASA ADS] [CrossRef] [Google Scholar]
  64. Masiero, J. R., Nugent, C., Mainzer, A. K., et al. 2017, AJ, 154, 168 [NASA ADS] [CrossRef] [Google Scholar]
  65. Masiero, J. R., Wright, E. L., & Mainzer, A. K. 2019, AJ, 158, 97 [NASA ADS] [CrossRef] [Google Scholar]
  66. Masiero, J. R., Mainzer, A. K., Bauer, J. M., et al. 2020a, Planet. Sci. J., 1, 5 [NASA ADS] [CrossRef] [Google Scholar]
  67. Masiero, J. R., Smith, P., Teodoro, L. D., et al. 2020b, Planet. Sci. J., 1, 9 [NASA ADS] [CrossRef] [Google Scholar]
  68. Masiero, J. R., Mainzer, A. K., Bauer, J. M., et al. 2021, Planet. Sci. J., 2, 162 [CrossRef] [Google Scholar]
  69. Mignard, F., Cellino, A., Muinonen, K., et al. 2007, Earth Moon Planets, 101, 97 [Google Scholar]
  70. Milani, A., & Gronchi, G. 2010, Theory of Orbit Determination (Cambridge University Press) [Google Scholar]
  71. Milani, A., Sansaturio, M. E., Tommei, G., Arratia, O., & Chesley, S. R. 2005, A&A, 431, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Minor Planet Center 2022, IAU MPC, http://minorplanetcenter.net [Google Scholar]
  73. Mouret, S. 2011, Phys. Rev. D, 84, 122001 [NASA ADS] [CrossRef] [Google Scholar]
  74. Mouret, S., & Mignard, F. 2011, MNRAS, 413, 741 [CrossRef] [Google Scholar]
  75. Mueller, M. 2012, ArXiv e-prints [arXiv:1200.3993] [Google Scholar]
  76. Mueller, M., Delbo’, M., Hora, J. L., et al. 2011, AJ, 141, 109 [NASA ADS] [CrossRef] [Google Scholar]
  77. Muinonen, K., Fedorets, G., Pentikäinen, H., et al. 2016, Planet. Space Sci., 123, 95 [Google Scholar]
  78. Müller, T., Kiss, C., Scheirich, P., et al. 2014, A&A, 566, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Myhrvold, N., Pinchuk, P., & Margot, J.-L. 2022, Planet. Sci. J., 3, 30 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nesvorny, D., & Bottke, W. F. 2004, Icarus, 170, 324 [NASA ADS] [CrossRef] [Google Scholar]
  81. Nugent, C., Margot, J., Chesley, S., & Vokrouhlický, D. 2012, AJ, 144, 60 [NASA ADS] [CrossRef] [Google Scholar]
  82. Nugent, C. R., Mainzer, A., Masiero, J., et al. 2015, ApJ, 814, 117 [NASA ADS] [CrossRef] [Google Scholar]
  83. Nugent, C. R., Mainzer, A., Bauer, J., et al. 2016, AJ, 152, 63 [Google Scholar]
  84. Okada, T., Fukuhara, T., Tanaka, S., et al. 2020, Nature, 579, 518 [NASA ADS] [CrossRef] [Google Scholar]
  85. Ostro, S. J., Margot, J.-L., Benner, L. A. M., et al. 2006, Science, 314, 1276 [NASA ADS] [CrossRef] [Google Scholar]
  86. Oszkiewicz, D., Muinonen, K., Virtanen, J., & Granvik, M. 2009, Meteor. Planet. Sci., 44, 1897 [NASA ADS] [CrossRef] [Google Scholar]
  87. Pérez-Hernández, J. A., & Benet, L. 2022, Commun. Earth Environ., 3, 1 [CrossRef] [Google Scholar]
  88. Rozitis, B., & Green, S. F. 2014, A&A, 568, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Rozitis, B., Duddy, S. R., Green, S. F., & Lowry, S. C. 2013, A&A, 555, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Rozitis, B., Maclennan, E., & Emery, J. P. 2014, Nature, 512, 174 [CrossRef] [Google Scholar]
  91. Rubincam, D. P. 1988, J. Geophys. Res.: Solid Earth, 93, 13805 [NASA ADS] [CrossRef] [Google Scholar]
  92. Scheirich, P., & Pravec, P. 2009, Icarus, 200, 531 [NASA ADS] [CrossRef] [Google Scholar]
  93. Scheirich, P., Pravec, P., Kušnirák, P., et al. 2021, Icarus, 360, 114321 [CrossRef] [Google Scholar]
  94. Sergeyev, A. V., & Carry, B. 2021, A&A, 652, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Shepard, M. K., Clark, B. E., Nolan, M. C., et al. 2008, Icarus, 193, 20 [NASA ADS] [CrossRef] [Google Scholar]
  96. Shimaki, Y., Senshu, H., Sakatani, N., et al. 2020, Icarus, 348, 113835 [Google Scholar]
  97. Spoto, F., Milani, A., & Kneževic, Z. 2015, Icarus, 257, 275 [NASA ADS] [CrossRef] [Google Scholar]
  98. Spoto, F., Tanga, P., Mignard, F., et al. 2018, A&A, 616, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Sugita, S., Honda, R., Morota, T., et al. 2019, Science, 364, eaaw0422 [Google Scholar]
  100. Tanga, P., Pauwels, T., Mignard, F., et al. 2023, A&A, 674, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Taylor, M. B. 2005, in ASP Conf. Ser., 347, Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, 29 [NASA ADS] [Google Scholar]
  102. Trilling, D. E., Mueller, M., Hora, J. L., et al. 2010, AJ, 140, 770 [NASA ADS] [CrossRef] [Google Scholar]
  103. Usui, F., Kuroda, D., Müller, T. G., et al. 2011, PASJ, 63, 1117 [Google Scholar]
  104. Vereš, P., Farnocchia, D., Chesley, S. R., & Chamberlin, A. B. 2017, Icarus, 296, 139 [CrossRef] [Google Scholar]
  105. Virtanen, J., Muinonen, K., & Bowell, E. 2001, Icarus, 154, 412 [NASA ADS] [CrossRef] [Google Scholar]
  106. Vokrouhlický, D. 1998, A&A, 335, 1093 [Google Scholar]
  107. Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015a, The Yarkovsky and YORP Effects, eds. P. Michel, F. DeMeo, & W. F. Bottke, 509 [Google Scholar]
  108. Vokrouhlický, D., Farnocchia, D., Capek, D., et al. 2015b, Icarus, 252, 277 [CrossRef] [Google Scholar]
  109. Warner, B. D. 2018, Minor Planet Bull., 45, 138 [NASA ADS] [Google Scholar]
  110. Watanabe, S., Hirabayashi, M., Hirata, N., et al. 2019, Science, 364, 268 [NASA ADS] [Google Scholar]
  111. Wolters, S. D., & Green, S. F. 2009, MNRAS, 400, 204 [Google Scholar]

All Tables

Table 1

Number of objects and observations.

In the text
Table 2

Summary of the data used for this study.

In the text
Table 3

Apophis orbital and physical parameters.

In the text
Table A.1

Estimated Yarkovsky effect for all accepted cases, orbital and physical parameters including determined densities.

In the text

All Figures

thumbnail Fig. 1

Parameter S as a function of S / NA2 for all NEA without using Gaia DR3 – top panel, using Gaia DR3 – bottom panel. Green circles represent accepted values (S / NA2 > 3 and S < 2) – consistent with the expected value scaled to the (99942) Apophis A2 value, blue circles are marginal cases with 2.5 < S / NA2 < 3 and S < 2 and red are values with S / NA2 > 3 or S > 2.5. The horizontal line represents S =2. The vertical line represents S / NA2 = 3.
In the text
thumbnail Fig. 2

Comparison of the A2 value determined in this work with the literature Greenberg et al. (2020), Ďurech et al. (2018), Del Vigna et al. (2018), Farnocchia et al. (2013), Nugent et al. (2012). S value computed for the A2 parameter determined in this work.
In the text
thumbnail Fig. 3

A2 value of (3200) Phaethon, depicted as a function of the observational arc utilized for orbit determination, with the cut-off date representing the date of the last observation included in the fit. The colorbar indicates the number of observations used for the determination of A2. The horizontal line is set at the value 0.
In the text
thumbnail Fig. 4

A2 value of (433) Eros as a function of observational arc. Axes, colours, horizontal line as in Fig. 3. The inside panel is zoomed in on the years 1893–1974.
In the text
thumbnail Fig. 5

Non-gravitational transverse acceleration as a function of the object diameter, D, for accepted and marginal NEA. Our analysis yields a diameter dependence of D−1.09±0.15, consistent with the theoretical expectation for the Yarkovsky effect of D−1.0 and the one estimated in Greenberg et al. (2020), D−1.06±0.05.
In the text
thumbnail Fig. 6

Example of density determination for (1566) Icarus. The cross indicates the best solution, and the dashed line the variation for each parameter. The reported density and uncertainties (Table A.1) are computed by fitting a two-sided Gaussian on the distribution of density.
In the text
thumbnail Fig. 7

Histogram displaying the density results, categorized by the taxonomic type of the asteroids.
In the text
thumbnail Fig. 8

Parameter S as a function of S / NA2 for all IMBAs and Mars-crossing asteroids using Gaia DR3. Axes, colours, horizontal and vertical lines as in Fig. 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.