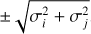| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202346930 | |
| Published online | 01 November 2023 | |
Constraints on the multiplicity of the most massive stars known: R136 a1, a2, a3, and c
1
Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Postbus 94249,
1090 GE
Amsterdam, The Netherlands
e-mail: T.Shenar@uva.nl
2
Departamento de Astrofísica, Centro de Astrobiología (CSIC-INTA),
Ctra. Torrejón a Ajalvir km 4,
28850
Torrejón de Ardoz, Spain
3
Institute of Astronomy, KU Leuven,
Celestijnenlaan 200D,
3001
Leuven, Belgium
4
Department of Physics & Astronomy, Hounsfield Road, University of Sheffield,
Sheffield
S3 7RH, UK
5
Steward Observatory, University of Arizona,
933 North Cherry Avenue,
Tucson, AZ
85721-0065, USA
6
Royal Observatory of Belgium,
Avenue circulaire/Ringlaan 3,
1180
Brussels, Belgium
7
Institute for Physics and Astronomy, University Potsdam,
14476
Potsdam, Germany
8
Zentrum für Astronomie der Universität Heidelberg, Astronomisches Rechen-Institut,
Mönchhofstr. 12–14,
69120
Heidelberg, Germany
Received:
17
May
2023
Accepted:
21
September
2023
Context. The upper stellar mass limit is a fundamental parameter for simulations of star formation, galactic chemical evolution, and stellar feedback. An empirical bound on this parameter is therefore highly valuable. The most massive stars known to date are R 136 a1, a2, a3, and c, with reported masses in excess of 150–200 M⊙ and initial masses of up to ≈300 M⊙. They are located within the central cluster R 136a of the Tarantula nebula in the Large Magellanic Cloud (LMC), However, the mass estimation of these stars relies on the assumption that they are single.
Aims. Via multi-epoch spectroscopy, we provide, for the first time, constraints on the presence of close stellar companions to the most massive stars known for orbital periods of up to ≈10 yr.
Methods. We collected three epochs of spectroscopy for R 136 a1, a2, a3, and c with the Space Telescope Imaging Spectrograph (STIS) of the Hubble Space Telescope (HST) in the years 2020–2021 to probe potential radial-velocity (RV) variations. We combined these epochs with an additional HST/STIS observation taken in 2012. For R 136 c, we also used archival spectroscopy obtained with the Very Large Telescope (VLT). We used cross-correlation to quantify the RVs and establish constraints on possible companions to these stars up to periods of ≈10 yr. Objects are classified as binaries when the peak-to-peak RV shifts exceed 50 km s−1 and when the RV shift is significant with respect to errors.
Results. R 136 a1, a2, and a3 do not satisfy the binary criteria and are thus classified as putatively single, although formal peak-to-peak RV variability on the level 40 km s−1 is noted for a3. Only R 136 c is classified as a binary, in agreement with the literature. We can generally rule out massive companions (M2 ≳ 50 M⊙) to R 136 a1, a2, and a3 out to orbital periods of ≲1 yr (separations ≲5 au) at 95% confidence, or out to tens of years (separations ≲100 au) at 50% confidence. Highly eccentric binaries (e ≳ 0.9) or twin companions with similar spectra could evade detection down to shorter periods (≳10 days), though their presence is not supported by the relative X-ray faintness of R 136 a1, a2, and a3. We derive a preliminary orbital solution with a 17.2 days period for the X-ray-bright binary R 136 c, though more data are needed to conclusively derive its orbit.
Conclusions. Our study supports a lower bound of 150–200 M⊙ on the upper-mass limit at LMC metallicity.
Key words: stars: Wolf–Rayet / binaries: spectroscopic / stars: massive / Magellanic Clouds
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The upper mass limit of stars (Mmax) as a function of metallicity (Z) is one of the most fundamental parameters that dictate the properties of galaxies. This is because the ecology, energy budget, and integrated spectral appearance of galaxies are largely determined by the most massive stars they host (M ≳ 50 M⊙; Crowther et al. 2010; Doran et al. 2013; Ramachandran et al. 2019). Moreover, the most massive stars are invoked in the context of a plethora of unique phenomena, from pair-instability supernovae and long-duration γ-ray bursts (Fryer et al. 2001; Woosley et al. 2007; Langer 2012; Smartt 2009; Quimby et al. 2011) to the early chemical enrichment of globular clusters (Gieles et al. 2018; Bastian & Lardo 2018; Vink 2018).
Establishing Mmax from first principles or simulations of star formation is challenging due to a variety of uncertainties, and estimates vary from ≈120 M⊙ to a few thousand M⊙, depending on Z and modelling assumptions (e.g. Larson & Starrfield 1971; Weidner & Kroupa 2004; Oey & Clarke 2005; Figer 2005). It is therefore essential to identify and weigh the most massive stars in our Galaxy and nearby lower-metallicity galaxies, such as the Small and Large Magellanic Clouds (SMC and LMC).
Stars initially more massive than ≈100 M⊙, dubbed very massive stars (VMSs), tend to have emission-line-dominated spectra stemming from their powerful stellar winds already on the main sequence. Such stars spectroscopically appear as Wolf–Rayet (WR) stars (de Koter et al. 1997). Due to the CNO burning cycle, they are N-rich and hence belong to the nitrogen WR sequence (WN). Unlike classical WR stars, which are evolved and massive H-depleted stars, VMSs typically show substantial surface hydrogen mass fractions (XH ≳ 40%) and are usually classified as WNh to indicate a H-rich atmosphere.
In the case of double-lined spectroscopic binaries (SB2s), the mass ratio and minimum masses of both components (M1‚2 sin3 i, where i is the orbital inclination) can be established via Newtonian mechanics. If the inclination is also known, then the true masses can be derived. Best constraints are obtained for eclipsing binaries, such as the massive Galactic binaries WR 43a (M1 = 116 ± 31 M⊙, M2 = 89 ± 16 M⊙; Schnurr et al. 2008), WR 21a (M1 = 93 ± 2 M⊙, M2 = 53 ± 1 M⊙; Tramper et al. 2016; Barbá et al. 2022), WR 20a (M1 = 83 ± 5 M⊙, M2 = 82 ± 5 M⊙; Rauw et al. 2004; Bonanos et al. 2004), and the SMC binary HD 5980, which hosts a luminous blue variable (LBV) and a WR star of masses 60–70 M⊙ (Koenigsberger et al. 2014). The inclination can also be constrained from interferometry (e.g. Richardson et al. 2016; Thomas et al. 2021) or from spatially resolved structures, such as the Homunculus nebula of of the Galactic binary η Car, a luminous LBV+WR system with masses ≈ 100 + 60 M⊙ (Madura et al. 2012; Strawn et al. 2023). Alternatively, the inclination can be constrained via polarimetry (Brown et al. 1978; Robert et al. 1992) or wind eclipses (Lamontagne et al. 1996), as was the case for the LMC binaries R 144 (alias BAT99 118) and R 145 (alias BAT99 119), which host similarmass components with current masses of ≈70–80 M⊙ and initial masses of ≈ 150 M⊙ (Shenar et al. 2017b, 2021).
When the inclination cannot be measured, the mass ratio and minimum masses nevertheless provide important parameters, which, in conjunction with other methods, constrain the true masses of the components. Examples include the LMC colliding-wind binary Melnick 33Na (M1 = 83 ± 19 M⊙, M2 = 48 ± 11 M⊙; Bestenlehner et al. 2022) and the most massive binary known to date, Melnick 34 (alias BAT99 116), with derived component masses of M1 = 139 ± 20 M⊙ and M2 = 127 ± 17 M⊙ (Tehrani et al. 2019).
In the absence of a companion, the mass of a star is estimated by matching the derived stellar properties (mainly the luminosity, L, effective temperature, Teff, and XH) with structure or evolution models, which yields the evolutionary current and initial masses. It is important to note that such mass estimates assume an internal structure for the star (e.g. H-burning or He-burning), which is not always trivial for WNh stars (e.g. the case of R 144; Shenar et al. 2021). Prominent examples for putatively single VMSs and WNh stars include the LMC WN5h star VFTS 682 (Bestenlehner et al. 2014) and several very massive WNh and Of stars in the Galactic clusters Arches (e.g. Figer et al. 2002; Najarro et al. 2004; Martins et al. 2008; Lohr et al. 2018) and NGC 3603 (Crowther et al. 2010). This method was also used to establish the masses of the most massive stars known, which are the subject of this study. These stars, which are classified as WN5h and reside in the dense central cluster R136 of the Tarantula nebula in the LMC, include R 136 a11 (alias BAT99 108, M = 200–300 M⊙, a1 hereafter), R 136 a2 (alias BAT99 109, M = 150–250 M⊙, a2 hereafter), R 136 a3 (alias BAT99 106, M = 150–200 M⊙, a3 hereafter), and R136 c (alias BAT99 112, VFTS 1025, M = 150–200 M⊙, c hereafter).
Studies in the 1980s identified the central region of R 136 as a single star with a mass ≳1000 M⊙ (Cassinelli et al. 1981; Savage et al. 1983), but later investigations with speckle interferometry and the Hubble Space Telescope (HST) showed that the central region comprises distinct stellar sources, including a1, a2, and a3 (Weigelt & Baier 1985); Lattanzi et al. 1994; Hunter et al. 1995). First measurements of these objects yielded masses of the order of 100 M⊙ (e.g. Heap et al. 1994; de Koter et al. 1997; Massey & Hunter 1998; Crowther & Dessart 1998). However, Crowther et al. (2010) reported masses in excess of 200 M⊙ using modern model atmospheres that account for iron line blanketing. Since then, the masses of a1, a2, a3, and c have been subject to several revisions (Hainich et al. 2014; Crowther et al. 2016; Rubio-Díez et al. 2017; Bestenlehner et al. 2020; Brands et al. 2022) but remain record-breaking in terms of current and initial masses. A visual companion to a1 was identified by Lattanzi et al. (1994) with the HST’s Fine Guidance Sensor (FGS), and later with HST imaging by Hunter et al. (1995). Recently, Khorrami et al. (2017) and Kalari et al. (2022) confirmed the presence of this companion and detected another faint companion to a3 via speckle imaging. Accounting for these com-panions potentially lowers the mass estimates of a1 and a3 by 10–20%.
A drawback for mass estimates of putatively single stars is the assumption that they are single. The presence of a contaminating companion could substantially alter the derived stellar parameters (especially L) and, in turn, the stellar masses. The realisation that the majority of massive stars reside in binary systems (Sana et al. 2012, 2013) forces us to consider that R 136 a1, a2, a3, and c may be members of binaries. In fact, relying on K-band spectroscopy acquired over 22 days, Schnurr et al. (2009) identified R 136 c as a potential binary with a 8.2 days period. The relatively high X-ray luminosity (≈1035 erg s−1) of R 136 c (Portegies Zwart et al. 2002; Townsley et al. 2006; Guerrero & Chu 2008; Crowther et al. 2022) suggests that it is a colliding-wind binary, where both companions possess a fast wind, although a compact object companion is also a viable option.
Until now, a1, a2, and a3 had not been probed for multiplic-ity for periods longer than a few weeks. In this study, we present results from a 1.5 yr spectroscopic monitoring of R136 a1, a2, a3, and c obtained with the HST, combined with a previous epoch obtained in 2012 and archival data for R 136 c. By deriv-ing the radial velocities (RVs) of the stars, we place constraints on potential companions. We additionally derive a new orbital solution for R136 c. The reduction of the data is described in Sect. 2, and their analysis is described in Sect. 3. We discuss our results in Sect. 4 and provide a brief summary in Sect. 5.
2 Data and reduction
Our investigation relies primarily on three epochs of spectroscopy obtained with the Space Telescope Imaging Spectrograph (STIS) mounted on the HST (PI: Shenar, proposal ID: 15942). We used a slit aperture of 52″ × 0.1″ with the G430M filter at the central wavelengths 3936 (37704101 Å), 4706 (4540–4872 Å), and 4961 (4795–5127 Å). Each pair of stars (a1, a2), (a3, c) defined a STIS slit positioning to enable the acquisition of the spectra of two stars during a single pointing (Fig. 1). The resulting position angles (PA) are 106° (or 286°) and 162.2° (or 342.2°) for the pairs (a1, a2) and (a3, c), respectively. The PA of the pair (a1, a2) is similar to the PA used by Crowther et al. (2016) in their scanning of the R 136 cluster with STIS (where the PA was 109° or 289°). Overall, three epochs of observations were acquired on 28 March 2020 (MJD 58936.20), 28 September 2020 (MJD 59120.07), and 14 September 2021 (MJD 59471.74) for the pair (a1, a2), and on 25 May 2020 (MJD 56023.42), 26 November 2020 (MJD 58994.06), and 14 May 2021 (MJD 59179.31) for the pair (аЗ, с) for each of the three spectral bands. Each exposure was divided into two dithered sub-exposures for removal of cosmics. The G430M filter has a spatial dispersion of 0.05″ pixel−1 The signal-to-noise ratio (S/N) of the data is ≈20–80 per pixel, depending on the star and the spectral domain. The spectral resolving power is R = λ/∆λ ≈ 6000 with a dispersion of ∆λ = 0.28 Å.
The extraction of the spectra of the stars R 136 аЗ and с acros s the slit is straightforward, since they are well separated spatially. The extraction of the pair (al, a2), however, is less trivial, since the point spread functions (PSFs) of the two sources overlap (see Fig. 1). To extract the spectra, we fitted Voigt profiles with identical width parameters (to mimic the PSF) to the flux across the cross-dispersion direction, as shown in Fig. 2. The fitting of the Voigt profile was performed in a wavelengthdependent fashion, such that the flux across the spatial direction was fitted for each wavelength bin. We fixed the separation between the Voigt profiles to 0.113″ (or 2.25 HST pixels), as found by Kalari et al. (2022), and fixed the amplitude ratios of the Voigt profiles to the magnitude ratio derived by Kalari et al. (2022). Attempts to avoid the latter had resulted in an instrumental wavy pattern that compromised the RV measurements. We fitted for the Voigt broadening parameters σ, γ as a function of wavelength but enforced both Voigt profiles of al and a2 to share the same parameters. The resulting spectral energy distributions are shown in Fig. 3.
The flux leveis of the four stars are relatively consistent in the three available epochs, though ≈10% variations are seen in al and a3. Such discrepancies are typical for the narrow-slit mode of STIS, which does not fully account for slit losses (e.g. Lennon et al. 2021). The overall flux level is consistent between the different epochs and is in agreement with the flux level presented by Crowther et al. (2010). However, we cannot rule out some contamination between al and a2 for strong fines such as He II λ4686 (see below), since in this case the PSFs are not well resolved. Results obtained for the He II λ4686 line for these components should be therefore taken with caution.
A similar technique was used by Crowther et al. (2016) for their analysis of STIS spectroscopy of the R 136 Cluster. The flux-calibrated spectra show a general agreement with those presented by Crowther et al. (2016), although the underlying spectral energy distribution for al and a2 depends on the PA, suggesting that the flux variability observed between the epochs is linked to the observational setup rather than intrinsic. For our study, only normalised spectra were used. The extracted spectra were rectified using a homogeneous set of pre-selected continuum points.
To verify our extraction methodology, we newly extracted the spectra of al, a2, and a3 from observations acquired in 2012 with STIS, which had been extracted and analysed by Crowther et al. (2016) using the MULTISPEC package (Maiz-Apellaniz 2005; Knigge et al. 2008). The extractions match well with each other. The 2012 spectra for a1, a2, and c are combined with the newly acquired 2020–2021 spectra in our investigation to boost the binary detection probability. We also inspected the interstellar Ca II K and H lines at 3934.77 Å and 3969.59 Å (wavelengths in vacuum) as a check on the absolute wavelength calibration of the spectra.
The extracted spectra (both the new data and the original 2012 epochs by Crowther et al. 2016) are shown in Fig. 4. The spectra only cover a few features that could correspond to cooler companions (e.g. He I λ4713), but these features appear flat for R 136 a1, a2, and a3 (for c, see Sect. 3.2), in agreement with previous studies of these objects. We therefore only show the main diagnostic lines: N IV λ4058, N V λλ4604,4620, He II λ4686, and N V λ4945.
Before advancing to the analysis, it is interesting to already note that no clear indications of RV variability are seen from an inspection of Fig. 4, with the exception of star c. Identifying companions on the basis of spectral appearance (as opposed to RV variability) is not viable here. Companions of interest in this study would have masses ≳50 M⊙, and such companions show primarily H and He II lines, which overlap with those of the WR primaries. Searching for RV variability is hence the method of choice with the available data.
For R 136 c, we used 34 archival spectra in addition to the HST data. These data cover five observing epochs (PI: Evans, ID: 182.D-0222) and were acquired in 2008–2010 with the Fibre Large Array Multi Element Spectrograph (FLAMES) ARGUS integral field unit mounted on UT2 of the Very Large Telescope (VLT). Each spaxel of ARGUS spatially covers 0.52″. The spectra cover the range 3960–4570 Å with a resolving power of R = 10500, a dispersion of ∆λ = 0.2 Å, and a typical S/N of 50–100 per pixel. The retrieval and reduction of the data are described in Evans et al. (2011). In addition, we retrieved a single spectroscopic observation acquired in 2001 with the Ultraviolet and Visual Echelle Spectrograph (UVES) mounted on UT2 of the VLT. We only used the spectrum covering the range 3700–5000 Å, which includes the N IV λ4058 line. The spectrum has a resolving power of R = 40 000 and a S/N of ≈20 per pixel, with a dispersion of ∆λ = 0.015 Å. The data are described in Cox et al. (2005), and are retrieved in reduced form from the European Southern Observatory (ESO) archive. We ensured wavelength calibratura to within a few km s−1 using the Cali H line at 3969.59Å, which is present in the HST, ARGUS, and UVES datasets.
 |
Fig. 1 Image of the central 3″ × 5″ (≈0.7 × 1.2 parsec) core of R 136 taken in 2009 with the HST’s Wide Field Camera 3 (WFC3) in the ultraviolet and visible light (UVIS) Channel with the F555W filter (λ0 ≈ 5500 Å, proposai ID 11360). Marked are the positions of our four targets and the two slit positions used to acquire the data. |
 |
Fig. 2 Fit of two Voigt proflies representing the PSFs of al and a2 to the flux across the cross-dispersion axis for the 28 March 2022 epoch at 4850.6 A. The Voigt profiles are used to compute the relative weight of each data point to the flux of each star at each given wavelength. |
 |
Fig. 3 Extracted calibrated fluxes for al, a2, аЗ, and с for the new epochs presented here (see the labels and legends). |
3 Analysis
3.1 Cross-correlation
The main tool with which our targets are probed for multiplicity is the measurement of RVs via maximisation of cross-correlation functions (CCFs). The technique is described by Zucker & Mazeh (1994), and is frequently implemented for WR binaries (e.g. Shenar et al. 2017b, 2019, 2021; Dsilva et al. 2020, 2022, 2023). Briefly, the CCF is computed in a particular spectral range (or multiple ranges) as a function of Doppler shift using a prespecified template that should represent the star. While for WR stars the template is usually produced by co-adding the individual observations, this does not yield satisfactory results in our case due to the limited number of observations and the modest S/N. Moreover, we refrained from cross-correlating multiple lines simultaneously since lines in WR spectra are formed in different radial layers and therefore often produce systematic shifts with respect to one another (e.g. Shenar et al. 2017a). Instead, we used a synthetic spectrum computed with the Potsdam Wolf–Rayet (PoWR) model atmosphere code (Hamann & Gräfener 2003); Sander et al. 2015) tailored for the analysis of these objects by Hainich et al. (2014). While this yields absolute RVs, an absolute RV calibration for WR stars is highly model dependent since the line centroids sensitively depend on the atmosphere parameters. However, this does not impact our study, since the detection of binaries relies on relative RVs. A comparison between the PoWR model used here and the spectrum of a1 is shown in Fig. 5.
The results from the CCF analysis for N IV λ4058, N V λλ4604,4620, He II λ4686, and N V λ4945 are shown in Fig. 6. Tables A.1 and A.2 provide a compilation of these measurements and the measured equivalent widths (EWs) of these lines. Upper bounds on the statistical errors on the EWs are computed as in Chalabaev & Maillard (1983). Significant EW variability is noted between the 2012 epoch and the other epochs in the He II λ4686 line belonging to a1. While such variability is not atypical for WR stars (e.g. Moffat & Bobert 1992; Lépine & Moffat 1999), this result could also be spurious given the difficulty in the more challenging extraction of the He II λ4686 line (see Sect. 2).
While the nitrogen lines are typically considered as the best RV probes of WN stars as they form relatively close to the stellar surface, the modest S/N becomes a limiting factor. In this context, the He II λ4686 line offers an important high S/N RV probe, but its interpretation should be treated with caution for a1 and a2 given possible cross-contamination in this line. The fact that the RVs of a1 and a2 from the N IV λ4058, N V λλ4604,4620, and N V λ4945 lines are consistent between the epochs, but the those of the He II λ4686 line are strongly variable, suggests that this RV variability is not genuine.
In principle, to classify RV variables into binaries versus putatively single, one commonly adopts a significance criteria on the peak-to-peak RV variability (see e.g. Sana et al. 2013). Due to the intrinsic variability of WR stars, it is often not trivial to find a single criterion. A significance criterion on the peak-to-peak (pp) RV shift that is commonly adopted is
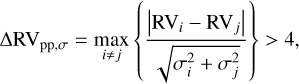 (1)
(1)
where σ is the corresponding error on the RV measurement. The threshold 4 is considered conservative, resulting in a falsepositive probability of roughly 0.1% (Sana et al. 2013). However, because of the intrinsic variability of WR stars, σ may be underestimated, and this criterion alone can lose validity. Hence, in addition, we also invoked a threshold criterion on the peak-to-peak RV difference, ∆RVpp = max{RVi− RVj}. Dsilva et al. (2023) conducted an RV monitoring survey of 11 late-type WN stars of spectral classes similar to those of a1, a2, a3, and c, and found the threshold ∆RVpp > 50 km s−1 clearly separated spectroscopic binaries from potentially single stars, and that intrinsic variability can lead to apparent RV variations of up to 50 km s−1, depending on the wind and stellar properties. Our second criterion for a binary classification is thus
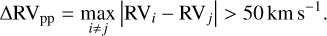 (2)
(2)
While the choice of this threshold impacts our classification to binary or single, the bias discussion provided in Sect. 4 addresses this issue. Table 1 summarises whether or not Eqs. (1) and (2) are fulfilled for each of the spectral diagnostics. When both conditions are satisfied, we flagged the star as a binary. Evidently, the only star that satisfies both conditions is R136 c (with the He II λ4686 line, and marginally with the nitrogen lines). In contrast, a1, a2, and a3 do not satisfy both conditions for any of the lines, and are hence flagged as putative single. The fact that R 136 c is classified as a binary is consistent with the findings of Schnurr et al. (2009), who derived a tentative 8.2 days orbital period for this object, and its high X-ray luminosity, suggestive of colliding winds or a compact object in the binary (Portegies Zwart et al. 2002; Crowther et al. 2022).
Before advancing to the interpretation of these results, one may wonder whether a 1D CCF method is valid if these objects are SB2s. Given the spectral appearance of our targets, the only companions that could be relevant in terms of contributing sufficient flux to bias the results are O-type stars or WR stars. O-type dwarfs typically have absorption-line-dominated spectra with weak to non-existing features belonging to N IV or N V, and much weaker features in the He II λ4686 line compared to a WR star (Walborn & Fitzpatrick 1990); Walborn et al. 2002). A contamination with an О dwarf therefore poses no danger to our RV measurement methodology.
However, a contamination with an Of star, a transition O/WR star (Crowther & Walborn 2011), or a WN star could impact our interpretation. For example, consider the case of two WN stars with similar ΝIVλ4058 or He II λ4686 line profiles. Typical peak-to-peak RV amplitudes may fall below the full-width half-maximum (FWHM) of these lines, implying that the line profiles would remain blended and show a marginai or even vanishing RV shift (e.g. Sana et al. 2011). The same argument holds for Ρ Cygni lines (such as N V λλ4604,4620), although the effect is more difficult to quantify. Thus, instead of an RV variation, one would observe a periodic change in the FWHM of the line. Excess emission stemming from wind-wind collisions may also be added to this line, further changing its profile (Luehrs 1997). For this reason, we also measured the FWHMs of the N IV λ4058 and He II λ4686 lines for the al, a2, a3, and с (Fig. 7). To obtain the FWHMs and their respective errors, we fitted Gaussian profiles to the N IV λ4058 and He II λ4686 lines and generate 1000 spectra with the same underlying Gaussian profile and S/N of the original data. The FWHM is then taken as the average of the FWHMs of these 1000 simulated spectra, and the error is their standard deviation. The results are shown in Fig. 7, and are also provided in Table A.3. Neither of the stars exhibits strong variability, with only the He II λ4686 line of R 136 с being significantly variable (on a 4σ levei). The interpretation of these results will be conducted in Sect. 4.
 |
Fig. 4 Extracted STIS spectra for a1, a2, a3, and c (from top to bottom), focusing on the diagnostic lines N IV λ4058, N V λλ4604,4620, He II λ4686, and N V λ4945 (from left to right). Epochs are listed in the legends. The spectra of a3 and c are binned at ∆λ = 0.5 Å for clarity. |
 |
Fig. 5 Comparison between the synthetic PoWR model (solid red line) used for cross-correlation and the normalised spectrum of al taken in March 2020 (noisy blue line). The line profiles of the PoWR model were shifted by 330 km s−1, and the EWs of the N IV λ4058 and Ν Vλ4945 proflies were scaled to the observations for the sake of plotting (the EW has no impact on the cross-correlation algorithm). The spectra of a2, a3, and с are comparable, and so is the match between the model and the data. |
 |
Fig. 6 Relative RVs measured for the four diagnostic spectral features in the spectra (when available; see the legend). The first RV is always calibrated to zero. Only component с, which satisfles the criteria in Eqs. (1) and (2), is classified as a binary. |
Binary status of R 136 al, a2, a3, and c.
3.2 Orbital analysis of R 136 с
We followed a similar analysis methodology using the 34 calibrated FLAMES spectra and single UVES spectrum available for R 136 с, which probe six distinct observational epochs in addition to the three HST epochs. The only robust RV probe in the available spectral range is the N IV λ4058 line, for which the same PoWR template is used as in Sect. 3.1. The full list of RVs is available in Tables A.1 and A.4. The amplitude of the RV variability is in apparent agreement with the HST data.
Figure 8 shows a Lomb-Scargle periodogram derived for the full set of RVs (HST + FLAMES + UVES). Multiple peaks are clearly present in the periodogram, with the most prominent peaks at P = 5.277, 5.345, 5.563, 17.20, 25.94, 47.15, and 83.06 days. For this set of periods, we used Python’s lmfit minimisation package2 with the differential evolution method to constrain the time of periastron (T0), systemic velocity (V0), RV semi amplitude (Κ1), argument of periastron (ω), and eccentric-ity (e) via
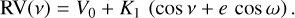 (3)
(3)
The lowest reduced χ2 (reduced χ2 = 0.46) is obtained for Ρ = 17.20 days, which is reflned to Ρ = 17.2051 days dur-ing the miηimisatiοη. We οbtaiη: T0 = 54737.8 + 1.5 [ΜJD], V0 = 307.6 + 2.8 km s−1Κ1 = 51 ±9 km s−1, ω = 148.5 + 3.7°, e = 0.31 + 0.08. Figures 9 and 10 compare this solution to the measurements. However, acceptable solutions are found for ail the periods listed above. We tried combining these RVs with those published by Schnurr et al. (2009) from IR data, but the period remains poorly constrained. Since the analysis involved a different spectral line than N IV λ14058, we refrained from including the RVs from Schnurr et al. (2009) in our final analysis. Moreover, the preliminary 8.2 days period derived by Schnurr et al. (2009) is not supported by our analysis.
Another interesting fact is the presence of He I absorption lines in the Spectrum of R136 с (Fig. 11). These Hei lines are seemingly static. The standard déviation of their RVs is 9.3 km s−1, comparable with the mean of the Statistical error (7.7 km s−1). If these lines originate in the physical companion of the WR star in R 136 с, then it must be a few times more massive than the WR star to avoid observed RV variability. This is somewhat in tension with the spectral type of the object, which is suggestive of a late-type О star or an early type В star. More likely, these lines belong to a distant tertiary source. Hénault-Brunet et al. (2012) noted that the ARGUS spaxel (which covers 0.52″, Sect. 2) included two sources, with R 136 c being significantly brighter. It is well possible that the second star produces the He I absorption lines.
The Hγ line shown in Fig. 11 likely stems from both the WN5h component and the late OB-type component. However, the variability seen in Balmer lines such as Hγ is likely dominated by the WNh5 component and its motion. WN5h stars, including a1, a2, and a3, typically show a combined emission + absorption profile in Hβ, Hγ, and Hδ (Crowther et al. 2010). Additional variability could stem from wind-wind collisions (e.g. Hill et al. 2000), although this remains speculative without knowledge of the nature of the companion of the WN5h component.
The nature of the secondary in R 136 c thus remains unclear, and, in light of the discrepant RVs among the spectral lines (Fig. 6) and the multiple possible periods (Fig. 8), more data will be necessary to unambiguously derive the orbit. The fact that it is X-ray-bright (Portegies Zwart et al. 2002) implies that the secondary is either another star with a strong wind (presumably an Of star or a WR star) or a compact object.
 |
Fig. 7 FWHMs of the N IV 14058 and He II 14686 lines for components al, a2, аЗ, and с. The values are offset relative to the FWHMs measured in the first available epoch for each star. The offset values are provided in the legend. Only the FWHMs of He II λ4686 for component с are significantly variable (on a 4σ level). |
 |
Fig. 8 Lomb-Scargle periodogram of the full RV set derived from the HST + FLAMES + UVES data for R 136 с. Our favoured period of 17.2 days is marked, along with the previously published 8.2 days period, which is not supported by this study. |
 |
Fig. 9 RVs measured for the FLAMES/ARGUS data for R 136 с as a function of MID, compared to the best-fitting RV curve corresponding to Ρ = 17.2051 days. |
 |
Fig. 10 Same as Fig. 9, but plotted as a function of phase and including the HST data and UVES data points. |
 |
Fig. 11 Comparison of ARGUS spectra of R 136 с taken during RV extremes, illustrating the apparent motion of the N IV λ4058 line and the presence of seemingly static He I absorption lines. |
4 Discussion
We could use the RVs measured in Sect. 3 to place constraints on possible companions to a1, a2, a3, and c. We used the RVs obtained for the NIV λ4058 line, which has the smallest measurement errors after the He II λ4686 line, for which cross-contamination between a1 and a2 cannot be ruled out. We performed Monte Carlo simulations to estimate the likelihood of specific binary configurations in reproducing the observed peak-to-peak RV variability. Specifically, for each pair of period P and companion mass M2 in the range 0.3 ≤ log Ρ[days] ≤ 4.5 and 2 ≤ M2 [M⊙] ≤ 150, respectively, we drew 1000 binaries from the following distributions: the eccentricities are drawn from a Gaussian distribution with a mean of 0.3 and a standard deviation of 0.2. In Appendix B, we explore the impact of highly eccentric binaries. The primary mass is drawn from a uniform distribution in the range 100–300 M⊙, the inclination i is drawn uniformly on cos i (corresponding to a random orientation of the orbital plane), the argument of periastron ω is drawn uniformly in the range 0−2 π, and the time of periastron T0 is drawn uniformly in the interval 0−P. The mass range 100–300 M⊙ for the primaries is justified by the WNh classification of our targets, which typically corresponds to M ≳ 100 M⊙, as well as by their previous mass determinations. For each star and for each mock binary, the RVs are computed using the actual dates of observations for that star. For each mock binary, the errors on the set of RVs are assumed to be identical to the actual measured errors, and the mock RVs are modified assuming these errors. Doing this, we formed a series of 1000 peak-to-peak measurements corresponding to Eqs. (1) and (2) for each P, M2 pair.
Since stars a1, a2, and a3 are not flagged as binaries in our study, for these stars, Fig. 12 shows the probability that a binary of a given P, M2 would yield values of ∆RVpp‚σ and ∆RVpp that are lower than those observed here for the N IV λ4058 line. The shaded areas correspond to configurations that can be rejected at 95% probability, corresponding to the probability of such binaries producing peak-to-peak RV variations larger than those observed. The probabilities for star c, which was flagged as a binary in our study, are discussed below. Evidently, companions with masses M2 ≲ 10 M⊙ (corresponding to mass ratios ≲0.1) cannot be ruled out at arbitrarily short periods. However, since our main focus is companions that could contribute significantly to the flux and bias the original mass estimates of these compo-nents, it is fair to focus our attention to M2 ≳ 50 M⊙. For such stars, we can confidently rule out companions up to periods of a few years (separations a ≲ 10 au) at 95% confidence, and up to tens of years (a ≲ 100 au) at 50% confidence, unless the periods coincide with one of the aliases of the limited HST time series. Constraints for a3 are somewhat less stringent.
Kalari et al. (2022) obtained speckle imaging of the R136 cluster and identified a companion at a projected separation of 2000 au from a1 and a3. The companion of a1 was already identified by Lattanzi et al. (1994), Hunter et al. (1995), and Khorrami et al. (2017). The Kalari et al. (2022) study is sensitive down to ≈1000 au (see their Fig. 1). Hence, in conjunction with Kalari et al. (2022), we cannot exclude massive companions in the range 10 ≲ a [au] ≲ 1000.
For star c, Fig. 12 shows the probability as a function of P, M2 that a star would reproduce the observed peak-to-peak variability. Specifically, we required that 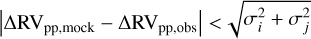 , where ai,σj are the errors on the RVs that produce ∆RVpp‚obs. This limits, within 95% confidence, the range of acceptable companion masses and periods to R 136 c. The results are consistent with the period of 17.20 days derived in our study.
, where ai,σj are the errors on the RVs that produce ∆RVpp‚obs. This limits, within 95% confidence, the range of acceptable companion masses and periods to R 136 c. The results are consistent with the period of 17.20 days derived in our study.
Finally, we considered the case of two WR-like stars with similar line profiles and light contributions, and considered the FWHM variability that could be expected in this case (see the discussion in Sect. 3). We focused on the N IV λ4058 line, to prevent possible cross-contamination between a1 and a2 in the He II λ4686 line from impacting our results. Like the exercise above, for each pair of M2, P, we drew 1000 binaries following the same distributions as before, focusing on 100 ≤ M2/M⊙ ≤ 150 and 0.3 ≤ log P [days] ≤ 3. We fitted the underlying N IV λ4058 profile of a1, a2, a3, and c with Gaussians. Then, we computed the FWHM of a Gaussian comprising the sum of two such Gaussians that are shifted relative to one another by ∆RV. We fitted a quadratic function to FWHM(∆RV) to obtain an analytical relation between the FWHM and ∆RVPP for each star. For each ∆RVpp value in a given simulation of a M2, P pair, we classified the mock binary as a binary if the ratio of the FWHM of the N IV λ4058 line to that of the unshifted Gaussian exceeds the values we observe. The results are shown in Fig. 13.
Evidently, the probability of detecting companions with similar spectra sharply drops in comparison with binaries containing only one WR star. Only very short period (≲3 days) can be rejected at high probability (90%); the 50% thresholds lie at periods of the order of 10–100 days. The results are insensitive to M2, recalling that the underlying assumption here is that the two stars have similar spectra. If the secondary is significantly fainter or does not show N IV λ4058 or He II λ4686 in emission, then the RVs become a sensitive probe, and Fig. 12 becomes the relevant diagnostic. We conclude that close companions of a similar spectral type cannot be readily excluded from the current data. A longer time coverage and higher data quality should allow for more stringent constraints in this case.
The absence of strong X-ray emission in a1, a2, and a3 does not favour the presence of close massive companions. For example, the X-ray luminosity of the WN5+WN5 binary Mk 34, with orbital period of 155 days, is ≈1035 erg s−1 (Pollock et al. 2018; Tehrani et al. 2019), which exceeds the combined X-ray luminosity of a1, a2, and nearby targets by an order of magnitude (Crowther et al. 2022). However, the colliding wind phenomenon occurs only in a subset of massive binaries – the X-ray emission of a majority of known spectroscopic binaries does not exceed average value LX/Lbol ~ 10−7 (Oskinova 2005; Sana et al. 2006; Rauw & Nazé 2016; Nebot Gómez-Morán & Oskinova 2018; Crowther et al. 2022). For example, R 144 is a colliding-wind binary hosting two WR stars bound on a 74 days period that does not exhibit strong X-ray excess (Shenar et al. 2021). Nazé (2009) noted that, for the short period massive binaries (Porb ≲ 30 days), the prevalence of enhanced X-rays is lower compared to longer period binaries. The physical reason could be the braking of stellar winds by the radiation of companions in close binaries, which dramatically reduces the strength of the wind collision (Gayley et al. 1997), or that the collision occurs within the wind acceleration zone (Sana et al. 2004). Furthermore, Krticka et al. (2015) suggest that intrinsic X-ray emission could lead to wind inhibition in massive binaries. Hence, generally, while X-ray excess provides indirect support for a companion with a powerful wind, lack of X-ray excess does not suffice to reject such a companion.
 |
Fig. 12 Allowed configurations for companions for a1, a2, a3, and c using the RV measurements for the N IV λ4058 line. The panels for a1, a2, and a3, which were not classified as binaries here, show the probability of a binary with the given M2, P producing values of ∆RVpp‚σ and ∆RVpp below our observed values. The 5% and 50% thresholds are marked. For star c, which is classified as a binary here, we show the probability that a binary in the given configuration would reproduce the observed ∆RVpp within |
 |
Fig. 13 Allowed configurations for companions for a1, a2, a3, and c for the case of two WR stars with identical spectra. The probabilities that the ratios between the largest and smallest FWHM values for the N IV λ4058 line are less than the observed values are shown (Fig. 7). The 5% and 50% thresholds are marked. The probabilities drop sharply in comparison with the RV case (Fig. 12). See the main text for details. |
5 Summary
We have investigated whether some of the most massive stars reported to date – R 136 a1, a2, a3, and c – may be binaries that host two massive stars, which would affect their previous mass determinations. To this end, we collected three epochs of optical spectroscopy over 1.5 yr in the years 2020–2021 with the STIS instrument on the HST to search for RV and EW variations or other indications of binary motion. These data were combined with an additional epoch in 2012 acquired by Crowther et al. (2016) to form a 10-yr baseline for our study. For R 136 c, we combined these data with archival FLAMES and UVES data to derive a preliminary orbital solution.
The data are not readily suggestive of close companions to the stars a1, a2, or a3. We can rule out companions more massive than ≈50 M⊙ out to orbital periods ≲1–3 yr (a ≲ 5–10 au) at 95% confidence, or periods of tens of years (a ≲ 100 au) at 50% confidence. Combining information from previous imaging studies (Khorrami et al. 2017; Kalari et al. 2022), we find that additional companions could only reside in the range ≈10–1000 au. However, ‘twin companions’ with similar light contributions and spectral appearances could avoid detection down to much shorter periods (P ≳ 10 days), though we see no direct indications of such companions (e.g. from the spectral appearance or X-ray behaviour). Hence, the masses of a1, a2, and a3 can still be considered to be ≳150 M⊙ (Crowther et al. 2010; Bestenlehner et al. 2020; Brands et al. 2022), although the faint visual companions to a1 and a3 (Hunter et al. 1995; Kalari et al. 2022) may lead to a modest downward revision of their masses.
In contrast, R 136 c is classified as a binary in our study. This is consistent with previous indications of binarity reported by Schnurr et al. (2009) and Hénault-Brunet et al. (2012), who reported this object as a binary candidate based on IR and VIS spectroscopy. Combining archival data with the new, we propose a tentative period of 17.2 days for R136 c, though more data will be needed to robustly constrain the orbital configuration and the true nature of the companion. Given the X-ray brightness of the system and the rarity of such very massive binaries, future monitoring of R 136 c would yield important constraints on the masses of the most massive stars and on massive binary evolution.
Acknowledgements
We thank the anonymous referee for improving our manuscript. TS acknowledges support from the European Union’s Horizon 2020 under the Marie Skłodowska-Curie grant agreement No 101024605 and from the Comunidad de Madrid (2022-T1/TIC-24117). This publication was made possible through the support of an LSSTC Catalyst Fellowship to K.A.B., funded through Grant 62192 from the John Templeton Foundation to LSST Corporation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of LSSTC or the John Templeton Foundation. AACS is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) in the form of an Emmy Noether Research Group – Project-ID 445674056 (SA4064/1-1, PI Sander) and acknowledges further support from the Federal Ministry of Education and Research (BMBF) and the Baden-Württemberg Ministry of Science as part of the Excellence Strategy of the German Federal and State Governments. P.A.C. is supported by the Science and Technology Facilities Council research grant ST/V000853/1 (PI V. Dhillon). F.N. acknowledges grant PID2019-105552RB-C4 funded by the Spanish MCIN/AEI/ 10.13039/501100011033. This publication was partially supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project 512 (Multiwavelength View on Massive Stars in the Era of Multimes-senger Astronomy (PI Oskinova). We appreciate discussions with Andy Pollock on the potential period of R136c from X-ray observations, and with Jesús Maíz Apellániz and Danny Lennon on reduction methods of the STIS dataset.
Appendix A Observation log and RV méasurements
Tables A.1 and A.4 compile the RV measurements for a1, a2, a3, and c using the STIS/HST data and the ARGUS/FLAMES data, respectively. Table A.2 compiles the EWs of several lines in the STIS/HST data, while Table A.3 provides the FWHM of the N IV λ4058 and He II λ4686 lines for the STIS/HST dataset.
RVs (in km s−1) for a1, a2, a3, and c, as derived from the STIS/HST data.
EWs for diagnostic lines of a1, a2, a3, and c, as derived from the STIS/HST data (in units of Å).(a)
FWHMs (in Å) of the N IV λ4058 and He IV λ4686 lines in the STIS/HST datasets.
RVs (in km s−1) for R 136 c, as derived from the UVES and FLAMES data.
Appendix B Detection probabilities for highly eccentric binaries
Some known massive binaries in the LMC exhibit high eccen-tricities (e.g. R 145, e = 0.79, Shenar et al. 2017a; R 144, e = 0.56, Shenar et al. 2021; Mk34, e = 0.76, Tehrani et al. 2019), while others exhibit more moderate eccentricities (e.g. Mk33Na, e = 0.33, Bestenlehner et al. 2022; R 139, e = 0.38, Taylor et al. 2011; Mahy et al. 2020). To explore the impact of potential high eccentricity in our targets, we repeated the exercise per-formed in Sect. 4 for a Gaussian eccentricity distribution with a mean of 〈e〉 = 0.8 and a standard deviation of 0.1 (Fig. B.1). As could be anticipated, the detection probability drops, though the exclusion domains are still comparable. Only highly eccen-tric binaries (e > 0.9) would have an appreciable likelihood to evade detection even at shorter (≲ 100 days) orbital periods. More epochs would certainly improve the detection probability of high eccentricity binaries.
 |
Fig. B.1 Same as Fig. 12, but for an underlying Gaussian eccentricity distribution with a mean of < e >= 0.8 and a standard deviation of 0.1. |
References
- Barbá, R. H., Gamen, R. C., Martín-Ravelo, P., Arias, J. I., & Morrell, N. I. 2022, MNRAS, 516, 1149 [CrossRef] [Google Scholar]
- Bastian, N., & Lardo, C. 2018, ARA & A, 56, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A & A, 570, A38 [CrossRef] [EDP Sciences] [Google Scholar]
- Bestenlehner, J. M., Crowther, P. A., Caballero-Nieves, S. M., et al. 2020, MNRAS, 499, 1918 [Google Scholar]
- Bestenlehner, J. M., Crowther, P. A., Broos, P. S., Pollock, A. M. T., & Townsley, L. K. 2022, MNRAS, 510, 6133 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanos, A. Z., Stanek, K. Z., Udalski, A., et al. 2004, ApJ, 611, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Brands, S. A., de Koter, A., Bestenlehner, J. M., et al. 2022, A & A, 663, A36 [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. C., McLean, I. S., & Emslie, A. G. 1978, A & A, 68, 415 [NASA ADS] [Google Scholar]
- Cassinelli, J. P., Mathis, J. S., & Savage, B. D. 1981, Science, 212, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- Chalabaev, A., & Maillard, J. P. 1983, A & A, 127, 279 [Google Scholar]
- Cox, N. L. J., Kaper, L., Foing, B. H., & Ehrenfreund, P. 2005, A & A, 438, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crowther, P. A., & Dessart, L. 1998, MNRAS, 296, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., & Walborn, N. R. 2011, MNRAS, 416, 1311 [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [Google Scholar]
- Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [Google Scholar]
- Crowther, P. A., Broos, P. S., Townsley, L. K., et al. 2022, MNRAS, 515, 4130 [NASA ADS] [CrossRef] [Google Scholar]
- de Koter, A., Heap, S. R., & Hubeny, I. 1997, ApJ, 477, 792 [Google Scholar]
- Doran, E. I., Crowther, P. A., de Koter, A., et al. 2013, A & A, 558, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dsilva, K., Shenar, T., Sana, H., & Marchant, P. 2020, A & A, 641, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dsilva, K., Shenar, T., Sana, H., & Marchant, P. 2022, A & A, 664, A93 [CrossRef] [EDP Sciences] [Google Scholar]
- Dsilva, K., Shenar, T., Sana, H., & Marchant, P. 2023, A & A, 674, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A & A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figer, D. F. 2005, Nature, 434, 192 [Google Scholar]
- Figer, D. F., Najarro, F., Gilmore, D., et al. 2002, ApJ, 581, 258 [Google Scholar]
- Fryer, C. L., Woosley, S. E., & Heger, A. 2001, ApJ, 550, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Gayley, K. G., Owocki, S. P., & Cranmer, S. R. 1997, ApJ, 475, 786 [Google Scholar]
- Gieles, M., Charbonnel, C., Krause, M. G. H., et al. 2018, MNRAS, 478, 2461 [Google Scholar]
- Guerrero, M. A., & Chu, Y.-H. 2008, ApJS, 177, 216 [Google Scholar]
- Hainich, R., Rühling, U., Todt, H., et al. 2014, A & A, 565, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamann, W. R., & Gräfener, G. 2003, A & A, 410, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heap, S. R., Ebbets, D., Malumuth, E. M., et al. 1994, ApJ, 435, L39 [CrossRef] [Google Scholar]
- Hénault-Brunet, V., Evans, C. J., Sana, H., et al. 2012, A & A, 546, A73 [CrossRef] [EDP Sciences] [Google Scholar]
- Hill, G. M., Moffat, A. F. J., St-Louis, N., & Bartzakos, P. 2000, MNRAS, 318, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Shaya, E. J., Holtzman, J. A., et al. 1995, ApJ, 448, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Kalari, V. M., Horch, E. P., Salinas, R., et al. 2022, ApJ, 935, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Khorrami, Z., Vakili, F., Lanz, T., et al. 2017, A & A, 602, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knigge, C., Dieball, A., Maíz Apellániz, J., et al. 2008, in Dynamical Evolution of Dense Stellar Systems, 246, eds. E. Vesperini, M. Giersz, & A. Sills, 321 [NASA ADS] [Google Scholar]
- Koenigsberger, G., Morrell, N., Hillier, D. J., et al. 2014, AJ, 148, 62 [Google Scholar]
- Krtička, J., Kubát, J., & Krtičková, I. 2015, A & A, 579, A111 [CrossRef] [EDP Sciences] [Google Scholar]
- Lamontagne, R., Moffat, A. F. J., Drissen, L., Robert, C., & Matthews, J. M. 1996, AJ, 112, 2227 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 2012, ARA & A, 50, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., & Starrfield, S. 1971, A & A, 13, 190 [NASA ADS] [Google Scholar]
- Lattanzi, M. G., Hershey, J. L., Burg, R., et al. 1994, ApJ, 427, L21 [CrossRef] [Google Scholar]
- Lennon, D. J., Maíz Apellániz, J., Irrgang, A., et al. 2021, A & A, 649, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lépine, S., & Moffat, A. F. J. 1999, ApJ, 514, 909 [CrossRef] [Google Scholar]
- Lohr, M. E., Clark, J. S., Najarro, F., et al. 2018, A & A, 617, A66 [CrossRef] [EDP Sciences] [Google Scholar]
- Luehrs S. 1997 PASP 109, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Madura, T. I., Gull, T. R., Owocki, S. P., et al. 2012, MNRAS, 420, 2064 [NASA ADS] [CrossRef] [Google Scholar]
- Mahy, L., Sana, H., Abdul-Masih, M., et al. 2020, A & A, 634, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiz-Apellaniz, J. 2005, Instrument Science Report STIS 2005-02 [Google Scholar]
- Martins, F., Hillier, D. J., Paumard, T., et al. 2008, A & A, 478, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massey, P., & Hunter, D. A. 1998, ApJ, 493, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Moffat, A. F. J., & Bobert, C. 1992, Nonisotropic and Variable Outflows from Stars, eds. L. Drissen, C. Leitherer, & A. Nota, Astronomical Society of the Pacific Conference Series, 22, 203 [Google Scholar]
- Najarro, F., Figer, D. F., Hillier, D. J., & Kudritzki, R. P. 2004, ApJ, 611, L105 [Google Scholar]
- Nazé, Y. 2009, A & A, 506, 1055 [CrossRef] [EDP Sciences] [Google Scholar]
- Nebot Gómez-Morán, A., & Oskinova, L. M. 2018, A & A, 620, A89 [CrossRef] [EDP Sciences] [Google Scholar]
- Oey, M. S., & Clarke, C. J. 2005, ApJ, 620, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M. 2005, MNRAS, 361, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Pollock, A. M. T., Crowther, P. A., Tehrani, K., Broos, P. S., & Townsley, L. K. 2018, MNRAS, 474, 3228 [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., Pooley, D., & Lewin, W. H. G. 2002, ApJ, 574, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Quimby, R. M., Kulkarni, S. R., Kasliwal, M. M., et al. 2011, Nature, 474, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Ramachandran, V., Hamann, W. R., Oskinova, L. M., et al. 2019, A & A, 625, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauw, G., & Nazé, Y. 2016, Adv. Space Res., 58, 761 [Google Scholar]
- Rauw, G., De Becker, M., Nazé, Y., et al. 2004, A & A, 420, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richardson, N. D., Shenar, T., Roy-Loubier, O., et al. 2016, MNRAS, 461, 4115 [NASA ADS] [CrossRef] [Google Scholar]
- Robert, C., Moffat, A. F. J., Drissen, L., et al. 1992, ApJ, 397, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Rubio-Díez, M. M., Najarro, F., García, M., & Sundqvist, J. O. 2017, in The Lives and Death-Throes of Massive Stars, 329, eds. J. J. Eldridge, J. C. Bray, L. A. S. McClelland, & L. Xiao, 131 [Google Scholar]
- Sana, H., Stevens, I. R., Gosset, E., Rauw, G., & Vreux, J. M. 2004, MNRAS, 350, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Rauw, G., Nazé, Y., Gosset, E., & Vreux, J. M. 2006, MNRAS, 372, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., Le Bouquin, J. B., De Becker, M., et al. 2011, ApJ, 740, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A & A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sander, A., Shenar, T., Hainich, R., et al. 2015, A & A, 577, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., Fitzpatrick, E. L., Cassinelli, J. P., & Ebbets, D. C. 1983, ApJ, 273, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Schnurr, O., Casoli, J., Chené, A. N., Moffat, A. F. J., & St-Louis, N. 2008, MNRAS, 389, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Schnurr, O., Chené, A. N., Casoli, J., Moffat, A. F. J., & St-Louis, N. 2009, MNRAS, 397, 2049 [NASA ADS] [CrossRef] [Google Scholar]
- Shenar, T., Oskinova, L. M., Järvinen, S. P., et al. 2017a, A & A, 606, A91 [CrossRef] [EDP Sciences] [Google Scholar]
- Shenar, T., Richardson, N. D., Sablowski, D. P., et al. 2017b, A & A, 598, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shenar, T., Sablowski, D. P., Hainich, R., et al. 2019, A & A, 627, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shenar, T., Sana, H., Marchant, P., et al. 2021, A & A, 650, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smartt, S. J. 2009, ARA & A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Strawn, E., Richardson, N. D., Moffat, A. F. J., et al. 2023, MNRAS, 519, 5882 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, W. D., Evans, C. J., Sana, H., et al. 2011, A & A, 530, A10 [Google Scholar]
- Tehrani, K. A., Crowther, P. A., Bestenlehner, J. M., et al. 2019, MNRAS, 484, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J. D., Richardson, N. D., Eldridge, J. J., et al. 2021, MNRAS, 504, 5221 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, L. K., Broos, P. S., Feigelson, E. D., Garmire, G. P., & Getman, K. V. 2006, AJ, 131, 2164 [NASA ADS] [CrossRef] [Google Scholar]
- Tramper, F., Sana, H., Fitzsimons, N. E., et al. 2016, MNRAS, 455, 1275 [CrossRef] [Google Scholar]
- Vink, J. S. 2018, A & A, 615, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walborn, N. R., & Fitzpatrick, E. L. 1990, PASP, 102, 379 [Google Scholar]
- Walborn, N. R., Howarth, I. D., Lennon, D. J., et al. 2002, AJ, 123, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., & Baier, G. 1985, A & A, 150, L18 [NASA ADS] [Google Scholar]
- Woosley, S. E., Blinnikov, S., & Heger, A. 2007, Nature, 450, 390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
EWs for diagnostic lines of a1, a2, a3, and c, as derived from the STIS/HST data (in units of Å).(a)
All Figures
 |
Fig. 1 Image of the central 3″ × 5″ (≈0.7 × 1.2 parsec) core of R 136 taken in 2009 with the HST’s Wide Field Camera 3 (WFC3) in the ultraviolet and visible light (UVIS) Channel with the F555W filter (λ0 ≈ 5500 Å, proposai ID 11360). Marked are the positions of our four targets and the two slit positions used to acquire the data. |
| In the text | |
 |
Fig. 2 Fit of two Voigt proflies representing the PSFs of al and a2 to the flux across the cross-dispersion axis for the 28 March 2022 epoch at 4850.6 A. The Voigt profiles are used to compute the relative weight of each data point to the flux of each star at each given wavelength. |
| In the text | |
 |
Fig. 3 Extracted calibrated fluxes for al, a2, аЗ, and с for the new epochs presented here (see the labels and legends). |
| In the text | |
 |
Fig. 4 Extracted STIS spectra for a1, a2, a3, and c (from top to bottom), focusing on the diagnostic lines N IV λ4058, N V λλ4604,4620, He II λ4686, and N V λ4945 (from left to right). Epochs are listed in the legends. The spectra of a3 and c are binned at ∆λ = 0.5 Å for clarity. |
| In the text | |
 |
Fig. 5 Comparison between the synthetic PoWR model (solid red line) used for cross-correlation and the normalised spectrum of al taken in March 2020 (noisy blue line). The line profiles of the PoWR model were shifted by 330 km s−1, and the EWs of the N IV λ4058 and Ν Vλ4945 proflies were scaled to the observations for the sake of plotting (the EW has no impact on the cross-correlation algorithm). The spectra of a2, a3, and с are comparable, and so is the match between the model and the data. |
| In the text | |
 |
Fig. 6 Relative RVs measured for the four diagnostic spectral features in the spectra (when available; see the legend). The first RV is always calibrated to zero. Only component с, which satisfles the criteria in Eqs. (1) and (2), is classified as a binary. |
| In the text | |
 |
Fig. 7 FWHMs of the N IV 14058 and He II 14686 lines for components al, a2, аЗ, and с. The values are offset relative to the FWHMs measured in the first available epoch for each star. The offset values are provided in the legend. Only the FWHMs of He II λ4686 for component с are significantly variable (on a 4σ level). |
| In the text | |
 |
Fig. 8 Lomb-Scargle periodogram of the full RV set derived from the HST + FLAMES + UVES data for R 136 с. Our favoured period of 17.2 days is marked, along with the previously published 8.2 days period, which is not supported by this study. |
| In the text | |
 |
Fig. 9 RVs measured for the FLAMES/ARGUS data for R 136 с as a function of MID, compared to the best-fitting RV curve corresponding to Ρ = 17.2051 days. |
| In the text | |
 |
Fig. 10 Same as Fig. 9, but plotted as a function of phase and including the HST data and UVES data points. |
| In the text | |
 |
Fig. 11 Comparison of ARGUS spectra of R 136 с taken during RV extremes, illustrating the apparent motion of the N IV λ4058 line and the presence of seemingly static He I absorption lines. |
| In the text | |
 |
Fig. 12 Allowed configurations for companions for a1, a2, a3, and c using the RV measurements for the N IV λ4058 line. The panels for a1, a2, and a3, which were not classified as binaries here, show the probability of a binary with the given M2, P producing values of ∆RVpp‚σ and ∆RVpp below our observed values. The 5% and 50% thresholds are marked. For star c, which is classified as a binary here, we show the probability that a binary in the given configuration would reproduce the observed ∆RVpp within |
| In the text | |
 |
Fig. 13 Allowed configurations for companions for a1, a2, a3, and c for the case of two WR stars with identical spectra. The probabilities that the ratios between the largest and smallest FWHM values for the N IV λ4058 line are less than the observed values are shown (Fig. 7). The 5% and 50% thresholds are marked. The probabilities drop sharply in comparison with the RV case (Fig. 12). See the main text for details. |
| In the text | |
 |
Fig. B.1 Same as Fig. 12, but for an underlying Gaussian eccentricity distribution with a mean of < e >= 0.8 and a standard deviation of 0.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.