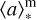| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346723 | |
| Published online | 31 October 2023 | |
Dust attenuation law in JWST galaxies at z ∼ 7–8
Scuola Normale Superiore,
Piazza dei Cavalieri 7,
56126
Pisa, Italy
e-mail: vladan.markov@sns.it
Received:
21
April
2023
Accepted:
30
August
2023
Context. Understanding the wavelength dependence of dust attenuation is vital for inferring the properties of galaxies from their spectral energy distribution (SED) fitting. The dust attenuation curves in star-forming galaxies depend on the complex interplay between the intrinsic physical dust properties and dust-to-star geometry. Due to the lack of observational constraints at high redshift, dust attenuation and extinction laws measured in the local Universe (e.g., the Calzetti attenuation law and the Small Magellanic Cloud and Milky Way extinction laws) have been employed to describe the dust attenuation at early epochs.
Aims. We exploit the high sensitivity and spectral resolution of the James Webb Space Telescope (JWST) to constrain dust attenuation laws in z ∼ 7–8 galaxies. Our goals are to: i) check whether dust attenuation curves at high-z differ from the ones measured in the local Universe and ii) quantify the dependence of the inferred galaxy properties on the assumed dust attenuation law.
Methods. We developed a modified version of the SED fitting code BAGPIPES by including a detailed dust attenuation curve parameterization. We applied our method to the JWST Near Infrared Spectrograph (NIRSpec) spectra in the ∼0.6–5.3 µm range to probe the nebular line (Hα, Hβ, Hγ, [O II] λ3727, [O III] λλ4959, 5007, [Ne III] λ3869) and continuum emissions of three star-forming galaxies at z = 7–8. Dust attenuation parameters and global galaxy properties are derived from the fit to the data.
Results. We find that the attenuation curves of the analyzed high-z galaxies differ from local templates. One out of the three galaxies shows a characteristic 2175Å bump, typically associated with the presence of small carbonaceous dust grains such as polycyclic aromatic hydrocarbons (PAHs). This is among the first pieces of evidence suggesting the presence of PAHs in early galaxies. Galaxy properties such as the stellar mass (M*) and star formation rate (SFR) inferred from the SED fitting are affected by the assumed attenuation curve (with deviations of up to ∼0.35 dex), however, the adopted star formation history plays the dominant role (up to ∼0.4 dex for the same galaxy properties).
Conclusions. Our results highlight the importance of accounting for the potential diversity among dust attenuation laws when analyzing the spectra of high-z galaxies, whose dust properties and dust-to-star geometry are still poorly understood. The application of our method to a larger sample of galaxies observed with JWST can provide important insights into the properties of dust and galaxies in the early Universe.
Key words: dust, extinction / Galaxy: evolution / Galaxy: fundamental parameters / galaxies: high-redshift / galaxies: ISM
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Much of our understanding of star-forming galaxies relies on the acquisition of photometric and spectroscopic (when available) multi-wavelength observations, ranging from the rest frame ultraviolet (UV) to the far infrared (FIR). Powerful ground-based instruments such as the Very Large Telescope (VLT) and spaceborne ones such as Hubble Space Telescope (HST) and Spitzer have enabled the collecting of data from galaxies up to the Epoch of Reionization (EoR, z ∼ 5–9; Finkelstein et al. 2015; Bouwens et al. 2021; see Dunlop et al. 2013; Stark 2016; Finkelstein 2016 for reviews), with just a few galaxies observed at z > 9 (Oesch et al. 2018; Bowler et al. 2020; Bagley et al. 2022). Thanks to the unprecedented sensitivity of James Webb Space Telescope (JWST), we are able to study galaxy candidates at much earlier epochs, with photometric candidates up to z ∼ 9–17 (Castellano et al. 2022; Bagley et al. 2023; Donnan et al. 2023; Harikane et al. 2023b; Atek et al. 2023b; Robertson et al. 2023), as well as spectroscopically confirmed sources up to z ∼ 13 (Curtis-Lake et al. 2023; Harikane et al. 2023a; Bunker et al. 2023).
These data carry information about the interactions between the radiation field of stars and the matter enclosed in the interstellar medium (ISM) of galaxies. In this context, dust grains play a key role at any wavelengths: on the one hand, dust scatters and absorbs preferentially short-wavelength (mostly optical and UV) photons emitted from stars; on the other hand, the dust heated by stellar radiation re-emits the absorbed energy as long-wavelength photons, giving rise to the so-called FIR bump (Meurer et al. 1999; Calzetti et al. 2000; see Draine 2003 for a review). Thus, the interpretation of the spectral energy distribution (SED) of galaxies requires a clear understanding of dust attenuation curves1, resulting from the complex interplay between the properties of dust (chemical composition, grain size distribution, mass, and temperature) and on the relative distribution of the interstellar dust grains in relation to stars and the ISM (Noll et al. 2009; Kriek & Conroy 2013; Seon & Draine 2016; Narayanan et al. 2018; Buat et al. 2019; Hirashita & Murga 2020; Trayford et al. 2020; Lower et al. 2022; see Salim & Narayanan 2020 for a review).
Dust attenuation curves that are broadly adopted for both nearby and high-z galaxies are the “Calzetti” attenuation curve (Calzetti et al. 1994, Calzetti et al. 2000), derived from the analysis of local starburst galaxies, and the extinction curves of nearby sources: the Milky Way (MW) extinction curve with a characteristic bump at ∼2175 Å, the steeply rising Small Magellanic Cloud (SMC) extinction curve, and the Large Magellanic Cloud (LMC) extinction curve, which is intermediate between the MW and SMC extinction curves (Weingartner & Draine 2001). However, the dust attenuation properties of high-z sources are generally unknown, and are not well described by the aforementioned described empirical dust laws, suggesting the evolution of the dust properties through cosmic times (Maiolino et al. 2004; Stratta et al. 2007; Li et al. 2008; Gallerani et al. 2010; Di Mascia et al. 2021; Ferrara et al. 2022). This is not surprising since dust properties depend on (1) the stellar populations responsible for dust formation and their corresponding timescales; (2) the dust re-processing mechanisms; and (3) the physical conditions of the ISM; which are generally unknown at high redshifts.
Dust formation requires physical gas conditions of low temperature (T < 2000 K) and high density (n > 108 cm−3, see Li & Greenberg 2003 and Tielens 2022, for reviews), which are expected to characterize both the atmospheres of low and intermediate-mass (M* < 8 M⊙) evolved stars during the asymptotic giant branch (AGB) phase (see Ferrarotti & Gail 2006; Valiante et al. 2009; Nanni et al. 2013, for reviews) and the expanding ejecta of core-collapse type II supernovae (SNelI, see Todini & Ferrara 2001; Bianchi & Schneider 2007, for reviews). The timescales associated with the dust formation in AGB and SNeII are ruled by the lifetimes of these stellar populations (∼108–109 and 106 yr, respectively; Morgan & Edmunds 2003). In the local Universe, dust formation is mostly ascribed to AGB stars, which are more numerous and, at these epochs, have plenty of time to evolve and enrich the ISM of galaxies. The origin of dust at high-z is instead much more uncertain. Star-forming galaxies are now routinely (sparsely) detected at z > 6 (z > 10), namely, when the age of the Universe tH < 0.9 Gyr (0.5 Gyr) starts becoming as long as (much shorter than) the AGB star lifetimes. It is thus questionable whether the primary sources of dust remain the same for high-z and local star-forming galaxies (Valiante et al. 2009; Mancini et al. 2015; Liu & Hirashita 2019; Leśniewska & Michałowski 2019; Burgarella et al. 2020; Nanni et al. 2020; Sommovigo et al. 2020, Sommovigo et al. 2022b,a; Dayal et al. 2022).
Independently from the actual nature of the stellar populations responsible for dust production, the final properties of dust further depend on several complex mechanisms of dust reprocessing in the ISM which likely modify the original dust properties. Dust grains can be completely destroyed and/or eroded as a consequence of (e.g.,) gas-grain sputtering, grain-grain collision (i.e., shattering Dwek & Scalo 1980; Tielens et al. 1994; Borkowski & Dwek 1995), dust sublimation (Laor & Draine 1993) occurring in the ISM, SN shocks, and hot plasma. These processes are expected to both decrease the total amount of dust and shift the grain size distribution towards smaller grains, steepening the attenuation curves of high-z galaxies. Conversely, dust grains can grow into larger grains by accreting gas-phase metals in the dense ISM or in molecular clouds (Spitzer 1978; Dwek & Scalo 1980; Draine 2009, but see also Ferrara et al. 2016), and/or via coagulation (Chokshi et al. 1993; Hirashita & Yan 2009). In these cases, the overall dust mass content increases and the grain size distribution becomes more populated at larger grains, flattening the attenuation curve.
These dust re-processing mechanisms are the main constituents of the dust cycle in galaxies and are deeply interconnected with the physical properties of galaxies (e.g., gas density, metallicity, star formation, stellar ages, and radiation fields). For instance, higher densities may favor the growth and coagulation into larger grains, while young stellar populations and/or strong radiation fields enhance the efficiency of dust destruction processes. There are several theoretical and observational studies suggesting that the ISM properties of high-z star-forming galaxies differ from their local counterparts (Olsen et al. 2017; Carniani et al. 2018; Lagache et al. 2018; Ferrara et al. 2019; Popping et al. 2019; Pallottini et al. 2019; Vallini et al. 2020, Vallini et al. 2021; Markov et al. 2022).
For all the aforementioned reasons, there is no physical justification for assuming that the dust attenuation in high-z sources resembles any of the well-studied dust empirical laws of local galaxies, such as the Calzetti attenuation law (e.g., Inami et al. 2022) or the SMC extinction law (e.g., Topping et al. 2022). Currently, there is no consensus on the shape of dust attenuation curves in early galaxies, although some dust laws seem to be favored over others (see e.g., Behrens et al. 2018, Ferrara et al. 2022).
In this work, we implement a “Drude-type” parameterization for the wavelength dependence of dust attenuation (Li et al. 2008) in the Bayesian Analysis of Galaxies for Physical Inference and Parameter EStimation (BAGPIPES) package (Carnall et al. 2018, Carnall et al. 2019b), which is a commonly used tool for modeling galaxy spectra and fitting spectroscopic and photometric observations. The goals of the present work are to: (i) characterize high-z galaxies properties without any a priori assumption of their unknown attenuation curve and (ii) infer the dust attenuation curves of a sample of star-forming galaxies at high-z.
This paper is organized in the following way: an overview of the Near Infrared Spectrograph (NIRSpec) JWST observations is presented in Sect. 2 and our methodology is outlined in Sect. 3. We present our results on new dust attenuation curves of high-z star-forming galaxies in Sect. 4. We analyze the dependence of the inferred galaxy properties on the adopted dust law and star formation history (SFH) model in Sect. 5. We discuss our main results on the shape of the dust laws of galaxies at the EoR in Sect. 6. Finally, we outline our main conclusions in Sect. 7.
2 Spectroscopic observations
We analyzed NIRSpec JWST data of three z ∼ 7–8 galaxies (previously published by Tang et al. 2023 and reported in Table 1) that were selected according to the process described below. The targets were originally identified as Lyman-break galaxies using HST (Bouwens et al. 2015, 2021). Most recently, Tang et al. (2023) analyzed the JWST/NIRSpec spectra of these sources taken at medium resolution (MR) gratings (R ∼ 1000) and reported multiple detections of the rest-frame optical lines (Hβ, Hγ, [O II] λ3727, [O III] λλ4959, 5007, and [Ne III] λ3869). The spectroscopic redshifts of these sources have been estimated based on the central wavelengths of the brightest detected lines (typically, the [O III] λλ4959, 5007 doublet and one of the hydrogen lines, e.g., Hβ or Hγ) in the NIRSpec medium resolution grating spectra.
We used publicly available data that are part of the Cosmic Evolution Early Release Science (CEERS) survey (Program ID: 1345, PI: Finkelstein) targeting the Extended Groth Strip (EGS) field. For each target, three adjacent micro shutters on the Micro-Shutter Assembly (MSA) were opened to create a slitlet in the cross-dispersion axis and a three-point nod pattern was adopted to achieve a total exposure of 3063 s. We analyzed the CEERS NIRSpec observations taken at R ∼ 100 (the nominal resolving power, or equivalently, the velocity resolution range of σ ∼ c/R ∼ 3000 km s−1) with the NIRSpec MultiObject Spectroscopy (MOS) mode, which spans the wavelength range λ ∼ 0.6–5.3 µm. This allows the nebular lines and continuum emission of high-redshift targets to be probed.
We visually inspected all the product level 3 spectra of the standard pipeline used for data reduction, in the Mikulski Archive for Space Telescopes (MAST) archive and we selected only those galaxies without negative features in their spectra, with a bright continuum and nebular lines at z > 5. The list of the three sources used in this work is provided in Table 1. We then downloaded from MAST the level 3 1D spectra for the targets that match our requirements.
The output 1D spectra containing the wavelength in units of µm, as well as the flux density and flux density errors in units of Jy, were converted to Å and erg s−1 cm−2 Å−1 units, respectively, in order to ensure the compatibility with BAGPIPES for performing the SED fitting (Sect. 3). A segment of the 1D spectra, originally containing ∼400 data points, was masked at the low-wavelength spectral region below the wavelength of the Lyα line (λ ≲ λLyα(1 + zsp), where zsp is the spectroscopic redshift; Tang et al. 2023). This masking step is necessary due to the potential attenuation of the flux by the intervening neutral IGM. The resulting masked spectra that were then fitted using our modified BAGPIPES tool contain ∼345–355 data points, with a varying channel resolution in the range of 75–204 Å.
The average signal-to-noise ratio (S/N) for the continuum emission across the entire spectra of the three sources is in the range S/N ∼ 2–4, whereas the S/N for the continuum emission around the position of the characteristic 2175 Å bump is S/N ∼ 3–6. Additionally, the S/Ns of the peak intensities of the three brightest spectral lines, namely [O III] λ5007, [O III] λ4959, and Hα (excluding Hα for s001149 since it is outside of the observed wavelength range), are S/N ∼ 23–35, S/N ∼ 13–15, and S/N ∼ 13, respectively. The resolving power R (R ∼ λ/Δλ) of the NIRSpec prism disperser is wavelength-dependent, and falls within the range R ∼ 50–300 (σ ∼ c/R ∼ 1000–6000 km s−1). In particular, the lowest resolution (R ≲ 50) is observed in the wavelength range of λ ∼ 0.5–2 µm, while the highest resolution (R ≳ 300) is achieved at a wavelength greater than λ ∼ 5 µm2. The low-velocity resolution (≳1000 km s−1) does not allow us to resolve nebular emission lines.
Overview of the high-z galaxies used in this paper (Tang et al. 2023).
3 Method
3.1 SED fitting procedure
BAGPIPES is a Python-based tool that is able to generate physically realistic galaxy spectra from FUV to microwave wavelengths, predict the spectroscopic and photometric observations, and fit the model to the data, using the MultiNest nested sampling algorithm (Feroz & Hobson 2008); Feroz et al. 2019). BAGPIPES has been widely used by the astronomical community for fitting the JWST observations of galaxies at the EoR and constraining their properties (Adams et al. 2023; Donnan et al. 2023; Leethochawalit et al. 2023; Carnall et al. 2023; Trussler et al. 2023).
BAGPIPES constructs the luminosity of a galaxy in the following way (Carnall et al. 2018):
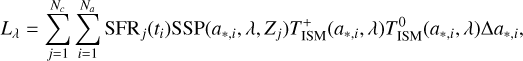 (1)
(1)
where simple stellar population (SSP) models are a function of the wavelength, λ, the age of the stellar population, α*3, metallicity, Z, and the initial mass function (IMF), SFRj(ti) is the star formation history (SFH), Nc and Na are the number of SFH and stellar age bins, respectively, and Δa*,i are the widths of age bins. Here, 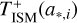 takes into account absorption, line emission, ionized continuum emission, and emission from warm dust present in H II regions (Charlot & Longhetti 2001);
takes into account absorption, line emission, ionized continuum emission, and emission from warm dust present in H II regions (Charlot & Longhetti 2001); 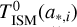 represents the transmission function of the neutral interstellar medium (ISM), which is caused by both diffuse dust attenuation and emission.
represents the transmission function of the neutral interstellar medium (ISM), which is caused by both diffuse dust attenuation and emission.
BAGPIPES uses the stellar population synthesis (SPS) models from the 2016 version of the Bruzual & Charlot (2003) model (Chevallard & Charlot 2016), generated by using the Mediumresolution Isaac Newton Telescope library of empirical spectra (MILES; Falcón-Barroso et al. 2011) and adopting a Kroupa & Boily (2002) IMF. The BAGPIPES code accepts the pre-defined SPS in the shape of grids of SSP models for a wide range of λ, a*, and Z.
Nebular line and continuum emission were pre-computed with CLOUDY, following the methodology of Byler et al. (2017). Calculations were performed with version 17.03 of the photoionization code CLOUDY, described in Ferland et al. (2017). CLOUDY uses grids of SSP models as input spectra and adopts the ionization parameter, U, as an input that is allowed to vary in the range of −4 < log (U) < 04, by changing the number of hydrogen-ionizing photons QH and assuming a constant hydrogen density of n = 100 atoms cm−3. For each value of log (U), Z, and a*, CLOUDY provides the output spectrum with contribution from the nebular line and continuum emission.
The resulting output spectrum includes the stellar and nebular emission and is attenuated by the dust. In the original implementation, BAGPIPES adopts three fixed templates as dust attenuation laws: Calzetti et al. (2000) attenuation law for local starbursts, the Gordon et al. (2003) SMC extinction law, and the Cardelli et al. (1989) MW extinction law; along with two flexible dust models with free parameters: the modified Charlot & Fall (2000) model, and the Salim et al. (2018) model. The functional form of each adopted dust attenuation curve is:
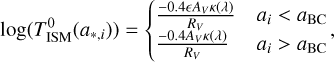 (2)
(2)
where aBC is the age of the stellar birth clouds, ϵ is a constant that regulates the additional attenuation towards the stellar birth clouds, κ(λ) and RV are the total attenuation curve and the total attenuation curve in the V band, respectively, that are specific to the adopted dust model.
Dust emission is accounted for with a hot dust component which is included in the CLOUDY continuum emission from the ionized (H II) region and a cold diffuse dust component that is modeled by the gray body emission.
The modeled galaxy luminosity is redshifted to the observed redshift (zobs) and transformed into a flux density:
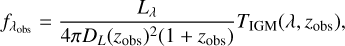 (3)
(3)
where DL(zobs) is the luminosity distance as a function of the redshift of the observation, zobs, and TIGM(λ, zobs) is the transmission function of the InterGalactic Medium (IGM; based on the Inoue et al. 2014 model). Besides the redshift zobs, an additional global parameter of the SED fitting procedure is σvel, designed to model the effects of dispersion on the observed spectral features.
Fundamental properties of galaxies that are not directly constrained, but are derived from the inferred SFH properties are the so-called “living” stellar mass, M* that is, the total stellar mass at the time of observation, the SFR which is averaged over the last 100 Myr, and the mass-weighted age 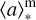 , namely, the age at which the stellar mass of galaxies was assembled. The mass-weighted time
, namely, the age at which the stellar mass of galaxies was assembled. The mass-weighted time 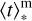 is given by:
is given by:
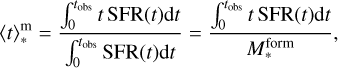 (4)
(4)
where 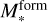 is the total stellar mass formed at the time of observation tobs = t(zobs) (e.g., Carnall et al. 2018).
is the total stellar mass formed at the time of observation tobs = t(zobs) (e.g., Carnall et al. 2018).
Once the model spectrum is constructed, we can fit it by using a Bayesian approach and a MultiNest sampling (Feroz & Hobson 2008); Feroz et al. 2019). We define the prior probability distributions for each of the parameters of a given model. Next, we fit the model and obtain the posterior probability distribution in parameter space. We can constrain the parameters of a given model, by using the best-fit values and 1σ uncertainties (i.e., the 16th, 50th, and 84th percentile) of the posterior distribution. Full details on the BAGPIPES SED fitting method are provided in Carnall et al. (2018).
3.2 Star formation history
In order to explore the dependence of our results on the adopted SFH model, we accounted for seven different SFH models among about ten models currently implemented in BAGPIPES. We considered five parametric SFH models: the constant, double power-law, exponentially declining (exponential hereafter), delayed exponentially declining (delayed hereafter), and lognormal. These parametric models are frequently adopted in the fitting of the SED of high-z galaxies (Carnall et al. 2018, Carnall et al. 2019a, Carnall et al. 2023; Laporte et al. 2021; Furtak et al. 2021). Additionally, we adopted a non-parametric model with a “continuity” and “bursty continuity” prior (Leja et al. 2019; Whitler et al. 2023; Tacchella et al. 2022).
For the fiducial model, we used the non-parametric SFH model with a continuity prior, since with respect to the above-mentioned parametric models, it allows us to recover all the empirical dust curves, along with the global physical properties of synthetic galaxies (as discussed in Appendix A). The non-parametric models allow more flexibility on the shape of the SFH model and generally provide a better fit to the often complex “true” SFHs of galaxies (Leja et al. 2019; Topping et al. 2022; Whitler et al. 2023). Consequently, the non-parametric models are able to recover the less biased, fundamental properties of galaxies (Leja et al. 2019; Lower et al. 2020).
Compared to the parametric models, where SFR(t) is modeled as a parametric function of time, the non-parametric models do not assume that SFR can be described as an explicit function of time, which allows for more flexibility on the shape of the SFH model. Instead, SFH is modeled by step functions in time, in which SFR is constant within each time bin. We put N = 7 time bins, taking into account Leja et al. (2019) who demonstrated that the results do not vary with the choice of the number of bins as long as N = 4–14 (see more details in Appendix A of Leja et al. 2019).
We set the first time bin as 0–10 Myr, while the rest of the bins were spaced equally in logarithmic lookback time, between 10 Myr and the lookback time at z = 20. The parameters of the non-parametric SFH model are the ratios of log(SFR) between two consecutive time bins, namely, log(SFRn/SFRn+1), where n goes from 1 to N − 1. Thus, the non-parametric SFH fits log(SFRn/SFRn+1), adopting the Student’s-t distribution:
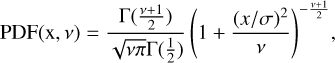 (5)
(5)
where x = log(SFRn/SFRn+1), Γ is the Gamma function, σ is a scale factor regulating the width of the distribution, and ν = 2 represents the degrees of freedom determining the behavior in the tails of the probability distribution. We fix σ = 0.3 for the continuity prior and σ = 1 for the bursty continuity prior. The Student’s t distribution is chosen for the continuity prior since it explicitly weights against sharp changes in SFR(t) such as rapid quenching or extreme burst (Leja et al. 2017), whereas bursty continuity prior allows a more “bursty” star formation (Tacchella et al. 2022). We direct the reader to Leja et al. (2019) for more details on the non-parametric models with different priors and the impact of the choice of the adopted prior on the constrained galaxy parameters.
While we use the non-parametric SFH model with a continuity prior as our fiducial model, we analyze the variations of the galaxy properties inferred from the SED fitting on the adopted SFH model in Sect. 5.
Drude model fit parameters for the Calzetti, SMC, MW, and the LMC curves from Li et al. (2008).
3.3 Dust parametrization
The parameterizations of dust attenuation laws in galaxies typically involve adaptations of the Calzetti dust law. Examples of variations of the Charlot & Fall (2000) recipe include a Calzetti dust curve with varying steepness of the curve and a Lorentzian-like Drude profile describing the characteristic ∼2175 Å bump and a two-component dust screen model (e.g., Noll et al. 2009; Kriek & Conroy 2013; Boquien et al. 2019; Trayford et al. 2020).
BAGPIPES includes two flexible dust attenuation models: a simple Charlot & Fall (2000) recipe and the Salim et al. (2018) model. However, the flexibility of the two models is somewhat limited, as they are not able to recover well all the empirical dust laws along with the global properties of the simulated galaxies. In this work, we adopted the analytical model for the parameterization of dust attenuation proposed by Li et al. (2008). While the dust parametrization recipe of Li et al. (2008) was originally proposed for modeling extinction curves along the line of sight of gamma-ray burst (GRB) afterglows, we take advantage of the flexibility of the model to explore dust attenuation curves in high-z galaxies. The main advantage of using this flexible model is that it is able both to reproduce empirical dust laws (Calzetti, MW, SMC, and LMC; Appendix A) and to recover potential non-conventional ones.
The analytical expression for the dust attenuation curve, normalized to the attenuation in the rest-frame optical range at 0.55 µm (AV) is:
![$ \matrix{ {{{{A_\lambda }} \mathord{\left/ {\vphantom {{{A_\lambda }} {{A_V}}}} \right. \kern-\nulldelimiterspace} {{A_V}}} = {{{c_1}} \over {{{\left( {{\lambda \mathord{\left/ {\vphantom {\lambda {0.08}}} \right. \kern-\nulldelimiterspace} {0.08}}} \right)}^{{c_2}}} + {{\left( {{{0.08} \mathord{\left/ {\vphantom {{0.08} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} \right)}^{{c_2}}} + {c_3}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{233\left[ {1 - {{c1} \mathord{\left/ {\vphantom {{c1} {\left( {{{6.88}^{{c_2}}} + {{0.145}^{{c_2}}} + {c_3}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {{{6.88}^{{c_2}}} + {{0.145}^{{c_2}}} + {c_3}} \right)}} - {{{c_4}} \mathord{\left/ {\vphantom {{{c_4}} {4.60}}} \right. \kern-\nulldelimiterspace} {4.60}}} \right]} \over {{{\left( {{\lambda \mathord{\left/ {\vphantom {\lambda {0.046}}} \right. \kern-\nulldelimiterspace} {0.046}}} \right)}^2} + {{\left( {{{0.046} \mathord{\left/ {\vphantom {{0.046} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} \right)}^2} + 90}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{{c_4}} \over {{{\left( {{\lambda \mathord{\left/ {\vphantom {\lambda {0.2175}}} \right. \kern-\nulldelimiterspace} {0.2175}}} \right)}^2} + {{\left( {{{0.2175} \mathord{\left/ {\vphantom {{0.2175} \lambda }} \right. \kern-\nulldelimiterspace} \lambda }} \right)}^2} - 1.95}},} \hfill \cr } $](/articles/aa/full_html/2023/11/aa46723-23/aa46723-23-eq11.png) (6)
(6)
where c1, c2, c3, and c4 are dimensionless parameters and λ is the wavelength in µm. The three terms of the Drude model describe the far ultraviolet (FUV) attenuation rise, attenuation in the optical and near-infrared (NIR) range, and the 2175 Å bump (which is pronounced in the MW extinction curve and, to a lesser extent, in the LMC extinction curve), respectively. The c1 – c4 parameters reproducing the Calzetti, SMC, LMC, and MW laws used as dust extinction templates in modeling the GRB afterglows are reported in Table 2.
The disadvantage of this method is that dust attenuation is described by four additional parameters with respect to the conventional fitting procedure. Thus, it can be used only with spectroscopic observations (as in our case) and/or when a sufficiently large number of photometric data points are available (e.g., with the JWST Public Release IMaging for Extragalactic Research; PRIMER large program). The advantage is that it can model any potential variation of the dust attenuation law from the ones derived from local star-forming galaxies. In fact, contrary to the standard fitting procedure, our method does not require a priori assumption on the dust law. This aspect is particularly important in the case of high-z galaxies since, as discussed in the introduction, there are no physical reasons supporting the idea that dust attenuation curves at early epochs resemble any of the dust laws found in the local Universe.
We implement the Drude parameterization in the BAGPIPES SED fitting software package. The four parameters (c1, c2, c3, and c4) of the Drude parameterization are constrained simultaneously with parameters of the SFH model and the global physical parameters of the source. The list of all the free parameters, along with their priors and ranges, is given in Table 3. The prior probability densities and allowed ranges for the model parameters are selected based on the suggestions from the literature (Carnall et al. 2018, 2019a,b, 2023; Leja et al. 2019) and the tests performed in retrieving the parameters of simulated galaxies (Appendix A). We allow the parameters of the dust parametrization model to vary in a wide range that covers all the values of the Drude model fit to the Calzetti, SMC, LMC, and MW dust laws (Table 2; see also Li et al. 2008), and any potential unconventional curve (Fig. 2, gray region). The prior limits for the c4 parameter, which characterizes the UV bump feature, are set so that c4 ≳ 0, since negative values have no physical meaning.
Free parameters and their priors that are used in the SED fitting procedure.
4 Dust attenuation law in early galaxies
In this section, we fit the NIRSpec JWST spectroscopic observations described in Sect. 2, with the SED fitting method outlined in Sect. 3.
4.1 Best-fit on the JWST spectra
We use BAGPIPES to load the galaxy spectra, masking the low-wavelength spectral region below the wavelength of the Lyα line. Next, we provide the instructions on the model that we use to fit the data, that is, the parameters of the model and their priors as summarized in Table 3. Using MultiNest, we sample the posterior distribution in parameter space and obtain the best-fit parameters of the model with their 1σ uncertainties. We report the corner plots with the 1D and 2D projections of the posterior distribution of all the parameters fitted by our model, for s00717, s01143, and s01149 in Figs. B.1, B.2, and B.3, respectively. The best-fit parameters of the three sources, along with the derived fundamental properties (e.g., log M*, SFR, 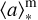 ) are summarized in Table 4.
) are summarized in Table 4.
Figure 1 depicts the JWST NIRSpec spectra of the three galaxies (s00717, s01143, and s01149) analyzed in this work, along with the best-fit posterior spectra (left panels: the blue and orange spectra, respectively). The shaded regions represent their respective 1σ uncertainties. Although the best-fit spectrum fits the narrower nebular lines at longer wavelengths (λobs ≳ 30000 Å), that is, the rest-frame optical lines, such as the [O III] λλ4959, 5007 doublet line, Hβ, Hγ, and [O II] λ3727, the fit to the potentially detected, broader, rest-frame UV lines (such as C III] λλ1907, 1909, C IV λλ1548, 1550, N III] λ1747, N IV λ1486, and He II λ1640) is somewhat poorer. The widths of the spectral lines vary due to the wavelength-dependent spectral resolution of the NIRSpec instrument, which increases with the wavelength and ranges from R ∼ 50–300. On the contrary, when performing the SED fitting of the input NIRSpec spectra, BAGPIPES (version 1.0.0) incorporates the broadening of the spectral features (due to the velocity dispersion and instrumental effects; e.g., Carnall et al. 2018) with a single parameter σvel. Consequently, it becomes challenging to achieve a satisfactory fit to both the rest-frame optical and UV lines. The resulting output best-fit spectra provide a better fit to the spectra at λobs ≳ 30 000 Å, including bright optical lines and lower uncertainties, with a lower σvel ∼ 400–700 km s−1 (Table 4). To test if this affects our results, we perform fit on the observed spectra that are smoothed (i.e., convolved with a Gaussian kernel) to the lower resolution of R ∼ 100, in order to fit both the rest-frame UV and optical lines, and we find that the inferred galaxy and dust attenuation parameters remain consistent (within ∼1–2σ).
Constrained properties of the three sources using the SED fitting procedure.
4.2 Dust attenuation curves of early galaxies
The dust attenuation curves derived for each source, along with the 1-σ uncertainties are illustrated on the right panels of Fig. 1 (orange solid lines with shaded regions). To estimate these uncertainties, we first boot-strap 1000 attenuation curves from a random sampling of the c1 − c4 from the 1D posterior distributions. Then, we plot the median attenuation curve with 1σ dispersion of the distribution.
For the three sources analyzed in this work, we report in Table 4 the c1 − c4 parameters of the best fitting attenuation curves. By comparing these results with Table 2 we find that the three high-z galaxies observed with JWST are characterized by dust attenuation curves that are different from the empirical laws typically adopted as dust law templates in the SED fitting procedure. Figure 2 further highlights this result: the overall shape of the inferred attenuation curve of s00717 resembles the LMC and MW dust extinction laws, but it is steeper at lower wavelengths (Fig. 2, blue curve). The inferred dust attenuation curves of the remaining two sources, s01143 and s01149, are similar to the Calzetti attenuation curve, but slightly flatter at short wavelengths (λ ≲ 0.2 microns; Fig. 2, orange and pink curves, respectively).
4.3 The characteristic 2175 Å bump
In the case of s00717, the strength of the broad UV absorption feature at 2175Å, characterized by the c4 parameter of the analytical dust model, (c4 ∼ 0.033 in Table 4), is ∼63% of the MW bump, and it falls within the range of the UV bumps of the MW and the LMC extinction curves (c4 ∼ 0.052 and c4 ∼ 0.022, respectively; Table 2). The dust attenuation curves of the remaining two sources show no significant evidence of the characteristic UV bump (Fig. 2, orange and pink curves), although there are some hints of the 2175 Å bump when assuming certain parametric SFHs (Fig. 5, middle and bottom panels).
To investigate the presence of the UV bump in the s00717 galaxy and its absence in the other two sources, we compare the fit to the spectra using two different versions of the fiducial dust attenuation model: with and without the bump, that is, with the c4 parameter-free and fixed at c4 = 0, respectively. For this purpose, we use Bayesian model selection through the Bayes factor5 (Jeffreys 1983; Kass & Raftery 1995; Berger & Pericchi 1996; MacKay 2003).
In Table 5, we provide the logarithm of Bayes factors obtained through the model evidences provided by the MultiNest nested sampling method (Feroz & Hobson 2008); Feroz et al. 2019) implemented in BAGPIPES. For the s00717 source, the Bayes factor is log(BF2−1) = 1.3, where models 1 and 2 are fiducial models without and with the bump, respectively. According to the scale proposed by Kass & Raftery (1995), the Bayes factor scales as strong (log(BF2−1) = 1−2), indicating substantial evidence in favor of the fiducial model with the bump over the model without the bump. On the contrary, for the remaining two sources, the model selection slightly favors the model without the bump (log(BF1−2) < 1).
 |
Fig. 1 Best fit on the SED and the inferred attenuation curves of three galaxies at the EoR. The left panels show the NIRSpec JWST spectrum of s00717 (top), s01143 (middle), and s01149 (bottom) in blue, with flux uncertainties illustrated in pale blue. Orange and pale orange colors indicate the best-fit posterior spectrum with 1σ uncertainties, respectively. Vertical dashed lines mark the prominent detected emission lines and positions of potential lines present in the spectra. In the bottom panel of each plot, we show the residuals of the best fit on the observed spectra, Δfλ, with 1σ uncertainties. The right panels depict the best-fit dust attenuation curves with 1σ uncertainties for s00717, s01143, and s01149 sources, which were obtained using the SED fitting method with the non-parametric SFH model. Drude model fits to the Calzetti, the MW, the SMC, and the LMC empirical curves are shown as green, red, purple, and brown dashed lines, respectively. |
5 Comparison with different dust and SFH models
While SED fitting is an effective method for getting insight into the galaxy properties from spectra and/or photometry, its accuracy may be restricted by the uncertainties in the dust attenuation and star formation history models, along with the wavelength coverage (Conroy et al. 2009; Maraston et al. 2010; Pforr et al. 2012; Mitchell et al. 2013; Buat et al. 2014; Reddy et al. 2015; Carnall et al. 2019a; Topping et al. 2022). In Sect. 5.1, we discuss how much the derived physical properties differ from our fiducial values if we assume a priori one of the empirical dust laws. In Sect. 5.2, we test whether our results depend on the adopted SFH model.
 |
Fig. 2 Best-fit dust attenuation curves obtained using the SED fitting method with the non-parametric SFH model, for our three sources. The median of the posterior with 1er uncertainties are shown as blue, orange, and pink solid lines with associated shaded regions for s00717, s01143, and s01149, respectively. The 3σ dispersion of the prior is estimated from a 99.7% sample of 1000 random draws from the prior limits for c1 − c4 parameters of the Drude model (gray shaded region). Drude model fits to the Calzetti, the MW, the SMC, and the LMC empirical curves are shown as in Fig. 1. |
Logarithm of the Bayes factor estimates derived comparing the fiducial SED fitting model with the analytical dust curve with and without the bump.
5.1 Comparison with the empirical dust laws
We carry out multiple BAGPIPES runs in order to perform the SED fitting of our spectroscopic data, as described in Sect. 3, but instead of using the Drude approach, we assume one of the empirical dust laws. Dust laws that have been frequently adopted a priori in the SED fitting procedure to infer the properties of high-z galaxies are the Calzetti attenuation law, and the SMC and MW extinction laws (Adams et al. 2023; Leethochawalit et al. 2023; Topping et al. 2022; Trussler et al. 2023). An overview of the derived physical properties of the three galaxies, obtained with the fiducial attenuation curve, and by assuming one of the frequently adopted empirical curves, is shown in Table 6.
We find that properties such as the redshift z, σvel (related to the width of the spectral lines and features due to velocity dispersion and instrumental broadening; e.g., Carnall et al. 2018), the mass-weighted stellar age, 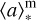 , metallicity, Z, and ionization parameter, log U, are practically independent (within ∼ 1σ) on the assumed dust law, for all the three sources. The only exception is the inferred metallicity of the s00717 source when adopting the SMC law, which is lower from its fiducial value by ∼4σ (0.18 dex). The remaining aforementioned properties mostly differ by ∼1−2σ, depending on the adopted dust law.
, metallicity, Z, and ionization parameter, log U, are practically independent (within ∼ 1σ) on the assumed dust law, for all the three sources. The only exception is the inferred metallicity of the s00717 source when adopting the SMC law, which is lower from its fiducial value by ∼4σ (0.18 dex). The remaining aforementioned properties mostly differ by ∼1−2σ, depending on the adopted dust law.
Conversely, properties such as the living stellar mass log M* SFR, and AV can deviate significantly from their fiducial values with the adopted dust law (see also e.g., Kriek & Conroy 2013). If a Calzetti dust law is assumed, most of the derived properties of the three galaxies are within 1−2σ from the fiducial value. Next, if the MW dust law is assumed, the properties of s00717 are within ∼1σ of their fiducial values, since the fiducial attenuation curve of s00717 resembles that of the MW curve (Fig. 2, blue solid line). However, for the remaining two sources, the choice of a MW dust law leads to significant deviations in properties such as the log M* SFR, and AV. For s01143, these three parameters are lower by 7σ (0.13 dex), 8σ (0.14 dex), and 10σ (0.12 dex), respectively. For s01149, log M*, SFR, and Av are lower by 4σ (0.16 dex), 6σ (0.16 dex), and 7.5σ (0.14 dex), respectively. Finally, when assuming the SMC law, most of the properties of s00717 resemble their fiducial values apart from AV, which is lower by >10σ (0.33 dex). For the remaining two sources, log M*, SFR, and AV deviate substantially (>10σ) from their fiducial values since their fiducial attenuation curve is much flatter than the SMC law (Fig. 2; orange and pink solid lines for s01143 and s01149, respectively). For example, for the s01143 and s01149 sources, log M*, SFR and Av are lower by 0.32–0.35 dex, 0.31–0.34 dex, and 0.32–0.38 dex, respectively.
We summarize the aforementioned findings in Fig. 3. Overall, the largest deviation is found for the s01143 and s01149 for which the parameters log M* and Av diverge the most from their fiducial values adopting the SMC law. This is unsurprising given that these sources have a much flatter fiducial attenuation curve than the steep SMC curve (Fig. 2, orange and pink curves, respectively).
In order to demonstrate that the fiducial model with the analytical dust attenuation curve provides a better fit to the observed spectra, with respect to the models with adopted empirical curves, we again make use of the Bayesian model selection. Model selection based on the Bayes factor favors the fiducial model over any of the models that rely on an a priori adoption of one of the empirical dust curves. In fact, the Bayes factors rank as either strong (log(BF) = 1−2) or decisive (log(BF) > 2), according to the proposed scale of Kass & Raftery (1995; more details are given in Table 7).
Our results are in overall agreement with previous studies in the literature that have analyzed the dependence of the fundamental galaxy properties with the adopted dust law, by employing various standard dust laws (Topping et al. 2022) and/or other dust attenuation recipes (Kriek & Conroy 2013); Reddy et al. 2015; Salim et al. 2016; Lo Faro et al. 2017; Buat et al. 2019). For instance, Reddy et al. (2015) found that the stellar masses and SFR differ by up to ∼0.16 dex and ∼0.30 dex, respectively, by comparing the Calzetti curve, the SMC curve, and the attenuation curve derived in their work, adopting the exponentially rising SFH as their fiducial model, for a sample of 224 star-forming galaxies at z ∼ 1.4−2.6. Next, Salim et al. (2016) compared the Calzetti and their modified dust attenuation curve, and found that a fraction of galaxies from their sample of ∼700 000 galaxies at z < 0.3 has stellar masses that vary by up to 0.4 dex, assuming the two-component exponential and delayed SFHs, with CIGALE (Boquien et al. 2019). Finally, Topping et al. (2022) found a weak dependence on the stellar mass (≲0.09 dex) and a significant dependence on the SFR (∼0.4 dex), on the choice of the dust attenuation law. Topping et al. (2022) considered the Calzetti, the SMC, and the MW curve, assuming a constant parametric SFH as fiducial, with the BEAGLE code (Chevallard & Charlot 2016).
To summarize, our study reveals that parameters like red-shift, velocity dispersion, stellar age, metallicity, and ionization parameters are largely unaffected by the choice of dust law. However, properties such as the stellar mass, SFR, and V-band dust attenuation can deviate significantly from their fiducial values based on the adopted dust law. Our analysis indicates that the fiducial model with the analytical dust attenuation curve provides a better fit to the observed spectra compared to models employing empirical curves, as supported by Bayesian model selection.
A summary of the constrained physical properties of the three galaxies with different empirical curves used in the SED fitting procedure assuming the fiducial non-parametric SFH model with a continuity prior.
 |
Fig. 3 Comparison of inferred galaxy properties (stellar mass, M*, and SFR, color-coded by the dust attenuation parameter, AV) when adopting one of the empirical curves as a dust law and with the fiducial dust attenuation curve for the three sources. The derived properties of the s00717, s01143, and s01149 galaxies are shown on the left, middle, and right panels, respectively. The relative variation in parameters inferred adopting the Calzetti, the SMC, and MW curves with the fiducial curve are represented as circle, square, and diamond, respectively. |
5.2 Comparison with different SFH models
We have so far assumed as a fiducial the non-parametric SFH model with a continuity prior. In this subsection, we investigate whether the inferred galaxy physical properties and the dust attenuation properties depend on the assumed SFH model.
The BAGPIPES code allows us to also consider the following parametric SFH models, where the SFR can be described as a function of time:
constant,
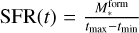 , where tmin and tmax are the time limits of the entire SFH;
, where tmin and tmax are the time limits of the entire SFH;double power-law (DPL), SFR(t) ∝ ((t/τ)α + (t/τ)−β)−1, where α and β are the falling and rising slopes, respectively, and τ is the turnover time;
exponential,
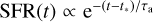 , where t* is the time of the SFR peak, and τa is the timescale of the SFR decline);
, where t* is the time of the SFR peak, and τa is the timescale of the SFR decline);delayed,
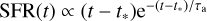 ;
;lognormal,
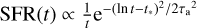 .
.
The list of all the parameters of the parametric SFH models, along with their priors and ranges, is given in Table 8.
We run the BAGPIPES code and perform the SED fitting of the spectroscopic data, adopting the Drude parametrization for the dust attenuation (Sect. 3), and assuming either one of the aforementioned parametric SFH models (constant, double power-law, exponential, delayed, and lognormal) or the non-parametric SFH model with a “bursty continuity” prior. We vary the free parameters of the aforementioned parametric and non-parametric SFH models, as summarized in Table 8 and Table 3, respectively.
Most of the inferred galaxy properties vary significantly depending on the assumed SFH model (see Table 9). In particular, the parameters closely associated with the SFH, such as the mass-weighted stellar age 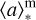 , and to a lesser extent, the stellar mass, M*, and SFR, reveal the strongest dependence on the assumed SFH. For instance, the mass-weighted stellar age,
, and to a lesser extent, the stellar mass, M*, and SFR, reveal the strongest dependence on the assumed SFH. For instance, the mass-weighted stellar age, 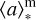 , fluctuates by >10σ (0.6–1.0 dex), for the three sources. Simultaneously, the stellar mass and SFR vary by 4–5σ (0.3–0.4 dex) and 5–8σ (0.3–0.4 dex), respectively. We illustrate the fluctuations of these parameters in Fig. 4 (top panels).
, fluctuates by >10σ (0.6–1.0 dex), for the three sources. Simultaneously, the stellar mass and SFR vary by 4–5σ (0.3–0.4 dex) and 5–8σ (0.3–0.4 dex), respectively. We illustrate the fluctuations of these parameters in Fig. 4 (top panels).
For s01143 and s01149 galaxies, there is a systematic difference in parameters inferred from the non-parametric and parametric SFH (Fig. 4, top middle and right panels). This is a consequence of the fact that the non-parametric models tend to favor a smoother SFH (Fig. 4, bottom middle and right panels) and, thus, higher mass-weighted ages 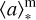 , higher stellar masses log M*, and higher SFR (averaged over 100 Myr). For the source s00717, the non-parametric SFHs are generally consistent with the more complex parametric SFH models (DPL, delayed, and lognormal), apart from the constant parametric SFH model that is biased towards a very bursty SFH (Fig. 4, bottom left panel). In this case, we infer a shorter
, higher stellar masses log M*, and higher SFR (averaged over 100 Myr). For the source s00717, the non-parametric SFHs are generally consistent with the more complex parametric SFH models (DPL, delayed, and lognormal), apart from the constant parametric SFH model that is biased towards a very bursty SFH (Fig. 4, bottom left panel). In this case, we infer a shorter 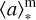 and a lower log M* and SFR (Fig. 4, top left panel).
and a lower log M* and SFR (Fig. 4, top left panel).
The metallicity Z shows a moderate dependence on the assumed SFH model, with variations of ∼1–2σ (∼0.05–0.15 dex) for all three sources. Next, the ionization parameter log U is largely independent (within 1σ) on the SFH for s00717, whereas it varies by 2–4σ (∼0.6–0.9 dex) for the remaining two sources, with a clear separation on the log U parameter estimate when using the parametric SFH with respect to the non-parametric models. Finally, the Av parameter is moderately dependent on the SFH model, with variations of up to ∼1σ (0.18 dex) for s00717, and up to ∼2–3σ (0.05–0.08 dex) for the remaining two galaxies; probably driven by the well-known degeneracy between the stellar age, metallicity, and dust attenuation (e.g., Papovich et al. 2001; Tacchella et al. 2022).
The dust attenuation curve is overall independent on the assumed SFH model. The properties of the dust model (c1 − c4) are in the 1–1.5σ range of the fiducial model. This variation does not strongly affect the overall shape of the attenuation curve, but the amplitude, the slope, and the UV bump of the dust curve fluctuate (see Fig. 5), probably driven mostly by the variation of the Av parameter, which acts as the normalization of the dust curve.
Various parametric SFH models have been compared using BAGPIPES in several studies (Carnall et al. 2018, 2019a). For instance, Carnall et al. (2019a) used a sample of z ∼ 0 mock galaxy photometric data, and found that the stellar mass, SFR, and mass-weighted age vary by at least ∼0.1, 0.3, and 0.2 dex, respectively, with the assumption on the four parametric SFH model: the DPL, exponential, delayed, and lognormal. For the same three parameters, our results indicate variations up to 0.11, 0.12, and 0.36 dex, respectively, taking into account the four aforementioned models.
Finally, Carnall et al. (2019a) showed that a correct recovery of the parameters depends more on the shape of the true SFHs than on the choice of the SFH model itself. Therefore, they concluded that there is no universal (parametric) SFH model that is able both to provide the best fit to the true SFH and to recover the unbiased properties of all the individual sources at all redshifts.
The exponentially declining model, often used as a fiducial model for nearby sources, generally does not provide a good fit for rising SFHs of intermediate-to-high redshift sources (z > 1; e.g., Maraston et al. 2010; Wuyts et al. 2011; Reddy et al. 2012; Buat et al. 2014). At intermediate-z (z ∼ 1–3), the double power-law can be a good choice for fitting the massive quiescent galaxies with an older stellar population (Carnall et al. 2018), whereas the exponentially rising SFHs provide a good fit for star-forming galaxies (Maraston et al. 2010; Pforr et al. 2012; Reddy et al. 2015). The constant and delayed SFH models often provide a good fit to the SED of high-z (z > 6) sources (Laporte et al. 2021; Furtak et al. 2021). In particular, the constant SFH model appears to be a more adequate choice for fitting the SEDs with the characteristic “Balmer jump” produced by very young stellar populations (a* < 10 Myr) in low-mass star-forming galaxies at high-z (Carnall et al. 2023). Finally, theoretical works found that exponentially rising SFHs are favored at high-z (Pallottini et al. 2017, 2022).
Although parametric SFH models are broadly used, they are often not flexible enough to fit the “true” galaxy SFHs in all their complexity (Leja et al. 2019; Lower et al. 2020). One approach to capture the complex “true” SFHs produced by composite stellar populations in galaxies is to combine multiple parametric SFH models (e.g., Buat et al. 2014, 2019; Ciesla et al. 2017, 2023; Bunker et al. 2023; Atek et al. 2023a). For example, a combination of a recent (< 10 Myr) burst of star formation and a delayed SFH can be employed to incorporate the star formation originating from younger and older stellar populations, respectively (Atek et al. 2023a). Another approach to retrieve more realistic SFHs and, thus, the global galaxy properties, is to fix the stellar age to a high value (e.g., 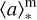 > 1 Gyr) instead of treating it as a free parameter in the SED fitting procedure (e.g., Maraston et al. 2010; Pforr et al. 2012; Buat et al. 2014 and references therein).
> 1 Gyr) instead of treating it as a free parameter in the SED fitting procedure (e.g., Maraston et al. 2010; Pforr et al. 2012; Buat et al. 2014 and references therein).
A favorable alternative to more rigid parametric SFH models are more flexible, non-parametric SFH models which are able to fit complex SFHs with greater variations in the SFR (Leja et al. 2019), often measured in high-z (z > 6) galaxies (Topping et al. 2022; Whitler et al. 2023). One of the drawbacks of the non-parametric models is that they tend to be more computationally expensive with respect to the parametric models since typically they require a larger parameter space to be explored by the Bayesian sampler (e.g., Leja et al. 2019). Another drawback is that the flexibility of non-parametric SFH models is somewhat limited by the assumed priors, which is either weighted in favor of a smooth or chaotic SFH (Leja et al. 2019; Whitler et al. 2023; Tacchella et al. 2022). Therefore, when assuming the non-parametric SFH models, it is important to choose a well-motivated prior that best mimics the realistic SFH, as it can have a significant impact on the SED fitting and the inferred galaxy properties (Leja et al. 2019; Whitler et al. 2023; Tacchella et al. 2022; Topping et al. 2022). However, the flexible non-parametric SFHs still provide a less biased fit with more accurate error estimates with respect to the more rigid parametric SFH models (Leja et al. 2019; Lower et al. 2020).
Overall, the non-parametric SFH models, and particularly models that explicitly weight against sharp transitions in the SFR history (e.g., models with the continuity prior) typically lead to more extended and complex SFHs, and fit older stellar populations and thus, recover higher 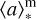 . Extended SFHs allow longer stellar mass assembly and, consequently, significantly larger inferred stellar masses (Fig. 4; see also, e.g., Topping et al. 2022; Whitler et al. 2023). On the contrary, the more rigid parametric SFH models are not flexible enough to fit both the recent burst of SFR originating from a young stellar population and a potentially more dominant older stellar population at earlier times. Consequently, the inferred stellar masses, SFRs, and ages of these sources will be systematically lower than their corresponding values obtained by adopting the non-parametric models. This is particularly evident for star-forming galaxies at the EoR, where a very young stellar population (<10 Myr) can outshine the possibly more massive, but fainter older stellar population (the so-called “outshining” effect; Leja et al. 2019; Whitler et al. 2023; Topping et al. 2022; Tacchella et al. 2022). For instance, Whitler et al. (2023) and Topping et al. (2022) found that adopting the non-parametric SFH model (with continuity prior) led to inferred stellar masses that were approximately an order of magnitude larger (≳1 dex) than those obtained using the parametric constant SFH model. However, in our study, we observed smaller fluctuations in stellar mass of around ∼0.4 dex when comparing the same SFH models.
. Extended SFHs allow longer stellar mass assembly and, consequently, significantly larger inferred stellar masses (Fig. 4; see also, e.g., Topping et al. 2022; Whitler et al. 2023). On the contrary, the more rigid parametric SFH models are not flexible enough to fit both the recent burst of SFR originating from a young stellar population and a potentially more dominant older stellar population at earlier times. Consequently, the inferred stellar masses, SFRs, and ages of these sources will be systematically lower than their corresponding values obtained by adopting the non-parametric models. This is particularly evident for star-forming galaxies at the EoR, where a very young stellar population (<10 Myr) can outshine the possibly more massive, but fainter older stellar population (the so-called “outshining” effect; Leja et al. 2019; Whitler et al. 2023; Topping et al. 2022; Tacchella et al. 2022). For instance, Whitler et al. (2023) and Topping et al. (2022) found that adopting the non-parametric SFH model (with continuity prior) led to inferred stellar masses that were approximately an order of magnitude larger (≳1 dex) than those obtained using the parametric constant SFH model. However, in our study, we observed smaller fluctuations in stellar mass of around ∼0.4 dex when comparing the same SFH models.
In summary, our study reveals that most of the inferred galaxy properties show significant variations depending on the assumed SFH model. Parameters directly associated with the SFH, such as mass-weighted stellar age, stellar mass, and SFR, exhibit the strongest dependence on the chosen SFH. The metallicity and ionization parameter, and the dust attenuation AV show moderate variations. We note that the dust attenuation curve remains largely independent of the SFH model, with only minor variations in its amplitude, slope, and UV bump. Finally, our study highlights the importance of considering both the advantages and limitations of flexible and parametric SFH modeling approaches.
Logarithm of the Bayes factor estimates derived comparing the fiducial fitting model with the analytical dust curve and the models with adopted Calzetti, SMC, and MW curves.
Free parameters and their priors of the different parametric SFH models.
Summary of constrained parameters of the three sources with the SED fitting procedure using different SFH models, assuming the Drude-type dust attenuation model.
 |
Fig. 4 Stellar mass M* and SFR, color-coded by the mass-weighted stellar age |
6 Discussion
The shape of dust attenuation curves (e.g., the steepness of the curve and the amplitude of the characteristic UV bump) both depend on the dust properties (chemical composition, size distribution, mass, temperature) and the dust-to-stars spatial distribution (see Salim & Narayanan 2020 for a review). Furthermore, Narayanan et al. (2018) demonstrated that even if a constant dust extinction law is employed in radiative transfer models, the resulting attenuation curves can have a wide range of variations of the derived shapes and ∼2175 Å bump strengths, primarily driven by the dust-to-star geometry. Thus, the interpretation of the constrained dust attenuation curves is challenging (see Conroy 2013 for a review). The number of galaxies analyzed in this work is too small to draw a firm conclusion about the dependence of the slope and/or bump strength on the galaxy properties. We find anyway instructive to make some considerations about our findings regarding this issue.
6.1 On the slope of dust attenuation curves
Numerous studies found a correlation between the steepness of the dust curve and/or the strength of the UV bump in relation to various galaxy properties. The dependence on the galaxy properties can often be attributed to the underlying dust-to-gas geometry or the intrinsic properties of the dust itself. From the analysis of nearby (z ∼ 0, Chevallard et al. 2013; Leja et al. 2017; Salim et al. 2018; see e.g., Salim & Narayanan 2020 for a review), intermediate-z (z ∼ 0–3, Battisti et al. 2020; Trayford et al. 2020) and high-z galaxies (z ∼ 4.4–5.5, Boquien et al. 2022), it results that the steepness of the dust curve strongly anti-correlates with the V-band attenuation optical depth τV (i.e., the V-band attenuation AV). Moreover, several studies on galaxies at nearby, intermediate and high-z have reported an inverse correlation between the steepness of the curve and various parameters such as the color excess E(B–V) (z ∼ 1.5–3, Salmon et al. 2016), the SFR (z ∼ 0–3, Battisti et al. 2020), the specific SFR (sSFR; z ∼ 0.5–2, Kriek & Conroy 2013), the stellar mass (z ∼ 0, Salim & Narayanan 2020; z ∼ 6–8; Mushtaq et al. 2023), and the metallicity (z ∼ 1.4–2.6, Shivaei et al. 2020). Conversely, a positive correlation has been reported between the slope of the dust curve and the rest-frame IR brightness of intermediate-z galaxies (z ∼ 1–2, Buat et al. 2012; Lo Faro et al. 2017). Notably, Salim & Narayanan (2020) analyzed the dependence of the slopes of attenuation curves of a large sample of nearby galaxies, on physical properties such as V-band dust attenuation, stellar mass, inclination, metallicity, and sSFR. They reported that once Av is fixed, none of the remaining properties have a significant effect on the slope of the attenuation curve, although a weak correlation was reported for the metallicity and an anti-correlation for the stellar mass.
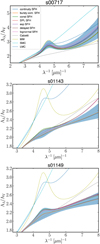 |
Fig. 5 Best-fit dust attenuation curves derived with the SED fitting method, adopting various aforementioned SFH models (solid lines). The attenuation curves of s00717, s01143, and s01149 are shown on the top, middle, and bottom panels, respectively. The 1σ uncertainties of the fiducial SFH model with the continuity prior are shown as blue-shaded regions. Drude model fits to empirical dust curves, frequently adopted as dust attenuation templates in the SED fitting methods are shown for comparison (dashed lines). |
6.2 On the strength of the 2175 Å bump
The 2175 Å bump represents a notable absorption feature in the ultraviolet spectrum that is often linked to the existence of small carbonaceous grains and/or PAHs (Stecher 1965; Desert et al. 1990; Weingartner & Draine 2001; Tress et al. 2019; Shivaei et al. 2022; Witstok et al. 2023; see Draine 2003 and Galliano et al. 2018 for reviews). The strength of the UV bump at 2175 Å was demonstrated to correlate with metallicity (z ∼ 1.4–2.7, Noll et al. 2009; Shivaei et al. 2020, 2022), stellar age (z ∼ 2, Noll et al. 2009), and stellar mass (z ∼ 1.4–2.7, Shivaei et al. 2022). Next, some authors found that the UV bump is anti-correlated with the sSFR in intermediate-z galaxies (z ∼ 0.5–2, Buat et al. 2012, Kriek & Conroy 2013). Finally, the strength of the UV bump is often found to correlate with the steepness of the dust attenuation curve (Kriek & Conroy 2013); Seon & Draine 2016; Narayanan et al. 2018), although the local extinction curves (the SMC, LMC, and MW) follow an opposite trend. To summarize, a steeper slope of the dust attenuation curve and the characteristic 2175 Å bump are typically observed in more evolved and metal-rich galaxies, with lower V-band attenuation. These trends are in overall agreement with our results on the constrained dust attenuation curves of our small sample.
6.3 About the sources analyzed in this work
The source s00717 is the galaxy of our sample characterized by the steepest attenuation curve and the presence of the 2175 Å bump. Simultaneously, the s00717 galaxy has a factor of ∼3.5–4 lower V-band attenuation (Av ∼ 0.3 mag), a factor of ∼1.5 higher metallicity (Z ∼ 0.3 Z⊙), a factor of ∼3.5 older stellar population (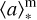 ∼ 46 Myr), and a factor of ∼1.8 lower SFR (∼5 M⊙ yr−1; Table 4), with respect to the other two sources of our sample, consistent with the literature predictions. Conversely, s01143 and s01149 show very flat and shallow attenuation curves, probably driven by high V-band dust attenuation Av (Fig. 2). In particular, we notice that the metallicity and the mass-weighted stellar age of s00717 are comparable to those of the JADES-GS-z6-0 source at z ∼ 6.7, analyzed by Witstok et al. (2023), which also exhibits the 2175 Å absorption feature. Finally, if we compare the stellar masses of our three sources and JADES-GS-z6-0, the most massive of these sources (s01143 and s01149) show no signs of a UV bump, in agreement with the trends found by Salim & Narayanan (2020), but opposite from the results of Shivaei et al. (2022).
∼ 46 Myr), and a factor of ∼1.8 lower SFR (∼5 M⊙ yr−1; Table 4), with respect to the other two sources of our sample, consistent with the literature predictions. Conversely, s01143 and s01149 show very flat and shallow attenuation curves, probably driven by high V-band dust attenuation Av (Fig. 2). In particular, we notice that the metallicity and the mass-weighted stellar age of s00717 are comparable to those of the JADES-GS-z6-0 source at z ∼ 6.7, analyzed by Witstok et al. (2023), which also exhibits the 2175 Å absorption feature. Finally, if we compare the stellar masses of our three sources and JADES-GS-z6-0, the most massive of these sources (s01143 and s01149) show no signs of a UV bump, in agreement with the trends found by Salim & Narayanan (2020), but opposite from the results of Shivaei et al. (2022).
Thus far, the characteristic 2175 Å feature has been identified at low-to-intermediate redshifts (z ∼ 1–3; Noll et al. 2009; Buat et al. 2012; Kriek & Conroy 2013; Battisti et al. 2020; Shivaei et al. 2020, 2022), with only one detection reported at high-z (z ∼ 6.7; Witstok et al. 2023). Therefore, the identification of the 2175 Å feature in s00717 represents one of the first evidence of the possible presence of the small carbonaceous dust grains and/or PAHs in the spectra of a galaxy at the EoR.
Finally, we notice that the strength of the 2175 Å bump, relatively high metallicity Z ∼ 0.3 Z⊙ and a relatively young stellar population (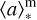 Myr) of the s00717 galaxy at z ∼ 6.9, suggests the need for a dust production mechanism on short timescales, that is possible to occur in the SNeII remnants (Mancini et al. 2015; Leśniewska & Michałowski 2019; Witstok et al. 2023) or dust grain growth in the ISM (Asano et al. 2013; Leśniewska & Michałowski 2019).
Myr) of the s00717 galaxy at z ∼ 6.9, suggests the need for a dust production mechanism on short timescales, that is possible to occur in the SNeII remnants (Mancini et al. 2015; Leśniewska & Michałowski 2019; Witstok et al. 2023) or dust grain growth in the ISM (Asano et al. 2013; Leśniewska & Michałowski 2019).
7 Summary and conclusions
In this paper, we presented a new method based on the BAGPIPES SED fitting code and a parametrization of the dust attenuation law which allows us to simultaneously constrain the fundamental physical properties of the galaxy, along with the dust attenuation curve. The flexibility of this dust attenuation parameterization allows us to fit the SEDs of galaxies attenuated by any of the well-known empirical curves (e.g., the Calzetti attenuation law, and the SMC and the MW extinction curves), as well as any unconventional dust attenuation curve. We test our tool against synthetic spectra, attenuated by empirical dust curves. We applied our tool on NIRSpec JWST spectroscopic observations of a sample of three star-forming galaxies at the Epoch of Reionization. Our main results are as follows:
We performed the SED fitting of the JWST spectroscopic data and constrained the global galaxy properties along with the dust attenuation curves of three galaxies at z ∼ 7–8; Although the shape of the constrained dust attenuation curve of s00717 resembles that of the LMC and MW extinction curves, the shape of the attenuation curves of the remaining two sources, s01143 and s01149, are similar to the Calzetti curve, we found that all three curves show different slopes and UV bump amplitudes;
We report the presence of the 2175 Å bump in the attenuation curve of s00717. This feature, frequently associated with the existence of small carbonaceous dust grains and/or PAHs, is one of the first indications of the presence of the PAHs in a galaxy at the EoR;
We investigated if the constrained galaxy physical properties change when including an a priori assumption of one of the empirical curves as a template in the SED fitting procedure. We showed that an important bias is introduced in the estimates of some of the fundamental physical properties of galaxies (log M* and SFR, as well as the dust attenuation parameter, Av), with fluctuations of up to ∼0.4 dex if the adopted dust law differs from the fiducial dust attenuation curve;
We probed the sensitivity of the fundamental properties of our galaxies on the assumed SFH model. We found that some properties related to the SFH can change significantly, with the mass-weighted age changing by an order of magnitude (1 dex); whereas the stellar mass and SFR vary by up to 0.4 dex. On the contrary, the inferred dust attenuation properties are independent on the assumed SFH model.
In the near future, applying our new robust method on the JWST spectroscopic and photometric data will provide the means to characterize the dust attenuation curves, along with the fundamental properties of a large sample of galaxies at the EoR. This will greatly enhance our understanding of the dust distribution, composition, and production mechanisms in the earliest and most distant galaxies in the Universe.
Acknowledgements
V.M. would like to thank Adam Carnall for his help and useful comments regarding the BAGPIPES code. V.M. would like to thank James Davies and Samuel Gagnon-Hartman for their useful comments on the Bayesian Analysis. V.M., A.F., and A.P. acknowledge support from the ERC Advanced Grant INTERSTELLAR H2020/740120. Partial support (AF) from the Carl Friedrich von Siemens-Forschungspreis der Alexander von Humboldt-Stiftung Research Award is kindly acknowledged. S.C. acknowledges support by the European Union’s HE ERC Starting Grant No. 101040227 – WINGS Any dissemination of results must indicate that it reflects only the author’s view and that the Commission is not responsible for any use that may be made of the information it contains. We gratefully acknowledge the computational resources of the Center for High Performance Computing (CHPC) at SNS.
Appendix A Fitting the synthetic spectra
We use BAGPIPES and our method outlined in Sect. 3, to generate the synthetic spectra. We fix the global, SFH, dust attenuation, and nebular emission parameters of the model galaxy to be identical to the inferred parameters of our sample galaxies (Table 4). The wavelength range and grid of the synthetic spectra are set to be identical to the wavelength range and grid of the observed spectra of the three sources. The flux density uncertainties are taken directly from the observed spectra. Synthetic spectra and their uncertainties are then masked below the Lyman break, in the same manner as for the observed spectra, due to the significant noise at lower wavelengths.
Next, we fit the synthetic spectra by the very same model, allowing the free properties of the synthetic galaxy to vary in the range as outlined in Table 3 when assuming the non-parametric SFH models. In the case of adopting one of the parametric SFH models, the additional free parameters of specific models are allowed to fluctuate in the limits summarized in Table 8. We test and validate our method by fitting the synthetic spectra and recovering the initial properties of the model galaxies, SFH model, and the adopted dust curve.
We showcase the usage of our method on example synthetic spectra (Fig. A.1, blue spectra in left panels), generated by fixing all the parameters of the model source to be equal to the constrained properties of the s01143 galaxy (Table 4), except the dust attenuation properties (c1 − c4), which are set to the values of one of the empirical dust curves: the Calzetti, the SMC, and the MW curves (Table 2). Next, we fit the synthetic spectra of the s01143 source, and demonstrate that we can recover any of the a priori adopted dust curves, namely, one of the empirical dust curves (Fig. A.1, left and right panels, respectively).
In Fig. A.2, we show a corner plot of the posterior of all the physical properties of the model galaxy, including the properties of the dust attenuation curves. The initial properties of the model galaxy are within the 1 – 2σ uncertainties of the posterior distribution (Fig. A.2: in blue and black, respectively).
 |
Fig. A.1 Synthetic dust-attenuated spectra of s01143 source, generated by using the SED fitting method, assuming the fiducial SFH, and adopting one of the empirical dust curves (top-left). The a priori adopted dust curves are the Calzetti attenuation law, and the SMC and the MW extinction curves (from top to bottom panels, respectively). The model spectra of our source are shown in blue, with flux uncertainties illustrated in pale blue. Orange and pale orange colors indicate the best-fit posterior spectra with 1er uncertainties, respectively. Bottom-left panel shows the residuals of the best fit on the synthetic spectra Δfλ with 1σ uncertainties. Right: The corresponding best-fit dust attenuation curve with 1σ uncertainties, on empirical dust curves. Drude model fits to empirical curves: the Calzetti, the SMC, the LMC, and the MW curves are shown as green, red, purple, and brown dashed lines, respectively. |
 |
Fig. A.2 Corner plot illustrating the 1D and 2D projections of the posterior distribution in the parameter space obtained from the SED fitting on the synthetic spectrum generated by fixing the model parameters to those of the s01143 source, assuming the SMC curve, and a fiducial SFH model. The initial (true) properties of the model galaxy are shown in blue. |
Appendix B Corner plots of our three sources
We show the corner plots with the 1D and 2D projections of the posterior distribution of all the parameters fitted by our model, for s00717, s01143, and s01149 (Figs. B.1, B.2, and B.3, respectively). Next, on the right top inset of Fig. B.1 we illustrate the 1D projection of the posterior of the global fundamental properties of the s00717 source: the living stellar mass log M*, the SFR, and the mass-weighted age of the galaxy 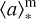 that we will focus on throughout the paper. Finally, on the right bottom inset of Fig. B.1, we illustrate the best-fit SFH of s00717 (that is, the SFR as a function of the age of the Universe), modeled by the fiducial non-parametric SFH with a continuity prior. We note that in a few cases, the posterior distribution of certain dust attenuation parameters is close to the assumed prior limits, making them poorly determined. Nonetheless, our capacity to constrain the dust attenuation curve remains unaffected, as shown by small variations induced by the parameter uncertainty (right panels of Fig. 1).
that we will focus on throughout the paper. Finally, on the right bottom inset of Fig. B.1, we illustrate the best-fit SFH of s00717 (that is, the SFR as a function of the age of the Universe), modeled by the fiducial non-parametric SFH with a continuity prior. We note that in a few cases, the posterior distribution of certain dust attenuation parameters is close to the assumed prior limits, making them poorly determined. Nonetheless, our capacity to constrain the dust attenuation curve remains unaffected, as shown by small variations induced by the parameter uncertainty (right panels of Fig. 1).
 |
Fig. B.1 Corner plot illustrating the 1D and 2D projections of the posterior distribution of the parameters derived from the SED fitting on the spectrum of s00717. 1D posterior of the additional properties derived from the SFH (the SFR, the living stellar mass, and the mass-weighted age of the galaxy) and SFH are shown on the right. |
 |
Fig. B.2 Corner plot illustrating the 1D and 2D projections of the posterior distribution of the parameters derived from the SED fitting on the spectrum of s01143. |
 |
Fig. B.3 Corner plot illustrating the 1D and 2D projections of the posterior distribution of the parameters derived from the SED fitting on the spectrum of s01149. |
References
- Adams, N. J., Conselice, C. J., Ferreira, L., et al. 2023, MNRAS, 518, 4755 [Google Scholar]
- Asano, R. S., Takeuchi, T. T., Hirashita, H., & Inoue, A. K. 2013, Earth Planets Space, 65, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Chemerynska, I., Wang, B., et al. 2023a, MNRAS, 524, 5486 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Shuntov, M., Furtak, L. J., et al. 2023b, MNRAS, 519, 1201 [Google Scholar]
- Bagley, M. B., Finkelstein, S. L., Rojas-Ruiz, S., et al. 2022, AAS J., submitted [arXiv:2285.12988] [Google Scholar]
- Bagley, M. B., Finkelstein, S. L., Koekemoer, A. M., et al. 2023, ApJ, 946, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Battisti, A. J., Cunha, E. D., Shivaei, I., & Calzetti, D. 2020, ApJ, 888, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Battisti, A. J., da Cunha, E., Shivaei, I., & Calzetti, D. 2020, ApJ, 888, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Behrens, C., Pallottini, A., Ferrara, A., Gallerani, S., & Vallini, L. 2018, MNRAS, 477, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, J. O., & Pericchi, L. R. 1996, J. Am. Stat. Assoc., 91, 109 [CrossRef] [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Buat, V., Burgarella, D., et al. 2022, A&A, 663, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkowski, K. J., & Dwek, E. 1995, ApJ, 454, 254 [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
- Bouwens, R. J., Oesch, P. A., Stefanon, M., et al. 2021, AJ, 162, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, R. A. A., Jarvis, M. J., Dunlop, J. S., et al. 2020, MNRAS, 493, 2059 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Noll, S., Burgarella, D., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Heinis, S., Boquien, M., et al. 2014, A&A, 561, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Ciesla, L., Boquien, M., Małek, K., & Burgarella, D. 2019, A&A, 632, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bunker, A. J., Saxena, A., Cameron, A. J., et al. 2023, A&A, 677, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgarella, D., Nanni, A., Hirashita, H., et al. 2020, A&A, 637, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Byler, N., Dalcanton, J. J., Conroy, C., & Johnson, B. D. 2017, ApJ, 840, 44 [Google Scholar]
- Calzetti, D. 2013, in Secular Evolution of Galaxies, eds. J. Falcón-Barroso, & J. H. Knapen, 419 [CrossRef] [Google Scholar]
- Calzetti, D., Kinney, A. L., & Storchi-Bergmann, T. 1994, ApJ, 429, 582 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carnall, A. C., McLure, R. J., Dunlop, J. S., & Davé, R. 2018, MNRAS, 480, 4379 [Google Scholar]
- Carnall, A. C., Leja, J., Johnson, B. D., et al. 2019a, ApJ, 873, 44 [Google Scholar]
- Carnall, A. C., McLure, R. J., Dunlop, J. S., et al. 2019b, MNRAS, 490, 417 [Google Scholar]
- Carnall, A. C., Begley, R., McLeod, D. J., et al. 2023, MNRAS, 518, L45 [Google Scholar]
- Carniani, S., Maiolino, R., Amorin, R., et al. 2018, MNRAS, 478, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Fontana, A., Treu, T., et al. 2022, ApJ, 938, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [Google Scholar]
- Charlot, S., & Longhetti, M. 2001, MNRAS, 323, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Chevallard, J., & Charlot, S. 2016, MNRAS, 462, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Chevallard, J., Charlot, S., Wandelt, B., & Wild, V. 2013, MNRAS, 432, 2061 [CrossRef] [Google Scholar]
- Chokshi, A., Tielens, A. G. G. M., & Hollenbach, D. 1993, ApJ, 407, 806 [Google Scholar]
- Ciesla, L., Elbaz, D., & Fensch, J. 2017, A&A, 608, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciesla, L., Gómez-Guijarro, C., Buat, V., et al. 2023, A&A, 672, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C. 2013, ARA&A, 51, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Gunn, J. E., & White, M. 2009, ApJ, 699, 486 [Google Scholar]
- Curtis-Lake, E., Carniani, S., Cameron, A., et al. 2023, Nat. Astron., 7, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., Sommovigo, L., et al. 2022, MNRAS, 512, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Desert, F. X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] [Google Scholar]
- Di Mascia, F., Gallerani, S., Ferrara, A., et al. 2021, MNRAS, 506, 3946 [NASA ADS] [CrossRef] [Google Scholar]
- Donnan, C. T., McLeod, D. J., Dunlop, J. S., et al. 2023, MNRAS, 518, 6011 [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2009, in ASP Conf. Ser., 414, Cosmic Dust – Near and Far, eds. T. Henning, E. Grün, & J. Steinacker, 453 [Google Scholar]
- Dunlop, J. S., Rogers, A. B., McLure, R. J., et al. 2013, MNRAS, 432, 3520 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., & Scalo, J. M. 1980, ApJ, 239, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., Cameron, E., & Pettitt, A. N. 2019, Open J. Astrophys., 2, 10 [Google Scholar]
- Ferrara, A., Viti, S., & Ceccarelli, C. 2016, MNRAS, 463, L112 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., Vallini, L., Pallottini, A., et al. 2019, MNRAS, 489, 1 [Google Scholar]
- Ferrara, A., Sommovigo, L., Dayal, P., et al. 2022, MNRAS, 512, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarotti, A. S., & Gail, H. P. 2006, A&A, 447, 553 [CrossRef] [EDP Sciences] [Google Scholar]
- Finkelstein, S. L. 2016, PASA, 33, e037 [Google Scholar]
- Finkelstein, S. L., Ryan, E., Russell, J., Papovich, C., et al. 2015, ApJ, 810, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Furtak, L. J., Atek, H., Lehnert, M. D., Chevallard, J., & Charlot, S. 2021, MNRAS, 501, 1568 [Google Scholar]
- Gallerani, S., Maiolino, R., Juarez, Y., et al. 2010, A&A, 523, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Nakajima, K., Ouchi, M., et al. 2023a, ApJ, submitted, [arXiv:2384.86658] [Google Scholar]
- Harikane, Y., Ouchi, M., Oguri, M., et al. 2023b, ApJS, 265, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hirashita, H., & Murga, M. S. 2020, MNRAS, 492, 3779 [CrossRef] [Google Scholar]
- Hirashita, H., & Yan, H. 2009, MNRAS, 394, 1061 [Google Scholar]
- Inami, H., Algera, H. S. B., Schouws, S., et al. 2022, MNRAS, 515, 3126 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K., Shimizu, I., Iwata, I., & Tanaka, M. 2014, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreys, H. 1983, Theory of Probability, International Series of Monographs on Physics (Clarendon Press) [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Kriek, M., & Conroy, C. 2013, ApJ, 775, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Boily, C. M. 2002, MNRAS, 336, 1188 [Google Scholar]
- Lagache, G., Cousin, M., & Chatzikos, M. 2018, A&A, 609, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, N., Meyer, R. A., Ellis, R. S., et al. 2021, MNRAS, 505, 3336 [NASA ADS] [CrossRef] [Google Scholar]
- Leethochawalit, N., Trenti, M., Santini, P., et al. 2023, ApJ, 942, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., Johnson, B. D., Conroy, C., van Dokkum, P. G., & Byler, N. 2017, ApJ, 837, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Leja, J., Carnall, A. C., Johnson, B. D., Conroy, C., & Speagle, J. S. 2019, ApJ, 876, 3 [Google Scholar]
- Leśniewska, A., & Michałowski, M. J. 2019, A&A, 624, L13 [Google Scholar]
- Li, A., & Greenberg, J. M. 2003, in Solid State Astrochemistry, 120, eds. V. Pirronello, J. Krelowski, & G. Manicò, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Liang, S. L., Kann, D. A., et al. 2008, ApJ, 685, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H.-M., & Hirashita, H. 2019, MNRAS, 490, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Buat, V., Roehlly, Y., et al. 2017, MNRAS, 472, 1372 [NASA ADS] [CrossRef] [Google Scholar]
- Lower, S., Narayanan, D., Leja, J., et al. 2020, ApJ, 904, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lower, S., Narayanan, D., Leja, J., et al. 2022, ApJ, 931, 14 [NASA ADS] [CrossRef] [Google Scholar]
- MacKay, D. J. C. 2003, Information Theory, Inference, and Learning Algorithms (Cambridge University Press) [Google Scholar]
- Maiolino, R., Schneider, R., Oliva, E., et al. 2004, Nature, 431, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, M., Schneider, R., Graziani, L., et al. 2015, MNRAS, 451, L70 [CrossRef] [Google Scholar]
- Maraston, C., Pforr, J., Renzini, A., et al. 2010, MNRAS, 407, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Markov, V., Carniani, S., Vallini, L., et al. 2022, A&A, 663, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meurer, G. R., Heckman, T. M., & Calzetti, D. 1999, ApJ, 521, 64 [Google Scholar]
- Mitchell, P. D., Lacey, C. G., Baugh, C. M., & Cole, S. 2013, MNRAS, 435, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, H. L., & Edmunds, M. G. 2003, MNRAS, 343, 427 [CrossRef] [Google Scholar]
- Mushtaq, M., Ceverino, D., Klessen, R. S., Reissl, S., & Puttasiddappa, P. H. 2023, MNRAS [Google Scholar]
- Nanni, A., Bressan, A., Marigo, P., & Girardi, L. 2013, MNRAS, 434, 2390 [NASA ADS] [CrossRef] [Google Scholar]
- Nanni, A., Burgarella, D., Theulé, P., Côté, B., & Hirashita, H. 2020, A&A, 641, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayanan, D., Conroy, C., Davé, R., Johnson, B. D., & Popping, G. 2018, ApJ, 869, 70 [Google Scholar]
- Noll, S., Pierini, D., Cimatti, A., et al. 2009, A&A, 499, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Illingworth, G. D., Labbé, I., & Stefanon, M. 2018, ApJ, 855, 105 [Google Scholar]
- Olsen, K., Greve, T. R., Narayanan, D., et al. 2017, ApJ, 846, 105 [Google Scholar]
- Pallottini, A., Ferrara, A., Bovino, S., et al. 2017, MNRAS, 471, 4128 [NASA ADS] [CrossRef] [Google Scholar]
- Pallottini, A., Ferrara, A., Decataldo, D., et al. 2019, MNRAS, 487, 1689 [Google Scholar]
- Pallottini, A., Ferrara, A., Gallerani, S., et al. 2022, MNRAS, 513, 5621 [NASA ADS] [Google Scholar]
- Papovich, C., Dickinson, M., & Ferguson, H. C. 2001, ApJ, 559, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Pforr, J., Maraston, C., & Tonini, C. 2012, MNRAS, 422, 3285 [NASA ADS] [CrossRef] [Google Scholar]
- Popping, G., Narayanan, D., Somerville, R. S., Faisst, A. L., & Krumholz, M. R. 2019, MNRAS, 482, 4906 [Google Scholar]
- Reddy, N. A., Pettini, M., Steidel, C. C., et al. 2012, ApJ, 754, 25 [Google Scholar]
- Reddy, N. A., Kriek, M., Shapley, A. E., et al. 2015, ApJ, 806, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Tacchella, S., Johnson, B. D., et al. 2023, Nat. Astron., 7, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., & Narayanan, D. 2020, ARA&A, 58, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [Google Scholar]
- Salmon, B., Papovich, C., Long, J., et al. 2016, ApJ, 827, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Seon, K.-I., & Draine, B. T. 2016, ApJ, 833, 201 [Google Scholar]
- Shivaei, I., Reddy, N., Rieke, G., et al. 2020, ApJ, 899, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Shivaei, I., Boogaard, L., Díaz-Santos, T., et al. 2022, MNRAS, 514, 1886 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 497, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Carniani, S., et al. 2022a, MNRAS, 517, 5930 [NASA ADS] [CrossRef] [Google Scholar]
- Sommovigo, L., Ferrara, A., Pallottini, A., et al. 2022b, MNRAS, 513, 3122 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1978, Physical processes in the interstellar medium (New York: Wiley) [Google Scholar]
- Stark, D. P. 2016, ARA&A, 54, 761 [Google Scholar]
- Stecher, T. P. 1965, ApJ, 142, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Stratta, G., Maiolino, R., Fiore, F., & D’Elia, V. 2007, ApJ, 661, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Finkelstein, S. L., Bagley, M., et al. 2022, ApJ, 927, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, M., Stark, D. P., Chen, Z., et al. 2023, MNRAS, 526, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2022, Front. Astron. Space Sci., 9, 908217 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., McKee, C. F., Seab, C. G., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Todini, P., & Ferrara, A. 2001, MNRAS, 325, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Topping, M. W., Stark, D. P., Endsley, R., et al. 2022, MNRAS, 516, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Trayford, J. W., Lagos, C. D. P., Robotham, A. S. G., & Obreschkow, D. 2020, MNRAS, 491, 3937 [NASA ADS] [CrossRef] [Google Scholar]
- Tress, M., Ferreras, I., Pérez-González, P. G., et al. 2019, MNRAS, 488, 2301 [NASA ADS] [CrossRef] [Google Scholar]
- Trussler, J. A. A., Adams, N. J., Conselice, C. J., et al. 2023, MNRAS, 523, 3423 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Bianchi, S., & Andersen, A. C. 2009, MNRAS, 397, 1661 [CrossRef] [Google Scholar]
- Vallini, L., Ferrara, A., Pallottini, A., Carniani, S., & Gallerani, S. 2020, MNRAS, 495, L22 [Google Scholar]
- Vallini, L., Ferrara, A., Pallottini, A., Carniani, S., & Gallerani, S. 2021, MNRAS, 505, 5543 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Whitler, L., Stark, D. P., Endsley, R., et al. 2023, MNRAS, 519, 5859 [NASA ADS] [CrossRef] [Google Scholar]
- Witstok, J., Shivaei, I., Smit, R., et al. 2023, Nature, 621, 267 [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Lutz, D., et al. 2011, ApJ, 738, 106 [Google Scholar]
We use the term “dust attenuation” to refer to the process of dust absorption and scattering on the spectrum of a source as a consequence of the presence of dust along the line of sight. Dust attenuation curves depend both on the intrinsic dust properties (chemical composition and grain size distribution) and the distribution of dust with respect to stars (see e.g., Calzetti 2013). When the latter can be described by a background source plus a uniform dust screen, the photon reduction along the line of sight is termed “dust extinction”, which depends only on the intrinsic dust properties. Since the actual distribution of dust and stars in distant or unresolved galaxies is unknown, we compare the dust attenuation curves of our sources both with dust attenuation and extinction curves found in the local and nearby Universe.
We make a distinction between times, t, measured from the beginning of the Universe, and ages, a, measured backward in time from the redshift of the observation zobs so that ti = t(zobs) − ai, following Carnall et al. (2018).
The default −4 < log (U) < −2 range in the built-in model grids in BAGPIPES has been extended in order to cover a wider range of values measured in galaxies at the EoR. For instance, Tang et al. (2023) measured −2.6 < log(U) < −1.3 for a sample of galaxies at z ∼ 7–9, including the three sources analyzed in this paper.
All Tables
Drude model fit parameters for the Calzetti, SMC, MW, and the LMC curves from Li et al. (2008).
Logarithm of the Bayes factor estimates derived comparing the fiducial SED fitting model with the analytical dust curve with and without the bump.
A summary of the constrained physical properties of the three galaxies with different empirical curves used in the SED fitting procedure assuming the fiducial non-parametric SFH model with a continuity prior.
Logarithm of the Bayes factor estimates derived comparing the fiducial fitting model with the analytical dust curve and the models with adopted Calzetti, SMC, and MW curves.
Summary of constrained parameters of the three sources with the SED fitting procedure using different SFH models, assuming the Drude-type dust attenuation model.
All Figures
 |
Fig. 1 Best fit on the SED and the inferred attenuation curves of three galaxies at the EoR. The left panels show the NIRSpec JWST spectrum of s00717 (top), s01143 (middle), and s01149 (bottom) in blue, with flux uncertainties illustrated in pale blue. Orange and pale orange colors indicate the best-fit posterior spectrum with 1σ uncertainties, respectively. Vertical dashed lines mark the prominent detected emission lines and positions of potential lines present in the spectra. In the bottom panel of each plot, we show the residuals of the best fit on the observed spectra, Δfλ, with 1σ uncertainties. The right panels depict the best-fit dust attenuation curves with 1σ uncertainties for s00717, s01143, and s01149 sources, which were obtained using the SED fitting method with the non-parametric SFH model. Drude model fits to the Calzetti, the MW, the SMC, and the LMC empirical curves are shown as green, red, purple, and brown dashed lines, respectively. |
| In the text | |
 |
Fig. 2 Best-fit dust attenuation curves obtained using the SED fitting method with the non-parametric SFH model, for our three sources. The median of the posterior with 1er uncertainties are shown as blue, orange, and pink solid lines with associated shaded regions for s00717, s01143, and s01149, respectively. The 3σ dispersion of the prior is estimated from a 99.7% sample of 1000 random draws from the prior limits for c1 − c4 parameters of the Drude model (gray shaded region). Drude model fits to the Calzetti, the MW, the SMC, and the LMC empirical curves are shown as in Fig. 1. |
| In the text | |
 |
Fig. 3 Comparison of inferred galaxy properties (stellar mass, M*, and SFR, color-coded by the dust attenuation parameter, AV) when adopting one of the empirical curves as a dust law and with the fiducial dust attenuation curve for the three sources. The derived properties of the s00717, s01143, and s01149 galaxies are shown on the left, middle, and right panels, respectively. The relative variation in parameters inferred adopting the Calzetti, the SMC, and MW curves with the fiducial curve are represented as circle, square, and diamond, respectively. |
| In the text | |
 |
Fig. 4 Stellar mass M* and SFR, color-coded by the mass-weighted stellar age |
| In the text | |
 |
Fig. 5 Best-fit dust attenuation curves derived with the SED fitting method, adopting various aforementioned SFH models (solid lines). The attenuation curves of s00717, s01143, and s01149 are shown on the top, middle, and bottom panels, respectively. The 1σ uncertainties of the fiducial SFH model with the continuity prior are shown as blue-shaded regions. Drude model fits to empirical dust curves, frequently adopted as dust attenuation templates in the SED fitting methods are shown for comparison (dashed lines). |
| In the text | |
 |
Fig. A.1 Synthetic dust-attenuated spectra of s01143 source, generated by using the SED fitting method, assuming the fiducial SFH, and adopting one of the empirical dust curves (top-left). The a priori adopted dust curves are the Calzetti attenuation law, and the SMC and the MW extinction curves (from top to bottom panels, respectively). The model spectra of our source are shown in blue, with flux uncertainties illustrated in pale blue. Orange and pale orange colors indicate the best-fit posterior spectra with 1er uncertainties, respectively. Bottom-left panel shows the residuals of the best fit on the synthetic spectra Δfλ with 1σ uncertainties. Right: The corresponding best-fit dust attenuation curve with 1σ uncertainties, on empirical dust curves. Drude model fits to empirical curves: the Calzetti, the SMC, the LMC, and the MW curves are shown as green, red, purple, and brown dashed lines, respectively. |
| In the text | |
 |
Fig. A.2 Corner plot illustrating the 1D and 2D projections of the posterior distribution in the parameter space obtained from the SED fitting on the synthetic spectrum generated by fixing the model parameters to those of the s01143 source, assuming the SMC curve, and a fiducial SFH model. The initial (true) properties of the model galaxy are shown in blue. |
| In the text | |
 |
Fig. B.1 Corner plot illustrating the 1D and 2D projections of the posterior distribution of the parameters derived from the SED fitting on the spectrum of s00717. 1D posterior of the additional properties derived from the SFH (the SFR, the living stellar mass, and the mass-weighted age of the galaxy) and SFH are shown on the right. |
| In the text | |
 |
Fig. B.2 Corner plot illustrating the 1D and 2D projections of the posterior distribution of the parameters derived from the SED fitting on the spectrum of s01143. |
| In the text | |
 |
Fig. B.3 Corner plot illustrating the 1D and 2D projections of the posterior distribution of the parameters derived from the SED fitting on the spectrum of s01149. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.