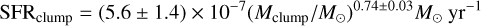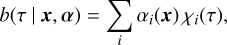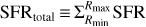EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 678 (October 2023) A&A, 678 (2023) A95 Full HTML
Open Access
Issue
A&A
Volume 678, October 2023
Article Number A95
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202347608
Published online 10 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The formation of stars marks the onset of the conversion of nuclear binding energy into radiative and mechanical energy that is then released into the interstellar medium (McKee & Ostriker 2007; Kennicutt & Evans 2012; Girichidis et al. 2020). Highmass stars regulate the composition, structure, and evolution of the interstellar medium by injecting energy and momentum through supernovae, ionizing photons, and winds (see, for example, Weaver et al. 1977; Krumholz et al. 2014). Thus, understanding the rate and distribution of star formation is crucial for understanding the workings of the Milky Way and other galaxies (see, Klessen & Glover 2016; Ballesteros-Paredes et al. 2020; Tacconi et al. 2020, for recent reviews).

The Milky Way’s star formation rate (SFR) has been estimated using various techniques. Radio free-free emission and [NII] 205 µm emission have been employed to reconstruct the Lyman continuum photon production rate from O stars in the Galactic disk (Smith et al. 1978). Assuming an initial mass function (IMF) of a newly formed generation of stars (Salpeter 1955; Bastian et al. 2010; Lee et al. 2020), these observations lead to SFR estimates of between 2.0 and 2.4 M⊙ yr−1 (Guesten & Mezger 1982; Bennett et al. 1994; McKee & Williams 1997; Murray & Rahman 2010). Robitaille & Whitney (2010) used the census of young stellar objects (YSOs) in the Galactic Legacy Infrared Mid-Plane Survey Extraordinaire (GLIMPSE) survey (Benjamin et al. 2003) to construct a population synthesis model of the Galaxy, which yields an SFR of between 0.68 and 1.45 M⊙ yr−1. Chomiuk & Povich (2011) normalized various estimates for the Galactic SFR to the same IMF and population synthesis models, which results in a global SFR of around 1.9 ± 0.4 M⊙ yr−1. Licquia & Newman (2015) revisited this result and, using a hierarchical Bayesian statistical method, obtained 1.65 ± 0.19 M⊙ yr−1. More recently, estimates of the SFR distribution across the Milky Way’s disk have become more precise thanks to the advent of high-resolution Galactic plane surveys in radio and far-infrared (FIR) frequencies as well as the unprecedented astrometric observations from the Gaia space observatory of the European Space Agency (ESA).

Elia et al. (2022, hereafter E22) derived the Milky Way’s SFR distribution based on the physical properties of clumps identified in the Berschel1 infrared Galactic Plane Survey (Hi-GAL; Molinari et al. 2016). Hi-GAL covered a two-degree-wide strip centered on the midplane of the Galactic disk and registered the emission in 70,160,250,350, and 500 µm wavelengths, which are dominated by the thermal emission from interstellar dust grains. Elia et al. (2017, 2021) identified compact sources in the Hi-GAL multifrequency maps, which were generically denominated as “clumps.”

The Hi-GAL catalog comprises 94604 clumps, 35 186 of which are considered protostellar, that is, at the earliest stage of star formation activity as indicated by their emission at 70 µm wavelength (Elia et al. 2021). Mège et al. (2021) assigned heliocentric kinematic distances to the clumps by using their morphological matching with the radial velocity channels in carbon monoxide (CO) emission surveys and additional information from three-dimensional dust density reconstructions and neutral atomic hydrogen (HI) emission. Using these distance estimates and the emission registered across the Herschel wavelength bands, Elia et al. (2021) computed the clumps’ sizes, masses, bolometric luminosities, and other physical properties.

E22 estimated the SFR for each protostellar clump from an empirical relation between the SFR and the clump mass derived using the method introduced in Veneziani et al. (2013, 2017). The initial hypothesis is that the YSO population is related to the SFR in a clump, an assumption that is justified in nearby clouds by the relatively similar ages inferred from the low spread of YSOs in the Hertzsprung-Russell diagram (Lada et al. 2010). The SFR is determined by combining the number of YSOs, their expected final mass, and their time to reach the main sequence. Models of stellar evolution indicate that a typical timescale estimated for the transition between the YSO phase and the start of the main sequence is roughly between 105 and 106 yr (see, for example, Molinari et al. 2008).

Due to the limited angular resolution, direct YSO counts are limited to the closest sources; thus, the SFR in distant clumps is estimated by applying a phenomenological relation between the YSO counts and the bolometric luminosity obtained in nearby clumps (Veneziani et al. 2013). E22 obtained the relation

SFRclump=(5.6±1.4)×10−7 (Mclump/M⊙)0.74±0.03M⊙ yr−1${\rm{SF}}{{\rm{R}}_{{\rm{clump}}}} = \left( {5.6 \pm 1.4} \right) \times {10^{ - 7}}\,{\left( {{{{M_{{\rm{clump}}}}} \mathord{\left/ {\vphantom {{{M_{{\rm{clump}}}}} {{M_ \odot }}}} \right. \kern-\nulldelimiterspace} {{M_ \odot }}}} \right)^{0.74 \pm 0.03}}{M_ \odot }\,{\rm{y}}{{\rm{r}}^{ - 1}}$(1)

to compute the SFR for 29704 protostellar clumps with reliable distance estimates. The clump SFRs were distributed and summed in a Cartesian grid with 0.5 kpc × 0.5 kpc spaxels to calculate the SFR surface density (∑SFR) distribution and radial profile within galactocentric radius Rgal = 16 kpc.

Wells et al. (2022) present a similar derivation of the Milky Way’s SFR using dense clumps. Their analysis is based on modeling the embedded stellar clusters to obtain bolometric luminosities from their parental dust clumps in mid-infrared and FIR frequencies. The result is a semi-empirical relation between the star formation efficiency and the clump mass, which was applied to obtain the star formation efficiency and SFR from the clumps identified in the 850 µm Atacama Pathfinder Experiment (APEX) telescope Large Area Survey of the Galaxy (ATLASGAL; Schuller et al. 2009; Urquhart et al. 2022). The general SFR trends in Wells et al. (2022) are not dissimilar to those obtained in E22, that is, the decrease in ΣSFR for Rgal > 5 kpc. However, the Galactic longitude range is limited to |l| < 60°, which restricts their reconstruction of the SFR profile to the inner Galaxy, and their clump selection corresponds to a high-density subset of the Hi-GAL sample. Thus, we focus our comparison on the results from E22.

Zari et al. (2023, hereafter Z23) present a map of the stellar age distribution across a 6kpc × 6kpc area of the Galactic disk centered on the Sun that was used to reconstruct the Galaxy’s recent (≤1 Gyr) star formation history. The sample used in Z23 consists of ~500 000 candidate O-, B-, and A-type stars selected in Zari et al. (2021) by combining Gaia Early Data Release 3 photometry and astrometry (Gaia Collaboration 2021) with photometric information from the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006). This sample is restricted to sources with Gaia G-band magnitudes <16 and absolute magnitudes in the 2MASS Ks band of less than zero, which roughly corresponds to a late B-type main-sequence star. Several color cuts were applied to clean the sample of bright red giant-branch and asymptotic giant-branch stars, as well as objects with unnaturally blue colors.

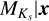Z23 modeled the distribution of absolute magnitudes, MKs${M_{{K_s}}}$, that is, n(MKs|x$\left. {{M_{{K_s}}}} \right|{\bf{x}}$, α), taken as a function of position x in Cartesian heliocentric coordinates with the x-axis oriented in the direction l = 0°. They assumed that at each x there is an underlying age or birthrate distribution, b(τ | x, α), whose temporal dependence is described by a set of parameters, α,

b(τ|x,α)=∑iαi(x) χi(τ),$b\left( {\left. \tau \right|{\bf{x}},{\bf{\alpha }}} \right) = \sum\limits_i {{\alpha _i}\left( {\bf{x}} \right)\,{\chi _i}\left( \tau \right)} ,$(2)

where the index i runs over five approximately logarithmic age bins:5 to 10Myr, 10 to 30Myr, 30 to 100Myr, 100 to 300Myr, and 300 Myr to 1 Gyr. The indicator function χ = 1 if τ is within the limits of the age bin, and χ = 0 otherwise. For each position, x, Z23 compared the observed and predicted 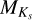MKs${M_{{K_s}}}$ distribution and derived the best-fit birthrate parameters, αbest, by optimizing the likelihood of the data.

Z23 hence derived number- or mass-density maps of mono-age stellar populations in five age bins across the 6 kpc × 6 kpc area of the Galactic disk surrounding the Sun. To derive a spatially resolved SFR, E23 divided the volume into 256 spaxels of different sizes, each containing roughly 1000 stars. They obtained an estimate of the SFR in that portion of the Galactic disk by summing over the entire area considered and multiplying b(τ |αbest) (units of yr−1) by the mean stellar mass derived from their assumed IMF, 〈M〉 = 0.22 M⊙.

In this paper we compare the independent state-of-the-art methods described above to study the recent star formation history of the Milky Way. In Sect. 2, we present the distribution and radial profiles of the SFR surface density (ΣSFR) and the comparison between the results of E22 and Z23. In Sect. 3, we discuss the main differences and similarities between the two estimates. Details on the construction of ΣSFR maps and radial profiles are given in Appendix A.

2 Comparison between ∑SFR estimates

We compared the two methods by distributing the E22 protostellar clumps into the spatial grid introduced in Z23, adding their contributions to the SFR to obtain an SFR for each spaxel. We accounted for the difference in the assumed galactocentric solar orbit radius (R⊙) in E22 (R⊙ = 8.35 kpc) and Z35 (R⊙ = 8.0kpc) by displacing the center of the Z23 SFR reconstruction in the local 6 kpc × 6 kpc to the Sun position in E22. The total SFR from E22 and Z23 in this region is 0.13 ± 0.06 M⊙ yr−1 and 0.28 ± 0.05 M⊙ yr−1, respectively.

We also compared the ΣSFR distributions in two ways. First, we used the Hi-GAL clumps to compute the ΣSFR radial profiles over the whole Galactic plane and for the region considered in Z23. Second, we computed ΣSFR in each spaxel of the grid introduced in Z23, dividing the SFR by the spaxel area.

2.1 ∑SFR radial profiles

We computed the Hi-GAL ΣSFR distribution across the Galactic plane in a polar grid across 1.35 < Rgal < 16.35 kpc, including the radial bins used by Z23, as shown in Fig. 1). We calculated ΣSFR by adding the SFRs from the Hi-GAL clumps in each spaxel and dividing by the area of the spaxel. We employed the clump positions in Galactic coordinates and the heliocentric distances reported in E22’s catalog to compute the galactocentric radius (Rgal) using the astronomical coordinate transformation tools in astropy (Astropy Collaboration 2022). Further details on the population of the grid are provided in Appendix A.

The ΣSFR distribution, presented in Fig. 1, illustrates the significant decrease in ΣSFR with increasing Rgal already identified in E22. It also shows a decrease in ΣSFR of at least one order of magnitude from the lowest to the largest Rgal within the area considered in Z23. The largest ΣSFR values within that area considered in Z23 are concentrated toward the lower-right corner of the region within the yellow rectangle in Fig. 1, which corresponds to the fourth Galactic quadrant for an observer located at the Sun’s position.

We calculated the Galactic ΣSFR radial profiles by binning and adding the SFRs from the Hi-GAL clumps in the radial grid used to construct Fig. 1 and dividing by the area of each annulus. For the local 6 kpc × 6 kpc considered in Z23 (yellow box in Fig. 1), we added the SFRs from the Hi-GAL clumps within the intersection between each annulus and the square patch and divided by the resulting area. The top panel of Fig. 2 shows the radial profiles obtained from the Hi-GAL clumps and the results of Z23 for the age interval 5<τ< 10Myr. We chose this age range since it is the closest to the timescales sampled by the FIR emission. Furthermore, the profiles obtained in other age bins are relatively flat (see Z23).

The global profile derived from the Hi-GAL clumps is around a factor of two below that obtained in Z23, but it shows a similar dependence on Rgal. This profile is particularly dominated by the significantly large ΣSFR shown by both methods for Rgal < 8 kpc. The radial profiles corresponding to the local 6 kpc × 6 kpc region show similar features at different galactocentric radii, as highlighted in the normalized SFR profile shown in the bottom panel of Fig. 2. For Rgal > 7 kpc, both tracers show significantly lower ΣSFR than at smaller Rgal, a bump in ΣSFR around Rgal ≈ 7.8 kpc, and a second bump at Rgal > 7.8 kpc. For Rgal < 7 kpc, both profiles show an increase in ΣSFR and a decrease close to Rgal ≈ 5 kpc. We further explored the structure in the ΣSFR profiles by considering the distribution within the area studied in Z23.

thumbnail Fig. 1

SFR surface density (∑SFR) derived from the Hi-GAL clumps. The yellow rectangle indicates the position of the 6 kpc × 6 kpc area around the Sun studied in Z23.
thumbnail Fig. 2

Profiles of the star formation surface density (∑SFR ; top) and normalized star formation (SFR/SFRtotal, where SFRtotal≡∑RminRmaxSFR${\rm{SF}}{{\rm{R}}_{{\rm{total}}}} \equiv \sum\nolimits_{{R_{{\rm{min}}}}}^{{R_{{\rm{max}}}}} {{\rm{SFR}}} $; bottom) obtained from modeling of the populations of high-mass stars in the age interval 5 <τ< 10Myr (orange; Zari et al. 2023) and the FIR emission from the Hi-GAL clumps (blue and cyan; Elia et al. 2022). The orange and cyan curves, labeled “local,” correspond to the profiles derived from an area of 6 kpc × 6 kpc around the Sun. The blue lines correspond to the profile from the full azimuthal range. The vertical segmented line indicates the assumed position of the Sun. The shaded areas indicate the 16th and 84th percentiles in the Zari et al. (2023) estimates and the upper and lower limits given by Eq. (1) in the E22 estimates.

2.2 Local ∑SFR distribution

We also computed the ΣSFR distribution from the Hi-GAL clumps using the same spatial grid as in Z23. As in the polar grid, we added the SFRs for the clumps in each spaxel and divided them by the spaxel area to obtain ΣSFR. We present the results of the two ΣSFR estimates in Fig. 3.

Figure 3 shows variations of more than an order of magnitude in ΣSFR as a function of position in the Galaxy. Such variations are also observed in nearby spiral galaxies (Kreckel et al. 2018; Sun et al. 2023). They imply that the instantaneous SFR varies dramatically throughout the Galactic disk.

The main similarities between the ΣSFR distributions are found toward well-known high-mass star-forming regions (counterclockwise and starting from the top of Fig. 3): Cygnus (Reipurth & Schneider 2008), the W3/W4/W5 region (Megeath et al. 2008), RCW38 (Wolk et al. 2008), and the Carina Nebula (Smith & Brooks 2008). The agreement is also good in the relatively high ΣSFR toward the M16, M17, M20, and Gem OB1 regions. The latter agreement is particularly notable since the uncertainty in the kinematic distances is particularly acute toward the Galactic center and anticenter.

Figure 4 shows the ratio of the two star formation surface density estimates 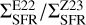ΣSFRE22/ΣSFRZ23${{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} \mathord{\left/ {\vphantom {{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}} \right. \kern-\nulldelimiterspace} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}$ across the local patch presented in Fig. 3. The ΣSFRE22/ΣSFRZ23${{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} \mathord{\left/ {\vphantom {{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}} \right. \kern-\nulldelimiterspace} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}$ distribution indicates that the ΣSFR estimates from Z23 are larger in most of the spaxels. There are, however, some regions where the ΣSFR from E22 are the largest, for example, toward the lower-left quadrant of the local patch (fourth Galactic quadrant).

The values of 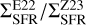ΣSFRE22/ΣSFRZ23${{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} \mathord{\left/ {\vphantom {{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}} \right. \kern-\nulldelimiterspace} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}$ shown in Fig. 4 appear to be consistently lower toward higher Rgal. Yet, there is no global trend in the distribution of the ratio, and regions at roughly the same Rgal show either 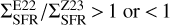ΣSFRE22/ΣSFRZ23>1 or <1${{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} \mathord{\left/ {\vphantom {{\Sigma _{{\rm{SFR}}}^{{\rm{E22}}}} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}}} \right. \kern-\nulldelimiterspace} {\Sigma _{{\rm{SFR}}}^{{\rm{Z23}}}}} > 1\,{\rm{or}}\,{\rm{ &gt; 1}}$, particularly for Rgal < 8 kpc. In the following section we discuss whether physical or systematic effects cause these differences.

thumbnail Fig. 3

SFR surface density (∑SFR) obtained from the Hi-GAL clumps (left) and modeling of the high-mass stellar population (right) in a 6 kpc × 6 kpc area centered on the Sun (indicated with the yellow star). The labels give the positions of the sources in the “Handbook of Star-Forming Regions” (Reipurth 2008a,b) with the distances estimated in Zucker et al. (2020). The dashed lines correspond to galactocentric circles with the indicated radii.

3 Discussion

We have presented ΣSFR as derived from the Hi-GAL clumps and the distribution of the high-mass stars, focusing on the end product of the two observational methods. In this section, we discuss whether the differences between the two estimates are explained by a systematic effect introduced by the underlying assumptions in either method or whether they reveal further physical insights into the dynamics of star formation in the Galactic plane.

3.1 Why the ∑SFR distributions are similar

The agreement between the ΣSFR profiles reported in Fig. 2 is noteworthy, given the differences in the observed quantities and the underlying assumptions involved in the two methods. However, this similarity is not entirely unexpected.

The molecular gas mass surface density (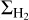ΣH2${{\rm{\Sigma }}_{{{\rm{H}}_2}}}$) traced by CO shows a sharp increase toward the inner Galaxy, reaching a peak value around 4 < Rgal < 5 kpc (see, for example, Heyer & Dame 2015; Miville-Deschênes et al. 2017; Riener et al. 2020). The star formation surface density is also expected to increase toward the inner Galaxy, directly following the strong correlation between ΣSFR and 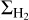ΣH2${{\rm{\Sigma }}_{{{\rm{H}}_2}}}$ observed toward nearby disk galaxies (see, for example, Kennicutt 1989; Schruba et al. 2011; Leroy et al. 2013). Hence, it is expected that ΣSFR increases at small Rgal

Z23 concluded that the Milky Way’s SFR increased during the past 10 Myr. Thus, it is foreseeable that the more recent SFR traced by the Hi-GAL clumps follows a similar distribution. If we assume that the difference between the two ΣSFR profiles in Fig. 2 has a physical origin, it would mean that the Milky Way SFR peaked between 5 and 10 Myr ago and has since slightly decreased. Yet, there are many systematic effects that may reconcile the two estimates without implying a change in the star formation history, as we discuss below.

thumbnail Fig. 4

Ratio between the ΣSFR estimates derived in E22 and Z23.

3.2 Why the ΣSFR values are different

The underlying assumptions in the estimation of ΣSFR are likely explanations for the factor of around two separating the total SFR and the ΣSFR profiles in Fig. 2. On the Hi-GAL clump SFR estimate, these assumptions include the use of kinematic distances, the selection of the dust properties to reconstruct masses from FIR emission, and the phenomenological model used to map masses into SFR. On the high-mass stellar population modeling, these assumptions include the adopted completeness of the sample and the choice of IMF.

The kinematic distances of the Hi-GAL clumps are derived by matching their emission to a particular component of CO emission (Mège et al. 2021). If the clump is on a circular orbit following a Galactic rotation model, the velocity with respect to the local standard of rest (υLSR) uniquely identifies the clump’s Rgal (see, for example, Wenger et al. 2018). This means that clumps close to the Galactic center or anticenter, where the radial component of the rotational motion is minimum, will have large uncertainties in their kinematic distances. Moreover, non-radial motions, such as those arising from supernova explosions or spiral arm shocks, will affect the location of clumps based on kinematic distances (see, for example, Burton 1971; Peek et al. 2022; Hunter et al., in prep.). The ΣSFR estimates from Z23 do not depend on kinematic distances but from Gaia parallaxes. Thus, because the two profiles in Fig. 2 are offset in ΣSFR rather than displaced in Rgal, it is likely that the kinematic distances are not critical for the global reconstruction of the SFR.

The SFR from the Hi-GAL clumps depends on the mass estimates, which were obtained using the source size, assumed distance, emission optical depth (τ), and dust opacity (κ) (Eq. (3) in Elia et al. 2017). The value of τ is usually parametrized as a power law with spectral index ß. Following the Herschel observations in nearby clouds regions (Sadavoy et al. 2013; Könyves et al. 2015), E22 adopted the reference value ß = 2. However, variations of ß between 1.8 and 2.6 have been inferred from Herschel observations toward the Galactic plane (Paradis et al. 2010). An increase in the assumed values of ß would push toward higher masses and higher SFRs, consequently closing the gap between the results of E22 and Z23. Yet, the selection of a single high ß for all the clumps is not justified by the observational evidence (see, for example, Planck Collaboration XI2014).

E22 set κ to a reference value at 300 µm, κ300 = 0.1 cm2 g−1, which includes the underlying assumption of a dust-to-gas ratio γ = 100 (Beckwith et al. 1990). Dust models indicate k values that span from κ300 = 0.13 cm2 g−1 in Ossenkopf & Henning (1994) to one of magnitude lower in Draine & Li (2007). Assuming a lower value of κ within the current observational limits is enough to reconcile the offset in Fig. 2. Fluctuations in κ are expected from the variety of physical conditions among the clumps, but it is unlikely that they conspire to make κ systematically lower than the reference value used in E22 and solely explain the offset in the ΣSFR profiles.

The phenomenological relation in Eq. (1) was obtained using plausible but coarse assumptions about the evolution between the protostellar phase and the start of the main sequence (Molinari et al. 2008). Assuming longer (shorter) timescales leads to an underestimation (overestimation) of the SFR. A shorter timescale would reconcile the ΣSFR profiles, although there is no observational evidence that would justify this choice.

Figure 3 shows that the ΣSFR as derived from the Hi-GAL clumps is lower than ΣSFR as derived from high-mass stars. The difference is more pronounced outside of the known star-forming regions. The spaxels showing good agreement most likely correspond to regions where the massive stars and YSOs coexist, while the spaxels with the largest differences correspond to regions with less dust and more stars.

The minimum mass recovered with the Hi-GAL survey is limited by the sensitivity of the Herschel instruments. This means that in regions of the sky with low FIR emission, the masses and SFRs derived from the Hi-GAL observations are underestimated. This may be the case toward the highest Rgal regions and the lower-left quadrant in Fig. 3 and the area between the W3/W4/W5 complex and Cygnus X. Additionally, the catalog used in E22 includes only “cold” clumps, that is, objects with reliable spectral energy density between 160 and 500 µm, from which their mass is derived. Multiple 70 µm-, 70 and 160 µm-, and 70, 160, and 250 µm-only sources are excluded from the SFR tally. Furthermore, the 70 µm emission employed to determine whether or not a clump is protostellar, and thus its inclusion in the SFR calculation, is an “on-off switch”; clumps with 70 µm emission close or below the detection limit are also excluded. Finally, clumps without reliable heliocentric distances are also not included. These omitted sources could account for an additional 20% to the global Galactic SFR, as estimated using random distance realizations (see Sect. 2.2.1 in Elia et al. 2022).

The discrepancy between the two ΣSFR estimates can also be caused by the fact that some O-, B-, and A-type stars might have moved from their birthplaces and populated the regions where the Hi-GAL emission is low, a hypothesis that is supported by the current observational evidence. The velocity dispersion of YSOs in the Orion high-mass star formation region is around 5 kms−1, which corresponds to an average displacement of roughly 50 pc in 10Myr (Großschedl et al. 2021). Furthermore, stars in the Galactic disk deviate from their birth orbits and experience radial migration and vertical heating.

Although based on older stars, the model of the secular evolution of the Milky Way disk presented in Frankel et al. (2020) indicates that the expected radial migration close to the solar circle in 10 Myr is around 100 pc. This is further supported by recent hydrodynamical simulations presented in Fujimoto (2023), where the numerical experiment set up to investigate the effect of gravitational interactions between giant molecular clouds (GMCs) and young stars in a Galactic disk analog indicates that GMCs efficiently scatter newborn stars in the first several hundred Myr after the stellar birth (see their Fig. 7). Moreover, observations of nearby spiral galaxies suggest that GMCs exist for less than roughly 5 Myr after the onset of massive star formation (see, for example, Kim et al. 2022). Together, these pieces of evidence suggest that the 5–10 Myr old OB stars should be located in different places than the ongoing star formation and thus partly explain why there is not a tighter agreement between the ΣSFR distribution presented in Fig. 3.

Finally, the choice of the IMF employed to model the stellar birth rate in Z23 can globally reconcile the profiles in Fig. 2. Since their sample is predominantly composed of massive stars, of which most are in unresolved binaries, Z23 used a four-component broken power law that accounts for unresolved binaries from Kroupa (2002). However, a two-component broken power law with Γ = 1.3 for masses between 0.1 and 0.5 M⊙ and Γ = 2.3 for masses between 0.5 and 100 M⊙ (Kroupa & Weidner 2003), leads to much better agreement with the E22 ∑SFR profile, as we show in Appendix B. This agreement does not justify the selection of a two-component IMF, but illustrates the quantitative agreement between the ΣSFR profiles within the range of assumptions of both observational methods.

4 Conclusions

We have presented a comparison of the Milky Way’s ΣSFR spatial distribution and radial profile inferred from two independent observational methods: the modeling of high-mass stellar populations and the FIR dust thermal emission from the clumps of the Hi-GAL survey. The two estimates show good agreement in the radial ΣSFR profile, within a factor of two, and considerable agreement in the SFR distribution within the 6kpc×6kpc area around the Sun. The factor of two separating the SFR estimates can be easily accounted for by the assumptions underlying the two methods. Together, these results indicate that the timescales of star formation sampled by each method are similar and suggest that the local SFR in the past 10 Myr has been approximately constant.

The agreement between the two independent SFR estimates presented here supports the robustness of both SFR reconstructions. The Hi-GAL results suggest that the conclusions drawn from the local populations of high-mass stars can be extended to the rest of the Galaxy. The outcome of the high-mass stellar population modeling indicates that the analysis of the dust thermal emission is not critically affected by the assumption of kinematic distances and dust properties. Given the difficulties derived from our position within the Galaxy, the agreement between these two estimates is comparable to characters in the parable of blind people encountering an elephant2 and agreeing with each other on their observations. In this case, the observations constitute a crucial hint about the workings of the Milky Way and a significant point of comparison with other nearby spiral galaxies.

Acknowledgements

J.D.S., S.M., C.M., R.S.K., P.H., S.C.O.G., and T.C. acknowledge funding by the European Research Council via the ERC Synergy Grant “ECOGAL – Understanding our Galactic ecosystem: From the disk of the Milky Way to the formation sites of stars and planets” (project ID 855130). R.S.K. and S.C.O.G. furthermore acknowledge funding from the German Excellence Strategy via the Heidelberg Cluster of Excellence (EXC 2181 - 390900948) “STRUCTURES” and from the German Ministry for Economic Affairs and Climate Action in project “MAINN” (funding ID 50OO2206). The team in Heidelberg also thanks for the computing resources provided by The Land and DFG through grant INST 35/1134-1 FUGG and for data storage at SDS@hd through grant INST 35/1314-1 FUGG. This project was partly developed at the Heidelberg-Harvard Star Formation workshop held in Heidelberg, Germany, in December 2022 and at the Lorentz Center workshop “Mapping the Milky Way”, held in Leiden, Netherlands, in February 2023. The authors acknowledge Interstellar Institute’s program “II6” and the Paris-Saclay University’s Institut Pascal for hosting discussions that nourished the development of the ideas behind this work. We thank the anonymous referee for the insightful comments that improved the quality of this paper. We also thank James Urquhart for his guidance through the ATLASGAL papers. J.D.S. thanks the following people who helped with their encouragement and conversation: João Alves, Henrik Beuther, Neal J. Evans II, Alyssa Goodman, Josefa Großschedl, Marc-Antoine Miville-Deschênes, Cameren Swiggum, and Catherine Zucker.

Appendix A Construction of radial profiles

In this appendix we present some of the quantities involved in the calculation of the ΣSFR radial profiles and maps presented in the main body of this paper. Figure A.1 shows the number of E22 clumps distributed in the polar grid presented in Fig. 1 and the maps in Fig. 3. We computed ΣSFR by adding the contributions derived from Eq. 1 for the clumps in each spaxel. For comparison, we present in Fig. A.2 the sum of the clump masses in each spaxel for the Galactic polar and Z23 grids.

thumbnail Fig. A.1

Number of Hi-GAL clumps in the polar and Cartesian grids presented in Figs. 1 and 3.

Appendix B Effect on the IMF selection

We considered the results of an alternative IMF selection in the modeling of the high-mass stellar population by employing a two-component broken power law with Γ = 1.3 for masses between 0.1 and 0.5 M⊙ and Γ = 2.3 for masses between 0.5 and 100 M⊙ (Kroupa & Weidner 2003). The results, presented in Fig. B.1, are much closer to the E22 ΣSFR profile. However, this selection of IMF does not account for unresolved binaries, which comprise a large portion of the objects in the Z23 source catalog.

thumbnail Fig. A.2

Total mass in Hi-GAL clumps in the polar and Cartesian grids presented in Figs. 1 and 3.
thumbnail Fig. B.1

Same as Fig. 2, but for a two-component broken-power-law IMF.

References

  1. Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ballesteros-Paredes, J., André, P., Hennebelle, P., et al. 2020, Space Sci. Rev., 216, 76 [Google Scholar]
  3. Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [Google Scholar]
  4. Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [Google Scholar]
  5. Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [Google Scholar]
  6. Bennett, C. L., Fixsen, D. J., Hinshaw, G., et al. 1994, ApJ, 434, 587 [NASA ADS] [CrossRef] [Google Scholar]
  7. Burton, W. B. 1971, A&A, 10, 76 [NASA ADS] [Google Scholar]
  8. Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [Google Scholar]
  9. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
  10. Elia, D., Molinari, S., Schisano, E., et al. 2017, MNRAS, 471, 100 [NASA ADS] [CrossRef] [Google Scholar]
  11. Elia, D., Merello, M., Molinari, S., et al. 2021, MNRAS, 504, 2742 [NASA ADS] [CrossRef] [Google Scholar]
  12. Elia, D., Molinari, S., Schisano, E., et al. 2022, ApJ, 941, 162 [NASA ADS] [CrossRef] [Google Scholar]
  13. Frankel, N., Sanders, J., Ting, Y.-S., & Rix, H.-W. 2020, ApJ, 896, 15 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fujimoto, Y., Inutsuka, S.-I., & Baba, J. 2023, MNRAS, 523, 3049 [Google Scholar]
  15. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Girichidis, P., Offner, S. S. R., Kritsuk, A. G., et al. 2020, Space Sci. Rev., 216, 68 [NASA ADS] [CrossRef] [Google Scholar]
  17. Großschedl, J. E., Alves, J., Meingast, S., & Herbst-Kiss, G. 2021, A&A, 647, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Guesten, R., & Mezger, P. G. 1982, Vistas Astron., 26, 159 [Google Scholar]
  19. Heyer, M., & Dame, T. M. 2015, ARA&A, 53, 583 [Google Scholar]
  20. Kennicutt, R. C. Jr. 1989, ApJ, 344, 685 [CrossRef] [Google Scholar]
  21. Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kim, J., Chevance, M., Kruijssen, J. M. D., et al. 2022, MNRAS, 516, 3006 [NASA ADS] [CrossRef] [Google Scholar]
  23. Klessen, R. S., & Glover, S. C. O. 2016, in Saas-Fee Advanced Course, 43, Saas-Fee Advanced Course, ed. Y. Revaz, P. Jablonka, R. Teyssier, & L. Mayer, 85 [NASA ADS] [CrossRef] [Google Scholar]
  24. Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [Google Scholar]
  25. Kreckel, K., Faesi, C., Kruijssen, J. M. D., et al. 2018, ApJ, 863, L21 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
  27. Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
  28. Krumholz, M. R., Bate, M. R., Arce, H. G., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 243 [Google Scholar]
  29. Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [Google Scholar]
  30. Lee, Y.-N., Offner, S. S. R., Hennebelle, P., et al. 2020, Space Sci. Rev., 216, 70 [NASA ADS] [CrossRef] [Google Scholar]
  31. Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [Google Scholar]
  32. Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
  33. McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [Google Scholar]
  34. McKee, C. F., & Williams, J. P. 1997, ApJ, 476, 144 [CrossRef] [Google Scholar]
  35. Mège, P., Russeil, D., Zavagno, A., et al. 2021, A&A, 646, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Megeath, S. T., Townsley, L. K., Oey, M. S., & Tieftrunk, A. R. 2008, in Handbook of Star Forming Regions, Volume I, 4, ed. B. Reipurth, 264 [NASA ADS] [Google Scholar]
  37. Miville-Deschênes, M.-A., Murray, N., & Lee, E. J. 2017, ApJ, 834, 57 [Google Scholar]
  38. Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Molinari, S., Schisano, E., Elia, D., et al. 2016, A&A, 591, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Murray, N., & Rahman, M. 2010, ApJ, 709, 424 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
  42. Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, A8 [Google Scholar]
  43. Peek, J. E. G., Tchernyshyov, K., & Miville-Deschenes, M.-A. 2022, ApJ, 925, 201 [NASA ADS] [CrossRef] [Google Scholar]
  44. Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Reipurth, B. 2008a, Handbook of Star Forming Regions, Volume I: The Northern Sky, 4 [Google Scholar]
  46. Reipurth, B. 2008b, Handbook of Star Forming Regions, Volume II: The Southern Sky, 5 [Google Scholar]
  47. Reipurth, B., & Schneider, N. 2008, in Handbook of Star Forming Regions, Volume I, 4, ed. B. Reipurth, 36 [NASA ADS] [Google Scholar]
  48. Riener, M., Kainulainen, J., Henshaw, J. D., & Beuther, H. 2020, A&A, 640, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Robitaille, T. P., & Whitney, B. A. 2010, ApJ, 710, L11 [NASA ADS] [CrossRef] [Google Scholar]
  50. Sadavoy, S. I., Di Francesco, J., Johnstone, D., et al. 2013, ApJ, 767, 126 [Google Scholar]
  51. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  52. Saxe, J. 1868, The Poems of John Godfrey Saxe: Complete in One Volume (Ticknor and Fields) [Google Scholar]
  53. Schruba, A., Leroy, A. K., Walter, F., et al. 2011, AJ, 142, 37 [NASA ADS] [CrossRef] [Google Scholar]
  54. Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  56. Smith, N., & Brooks, K. J. 2008, in Handbook of Star Forming Regions, Volume II, 5, ed. B. Reipurth, 138 [NASA ADS] [Google Scholar]
  57. Smith, L. F., Biermann, P., & Mezger, P. G. 1978, A&A, 66, 65 [NASA ADS] [Google Scholar]
  58. Sun, J., Leroy, A. K., Ostriker, E. C., et al. 2023, ApJ, 945, L19 [NASA ADS] [CrossRef] [Google Scholar]
  59. Tacconi, L. J., Genzel, R., & Sternberg, A. 2020, ARA&A, 58, 157 [NASA ADS] [CrossRef] [Google Scholar]
  60. Urquhart, J. S., Wells, M. R. A., Pillai, T., et al. 2022, MNRAS, 510, 3389 [NASA ADS] [CrossRef] [Google Scholar]
  61. Veneziani, M., Elia, D., Noriega-Crespo, A., et al. 2013, A&A, 549, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Veneziani, M., Schisano, E., Elia, D., et al. 2017, A&A, 599, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [Google Scholar]
  64. Wells, M. R. A., Urquhart, J. S., Moore, T. J. T., et al. 2022, MNRAS, 516, 4245 [NASA ADS] [CrossRef] [Google Scholar]
  65. Wenger, T. V., Balser, D. S., Anderson, L. D., & Bania, T. M. 2018, ApJ, 856, 52 [Google Scholar]
  66. Wolk, S. J., Bourke, T. L., & Vigil, M. 2008, in Handbook of Star Forming Regions, Volume II, 5, ed. B. Reipurth, 124 [NASA ADS] [Google Scholar]
  67. Zari, E., Rix, H. W., Frankel, N., et al. 2021, A&A, 650, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Zari, E., Frankel, N., & Rix, H.-W. 2023, A&A, 669, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2020, A&A, 633, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
1

Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.

2

“It was six men oflndostan To learning much inclined, Who went to see the Elephant (Though all ofthem were blind), That each by observation Might satisfy his mind… ” (Saxe 1868).

All Figures

thumbnail Fig. 1

SFR surface density (∑SFR) derived from the Hi-GAL clumps. The yellow rectangle indicates the position of the 6 kpc × 6 kpc area around the Sun studied in Z23.
In the text
thumbnail Fig. 2

Profiles of the star formation surface density (∑SFR ; top) and normalized star formation (SFR/SFRtotal, where SFRtotal≡∑RminRmaxSFR${\rm{SF}}{{\rm{R}}_{{\rm{total}}}} \equiv \sum\nolimits_{{R_{{\rm{min}}}}}^{{R_{{\rm{max}}}}} {{\rm{SFR}}} $; bottom) obtained from modeling of the populations of high-mass stars in the age interval 5 <τ< 10Myr (orange; Zari et al. 2023) and the FIR emission from the Hi-GAL clumps (blue and cyan; Elia et al. 2022). The orange and cyan curves, labeled “local,” correspond to the profiles derived from an area of 6 kpc × 6 kpc around the Sun. The blue lines correspond to the profile from the full azimuthal range. The vertical segmented line indicates the assumed position of the Sun. The shaded areas indicate the 16th and 84th percentiles in the Zari et al. (2023) estimates and the upper and lower limits given by Eq. (1) in the E22 estimates.
In the text
thumbnail Fig. 3

SFR surface density (∑SFR) obtained from the Hi-GAL clumps (left) and modeling of the high-mass stellar population (right) in a 6 kpc × 6 kpc area centered on the Sun (indicated with the yellow star). The labels give the positions of the sources in the “Handbook of Star-Forming Regions” (Reipurth 2008a,b) with the distances estimated in Zucker et al. (2020). The dashed lines correspond to galactocentric circles with the indicated radii.
In the text
thumbnail Fig. 4

Ratio between the ΣSFR estimates derived in E22 and Z23.
In the text
thumbnail Fig. A.1

Number of Hi-GAL clumps in the polar and Cartesian grids presented in Figs. 1 and 3.
In the text
thumbnail Fig. A.2

Total mass in Hi-GAL clumps in the polar and Cartesian grids presented in Figs. 1 and 3.
In the text
thumbnail Fig. B.1

Same as Fig. 2, but for a two-component broken-power-law IMF.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.