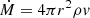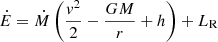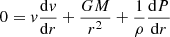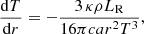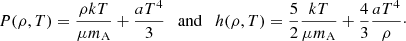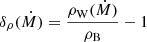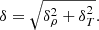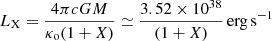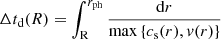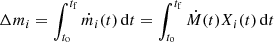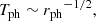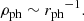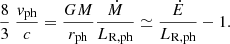| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A156 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346190 | |
| Published online | 17 October 2023 | |
Mass-loss and composition of wind ejecta in type I X-ray bursts
1
Departament de Física, EEBE, Universitat Politècnica de Catalunya, c/Eduard Maristany 16, 08019 Barcelona, Spain
2
Institut d’Estudis Espacials de Catalunya, c/Gran Capità 2-4, Ed. Nexus-201, 08034 Barcelona, Spain
3
Institute of Space Sciences, c/Can Magrans, 08193 Cerdanyola del Vallès, Barcelona, Spain
e-mail: herrera@ice.csic.es
Received:
20
February
2023
Accepted:
5
May
2023
Context. X-Ray bursts (XRBs) are powerful thermonuclear events on the surface of accreting neutron stars (NSs) where nucleosynthesis of intermediate-mass elements occurs. The high surface gravity of an NS prevents the ejection of material by the XRB thermonuclear explosion. However, the predicted and observed XRB luminosities sometimes exceed Eddington’s value, and some of the material may escape by means of stellar wind.
Aims. This work aims to determine the mass-loss and chemical composition of the material ejected through radiation-driven winds and its significance for Galactic abundances. It also reports on the evolution of observational quantities during the wind phase, which can help constrain the mass-radius relation in NSs.
Methods. A non-relativistic radiative wind model was implemented, with modern opacity tables and treatment of the critical point, and linked through a new technique to a series of XRB hydrodynamic simulations that include over 300 isotopes. This allowed us to construct a quasi-stationary time evolution of the wind during the XRB.
Results. In the models we studied, the total mass ejected by the wind was about 6 × 1019 g; the average ejected mass per burst represented 2.6% of the accreted mass between bursts, with 0.1% of the envelope mass ejected per burst; and approximately 90% of the ejecta was composed by 60Ni, 64Zn, 68Ge, and 58Ni. The ejected material also contained a small fraction (10−4 − 10−5) of some light p-nuclei, but not enough to account for their Galactic abundances. Additionally, the observable magnitudes during the wind phase showed remarkable correlations, partly due to the fact that photospheric luminosity stays close to the Eddington limit. Some of these correlations involve wind parameters, such as energy and mass outflows, that are determined by the conditions at the base of the wind envelope.
Conclusions. The simulations resulted in the first realistic quantification of mass-loss for each isotope synthesized in the XRB. The photospheric correlations we found could be used to link observable magnitudes to the physics of the innermost parts of the envelope, close to its interface with the NS crust. This is a promising result regarding the issue of NS radius determination.
Key words: X-rays: bursts / stars: winds / outflows / stars: neutron / Galaxy: abundances / stars: mass-loss / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Type I X-ray bursts (XRBs) are highly energetic and recurrent thermonuclear events occurring in the envelope of accreting neutron stars (NSs) in binary systems where the secondary star is usually a main sequence star or red giant. Most observed XRBs have short orbital periods in the range of 0.2−15 h1. As a result, the secondary star overfills its Roche lobe, and mass transfer ensues through the inner Lagrangian point (L1) of the system. The material stripped from the secondary star has angular momentum such that it forms an accretion disk around the NS. Viscous forces progressively remove angular momentum from the disk, forcing the material to spiral in and pile up on top of the NS. The accreted material accumulates under mildly degenerate conditions, driving a temperature increase and the onset of nuclear reactions. As a result, a thermonuclear runaway occurs, generating a massive luminosity increase as well as nucleosynthesis of intermediate-mass elements, mostly around A = 64 (see, e.g., Woosley et al. 2004; Fisker et al. 2008; José et al. 2010). The presence of such elements can, in principle, be detected (see Bildsten et al. 2003; Chang et al. 2005, 2006; Weinberg et al. 2006) in the form of gravitationally redshifted absorption features in the spectrum, which mostly lies in the X-ray range. (For further information on XRBs, see Strohmayer & Bildsten 2006; Keek & in’t Zand 2008; Galloway et al. 2008; José 2016).
A typical NS (MNS ∼ 1.4 M⊙, RNS ∼ 10 km) has a strong surface gravity that allows only a limited envelope expansion before the nuclear fuel is consumed. However, for some accretion rate values, a considerable photospheric radius expansion (PRE) takes place. In these cases, the luminosity can approach, or even exceed, the Eddington limit in the outer layers of the expanded envelope, which may lead to the ejection of some material through a radiation-driven wind (see Herrera et al. 2020, and references therein). The potential impact of XRBs on the Galactic abundances is still a matter of debate.
Additionally, the study of XRB wind can lead to a more accurate determination of the radii of NSs. Several theoretical mass-radius relations are available for NSs, depending on the choice of equation of state when modeling their inner structure (see Lattimer & Prakash 2006). Thus, accurate measurements of NS masses and radii, taken independently, are needed to test the validity of these theoretical models. Neutron star masses, for instance, can be determined from bolometric luminosities during XRBs with significant envelope expansion (assuming the maximum corresponds to the Eddington limit). The radius is more difficult to measure, and methods that have been proposed carry varied sensitivity to systematic errors (see Damen et al. 1990; Steiner et al. 2010; Güver et al. 2012; Sala et al. 2012). A detailed study of the NS envelope evolution during XRBs, which includes stellar wind features, can bring more light to this matter.
Motivated by the aforementioned unanswered questions and by the new possibilities brought by recent technical advancements, the interest of the scientific community in stellar winds in the context of XRBs has been renewed. For instance, Yu & Weinberg (2018) used MESA code (see Paxton et al. 2011) to perform a hydrodynamic simulation of the wind after the Eddington limit was reached during a hydrostatic burst, and Guichandut et al. (2021) studied the transition from static expanded envelopes to radiatively driven stellar wind and discussed the applicability of steady-state wind models during XRBs. The results from our simulations of radiative winds applied to a generic NS scenario were published in Herrera et al. (2020). There, the focus was set on the exploration of parameter space, the characterization of different types of solutions and their self-consistency with model hypotheses, and analysis of possible predictions related to observable variables, paving the road for the application of the wind models to a more complex XRB scenario.
In this work, we applied the stellar wind model, implemented through a simulation code entirely developed for the present work, to the physical conditions of type I XRBs. We proceeded toward this goal by matching numerical solutions of the stellar wind model to a set of XRB hydrodynamic models (José et al. 2010). This way, we could obtain physical predictions about the evolution of the entire neutron star atmosphere, including both the nuclear burning shells and the expanded wind envelope. On one hand, this allowed us to study the evolution of the observable magnitudes in more realistic conditions and their relation to such parameters as NS mass and radius, potentially leading to the development of better measuring techniques. And, on the other hand, we could obtain the composition of the envelope layers blown by the wind. This allowed us to study the possible contribution of XRBs to Galactic abundances.
This work is organized as follows. In Sect. 2, a summarized description of both stellar wind and XRB hydrodynamic models is followed by an account of the methods employed to match them. An analysis of the results obtained in our best matching model, including the wind-related mass-loss and its contribution of key isotope species to galactic abundances, as well as the impact on observable features, is shown in Sect. 3. Finally, the significance of our results and our main conclusions are summarized in Sect. 4.
2. Models, input physics, and methods
Our objective was to determine if the physical conditions given by the XRB hydrodynamic models are suitable for a stellar wind to appear at some point during the evolution of the burst. In other words, we wanted to find if there is a compatible match in physical variables between the possible wind profiles obtained as solutions of the model developed in Herrera et al. (2020) and the boundary values taken as a result from the XRB hydrodynamic models developed by José et al. (2010; and unpublished data). These extra boundary conditions can constrain the free parameters in the wind model (see Sect. 2.1), and could be used to determine a unique wind profile at each time in the XRB evolution, if a solution exists. We worked under the assumption that the chemical composition of the whole wind envelope is determined by the XRB hydrodynamic models at the matching point for each time step. That is, we re-compute wind profiles by adjusting all their free parameters (including mean molecular mass) to match those resulting from the hydrodynamic model at each time step (see Sect. 2.3). If successful, the ultimate goal is to study the consequent mass-loss and predicted observable magnitudes.
An important aspect to take into consideration was the fact that wind and XRB models differ in some key features and basic hypotheses. For instance, the wind model describes a stationary regime, while XRB models are time dependent. However, if the evolution of the XRB conditions is slow enough, under some criteria, a matching sequence of steady wind solutions can still be considered a good quasi-stationary approximation. Additionally, convective energy transport, degenerate matter contributions to the equation of state, and energy generation by nuclear reactions were also only considered in the XRB hydrodynamic models, since they were not necessary for wind models. These issues are taken into consideration when assessing the validity of the results.
In the following subsections, we first summarize the relevant features of both stellar wind (Sect. 2.1) and XRB hydrodynamic models (Sect. 2.2). The model matching technique is then described in Sect. 2.3.
2.1. Stellar wind model
The simulations reported in this work rely on a stationary, non-relativistic wind model with spherical symmetry. The radiation-driven wind, treated as a fully ionized perfect gas, was assumed to be optically thick and in local thermodynamic equilibrium (LTE) with radiation. In this framework, the basic hydrodynamic equations for mass (1), energy (2), momentum conservation (3), and radiative energy transport (4) become:
where the variables r, T, v, ρ, LR stand for the radial coordinate, temperature, wind velocity, gas density, and radiative luminosity, respectively. The total pressure, P, and specific enthalpy, h, include the contributions of gas and radiation in the form:
In this work, the opacity, κ, was taken from OPAL (Iglesias & Rogers 1996) and The Opacity Project (Seaton et al. 1994), and it is a function of temperature, density, and composition of the gas only2.
From the mass and energy conservation laws, the total mass and energy outflows (Ṁ, Ė) arise as integration constants and can be determined by imposing extra conditions at the base of the wind. Therefore, Ṁ and Ė can be considered free model parameters. During an XRB, these parameters vary in time, but in a quasi-stationary approach, they are assumed to be approximately constant across the wind for a fixed time. The mass of the NS core, M, is another model parameter that was considered fixed in this work, and it constitutes the only relevant source of gravity (the contribution of the envelope mass can be neglected). Lastly the mean molecular mass, μ, is a function of the mass fractions Xi of the different species present in the envelope. The rest of the symbols have their usual meaning: G for gravitational constant, c for speed of light, k for Boltzmann constant, 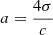 for radiation energy density constant (σ is the Stefan–Boltzmann constant), and mA for atomic mass unit.
for radiation energy density constant (σ is the Stefan–Boltzmann constant), and mA for atomic mass unit.
Two boundary conditions are required to solve the system of two first-order differential Eqs. (3) and (4). These conditions are normally given at the photosphere (usual for any stellar envelope, but with a slight difference for winds) and at a critical point (for stellar wind solutions with non-zero velocity at large radii).
As stated before, an extra set of boundary conditions can be set to fix the value of the free model parameters Ṁ and Ė, adjusting the resulting solution to describe different physical scenarios. In Herrera et al. (2020), we explored a subset of possible wind solutions that are compatible with a very general boundary condition expected at the base of the envelope for NSs with radii lying within a wide possible range (7 − 20 km)3. For a particular NS radius of 13 km, we found that a sequence of solutions aligned in the parameter space, with correlated energy and mass outflows. Although these values were within the expected ranges for an XRB, no specification was made as to whether these solutions correspond to actual XRB conditions or how they evolve in time. In this work, we want to connect the stellar wind models to a more realistic burst scenario, as described through the aforementioned XRB hydrodynamic models.
2.2. XRB hydrodynamic simulations
The XRB hydrodynamic models analyzed in this work couple a nuclear reaction network that includes 324 isotopes linked by 1392 nuclear interactions, with a modified version of the SHIVA hydrodynamic evolution code (see José & Hernanz 1998; José 2016). The main features and hypotheses of this code are: spherical symmetry, Newtonian gravity, and energy transport by radiative diffusion and convection4. The equation of state includes contributions from electron gas (with different degrees of degeneracy), ion plasma, and radiation. Coulomb corrections to the electronic pressure are taken into account. Aside from the energy generated by nuclear reactions, the models took into account neutrino energy losses as well.
In the present work, we focus on a model computed with the following physical input parameters: MNS = 1.4 M⊙, RNS = 13.1 km, accreted material of solar composition, and an accretion rate of 1.75 × 10−9 M⊙ yr−1. All bursts from this model show similar resulting features: burst recurrence times ranging around 5 − 6.5 h, burst durations of 55 − 75 s, peak luminosities within ∼[1 − 2]×105 L⊙, and peak temperatures in [1 − 1.25]×109 K. We show a study on one burst corresponding to a 200-shell envelope simulation, which we refer to as XRB-A (Model 2 in José et al. 2010, and unpublished data)5.
We remark that, even though José et al. (2010) report that no matter is ejected in their simulations, this refers to explosive ejection (i.e., material reaching escape velocity). They also state that the ejection of a tiny fraction by radiation-driven wind (i.e., when luminosity exceeds the Eddington limit) is still possible.
2.3. Model matching method
Ideally at a given matching point, all relevant physical variables should be continuous functions. However, given that both models have different hypotheses corresponding to different physical regimes, the ideal match may not always be sensible, or possible. For instance, we cannot expect a realistic match whenever degenerate gas pressure or convection are relevant terms in the equations of XRB hydrodynamic models, given that they are not present in the wind models. Nevertheless, whenever the conditions are such that these terms can be neglected, we could expect to find a valid match.
Another aspect we found important to take into consideration is whether energy or mass outflows, Ė and Ṁ, resulting from the conditions in the XRB hydrodynamic model lie in the region of the wind parameter space where solutions can be found and are consistent with the wind model hypotheses. In this regard, the study of the wind parameter space discussed in Herrera et al. (2020) resulted in great significance by providing an insight on the shape and location of this region in parameter space. Though, we note that it is worth keeping in mind that the location and shape of this region also depends on the abundances of elements present in the envelope, especially hydrogen, and on the mass of the NS. The latter is fixed for the XRB hydrodynamic models considered in this work, but the former changes dynamically within the evolution of each XRB and across their shells. The wind model free parameters, Ė and Ṁ, can be uniquely determined by imposing two additional boundary conditions, for instance the temperature and density, at a particular matching radius. The energy outflow Ė can be equated to the total luminosity reported in the XRB models, which varies with the radial coordinate, since the envelope in the XRB hydrodynamic models extends over a few meters above the NS core. In practice, this translates into finding which shell has a better match.
The general idea for the matching procedure employed is as follows. For a given XRB hydrodynamic simulation, we explored the 2-dimensional (shell, time step) grid, focusing first on every point with an energy outflow Ė that lies within the range of acceptable wind solutions in the parameter space. Since this range depends on the current element abundances and its exact extension is not known a priori, a typically safe and reduced region was chosen in terms of the ratio Ė/LX, for the first of several grid sweeps. In each sweep, every selected grid point was tested for a possible match by trying different wind profiles with varying mass outflows Ṁ, while the rest of the wind parameters (Ė,μ(Xi)) were fixed to those given by the current XRB simulation grid point, until we found the one that matches one of the boundary conditions at the radius given by the current grid point. For this initial step (which we call “first” match), we chose a match in density. That is, we used a suitable root-finding method to find zeros of the following δρ function that parametrizes the match relative error as a function of the mass outflow6:
where the subindices W and B stand for “wind” and “burst” (i.e., from the hydrodynamic simulation) values at the matching radius, respectively. Grid points where this match relative error was smaller than a desired threshold (e.g. δρ < 0.01) were considered successful first matches, or “hits”.
After the first sweep was completed, the exploration was sequentially extended to previously unexplored grid points adjacent to those for which a “hit” was found. The whole process was repeated until no further hits were found. The aim was to avoid missing possible hits outside the initially guessed safe region while at the same time preventing a waste of effort (and computing time) by unnecessarily testing points with parameters outside the wind model acceptable region.
At each point, we also computed a “second” matching error for temperature, δT, with an expression analogous to Eq. (6) in order to construct the total matching error7:
Grid points where this match error was lower than a desired threshold were considered to be successful XRB wind matches. Matching points were tested for hypothesis consistency in both XRB hydrodynamic and wind models.
3. Results
The search for XRB wind model matching points was successful for some of the studied XRB hydrodynamic simulations. This means that these XRB hydrodynamic models gave way to a brief stellar wind and the consequent mass-loss.
3.1. Wind-burst matching solutions
The wind-burst matching analysis for the hydrodynamic burst model, XRB-A, resulted in the sequence of matching points shown in Fig. 1. The figure shows a very well defined progression from the inner (hotter and denser) layers to the outer (cooler and less dense) layers and allowed us to reconstruct a continuous evolution of all physical variables (see Sects. 3.2 and 3.3). The matching error (Eq. (7)) for these points was significantly low: δ < 0.01. The resulting mass outflow, Ṁ, color coded in Fig. 1, evolved from higher values at the inner matching layers, diminishing as the matching point moves outward, until no further match was found. Matching points for deeper layers (and earlier times) than the ones shown in the figure can be found with the same method. However, in that direction, the XRB models enter a region of temperature and density where the effects from electron degeneracy and energy generation from nuclear reactions become significant. Convective energy transport also becomes relevant in deeper layers. The wind model does not consider these effects; therefore, possible matches toward deeper layers were not explored further.
 |
Fig. 1. Wind matching points during XRB evolution (model XRB-A). The gray dotted lines show the radial expansion of each XRB model shell as a function of time. Points for which matching wind solutions were found (δ < 0.01, see text) are marked with colored circles. The color indicates the mass outflow Ṁ of the matching wind solution. |
The distribution of matching solutions in the wind parameter space is shown in Fig. 2. At a first glance, the sequence of matching points displays a similar distribution in parameter space to the one found in our previous work (see, e.g., Fig. 4 in Herrera et al. 2020), but the overall energy outflow is slightly higher here. In contrast with our previous work, where X = 0 and normalization was therefore constant, the wind parameters have been normalized here in terms of a non-constant Eddington luminosity corresponding to electron scattering, LX, which depends on local hydrogen mass fraction, X, as:
 |
Fig. 2. Evolution of wind-burst matching points in the parameter space (for model XRB-A). The colored dots represent matching points with a relative error of δ < 0.01. The color scale corresponds to the time since burst peak expansion. Both energy outflow, Ė, and mass outflow, Ṁ, were normalized in terms of Eddington luminosity in the electron scattering case, LX (see text). A reference value for Ṁ = 1018 g s−1 is indicated by a vertical red dashed line. |
with κo = 0.2 cm2 g−1. Without this new normalization, each of the matching points would deviate slightly from the observed aligned disposition, according to their corresponding hydrogen abundance. Also in comparison to the previous work, the time evolution can now be followed, as given by the color scale. The wind total energy outflow evolves from lower to higher values, while the opposite occurs with mass outflow. The matching point time progression in the parameter space was slower for earlier times and sped up considerably in the final few seconds.
A selection of radial profiles for some of the matching wind solutions is shown in Fig. 3. The profiles show features similar to the ones reported in Herrera et al. (2020). The main difference is that the overall radial extension of the wind profiles shown here is smaller, which is characteristic of wind solutions with higher energy outflows. The radial extension of the wind envelope shrank with time, as was made evident by the position of the critical (sonic) point and photosphere, indicated in each profile in the figure. This shrinking is expected for the final part of the wind evolution: the expanded wind envelope should eventually recede and finally meet the original boundaries reported by the XRB hydrodynamic models, when the wind stops.
 |
Fig. 3. Wind profiles obtained for model XRB-A. The time evolution is indicated by the line color. Locations of the critical sonic point (⬧) and photosphere (°) are indicated in each curve. Panels in reading order are: velocity, temperature, characteristic time, and luminosity ratio Γ (i.e. LR in terms of local Eddington luminosity, LEdd). All plotted as a function of radius. The NS radius is 13.1 km (vertical dashed line). |
Values of wind velocity at the photosphere and critical point did not vary much (vph ∼ 10−2 c, vcr ∼ 10−3 c) for most of the duration of the wind, reflecting a similar behavior to the solutions reported in our previous work (Herrera et al. 2020). Temperature values at these points are also similar to our previous work (log Tph(K)∼6.5 − 7, log Tcr(K)∼7.5), minding the fact that the profiles shown here extend only to about 500 km, corresponding to log r(km)≃2.7 in Fig. 1 from Herrera et al. (2020). The radiative luminosity ratio profiles, Γ = LR/LEdd, also exhibited a similar behavior to the ones reported in Herrera et al. (2020). They all show a sharp rise close to the envelope base, quickly stabilizing outwards around a value of Γ ∼ 1, with tiny variations of about 10−3. This sharp rise in Γ is also a sign of a quick change from gas pressure-driven to radiation-driven wind.
In Herrera et al. (2020), we showed a characteristic time plot following the prescription used by Quinn & Paczyński (1985). However, according to Guichandut et al. (2021), this flow time is not a good measure of the feasibility of the quasi-stationary approach. They stated the problem is that it is highly dominated by the very slow wind velocity at the wind base. Instead of the flow time, they proposed a combined characteristic time that uses the much higher sound speed for the subsonic part and the regular wind speed for the supersonic part, giving a much smaller characteristic time than the typical wind duration. That is, in general, for any starting radius R below the photosphere, this new dynamic characteristic time would be:
where cs is the sound speed and the other symbols have their usual meaning. The total dynamic time of a wind solution is then obtained by evaluating at the wind base radius (i.e., R = rwb). The reasoning behind this choice can be understood as follows. A small change in physical conditions at the base can be thought of as a perturbation from the stationary regime solution. This perturbation will travel at the speed of sound as long as the flow is subsonic, readjusting the profile on its way up, and will travel with the flow velocity when it is supersonic. This effectively means that Δtd is associated with the propagation speed of information through the wind envelope. As long as this information travel time is small enough compared to the duration of the wind, we can consider the quasi-stationary regime as a good approximation. Given the fact that Δtd < 0.5 s in all profiles (as shown in Fig. 3, bottom-left panel) and that the wind duration is above 30 s, we can safely conclude that the quasi-stationary hypothesis holds. A similar argument could be made to test another assumption, which is that the composition of the whole wind profile is determined by the composition of the matching point (see Sect. 2). Changes in composition have an impact on the wind profiles mainly through the mean molecular mass μ(Xi). However, given that the total change is 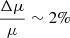 for the duration of the wind (i.e., ≲0.03% for the typical Δtd), we can safely assume that this is a valid approximation8.
for the duration of the wind (i.e., ≲0.03% for the typical Δtd), we can safely assume that this is a valid approximation8.
A detailed view of the match between temperature profiles from wind and XRB hydrodynamic models is displayed in Fig. 4. In the figure, one can graphically appreciate not only the precise match in temperature at different times but also the fact that the temperature gradient at the matching point is also continuous. This feature is expected if convection is negligible, making radiative diffusion the only relevant term in the energy transport equation. However, the same cannot be said for the density match. Despite the match in density being more accurate in most cases, the density gradient is not continuous. A density gradient appears in the mass conservation equation, and this discontinuity may be caused by a significant contribution to the integrated mass outflow from the time-dependent term. Alternatively, it may come from the different choice of surface boundary conditions in XRB hydrodynamic models, especially P = PRad, which is typically used for modeling non-expanded envelopes but does not admit wind-related mass-loss. These conditions can shape radial profiles differently, especially in upper shells close to the boundary, where the discontinuity in density gradient seems to be more prominent.
 |
Fig. 4. Detailed match of temperature (top) and density (bottom) radial profiles between wind (continuous lines) and hydrodynamic model (dashed lines) in XRB-A. The wind-burst profile matching points are indicated with circles. The color scale indicates the time since burst peak expansion. |
3.2. Mass-loss
After determining the sequence of the matching solutions between the wind and hydrodynamic XRB models, we could take a look at the chemical composition present at the matching points. Under our working hypothesis, we consider this to be the composition of the wind. Every isotope present at the matching point would ride this wind, escape the NS gravitational potential, and go out into the interstellar medium.
In order to calculate the total mass-loss for each species, Δmi, we needed to integrate the mass outflow rate of every isotope, ṁi(t), with respect to time and over the duration of the wind. That is:
where Ṁ(t) is the total mass outflow as a function of time, and to and tf are the initial and final times of the wind.
Although the accuracy of the match was relatively high in model XRB-A, with a significantly low matching error of δ < 0.01, the matching points still showed some degree of fluctuation in most physical variables and irregularity in time distribution (see Fig. 5, for instance). A smoothing technique using local regression was applied, incorporating the matching error as a weight factor in the form ω = δ−2 so that the smoothing favors points with a smaller error. Additionally, interpolation was used to reconstruct a curve in order to fill in time gaps related to shell resolution, obtain a large number of equally distributed points, and better approximate the integral in Eq. (10). Figure 5 shows both the matching point data and this smoothed, interpolated predictive curve, for the mass outflow, Ṁ, and total energy outflow, Ė.
 |
Fig. 5. Time evolution of mass outflow, Ṁ (top), and energy outflow, Ė (bottom), in model XRB-A, and predictive curves using the smoothing-interpolating technique (see text). The wind-burst matching data points are indicated with dots, and predicted values are shown with a line. The color scale indicates the matching error as defined by Eq. (7). |
Figure 6 shows both the predicted time-evolution curves of the mass outflow rates for the top five species and their time-integrated ejected mass. The total mass outflow seemed to increase toward earlier times than the ones shown in the figure. The matching technique could still be applied, in principle, to find earlier matching points, but this was dismissed due to hypothesis inconsistency between models (see Sect. 3.1). However, the total mass outflow was expected to go back down by the time of the actual wind onset. The total mass yield obtained is Δm = 6.16 × 1019 g for the time interval analyzed9. Considering that model XRB-A has a recurrence time of 5.9 h and assuming no period of inactivity (i.e., an upper limit to its real contribution), this implies a yearly output of 4.6 × 10−11 M⊙ yr−1, that is, 2.6% of the mass-accretion rate.
 |
Fig. 6. Time evolution of mass ejection for the top five species (by ejected mass) in model XRB-A. Top: mass outflow (Ṁ). Bottom: time-integrated ejected mass (Δm). The wind-burst model matching points are indicated with dots and the predictive curves with dashed lines. |
Figure 7 shows the total mass yield of every isotope produced in the XRB and ejected by the stellar wind. The mass yield is color coded only for species with a mass output of Δmi > 1010 g. Most of the isotopes produced in the XRB are unstable and will eventually decay (mainly through β process) into stable isotopes. The final resulting stable isotopes were also computed and are shown in Fig. 8. Values for the top ten mass-yielding isotopes are shown in Table 1. Almost 90% of the total expelled mass is constituted by the first four isotopes listed in the table: 60Ni, 64Zn, 68Ge, 56Ni. All ten species shown in the table account for over 97% of the overall mass ejected.
 |
Fig. 7. Mass ejected per isotope for the overall duration of the wind, from model XRB-A. The color scale indicates the mass ejected only for isotopes for which log Δm > 10; the rest is gray. Some species of interest are also marked. |
Top ten stable isotopes (after radioactive decay) by mass yield, from stellar wind in model XRB-A.
It has been suggested that if a tiny fraction of the accreted envelope is ejected through radiation-driven winds, XRBs may potentially be the source of some light p-nuclei, such as 92, 94Mo and 96, 98Ru (see Schatz et al. 1998, 2001), which are systematically under produced in all canonical scenarios proposed to date for the synthesis of such species. With the results we found here, we could make a rough estimate regarding the possible contribution of p-nuclei. Their progenitor (92Pd, 94Ag and 98In) and available final stable species are all marked in Figs. 7 and 8, respectively. The significant mass yields were Δm92Mo = 1.57 × 1016 g, Δm96Ru = 5.75 × 1015 g, and Δm98Ru = 4.72 × 1015 g, for the duration of the wind, corresponding to mass fractions of X92Mo = 2.57 × 10−4, X96Ru = 9.33 × 10−5, and X98Ru = 7.67 × 10−5. With a burst recurrence time of τrec = 5.9 h, this gives annual yields of 1.18 × 10−14 M⊙ yr−1, 4.29 × 10−15 M⊙ yr−1, and 3.53 × 10−15 M⊙ yr−1, respectively.
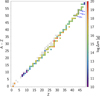 |
Fig. 8. Mass yield of stable isotopes from stellar wind in model XRB-A. These values correspond to the final products from the radioactive decay of the unstable isotopes shown in Fig. 7. |
Now, let us evaluate the significance of the XRB wind contribution we found for the observed Galactic abundance of the light p-nuclei. Current measurements in primitive meteorites (see Lodders et al. 2009, and references therein) report the following abundances: 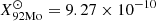 ,
, 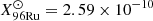 , and
, and 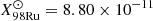 . For an estimation of the XRB wind contribution to the Galactic abundances, the total net mass of each element ejected by the XRB winds must be compared to the total mass of that element present in the Galaxy. A raw estimate could be obtained in the following way (results are summarized in Table 2). The total observable mass of the Milky Way is believed to lie in the range of [100 − 400]×109 M⊙10. Assuming a value of 200 × 109 M⊙, and the mass fractions inferred from meteoritic samples in our Solar System, we would obtain the following estimates for the amount of the p-nuclei present in our Galaxy:
. For an estimation of the XRB wind contribution to the Galactic abundances, the total net mass of each element ejected by the XRB winds must be compared to the total mass of that element present in the Galaxy. A raw estimate could be obtained in the following way (results are summarized in Table 2). The total observable mass of the Milky Way is believed to lie in the range of [100 − 400]×109 M⊙10. Assuming a value of 200 × 109 M⊙, and the mass fractions inferred from meteoritic samples in our Solar System, we would obtain the following estimates for the amount of the p-nuclei present in our Galaxy: 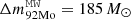 ,
, 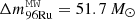 , and
, and 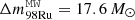 , where the “MW” superscript stands for Milky Way. Next, assuming that all XRB sources contribute a chemical abundance pattern similar to that in the XRB-A model and assuming no periods of inactivity (i.e., all sources experience one burst after 5.9 h continuously throughout their entire lifetime), we could get an upper limit of the overall mass contribution of each species to the galactic abundance by simply multiplying the annual yields by the estimated lifetime of X-ray binaries (5 Gyr)11. This would result in
, where the “MW” superscript stands for Milky Way. Next, assuming that all XRB sources contribute a chemical abundance pattern similar to that in the XRB-A model and assuming no periods of inactivity (i.e., all sources experience one burst after 5.9 h continuously throughout their entire lifetime), we could get an upper limit of the overall mass contribution of each species to the galactic abundance by simply multiplying the annual yields by the estimated lifetime of X-ray binaries (5 Gyr)11. This would result in 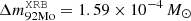 ,
, 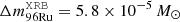 , and
, and 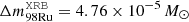 . The ratio between the mass of each species present in the Galaxy and the amount ejected by our typical XRB source throughout its lifetime (i.e.,
. The ratio between the mass of each species present in the Galaxy and the amount ejected by our typical XRB source throughout its lifetime (i.e., 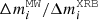 ) would yield an estimate of the number of XRB sources similar to XRB-A that would be needed to account for the origin of these p-nuclei. The values obtained for this ratio were different for each isotope. Between a few hundred thousand to over a million sources like XRB-A would be needed for this ratio to be of the order of one. In contrast, the total number of identified XRB sources so far is around one hundred12. That is, assuming that XRBs are the only source for these species and that our XRB-A is a representative case, then 103 − 104 times more sources than the ones already discovered would be needed to explain the observed mass abundances of these light p-nuclei. This suggests that XRBs are unlikely to be the main origin of these isotopes.
) would yield an estimate of the number of XRB sources similar to XRB-A that would be needed to account for the origin of these p-nuclei. The values obtained for this ratio were different for each isotope. Between a few hundred thousand to over a million sources like XRB-A would be needed for this ratio to be of the order of one. In contrast, the total number of identified XRB sources so far is around one hundred12. That is, assuming that XRBs are the only source for these species and that our XRB-A is a representative case, then 103 − 104 times more sources than the ones already discovered would be needed to explain the observed mass abundances of these light p-nuclei. This suggests that XRBs are unlikely to be the main origin of these isotopes.
3.3. Observables, correlations, and other physical magnitudes
Another important aspect we analyzed from the XRB-wind matching results is the evolution of observable features and how they relate to other predicted physical variables. Time evolution of photospheric magnitudes in XRB-A is shown in Fig. 9. In the figure, photospheric radial expansion steadily recedes from over 600 km for most of the time interval displayed, and it drops rapidly in the last few seconds, seemingly toward the final XRB-wind matching radius (∼13.17 km), close to the NS core surface. The effective temperature appears to evolve in an exactly inverse manner, rising from around 4 × 106 K in the earlier moments, when the wind atmosphere is most expanded, and ending in a quick spike (> 1.6 × 107 K) that seems to sharply rise up toward the much higher photospheric temperature (∼5 × 108 K) of the envelope after the wind phase. Wind velocity at the photosphere varies little around ∼0.01 c for the most part and drops abruptly by the end. Density shows an almost identical behavior to temperature.
 |
Fig. 9. Time evolution of photospheric magnitudes, in model XRB-A. In reading order, radius, temperature, wind velocity, density, radiative luminosity and its ratio to local Eddington luminosity. Values corresponding to matching wind profiles are indicated with dots, and predicted values (using smoothing-interpolating technique) with a line. |
Photospheric luminosity rises slowly through most of the wind and spikes toward the end, in a similar way to temperature. Analysis of the full wind evolution from lower-resolution models (i.e., Model 1 in José et al. 2010) hint that this rise may in fact be the recovery part of an overall small dip in luminosity (∼5 − 6%), with respect to the average luminosity while the wind is active (LX ∼ 3.52 × 1038 erg s−1). This average luminosity is in turn much smaller than the values typically reported in XRB hydrodynamic simulations, especially if the wind phase appears during their peak expansion. The onset of the stellar wind expands the envelope further, cooling it down toward the photosphere. This in turn raises opacity and allows for the absorption of more radiative energy into the gas, which is transformed into kinetic energy and makes the photospheric luminosity drop. This drop in photospheric luminosity during the wind phase with respect to the wind-less envelope could, in principle, be observed as a flattening of the luminosity peak for the duration of the wind or, if the drop is significant and the wind short-lived, as a double peak. From the observational point of view, such a feature could be a clear signal of the presence of a stellar wind.
In the first paragraph of the current section, we noted the similarity between photospheric temperature and density time evolution curves and their apparent inverse relation to photospheric radius. In the characterization study shown in Herrera et al. (2020), we found similar correlations due to the fact that photospheric luminosity was close to Eddington luminosity. That is:
We also stated the correlation between observable features, such as photospheric luminosity and wind velocity, and the wind parameters determined by physical conditions of the inner parts of the envelope,
After assessment, we are able to confirm that these correlations hold for the more realistic scenario studied in this article. The regression results are shown in Table 3.
Regression results from correlations among observable variables and wind parameters in model XRB-A.
Finally, Figs. 10 and 11 show the time evolution of physical magnitudes at the critical point and wind base (XRB model matching point), respectively. The critical point remains much closer to the base, extending only a few times the NS radius and receding at a somewhat uniform rate. Temperature, velocity, and density at the critical point evolve in the opposite direction, slowly growing and with an overall smaller change of velocity around vcr ∼ 10−3 c, but there is an abrupt drop right before the end of the wind. Luminosity stays just below the local Eddington luminosity. The effective optical depth of the critical point always stays higher than the required threshold of ten, which is needed to consider the wind as optically thick (see Herrera et al. 2020, and references therein), but it seems to drop very quickly by the end of the wind. This may be a hint that there could be a continuation of the wind with an optically thin regime, which our wind simulation code does not consider. However, the XRB wind matching point moves quickly toward the outermost shells of the XRB hydrodynamic model where the boundary condition Pg = 0 was set, making the appearance of a thin wind unlikely and, in practice, the search of further matches impossible, even if the wind code were capable of dealing with an optically thin wind.
 |
Fig. 10. Same as Fig. 9 but for magnitudes evaluated at the critical point. In reading order, the panels show: radius, temperature, density, ratio of radiative luminosity to local Eddington limit, and effective optical depth. |
 |
Fig. 11. Same as Fig. 9 but for magnitudes evaluated at the wind base. In reading order, the panels show: radius, temperature, density, velocity luminosity ratio Γ, and gas-to-radiation pressure gradient ratio. |
The ratio of the gas pressure gradient to the radiation pressure gradient at the wind base (last panel of Fig. 11) shows values very close to unity. This result rests in good agreement with the very “generic” boundary condition assumed for the characterization study in Herrera et al. (2020). This agreement does not come as a surprise, since the previously assumed boundary condition was inspired by (and is a necessary condition for) a situation in which wind velocity can be neglected and radiation pressure is not dominant, both of which correspond to a transition region between a stellar wind and static envelope. These assumptions turned out to be good approximations of the physical conditions at the wind base for all the XRB hydrodynamic models we studied, as can be seen for the current model of XRB-A (Fig. 11, last three panels), where the wind velocity is smaller than 1 cm s−1, the radiative luminosity is about one half of the local Eddington limit needed to accelerate the wind, and the remaining half of the driving force is provided by the gas pressure gradient, due to the abrupt temperature and density changes.
4. Conclusions and discussion
We linked the stellar wind model developed in Herrera et al. (2020) to a series of XRB hydrodynamic models developed in José et al. (2010). For this, we developed a technique that successfully matched different wind profiles to the boundary conditions given at different points during the evolution of each burst, with a quasi-stationary approach. This allowed us to construct a time evolution of wind profiles and to quantify the mass-loss of each isotope produced by nucleosynthesis during the burst. The overall ejected mass in XRB-A was about 6 × 1019 g13. The average ejected mass per unit time represents 2.6% of the accretion rate, with 0.1% of the envelope mass ejected per burst, and 90% of the ejecta was composed by 60Ni, 64Zn, 68Ge, and 58Ni. Additionally, the amounts of 1H and 4He add up to less than 5% of the ejected mass.
The ejected material also contained a small fraction (10−4 − 10−5) of some light p-nuclei that was of interest. The species with the highest amount was 92Mo, with ∼1.5 × 1016 g in XRB-A. However, an estimation of their significance showed that an unreasonable number of XRB sources, like the one analyzed (corresponding to a typical XRB episode), were required to account for the Galactic abundances of each isotope. When applied to the sequence of lower-resolution bursts (i.e., Model 1 in José et al. 2010) with evolving metallicities and ignition conditions between them, our method showed varying quantities of these isotopes, but all of them were smaller by at least an order of magnitude. Therefore, we concluded that XRB sources are unlikely to constitute the sole explanation of their origin.
Much as in Herrera et al. (2020), the resulting wind profiles were all observed to transition from a gas pressure-driven regime at the inner parts, close to the wind base where opacity is low, to a full radiatively driven wind in the outer parts. Most notably, photospheric magnitudes showed the same correlations, namely 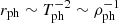 , independently of the radius at which the aforementioned wind base condition was found. These correlations are apparently independent from model parameters (Ṁ, Ė) too, so they are expected to appear in every scenario. They seem to derive from the choice of boundary conditions at the photosphere and the fact that photospheric luminosity takes on values very close to Eddington luminosity
, independently of the radius at which the aforementioned wind base condition was found. These correlations are apparently independent from model parameters (Ṁ, Ė) too, so they are expected to appear in every scenario. They seem to derive from the choice of boundary conditions at the photosphere and the fact that photospheric luminosity takes on values very close to Eddington luminosity 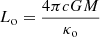 for every choice of parameters (Ṁ, Ė).
for every choice of parameters (Ṁ, Ė).
Another set of correlations we found to hold in the present work involved parameters (Ṁ, Ė) as well as photospheric magnitudes (see Eq. (13)). Since wind parameters are determined by imposing conditions for all physical variables at the wind base, the correlations effectively link observable magnitudes to the physics of the innermost parts of the envelope, close to its interface with the NS core. This could lead to a technique that allows for the indirect determination of the radius of the NS from photospheric magnitudes. This possibility requires further study, but a possible general idea is outlined as follows: For a fixed set of wind parameters (Ṁ, Ė, NS mass M, and gas composition Xi), one can determine the location of the wind base rwb, understood now as the point where the wind profile transitions from being gas-pressure driven to radiation driven, that is ∇Pgas = ∇Prad. Such a wind base rwb would remain very close (∼20 − 60 m) to the actual NS radius (see Fig. 11, first and last panels). Now, as Ṁ, Ė evolve with the burst, they would follow a path (see Fig. 2) that notably resembles that of constant rwb value in the parameter space from Fig. 3, panel 3 in Herrera et al. (2020). The actual (Ṁ, Ė) path would not be exactly the same, since composition also evolves, but it would traverse a rather small range of values of the rwb in an analogous parameter space plot calculated with an average value of μ(Xi), which varies little (as stated previously when discussing the validity of quasi-stationary approach in Sect. 3.1). For high Ṁ and low Ė, which in Model XRB-A corresponds to the earliest available times of the wind phase, this value of rwb would be closer to the actual NS radius. This could give us an estimation with an error as low as only a few tens of meters. Nevertheless, further study is required to determine whether these results are affected by the inclusion of more complex input physics, such as relativistic wind models, or a more detailed treatment of radiative transfer.
The tables and calculation routines from The Opacity Project were especially useful since they allow dynamical changes in the gas composition and higher values of metallicity. However, for such values, they are limited to log T < 8. For higher temperatures, opacity was extrapolated using a formula introduced by Paczyński (1983).
General relativity corrections can be determined a posteriori and rely on the factor (1 + z), where z is the gravitational redshift (see discussion section in José et al. 2010).
A study on lower-resolution bursts (e.g., Model 1 in José et al. 2010) yielded similar resulting characteristics, but with lower matching accuracy and lower overall mass ejected by the wind, with varying composition. In both cases, the unpublished data mentioned includes detailed chemical composition and additional physical properties of each numerical shell.
It is worth mentioning that since the valid domain for Ṁ is not known a priori, derivative-based root-finding methods, such as the commonly used Newton-Raphson, are not well suited for the task, since they may wander outside any initial guess of a valid domain and they also require a numerical approximation of the derivative of the δρ function, which demands calculating additional wind model solutions at each step. A custom root-finding algorithm based on the safer (but often slower) bisection method was developed for dealing with this problem.
Several pairs of matching variables could be used here ((ρ, T), (PR, Pg), etc.), and in any order. Which variable is chosen for the first match will affect the precision requirement of the root-finding employed, as well as the overall error obtained for the second match. After trying several combinations, we found that the best results for the method employed, in terms of number of matches, speed and matching errors, is obtained with the ordered pair (ρ, T).
Changes in opacity may also be relevant in principle, which at such high temperature can be approximated with the formula given by Paczyński (1983), giving 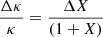 . In the models analyzed, this value is ∼0.4% for the whole duration of the wind.
. In the models analyzed, this value is ∼0.4% for the whole duration of the wind.
Here, we consider only baryonic matter; no dark matter estimate is included (see, e.g., Kafle et al. 2014; McMillan 2017; Watkins et al. 2019).
This is a traditionally assumed value for the lifetime of X-ray binaries, but it is currently not very well constrained. Other works suggest much shorter lifetimes, by even three orders of magnitude (see Iben et al. 1995; Podsiadłowski et al. 2002; Pfahl et al. 2003). In such a case, our final conclusion (see further ahead) is strengthened since even more XRB sources would be needed to explain the observed mass abundances.
See http://www.sron.nl/~jeanz/bursterlist.html for an updated list of known galactic type I XRB systems.
Acknowledgments
This work has been partially supported by the Spanish MINECO grant PID2020-117252GB-I00, by the E.U. FEDER funds, and by the AGAUR/Generalitat de Catalunya grant SGR-386/2021. This article benefited from discussions within the EU’ H2020 project No. 101008324 “ChETEC-INFRA”. This work was also partly supported by the Spanish program Unidad de Excelencia María de Maeztu CEX2020-001058-M, financed by MCIN/AEI/10.13039/501100011033.
References
- Bildsten, L., Chang, P., & Paerels, F. 2003, ApJ, 591, L29 [CrossRef] [Google Scholar]
- Chang, P., Bildsten, L., & Wasserman, I. 2005, ApJ, 629, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., Morsink, S., Bildsten, L., & Wasserman, I. 2006, ApJ, 636, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Damen, E., Magnier, E., Lewin, W. H. G., et al. 1990, A&A, 237, 103 [NASA ADS] [Google Scholar]
- Fisker, J. L., Schatz, H., & Thielemann, F.-K. 2008, ApJS, 174, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Guichandut, S., Cumming, A., Falanga, M., Li, Z., & Zamfir, M. 2021, ApJ, 914, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., Psaltis, D., & Özel, F. 2012, ApJ, 747, 76 [CrossRef] [Google Scholar]
- Herrera, Y., Sala, G., & José, J. 2020, A&A, 638, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, I., Jr., Tutukov, A. V., & Yungelson, L. R. 1995, ApJS, 100, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- José, J. 2016, Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton: CRC/Taylor and Francis) [Google Scholar]
- José, J., & Hernanz, M. 1998, ApJ, 494, 680 [Google Scholar]
- José, J., Moreno, F., Parikh, A., & Iliadis, C. 2010, ApJS, 189, 204 [CrossRef] [Google Scholar]
- Kafle, P. R., Sharma, S., Lewis, G. F., & Bland-Hawthorn, J. 2014, ApJ, 794, 59 [Google Scholar]
- Keek, L., & in’t Zand, J. J. M. 2008, Proceedings of the 7th INTEGRAL Workshop, 32 [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2006, Nucl. Phys. A, 777, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. P. 2009, Landolt Börnstein, 4B, 712 [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1983, ApJ, 267, 315 [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Pfahl, E., Rappaport, S., & Podsiadłowski, P. 2003, ApJ, 597, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadłowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, T., & Paczyński, B. 1985, ApJ, 289, 634 [CrossRef] [Google Scholar]
- Sala, G., Haberl, F., José, J., et al. 2012, ApJ, 752, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., Aprahamian, A., Görres, J., et al. 1998, Phys. Rep., 294, 167 [CrossRef] [Google Scholar]
- Schatz, H., Aprahamian, A., Barnard, V., et al. 2001, Phys. Rev. Lett., 86, 3471 [CrossRef] [PubMed] [Google Scholar]
- Seaton, M. J., Yan, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, New Views of Thermonuclear Bursts (Cambridge: Cambridge University Press) [Google Scholar]
- Watkins, L. L., van der Marel, R. P., Sohn, S. T., & Evans, N. W. 2019, ApJ, 873, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, N. N., Bildsten, L., & Schatz, H. 2006, ApJ, 639, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., & Weinberg, N. N. 2018, ApJ, 863, 53 [CrossRef] [Google Scholar]
All Tables
Top ten stable isotopes (after radioactive decay) by mass yield, from stellar wind in model XRB-A.
Regression results from correlations among observable variables and wind parameters in model XRB-A.
All Figures
 |
Fig. 1. Wind matching points during XRB evolution (model XRB-A). The gray dotted lines show the radial expansion of each XRB model shell as a function of time. Points for which matching wind solutions were found (δ < 0.01, see text) are marked with colored circles. The color indicates the mass outflow Ṁ of the matching wind solution. |
| In the text | |
 |
Fig. 2. Evolution of wind-burst matching points in the parameter space (for model XRB-A). The colored dots represent matching points with a relative error of δ < 0.01. The color scale corresponds to the time since burst peak expansion. Both energy outflow, Ė, and mass outflow, Ṁ, were normalized in terms of Eddington luminosity in the electron scattering case, LX (see text). A reference value for Ṁ = 1018 g s−1 is indicated by a vertical red dashed line. |
| In the text | |
 |
Fig. 3. Wind profiles obtained for model XRB-A. The time evolution is indicated by the line color. Locations of the critical sonic point (⬧) and photosphere (°) are indicated in each curve. Panels in reading order are: velocity, temperature, characteristic time, and luminosity ratio Γ (i.e. LR in terms of local Eddington luminosity, LEdd). All plotted as a function of radius. The NS radius is 13.1 km (vertical dashed line). |
| In the text | |
 |
Fig. 4. Detailed match of temperature (top) and density (bottom) radial profiles between wind (continuous lines) and hydrodynamic model (dashed lines) in XRB-A. The wind-burst profile matching points are indicated with circles. The color scale indicates the time since burst peak expansion. |
| In the text | |
 |
Fig. 5. Time evolution of mass outflow, Ṁ (top), and energy outflow, Ė (bottom), in model XRB-A, and predictive curves using the smoothing-interpolating technique (see text). The wind-burst matching data points are indicated with dots, and predicted values are shown with a line. The color scale indicates the matching error as defined by Eq. (7). |
| In the text | |
 |
Fig. 6. Time evolution of mass ejection for the top five species (by ejected mass) in model XRB-A. Top: mass outflow (Ṁ). Bottom: time-integrated ejected mass (Δm). The wind-burst model matching points are indicated with dots and the predictive curves with dashed lines. |
| In the text | |
 |
Fig. 7. Mass ejected per isotope for the overall duration of the wind, from model XRB-A. The color scale indicates the mass ejected only for isotopes for which log Δm > 10; the rest is gray. Some species of interest are also marked. |
| In the text | |
 |
Fig. 8. Mass yield of stable isotopes from stellar wind in model XRB-A. These values correspond to the final products from the radioactive decay of the unstable isotopes shown in Fig. 7. |
| In the text | |
 |
Fig. 9. Time evolution of photospheric magnitudes, in model XRB-A. In reading order, radius, temperature, wind velocity, density, radiative luminosity and its ratio to local Eddington luminosity. Values corresponding to matching wind profiles are indicated with dots, and predicted values (using smoothing-interpolating technique) with a line. |
| In the text | |
 |
Fig. 10. Same as Fig. 9 but for magnitudes evaluated at the critical point. In reading order, the panels show: radius, temperature, density, ratio of radiative luminosity to local Eddington limit, and effective optical depth. |
| In the text | |
 |
Fig. 11. Same as Fig. 9 but for magnitudes evaluated at the wind base. In reading order, the panels show: radius, temperature, density, velocity luminosity ratio Γ, and gas-to-radiation pressure gradient ratio. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.