| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 19 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202346010 | |
| Published online | 17 October 2023 | |
General relativistic hydrodynamic simulations of perturbed transonic accretion⋆
1
Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010 6500 GL Nijmegen, The Netherlands
e-mail: holivares@science.ru.nl
2
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
Received:
27
January
2023
Accepted:
31
March
2023
Contact. Comparing horizon-scale observations of Sgr A* and M 87* with numerical simulations has provided considerable insight into their interpretation. Most of these simulations are variations of the same physical scenario consisting of a rotation-supported torus seeded with poloidal magnetic fields. However, this approach has several well-known limitations such as secular decreasing trends in mass-accretion rates that render long-term variability studies difficult; a lack of connection with the large-scale accretion flow, which is replaced by an artificial medium emulating vacuum; and significant differences with respect to the predictions of models of accretion onto Sgr A* fed by stellar winds.
Aims. We aim to study the flow patterns that arise on horizon scales in more general accretion scenarios that have a clearer connection with the large-scale flow, and are at the same time controlled by a reduced set of parameters.
Methods. As a first step in this direction, we performed three-dimensional general relativistic hydrodynamic simulations of rotating transonic flows with velocity perturbations injected from a spherical boundary located far away from the central object (1000 gravitational radii). We studied the general properties of these flows with varying perturbation amplitudes and angular momentum. We analyzed time series of mass and angular-momentum radial fluxes, angle- and time-averaged profiles, and synthetic bremsstrahlung light curves, as well as the three-dimensional structure of the flow, and quantified shock and sonic transitions in the solutions.
Results. We observe a rich phenomenology in accretion patterns, which includes smooth Bondi-like flows, turbulent torus-like structures, shocks, filaments, and complex sonic structures. For sufficiently large perturbations and angular momentum, radial profiles deviate from the constant entropy and constant angular-momentum profiles used for initialization and resemble those of advection-dominated accretion flows, showing evidence of entropy generation and angular-momentum redistribution not mediated by magnetic fields. Time series do not show the secular decreasing trend and are suitable for long-term variability studies. We see that the fluctuations are amplified and extend further in frequency than the injected spectrum, producing a red noise spectrum both for the mass-accretion rate and the synthetic light curves.
Conclusions. We present a simulation setup that can produce a wide variety of flow patterns at horizon scales and incorporate information from large scale accretion models. The future inclusion of magnetic fields and radiative cooling could make this type of simulation a viable alternative for the numerical modeling of general low-luminosity active galactic nuclei (AGNs).
Key words: accretion / accretion disks / black hole physics / relativistic processes / methods: numerical
Movies (Fig. 4) are available at https://www.aanda.org.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Accretion onto compact objects such as black holes and neutron stars powers some of the most spectacular phenomena in astrophysics. While the focus of numerous studies in accretion theory is on how matter and angular momentum are transported through an accretion disk, far fewer studies focus on the formation of the accretion disk itself. In particular, numerical simulations of accretion disk formation are encumbered by the large-scale separation between the circularization radius of incoming matter and the size of the accretor. There are certain applications, however, where the accreted matter has comparatively low angular momentum, leading to circularization radii not much larger than the accretor itself. Prime examples are the high-mass X-ray binaries (HMXBs) and chaotic, stellar-wind-fed accretion in galactic nuclei such as our own Galactic center Sgr A*.
A central role in the interpretation of the event-horizon-scale observations of Sgr A* and M 87* by the Event Horizon Telescope (EHT) Collaboration is played by general relativistic magnetohydrodynamic (GRMHD) simulations (Porth et al. 2019; Event Horizon Telescope Collaboration 2019, 2022). To date, all of the models in the simulation library for Sgr A* and most of those used for M 87* follow variations of the same initial conditions of a rotation-supported torus (Fishbone & Moncrief 1976) seeded with a weak poloidal magnetic field. While a lot of physical insights have already been gained by comparing observational data against GRMHD simulations – leading to increasingly tight constraints of the parameters such as black hole mass, accretion rate, inclination and black hole spin (Event Horizon Telescope Collaboration 2019, 2021, 2022) – there are several limitations intrinsic to the considered black hole-torus (BHT) simulations. For example, since they are initialized with a finite amount of matter contained in the torus, the matter content in the simulation decreases over time, accompanied by a corresponding decrease in mass-accretion rate. This secular trend renders the study of long-term variability difficult. This systematic is particularly important since the current set of GRMHD simulations produces highly varying light curves that are tightly constrained by the less variable data for Sgr A* (Murchikova & Witzel 2021; Event Horizon Telescope Collaboration 2022; Wielgus et al. 2022; Murchikova et al. 2022).
The most important limitation of the BHT simulations, however, concerns physical realism. It is now widely believed that our galactic center black hole, Sgr A*, can be fed from the winds of ∼30 massive stars that orbit on the parsec scale (Quataert 2004; Cuadra et al. 2008; Ressler et al. 2018). Whether an accretion disk (torus) forms in this scenario depends not only on the initial wind parameters (Mościbrodzka et al. 2006; Shcherbakov & Baganoff 2010), but also on the interactions of the unbound winds, which can give rise to shocks and hydrodynamic turbulence. The flow patterns of realistic stellar wind accretion models for low luminosity active galactic nuclei (AGNs) differ significantly from the BHT scenario described above. In stellar-wind accretion, material forms clumpy structures and has a broad distribution of angular momentum without sufficient time to circularize, and it is not generally rotation supported. Instead, it is accreted mainly due to an originally low angular momentum and remains unbound for the most part (Ressler et al. 2018).
This latter property is shared by different models of large-scale accretion such as the constant-entropy solutions by Bondi (1952), Michel (1972), and Chakrabarti (1996), and models that include dissipation such as the well-known advection dominated accretion flows (ADAFs; Narayan & Yi 1994). Recent magnetohydrodynamics (MHD) simulations that focus on the large-scale dynamics have revealed further differences to the standard BHT scenario: while magnetic fields from stellar winds are initially weak and passively advected, at horizon scales they accumulate and become dynamically important and start to regulate accretion in a way similar to magnetically arrested disks (MADs; Ressler et al. 2020a,b). The submillimeter light curves produced by these wind-fed models are less variable than those typically obtained from BHT simulations, which is in better agreement with the variability statistics from Sgr A* observations Murchikova et al. (2022). On much larger timescales, the lack of a predominant angular momentum or magnetic field direction leads to erratic changes in the orientation of the accretion disk (Ressler et al. 2021). Similar transient behavior can be seen in the direction and power of the jet before the formation of a steady jet (Lalakos et al. 2022). Simulations of accretion from kiloparsec scales onto the black hole (BH) event horizon have also shown that the accretion flow in elliptic galaxies as M 87 can acquire a variety of patterns that range from rotation-supported disks to chaotic streams (Guo et al. 2023).
In general, simulation-based studies of the horizon-scale structure of the accretion flow resulting from large-scale feeding present the computational challenge of having to simulate length and timescales spanning ∼6 orders of magnitude or dealing with uncertain factors such as the details of stellar-wind astrophysics. It would therefore be desirable to gain more insight into the properties of the accretion flow from the study of transonic solutions connecting the event horizon to infinity, in a similar manner to the way the theory of accretion disks has benefitted from the study of analytic solutions for fluids in circular motion around black holes. Depending on the specific angular momentum and energy, analytic studies of transonic low-angular-momentum accretion flows (e.g., Fukue 1987; Chakrabarti 1989, 1996; Chakrabarti & Das 2004) have revealed different regimes characterized by smooth, Bondi-like flows, standing accretion shocks, or the formation of circularized tori. Furthermore, the solutions have been studied including the effects of viscosity (Chakrabarti & Molteni 1995; Lanzafame et al. 1998), radiative cooling (Molteni et al. 1996; Okuda et al. 2004), and magnetic fields (Proga & Begelman 2003b; Okuda et al. 2019; Mitra et al. 2022), often with particular focus on the stability and dynamics of the accretion shock. The effects of non-axisymmetry and boundary conditions on these flows were studied by Janiuk et al. (2008, 2009) and Garain & Kim (2023) using three-dimensional pseudo-Newtonian numerical simulations. Numerical simulations of transonic hydrodynamic solutions were presented more recently by Kim et al. (2017, 2019) for the Schwarzschild and Kerr space-times, showing that certain perturbations can trigger long-surviving shocks at the location of predicted standing shocks (Chakrabarti 1996).
In fact, a realistic approach to the problem should consider the destabilizing effect of inhomogeneities in the surrounding medium. The stability of spherical Bondi accretion has been studied analytically in a number of works (see, e.g., Moncrief 1980; Kovalenko & Eremin 1998). In the latter work, it is shown that this solution is unstable for nonradial perturbations, although for the instability to manifest itself the size of the accretor needs to be sufficiently small compared to the Bondi radius, as is the case for the nearest supermassive black holes (SMBHs).
In this work, we studied a simulation setup that aims to address the above-described limitations of the BHT paradigm and facilitate the incorporation of information gained from larger scale simulations. This model depends on a reduced set of parameters that can in principle be chosen to match the properties inferred for known SMBHs such as Sgr A*, M 87, and other targets of the EHT. By incorporating time-dependent properties of the surrounding medium in the boundary conditions, the simulation domain can be of a modest size comparable to that of existing GRMHD simulations in the EHT library. The simulations presented here were run in pure general relativistic hydrodynamics (GRHD), that is, with zero magnetic field, as an intermediate step toward the GRMHD simulations that will be presented in a forthcoming work. We show that the proposed setup produces steady time series that are in principle suitable for long-term variability studies and exhibits a rich phenomenology that can differ significantly both from typical BHT simulations and from unperturbed, Bondi-like accretion. We describe this setup in Sect. 2 and provide justification for the physical parameters employed (Sect. 2.2). In Sect. 3, we report on the properties observed in the simulations, such as time series of mass and angular-momentum accretion rates and radial profiles (Sect. 3.1); three-dimensional morphology, including the presence of shocks and complex sonic structures (Sect. 3.2); and variability properties (Sect. 3.3). We summarize and discuss our results in Sect. 4, and we complement this work with more information on the simulation setup in the appendices.
2. Simulation setup
2.1. Setup description
To explore the flow patterns arising from transonic accretion of an inhomogeneous interstellar medium, we performed three-dimensional GRHD simulations that continuously inject matter from an outer boundary. The equations solved are those for the conservation of particle number and energy-momentum,
where ρ is the particle number density, uμ is the fluid four-velocity, and 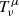 is the fluid energy-momentum tensor. The latter reads
is the fluid energy-momentum tensor. The latter reads
where h is the specific enthalpy, p is the fluid pressure, and gμν is the space-time metric. We employed units such that the gravitational constant and the speed of light are G = c = 1; so, the gravitational radius rg = GM/c2 and the gravitational timescale tg = rg/c are rg = tg = M, where M is the mass of the black hole. We adopted a Kerr space time with a dimensionless spin parameter of a := J/M = 0.95, where J is the black hole angular momentum, and the event horizon located at 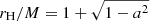 . For all of our simulations, we set the sonic radius to rs = 500 M and placed the boundary at r = 1000 M. We initialized the simulations with a smooth, quasi-stationary background solution with a latitude-dependent angular-momentum profile. Following Proga & Begelman (2003b), we adopted an angular-momentum profile that peaks at the equator and vanishes at the poles (see Appendix A for a detailed discussion of the background flow):
. For all of our simulations, we set the sonic radius to rs = 500 M and placed the boundary at r = 1000 M. We initialized the simulations with a smooth, quasi-stationary background solution with a latitude-dependent angular-momentum profile. Following Proga & Begelman (2003b), we adopted an angular-momentum profile that peaks at the equator and vanishes at the poles (see Appendix A for a detailed discussion of the background flow):
where ℓ := −uϕ/u. The background flow is characterized by only two parameters, the angular momentum at the equator, ℓ0, and the sonic radius (or, alternatively, fluid internal energy ℰ = hut at the equator).
To model inhomogeneities in the interstellar medium, we injected perturbations of varying amplitude to the (tangential-) velocity components at the outer boundary. Perturbations are modeled as a time-varying Gaussian random field with a white-noise spectrum,
in the λk/M = 2π/kM ∈ [214, 2400] wavelength range and in the fk ∈ [3.7, 41]×10−5 M−1 frequency range, where k is the wave number (see Appendix B for more details). The remaining fluid variables at the boundary are set consistently with the initial condition and are therefore constantly injecting matter that should preserve the initial state in absence of perturbations. The injected noise is controlled by the parameter δ, which specifies the ratio of the variance of velocity perturbations to the radial component of the four-velocity of the unperturbed flow at the boundary, δ = ⟨δu2⟩1/2/ur. We adopted the equation of state of an ideal gas with adiabatic index 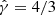 .
.
We performed several simulations while varying ℓ0 and δ. In order to isolate the effect of perturbations, we ran a set of simulations in a Bondi-Michel accretion scenario, that is, ℓ0 = 0 and a = 0. The list of runs and parameters used is displayed in Table 1.
Table of runs.
To run the simulations, we used the code BHAC (Porth et al. 2017; Olivares et al. 2019). We used a spherical polar grid in modified Kerr-Schild coordinates with logarithmic spacing in the radius. The base resolution is Nr × Nθ × Nϕ = 96 × 48 × 48, and we employed three levels of adaptive mesh refinement (AMR), obtaining an effective resolution of 384 × 192 × 192. Refinement is activated by Löhner’s error estimator (Löhner 1987) applied to the density field, with the tolerance set to 0.1. More details on the implementation of this scheme in BHAC can be found in Porth et al. (2017). AMR blocks in contact with the inner boundary and the polar axis are kept at the coarsest level in order to avoid small time steps.
The inner boundary is located inside the central black hole event horizon, at r = 1.19 M, in order to avoid boundary effects. We employed a finite volume method with piecewise parabolic reconstruction (PPM), a total variation diminishing Lax-Friedrichs (TVDLF) approximate Riemann solver, and a two-step method for time integration (see Porth et al. 2017 for more details on coordinates and numerical methods).
To reduce the cost of simulations, we evolved a passive tracer f that was initialized as f = 0 inside the domain and f = 1 for the injected matter at the boundary, and we only evolved the blocks of 8 × 8 × 8 cells for which f > 0.1 or which were surrounded by blocks that satisfied this condition. For all of the simulations, this tracer reached the event horizon at t ≲ 30 000 M, after which the simulation domain became active everywhere. We continued the evolution up to t = 60 000 M, which corresponds to a total simulation time of nearly five free-fall timescales from the sonic radius, tff = π(rs/2)3/2 ≈ 12 418 M.
Finally, to avoid negative densities and pressures, we prescribed floor values given by ρfloor = ρmin r−3/2 and pfloor = pmin r−5/2, where ρmin = 10−5 and pmin = (1/3)×10−7. Whenever ρ < ρfloor or p < pfloor, we set values in that cell to ρ = ρfloor and p = pfloor. However, since the matter injected at the boundary has density and pressure orders of magnitude higher than the floors, these are almost never applied.
2.2. Physical parameters
Accretion onto an object at rest with respect to a spherically symmetric, asymptotically uniform medium can be considered to start at the Bondi radius, rB, the distance at which the asymptotic sound speed c∞ equals the escape velocity, that is, 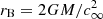 . Temperatures inferred from Chandra X-ray observations of the hot gas surrounding Sgr A* (Baganoff et al. 2003) and the central black hole of M 87 (Russell et al. 2015), combined with the assumption of a monoatomic ideal gas with
. Temperatures inferred from Chandra X-ray observations of the hot gas surrounding Sgr A* (Baganoff et al. 2003) and the central black hole of M 87 (Russell et al. 2015), combined with the assumption of a monoatomic ideal gas with 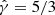 , yield estimates for the Bondi radius of 6 × 105 M and 4 × 105 M, respectively. The several orders of magnitude separation between the Bondi radius and the event horizon makes simulations of accretion from the Bondi radius onto SMBHs prohibitive for most numerical codes. In practice, due to temperature gradients, the local sound speed cs does not coincide with the escape velocity at the Bondi radius. This happens instead at the sonic radius
, yield estimates for the Bondi radius of 6 × 105 M and 4 × 105 M, respectively. The several orders of magnitude separation between the Bondi radius and the event horizon makes simulations of accretion from the Bondi radius onto SMBHs prohibitive for most numerical codes. In practice, due to temperature gradients, the local sound speed cs does not coincide with the escape velocity at the Bondi radius. This happens instead at the sonic radius 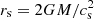 , which marks the transition from subsonic to supersonic flow. In Newtonian hydrodynamics, the case
, which marks the transition from subsonic to supersonic flow. In Newtonian hydrodynamics, the case  is degenerate and pushes the sonic radius to the origin. However, by incorporating relativistic corrections and assuming c∞ ≪ c, it takes a finite value that can be approximated as rs ≈ 3Mc/4c∞ (see, e.g., Rezzolla & Zanotti 2013). For the value of c∞ reported above, this corresponds to rs ≈ 409 M for Sgr A* and rs ≈ 335 M for M 87. The value rs = 500 M in our simulations is chosen accordingly within the same order of magnitude.
is degenerate and pushes the sonic radius to the origin. However, by incorporating relativistic corrections and assuming c∞ ≪ c, it takes a finite value that can be approximated as rs ≈ 3Mc/4c∞ (see, e.g., Rezzolla & Zanotti 2013). For the value of c∞ reported above, this corresponds to rs ≈ 409 M for Sgr A* and rs ≈ 335 M for M 87. The value rs = 500 M in our simulations is chosen accordingly within the same order of magnitude.
Following the same relativistic Bondi models, the dimensionless temperature at the sonic radius can be estimated to be Θ := kBT/mc2 = 7.3 × 10−4 − 8.8 × 10−4, where m is the ion mass and kB is the Boltzmann constant. For monoatomic hydrogen, this corresponds to T ≈ 8 × 109 K–1010 K (higher values correspond to M 87). The dimensionless temperatures attained at the sonic radius for our simulations are, similarly, Θ ≈ 8 × 10−4. Expecting it to to increase by orders of magnitude when approaching the black hole, we set 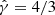 . The effective adiabatic index in this regime is very dependent on uncertain factors such as cooling and the ratio between ion and electron temperatures, and a more self-consistent generation the background solution may require the use of a relativistic equation of state as in Aguayo-Ortiz et al. (2021). However, a fully accurate modeling of these effects is beyond the scope of this project.
. The effective adiabatic index in this regime is very dependent on uncertain factors such as cooling and the ratio between ion and electron temperatures, and a more self-consistent generation the background solution may require the use of a relativistic equation of state as in Aguayo-Ortiz et al. (2021). However, a fully accurate modeling of these effects is beyond the scope of this project.
Turning to the second parameter, ℓ0, the specific angular momentum from stellar-wind accretion can be roughly estimated by 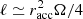 (Frank et al. 2002). Here, Ω is the orbital angular velocity of the star and
(Frank et al. 2002). Here, Ω is the orbital angular velocity of the star and 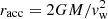 is the accretion radius for an assumed cold wind with a velocity of vw. Scaled to geometric units and for a star in Keplerian orbit with the semi-major axis a, we have
is the accretion radius for an assumed cold wind with a velocity of vw. Scaled to geometric units and for a star in Keplerian orbit with the semi-major axis a, we have
Thus, low-angular-momentum flows are indeed expected for these fiducial values. Focusing on a particular source, it was argued in Mościbrodzka et al. (2006) that the stellar complex known as IRS 13 E3 (Maillard et al. 2004) exerts the strongest ram pressure at the Galactic center, which renders it the dominant wind-accretion source. Thus, taking IRS 13 E3 with a fiducial wind velocity of 1000 km s−1 as an exemplary case and using the orbital fits by Mužić et al. (2008), we obtain ℓ in the 0.1 − 16 range. This large spread is caused by the wide range of admitted semi-major axes 0.1 pc−2.6 pc reported in Mužić et al. (2008).
As there are large uncertainties associated with the value of ℓ in the Galactic center and to gain insight into the parameter dependence, we here investigate three cases that correspond to the different qualitative behaviors of the background solution: a nonrotating case (ℓ = 0), a rotating case where the solution is complete, that is, it connects infinity and the event horizon (ℓ = 2.25) smoothly, and a rotating case with an incomplete solution (ℓ = 3.25). Incomplete solutions of flows coming from infinity are expected either to pass through a shock and transition to another smooth solution that reaches horizon or to represent flows that are unstable in the absence of viscosity. For a sufficiently viscous flow, some of these incomplete solutions can transition to a torus (Chakrabarti 1996). It should be noted that a complete solution can exist for ℓ, even when there is a circularization radius rcirc > rH at which ℓ is equal to the Keplerian angular momentum, as is the case for ℓ = 2.25 (rcirc ≈ 3.6 M). The reason is that fluid elements have a nonzero radial velocity and depending on their energy (part of which is internal) their centrifugal barrier is located further inside rcirc, and in some cases they can even cross the event horizon smoothly.
Although Ressler et al. (2020b) showed that the orientation of the flow angular momentum at horizon scales can vary wildly, these variations occur on scales of hundreds of years for Sgr A*. The simulations presented here have a much shorter duration – comparable to 14 days for the same source – which justifies the assumption that the orientation of the angular momentum is fixed.
Finally, the most uncertain parameter is the amplitude of injected perturbations. To explore several possibilities, we have considered a wide range with cases varying by orders of magnitude with respect to the inflow velocity at the boundary.
3. Results
3.1. Global properties
In this section, we briefly discuss and compare the salient global features of the simulations. We start by computing time series of the mass and angular-momentum flux through the event horizon:
where g is the metric determinant. To set a typical scale that can be compared with real systems, we normalized the accretion rate to the Bondi rate:
where
and ρ∞ and c∞ are the density and sound speed at infinity. In the units employed here, ρ is normalized so that ρ = 1 at r = 6 M, which leads to the numeric value ṀB ≈ 246 code mass units per gravitational timescale.
Figure 1 shows the time series in the interval t/M ∈ [30 000, 60 000]. The first important feature shown in Fig. 1 is the long-term stability of the horizon penetrating fluxes over the simulated timescales. While a quasi-stationary state is expected due the constant mass supply at the inflow boundaries, it is reassuring that accretion rates are nearly constant after ∼2 free-fall timescales.
 |
Fig. 1. Mass and angular-momentum flux through the event horizon for all of the simulations, starting from a time where perturbations reached the event horizon for all simulations. The upper horizontal scale measures time in units of the free-fall timescale from the sonic radius. |
As expected, there is a trend that relates a higher angular momentum with a lower mass-accretion rate. A larger amplitude of perturbations also appears to result in smaller accretion rates, likely due to the extra angular momentum provided by perturbations, which also contribute to centrifugal support. For instance, the addition of δ = 10 perturbations for the ℓ = 0 case reduces the accretion rate to a value of ∼ 0.75 ṀB, which is comparable to that obtained for the simulations for ℓ = 2.25 with smaller perturbations. The simulation with the largest perturbation and angular momentum possesses the smallest accretion rate, ≲ 0.25 ṀB.
Inspecting the accretion of angular momentum, the solutions show a surprising behavior; although it could be expected that a flow with larger angular momentum would result in more angular momentum accreted by the black hole, the simulations with ℓ = 2.25 actually register slightly more angular momentum accretion than those with ℓ = 3.25. Normalizing the angular momentum accretion rate by the mass-accretion rate, as it appears in the bottom panel of Fig. 1, both cases show about the same value of 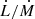 . The reason is likely that centrifugal support prevents matter from accreting and carrying angular momentum through the event horizon. In this respect, it is important to recall the qualitative difference between the unperturbed flow configurations corresponding to these two values; while ℓ = 2.25 allows solutions that connect smoothly infinity with the event horizon, ℓ = 3.25 produces an incomplete solution, which for the viscous case should connect to a rotation-supported torus where the flow is stalled (Chakrabarti 1996). It has been reported that pseudo-Newtonian numerical simulations performed using comparable angular momentum profiles form a thick torus close to the black hole. This torus has a nearly-constant angular momentum smaller than ℓ0 as a result of the replacement of high angular momentum material by low angular momentum material that inflows in the polar region and outflows along the equator (Proga & Begelman 2003a).
. The reason is likely that centrifugal support prevents matter from accreting and carrying angular momentum through the event horizon. In this respect, it is important to recall the qualitative difference between the unperturbed flow configurations corresponding to these two values; while ℓ = 2.25 allows solutions that connect smoothly infinity with the event horizon, ℓ = 3.25 produces an incomplete solution, which for the viscous case should connect to a rotation-supported torus where the flow is stalled (Chakrabarti 1996). It has been reported that pseudo-Newtonian numerical simulations performed using comparable angular momentum profiles form a thick torus close to the black hole. This torus has a nearly-constant angular momentum smaller than ℓ0 as a result of the replacement of high angular momentum material by low angular momentum material that inflows in the polar region and outflows along the equator (Proga & Begelman 2003a).
The time series in Fig. 1 shows different variability properties for each simulation, with those having higher ℓ and larger perturbations appearing more ‘noisy’. For the cases with ℓ = 3.25, this can be attributed again to the fact that the unperturbed solution is incomplete, producing shocks and complex interactions between the flow close to the centrifugal barrier even when the injected perturbations are small. However, it is interesting to see that the most variable time series corresponds to ℓ = 2.25, for the simulation l2p10, where peaks in Ṁ are sometimes even larger than the Bondi accretion rate. We diagnose the variability properties of the different solutions in more detail in Sect. 3.3.
Simulations with δ ≤ 1 and ℓ ≤ 2.25 show transient oscillations near the time at which the innermost grids become active (t ≈ 30 000 M) and decrease in amplitude and frequency as the evolution proceeds. These are especially noticeable for the cases ℓ = 0 for Ṁ and ℓ = 2.25 for 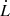 . For the other cases, the oscillations are masked by the larger perturbations.
. For the other cases, the oscillations are masked by the larger perturbations.
To quantify the departure of the perturbed solutions from the initial background solution, in Fig. 2 we show the angle- and time-averaged radial profiles for all simulations. These are computed as
where q = ρ, p/ρ. We also show ϕ averages of the rotation angular velocity on the equatorial plane Ω = uϕ/ut,
where axial symmetry has been used to eliminate the metric determinant. All quantities are then time-averaged over the interval t/M ∈ [50 000, 60 000]. We also plot the radial profiles expected for a self-similar ADAF model (Narayan & Yi 1994) with 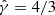 and no radiative cooling, as well as those of the unperturbed Chakrabarti solutions with ℓ = 0, 2.25, and 3.25, which are used as initial conditions and are exact on the equatorial plane.
and no radiative cooling, as well as those of the unperturbed Chakrabarti solutions with ℓ = 0, 2.25, and 3.25, which are used as initial conditions and are exact on the equatorial plane.
 |
Fig. 2. Radial profiles of density (left column), dimensionless temperature (middle column), and equatorial angular velocity (right column) averaged over angle and time in the interval t/M ∈ [50 000, 60 000] for all simulations. From top to bottom, the rows correspond to ℓ0 = 0, ℓ0 = 2.25, and ℓ0 = 3.25, and the different values of δ are indicated by the different colors. The shaded regions indicate the standard deviation. The dot-dashed lines show the power laws expected for an ADAF with |
For all simulations, the density profiles (left column of Fig. 2) are well described by an ADAF profile of ρ ∝ r−3/2, which also holds approximately for the initial condition. In particular, the profiles are inconsistent with the shallower convective solution ρ−1/2, indicating that convection is not important in our parameter regime (Narayan et al. 2000).
Although the averaged density profiles shown in Fig. 2 are smooth, some of the simulations exhibit density jumps at individual snapshots, in which case the profile possess the same slope at either side of the jump. These are present in the simulations with high angular momentum and large perturbations. As we discuss in Sect. 3.2, they are related to shocks that propagate outwards as they are smoothed away. Traces of these jumps are visible in the profiles of simulations with ℓ = 3.25 (especially of l3p10) at scales of r = 102 − 103 M. These are expanding shocks produced by the fluid colliding with the centrifugal barrier, such as those studied by Suková et al. (2017). The slow evolution timescales near the outer boundary prevent them from being smoothed by the time average.
The averaged profiles of p/ρ ∝ Θ in the central column of Fig. 2 show a more interesting behavior. While initially they coincide with those of the Chakrabarti solutions, those corresponding to ℓ = 3.25 and δ = 10 gradually transition to the profile of the ADAF solution. The clearest case is that of simulations l0p10 and l2p10, which transition form the constant-entropy initial profile (∝r−1/2 for the Bondi solution) to that of the ADAF model ∝r−1 at r ≈ 40 M.
The rise of the temperature profile close to the black hole is likely a result of heating by shocks and turbulence, which transform the kinetic energy injected through the perturbations in the velocity to thermal energy. It can be noticed that the temperature profiles of l0p1 and l2p1 start rising as well and deviate from the initial profile at a shorter distance from the black hole. This suggests that the radius at which the transition to an ADAF-like profile occurs is indeed related to the amplitude of perturbations in the medium. The fact that l0p10 acquires an ADAF-like temperature profile close to the black hole is interesting. In fact, this simulation differs from the scenario studied by Narayan & Yi (1994) from which the self-similar solution is derived. Here, there is no coherent disk-like structure, and the average of Ω is close to zero (see rightmost panel of Fig. 2). It is therefore surprising that the heating provided by incoherent shocks and turbulence results in a temperature profile similar to that of a coherent viscous rotating flow.
The rightmost column of Fig. 2 shows the angular velocity profile for all simulations. As expected, the profiles corresponding to the cases with zero angular momentum in the unperturbed solution show negligible rotation velocity on the equatorial plane. The rest of the profiles behave in a similar way to those of dimensionless temperature: they follow the Chakrabarti constant angular momentum profile at large radii (yielding a power-law slope of −2 far from the black hole) and transition to the ADAF-like Keplerian profile, ∝r−3/2, at smaller radii.
In general, it appears that at large distances the system is well described by the adiabatic Bondi- and Chakrabarti-like solutions, while once perturbations become sufficiently amplified by the geometry of the flow to produce shocks and turbulence, entropy production starts and the system becomes better described by ADAF-like profiles.
We also obtain information on the overall structure of the horizon-scale flow by computing ϕ- and time-averaged angular profiles evaluated at a fixed radius. Figure 3 shows these θ profiles for density, temperature, and the radial component of the four-velocity, evaluated at r = 20 M and normalized by the values of the Bondi-Michel solution at the same radius.
 |
Fig. 3. Angular profiles of density (left column), dimensionless temperature (middle column), and radial component for the four-velocity (right column) measured at r = 20 M, averaged over the time interval t/M ∈ [50 000, 60 000] for all simulations. All quantities are normalized to those of the Bondi-Michel solution at the same radius. Similarly to what is shown in Fig. 2, the rows from top to bottom correspond to ℓ0 = 0, ℓ0 = 2.25, and ℓ0 = 3.25, and the different values of δ are indicated by the different colors. The shaded regions indicate the standard deviation. In most of the panels, the profiles for δ = 0.01 and δ = 0.1 overlap completely. |
As could be expected, the cases with ℓ0 ≠ 0 break the spherical symmetry and produce a decrease in the inflow velocity around the equatorial plane as a consequence of the centrifugal support. For the largest angular momentum cases, the averaged radial velocity becomes positive, indicating the presence of an equatorial outflow. The decrease in radial velocity is accompanied by a maximum in averaged density on the equatorial plane for all cases with ℓ0 = 3.25 and almost all cases with ℓ0 = 2.25. The only exception is the case with the largest perturbation amplitude, for which the effect of chaotic motion prevails over that of rotation.
Cases with the largest perturbation amplitude also show profiles with larger densities and temperatures. This is a consequence of the modified radial profiles due to entropy production at shocks, as it was discussed above when describing Fig. 2.
Although these angular profiles are very informative, they have limited use when attempting to extract other quantities, such as the disk scale ratio, which are reliable only if the structure is symmetric with respect to the z axis. This is not always the case in our models; therefore, averaging regions inside and outside disk-like structures together results in the underestimation of outflows and density peaks in the disk plane and the overestimation of the disk thickness. In the next section, we explore the three-dimensional morphology of our models in more detail.
3.2. Three-dimensional morphology
Figures 4 and 5 show the density distribution for all the simulations on the equatorial and the meridional plane, respectively, at t = 60 000 M. The four simulations with lowest ℓ and perturbation amplitude, l0p001, l2p001, l0p01, l2p01 are always smooth and highly symmetric, and are practically indistinguishable from the initial conditions. Changes start becoming visible for those with perturbations comparable to the incoming radial velocity, l0p1 and l2p1, for which near-radial filaments can be seen.
 |
Fig. 4. Logarithmic density maps for all simulations at t = 60 000 M on the equatorial plane. Panels are organized in the same way as simulations in Table 1, that is, increasing angular momentum from left to right and perturbation amplitude from top to bottom. Movies of simulations l0p10, l2p10, and l3p10, are available online. |
The simulations with higher angular momentum are qualitatively different, as could be expected due to the incompleteness of the Chakrabarti solution. In all of the ℓ = 3.25 runs, it is possible to see the formation of a turbulent torus-like structure close to the black hole. The larger the perturbations are, the more misaligned this structure becomes with respect to the large-scale angular momentum, which points into the +z direction (rightmost panels of Fig. 5).
Despite the apparent similarity of these configurations with those in BHT simulations, they exhibit significant differences. While for BHT simulations the toroidal structure is confined mainly by the equilibrium between gravity and the centrifugal force, for the simulations presented here it consists in large part of unbound outflowing matter that is confined by its interaction with inflowing matter. In addition, while for BHT simulations most of the accretion flow occurs in the equatorial plane, here the toroidal structure is an obstacle for the inflowing matter, causing most of the accretion to occur through the poles. This behavior is consistent with that observed for similar systems in the absence of magnetic fields, for example, by Proga & Begelman (2003a), Moscibrodzka & Proga (2008), and Suková et al. (2017). We also expect that the inclusion of magnetic fields will reverse the situation by producing accretion on the equatorial plane and a polar outflow (Proga & Begelman 2003b).
Figures 6 and 7 show the relative pressure gradient as proxy for the location of shocks. The simulations with low ℓ0 and δ (l0p001, l2p001, l0p01, l2p01) do not show significant pressure gradients. In contrast, those with ℓ0 = 3.25 and δ ≤ 1 (l3p001, l3p01, and l3p1) show clear spiral shocks. This coherent large-scale shock does not form in the strongly perturbed case δ = 10. The color map in Figs. 6 and 7 also allows us to see sound waves traveling within the shocked regions.
 |
Fig. 6. Shocks and sonic surfaces for all simulations at t = 60 000 M. The color scale displays the relative pressure gradient, which is used as a proxy for shock locations, and the dashed lines indicate the static limits of the sonic metric. |
It is also interesting to examine to what extent the causal structure of the flow is preserved in the presence of perturbations and high angular momentum. The dashed lines in Figs. 6 and 7 mark the surfaces for which the four-velocity of an observer at rest at infinity, ∂t = (1, 0, 0, 0), becomes null with respect to the sonic metric (Moncrief 1980)
where ρ is the rest-mass density, h is the enthalpy, cs is the sound speed, and uμ is the four-velocity of the fluid. This condition is analogous to that defining static surfaces such as ergoregions and event horizons for the space-time metric, gμν, and can be used to characterize transitions between subsonic and supersonic flows in an invariant way (Aguayo-Ortiz et al. 2021), especially in situations that lack symmetries such as the perturbed flows studied here.
The sonic surface for the unperturbed solutions is a sphere with a radius of rs = 500 M centered at the black hole. Its structure is practically unchanged for the four cases with lowest ℓ0 and δ (l0p001, l2p001, l0p01, l2p01). Cases with ℓ0 ≤ 2.25 and δ = 1 (l0p1, l2p1) exhibit slight but noticeable changes in the shape of the sonic surface, although it remains close to rs. This is remarkable since perturbations already have an amplitude similar to the magnitude of the inflow radial velocity at the boundary. Only when the perturbation amplitude is ten times the inflow radial velocity (l0p10, l2p10) do we see large incursions of subsonic matter inside rs, as well as islands of supersonic (subsonic) flow within the former subsonic (supersonic) regions.
Models with ℓ0 = 3.25 show a more complex causal structure. The spiral shock produces an additional transition from supersonic to subsonic flow, and it can erase the original sonic surface as it propagates outwards. However, downstream the flow can become supersonic again. The spiral structure can then produce several sonic transitions between the distant regions, where matter is injected subsonically, and the event horizon, which needs to be crossed supersonically. For instance, in the panel of Fig. 6 that corresponds to simulation l3p1, there can even be five sonic transitions when approaching the black hole from certain directions. For the case with δ = 10, l3p10, the original sonic surface has disappeared completely and a new one has formed closer to the black hole. Also in this case, the spiral shock produces more than one sonic transition in some directions.
In addition to the entropy increase due to shocks, turbulence could also play a role in heating the fluid and contribute to the transition from a constant entropy temperature profile to an ADAF-like profile, as shown in the middle panel of Fig. 2. In order to highlight the presence of turbulence, Fig. 8 shows the z-component of the vorticity vector on the equatorial plane for simulations l3p001 and l0p10. The ℓ0 = 0 case shows vorticity sheets that can be associated with fluid streams approaching the black hole at different speeds and suggests the emergence of smaller turbulent structures if simulated at a higher resolution.
 |
Fig. 8. Vertical component of equatorial plane vorticity for simulations l3p001 and l0p10. |
For the incomplete ℓ0 = 3.25 analytical solution, the fluid is expected to form a torus at the circularization radius rcirc ≈ 8.8 M, and no presence of fluid is expected at smaller radii. However, in all of our simulations we observe the flow occupying this region without impediment, meaning that a means of angular momentum redistribution is operating. The same can also be inferred from the rotation velocity profiles in the rightmost panel of Fig. 2, where several of them transition from constant to Keplerian angular momentum profiles. This indicates that even in the absence of magnetic fields, and thus MRI and large-scale Maxwell stresses, angular momentum redistribution occurs, and it can be attributed to shocks and turbulence that could easily appear in nature.
3.3. Variability properties
To have a rough estimation of the observable properties of the variability in our simulations, we computed synthetic X-ray light curves by integrating the total bremsstrahlung emissivity from free-free electron-ion collisions (Rybicki & Lightman 1986):
where Z is the atomic number of ions, mi is the ion mass, mp is the proton mass, and ni is the scaling factor that relates the dimensionless code density ρ with the ion number density niρ. The Gaunt factor has been assumed to be constant and equal to 1.2. The integration is performed as
where Γ is the Lorentz factor, and the prefactor comes from the conversion of volume in geometrized code units to physical units. Here, γ is the determinant of the spatial metric, γμν = gμν + nμnν, where nμ is the four-velocity of Eulerian observers.
The synthetic light curves within t/M ∈ [50 000, 60 000] for each simulation are shown in Fig. 9. The parameters have been chosen for monoatomic hydrogen, with ni = 106 cm−3 and M as the mass of Sgr A*, M = 4.15 × 106 M⊙. This gives luminosities that agree in terms of order of magnitude with the ≈2.4 × 1033 erg s−1 estimated by Baganoff et al. (2003). For this source, the time interval corresponds to ≈55.5 h of observing time. We calculated spectrograms in this interval using the Welch method (Welch 1967) with time windows overlapping by 128 points (=128 M). The power spectral densities (PSDs) are shown in the left panel of Fig. 10. It can be seen that, as expected, the power of fluctuations increases with the amplitude of the injected perturbations and with the angular momentum. The two simulations with zero angular momentum and smallest perturbations show small frequency peaks that are lost into the noise for the other cases.
 |
Fig. 9. Synthetic light curves of total bremsstrahlung luminosity using parameters of Sgr A*, for all simulations. The curve corresponding to l0p001 overlaps that of l0p01 completely. The upper horizontal axis displays the time in hours. |
 |
Fig. 10. Spectrograms (left) and correlation functions (right) of bremsstrahlung light-curve proxy of all simulations. Dashed lines with slopes of power laws are shown for comparison in the left panel, and they bind the region between ±1/e in the right panel. The upper horizontal axes have been scaled for Sgr A*. |
As perturbations and angular momentum increase, it is possible to observe a steepening in the slope of the PSD. Simulations with ℓ0 = 3.25 or δ = 10 show a very similar spectrum with a break from white noise to red noise around f ∼ 10−2 M−1. Power laws of red noise f−2 and f−4 are shown for comparison. Spectrograms are calculated over a frequency range higher than that of the injected perturbations (see Sect. 2), which therefore do not appear in the PSD.
We Fourier-transformed these spectrograms in order to obtain autocorrelation functions, corr(LBR, LBR), for the synthetic light curve. For all of the simulations, positive correlations decay below 1/e in about τ ∼ 5 − 15 M. However, autocorrelations for noisier simulations (ℓ0 = 3.25 or δ = 10), are close to zero for τ ∼ 30 M (≈10 min for Sgr A*), while simulations with small angular momentum and perturbations still exhibit longer term positive and negative correlations.
Overall, the correlation timescales are shorter than 40 M for all simulations, which allows us to calculate modulation indices σ/μ for statistically uncorrelated data by computing the standard deviation σ and average μ over points separated by 50 M. Modulation indices are shown in Table 2. The modulation index of the mass-accretion rate through the event horizon in the same time interval is shown in parentheses. The fact that the latter does not show as much variation when the former varies by orders of magnitude indicates that a significant portion of bremsstrahlung variability is not related to fluctuations in the accretion rate close to the horizon. Instead, the bremsstrahlung modulation index clearly increases for simulations in which shocks and turbulence are present.
Modulation index of the bremsstrahlung luminosity light curve and the mass-accretion rate through the event horizon (in parentheses), computed over the interval t/M = [50 000, 60 000].
In order to investigate the origin and properties of the fluctuations observed in the mass-accretion rate, we calculated PSDs of Ṁ(r,t) at several radial shells. These are shown for selected radii and for all the simulations in Fig. 11, for the same interval used for the analysis of the synthetic bremsstrahlung light curve and using the same methodology as in Sect. 3.3.
 |
Fig. 11. Power spectral density of mass-accretion rate measured at different radii for all simulations during t/M ∈ [50 000, 60 000] interval. The dashed line represents a power law proportional to f−2. |
It is evident that in general the spectrum at event-horizon scales differs significantly from that at large distances. In most of the panels it is possible to see higher frequencies increasingly populated as one moves closer to the black hole. This can be interpreted as the transfer of energy from longer lower frequency modes to smaller and faster modes, and it could be due to the change in the characteristic scale of the system as the fluid moves inwards, as well as to the development of turbulence. Cases producing shocks (ℓ0 = 3.25 and δ > 1) show a larger power, and the spectrum at the smaller radius acquires the form of a power law ∝r−2 or steeper. The rest of the cases with ℓ0 = 2.25 show a flatter spectrum close to white noise. Similarly as for bremsstrahlung spectrograms, for cases with ℓ0 = 0 and δ = 0.01, 0.1, the spectrum of Ṁ has very little power and is dominated by oscillation peaks. These appear within r ≤ 15 M, indicating that, for almost unperturbed Bondi-like accretion, fluctuations in bremsstrahlung emission do appear related to these fluctuations in Ṁ close to the horizon. In contrast, our results suggest that for sufficiently large perturbations, as those injected manually or those produced by the movement of the spiral shock, a red noise spectrum will be recovered, regardless of the injected perturbation spectrum.
Finally, it should be mentioned that a realistic X-ray emission model for the flow at these scales, if applied to Sgr A*, should also take into account synchrotron radiation and Compton scattering, which for our non-magnetized models would require additional assumptions. In addition, observed X-ray light curves are believed to contain an important component from near-horizon flares, which were not modeled in this work. However, although not directly comparable to Sgr A* observations, the analysis performed in this section is useful as a first step to understand the variability properties of our models. We leave a more realistic modeling for a future work including magnetic fields, which will also make the generation of synthetic light curves at 230 GHz possible.
4. Discussion and conclusions
In this work, we used three-dimensional GRHD simulations to study the structure and variability patterns in perturbed transonic accretion flows with low-angular momentum. Our aim was to explore an accretion scenario that generalizes torus simulations, is more consistent with the properties of stellar wind-fed accretion, and is controlled by a reduced set of parameters. Our simulation setup also aims to overcome two of the known limitations of the BHT simulation paradigm, namely the secular decrease in torus mass that complicates long-term variability studies and the artificiality of the medium beyond the close vicinity of the black hole. We evaluated the general properties of this accretion scenario using several diagnostics, namely (1) the time series of the mass-accretion rate and angular momentum flux through the event horizon, (2) shell- and time-averaged profiles of several quantities of interest, and (3) a synthetic bremsstrahlung light curve used to analyze its variability properties. We also investigated the three-dimensional morphology of the models, including the location of shocks and sonic surfaces.
Our models, contrary to BHT simulations, have accretion rates that do not decay exponentially, allowing for long-term variability studies. We observe that Ṁ decreases significantly for models with larger angular momentums and perturbation amplitudes. This is consistent with the additional centrifugal support provided by angular velocities and the additional pressure support due to heating caused by turbulence and shocks, which are also more important for the same models. The reduction in mass-accretion rate for larger angular momentum models also results in a smaller net angular momentum flux through the horizon, suggesting that there is a finite value of ℓ0 that maximizes the accretion of angular momentum.
The fact that these models are fed from solutions that extend to infinity allows us to relate the mass-accretion rate on horizon scales to the Bondi accretion rate from the medium properties on large scales. This in turn permits us to obtain tighter constraints on the models. For example, density scales need to match large-scale fluid properties in addition to electromagnetic flux constraints derived from radiative transfer calculations.
In addition to their significant variations in accretion rate, the flows we studied possess a rich phenomenology and are in some respects qualitatively different both from BHT simulations and from unperturbed transonic flows. Some of the salient features we observe include outflowing toroidal structures, turbulence, shocks, filaments, and multiple sonic transitions.
Deviations from the transonic solutions used as initial conditions are in some cases large enough to lead to different averaged temperature and velocity profiles. In particular, models with large perturbations and angular momentum deviate from the isentropic temperature profiles and transition to profiles similar to those of an ADAF. For the cases initialized from complete solutions (ℓ0 = 0 and ℓ0 = 2.25), the radius at which the transition occurs seems related to the amplitude of perturbations. This can be explained from the instability of supersonic spherical accretion to nonradial perturbations (Kovalenko & Eremin 1998). These perturbations grow without limit with smaller radii, producing the “ADAF transition” when they become large enough to produce shocks and generate entropy, which depends on the injected perturbation amplitude.
For the cases initialized from the incomplete solutions with small perturbation amplitudes, large-scale spiral shocks are produced by the interaction between the inflowing fluid and the centrifugal barrier. They likely play an important role in transporting angular momentum outwards and thus enabling accretion of matter and the transition to a Keplerian rotation profile at small radii in the absence of a magnetic field.
In the context of chaotic cold accretion (e.g., Gaspari et al. 2017; Prasad et al. 2017), it has been suggested that inelastic collisions between clouds can cancel angular momentum, leading to an increased accretion rate. In the simulations presented here, shocks could be expected to play a similar role; however, even simulations where shocks are present show the same trend that relates larger perturbations and angular momentum with smaller accretion rates. The reason could be that shocked simulations are precisely those with larger perturbations and angular momentum, and this effect needs to compete with the additional support provided by angular velocities and the pressure from gas heated by shocks and turbulence.
As could be expected, the different qualitative behavior results in different variability properties of the simulations. However, we found that for sufficiently large angular momentum and perturbations, a red noise spectrum is robustly recovered, even from white noise injection perturbations.
Our simulations are complementary to similar hydrodynamical simulations carried out by other authors. Ressler et al. (2018) used a conservative hydrodynamics code to study the formation of the accretion flow onto Sgr A* in which matter is constantly supplied by stars on orbits around the central black hole. This setup leads to a somewhat chaotic accretion. Although their simulation domain is much larger in comparison to ours, their inner boundary overlaps with our outer boundary. Ressler et al. (2018) obtained solutions with density and temperature power-law profiles, ∝r−1, that are different to our results. Also, the angular momentum in our simulations is significantly lower than the value they obtained at comparable radii (Ressler et al. 2018, Fig. 14 reports that the ℓ ≈ 0.4 − 0.5ℓK at the inner boundary). These differences in the profiles could be explained by the differences in the physical scenario considered. In their case, these include stronger rotation, the presence of important outflows, as well as line and bremsstrahlung cooling, which becomes significant at the scales they considered. Similarly, very large-scale simulations performed by Guo et al. (2023) studied the formation of the accretion pattern at event horizon scales following material from the Bondi radius scale in elliptical galaxies such as M 87. The information obtained from these works and future large-scale simulations can be incorporated to smaller scale simulation setups such as those presented in this work (e.g., by specifying initial density profiles and the spatial and temporal spectrum of injected perturbations).
In a setting more similar to ours, Suková et al. (2017) used two-dimensional and three-dimensional conservative GRHD simulations to study low-angular-momentum flows on closer-to-horizon scales, but without manually injecting perturbations. In the tests we performed while implementing our initial condition, we recovered the general behavior of some of their two-dimensional models, although there were some differences in implementation and parameter choices, which we describe in Appendix A.
The inclusion of magnetic fields in the simulations will be presented in a forthcoming publication; however, there are a few expectations we can draw from our hydrodynamic models that could be relevant for observations. For example, the fact that the accretion pattern is almost isotropic for cases with low angular momentum ℓ0 ≤ 2.25 may result in images that are also independent of orientation, in particular in contrast to Standard and Normal Evolution (SANE) BHT models. In addition, the possibility of producing synthetic synchrotron light curves that do not suffer from secular torus depletion may contribute to some extent to unravelling the ongoing discussion on the suitability of GRMHD models to meet the tight variability constraints given by 230 GHz observations of Sgr A* (Event Horizon Telescope Collaboration 2022). We also expect magnetic fields to introduce an even richer phenomenology, which may include reconnection-driven turbulence and the formation of relativistic jets and outflows. These expectations are based on the simulations of magnetized low angular-momentum accretion, which can be found in the works of Igumenshchev & Narayan (2002), Pen et al. (2003), Pang et al. (2011), and Ressler et al. (2021). Overall, we believe our simulations are an important middle step towards obtaining more realistic models of relativistic accretion flows in which matter is supplied by the turbulent interstellar medium.
Movies
Movie 1 associated with Fig. 4 (rho_l0p10_comp) Access here
Movie 2 associated with Fig. 4 (rho_l2p10_comp2) Access here
Movie 3 associated with Fig. 4 (rho_l3p10_comp2) Access here
Acknowledgments
We thank Jesse Vos, Aristomenis Yfantis, Alejandra Jimenez-Rosales, Christiaan Brinkerink and other members of the EHT group at Radboud University for discussions. We also thank Jordy Davelaar, Agnieszka Janiuk and Daniel Proga for their comments. H.R.O.S. was supported part by a Virtual Institute of Accretion (VIA) postdoctoral fellowship from the Netherlands Research School for Astronomy (NOVA). We acknowledge that the results of this research have been achieved using the DECI resource Snellius based in the Netherlands at SURF with support from the PRACE AISBL. This work made use of the following software libraries not cited in the text: MATPLOTLIB (Hunter 2007) and NumPy (Harris et al. 2020). This research has made use of NASA’s Astrophysics Data System.
References
- Aguayo-Ortiz, A., Tejeda, E., Sarbach, O., & López-Cámara, D. 2021, MNRAS, 504, 5039 [CrossRef] [Google Scholar]
- Baganoff, F. K., Maeda, Y., Morris, M., et al. 2003, ApJ, 591, 891 [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [Google Scholar]
- Chakrabarti, S. K. 1989, ApJ, 347, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K. 1996, ApJ, 471, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., & Das, S. 2004, MNRAS, 349, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S. K., & Molteni, D. 1995, MNRAS, 272, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Cuadra, J., Nayakshin, S., & Martins, F. 2008, MNRAS, 383, 458 [NASA ADS] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L5 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2021, ApJ, 910, L13 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Fishbone, L. G., & Moncrief, V. 1976, ApJ, 207, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition (Cambridge: Cambridge University Press) [Google Scholar]
- Fukue, J. 1987, PASJ, 39, 309 [NASA ADS] [Google Scholar]
- Garain, S. K., & Kim, J. 2023, MNRAS, 519, 4550 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Temi, P., & Brighenti, F. 2017, MNRAS, 466, 677 [Google Scholar]
- Guo, M., Stone, J. M., Kim, C.-G., & Quataert, E. 2023, ApJ, 946, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Igumenshchev, I. V., & Narayan, R. 2002, ApJ, 566, 137 [CrossRef] [Google Scholar]
- Janiuk, A., Proga, D., & Kurosawa, R. 2008, ApJ, 681, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Sznajder, M., Mościbrodzka, M., & Proga, D. 2009, ApJ, 705, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J., Garain, S. K., Balsara, D. S., & Chakrabarti, S. K. 2017, MNRAS, 472, 542 [CrossRef] [Google Scholar]
- Kim, J., Garain, S. K., Chakrabarti, S. K., & Balsara, D. S. 2019, MNRAS, 482, 3636 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalenko, I. G., & Eremin, M. A. 1998, MNRAS, 298, 861 [CrossRef] [Google Scholar]
- Lalakos, A., Gottlieb, O., Kaaz, N., et al. 2022, ApJ, 936, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzafame, G., Molteni, D., & Chakrabarti, S. K. 1998, MNRAS, 299, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Löhner, R. 1987, Comput. Meth. Appl. Mech. Eng., 61, 323 [CrossRef] [Google Scholar]
- Maillard, J. P., Paumard, T., Stolovy, S. R., & Rigaut, F. 2004, A&A, 423, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel, F. C. 1972, Astrophys. Space Sci., 15, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra, S., Maity, D., Dihingia, I. K., & Das, S. 2022, MNRAS, 516, 5092 [CrossRef] [Google Scholar]
- Molteni, D., Sponholz, H., & Chakrabarti, S. K. 1996, ApJ, 457, 805 [CrossRef] [Google Scholar]
- Moncrief, V. 1980, ApJ, 235, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Moscibrodzka, M., & Proga, D. 2008, ApJ, 679, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Mościbrodzka, M., Das, T. K., & Czerny, B. 2006, MNRAS, 370, 219 [CrossRef] [Google Scholar]
- Murchikova, L., & Witzel, G. 2021, ApJ, 920, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Murchikova, L., White, C. J., & Ressler, S. M. 2022, ApJ, 932, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Mužić, K., Schödel, R., Eckart, A., Meyer, L., & Zensus, A. 2008, A&A, 482, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [Google Scholar]
- Narayan, R., Igumenshchev, I. V., & Abramowicz, M. A. 2000, ApJ, 539, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Okuda, T., Teresi, V., Toscano, E., & Molteni, D. 2004, PASJ, 56, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Okuda, T., Singh, C. B., Das, S., et al. 2019, PASJ, 71, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Olivares, H., Porth, O., Davelaar, J., et al. 2019, A&A, 629, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pang, B., Pen, U.-L., Matzner, C. D., Green, S. R., & Liebendörfer, M. 2011, MNRAS, 415, 1228 [NASA ADS] [CrossRef] [Google Scholar]
- Pen, U.-L., Matzner, C. D., & Wong, S. 2003, ApJ, 596, L207 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Olivares, H., Mizuno, Y., et al. 2017, Comput. Astrophys. Cosmol., 4, 1 [Google Scholar]
- Porth, O., Chatterjee, K., Narayan, R., et al. 2019, ApJS, 243, 26 [Google Scholar]
- Prasad, D., Sharma, P., & Babul, A. 2017, MNRAS, 471, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., & Begelman, M. C. 2003a, ApJ, 582, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., & Begelman, M. C. 2003b, ApJ, 592, 767 [CrossRef] [Google Scholar]
- Quataert, E. 2004, ApJ, 613, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2018, MNRAS, 478, 3544 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., Quataert, E., & Stone, J. M. 2020a, MNRAS, 492, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- Ressler, S. M., White, C. J., Quataert, E., & Stone, J. M. 2020b, MNRAS, 896, L6 [Google Scholar]
- Ressler, S. M., Quataert, E., White, C. J., & Blaes, O. 2021, MNRAS, 504, 6076 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., & Zanotti, O. 2013, Relativistic Hydrodynamics (Oxford: Oxford University Press) [CrossRef] [Google Scholar]
- Russell, H. R., Fabian, A. C., McNamara, B. R., & Broderick, A. E. 2015, MNRAS, 451, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Berlin: Wiley-VCH) [Google Scholar]
- Shcherbakov, R. V., & Baganoff, F. K. 2010, ApJ, 716, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Suková, P., Charzyński, S., & Janiuk, A. 2017, MNRAS, 472, 4327 [CrossRef] [Google Scholar]
- Welch, P. D. 1967, IEEE Trans. Audio Electroacoust., 15, 70 [CrossRef] [Google Scholar]
- Wielgus, M., Moscibrodzka, M., Vos, J., et al. 2022, A&A, 665, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Initial conditions
Our initial data are constructed from the semi-analytic rotating transonic solutions by Chakrabarti (1996). These can be thought of as a generalization of a Michel accretion (Michel 1972) for a rotating flow and for the Kerr metric.
To solve for the fluid properties, one assumes that streamlines are radial when projected on the meridional plane (that is, θ components of the velocity are neglected). The mass flux 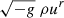 , entropy, internal energy ℰ = hut, and angular momentum ℒ = −huϕ = ℓℰ are conserved along each streamline.
, entropy, internal energy ℰ = hut, and angular momentum ℒ = −huϕ = ℓℰ are conserved along each streamline.
Similarly to the cases of Michel and Bondi accretion, once ℒ is specified, ℰ can be chosen so that the sonic radius is at the desired position. The flow configuration is then found by solving a pair of coupled, nonlinear algebraic equations for the sound speed and the radial velocity in the co-rotating frame at every point (Equations 30a,b of Chakrabarti 1996). The equations do not constrain the density scale, which can be chosen later. In our case, we set it so that ρ = 1 at r = 6 M.
Accretion solutions of these equations have a wide variety of qualitative behaviors. A class of solutions connects infinity and the event horizon smoothly, similarly to the Michel solution. Other solutions possess incomplete interior or exterior branches that can be connected by a shock, and incomplete solutions that have a sonic point but do not extend supersonically to the event horizon also exist (see Figure 2 and Section 4.1 of Chakrabarti 1996 for a complete description). For simplicity, we always solve only the exterior branch of the solution.
To initialize our simulations, we solve the system on a grid covering the range θ ∈ [0, π/2] with 300 points. The supersonic part of each streamline was solved with 300 points and the subsonic part with 100 points, both logarithmically spaced in radius. The calculated part of the subsonic region extends beyond the simulation domain by 10% in order to be be used for the boundary conditions.
The approximation of projected radial streamlines is, in general, inconsistent with vertical equilibrium, however it holds on the equatorial plane. For this reason, we chose an angular momentum profile with a sharp peak at the equator that decays to ℓ = 0 at the poles, where again vertical equilibrium is fulfilled (Equation 4).
In order to evaluate the adequacy of this approximation and to test that the solution reproduced the expected qualitative behavior, we performed two-dimensional simulations evolving only the initial condition without injecting any perturbation. Figure A.1 shows two-dimensional maps of rest-mass density and mass-accretion rate per θ angle for some of the two-dimensional simulations we performed for a = 0.95 and different angular momenta. As expected, for cases where the equatorial solution connects the event horizon and infinity (ℓ = 1.75, 2.25), the artificial initial condition quickly relaxes to a true solution in vertical equilibrium and remains stable until the end of the simulation. Figure A.2 shows the evolution of the radial four-velocity profile of the unperturbed solution used for simulations with ℓ = 2.25 at different latitudes. At ∼150 M, the configuration has already relaxed to a stationary flow. This is adequate for our simulations, which have durations over 100 times longer.
 |
Fig. A.1. Rest-mass density and mass-accretion rate per θ angle for two-dimensional evolutions of unperturbed initial conditions with different angular momentum. |
 |
Fig. A.2. Equatorial cuts of radial velocity of background flow at different times and latitudes for the case of ℓ = 2.25. |
For incomplete solutions (ℓ = 2.75, 3.25), material accreting on the equatorial plane starts piling up due to the centrifugal barrier, while accretion continues through the poles. The dense toroidal structure that forms is different from the tori commonly used in simulations in that it consists of “outflowing” unbound material, which produces a shock when interacting with the incoming accretion flow. Since there is no cooling, these structures grow until the end of the simulation (Molteni et al. 1996). As described in Section 3.2, these shocks are also present in three-dimensional simulations; however, the lack of azimuthal symmetry introduces important differences, such as the presence of turbulence in the ϕ direction and the change in shape of the shock from spheroidal to spiral.
Our two-dimensional unperturbed simulations show a behavior that is consistent with that reported by Suková et al. (2017). A difference with respect to that work is that their initial condition is a Bondi flow to which rotation has been added, while in our case it is a solution including rotation in a more self-consistent way (albeit exact only on the equatorial plane and the poles), for which the assumption of low angular momentum is not necessary. Another difference is that Suková et al. (2017) largely focused on studying the parameter regime that produces oscillating shocks, which we did not explore.
Appendix B: Boundary conditions
To emulate the turbulent flow entering from the boundary, we filled the ghost zones with the same transonic solution used as initial condition and added time-dependent noise in the form of Gaussian random fields (GRFs). These fields are generated as the superposition of plane waves with random phases.
The usual way of generating a time-dependent GRF in N dimensions is by Fourier-transforming white noise in N + 1 dimensions, multiplying the Fourier transform by the desired PSD, and then transforming it back. One can then obtain time-dependent noise by successively applying slices of the resulting N + 1-dimensional array.
Although this way of generating GRFs is very fast due to the elegance of the fast-Fourier transform (FFT) algorithm, it has some disadvantages that lead us to follow a different procedure. First, storing a large four-dimensional array and communicating it among different parallel processes to perform interpolations can be a source of implementation and performance problems, and, second, we did not desire to apply the noise in a full three-dimensional box, but only on the outer ghost cells, which make an almost two-dimensional spherical shell embedded in three-dimensional space.
For this reason, we built the GRF by directly evaluating a series of sine functions corresponding to plane waves with random phases at the cells of interest. This sum has the following form:
where k is a three-dimensional vector of integers, λmax is the maximum wavelength, f(k) is a function determined by a user-defined dispersion relation, and φk is the random phase corresponding to k. We drew random phases from a uniform distribution over [0, 1) using a pseudo-random number generator with a fixed seed, which allowed us to use the same random phases without the need to store them between restarts. In order to ensure causality, we used the constant dispersion relation f(k) = cs, where cs is the sound speed at the simulation boundary, although more complicated relations are also possible. The coefficients Ak are set according to the desired power spectral density Sk, such as Ak ∝ (Sk)1/2, and can be normalized to give the desired rms perturbation amplitude. We set Ak = 0 for k = (0, 0, 0) in order to keep the average of the GRF to zero.
In our simulation, we generated three GRFs to perturb the three spatial components of the four-velocity in Cartesian coordinates. We then transformed them to the code coordinates and added them only to the angular components of the velocity given by the background transonic solution.
As we decided not to use the FFT, we paid the price of having to evaluate a large number of transcendental functions, which can slow down the code significantly. We find that Nk = 5 gives a negligible slow down, and the smallest-wavelength mode has a size comparable to ∼1.6 cells of the outer boundary. This leads to Nθ × Nϕ × Nghost × Nfields × (2Nk + 1)3 = 12 266 496 evaluations of the sine function per time step, or 340 736 evaluations for each of the 8 × 8 × 8 AMR blocks at the boundary. Here, Nghost = 4 is the number of ghost zones in the radial direction and Nfields = 3, since each of the spatial components of the velocity is perturbed with a different GRF.
Finally, it is worth mentioning that, as it is a sum of periodic functions, the noise is also periodic with the period of the longest wavelength mode. Although this will generally not result in a periodic behavior of the simulation due to the changing chaotic dynamics inside the domain, it may be desirable to produce non-periodic noise models. One possibility could be to slightly change the dispersion relation so that the period of some of the modes is an irrational multiple of that of others. The search for more appropriate non-periodic noise models is, however, out of the scope of this work.
All Tables
Modulation index of the bremsstrahlung luminosity light curve and the mass-accretion rate through the event horizon (in parentheses), computed over the interval t/M = [50 000, 60 000].
All Figures
 |
Fig. 1. Mass and angular-momentum flux through the event horizon for all of the simulations, starting from a time where perturbations reached the event horizon for all simulations. The upper horizontal scale measures time in units of the free-fall timescale from the sonic radius. |
| In the text | |
 |
Fig. 2. Radial profiles of density (left column), dimensionless temperature (middle column), and equatorial angular velocity (right column) averaged over angle and time in the interval t/M ∈ [50 000, 60 000] for all simulations. From top to bottom, the rows correspond to ℓ0 = 0, ℓ0 = 2.25, and ℓ0 = 3.25, and the different values of δ are indicated by the different colors. The shaded regions indicate the standard deviation. The dot-dashed lines show the power laws expected for an ADAF with |
| In the text | |
 |
Fig. 3. Angular profiles of density (left column), dimensionless temperature (middle column), and radial component for the four-velocity (right column) measured at r = 20 M, averaged over the time interval t/M ∈ [50 000, 60 000] for all simulations. All quantities are normalized to those of the Bondi-Michel solution at the same radius. Similarly to what is shown in Fig. 2, the rows from top to bottom correspond to ℓ0 = 0, ℓ0 = 2.25, and ℓ0 = 3.25, and the different values of δ are indicated by the different colors. The shaded regions indicate the standard deviation. In most of the panels, the profiles for δ = 0.01 and δ = 0.1 overlap completely. |
| In the text | |
 |
Fig. 4. Logarithmic density maps for all simulations at t = 60 000 M on the equatorial plane. Panels are organized in the same way as simulations in Table 1, that is, increasing angular momentum from left to right and perturbation amplitude from top to bottom. Movies of simulations l0p10, l2p10, and l3p10, are available online. |
| In the text | |
 |
Fig. 5. Similar to Fig. 4, but for the meridional plane. |
| In the text | |
 |
Fig. 6. Shocks and sonic surfaces for all simulations at t = 60 000 M. The color scale displays the relative pressure gradient, which is used as a proxy for shock locations, and the dashed lines indicate the static limits of the sonic metric. |
| In the text | |
 |
Fig. 7. Similar to Fig. 6, but for the meridional plane. |
| In the text | |
 |
Fig. 8. Vertical component of equatorial plane vorticity for simulations l3p001 and l0p10. |
| In the text | |
 |
Fig. 9. Synthetic light curves of total bremsstrahlung luminosity using parameters of Sgr A*, for all simulations. The curve corresponding to l0p001 overlaps that of l0p01 completely. The upper horizontal axis displays the time in hours. |
| In the text | |
 |
Fig. 10. Spectrograms (left) and correlation functions (right) of bremsstrahlung light-curve proxy of all simulations. Dashed lines with slopes of power laws are shown for comparison in the left panel, and they bind the region between ±1/e in the right panel. The upper horizontal axes have been scaled for Sgr A*. |
| In the text | |
 |
Fig. 11. Power spectral density of mass-accretion rate measured at different radii for all simulations during t/M ∈ [50 000, 60 000] interval. The dashed line represents a power law proportional to f−2. |
| In the text | |
 |
Fig. A.1. Rest-mass density and mass-accretion rate per θ angle for two-dimensional evolutions of unperturbed initial conditions with different angular momentum. |
| In the text | |
 |
Fig. A.2. Equatorial cuts of radial velocity of background flow at different times and latitudes for the case of ℓ = 2.25. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



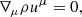
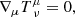
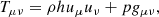
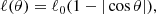
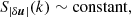
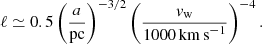
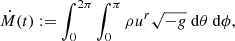
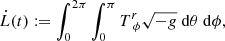
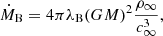
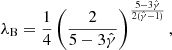
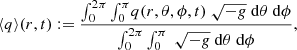
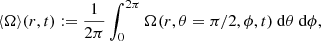
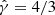
![$$ \begin{aligned} {\mathcal{G} }_{\mu \nu }= \frac{\rho }{h c_{\rm s}}\left[g_{\mu \nu } + (1 - c_{\rm s}^2) u_\mu u_\nu \right], \end{aligned} $$](/articles/aa/full_html/2023/10/aa46010-23/aa46010-23-eq27.gif)
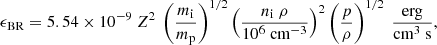
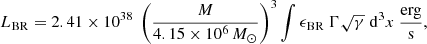
![$$ \begin{aligned} \mathrm{GRF}(t,x^i) = \sum _{k_1, k_2, k_3=-N_k}^{N_k} A_{\boldsymbol{k}} \sin \left[\frac{2\pi }{\lambda _{\rm max}} \left( \boldsymbol{k}\cdot \boldsymbol{x} - f(\boldsymbol{k})\ t - \varphi _{\boldsymbol{k}} \right) \right], \end{aligned} $$](/articles/aa/full_html/2023/10/aa46010-23/aa46010-23-eq31.gif)