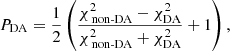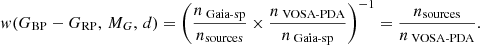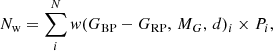| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346977 | |
| Published online | 21 September 2023 | |
White dwarf spectral type-temperature distribution from Gaia DR3 and the Virtual Observatory⋆
1
Departament de Física, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
e-mail: santiago.torres@upc.edu
2
Institute for Space Studies of Catalonia, c/Gran Capità 2–4, Edif. Nexus 104, 08034 Barcelona, Spain
3
Centro de Astrobiología (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, campus ESAC, 28692 Villanueva de la Cañada, Madrid, Spain
4
École d’ingénieurs (EPF), 55 Av. du Président Wilson, 94230 Cachan, France
Received:
23
May
2023
Accepted:
25
July
2023
Context. The characterization of white dwarf atmospheres is crucial for accurately deriving stellar parameters such as effective temperature, mass, and age. However, the inclusion of physical processes such as convective mixing and convective dilution in current white dwarf atmospheric models offers a prediction of the spectral evolution of these objects. To constrain these models, accurate observational data and analyses are necessary.
Aims. We aim to classify the population of white dwarfs up to 500 pc into hydrogen-rich or hydrogen-deficient atmospheres based on Gaia spectra and to derive an accurate spectral type-temperature distribution, namely, the ratio between the number of non-DAs to the total number of white dwarfs as a function of the effective temperature for the largest observed unbiased sample of these objects.
Methods. We took advantage of the recent Gaia low-resolution spectra available for 76 657 white dwarfs up to 500 pc. We calculated the synthetic J-PAS narrow-band photometry and fit the spectral energy distribution of each object with up-to-date models for hydrogen-rich and helium-rich white dwarf atmospheres. We estimated the probability for a white dwarf to have a hydrogen-rich atmosphere and validated the results using the Montreal White Dwarf Database. Finally, precise effective temperature values were derived for each object using La Plata evolutionary models.
Results. We successfully classified a total of 65 310 white dwarfs (57 155 newly classified objects) into DAs and non-DAs with an accuracy of 94%. An unbiased subsample of nearly 34 000 objects was built, from which we computed a precise spectral distribution spanning an effective temperature range from 5500 to 40 000 K, while accounting for potential selection effects.
Conclusions. Some characteristic features of the spectral evolution, such as the deficit of helium-rich stars at Teff ≈ 35 000 − 40 000 K and in the range of 22 000 ≲ Teff ≲ 25 000 K, as well as a gradual increase from 18 000 K to Teff ≈ 7000 K, where the non-DA stars percentage reaches its maximum of 41%, followed by a decrease for cooler temperatures, are statistically significant. These findings will provide precise constraints for the proposed models of spectral evolution.
Key words: white dwarfs / stars: atmospheres / virtual observatory tools / catalogs
The catalogue is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/677/A159
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Gaia mission has revealed important features of the white dwarf population with unprecedented precision. That is the case, for instance, with respect to the existence of two well-defined branches in the colour-magnitude diagram (roughly between 0.0 ≲ GBP − GRP ≲ 0.5) referred to as the A and B branches, which correspond to the majority of white dwarfs with hydrogen-rich and helium-rich atmospheres (see Gaia Collaboration 2018). The most plausible explanation to reproduce the B branch invokes the presence of small amount of hydrogen or carbon into helium-dominated atmospheres (Bergeron et al. 2019; Camisassa et al. 2023; Blouin et al. 2023). These models are based on well-studied physical processes that can alter the composition of the outer layers, such as convective mixing and convective dilution, among others (e.g. Rolland et al. 2018, and references therein). The specific characteristics of each model, such as the hydrogen content, the depth of the convective zone as a function of the effective temperature, or even the possibility of accreting material from surrounding asteroids, give rise to different channels of formation and evolution of white dwarf spectral types1 (e.g., Rolland et al. 2018; Ourique et al. 2018; Cunningham et al. 2019, 2020; Bédard et al. 2020). Therefore, accurate observational data is required to constrain these models.
The proper explanation for the formation of the Gaia A and B branches extends beyond the effective temperature range of these branches, encompassing a broader issue. A crucial observational factor in analysing the spectral evolution of white dwarfs is the ratio of non-DA to DA stars as a function of effective temperature2. Extensive efforts have been made since the pioneering work of Sion (1984) to obtain statistically significant spectral distributions (e.g., Tremblay & Bergeron 2008). However, the advent of large spectroscopic and photometric surveys such as the Sloan Digital Sky Survey (SDSS; York et al. 2000), Galaxy Evolution Explorer (GALEX; Morrissey et al. 2007), and Gaia (Gaia Collaboration 2016) has significantly increased both the quantity and quality of available data (e.g., Ourique et al. 2018; Genest-Beaulieu & Bergeron 2019; Blouin et al. 2019; Cunningham et al. 2020; McCleery et al. 2020; López-Sanjuan et al. 2022). However, complete spectroscopic samples have been limited to a distance of up to 40 pc. In other cases, magnitude-selection effects introduce significant biases in the final distribution.
Nevertheless, we can leverage the exceptional quality of astrometric and photometric data provided by the Gaia mission. The third data release (DR3) of Gaia includes low-resolution spectra for nearly 100 000 white dwarfs (Montegriffo 2023), making it the largest sample of white dwarfs available for analysis. In our recent study (Jiménez-Esteban et al. 2023), we classified 8150 white dwarfs within a nearly volume-complete 100 pc sample into DA or non-DA categories. The achieved accuracy of 90% was remarkable and allowed us to derive a detailed spectral distribution within the range of temperatures from 5500 K up to 23 000 K.
In this paper, we extend our previous analysis to a distance of 500 pc, significantly increasing the expected number of white dwarfs, particularly for hotter effective temperatures. Our goal is to derive, for the first time, the spectral distribution in the entire range of temperatures between 5500 K and 40 000 K, where spectral evolution is significant.
The paper is structured as follows. In Sect. 2, we describe the selection procedure used to obtain our white dwarf sample from Gaia data. We provide a summary of the main steps of our classification methodology in Sect. 3. Once our sample is classified and validated, Sect. 4 focuses on analysing selection effects and addressing the completeness correction of the sample. In Sect. 5, we present our spectral distribution, discuss our findings, and compare them to previous works. We summarise our key results and draw our main conclusions in Sect. 6.
2. The Gaia-DR3 white dwarf sample
We selected our objects from Gaia-DR3 catalogue3 following the criteria used in Jiménez-Esteban et al. (2023) but extended up to 500 pc: (1) ω − 3σω ≥ 2 mas and ω/σω ≥ 10; (2) FBP/σFBP ≥ 10 and FRP/σFRP ≥ 10; (3) with a renormalised unit weight error (RUWE) of less than 1.4, aimed at preventing poor astrometric solutions (Lindegren et al. 2021); (4) |C*|< 3σC*, where |C*| is an estimate of the BP and RP flux excess factor and σC* is its scatter, following the prescription by Riello et al. (2021).
Selected objects were corrected from extinction following the 3D interstellar Galactic extinction maps from Lallement et al. (2022)4. In principle, we selected only those objects falling below the 0.45 M⊙ cooling track on the Hertzsprung–Russell (HR) diagram. Additionally, as the atmospheric models we used (see Sect. 3) provide a reliable estimate of the effective temperature in the range from 5500 K up to 40 000 K, we chose those objects with unreddened colour between −0.5 < BP − RP < 0.86. A total number of 100 173 objects were selected, from which 76 657 have Gaia low-resolution spectra available.
Figure 1 displays the distance distribution (left panel) and cumulative distribution of apparent magnitude G (right panel) for our entire sample (red histogram) and white dwarfs with Gaia spectra (blue histogram). The use of inverse parallax as a distance estimator, combined with a parallax error threshold of less than 10%, introduces negligible discrepancies (less than ≈4%) compared to other distance estimators (Bailer-Jones et al. 2021). Most of our selected white dwarfs (73%) are within 250 pc, with a long tail extending up to 500 pc. The cumulative G magnitude distribution reveals a deficit of objects starting at G ∼ 20 mag for the entire sample and around G ∼ 19.5 mag for white dwarfs with Gaia spectra. Although the nominal limiting Gaia magnitude is ∼21.0, we adopted a conservative value of Glim = 19.5 mag for our completeness analysis (see Sect. 4).
 |
Fig. 1. Distance distribution (left panel) and apparent G magnitude cumulative distribution (right panel) for the entire sample of white dwarfs that fulfil our selection criteria (red histogram) and for the subsample of objects that have Gaia spectra (blue histogram). A constant cumulative slope is shown (black line) as indicative of the completeness of the sample. |
3. White dwarf spectral classification
For those sources of our selected sample with available Gaia spectra, we followed the same procedure described in Jiménez-Esteban et al. (2023). A brief description of the methodology for classifying white dwarfs into DA and non-DA types used in that work is provided as follows.
First, for each white dwarf of our sample with available Gaia spectrum we determined, by means of the Python package Gaia XPy5 and taking into account all the coefficients of the Gaia spectrum, the synthetic Javalambre-Physics of the Accelerating Universe Astrophysical Survey (J-PAS; Benitez et al. 2014) filter system (Marín-Franch et al. 2012) photometry. We focused on those filters covering the range from 4000 to 9590.54 Å and discarding those filters with effective wavelength shorter than 4000 Å. Second, for each object we built a spectral energy distribution (SED) using the derived J-PAS photometry. Although most of the SEDs have 56 photometric points, in some noisy spectra the number of points is lower, due to our threshold in the photometric error of 10% to each individual photometric measurement obtained with Gaia XPy.
We analysed 67 340 new white dwarfs spectra, which had not previously been studied in our 100 pc sample (Jiménez-Esteban et al. 2023). For those objects with more than four photometric points (57 155), their SEDs were fitted using either pure hydrogen white dwarf atmospheric models (DA) or models with helium and a small trace of hydrogen (non-DA, log N(H)/N(He) = −6). Both DA and non-DA models covered the temperature range of interest for this study (5500–40 000 K) and surface gravities from 7 to 9 dex (see Sect. 3.1 in Jiménez-Esteban et al. 2023 for detailed model information). The fitting process was performed using the Virtual Observatory spectral energy distribution Analyser6 (VOSA; Bayo et al. 2008), a powerful tool developed by the Spanish Virtual Observatory. Among the new 57 155 analysed objects, only three had Vgfb7 greater than 15 and were disregarded. For each object, two reduced chi-squared values (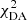 and
and 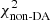 ) were obtained. Finally, the estimator of the probability of being a DA white dwarf (PDA) was defined as:
) were obtained. Finally, the estimator of the probability of being a DA white dwarf (PDA) was defined as:
where we classified an object as DA if PDA ≥ 0.5, otherwise as a non-DA.
We validated our classification procedure by means of the spectroscopically labelled white dwarf sample of the Montreal White Dwarf Database8 (MWDD; Dufour et al. 2017). A total of 8482 objects from the MWDD were used in our validating test (including those at distances closer than 100 pc). We adopted all MWDD objects whose primary spectral type is DA as DA class, regardless of their secondary types. The rest of the objects were considered as non-DA. In the left panel of Fig. 2, we show the distribution of the probability of being a DA, PDA, for white dwarfs labelled as DA (blue histogram) or non-DA (red histogram) in the MWDD. The distribution confirms that the adopted threshold at PDA = 0.5 effectively separates both populations and that the percentage of misclassified object is reasonable small, ≲7%. In the right panel of Fig. 2, we show the confusion matrix, where rows represent the number of already labelled spectral objects, while columns are the prediction of our classification (in parentheses the percentages with respect to the total population). The results of the confusion matrix reveal that the performance of our spectral type estimator is excellent, as it is corroborated by the derived metrics9: accuracy of 0.94, F1-score of 0.96, recall of 0.94, and precision of 0.98.
 |
Fig. 2. Probability distribution of being DA for the white dwarf labelled as DA or non-DA (blue and red histograms, respectively) in the MWDD (top panel). Confusion matrix of our estimator of being DA (bottom panel). Displayed values represent the total number of objects, while in brackets the percentages with respect to the total population. |
A last check was performed before applying our classification method to the observed Gaia white dwarf sample. In Fig. 3, we depicted the distribution of the G apparent magnitude for the entire sample of white dwarfs with Gaia spectra (blue histogram) and those with spectral classification in MWDD (gray histogram). We verified that the MWDD sample covers the full range of magnitudes and closely resemble the observed Gaia sample distribution. These facts guarantee the proper use of the MWDD sample for testing our classification method. Moreover, in Fig. 3, we present the magnitude distribution of the white dwarfs misclassified by our method (red histogram). As expected, the fainter the magnitude the larger the fraction of misclassified objects. Considering the percentage of error as a function of magnitude and extrapolating it to the Gaia sample, we estimated that the error in the final classification should not exceed 10%.
 |
Fig. 3. Distribution of G apparent magnitude for the entire sample of white dwarfs with Gaia spectra (blue histogram), those with spectral classification in MWDD (grey histogram) and those of the previous sample misclassfied by our method (red histogram). |
Once we have validated the reliability of our classification method, we applied it to the sample of white dwarfs with Gaia spectra within 500 pc. A total of 65 310 white dwarfs (including those previously classified in Jiménez-Esteban et al. 2023) have been classified into the spectral types DA (50 189; 77%) and non-DA (15 121; 23%) with an accuracy of 0.94. The catalogue with the spectral classification is available at the CDS and at The SVO archive of Gaia white dwarfs10 at the Spanish Virtual Observatory portal11.
In Fig. 4, we show the HR diagram of the corresponding DA and non-DA populations. For visual reference, we also show the cooling sequence of a 0.58 M⊙ DA white dwarf (Camisassa et al. 2016). The distribution of DA and non-DA white dwarfs clearly follows different tracks, with the latter group being, on average, less luminous for a certain colour (in particular for BP − RP > ;0) than the first one. It is worth mentioning that our classification into DA and non-DA groups is less model-dependent than H- vs. He-rich classification. However, such a classification is still needed for a correct astrophysical interpretation. Thus, higher resolution spectroscopy is required to flag misclassified objects, identify He-rich DAs and magnetic DAH with distorted Balmer jumps, as well as DZ and DQ with unusual colours, among other cases.
 |
Fig. 4. Gaia HR diagram for the population of white dwarfs classified by our probability estimator as DA (left panel) and non-DA (right panel). As a visual reference, we plotted the cooling sequence of a 0.58 M⊙ DA white dwarf according to La Plata models. |
4. Completeness correction
We analysed the different selection effects and how they can be corrected or at least mitigated. First of all, as our sample is initially built as a magnitude-selected sample, objects fainter than a certain magnitude limit would be absent from our sample. A standard 1/𝒱max method (Schmidt 1968) will provide an unbiased estimate of the space density. However, it requires extra conditions of completeness and homogeneity to be fulfilled (see Geijo et al. 2006, and references therein). These conditions are not guaranteed in our sample, as the requirement to have a Gaia spectrum adds a new selection effect and also mainly because DA and non-DA populations have, as previously stated, a different distribution in the colour–magnitude diagram (see Fig. 4).
In order to avoid this bias that would distort the spectral distribution, we developed a strategy in which we consider objects contributing to the spectral distribution only if they are brighter than a certain magnitude and hotter than a certain temperature (colour). We adopted the cooling sequence for a 1.05 M⊙ white dwarf as our faint limiting region. For a given distance of the white dwarf, the Gaia limiting magnitude we adopted is Glim = 19.5 (see Sect. 2), which is meant to fix the absolute observable magnitude limit. The corresponding colour at this magnitude for the 1.05 M⊙ white dwarf cooling sequence delimits the possible contribution to the spectral distribution. Only objects with a bluer colour than this value will contribute, while redder objects will be disregarded. In the left panel of Fig. 5, we present an example of this strategy. White dwarfs beyond a distance of 250 pc are highlighted in the Gaia HR diagram. Only those objects (marked in blue) above the horizontal line are observable and those to the left of the vertical line and above the 1.05 M⊙ track are included in the final sample to construct our spectral distribution. Thus, we prevented non-DA objects (which, on average, are fainter than DAs for a given colour; see Fig. 4) from being underestimated in the spectral distribution. It should be noted that this procedure automatically eliminates any massive white dwarf from our sample. However, their contribution is estimated to be less than ≈3% of the entire population (e.g., Kilic et al. 2020; Jiménez-Esteban et al. 2023).
 |
Fig. 5. Gaia colour–magnitude diagram of our population of DA and non-DA white dwarfs, shown as yellow dots in the left panel. Highlighted in blue are those objects at distances d > ;250 pc. Assuming a limiting magnitude of Glim = 19.5, only those brighter than MG < 12.5 (horizontal red line) are observable. The cooling track for a 1.05 M⊙ white dwarf (black line) is adopted as our lower selection function limit. For a given distance, only objects (marked in dark blue) at the left of the corresponding colour value (vertical red line) contribute to the final spectral distribution. The white dwarfs selected for building our spectral distribution are highlighted in red in the right panel. Objects above or below the cooling track for a 0.51 M⊙ helium-rich and a 1.05 M⊙ hydrogen-rich white dwarf, respectively, were discarded. |
A second important source of incompleteness comes from the fact that not all white dwarf sources have an available Gaia spectrum. Moreover, even those sources that have it may not have a good VOSA determination of the probability of being DA or non-DA. It is expected that the number of sources without a determination of this probability increases for fainter and distant objects. We take into account this fact by introducing a weight function that depends on the distance, d, of the object and its specific location within the HR diagram, w(GBP − GRP, MG, d). For a given source with parameters (GBP − GRP, MG, d)0, we computed the number of sources, nsources, within a volume of 𝒱 = Δ(GBP − GRP)×ΔMG × Δd centred at the previous value and with Δ(GBP − GRP) = 0.1, ΔMG = 0.1 and Δd = 50 pc. Besides the number of sources within 𝒱, we also computed the number of objects with available Gaia spectra, nGaia-sp, and the number of those who have a VOSA estimation of the probability of being DA, nVOSA-PDA. Assuming that the completeness weight function should be inversely proportional to the probability of an object of belonging to the final sample, a straightforward application of the Bayes’ theorem for conditional probability leads to:
Finally, in addition to the selection function previously described (i.e., the selection of objects hotter than a given colour determined by the 1.05 M⊙ evolutionary track for a given distance), we considered objects located in the HR diagram below the cooling track for a 0.51 M⊙ helium-rich white dwarf. This way, we avoid unresolved binary white dwarf systems and the contribution of white dwarfs evolved from binary evolution (Jiménez-Esteban et al. 2023). Furthermore, the existence of low-mass white dwarfs with helium-rich atmospheres has not been proven (see, for instance, Genest-Beaulieu & Bergeron 2019; Battich et al. 2020). Thus, we adopted the 0.51 M⊙ low-mass limit as a conservative criterion. For each object of our final sample we determined the effective temperature by interpolating the Gaia photometry in the La Plata models. Those objects classified as DA were interpolated in the models of Camisassa et al. (2016), while for those labelled as non-DA, we used the hydrogen-deficient cooling models of Camisassa et al. (2017); in both cases, for carbon-oxygen-core white dwarfs (see Jiménez-Esteban et al. 2023, for details). Atmospheric models where those used in the SED analysis (see Sect. 3.1 from Jiménez-Esteban et al. 2023), namely, Koester’s models with pure hydrogen composition for DAs and helium with a small trace of hydrogen (log N(H)/N(He) = −6) for non-DAs (Koester 2010). It is worth noting here that recent studies have emphasised the importance of considering the carbon content in non-DA atmospheres (Camisassa et al. 2023; Blouin et al. 2023). Assuming the maximum non-observable carbon enrichment prescription from Camisassa et al. (2023), that is, carbon sequence −1 dex, the difference with respect to a pure helium model is ∼10% at 12 000 K, and approximately 5% at 6000 K. The differences are not larger than 1500 K, which corresponds to the bin width of our spectral distribution. Thus, no major effects are expected in this regard. Our final sample to estimate the spectral fraction, consisting of 33 997 white dwarfs, is shown in Fig. 5, with 25 984 (76.4%) classified as DAs and 8013 (23.6%) as non-DAs.
5. The spectral type-temperature distribution
The spectral type-temperature distribution, f, is defined as the ratio of weighted non-DA white dwarfs, to the total number of weighted objects, Nw, per effective temperature interval. We adopted that the contribution of each object to its temperature bin depends on its weight function, w, and the probability of classification, Pi (that is PDA, i for DAs, 1 − PDA, i for non-DAs). Hence, the weighted number of objects is defined as:
where N is the number of objects in that interval, w the weighted function and Pi the probability aforementioned. Error bars were estimated taking into account Poissonian error and the corresponding object weight, that is 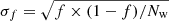 .
.
In Fig. 6, we displayed our final spectral distribution (black solid circles and black line). To evaluate the extent of the completeness correction introduced in our sample, we included the ratio distribution of the entire classified white dwarf population (raw sample consisting of 65 310 objects) when no selection function is applied at all (blue open triangles). For purposes of comparison, we also plotted the spectral distribution for the sample of 100 pc (red circles; Jiménez-Esteban et al. 2023). The analysis of the different spectral distributions revealed that the effects due to completeness correction are of minor order. The general trend is practically coincident, and only small discrepancies appear for the coolest bin, where the error bars underestimate the fact that the classification is less certain. In any case, we can conclude that our weighted spectral distribution provides a robust estimate of the ratio of DA vs. non-DA white dwarfs.
 |
Fig. 6. Spectral distribution presented in this work (black lines and solid circles) and when no selection criteria and correction function is applied at all (blue open triangles). The one obtained for the 100 pc sample (Jiménez-Esteban et al. 2023, red circles) is also shown. |
In Fig. 7, we show a comparison of the spectral distribution found in this work (black solid circles) with some of the most recent ratio distributions found in the literature. The first remarkable characteristic of the spectral distribution found in this work is the wider range of effective temperatures covered by it, thus constituting a solid estimate of the spectral evolution of white dwarfs. While a detailed analysis of the implications for spectral evolution is outside the scope of this work, in what follows, we present a brief analysis of the most relevant points found.
 |
Fig. 7. Spectral distribution for our final white dwarf sample (black points and lines). For comparison, we also show the spectral distributions from other works found in literature. |
At the hottest end, that is, Teff ≈ 35 000 − 40 000 K, the lowest ratio of non-DAs was found. As previously reported, there is not a complete absence of non-DAs in this region, but an average ∼5% is indicative of the presence of the so called “DB-gap” (e.g., Bergeron et al. 2011; Koester & Kepler 2015, and references therein). An additional statistical significant deficit of non-DAs was also found for effective temperatures in the range of 22 000 ≲ Teff ≲ 25 000 K, in perfect agreement with the ratios found by Ourique et al. (2018) and López-Sanjuan et al. (2022). Finally, for temperatures cooler than ∼18 000 K, coinciding with the onset of convection mixing in DAs (e.g., Cunningham et al. 2020), a marked increase in the ratio of non-DAs was found, leading from ∼10% at 18 000 K up to ∼40% at 8000 K and in agreement with most of the spectral distributions found in the literature.
It is worth mentioning that our spectral distribution presented a peak around Teff ≈ 7000 K with a ratio of non-DA objects of f ≈ 0.41. This maximum is found at lower temperatures than that of our previous work (Jiménez-Esteban et al. 2023) and others retrieved in literature such as Ourique et al. (2020), probably as a consequence of an unweighted distribution in these cases. However, the weighted distribution presented here is in agreement with the 40 pc spectroscopic complete sample analysed in McCleery et al. (2020). Moreover, a statistically significant decrease in the ratio of non-DAs is found at the coolest bin, Teff ≈ 6000 K, dropping to f ≈ 0.35. This behaviour was also reported in our previous work (Jiménez-Esteban et al. 2023) and is also in agreement with Blouin et al. (2019) and McCleery et al. (2020), although no known physical mechanism can be associated with it (Blouin et al. 2019).
6. Conclusions
Following the methodology presented in Jiménez-Esteban et al. (2023), we have expanded our white dwarf study sample up to 500 pc. A total of 65 310 white dwarfs have been classified as DAs and non-DAs based on their Gaia spectra, with an accuracy of 94%. This has allowed us to construct a statistically significant and precise distribution of the DA vs. non-DA ratio as a function of effective temperature. Nearly 34 000 white dwarfs have contributed to the final selected sample, making it the largest sample to date in terms of the number of objects and the range of effective temperatures analysed, from 5500 K to 40 000 K.
The comparative analysis of our distribution with others found in the literature reveals statistically significant features such as: the deficit of DBs within the effective temperature range of approximately 35 000 − 40 000 K and between 22 000 − 25 000 K, along with a gradual rise starting from 18 000 K up to around 7000 K, where the proportion of non-DA white dwarfs peaks at 41%, followed by a decline for lower temperatures.
Finally, we can state that selection effects have been taken into account in the construction of the final sample. This fact, along with the high number of objects per interval in the sample, ensures that our spectral distribution can be considered a robust and precise element in the analysis of the spectral evolution of white dwarfs.
White dwarfs are classified as DAs or non-DAs based on the presence or absence of hydrogen lines in their spectra, respectively. This last group is formed by those who exhibits helium lines (DB), metal lines (DZ), carbon lines (DQ), or no lines at all (DC), among others (Sion et al. 1983).
Throughout the paper, we use the term ‘spectral type-temperature distribution’ or simply ‘spectral distribution’ to refer to the ratio of non-DA to the total number of objects as a function of the effective temperature. We prefer it to the term ‘spectral evolution’ as we consider this case specifically refers to the physical processes that result in a change in spectral type.
For a definition of these parameters, please refer for instance to Appendix A from Echeverry et al. (2022).
Acknowledgments
We acknowledge support from MINECO under the PID2020-117252GB-I00 grant and by the AGAUR/Generalitat de Catalunya grant SGR-386/2021. P.C. acknowledges financial support from the Government of Comunidad Autónoma de Madrid (Spain) via postdoctoral grant ‘Atracción de Talento Investigador’ 2019-T2/TIC-14760. R.M.O. is funded by INTA through grant PRE-OBSERVATORIO. MC acknowledges grant RYC2021-032721-I, funded by MCIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR. RR acknowledges support from Grant RYC2021-030837-I funded by MCIN/AEI/ 10.13039/501100011033 and by “European Union NextGenerationEU/PRTR”. F.J.E. acknowledges support from ESA through the Faculty of the European Space Astronomy Centre (ESAC) – Funding reference 4000139151/22/ES/CM. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work has made use of the Python package Gaia XPy, developed and maintained by members of the Gaia Data Processing and Analysis Consortium (DPAC) and in particular, Coordination Unit 5 (CU5), and the Data Processing Centre located at the Institute of Astronomy, Cambridge, UK (DPCI). This publication makes use of VOSA, developed under the Spanish Virtual Observatory (https://svo.cab.inta-csic.es) project funded by MCIN/AEI/10.13039/501100011033/ through grant PID2020-112949GB-I00. We extensively made used of Topcat (Taylor 2005). This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. We acknowledge use of the ADS bibliographic services.
References
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, VizieR Online Data Catalog: I/352 [Google Scholar]
- Battich, T., Althaus, L. G., & Córsico, A. H. 2020, A&A, 638, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bédard, A., Bergeron, P., Brassard, P., & Fontaine, G. 2020, ApJ, 901, 93 [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2014, arXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Bergeron, P., Wesemael, F., Dufour, P., et al. 2011, ApJ, 737, 28 [Google Scholar]
- Bergeron, P., Dufour, P., Fontaine, G., et al. 2019, ApJ, 876, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Blouin, S., Dufour, P., Thibeault, C., & Allard, N. F. 2019, ApJ, 878, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Blouin, S., Bédard, A., & Tremblay, P.-E. 2023, MNRAS, 523, 3363 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2016, ApJ, 823, 158 [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Rohrmann, R. D., et al. 2017, ApJ, 839, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M., Torres, S., Hollands, M., et al. 2023, A&A, 674, A213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cunningham, T., Tremblay, P.-E., Freytag, B., Ludwig, H.-G., & Koester, D. 2019, MNRAS, 488, 2503 [NASA ADS] [CrossRef] [Google Scholar]
- Cunningham, T., Tremblay, P.-E., Gentile Fusillo, N. P., Hollands, M., & Cukanovaite, E. 2020, MNRAS, 492, 3540 [NASA ADS] [CrossRef] [Google Scholar]
- Dufour, P., Blouin, S., Coutu, S., et al. 2017, in 20th European White Dwarf Workshop, eds. P. E. Tremblay, B. Gaensicke, & T. Marsh, ASP Conf. Ser., 509, 3 [Google Scholar]
- Echeverry, D., Torres, S., Rebassa-Mansergas, A., & Ferrer-Burjachs, A. 2022, A&A, 667, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geijo, E. M., Torres, S., Isern, J., & García-Berro, E. 2006, MNRAS, 369, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Genest-Beaulieu, C., & Bergeron, P. 2019, ApJ, 882, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Esteban, F. M., Torres, S., Rebassa-Mansergas, A., et al. 2023, MNRAS, 518, 5106 [Google Scholar]
- Kilic, M., Bergeron, P., Kosakowski, A., et al. 2020, ApJ, 898, 84 [Google Scholar]
- Koester, D. 2010, Mem. Soc. Astron. Ital., 81, 921 [Google Scholar]
- Koester, D., & Kepler, S. O. 2015, A&A, 583, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lallement, R., Vergely, J. L., Babusiaux, C., & Cox, N. L. J. 2022, A&A, 661, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Tremblay, P. E., Ederoclite, A., et al. 2022, A&A, 658, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marín-Franch, A., Chueca, S., Moles, M., et al. 2012, in Modern Technologies in Space- and Ground-based Telescopes and Instrumentation II, eds. R. Navarro, C. R. Cunningham, & E. Prieto, SPIE Conf. Ser., 8450, 84503S [Google Scholar]
- McCleery, J., Tremblay, P.-E., Gentile Fusillo, N. P., et al. 2020, MNRAS, 499, 1890 [Google Scholar]
- Montegriffo, P. 2023, A&A, 674, A33 [CrossRef] [EDP Sciences] [Google Scholar]
- Morrissey, P., Conrow, T., Barlow, T. A., et al. 2007, ApJS, 173, 682 [Google Scholar]
- Ourique, G., Romero, A. D., Kepler, S. O., Koester, D., & Amaral, L. A. 2018, MNRAS, 482, 649 [Google Scholar]
- Ourique, G., Kepler, S. O., Romero, A. D., Klippel, T. S., & Koester, D. 2020, MNRAS, 492, 5003 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rolland, B., Bergeron, P., & Fontaine, G. 2018, ApJ, 857, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [Google Scholar]
- Sion, E. M. 1984, ApJ, 282, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Sion, E. M., Greenstein, J. L., Landstreet, J. D., et al. 1983, ApJ, 269, 253 [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Tremblay, P.-E., & Bergeron, P. 2008, ApJ, 672, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr, et al. 2000, AJ, 120, 1579 [Google Scholar]
All Figures
 |
Fig. 1. Distance distribution (left panel) and apparent G magnitude cumulative distribution (right panel) for the entire sample of white dwarfs that fulfil our selection criteria (red histogram) and for the subsample of objects that have Gaia spectra (blue histogram). A constant cumulative slope is shown (black line) as indicative of the completeness of the sample. |
| In the text | |
 |
Fig. 2. Probability distribution of being DA for the white dwarf labelled as DA or non-DA (blue and red histograms, respectively) in the MWDD (top panel). Confusion matrix of our estimator of being DA (bottom panel). Displayed values represent the total number of objects, while in brackets the percentages with respect to the total population. |
| In the text | |
 |
Fig. 3. Distribution of G apparent magnitude for the entire sample of white dwarfs with Gaia spectra (blue histogram), those with spectral classification in MWDD (grey histogram) and those of the previous sample misclassfied by our method (red histogram). |
| In the text | |
 |
Fig. 4. Gaia HR diagram for the population of white dwarfs classified by our probability estimator as DA (left panel) and non-DA (right panel). As a visual reference, we plotted the cooling sequence of a 0.58 M⊙ DA white dwarf according to La Plata models. |
| In the text | |
 |
Fig. 5. Gaia colour–magnitude diagram of our population of DA and non-DA white dwarfs, shown as yellow dots in the left panel. Highlighted in blue are those objects at distances d > ;250 pc. Assuming a limiting magnitude of Glim = 19.5, only those brighter than MG < 12.5 (horizontal red line) are observable. The cooling track for a 1.05 M⊙ white dwarf (black line) is adopted as our lower selection function limit. For a given distance, only objects (marked in dark blue) at the left of the corresponding colour value (vertical red line) contribute to the final spectral distribution. The white dwarfs selected for building our spectral distribution are highlighted in red in the right panel. Objects above or below the cooling track for a 0.51 M⊙ helium-rich and a 1.05 M⊙ hydrogen-rich white dwarf, respectively, were discarded. |
| In the text | |
 |
Fig. 6. Spectral distribution presented in this work (black lines and solid circles) and when no selection criteria and correction function is applied at all (blue open triangles). The one obtained for the 100 pc sample (Jiménez-Esteban et al. 2023, red circles) is also shown. |
| In the text | |
 |
Fig. 7. Spectral distribution for our final white dwarf sample (black points and lines). For comparison, we also show the spectral distributions from other works found in literature. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.