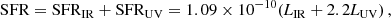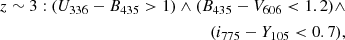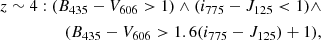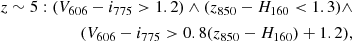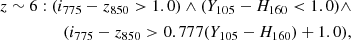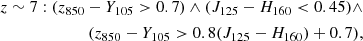EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 677 (September 2023) A&A, 677 (2023) A34 Full HTML
Open Access
Issue
A&A
Volume 677, September 2023
Article Number A34
Number of page(s) 13
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202346673
Published online 29 August 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Until JWST came online, our understanding of the early (z > 3) cosmic history of galaxies was mainly based on samples selected from their rest-frame ultraviolet (UV) light (see Madau & Dickinson 2014, for a review). However, this view is limited, as classical color selections to find distant star-forming galaxies (SFGs), such as the Lyman break galaxies (LBGs; e.g., Steidel et al. 1996; Giavalisco et al. 2004; Bouwens et al. 2012), are effective at identifying blue galaxies with low dust attenuation, but are generally biased against redder dusty SFGs (see Casey et al. 2014; Hodge & da Cunha 2020, for a review).

In recent years, Spitzer Space Telescope (Spitzer) and Atacama Large Millimeter/submillimeter Array (ALMA) observations from numerous studies have uncovered a population of massive dusty SFGs completely missed in deep optical/near-infrared (optical/near-IR) surveys, but bright at longer far-infrared/millimeter (far-IR/mm) wavelengths (see e.g., Simpson et al. 2014; Wang et al. 2016, 2019; Franco et al. 2018; Alcalde Pampliega et al. 2019; Yamaguchi et al. 2019; Williams et al. 2019; Romano et al. 2020; Toba et al. 2020; Umehata et al. 2020; Zhou et al. 2020; Gruppioni et al. 2020; Talia et al. 2021; Smail et al. 2021; Fudamoto et al. 2021; Manning et al. 2022; Gómez-Guijarro et al. 2022a; Shu et al. 2022; Enia et al. 2022; Xiao et al. 2023, so-called optically dark/faint galaxies (OFGs), or, alternatively, optically invisible galaxies, optical/near-IR-dark, HST-dark, among others). These dusty SFGs are different from the rare extreme dusty starbursts (e.g., Walter et al. 2012; Riechers et al. 2013; Marrone et al. 2018), as they are more numerous, with number densities two orders of magnitude greater, and are characterized by milder star formation rates (SFRs; e.g., Wang et al. 2019) typical of galaxies in the main sequence of SFGs (MS; e.g., Brinchmann et al. 2004; Daddi et al. 2007; Elbaz et al. 2007; Noeske et al. 2007; Whitaker et al. 2012; Speagle et al. 2014; Schreiber et al. 2015). These galaxies are believed to be a dominant contributor to the massive (M* > 1010.3 M⊙) end of the SFR density of the Universe at z ∼ 3–6 (e.g., Wang et al. 2019; Xiao et al. 2023; Barrufet et al. 2023). However, the dearth of available secure spectroscopic redshifts and determinations of their stellar mass is a hinderance to the interpretation of these sources among the SFG population. It is still unclear as to how many owe their faintness at optical/near-IR wavelengths to a dusty or a quiescent nature. In addition, being so faint or completely dark to the Hubble Space Telescope (HST) has rendered the study and understanding of the role of their stellar morphologies impossible.

The JWST recently began to be used to investigate this galaxy population, unveiling the stellar light of galaxies previously undetected by HST (HST-dark). In a general sense, it should be noted that there is no consensus definition of this galaxy population and the properties of its members heavily depend on the specific magnitude and color cuts (e.g., Xiao et al. 2023). Among these JWST studies, Barrufet et al. (2023), based on a red (F160W–F444W) color selection, reported their relatively high-redshift, massive, MS-like SFRs, a dusty nature (z ∼ 2–8; M* > 1010 M⊙; AV ∼ 2 mag), and their important contribution to the cosmic SFR density at z ∼ 6. Nelson et al. (2023) measured a prevalence of low axis ratios and linked their elusiveness to a dusty disk-like and edge-on nature. Pérez-González et al. (2023), based on a red (F150W–F356W) color selection, described this galaxy population as threefold, including a majority (∼70%) of dusty SFGs at z = 2–6, with M* = 109 − 10 M⊙, ∼20% quiescent galaxies (QGs) with M* > 1010 M⊙ at z = 3–4, and ∼10% young starbursts at z = 6–7 with M* ∼ 109.5 M⊙. Rodighiero et al. (2023) reported evolved z = 8–13 massive M* = 109 − 10 M⊙ galaxies with high dust attenuation (AV > 5 mag). Kokorev et al. (2023) presented a spatially resolved study of a z ∼ 2.5 massive (M* ∼ 1011.3 M⊙) dark galaxy, finding very high levels of dust attenuation (AV ∼ 4 mag) all across its stellar extent.

In this work, we investigate the drivers of dust attenuation in the JWST era, focusing on understanding the nature of obscured galaxies to unveil the reason behind their elusiveness in the pre-JWST era. We study the roles of stellar mass and morphology as proxies for dust attenuation. The layout of the paper is as follows. The data used in this work are described in Sect. 2. In Sect. 3, we present the catalog and photometry, along with the derivation of stellar-based properties, including morphological measurements. Section 4 describes the sample selection, classification into LBGs and OFGs, and evaluation of the star-forming or quiescent nature of OFGs. In Sect. 5, we characterize the stellar-based properties, including redshift, stellar mass, dust attenuation, SFR, and morphological measurements. We investigate the relevance of the stellar mass and morphology in driving dust attenuation in Sect. 6. In Sect. 7, we discuss and interpret our results. We summarize our main findings and conclusions in Sect. 8.

Throughout this work, we adopt a concordance cosmology [ΩΛ, ΩM, h]=[0.7, 0.3, 0.7] and a Chabrier initial mass function (IMF, Chabrier 2003). When magnitudes are quoted, they are in the AB system (Oke 1974).

2. Data

2.1. JWST data

In this work, we used JWST data from the Cosmic Evolution Early Released Science (CEERS) survey, an early release science program in the Extended Groth Strip (EGS) field (Finkelstein et al. 2022). The CEERS data include JWST/NIRCam imaging over ten pointings, the first four (CEERS1, CEERS2, CEERS3, CEERS6) observed in June 2022 and the remaining six (CEERS4, CEERS5, CEERS7-10) observed in December 2022, together covering a total area of 97 arcmin2. This dataset comprises observations with seven NIRCam filters F115W, F150W, F200W, F277W, F356W, F410M, and F444W, reaching an average 5σ point source depth of 29.15, 29.00, 29.17, 29.19, 29.17, 28.38, and 28.58 mag, respectively.

For details about the observations and data reduction process, we refer the reader to Bagley et al. (2023). Briefly, the June pointings were processed using the JWST Calibration Pipeline version 1.7.2 and CRDS pmap 0989, while the December pointings were processed using the pipeline version 1.8.5 and CRDS pmap 1023. For both June and December pointings, the reduction steps were the same, with the raw images passing through all pipeline stages with some additional steps, including 1/f noise subtraction and wisp removal. The mosaics were aligned to the Gaia-EDR3 astrometry (Gaia Collaboration 2021), mapped into a pixel scale of 0 . ″ $ \overset{\prime \prime }{.} $03/pixel, and background subtracted.

2.2. Ancillary data

In order to complement shorter wavelengths, we used HST imaging in the EGS field from its public release reprocessed by the CEERS team, matching the astrometry and pixel scale of the JWST data (see Koekemoer et al. 2011). This dataset comprises observations with six filters: ACS/WFC F606W, F814W, WFC3/IR F105W, F125W, F140W, and F160W, reaching an average 5σ point source depth of 28.62, 28.30, 27.11, 27.31, 26.67, and 27.37 mag, respectively.

We also used the publicly available ground-based imaging from the Canada-France-Hawaii Telescope (CFHT)/MegaCam observations in the EGS field in u*, g′, r′, i′, and z′-band, reaching average 5σ point source depths of 27.1, 27.3, 27.2, 27.0, and 26.1 mag, respectively. This dataset corresponds to the D3 field of the CFHT Legacy Survey (CFHTLS, Gwyn 2012).

3. Catalog

3.1. Source detection and photometry

For source detection, we followed a similar approach to that used in the CANDELS catalog in the EGS field (Stefanon et al. 2017). We employed SExtractor (Bertin & Arnouts 1996) using the F444W-band as a detection image. This band was found to be optimal for our science case, because our goal is to unveil galaxies that become increasingly faint at shorter wavelengths. The F444W-band comprises the longest wavelengths of the JWST/NIRCam bands. We carried out the source detection in both the so-called cold and hot modes, that is, with tailored parameters optimized to detect from bright extended to faint compact sources. We also employed a RMS map (defined as 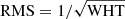RMS = 1 / WHT $ \mathrm{RMS} = 1 / \sqrt{\mathrm{{WHT}}} $, where the WHT map is a weight image giving the relative weight of the output pixels) scaled to the median value of the ERR map (data array containing resampled uncertainty estimates, given as standard deviation) as a weighting image for detection. The final merged catalog comprises all cold sources and the hot sources that are not part of a cold source. Discarded hot sources are those that fall within the Kron ellipse of a cold source.

In the 13 JWST and HST bands, we measured fluxes using SExtractor in dual image mode. In this mode, one image is used for detections (F444W-band in our case), while measurements are carried out on another image. Running SExtractor with various measurement images while keeping the same detection image, one ends up with a catalog with the same sources measured through different bands. Measurements were carried out on images PSF-matched to the angular resolution of the detection F444W-band image (0 . ″ $ \overset{\prime \prime }{.} $16 FWHM), which provides the coarsest angular resolution of the JWST/NIRCam bands and a resolution that is comparable to those of the HST WFC3 bands. PSF-matching was performed on JWST/NIRCam and HST/ACS images by convolving them with a convolution kernel created using the software PyPHER (Boucaud et al. 2016), from PSF images of the different bands constructed by stacking point sources that were selected in the mosaics using the software PSFEx (Bertin et al. 2011). Total flux measurements and uncertainties in both the cold and hot modes in the detection F444W-band image were calculated using Kron elliptical apertures (FLUX_AUTO with PHOT_AUTOPARAMS = 2.5, 3.5). For the remaining bands, SExtractor dual mode uses the segmentation map of the detection image to measure isophotal fluxes and uncertainties (FLUX_ISO) that we corrected to total fluxes by multiplying them with the ratio FLUX_AUTO/FLUX_ISO as measured in the detection F444W-band (see Stefanon et al. 2017). HST/WFC3 fluxes and uncertainties were scaled to account for the missing flux when comparing their PSF with the F444W-band PSF. An additional aperture correction optimized for point sources was added in all bands to account for the flux missed outside of the Kron elliptical apertures. For each source, we scaled their fluxes and uncertainties by the fraction of flux outside of the area covered by its Kron ellipse as measured in the F444W-band PSF.

In the five ground-based CFHT bands, we measured fluxes using aperture photometry on images PSF-matched to the angular resolution of the u*-band (0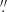 . ″ $ \overset{\prime \prime }{.} $9 FWHM), which provides the coarsest angular resolution of the CFHT bands (i.e., the poorest seeing conditions at the moment of observation). We measured fluxes in 1 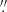. ″ $ \overset{\prime \prime }{.} $2 diameter apertures, which provides an optimal trade-off between total flux retrieval and signal-to-noise ratio (S/N; see also, e.g., Straatman et al. 2016). Total flux measurements were then calculated using aperture corrections derived tracing the u*-band PSF growth curve to account for the flux losses outside the chosen aperture.

Fluxes and uncertainties in all bands were corrected for Milky Way attenuation following a Cardelli et al. (1989) extinction function with an average E(B − V) = 0.006 in the EGS field (Schlafly & Finkbeiner 2011).

3.2. Redshift, stellar mass, and dust attenuation

We estimated photometric redshifts from spectral energy distribution (SED) fitting to the 18 bands in our catalog (u* to F444W) using the code EAZy (Brammer et al. 2008) in its updated Python version EAZy-py. We employed the set of 13 Flexible Stellar Population Synthesis (FSPS; Conroy & Gunn 2010) templates (corr_sfhz_13; see Kokorev et al. 2022, for details). These templates cover redshift-dependent star formation histories (SFHs), which disfavor SFHs that start earlier than the age of the Universe at a given epoch, span a large range in ages and dust attenuation, and include emission lines. Additionally, the set was complemented with the best-fit template to the extreme emission line galaxy 4590 at z = 8.5 with a JWST/NIRSpec spectrum (Carnall et al. 2023) rescaled to match the normalization of the FSPS templates (see e.g., Kokorev et al. 2022; Gould et al. 2023; Valentino et al. 2023, for a similar approach). EAZy-py finds the best linear combination of templates for the flux densities and uncertainties of each source. We searched for updated spectroscopic redshifts by cross-matching the source catalog (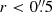 r < 0 . ″ 5 $ r < 0{{\overset{\prime\prime}{.}}}5 $) with the ancillary spectroscopic compilation in Stefanon et al. (2017) and the MOSDEF survey in the EGS field (Kriek et al. 2015). When a high-quality measurement was available, we substituted the photometric redshift by its spectroscopic value. In addition, we used the best-quality spectroscopic redshifts to derive zero-point corrections applied iteratively to the EAZy-py run to improve photometric redshifts (N = 320, σ = 0.02, corrections < 10%).

The set of EAZy templates is best suited for redshift determination, but they are limited in terms of their physical parameters. Therefore, we estimated stellar masses and dust attenuation (AV) using the SED fitting code FAST++1, which is an updated version of the SED fitting code FAST (Kriek et al. 2009), fixing the redshifts to the values previously obtained. The stellar population models were from Bruzual & Charlot (2003), with delayed exponentially declining SFHs (τ = 100 Myr–30 Gyr; age = 50 Myr–age of the universe at a given redshift), a Calzetti et al. (2000) dust attenuation law (AV = 0.0–5.0) –which is common in similar studies and provides a benchmark for comparison– and metallicity (Z = 0.004, 0.008, 0.02 (solar), 0.05).

3.3. Star formation rate

We estimated SFR values from a ladder of SFR estimators (see e.g., Wuyts et al. 2011; Magnelli et al. 2014; Barro et al. 2019, for a similar approach).

First, we checked whether there are counterparts in the mid-IR-to-mm bands in the “super-deblended” catalog in the EGS field (Le Bail et al., in prep.). This catalog is built using a state-of-the-art de-blending methodology similar to that of similar catalogs in the GOODS-North (Liu et al. 2018) and COSMOS (Jin et al. 2018) fields. These mid-IR-to-mm bands include Spitzer/MIPS/24 μm, Herschel/PACS/100, 160 μm, Herschel/SPIRE/250, 350, 500 μm, JCMT/SCUBA2/450, 850 μm, and ASTE/AzTEC 1.1 mm. For galaxies with S/NIR > 5 (sum in quadrature of the S/N of all the bands beyond and not including Spitzer/MIPS/24 μm), we fit Draine & Li (2007) dust emission templates with the correction from Draine et al. (2014) using the code CIGALE (Burgarella et al. 2005; Noll et al. 2009; Boquien et al. 2019) to derive total IR luminosity estimates (LIR, 8–1000 μm rest-frame). For galaxies with S/NIR < 5, but S/N24 μm > 5, we renormalized IR templates from Schreiber et al. (2018) to the Spitzer/MIPS/24 μm fluxes, obtaining LIR. The total SFR accounts for the contribution of the obscured star formation probed in the IR (SFRIR) and the unobscured star formation probed in the UV (SFRUV), following the prescription of Bell et al. (2005; for a Chabrier 2003, IMF):

SFR = SFR IR + SFR UV = 1.09 × 10 − 10 ( L IR + 2.2 L UV ) , $$ \begin{aligned} \mathrm {SFR} = \mathrm {SFR_{IR}} + \mathrm {SFR_{UV}} = 1.09 \times 10^{-10} (\textit{L}_{\rm {IR}} + 2.2\textit{L}_{\rm {UV}})\,, \end{aligned} $$(1)

where LUV = 1.5νlν, 2800 is the total UV luminosity in the range 1260–3000 Å rest frame derived from the rest frame 2800 Å luminosity density (lν, 2800).

For galaxies with S/NIR < 5 and S/N24 μm < 5, or for those without counterparts in the mid-IR-to-mm bands in the super-deblended catalog, the total SFR is given by the SFRUV corrected from dust attenuation (SFRUV, cor). We calculated SFRUV, cor following the same prescription above for the UV term, but with LUV,cor = 1.5νlν,2800,cor, and with lν,2800,cor being the rest-frame 2800 Å luminosity density corrected for dust attenuation (A2800) using the Calzetti et al. (2000) law.

3.4. Morphology

In order to estimate morphological structural parameters, we used surface brightness profile fitting to the JWST/NIRCam F444W images by employing the code statmorph (Rodriguez-Gomez et al. 2019). The F444W-band is the reddest NIRCam filter available, probing 0.52 < λrf < 1.1 μm in the redshift range of interest (3 < z < 7.5, see Sect. 4) at 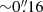∼ 0 . ″ 16 $ {\sim} 0{{\overset{\prime\prime}{.}}}16 $ angular resolution (PSF FWHM). Therefore, the F444W-band probes optical-to-near-IR rest-frame morphologies, mitigating the morphological differences that can occur at shorter wavelengths, especially in the rest-frame UV (see e.g., Suess et al. 2022; Miller et al. 2023). statmorph performs 2D Sérsic profile fitting and nonparametric morphological diagnostics of a given background-subtracted image and associated segmentation map with the sources of interest. The code includes a flag for the fit quality, where flag = 0 indicates a good fit and flag ≥ 2 indicates a problem with the measurements (e.g., artefacts, foreground stars, or incompletely masked secondary sources). Following the documentation, we restricted our analysis to flag ≤ 1 and flag_sersic = 0 when considering morphological measurements.

4. Sample definitions

4.1. General parent SFGs sample

In order to include new insight from JWST/NIRCam into the rest-frame UV, we introduced a lower limit in the redshift for our study. We focused our work on the redshift range 3 < z < 7.5. The lower redshift limit was imposed to cover the rest-frame UV (λrf < 4000 Å) at all redshifts with at least two NIRCam bands (F115W and F150W), while the higher redshift limit was imposed because of the scarcity of galaxies at higher redshifts. We also introduced a lower limit in the stellar mass of log(M*/M⊙)≥9.0 to focus our work on intermediate-to-massive galaxies.

We classified this redshift- and stellar mass-limited sample into SFGs and QGs through a UVJ classification. The UVJ plane is a classical color diagram widely used to make this discrimination (e.g., Wuyts et al. 2007; Williams et al. 2009; Patel et al. 2012). We employed the definition by Williams et al. (2009). The rest-frame colors were obtained from FAST++ and the resulting best-fit SEDs. Although the UVJ diagram has proven to be a useful tool for SFGs and QGs discrimination, it is not free of some plausible contamination. In order to mitigate contaminants, we checked that the galaxies classified as QGs by the UVJ criteria are undetected (< 2σ) in mid-IR-to-mm bands (from Herschel/PACS/100 μm to ASTE/AzTEC 1.1 mm) in the super-deblended catalog in the EGS field (Le Bail et al., in prep.); otherwise we classified them as SFGs.

As a result, we defined a redshift- (3 < z < 7.5) and stellar mass-limited (log(M*/M⊙)≥9.0) sample of UVJ-selected SFGs (parent SFGs sample), which serves as a benchmark for comparisons. In total, the parent SFG sample comprises 1490 galaxies.

4.2. Lyman break galaxies

The Lyman limit (λrf = 912 Å) is a signature that allows the identification of high-redshift SFGs. SFGs exhibit a prominent break beyond their Lyman limit owing to absorption by intervening hydrogen. These galaxies are called LBGs. An LBG will appear very faint or invisible in all bands bluewards of its Lyman limit and prominent again redwards of its Lyman limit. The more redshifted the Lyman limit, the more distant the galaxy. Therefore, the Lyman break technique is an efficient way of selecting high-redshift SFGs (e.g., Steidel et al. 1996; Giavalisco et al. 2004; Bouwens et al. 2012). The technique was used up to z ∼ 10 in the pre-JWST era (e.g., Bouwens et al. 2015).

In this work, we label LBGs in the parent SFGs sample galaxies; these are selected by applying the LBG color criteria as defined by Bouwens et al. (2020):

z ∼ 3 : ( U 336 − B 435 > 1 ) ∧ ( B 435 − V 606 < 1.2 ) ∧ ( i 775 − Y 105 < 0.7 ) , $$ \begin{aligned} z\sim 3: (U_{336}-B_{435}>1)\wedge (B_{435}-V_{606}<1.2)\wedge \\ (i_{775}-Y_{105} < 0.7), \end{aligned} $$

z ∼ 4 : ( B 435 − V 606 > 1 ) ∧ ( i 775 − J 125 < 1 ) ∧ ( B 435 − V 606 > 1.6 ( i 775 − J 125 ) + 1 ) , $$ \begin{aligned} z\sim 4: (B_{\rm 435}-V_{\rm 606}>1)\wedge (i_{\rm 775}-J_{\rm 125} < 1) \wedge \\ (B_{\rm 435}-V_{\rm 606} > 1.6(i_{\rm 775}-J_{\rm 125})+1), \end{aligned} $$

z ∼ 5 : ( V 606 − i 775 > 1.2 ) ∧ ( z 850 − H 160 < 1.3 ) ∧ ( V 606 − i 775 > 0.8 ( z 850 − H 160 ) + 1.2 ) , $$ \begin{aligned} z\sim 5: (V_{\rm 606}-i_{\rm 775}>1.2)\wedge (z_{\rm 850}-H_{\rm 160} < 1.3) \wedge \\ (V_{\rm 606}-i_{\rm 775} > 0.8(z_{\rm 850}-H_{\rm 160})+1.2), \end{aligned} $$

z ∼ 6 : ( i 775 − z 850 > 1.0 ) ∧ ( Y 105 − H 160 < 1.0 ) ∧ ( i 775 − z 850 > 0.777 ( Y 105 − H 160 ) + 1.0 ) , $$ \begin{aligned} z\sim 6: (i_{\rm 775}-z_{\rm 850}>1.0)\wedge (Y_{\rm 105}-H_{\rm 160} < 1.0) \wedge \\ (i_{\rm 775}-z_{\rm 850} > 0.777(Y_{\rm 105}-H_{\rm 160})+1.0), \end{aligned} $$

z ∼ 7 : ( z 850 − Y 105 > 0.7 ) ∧ ( J 125 − H 160 < 0.45 ) ∧ ( z 850 − Y 105 > 0.8 ( J 125 − H 160 ) + 0.7 ) , $$ \begin{aligned} z\sim 7: (z_{\rm 850}-Y_{\rm 105}>0.7)\wedge (J_{\rm 125}-H_{\rm 160} < 0.45) \wedge \\ (z_{\rm 850}-Y_{\rm 105} > 0.8(J_{\rm 125}-H_{\rm 160})+0.7), \end{aligned} $$

where ∧ and ∨ represent the logical AND and OR symbols, respectively. The bands involved in these LBG color criteria correspond to HST. In order to properly mimic this selection in the absence of observations in the exact same bands, the magnitudes in the relevant filters were calculated by convolving their transmission curves with the resulting best-fit SEDs from FAST++. In addition, to avoid classifying galaxies based on model extrapolations of observationally unconstrained regions of the SED, we required at least two (> 5σ) detections in the rest-frame UV (λrf < 4000 Å) of the SED to perform the classification. The LBGs sample comprises 1182 galaxies within the parent SFGs sample.

4.3. Optically dark/faint galaxies

Optically dark/faint galaxies (OFGs) is a general term referring to the intrinsic faintness of these galaxies around optical/near-IR wavelengths (Gómez-Guijarro et al. 2022a; Xiao et al. 2023). In this sense, they are defined as galaxies undetected or very faint in all optical and near-IR bands up to and including the H-band in the deepest cosmological fields (typical 5σ point source depth H > 27 mag) but bright at longer near-IR bands ([3.6] or [4.5]-band). Their redshifts, stellar masses, dust attenuation, and star-forming or quiescent nature heavily depend on the specific magnitude and color cuts.

A typical selection consists in targeting sources that are H-band dropouts (with studies defining them below a given magnitude limit or as absent in catalogs) but bright at 3.6/4.5 μm, or galaxies with very red colors (e.g., H − 3.6/4.5 > 2–4 mag) (see e.g., Wang et al. 2016, 2019; Alcalde Pampliega et al. 2019; Pérez-González et al. 2023). This selection typically yields z > 3 massive and dust obscured galaxies (see also Bisigello et al. 2023, for low-mass dusty SFG selection criteria). Xiao et al. (2023), with the purpose of bridging more extreme optically dark galaxies with more common lower-mass, less-dust attenuated galaxies, such as LBGs, formally define OFGs based on the following criteria: (1) H > 26.5 mag; (2) [4.5]< 25 mag. The H > 26.5 cut selects both the extreme optically dark and intrinsically fainter galaxies with less dust attenuation. This cut also weeds out typical massive (log(M*/M⊙) > 10) QGs. The [4.5]< 25 mag cut selects not only massive galaxies, but also galaxies with intermediate stellar masses (see Xiao et al. 2023, for details).

In this work, we applied the magnitude cuts as defined by Xiao et al. (2023) using the new insight from the JWST/NIRCam bands: (1) F150W > 26.5 mag; (2) F444W < 25 mag. This parent OFG sample comprises 35 galaxies. There are 25/35 (71%) in the parent SFG sample and 3/35 (8.6%) QGs based on the UVJ classification. The remaining 7/35 (20%) galaxies belong to a lower-redshift tail (1.5 < z < 3). This tail is left out of the parent SFG sample when we impose the lower redshift limit (z > 3) to cover the rest-frame UV (λrf < 4000 Å) at all redshifts with at least two NIRCam bands (F115W and F150W). Nevertheless, the OFG criteria appear to be an effective filter for relatively high-redshift (3 < z < 7.5), intermediate-to-massive (M* > 109 M⊙), dusty (AV ≳ 1) SFGs (25/35, 71%), with little contamination from QGs (3/35, 8.6%). Hereafter, we continued the analysis focusing on the OFGs sample that is part of the parent SFGs sample (see Sect. 5, for details on their redshift, stellar mass, and dust attenuation distributions).

Figure 1 shows the (F150W − F444W) color versus F444W magnitude distribution, including the parent SFGs, LBGs, and OFGs samples. The distribution of LBGs follows the bulk of the parent SFGs population, although we see that the LBG sample starts to miss galaxies as they become redder. The OFG sample is complementary to the LBG sample by selecting bright F444W < 25 mag galaxies missed by the LBG criteria. We note that LBGs and OFGs are not mutually exclusive galaxy types; at the edges of the OFGs selection region, seven galaxies are both LBG and OFG. An example OFG is shown in Fig. 2.

thumbnail Fig. 1.

(F150W − F444W) color versus F444W magnitude distribution for the parent SFG (black), LBG (cyan circles), and OFG (orange circles) samples. The OFG selection criteria is displayed with orange segments.

thumbnail Fig. 2.

Example OFG at zphot = 3.52, with log(M*/M⊙) = 10.39 and AV = 2.16. While the galaxy is not detected (S/N < 1) in the HST/WFC3 F160W image, it is detected (S/N > 5) in all JWST/NIRCam bands. Images are 2″ × 2″ with north up and east to the left.

In light of the small percentage of QG contaminants in the OFG sample, we find that most of the z > 3 massive galaxies missed by the LBG criteria in the pre-JWST era were missed mainly because of high dust attenuation rather than because of old stellar populations. In order to illustrate the effect of dust attenuation in the selection criteria for LBGs and OFGs, we performed the following experiment: First, we took the intrinsic (before applying the dust attenuation law) best-fit SEDs of the parent SFG sample from FAST++. We used the SEDs of the parent SFG sample to build a representative set of SEDs, as opposed to taking all the SED templates of FAST++. We then progressively applied increasing AV values following the Calzetti et al. (2000) dust attenuation law. In every AV step, we obtained the magnitudes in the relevant filters for the selection criteria for LBGs and OFGs by convolving their transmission curves with the best-fit SEDs. In each AV step, we calculated the fraction of galaxies that meet the selection criteria for LBGs and OFGs, that is, fLBGs = NLBGs/NSFGs, where NSFG is the number of galaxies in the parent SFG sample; and fOFGs = NOFGs/NSFGs, bright, where NSFG, bright is the number of galaxies in the parent SFG sample with F444W < 25 mag. Figure 3 presents these fractions as a function of increasing AV. This illustrates how the Lyman break technique naturally misses galaxies as a function of increasing AV (∼50% for AV = 2 mag and ∼0% for AV > 3 mag). On the contrary, the higher the AV, the higher the fraction of OFGs (∼50% for AV = 1 mag and ∼100% for AV > 5 mag).

thumbnail Fig. 3.

Fraction of LBGs (left axis) and fraction of OFGs (right axis) as a function of increasing AV (see main text, for details on the calculation), where NSFG is the number of galaxies in the parent SFG sample and NSFGs, bright is the number of galaxies in the parent SFG sample with F444W < 25 mag.

5. Stellar-based properties and morphologies

In this section, we characterize the stellar-based properties, including redshift, stellar mass, dust attenuation, SFR, and morphological measurements, as derived in Sect. 3. We compare the samples defined as in the previous section with regard to these stellar properties. In Fig. 4, we present the redshift, stellar mass, and dust attenuation distributions of the parent SFG, LBG, and OFG samples to illustrate the parameter space covered by these galaxies. All samples exhibit a similar redshift distribution. In terms of stellar mass and dust attenuation distributions, the main difference is in the OFG sample. These galaxies are more massive and dust attenuated than LBGs and the parent sample of SFGs. This reflects the OFG criteria, which are designed to select intermediate to massive galaxies with moderate to high levels of dust attenuation.

thumbnail Fig. 4.

Redshift (left column), stellar mass (middle column), and dust attenuation (right column) histograms of the parent SFG (top row, gray), LBG (middle row, cyan), and OFG (bottom row, orange) samples. We show the median values (filled squares) along with the 16% and 84% percentiles (segments) of the distributions in the insets.

In Fig. 5, we place our different samples in the stellar mass versus SFR plane, along with the MS of SFGs as defined by Schreiber et al. (2015), assuming that this MS definition can be extrapolated to z > 4. The SFR values are scaled to a common redshift, corresponding to the median value of the parent SFGs sample (zmed = 3.95). The scaled SFR values do not represent the true SFR values, but the overall distribution of the different samples in the SFR–M* plane, maintaining the ΔMS = SFR/SFRMS each galaxy would have if plotted against the MS associated with its redshift. The parent SFG sample has a median 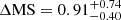Δ MS = 0 . 91 − 0.40 + 0.74 $ \Delta \rm{MS} = 0.91_{-0.40}^{+0.74} $ (where the uncertainties are the 16% and 84% percentiles of the distributions), tracing the MS of SFGs. Similarly, LBGs have 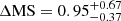Δ MS = 0 . 95 − 0.37 + 0.67 $ \Delta \rm{MS} = 0.95_{-0.37}^{+0.67} $ and therefore trace the bulk of the MS of SFGs. In the case of OFGs, 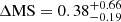Δ MS = 0 . 38 − 0.19 + 0.66 $ \Delta \rm{MS} = 0.38_{-0.19}^{+0.66} $ locates them slightly below the MS of SFGs. Previous studies revealed that the SFR of the OFGs (or comparable selections) is consistent with the typical MS SFGs as constrained from stacked mid-IR-to-mm photometry or deep mm individual detections from ALMA (e.g., Wang et al. 2019; Gómez-Guijarro et al. 2022b; Xiao et al. 2023). SFR could be underestimated in OFGs in the absence of counterparts in the mid-IR-to-mm that typically offer the best SFR constraints. In this work, none of the OFGs have counterparts in the mid-IR-to-mm bands in the super-deblended catalog in the EGS field, and so SFRs would be underestimated, likely because of an underestimated dust attenuation, which already reaches saturation in the SED fitting of such highly dust-attenuated systems. The extreme cases are the OFGs that are still undetected in their rest-frame UV by JWST (9/25), for which dust attenuation constraints are heavily dependent on extrapolations of the best-fit SED. These galaxies do not show differences in terms of redshift when compared to the OFG sample (∼5% difference in the medians) and exhibit 1.7 times higher stellar masses and 1.2 times higher dust attenuation. Pérez-González et al. (2023) reported a similar SFR behaviour compared to the MS for HST-dark galaxies, which is mitigated when performing 2D SED-fitting.

thumbnail Fig. 5.

SFR–M* plane, with the MS from Schreiber et al. (2015) displayed as a solid blue line. Its 1σ scatter associated with 0.5 < ΔMS < 2 (∼0.3 dex) is represented as a shaded blue area, with a more extended typical scatter of 0.33 < ΔMS < 3 (∼0.5 dex) in lighter blue. We note that the values are scaled to a common redshift (zmed = 3.95) as explained in the main text.

In terms of morphological parameters, in Fig. 6, we present the (circularized) effective radius (Re), axis ratio (q = b/a), and Sérsic index (n) distributions of the parent SFG, LBG, and OFG samples (flagged as good fits). We recall that these were measured in the JWST/NIRCam F444W-band and that we restricted our analysis to flag ≤ 1 and flag_sersic = 0 when considering morphological measurements. Among the OFGs sample, 6/25 galaxies were flagged as poor fits, in all cases being found to be consistent with point sources. Therefore, while it was not possible in these cases to measure their morphologies, a limit on their effective radii is 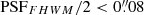PSF FHWM / 2 < 0 . ″ 08 $ {\mathrm{PSF}_{FHWM}} / 2 < 0{{\overset{\prime\prime}{.}}}08 $. At first order, the distributions are rather similar in the different samples. The main difference is in the lower scatter around small effective radii and Sérsic index n ∼ 1 in the case of the OFGs sample compared to LBGs and the parent SFGs sample. In addition, the distribution of axis ratios appears skewed toward larger values in the case of OFGs. While not displayed here, the upper limits on the sizes for the 6/25 OFGs classified as point sources are also consistent with these sources being clustered around smaller effective radii. Their compact sizes could also explain the skewness toward large axis ratios, as the latter are more difficult to constrain when the angular resolution starts to be comparable with the intrinsic size of the galaxy (marginally resolved sources).

thumbnail Fig. 6.

(Circularized) effective radius (left column), axis ratio (middle column), and Sérsic index (right column) histograms of the parent SFG (top row, grey), LBG (middle row, cyan), and OFG (bottom row, orange) samples. We show the median values (filled squares) along with the 16% and 84% percentiles (segments) of the distributions in insets.

6. Drivers of dust attenuation

In this section, we study the relevance of stellar mass and morphology in driving dust attenuation in a general sense and, specifically, in the case of highly dust attenuated galaxies, such as OFGs. We note that drivers in this case refer to parameters that show correlations, and these can therefore be interpreted as predictors of the dust attenuation. For a discussion on the relevant physical processes involved, we refer to Sect. 7.

6.1. Stellar mass

Figure 7 shows dust attenuation as a function of stellar mass. Dust attenuation correlates with stellar mass in SFGs, as reported before in numerous studies (e.g., Garn & Best 2010; Zahid et al. 2013; Heinis et al. 2014; Pannella et al. 2015; Álvarez-Márquez et al. 2016). The parent sample of SFGs establishes the general trend. LBGs exhibit a shallower trend, while OFGs display a steeper trend populating a much more dust attenuated regime.

thumbnail Fig. 7.

Dust attenuation as a function of stellar mass (left panel), (circularized) effective radius (middle panel), and axis ratio (right panel). Sliding medians for the different galaxy types shown in the legend are displayed with colored squares, with the error bars representing the uncertainty of the medians. Bins with less than three galaxies are not displayed (see Figs. 4 and 6 for the distributions).

The dust attenuation and stellar mass correlation arises from the mass–metallicity relation (e.g., Tremonti et al. 2004; Erb et al. 2006; Sánchez et al. 2013; Genzel et al. 2015; Ma et al. 2015). Massive SFGs are capable of more efficiently producing and retaining their metals than low-mass SFGs, which tend to expel them in galactic winds. Therefore, massive SFGs tend to be more dusty than low-mass SFGs.

Stellar mass acts as a primary proxy for dust attenuation in SFGs. However, it remains unclear as to whether or not additional parameters can drive dust attenuation. In the following section, we study the role of morphology.

6.2. Morphology

We studied whether dust attenuation shows signs of correlation with basic morphological structural parameters. In Fig. 7, we show dust attenuation as a function of effective radius and axis ratio. The behavior of AV for the parent sample of SFGs and LBGs is generally flat across the range of effective radii and axis ratios. The main difference arises in the case of OFG sizes. The effective radii of OFGs are clustered around small sizes (as shown in Fig. 6) that are associated to high dust-attenuation values. In addition, we see an increase in AV when moving toward smaller effective radii. On the contrary, we do not see an increase in AV toward lower axis ratios (i.e., edge-on galaxies).

Generally, there is no clear link –as in the one involving stellar mass– between the studied basic structural parameters and dust attenuation. However, galaxy size appears to be related in the most dust attenuated galaxy type, the OFG sample. The question that rises is whether or not OFGs are indeed smaller when compared to the typical SFG sizes at similar stellar mass and redshift.

Figure 8 shows the ratio between median (circularized) effective radius of the different galaxy types and the median (circularized) effective radius of the parent sample of SFGs. For better statistics, we focus on a single redshift bin (3 < z < 5) of massive galaxies (log(M*/M⊙) > 10). In addition, we also move beyond the selection criteria for LBGs and OFGs by simply defining galaxies with higher dust attenuation (AV > 1 sample), of which OFGs would be specific cases, and galaxies with lower dust attenuation (AV < 1 sample), which would comprise the majority of LBGs. The AV > 1 and OFG samples are indeed smaller than the parent sample of SFGs at the same redshift and stellar mass bin. In the case of axis ratios, these appear generally consistent with the values of the parent sample of SFGs, albeit slightly skewed toward larger values, which is consistent with the picture in which axis ratios are more difficult to constrain when the angular resolution starts to be comparable with the intrinsic size of the galaxy. This affects more galaxy types that are intrinsically smaller, such as the AV > 1 and OFG samples and, generally, galaxies at higher redshifts following the decreasing sizes of SFGs with increasing redshift (e.g., van der Wel et al. 2014). We note that the upper limits in the sizes for the 6/25 OFGs classified as point sources are not included here. If included, they would lower the size ratio even further, in line with AV > 1 and OFG samples exhibiting smaller sizes than the parent sample of SFGs.

thumbnail Fig. 8.

Ratio of the (circularized) effective radius (left panel) and axis ratio (right panel) for different galaxy types to those of the parent SFG sample. Galaxies are in the redshift bin 3 < z < 5 and are massive (log(M*/M⊙) > 10). In the case of the effective radius, ratios calculated after applying a correction to a common redshift and stellar mass are displayed with open squares. The ratios are obtained by dividing the median values of a given galaxy type by the median values of the parent SFG sample, with the error bars representing the uncertainty of the ratio of the medians.

While we studied a given galaxy type compared with the parent sample of SFGs in the same redshift and stellar mass bin, there are still differences in the redshift and stellar mass distributions. In Fig. 8, measurements (filled squares) are placed at the median stellar mass of the galaxy type. These galaxy types do not have the exact same median stellar mass (or redshift) between them and they do not have the exact same median stellar mass (or redshift) as the parent SFG sample. This could have an impact on the comparison. However, we know from literature studies that SFG sizes decrease with increasing redshift and increase with increasing stellar mass (e.g., Shen et al. 2003; van der Wel et al. 2014; Barro et al. 2017; Suess et al. 2019; Mowla et al. 2019). While these studies were carried out in the pre-JWST era, and therefore they are typically limited to z < 3 for stellar sizes in the rest-frame optical/near-IR, if we assume that the same trends can be extrapolated to higher redshifts, we can correct for the differential effect that redshift and stellar mass have on the sizes (see also Gómez-Guijarro et al. 2022a, for a similar analysis). Following this approach, we corrected the effective radii of each galaxy to a common redshift and stellar mass as given by the median values of the 3 < z < 5 massive (log(M*med/M⊙) > 10) parent sample of SFGs (open squares in Fig. 8). After this exercise, AV > 1 and OFG samples are a factor 1.3 smaller than the parent sample of SFGs and a factor 1.5 smaller than the AV < 1 sample at the same redshift and stellar mass bin.

6.3. Random forest analysis

The results above indicate that stellar mass is a primary proxy for dust attenuation. In a general sense, effective radius and axis ratio do not play a clear role in dust attenuation. However, when considering massive galaxies at similar redshifts, highly dust-attenuated galaxies exhibit more compact (smaller effective radii) stellar light profiles. We check these results by performing a random forest analysis (see e.g., Ellison et al. 2020; Baker et al. 2022; Bluck et al. 2022, for a similar analysis).

A random forest is a machine learning technique that identifies the most important parameter in driving a given quantity, especially when several parameters are inter-correlated. A target quantity is selected and removed from the data, leaving a dataset containing the features that the target quantity imprinted on it. These two datasets (target and features) are then split into a training and a test sample. The algorithm is employed in the training sample, which sorts the data in different nodes into the different decision trees with the goal being to minimize the Gini Impurity (Pedregosa et al. 2011). The final model is then applied to the test sample in order to check its performance.

We used a random forest regressor in order to identify the most predictive parameter of AV between M*, SFR, Re, and q. These parameters are chosen to reflect different aspects of galaxies, going from the total amount of stars (M*), the rate of creating new stars (SFR), the extent of the stellar light Re, and the way the stellar light is oriented (q). We also added a random uniform variable (Rand) as a control variable. Using a randomized cross-search validation method we fine-tuned the hyperparameters. We checked the performance of the fit by calculating the mean squared errors (MSEs) between model and test sample.

Figure 9 shows the relative importance of the studied parameters in predicting AV from the random forest regressor. Stellar mass is the most predictive parameter, followed by SFR. The morphological parameters of effective radius and axis ratio do not appear as strong predictors of dust attenuation, with the axis ratio being close to random. These results are in line with the results shown in Sect. 6.

thumbnail Fig. 9.

Relative importance of the different parameters explored in predicting dust attenuation from a random forest regressor analysis. The bar height displays the median value of the distribution of 10 000 realizations of training and test samples, while the error bars represent the 16% and 84% percentiles of the distributions.

7. Discussion

The results in this work show that stellar mass is a primary predictor of dust attenuation. The correlation between dust attenuation and stellar mass was studied in the pre-JWST era, especially at z < 4 using statistical galaxy samples (e.g., Garn & Best 2010; Zahid et al. 2013; Heinis et al. 2014; Pannella et al. 2015; Álvarez-Márquez et al. 2016), with some studies peering into the z > 4 Universe using smaller samples (e.g., Fudamoto et al. 2020; Bogdanoska & Burgarella 2020). In the JWST era, some works started to investigate the relation between dust attenuation and stellar mass at z > 3 (e.g., Shapley et al. 2023), with models predicting similar trends (e.g., Yung et al. 2019). Stellar mass is a tracer of the integrated history of star formation in galaxies and therefore the history of metal and dust production. The stellar mass defines the depth of the galaxy potential well and therefore massive galaxies are able to keep their metals and dust more efficiently than low-mass galaxies, which are prone to lose them through galactic winds. The mass–metallicity relation is strong observational proof of these physical processes (e.g., Tremonti et al. 2004; Erb et al. 2006; Sánchez et al. 2013; Genzel et al. 2015; Ma et al. 2015).

Once the stellar mass has been accounted for, SFR appears as another strong predictor of dust attenuation. The two are correlated in SFGs, as shown by the existence of the MS of SFGs (e.g., Brinchmann et al. 2004; Daddi et al. 2007; Elbaz et al. 2007; Noeske et al. 2007; Whitaker et al. 2012; Speagle et al. 2014; Schreiber et al. 2015). At fixed stellar mass, a number of studies in the literature explain the dust attenuation scatter through variations in the SFR (e.g., Garn & Best 2010; Wuyts et al. 2011; Zahid et al. 2013). However, one interesting aspect of the random forest analysis in Sect. 6.3 is that stellar mass appears as a stronger predictor of dust attenuation than SFR. While the mass–metallicity relation can be considered a first-order relation in galaxy evolution, the fundamental metallicity relation (FMR; Mannucci et al. 2010) comes as a second-order indicator of the metal content in galaxies. The FMR indicates that, at fixed stellar mass, galaxies with higher SFR have lower metallicities. Therefore, the FMR would favor stellar mass as a stronger predictor of dust attenuation than SFR.

Orientation has been studied in the literature as a proxy for dust attenuation. Disk galaxies can exhibit higher dust attenuation levels for higher inclinations, owing to the thicker projected dust columns (e.g., Wild et al. 2011; Patel et al. 2012; Zuckerman et al. 2021). Zuckerman et al. (2021) explains the dust attenuation scatter at fixed stellar mass as due to inclination effects in thin dust disks, but also shows that when the dust disk is thick, inclination becomes irrelevant. The results presented in this work show that at z > 3, inclination has a negligible effect on dust attenuation, and is almost indistinguishable from a random variable. Highly dust attenuated systems in this work do not exhibit a preference for more inclined orientations (i.e., edge-on disks). In particular, OFGs are not biased toward edge-on disks, contrary to the interpretation of Nelson et al. (2023), who links the obscuration of similar galaxies to an edge-on nature. A very recent study by Lorenz et al. (2023) also reaches the same conclusion at lower redshifts, showing that none of the dust properties studied (Balmer decrement, AV, rest-frame UV slope) vary with axis ratio in a sample of 308 spectroscopically characterized SFGs at 1.3 < z < 2.6. The authors propose an interpretation in which already at z > 1 the dust attenuation in SFGs would be dominated by dust in dense star-forming regions rather than by the dust in the diffuse ISM, which would mean a negligible effect of inclination on dust attenuation. Some examples of dust swept in dense clouds and depleted diffuse components have also been observed in the local Universe (Holwerda & Keel 2013; Keel et al. 2014).

While stellar mass and SFR come as strong predictors of dust attenuation for the parent sample of SFGs, our results show that there is a subset of galaxies that, even at fixed stellar mass, SFR, and redshift, are fainter than the average SFG at rest-frame UV wavelengths with higher levels of dust attenuation (AV > 1). OFGs are a specific case of these galaxies, and exhibit a factor 2.4 higher AV than the parent sample of SFGs (for 3 < z < 5 and log(M*/M⊙) > 10). We find that the key distinctive feature is their compact size (smaller effective radii) compared to the average SFG at the same stellar mass and epoch (as given by the parent sample of SFGs). The physical interpretation of this is that the galaxy size is the parameter that modulates how the density profile of the galaxy is distributed. More compact stellar profiles could therefore contribute to more efficiently keeping metals and dust in a galaxy compared to a more extended stellar profile. For galaxies with similar levels of dust mass (determined at first order by their redshift, stellar mass, and SFR), the dust column density would be thicker when embedded in more compact stellar profiles than in more extended stellar profiles.

More compact stellar profiles in OFGs are in line with the view of ALMA-detected OFGs; they exhibit enhanced SFR surface densities associated with compact dust morphologies with high dust covering fractions. Therefore, these galaxies are capable of forming stars in concentrated areas –which would result in the compact stellar light profiles we see in this work– and of obscuring the stellar light behind thick dust columns (e.g., Smail et al. 2021; Xiao et al. 2023; Kokorev et al. 2023). The compact stellar sizes of OFGs are comparable to those of QGs. Massive (log(M*/M⊙) > 10) OFGs in the redshift bin 3 < z < 4 have a median (circularized) effective radius of Re = 0.75 ± 0.25 kpc (where the uncertainty is given by the median absolute deviation). As a reference, QGs at z = 3 of similar stellar mass have a typical effective radius of Re = 0.73 kpc (van der Wel et al. 2014). In the classical view of galaxy structural evolution, SFGs evolve mostly as extended star-forming disks, while QGs are typically more compact than SFGs at a fixed stellar mass and redshift (e.g., Shen et al. 2003; van der Wel et al. 2014; Barro et al. 2017; Suess et al. 2019; Mowla et al. 2019). The buildup of a central stellar core appears to be linked to the quenching of star formation (e.g., Kauffmann et al. 2003; Whitaker et al. 2017; Barro et al. 2017; Gómez-Guijarro et al. 2019; Suess et al. 2021). SFGs with compact star forming regions (e.g., Toft et al. 2014; Gómez-Guijarro et al. 2018, 2022b; Franco et al. 2020; Puglisi et al. 2021; Magnelli et al. 2023) and SFGs with a developed compact stellar core (e.g., Barro et al. 2013; Nelson et al. 2014; Williams et al. 2014; van Dokkum et al. 2015; Gómez-Guijarro et al. 2019) have been proposed as the link between the more extended SFGs and the more compact QGs. The compact sizes (smaller effective radius) in OFGs when compared to the general SFG population shown in this work and the higher SFR surface densities in OFGs shown in literature studies are in line with a progressive buildup of the compact stellar profiles of QGs. Therefore, OFGs (at a higher redshift bin) could be progenitors of massive compact QGs (at a lower redshift bin).

8. Summary and conclusions

In this work, we investigate the drivers of dust attenuation in the JWST era, with a special focus on understanding why the galaxies known as optically faint/dark galaxies (OFGs) are so faint at optical/near-IR wavelengths. To this end, we use data from JWST to unveil their nature and characterize their basic stellar and morphological properties. Our findings can be summarized as follows:

  • Stellar mass is a primary proxy of dust attenuation, among the properties studied. Effective radius and axis ratio do not show a clear link with dust attenuation, with the effect of orientation being found to be close to random.

  • There is a subset of highly dust attenuated (AV > 1) SFGs, of which OFGs are a specific case. Even at the same stellar mass, SFR, and redshift, this subset of galaxies are still fainter than the average SFG at rest-frame UV wavelengths with high levels of dust attenuation. We find that their key distinctive feature is their compact size, with 30% smaller effective radius than the average SFG at the same stellar mass and redshift (for massive systems with log(M*/M⊙) > 10). These galaxies do not show a preference for low axis ratios (i.e., edge-on disks).

  • The OFG selection criteria (F150W > 26.5 mag; F444W < 25 mag) are an effective filter for relatively high-redshift (3 < z < 7.5), intermediate to massive (log(M*/M⊙)≥9.0), dusty (AV ≳ 1) SFGs, with little contamination from QGs (∼8.6%). Compared to the general SFG population, OFGs exhibit smaller effective radii, with Sérsic indices of n ∼ 1 and axis ratios of around q ∼ 0.5.

The results in this work show that stellar mass is a primary proxy for dust attenuation and compact stellar light profiles behind the thick dust columns obscuring typical massive SFGs.

Acknowledgments

C.G.G. acknowledges support from CNES. PGP-G acknowledges support from Spanish Ministerio de Ciencia e Innovación MCIN/AEI/10.13039/501100011033 through grant PGC2018-093499-B-I00. This work is based on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST. These observations are associated with program #1345. We would acknowledge the following open source software used in the analysis: Astropy (Astropy Collaboration 2013, 2018, 2022), photutils (Bradley et al. 2022), APLpy (Robitaille & Bressert 2012), pandas (The pandas development team 2020), NumPy (Harris et al. 2020). We are grateful to the anonymous referee, whose comments have been very useful to improving our work.

References

  1. Alcalde Pampliega, B., Pérez-González, P. G., Barro, G., et al. 2019, ApJ, 876, 135 [NASA ADS] [CrossRef] [Google Scholar]
  2. Álvarez-Márquez, J., Burgarella, D., Heinis, S., et al. 2016, A&A, 587, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  5. Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bagley, M. B., Finkelstein, S. L., Koekemoer, A. M., et al. 2023, ApJ, 946, L12 [NASA ADS] [CrossRef] [Google Scholar]
  7. Baker, W. M., Maiolino, R., Bluck, A. F. L., et al. 2022, MNRAS, 510, 3622 [NASA ADS] [CrossRef] [Google Scholar]
  8. Barro, G., Faber, S. M., Pérez-González, P. G., et al. 2013, ApJ, 765, 104 [Google Scholar]
  9. Barro, G., Faber, S. M., Koo, D. C., et al. 2017, ApJ, 840, 47 [Google Scholar]
  10. Barro, G., Pérez-González, P. G., Cava, A., et al. 2019, ApJS, 243, 22 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barrufet, L., Oesch, P. A., Weibel, A., et al. 2023, MNRAS, 522, 449 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [Google Scholar]
  13. Bertin, E. 2011, ASP Conf. Ser., 442, 435 [Google Scholar]
  14. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bisigello, L., Gandolfi, G., Grazian, A., et al. 2023, A&A, 676, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bluck, A. F. L., Maiolino, R., Brownson, S., et al. 2022, A&A, 659, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Bogdanoska, J., & Burgarella, D. 2020, MNRAS, 496, 5341 [NASA ADS] [CrossRef] [Google Scholar]
  18. Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Boucaud, A., Bocchio, M., Abergel, A., et al. 2016, A&A, 596, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2012, ApJ, 754, 83 [Google Scholar]
  21. Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [Google Scholar]
  22. Bouwens, R., González-López, J., Aravena, M., et al. 2020, ApJ, 902, 112 [NASA ADS] [CrossRef] [Google Scholar]
  23. Bradley, L., Sipőcz, B., Robitaille, T., et al. 2022, https://doi.org/10.5281/zenodo.6825092 [Google Scholar]
  24. Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [Google Scholar]
  25. Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
  26. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  27. Burgarella, D., Buat, V., & Iglesias-Páramo, J. 2005, MNRAS, 360, 1413 [NASA ADS] [CrossRef] [Google Scholar]
  28. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  29. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  30. Carnall, A. C., Begley, R., McLeod, D. J., et al. 2023, MNRAS, 518, L45 [Google Scholar]
  31. Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [Google Scholar]
  32. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  33. Conroy, C., & Gunn, J. E. 2010, ApJ, 712, 833 [Google Scholar]
  34. Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
  35. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
  36. Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [Google Scholar]
  37. Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Ellison, S. L., Thorp, M. D., Lin, L., et al. 2020, MNRAS, 493, L39 [CrossRef] [Google Scholar]
  39. Enia, A., Talia, M., Pozzi, F., et al. 2022, ApJ, 927, 204 [NASA ADS] [CrossRef] [Google Scholar]
  40. Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
  41. Finkelstein, S. L., Bagley, M. B., Arrabal Haro, P., et al. 2022, ApJ, 940, L55 [NASA ADS] [CrossRef] [Google Scholar]
  42. Franco, M., Elbaz, D., Béthermin, M., et al. 2018, A&A, 620, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Franco, M., Elbaz, D., Zhou, L., et al. 2020, A&A, 643, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020, A&A, 643, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Fudamoto, Y., Oesch, P. A., Schouws, S., et al. 2021, Nature, 597, 489 [CrossRef] [Google Scholar]
  46. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Garn, T., & Best, P. N. 2010, MNRAS, 409, 421 [Google Scholar]
  48. Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [Google Scholar]
  49. Giavalisco, M., Ferguson, H. C., Koekemoer, A. M., et al. 2004, ApJ, 600, L93 [NASA ADS] [CrossRef] [Google Scholar]
  50. Gómez-Guijarro, C., Toft, S., Karim, A., et al. 2018, ApJ, 856, 121 [Google Scholar]
  51. Gómez-Guijarro, C., Magdis, G. E., Valentino, F., et al. 2019, ApJ, 886, 88 [Google Scholar]
  52. Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022a, A&A, 658, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022b, A&A, 659, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Gould, K. M. L., Brammer, G., Valentino, F., et al. 2023, AJ, 165, 248 [NASA ADS] [CrossRef] [Google Scholar]
  55. Gruppioni, C., Béthermin, M., Loiacono, F., et al. 2020, A&A, 643, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Gwyn, S. D. J. 2012, AJ, 143, 38 [Google Scholar]
  57. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]
  58. Heinis, S., Buat, V., Béthermin, M., et al. 2014, MNRAS, 437, 1268 [Google Scholar]
  59. Hodge, J. A., & da Cunha, E. 2020, Roy. Soc. Open Sci., 7, 200556 [NASA ADS] [CrossRef] [Google Scholar]
  60. Holwerda, B. W., & Keel, W. C. 2013, A&A, 556, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Jin, S., Daddi, E., Liu, D., et al. 2018, ApJ, 864, 56 [Google Scholar]
  62. Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
  63. Keel, W. C., Manning, A. M., Holwerda, B. W., Lintott, C. J., & Schawinski, K. 2014, AJ, 147, 44 [NASA ADS] [CrossRef] [Google Scholar]
  64. Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kokorev, V., Brammer, G., Fujimoto, S., et al. 2022, ApJS, 263, 38 [NASA ADS] [CrossRef] [Google Scholar]
  66. Kokorev, V., Jin, S., Magdis, G. E., et al. 2023, ApJ, 945, L25 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [Google Scholar]
  68. Kriek, M., Shapley, A. E., Reddy, N. A., et al. 2015, ApJS, 218, 15 [NASA ADS] [CrossRef] [Google Scholar]
  69. Liu, D., Daddi, E., Dickinson, M., et al. 2018, ApJ, 853, 172 [Google Scholar]
  70. Lorenz, B., Kriek, M., Shapley, A. E., et al. 2023, ApJ, 951, 29 [NASA ADS] [CrossRef] [Google Scholar]
  71. Ma, X., Kasen, D., Hopkins, P. F., et al. 2015, MNRAS, 453, 960 [NASA ADS] [CrossRef] [Google Scholar]
  72. Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [Google Scholar]
  73. Magnelli, B., Lutz, D., Saintonge, A., et al. 2014, A&A, 561, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Magnelli, B., Gómez-Guijarro, C., Elbaz, D., et al. 2023, A&A, submitted, [arXiv:2305.19331] [Google Scholar]
  75. Manning, S. M., Casey, C. M., Zavala, J. A., et al. 2022, ApJ, 925, 23 [CrossRef] [Google Scholar]
  76. Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
  77. Marrone, D. P., Spilker, J. S., Hayward, C. C., et al. 2018, Nature, 553, 51 [NASA ADS] [CrossRef] [Google Scholar]
  78. Miller, T. B., van Dokkum, P., & Mowla, L. 2023, ApJ, 945, 155 [NASA ADS] [CrossRef] [Google Scholar]
  79. Mowla, L. A., van Dokkum, P., Brammer, G. B., et al. 2019, ApJ, 880, 57 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nelson, E., van Dokkum, P., Franx, M., et al. 2014, Nature, 513, 394 [NASA ADS] [CrossRef] [Google Scholar]
  81. Nelson, E. J., Suess, K. A., Bezanson, R., et al. 2023, ApJ, 948, L18 [NASA ADS] [CrossRef] [Google Scholar]
  82. Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [CrossRef] [Google Scholar]
  83. Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Oke, J. B. 1974, ApJS, 27, 21 [Google Scholar]
  85. Pannella, M., Elbaz, D., Daddi, E., et al. 2015, ApJ, 807, 141 [Google Scholar]
  86. Patel, S. G., Holden, B. P., Kelson, D. D., et al. 2012, ApJ, 748, L27 [NASA ADS] [CrossRef] [Google Scholar]
  87. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  88. Pérez-González, P. G., Barro, G., Annunziatella, M., et al. 2023, ApJ, 946, L16 [CrossRef] [Google Scholar]
  89. Puglisi, A., Daddi, E., Valentino, F., et al. 2021, MNRAS, 508, 5217 [NASA ADS] [CrossRef] [Google Scholar]
  90. Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
  91. Robitaille, T., & Bressert, E. 2012, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
  92. Rodighiero, G., Bisigello, L., Iani, E., et al. 2023, MNRAS, 518, L19 [Google Scholar]
  93. Rodriguez-Gomez, V., Snyder, G. F., Lotz, J. M., et al. 2019, MNRAS, 483, 4140 [NASA ADS] [CrossRef] [Google Scholar]
  94. Romano, M., Cassata, P., Morselli, L., et al. 2020, MNRAS, 496, 875 [Google Scholar]
  95. Sánchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  97. Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Schreiber, C., Elbaz, D., Pannella, M., et al. 2018, A&A, 609, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Shapley, A. E., Sanders, R. L., Reddy, N. A., Topping, M. W., & Brammer, G. B. 2023, ApJ, submitted, [arXiv:2301.03241] [Google Scholar]
  100. Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
  101. Shu, X., Yang, L., Liu, D., et al. 2022, ApJ, 926, 155 [NASA ADS] [CrossRef] [Google Scholar]
  102. Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
  103. Smail, I., Dudzevičiūtė, U., Stach, S. M., et al. 2021, MNRAS, 502, 3426 [NASA ADS] [CrossRef] [Google Scholar]
  104. Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
  105. Stefanon, M., Yan, H., Mobasher, B., et al. 2017, ApJS, 229, 32 [NASA ADS] [CrossRef] [Google Scholar]
  106. Steidel, C. C., Giavalisco, M., Pettini, M., Dickinson, M., & Adelberger, K. L. 1996, ApJ, 462, L17 [Google Scholar]
  107. Straatman, C. M. S., Spitler, L. R., Quadri, R. F., et al. 2016, ApJ, 830, 51 [NASA ADS] [CrossRef] [Google Scholar]
  108. Suess, K. A., Kriek, M., Price, S. H., & Barro, G. 2019, ApJ, 877, 103 [NASA ADS] [CrossRef] [Google Scholar]
  109. Suess, K. A., Kriek, M., Price, S. H., & Barro, G. 2021, ApJ, 915, 87 [NASA ADS] [CrossRef] [Google Scholar]
  110. Suess, K. A., Bezanson, R., Nelson, E. J., et al. 2022, ApJ, 937, L33 [NASA ADS] [CrossRef] [Google Scholar]
  111. Talia, M., Cimatti, A., Giulietti, M., et al. 2021, ApJ, 909, 23 [NASA ADS] [CrossRef] [Google Scholar]
  112. Toba, Y., Goto, T., Oi, N., et al. 2020, ApJ, 899, 35 [Google Scholar]
  113. The pandas development team 2020, https://doi.org/10.5281/zenodo.3509134 [Google Scholar]
  114. Toft, S., Smolčić, V., Magnelli, B., et al. 2014, ApJ, 782, 68 [Google Scholar]
  115. Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
  116. Umehata, H., Smail, I., Swinbank, A. M., et al. 2020, A&A, 640, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Valentino, F., Brammer, G., Gould, K. M. L., et al. 2023, ApJ, 947, 20 [NASA ADS] [CrossRef] [Google Scholar]
  118. van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [Google Scholar]
  119. van Dokkum, P. G., Nelson, E. J., Franx, M., et al. 2015, ApJ, 813, 23 [NASA ADS] [CrossRef] [Google Scholar]
  120. Walter, F., Decarli, R., Carilli, C., et al. 2012, Nature, 486, 233 [Google Scholar]
  121. Wang, T., Elbaz, D., Schreiber, C., et al. 2016, ApJ, 816, 84 [Google Scholar]
  122. Wang, T., Schreiber, C., Elbaz, D., et al. 2019, Nature, 572, 211 [Google Scholar]
  123. Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [Google Scholar]
  124. Whitaker, K. E., Bezanson, R., van Dokkum, P. G., et al. 2017, ApJ, 838, 19 [NASA ADS] [CrossRef] [Google Scholar]
  125. Wild, V., Charlot, S., Brinchmann, J., et al. 2011, MNRAS, 417, 1760 [NASA ADS] [CrossRef] [Google Scholar]
  126. Williams, C. C., Giavalisco, M., Cassata, P., et al. 2014, ApJ, 780, 1 [NASA ADS] [Google Scholar]
  127. Williams, C. C., Labbe, I., Spilker, J., et al. 2019, ApJ, 884, 154 [Google Scholar]
  128. Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
  129. Wuyts, S., Labbé, I., Franx, M., et al. 2007, ApJ, 655, 51 [NASA ADS] [CrossRef] [Google Scholar]
  130. Wuyts, S., Förster Schreiber, N. M., van der Wel, A., et al. 2011, ApJ, 742, 96 [NASA ADS] [CrossRef] [Google Scholar]
  131. Xiao, M. Y., Elbaz, D., Gómez-Guijarro, C., et al. 2023, A&A, 672, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  132. Yamaguchi, Y., Kohno, K., Hatsukade, B., et al. 2019, ApJ, 878, 73 [Google Scholar]
  133. Yung, L. Y. A., Somerville, R. S., Finkelstein, S. L., Popping, G., & Davé, R. 2019, MNRAS, 483, 2983 [NASA ADS] [CrossRef] [Google Scholar]
  134. Zahid, H. J., Yates, R. M., Kewley, L. J., & Kudritzki, R. P. 2013, ApJ, 763, 92 [NASA ADS] [CrossRef] [Google Scholar]
  135. Zhou, L., Elbaz, D., Franco, M., et al. 2020, A&A, 642, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  136. Zuckerman, L. D., Belli, S., Leja, J., & Tacchella, S. 2021, ApJ, 922, L32 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

(F150W − F444W) color versus F444W magnitude distribution for the parent SFG (black), LBG (cyan circles), and OFG (orange circles) samples. The OFG selection criteria is displayed with orange segments.
In the text
thumbnail Fig. 2.

Example OFG at zphot = 3.52, with log(M*/M⊙) = 10.39 and AV = 2.16. While the galaxy is not detected (S/N < 1) in the HST/WFC3 F160W image, it is detected (S/N > 5) in all JWST/NIRCam bands. Images are 2″ × 2″ with north up and east to the left.
In the text
thumbnail Fig. 3.

Fraction of LBGs (left axis) and fraction of OFGs (right axis) as a function of increasing AV (see main text, for details on the calculation), where NSFG is the number of galaxies in the parent SFG sample and NSFGs, bright is the number of galaxies in the parent SFG sample with F444W < 25 mag.
In the text
thumbnail Fig. 4.

Redshift (left column), stellar mass (middle column), and dust attenuation (right column) histograms of the parent SFG (top row, gray), LBG (middle row, cyan), and OFG (bottom row, orange) samples. We show the median values (filled squares) along with the 16% and 84% percentiles (segments) of the distributions in the insets.
In the text
thumbnail Fig. 5.

SFR–M* plane, with the MS from Schreiber et al. (2015) displayed as a solid blue line. Its 1σ scatter associated with 0.5 < ΔMS < 2 (∼0.3 dex) is represented as a shaded blue area, with a more extended typical scatter of 0.33 < ΔMS < 3 (∼0.5 dex) in lighter blue. We note that the values are scaled to a common redshift (zmed = 3.95) as explained in the main text.
In the text
thumbnail Fig. 6.

(Circularized) effective radius (left column), axis ratio (middle column), and Sérsic index (right column) histograms of the parent SFG (top row, grey), LBG (middle row, cyan), and OFG (bottom row, orange) samples. We show the median values (filled squares) along with the 16% and 84% percentiles (segments) of the distributions in insets.
In the text
thumbnail Fig. 7.

Dust attenuation as a function of stellar mass (left panel), (circularized) effective radius (middle panel), and axis ratio (right panel). Sliding medians for the different galaxy types shown in the legend are displayed with colored squares, with the error bars representing the uncertainty of the medians. Bins with less than three galaxies are not displayed (see Figs. 4 and 6 for the distributions).
In the text
thumbnail Fig. 8.

Ratio of the (circularized) effective radius (left panel) and axis ratio (right panel) for different galaxy types to those of the parent SFG sample. Galaxies are in the redshift bin 3 < z < 5 and are massive (log(M*/M⊙) > 10). In the case of the effective radius, ratios calculated after applying a correction to a common redshift and stellar mass are displayed with open squares. The ratios are obtained by dividing the median values of a given galaxy type by the median values of the parent SFG sample, with the error bars representing the uncertainty of the ratio of the medians.
In the text
thumbnail Fig. 9.

Relative importance of the different parameters explored in predicting dust attenuation from a random forest regressor analysis. The bar height displays the median value of the distribution of 10 000 realizations of training and test samples, while the error bars represent the 16% and 84% percentiles of the distributions.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.