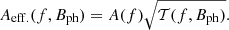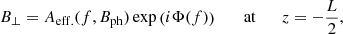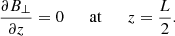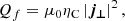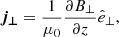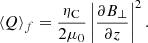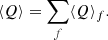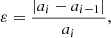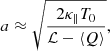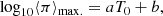| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 12 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202346459 | |
| Published online | 31 July 2023 | |
Self-consistent equilibrium models of prominence thin threads heated by Alfvén waves propagating from the photosphere
1
Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
e-mail: llorencmssil1997@gmail.com
2
Institut d’Aplicacions Computacionals de Codi Comunitari (IAC3), Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
Received:
20
March
2023
Accepted:
22
May
2023
The fine structure of solar prominences is composed of thin threads that outline the prominence magnetic field lines. Observations have shown that transverse waves of Alfvénic nature are ubiquitous in prominence threads. These waves are driven at the photosphere and propagate to prominences suspended in the corona. Heating due to Alfvén wave dissipation could be a relevant mechanism in the cool and partially ionised prominence plasma. In this work, we explore the construction of 1D equilibrium models of prominence thin threads that satisfy an energy balance condition between radiative losses, thermal conduction, and Alfvén wave heating. We assumed the presence of a broadband driver at the photosphere that launches Alfvén waves towards the prominence. An iterative method was implemented in which the energy balance equation and the Alfvén wave equation are consecutively solved. From the energy balance equation and considering no wave heating initially, we computed the equilibrium profiles along the thread of the temperature, density, ionisation fraction, and other relevant parameters. On these equilibrium profiles, we used the Alfvén wave equation to compute the wave heating rate, which was then put back in the energy balance equation to obtain new equilibrium profiles, and so on. The process was repeated until convergence to a self-consistent thread model heated by Alfvén waves was achieved. We obtained equilibrium models composed of a cold and dense thread, an extremely thin prominence-corona transition region, and an extended coronal region. We found that the length of the cold thread decreases with the temperature at the prominence core and increases with the Alfvén wave energy flux injected at the photosphere. However, computed equilibrium models for large wave energy fluxes are not possible when the wave heating rate inside the cold thread becomes larger than the radiative losses. The maximum value of the wave energy flux that allows for an equilibrium depends on the prominence core temperature. This constrains the existence of thread equilibria in realistic conditions.
Key words: magnetohydrodynamics (MHD) / Sun: atmosphere / Sun: corona / Sun: filaments / prominences / Sun: oscillations / waves
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Solar prominences consist of masses of relatively cool and dense plasma suspended in the solar corona that have physical properties similar to those in the chromosphere (see, e.g. Vial & Engvold 2015). High-resolution observations have shown that prominences are composed by a myriad of thin threads, and they seem to outline particular field lines of the general magnetic structure of prominences (see, e.g. Lin 2011; Martin 2015). The mechanical equilibrium of prominences suspended above the photosphere can be established when the upward force provided by the magnetic field compensates gravity (see, e.g. Parenti 2014; Gilbert 2015; Heinzel 2015). On the other hand, the energy balance in solar prominences is a problem not so well understood (Gilbert 2015). A detailed knowledge of the heating and cooling processes operating in prominences is needed to explain the temperatures at prominence cores, which are estimated to be in the range of 7000–9000 K (see Parenti 2014). According to radiative equilibrium models, heating due to radiative illumination is believed to be the main heating source (e.g. Heasley & Mihalas 1976; Anzer & Heinzel 1999; Heinzel et al. 2010; Heinzel & Anzer 2012). Using a slab model, Heinzel & Anzer (2012) computed radiative equilibrium temperatures within the expected range of values for a plasma composed of hydrogen alone. However, if CaII losses are added, much lower radiative equilibrium temperatures are obtained, and for certain conditions, they can be as low as 4400 K (see details in Heinzel & Anzer 2012). To the best of our knowledge, the effect of additional coolants has not been explored, but it may be that even lower radiative equilibrium temperatures would be obtained if additional coolant species are added. Therefore, although radiative heating would be dominant in prominences, we cannot presently discard that additional sources of heating play a role. The purpose of the present paper is to explore the role of Alfvén wave dissipation as a potential heating mechanism in solar prominences.
Mechanical and thermal equilibrium models of prominence thin threads have been studied before. For instance, Degenhardt & Deinzer (1993) studied the equilibrium between cooling and an imposed heating without considering the effect of thermal conduction. More detailed equilibrium models of threads were constructed by Terradas et al. (2021), who studied the balance between radiative cooling, thermal conduction, and heating. However, the heating considered by Terradas et al. (2021) was arbitrarily imposed, rather than being the result of an actual physical process. The present work follows the method of Terradas et al. (2021) to construct equilibrium models but uses a consistently computed heating from the dissipation of Alfvén waves.
Observations have shown that transverse waves are ubiquitous in fine structures of solar prominences (see the review by Arregui et al. 2018). These waves are interpreted as magnetohydrodynamic waves of Alfvénic nature (see, e.g. Lin et al. 2009; Ballester 2015). There are strong indications that the transverse waves observed in prominences are driven at the photosphere, where the prominence magnetic field is anchored (Hillier et al. 2013). It has been shown that Alfvénic waves can travel from the photosphere to the coronal structures, such as prominences or coronal loops, transporting a significant amount of energy (see Soler et al. 2019, 2021). The existence of an efficient dissipation mechanism in the prominence plasma could provide a way to thermalise the wave energy. The fact that the prominence plasma is only partially ionised introduces important dissipation mechanisms for Alfvén waves, namely, ambipolar diffusion due to ion-neutral collisions and enhanced Ohm’s diffusion due to electron-neutral collisions (see Ballester et al. 2018). Thus, heating due to Alfvénic waves arises as a possible heating mechanism in solar prominences whose importance needs to be explored.
There are some previous works that have explored the role of Alfvén wave heating in prominences. Using monochromatic waves and considering ion-neutral collisions, Pécseli & Engvold (2000) concluded that Alfvén wave heating may only compensate for a tiny part of radiative losses. However, these authors did not consider a more realistic broadband spectrum of waves with an observationally confirmed presence (Hillier et al. 2013). Conversely, Parenti & Vial (2007) estimated that the heating produced by the dissipation of unresolved non-thermal motions in prominences, which they attributed to Alfvén waves, could indeed compensate for a large fraction of radiative losses. Later, Soler et al. (2016) used an idealised slab model with a straight magnetic field transverse to the slab axis. The slab was filled with a homogeneous and partially ionised prominence plasma and was embedded in a fully ionised corona. No fine structure was considered. Alfvén waves were launched towards the prominence slab, and heating due to ion-neutral collisions was computed. Soler et al. (2016) estimated that the heating could account for about 10% of radiative losses if a spectrum of wave periods between 0.1 to 100 s is considered. Although the model was simple, the results of Soler et al. (2016) evidenced the potential of wave heating in solar prominences.
A further study of wave heating in solar prominences was done in Melis et al. (2021), and the model implemented was more elaborated. An important difference with the previous work by Soler et al. (2016) is that Melis et al. (2021) considered a model for a thin thread that included longitudinal non-uniformity and had the anchoring of the magnetic field at the ends of the model representing the base of the corona. In the central part of the thread, where the plasma is the densest and coolest, partial ionisation and the roles of Ohm’s and ambipolar diffusion were included. In the model of Melis et al. (2021), Alfvén waves were driven at one end of the thread to mimic photospheric excitation. Their results showed that wave heating could compensate for radiative losses in the cool part of the thread where the plasma was partially ionised, although the energy balance was not consistently satisfied because the density and temperature profiles were assumed ad hoc and the back reaction of wave heating upon those profiles was not considered.
The aim of the present work is to continue and go further into the study of Alfvén wave heating in prominence thin threads. Specifically, the goal is to investigate the effect of wave heating in the equilibrium of threads. To this end, we combined the method to compute the wave heating rate of Melis et al. (2021) with the method to compute equilibrium models of Terradas et al. (2021). In the presence of wave heating, threads should tend to form an equilibrium configuration where wave heating affects the profiles of density, temperature, and other variables along the thread. To study such influence and to investigate under what conditions an equilibrium is possible, we implemented a self-consistent approach loosely inspired by that used in Ofman et al. (1998) for heating by resonant absorption in coronal loops. Starting from a thread model that includes no wave heating, the wave heating rate was computed following Melis et al. (2021). Then, following Terradas et al. (2021), the energy balance equation was solved, including wave heating, and a new thread model was obtained. The wave heating rate was re-calculated in the new thread model, and an energy balance was imposed again. This, in turn, led to a different thread model, and so on. This scheme was run iteratively until convergence to a self-consistent model was reached.
This paper is structured as follows. Section 2 contains an explanation of the thread model, the basic equations, and the implementation of the self-consistent method. In Sect. 3, we present and discuss the results. Finally, some conclusions are given in Sect. 4.
2. Method
2.1. Thread models satisfying energy balance condition
As in Melis et al. (2021), we used a 1D prominence thread model composed of a single magnetic field line of length L = 108 m. Curvature and gravity were not considered; hence, the magnetic field line is straight with a uniform value of B = 10 G. We aligned the magnetic field with the z-axis for convenience. The centre of the thread was placed at z = 0, whereas we located its ends at z = ±L/2. For simplicity, we assumed a uniform gas pressure of p = 5 × 10−3 Pa. A sketch of the thread model is shown in Fig. 1.
 |
Fig. 1. Sketch of the 1D thread model. The grey areas denote the photosphere where the thread ends are anchored. The red colour gradient aims to represent the density distribution along the thread. |
The density, ρ, and temperature, T, profiles were expected to be non-uniform along the thread, but p was assumed to be uniform in order to preserve the hydrostatic equilibrium. Density and temperature are related with the pressure through the ideal gas law, which for a hydrogen plasma is
where ξi is the ionisation fraction defined as the ratio between ion density with total density and R is the ideal gas constant. In the cool parts of the thread, we expected the plasma to be partially ionised, and so ξi < 1. In order to realistically obtain the ionisation fraction in a solar prominence thread, we needed to solve the full radiative transfer equations, including incident radiation. This was far beyond the aims of this work. Thus, we instead approximated the ionisation degree using the tabulated values given in Heinzel et al. (2015), which are based on non local thermodynamic equilibrium (non LTE) computations for 1D prominence slabs. In Table 1, we indicate the values of the ionisation fraction as a function of the temperature for the pressure value considered in this work. The data of Table 1 was interpolated for intermediate temperatures, and ξi = 1 was imposed for T ≥ 20 000 K. If either T or ρ is known, Eq. (1) can be used to compute the other variable. Hence, we focused on the computation of T.
Values of the ionisation fraction, ξi, for various values of the temperature (in K) for a gas pressure of 5 × 10−3 Pa and an altitude above the photosphere of 20 000 km.
In order to obtain the temperature profile, we solved the energy balance equation given by
where ⟨Q⟩ denotes the heating rate (this represents the wave heating, as explained later); q = −κ∥∇T is the heat flux due to thermal conduction with κ∥ as the parallel thermal conductivity; ℒ represents the energy losses caused by radiative cooling; and C may represent other heating sources, such as heating due to viscous dissipation or radiative heating. Alfvén wave dissipation due to viscosity is less efficient than ambipolar dissipation in prominences, but a consistent treatment of radiative heating is well beyond our aims. Therefore, these additional sources are ignored here.
In a partially ionised plasma, the parallel component of the thermal conductivity with respect to the magnetic field can be approximated by κ∥ ≈ κe + κn. Here, κe and κn are the contributions of electrons and neutrals, respectively, and are given by
where kB is the Boltzmann constant; ne and nn are the number density of electrons and neutrals, respectively; αe and αn are the corresponding electron and neutral total friction coefficients; and αee and αnn are the electron and neutral friction coefficients accounting for self-collisions. The total friction coefficients are computed as
where β and β′ denote the different species that collide, which could be electrons (e), neutrals (n), or ions (i), and αββ′ = αβ′β are the symmetric friction coefficients between individual particles. If the collision is between charged particles, the friction coefficient is
where mββ′ = mβmβ′/(mβ+mβ′) is the reduced mass, e is the electron charge, ϵ0 is the electrical permittivity, nβ is the number density, and lnΛββ′ is the Coulomb’s logarithm, expressed as
If at least one particle is neutral, the friction coefficient is
where σβn is the collision cross-section. See details in Melis et al. (2021).
The radiative cooling rate was computed using the function provided in Athay (1986), which is frequently used in the literature to approximate radiative losses in cool prominence plasmas (see, e.g. Mok et al. 1990). We used Athay’s function because it provides lower radiative losses than other cooling tables based on the optically thin approximation that may overestimate the actual losses for cool prominence temperatures. However, we note that other approaches are possible (see Dalgarno & McCray 1972), and more recent cooling functions implement them (e.g. Schure et al. 2009; Hermans & Keppens 2021; Brughmans et al. 2022). The radiative function we adopted is written as
where mp is the proton mass and fp is an analytical function of the temperature that can be cast in MKS units as
We note that because of the variation along the thread of the temperature, density, and ionisation degree, both the thermal conductivity, κ∥, and the radiative cooling rate, ℒ, are functions of z. For a given profile of the heating rate, ⟨Q⟩, Eq. (2) results in a complicated second order ordinary differential equation for the temperature profile, T, that needs to be solved numerically. To do so, we considered the same boundary conditions as in Terradas et al. (2021). We prescribed the temperature at the thread centre, T0, and imposed that this must correspond to the temperature minimum so that the boundary conditions are
Terradas et al. (2021) showed that the following relation must be satisfied at the thread centre,
For a cold thread, the temperature at the centre must be a minimum. According to Eq. (13), this is satisfied only when ℒ > ⟨Q⟩ at z = 0. This gave us a restriction on the value of the heating rate that is explored further.
The numerical integration of Eq. (2) was performed in two separate stages: first from z = 0 to z = L/2 and later from z = 0 to z = −L/2. Then, the two solutions were joined together to construct the whole profile. This was done to correctly account for asymmetries in the heating rate, ⟨Q⟩. The integration was performed in Wolfram Mathematica with the routine NDSolve, which automatically adapts the step size to minimise numerical errors.
2.2. Alfvén wave heating
As in Melis et al. (2021), the heating rate ⟨Q⟩ was computed from the dissipation of Alfvén waves. In the single-fluid magnetohydrodynamic approximation and assuming linear waves, an equation that governs the stationary state propagation of Alfvén waves along the thread was derived by Melis et al. (2021), namely,
where B⊥ is the transverse perturbation of the magnetic field; ω is the angular wave frequency related with the linear frequency as f = ω/2π; 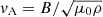 is the Alfvén speed, with μ0 as the magnetic permeability; and ηC is the Cowling’s diffusion coefficient. Again, we note that both vA and ηC are functions of z.
is the Alfvén speed, with μ0 as the magnetic permeability; and ηC is the Cowling’s diffusion coefficient. Again, we note that both vA and ηC are functions of z.
The Cowling’s diffusion is the joint effect of Ohm’s and ambipolar diffusion in a partially ionised plasma. The Ohm’s diffusion is caused by the collisions of electrons with other particles, whereas the ambipolar diffusion is related to the collisions between neutrals and charged particles. Their coefficients are written as
where η is the Ohm’s coefficient, and ηA is the ambipolar coefficient, with ξn = 1 − ξi as the fraction of neutrals. Then, the Cowling’s or total diffusion coefficient was computed as ηC = η + B2ηA.
The wave equation (Eq. (14)) needed to be solved considering appropriate boundary conditions at the ends of the thread. We assumed that the wave driver was located at the left end of the thread, z = −L/2. The Alfvén waves with a frequency, f, were driven with a prescribed amplitude that depends upon the adopted spectral weighting function, A(f). Following Tu & Song (2013) and Arber et al. (2016), the spectral weighting function was assumed to be a piece-wise power-law function expressed as
where fb is the break frequency and A0 is a constant. The break frequency was set to 1.59 mHz, as in Tu & Song (2013). The choice of this frequency was based on the observed spectrum of horizontal photospheric motions, which suggests that this frequency is between 1 and 10 mHz (see, e.g. Matsumoto & Kitai 2010). Physically, this break frequency should correspond to the beginning of the inertial range governed by the photospheric turbulence. The constant A0 depends on the wave energy flux injected by the driver. The energy flux for an Alfvén wave of frequency f averaged over one full period 1/f is
where * denotes the complex conjugate and v⊥ is the transverse velocity perturbation, which can be expressed in terms of B⊥ as (see Melis et al. 2021)
The energy flux can be decomposed as ⟨Π⟩=⟨Π⟩↑ − ⟨Π⟩↓, where ⟨Π⟩↑ and ⟨Π⟩↓ are the parallel and anti-parallel components of ⟨Π⟩, with respect to the direction of the background magnetic field. Their expressions are
where 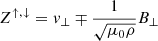 are the so-called Elsässer variables that represent parallel-propagating and anti-parallel-propagating Alfvénic disturbances, respectively. At z = −L/2, the quantity ⟨Π⟩↑ corresponds to the wave energy flux injected by the driver for one particular frequency, f. Thus, Σf⟨Π⟩↑ is the total energy flux injected by the driver for all the frequencies in the spectrum. The constant A0 was computed by assuming that the total injected energy flux is equal to a prescribed value, which is hereafter denoted by ⟨π⟩.
are the so-called Elsässer variables that represent parallel-propagating and anti-parallel-propagating Alfvénic disturbances, respectively. At z = −L/2, the quantity ⟨Π⟩↑ corresponds to the wave energy flux injected by the driver for one particular frequency, f. Thus, Σf⟨Π⟩↑ is the total energy flux injected by the driver for all the frequencies in the spectrum. The constant A0 was computed by assuming that the total injected energy flux is equal to a prescribed value, which is hereafter denoted by ⟨π⟩.
The wave driver is actually located at the photosphere, but the thread model only includes the coronal part. It is known that the transmission of Alfvén waves from the photosphere to the corona is heavily influenced by the conditions in the chromosphere, where reflection and dissipation can be equally important (see Soler et al. 2017, 2019). To account for the chromospheric filtering, we used the empirical wave energy transmission coefficient from Soler et al. (2019), 𝒯(f, Bph), which is a function of the wave frequency, f, and the magnetic field strength at the photosphere, Bph, namely:
where erf is the error function, and a0, μ, σ, and α are the amplitude, location, scale, and shape parameters, respectively, which are given in Soler et al. (2019) and depend upon Bph. In the present work, we took Bph = 100 G. Therefore, the effective spectral weighting function at the base of the corona was
We note that Aeff. is proportional to the square root of 𝒯(f, Bph) because there is quadratic relation between the wave energy and magnetic field perturbations.
Figure 2 compares the photospheric spectral weighting function, A(f), with the effective coronal one, Aeff.(f). Reflection at the chromosphere decreases the spectrum amplitude in the low frequency range, while the strong ion-neutral damping produces a rapid decrease of the amplitude as the frequency increases. Indeed, the highest frequencies in the spectrum are effectively suppressed by the chromospheric filtering.
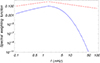 |
Fig. 2. Photospheric spectral weighting function (dash-dotted red line) and effective coronal spectral weighting function (dashed blue line) as functions of the wave driver frequency. We note that both axes are in logarithmic scale. For the purpose of this plot, we set A0 = 1. |
Hence, the form of the magnetic field perturbation at the driver location is prescribed as
where 0 < Φ(f) < 2π represents a random phase that is different for each frequency in the spectrum. On the other hand, the right end of the thread was treated as a perfectly reflecting boundary for the waves. Contrary to the empirical transmissivity used at the left boundary, there is no available empirical reflection coefficient that can be used at the right boundary to account for the effect of the chromosphere, so we had to impose a boundary condition arbitrarily. Melis et al. (2021) tested different boundary conditions, namely total reflection, total transmission, and partial reflection. Concerning the wave heating rate in the cool part of the thread, they found no significant differences between the results for the different boundary conditions. The physical explanation for this finding is that the high frequency waves that actually produce most of the heating have short damping lengths and are almost completely dissipated during their first passing through the thread such that little energy is left to reach and reflect at the boundary. Thus, we restricted ourselves to the perfectly reflecting scenario, and the boundary condition at the right end was
We discretised the spectrum of the driver into 101 individual frequencies between 0.1 and 100 mHz with a logarithmic spacing. For each of the frequencies in the discretised spectrum, Eq. (14) with the above boundary conditions (Eqs. (24) and (25)) was numerically solved in Wolfram Mathematica using, again, the routine NDSolve. This time, however, we used finite elements to perform the integration with a customised non-uniform mesh whose resolution depended upon the considered frequency, f. Results from Terradas et al. (2021) point out that temperature and density profiles are expected to have sharp variations at the prominence-corona transition region (PCTR). Concerning the Alfvén waves, the PCTR needed to be resolved with a sufficient high resolution in order to correctly compute the transmission of the waves into the dense part of the thread. Otherwise, artificial reflections could occur, which can heavily influence the results. The custom grid was divided into five different regions: the central part where the plasma is the coolest and partially ionised; two PCTR zones surrounding the centre, where there is a sharp variation of temperature and density; and two outermost parts that represent the coronal regions. For a prescribed wave frequency, the mesh resolution in the central and coronal regions was determined by the local Alfvén wavelength at the centre, λ0 = vA(z = 0)/f, or at the ends, λc = vA(z = L/2)/f, of the thread, respectively. We set the resolution in each region as equal to a small fraction of their respective local wavelengths, that is, λ0/100 for the central region and λc/20 for the coronal regions. In the PCTR zones, a fixed mesh resolution of 100 m was used for all frequencies. The width of the two high-resolution PCTR zones was set to 40 km, and their location was determined by a routine that detects the position at which the derivative of the temperature profile with respect to z is the maximum or minimum.
The numerical solution of Eq. (14) provided us with the magnetic field perturbation, B⊥, along the thread caused by the propagation of Alfvén waves with frequency, f. The next step was to compute the wave heating rate. The plasma heating is a consequence of the wave energy absorption, that is, the part of the wave energy flux that is deposited into the plasma due to Cowling’s diffusion. The instantaneous heating rate was computed as
where j⊥ is the perpendicular component of the current density given by
where 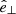 denotes the unit vector in the direction perpendicular to the magnetic field. The instantaneous heating rate needed to be averaged over one full period of the wave, 1/f, to obtain the net heating produced by that particular frequency, namely
denotes the unit vector in the direction perpendicular to the magnetic field. The instantaneous heating rate needed to be averaged over one full period of the wave, 1/f, to obtain the net heating produced by that particular frequency, namely
In order to obtain the total heating rate, we added together the net heatings produced by all the frequencies in the broadband spectrum. Thus,
The resulting heating profile is the one we used in the energy balance equation (Eq. (2)).
2.3. Self-consistent strategy
Our goal was to obtain prominence thread models in which the Alfvén wave heating obtained from the solution of Eq. (14) satisfies the energy balance condition (Eq. (2)). Thus, threads heated by Alfvén waves would be in thermal equilibrium. This equilibrium is studied in terms of two parameters: the central temperature, T0, and the wave energy flux injected at the photosphere, ⟨π⟩. For T0, we considered values between 7000 to 10 000 K as consistent with the temperatures in prominence cores. Regarding the injected energy flux, we expected that the wave heating rate increases with the injected flux. Thus, we progressively increased the value of ⟨π⟩ until the requirement of Eq. (13) was no longer satisfied and so no equilibrium models would be possible for such conditions.
The construction of self-consistent thread models heated by Alfvén waves posed a circular problem. We had to solve Eq. (14) to compute the wave heating rate. Since the Alfvén speed and the Cowling’s coefficient appear in Eq. (14), we needed the temperature and density profiles to be known beforehand. However, the temperature profile is computed from Eq. (2), which in turn requires the wave heating rate to be known. The solution to this circular problem was therefore approached using an iterative strategy.
To start with, we selected particular values of T0 and ⟨π⟩ for which the self-consistent thread model was to be computed. A thread model satisfying the energy balance condition (Eq. (2)) was obtained for the case with no wave heating (i.e. ⟨Q⟩ = 0). Subsequently, the Alfvén wave equation (Eq. (14)) was solved in that initial thread model, and the wave heating rate was obtained. This heating rate was put back in Eq. (2), and a new thread model now including wave heating was computed. This completed the first iteration of the process. Generally, the initial thread model obtained for ⟨Q⟩ = 0 and that obtained after the first iteration would be different. To quantify the difference between the models, we studied the variation of the length of the cool part of the thread, hereafter called the ‘thread length’ and denoted by a. The thread lengths were computed by automatically detecting the position of the two PCTR zones, as explained in Sect. 2.2. The location of PCTR and the thread length were computed by using the second derivative of temperature and detecting the values of z for which it equals zero. We used the parameter ε, which is defined as the relative error norm of the thread length, namely,
where ai and ai − 1 are the thread lengths for the iteration i and the previous iteration, respectively. We assumed that a self-consistent model was achieved when ε < ε0, where ε0 is a prescribed small tolerance. We used ε0 = 10−7. Therefore, the process explained before for the first iteration would be repeated as many times as necessary until convergence, if possible, was reached. If the requirement of Eq. (13) was satisfied, the value of ε decreased with the number of iterations, leading to successful convergence. However, if the requirement of Eq. (13) was not satisfied, convergence could never be achieved, and the value of ε would even increase with the number of iterations. Figure 3 displays the variation of ε with the number of iterations in two example cases: a case in which the chosen values of T0 and ⟨π⟩ allow convergence and a self-consistent model is obtained and another case that does not converge. Figure 4 summarises in a schematic way how the iterative strategy works to compute a self-consistent model.
 |
Fig. 3. Variation of the parameter ε with the number of iterations for a case that converges (dash-dotted red line) and a case that does not converge (dashed blue line). The tolerance value of ε0 = 10−7 is denoted by a horizontal line. We note that the vertical axis is in logarithmic scale. |
 |
Fig. 4. Flux diagram of the iterative strategy that we used to compute self-consistent thread models. All parameters are defined in the text. |
3. Results
3.1. A typical thread model
We start the presentation of results by analysing a typical thread model obtained for a certain combination of T0 and ⟨π⟩. This helps to better understand the results of the subsequent parameter study.
Hence, we consider T0 = 7000 K and ⟨π⟩= 0.2 W m−2. Figure 5 displays the profiles of temperature, density, ionisation fraction, Ohm’s and ambipolar coefficients, and heating rate along the thread. The temperature profile (Fig. 5a) was directly computed from Eq. (2), and its shape in the figure is similar to that obtained of the models of Terradas et al. (2021) with a constant heating term. The temperature profile can be divided into three distinct regions: a cold central region with a parabolic-like shape around the temperature minimum; then a region with a sharp increase of temperature by several orders of magnitude in a very thin layer, which clearly matches the expected PCTR mentioned before; and a wider region with a smooth increase of temperature that extends up to the ends of the thread where typical coronal temperatures on order of ∼106 K are reached. The temperature profile is largely symmetric with respect to z = 0. Very small asymmetries exist but are not noticeable at the scale of the figure. In this particular model, the thread length is a ≈ 2.66 Mm, which corresponds to a small fraction of the total length of the magnetic field line, namely a/L ≈ 0.027.
 |
Fig. 5. Equilibrium profiles along the thread: (a) temperature, (b) density, (c) ionisation fraction, (d) Ohm’s diffusion coefficient, (e) ambipolar diffusion coefficient, and (f) volumetric wave heating rate. These results are for T0 = 7000 K and ⟨π⟩= 0.2 W m−2. |
Figure 5b shows the density profile, which was computed from the temperature profile with the help of Eq. (1). The density shows an inverse profile with respect to that of the temperature. The largest density of ∼10−11 kg m−3 is located at the centre. In the outermost coronal part of the model, the density decreases to ∼10−13 kg m−3 near the ends. The ionisation fraction is plotted in Fig. 5c. We recall that the ionisation fraction was computed from the temperature using Table 1. We obtained a very narrow, partially ionised region around the thread centre, where the plasma is coldest and densest, with a minimum of ξi ≈ 0.5. The plasma rapidly becomes fully ionised in the PCTR so that ξi = 1 in the coronal part of the model.
The Ohm’s diffusion coefficient, η, can be seen in Fig. 5d. Essentially, the spatial profile of η follows that of the density. The maximum of η is located at the central part, η ∼ 1 × 103 m2 s−1, and it decreases sharply towards the coronal part of the model where η ∼ 1 m2 s−1. Therefore, the Ohm’s diffusion is three orders of magnitude more efficient in the cool central part than in the hot coronal part. The ambipolar diffusion coefficient, ηA, is shown in Fig. 5e. The ambipolar coefficient is zero in the coronal region of the model where the plasma is fully ionised. Inside the partially ionised zone, ηA has two relative maxima slightly displaced from the centre of the thread. The maximum value is ηA ∼ 1 × 1013 m2 s−1 T−2. Considering that the background magnetic field strength is B = 10 G, the maximum value of the effective ambipolar diffusion coefficient is B2ηA ∼ 1 × 107 m2 s−1, which reveals that ambipolar diffusion is much more efficient than the Ohm’s diffusion in the partially ionised region.
The wave heating rate consistent with this particular model can be seen in Fig. 5f. The heating is very non-uniform along the thread. When approaching the cold central region, the heating rate increases several orders of magnitude compared to the values obtained in the hot coronal part. Ambipolar diffusion is the dominant dissipation mechanism in our model, and it produces most of the heating in the cold, partially ionised region. In addition, unlike the rest of the quantities, the heating rate displays a clear asymmetry (see Fig. 5f). Towards the right end, the heating rate tends to zero. The reason for this asymmetry resides in the fact that the wave driver is only located at the left end of the model, while the boundary condition at the right end imposes total reflection. However, the asymmetry is much less noticeable in the central region and, indeed, the profiles obtained for the rest of model quantities are nearly symmetric with respect to z = 0.
3.2. Effect of the central temperature
After presenting the results for a particular case, we next explore the effect of changing the central temperature, T0. In all cases, we kept ⟨π⟩= 0.2 W m−2 as before. According to Terradas et al. (2021), the thread length decreases when the central temperature increases. This result is confirmed in Fig. 6, which displays the equilibrium profiles for thread models with different values of the central temperature. Due to the near symmetry of the models, Fig. 6 only shows the profiles for positive values of z corresponding to the central part of the thread and the PCTR because it is where the main differences appear, while the profiles in the coronal part would appear as nearly identical.
 |
Fig. 6. Same as Fig. 5 but for different values of the central temperature. Namely, the values are T0 = 7000 K (solid blue line), T0 = 8000 K (dashed red line), T0 = 9000 K (dash-dotted green line), and T0 = 10 000 K (solid black line). Only a close-up view of the central part and the PCTR of the thread for z ≥ 0 are displayed. These results are for ⟨π⟩= 0.2 W m−2. |
In agreement with Terradas et al. (2021), when the central temperature increases, the cold part of the thread becomes narrower. The decrease of the thread length can be explained by the relative importance of the various terms in the energy balance equation (Eq. (2)). If the effect of heating is small, which would happen for the small wave energy flux assumed here, thermal conduction would mostly be responsible for balancing radiative losses in the equilibrium (Terradas et al. 2021). As T0 increases, radiative losses become more efficient in the central region. Hence, thermal conduction requires a stronger temperature gradient to compensate for the increase of radiation that results in narrower threads.
Another consequence of an increase in the central temperature is that the partially ionised plasma gets confined to a thinner region and the lowest value of ξi increases. This is explained by the relation between temperature and ionisation fraction, as seen in Table 1. The fact that the plasma gets more ionised as T0 increases impacts the efficiency of Ohm’s and ambipolar diffusion. The coefficients associated with both effects become smaller in magnitude when T0 increases.
Despite the fact that the thread length changes, the shapes of the profiles for the different values of the central temperature are quite similar, except for the ambipolar diffusion coefficient (Fig. 6e). For high central temperatures, the maximum of ηA is located at the centre of the thread instead of being displaced from the centre when the central temperature is low. The ambipolar diffusion coefficient has a complicated dependence on the temperature and ionisation degree that results in this peculiar behaviour. In turn, the heating rate (Fig. 6f) also has a similar shape for all the central temperatures considered, but its value at the thread centre increases or decreases with T0 according to the behaviour of the ambipolar diffusion coefficient at z = 0.
3.3. Effect of the wave energy flux
In addition to the role of the central temperature, which was already explored by Terradas et al. (2021), we are also interested in the effect of the injected wave energy flux. Therefore, we set the central temperature to T0 = 7000 K and considered three different values of the injected energy flux, namely: ⟨π⟩= 0.2, 0.4, and 0.8 W m−2. The computed models for those values of wave energy flux are displayed in Fig. 7, where, again, only positive values of z corresponding to the central part of the thread and the PCTR are displayed.
 |
Fig. 7. Same as Fig. 6 but with T0 = 7000 K and three different values of injected wave energy flux. The values of the injected wave energy flux are ⟨π⟩= 0.2 W m−2 (solid blue line), ⟨π⟩= 0.4 W m−2 (dashed red line), and ⟨π⟩= 0.8 W m−2 (dash-dotted green line). |
Two main effects of varying ⟨π⟩ can be seen in Fig. 7. First of all, the larger ⟨π⟩, the larger the wave heating rate ⟨Q⟩ (see Fig. 7f). This result is not surprising, because the wave heating rate is expected to be proportional to the injected wave energy flux. In other words, the larger the available wave energy, the larger the energy that is dissipated. The second effect that is obvious from the Fig. 7 is the growth of the thread length as ⟨π⟩ increases. Indeed, this result is a consequence of the increase of the heating rate discussed before. Following Terradas et al. (2021), the increase of the thread length can be understood by using an approximate analytic expression for this quantity given by
where κ∥, ℒ, and ⟨Q⟩ need to be evaluated at the thread centre, z = 0. If the central temperature remains constant and the wave heating rate increases at z = 0 and approaches the minimum value of radiative loses, then the denominator in Eq. (31) decreases. Consequently, the thread length increases. In Terradas et al. (2021), a similar conclusion was reached, although for a spatially uniform heating term. Here, the heating rate is very non-uniform along the field line, but Eq. (31) can still be used to understand the effect of the heating on the thread length. In this regard, and for a fixed central temperature, only the value of ⟨Q⟩ at the centre seems to be relevant, while its spatial profile does not play a role according to Eq. (31). The effect of the wave heating on the thread length is investigated further in Sect. 3.5.
3.4. Role of wave heating in the energy balance
In this section, we explore the role of wave heating in the energy balance. We consider an illustrative example of self-consistent thread models obtained for a central temperature of 9000 K and two different injected wave energy fluxes, namely, ⟨π⟩= 0.1 and 30 W m−2. Figure 8 compares the importance along the thread of the various terms that appear in the energy balance equation (Eq. (2)), namely, radiation losses, thermal conduction, and wave heating. To better visualise the results, Fig. 8 only displays the cool central part, the PCTR, and the beginning of the coronal part.
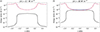 |
Fig. 8. Comparison of the various terms in the energy balance equation (Eq. (2)) in models with T0 = 9000 K and two values of the injected wave energy flux: (a) ⟨π⟩= 0.1 W m−2 and (b) ⟨π⟩= 30 W m−2. The solid black line corresponds to the wave heating rate, the dot-dashed blue line denotes radiative losses, and the dashed red line represents the thermal conduction term. Only a close-up view of the central part and the PCTR of the thread are displayed. |
In the figure, the shape of the wave heating rate is similar for both values of ⟨π⟩. The maximum of ⟨Q⟩ is located at the centre of the thread and then there is a sharp decrease of several orders of magnitudes in the PCTR so that the values of ⟨Q⟩ in the coronal part of the model are much smaller than in the central cool part. Indeed, as already pointed out, ⟨Q⟩ seems to mimic the profile of the Cowling’s diffusion coefficient, ηC, in the central and PCTR regions, while in the coronal zone it approximately follows the profile of the Ohm’s diffusion coefficient, η. This highlights the dominance of each mechanism in the different regions.
In the case with ⟨π⟩= 0.1 W m−2, the wave heating rate is much less important than the radiative losses and thermal conduction, even in the central cool part. In this case (see Fig. 8a), wave heating has an almost negligible influence on the energy balance since radiative losses and thermal conduction essentially compensate each other everywhere along the field line. Radiative loses have a minimum located at the centre of the thread, while their maximum is located inside the PCTR around T ≈ 58 000 K. In this case, the thermal conduction term just follows the spatial dependence of radiative losses. Comparing the results with the work of Terradas et al. (2021), the shapes of the radiative losses and thermal conduction terms obtained here are identical to those obtained in the previous work, although Terradas et al. (2021) used constant heating instead of a function depending on position.
The situation changed when we considered a larger wave energy flux of ⟨π⟩= 30 W m−2 (see Fig. 8b). In this case, a significantly larger heating rate was obtained in the central region, which approaches the minimum of radiative losses. This large value of the wave energy flux brought us close to the upper boundary of ⟨Q⟩ imposed by Eq. (13) to obtain a self-consistent model. Around the thread centre, wave heating compensates a large fraction of radiation losses, while thermal conduction has a lower weight in the energy balance. The relevance of wave heating only applies in the central part of the thread, where the plasma is cool and partially ionised, while in the PCTR and especially in the coronal region, its contribution remains almost negligible, and thermal conduction entirely compensates cooling. These results are consistent with the work of Melis et al. (2021), where the heating rate in the cool central region was estimated to be as important as radiative loses for large enough wave energy fluxes.
As already discussed in Sect. 3.3, another difference between the results for the two considered wave energy fluxes is that the length of the thread increases when ⟨π⟩= 30 W m−2 compared to the case with ⟨π⟩= 0.1 W m−2. The computed lengths are a ≈ 0.59 Mm for ⟨π⟩= 0.1 W m−2 and a ≈ 0.77 Mm for ⟨π⟩= 30 W m−2.
3.5. Thread length: Parameter survey
Since the main effect of wave heating is to modify the thread length, in this section we perform a parameter study on the variation of this quantity as a function of T0 and ⟨π⟩. Although some results have already been obtained in previous sections, here we carry out a more detailed investigation.
Figure 9a shows the variation of thread length as a function of the injected wave energy flux for the various central temperatures considered. For each central temperature, the wave energy flux has been varied between ⟨π⟩= 0.1 W m−2 and the maximum flux that allows the requirement of Eq. (13) to be satisfied, hereafter denoted by ⟨π⟩max.. Comparing the results for different temperatures, we found that for low central temperatures, the thread length is larger than for high central temperatures, as already discussed in Sect. 3.2, but the evolution of the thread length when ⟨π⟩ increases is similar for all the considered central temperatures. Three different regimes were found. First, for ⟨π⟩≪⟨π⟩max., the thread length smoothly increases with ⟨π⟩ following an approximate linear dependence. Then, when ⟨π⟩ approaches ⟨π⟩max., the thread length starts to increase more abruptly in an approximately exponential fashion. Finally, for ⟨π⟩→⟨π⟩max., the thread length asymptotically tends to infinity. Although our iterative strategy allowed us to consider large values of ⟨π⟩ that differ from ⟨π⟩max. by a tiny percentage, the method becomes unstable when ⟨π⟩ is too close to ⟨π⟩max.. For this reason, the third regime (i.e. the asymptotic behaviour of the thread length when ⟨π⟩→⟨π⟩max.) is only partially captured by the results shown in Fig. 9a. Such asymptotic behaviour can be better visualised in Fig. 9b, which displays the percentage increase of the thread length as a function of ⟨π⟩ with respect to the length obtained in the absence of wave heating. Depending on the central temperature, a percentage increase of the thread length between 15% and 30% was obtained for wave energy fluxes just below ⟨π⟩max..
 |
Fig. 9. Dependence of the thread length with the wave energy flux. Panel (a): Thread length, a, as a function of the injected wave energy flux, ⟨π⟩, for different values of central temperature. Panel (b): Percentage increase of the thread length with respect to the value without wave heating as a function of ⟨π⟩ for the same central temperatures. The vertical lines in panel (b) denote the value of ⟨π⟩max. corresponding to each temperature. |
Figure 10 presents the same results of Fig. 9 but in a complementary way. Figure 10 displays the thread length as a function of the central temperature in two cases: the length obtained when no wave heating is present (i.e. for ⟨π⟩ = 0) and the length obtained for a wave energy flux just below ⟨π⟩max. (i.e. at the beginning of the asymptotic regime). As stated before, the thread length decreases when the central temperature increases, which is consistent with the previous results of Terradas et al. (2021). For a given central temperature, Fig. 10 shows the range of values of the thread length for which our iterative method converges and a self-consistent model is obtained. Threads with smaller lengths are not possible. Threads with larger lengths are indeed possible, but only in the asymptotic regime when ⟨π⟩→⟨π⟩max., which happens in a extremely narrow range of values of ⟨π⟩ just below ⟨π⟩max..
 |
Fig. 10. Thread length, a, as a function of the central temperature, T0, in the absence of wave heating (red line) and for ⟨π⟩≈⟨π⟩max. (blue line). The grey area indicates the range of possible thread lengths for which a self-consistent model can be found. |
Another interesting result is that ⟨π⟩max. is a function of the central temperature (see Fig. 11). High central temperatures are able to accommodate larger wave energy fluxes than low central temperatures. Again, the reason for this result can be found in the requirement of Eq. (13) that an equilibrium model must satisfy. At z = 0, the radiative losses provided by Athay’s function (Eq. (10)) increase with T0. Therefore, the maximum wave heating rate at z = 0 that is consistent with Eq. (13) also becomes larger when T0 increases. Obviously, larger wave heating rates, ⟨Q⟩, are associated with larger wave energy fluxes, ⟨π⟩. The results of Fig. 11 suggest a power-law dependence of ⟨π⟩max. with T0. Therefore, we performed a least squares fit to the results of Fig. 11 considering the following form:
 |
Fig. 11. Maximum wave energy flux injected at the photosphere, ⟨π⟩max. as a function of the thread central temperature, T0. The symbols are the results of the computations, while the dashed line is the fit of Eq. (32). We note that the vertical axis is in logarithmic scale. |
where a = (770 ± 18)×10−6 and b = −5.49 ± 0.15 with ⟨π⟩max. are expressed in Watts per metre squared and T0 in Kelvins. The R2 coefficient of the fit is R2 = 0.997. The fitted function is overplotted in Fig. 11, showing a very good approximation to the numerical data. Hence, for a given central temperature, Eq. (32) can be used to predict the maximum wave energy flux that allows an equilibrium model to exist.
4. Conclusions
In this paper, we studied 1D models of prominence thin threads that satisfy an energy balance condition, including heating due to Alfvén waves. Our investigation is built upon the previous works of Terradas et al. (2021) and Melis et al. (2021), where equilibrium models and Alfvén wave heating were studied separately. We computed the thread models using an iterative method involving the solution of the energy balance equation together with the Alfvén wave equation until convergence to a self-consistent model of a thin thread was achieved. The Alfvén waves were assumed to be launched from the photosphere by a broadband driver that injects a prescribed value of the wave energy flux. The waves were then dissipated in the prominence by Ohm’s and ambipolar diffusion.
The computed thread models were composed of a cold central region that corresponds to the prominence core (the prominence thread itself), a thin PCTR in which there is a sharp increase of temperature, and an external region with solar coronal properties. The wave heating rate was at its maximum in the central part of the thread, where the plasma is partially ionised and ambipolar diffusion is responsible for wave dissipation. In the outermost coronal part, wave heating was negligible because of the irrelevance of Ohm’s diffusion for fully ionised coronal conditions.
The magnitude of the wave heating rate in the cold central region depended on the wave energy flux injected by the driver at the photosphere such that the larger the injected energy flux, the larger the heating rate. Increasing the value of the injected energy flux resulted in obtaining models with longer cold regions (i.e. longer threads). Self-consistent models could be obtained until the injected wave energy flux produced a heating rate at the thread centre that was equal to the radiative losses. We performed a parametric survey in order to explore how the thread length correlates with the injected wave energy flux and the central temperature. The thread length decreased with increasing central temperature and increased with the injected wave energy flux. The maximum value of the wave energy flux that allows self-consistent models to exist was found to increase with the value of the central temperature, so hot threads are able to accommodate more wave heating than cool ones.
We used the injected wave energy flux as a free parameter of the model. Unfortunately, there are no determinations of the Alfvén wave energy flux driven at the footpoints of the magnetic structure of prominences. In intense photospheric flux tubes, calculations of the transverse wave energy flux driven by horizontal motions show that the flux generated within the photospheric flux tubes can be as large as ∼106 W m−2 (see, e.g. Spruit 1981; Ulmschneider 2000; Noble et al. 2003; Shelyag et al. 2011). When averaged over the entire photosphere and considering the photospheric filling factor, the resulting averaged driven flux is of the order of ∼104 W m−2 (see, e.g. De Pontieu et al. 2001; Goodman 2011; Tu & Song 2013; Arber et al. 2016). This estimated wave energy flux applies in the case of photospheric bright points, but it is probably much larger than the wave energy flux driven in the case of prominences. If this large energy flux were applicable to prominences, then our results indicate that no equilibrium models of threads would be possible, as wave heating would simply be too large. Stable threads cannot sustain such large wave energy fluxes. In essence, the existence or absence of equilibrium models depends upon the balance between wave heating and radiation losses at the thread centre. While radiation losses mainly depend on the local properties of the thread, the magnitude of wave heating is determined by how the waves are driven at the photospheric regions where the prominence magnetic field is anchored. Recently, Li et al. (2022) reported Alfvénic waves along prominence threads with an estimated energy flux of 16.2–37.3 W m−2, which is more compatible with the wave energy fluxes needed to obtain equilibrium models.
For simplicity and to consider the same setup as in Melis et al. (2021), a perfectly reflecting boundary was implemented at the right end of the thread, instead of considering the presence of two different drivers located at both ends. The expected results of adding a second driver to the model are straightforward. If the second driver injects the same energy flux as the first one, the heating rate in the cool region would double its value. In turn, the maximum value of the wave energy flux to obtain a self-consistent model would then need to account for the sum of the fluxes injected by both drivers.
A limitation of this work is that the computation of the wave heating rate assumes the stationary state of wave propagation. In other words, we assumed that the waves had been propagating and reflecting along the thread for enough time to reach a stationary pattern. An alternative approach would be to solve the time-dependent problem, which would require full numerical simulations. The comparison of time-dependent results with those of the stationary problem is relevant and may be tackled in the future.
Although the present method of constructing thread models heated by Alfvén waves provides interesting results, the background configuration is still simple compared to the observed complexity of prominences. A further extension would be to consider 2D models in cylindrical geometry, which should include the perpendicular component of thermal conduction. Concerning the Alfvén waves, the use of 2D models would introduce the presence of resonances in the Alfvén continuum. Adding these new aspects would allow us to obtain more accurate information about the efficiency of wave heating in solar prominences and the conditions for the existence of equilibrium models. This could also be undertaken in follow-up work.
Finally, we return to the comment made in the introduction of this work about the possible role that Alfvén wave heating may have in complementing radiative heating of prominences. In our approach, we computed thread models with realistic lengths and central temperatures without including radiative heating. This suggests that Alfvén wave heating may not only play a complementary role but an important part in the energy balance of prominence threads, which is an aspect that future works should keep investigating. Ideally, future models should include both radiative and wave heating, which is a challenging task.
Acknowledgments
This publication is part of the R+D+i project PID2020- 112791GB-I00, financed by MCIN/AEI/10.13039/501100011033. This research was supported by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project #457 (The Role of Partial Ionization in the Formation, Dynamics and Stability of Solar Prominences). We thank Ramón Oliver for some comments regarding the importance of correctly resolving the PCTR. We acknowledge the unknown referee for very constructive comments that helped us to improve the paper.
References
- Anzer, U., & Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] [Google Scholar]
- Arber, T. D., Brady, C. S., & Shelyag, S. 2016, ApJ, 817, 94 [Google Scholar]
- Arregui, I., Oliver, R., & Ballester, J. L. 2018, Liv. Rev. Sol. Phys., 15, 3 [Google Scholar]
- Athay, R. G. 1986, ApJ, 308, 975 [Google Scholar]
- Ballester, J. L. 2015, in Solar Prominences, eds. J. C. Vial, & O. Engvold, Astrophys. Space Sci. Lib., 259, 415 [Google Scholar]
- Ballester, J. L., Alexeev, I., Collados, M., et al. 2018, Space Sci. Rev., 214, 58 [Google Scholar]
- Brughmans, N., Jenkins, J. M., & Keppens, R. 2022, A&A, 668, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalgarno, A., & McCray, R. A. 1972, ARA&A, 10, 375 [Google Scholar]
- De Pontieu, B., Martens, P. C. H., & Hudson, H. S. 2001, ApJ, 558, 859 [Google Scholar]
- Degenhardt, U., & Deinzer, W. 1993, A&A, 278, 288 [NASA ADS] [Google Scholar]
- Gilbert, H. 2015, in Solar Prominences, eds. J. C. Vial, & O. Engvold, Astrophys. Space Sci. Lib., 415, 157 [Google Scholar]
- Goodman, M. L. 2011, ApJ, 735, 45 [Google Scholar]
- Heasley, J. N., & Mihalas, D. 1976, ApJ, 205, 273 [Google Scholar]
- Heinzel, P. 2015, in Solar Prominences, eds. J. C. Vial, & O. Engvold, Astrophys. Space Sci. Lib., 415, 103 [Google Scholar]
- Heinzel, P., & Anzer, U. 2012, A&A, 539, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Anzer, U., & Gunár, S. 2010, Mem. Soc. Astron. It., 81, 654 [NASA ADS] [Google Scholar]
- Heinzel, P., Gunár, S., & Anzer, U. 2015, A&A, 579, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hermans, J., & Keppens, R. 2021, A&A, 655, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillier, A., Morton, R. J., & Erdélyi, R. 2013, ApJ, 779, L16 [Google Scholar]
- Li, D., Xue, J., Yuan, D., & Ning, Z. 2022, Sci. China-Phys. Mech. Astron., 65, 239611 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y. 2011, Space Sci. Rev., 158, 237 [Google Scholar]
- Lin, Y., Soler, R., Engvold, O., et al. 2009, ApJ, 704, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F. 2015, in Solar Prominences, eds. J. C. Vial, & O. Engvold, Astrophys. Space Sci. Lib., 415, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., & Kitai, R. 2010, ApJ, 716, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Melis, L., Soler, R., & Ballester, J. L. 2021, A&A, 650, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mok, Y., Drake, J. F., Schnack, D. D., & van Hoven, G. 1990, ApJ, 359, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Noble, M. W., Musielak, Z. E., & Ulmschneider, P. 2003, A&A, 409, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., Klimchuk, J. A., & Davila, J. M. 1998, ApJ, 493, 474 [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Parenti, S., & Vial, J. C. 2007, A&A, 469, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pécseli, H., & Engvold, O. 2000, Sol. Phys., 194, 73 [Google Scholar]
- Schure, K. M., Kosenko, D., Kaastra, J. S., Keppens, R., & Vink, J. 2009, A&A, 508, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shelyag, S., Fedun, V., Keenan, F. P., Erdélyi, R., & Mathioudakis, M. 2011, Ann. Geophys., 29, 883 [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., & Ballester, J. L. 2016, A&A, 592, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., & Ballester, J. L. 2017, ApJ, 840, 20 [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., & Ballester, J. L. 2019, ApJ, 871, 3 [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., & Ballester, J. L. 2021, ApJ, 909, 190 [Google Scholar]
- Spruit, H. C. 1981, A&A, 98, 155 [NASA ADS] [Google Scholar]
- Terradas, J., Luna, M., Soler, R., et al. 2021, A&A, 653, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tu, J., & Song, P. 2013, ApJ, 777, 53 [Google Scholar]
- Ulmschneider, P. 2000, in Chromosphere: Heating Mechanisms, Encyclopedia of Astronomy and Astrophysics, ed. P. Murdin (Nature Publishing Group), 2260 [Google Scholar]
- Vial, J.-C., & Engvold, O. 2015, Solar Prominences, 415, 490 [NASA ADS] [Google Scholar]
All Tables
Values of the ionisation fraction, ξi, for various values of the temperature (in K) for a gas pressure of 5 × 10−3 Pa and an altitude above the photosphere of 20 000 km.
All Figures
 |
Fig. 1. Sketch of the 1D thread model. The grey areas denote the photosphere where the thread ends are anchored. The red colour gradient aims to represent the density distribution along the thread. |
| In the text | |
 |
Fig. 2. Photospheric spectral weighting function (dash-dotted red line) and effective coronal spectral weighting function (dashed blue line) as functions of the wave driver frequency. We note that both axes are in logarithmic scale. For the purpose of this plot, we set A0 = 1. |
| In the text | |
 |
Fig. 3. Variation of the parameter ε with the number of iterations for a case that converges (dash-dotted red line) and a case that does not converge (dashed blue line). The tolerance value of ε0 = 10−7 is denoted by a horizontal line. We note that the vertical axis is in logarithmic scale. |
| In the text | |
 |
Fig. 4. Flux diagram of the iterative strategy that we used to compute self-consistent thread models. All parameters are defined in the text. |
| In the text | |
 |
Fig. 5. Equilibrium profiles along the thread: (a) temperature, (b) density, (c) ionisation fraction, (d) Ohm’s diffusion coefficient, (e) ambipolar diffusion coefficient, and (f) volumetric wave heating rate. These results are for T0 = 7000 K and ⟨π⟩= 0.2 W m−2. |
| In the text | |
 |
Fig. 6. Same as Fig. 5 but for different values of the central temperature. Namely, the values are T0 = 7000 K (solid blue line), T0 = 8000 K (dashed red line), T0 = 9000 K (dash-dotted green line), and T0 = 10 000 K (solid black line). Only a close-up view of the central part and the PCTR of the thread for z ≥ 0 are displayed. These results are for ⟨π⟩= 0.2 W m−2. |
| In the text | |
 |
Fig. 7. Same as Fig. 6 but with T0 = 7000 K and three different values of injected wave energy flux. The values of the injected wave energy flux are ⟨π⟩= 0.2 W m−2 (solid blue line), ⟨π⟩= 0.4 W m−2 (dashed red line), and ⟨π⟩= 0.8 W m−2 (dash-dotted green line). |
| In the text | |
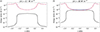 |
Fig. 8. Comparison of the various terms in the energy balance equation (Eq. (2)) in models with T0 = 9000 K and two values of the injected wave energy flux: (a) ⟨π⟩= 0.1 W m−2 and (b) ⟨π⟩= 30 W m−2. The solid black line corresponds to the wave heating rate, the dot-dashed blue line denotes radiative losses, and the dashed red line represents the thermal conduction term. Only a close-up view of the central part and the PCTR of the thread are displayed. |
| In the text | |
 |
Fig. 9. Dependence of the thread length with the wave energy flux. Panel (a): Thread length, a, as a function of the injected wave energy flux, ⟨π⟩, for different values of central temperature. Panel (b): Percentage increase of the thread length with respect to the value without wave heating as a function of ⟨π⟩ for the same central temperatures. The vertical lines in panel (b) denote the value of ⟨π⟩max. corresponding to each temperature. |
| In the text | |
 |
Fig. 10. Thread length, a, as a function of the central temperature, T0, in the absence of wave heating (red line) and for ⟨π⟩≈⟨π⟩max. (blue line). The grey area indicates the range of possible thread lengths for which a self-consistent model can be found. |
| In the text | |
 |
Fig. 11. Maximum wave energy flux injected at the photosphere, ⟨π⟩max. as a function of the thread central temperature, T0. The symbols are the results of the computations, while the dashed line is the fit of Eq. (32). We note that the vertical axis is in logarithmic scale. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



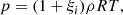
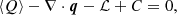
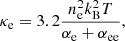
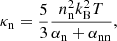
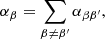
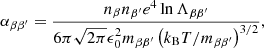
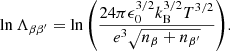
![$$ \begin{aligned} \alpha _{\beta n}= n_{\beta } n_{\rm n} m_{\beta \mathrm{n}} \left[ \frac{8 k_{\rm B} T}{\pi m_{\beta \mathrm{n}}} \right]^{1/2} \sigma _{\beta \mathrm{n}}, \end{aligned} $$](/articles/aa/full_html/2023/08/aa46459-23/aa46459-23-eq8.gif)
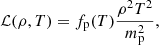
![$$ \begin{aligned} f_{\rm p}(T)&= 10^{-35} T^{-2} \Bigl \{ 0.4 \exp \left[ -30 \left( \log _{10} T -4.6 \right)^{2} \right] \nonumber \\&\quad + 4 \exp \left[ -20 \left( \log _{10} T -4.9 \right)^{2} \right] \nonumber \\&\quad + 4.5 \exp \left[ -16 \left( \log _{10} T - 5.35 \right)^{2} \right] \nonumber \\&\quad + 2 \exp \left[ -4 \left( \log _{10} T -6.1 \right)^{2} \right] \Bigr \}. \end{aligned} $$](/articles/aa/full_html/2023/08/aa46459-23/aa46459-23-eq10.gif)
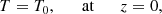
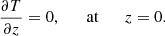
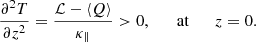
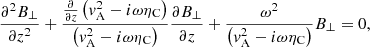
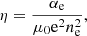
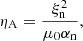
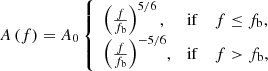
![$$ \begin{aligned} \langle \boldsymbol{\Pi } \rangle = -\frac{1}{2 \mu _0} \mathrm{Re} \left[ {v}_{\perp } B_{\perp }^{*} \right]\boldsymbol{B}, \end{aligned} $$](/articles/aa/full_html/2023/08/aa46459-23/aa46459-23-eq19.gif)
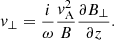
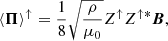
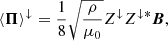
![$$ \begin{aligned} \begin{split} \mathcal{T} (f,B_{\rm ph})&\approx a_{0}(B_{\rm ph}) \frac{1}{\sqrt{2\pi \sigma {(B_{\rm ph})}^{2}}} \exp \left( -\frac{\left( \log _{10} f -\mu (B_{\rm ph})\right)^{2}}{2\sigma {(B_{\rm ph})}^{2}} \right) \\&\times \left[ 1 + \mathrm{erf} \left( \frac{\alpha (B_{\rm ph})}{\sqrt{2}} \frac{\log _{10}f - \mu (B_{\rm ph})}{\sigma (B_{\rm ph})} \right) \right], \end{split} \end{aligned} $$](/articles/aa/full_html/2023/08/aa46459-23/aa46459-23-eq24.gif)