| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245197 | |
| Published online | 01 June 2023 | |
Particle-in-cell modelling of comet 67P/Churyumov-Gerasimenko
Spatial structures of densities and electric fields
1
Department of Physics, Umeå University,
901 87
Umeå,
Sweden
e-mail: herbert.gunell@physics.org
2
Department of Mathematics, Physics and Electrical Engineering, Northumbria University,
Newcastle upon Tyne,
UK
e-mail: charlotte.goetz@northumbria.ac.uk
3
Formerly at Space Research and Technology Centre, European Space Agency,
Keplerlaan 1,
2201AZ
Noordwijk,
The Netherlands
Received:
12
October
2022
Accepted:
31
March
2023
Context. Sufficiently far from the Sun, all comets go through a phase of low activity. Rosetta observations at large heliocentric distances of approximately 3 au showed that the plasma at a low-activity comet is affected by both steady state electric fields and low-frequency waves.
Aims. Our goal is to provide a model for the electric fields in the inner coma at a low-activity comet and to simulate waves and field structures farther away from the nucleus.
Methods. We compare analytical models for the convective, ambipolar, and polarisation electric fields to the results of an electrostatic particle-in-cell simulation of a scaled-down low-activity comet.
Results. We find good agreement between the steady state field model and the simulation results close to the nucleus. At larger cometocentric distances, waves dominate the electric field. These waves are interpreted as the scaled-down electrostatic limit of the previously observed singing comet waves. The comet ion density is not spherically symmetric.
Conclusions. Low-activity comets can be modelled using electrostatic particle-in-cell simulations of a scaled-down system. Outside the innermost part of the coma (r ≳ 40 km), the plasma is not spherically symmetric and the electric field is dominated by waves.
Key words: comets: general / comets: individual: 67P/Churyumov-Gerasimenko / plasmas / methods: numerical / waves
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In this paper, we present the results of electrostatic particle-in-cell simulations of comet 67P/Churyumov-Gerasimenko (67P) when it was at a heliocentric distance of 3 au. Comet 67P was visited by the Rosetta orbiter during two years from 2014 to 2016, and results in cometary plasma physics based on Rosetta measurements were reviewed by Goetz et al. (2022b). When the Rosetta spacecraft arrived at comet 67P in August 2014, it was at approximately 3.6 au from the Sun. The comet was in a weak activity stage with an outgassing rate of (2−4)×1025 s−1 (Simon Wedlund et al. 2016; Hansen et al. 2016). The comet interacted with the solar wind through weak mass loading; water group ions formed by ionisation of the neutral coma were accelerated by the convective electric field of the solar wind, and solar-wind protons were deflected by approximately 20° (Nilsson et al. 2015a).
Closer to the Sun, the comet–solar-wind interaction entered a different regime. An infant bow shock was first observed when the heliocentric distance of comet 67P fell below 3 au (Gunell et al. 2018; Goetz et al. 2021). When the comet moved even closer to the Sun, both a solar-wind ion cavity (Simon Wedlund et al. 2019) and a diamagnetic cavity appeared (Goetz et al. 2016b,a). Heliocentric distances of approximately 3 au have been the subject of a few simulation studies in the past, using hybrid models (Koenders et al. 2016); comparing multi-fluid and hybrid models (Rubin et al. 2014); employing implicit particle-in-cell simulations (Deca et al. 2017); and using an electrostatic particle-in-cell model (Gunell et al. 2019). At 3 au, the weak mass-loading stage of the comet–solar-wind interaction was coming to an end, but the qualitative change represented by the formation of shocks and plasma boundaries had not yet occurred. This is also the regime that is examined in this work.
One aspect of interest is how the density of the cometary plasma is distributed in the head of the comet. The density of the neutral gas that is sublimated from the surface follows a Haser model (Haser 1957). For cometocentric distances relevant to the Rosetta mission, ionisation has only a negligible influence on the neutral density, which is therefore proportional to r−2. Galand et al. (2016) derived a radial ion density profile proportional to r−1 under the assumptions that the ions are collisionally coupled to the neutrals and therefore move at the same velocity. Vigren & Eriksson (2017) considered an energy-dependent cross section for ion–neutral collisions and an ambipolar electric field accelerating ions outward. In their model, the ions moves significantly faster than the neutrals, and the speed of the ions also affects the density. That the ions move faster than the neutrals was also observed by Rosetta (Odelstad et al. 2018). Edberg et al. (2022) used data from six periods when Rosetta moved along the radial dimension, and found that the ion density on average followed an approximate r−1 profile, but these authors also found that there were intervals when the deviations were significant.
Immediately upon arrival, Rosetta observed waves in the 10–100 mHz range, and these were given the name ‘singing comet waves’ (Richter et al. 2015, 2016). These waves continued to be observed until the end of March 2015 (at 2 au heliocentric distance) after which the spacecraft was located too deep into the inner coma for suitable observations to be made (Goetz et al. 2020). The observations of singing comet waves have been interpreted in terms of an ion Weibel instability (Meier et al. 2016), and similar waves have been seen in simulations (Rubin et al. 2014; Koenders et al. 2016; Deca et al. 2017).
When comet 67P moved closer to the Sun, a multitude of different waves could be observed: ion acoustic waves both in the diamagnetic cavity (Gunell et al. 2017a), at the boundary of this cavity (Madsen et al. 2018), and during times when the cavity has not yet formed (Gunell et al. 2017b, 2021); Langmuir waves were seen throughout the escort phase of the mission (Myllys et al. 2021); and lower hybrid waves (André et al. 2017; Karlsson et al. 2017) often in connection with steepened magnetosonic waves (Stenberg Wieser et al. 2017; Ostaszewski et al. 2021).
Stationary waves can develop when the wave propagates with an equal and opposite velocity to a plasma flow. One example is planetary bow shocks, which are stationary when viewed on large scales, although constantly moving and reforming, they are non-stationary on small scales (Balogh & Treumann 2013). Another examples is stationary Alfvén waves that have been suggested as a way to accelerate electrons in the aurora (Knudsen 1996) and that have been shown to exist in laboratory plasmas (Finnegan 2008; Koepke et al. 2016). In this paper we use electrostatic particle-in-cell simulations to model the interaction between the comet and the solar wind. This approach has previously been applied to plasmoids encountering magnetic barriers (Hurtig et al. 2003; Gunell et al. 2008, 2009). Being electrostatic, the model cannot reproduce any changes in the magnetic field. However, the electrostatic aspects are still adequately modelled as long as the currents are small enough that those changes are insignificant, as can be seen by comparison to electromagnetic simulations of the same phenomena (Voitcu & Echim 2016, 2017). No wave is completely electrostatic, as the currents associated with the waves give rise to time-variable magnetic fields. Waves can transition between electrostatic and electromagnetic in different parameter regimes, and energy can be transferred between electrostatic and electromagnetic waves in non-linear interactions (Tejero et al. 2015a,b, 2016). In this work, we consider a comet where the length scales have been reduced by a factor of either 1/400 or 1/200 in different simulation runs. As currents scale with cross-sectional area, this also scales down the magnetic-field variations, the system becomes predominantly electrostatic, and what we explore is the electrostatic limit of the real comet.
2 Models and methods
2.1 Particle-in-cell model
We used the electrostatic particle-in-cell model Picard (Lindkvist & Gunell 2019) to simulate a scaled-down comet at low activity. The model and first results were described by Gunell et al. (2019), and we only summarise the most important facts here.
Poisson’s equation is solved using the conjugate gradient method (e.g. Shewchuk 1994) and open boundary conditions, meaning that space outside the simulation box is assumed to be empty and the potential at the boundary derived from the charge density inside the simulation box is specified as a Dirichlet boundary condition. Poisson’s equation is solved in the solar-wind frame of reference, where the convective electric field vanishes, but all results presented here are in the comet frame of reference. The electric field in the comet frame is obtained by addition of the convective term −υSW × B to the field in the solar-wind frame of reference. The ions and electrons are advanced in phase space using Boris’ algorithm (see e.g. Birdsall & Langdon 1991). There are four particle species: solar-wind protons and electrons and cometary water ions (H2O+) and electrons. The solar-wind species are created at all the boundaries at every time step. This is also done at the downstream boundary, but there the vast majority of the protons never enter the simulation domain as the outwardly directed bulk velocity is much higher than the thermal speed. For electrons, there is a significant inflow at all boundaries. All particles that reach the boundaries from the interior of the simulation box during one time step are removed.
The simulation box is a cube with a side of Nx grid cells, and each grid cell is a cube whose side is ∆x. These and other parameters used in the three different runs presented in this paper are shown in Table 1. The present version of the simulation code includes a source of the cometary plasma species by photo-ionisation of an approximate Haser model neutral-density profile. The nucleus is not modelled; instead the neutral density is kept constant inside the cometocentric distance r = rn where the nucleus would be, and is decreased linearly to zero in the range r1 ≤ r ≤ r2 to avoid artefacts at the boundaries. Here, rc is the radius of the nucleus, which together with r1 and r2 is listed in Table 1. The exponential factor in Haser’s model (Haser 1957) is approximated to unity, because the typical length scale for ionisation is much larger than the simulated region. Thus, for the neutral density, we have
where Q is the gas-production rate and u is the speed with which the neutrals move radially outwards. For the initial density of the cometary plasma, we use the profile derived by Galand et al. (2016) and Vigren et al. (2017), which in analogy with the neutral profile is capped at small cometocentric distances and linearly decreased to zero at large values of r. We have
where νi is the ionisation frequency. The profile in Eq. (2) is only imposed as an initial condition. After t = 0, the plasma density is allowed to evolve self-consistently with the neutral density given by Eq. (1). The initial density profiles for simulation runs A and C are shown by the solid black lines in Figs. 1a and b, respectively. The inclusion of this cometary plasma source allows us to simulate longer timescales than in our previous study, where the cometary plasma started to disperse enough to affect the results after approximately 30 ms (Gunell et al. 2019).
To reduce computational cost, the size of the comet was scaled down by a factor of 1/400 in runs A and B (same factor as used by Gunell et al. 2019) and by a factor of 1/200 in run C. The scaling of the characteristic length scale for the density variation is achieved by adjusting the gas production rate Q in Eqs. (1) and (2). The gyro radii by the particles are scaled via the magnitude of the magnetic field B0. The values used for Q and B0 in the different runs are shown in Table 1. The grid cell size is controlled by the Debye length, which is not scaled, and the smaller comet therefore requires fewer grid cells than a full-scale comet. This is what makes the simulation numerically feasible. How this scaling influences the results is discussed in Sect. 3.1. The magnetic field is prescribed, and directed in the y direction. In runs A and C, the field is constant. The values are shown in Table 1 and are scaled up with the scaling factors of each run from the approximately 5 nT field observed by Rosetta (Goetz et al. 2017). In order to determine the influence of a spatially varying magnetic field, we performed one run with a non-uniform magnetic field, namely run B, where the field is cylindrically symmetric around the y axis as shown in Fig. 2. This magnetic field profile is scaled up from the Rosetta observation at its first approach of comet 67P (cf. Fig. A.1. of Gunell et al. 2019).
Parameters for the solar wind and comet for the three simulation runs and for comet 67P as encountered by the Rosetta spacecraft at 3 au.
 |
Fig. 1 Water-ion densities and velocities in runs A and C, illustrating the influence of the scaling factor. (a) Water-ion density, nwi, as a function of r in run A for different radial directions, following the axes of the coordinate system as indicated in the legend. (b) nwi for run C. (c) The radial-velocity component υr,wi for run A. (d) υrwi for run C. The legend in panel a also applies to panels a to d. (e) Velocity components in the x−z plane for run A. (f) Velocity components in the x−z plane for run C. (g) Velocity components in the x−y plane for run A. (h) Velocity components in the x−y plane for run C. The axis limits for r, x, y, and z are different for the different scalings. The dotted lines in panels c and d indicate |
 |
Fig. 2 Prescribed magnetic field By in the three runs. In runs A and C, the field is constant, and in run B it depends on the distance to the y axis |
2.2 Analytical model
For comparison with the particle-in-cell simulations, we use a simplified model of the electric field that includes three contributions, namely the convective electric field Ec, an ambipolar field Ea, and a polarisation electric field Ep:
The convective electric field is
where υSW is the solar-wind velocity and B the magnetic–flux density. The ambipolar electric field is modelled assuming that the electron pressure gradient is balanced by the force from Ea on the electrons and that the electron temperature Te is constant in the region where the ambipolar field is important. Under these conditions, we have Ea = −(kBTe/(nee))∇ne. If the plasma density ne is spherically symmetric and depends on the cometocentric distance r as
where n0 is the density at a reference distance r0 and α is a constant describing how fast the plasma density decreases with cometocentric distance, then the ambipolar electric field becomes
where er is a unit vector directed radially outward from the centre of the cometary nucleus.
The polarisation electric field is modelled using the field from a polarised spherically symmetric plasma where the density is inversely proportional to the spherical coordinate r over an interval b < r ≤ d is derived in Appendix A. The ions are then displaced from the electrons by a small distance ∆x along the x axis. The polarisation electric field is then
A strong magnetic field may also impose a cylindrical symmetry on the plasma, and cylindrical models have been used in the past (Brenning et al. 1991; Nilsson et al. 2018). Therefore, it is of interest to compare the fields from both spherically and cylindrically symmetric plasma models with simulations to see where the different models are applicable. The polarisation field in a cylindrically symmetric system is (Nilsson et al. 2018)
where the cylinder axis is directed along the y axis, that is to say it is parallel to the magnetic field, and the cylindrical coordinate 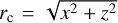 is the distance from the field point to the y axis. Typical parameters for the model used in this paper are shown in Table 2. This model is not self-consistent. Moreover, the two density profiles in Eqs. (5) and Eq. (A.3) are inconsistent outside the x–z plane. Not being self-consistent, this analytical model cannot be used to compute how the electric fields develop from their initial and boundary conditions. However, if agreement can be found with either a self-consistent simulation, such as the particle-in-cell simulation presented in this article, or space observations, this implies that the electric field is built up from the contributions included in the model, and one can obtain information about the relative importance of these components. The results and a comparison between the analytical and particle-in-cell models is discussed in Sect. 3.3.
is the distance from the field point to the y axis. Typical parameters for the model used in this paper are shown in Table 2. This model is not self-consistent. Moreover, the two density profiles in Eqs. (5) and Eq. (A.3) are inconsistent outside the x–z plane. Not being self-consistent, this analytical model cannot be used to compute how the electric fields develop from their initial and boundary conditions. However, if agreement can be found with either a self-consistent simulation, such as the particle-in-cell simulation presented in this article, or space observations, this implies that the electric field is built up from the contributions included in the model, and one can obtain information about the relative importance of these components. The results and a comparison between the analytical and particle-in-cell models is discussed in Sect. 3.3.
Parameters of the analytical model used for comparison with runs A and C, respectively.
2.3 Wave identification using singular value decomposition
As the plasma in the inner coma is non-uniform, with density values spanning 1–2 orders of magnitude in the relevant region, we use a singular value decomposition (SVD) technique to make waves visible also when their amplitudes are low compared to the large-scale structures of the coma. In SVD, a two-dimensional data array, that is, an image, is written as a weighted sum of principal components. The largest weights or principal values correspond to the large-scale features of the image. Our analysis follows those of Finnegan (2008) and Koepke et al. (2016), who used SVD to bring forward stationary Alfvén waves observed in a laboratory experiment. In the images in the x–z plane presented in Sect. 3.5, we have subtracted the large-scale variations of the displayed quantities by removing the principal components corresponding to the 6 largest principal values. We have also removed the principal components smaller than the 40th largest principal value in order to suppress small-scale noise. The numbers of principal components to remove were found by testing different values, and 6 and 40 were found to sufficiently suppress large-scale variations and small-scale noise, respectively. For the images in the x–y plane, the principal components corresponding to the 4 largest principal values and those smaller than the 20th principal value were removed.
We use Fig. 8 as an example; the figure is discussed further in Sect. 3.5. Figure 8a shows the plasma density in the x–z plane for t = 300 ms with the mean density subtracted. It was necessary to remove all data points within 300 m from the origin, that is to say, within the white circle; otherwise they dominate the mean value. The waves are visible in the figure, but only far from the origin. Figure 8d shows the SVD of the density for the same time, and here the waves can be discerned all the way in to the origin. In the same way, Fig. 8e shows the Ex component of the electric field, and Fig. 8f highlights waves in Ex, the large-scale variations having been removed using the SVD technique.
3 Results
3.1 Scaling
We scaled down the size of the comet 400 times in runs A and B and 200 times in run C. The advantage of this is that, simulating a smaller comet, fewer grid cells and fewer particles are needed. With the parameters we use as an initial condition, the Debye length is approximately 3 m at the density maximum near the nucleus. As the simulation progresses, the Debye length increases into the 10–30m range as shown in Fig. 3 (bottom row). The cometary electron Debye length is only shown near the origin where the density is high enough for an accurate estimate. The minimum cometary electron Debye length is approximately 9 m at the end of the simulation. The cometary electron temperature remains close to the initial 10eV, and the increase in Debye length from 3 m is mostly due to the decreased density; see Figs. 1b and 3a, d, and g. In most of the simulation box, it is the Debye length of the solar-wind electrons that is important. For comparison, the gyro radius for a 10eV electron in a 990 nT magnetic field, that is to say, conditions as in run C, is 34m. Thus, typical scales for phenomena that depend on the Debye length are approximately the same as for those that depend on the gyro radius. Both gyro radius and Debye length scales are resolved by the spatial grid size of ∆x = 8 m.
The Debye length is of the same order as the radius of the nucleus for the simulations with 400 times scaling. This means that a sheath will form around the nucleus. Furthermore, in this near-nucleus region space, charge effects will be more important than in a less scaled simulation or indeed at the real comet. The stronger electric field in the more scaled run removes ions faster from the near-nucleus space, and this leads to a lower water-ion density for high scale factors. This can be seen in Figs. 1a and b, which show the water-ion density along the axes of the coordinate system for runs A and C, respectively. In run A, with 400 times scaling, the water ion density is lower than in run C, which is scaled only 200 times. It is worthwhile noticing that since the width of the sheath depends on the Debye length, which is not affected by our scaling, this width does not scale by the factors of 200 or 400. Instead the Debye length will in the simulation and around the real comet will be of similar size. Also, as the nucleus itself is not modelled as a solid surface, we cannot draw conclusions about the details of the sheath at the nucleus of the comet from these simulations. The results presented here were recorded after the initial transients had faded away. The transients themselves were examined more closely by Gunell et al. (2019).
During its descent to the comet surface at the end of the mission, Rosetta observed a plasma-density peak at a cometocentric distance of twice the radius of the nucleus (Heritier et al. 2017). This cannot be reproduced in our simulations, because we do not model the solid nucleus and instead let the plasma source extend all the way to the origin (see the discussion of Eqs. (1) and (2) in Sect. 2.1). Although a different choice is possible, a careful study of the plasma density as a function of the spatial coordinates on length scales the size of the nucleus would also require a smaller grid size than what could be achieved here. The grid cell is of the same order of magnitude as the radius of the nucleus in all our runs (see Table 1).
In both runs A and C, the water-ion density is significantly below the initial density. With decreased scaling, going from 400 to 200 times, the density increases. However, we would not expect the density to precisely follow the initial profile even if no scaling was applied, because that profile was derived assuming that the ions move radially outward with the neutrals without the influence of electric fields (Galand et al. 2016; Vigren et al. 2017). At a low-activity comet, where the plasma is not dominated by collisions, the ions move along more complicated trajectories as is seen by the velocity vectors in Figs. 1e–h. The axis limits for r, x, y, and z in Fig. 1 are different for the two different scale factors. It can be seen that any fixed speed is reached at approximately twice the cometocentric distance for a scale factor of 200 compared to the run that is scaled 400 times. Thus, the spatial dimensions of the structure that accelerates the ions scale linearly with the scale factor applied. The ion speed reaches 20 km s−1 at z ≈ 75 m in run A, and z ≈ 150 m in run C, corresponding to 30 km cometocentric distance if scaled back to the real comet. This speed corresponds to a water-ion energy of a few tens of eV, which agrees with observations of the energy of the bulk of the cometary ions made by Rosetta in the beginning of November 2014 (Nilsson et al. 2015b), even though the energies in the tail of the distributions observed by Rosetta reached the keV range.
Another effect of the scaling is that the system becomes electrostatic. The electrostatic simulation code we use is suitable for the scaled-down problem. The magnetic field caused by the waves can be estimated to be 1 pT by assuming that 30 nA flows in a cylinder with a diameter of 100m (see Sect. 3.5 for wave currents). This means that the wave field is ~ 10−6 times the background field for the simulations scaled down 400 times. Thus, the magnetic perturbations are negligible and the use of an electrostatic code justified. However, if the system were to be scaled back up to its natural size, keeping current densities constant, the wave magnetic field would increase by a factor of 400 while the background field would decrease by the same factor. The wave field would then be a fraction of ~10−1 of the background, and in that case an electromagnetic treatment would be necessary.
 |
Fig. 3 Electron densities, temperatures, and Debye lengths along the three coordinate axes. (a) Density of the solar-wind electrons (black) and cometary electrons (red) along the x axis. (b) Temperatures in the x (blue), y (green), and z (red) directions shown along the x axis. (c) Debye length of the solar-wind electrons (black) and cometary electrons (red). The cometary electron Debye length is only shown near the origin where the density is high enough for an accurate estimate. (d–f) Same quantities as a–c shown along the y axis. (g–i) Same quantities as a–c shown along the z axis. |
3.2 Electric fields and structures
The upper row of panels in Fig. 4 shows the densities of protons and water ions in the x–z and x–y planes in run A for t = 150 ms. A proton wake is seen downstream of the nucleus (x < 0) in Figs. 4a and b, showing the x–z and x–y planes, respectively. In the x–z plane, there is also a proton-density enhancement next to the wake due to the deflection of the protons that otherwise would have passed through the wake region. Such a wake has also been seen in hybrid simulations (Koenders et al. 2016), multi-fluid MHD simulations (Huang et al. 2016), and intrinsic particle-in-cell simulations (Divin et al. 2020). A proton wake was also seen to develop in our previous simulations (Gunell et al. 2019). The difference is that, as the previous version of the simulation code did not include ionisation, only the first 30 ms could be simulated. Therefore, only the buildup of structures in the plasma could be studied before loss of plasma from the system would render the results unrealistic. In the present version, the plasma is replenished by ionisation, and we can follow the development towards a steady state.
Figures 4c and d show the water-ion density in the x–z and x–y planes, respectively. For z > 0, a structure has developed that is elongated in the anti-sunward direction, that is, towards negative x values. The arrows showing the direction of the water-ion velocity point in the positive z direction for z < 0, but tilt in the anti-sunward direction for z > 0. This ion-motion pattern is consistent with the density structure. The water-ion density is higher for z > 0 than for z < 0, forming a plume in the +z space due to the ions moving in that direction from the source under the influence of the convective electric field.
The bottom row of panels in Fig. 4 shows the same quantities as the upper row but for run B, in which the magnetic field is non-uniform and follows the black curve in Fig. 2. The non-uniformity of the magnetic field has no major influence on the ion densities. The only significant effect that can be seen in Fig. 4 is the density enhancement at 300 m ≲ z ≲ 400 m for x < 0 in panel e. Protons in this z range pass through the region where there is a magnetic-field gradient and hence also a gradient in the convective electric field, and this causes the focusing effect, increasing the proton density in the region downstream. The effect the non-uniform magnetic field has on the electric field is illustrated in Fig. 5, where panel a shows the electric field in the x–z plane for the uniform magnetic field of run A and panel b the same quantity in run B, where the field is non-uniform. The main difference between the two runs is that the electric field becomes weaker in run B for distances of 300 m or more from the y axis, which is also where the magnetic field decreases quickly as seen in Fig. 2.
 |
Fig. 4 Densities of protons and water ions for uniform and non-uniform magnetic fields. (a) Proton density in the x–z plane in the simulation with a uniform magnetic field (run A). (b) Proton density in the x–y plane in run A (c) Water-ion density in the x–z plane in run A. (d) Water-ion density in the x–y plane in run A. (e) Proton density in the x–z plane in the simulation with a non-uniform magnetic field (run B). (f) Proton density in the x–y plane in run B. (g) Water-ion density in the x–z plane in run B. (h) Water-ion density in the x–y plane in run B. The proton densities are shown on a linear colour scale, while the colour scale for the water ions is logarithmic. The arrows indicate the direction of the ion velocity. |
3.3 Analytical–particle-in-cell comparison
The steady state electric field around a comet was previously found to be described by three contributions: the convective, the ambipolar, and the polarisation fields (Gunell et al. 2019). Here, we make a quantitative comparison between the simple analytical model for those three contributions described in Sect. 2.2 and the particle-in-cell results. Figure 6 shows the three contributions both individually and added together for comparison with simulation run C. The upper row of panels shows the fields in the x–z and the lower row shows the x–y plane. The magnitude of the field component in the respective plane is colour coded, and the arrows show the direction of this in-plane component.
Comparing Figs. 6d and e for the x–z and Figs. 6i and j for the x–y plane, we find that there is good agreement between the analytical model and the particle-in-cell results for both the magnitude and direction of the electric field out to approximately 200 m cometocentric distance. As this is for a comet scaled-down 200 times, it would scale back to 40 km for comet 67P, and Rosetta was in this region when the comet was at a heliocentric distance of around 3 au during the October to December 2014 period (e.g. Nilsson et al. 2015b; Edberg et al. 2015). Overall, the dominant contribution is the convective electric field, although at small cometocentric distances, the combination of the ambipolar and polarisation fields can cause the electric field to be turned close to the anti-sunward direction as seen in Fig. 6e. The convective electric field has no component in the x–y plane; the electric field is directed anti-sunward in most of the r < 200 m region due to the contribution from the polarisation field.
Farther away from the centre of the comet, for r ≳ 200 m, the polarisation and ambipolar field fade away and the convective contribution dominates the electric field. There are three features that can be seen in Figs. 6e and j that cannot be explained by the analytical model. First, there is an electric-field enhancement for x < −200 m and z ≈ −100 m, that is to say, on the left hand side of the origin in Fig. 6e. This field enhancement is at its maximum in between the proton density enhancement and the proton density wake seen in Fig. 4e. Secondly, a region where the electric field is more anti-sunward and slightly weaker than in the surrounding plasma extends from the origin to the upper left-hand corner of Fig. 6e (negative x and positive z values). Thirdly, a wing-shaped region extends across all y values and downstream to x ≈ −400 m in Fig. 6j. The first feature is associated with the proton wake, and in Sect. 3.5 we propose an explanation for the latter two based on stationary waves.
Nilsson et al. (2018) estimated the angle between the electric field and the anti-sunward direction based on a model including the convective electric field and a polarisation field computed in a cylindrical geometry according to Eq. (8). The model used by Nilsson et al. (2018) also did not contain an ambipolar electric field. We compare the electric fields produced by the two models in Fig. 7. The region of space with a significant anti-sunward electric-field component is larger in the Nilsson et al. (2018) model than the one presented here. This is seen in both the x–z and x–y planes. One reason for this is the absence of an ambipolar field in the cylindrical model, and another reason for this is that the ambipolar and polarisation fields cancel each other out in some regions for the spherical model. The other reason, which applies in the x–y plane (Figs. 7c and d) is that the cylinder extends to infinity along the y axis. The spherical model is in better agreement with the simulations both because it includes the ambipolar field and because the strong polarisation field in the simulation does not extend along the y axis. However, the agreement between the two models is reasonable close to the x–z plane, and that is where the cylindrical model was meant to be applied. The wing-shaped region with an anti-sunward field in the simulation cannot be explained by the cylindrical model either, as there is no extended cylindrical density structure that could cause such a spatially extended polarisation field.
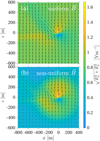 |
Fig. 5 Electric-field topology in two different magnetic-field models (a) Electric field in the x–z plane in the simulation with a uniform magnetic field (run A). (b) Electric field in the x–z plane in the simulation with a non-uniform magnetic field (run B). |
3.4 Electrons
The temperature of the solar-wind electrons and the densities of both electron populations are shown in Fig. 3. All quantities are shown along the three coordinate axes in the three columns of the figure. The solar-wind electrons reach an increased temperature as they get closer to the origin. Figures 3b, e, and h, that is, the middle row, show the temperatures in the x (blue), y (green), and z (red) directions for the solar-wind electrons. The temperature in the y direction, along the magnetic field, is greater than the temperature in the other two directions, which are approximately equal to each other. Thus, the distribution can be described by a parallel, T‖, and a perpendicular, T⊥, temperature. The temperature of the cometary electrons is not shown. It remains close to the initial value of 10 eV, and is only relevant close to the origin, where the density of the cometary population is significant. In the top row of Fig. 3, the densities of the two populations are shown. It is seen that the cometary electrons are mostly confined to the vicinity of the origin. The solar-wind electron density in a larger volume around the origin is higher than its upstream value.
The ambipolar field creates a potential structure that has its maximum at the origin. When solar-wind electrons enter this structure they are accelerated by the ambipolar field, and the energy they gain in this way is behind the increased temperature. The component of the ambipolar field that is parallel to the electric field contributes more to the energisation of the electrons than the perpendicular component. A parallel electric field can accelerate electrons to large energies, when a perpendicular electric field of the same strength only leads to a slow drift. This explains the temperature anisotropy. The solar-wind electrons can bounce back and forth along the magnetic field, contributing to the increased density of the solar-wind electrons, which is seen in Fig. 3. Eventually they will drift out of the potential structure, primarily because of the superimposed convectional electric field, but also the polarisation field and the component of the ambipolar field that is perpendicular to B contribute to this drift. Similar results were found by Divin et al. (2020), using an electromagnetic implicit particle-in-cell simulation.
3.5 Waves
During the simulation, waves are generated and can be seen in the electric field, the density, and currents. In Fig. 8, we use singular value decomposition to highlight these waves as described in Sect. 2.3. Waves are seen throughout the simulation box already early in the course simulation run. The presence of waves was mentioned by Gunell et al. (2019) but not explored further. Panels b, c, and d of Fig. 8 uses SVD to show waves in the plasma density for times t = 100,200, and 300 ms, respectively. All plasma quantities go through a period dominated by transients before the system settles into a steady state. This also applies to the waves. In Fig. 8b, at t = 100 ms the amplitude is higher for z < 0 than for z > 0. In Fig. 8c, the waves in the z < 0 half space have faded out considerably, and in Fig. 8d a steady state has been reached where the high amplitude waves are mostly located in the z > 0 half space but extending down to approximately z = −400 m, corresponding to −80 km when scaled back to comet 67P. The colour scales of the individual panels are different, and the ∆ne amplitude for z > 0 in panels b, c and d are of the same order of magnitude even though the colours are different. The significant development between the panels is the decrease in the amplitude for z < 0.
Besides the density, the same waves are visible in other quantities. Figure 8e shows the Ex component of the electric field, and in Fig. 8f the wave part of Ex is highlighted using the SVD technique. A comparison between the density and Ex wave fronts shows that the peaks in the two quantities do not coincide, but instead the field maxima occur between the density peaks. However, the density wave peaks in Fig. 8d do coincide with the current density peaks in Fig. 8g reasonably well. Figure 8h shows the result of applying the SVD technique to the magnitude of the in-plane component of the electric field, 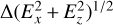 . This creates the illusion that the wavelength is shorter for
. This creates the illusion that the wavelength is shorter for 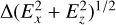 than ∆ne and ∆Ex, because when the direction of the field oscillates, peaks in both directions will have the same colour in Fig. 8h. The current density in Fig. 8g is also the magnitude of a vector quantity, but this latter effect does not occur there as the wave amplitude is not high enough to change the direction of the current. The wavelengths in run A (not shown) are approximately half of those seen in Fig. 8, and this means that the wavelength scales with the same factor we used for the magnetic field. The value of the wavelength is in the range 150 m ≲ λ ≲ 550 m, which if scaled back to the real comet using the scale factor of 200 would correspond to (30–110) km. The scaled-back values are within the range that has been observed at comet 67P (Richter et al. 2016; Goetz et al. 2020).
than ∆ne and ∆Ex, because when the direction of the field oscillates, peaks in both directions will have the same colour in Fig. 8h. The current density in Fig. 8g is also the magnitude of a vector quantity, but this latter effect does not occur there as the wave amplitude is not high enough to change the direction of the current. The wavelengths in run A (not shown) are approximately half of those seen in Fig. 8, and this means that the wavelength scales with the same factor we used for the magnetic field. The value of the wavelength is in the range 150 m ≲ λ ≲ 550 m, which if scaled back to the real comet using the scale factor of 200 would correspond to (30–110) km. The scaled-back values are within the range that has been observed at comet 67P (Richter et al. 2016; Goetz et al. 2020).
The black arrows in Figs. 8d and h show the direction of the in-plane component of the current density. All arrows have the same length regardless of the magnitude of the current density. We can observe that the wave fronts are approximately perpendicular to the current density, which means that the wave vector is approximately parallel to the current. In Sect. 4, this result is compared to model calculations by Meier et al. (2016). The three-dimensional current system is illustrated by streamlines in Fig. 9. The streamlines are colour coded with the current density1. Most of the current flows in the same way as already shown in Fig. 8d and (h), but there is also a weak component in the positive and negative y directions, that is to say, parallel and anti-parallel to B.
Figure 10 shows waves in the plane z = 100 m, which is parallel to the x–y plane for the in-plane current density (a) and the magnitude of the electric field (b), using the SVD technique. The black arrows show the direction of the in-plane component of the current density. In this plane, the direction of the current is largely parallel to the wave fronts, in contrast to the situation in the x–z plane shown in Fig. 8. Figure 10a also shows that the wavelength is longer in this plane, up to 700 m. As mentioned above for the x–z plane, the appearance of a shorter wavelength for the electric field magnitude is also an artefact seen in Fig. 10b. The shape of the wave structure resembles that of the region of high electric field shown in Fig. 6j.
After the initial transients have faded away, the wave structures become stationary in the rest frame of the comet. This means that in the plasma frame of reference the waves are propagating with the same speed but in the opposite direction to the plasma velocity. As no nucleus is included in the simulation, it is instead the density peak at the origin that anchors the waves in the comet rest frame. Both the density and the velocities of the different particle species are non-uniform in space, leading to the complicated shape of the wave structures around the centre of the comet.
 |
Fig. 6 Electric fields in the x–z plane (top row) and x–y plane (bottom row) from both the analytical model and simulation run C. Panels (a) and (f) show the convective electric field of the analytical model; (b) and (g) the ambipolar field; (c) and (h) the polarisation field; (d) and (i) the sum of the three electric field contribution in the analytical model; and panels (e) and (j) show the electric field obtained in run C of the particle-in-cell simulation. |
4 Discussion and conclusions
In an electromagnetic implicit particle-in-cell simulation, Deca et al. (2019) computed the contributions to the electric field that correspond to the terms of a generalised Ohm’s law. These authors found several features similar to those that we find in the total simulated electric field presented in Fig. 6: a decreased electric field magnitude near the nucleus on its sunward side; a wing-shaped field structure in the x–y plane, which Deca et al. (2019) attribute to the Hall field; and a region of coherent fields extending diagonally anti-sunward into the hemisphere towards which the solar-wind convective field is pointing. The shapes of these regions are affected by field-line draping in the simulation of Deca et al. (2019), while in our electrostatic simulation there is no draping. These latter authors do not treat waves in their article. However, a wave structure in the magnetic field magnitude can be discerned in their Fig. 1, resembling both the magnetic structures reported by Koenders et al. (2016) and the wave structures presented in this work that appear in the plasma density, electric field, and current.
Koenders et al. (2016) modelled comet 67P using an electromagnetic hybrid simulation code, where the ions are treated as particles and the electrons as a fluid. These authors found waves that, like those reported here, appear as wave fronts in densities and fields, spanning out from the nucleus diagonally in the anti-sunward direction. In both the present paper and the one by Koenders et al. (2016), the waves appear mostly in the hemisphere towards which the convective electric field is pointing, and as bow-shaped structures in the x–y plane. As the simulation by Koenders et al. (2016) is electromagnetic, these authors also observed waves in the magnetic field. The simulation in the present work is electrostatic, and can therefore not reproduce any time-dependent magnetic fields. Another difference is that while our waves eventually become stationary, the waves in the electromagnetic hybrid simulation continued to propagate throughout the simulation run (Koenders et al. 2016). The stationarity we observe is also a result of the model being electrostatic: a plasma element that is magnetically connected to the density peak at the origin will always remain connected to it, as the magnetic field cannot change. In an electromagnetic simulation, on the other hand, such changes are happening continuously, allowing for the wave propagation. As pointed out in Sect. 3.1, the scaling down of the size of the system makes it electrostatic in nature. Therefore, we expect that if a similarly scaled comet was simulated electromagnetically, the electrostatic limit would be retained, and the wave structures would be stationary over long timescales.
Our simulations assume a constant magnetic field, and therefore it is difficult to compare to observations directly, because the singing comet waves are mostly observed in the magnetic field. However, some density observations exist (Breuillard et al. 2019).
From the previous section, we see that the wavefronts are parallel to the current, which is either parallel or anti-parallel to the background magnetic field. Thus, the wavefronts seem to be parallel to the magnetic field. The parallel to the current case was also investigated by Meier et al. (2016) using the dispersion relation of an ion-Weibel instability. These authors found that the typical wavelength was 18 000 km for 17 mHz and 4.1 mHz. These wavelengths are substantially longer than what is observed in our simulations.
The wavelengths in our simulation (~100 km, scaled back up to the real comet scale) are within the range of wavelengths from below 100 km up to 800 km observed by Richter et al. (2016). These authors used two-point observations to derive a projected wavelength along the Rosetta-Philae line and obtained mean values of (251 ± 31) km and (278 ± 19) km from two independent methods. The theory proposed by Meier et al. (2016) assumes a uniform plasma, where the solar-wind and cometary species move at different, but still uniform, velocities. The plasma in our simulations, as well as at a real comet, is non-uniform, and particles of different species move along complicated trajectories. A non-uniform wave theory is beyond the scope of this paper, but we expect that the limited size of the interaction region, which is set by the density gradients near the nucleus, favours shorter wavelengths than those in a uniform plasma of infinite extent.
In our simulations, the waves are moving sunward in the frame of reference of the bulk flow, which means they are stationary in that of the comet (and that of a potential spacecraft), but observations have indicated that the opposite is the case for the singing comet waves, which are stationary in the reference frame of the flow and propagating in that of the comet. In particular, Breuillard et al. (2019) hypothesise that the change in Doppler shift due to the change in bulk-flow velocity increases or decreases the peak wave frequency measured by the Rosetta instruments following a cometary outburst. On the other hand, such a correlation was not found through a statistical study: Goetz et al. (2020) reported that the density of the background plasma did not correlate with the frequency. This led these authors to speculate that the wave-generation region was much larger than what was covered by the observation (~100s km). Our simulation is electrostatic. Therefore, the magnetic field cannot change, and a point that is magnetically connected to the nucleus will always remain in that state. When a steady state has developed, the large-scale structure that the waves constitute is anchored to the density maximum at the nucleus and the waves are stationary in the cometary frame of reference. In an electromagnetic model (e.g. Koenders et al. 2016), the waves are allowed to propagate in the comet frame. In our simulation, waves appear as transients all over the simulation domain, but after these transients have faded away, the waves are generated mostly in one hemisphere of the environment. This can be seen by comparing Figs. 8b, c, and d. Volwerk et al. (2018) did find that the singing comet waves were confined to one hemisphere in a system not aligned with the electric field. However, Goetz et al. (2020) could not reproduce this finding for the system aligned with the electric field, which is more similar to the simulation frame of reference. This discrepancy could be caused by changes in the cometary or solar-wind environments occurring so frequently that the system is always in a transient state.
Based on these discussions, we propose that the waves observed in the simulation presented here are the electrostatic manifestation of the singing comet waves for a scaled-down comet. What is the nature of these waves in the simulations? A precise determination is not a trivial task as the plasma is nonuniform and contains several different particle populations. The observation in Sect. 3.5 that the wavelength scales with the magnetic field rather than the Debye length suggests that they are not ion acoustic. Also, the ion acoustic speed of a few km s−1 does not match the solar-wind speed. It could match the speed of the cometary ions, but the direction of the wavefronts is not consistent with ion acoustic waves propagating against the water ion flow direction. The waves are more likely to belong to (the electrostatic limit of) the family of ion cyclotron and lower hybrid waves that can be generated by modified two-stream instabilities for example (e.g. Treumann & Baumjohann 1997).
Edberg et al. (2022) analysed Rosetta data by fitting power laws to the measured density as a function of cometocentric distance, and pointed out that the density profile is not only influenced by non-uniform outgassing and the rotation of the nucleus but also by the presence of non-radial electric fields. The density structures reported in Sect. 3.2 deviate significantly from spherical symmetry as a consequence of the convective and polarisation electric fields, which cause the ions to move along trajectories that are more complicated than radial straight lines. Apart from the singing comet wave observations during the descent of the Philae lander, all in situ observations at comets are single point measurements. This limits the possibility to assess the spatio-temporal development of field and density structures and of wave properties. In future, this may be improved by the upcoming Comet Interceptor mission (Snodgrass & Jones 2019), which has been designed to perform three point measurements during a fast flyby of a comet, and by multi-spacecraft missions accompanying comets, such as those suggested by Goetz et al. (2022a).
 |
Fig. 7 Model electric fields, using a cylindrical (left) and spherical (right) model for the polarisation field. Panels (a) and (b) show the field in the x–y plane and (c) and (d) show the field in the x–y plane. The colour-coded quantity is the magnitude of the component of the field in the plane shown, and the arrows indicate the direction of that in-plane component. The polarisation field models differ between the panels, and the cylindrical model also follows Nilsson et al. (2018) in that it does not include an ambipolar electric field. The parameters used correspond to simulation run C. |
 |
Fig. 8 Wave structures in simulation run C. (a) Plasma density variation, ne− < ne >, in the x–z plane for t = 300 ms. The subtracted mean, < ne > is formed over the region shown. The circle in the centre has been removed as the high density in that region would otherwise dominate the mean. (b) Singular value decomposition (SVD) of the plasma density at t = 100 ms with the first four principal images removed. (c) SVD of the plasma density at t = 200 ms. (d) SVD of the plasma density at t = 300 ms. (e) The Ex component of the electric field at t = 300 ms. (f) SVD of the Ex component of the electric field at t = 300 ms. (g) SVD of the current density magnitude |j| at t = 300 ms. (h) SVD of the magnitude of the in-plane electric field, |
 |
Fig. 9 Three-dimensional representation of the current density in run A. The magnitude of the current density is colour coded on each line, and the direction of the current is shown by the black cones on a few selected lines1. |
 |
Fig. 10 Wave structures in the x–y plane of simulation run C. (a) Singular value decomposition of the plasma density at t = 300 ms with the first four principal images removed. (b) SVD of the electric-field magnitude at t = 300 ms. The black arrows show the direction of the current density. |
A video clip of this image rotating has been deposited with the latest version of the simulation code at (https://doi.org/10.5281/zenodo.7664037>
Acknowledgements
This work was supported by the Swedish National Space Agency contract 108/18. C.G. is supported by an ESA Research Fellowship. This research was conducted using the resources of High Performance Computing Center North (HPC2N). The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC), partially funded by the Swedish Research Council through grant agreement no. 2018-05973. The software used in this work was developed by J. Lindkvist and H. Gunell and is available for download at (https://doi.org/10.5281/zenodo.7664037).
Appendix A Polarisation electric field
In this Appendix, we derive the polarisation field that is caused when displacing the electrons with respect to the ions in a plasma where the density is spherically symmetric and proportional to 1/r, where r is the spherical coordinate. The strategy is to integrate the contributions from infinitesimally thin shells that generate the same fields as would have produced by the same displacement, ∆x, of the electrons in a sphere of constant density, n0. Inside such a sphere of constant density, the electric field is (Tonks 1931)
Assuming the radius of the sphere is R, the electric field outside r = R is the field from an electric dipole at the origin with the dipole moment p = (∆xn04πR3/3)ex, which is
We use a density profile that is constant close to the origin (r ≤ b), and then falls off as 1/r until it becomes constant again for r > d. We have
where R0 is the cometocentric distance where ne = n0. The constant b is the cometocentric distance beneath which the density is constant, that is, approximately two comet radii, and r = d is the larger distance where the density becomes constant again. The latter represents the point at which the density has dropped close enough to the solar-wind value that polarisation contributions are insignificant.
The centres of the electron and ion distributions are displaced from the origin to −∆x/2 and ∆x/2, respectively. The electric field is then obtained by integrating the contributions from an infinite number of concentric spheres with the following charge distribution along the x axis:
The field at a given point (x, y, z) can be written as a sum:
where E1 is the contribution from sources outside a sphere of radius r, and E2 is the contribution from sources inside that sphere. Thus, the contributions to E1 come from a superposition of spheres larger than r, as in Eq. (A.1), and only have an x component:
For r ≤ b we have
For r > d, we have Ex1 = 0, as there are no sources outside the field point in that region. The approximations in Eq. (A.6) and Eq. (A.7) rely on ∆x ≪ r and∆x ≪ b.
Letting (x′, y′, z′) denote the coordinates of the source point, E2 in Eq. (A.5) stems from sources in the region b ≤ 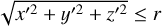 , that is to say outside of a sphere of radius b but inside a sphere of radius r. E2 is found by integrating contributions of the form given by Eq. (A.2). To simplify the notation of Eq. (A.2), we define the vector a, which depends only on the coordinates of the field point:
, that is to say outside of a sphere of radius b but inside a sphere of radius r. E2 is found by integrating contributions of the form given by Eq. (A.2). To simplify the notation of Eq. (A.2), we define the vector a, which depends only on the coordinates of the field point:
The electric-field contribution E2 for b < r ≤ d is then
The approximation relies on ∆x ≪ r, b and (∆x/2)2 · 2 · ln (r/b) ≪ r2, b2. There is no net charge inside the sphere r = b, and therefore
and outside the region where there are space charges E2 is given by Eq. (A.9) with r = d, that is to say
In summary, the total field for small ∆x can be written
where we have used the approximate expressions found above.
References
- André, M., Odelstad, E., Graham, D. B., et al. 2017, MNRAS, 469, S29 [Google Scholar]
- Balogh, A., & Treumann, R. A. 2013, Physics of Collisionless Shocks (New York, NY: Springer), ISSI Scientific Report Series, 12 [CrossRef] [Google Scholar]
- Birdsall, C. K., & Langdon, A. B. 1991, Platsma Physics via Computer Simulation (Dirac House, Temple Back, Bristol, UK: IOP Publishing Ltd [CrossRef] [Google Scholar]
- Brenning, N., Kelley, M. C., Providakes, J., Swenson, C., & Stenbaek-Nielsen, H. C. 1991, J. Geophys. Res., 96, 9735 [NASA ADS] [CrossRef] [Google Scholar]
- Breuillard, H., Henri, P., Bucciantini, L., et al. 2019, A & A, 630, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deca, J., Divin, A., Henri, P., et al. 2017, Phys. Rev. Lett., 118, 205101 [Google Scholar]
- Deca, J., Henri, P., Divin, A., et al. 2019, Phys. Rev. Lett., 123, 055101 [Google Scholar]
- Divin, A., Deca, J., Eriksson, A., et al. 2020, ApJ, 889, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Edberg, N. J. T., Eriksson, A. I., Odelstad, E., et al. 2015, Geophys. Res. Lett., 42, 4263 [NASA ADS] [CrossRef] [Google Scholar]
- Edberg, N. J. T., Johansson, F. L., Eriksson, A. I., et al. 2022, A & A, 663, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finnegan, S. M. 2008, PhD thesis, West Virginia University, USA [Google Scholar]
- Galand, M., Héritier, K. L., Odelstad, E., et al. 2016, MNRAS, 462, S331 [Google Scholar]
- Goetz, C., Koenders, C., Hansen, K. C., et al. 2016a, MNRAS, 462, S459 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, C., Koenders, C., Richter, I., et al. 2016b, A & A, 588, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goetz, C., Volwerk, M., Richter, I., & Glassmeier, K.-H. 2017, MNRAS, 469, S268 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, C., Plaschke, F., & Taylor, M. G. G. T. 2020, Geophys. Res. Lett., 47, e2020GL087418 [Google Scholar]
- Goetz, C., Gunell, H., Johansson, F., et al. 2021, Ann. Geophys., 39, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, C., Gunell, H., Volwerk, M., et al. 2022a, Exp. Astron., 54, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, C., Behar, E., Beth, A., et al. 2022b, Space Sci. Rev., 218, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Gunell, H., Hurtig, T., Nilsson, H., Koepke, M., & Brenning, N. 2008, Plasma Phys. Controlled Fusion, 50, 074013 [NASA ADS] [CrossRef] [Google Scholar]
- Gunell, H., Walker, J. J., Koepke, M. E., et al. 2009, Phys. Plasmas, 16, 112901 [NASA ADS] [CrossRef] [Google Scholar]
- Gunell, H., Goetz, C., Eriksson, A., et al. 2017a, MNRAS, 469, S84 [NASA ADS] [CrossRef] [Google Scholar]
- Gunell, H., Nilsson, H., Hamrin, M., et al. 2017b, A & A, 600, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunell, H., Goetz, C., Simon Wedlund, C., et al. 2018, A & A, 619, A2 [Google Scholar]
- Gunell, H., Lindkvist, J., Goetz, C., Nilsson, H., & Hamrin, M. 2019, A & A, 631, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunell, H., Goetz, C., Odelstad, E., et al. 2021, Ann. Geophys., 39, 53 [CrossRef] [Google Scholar]
- Hansen, K. C., Altwegg, K., Berthelier, J.-J., et al. 2016, MNRAS, 462, S491 [Google Scholar]
- Haser, L. 1957, Bull. Soc. Roy. Sci. Liège, 43, 740 [Google Scholar]
- Heritier, K. L., Henri, P. X., Vallières, X., et al. 2017, MNRAS, 469, S118 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z., Tóth, G., Gombosi, T. I., et al. 2016, J. Geophys. Res.: Space Phys., 121, 4247 [NASA ADS] [CrossRef] [Google Scholar]
- Hurtig, T., Brenning, N., & Raadu, M. A. 2003, Phys. Plasmas, 10, 4291 [NASA ADS] [CrossRef] [Google Scholar]
- Karlsson, T., Eriksson, A. I., Odelstad, E., et al. 2017, Geophys. Res. Lett., 44, 1641 [NASA ADS] [Google Scholar]
- Knudsen, D. J. 1996, J. Geophys. Res., 101, 10761 [NASA ADS] [CrossRef] [Google Scholar]
- Koenders, C., Perschke, C., Goetz, C., et al. 2016, A & A, 594, A66 [CrossRef] [EDP Sciences] [Google Scholar]
- Koepke, M. E., Finnegan, S. M., Vincena, S., et al. 2016, Plasma Phys. Controlled Fusion, 58, 084006 [NASA ADS] [CrossRef] [Google Scholar]
- Lindkvist, J., & Gunell, H. 2019, https://doi.org/10.5201/zenodo.2656629 [Google Scholar]
- Madsen, B., Simon Wedlund, C., Eriksson, A., et al. 2018, Geophys. Res. Lett., 45, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, P., Glassmeier, K.-H., & Motschmann, U. 2016, Ann. Geophys., 34, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Myllys, M., Henri, P., Vallières, X., et al. 2021, A & A, 652, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2015a, Science, 347, aaa0571 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2015b, A & A, 583, A20 [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, H., Gunell, H., Karlsson, T., et al. 2018, A & A, 616, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Odelstad, E., Eriksson, A. I., Johansson, F. L., et al. 2018, J. Geophys. Res. (Space Phys.), 123, 5870 [NASA ADS] [CrossRef] [Google Scholar]
- Ostaszewski, K., Glassmeier, K.-H., Goetz, C., et al. 2021, Ann. Geophys. Discuss., 2021, 1 [Google Scholar]
- Richter, I., Koenders, C., Auster, H.-U., et al. 2015, Ann. Geophys., 33, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Richter, I., Auster, H.-U., Berghofer, G., et al. 2016, Ann. Geophys., 34, 609 [CrossRef] [Google Scholar]
- Rubin, M., Koenders, C., Altwegg, K., et al. 2014, Icarus, 242, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Shewchuk, J. R. 1994, An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, Tech. rep., USA [Google Scholar]
- Simon Wedlund, C., Kallio, E., Alho, M., et al. 2016, A & A, 587, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon Wedlund, C., Behar, E., Kallio, E., et al. 2019, A & A, 630, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snodgrass, C., & Jones, G. H. 2019, Nat. Commun., 10, 5418 [NASA ADS] [CrossRef] [Google Scholar]
- Stenberg Wieser, G., Odelstad, E., Nilsson, H., et al. 2017, MNRAS, 469, S522 [NASA ADS] [CrossRef] [Google Scholar]
- Tejero, E. M., Crabtree, C., Blackwell, D. D., et al. 2015a, Phys. Plasmas, 22, 091503 [NASA ADS] [CrossRef] [Google Scholar]
- Tejero, E. M., Crabtree, C., Blackwell, D. D., et al. 2015b, Sci. Rep., 5, 17852 [NASA ADS] [CrossRef] [Google Scholar]
- Tejero, E. M., Crabtree, C., Blackwell, D. D., et al. 2016, Phys. Plasmas, 23, 055707 [NASA ADS] [CrossRef] [Google Scholar]
- Tonks, L. 1931, Phys. Rev., 37, 1458 [NASA ADS] [CrossRef] [Google Scholar]
- Treumann, R. A., & Baumjohann, W. 1997, Advanced Space Plasma Physics (Imperial College Press) [CrossRef] [Google Scholar]
- Vigren, E., & Eriksson, A. I. 2017, AJ, 153, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Vigren, E., André, M., Edberg, N. J. T., et al. 2017, MNRAS, 469, S142 [Google Scholar]
- Voitcu, G., & Echim, M. 2016, J. Geophys. Res. (Space Phys.), 121, 4343 [NASA ADS] [CrossRef] [Google Scholar]
- Voitcu, G., & Echim, M. 2017, Geophys. Res. Lett., 44, 5920 [NASA ADS] [CrossRef] [Google Scholar]
- Volwerk, M., Goetz, C., Richter, I., et al. 2018, A & A, 614, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameters for the solar wind and comet for the three simulation runs and for comet 67P as encountered by the Rosetta spacecraft at 3 au.
Parameters of the analytical model used for comparison with runs A and C, respectively.
All Figures
 |
Fig. 1 Water-ion densities and velocities in runs A and C, illustrating the influence of the scaling factor. (a) Water-ion density, nwi, as a function of r in run A for different radial directions, following the axes of the coordinate system as indicated in the legend. (b) nwi for run C. (c) The radial-velocity component υr,wi for run A. (d) υrwi for run C. The legend in panel a also applies to panels a to d. (e) Velocity components in the x−z plane for run A. (f) Velocity components in the x−z plane for run C. (g) Velocity components in the x−y plane for run A. (h) Velocity components in the x−y plane for run C. The axis limits for r, x, y, and z are different for the different scalings. The dotted lines in panels c and d indicate |
| In the text | |
 |
Fig. 2 Prescribed magnetic field By in the three runs. In runs A and C, the field is constant, and in run B it depends on the distance to the y axis |
| In the text | |
 |
Fig. 3 Electron densities, temperatures, and Debye lengths along the three coordinate axes. (a) Density of the solar-wind electrons (black) and cometary electrons (red) along the x axis. (b) Temperatures in the x (blue), y (green), and z (red) directions shown along the x axis. (c) Debye length of the solar-wind electrons (black) and cometary electrons (red). The cometary electron Debye length is only shown near the origin where the density is high enough for an accurate estimate. (d–f) Same quantities as a–c shown along the y axis. (g–i) Same quantities as a–c shown along the z axis. |
| In the text | |
 |
Fig. 4 Densities of protons and water ions for uniform and non-uniform magnetic fields. (a) Proton density in the x–z plane in the simulation with a uniform magnetic field (run A). (b) Proton density in the x–y plane in run A (c) Water-ion density in the x–z plane in run A. (d) Water-ion density in the x–y plane in run A. (e) Proton density in the x–z plane in the simulation with a non-uniform magnetic field (run B). (f) Proton density in the x–y plane in run B. (g) Water-ion density in the x–z plane in run B. (h) Water-ion density in the x–y plane in run B. The proton densities are shown on a linear colour scale, while the colour scale for the water ions is logarithmic. The arrows indicate the direction of the ion velocity. |
| In the text | |
 |
Fig. 5 Electric-field topology in two different magnetic-field models (a) Electric field in the x–z plane in the simulation with a uniform magnetic field (run A). (b) Electric field in the x–z plane in the simulation with a non-uniform magnetic field (run B). |
| In the text | |
 |
Fig. 6 Electric fields in the x–z plane (top row) and x–y plane (bottom row) from both the analytical model and simulation run C. Panels (a) and (f) show the convective electric field of the analytical model; (b) and (g) the ambipolar field; (c) and (h) the polarisation field; (d) and (i) the sum of the three electric field contribution in the analytical model; and panels (e) and (j) show the electric field obtained in run C of the particle-in-cell simulation. |
| In the text | |
 |
Fig. 7 Model electric fields, using a cylindrical (left) and spherical (right) model for the polarisation field. Panels (a) and (b) show the field in the x–y plane and (c) and (d) show the field in the x–y plane. The colour-coded quantity is the magnitude of the component of the field in the plane shown, and the arrows indicate the direction of that in-plane component. The polarisation field models differ between the panels, and the cylindrical model also follows Nilsson et al. (2018) in that it does not include an ambipolar electric field. The parameters used correspond to simulation run C. |
| In the text | |
 |
Fig. 8 Wave structures in simulation run C. (a) Plasma density variation, ne− < ne >, in the x–z plane for t = 300 ms. The subtracted mean, < ne > is formed over the region shown. The circle in the centre has been removed as the high density in that region would otherwise dominate the mean. (b) Singular value decomposition (SVD) of the plasma density at t = 100 ms with the first four principal images removed. (c) SVD of the plasma density at t = 200 ms. (d) SVD of the plasma density at t = 300 ms. (e) The Ex component of the electric field at t = 300 ms. (f) SVD of the Ex component of the electric field at t = 300 ms. (g) SVD of the current density magnitude |j| at t = 300 ms. (h) SVD of the magnitude of the in-plane electric field, |
| In the text | |
 |
Fig. 9 Three-dimensional representation of the current density in run A. The magnitude of the current density is colour coded on each line, and the direction of the current is shown by the black cones on a few selected lines1. |
| In the text | |
 |
Fig. 10 Wave structures in the x–y plane of simulation run C. (a) Singular value decomposition of the plasma density at t = 300 ms with the first four principal images removed. (b) SVD of the electric-field magnitude at t = 300 ms. The black arrows show the direction of the current density. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



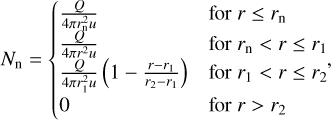
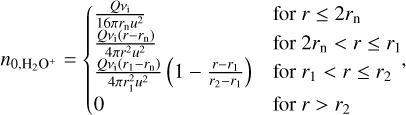
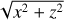
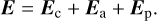
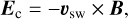
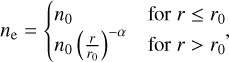
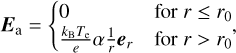
![${{\bf{E}}_{\rm{p}}} \approx \left\{ {\matrix{ { - {{e{n_0}{R_0}{\rm{\Delta }}x} \over {3{_0}}}\left( {{1 \over b} - {1 \over d}} \right){{\bf{e}}_x}} \hfill & {{\rm{for}}\,r \le b} \hfill \cr {\matrix{ {{{e{n_0}{R_0}{\rm{\Delta }}x} \over {3{_0}}}\left[ {\left( {{{2{x^2} - {y^2} - {z^2}} \over {{r^5}}}{{{r^2} - {b^2}} \over 2} - {1 \over r} + {1 \over d}} \right){{\bf{e}}_x}} \right.} \cr {\left. {\quad \quad \quad \quad + \left( {{{3xy} \over {{r^5}}}{{{r^2} - {b^2}} \over 2}} \right){{\bf{e}}_y} + \left( {{{3xz} \over {{r^5}}}{{{r^2} - {b^2}} \over 2}} \right){{\rm{e}}_z}} \right]} \cr } } \hfill & {{\rm{for}}\,b < r \le d} \hfill \cr {{{e{n_0}{R_0}{\rm{\Delta }}x\left( {{d^2} - {b^2}} \right)} \over {6{_0}}}\left[ {{{2{x^2} - {y^2} - {z^2}} \over {{r^5}}}{{\bf{e}}_x} + {{3xy} \over {{r^5}}}{{\bf{e}}_y} + {{3xz} \over {{r^5}}}{{\bf{e}}_z}} \right]} \hfill & {{\rm{for}}\,r > d.} \hfill \cr } } \right.$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq12.png)
![${{\bf{E}}_{\rm{p}}} = \left\{ {\matrix{ { - {{e{n_0}{R_0}{\rm{\Delta }}x} \over {2{_0}}}\left( {{1 \over b} - {1 \over d}} \right){{\bf{e}}_x}} \hfill & {{\rm{for}}\,{r_{\rm{c}}} \le b} \hfill \cr {\matrix{ {{{e{n_0}{R_0}{\rm{\Delta }}x} \over {2{_0}}}\left[ {\left( {\left( {{r_{\rm{c}}} - b} \right){{{x^2} - {z^2}} \over {r_c^4}} - {1 \over {{r_{\rm{c}}}}} + {1 \over d}} \right){{\bf{e}}_x}} \right.} \cr {\left. {\quad \quad + {{\left( {{r_{\rm{c}}} - b} \right)2xz} \over {r_{\rm{c}}^4}}{{\bf{e}}_z}} \right]} \cr } } \hfill & {{\rm{for}}\,b < {r_{\rm{c}}} \le d} \hfill \cr {{{e{n_0}{R_0}{\rm{\Delta }}x} \over {2{_0}}}\left[ {\left( {d - b} \right){{{x^2} - {z^2}} \over {r_{\rm{c}}^4}}{{\bf{e}}_x} + \left( {d - b} \right){{2xz} \over {r_{\rm{c}}^4}}{{\bf{e}}_z}} \right]} \hfill & {{\rm{for}}\,{r_{\rm{c}}} > d,} \hfill \cr } } \right.$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq13.png)
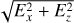
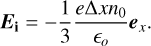
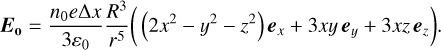
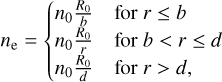
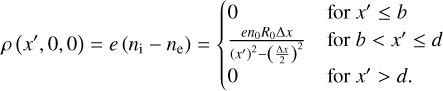
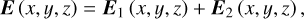
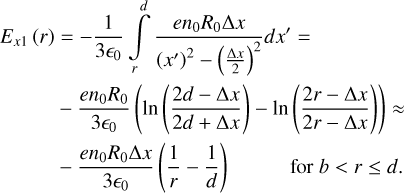
![$\matrix{ {{E_{x1}} = - {{e{n_0}{R_0}} \over {3{_0}}}\,\left[ {\ln \,\left( {{{2d - {\rm{\Delta }}x} \over {2d + {\rm{\Delta }}x}}} \right) - \ln \,\left( {{{2b - {\rm{\Delta }}x} \over {2b - {\rm{\Delta }}x}}} \right)} \right] \approx } \hfill \cr {\,\,\,\,\,\,\,\,\, - {{e{n_0}{R_0}{\rm{\Delta }}x} \over {3{_0}}}\,\left( {{1 \over b} - {1 \over d}} \right).} \hfill \cr }$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq24.png)
![${\bf{a}} = {1 \over {{r^5}}}\,\left[ {\left( {2{x^2} - {y^2} - {z^2}} \right)\,{{\bf{e}}_x} + 3xy{{\bf{e}}_y} + 3xz{{\bf{e}}_z}} \right].$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq26.png)
![$\matrix{ {{{\bf{E}}_{\bf{2}}}\left( {x,y,z} \right) = {\bf{a}}{{e{n_0}{R_0}{\rm{\Delta }}x} \over {3{_0}}}\int\limits_b^r {{{{{\left( {R'} \right)}^3}} \over {{{\left( {R'} \right)}^2} - {{\left( {{\textstyle{{{\rm{\Delta }}x} \over 2}}} \right)}^2}}}dR' = } } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\bf{a}}{{e{n_0}{R_0}{\rm{\Delta }}x} \over {6{_0}}}\,\left[ {{r^2} - {b^2} + {{\left( {{{{\rm{\Delta }}x} \over 2}} \right)}^2}\ln \,\,\left( {{{{r^2} - {{\left( {{\textstyle{{{\rm{\Delta }}x} \over 2}}} \right)}^2}} \over {{b^2} - {{\left( {{\textstyle{{{\rm{\Delta }}x} \over 2}}} \right)}^2}}}} \right)} \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\bf{a}}{{e{n_0}{R_0}{\rm{\Delta }}x} \over {6{_0}}}\,\left( {{r^2} - {b^2}} \right).} \hfill \cr } \, \approx$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq27.png)

![$\matrix{ {{{\bf{E}}_{\bf{2}}}\left( {x,y,z} \right) = {\bf{a}}{{e{n_0}{R_0}{\rm{\Delta }}x} \over {6{_0}}}\left[ {{d^2} - {b^2} + {{\left( {{{{\rm{\Delta }}x} \over 2}} \right)}^2}\ln \left( {{{{d^2} - {{\left( {{\textstyle{{{\rm{\Delta }}x} \over 2}}} \right)}^2}} \over {{b^2} - {{\left( {{\textstyle{{{\rm{\Delta }}x} \over 2}}} \right)}^2}}}} \right)} \right]\,\, \approx } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\bf{a}}{{e{n_0}{R_0}{\rm{\Delta }}x} \over {6{_0}}}\left( {{d^2} - {b^2}} \right)\quad \quad \,\,\,\,\,{\rm{for}}\,r\,{\rm{ > }}\,d.} \hfill \cr }$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq29.png)
![${\bf{E}} \approx \left\{ {\matrix{ { - {{e{n_0}{R_0}{\rm{\Delta }}x} \over {3{_0}}}\left( {{1 \over b} - {1 \over d}} \right){{\bf{e}}_x}} \hfill & {{\rm{for}}\,r \le b} \hfill \cr {\matrix{ {{{e{n_0}{R_0}{\rm{\Delta }}x} \over {3{_0}}}\left[ {\left( {{{2{x^2} - {y^2} - {z^2}} \over {{r^5}}}{{{r^2} - {b^2}} \over 2} - {1 \over r} + {1 \over d}} \right){{\bf{e}}_x}} \right. + } \cr {\left. {\quad \quad \quad \quad \left( {{{3xy} \over {{r^5}}}{{{r^2} - {b^2}} \over 2}} \right){{\bf{e}}_y} + \left( {{{3xz} \over {{r^5}}}{{{r^2} - {b^2}} \over 2}} \right){{\bf{e}}_z}} \right]} \cr } } \hfill & {{\rm{for}}\,b < r \le d} \hfill \cr {{{e{n_0}{R_0}{\rm{\Delta }}x\left( {{d^2} - {b^2}} \right)} \over {6{_0}}}\left[ {{{2{x^2} - {y^2} - {z^2}} \over {{r^5}}}{{\bf{e}}_x} + {{3xy} \over {{r^5}}}{{\bf{e}}_y} + {{3xz} \over {{r^5}}}{{\bf{e}}_z}} \right]} \hfill & {{\rm{for}}\,r > d,} \hfill \cr } } \right.$](/articles/aa/full_html/2023/06/aa45197-22/aa45197-22-eq30.png)