| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 13 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202346073 | |
| Published online | 04 May 2023 | |
Reaction dynamics on amorphous solid water surfaces using interatomic machine-learned potentials
Microscopic energy partition revealed from the P + H → PH reaction
1
Department of Astronomy, Graduate School of Science, The University of Tokyo,
113-0033,
Tokyo, Japan
e-mail: molpeceres@astron.s.u-tokyo.ac.jp
2
University of Stuttgart, Faculty of Chemistry, Institute for Theoretical Chemistry,
70569
Stuttgart, Germany
e-mail: zaverkin@theochem.uni-stuttgart.de
3
National Astronomical Observatory of Japan,
181-8588
Tokyo, Japan
Received:
3
February
2023
Accepted:
6
March
2023
Context. Energy redistribution after a chemical reaction is one of the few mechanisms that can explain the diffusion and desorption of molecules which require more energy than the thermal energy available in quiescent molecular clouds (10 K). This energy distribution can be important in phosphorous hydrides, elusive yet fundamental molecules for interstellar prebiotic chemistry.
Aims. Our goal with this study is to use state-of-the-art methods to determine the fate of the chemical energy in the simplest phosphorous hydride reaction.
Methods. We studied the reaction dynamics of the P + H → PH reaction on amorphous solid water, a reaction of astrophysical interest, using ab initio molecular dynamics with atomic forces evaluated by a neural network interatomic potential.
Results. We found that the exact nature of the initial phosphorous binding sites is less relevant for the energy dissipation process because the nascent PH molecule rapidly migrates to sites with higher binding energy after the reaction. Non-thermal diffusion and desorption after reaction were observed and occurred early in the dynamics, essentially decoupled from the dissipation of the chemical reaction energy. From an extensive sampling of on-site reactions, we constrained the average dissipated reaction energy within the simulation time (50 ps) to be between 50 and 70%. Most importantly, the fraction of translational energy acquired by the formed molecule was found to be mostly between 1 and 5%.
Conclusions. Including these values, specifically for the test cases of 2% and 5% of translational energy conversion, in astrochemical models, reveals very low gas-phase abundances of PHx molecules and reflects that considering binding energy distributions is paramount to correctly merging microscopic and macroscopic modelling of non-thermal surface astrochemical processes. Finally, we found that PD molecules dissipate more of the reaction energy. This effect can be relevant for the deuterium fractionation and preferential distillation of molecules in the interstellar medium.
Key words: ISM: molecules / molecular data / astrochemistry / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Phosphorous is an element of great relevance for the chemistry of the interstellar medium (ISM). This is due to the intrinsic connection between abiotic and prebiotic phosphorous, with abiotic molecules such as phosphine (PH3) serving as an indicator of the potential presence of more complex oxoacids (Turner et al. 2018). Biocompatible phosphorous can be found in several essential biomolecules, such as DNA, RNA, or phospho-lipids. So far, phosphorous has been unambiguously detected in different regions of the ISM in the form of CP, HCP, PN, PO, or HPO (Turner & Bally 1987; Guelin et al. 1990; Agúndez et al. 2007, 2014; Fontani et al. 2016; Lefloch et al. 2016; Rivilla et al. 2016, 2018; Ziurys et al. 2018). However, the detection of phosphorous-bearing molecules in cold star-forming regions is limited to PN, PO, and, recently, PO+ (Yamaguchi et al. 2011; Lefloch et al. 2016; Rivilla et al. 2016, 2018, 2020, 2022). Despite laboratory experiments and computational simulations show that PH3 must be easily hydrogenated on dust grains (Nguyen et al. 2020, 2021; Molpeceres & Kästner 2021), no single phosphorous hydride has been detected in the cold ISM (Chantzos et al. 2020).
The sequence of hydrogenation of phosphorous atoms in the ISM is known to finalise with the formation of phos-phine, PH3 (Molpeceres & Kästner 2021; Nguyen et al. 2021), and proceeds on interstellar dust grains through a sequence: 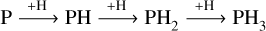 . Competing with this sequence, there are backwards reactions mediated by quantum tunnelling PH3+H→PH2+H2, PH2+H→PH+H2, PH+H→P+H2 that proceed with very low activation barriers and are very rapid, even at 10 K (Molpeceres & Kästner 2021). These establish a pseudo-equilibrium that favours addition (PH3 as end molecule) in the absence of other mechanisms that reduce the intermediate species’ abundance. We find chemical desorption and non-thermal diffusion among this sequence’s possible mechanisms. The low binding energies (BE) of the P-bearing molecules (Molpeceres & Kästner 2021) combined with the confirmation of chemical desorption of phosphine under astro-physical conditions (Nguyen et al. 2020; Furuya et al. 2022) indicate that the hydrogenation sequence may be altered non-thermally, such as the release of intermediates to the gas phase or by fast diffusive reactions with other atoms or radicals, promoted by the release of chemical energy.
. Competing with this sequence, there are backwards reactions mediated by quantum tunnelling PH3+H→PH2+H2, PH2+H→PH+H2, PH+H→P+H2 that proceed with very low activation barriers and are very rapid, even at 10 K (Molpeceres & Kästner 2021). These establish a pseudo-equilibrium that favours addition (PH3 as end molecule) in the absence of other mechanisms that reduce the intermediate species’ abundance. We find chemical desorption and non-thermal diffusion among this sequence’s possible mechanisms. The low binding energies (BE) of the P-bearing molecules (Molpeceres & Kästner 2021) combined with the confirmation of chemical desorption of phosphine under astro-physical conditions (Nguyen et al. 2020; Furuya et al. 2022) indicate that the hydrogenation sequence may be altered non-thermally, such as the release of intermediates to the gas phase or by fast diffusive reactions with other atoms or radicals, promoted by the release of chemical energy.
Regrettably, there is no way of determining the efficiency of non-thermal effects from static quantum chemical calculations, not only in phosphorous chemistry but also in interstellar surface chemistry. This is because the appearance of non-thermal effects requires the interplay between energy dissipation to the bulk and the conversion of the reaction energy to kinetic energy. Classical molecular dynamics simulations have been used to that end, targeting, for example, HCO formation on H2O (Pantaleone et al. 2020), H2 formation on H2O (Pantaleone et al. 2021), or energy dissipation of CO2, H2O and CH4 on water ice after inoculation of a significant amount of energy (Fredon et al. 2017, 2021; Fredon & Cuppen 2018; Upadhyay et al. 2021; Upadhyay & Meuwly 2022). Finally the hydrogenation sequence of the nitrogen atom was very recently studied on H2O (Ferrero et al. 2022b). The interaction potentials for these studies vary in their objectives, such as empirical pair potentials or on-the-fly ab initio molecular dynamics simulations. The former’s low computational cost is the latter’s main drawback. Likewise, ab initio molecular dynamics’ main advantage is that it is, in principle, general, can treat reactive systems, and new potentials do not need to be generated for each system.
In this work, we studied the energy dissipation following the first hydrogenation step of the phosphorous atom (P) with a twofold aim. First of all, we studied the energy dissipation dynamics of a relatively heavy radical PH after its formation via P + H → PH. The energy dissipation and reaction energy redistribution to the different degrees of freedom of the molecule is the crucial quantity behind non-thermal events and, ultimately, its fate depends on phosphorous hydrides in the ISM. The second aim of this paper is to serve as a proof-of-concept for applying interatomic neural network potentials to study reactions in the context of surface astrochemistry. These potentials permit an extensive sampling of reaction trajectories while maintaining a reasonable computational cost, yet somewhat higher than empirical potentials. Using neural-network potentials opens new avenues for studying any adsorbate on any substrate, provided that the chosen reference method can reproduce the electronic structure of the system. The PH radical is especially suitable as a test case for several reasons. First, its formation reaction is barrierless and exothermic (~305–315 kJ mol−1). Secondly, the binding energy of the PH radical is relatively low, especially compared to the reaction energy, permitting the study of various outcomes after the reaction. Third, the reaction occurs on a triplet potential energy surface (PES), which facilitates the construction of the training set compared with more complex radical–radical recombinations occurring in the singlet channel. Fourth and finally, PH is a sufficiently heavy molecule in which the drawbacks of using classical dynamics not accounting for nuclear quantum effects can be partially palliated.
This paper’s structure is as follows. In Sect. 2, we briefly introduce the methodology employed in the paper and the particularities of the training set used to train the interatomic neural network potential. In Sect. 3, we present the results derived from the present study, starting with the adsorption energetics of the P atom at our level of theory and continuing with exploratory molecular dynamics simulations of different binding sites. Later, we focus on extensive sampling, extracting statistical values on energy dissipation and translational kinetic energy of the newly formed PH radical. Finally, we discuss our results under an astrochemical prism in Sect. 4, and include our results in an astrochemical model of a molecular cloud.
2 Methods
2.1 Interatomic potential model
In this work, we developed an entirely reactive machine-learned interatomic potential (MLIP) to study the reaction dynamics for forming the PH molecule on top of amorphous solid water (ASW). Our approach resembles Born–Oppenheimer molecular dynamics at a fraction of its cost. In our simulations, we must sample many trajectories with different reaction outcomes for sufficiently long timescales. Moreover, we need sufficient energy conservation to obtain correct dynamics, especially during the initial step of the reaction. Small integration time steps ensure the desired energy conservation, vide infra. We have achieved all these prerequisites by combining ample sampling with a Gaussian-moment neural network (GMNN) potential (Zaverkin & Kästner 2020; Zaverkin et al. 2021a) trained on energies and atomic forces obtained from density functional theory (DFT). The GMNN source code is freely available1.
To calculate reference energy and atomic force values, we used the DFT method PBE-D3BJ/def2-TZVP (Perdew et al. 1996; Weigend & Ahlrichs 2005; Grimme et al. 2011) as it provides similar energetics to those obtained by Molpeceres & Kästner (2021); Nguyen et al. (2021). The P + H → PH reaction energy (without zero-point vibrational energy, ZPVE) in the gas phase is within 9 kJ mol−1 of reference UCCSD(T)-F12/cc-pVTZ-F12 calculations, −314 versus −305 kJ mol−1. We studied the reaction in the triplet channel since the quintet channel was found to be repulsive in an earlier publication (Molpeceres & Kästner 2021). The training data set generated to train the GMNN model comprises 11 249 structures. The training set size required to achieve the accuracy of 1 kcal mol−1 with respect to the reference electronic structure method is smaller than in our previous works (Molpeceres et al. 2020, 2021; Zaverkin et al. 2021b), owing to the recent improvements in our model (Zaverkin et al. 2021a). The electronic structure calculations were carried out using the ORCA (v 5.0.3) code (Neese 2012; Neese et al. 2020).
A summary of the structures that comprise the training set can be found in Table 1. As in our previous work (Molpeceres et al. 2020, 2021), we generated the training structures by running ab initio molecular dynamics at exploratory, computationally cheaper levels of theory. Here, we used a combination of HF-3c (Sure & Grimme 2013) for the exploration of reactions on clusters and GFN2-xTB (Bannwarth et al. 2019), as well as GFNFF (Spicher & Grimme 2020) to study water clusters and isolated adsorbates on water clusters. The training set includes subsets tailored to reproduce the water–water interaction, for which molecular dynamics in the canonical (NVT) ensemble was carried out, and other subsets simulating collision and reactions, where a microcanonical ensemble (NVE) was used.
Three independent MLIP models were then trained for 1000 epochs. All models were trained on 9000 structures from the data set in Table 1, while another 1500 structures were reserved for the early stopping technique (Prechelt 2012). The achieved mean absolute error with respect to the reference DFT level is about 0.5 kcal mol−1 and 0.3 kcal mol−1 Å−1 for total energies and atomic forces, respectively. The provided errors were evaluated on the test data set consisting of the remaining 749 structures. We then used an ensemble of the three models to predict energies and atomic forces while running our simulations. The cut-off radius is set to 5.5 Å because we are interested in short- and medium-range interactions of the adsorbates with the surface. All other relevant hyper-parameters used for training our NN potentials can be found in the original work (Zaverkin et al. 2021a).
The advantage of using an ensemble is two-fold. First, lower error values in the potential energy can be achieved, and the predicted atomic forces are much smoother than for a single model. The latter is crucial for energy conservation. Second, the variance or disagreement between the three independent models estimates the uncertainty in predicted energy and atomic force values. Thus, using an ensemble of at least three NN potentials provides the means for running a more stable molecular dynamics simulation and allows for estimating uncertainties in predicted values such as binding energy, reaction energy, and reaction profiles. Finally, a detailed analysis of the accuracy of the employed NN ensemble is provided in Appendix A.
Composition of the data set used for training the machine-learned interatomic potentials.
2.2 Water ice surface model
With the MLIP trained, we created a slab model for an amorphous solid water surface by running heating and cooling cycles of molecular dynamics simulations. Very briefly, from a randomly pre-optimised and fully periodic packed simulation cell with 500 water molecules at ρ=0.998 g cm−3, we ran NVT dynamics at 300 K for 100 ps using a Langevin thermostat to control the temperature (friction coefficients of 0.02 ps−1 and 0.5 fs timestep). Five different snapshots along the trajectory are chosen and later quenched to 10 K for 10.0 ps (friction coefficients of 0.05 ps−1 and 0.5 fs timestep), serving as initial models for the subsequent reactivity studies. This system is periodic in the X and Y directions but not in the Z direction. We propagate our dynamics in periodic systems after having trained it on cluster data. We refer the reader to our recent publication for details on this procedure (Zaverkin et al. 2022).
We fixed the bottom layers of the simulation cell in the Z direction to simulate a bulk structure. Once we had the structural models for the ice ready, we sampled the binding energy distribution of the P atom by placing P atoms atop the surface and relaxing the structure. Finally, from representative configurations of the binding energy distribution (see Sect. 3.1), we started NVE simulations to trace the reaction dynamics. The chemical reaction under investigation is P + H → PH. The incoming H atoms are placed around the pre-adsorbed P atom in different binding sites at a distance of 3.5 Å. For all simulations, we ran NVE dynamics for 50 ps using an integration timestep of 0.25 fs. All molecular dynamics calculations were performed with the ASE simulation package (Hjorth Larsen et al. 2017).
3 Results
3.1 Binding energy distribution calculation
The binding energy distribution of the P atom and the PH molecule on ASW, computed with the MLIP, is very similar to in our previous work (Molpeceres & Kästner 2021), which used more sophisticated density functional explicit calculations. To clarify the findings shown in Fig. 1, we identify several segments. One corresponds to high binding (HB), at values of >120% of the average binding energy (which for P is at 1371 K, the equivalent of 1241 K of our previous work (Molpeceres & Kästner 2021) and other works Nguyen et al. 2021). We also sample medium binding (MB) sites, around the average binding energy, weak binding (WB) sites at 70−40% of the average binding energy, and very weak binding (VW) sites at <40% of the average binding energy. Overall, the binding energy of P on ASW is relatively small for an atom as heavy as phosphorus. The average binding energy for PH is 1843 K, which is also in good agreement with our previous work (1616 K; Molpeceres & Kästner 2021), especially considering that we omitted ZPVE in the distributions because we cannot capture the ZPVE during the reaction dynamics.
As mentioned above, we selected four initial configurations to study the reaction from the distribution of binding energies for the P atom. The local environments for each configuration in one of our ice models are depicted in Fig. 2. The figure illustrates that more oxygen neighbours increase the binding energy, as predicted previously (Cuppen et al. 2013). On the contrary, interactions with H atoms lead to weaker binding. The first part of our study evaluated the binding site’s dependence on the dynamics, which was sampled for 19 trajectories because we faced difficulties finding a VW situation for one of the ice models. As mentioned, the P–Hincoming distance was set to 3.5 Å. We ran a short (~2 ps) NVT simulation to initialise the velocities of the water molecules to 10 K before the production run. During this short pre-equilibration, both P and H positions were allowed to relax, but we enforced a constraint in the internuclear distance to the above-mentioned value.
 |
Fig. 1 Distribution of binding energies of P (top) and PH (bottom) on ASW. Each bar is coloured according to the approximated attributed binding site. The colour-code is as follows: high binding (HB) in red, medium binding (MB) in blue, weak binding (WB) in purple, very weak binding (VW) in green. We sampled 245 binding sites to obtain these distributions. |
3.2 Exploratory PH reaction dynamics
An example of the onset of the NVE dynamics for a binding site is presented in Fig. 3. From each of the trajectories, we monitored the evolution of the kinetic energy of the nascent PH molecule along the trajectory and the kinetic energy of all the water molecules within the ice. Two exemplary kinetic energy profiles for the reaction can be found in Fig. 4, left panels. For comparison, we selected two trajectories with very similar binding energies but different energy dissipation behaviour. In the case shown on top, the ice structure accommodates the excess reaction energy into the ice lattice quite fast, whereas, in the one shown at the bottom, most of the reaction energy remains longer as vibrational and rotational energy within the molecule. While this does not mean that energy dissipation does not occur, it hints at different dissipation timescales but without a significant dependence on the binding site.
To check the dependence of the energy dissipation process on the initial binding site, we gathered the outcome of all these trajectories and compared their initial P binding energy with their final PH binding energy. The results can be found in Table 2. We represent the population of P atoms in a given binding site before and after the reaction, along with the fraction of dissipated energy for each binding site in each ice model. The fraction of dissipated energy is calculated as
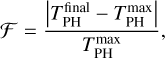 (1)
(1)
where 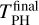 is the final kinetic energy averaged over the last 2.5 ps (to avoid oscillations) of the PH molecule and
is the final kinetic energy averaged over the last 2.5 ps (to avoid oscillations) of the PH molecule and 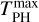 is the maximum of the kinetic energy of PH along the trajectory. Both quantities are calculated from the running averages with a window size of 25 fs. We found different values of ℱ for different binding sites and ice models. However, the dependence on the different binding sites is unclear, indicating that further sampling is required. We increased the sampling for MB and HB sites in Sect. 3.3.
is the maximum of the kinetic energy of PH along the trajectory. Both quantities are calculated from the running averages with a window size of 25 fs. We found different values of ℱ for different binding sites and ice models. However, the dependence on the different binding sites is unclear, indicating that further sampling is required. We increased the sampling for MB and HB sites in Sect. 3.3.
The lack of correlation between ℱ and the binding site can be found by looking at the different populations of P binding sites before the reaction and PH binding sites after the reaction shown by the second and the third columns in Table 2. While we start our sequential simulations with P atoms in VW and WB binding sites along with MB and HB, we find that PH only populates HB and MB sites at the end. This is an essential conclusion of our work, pointing to the fact that nascent molecules arising from exothermic radical-radical recombination are unlikely to be found in the weak binding sites on a pristine surface and affecting the (effective) distributions of binding energies recently reported in the literature for low-temperature studies (Ferrero et al. 2020; Duflot et al. 2021; Molpeceres & Kästner 2021; Bovolenta et al. 2022). The population of HB and MB sites comes as a result of non-thermal diffusion of the nascent PH molecule that uses part of the reaction energy to freely roam the surface until landing on an HB or MB site.
We also evaluated the translational energy (part of the kinetic energy corresponding to the translational motion of the whole PH molecule) depicted in the right panels of Fig. 4 as the instantaneous kinetic energy (no running average). It is calculated as the kinetic energy of the centre of mass (TCOM). From the right panels of Fig. 4, we observe that, despite having similar P binding energies, these PH molecules acquire different translational energies. Both roam the surface before thermally equilibrating and land at a site where they remain for the rest of the simulation. The maximum of the translational energy is, on average, only between 1 and 5% of the reaction energy (−314 kJ mol−1, as a univocal value), with significant variability. Later, we incorporate these values into astrochemical models.
The key to energy dissipation is the binding site where the particles land rather than the binding site where the molecule is formed, in contrast to non-thermal events (like non-thermal diffusion) that depend on the initial site. That conclusion highlights the importance of the ice morphology in the whole energy dissipation versus non-thermal processes interplay. Non-thermal events are characteristic of VW and WB sites, where P (and PH) interacts with fewer neighbours. Hence, a molecule formed in a region with a low density of water molecules will be more likely to experience non-thermal diffusion or desorption. It is essential to mention that even starting the reaction from HB and MB sites, the newly formed PH molecule still may non-thermally diffuse to other (different) HB and MB sites. The fraction of PH molecules diffusing from MB and HB sites can be as low as 7% for HB, indicating the correlation between the binding energy and non-thermal events.
In one out of the 19 trajectories, we observed chemical desorption. We can attribute the mechanism of desorption to the interaction of a highly rotationally excited PH molecule with a dangling O–H bond during an instantaneous exploration of a very repulsive part of the potential (short H–H distance of 1.51 Å), counteracted by momentum conservation and desorption (see Fig. 5). Another important observation of the present work is that the type of non-thermal process, either diffusion or desorption, is determined early in the dynamics (1–10 ps, inferred from the time at which peaks in the translational energy of Figs. 4 and 5 take place) indicating essentially different timescales between non-thermal processes and energy dissipation. The latter, for example, can take up to a few nanoseconds, for CO2 molecules (Upadhyay & Meuwly 2022), for example. In Upadhyay & Meuwly (2022), the authors also found that there are two components for the energy dissipation: one rapid, occurring in tens of picoseconds, which is coherent with our observed behaviour in Table 2 for ℱ; one occurring on the nanosecond scale that is not captured in our simulations because of the simulated time window. We note that the PH molecule of the desorbing trajectory possesses a translational kinetic energy three times lower than the average binding energy for the PH radical on ASW. This shows that the likelihood of chemical desorption, such as adsorption or diffusion, depends on the overall distribution of binding energies rather than only its average.
Our results are also in line with recent results on the N + 3H → NH3 system, with dissipation fractions between 58 and 90% within the first picoseconds of the reaction dynamics (Ferrero et al. 2022b). We observe a similar qualitative behaviour on longer timescales (e.g. Fig. 4, left panels, and Table 2), which can be attributed to the different masses and vibrational frequencies of PH and NH.
 |
Fig. 2 Local environments of P atom prior to the reaction with H. The models portrayed in this figure come from different ice models. |
 |
Fig. 3 Onset for title reaction in our simulations. The figure represents around 50 ſs of the total dynamics (50 ps). The distance of 3.5 Å represents the P–H initial distance. |
 |
Fig. 4 Evolution of total kinetic energy of water ice and PH molecules (left panels) and PH translational energy (right panels) for two P + H → PH reaction trajectories, one with significant energy dissipation in the time-lapse of the simulation (BE=739 K, top panel) and without significant energy dissipation (BE=805 K, bottom panel). The pale blue colour in the left panels shows the instantaneous kinetic energy of the PH molecule. The dark blue colour shows the running average evaluated over a window size of 25 fs. The black dashed line in both panels depicts the average PH binding energy. X, Y, and Z indicate the component along the translational energy is distributed, with Z being the normal to the surface. |
Initial and final binding sites of our exploratory simulations for the P + H → PH reaction on ASW, including all types of binding sites along with the fraction of the reaction energy dissipated into the ice bulk for each trajectory.
3.3 Extended sampling
In the previous section, we determined that the timescales for non-thermal diffusion and desorption are different compared to the energy dissipation. Based on that, we also conclude that, except for the trajectories leading to immediate desorption of PH, the MB and HB are especially interesting for investigating/evaluating energy dissipation because, after the few picoseconds of a simulation, they are the only sites with a PH population different from zero (Table 2), whereas WB sites are the most interesting from a chemical desorption perspective. P is a physisorbed species with relatively low binding energy, so VW binding sites are most likely transient.
To extract reliable statistics on ℱ and related quantities, namely the maximum translational energy (TCOM), the linear displacement (d) of the PH molecule after formation, and the number of trajectories with significant non-thermal diffusion (Ndiff, defined as the fraction of trajectories with d > 2 Å), we carried out an extensive sampling of MD trajectories (358 trajectories, similar to the ones presented before) starting only from MB, HB, and WB situations. We observed explicit chemical desorption in three of 358 trajectories, all of which have been initialised from a WB site. These results correspond to about 1% and 3% of total chemical desorption probability and chemical desorption probability coming from WB sites, respectively. The latter number is similar to the one found for PH3 (a similar system with more degrees of freedom) in experiments (Nguyen et al. 2020), suggesting that the experimental observations may also come from WB sites. We note, however, that the sampling is not enough to guarantee a statistical match between theory and experiments, summed to the inherent differences between the PH and PH3 system. That is why we refer to our discussion in terms of translational energy in Sect. 4.
The significant quantities for these trajectories are shown in Table 3. There, we also include statistics of further 233 trajectories, in which the reactive H atom was replaced by D for MB and HB sites (i.e. MB-D and HB-D). We did not include the study with deuterium in WB sites because of the computational expense of the respective calculations. With the deuterium substitution, we want to observe whether the different vibrational properties of PH and PD affect the dynamics of the nascent molecule. For example, PD has its fundamental vibrational mode in the range of water bendings (~ 1600 cm−1), unlike PH, which appears in a clean region of the spectra at 2218 cm−1, which can facilitate the energy dissipation through the bending modes of water.
The analysis of the trajectories for the MD runs reveals several important conclusions. First, we find that the type of binding site significantly affects the energy dissipation in the considered timescales. This fact could be inferred from previous studies (Garrod et al. 2007; Minissale et al. 2016; Fredon & Cuppen 2018; Fredon et al. 2021), where the efficiency of chemical desorption is a function of BE. However, as previously indicated for thermal desorption studies (Molpeceres & Kästner 2021; Ferrero et al. 2022a; Molpeceres et al. 2022), we must emphasise that considering the whole distribution of binding sites is essential in order to unravel the role of non-thermal mechanisms. Here, we found that the binding energy anticorrelates with the fraction of energy dissipated into the lattice and the acquired translational energy of the nascent molecule. On average, the reaction energy dissipates 12% more in medium-energy binding sites. Likewise, 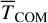 , Ndiff, and
, Ndiff, and 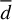 are significantly higher for MB sites than HB sites. This indicates the importance of different factors in energy dissipation and related properties.
are significantly higher for MB sites than HB sites. This indicates the importance of different factors in energy dissipation and related properties.
It is essential to mention that, even though at the end of the dynamics, the reaction energy is not entirely dissipated (see Fig. 4), the translational component TCOM is already wholly dissipated. For WB sites, we observe the highest 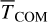 , Ndiff, and
, Ndiff, and 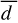 , which reinforces the idea that non-thermal events are maximised on WB sites. It is worth mentioning that with any trajectory starting from WB, PH migrates to a deep binding site. Moreover,
, which reinforces the idea that non-thermal events are maximised on WB sites. It is worth mentioning that with any trajectory starting from WB, PH migrates to a deep binding site. Moreover, 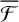 for WB does not follow the trend that we saw for MB and HB, with
for WB does not follow the trend that we saw for MB and HB, with 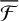 values in between HB and MB. As we mention in Sect. 3.2, WB sites are not populated after the reaction, and the reaction energy dissipation takes place either in MB and HB sites following rapid diffusion after formation; this observation is further reinforced by the values of
values in between HB and MB. As we mention in Sect. 3.2, WB sites are not populated after the reaction, and the reaction energy dissipation takes place either in MB and HB sites following rapid diffusion after formation; this observation is further reinforced by the values of 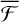 starting from WB sites, appearing in between MB and HB values. For
starting from WB sites, appearing in between MB and HB values. For 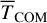 , we keep finding values corresponding to 1–5% of the total reaction energy (rarely going as high as 6.8% in just a single case) in a case starting from a WB situation.
, we keep finding values corresponding to 1–5% of the total reaction energy (rarely going as high as 6.8% in just a single case) in a case starting from a WB situation.
The efficiency of energy dissipation also depends on the hydrogen isotope under consideration. We found that, on average, the energy dissipates 6–7% faster when the incoming particle is deuterium, a fact that could be attributed to the coupling of PD with the bending vibration modes of water, as mentioned above. Similarly, we observed that the average diffusion length of the nascent deuterated molecule is lower than for hydrogen additions by ~0.5 Å on average (which corresponds to 10% of the total traversed distance). At this point, it is important to stress that our classical MD simulations disregard the differences that arise from the quantum nature of H and D. For example, ZPVE is not included in our simulations. We do not expect significant changes in the dynamics on short timescales because of how energetic the reaction is. However, quantum effects may be significant during thermalisation and are vital in supporting quantitative claims in the deuterations.
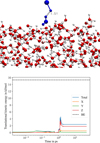 |
Fig. 5 Molecular dynamics snapshot before chemical desorption (top panel) and translational kinetic energy of the respective trajectory (bottom panel). We note that even in such repulsive parts of the PES, our potential only has an uncertainty of around 10% between models, indicating high-quality predictions of the PES also during the reaction. |
Number of trajectories, average dissipation fraction (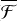 ), average translational kinetic energy (
), average translational kinetic energy (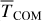 , in kJ mol−1), the fraction of trajectories exhibiting non-thermal diffusion (Ndiff, see text), and average diffusion distance for the diffusing trajectories (
, in kJ mol−1), the fraction of trajectories exhibiting non-thermal diffusion (Ndiff, see text), and average diffusion distance for the diffusing trajectories (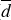 , in Å, the standard deviation in parentheses).
, in Å, the standard deviation in parentheses).
4 Astrochemical implications
4.1 Non-thermal effects of relevance to interstellar chemistry: Astrochemical models
The findings presented in this paper carry significant implications for the chemistry of phosphorous-bearing species in particular and interstellar chemistry in general. As we presented in the introduction, there is no single detection of phosphorous hydrides, including phosphine (PH3), in cold astronomical environments. One common explanation for the absence of a molecule (or family of molecules) in the cold ISM relies on chemical conversions and the appearance of proxy species, a hypothesis applicable to the gas and solid phase (Shingledecker et al. 2019, 2020, 2022; Cooke et al. 2020)). The PH molecule is the most simple phosphorous hydride, and it is thought to be the current onset in the formation of interstellar PH3 (Chantzos et al. 2020; Molpeceres & Kästner 2021), but an early release to the gas-phase or efficient non-thermal diffusion to encounter other radicals and react may decrease its abundance.
Our simulations reveal that between 1 and 5% of the reaction energy is transferred to translation, a quantity labelled χ in the literature (Fredon et al. 2021). This number is in agreement with the current formulation of chemical desorption in terms of RRKM theories (Garrod et al. 2007; Minissale et al. 2016), where a value between 0.5 and 1.0% is assumed for the fraction of energy going to the desorption mode (e.g. oscillation of the z coordinate of the molecule’s centre of mass). Since we are considering three translational degrees of freedom instead of the single one used in the statistical study of chemical desorption, our values are in the range predicted by those models. Our results also fall within the lower bounds considered in the chemical models of Fredon et al. (2021) and specifically with their low-conversion energy model of an assumed 5% of energy conversion. For the specific P + H → PH reaction, 1–5% of energy conversion corresponds to 3.14–15.7 kJ mol−1 energy available for diffusion or desorption, assuming a univocal value of the reaction energy corresponding to −314 kJ mol−1 (the value in the gas phase).
Regarding non-thermal diffusion, 1–5% of the reaction energy corresponds to more or less the average binding energy of the PH molecule, and, assuming a diffusion energy that is a fraction of that energy (even though such an assumption must be done with care under astrophysical conditions; see Furuya et al. 2022), the PH molecule can visit several binding sites, in the process reacting with other pre-adsorbed molecules. However, the translation energy may not be enough to overcome any diffusion barriers for reactions starting in high-energy binding sites. This is illustrated by the value of 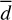 , Table 3. From an astrochemical perspective, one important factor is missing in our simulations: the H2 molecule coverage on the surface. At 10 K, most high-energy binding sites will be populated by H2 molecules (ten orders of magnitude more abundant than the most abundant phosphorous bearing molecule, Chantzos et al. 2020), and PH would likely not be locked on high binding sites. Our average diffusing distance (
, Table 3. From an astrochemical perspective, one important factor is missing in our simulations: the H2 molecule coverage on the surface. At 10 K, most high-energy binding sites will be populated by H2 molecules (ten orders of magnitude more abundant than the most abundant phosphorous bearing molecule, Chantzos et al. 2020), and PH would likely not be locked on high binding sites. Our average diffusing distance (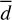 ) is, therefore, a lower bound of the real one. Hence, PH can perform a few hops on the grain, meeting reaction partners and converting to more complex P-bearing molecules. This is in contrast with the classical picture of PHx forming under thermal conditions by hydrogenation in which only hydrogen can move. Thus, we suggest that the effective binding energy applicable to non-thermal events should be lower than the average binding energy computed from distributions, which we tested later in our chemical models (see below).
) is, therefore, a lower bound of the real one. Hence, PH can perform a few hops on the grain, meeting reaction partners and converting to more complex P-bearing molecules. This is in contrast with the classical picture of PHx forming under thermal conditions by hydrogenation in which only hydrogen can move. Thus, we suggest that the effective binding energy applicable to non-thermal events should be lower than the average binding energy computed from distributions, which we tested later in our chemical models (see below).
The other critical non-thermal process is chemical desorption, a phenomenon vital for explaining the return of interstellar adsorbates to the gas phase, where they are ultimately detected. Chemical desorption has been treated analytically in the astrochemical literature. Corresponding approaches are briefly reviewed here. The most straightforward scheme assumes a constant desorption probability of normally 1% for every reaction. The second scheme, described in Garrod et al. (2007) proposes a scheme based on RRKM theory explicitly introducing the binding energy and reaction enthalpy in the formalism. Improving on that, Minissale et al. (2016) also included a collisional parameter (ϵ) where a mass term is introduced, allowing for good agreement for rigid surfaces (graphite) under the assumption of a purely elastic collision. The last attempt to analytically formulate this phenomenon can be found in Fredon et al. (2021), where the authors explicitly consider the fraction of energy inoculated into translational degrees of freedom (χ), which is a step beyond the equipartition of the reaction energy predicted by RRKM theory. In the latter study, the authors indicate that the least known part of their model is the determination of χ, which is most likely not constant for every reaction. Here, we have found χ to be between 1 and 5%, with average values of around 2% for the P + H → PH reaction (Table 3) depending on the binding site under consideration. The probability of chemical desorption (p) as a function of χ, ∆Hr (the enthalpy of the reaction), and EB (the binding energy) proposed in Fredon et al. (2021) for one-product reactions is
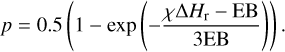 (2)
(2)
We explicitly addressed the impact of our derived χ values in a three-phase (e.g. gas, grain and (inert) mantle) astrochemical model of a molecular cloud. The model is a recent modification of the model reported by Furuya et al. (2022) using the chemical network of Garrod (2013) and adding the hydrogenation sequence of the P atom based on our recent study Molpeceres & Kästner (2021) and the H2 abstraction reactions for these species. The physical conditions of the model are gathered in Table 4 and are the standard conditions of a pseudo-time-dependent molecular cloud model. Reaction-diffusion competition is explicitly considered in our models with diffusion energy assumed to be 0.4 of the binding energy. Quantum tunnelling of atomic H is taken into account in the evaluation of the diffusion-reaction competition (Chang et al. 2007). Non-thermal mechanisms are accounted for, including photodesorption (with a constant photodesorption yield per photon of 1×10−3), desorption induced by cosmic rays in its Hasegawa and Herbst formulation (Hasegawa & Herbst 1993) with a cosmic-ray-ionisation-rate (ζ) of 1.3×10−17 s−1 and (most relevant for this paper) chemical desorption.
To see the impact on the phosphorous hydrides chemistry, we evaluated two chemical desorption schemes, one assuming a constant desorption probability for all phosphorous hydrogenation reactions of p = 3% following the recent experimental and modelling studies (Nguyen et al. 2021; Furuya et al. 2022) (and 1% for all the other reactions) and another one using the Fredon et al. (2021) approach and explicitly including the χ values derived here for the P + H → PH. Specifically, we took χ values of 2.0 and 5.0 %. The former corresponds to the average value obtained in this work, while the latter represents an upper value of it. For simplicity, we assumed that χ is equal throughout the whole hydrogenation sequence. The χ value for all the other reactions in the reaction network is set to 1%. The binding energies for P and PHx molecules are taken from Molpeceres & Kästner (2021). The elemental abundances for the model are taken from Aikawa & Herbst (1999); these correspond, for example, to the low metallicity values, with initial P fractional abundances of 1×10−9 with respect to H nuclei, and where all the elements are in atomic or ionic form except for H, which is contained in H2. Enthalpies of formation used to compute ∆Hr are taken from the original Ruaud et al. (2016) reaction network for P + H → PH and PH + H → PH2, based on the KIDA database data (Wakelam et al. 2012). In contrast, for PH3, we took it from the NIST database because it was unavailable in the original reaction network.
The results for the model are presented in Fig. 6 with peak abundances, and abundances at t = 1 ×107 yr gathered in Table 5. From the figure, we draw several conclusions. First, we observe that the model with χ = 2.0% yields gas abundances of P hydrides that are very low, which is partially palliated for χ = 5.0%. This trend is inverted for ice abundance. In all models explicitly using χ, the abundance of PH3 is very low, in contrast with the model assuming a constant desorption probability that is supported by recent experiments (Nguyen et al. 2021). We believe that the reduced efficiency for chemical desorption that we found for χ = 2% and 5% stems from considering a single BE and a single χ parameter for our systems. From Table 3, we learned that there is an anti-correlation between BE and 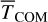 (a proxy of χ) with a significant variability for χ.
(a proxy of χ) with a significant variability for χ.
We ran the same chemical models with χ = 5% (as an upper value), using an average BE for PHx that does not include the high binding sites (modified value A), or, taking into account the BE 0.7 of the real binding energy to only consider weak binding sites (modified value B). Hence, the original values of Molpeceres & Kästner (2021) are re-weighted according to these rules and included in the model. Table 6 enumerates these changes, where for the modified value A we excluded the binding sites with energies higher than 120% of the average BE. The abundances for this chemical model are shown in Fig. 7 with peak fractional abundances and abundances at t = 1 × 107 collated in Table 7.
Even though the changes portrayed in Table 6 (modified value A) are minimal and fall within the variability for binding energies as presented by various methods for other adsorbates (Das et al. 2018; Ferrero et al. 2020; Bovolenta et al. 2022), we observe a significant increase in the abundance of gas-phase PH3 by four orders of magnitude. The changes for the modified values B are even more drastic because they disregard average and deep binding sites (MB and HB), and we equally observe variations of five orders of magnitude in the P-bearing abundances with respect to the values using the original average BE, approaching the values predicted by a constant probability of chemical desorption. This is the key finding of our work because even with an average BE lower than reaction energies by two orders of magnitude, the binding site is still defining the dynamics of chemical desorption of the nascent molecule. For all of our portrayed molecules, both in Figs. 6 and 7, we can calculate the analytic chemical desorption probability (p) as a function of χ. This is shown in Fig. 8 and is helpful to rationalise our observations. We see that for the model with the Molpeceres & Kästner (2021) BE and χ = 2% (Fig. 6, middle panel), the chemical desorption probability is null for all reactions. The molecules’ release to the gas phase is driven only by cosmic-ray-induced desorption and photodesorption, mechanisms that are insufficient to release a significant portion of the phosphorous hydrides contained in the ice. For χ = 5% (Fig. 6, bottom panel) and PH and PH2, there is a real value of the chemical desorption probabilities that is higher for PH2 owing to its higher ∆Hr. Reducing the effective binding energy with the modified values B of Table 6 finally enables desorption of PH3 for χ = 5% (Fig. 7, bottom panel).
A model based on translational energy gained by the nascent molecule, such as the one presented in Fredon et al. (2021), is a significant step forward in our understanding of chemical desorption. Furthermore, it is physically sound and allows us to go beyond equipartition into vibration, rotation, and translational degrees of freedom, something that we also do in our simulations. However, in this work, we found that such a model is susceptible to the χ parameter, which, in addition, is not only species-dependent, but also binding-site-dependent. In line with our results, to reproduce the experimental abundances for the chemical desorption probability of PH3, Furuya et al. (2022) derived a χ value for chemical desorption of 7% to account for a chemical desorption probability per reactive event of 3% in the PH2 + H → PH3 reaction, the same value obtained in this work (continuous green line in Fig. 8). However, based on our simulations on PH, we cannot explain a value of 7% for χ, where our upper bound for the distribution is 5% and the absolute maximum value found for a single trajectory is 6.7%, occurring only once, and in a system (PH) with fewer degrees of freedom to distribute the reaction energy into the molecule. The difference between 1 and 5 % of our simulations and 7% obtained from the fit of experimental data stems from the range of values in EB, ∆Hr, and χ, making it challenging to establish a clear and univocal relation between our microscopically derived data with macroscopical models of chemical desorption. We continue to investigate ways of improving on the basis provided by Eq. (2) and encourage further work on this subject.
Finally, from an astrochemical point of view, we cannot confidently determine the abundances of PH3 in molecular clouds, but it is not our intention with this paper. We refer the reader to Chantzos et al. (2020) for a much more in-depth analysis of interstellar phosphorous chemistry. The purpose of the chemical models presented here is to evaluate the sensitivity of the models to the parameters governing chemical desorption, reiterating the extreme variability induced by the BE distributions.
Initial physical conditions utilised in the molecular cloud model.
 |
Fig. 6 Astrochemical models for the evolution of PHx species in the gas (solid lines) and in the ice (dashed lines) for models with different treatment of chemical desorption. Labels in the top graph apply to all graphs. |
Update of the PHx binding energies to exclude high binding energy sites (modified value A), and to only consider weak-binding sites (0.70 of EB; modified value B).
 |
Fig. 7 Astrochemical models equivalent to bottom panel in Fig. 6, but with updated binding energies according to Table 6. Labels in the top graph apply to all graphs. |
 |
Fig. 8 Chemical desorption probability (p) in the Fredon et al. (2021) formulation as a function of the translational energy conversion fraction χ. |
4.2 Deuteration reactions and PD dynamics
Finally, we dedicate a few words to our study of the energy dissipation of PD versus PH. Although we are aware that the main caveat of our simulations remains the classical nature of the nuclear motion, we find that energy dissipation is, on average, more efficient for PD than for PH. It remains to be established if such an effect is a particularity of PD because of a coupling between the fundamental stretching mode of PD and the water bending modes or if, by contrast, it is a consequence of the different mass terms during the dynamics. Suppose this effect is due to the coupling between vibrational frequencies. In that case, we can expect a preferential distillation of molecules whose vibrational modes are compatible with the substrate’s composition, which will be important for desorption of molecules as a function of the surface composition. In contrast, if the greater energy dissipation is general to all deuterations, that would imply that molecules on grains would be deuterium enriched compared to their gas counterparts.
Although the limitation of our method does not allow for strong conclusions in this regard, we encourage further work in this direction because of the crucial implications that our simulations carry for the deuterium fractionation in the ISM. We postpone the aforementioned study to future work.
5 Conclusions
In this work, we used a novel methodology based on neural-network interatomic potentials to study the chemical energy dissipation in the surface reaction P + H → PH on ASW. The main finding of our work, that is extremely counterintuitive, is that, even with the reaction energy being two orders of magnitude higher than the binding energy, the initial binding energy of the adsorbate prior to reaction is absolutely crucial, to the point that in our study, only adsorbates on WB sites are susceptible to experience chemical desorption. From our study, we draw several conclusions, which we list below:
Our MLIP achieves high accuracy levels, comparable to the reference level of theory, even in reactivity studies where very abrupt changes in the potential occur on very short timescales.
The binding energies of P and PH on ASW, obtained by neural-network potentials, are, on average, 1317 and 1843 K; these values are in very good agreement with those of our previous study (1241 and 1616 K).
Our exploratory simulations of four types of binding sites show that below-average binding energy sites are not likely to be populated after a reaction on a pristine surface. By contrast, medium- and high-energy binding sites are likely to be the endpoint of a nascent molecule, where the reaction energy is dissipated.
Non-thermal effects such as diffusion and desorption are determined early in the dynamics, approximately in the first 10 ps. Energy dissipation and non-thermal events seem to be decoupled processes with a marked dependence on the binding energy of the adsorbate.
From a more extensive pool of simulations on high, medium, and weak binding energy sites, we were able to constrain the fraction of dissipated energy and, most importantly, the translational kinetic energy acquired by the PH molecule after the reaction. We showed that on medium-energy binding sites, energy dissipates 12% more than on high binding sites. Concerning transfer to translational energies, we found that it is a rather inefficient process, and we constrained it to a yield of 1–5%. Molecules formed on medium-energy binding sites acquire, on average, nearly double the translational energy that molecules formed on high-energy binding sites need. In weak binding sites, the energy dissipation fraction is meaningless because the population of weak binding sites is null after the reaction, with a consequential maximum of translational energy.
We found the differences between the deuteration reaction and the hydrogenation, P + D → PD. On average, energy dissipates 6–7% more for the same binding site for the deuteration reaction, and PD acquires around 10% less translational energy.
We incorporated our derived values into astrochemical models accounting for chemical desorption. We found that the latest literature model for chemical desorption (Eq. (2)) is extremely sensitive to the molecule’s binding energy and the fraction of energy redistributed to translational degrees of freedom. Using our average value, χ = 2%, we obtain that PHx gas abundances must be very low, which confronts recent studies (Nguyen et al. 2020; Furuya et al. 2022). Using an upper limit of χ along with updating binding energies to exclude high-energy binding sites (a situation expected in the ISM for P-bearing molecules), we found changes of one-to-five orders of magnitude in the abundances of PHx compounds, reconciling our values with those of recent studies mentioned above. This strongly suggests that chemical desorption, similarly to thermal diffusion or desorption, is sensitive to the binding site under consideration.
Continuations to this work will deepen the connection between the atomistic simulations and the analytical formulas for chemical desorption (and diffusion), ideally tackling the problem of using a single binding energy/translational energy value in contrast to the distribution of such values.
Acknowledgements
G.M. thanks the Japan Society for the Promotion of Science (JSPS International Fellow P22013, and Grant-in-aid 22F22013) for its support. V.Z. and J.K. acknowledge the support by the Stuttgart Center for Simulation Science (SimTech). Funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2075 – 390740016. The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster). KF acknowledges support from JSPS KAKENHI grant Numbers 20H05847 and 21K13967. Y.A. acknowledges support by Grant-in-Aid for Scientific Research (S) 18H05222, and Grant-in-Aid for Transformative Research Areas (A) grant Nos. 20H05847.
Appendix A Quality assessment for employed MLIPs
In this section, we assess the quality of the GMNN-based MLIPs employed to study the reaction dynamics of the PH formation. For this purpose, we first analysed the errors obtained on the test data, that is, the data drawn from the original data set but not seen during training, including the early stopping technique. Fig. A.1 shows the correlation of predicted energies and atomic forces with the respective reference values. All values lie tightly on the diagonal, indicating an excellent performance of developed MLIPs. We obtained a mean absolute error (MAE) of 0.01 kcal/mol/atom and 0.28 kcal/mol/Å for predicted energies and atomic forces, respectively. The respective root-mean-square errors (RMSEs) are 0.01 kcal/mol/atom and 0.42 kcal/mol/Å.
The MAE and RMSE values in predicted energies and atomic forces are abstract quality measures for MLIPs. To assess the potential’s robustness and reliability, we investigated their uncertainty during real-time applications. For this purpose, we considered two possible outcomes, namely a reaction with subsequent desorption (1) and diffusion (2) of created PH species and the distributions of uncertainties corresponding to them. Fig. A.2 (top) shows the distribution of uncertainties for the case where PH desorbs after the reaction (1), obtained through a disagreement among three models. The figure shows that most uncertainties are of values less than 1 kcal/mol/Å, an empirical threshold used to make statements concerning the model’s reliability. Thus, the model performs overall robustly and leads to correct dynamics.
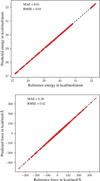 |
Fig. A.1 Evaluation of model’s performance on test data. Correlation of the predicted potential energies (top) and atomic forces (bottom) with the corresponding reference values for all structures in the test data. Mean absolute errors (MAEs) and root-mean-square errors (RMSEs) are shown as an inset. |
 |
Fig. A.2 Tracking force uncertainties along MD trajectory leading to desorption of created PH species. Top: Norm uncertainty of the atomic forces predicted by an ensemble of three GM-NN models. Bottom: Comparison of the force norm and the respective uncertainty for the hydrogen atom during first steps of an MD simulation leading to the desorption of the created PH species. The timescale is restricted to the reaction of P and H and the desorption of the resulting PH molecule. The uncertainty of the ensemble does not exceed 9.6% of the respective force norm. |
However, at least one of the atoms participating in the reaction requires more rigorous analysis. Fig. A.2 (bottom) shows the norm of the force acting on the hydrogen atom evaluated along a molecular dynamics trajectory. Additionally, we show the uncertainty of the force norm in Fig. A.2 (bottom). The figure shows that the maximal uncertainty does not exceed 9.6 % of the value of the respective force norm. However, additional inspection has shown that those uncertainties correspond to high-energy regions where, the vibrations stimulated by the reaction, for example, should be accounted for. In this case, the distance between P and H reaches values smaller than those sampled by the training set, leading to a higher model uncertainty. As this part of the potential energy surface is irrelevant to the performed study and its results, the uncertainty in those high-energy regions could not influence them. Similar results have been obtained for the case where PH species diffuse on the surface after the reaction (2). The respective uncertainties are shown in Fig. A.3.
 |
Fig. A.3 Tracking force uncertainties along MD trajectory leading to diffusion of the created PH species. Top: Norm uncertainty of atomic forces predicted by three GM-NN models. Bottom: Comparison of force norm and respective uncertainty for the hydrogen atom during first steps of an MD simulation leading to the diffusion of the created PH species. The timescale is restricted to the reaction of P and H and the diffusion of the resulting PH molecule. The uncertainty of the ensemble does not exceed 12 % of the respective force norm. |
Finally, we considered a geometry optimisation profile on 20 (H2O)20 using explicit DFT calculations at the reference level and using the MLIP Fig. A.4 shows that both energy profiles almost coincide with an MAE of 0.002 kcal/mol/atom and an RMSE of 0.01 kcal/mol/atom. Moreover, atomic forces correlate very well with the reference values that correspond to low MAE and RMSE values of 0.21 kcal/mol/Å and 0.69 kcal/mol/Å, respectively. This indicates that the MLIP reproduces the exact reaction profile predicted by DFT.
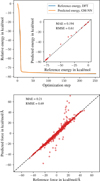 |
Fig. A.4 Evaluating the model’s performance during geometry optimisation. Top: Comparison of reference and predicted potential energy profiles obtained during a geometry optimisation. (Bottom: Correlation of atomic forces predicted by the developed MLIP with the corresponding reference values. |
References
- Agúndez, M., Cernicharo, J., & Guélin, M. 2007, ApJ, 662, L91 [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., Decin, L., Encrenaz, P., & Teyssier, D. 2014, ApJ, 790, L27 [CrossRef] [Google Scholar]
- Aikawa, Y., & Herbst, E. 1999, ApJ, 526, 314 [Google Scholar]
- Bannwarth, C., Ehlert, S., & Grimme, S. 2019, J. Chem. Theory Comput., 15, 1652 [CrossRef] [Google Scholar]
- Bovolenta, G. M., Vogt-Geisse, S., Bovino, S., & Grassi, T. 2022, ApJS, 262, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Q., Cuppen, H. M., & Herbst, E. 2007, A&A, 469, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chantzos, J., Rivilla, V. M., Vasyunin, A., et al. 2020, A&A, 633, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooke, I. R., Gupta, D., Messinger, J. P., & Sims, I. R. 2020, ApJ, 891, L41 [Google Scholar]
- Cuppen, H. M., Karssemeijer, L. J., & Lamberts, T. 2013, Chem. Rev., 113, 8840 [NASA ADS] [CrossRef] [Google Scholar]
- Das, A., Sil, M., Gorai, P., Chakrabarti, S. K., & Loison, J. C. 2018, ApJS, 237, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Duflot, D., Toubin, C., & Monnerville, M. 2021, Front. Astron. Space Sci., 8, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrero, S., Zamirri, L., Ceccarelli, C., et al. 2020, ApJ, 904, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrero, S., Grieco, F., Ibrahim Mohamed, A.-S., et al. 2022a, MNRAS, 516, 2586 [CrossRef] [Google Scholar]
- Ferrero, S., Pantaleone, S., Ceccarelli, C., et al. 2022b, ApJ, 944, 142 [Google Scholar]
- Fontani, F., Rivilla, V. M., Caselli, P., Vasyunin, A., & Palau, A. 2016, ApJ, 822, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Fredon, A., & Cuppen, H. M. 2018, Phys. Chem. Chem. Phys., 20, 5569 [NASA ADS] [CrossRef] [Google Scholar]
- Fredon, A., Lamberts, T., & Cuppen, H. M. 2017, ApJ, 849, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Fredon, A., Groenenboom, G. C., & Cuppen, H. M. 2021, ACS Earth Space Chem., 5, 2032 [NASA ADS] [CrossRef] [Google Scholar]
- Furuya, K., Oba, Y., & Shimonishi, T. 2022a, ApJ, 926, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comp. Chem., 32, 1456 [CrossRef] [Google Scholar]
- Guelin, M., Cernicharo, J., Paubert, G., & Turner, B. E. 1990, A&A, 230, L9 [NASA ADS] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth Larsen, A., Jørgen Mortensen, J., Blomqvist, J., et al. 2017, J. Condens. Matter Phys., 29, 273002 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Vastel, C., Viti, S., et al. 2016, MNRAS, 462, 3937 [CrossRef] [Google Scholar]
- Minissale, M., Dulieu, F., Cazaux, S., & Hocuk, S. 2016, A&A, 585, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molpeceres, G., & Kästner, J. 2021, ApJ, 910, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Molpeceres, G., Zaverkin, V., & Kästner, J. 2020, MNRAS, 499, 1373 [Google Scholar]
- Molpeceres, G., Zaverkin, V., Watanabe, N., & Kästner, J. 2021, A&A, 648, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molpeceres, G., Kästner, J., Herrero, V. J., Peláez, R. J., & Maté, B. 2022, A&A, 664, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neese, F. 2012, WIREs Comput. Mol. Sci., 2, 73 [CrossRef] [Google Scholar]
- Neese, F., Wennmohs, F., Becker, U., & Riplinger, C. 2020, J. Chem. Phys., 152, 224108 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, T., Oba, Y., Shimonishi, T., Kouchi, A., & Watanabe, N. 2020, ApJ, 898, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, T., Oba, Y., Sameera, W. M. C., Kouchi, A., & Watanabe, N. 2021, ApJ, 918, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Pantaleone, S., Enrique-Romero, J., Ceccarelli, C., et al. 2020, ApJ, 897, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Pantaleone, S., Enrique-Romero, J., Ceccarelli, C., et al. 2021, ApJ, 917, 49 [CrossRef] [Google Scholar]
- Perdew, J. P., Burke, K., & Ernzerhof, M. 1996, Phys. Rev. Lett., 77, 3865 [CrossRef] [PubMed] [Google Scholar]
- Prechelt, L. 2012, in Neural Networks: Tricks of the Trade, 2nd edn., eds. G. Montavon, G. B. Orr, & K.-R. Müller (Berlin, Heidelberg: Springer), 53 [CrossRef] [Google Scholar]
- Rivilla, V. M., Fontani, F., Beltrán, M. T., et al. 2016, ApJ, 826, 161 [CrossRef] [Google Scholar]
- Rivilla, V. M., Jiménez-Serra, I., Zeng, S., et al. 2018, MNRAS, 475, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Rivilla, V. M., Drozdovskaya, M. N., Altwegg, K., et al. 2020, MNRAS, 492, 1180 [Google Scholar]
- Rivilla, V. M., García De La Concepción, J., Jiménez-Serra, I., et al. 2022, Front. Astron. Space Sci., 9 [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [Google Scholar]
- Shingledecker, C. N., Álvarez-Barcia, S., Korn, V. H., & Kästner, J. 2019, ApJ, 878, 80 [Google Scholar]
- Shingledecker, C., Molpeceres, G., Rivilla, V., Majumdar, L., & Kästner, J. 2020, ApJ, 897, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Shingledecker, C. N., Banu, T., Kang, Y., et al. 2022, J. Phys. Chem. A, 126, 5343 [NASA ADS] [CrossRef] [Google Scholar]
- Spicher, S., & Grimme, S. 2020, Angew. Chem. Int. Ed., 59, 15665 [Google Scholar]
- Sure, R., & Grimme, S. 2013, J. Comput. Chem., 34, 1672 [CrossRef] [Google Scholar]
- Turner, B. E., & Bally, J. 1987, ApJ, 321, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, A. M., Bergantini, A., Abplanalp, M. J., et al. 2018, Nat. Commun., 9, 3851 [NASA ADS] [CrossRef] [Google Scholar]
- Upadhyay, M., & Meuwly, M. 2022, Energy Redistribution Following CO2 Formation on Cold Amorphous Solid Water [Google Scholar]
- Upadhyay, M., Pezzella, M., & Meuwly, M. 2021, J. Phys. Chem. Lett., 12, 6781 [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [Google Scholar]
- Weigend, F., & Ahlrichs, R. 2005, Phys. Chem. Chem. Phys., 7, 3297 [Google Scholar]
- Yamaguchi, T., Takano, S., Sakai, N., et al. 2011, PASJ, 63, L37 [NASA ADS] [Google Scholar]
- Zaverkin, V., & Kästner, J. 2020, J. Chem. Theory Comput., 16, 5410 [Google Scholar]
- Zaverkin, V., Holzmüller, D., Steinwart, I., & Kästner, J. 2021a, J. Chem. Theory Comp., 17, 6658 [CrossRef] [Google Scholar]
- Zaverkin, V., Molpeceres, G., & Kästner, J. 2021b, MNRAS, 510, 3063 [Google Scholar]
- Zaverkin, V., Holzmüller, D., Schuldt, R., & Kästner, J. 2022, J. Chem. Phys., 156, 114103 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M., Schmidt, D. R., & Bernal, J. J. 2018, ApJ, 856, 169 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Composition of the data set used for training the machine-learned interatomic potentials.
Initial and final binding sites of our exploratory simulations for the P + H → PH reaction on ASW, including all types of binding sites along with the fraction of the reaction energy dissipated into the ice bulk for each trajectory.
Number of trajectories, average dissipation fraction (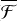 ), average translational kinetic energy (
), average translational kinetic energy (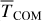 , in kJ mol−1), the fraction of trajectories exhibiting non-thermal diffusion (Ndiff, see text), and average diffusion distance for the diffusing trajectories (
, in kJ mol−1), the fraction of trajectories exhibiting non-thermal diffusion (Ndiff, see text), and average diffusion distance for the diffusing trajectories (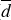 , in Å, the standard deviation in parentheses).
, in Å, the standard deviation in parentheses).
Update of the PHx binding energies to exclude high binding energy sites (modified value A), and to only consider weak-binding sites (0.70 of EB; modified value B).
All Figures
 |
Fig. 1 Distribution of binding energies of P (top) and PH (bottom) on ASW. Each bar is coloured according to the approximated attributed binding site. The colour-code is as follows: high binding (HB) in red, medium binding (MB) in blue, weak binding (WB) in purple, very weak binding (VW) in green. We sampled 245 binding sites to obtain these distributions. |
| In the text | |
 |
Fig. 2 Local environments of P atom prior to the reaction with H. The models portrayed in this figure come from different ice models. |
| In the text | |
 |
Fig. 3 Onset for title reaction in our simulations. The figure represents around 50 ſs of the total dynamics (50 ps). The distance of 3.5 Å represents the P–H initial distance. |
| In the text | |
 |
Fig. 4 Evolution of total kinetic energy of water ice and PH molecules (left panels) and PH translational energy (right panels) for two P + H → PH reaction trajectories, one with significant energy dissipation in the time-lapse of the simulation (BE=739 K, top panel) and without significant energy dissipation (BE=805 K, bottom panel). The pale blue colour in the left panels shows the instantaneous kinetic energy of the PH molecule. The dark blue colour shows the running average evaluated over a window size of 25 fs. The black dashed line in both panels depicts the average PH binding energy. X, Y, and Z indicate the component along the translational energy is distributed, with Z being the normal to the surface. |
| In the text | |
 |
Fig. 5 Molecular dynamics snapshot before chemical desorption (top panel) and translational kinetic energy of the respective trajectory (bottom panel). We note that even in such repulsive parts of the PES, our potential only has an uncertainty of around 10% between models, indicating high-quality predictions of the PES also during the reaction. |
| In the text | |
 |
Fig. 6 Astrochemical models for the evolution of PHx species in the gas (solid lines) and in the ice (dashed lines) for models with different treatment of chemical desorption. Labels in the top graph apply to all graphs. |
| In the text | |
 |
Fig. 7 Astrochemical models equivalent to bottom panel in Fig. 6, but with updated binding energies according to Table 6. Labels in the top graph apply to all graphs. |
| In the text | |
 |
Fig. 8 Chemical desorption probability (p) in the Fredon et al. (2021) formulation as a function of the translational energy conversion fraction χ. |
| In the text | |
 |
Fig. A.1 Evaluation of model’s performance on test data. Correlation of the predicted potential energies (top) and atomic forces (bottom) with the corresponding reference values for all structures in the test data. Mean absolute errors (MAEs) and root-mean-square errors (RMSEs) are shown as an inset. |
| In the text | |
 |
Fig. A.2 Tracking force uncertainties along MD trajectory leading to desorption of created PH species. Top: Norm uncertainty of the atomic forces predicted by an ensemble of three GM-NN models. Bottom: Comparison of the force norm and the respective uncertainty for the hydrogen atom during first steps of an MD simulation leading to the desorption of the created PH species. The timescale is restricted to the reaction of P and H and the desorption of the resulting PH molecule. The uncertainty of the ensemble does not exceed 9.6% of the respective force norm. |
| In the text | |
 |
Fig. A.3 Tracking force uncertainties along MD trajectory leading to diffusion of the created PH species. Top: Norm uncertainty of atomic forces predicted by three GM-NN models. Bottom: Comparison of force norm and respective uncertainty for the hydrogen atom during first steps of an MD simulation leading to the diffusion of the created PH species. The timescale is restricted to the reaction of P and H and the diffusion of the resulting PH molecule. The uncertainty of the ensemble does not exceed 12 % of the respective force norm. |
| In the text | |
 |
Fig. A.4 Evaluating the model’s performance during geometry optimisation. Top: Comparison of reference and predicted potential energy profiles obtained during a geometry optimisation. (Bottom: Correlation of atomic forces predicted by the developed MLIP with the corresponding reference values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


