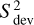| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202245089 | |
| Published online | 04 May 2023 | |
Improved precision of radial velocity measurements after correction for telluric absorption★
1
LATMOS, Université Versailles-Saint-Quentin,
11 Bd D’Alembert,
78280
Guyancourt, France
e-mail: anastasia.ivanova@latmos.ipsl.fr
2
Space Research Institute (IKI), Russian Academy of Science,
Profsoyusnaya street, 84/32,
Moscow
117997, Russia
3
GEPI, Observatoire de Paris, PSL University, CNRS,
5 place Jules Janssen,
92190
Meudon, France
e-mail: rosine.lallement@obspm.fr
4
LATMOS, Sorbonne Université,
4 place Jussieu,
75005
Paris, France
Received:
29
September
2022
Accepted:
5
February
2023
Context. The detection of planets around other stars by measurement of stellar radial velocity (RV) variations benefits from improvements to dedicated spectrographs that can lead to the achievement of a precision of 1 m s−1 or better. Spectral intervals within which stellar lines are contaminated by telluric lines are classically excluded from the RV processing.
Aims. We aim to estimate the potential improvement of the precision of radial velocity measurements from telluric-absorption removal and subsequent extension of the useful spectral domain.
Methods. We developed a correction method based on the online web service TAPAS that allows a synthetic atmospheric transmission spectrum to be determined for the time and location of observations. This method was applied to telluric H2O and O2 absorption removal from a series of 200 consecutive ESPRESSO exposures of the K2.5V star HD40307 available in ESO archives. We calculated the radial velocity using the standard cross-correlation function (CCF) method and Gaussian fit of the CCF, with uncorrected spectra and the ESPRESSO standard stellar binary mask on one hand, and telluric-corrected spectra and an augmented binary mask with 696 additional lines on the other.
Results. We find that the precision of radial velocity measurements is improved in the second case, with a reduction of the average formal error from 1.04 m s−1 down to 0.78 m s−1 in the case of these ESPRESSO data and this stellar type for the red arm. Using an estimator of the minimal error based on the photon noise limit applied to the full CCF, the error is reduced from 0.89 m s−1 down to 0.78 m s−1. This corresponds to a significant decrease (by about 35%) in the observing time required to reach the same precision in the red part.
Key words: methods: data analysis / techniques: spectroscopic / planets and satellites: detection
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
After the discovery of the first exoplanet (Mayor & Queloz 1995), the radial velocity (RV) method brought us another ≃2000 exoplanets1. Although the method of transit photometry is currently the most productive, the RV method is still important, because in addition to enabling the discovery of new exoplanets and the determination of their apparent mass m sin i, it can be used to confirm exoplanets discovered with other methods and to measure the masses of transiting exoplanets (sin i ≃ 1). However, the RV method is limited by technical capabilities: the size and availability of the telescope and the stability and accuracy of the wavelength calibration of the spectrograph. Therefore, any improvement of the processing associated to the radial velocity retrieval will result in improved precision or a decrease in the telescope time required to achieve a defined-goal precision (when this latter is limited by photon shot noise).
The RV method (Connes 1985; Baranne et al. 1996) is based on measuring the Doppler shifts of the stellar lines caused by the reflex motion of the star around the center of mass of the star-planet system. As spectra for RV measurements are taken from Earth, the absorption lines produced by Earth’s atmosphere are also implanted on the star spectrum along with the stellar lines. Absorptions by Earth’s atmosphere, or telluric absorptions, are unavoidable and produce a system of absorption features whose wavelengths are essentially fixed in the wavelength reference system of the spectrograph. On the contrary, even if the radial velocity of a star with respect to the barycenter of the Solar System is constant (case of no planet), the motion of the Earth (rotation and orbital) induces a change in the Doppler shift of the star as seen from the telescope, which is referred to as barycentric Earth radial velocity (BERV).
The classical method of measuring RV in spectra is to cross-correlate them with a template, or binary mask (BM; Baranne et al. 1979). Binary masks were initially mechanical (Baranne et al. 1979), with holes at the positions of stellar absorption lines, and required the refocusing of the whole spectrum light that passed through the mask onto a single photometric detector. Later on, masks were numerical, and in the form of a set of boxcar functions (e.g., Baranne et al. 1996). Subsequent improvements to the cross-correlation function (CCF) method consisted in assigning different weights to different lines of the BM (Pepe et al. 2002; Lafarga et al. 2020).
Most RV measurements excluded from consideration those spectral regions with, or adjacent to, telluric absorption. Figure 1 illustrates those wavelength intervals that are excluded from computation because of telluric contamination by restricting the official ESPRESSO BM lines to spectral regions clear of strong to moderate telluric lines. If we convert these regions into orders of the new, high-accuracy ESPRESSO spectrograph at ESO-VLT, 16 orders out of 170 are not used in RV calculation for this reason, while 30 others have a relatively small number of lines of the binary mask (Fig. 2). Our goal is to show that it is possible to correct the spectra for telluric absorption based on a highly detailed state-of-the-art synthetic atmospheric transmission spectrum available online and a rather simple fitting technique, and to use the previously discarded spectral regions for RV measurement. To check the correction and test its benefits, we took advantage of a quite unusual series of very short ESPRESSO exposures made in a single night.
Several methods have been developed to correct spectra for telluric absorption. We describe the different types of the existing methods and the differences between them in Sect. 2, where we also describe our method and how it fits into this typology. In Sect. 3, we describe the archive ESPRESSO data that we used for this study. Section 4 describes the steps toward the removal of telluric contamination from all exposures. In Sect. 5, we describe the classical CCF method, and explain how we constructed a new binary mask relevant to corrected parts of the spectrum. In Sect. 6, we describe our results when the CCF technique is applied to various parts of the spectrum, and show how we quantified the improvement in RV retrieval precision. In Appendix A, we describe the method used to estimate the uncertainties on RVs as a function of photon noise and spectrum quality, and how uncertainties derived in this way compare with our results. Finally, a comparison of radial velocity fluctuations seen with the blue arm and the red arm of ESPRESSO is presented in Sect. 7, followed by conclusions.
 |
Fig. 1 Binary masks (left scale) and telluric lines (right scale). Black bars represent the contrast (relative depths) of the stellar lines of the standard K2 binary mask BM1 used in the ESPRESSO pipeline. Red bars show the contrast of the newly added lines forming the mask BMc. TAPAS telluric H2O and O2 transmission spectra are shown in blue and green, respectively. |
 |
Fig. 2 Number of stellar lines per order from the standard BM1 (black) and the augmented binary mask BM2 = BMl +BMc (red) restricted to the lines used in our study that have a contrast of ≥0.2. For the red arm, the new mask contains 724 more lines than the 1060 lines of the original mask (Table 2). |
2 Overview of telluric correction existing techniques
One prominent technique is the division of each spectrum by the spectrum of a fast-rotating star (the so-called telluric standard) observed as close as possible in time and direction to the science target. This method has the disadvantage of requiring substantial additional observing time and the spectrum is affected by features present in the standard star. It is well adapted to multi-object spectrographs; in this case a number of fibers are devoted to the telluric target stars, but it is not well adapted to high-precision radial velocity measurements. A second, data-driven category of techniques builds on a series of auxiliary observations. Among these, Artigau et al. (2014) used a series of hot, fast-rotating stars to construct libraries of empirical telluric absorption spectra and performed a principal component analysis (PCA) of the dataset. These authors showed that the simultaneous adjustment of the first five principal components of an observed star spectrum allows them to obtain a good correction, to extend the spectral domain for RV extraction, and to increase the RV accuracy. More recently, Leet et al. (2019) used a series of fast-rotator spectra observed in various different humidity conditions to empirically extract the whole series of water vapor lines, including the very weak, microtelluric absorptions. Bedell et al. (2019) developed a modern, sophisticated method of learning template spectra for stars and telluric absorptions directly from the data, a method adapted to a series of observations of cool stars covering sufficiently wide Doppler shifts between the stars and Earth. Recently, Cretignier et al. (2021) developed a PCA on a spectral time series, using prior information to disentangle contaminations from real Doppler shifts, that is, to eliminate both instrumental systematic errors and atmospheric contamination.
A third category of telluric decontamination relies on realistic atmospheric transmission spectra. Extremely detailed models of the global atmosphere and of time- and location-dependent atmospheric profiles are now available, the most detailed being the Global Data Assimilation System (GDAS) and the European Centre for Medium-Range Weather Forecasts (ECMWF). These give the altitude distribution of pressure, temperature, and H2O concentration. Several tools have been constructed over recent decades to compute the resulting transmission spectra based on these profiles and the HITRAN molecular database (Rothman 2021; Gordon et al. 2017). The MolecFit facility developed by Smette et al. (2015) and the Telfit tool by Gullikson et al. (2014) make use of GDAS atmospheric profiles, while the TAPAS online service (see Bertaux et al. 2014) is extracting vertical profiles from the ECMWF. Both MolecFit and TAPAS use the state-of-the-art Line-By-Line Radiative Transfer Model (LBLRTM) code and the HITRAN database to compute the atmospheric transmission. Telfit and MolecFit also include software allowing users to correct spectral observations based on fits of the atmospheric transmission to the data, by adjusting the wavelength solution, a polynomial continuum and molecule abundances. To do so, MolecFit automatically retrieves the atmospheric profile at the time and place of the observations from an ESO repository. The advantage of this third category is the lack of a requirement for additional measurements and the adaptability of the methods to any instrument or observatory.
Very recently, Allart et al. (2022; hereafter A22) presented a fourth type of method for correcting stellar spectra from telluric absorptions. Similarly to the previous techniques, A22 use the HITRAN spectral data base to compute the transmittance of H2O and O2; however, instead of a worldwide time-variable grid of detailed atmospheric altitude profiles, the authors model the atmosphere as a single layer, characterized by a unique pressure p, unique temperature T, and a global H2O column. The line profiles are less accurate, because the resulting atmospheric transmission does not take into account the different widths that correspond to different altitudes, contrary to the realistic atmosphere, but the advantage of this technique is the absence of a dependence on a meteorological field. A22 adjust p, T, and H2O abundance by piling up 20 H2O lines in a CCF.
Our work enters into the third category. Here, for the model of the Earth’s atmosphere and the simulated transmission spectra, we used the TAPAS facility (Bertaux et al. 2014). TAPAS2 is a free online web service that simulates with exquisite detail the atmospheric transmission spectra due to the main absorbing species as a function of date, observing site, and either zenith angle or target coordinates. TAPAS uses the ESPRI/AERIS ETHER (a French Atmospheric Chemistry Data Center) facility to obtain pressure, temperature, and constituent vertical profiles of the ECMWF, which are refreshed every 6 h. These are used to compute the atmospheric transmittance from the top of the atmosphere down to the observatory in each of 137 altitude layers based on the HITRAN database and LBLRTM (Clough & Iacono 1995; Clough et al. 2005). For each species and each altitude layer, the local temperature and pressure are used to compute air- and self-broadening as well as pressure line shift for each HITRAN transition. The basic mode gives access to spectra with wavelength grid steps on the order of 1 mÅ (R ≃ 5 × 106), and the transmission spectra may be obtained separately for individual gases. TAPAS does not include correction tools and serves as a basis for line identifications or for various post-processing correction techniques. For example, Artigau et al. (2021) used TAPAS for a first data-model adjustment followed by a refined PCA-based correction for residuals. Bertaux et al. (2014) describe the TAPAS product, a synthetic atmospheric transmission spectrum for the time, place, and direction of any astronomical observation. These authors mention a potential application to the RV method of exoplanet searches, and a way to adapt the H2O quantity of the model to a real observation is briefly outlined; this latter makes use of TX(H2O), which is the model transmission T(H2O) elevated to the power X, which can be determined by comparison with the observed spectrum. In the present paper, we put the method sketched out in this latter paper into practice.
3 Data
3.1 Brief description of the ESPRESSO spectrograph
The new-generation spectrograph ESPRESSO was chosen because of its high resolution, its excellent wavelength calibration, and, in particular, its impressive stability and the quality the data it provides. Indeed, ESPRESSO can achieve a precision on measurements of 30 cm s−1, as reported in Pepe et al. (2021). These latter authors present a detailed description of the spectrograph, as well as an assessment of its performance. Installed by ESO at the Paranal observatory, the ESPRESSO spectrograph can be coupled to either one of the four VLT telescopes using optical fibers. It is an echelle-grating spectrograph with cross-dispersion installed in a vacuum chamber. It covers the wavelength range from 378.2 to 788.7 nm divided in two arms with two different detectors. We used the High Resolution mode, which provides a resolving power that varies between ≃100 000 and ≃160 000 depending on the position on the detectors. In this mode, an image slicer is used, which provides two images of the same echelle-grating physical diffraction order. All the useful parts of the spectra are numbered from 0 (start of the blue arm) to 169 (end of the red arm), and are called «orders» in the official nomenclature of ESPRESSO (used throughout this paper); not to be confused with true echelle-grating diffraction orders. In this nomenclature, one even-number order is followed by an odd-number order with the same wavelength coverage (due to the image slicer). The ESPRESSO processing pipeline has several versions of outputs. We selected the ES_S2BA-type data, that is, one spectrum per order, without flux calibration, not corrected for blaze function, with 9111 spectels in the red and 6541 in the blue. We used the wavelength assignment of each spectel in the laboratory system in which the telluric line absorption system should be fixed (except for the local wind). The blue arm contains orders 0 to 89 and covers the range 3781-5251 Å, while the red arm contains orders 90–169 and covers 5195–7908 Å. The intensity for each spectel is given in adu (analog to digital units). The electronic gain that was used for the archive data discussed here is ≃0.9 electron/adu.
3.2 Selected data
We used ESO VLT/ESPRESSO spectra of the K2.5V star HD 40307 (V = 7.1). The star has a mean radial velocity of ≃31.3 km s−1 and at least four discovered exoplanets with periods from 4.3 to 197 days (Díaz et al. 2016). The target star HD 40307 was chosen for two main reasons: first, detailed measurements of radial velocities of this target with ESPRESSO were obtained as part of an asteroseismological campaign on the star3. The results of the full campaign are presented by Pepe et al. (2021).
Second, the ESO archive makes available all 1150 spectra of this star recorded over 5 nights. Here, we made use of the set of 200 consecutive exposures taken during one single night from 24 to 25 December 2018. The exposure time was set to 30 s for all data. The reason for the choice of such short and frequent observations by the proposing team was the attempted detection of stellar activity, namely p-mode oscillations. For the present study, this exceptional dataset of a very large number of exposures in a single night is ideal. First, the number of exposures is high enough to perform statistics on the RV measurements. Second, the total duration corresponds to ≃240 m s−1 Doppler-shift variation of telluric lines with respect to stellar lines, which is a sufficiently large value to detect potential effects of the telluric correction on the absolute value of RV. Finally, the total duration of 4.3 h for the 200 selected exposures is too short to correspond to a detectable RV variation for the exoplanet given its period of 4.31 days, especially for the sequence of that particular night, which corresponds to a maximum-velocity region (data points around phase 130 in Fig. 25 of Pepe et al. 2021) and to an RV variation of less than a few tenths of a m s−1. Because one criterion with which to verify the validity of our telluric correction is to check that the retrieved RV is constant over the period of observations, this is an important aspect.
We used the fully reduced spectra from the ESPRESSO pipeline. For each spectral order, the data are given separately for each of the two parts of the image slicer and we used these distinct spectra as if they were individual orders (e.g., orders 154–155 in the following sections correspond to a unique spectral order and the two images of the slicer). For RV measurements, all available spectra are shifted to the barycentric frame. For the purpose of telluric correction, we also used recorded spectra with a wavelength scale in the laboratory frame (see Sect. 4).
4 Correction of the data from telluric absorption
4.1 Principle of the correction
The main steps of the correction are as follows:
- (1)
First we construct a binary mask that eliminates stellar lines in order to let telluric lines only (hereafter referred to as the BMT). This mask is equal to 1 in spectral intervals free of stellar lines and zero elsewhere. It can be considered as a kind of complementary mask to the BM. This mask is constructed for the orders that are used in the next step.
- (2)
We then determine the atmospheric H2O and O2 columns present during each of the 200 exposures. These are obtained by fitting TAPAS synthetic atmospheric spectra in unmasked regions of specific appropriate orders. We checked that H2O and O2 are the two dominant gases in the wavelength range of ESPRESSO and that other atmospheric constituents produce negligible absorption.
- (3)
We then compute the product of the two H2O and O2 transmission spectra for each exposure and for all orders contaminated by tellurics using the previous results for the absorbing columns. The resulting transmission spectra are convolved by the appropriate order and wavelength-dependent ESPRESSO point spread function (PSF).
- (4)
Finally, we divide the contaminated data by the computed transmission spectra.
4.2 Preparation of the binary mask eliminating stellar lines
Telluric corrections are relatively easy in the case of hot stars. Their spectra are featureless and one can fit data directly to the product of a continuum and one or several atmospheric transmission spectra to adjust the columns of absorbing gases, the telluric line Doppler shift, and the PSF. The data are divided by this adjusted synthetic transmittance. For colder stars, this simple procedure is often not applicable because of the huge number of stellar lines. HD40307 is relatively cool with a temperature of ≃4980 K. However, we took advantage of its low metallicity of ≃−0.3 and the high resolution of ESPRESSO, resulting in lines narrow and weak enough to allow us to distinguish between tellurics and stellar features in some spectral regions where the former are separated from the latter, and to allow stellar continuum fitting, as in those regions the stellar continuum is well recovered between the lines. This means that, in such regions, it is possible to mask the stellar lines and fit the spectral regions free of stellar lines to atmospheric transmission model spectra.
The masks were constructed based on a semi-automated comparison between three spectra: a high-S/N spectrum of the star obtained by stacking ten consecutive exposures; a TAPAS transmission of atmospheric H2O and O2 adapted to the Paranal site and to the date of observations; and a stellar synthetic spectrum computed for a set of values of temperature, metallicity, and gravity adapted to those of HD 40307. This allows us to select areas that are devoid of non-negligible stellar lines and where telluric lines are dominant. Three masks were built for orders 130–131, 146–147, (for O2 lines) and 154–155 (for H2O lines), respectively. These can be seen in Figs. 3 and 4. The masked intervals are listed in Table 1.
4.3 Determination of H2O or O2 columns
Telluric lines vary during the night in response to airmass evolution along the line of sight to the star and also variations of atmospheric constituents. In particular, water vapor is highly variable and may change on timescales as short as a few minutes. Therefore, it is mandatory to measure the evolution of H2O and O2 during the series of measurements in order to obtain a good correction.
The individual exposures were divided into sections of about 2 nm and each section was fitted in the unmasked regions to a product of a second-order polynomial to represent the stellar continuum and a telluric transmittance convolved by a Gaussian PSF. The free parameters are the O2 (for orders 130–131 and 146–147) or H2O (for orders 154–155) columns and the coefficients of the second-order polynomial. The telluric transmittance varies as a power law of TX(H2O), (respectively TX(O2)) where the factor X is proportional to the H2O (respectively O2) column (Bertaux et al. 2014). During the fitting procedure (which makes use of the Levenberg–Marquardt convergence scheme), the resolving power (and its associated Gaussian PSF) was fixed to a single value for the whole order estimated from Fig. 11 of Pepe et al. (2021). Examples of fits are shown in Figs. 3 (and 5) and 4 for the first exposure. The results for the various chunks are averaged along a full order to obtain H2O or O2 column temporal evolutions.
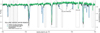 |
Fig. 3 Illustration of the procedure used to determine the H2O column for each exposure (here exposure 0 and order 154) and the telluric H2O removal. The mask of stellar lines, i.e., the BMT, is shown as a black dashed lines. The data and adjusted TAPAS transmittance are shown in black and light blue, respectively. The division of the data by the fit is shown in green. The correction works for isolated telluric lines and also for blended telluric and stellar lines (e.g., at 7240 A; see Fig. 5). |
 |
Fig. 4 Illustration of the procedure used to determine the O2 column for each exposure (here exposure 0 and order 130). The BMT is shown as a black dashed line. The normalized data and the fitted TAPAS transmission are shown in black and green, respectively. The division of the data by the fit is shown in blue. |
4.3.1 H2O temporal evolution
The value of reference for the column chosen in the fitting procedure and the corresponding transmission spectrum were chosen as follows. We started with the spectrum predicted by the TAPAS website for the first exposure (25 December 2018, 00:24:00 GMT). The corresponding water vapor vertical column indicated by TAPAS COL(T) does not correspond to the column COL(P) estimated locally thanks to the infrared radiometer installed at Paranal, which continuously monitors the night sky and estimates this vertical column of H2O in mm of precipitable water vapor. This information is included in the header of each exposure. This difference is not surprising given the strong temporal and local variability of the humidity and the fact that TAPAS interpolates temporally within ECMWF meteorological models refreshed every 6 h and spatially within nodes that may be distant with respect to the spatial scale of the variability. We used the two values to adapt the spectrum to the Paranal conditions by elevating it to the power of the ratio COL(P)/COL(T) and attributed a coefficient X = 1 to this reference spectrum.
The variation of the average fitted H2O column for the 200 exposures is shown in Fig. 6. It is the product of the reference column COL(P) by the fitted coefficient X. It is compared with the vertical column estimated at Paranal. The comparison shows that the adjusted column of H2O correlates well with the estimate from the infrared radiometer; in particular both have a similar amplitude of variation of about 15% and a similar time for minimum column. They also have very similar absolute levels, showing that the chosen reference was appropriate. More precisely, the fitted value for the first exposure is X = 0.93, which is not exactly 1 but is of the same order. During some time intervals, the values deduced from the spectral adjustment differ slightly from the on-site measurements. This is probably due to the sensitivity of the radiometric data to parameters other than the molecular column. In the subsequent correction for H2O lines, we made use of the ESPRESSO spectral measurements that are the most direct.
4.3.2 O2 temporal evolution
The retrieved O2 column in the line of sight (LOS) is shown in Fig. 7. The chosen transmission spectrum of reference for the first exposure is exactly that predicted by the TAPAS website and was attributed a reference value X = 1 in the fitting procedure. The results of two series of fits are displayed, one for the order 130, which contains part of the O2 γ band near 630 nm, and one for order 146, which contains part of the O2 B band near 688 nm. Also shown is the evolution of the airmass for all exposures, as indicated in the headers. It can be seen that both fitted values follow the temporal evolution of the airmass very closely, which is expected. A small difference can also be seen between the two determinations. The γ band provides a more noisy determination but at the exact expected level (X=1 for the first exposure, which happens if the fitted column is exactly the reference value for the O2 column of this exposure). The B band provides a less noisy determination, but with a small relative difference of about 3%. The reason for this small discrepancy is unclear. It is not likely to be a cross-section error in the HITRAN database. It might be due to small differences between the modeled and actual atmospheric profiles, or, more likely, to a lack of precision in the modeled PSF, in particular departures from the Gaussian approximation. In view of these results, we decided to use the B band result for the absolute value of X during the subsequent telluric-line removal, because the B band lines are stronger, and for the temporal evolution we chose to use quite simply the airmass as the multiplicative factor for the O2 vertical column.
Stellar mask for orders 130/131, 146/147, and 154/155.
4.4 Correction for telluric lines based on the H2O and O2 adjusted columns
The next and final step of the correction procedure is, for the full wavelength range, the division of the data by a synthetic transmission computed for each exposure for the adjusted H2O and O2 values and adapted to the instrument resolution in an optimal way. The spectral resolution is not constant along an order and from one order to another, as is well known. Fortunately, the information on the resolution is available from Fig. 11 of Pepe et al. (2021). We digitized this figure and the associated color scale and derived the spectral resolution as a function of order and wavelength. The resolution for the three orders used for the O2 and H2O estimate are displayed in Fig. 8, showing variations with amplitudes of approximately 15% along an order. We used the results of this digitization to convolve the atmospheric transmission by the correct wavelength-dependent resolution, that is, taking into account the true PSF for each order and each wavelength. The last operation, namely the division of the data by the convolved synthetic transmission, is not fully mathematically correct. In principle, the recorded spectrum should be de-convolved first, and then divided by the transmission, and the result of the division should be re-convolved (Bertaux et al. 2014). However, for a high resolving power, the first simplified approach is a good approximation. Examples of the divisions are shown in Figs. 3, 5, and 4 for H2O and O2.
For the whole correction, we assumed an exactly Gaussian PSF and only varied its width according to the wavelength and the order. We did this for the following reasons. First, in the case of hot stars with smooth continua, it is possible to deconvolve isolated telluric lines to infer the PSF shape; however, here in the case of this Κ star, the result of the deconvolution would be somewhat hazardous. Second, there are no indications of departures from a Gaussian shape in the ESPRESSO documents and, to our knowledge, no mention of departures in articles based on ESPRESSO data. Third, and most important, significant departures would introduce features at the locations of the wings of the corrected lines that would repeat along all lines, and be especially strong for a deep absorption; we did not notice any specific, repetitive shape in the residuals in the wings that would indicate such departures. On the contrary, the residuals, when present, do vary from one line to another.
 |
Fig. 5 Zoom onto Fig. 3. Even stellar lines heavily contaminated by H2O lines may be kept for RV retrieval after correction from an adjusted telluric transmission. The BMT is shown as a black dashed lines. |
 |
Fig. 6 Comparison between the vertical column of water vapor adjusted through spectral fitting (black curve) and the column estimated from the infrared monitor at Paranal (in red) for the 200 consecutive exposures. |
 |
Fig. 7 Comparison between the column of O2 adjusted through spectral fitting of the Β band and the γ band (black and red curves) and the air mass (green curve). The retrieved columns of O2 follow the air mass relatively well, which means that, unlike the H2O variations, there is no significant variation of the O2 vertical column. |
 |
Fig. 8 Spectral resolution as a function of pixel number based on the digitization of Fig. 11 of Pepe et al. (2021). Shown are three examples for three orders of the red arm. |
5 Standard and extended binary masks to be used in the classical cross-correlation function method
In order to quantify the quality gain obtained by correcting the spectra from telluric absorptions, we need to compare the retrieved RVs with exactly the same algorithm, applied either to the noncorrected data (i.e., the wavelength regions not contaminated by tellurics), and to the corrected data (including wavelength regions corrected for tellurics). There are several types of RV-retrieval algorithm, but for our purpose we do not need to use the absolute best one, as long as we use exactly the same one for the two cases.
The historical and classical approach of RV retrieval is the CCF with a binary mask (Baranne et al. 1996; Pepe et al. 2002), which is used in the official ESPRESSO pipeline for the official RV retrieval. This approach has the advantage of being robust. One of the recent papers describing this method in detail is Lafarga et al. (2020), from which we borrowed some details when coding our own version of this algorithm.
For processing the non-corrected data, we used the standard binary mask of ESPRESSO corresponding to the spectral type K2.5 of HD40307. This mask is made of a series of wavelengths in air and the relative depth of the star line (called the contrast), which is represented in Fig. 1 as a function of wavelength. When compared to the model transmission computed by TAPAS (Fig. 1), it is clear that this standard binary mask is avoiding regions seriously contaminated by atmospheric H2O and O2 lines. We selected all the lines of the standard mask with a contrast of >0.2, which constituted the BM1 mask that was used to process the noncorrected data. A second mask, BM2, was built by adding a series of new lines to the BM1 mask, specifically in regions contaminated by telluric absorption, constituting the mask BMc. There are many orders where there were no lines in BM1: 118, 136, 148, 150, 152, 154, 156, and 164 (and their odd number twins). In order to find the new lines of BM2 = BM1 + BMc, we stacked together the 200 spectra after telluric correction, and to this stacked spectrum we assigned the wavelengths of exposure number 100 in the reference frame of ESPRESSO. Then, for a set of observed stellar spectral features, we determined the precise wavelength (using a Gaussian fit) of the minimum and kept those lines that had a contrast of >0.2. In Fig. 2, we plot the number of lines per order for the two masks BM1 and BM2 as a function of order number. For some orders (116–123, 128–148, 158–159), the number of lines from BM1 was not zero but small; the lines were kept for BMc but their wavelengths were also taken from the stacked spectrum (after telluric correction). Table 2 lists the numbers of the initial lines (BM1), the additional selected lines (BMc), and the total lines of the binary mask. There is only one more line for the blue arm, and 724 more lines for the red arm, added to the 1060 lines of the original mask BM1. For the analysis of the time series of measurements, we dropped the last six orders (A band of O2 and weak signal); the selected orders for the red arm contain 696 lines more than the 1050 lines of BM1. The gain in RV measurement precision is entirely due to the use of those 696 extra lines of the BMc mask. Table 3 lists the BMc lines for order 130. The full list of additional lines will be made available on request.
Figure 9 shows the order 130 of the stacked spectrum, as well as the TAPAS model transmission and the position of the lines represented by vertical bars of different colors for BM1 and BMc. This order is contaminated by the γ band of di-oxygen O2, and as a result there are only three lines in this order in the BM1 mask (position indicated by vertical red lines at the bottom). We found 33 more lines for the BMc lines (vertical blue lines), giving a total of 36 lines for this order.
Figure 10 is a zoom onto Fig. 9 around a particular line at 6344.8 Å, which was already in BM1 and whose position is indicated by the black vertical line at the bottom of the figure. The blue line is the contrast (right scale) of the spectral line and is centered on the observed spectral line, which is displaced by a Doppler shift from the BM1 line. In order to allow it to serve as a line in a binary mask, we need to shift this new line back to a reference system with RV=0. Therefore, to carry out this back-shift we have to precisely select the RV of the star HD 40307. We chose Vrad0 = 31381.572 m s−1, as determined with the mask BM1 with orders 92–115. When this line is back-shifted, it comes to the position of the red vertical bar, very near the original BM1 line. All new lines from the telluric-corrected stacked spectrum were back-shifted by the same stretch factor (the Doppler shift is actually a stretch) to constitute the mask BMc, and this was added to BM1 to form BM2.
In Fig. 11, we show the extreme case of the order 146, which is heavily contaminated by the O2 Β band. The correction is poor at the location of the strongest absorption lines, and strong residual spikes are visible. A better correction would require a detailed adjustment of the exact shape of the PSF, which is beyond the scope of this work. This order is also characterized by a low number of stellar lines. We could also simply add 18 lines to the binary mask. To do so, we avoided the regions with poor correction.
In the CCF scheme adopted here, and described by Lafarga et al. (2020), each order is treated separately. The CCFs of all the lines of one order are added together with a weight attached to each line. The total CCF is then fitted by a Gaussian whose central position (the minimum) is the radial velocity for this order. The uncertainty σord attached to this determination is that returned by the Gaussian fit routine. Once the RVs for each order are determined, they are averaged together, accounting in a standard way for their uncertainties: the weighted average with 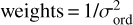 , and the error for the exposure σexp, such that
, and the error for the exposure σexp, such that 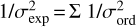 .
.
While Lafarga et al. (2020) took the ratio contrast/width as a weight attached to each line of a BM, we took only the contrast of each line as its weight for its CCF. We did this because the mask BM1 contains only the contrast and not the width. As we wanted to use exactly the same algorithm for comparing the RV results with BM1 and BM2, we were forced to use only the contrast for the two cases. We carried out a limited comparison with the two versions of the weight: either the contrast only, or the contrast/width. We find a very modest decrease (2.9%) in the uncertainty in the latter case and a ≃3% decrease for the spread of all RV measurements (standard deviation) among the series of 200 exposures. Therefore, while clearly it would be slightly better to use the contrast/width weight, using only the contrast will not be detrimental for the comparison between the use of BM1 applied to original spectra and BM2 applied to telluric-corrected spectra.
The CCF of one line of the BM with one observed line is done by computing the signal contained in a boxcar centered on the BM line, and displaced by a variable RV (by steps of 492 m s−1, the mean size of one spectel) around the observed minimum. Following the recommendation of Lafarga et al. (2020), we chose to use a boxcar width of approximately one spectel of the observed spectrum. As a result, the CCF is very similar to the observed line, because both the boxcar width and the step of the RV grid are of the size of one spectel. This method also has the advantage of providing independent points of the CCF. Indeed, the Gaussian fit algorithm used in Igor language (but this is the same for most coding languages used to code the Numerical Recipe library, Press et al. 1992) assumes that all points to be fitted are independent, and the error bars returned by the fit routine rely on this hypothesis. This would not be the case if the boxcar width was larger than one pixel, or if the RV grid step was smaller than one spectel. We find that one important parameter of the Gaussian fit to the total CCF for one order is the number of CCF steps over which the CCF is fitted, because we find that the exact position of the CCF minimum depends substantially on this number; it was fixed to ten points in all the presented results.
The blaze effect is relatively conspicuous in Fig. 9. We did not attempt to correct the blaze before performing the CCF. When fitting a tilted (from constant) signal, any blaze introduces a bias on the position of the minimum. However, we determined that with the observed slopes due to the ESPRESSO blaze, the bias does not exceed about 12 m s−1. This systematic bias is constant along all exposures for one particular line and does not increase the spread of all measurements, nor the (shot noise associated) uncertainty on RV. Furthermore, being of opposite sign on the two sides of the order, the two biases approximately compensate for one another when performing the CCF for a full order. Also, we find out that for some lines of the BM1 mask (probably those determined from laboratory measurements of transitions), the bias is much larger – of the order of ≃100 m s−1 - due to convection and granulation, as pointed out by González Hernández et al. (2020), which is therefore much larger than the biasing blaze effect.
There are several adjustable parameters in this CCF algorithm (as described above), and therefore, for each exposure, we do not expect to find exactly the same RV value as the one contained in the archive product of HD 40307 (for which the exact values of the parameters are different from ours and are unknown to us). However, this is not our objective. Our purpose is to compare the RV series results obtained with BM1 and BM2 with exactly the same algorithm and its parameters. Also, we have not used all the lines of the original mask, keeping only those with a contrast larger than 0.2.
As suggested by our reviewer, we also computed another estimator of the error on RV based on a quality factor and photon noise as first devised by Connes (1985) and revived by Bouchy et al. (2001). To do so, we used the approach from Boisse et al. (2010), in which the authors consider a CCF for one order as an averaged noise-free spectral line. This provides an estimate of the minimal error. We detail this approach and present our calculations in Appendix A.
Number of lines in the binary mask.
Binary mask lines for order 130/131.
 |
Fig. 9 Augmented mask of order 130. The intensity of the stacked spectrum (high S/N) after correction of telluric absorption is shown in black (left scale). The atmospheric transmission computed from TAPAS (green, right scale) displays the γ band of O2. The original binary mask BM1 contains only three lines, whose wavelengths are indicated at the bottom by red vertical bars. These lines avoid the O2-contaminated region. A new Binary Mask BM2 containing 36 lines is made from the observed stacked spectrum with stellar lines whose depths are ≥0.2. The wavelength assigned to the stacked spectrum is that of exposure number 100, in the middle of the series of exposures. The three red lines of BM1 are seen shifted to the left from their blue-line counterpart detected in the stacked spectrum. |
 |
Fig. 10 Adjustment of the two masks. The vertical blue line gives the wavelength position of the center of one stellar line of the observed spectrum, after telluric correction and stacking of all exposures. Its height is the contrast of the line (relative depth, 0.64). The red line represent the same line, back-shifted to account for the radial velocity Vrad0 of the star. The velocity Vrad0 was determined with the original mask BM1 and data from orders 92–115. As a result, the position of the red line coincides well (but not perfectly) with the corresponding line of the original BM1 mask (vertical bar, bottom). |
 |
Fig. 11 Same as Fig. 9 for order 146, which is heavily contaminated by deep, narrow lines of the O2 B band. The corrected spectrum exhibits conspicuous residuals (see text) at the location of the strongest absorption; however we were able to add 18 lines in the new mask in addition to the initial three lines. |
6 Results
In this section, we show a series of comparisons between two separate applications of the CCF code. On one hand, the code is applied to the uncorrected data on the basis of the standard binary mask BM1. On the other hand, it is applied to corrected data on the basis of the combination BM2 of the standard mask and the newly created mask. We show three different cases: relatively straightforward H2O correction (116–117), less straightforward O2 correction (γ band, orders 130–131), and the more difficult case of the O2 Β band (orders 146–147).
 |
Fig. 12 Radial velocity of star HD40307 for order 130, which is contaminated by O2. The result with the standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 372.4 and 31 384.2 m s−1 were subtracted from the series before and after correction, respectively. |
 |
Fig. 13 Radial velocity of star HD40307 for order 116, which is contaminated by H2O. The result with the standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 386.4 and 31 388 m s−1 were subtracted from the series before and after correction, respectively. |
6.1 Order 130 contaminated by O2
The order 130 (λ ≃ 6316 Å) and its twin order 131 are contaminated by the γ band of O2 (Fig. 9). Only three lines are contained in the official BM1 of ESPRESSO, while our new mask BM2, as described above, contains 38 lines for this order.
Figure 12 compares the RV measurements (for the whole series of 200 exposures) coming from our CCF algorithm before correction and after correction of tellurics. The average (over time) of RV has been subtracted from the whole series in order to ease the comparison of the dispersion. In principle, we should find a constant signal over the ≃4 h of measurements. We see by eye that the signal is approximately constant on average. Both the error bars and the spread of measurements (fluctuations, quantified by the standard deviation Sdev) are very much decreased with the telluric-corrected data. Quantitatively, the average error bar of this order over the 200 measurements is reduced from 22.5 to 5.3 m s−1 for the new mask, while the spread of RV measurements Sdev is reduced from 35.4 to 7.0 m s−1. This is of course a somewhat extreme example of what can be gained by the addition of new portions of star spectra once they are corrected for tellurics. Independently of this improvement, the constancy of the RV value over the exposures constitutes an additional test of the telluric correction.
6.2 Order 116 contaminated by H2O
Similarly, the order 116 (λ = 5891Å) and its twin order 117 are contaminated by the blue end of a region contaminated by H2O lines (Fig. 1). BM1 contains only 5 lines, while BM2 contains 20 lines for this order.
Figure 13 compares the RV measurements before correction and after correction of tellurics. Again, the time-averaged RV has been subtracted. The average error bar of this order is reduced from 12.8 to 7.1 m s−1 for the new mask, while the spread of RV measurements Sdev is reduced from 20.5 to 9.6 m s−1. The vertical scale of RV covers the same extent of 260 m s−1.
Figure 14 is identical to Fig. 12, but for order 146, which is heavily contaminated by the strong O2 Β band (see Fig. 11). We include this order as an extreme case because a number of telluric lines are saturated before convolution by the PSF and there are strong residuals. As mentioned above, a better correction would require a specific determination of the exact shape of the instrumental PSF, which is beyond the scope of this work. The standard binary mask contains only three stellar lines, while our binary mask created after telluric correction contains 18 stellar lines. Here, the spread decreased from 47 m s−1 to 32 m s−1. However, the formal error increased from the rather high value of 21 to 25 m s−1, a somewhat puzzling result. We note a similar behavior for order 144, which is not contaminated by telluric absorption.
 |
Fig. 14 Radial velocity of star HD40307 for the extreme case of order 146, which is heavily contaminated by O2. The result with the standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 386.4 and 31 388 m s−1 were subtracted from the series before and after correction, respectively. |
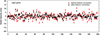 |
Fig. 15 Radial velocity of star HD 40307 for orders from 90 to 163. The result with standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 382.5 and 31 384.4 m s−1 were subtracted from the series before and after correction, respectively. |
6.3 Red arm
Figure 15 compares the series of RV measurements when the orders of the red arm are combined, with a weight of 1/err2 where err is the formal error returned for each order. We note that the red arm contains the orders 90–169, while we kept only orders 90 to 163, dropping the four orders 164–167 which are heavily contaminated by the strongest A band from O2, and contain saturated lines. Moreover, the last orders 168–169 are characterized by a low signal. The vertical scale of RV covers a 40 m s−1 full extent.
The average error bar of this red arm is reduced from 1.04 to 0.78 m s−1 for the new mask BM2 (Table 4). If we use the photon-noise estimation on the CCF (see Appendix A), the error bar decreases from 0.89 to 0.72 m s−1, a reduction factor of 1.24. As discussed in the Appendix, the difference is due to our choice of using ten points of the CCF instead of the CCF in its entirety. Therefore, it is likely that the photon-noise estimator is more robust than the ten-point Gaussian fit. For both cases, this gain is entirely due to additional photons from the 696 new stellar lines from BMc included in the spectral regions made available by the telluric correction. The spread of RV measurements Sdev is reduced from 2.83 to 2.37 m s−1 (see Table 4). The reduction of the spread, by a factor of 1.19, is slightly smaller than the reduction of the formal error, which is reduced by a factor of 1.33.
CCF statistical results.
 |
Fig. 16 Radial velocity of star HD 40307 for orders from 40 to 163. The result with standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 386.9 and 31 385.9 m s−1 were subtracted from the series before and after correction, respectively. |
6.4 Red+Blue arms
Finally, we performed the same comparison as above for a combination of red and blue arm data. More precisely, we combined data for orders 40 to 163 coming from both arms. Orders below 40 were dropped because of a very low signal for this K2.5 star. The comparison is shown in Fig. 16. The average error bar of blue+red arms is reduced from 0.77 to 0.64 m s−1 for the new mask BM2, while the spread of RV measurements Sdev is reduced from 3.53 to 2.59 m s−1 (see Table 4). The vertical scale of RV again covers a 40 m s−1 full extent. The reduction of the spread, by a factor of 1.36, is slightly larger than the reduction of the formal error, which is reduced by a factor of 1.20.
6.5 Absence of an RV trend in the RV time series
Figure 17 compares four time series of RV measurements: (1) The original RV measurements found in the archive (similar to Fig. 21 of Pepe et al. 2021). (2) The RV measurements from our processing after telluric correction restricted to blue orders (from 40 to 89, λ from 4319 to 5206 Å); this determination is almost identical to our processing of data not corrected for tellurics (not shown here). (3) Our RV measurements after telluric correction restricted to red orders (from 90 to 163, λ from 5195 to 7504 Å), and (4) the RV measurements after telluric correction for a combination of blue and red orders. All curves were obtained after subtraction of their mean value, and are plotted on the same scale. We recall that we did not do any filtering and used a threshold for the contrast, and for this reason we do not obtain the same final result for each RV point as Pepe et al. (2021). All the time series show a constant value, with some fluctuations, as discussed further in Sect. 7. A linear fit to the red arm RV values indicates a change of RV (a drift) of less than 0.064 m s−1 (the error bar encompasses 0), while the BERV had a change of 240 m s−1 over the whole series: the telluric system of lines has moved with respect to the star system of lines by this amount along the time series. The fact that there is no measurable trend over the time series is a serious indication that the telluric system has indeed been well removed from the telluric-corrected spectra. Unfortunately, the time series that we analyzed covers only 240 m s−1, while the BERV could change by ≃30 km s−1, corresponding to a maximum drift of 8 m s−1. The campaign of HD40307 observations covered only a limited excursion of BERV and we cannot significantly improve on this with this campaign. However, Allart et al. (2022) indeed showed on Tau Ceti that possible drifts due to uncorrected remnants of tellurics are smaller than ≃0.2 m s−1 over a large BERV excursion (±28 km s−1, their Fig. 12) in the case of their correction technique. As we perform an accurate computation of the atmospheric transmission (by taking the whole p-T vertical profile into account instead of a monolayer) and are using the same HITRAN molecular database, we may not expect our atmospheric correction scheme to produce more drift. The study of the exact amount of drift is an interesting subject, but is beyond the scope of this paper; it would require another target, because the planetary orbits are not yet known with enough precision to detect drifts on the order of 0.2 m s−1.
 |
Fig. 17 Temporal and BLUE-RED dependence of the measured RV. Top blue graph: RV measurements from our processing after telluric correction restricted to blue orders. Top red graph: Same for the red orders. Bottom purple graph: Combination of blue and red orders above. Bottom black graph: RV measurements reported by Pepe et al. (2021). |
7 Temporal and wavelength dependence of radial velocity fluctuations
During our analysis, we discovered the presence of RV signal fluctuations, as previously mentioned in Pepe et al. (2021). What we refer to as jitter here is these rapid fluctuations of the RV signal, with amplitudes far above the formal error, without hypothesising as to the physical nature of the cause of this jitter. The existence of the time series of 200 exposures of the star HD 40307 offers the opportunity to identify some time periods where the dispersion of RV values is larger than usual (Fig. 17). In order to investigate these fluctuations further, we considered the blue and red arms of ESPRESSO data separately.
7.1 Temporal dependence
The difference in observed jitter between the blue arm and the red arm is striking. While the blue arm reproduces the time variation of the jitter presented in Pepe et al. (2021), with a sudden increase approximately after exposure 130, the red arm does not see such an increase. We divided the time series into two groups: a first group for exposures 0–99, and a second group for exposures 100–199. The change of the standard deviation Sdev from group 1 to group 2 is quite different for the blue arm and the red arm, as seen in Table 4. Quantitatively, going from group 1 to group 2, for the blue arm, Sdev increased substantially from 4.13 to 6.71 m s−1. At the same time, for the red arm, Sdev decreased (slightly) from 2.50 to 2.33 m s−1.
Our results in Fig. 17 imply that the fluctuations occur only on the blue detector. It is a little worrisome to see this dichotomy arriving between the blue arm and the red arm, because they have two different detectors, and because the telluric correction was mostly relevant to the red arm. Nevertheless, such a change in radial velocity detected by only one arm of the spectrograph is difficult to relate to stellar p-mode oscillations, because implied Doppler shifts of the stellar atmosphere would affect the RVs equally in the red and blue parts of the spectrum. Fortunately, our referee pointed out to us that until a major instrument intervention in May 2022, ESPRESSO had a blue cryostat thermal stability problem (Figueira et al. 2021). Therefore, this type of fluctuation (jitter), which affects only the blue arm that we have detected, is certainly mainly caused by the thermal instability of the blue detector, and is not related to the onset of p-mode oscillations. The fact that our separate blue arm and red arm measurements clearly reveal this behavior shows that our telluric correction, mostly applied in the red arm, does not introduce artefacts that would mask this difference in red and blue arm fluctuation levels.
 |
Fig. 18 Wavelength and temporal dependence of the observed RV. Top: standard deviation Sdev (black line) and formal error on RV measurements (red line) for each order from our processing, averaged over the first 100 exposures only. The ratio between the two quantities is shown in violet. Bottom: same as top but for the last 100 exposures. We note the high ratio found in the blue orders during the second half of the observational time, a sign of spurious jitter due to a blue cryostat thermal instability. |
7.2 Wavelength dependence
In order to refine the wavelength dependence of the jitter (to decipher whether or not it coincides with the blue arm only), the time series of retrieved RVs were also studied for each order separately. In particular, we examined the variation versus the ESPRESSO order of three variables: the mean (formal) error ‘err’ of the RV averaged over exposures, the standard deviation Sdev of the RV values among exposures, and the ratio Sdev/err displayed in Fig. 18 as a function of order number (equivalent to wavelength) and separately for the two groups of exposures. Our reasoning here is that, in the frame of the theory of Gaussian errors, the standard deviation Sdev should be equal to the mean error of a series of measurements. This would hold if the error were well estimated, and if the spectra were not changing (otherwise from shot noise), implying a constant retrieved RV (within shot noise limits).
We note in Fig. 18 that both the error and Sdev are changing for three reasons: the intensity of the spectrum in the order (shot noise), the number of masked lines for this order, and their depths (contrast).
However, the value of Sdev is systematically larger than the value of the error, with a strong correlation (from order to order) between Sdev and the error. There are usually two reasons for which the standard deviation is found to be larger than the mean error: either the error bar has been underestimated or there are time fluctuations (jitter) in the data superimposed to a constant mean RV value, or a combination of both effects.
It can be shown mathematically (with the theorem of the variance of a sum of independent variables X and Y) that Sdev may be related to the formal error and the jitter amplitude as
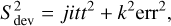 (1)
(1)
where jitt is the amplitude of the jitter (affecting the RV), and k is a factor by which the formal error is underestimated with respect to the true error. This factor k is likely valid at all times and all orders, because it is intrinsic to the retrieval algorithm.
For the second group of exposures (100–199), a dichotomy is observed between the left part (blue arm) and the right part (red part). The behavior of the right part is quite similar to the whole top curve (0–99), both for the correlation between error (RV) and Sdev, and the approximately constant value of the ratio around 1.41 (which is lower than for the first group, which is 1.55 for the red arm). On the contrary, for the blue arm, the Sdev curve is detached above the RV curve, there is no correlation between error(RV) and Sdev, and the ratio is much larger, with a mean of 2.67. Therefore, the jitter, which appears mostly during the second half of the series of exposures, happens only in all the orders of the blue arm.
As mentioned above, the explanation of this blue jitter is related to the instrument, and linked to thermal instabilities of the cryostat containing the blue detector. The smallest values of the ratio Sdev/err are found in the red arm for exposures 100–199 (Fig. 18). Let us assume that the jitter amplitude is the same for all red orders in this time frame. Figure 19 shows Sdev2 as a function of the squared formal error err2, each point representing one order from 92 to 169. After the exclusion of a few outliers, there is a clear linear relationship of the form a + bx, where the slope b = k2 is found to be 2. 1 ± 0. 07. This means that our formal error is underestimated (with respect to the true error) by a factor of ≃1.4.
Extrapolating the linear fit to err = 0, the value of 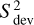 becomes equal to jitt2. This value is found equal to −8.6 ± 7m2 s−2. As a squared quantity cannot be negative, the jitter is likely weak, and undetectable in this portion of the spectrum and exposures 100–199.
becomes equal to jitt2. This value is found equal to −8.6 ± 7m2 s−2. As a squared quantity cannot be negative, the jitter is likely weak, and undetectable in this portion of the spectrum and exposures 100–199.
 |
Fig. 19 Linear fit of the scatter plot of |
8 Conclusions
We used an exceptional series of consecutive short exposures of the ESPRESSO spectrograph for a K2.5V type star to test and estimate the potential increase in precision of the RV measurement brought by telluric-line removal when this correction is based on a publicly available, location-, and time-matched atmospheric transmission spectrum and a simple and conventional fitting code to be performed locally.
We used theoretical transmissions of H2O and O2 downloaded from the TAPAS online facility and adjusted them to each exposure before dividing each recorded spectrum by this adjusted transmission. TAPAS conducts a high-quality computation of the telluric absorption based on the vertical T-P profile provided by the ECMWF meteorological field, the HITRAN spectroscopic data base and the LBLRTM code. To perform the adjustment of H2O and O2 columns, we took advantage of the characteristics of the target star, that is, a temperature of ≃4980K and a low metallicity of ≃−0.3, resulting in lines narrow and weak enough to allow easy stellar continuum fitting and distinction between tellurics and stellar features in some spectral regions. This process makes it possible to mask the stellar lines, adjust the telluric transmission in a very precise way, and divide the data by the adjusted telluric model, without direct use of a stellar synthetic spectrum. The quality of the adjustment is illustrated by the close correspondence between the fitted H2O column and the column deduced for each exposure from the infrared radiometer located at Paranal, as well as the close correspondence between the adjusted O2 column and the airmass.
We augmented the ESPRESSO binary mask with 696 additional stellar lines located within regions previously excluded due to the presence of tellurics (additional mask: BMc). We applied the same standard CCF method, with the same parameters, to the initial data and the standard binary mask as well as to the corrected data and the augmented mask.
We compared the average error on RV as well as the average spread of the results before and after the telluric correction and mask extension. For data from orders 90 to 163 (the ESPRESSO red arm), we find that the average error on RV measurements decreases from E(BM1) = 1.04 m s−1 for the standard binary mask BM1 to E(BM2) = 0.78 m s−1 when using spectra corrected for telluric absorption and the new binary mask adapted to corrected regions. The blue arm is almost unaffected by the telluric absorptions. The red arm error values of E(BM1) = 1.04 and E(BM2) = 0.78 m s−1 are for a 30 s exposure of the star HD40307, which is of spectral type K2.5, and has visual and red magnitudes of V = 7.1, R = 6.6, giving ≃7094 electrons per pixel at the center of order 146 (S/N ≃ 84). For the same stellar spectral type, we expect that both errors will scale inversely to the S/N per pixel (from shot noise), and therefore their ratio will remain constant. For cooler stars, which have more flux in the red part for the same visual magnitude V, the reduction factor of the error will be larger. On the other hand, in the course of our study of the series of measurements of HD 40307, we noted that some jitter affects the RV signal, revealing some sudden increase in stellar activity, as reported by Pepe et al. (2021). We were surprised to find that this jitter has a greater affect on the bluest part of the spectrum than on the red part. We recently learned that this fluctuation was produced by thermal fluctuations of the blue arm cryostat.
When using the full spectrum (blue+red arms), the formal error after telluric correction is reduced from 0.77 to 0.64 m s−1 (or, if using the photon noise minimal uncertainty estimation, from 0.55 to 0.51 m s−1). This improvement corresponds to a saving of about 45% in the telescope time required to reach the same precision (or 16% in the telescope time if using the photon-noise minimal uncertainty estimation). This is important when considering the huge need for telescope time when monitoring target stars in order to determine their populations of planets. Furthermore, it has been shown that long-term stellar activity (e.g., associated to the rotation period of the star) induces some spurious RV variations that are smaller in the red than in the blue, at least in the case of Proxima Centauri (Suárez Mascareño et al. 2020). This increases the benefit of telluric corrections, as they broaden the spectral intervals available for RV retrievals. Similarly, all stellar spectra taken before the correction of the blue detector instability (introducing a short-term artificial “jitter” in the RV data derived from the blue detector) could be reprocessed with our TAPAS-derived procedure for a better RV estimate.
The binary mask BMc built for the telluric contaminated regions is probably also valid for other spectral types close to K2.5, but this needs to be explored. Cooler-type stars with more numerous lines (e.g., M stars) and/or stars with higher metallicity might be more difficult to treat; however, state-of-the-art atmospheric transmission spectra and synthetic stellar spectra allow us to predict atmospheric lines or fractions of lines free of stellar absorption. Moreover, it has been shown that in this case, fitting the observed spectrum with a forward model of the product of a stellar synthetic spectrum and a telluric transmission spectrum is also feasible (see, e.g., Puspitarini et al. 2015), allowing the quantity of H2O to be determined and the quantity of O2 in the atmosphere to be verified at the time of observations. Such procedures allow us to retrieve the stellar spectrum corrected for atmospheric absorption.
The present technique has the advantage of being applicable to any individual recorded spectrum; that is, it does not require time series or libraries of spectra. Also, it benefits from the very highly detailed transmission spectra publicly available from the TAPAS facility. Telluric lines associated with observatories located at different altitudes and in different regions have different shapes, and these differences are not entirely smoothed out after convolution by the spectrograph PSF. There are also changes according to the season. This is why computations made for a stratified atmosphere adapted to both location and date provides an optimal input for the corrections. As we show here, the O2 transmission spectrum can be directly used after scaling to the airmass, while the H2O transmission spectrum requires scaling. Moreover, the atmospheric water vapor is changing rapidly, often on timescales of shorter than 1 h, and the 6 h interval between ECMWF computations is too long to follow its variations. We show that the H2O columns we have adjusted for all individual exposures very closely follow the values derived from the Paranal infrared radiometer and indicated in the data file for each exposure. This implies that, if an on-site measurement of precipitable water vapor column is provided, an initial scaling can be performed using the ratio between this measured column and the one predicted by TAPAS/ECMWF indicated in the accompanying information. Equivalently, one may enter the onsite value in the TAPAS request form and the computed profile will be adjusted accordingly. This provides a preliminary H2O transmission very close to the true solution.
The correction method we present here requires that TAPAS transmission spectra be downloaded. TAPAS computations are now very fast and interruptions are very rare since the website has been upgraded. Because species other than H2O follow the airmass, as we show here for O2, it is possible to retrieve TAPAS transmissions for the different species at the beginning of the observing night or during an exposure and to adapt them to the airmass of each observation. Adjustments of H2O are required for each exposure, as mentioned above, but they are also very fast provided one has prepared the mask appropriate to the stellar type in advance. For this work, the H2O adjustment, the computation of the profiles order by order, and the correction take less than 1 min per exposure on a laptop with a 2.4 GHz Intel Core I9. TAPAS now covers the 300–3500 nm interval and is well adapted to both the near-UV, for example for the CUBES spectrograph under development (Covino et al. 2022), and to near-IR spectrographs such as SPIROU (Donati et al. 2020) or NIRPS (Bouchy et al. 2019). The available species in TAPAS are O2, H2O, Oз, CO2, CH4, and N2O. Both NO2 and NO3 are also expected to become available soon.
Acknowledgements
We thank our referee for his/her very constructive comments and for having pointed out the instrumental reason of increased jitter for the blue detector data. We deeply thank Piercarlo Bonifacio for providing his personal ATLAS-SYNTHE environment and helping us to compute an appropriate stellar synthetic spectrum, used for comparison tests (template matching) and stellar line identification. We acknowledge a very useful support from Burkhard Wolff from ESO who helped us with ESPRESSO instrumental details and the binary mask. A.I. acknowledges the support of a Vernadski Scholarship for PhD students, sponsored by the French Government and the Ministry of Science and Higher Education of the Russian Federation under the grant 075-15-2020-780 (N13.1902.21.0039). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
Appendix A The RV uncertainty estimation based on photon-noise and CCF
The photon noise is one limiting factor for the precision of RV time-change measurements, the other being the richness of the spectral features to be used to detect a Doppler shift of the star. A mathematical expression of the limitation was developed by Connes (1985) and tested for different types of stars and spectrographs by Bouchy et al. (2001). It uses the quality factor Q devised by Connes (1985) and revived in Bouchy et al. (2001), which represents the spectral-line richness of the spectrum; it is independent of the actual size of the spectral range, but is a function of the complexity of the spectral profile within that range. The estimation of the RV uncertainty δVQ based on the quality factor Q is:
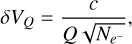 (A.1)
(A.1)
where c is the speed of light, Q the quality factor, and 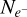 is the total number of photo-electrons counted over the whole spectral range. The quality factor Q makes use of the derivative of the intensity with respect to the wavelength and should be estimated from a noise-free spectrum. The derivative is computed as the finite difference in intensity from one spectel to the next. In reality, an observed spectrum is not noise free. Therefore, with noisy data the quality factor will be spuriously higher and the RV uncertainty will be lower than the true optimal uncertainty. Boisse et al. (2010) described an approach to apply this formalism; not to a spectrum as in Connes (1985), but to a CCF. As the CCF for an order is constructed by piling up all the lines of this order, it can be considered as an average spectral line of the order and also as noise free. In Boisse et al. (2010), the quality factor of the spectrum is calculated as
is the total number of photo-electrons counted over the whole spectral range. The quality factor Q makes use of the derivative of the intensity with respect to the wavelength and should be estimated from a noise-free spectrum. The derivative is computed as the finite difference in intensity from one spectel to the next. In reality, an observed spectrum is not noise free. Therefore, with noisy data the quality factor will be spuriously higher and the RV uncertainty will be lower than the true optimal uncertainty. Boisse et al. (2010) described an approach to apply this formalism; not to a spectrum as in Connes (1985), but to a CCF. As the CCF for an order is constructed by piling up all the lines of this order, it can be considered as an average spectral line of the order and also as noise free. In Boisse et al. (2010), the quality factor of the spectrum is calculated as
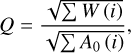 (A.2)
(A.2)
where i is the pixel number of the spectrum and 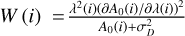 , where A0 is a reference noise-free spectrum intensity and
, where A0 is a reference noise-free spectrum intensity and 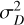 is the detector noise.
is the detector noise.
In the case of the CCF, the wavelength scale is replaced by a velocity scale. The quality factor QCCF shown in Boisse et al. (2010) becomes
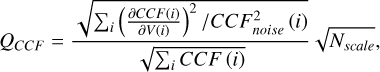 (A.3)
(A.3)
where CCFnoise(i) is the quadratic sum of the photon noise and the read-out detector noise integrated inside the CCF mask holes for the velocity i, which is analogous to the 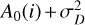 in the W(i) formulation from Bouchy et al. (2001); and Nscale is a correction factor corresponding to the scale of the velocity step in detector pixel units. The velocity uncertainty is equal to
in the W(i) formulation from Bouchy et al. (2001); and Nscale is a correction factor corresponding to the scale of the velocity step in detector pixel units. The velocity uncertainty is equal to
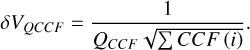 (A.4)
(A.4)
Uncertainties computed both from our Gaussian fit of the CCF δVG and from the application of the above quality factor to the CCF δVQCCF are shown in figures A.1 and A.2. In both cases, estimated uncertainties decrease after telluric correction. We verified that the fluctuations of δVQCCF (Fig. A.2) are almost entirely due to intensity fluctuations reflected on 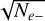 . This explains the parallelism of both curves, before and after telluric correction. In the last figure A.3, we show a comparison between our estimates based on a Gaussian fit δVG and those based on the quality factor δVQCCF for all orders (blue and red) simultaneously. We can see that, generally, the uncertainty estimation obtained from the quality factor δVQCCF is smaller than the one obtained by a Gaussian fit and also displays smaller fluctuations. This is because Boisse et al. (2010) used the full CCF to perform their estimate while we used only ten points of the CCF for our Gaussian fit (we reiterate that in this way we attempt to avoid RV biases appearing when fitting a whole spectral line as described by González Hernández et al. (2020).
. This explains the parallelism of both curves, before and after telluric correction. In the last figure A.3, we show a comparison between our estimates based on a Gaussian fit δVG and those based on the quality factor δVQCCF for all orders (blue and red) simultaneously. We can see that, generally, the uncertainty estimation obtained from the quality factor δVQCCF is smaller than the one obtained by a Gaussian fit and also displays smaller fluctuations. This is because Boisse et al. (2010) used the full CCF to perform their estimate while we used only ten points of the CCF for our Gaussian fit (we reiterate that in this way we attempt to avoid RV biases appearing when fitting a whole spectral line as described by González Hernández et al. (2020).
 |
Fig. A.1 Estimated uncertainty δVG based on the Gaussian fit for the red arm. The red and black curves show the uncertainty before and after telluric correction, respectively. |
 |
Fig. A.2 Estimated uncertainty δVQCCF based on the quality factor for CCF from Boisse et al. (2010) for the red arm. The red and black curves show the uncertainty before and after telluric correction, respectively. Fluctuations are connected to the fluctuations of spectral intensity (see text). |
 |
Fig. A.3 Comparison of estimated uncertainties: based on Gaussian fit of the CCF (δVG, in red) and on the quality factor for the CCF from Boisse et al. (2010), (δVQCCF, in black), for red and blue arms combined. |
References
- Allart, R., Lovis, C., Faria, J., et al. 2022, A&A, 666, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artigau, É., Astudillo-Defru, N., Delfosse, X., et al. 2014, SPIE Conf. Ser., 9149, 914905 [NASA ADS] [Google Scholar]
- Artigau, É., Hébrard, G., Cadieux, C., et al. 2021, AJ, 162, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Mayor, M., & Poncet, J. L. 1979, Vistas Astron., 23, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedell, M., Hogg, D. W., Foreman-Mackey, D., Montet, B. T., & Luger, R. 2019, AJ, 158, 164 [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Eggenberger, A., Santos, N. C., et al. 2010, A&A, 523, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Doyon, R., Pepe, F., et al. 2019, in EPSC-DPS Joint Meeting 2019, 1860 [Google Scholar]
- Clough, S. A., & Iacono, M. J. 1995, J. Geophys. Res., 100, 16, 519 [NASA ADS] [Google Scholar]
- Clough, S. A., Shephard, M. W., Mlawer, E. J., et al. 2005, J. Quant. Spec. Radiat. Transf., 91, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Connes, P. 1985, Ap&SS, 110, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, S., Cristiani, S., Alcala’, J. M., et al. 2022, arXiv e-prints, [arXiv:2212.12791] [Google Scholar]
- Cretignier, M., Dumusque, X., Hara, N. C., & Pepe, F. 2021, A&A, 653, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Ségransan, D., Udry, S., et al. 2016, A&A, 585, A134 [Google Scholar]
- Donati, J. F., Kouach, D., Moutou, C., et al. 2020, MNRAS, 498, 5684 [Google Scholar]
- Figueira, P., Lo Curto, G., & Mehner, A. 2021, Very Large Telescope Paranal Science Operations ESPRESSO User Manual [Google Scholar]
- González Hernández, J. I., Rebolo, R., Pasquini, L., et al. 2020, A&A, 643, A146 [EDP Sciences] [Google Scholar]
- Gordon, I. E., Rothman, L. S., Tan, Y., Kochanov, R. V., & Hill, C. 2017, in 72nd International Symposium on Molecular Spectroscopy (Urbana-Champaign: The University of Illinois), TJ08 [Google Scholar]
- Gullikson, K., Dodson-Robinson, S., & Kraus, A. 2014, AJ, 148, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lafarga, M., Ribas, I., Lovis, C., et al. 2020, A&A, 636, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leet, C., Fischer, D. A., & Valenti, J. A. 2019, AJ, 157, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Puspitarini, L., Lallement, R., Babusiaux, C., et al. 2015, A&A, 573, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L. S. 2021, Nat. Rev. Phys., 3, 302 [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Faria, J. P., Figueira, P., et al. 2020, A&A, 639, A77 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Binary masks (left scale) and telluric lines (right scale). Black bars represent the contrast (relative depths) of the stellar lines of the standard K2 binary mask BM1 used in the ESPRESSO pipeline. Red bars show the contrast of the newly added lines forming the mask BMc. TAPAS telluric H2O and O2 transmission spectra are shown in blue and green, respectively. |
| In the text | |
 |
Fig. 2 Number of stellar lines per order from the standard BM1 (black) and the augmented binary mask BM2 = BMl +BMc (red) restricted to the lines used in our study that have a contrast of ≥0.2. For the red arm, the new mask contains 724 more lines than the 1060 lines of the original mask (Table 2). |
| In the text | |
 |
Fig. 3 Illustration of the procedure used to determine the H2O column for each exposure (here exposure 0 and order 154) and the telluric H2O removal. The mask of stellar lines, i.e., the BMT, is shown as a black dashed lines. The data and adjusted TAPAS transmittance are shown in black and light blue, respectively. The division of the data by the fit is shown in green. The correction works for isolated telluric lines and also for blended telluric and stellar lines (e.g., at 7240 A; see Fig. 5). |
| In the text | |
 |
Fig. 4 Illustration of the procedure used to determine the O2 column for each exposure (here exposure 0 and order 130). The BMT is shown as a black dashed line. The normalized data and the fitted TAPAS transmission are shown in black and green, respectively. The division of the data by the fit is shown in blue. |
| In the text | |
 |
Fig. 5 Zoom onto Fig. 3. Even stellar lines heavily contaminated by H2O lines may be kept for RV retrieval after correction from an adjusted telluric transmission. The BMT is shown as a black dashed lines. |
| In the text | |
 |
Fig. 6 Comparison between the vertical column of water vapor adjusted through spectral fitting (black curve) and the column estimated from the infrared monitor at Paranal (in red) for the 200 consecutive exposures. |
| In the text | |
 |
Fig. 7 Comparison between the column of O2 adjusted through spectral fitting of the Β band and the γ band (black and red curves) and the air mass (green curve). The retrieved columns of O2 follow the air mass relatively well, which means that, unlike the H2O variations, there is no significant variation of the O2 vertical column. |
| In the text | |
 |
Fig. 8 Spectral resolution as a function of pixel number based on the digitization of Fig. 11 of Pepe et al. (2021). Shown are three examples for three orders of the red arm. |
| In the text | |
 |
Fig. 9 Augmented mask of order 130. The intensity of the stacked spectrum (high S/N) after correction of telluric absorption is shown in black (left scale). The atmospheric transmission computed from TAPAS (green, right scale) displays the γ band of O2. The original binary mask BM1 contains only three lines, whose wavelengths are indicated at the bottom by red vertical bars. These lines avoid the O2-contaminated region. A new Binary Mask BM2 containing 36 lines is made from the observed stacked spectrum with stellar lines whose depths are ≥0.2. The wavelength assigned to the stacked spectrum is that of exposure number 100, in the middle of the series of exposures. The three red lines of BM1 are seen shifted to the left from their blue-line counterpart detected in the stacked spectrum. |
| In the text | |
 |
Fig. 10 Adjustment of the two masks. The vertical blue line gives the wavelength position of the center of one stellar line of the observed spectrum, after telluric correction and stacking of all exposures. Its height is the contrast of the line (relative depth, 0.64). The red line represent the same line, back-shifted to account for the radial velocity Vrad0 of the star. The velocity Vrad0 was determined with the original mask BM1 and data from orders 92–115. As a result, the position of the red line coincides well (but not perfectly) with the corresponding line of the original BM1 mask (vertical bar, bottom). |
| In the text | |
 |
Fig. 11 Same as Fig. 9 for order 146, which is heavily contaminated by deep, narrow lines of the O2 B band. The corrected spectrum exhibits conspicuous residuals (see text) at the location of the strongest absorption; however we were able to add 18 lines in the new mask in addition to the initial three lines. |
| In the text | |
 |
Fig. 12 Radial velocity of star HD40307 for order 130, which is contaminated by O2. The result with the standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 372.4 and 31 384.2 m s−1 were subtracted from the series before and after correction, respectively. |
| In the text | |
 |
Fig. 13 Radial velocity of star HD40307 for order 116, which is contaminated by H2O. The result with the standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 386.4 and 31 388 m s−1 were subtracted from the series before and after correction, respectively. |
| In the text | |
 |
Fig. 14 Radial velocity of star HD40307 for the extreme case of order 146, which is heavily contaminated by O2. The result with the standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 386.4 and 31 388 m s−1 were subtracted from the series before and after correction, respectively. |
| In the text | |
 |
Fig. 15 Radial velocity of star HD 40307 for orders from 90 to 163. The result with standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 382.5 and 31 384.4 m s−1 were subtracted from the series before and after correction, respectively. |
| In the text | |
 |
Fig. 16 Radial velocity of star HD 40307 for orders from 40 to 163. The result with standard binary mask BM1 before telluric correction is shown in red; the result with our new binary mask BM2 after telluric correction is shown in black. The average radial velocities of 31 386.9 and 31 385.9 m s−1 were subtracted from the series before and after correction, respectively. |
| In the text | |
 |
Fig. 17 Temporal and BLUE-RED dependence of the measured RV. Top blue graph: RV measurements from our processing after telluric correction restricted to blue orders. Top red graph: Same for the red orders. Bottom purple graph: Combination of blue and red orders above. Bottom black graph: RV measurements reported by Pepe et al. (2021). |
| In the text | |
 |
Fig. 18 Wavelength and temporal dependence of the observed RV. Top: standard deviation Sdev (black line) and formal error on RV measurements (red line) for each order from our processing, averaged over the first 100 exposures only. The ratio between the two quantities is shown in violet. Bottom: same as top but for the last 100 exposures. We note the high ratio found in the blue orders during the second half of the observational time, a sign of spurious jitter due to a blue cryostat thermal instability. |
| In the text | |
 |
Fig. 19 Linear fit of the scatter plot of |
| In the text | |
 |
Fig. A.1 Estimated uncertainty δVG based on the Gaussian fit for the red arm. The red and black curves show the uncertainty before and after telluric correction, respectively. |
| In the text | |
 |
Fig. A.2 Estimated uncertainty δVQCCF based on the quality factor for CCF from Boisse et al. (2010) for the red arm. The red and black curves show the uncertainty before and after telluric correction, respectively. Fluctuations are connected to the fluctuations of spectral intensity (see text). |
| In the text | |
 |
Fig. A.3 Comparison of estimated uncertainties: based on Gaussian fit of the CCF (δVG, in red) and on the quality factor for the CCF from Boisse et al. (2010), (δVQCCF, in black), for red and blue arms combined. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.