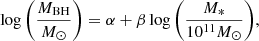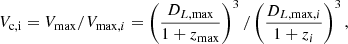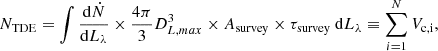| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245065 | |
| Published online | 12 May 2023 | |
AT 2020wey and the class of faint and fast tidal disruption events
1
DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
e-mail: pngchr@space.dtu.dk
2
Department of Physics and Astronomy, University of Turku, Vesilinnantie 5 20500, Finland
3
The School of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978, Israel
4
CIFAR Azrieli Global Scholars program, CIFAR, ON M5G 1M1 Toronto, Canada
5
Las Cumbres Observatory, 6740 Cortona Dr, Suite 102, Goleta, CA 93117-5575, USA
6
Department of Physics, University of California, Santa Barbara, CA 93106-9530, USA
7
The Oskar Klein Centre, Department of Astronomy, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
8
School of Physics and Astronomy, University of Birmingham, Birmingham B15 2TT, UK
9
Institute for Gravitational Wave Astronomy, University of Birmingham, Birmingham B15 2TT, UK
Received:
26
September
2022
Accepted:
21
February
2023
We present an analysis of the optical and ultraviolet properties of AT 2020wey, a faint and fast tidal disruption event (TDE) at 124.3 Mpc. The light curve of the object peaked at an absolute magnitude of Mg = −17.45 ± 0.08 mag and a maximum bolometric luminosity of Lpeak = (8.74 ± 0.69)×1042 erg s−1, making it comparable to iPTF16fnl, the faintest TDE to date. The time from the last non-detection to the g-band peak is 23 ± 2 days, and the rise is well described by L ∝ t1.80 ± 0.22. The decline of the bolometric light curve is described by a sharp exponential decay steeper than the canonical t−5/3 power law, making AT 2020wey the fastest declining TDE to date. The multi-band light curve analysis shows first a slowly declining blackbody temperature of TBB ∼ 20 000 K around the peak brightness followed by a gradual temperature increase. The blackbody photosphere is found to expand at a constant velocity (∼1300 km s−1) to a value of RBB ∼ 3.5 × 1014 cm before contracting rapidly. Multi-wavelength fits to the light curve indicate a complete disruption of a star of M⋆ = 0.11−0.02+0.05 M⊙ by a black hole of MBH = 106.46−0.09+0.09 M⊙. Our spectroscopic dataset reveals broad (∼104 km s−1) Balmer and He II 4686 Å lines, with Hα reaching its peak with a lag of ∼8.2 days compared to the continuum. In contrast to previous faint and fast TDEs, there are no obvious Bowen fluorescence lines in the spectra of AT 2020wey. There is a strong correlation between the MOSFIT-derived black hole masses of TDEs and their decline rate. However, AT 2020wey is an outlier in this correlation, which could indicate that its fast early decline may be dictated by a different physical mechanism than fallback. After performing a volumetric correction to a sample of 30 TDEs observed between 2018 and 2020, we conclude that faint TDEs are not rare by nature; they should constitute up to ∼50–60% of the entire population and their numbers could alleviate some of the tension between the observed and theoretical TDE rate estimates. We calculate the optical TDE luminosity function and we find a steep power-law relation dN/dLg ∝ Lg−2.36±0.16.
Key words: black hole physics / methods: observational / Galaxy: nucleus
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The immense gravitational force of supermassive black holes (SMBHs) located in the nuclei of galaxies can lead to the tidal disruption of orbiting stars. When the trajectory of an orbiting star (with stellar radius R* and mass M*) intersects the tidal radius Rt of the SMBH (with mass MBH), the pericenter distance of the star Rp becomes smaller than the tidal radius defined as Rt ≈ R*(MBH/M*)1/3 (Hills 1975). The gravitational field of the SMBH causes a large spread in the specific orbital binding energy of the star, which ends up being much greater than its mean binding energy, leading to the star being ripped apart (Rees 1988) in a tidal disruption event (TDE).
The stellar debris is stretched into a thin elongated stream, half of which escapes the system in unbound orbits, while the rest stay bound and start to fall back toward the SMBH on highly eccentric orbits (Rees 1988; Evans & Kochanek 1989). A strong, transient flare arises (Lacy et al. 1982; Rees 1988; Evans & Kochanek 1989; Phinney et al. 1989) as the debris circularizes around the black hole with luminosites of Lbol ∼ 1041 − 45 erg s−1, which are sometimes super-Eddington (Strubbe & Quataert 2009; Lodato & Rossi 2011), that is, their luminosity exceeds the Eddington luminosity (which depends linearly on the BH mass). Theory spredicted TDEs almost five decades ago (Hills 1975); however, they started being observed about two decades ago, first in the X-ray regime (Komossa & Bade 1999), then in the ultraviolet (UV; Gezari et al. 2006), and finally in the optical wavelengths (Gezari et al. 2012). Moreover, TDEs have been discovered in the mid-infrared (Mattila et al. 2018; Kool et al. 2020; Jiang et al. 2021; Reynolds et al. 2022) and in the gamma-ray, X-ray and radio wavelengths; emission attributed to the launch of relativistic jets and outflows (e.g., Zauderer et al. 2011; Van Velzen et al. 2016; Alexander et al. 2020; Goodwin et al. 2022). However, there is a discrepancy of an order of magnitude between the observed rates of TDEs and the theoretical estimations (see, e.g., Magorrian & Tremaine 1999; Wang & Merritt 2004; Stone & Metzger 2016 and review by Stone et al. 2020).
In the optical TDEs are considered to be bright with peak absolute magnitudes on the order of −20 ≲ M ≲ −19 (van Velzen et al. 2020). However, there have been a few nearby TDEs (∼60–70 Mpc) that are significantly fainter, but also faster than expected. iPTF16fnl (Blagorodnova et al. 2017; Brown et al. 2018; Onori et al. 2019) is the faintest TDE to date (Mg = −17.45 mag), and was also very fast-decaying TDE. AT 2019qiz (Nicholl et al. 2020; Hung et al. 2021) was a fast-decaying TDE with a luminosity intermediate between the bulk of the population and the faint and fast event iPTF16fnl. These two TDEs belong to the spectroscopic class of H+He TDEs with strong N III lines as well (Leloudas et al. 2019; van Velzen et al. 2020; Charalampopoulos et al. 2022). Two more TDEs of similar brightness to AT 2019qiz are AT 2018ahl (Hinkle et al. 2022) and AT 2020neh (Angus et al. 2022; this study was published when our work was in a very late stage). The latter features the fastest rise time among all TDEs, and it has been suggested that it might originate from an intermediate-mass black hole.
Although TDEs are considered to have a steep luminosity function (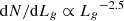 , van Velzen 2018), we are biased in discovering bright ones in flux limited surveys. This is an effect of the Malmquist bias, which describes the preferential detection of intrinsically brighter objects in brightness-limited surveys (Malmquist 1922). Recently, a photometric sample study (Hammerstein et al. 2023) presented a uniformly selected sample of 30 spectroscopically classified TDEs observed by the Zwicky Transient Facility Phase-I survey operations (∼2.5 years) and the mean peak absolute magnitude of the sample is ⟨Mg,peak⟩ = −19.85 mag. A faint and fast TDE in this sample, AT 2020wey, was first discovered by the Zwicky Transient Facility (ZTF; Bellm et al. 2019; Masci et al. 2019; Patterson et al. 2019) as ZTF20acitpfz on 2020 October 13 (Nordin et al. 2020) at coordinates RA = 09:05:25.880, Dec = +61:48:09.18. It is coincident with the center of the galaxy SDSS J090525.86+614809.1 (also known as WISEA J090525.88+614809.2), an r = 16.71 mag galaxy found in the Sloan Digital Sky Survey (SDSS) catalog (Gunn et al. 2006). The transient was also independently reported by the Asteroid Terrestrial impact Last Alert System (ATLAS; Tonry et al. 2018) as ATLAS20belb on 2020 October 23 UT, and by Gaia Science Alerts (Hodgkin et al. 2013) as Gaia20fck on 2020 November 06 UT. The transient appeared in our custom query in Lasair alert broker1 (Smith et al. 2019), a query created to look for nuclear transients within a catalog of quiescent Balmer-strong (QBS) galaxies, otherwise known as E+A galaxies (i.e., an elliptical galaxy showing absorption lines from A-type star atmospheres). TDEs are over-represented in such galaxies by a factor of 30–35 (Arcavi et al. 2014; French et al. 2016, 2020; Graur et al. 2018). This catalog of E+A galaxies was retrieved from French & Zabludoff (2018) and was implemented in the query. The transient was subsequently classified as a TDE by Arcavi et al. (2020) on 2020 October 23 UT, based on a spectrum taken with the FLOYDS-N instrument mounted on the Faulkes Telescope North. The spectroscopic redshift of AT 2020wey, measured from narrow galactic absorption lines in the TDE spectrum, is z = 0.02738. This corresponds to a distance of 124.3 Mpc assuming a ΛCDM cosmology with H0 = 67.4 km s−1 Mpc−1, Ωm = 0.315, and ΩΛ = 0.685 (Planck Collaboration VI 2020).
, van Velzen 2018), we are biased in discovering bright ones in flux limited surveys. This is an effect of the Malmquist bias, which describes the preferential detection of intrinsically brighter objects in brightness-limited surveys (Malmquist 1922). Recently, a photometric sample study (Hammerstein et al. 2023) presented a uniformly selected sample of 30 spectroscopically classified TDEs observed by the Zwicky Transient Facility Phase-I survey operations (∼2.5 years) and the mean peak absolute magnitude of the sample is ⟨Mg,peak⟩ = −19.85 mag. A faint and fast TDE in this sample, AT 2020wey, was first discovered by the Zwicky Transient Facility (ZTF; Bellm et al. 2019; Masci et al. 2019; Patterson et al. 2019) as ZTF20acitpfz on 2020 October 13 (Nordin et al. 2020) at coordinates RA = 09:05:25.880, Dec = +61:48:09.18. It is coincident with the center of the galaxy SDSS J090525.86+614809.1 (also known as WISEA J090525.88+614809.2), an r = 16.71 mag galaxy found in the Sloan Digital Sky Survey (SDSS) catalog (Gunn et al. 2006). The transient was also independently reported by the Asteroid Terrestrial impact Last Alert System (ATLAS; Tonry et al. 2018) as ATLAS20belb on 2020 October 23 UT, and by Gaia Science Alerts (Hodgkin et al. 2013) as Gaia20fck on 2020 November 06 UT. The transient appeared in our custom query in Lasair alert broker1 (Smith et al. 2019), a query created to look for nuclear transients within a catalog of quiescent Balmer-strong (QBS) galaxies, otherwise known as E+A galaxies (i.e., an elliptical galaxy showing absorption lines from A-type star atmospheres). TDEs are over-represented in such galaxies by a factor of 30–35 (Arcavi et al. 2014; French et al. 2016, 2020; Graur et al. 2018). This catalog of E+A galaxies was retrieved from French & Zabludoff (2018) and was implemented in the query. The transient was subsequently classified as a TDE by Arcavi et al. (2020) on 2020 October 23 UT, based on a spectrum taken with the FLOYDS-N instrument mounted on the Faulkes Telescope North. The spectroscopic redshift of AT 2020wey, measured from narrow galactic absorption lines in the TDE spectrum, is z = 0.02738. This corresponds to a distance of 124.3 Mpc assuming a ΛCDM cosmology with H0 = 67.4 km s−1 Mpc−1, Ωm = 0.315, and ΩΛ = 0.685 (Planck Collaboration VI 2020).
In this paper we present the follow-up and thorough photometric and spectroscopic analysis of the faint and fast TDE candidate AT 2020wey. We describe our observations and data reduction in Sect. 2. We present a comprehensive analysis of the photometric and spectroscopic properties of AT 2020wey in Sect. 3, and we discuss their implications in Sect. 4. In Sect. 5 we present our summary and conclusions.
2. Observations and data reduction
Throughout this work we assume a Cardelli et al. (1989) extinction law with RV = 3.1 and use a foreground Galactic extinction of AV = 0.127 mag (Schlafly & Finkbeiner 2011) to de-redden our photometry and spectra.
2.1. Ground-based imaging
Well-sampled host subtracted light curves of AT 20202wey were obtained by the ZTF public survey in the g and r bands, which were accessed using the Lasair alert broker. Las Cumbres Observatory (LCO) BVgri-band data were obtained using the Sinistro cameras on Las Cumbres 1m telescopes. PSF fitting was performed on the host-subtracted images using the lcogtsnpipe pipeline (Valenti et al. 2016), which uses HOTPANTS (Becker 2015) for the subtraction, with template images also obtained at Las Cumbres after the event became non-detectable. BV-band photometry was calibrated to the Vega system using APASS, while gri-band photometry was calibrated to the AB system using the Sloan Digital Sky Survey (Smith et al. 2002). We measured the TDE position in a LCO V-band image taken ∼5 days before the peak of the optical light curve of the transient (MJD = 59 146.4) and the centroid of the galaxy taken as a template image in the same filter, about six months later. We measure an offset of 0.096″ in RA and 0.111″ in Dec. leading to an offset of 0.147″ from the galactic nucleus. This corresponds to an offset of ∼80 parsecs at the redshift of the transient (z = 0.02738), making AT 2020wey a nuclear transient (with a root mean square error of ∼0.18″ in the images, i.e., ∼±100 parsecs).
Finally, we obtained two epochs of Campo Imperatore photometry and the g and r filters. The Campo Imperatore Station of the INAF-Astronomical Observatory of Abruzzo has a 90 cm Schmidt telescope, equipped with an Apogee 4096 × 4096 CCD, covering a field of view of 1.15 × 1.15 square degrees and a ugriz Sloan filter set. For our analysis and plots, all the photometric data were converted to the AB system.
2.2. Swift UVOT photometry
Target-of-opportunity observations spanning 39 epochs (PIs Arcavi and Charalampopoulos) were obtained with the UV-Optical Telescope (UVOT) and X-ray Telescope (XRT) on board the Neil Gehrels Swift Observatory (Swift). The UVOT data were reduced using the standard pipeline available in the HEAsoft software package2. Observation of every epoch was conducted using one or several orbits. To improve the signal-to-noise ratio (S/N) of the observation in a given band in a particular epoch, we co-added all orbit data for that corresponding epoch using the HEAsoft routine uvotimsum. We used the routine uvotsource to measure the apparent magnitude of the transient (using the most recent UVOT photometric zero-points of Poole et al. 2007) by performing aperture photometry using a 5 arcsec aperture for the source and a 25 arcsec aperture for the background. No host galaxy images in the UV are available for subtraction hence we estimated the host contribution using a spectral energy distribution (SED) fit to archival data for this galaxy (details in Sect. 3.1). The computed synthetic UVOT host magnitudes can be found in Table 1.
Synthetic host-galaxy magnitudes.
The complete, host-subtracted and de-reddened UV and optical light curves from Swift, LCO, ZTF, and Campo imperatore are shown in Fig. 1 and all magnitudes are listed in Tables A.1, A.2, and A.4.
 |
Fig. 1. De-reddened and host-subtracted light curves of AT 2020wey. After the peak, it seems that the light curve goes under two distinct phases: one until ∼20 days and another after 20 days. The inset shows fits in the g band (dashed lines), to the first phase (from peak to ∼20 days), and to the entire evolution. The first phase is fit with a linear fit (black line) and the full decline is fit with an exponential (green line). The same fits are plotted in the main plot (dashed lines) but in magnitude space. The exponential fit describes the late-time data nicely, but fails in following the early phase decline. As the event rises to peak, there seems to be a pre-peak precursor (ZTF g and r bands), never observed before in a TDE, between ∼ − 18 days and −10 days before the peak. |
2.3. X-ray and infrared upper limits
We looked for X-ray emission from the position of the source in the XRT data, and we report that AT 2020wey was not bright in X-rays. After stacking all available observations (eight epochs) we place an upper limit at 8 × 10−4 counts per second. Using the webPIMMS tool3 and assuming a Galactic column density NH of 6.22 × 1020 cm−2, we convert the count rate to an unabsorbed flux upper limit of 3.91 × 10−14 erg cm−2 s−1 (0.3–10 keV, assuming a blackbody model with kT = 0.1 keV), which translates to an upper limit for the X-ray luminosity of ∼ 6.64 × 1040 erg s−1 (a power-law model with n = 2 results in an upper limit of ∼ 6.09 × 1040 erg s−1).
We also looked for mid-infrared data from the NEOWISE survey (Mainzer et al. 2011, 2014) by the Wide-field Infrared Survey Explorer (WISE) satellite in its W1 and W2 channels. We do not detect any transient activity up to approximately one year after the event and we measure the host galaxy levels at 16.85 ± 0.02 mag for W1, and at 17.43 ± 0.04 mag for W2 (AB system). That places three-sigma upper limits on the IR detection of the transient at 16.67 mag for W1 and 17.02 mag for W2.
2.4. Optical spectroscopy
We obtained low resolution spectra of AT 2020wey using the FLOYDS instrument on the LCO4 2m telescope in Siding Spring, Australia (Brown et al. 2013) and the Alhambra Faint Object Spectrograph and Camera (ALFOSC) mounted on the 2.56m Nordic Optical Telescope (NOT) located at La Palma, Spain. The LCO spectra were extracted, and flux and wavelength calibrated using the floyds_pipeline5 (Valenti et al. 2014). The ALFOSC spectra were reduced using the spectroscopic data reduction pipeline PyPeIt6 (Prochaska et al. 2020). Although an archival SDSS spectrum existed, we obtained a high S/N host galaxy spectrum with the NOT at 463 d after peak (rest frame) in order to host-subtract our spectra with the same instrument. A spectroscopic log can be found in Table 2 and the host-subtracted spectral series along with the host is shown in the left panel of Fig. 2. We note that there were four more LCO spectra acquired, one on November 08 and three within January. We do not show those spectra in Fig. 2 nor include them in the analysis as we have a higher S/N spectrum from the NOT on November 08, and the late ones were acquired after the optical emission had reached host levels. The host subtraction was performed similarly to Charalampopoulos et al. (2022).
 |
Fig. 2. Spectral evolution of AT 2020wey. Left panel: De-reddened and host-subtracted spectra of AT 2020wey. The spectrum at +463.3 days is the host galaxy spectrum used for host subtraction. The green dashed lines are the polynomial fits to the continuum. Right panel: De-reddened, host-subtracted, and continuum-subtracted spectra of AT 2020wey. |
Spectroscopic observations of AT 2020wey.
3. Analysis
3.1. Host galaxy and SED model fit
The host galaxy (presented in the left panel of Fig. 2) shows Balmer absorption lines and lacks emission lines like Hα and O II, which is typical of quiescent Balmer-strong galaxies. It was spectroscopically (SDSS archival spectrum) classified by French & Zabludoff (2018) as a quiescent Balmer-strong galaxy, with Hα equivalent width of 0.08 Å (in emission) and a Lick HδA of 2.92 (in absorption).
We retrieved archival photometry of the host galaxy from the PanSTARRS catalog (Huber et al. 2015) in the g, r, i, z, y filters and from the Sloan Digital Sky Survey (SDSS; York et al. 2000) in the g, r, i, z filters. Furthermore, we retrieved archival photometry from the 2 Micron All Sky Survey (2MASS; Skrutskie et al. 2006), and the Galaxy Evolution Explorer (GALEX; Martin et al. 2005). We used PROSPECTOR (Leja et al. 2017) in order to fit archival photometry and produce the best-fitting SED model (see Schulze et al. 2021 for a description of the methods), which is shown compared to the archival photometry in Fig. 3. The SED model includes a stellar component and emission from the H II regions. We used the software package Lambda Adaptive Multi-Band Deblending Algorithm in R (Wright 2016) to obtain matched-aperture photometry from the far-UV to the near-infrared, and included the entire host galaxy light in order to quantify the properties of the host galaxy. We find a stellar mass of 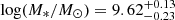 , a star formation rate of
, a star formation rate of 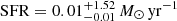 corresponding to a low specific star formation rate of
corresponding to a low specific star formation rate of 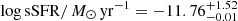 . The reported values and uncertainties are the median and 16th and 84th percentiles of the marginalized posterior distributions. These values confirm that the host is indeed a quiescent galaxy. The model predicts a color excess of
. The reported values and uncertainties are the median and 16th and 84th percentiles of the marginalized posterior distributions. These values confirm that the host is indeed a quiescent galaxy. The model predicts a color excess of 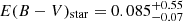 mag. The stellar mass reported by PROSPECTOR is the integral of the star formation history, and so includes stars and stellar remnants. Finally, in order to retrieve the UVOT host magnitudes (needed for host subtraction; see Table 1) we used an aperture of 5 arcsecs, similar to what was used for the photometry of UVOT.
mag. The stellar mass reported by PROSPECTOR is the integral of the star formation history, and so includes stars and stellar remnants. Finally, in order to retrieve the UVOT host magnitudes (needed for host subtraction; see Table 1) we used an aperture of 5 arcsecs, similar to what was used for the photometry of UVOT.
 |
Fig. 3. Host galaxy SED fit with PROSPECTOR. The dashed vertical lines show the effective wavelengths of the Swift UVOT filters for which synthetic magnitudes have been derived (see Table 1). |
3.2. Photometric analysis
The complete, host-subtracted and de-reddened UV and optical light curves from Swift, LCO, and ZTF are shown in Fig. 1. After fitting a third-order polynomial around the maximum of the ZTF r band, we conclude that the date of r-band maximum is at MJD = 59 152.00 ± 0.45. From here on we use this date as the peak of AT 2020wey.
3.2.1. Broadband light curve evolution
We study the broadband light curve evolution of AT 2020wey in the g band. The time from the last non-detection to the ZTF g-band peak is (22.94 ± 2.03) days. The rise to peak is nicely covered by the ZTF g and r bands. We note that in both bands there seems to be a variation in the smooth rise of the light curve between ∼ − 18 d and −10 d, not identified before in TDEs. This “precursor” activity can be interpreted either as a bump (third and fourth points in g band and second point in r band) or as a dip (fourth point in g band and second point in r band), with the dip being more statistically significant as an outlier. The physical processes that drive the light curve rise of TDEs are still under debate, and hence we cannot conclude on the nature or physical origin of the precursor. However, based on the different scenarios of the TDE emission mechanism (and whether it is seen as a bump or a dip), such a feature could be evidence of a fallback–rapid accretion episode or, if an outflow drives the early pre-peak emission of TDEs (Nicholl et al. 2020), such a feature could be related to an uneven density distribution of the expanding optically thick outflow. Alternatively, it could arise from debris stream-crossing shocks during circularization, followed by the main peak.
After the peak, the light curve undergoes two distinct phases, one until ∼+20 days and one after. During the first phase the decay of the light curve is surprisingly fast for a TDE and the luminosity decline is best described by a linear fit in luminosity space (see inset of Fig. 1). During the second phase the event drops close to host galaxy levels and the evolution becomes very slow. We fit the combined ZTF and LCO g band with a power-law model and an exponential model, and we find that the exponential model provides a much better fit to the data with a reduced chi-square statistic of 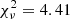 (compared to the
(compared to the 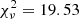 of the power law). Nonetheless, it cannot describe the data during the first decline phase (until ∼+20 days) as accurately as the linear fit (
of the power law). Nonetheless, it cannot describe the data during the first decline phase (until ∼+20 days) as accurately as the linear fit (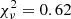 ), as shown in the inset of Fig. 1.
), as shown in the inset of Fig. 1.
3.2.2. Bolometric light curve
We construct the bolometric light curve of AT 2020wey by interpolating the host-subtracted and de-reddened photometry of each band in time, to any epoch with data in the three UV bands of UVOT (reference filters), using SUPERBOL (Nicholl 2018). For the interpolation of the light curves we used polynomials of third to fifth order. Then we integrate under the spectral energy distribution (from 1 to 25 000 Å) at each epoch in order to retrieve the luminosity and fit the SED with a blackbody function to estimate the temperature and the radius, and also in order to calculate the missing energy outside of the observed wavelength range. Before the peak, for the epochs where the reference filters were not observed, we extrapolated assuming constant color based on the ZTF g − r color. We find this choice fair, as TDEs have been speculated to show a generally constant color evolution (Holoien et al. 2019a; van Velzen et al. 2021). The constant color assumption is further validated by looking at the shape of the strong blue continuum in the spectra, which is very similar in the first three epochs. The bolometric light curve, temperature, and radius evolution are plotted in Fig. 4. The epochs for which we used the constant color extrapolation method are shaded in gray.
 |
Fig. 4. Bolometric light curve, temperature, and radius evolution derived using SUPERBOL. The shaded regions indicate the time regions where constant color was assumed for extrapolation purposes. |
The bolometric light curve analysis shows a blackbody temperature in the range ∼20 000 K − 25 000 K, that slowly declines from ∼25 000 K to TBB ∼ 20 000 K at peak and is followed by a slow return to ∼ 25 000 K. The blackbody photosphere expands to the peak value of RBB ∼ 3.5 × 1014 cm before it starts contracting. The expansion of the radius up to the peak is best described by a linear expansion with a constant velocity of ≳ 1300 km s−1 (top panel of Fig. 5). Nicholl et al. (2020) find a linear expansion to the peak radius of the moderately faint TDE AT 2019qiz as well, but with a higher expansion velocity of 2200 km s−1. The higher luminosity TDE AT 2020zso was measured to have an ever higher expansion velocity of 2900 km s−1 (Wevers et al. 2022). Extrapolating back to radius RBB = 0, we infer the start of the light curve rise to be at 29.6d before peak, similar to the value that Nicholl et al. (2020) find for AT 2019qiz (−30.6d) and for AT 2020zso (−35d Wevers et al. 2022). We fit the rise of the bolometric light curve with a power law of the form L = L0[(t − t0)/τ]α using the lmfit7 package (Newville et al. 2016), where a Levenberg–Marquardt algorithm (i.e., least-squares method) was used for fitting. We fix the initial time to t0 = −29.6d and we get a best-fit power-law index a = 1.8 ± 0.22, similar to AT 2019qiz (a = 1.99 ± 0.01), AT 2019ahk (a = 2.1 ± 0.12; Holoien et al. 2019b), and AT 2019azh (a = 1.9 ± 0.39; Hinkle et al. 2021a). We present this fit alongside the fit to the radius expansion in Fig. 5. In the bottom panel of Fig. 5 we present our fits to the sharply declining part of the bolometric luminosity curve. We fit the decline of the bolometric light curve with a power law and with an exponential decay function (L ∝ e−t/τ). We find that both fits can properly describe the data, but the exponential fit returns a better reduced chi-square statistic (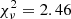 and
and 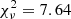 , respectively). The exponential fit has a τ = 7.86 ± 0.48. Onori et al. (2019) find that the bolometric luminosity of the faintest TDE to date iPTF16fnl, is also best described by an exponential decay with τ = 17.6 ± 0.2. That makes AT 2020wey faster and more sharply declining. Our power-law fit returns a power-law index of b = −2.84 ± 0.18, much steeper than the canonical L ∝ t−5/3 expected from simple fallback arguments (Rees 1988) and even steeper than the fast AT 2019qiz (b = −2.51 ± 0.03). AT 2020neh, which is the fastest rising TDE, has a moderate decline (b = −1.44 ± 0.19). The declining rates of the broadband (see Fig. 1) and the bolometric light curve of AT 2020wey are surprisingly sharp and make it the fastest declining TDE to date. The peak of the bolometric luminosity Lpk = (8.74 ± 0.69) × 1042 erg s−1 is very low for a TDE, making it equally faint to iPTF16fnl, the faintest TDE to date. In Fig. 6 we plot the bolometric light curve compared to other well observed TDEs studied in Nicholl et al. (2020, see their Fig. 10). We see that AT 2020wey is the faintest discovered TDE along with iPTF16fnl and that the two TDEs seem identical, almost clones of each other in the bolometric luminosity space.
, respectively). The exponential fit has a τ = 7.86 ± 0.48. Onori et al. (2019) find that the bolometric luminosity of the faintest TDE to date iPTF16fnl, is also best described by an exponential decay with τ = 17.6 ± 0.2. That makes AT 2020wey faster and more sharply declining. Our power-law fit returns a power-law index of b = −2.84 ± 0.18, much steeper than the canonical L ∝ t−5/3 expected from simple fallback arguments (Rees 1988) and even steeper than the fast AT 2019qiz (b = −2.51 ± 0.03). AT 2020neh, which is the fastest rising TDE, has a moderate decline (b = −1.44 ± 0.19). The declining rates of the broadband (see Fig. 1) and the bolometric light curve of AT 2020wey are surprisingly sharp and make it the fastest declining TDE to date. The peak of the bolometric luminosity Lpk = (8.74 ± 0.69) × 1042 erg s−1 is very low for a TDE, making it equally faint to iPTF16fnl, the faintest TDE to date. In Fig. 6 we plot the bolometric light curve compared to other well observed TDEs studied in Nicholl et al. (2020, see their Fig. 10). We see that AT 2020wey is the faintest discovered TDE along with iPTF16fnl and that the two TDEs seem identical, almost clones of each other in the bolometric luminosity space.
 |
Fig. 5. Fits to the bolometric light curve during rise (top) and decline (bottom) of the light curve. Top: the photospheric radius (blue triangles) before peak grows linearly with a velocity v ≈ 1300 km s−1, while the luminosity (black circles) is best fit as L ∝ t1.8. Bottom: exponential and power-law fits to the declining bolometric light curve. The decline is much steeper than the canonical t−5/3. For comparison, iPTF16fnl and AT 2019qiz are overplotted and their bolometric light curves normalized in order for the three events to have the same peak; AT 2020wey is the fastest declining TDE to date. |
 |
Fig. 6. Comparison of the bolometric light curve of AT 2020wey with the TDEs presented in Fig. 10 of Nicholl et al. (2020) and with AT 2020neh (Angus et al. 2022). The resemblance of AT 2020wey with iPTF16fnl is striking. AT 2020neh rises faster, but is brighter and decays more slowly. |
3.2.3. TDE model fit
To estimate the physical parameters of the disruption, we fit our host-subtracted multi-band light curves using the Modular Open Source Fitter for Transients (MOSFIT; Guillochon et al. 2018) with the TDE model from Mockler et al. (2019). This model assumes a mass fallback rate derived from simulated disruptions of polytropic stars by a SMBH of 106 M⊙ (Guillochon et al. 2014), and uses scaling relations and interpolations for a range of black hole masses, star masses, and encounter parameters. It generates a bolometric light curve and, in turn, multi-band light curves, which are fitted to the observed data. Finally, it reaches the combination of parameters that yield the highest likelihood match, using one of the various sampling methods. Here, we ran MOSFIT using dynamic nested sampling with DYNESTY (Speagle 2020) in order to evaluate the posterior distributions of the model. We list the free parameters of the model (as defined by Mockler et al. 2019), their priors, and their posterior probability distributions in Table 3, with two-dimensional posteriors plotted in Fig. B.1.
Priors and marginalized posteriors for the MOSFIT TDE model.
In Fig. 7 we present the fits to the multi-band light curves of AT 2020wey. The model struggles to reproduce the UV data around the peak and the optical data after +20d post-peak. The latter might be reasonable since this is when the transient has almost faded and reached host levels. For the SMBH and the stellar mass, we find a 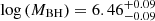 and
and 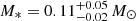 , respectively. We note that even though the fit struggles to reproduce the data, the posteriors of these values are narrow. This means that the true uncertainties in our estimates of these quantities must be driven by the systematic errors of the MOSFIT fits. This is addressed by Mockler et al. (2019) who calculated the systematic uncertainties of MOSFIT TDE fitting and found a ±0.2 dex uncertainty in the BH mass and a ±0.66 dex in the stellar mass. Furthermore we find a scaled impact parameter,
, respectively. We note that even though the fit struggles to reproduce the data, the posteriors of these values are narrow. This means that the true uncertainties in our estimates of these quantities must be driven by the systematic errors of the MOSFIT fits. This is addressed by Mockler et al. (2019) who calculated the systematic uncertainties of MOSFIT TDE fitting and found a ±0.2 dex uncertainty in the BH mass and a ±0.66 dex in the stellar mass. Furthermore we find a scaled impact parameter, 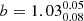 . This scaled impact parameter is defined such that b ≥ 1 leads to a complete disruption and b = 0 to no disruption (for further discussion see Mockler et al. 2019). To summarize all of the above, our MOSFIT posteriors suggest the complete disruption of a sub-solar mass star from a moderate mass supermassive black hole.
. This scaled impact parameter is defined such that b ≥ 1 leads to a complete disruption and b = 0 to no disruption (for further discussion see Mockler et al. 2019). To summarize all of the above, our MOSFIT posteriors suggest the complete disruption of a sub-solar mass star from a moderate mass supermassive black hole.
 |
Fig. 7. Fits to the multi-color light curve using the TDE model in MOSFIT (Guillochon et al. 2018; Mockler et al. 2019). |
3.3. Spectroscopic analysis
In the spectra of AT 2020wey, we identify Balmer Hα and Hβ lines as well as the typical TDE line He II 4686 Å. A faint He I 5876 Å also appears at 15 d post-peak. Frequently, the broad He II 4686 Å line in TDEs is found to be blended with N III 4640 Å and, depending on the S/N of the spectrum and the width of the lines, it may be impossible to distinguish between the two peaks. The reason why other TDEs (see, e.g., Nicholl et al. 2020 and Leloudas et al. 2019) are classified as N III rich TDEs (Bowen) is that they show a clear strong peak of N III ∼ 4100 Å, which is clearly absent for AT 2020wey in all of our spectra. In order to further quantify the non-detection of the N III ∼ 4100 Å line, we measure a two-sigma upper limit of 3.47 × 1039 erg s−1, by integrating the error spectrum of our +8.8-day NOT spectrum over a region of two times the full width at half maximum of the Hα line measured in the same spectrum. Based on the above, AT 2020wey is a hydrogen and helium (H+He) TDE, but without Bowen lines, a quite rare class as usually H+He TDEs also show Bowen lines. Based on the spectroscopic classification of Charalampopoulos et al. (2022), it is similar to TDE AT 2017eqx (Nicholl et al. 2019).
We performed a series of processes before fitting the emission lines of our spectra (see Charalampopoulos et al. 2022 for a detailed description). The spectra (including the host) were first scaled with the ZTF g- and r-band photometry, and the host galaxy spectrum was subtracted from the transient plus host spectra. Then we corrected the spectra for galactic extinction and finally we removed the continuum by fitting the emission-free regions of each host-subtracted spectrum with a fourth-order polynomial. The host-subtracted and continuum-subtracted spectral series can be seen in the right panel of Fig. 2. After we obtained the emission line spectra, we performed our spectroscopic line study using customized Python scripts employing the lmfit package. We focus here on Hα, and we quantify the line luminosity by integrating under the line profile. In order to measure the velocity width, we used a custom script in Python that first smooths the spectrum and then locates the data points to the left and right of the maximum that have flux values closest to half of the maximum; the script then calculates the distance between them on the x-axis. We use a custom Monte Carlo method (10 000 iterations of re-sampling the data assuming Gaussian error distribution) in order to calculate uncertainties for the flux (luminosity) and line width. In the sub-panels of Fig. 8, we present the luminosity (left panel) and line width (right panel) and we compare them with those of the sample of Charalampopoulos et al. (2022). The line luminosity is below 1041 erg s−1 and is identical to that of iPTF16fnl. We find that Hα peaks with a lag of ∼8.2 ± 2.8 days compared to the light curve peak, and in Fig. 9 we plot this lag as a function of the peak of the blackbody radius. Charalampopoulos et al. (2022) found that there is a correlation between the two parameters, and AT 2020wey is indeed within 1σ from the best linear fit, and its lag is similar to that of iPTF16fnl. The line width of Hα is on the order of 10 000 km s−1, and reaches the value of ∼20 000 km s−1 only at 8.8d, where the line luminosity peaks. We note that Hα has an asymmetric profile, as seen in many previous TDEs (see, e.g., Fig. 17 of Charalampopoulos et al. 2022). In the first three spectra, Hα seems to show a bump on the blue side of the main peak. Such broad, multiple peak profiles have been seen in some TDEs and, after careful modeling, have been attributed to the formation of highly inclined, highly elliptical, and relatively compact accretion disks (e.g., PTF09-djl; Arcavi et al. 2014; Liu et al. 2017, AT 2020zso; Wevers et al. 2022), consistent with theoretical works predicting that the returning debris should form an extended eccentric accretion flow (Shiokawa et al. 2015). Such modeling is not attempted in our work since the host-subtracted optical spectra are of low S/N and the transient has faded very quickly in the optical wavelengths (within ∼20 days after peak).
 |
Fig. 8. Hα properties as a function of time. Left panel: Hα luminosity evolution of AT 2020wey as a function of time, compared with the sample of Charalampopoulos et al. (2022). The dashed vertical line denotes the time of peak or discovery of each TDE. Right panel: Hα line width evolution of AT 2020wey as a function of time, compared with the sample of Charalampopoulos et al. (2022). |
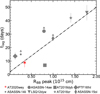 |
Fig. 9. Comparison of the Hα lag as a function of the peak of the blackbody radius of AT 2020wey with the other TDEs (Charalampopoulos et al. 2022). The dot-dashed line is a linear regression fit that does not include the three lower limits. |
4. Discussion
4.1. The nature of faint and fast TDEs
The physical origin of what makes a TDE faint and fast remains a mystery to the community. Here, we try to get further insight into this question by comparing two well-studied faint and fast TDEs in the literature, iPTF16fnl (Blagorodnova et al. 2017; Brown et al. 2018; Onori et al. 2019) and AT 2019qiz (Nicholl et al. 2020; Hung et al. 2021), as well as the recently studied AT 2018ahl (Hinkle et al. 2022) and AT 2020neh (Angus et al. 2022). The following discussion in this section and the comparison of the faint and fast TDEs AT 2020wey, iPTF16fnl, AT 2019qiz, and AT 2020neh is summarized in Table 4 where we list their properties.
Comparison of different properties of AT 2020wey with three well-studied faint and fast TDEs (iPTF16fnl, AT 2019qiz, and AT 2020neh).
In Fig. 10 we compare the broadband light curve evolution, for the ZTF g and r bands in the left panels (optical) and for the UVOT bands W2, M2, W1 and U, in the right panels (UV). We also compare it with AT 2018ahl in the g band alone since there are no observations in r or the UVOT bands. For the comparison in the UVOT bands, we retrieved data from Hinkle et al. (2021b), who use the updated calibrations of Swift. The data in this plot are not k-corrected as all those TDEs were found at comparably low redshifts. In the optical, the decays of the faintest TDEs AT 2020wey and iPTF16fnl look very similar. In the UV, although AT 2020wey and iPTF16fnl have similar magnitudes and evolution until ∼8 days after the peak, interestingly AT 2020wey starts decaying much faster. At 20 days after peak, AT 2020wey has dropped 0.65–0.73 mag more in the three UV bands (i.e., UVW1, UVM2, UVW2) compared to iPTF16fnl.
 |
Fig. 10. Light curves of AT 2020wey and other faint and fast TDEs. Left panels: comparison of the ZTF and LCO host-subtracted and de-reddened magnitudes of AT 2020wey with three faint and fast TDEs (iPTF16fnl, AT 2019qiz, and AT 2018ahl). Right panels: comparison of the UVOT host-subtracted and de-reddened magnitudes of AT 2020wey with two faint and fast TDEs (iPTF16fnl and AT 2019qiz). At +8 days post-peak, AT 2020wey starts declining very quickly in the UV; at 20 days after peak it has dropped an average of 0.69 mag more in the three UV bands (i.e., UVW1, UVM2, UVW2) compared to iPTF16fnl. |
4.1.1. Photometric properties and black hole masses
In order to make a further comparison in the photometric properties of faint and fast TDEs we retrieved MBH, M⋆, and the scaled impact parameter b for iPTF16fnl and AT 2019qiz from Nicholl et al. (2022), and for AT 2020neh from Angus et al. (2022), where they fitted the light curves of a sample of TDEs with MOSFIT. We also use the BH mass of AT 2018ahl from Hinkle et al. (2022), where they estimate it using a stellar mass–black hole mass relation. AT 2020wey and AT 2018ahl have the highest BH masses (log(MBH/ M⊙)∼6.4) with iPTF16fnl being the lowest (log(MBH/ M⊙)∼5.9) and AT 2019qiz being an intermediate case (log(MBH/M⊙)∼6.22). Blagorodnova et al. (2017) suggests that the reason for faint and fast TDEs could be the low SMBH mass of the host galaxy. However, Nicholl et al. (2020) argues that the estimated mass of AT 2019qiz is not significantly lower compared to the other more slowly evolving TDEs, and that faint and fast events can occur in more massive galaxies. They argue, however, that low BH masses could have an effect on the outflow velocity launched from a TDE since the velocity scales as 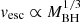 , meaning an outflow can escape more easily at low MBH. They also note that the effect could be more prominent in the early phases of the TDE, when the outflow dynamics most likely govern the light curve evolution. Angus et al. (2022) draw the same conclusion for the fastest rising TDE to date, AT 2020neh, for which they measure an intermediate BH mass (4.8 ≲ log(MBH/ M⊙)≲5.9). If all TDEs have similar Eddington ratios (bolometric-to-Eddington luminosity ratio) as a class, the low BH mass via the early outflow properties could dictate whether a TDE is faint and fast. Here we find that the higher BH mass of AT 2020wey has a slower photospheric radius expansion than AT 2019qiz (see Fig. 5) as expected with the above scenario, if the outflow drives the early phase photospheric expansion. However, AT 2020wey then decays more quickly and is also less luminous than AT 2019qiz and AT 2020neh. Here we note that the BH mass of AT 2020wey was measured with MOSFIT which only provides a model-dependent estimation based on several assumptions. Unfortunately, without a high-resolution host galaxy spectrum we cannot estimate the BH mass via the M − σ relation. However, we can use the stellar mass of the host galaxy derived from the PROSPECTOR fit (see Sect. 3.1) in order to make an estimation of the BH mass using a scaling relation between the central BH mass and total galaxy stellar mass (similarly to Angus et al. 2022) for low-mass galaxies (Reines & Volonteri 2015),
, meaning an outflow can escape more easily at low MBH. They also note that the effect could be more prominent in the early phases of the TDE, when the outflow dynamics most likely govern the light curve evolution. Angus et al. (2022) draw the same conclusion for the fastest rising TDE to date, AT 2020neh, for which they measure an intermediate BH mass (4.8 ≲ log(MBH/ M⊙)≲5.9). If all TDEs have similar Eddington ratios (bolometric-to-Eddington luminosity ratio) as a class, the low BH mass via the early outflow properties could dictate whether a TDE is faint and fast. Here we find that the higher BH mass of AT 2020wey has a slower photospheric radius expansion than AT 2019qiz (see Fig. 5) as expected with the above scenario, if the outflow drives the early phase photospheric expansion. However, AT 2020wey then decays more quickly and is also less luminous than AT 2019qiz and AT 2020neh. Here we note that the BH mass of AT 2020wey was measured with MOSFIT which only provides a model-dependent estimation based on several assumptions. Unfortunately, without a high-resolution host galaxy spectrum we cannot estimate the BH mass via the M − σ relation. However, we can use the stellar mass of the host galaxy derived from the PROSPECTOR fit (see Sect. 3.1) in order to make an estimation of the BH mass using a scaling relation between the central BH mass and total galaxy stellar mass (similarly to Angus et al. 2022) for low-mass galaxies (Reines & Volonteri 2015),
where α = 7.45 ± 0.08 and β = 1.05 ± 0.11. Using this method we estimate a BH mass of 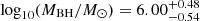 . This value is within 1σ of the MOSFIT estimation. Furthermore, in order to make an estimation of the BH mass based on the stream collision scenario (Piran et al. 2015; Jiang et al. 2016), we use TDEmass (Ryu et al. 2020), which assumes that the UV–optical emission is powered by shocks occurring due to the debris-stream collision, and extracts the BH and stellar mass based on the observed bolometric luminosity and temperature at the peak. We find a BH mass of
. This value is within 1σ of the MOSFIT estimation. Furthermore, in order to make an estimation of the BH mass based on the stream collision scenario (Piran et al. 2015; Jiang et al. 2016), we use TDEmass (Ryu et al. 2020), which assumes that the UV–optical emission is powered by shocks occurring due to the debris-stream collision, and extracts the BH and stellar mass based on the observed bolometric luminosity and temperature at the peak. We find a BH mass of 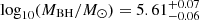 and a stellar mass of
and a stellar mass of 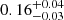 . The stellar mass is consistent with the MOSFIT estimate, but the BH mass is not, as TDEmass returns a significantly lower value (almost an order of magnitude lower).
. The stellar mass is consistent with the MOSFIT estimate, but the BH mass is not, as TDEmass returns a significantly lower value (almost an order of magnitude lower).
In Fig. 11 we present the peak bolometric luminosity (top panel) and its decline rate within the first 20 days (ΔL20 = log10(L20/Lpeak); bottom panel) as a function of the BH mass, for the sample of optical TDEs presented in Fig. 6. The BH masses of the TDEs were computed with MOSFIT and retrieved from Nicholl et al. (2022; and from Angus et al. 2022 for AT 2020neh). There is no correlation between the black hole mass and the peak luminosity (upper panel), which is consistent with previous studies (Blanchard et al. 2017; Hung et al. 2017; Wevers et al. 2019b). In the same panel we show the Eddington ratios (bolometric-to-Eddington luminosity ratio). An interesting feature of AT 2020wey is that it stands out as the one with the lowest Eddington ratio of the sample.
 |
Fig. 11. Peak bolometric luminosity (top panel) and its decline rate within the first 20 days (ΔL20 = log10(L20/Lpeak); bottom panel) as a function of the BH mass, for a sample of optical TDEs. The BH masses are computed with MOSFIT (Mockler et al. 2019; Nicholl et al. 2022). There is no correlation between the peak bolometric luminosity and the decline rate. However, there is a strong correlation between the decline rate and the BH mass of TDEs, where AT 2020wey is an outlier. |
However, there is a strong correlation between the MOSFIT-derived BH masses of TDEs and their decline rate even though AT 2020wey is an outlier in this strong trend. We ran a Pearson’s correlation coefficient test which measures the linear correlation between two sets of data. In order to ensure that any measured correlation is not driven by a few extreme data points, we applied a bootstrapping method where, within each iteration (out of 105), we randomly draw N data points with replacement (where N is the number of data points for which we want to measure the correlation for). Without AT 2020wey, the score of Pearson’s r test is 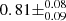 , indicating a very strong correlation (p value of
, indicating a very strong correlation (p value of 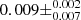 ). If we include AT 2020wey the score drops to
). If we include AT 2020wey the score drops to 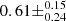 , as expected since Pearson’s r test is sensitive to outliers (p value of
, as expected since Pearson’s r test is sensitive to outliers (p value of 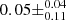 ). Spearman’s ρ test for monotonicity is less sensitive to outliers, and results in a score of
). Spearman’s ρ test for monotonicity is less sensitive to outliers, and results in a score of 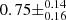 (
(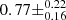 without AT 2020wey). Hence we show that there is a significant (p ≤ 0.05) linear (and monotonic) correlation between the BH mass and the luminosity decline rate of TDEs. We note that this correlation might be expected as MOSFIT estimates the BH mass exactly through fitting the light curves and assuming fallback, whose rate is dependant on the BH mass. What is important, however, is that AT 2020wey appears to be an outlier in this strong correlation. This could indicate that its fast decline from the peak, may be driven by different physical processes than in other TDEs or than those assumed in the MOSFIT model. Even if this is so, the posteriors we derived for the BH and the stellar mass should still stand since the uncertainty on the driving mechanism is encapsulated in the efficiency parameter ϵ, as it is possible that quite different mechanisms (shock heating or accretion) could track the mass return rate, just with different normalizations (i.e., efficiencies). In the Appendix we provide a plot similar to Fig. 11, with the difference that the BH masses have been estimated through the M–σ relation (Wevers et al. 2019a; Leloudas et al. 2019; Short et al. 2020; Nicholl et al. 2020; Angus et al. 2022). Unfortunately, this estimate does not exist for AT 2020wey, and it is therefore not included in the plot. Although weaker (Pearson’s r test result of
without AT 2020wey). Hence we show that there is a significant (p ≤ 0.05) linear (and monotonic) correlation between the BH mass and the luminosity decline rate of TDEs. We note that this correlation might be expected as MOSFIT estimates the BH mass exactly through fitting the light curves and assuming fallback, whose rate is dependant on the BH mass. What is important, however, is that AT 2020wey appears to be an outlier in this strong correlation. This could indicate that its fast decline from the peak, may be driven by different physical processes than in other TDEs or than those assumed in the MOSFIT model. Even if this is so, the posteriors we derived for the BH and the stellar mass should still stand since the uncertainty on the driving mechanism is encapsulated in the efficiency parameter ϵ, as it is possible that quite different mechanisms (shock heating or accretion) could track the mass return rate, just with different normalizations (i.e., efficiencies). In the Appendix we provide a plot similar to Fig. 11, with the difference that the BH masses have been estimated through the M–σ relation (Wevers et al. 2019a; Leloudas et al. 2019; Short et al. 2020; Nicholl et al. 2020; Angus et al. 2022). Unfortunately, this estimate does not exist for AT 2020wey, and it is therefore not included in the plot. Although weaker (Pearson’s r test result of 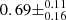 with a p value of
with a p value of 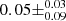 ), the correlation between BH mass and light curve decline rate still exists, showing that it is not uniquely driven by the MOSFIT systematics.
), the correlation between BH mass and light curve decline rate still exists, showing that it is not uniquely driven by the MOSFIT systematics.
Hinkle et al. (2021b) report a correlation between the peak value of the bolometric luminosity and the decline rate within the first 40 days (ΔL40 = log10(L40/Lpeak)) in optical TDEs and derives an empirical relation between the two quantities (see their Equation 1). We measure the ΔL40 of AT 2020wey and find it to be −1.28, within 1σ of the expected value derived from their empirical relation (i.e., 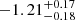 ). Therefore, AT 2020wey is consistent with the correlation proposed by Hinkle et al. (2021b) at the low-luminosity end.
). Therefore, AT 2020wey is consistent with the correlation proposed by Hinkle et al. (2021b) at the low-luminosity end.
4.1.2. Other observables and spectroscopic properties
In this section we investigate whether there is any single observable property that is common among faint TDEs. MOSFIT suggests that iPTF16fnl and AT 2019qiz were caused by the partial disruption of solar mass stars, while AT 2020wey by the complete disruption of a sub-solar mass star (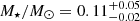 ). We also investigated if the faint and fast TDEs were similar regarding their X-ray properties, but we could not identify a clear tendency; AT 2019qiz was detected in X-rays, while the others were not detected (or were marginally detected). AT 2019qiz had some time-resolved detections in X-rays and was measured in a single deep stack image to have a luminosity of ∼ 5.1 × 1040 erg s−1 in the 0.3–10 keV band. A single deep stack image in the same energy band for iPTF16fnl provided an extremely weak marginal detection of ∼ 2.4 × 1039 erg s−1. We also consider that the host galaxies of the events and AT 2019qiz occurred in a spiral galaxy that probably harbored a weak AGN; however, iPTF16fnl and AT 2018ahl occurred in quiescent Balmer-strong galaxies, while AT 2020neh occurred in a dwarf galaxy.
). We also investigated if the faint and fast TDEs were similar regarding their X-ray properties, but we could not identify a clear tendency; AT 2019qiz was detected in X-rays, while the others were not detected (or were marginally detected). AT 2019qiz had some time-resolved detections in X-rays and was measured in a single deep stack image to have a luminosity of ∼ 5.1 × 1040 erg s−1 in the 0.3–10 keV band. A single deep stack image in the same energy band for iPTF16fnl provided an extremely weak marginal detection of ∼ 2.4 × 1039 erg s−1. We also consider that the host galaxies of the events and AT 2019qiz occurred in a spiral galaxy that probably harbored a weak AGN; however, iPTF16fnl and AT 2018ahl occurred in quiescent Balmer-strong galaxies, while AT 2020neh occurred in a dwarf galaxy.
We finally compare the faint and fast TDEs based on their spectroscopic properties. Figure 12 shows the host-subtracted and de-reddened spectra of AT 2020wey (+ 8.8d) (our best S/N spectrum) with iPTF16fnl (+ 17.0d) and AT 2019qiz (+ 19.0d). The spectra of the three events are very similar. We see broad and asymmetric Hα; we see that the peak of Hβ is nicely resolved in the ∼4600 Å blend; and there is evidence for weak He I in all of them. All three events have a strong peak at He II 4686 Å, which may be blended with N III 4640 Å. The reason why iPTF16fnl and AT 2019qiz are classified as N III rich TDEs (Bowen) is that they show a clear strong peak of N III ∼ 4100Å, which is absent for AT 2020wey in all of our spectra. Hence, we can robustly classify AT 2020wey as a H+He TDE with no Bowen features. This means that there does not seem to be a connection between faint and fast TDEs and the physical origin of Bowen fluorescence lines.
 |
Fig. 12. Comparison of the host-subtracted (and de-reddened) spectra of AT 2020wey with two more faint and fast TDEs (iPTF16fnl and AT 2019qiz). The three events are spectroscopically similar, but AT 2020wey lacks the strong nitrogen line at 4100 Å. |
The faint and fast TDEs appear to be different in many observables, and we conclude that none of these properties shows a tendency for the four faint and fast TDEs.
4.2. Luminosity function and TDE rates
In order to further probe the nature of faint TDEs, we investigate whether they are indeed rare by nature or if we have been biased toward bright nuclear flares (peak absolutes magnitudes of ∼−20 mag) and and have caused fainter TDEs to go unnoticed in searches within the new detections of wide-field surveys. That is, we want to account for observational biases, for example the Malmquist bias, which describes the preferential detection of intrinsically brighter objects in brightness-limited surveys (Malmquist 1922) and quantify how many faint TDEs are missed.
For this reason, we use the same sample presented by Hammerstein et al. (2023), which consists of 30 spectroscopically classified TDEs observed by ZTF Phase-I survey (see further details and their selection criteria therein). This sample includes two well-studied faint and fast TDEs: AT 2020wey and AT 2019qiz. We first took the public ZTF difference photometry of those TDEs at peak, and isolated the peak of each event in the g and r bands. Then we computed the absolute magnitudes after correcting for galactic extinction (host galaxy extinction is not considered) and performing a k-correction. A k-correction is an important correction for such samples because of the vast redshift interval between the different events. We computed a 0.98 mag correction in the r band for the highest redshift event in the sample (AT 2020riz; z = 0.435). We performed the k-correction using the peak blackbody temperatures of each TDE as estimated by Hammerstein et al. (2023). In the top panel of Fig. 13 we show the peak luminosity distribution of the 30 TDEs in Hammerstein et al. (2023), in the ZTF g (left) and r (right) bands. In order to visualize faint TDEs we set an arbitrary cut for events being fainter than or equally faint to AT 2019qiz and we plot those histogram bins in green for the g band and in red for the r band. We find an average peak of ⟨Mg,peak⟩ = −19.85 mag for the g band and ⟨Mr,peak⟩ = −19.54 mag for the r band.
 |
Fig. 13. Absolute peak magnitude distributions (k-corrected) of the Hammerstein et al. (2023) TDE sample, with g band on the left and r band on the right. Shown in the top panel are the histograms of the original data (observed distributions) and in the bottom panel the data after volumetric correction (i.e., expected yields, number of TDEs). The colored bins contain TDEs that are fainter than or equally faint to AT 2019qiz. |
However, in order to make a fair comparison we need to properly address observational biases. The Malmquist bias is taken account of by normalizing the numbers of each bin to the same co-moving volume. We calculate the volumetric correction Vc for each TDE as the ratio of the volume Vmax probed by the most luminous TDE in the Hammerstein et al. (2023) sample (AT 2018jbv with Mg, max = −22.07 mag and Mr,max = −21.58 mag) to the volume Vmax, i probed by each individual TDE, if they were observed at a brightness equal to the faintest apparent magnitude of the sample (AT 2020ocn with mg, min = 19.65 mag and mr, min = 19.79 mag). The redshift at which each TDE would have been observed with this apparent magnitude is defined as zi, with zmax being the highest of them all (attributed to AT 2018jbv). The volumetric correction factor Vc, i for each TDE (see, e.g., De Cia et al. 2018) can be written as
where the luminosity distance of the brightest TDE in the sample (in each respective band λ) is 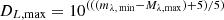 , and the luminosity distance at which each individual TDE would have been observed with the faintest apparent magnitude is
, and the luminosity distance at which each individual TDE would have been observed with the faintest apparent magnitude is 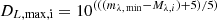 . The bottom panel of Fig. 13 shows the peak magnitude distribution after applying the volumetric correction. We find that the mean peak absolute magnitudes of the sample reduces to ⟨Mg,peak⟩ = −18.52 mag and ⟨Mr,peak⟩ = −18.34 mag, which implies a magnitude difference from the observed sample of 1.33 mag and 1.2 mag in g and r band, respectively. These large differences suggest that we are indeed biased toward finding bright nuclear flares, and that faint events like AT 2020wey are not as rare as they are considered to be. The events that are fainter than or as faint as AT 2019qiz in the observed sample constitute barely 10% in the g band (16% in r band) but they are estimated to be 52% (64%) after the volumetric correction. The fact that faint TDEs should constitute up to (50–60)% of the whole population could alleviate some of the tension between the observed and theoretical TDE rate estimates (about an order of magnitude discrepancy; see, e.g., review of Stone et al. 2020).
. The bottom panel of Fig. 13 shows the peak magnitude distribution after applying the volumetric correction. We find that the mean peak absolute magnitudes of the sample reduces to ⟨Mg,peak⟩ = −18.52 mag and ⟨Mr,peak⟩ = −18.34 mag, which implies a magnitude difference from the observed sample of 1.33 mag and 1.2 mag in g and r band, respectively. These large differences suggest that we are indeed biased toward finding bright nuclear flares, and that faint events like AT 2020wey are not as rare as they are considered to be. The events that are fainter than or as faint as AT 2019qiz in the observed sample constitute barely 10% in the g band (16% in r band) but they are estimated to be 52% (64%) after the volumetric correction. The fact that faint TDEs should constitute up to (50–60)% of the whole population could alleviate some of the tension between the observed and theoretical TDE rate estimates (about an order of magnitude discrepancy; see, e.g., review of Stone et al. 2020).
Based on our volumetric correction of the Hammerstein et al. (2023) sample, we calculate the volumetric rate of TDEs. The number of TDEs detected by the survey (see, e.g., Hung et al. 2018) can be expressed as
where dṄ/dLλ is the luminosity function of TDEs (the volumetric TDE rate with respect to peak g-band luminosity), DL,max is the maximum distance (redshift) within which a TDE can be detected by the flux-limited survey (and is a function of the peak magnitude of the flare), and Asurvey × τsurvey is used to label the product of the effective survey area (ZTF areal coverage of 23 675 deg2 over the total area of the celestial sphere) and duration. For the duration τsurvey, we set a starting date at 1 October 2018 and an end date at 1 December 2020. The Hammerstein et al. (2023) sample consists of 30 spectroscopically classified TDEs observed by ZTF during the ZTF Phase-I survey. However, we see that while AT 2018zr was observed in March 2018 and AT 2018bsi in April 2018, the next TDE is observed on 4 October 2018 (i.e., ∼ six months later) and there is a regular cadence in TDE observations from then on. Hence, we exclude the first two events from our calculations and we consider the start of the survey that observed 28 TDEs to be 1 October 2018. All these assumptions, combined with the selection criteria based on which a discovered transient was spectroscopically classified (i.e., some TDEs during ZTF Phase-I might never got classified, and Hammerstein et al. 2023 do not claim that their sample is spectroscopically complete), make our estimate of the TDE volumetric rate a rough lower limit.
On the primary y-axis (left) of Fig. 14, we show the expected yield, the expected number of TDEs observed by the survey within each magnitude bin range (same ranges as in Fig. 13). On the secondary y-axis (right) we present the volumetric rate dṄ/dLλ binned by the peak absolute magnitude, for the g band in the left panel and for the r band in the right panel. We fit the volumetric rate in each band with a power law and we get the same power-law index for both bands: b = −2.36 ± 0.16 for g band and b = −2.36 ± 0.31 for r band. Hence, we find that the luminosity function of TDEs can be described by dṄ/dLλ ∝ L−2.36 and we conclude, similarly to van Velzen (2018), that a steep power law is required to explain the observed rest-frame luminosities of TDEs (they find dṄ/dLg ∝ L−2.5). When our work was at a late stage, a thorough study on the luminosity function of TDEs from the ZTF-I survey was published by Lin et al. (2022), who studied almost the same sample as ours. In their work, they find a luminosity function of 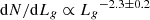 , practically the same as we do.
, practically the same as we do.
 |
Fig. 14. Fits to the volumetric rates based on the Hammerstein et al. (2023) sample, for the ZTF g band (left) and ZTF r band (right). The histograms denote the expected yields (number of TDEs) after the volumetric correction, and they are the same as the bottom panel of Fig. 13. The colored bins include TDEs that are fainter than or equally faint to AT 2019qiz. |
Finally, if we sum the contributions of each volumetric rate bin (see Fig. 14) we can derive a lower limit for the TDE rate, and we calculate it to be Ṅ ∼ 2 × 10−8 Mpc−3 yr−1. Hung et al. (2018) calculate a lower limit for TDEs in red galaxies of 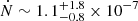 Mpc−3 yr−1; this value is consistent with ours since their study focuses on TDEs in red galaxies (easier to detect since TDEs have intrinsically blue colors). The two values would most likely be within one sigma of each other if we could calculate error bars on our measurement, but we cannot since the largest source of uncertainty is systematic (whether the Hammerstein et al. 2023 sample is spectroscopically complete or not) and was not controlled by us. Lin et al. (2022) calculated a TDE rate of Ṅ ∼ 6.3 × 10−8 Mpc−3 yr−1, that is ∼ three times larger than ours. A possible explanation for the small discrepancy is that they used a limiting magnitude of mr = 19.5 mag, while ours was set by the faintest TDE in the sample ( mr,min = 19.79 mag). Another possible reason is that they included the two early TDEs of the ZTF-I survey that we did not, and also included three more than those in the Hammerstein et al. (2023) sample (AT2020neh, AT2020nov, AT2020vwl), setting the effective survey duration to 2.7 years (compared to our 2.16 years). We made a calculation including the two early TDEs (raising our sample to 30), and thus extending the effective survey duration, as well as setting our limiting magnitude to 19.5. In this way we find a TDE rate of Ṅ ∼ 3.5 × 10−8 Mpc−3 yr−1, which is 1.8 times smaller than that found by Lin et al. (2022). Hence, we conclude that adding those three extra TDEs is most likely the reason for this small discrepancy. van Velzen (2018) found a rate of (8 ± 4)×10−7 Mpc−3yr−1; here the discrepancy is very large and more extensive. A thorough analysis on why this discrepancy exists can be found in the recent work of Lin et al. (2022). However the authors cannot conclude on the reason for their lower volumetric rate compared to the one of van Velzen (2018).
Mpc−3 yr−1; this value is consistent with ours since their study focuses on TDEs in red galaxies (easier to detect since TDEs have intrinsically blue colors). The two values would most likely be within one sigma of each other if we could calculate error bars on our measurement, but we cannot since the largest source of uncertainty is systematic (whether the Hammerstein et al. 2023 sample is spectroscopically complete or not) and was not controlled by us. Lin et al. (2022) calculated a TDE rate of Ṅ ∼ 6.3 × 10−8 Mpc−3 yr−1, that is ∼ three times larger than ours. A possible explanation for the small discrepancy is that they used a limiting magnitude of mr = 19.5 mag, while ours was set by the faintest TDE in the sample ( mr,min = 19.79 mag). Another possible reason is that they included the two early TDEs of the ZTF-I survey that we did not, and also included three more than those in the Hammerstein et al. (2023) sample (AT2020neh, AT2020nov, AT2020vwl), setting the effective survey duration to 2.7 years (compared to our 2.16 years). We made a calculation including the two early TDEs (raising our sample to 30), and thus extending the effective survey duration, as well as setting our limiting magnitude to 19.5. In this way we find a TDE rate of Ṅ ∼ 3.5 × 10−8 Mpc−3 yr−1, which is 1.8 times smaller than that found by Lin et al. (2022). Hence, we conclude that adding those three extra TDEs is most likely the reason for this small discrepancy. van Velzen (2018) found a rate of (8 ± 4)×10−7 Mpc−3yr−1; here the discrepancy is very large and more extensive. A thorough analysis on why this discrepancy exists can be found in the recent work of Lin et al. (2022). However the authors cannot conclude on the reason for their lower volumetric rate compared to the one of van Velzen (2018).
Finally, we calculate the rate of faint TDEs (defined as being as faint as or fainter than AT 2019qiz) to be Ṅ ∼ 10−8 Mpc−3 yr−1 making faint TDEs half of the entire TDE population. In order to investigate whether we might be biased in finding faint TDEs in faint-nucleus galaxies, in Fig. 15 we plot the absolute magnitudes of the TDEs in the Hammerstein et al. (2023) sample against the absolute magnitude of the nucleus of their respective hosts (retrieved from the Lasair alert broker), in the ZTF g and r bands. We do not find a strong correlation between the two quantities, meaning that we are not actually biased in discovering faint TDEs because of the faint nuclei of their respective hosts. However, AT 2020wey and AT 2019qiz both have a faint host nucleus compared to the rest of the sample, making them easier targets to initiate a follow-up campaign for.
 |
Fig. 15. Absolute magnitudes of the TDEs in the Hammerstein et al. (2023) sample against the absolute magnitude of the nucleus of their respective hosts, in the ZTF g (top panel) and r (bottom panel) bands. AT 2020wey is plotted as a star and AT 2019qiz as a square. Even though the two TDEs have a faint host nucleus compared to the rest of the sample, a bias was not found to be present in discovering faint TDEs because of the faint nuclei of the respective hosts. |
5. Conclusions
We presented the follow-up and detailed study of AT 2020wey, an optical–UV TDE candidate in a quiescent, Balmer-strong galaxy at 124.3 Mpc, along with a comprehensive analysis of its photometric and spectroscopic properties and evolution. We summarize our key findings here:
-
AT 2020wey is a very faint TDE with a peak absolute magnitude of Mg = −17.45 mag and a peak bolometric luminosity of Lpk = (8.74 ± 0.69) × 1042 erg s−1, making it equally faint to iPTF16fnl, the faintest TDE to date.
-
AT 2020wey is a fast-evolving TDE. The time from the last non-detection to the g-band peak is (23 ± 2) days, and the decline rate within the first 20 days after peak (ΔL20 = log10(L20/Lpeak) is the fastest measured in any TDE. The broadband luminosity decline during the first 20 days is linear with time.
-
The bolometric light curve analysis shows a blackbody temperature of TBB ∼ 20 000 K around peak followed by a slow rise, and a blackbody photosphere that expands with a constant velocity (∼ 1300 km s−1) to a peak value of RBB ∼ 3.5 × 1014 cm before it starts shrinking.
-
The early optical emission shows a luminosity evolution L ∝ t1.8 (consistent with other TDE pre-peak evolution timescales) followed by a sharp fading (best described as an exponential decay) that is steeper than the canonical t−5/3 as well as other fast TDEs. This makes AT 2020wey the fastest decaying TDE to date.
-
Our spectroscopic dataset reveals broad (∼ 104 km s−1) Balmer and He II 4686 Å lines and that Hα peaks with a lag of ∼ 8.2 ± 2.8d compared to the light curve maximum light. The spectrum of AT 2020wey is very similar to those of iPTF16fnl and AT 2019qiz (around + 10d post-peak) with the exception that AT 2020wey does not show any N III Bowen lines. The lack of obvious Bowen lines suggests that there is no connection between the physical origin of Bowen fluorescence lines and faint and fast TDEs.
-
After making a comparison between the properties of a sample of faint and fast TDEs, we conclude that there is not a single observable that is common between all of them.
-
There is a strong correlation between the MOSFIT-derived BH masses of TDEs and their decline rate within the first 20 days (ΔL20 = log10(L20/Lpeak). However, AT 2020wey is an outlier in this correlation, possibly indicating that its fast early decline could be dictated by a different physical mechanism than fallback.
-
After performing a volumetric correction to a sample of 30 TDEs observed between 2018 and 2020 (Hammerstein et al. 2023), we conclude that faint TDEs are not rare by nature and that they should constitute up to ∼(50–60)% of the entire population.
-
We calculated the optical TDE luminosity function and we find a steep power-law relation
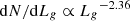 , and a lower limit for the TDE rate of Ṅ ∼ 2 × 10−8 Mpc−3 yr−1, both consistent with previous measurements.
, and a lower limit for the TDE rate of Ṅ ∼ 2 × 10−8 Mpc−3 yr−1, both consistent with previous measurements.
The upcoming time-domain survey of the Rubin Observatory (LSST; Ivezić et al. 2019) is expected to observe 3500 to 8000 TDEs per year, depending on the assumed SMBH mass distribution (Bricman & Gomboc 2019). In this work we showed that faint TDEs should constitute up to 50–60% of the entire population of these exotic transients. In addition, it is possible that there are fainter TDEs but their population is hard to detect, especially in bright galaxies. Although technically difficult, we encourage the classification and follow-up of fainter nuclear transients in order to better understand the TDE rates and luminosity function.
Acknowledgments
We kindly thank D.B. Malesani for his help with Swift triggering and valuable comments and C. Angus for sharing the bolometric light curves of AT 2020neh. We thank the anonymous referee for comments that helped improve this paper. P.C, M.P and G.L are supported by a research grant (19054) from VILLUM FONDEN. P.C. acknowledges support via an Academy of Finland grant (340613; P.I. R. Kotak). IA is a CIFAR Azrieli Global Scholar in the Gravity and the Extreme Universe Program and acknowledges support from that program, from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement number 852097), from the Israel Science Foundation (grant number 2752/19), from the United States – Israel Binational Science Foundation (BSF), and from the Israeli Council for Higher Education Alon Fellowship. This work is based on observations made with the Nordic Optical Telescope, owned in collaboration by the University of Turku and Aarhus University, and operated jointly by Aarhus University, the University of Turku and the University of Oslo, representing Denmark, Finland and Norway, the University of Iceland and Stockholm University at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. This work used data taken with the Campo Imperatore Station as part of the first commissioning phase of Schmidt telescope’s upgrade. The Campo Imperatore Station is part of the INAF-Astronomical Observatory of Abruzzo. We thank the observers Francesca Onori, Roberta Carini and Fiore De Luise.
References
- Alexander, K. D., van Velzen, S., Horesh, A., & Zauderer, B. A. 2020, Space Sci. Rev., 216, 81 [CrossRef] [Google Scholar]
- Angus, C. R., Baldassare, V. F., Mockler, B., et al. 2022, Nat. Astron., 6, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Arcavi, I., Gal-Yam, A., Sullivan, M., et al. 2014, ApJ, 793, 38 [Google Scholar]
- Arcavi, I., Burke, J., Nyiha, I., et al. 2020, Transient Name Serv. Classif. Rep., 2020–3228, 1 [Google Scholar]
- Becker, A. 2015, Astrophysics Source Code Library [record ascl:1504.004] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
- Blagorodnova, N., Gezari, S., Hung, T., et al. 2017, ApJ, 844, 46 [Google Scholar]
- Blanchard, P. K., Nicholl, M., Berger, E., et al. 2017, ApJ, 843, 106 [Google Scholar]
- Bricman, K., & Gomboc, A. 2019, ApJ, 890, 73 [Google Scholar]
- Brown, J. S., Kochanek, C. S., Holoien, T. W., et al. 2018, MNRAS, 473, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Charalampopoulos, P., Leloudas, G., Malesani, D. B., et al. 2022, A&A, 659, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cia, A., Gal-Yam, A., Rubin, A., et al. 2018, ApJ, 860, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. R., & Kochanek, C. S. 1989, ApJ, 346, L13 [Google Scholar]
- French, K. D., & Zabludoff, A. I. 2018, ApJ, 868, 99 [NASA ADS] [CrossRef] [Google Scholar]
- French, K. D., Arcavi, I., & Zabludoff, A. 2016, ApJ, 818, L21 [NASA ADS] [CrossRef] [Google Scholar]
- French, K. D., Wevers, T., Law-Smith, J., Graur, O., & Zabludoff, A. I. 2020, Space Sci. Rev., 216, 32 [CrossRef] [Google Scholar]
- Gezari, S., Martin, D. C., Milliard, B., et al. 2006, ApJ, 653, L25 [Google Scholar]
- Gezari, S., Chornock, R., Rest, A., et al. 2012, Nature, 485, 217 [Google Scholar]
- Goodwin, A. J., Van Velzen, S., Miller-Jones, J. C., et al. 2022, MNRAS, 511, 5328 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., French, K. D., Zahid, H. J., et al. 2018, ApJ, 853, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Guillochon, J., Manukian, H., & Ramirez-Ruiz, E. 2014, ApJ, 783, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Guillochon, J., Nicholl, M., Villar, V. A., et al. 2018, ApJS, 236, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Hammerstein, E., van Velzen, S., Gezari, S., et al. 2023, ApJ, 942, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1975, Nature, 254, 295 [Google Scholar]
- Hinkle, J. T., Holoien, T. W., Auchettl, K., et al. 2021a, MNRAS, 500, 1673 [Google Scholar]
- Hinkle, J. T., Holoien, W. S. T., Shappee, B. J., & Auchettl, K. 2021b, ApJ, 910, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, J. T., Tucker, M. A., Shappee, B. J., et al. 2022, MNRAS, 519, 2035 [CrossRef] [Google Scholar]
- Hodgkin, S. T., Wyrzykowski, Ł., Blagorodnova, N., & Koposov, S. 2013, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 371, 20120239 [NASA ADS] [CrossRef] [Google Scholar]
- Holoien, T. W.-S., Huber, M. E., Shappee, B. J., et al. 2019a, ApJ, 880, 120 [Google Scholar]
- Holoien, T. W.-S., Vallely, P. J., Auchettl, K., et al. 2019b, ApJ, 883, 111 [Google Scholar]
- Huber, M., Chambers, K., Flewelling, H., et al. 2015, Astron. Telegr., 7153 [Google Scholar]
- Hung, T., Gezari, S., Blagorodnova, N., et al. 2017, ApJ, 842, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Hung, T., Gezari, S., Cenko, S. B., et al. 2018, ApJS, 238, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hung, T., Foley, R. J., Veilleux, S., et al. 2021, ApJ, 917, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
- Jiang, N., Wang, T., Hu, X., et al. 2021, ApJ, 911, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Y.-F., Guillochon, J., & Loeb, A. 2016, ApJ, 830, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., & Bade, N. 1999, A&A, 343, 775 [NASA ADS] [Google Scholar]
- Kool, E. C., Reynolds, T. M., Mattila, S., et al. 2020, MNRAS, 498, 2167 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, J. H., Townes, C. H., & Hollenbach, D. J. 1982, ApJ, 262, 120 [Google Scholar]
- Leja, J., Johnson, B. D., Conroy, C., van Dokkum, P. G., & Byler, N. 2017, ApJ, 837, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Leloudas, G., Dai, L., Arcavi, I., et al. 2019, ApJ, 887, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Z., Jiang, N., Kong, X., et al. 2022, ApJ, 939, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F. K., Zhou, Z. Q., Cao, R., Ho, L. C., & Komossa, S. 2017, MNRAS, 472, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., & Rossi, E. M. 2011, MNRAS, 410, 359 [Google Scholar]
- Magorrian, J., & Tremaine, S. 1999, MNRAS, 309, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Bauer, J., Grav, T., et al. 2011, ApJ, 731, 53 [Google Scholar]
- Mainzer, A., Bauer, J., Cutri, R. M., et al. 2014, ApJ, 792, 30 [Google Scholar]
- Malmquist, K. G. 1922, Medd. fran Lunds Astron. Obs. Ser. I, 100, 1 [NASA ADS] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Masci, F. J., Laher, R. R., Rusholme, B., et al. 2019, PASP, 131, 018003 [Google Scholar]
- Mattila, S., Pérez-Torres, M., Efstathiou, A., et al. 2018, Science, 361, 482 [Google Scholar]
- Mockler, B., Guillochon, J., & Ramirez-Ruiz, E. 2019, ApJ, 872, 151 [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., et al. 2016, Astrophysics Source Code Library [record ascl:1606.014] [Google Scholar]
- Nicholl, M. 2018, Res. Notes AAS, 2, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholl, M., Blanchard, P. K., Berger, E., et al. 2019, MNRAS, 488, 1878 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholl, M., Wevers, T., Oates, S. R., et al. 2020, MNRAS, 499, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholl, M., Lanning, D., Ramsden, P., et al. 2022, MNRAS, 515, 5604 [NASA ADS] [CrossRef] [Google Scholar]
- Nordin, J., Brinnel, V., Giomi, M., et al. 2020, Transient Name Serv. Discov. Rep., 2020–3103, 1 [Google Scholar]
- Onori, F., Cannizzaro, G., Jonker, P. G., et al. 2019, MNRAS, 489, 1463 [CrossRef] [Google Scholar]
- Patterson, M. T., Bellm, E. C., Rusholme, B., et al. 2019, PASP, 131, 018001 [Google Scholar]
- Phinney, E. S. 1989, Manifestations of a Massive Black Hole in the Galactic Center, ed. M. Morris, 136, 543 [NASA ADS] [Google Scholar]
- Piran, T., Svirski, G., Krolik, J., Cheng, R. M., & Shiokawa, H. 2015, ApJ, 806, 8 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2007, MNRAS, 383, 627 [CrossRef] [Google Scholar]
- Prochaska, J., Hennawi, J., Westfall, K., et al. 2020, J. Open Source Softw., 5, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1988, Nature, 333, 523 [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, T. M., Mattila, S., Efstathiou, A., et al. 2022, A&A, 664, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryu, T., Krolik, J., & Piran, T. 2020, ApJ, 904, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schulze, S., Yaron, O., Sollerman, J., et al. 2021, ApJS, 255, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Shiokawa, H., Krolik, J. H., Cheng, R. M., Piran, T., & Noble, S. C. 2015, ApJ, 804, 85 [Google Scholar]
- Short, P., Nicholl, M., Lawrence, A., et al. 2020, MNRAS, 498, 4119 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. A., Tucker, D. L., Kent, S., et al. 2002, AJ, 123, 2121 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. W., Williams, R. D., Young, D. R., et al. 2019, Res. Notes AAS, 3, 26 [Google Scholar]
- Speagle, J. S. 2020, MNRAS, 493, 3132 [Google Scholar]
- Stone, N. C., & Metzger, B. D. 2016, MNRAS, 455, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, N. C., Vasiliev, E., Kesden, M., et al. 2020, Space Sci. Rev., 216, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Strubbe, L. E., & Quataert, E. 2009, MNRAS, 400, 2070 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Denneau, L., Heinze, A. N., et al. 2018, PASP, 130, 064505 [Google Scholar]
- Valenti, S., Sand, D., Pastorello, A., et al. 2014, MNRAS, 438, L101 [Google Scholar]
- Valenti, S., Howell, D. A., Stritzinger, M. D., et al. 2016, MNRAS, 459, 3939 [NASA ADS] [CrossRef] [Google Scholar]
- van Velzen, S. 2018, ApJ, 852, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Van Velzen, S., Anderson, G. E., Stone, N. C., et al. 2016, Science, 351, 62 [NASA ADS] [CrossRef] [Google Scholar]
- van Velzen, S., Holoien, T. W., Onori, F., Hung, T., & Arcavi, I. 2020, Space Sci. Rev., 216, 124 [CrossRef] [Google Scholar]
- van Velzen, S., Gezari, S., Hammerstein, E., et al. 2021, ApJ, 908, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., & Merritt, D. 2004, ApJ, 600, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Wevers, T., Pasham, D. R., van Velzen, S., et al. 2019a, MNRAS, 488, 4816 [Google Scholar]
- Wevers, T., Stone, N. C., Van Velzen, S., et al. 2019b, MNRAS, 487, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Wevers, T., Nicholl, M., Guolo, M., et al. 2022, A&A, 666, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, A. H. 2016, Astrophysics Source Code Library [record ascl:1604.003] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr, et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zauderer, B. A., Berger, E., Soderberg, A. M., et al. 2011, Nature, 476, 425 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Photometry tables
ZTF photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
LCO photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
Campo Imperatore photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
SWIFT photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
Appendix B: MOSFIT posteriors
The priors and marginalized posteriors of our MOSFIT TDE model were listed in Table 3. In Fig. B.1 we plot the full two-dimensional posteriors.
 |
Fig. B.1. Posterior probability density functions for the free parameters of the model light curves in Fig. 7. |
 |
Fig. B.2. Same as Fig. 11, but for BH mass estimated using the M–σ scaling relation. The correlation between the BH mass and the decline rate within the first 20 days (ΔL20) stands when the M–σ relation is used, even though it is not as strong as the correlation detected in Fig. 11. |
All Tables
Comparison of different properties of AT 2020wey with three well-studied faint and fast TDEs (iPTF16fnl, AT 2019qiz, and AT 2020neh).
ZTF photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
LCO photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
Campo Imperatore photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
SWIFT photometry in the AB system. All reported magnitudes are host-subtracted and de-reddened.
All Figures
 |
Fig. 1. De-reddened and host-subtracted light curves of AT 2020wey. After the peak, it seems that the light curve goes under two distinct phases: one until ∼20 days and another after 20 days. The inset shows fits in the g band (dashed lines), to the first phase (from peak to ∼20 days), and to the entire evolution. The first phase is fit with a linear fit (black line) and the full decline is fit with an exponential (green line). The same fits are plotted in the main plot (dashed lines) but in magnitude space. The exponential fit describes the late-time data nicely, but fails in following the early phase decline. As the event rises to peak, there seems to be a pre-peak precursor (ZTF g and r bands), never observed before in a TDE, between ∼ − 18 days and −10 days before the peak. |
| In the text | |
 |
Fig. 2. Spectral evolution of AT 2020wey. Left panel: De-reddened and host-subtracted spectra of AT 2020wey. The spectrum at +463.3 days is the host galaxy spectrum used for host subtraction. The green dashed lines are the polynomial fits to the continuum. Right panel: De-reddened, host-subtracted, and continuum-subtracted spectra of AT 2020wey. |
| In the text | |
 |
Fig. 3. Host galaxy SED fit with PROSPECTOR. The dashed vertical lines show the effective wavelengths of the Swift UVOT filters for which synthetic magnitudes have been derived (see Table 1). |
| In the text | |
 |
Fig. 4. Bolometric light curve, temperature, and radius evolution derived using SUPERBOL. The shaded regions indicate the time regions where constant color was assumed for extrapolation purposes. |
| In the text | |
 |
Fig. 5. Fits to the bolometric light curve during rise (top) and decline (bottom) of the light curve. Top: the photospheric radius (blue triangles) before peak grows linearly with a velocity v ≈ 1300 km s−1, while the luminosity (black circles) is best fit as L ∝ t1.8. Bottom: exponential and power-law fits to the declining bolometric light curve. The decline is much steeper than the canonical t−5/3. For comparison, iPTF16fnl and AT 2019qiz are overplotted and their bolometric light curves normalized in order for the three events to have the same peak; AT 2020wey is the fastest declining TDE to date. |
| In the text | |
 |
Fig. 6. Comparison of the bolometric light curve of AT 2020wey with the TDEs presented in Fig. 10 of Nicholl et al. (2020) and with AT 2020neh (Angus et al. 2022). The resemblance of AT 2020wey with iPTF16fnl is striking. AT 2020neh rises faster, but is brighter and decays more slowly. |
| In the text | |
 |
Fig. 7. Fits to the multi-color light curve using the TDE model in MOSFIT (Guillochon et al. 2018; Mockler et al. 2019). |
| In the text | |
 |
Fig. 8. Hα properties as a function of time. Left panel: Hα luminosity evolution of AT 2020wey as a function of time, compared with the sample of Charalampopoulos et al. (2022). The dashed vertical line denotes the time of peak or discovery of each TDE. Right panel: Hα line width evolution of AT 2020wey as a function of time, compared with the sample of Charalampopoulos et al. (2022). |
| In the text | |
 |
Fig. 9. Comparison of the Hα lag as a function of the peak of the blackbody radius of AT 2020wey with the other TDEs (Charalampopoulos et al. 2022). The dot-dashed line is a linear regression fit that does not include the three lower limits. |
| In the text | |
 |
Fig. 10. Light curves of AT 2020wey and other faint and fast TDEs. Left panels: comparison of the ZTF and LCO host-subtracted and de-reddened magnitudes of AT 2020wey with three faint and fast TDEs (iPTF16fnl, AT 2019qiz, and AT 2018ahl). Right panels: comparison of the UVOT host-subtracted and de-reddened magnitudes of AT 2020wey with two faint and fast TDEs (iPTF16fnl and AT 2019qiz). At +8 days post-peak, AT 2020wey starts declining very quickly in the UV; at 20 days after peak it has dropped an average of 0.69 mag more in the three UV bands (i.e., UVW1, UVM2, UVW2) compared to iPTF16fnl. |
| In the text | |
 |
Fig. 11. Peak bolometric luminosity (top panel) and its decline rate within the first 20 days (ΔL20 = log10(L20/Lpeak); bottom panel) as a function of the BH mass, for a sample of optical TDEs. The BH masses are computed with MOSFIT (Mockler et al. 2019; Nicholl et al. 2022). There is no correlation between the peak bolometric luminosity and the decline rate. However, there is a strong correlation between the decline rate and the BH mass of TDEs, where AT 2020wey is an outlier. |
| In the text | |
 |
Fig. 12. Comparison of the host-subtracted (and de-reddened) spectra of AT 2020wey with two more faint and fast TDEs (iPTF16fnl and AT 2019qiz). The three events are spectroscopically similar, but AT 2020wey lacks the strong nitrogen line at 4100 Å. |
| In the text | |
 |
Fig. 13. Absolute peak magnitude distributions (k-corrected) of the Hammerstein et al. (2023) TDE sample, with g band on the left and r band on the right. Shown in the top panel are the histograms of the original data (observed distributions) and in the bottom panel the data after volumetric correction (i.e., expected yields, number of TDEs). The colored bins contain TDEs that are fainter than or equally faint to AT 2019qiz. |
| In the text | |
 |
Fig. 14. Fits to the volumetric rates based on the Hammerstein et al. (2023) sample, for the ZTF g band (left) and ZTF r band (right). The histograms denote the expected yields (number of TDEs) after the volumetric correction, and they are the same as the bottom panel of Fig. 13. The colored bins include TDEs that are fainter than or equally faint to AT 2019qiz. |
| In the text | |
 |
Fig. 15. Absolute magnitudes of the TDEs in the Hammerstein et al. (2023) sample against the absolute magnitude of the nucleus of their respective hosts, in the ZTF g (top panel) and r (bottom panel) bands. AT 2020wey is plotted as a star and AT 2019qiz as a square. Even though the two TDEs have a faint host nucleus compared to the rest of the sample, a bias was not found to be present in discovering faint TDEs because of the faint nuclei of the respective hosts. |
| In the text | |
 |
Fig. B.1. Posterior probability density functions for the free parameters of the model light curves in Fig. 7. |
| In the text | |
 |
Fig. B.2. Same as Fig. 11, but for BH mass estimated using the M–σ scaling relation. The correlation between the BH mass and the decline rate within the first 20 days (ΔL20) stands when the M–σ relation is used, even though it is not as strong as the correlation detected in Fig. 11. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.