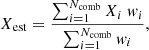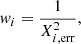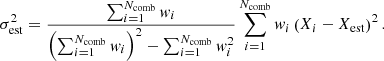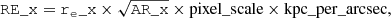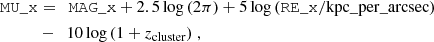| Issue |
A&A
Volume 671, March 2023
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202346151 | |
| Published online | 09 March 2023 | |
Letter to the Editor
The Kormendy relation of early-type galaxies as a function of wavelength in Abell S1063, MACS J0416.1-2403, and MACS J1149.5+2223⋆
1
University Observatory, Faculty of Physics, Ludwig-Maximilians-Universität München, Scheinerstr. 1, 81679 Munich, Germany
e-mail: Luca.Tortorelli@physik.lmu.de
2
Dipartimento di Fisica “E.R. Caianiello”, Università Degli Studi di Salerno, Via Giovanni Paolo II, 84084 Fisciano (SA), Italy
3
INAF-Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
4
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
5
INAF – IASF Milano, via Corti 12, 20133 Milano, Italy
6
Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, Via Saragat 1, 44122 Ferrara, Italy
7
INAF – Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
8
INAF – OAS, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, via Gobetti 93/3, 40129 Bologna, Italy
9
Technical University of Munich, TUM School of Natural Sciences, Department of Physics, James-Franck-Str 1, 85748 Garching, Germany
10
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
Received:
15
February
2023
Accepted:
24
February
2023
Context. The wavelength dependence of the projection of the fundamental plane along the velocity dispersion axis, namely the Kormendy relation, is well characterised at low redshift but poorly studied at intermediate redshifts. The Kormendy relation provides information on the evolution of the population of early-type galaxies (ETGs). Therefore, by studying it, we may shed light on the assembly processes of these objects and their size evolution. As studies at different redshifts are generally conducted in different rest-frame wavebands, it is important to investigate whether the Kormendy relation is dependent on wavelength. Knowledge of such a dependence is fundamental to correctly interpreting the conclusions we might draw from these studies.
Aims. We analyse the Kormendy relations of the three Hubble Frontier Fields clusters, Abell S1063 at z = 0.348, MACS J0416.1-2403 at z = 0.396, and MACS J1149.5+2223 at z = 0.542, as a function of wavelength. This is the first time the Kormendy relation of ETGs has been explored consistently over such a large range of wavelengths at intermediate redshifts.
Methods. We exploit very deep Hubble Space Telescope photometry, ranging from the observed B-band to the H-band, and VLT/MUSE integral field spectroscopy. We improve the structural parameter estimation we performed in a previous work by means of a newly developed PYTHON package called MORPHOFIT.
Results. With its use on cluster ETGs, we find that the Kormendy relation slopes increase smoothly with wavelength from the optical to the near-infrared (NIR) bands in all three clusters, with the intercepts becoming fainter at lower redshifts due to the passive ageing of the ETG stellar populations. The slope trend is consistent with previous findings at lower redshifts.
Conclusions. The slope increase with wavelength implies that smaller ETGs are more centrally concentrated than larger ETGs in the NIR with respect to the optical regime. As different bands probe different stellar populations in galaxies, the slope increase also implies that smaller ETGs have stronger internal gradients with respect to larger ETGs.
Key words: galaxies: evolution / galaxies: elliptical and lenticular, cD / galaxies: clusters: individual: Abell S1063 / galaxies: clusters: individual: MACS J1149.5+2223 / galaxies: clusters: individual: MACS J0416.1-2403 / galaxies: photometry
The table of structural parameters described in Appendix A is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/671/L9
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Studies of how the structural parameters of galaxies are linked to their dynamics and stellar properties via scaling relations and how these change as a function of redshift, environment, and wavelength have been used many times as probes to understand the formation and evolution of galaxies. The fundamental plane (FP; Dressler et al. 1987; Djorgovski & Davis 1987; Bender et al. 1992; Saglia et al. 1993; D’Onofrio & Chiosi 2022; D’Onofrio & Chiosi 2023) and its projections are among the most important galaxy scaling relations. The FP links the structural properties of early-type galaxies (ETGs), such as their surface brightnesses and effective radii, with their dynamics. One of its projections is the Kormendy relation (KR; Kormendy 1977). The KR links the effective radius Re of an ETG to its average surface brightness within that radius ⟨μ⟩e, ⟨μ⟩e = α + βlogRe. The KR is a physical correlation, presumably reflecting the difference in the origin of bright and faint ellipticals and bulges; it provides information on how the size and light distribution in ETGs evolve as a function of redshift. This implies that the KR can be used to understand whether ETGs have completed their growth in mass and size at their redshift or if there is still significant growth up to z = 0. Furthermore, the KR can also be used to study the bulge formation of disk galaxies (Gadotti 2009): classical bulges can be disentangled from pseudobulges, the latter being 3σ outliers with respect to the best-fitting KR (Costantin et al. 2018; Gao et al. 2020).
The KR has been studied extensively in the literature (Ziegler et al. 1999; La Barbera et al. 2003; Longhetti et al. 2007; Rettura et al. 2010; Saracco et al. 2014). However, the conclusions drawn from it are contrasting; in particular, they depend on how the sample of galaxies is selected, that is, whether this selection is based on colours, Sérsic indices, or stellar populations (e.g., Saracco et al. 2010; Andreon et al. 2016; Fagioli et al. 2016). In Tortorelli et al. (2018), we investigated the effect of sample selection and found that a selection purely based on colours may bias the KR parameter estimates, while galaxies selected through Sérsic indices (ETGs), visual inspection (ellipticals), and spectra (passives) constitute a more coeval population.
Additionally, the morphologies and therefore the sizes of galaxies may appear different at different wavelengths. As different wavelengths probe different regions and physical processes inside the galaxies, the KR does not necessarily hold or have the same parameters at all wavelengths. The surface brightness in the near-infrared (NIR) is less affected by gas and dust extinction; it is instead dominated by the older stellar population of galaxies, which constitutes their main stellar mass component, especially that of ETGs. Therefore, the contrast between the NIR and the optical observations translates into the contrast between the underlying mass component (older stellar population) and the younger stellar population component. Therefore, the wavelength range used to study the KR may impact the conclusions that we can draw from it. Studies of the wavelength dependence of the KR at low redshift have been conducted by La Barbera et al. (2010), for example. These studies show that there is evolution of the KR slope as a function of wavelength for Sloan Digital Sky Survey (SDSS) ETGs selected via colours in the form of a steepening of the relation from the g to the K observed bands. However, studies at higher redshifts (z > 0.3) with samples of ETGs consistently selected at different redshifts are still missing.
In this Letter, we use data from the Hubble Space Telescope (HST) Frontier Fields (FF) survey (Lotz et al. 2017) to study the KR of ETGs as a function of wavelength in three clusters at intermediate redshift, namely Abell S1063 at z = 0.348, MACS J0416.1-2403 at z = 0.396, and MACS J1149.5+2223 at z = 0.542. We build the KR for ETGs selected via Sérsic indices only, following the conclusions in Tortorelli et al. (2018) regarding the consistent selection of ETGs at different redshifts.
We measured the structural parameters using a new PYTHON package we developed called MORPHOFIT (Tortorelli & Mercurio 2023). We used the data-analysis pipeline first introduced in Tortorelli et al. (2018) and refined in Tortorelli & Mercurio (2023), which involves fitting the surface-brightness profiles of galaxies in images of increasing size.
The Letter is structured as follows. In Sect. 2, we describe the photometric and spectroscopic data used for this analysis. In Sect. 3, we summarise the structural parameter estimation process using MORPHOFIT. In Sect. 4, we present our results for the Kormendy-relation behaviour as a function of wavelength. Finally, we provide our main conclusions in Sect. 5.
Unless otherwise stated, we give errors at the 68 per cent confidence level, and we report the circularised effective radii. Throughout this Letter, we use H0 = 70 km s−1 Mpc−1 in a flat cosmology with ΩM = 0.3 and ΩΛ = 0.7. In the adopted cosmology, 1″ corresponds to 4.921 kpc at z = 0.348, to 5.340 kpc at z = 0.396, and to 6.364 kpc at z = 0.542.
2. Dataset
We analysed the three clusters Abell S1063 (AS1063) at z = 0.348, MACS J0416.1-2403 (M0416) at z = 0.396, and MACS J1149.5+2223 (M1149) at z = 0.542. A wealth of multi-wavelength and wide-field data are available for AS1063, M0416, and M1149 from photometry and spectroscopy (Rosati et al. 2014; Karman et al. 2015; Grillo et al. 2016; Mercurio et al. 2021). The photometric data we use in this study are available at the STScI Mikulski Archive for Space Telescopes (MAST) 1. These data belong to the FF programme2 (PI: J. Lotz, Lotz et al. 2017), which was designed to combine the power of HST and Spitzer with the natural gravitational telescope effect of massive high-magnification clusters of galaxies. These datasets allow us, for instance, to test predictions of the ΛCDM model (Annunziatella et al. 2017; Sartoris et al. 2020), to measure the Hubble constant value (Grillo et al. 2018, 2020), to refine weak and strong lensing models in order to map the total mass distribution in clusters (Gruen et al. 2013; Caminha et al. 2016; Bergamini et al. 2019; Granata et al. 2022), and to serendipitously discover very distant lensed galaxies up to z ∼ 6 (Vanzella et al. 2016; Balestra et al. 2018).
In order to measure the structural parameters (i.e. effective radii and surface brightnesses), we used the 0.060 arcsec/pixel images in all seven optical/NIR bands of the FF programme. The three optical bands F435W, F606W, F814W belong to the Advanced Camera for Surveys (ACS), while the four NIR bands F105W, F125W, F140W, F160W belong to the Wide Field Camera 3 (WFC3) IR imager. These bands span a wavelength range from ∼3500 Å, corresponding to the observed Johnson B-band filter, to ∼17 400 Å, corresponding to the observed H filter. This roughly corresponds to the rest-frame ranges: u to J band for AS1063 and M0416, and near-UV to Y band for M1149. We use the drz science images, the rms images, and the exp exposure-time-map images.
The AS1063 and M1149 spectroscopically confirmed cluster members we use in our analysis are the same as those selected in Tortorelli et al. (2018) using the Multi Unit Spectroscopic Explorer (MUSE) spectrograph integral field unit (IFU) spectra. The confirmed members are 95 for AS1063, which have redshifts in the range 0.335 ≤ z ≤ 0.361 (Karman et al. 2015), and 68 for M1149, which have redshifts of 0.52 ≤ z ≤ 0.57 (Grillo et al. 2016). HST imaging and MUSE IFU spectra allow us to reach a completeness in apparent magnitude of 1.0 down to a value of 22.5 in the F814W waveband (Caminha et al. 2016). This limit roughly corresponds to a stellar mass value of M* ∼ 109.8 M⊙ and M* ∼ 1010.0 M⊙ for AS1063 and M1149, respectively, for the typical spectral energy distribution of the sources we are interested in and considering a Salpeter initial mass function (IMF; Salpeter 1955). The cluster members for M0416 are also those for which MUSE spectra are available; there are 119 members, which have redshifts of 0.38 ≤ z ≤ 0.41. The description of the member selection is detailed in Annunziatella et al. (2017) and Caminha et al. (2017).
In Tortorelli et al. (2018), we defined and compared four different galaxy samples according to (a) Sérsic indices: early-type (‘ETG’), (b) visual inspection: ‘ellipticals’, (c) colours: ‘red’, (d) spectral properties: ‘passive’. We showed that the KR built with the ‘ETG’ sample is fully consistent with the ones obtained with the ‘elliptical’ and ‘passive’ samples. On the other hand, the KR slope built with the ‘red’ sample is only marginally consistent with those obtained with the other samples. Therefore, in this work, we analyse the results using only the sample of ETGs selected via Sérsic indices.
3. Structural parameter estimates with MORPHOFIT
In order to build the KR, we need to estimate the structural parameters of spectroscopically confirmed cluster members. We do this using the PYTHON package MORPHOFIT3 (Tortorelli & Mercurio 2023). The package uses SEXTRACTOR (Bertin & Arnouts 1996) and GALFIT (Peng et al. 2011) to automatically fit the surface-brightness profile of a set of user-defined galaxies. The code is highly parallelisable, making it suitable for modern wide-field photometric surveys. A complete description of the software features can be found in Tortorelli & Mercurio (2023).
The methodology for the estimation of structural parameters is a refined version of that highlighted in Tortorelli et al. (2018). To deal with the cluster-crowded environment and the intracluster light contribution, we adopt an iterative approach that analyses images of increasing size (from stamps to the full images) using different point-spread-function (PSF) images, background-estimation methods, and sigma image creation.
The analysis with MORPHOFIT starts by running SEXTRACTOR in forced photometry mode on the drizzled images of the three clusters in all seven wavebands. The structural parameters estimated with SEXTRACTOR constitute the initial values of the surface-brightness profile fits with GALFIT. As GALFIT requires a PSF image for the light-profile convolution, and it has been proven that different PSFs may lead to different structural parameter estimates (Vanzella et al. 2019), we built four different PSF images with four different methods for each cluster and each waveband (see Fig. 2 in Tortorelli & Mercurio 2023) to average out systematic effects arising from a specific model PSF. We used the SEXTRACTOR catalogue to select stars on the images based on their loci on the magnitude–size (MAG_AUTO vs. FLUX_RADIUS SEXTRACTOR parameters) and magnitude–maximum surface brightness (MAG_AUTO vs. MU_MAX SEXTRACTOR parameters) planes and then cut stamps of 50 pixels in size around them. The sample of stars is further refined based on a signal-to-noise ratio (100 ≤ S/N ≤ 800) and isolability criterion (no detected sources around).
MORPHOFIT then cuts stamps around the spectroscopically confirmed cluster members and fits their light profiles and those of the neighbouring objects in the stamps with GALFIT. We fit single Sérsic profiles with initial values of the positions, magnitudes, half-light radii, axis ratios, and position angles given by the SEXTRACTOR parameters XWIN_IMAGE, YWIN_IMAGE, MAG_AUTO, FLUX_RADIUS, BWIN_IMAGE/AWIN_IMAGE, and THETAWIN_IMAGE, respectively. The initial values of the Sérsic indices are kept fixed at 2.5. The fit is performed on each member for all seven wavebands with different combinations of four kinds of PSF images, two background estimate methods and two different ways of providing GALFIT with sigma images (see Sects. 2 and 4 in Tortorelli & Mercurio 2023 for more details). For each galaxy, we combine the measurements Xi obtained with the various combinations (‘comb’) into a single estimate Xest of the structural parameters via an error-weighted mean:
where wi and Xi, err are the weights and the errors quoted by GALFIT for each fit, respectively. The error on the estimates σest is computed as the square root of the unbiased, weighted estimator sample variance:
These structural parameters are, in turn, used as initial values for the light-profile fit of galaxies in images of increasing size, first on image regions and then on the full images. We used the same combination of PSF images, background, and sigma images as the fit on stamps. The final structural parameters we used to build the KR at different wavelengths are a weighted mean (Eq. (A.2)) of those obtained with the different combinations in the seven wavebands on the full images. The structural parameters for the three clusters are provided as supplementary material to this Letter (Appendix A).
4. The Kormendy relation as a function of wavelength
We used the structural parameters estimated in Sect. 3 to select the sample of ETGs we used to build the KR. Following Tortorelli et al. (2018), we fit galaxies with single Sérsic profiles and select ETGs as those having Sérsic indices in the F814W waveband, nF814W ≥ 2.5. Additionally, we limit our analysis to galaxies brighter than the completeness limit, mF814W ≤ 22.5 ABmag, and we do not consider BCGs in the fit. The number of galaxies satisfying this criterion is 42, 50, and 35 for AS1063, M0416, and M1149, respectively.
We performed the linear regression analysis of the KR, ⟨μ⟩e = α + βlogRe, as in Tortorelli et al. (2018), using the bivariate correlated errors and intrinsic scatter estimator (BCES; Akritas & Bershady 1996) method. ⟨μ⟩e and Re are in units of mag arcsec−2 and kpc, respectively, and the surface brightness is corrected for the cosmological dimming effect. Table 1 reports the slopes, intercepts, scatters, and their 1σ uncertainties of the best-fitting KRs built with the ETG samples for the three clusters in the seven wavebands.
Best-fitting slopes, intercepts, observed scatters, and their 1σ errors obtained by fitting the KR to the ETG samples.
Figure 1 shows the slope and intercept evolution with wavelength for AS1063, M0416, and M1149. We fit a linear relation to the slopes as a function of wavelength. We find the slopes of the three clusters evolve with wavelength, smoothly increasing their values from the observed B-band to the observed H-band. This result extends the trend of the KR slope increase with wavelength already found at low redshift by La Barbera et al. (2010) to intermediate redshift. In our work, the NIR slopes have higher values and are only marginally consistent within the errors with the values quoted by La Barbera et al. (2010), despite our errors being larger due to the much smaller number of objects.
 |
Fig. 1. Best-fitting KR slope β (left panel) and intercept α (right panel) evolution as a function of wavelength for AS1063, M0416, and M1149 (blue, green, and red points, respectively). The scatter points refer to the best-fitting KR slopes and intercepts obtained from the linear regression on the galaxy structural parameters measured with MORPHOFIT. The dashed lines in the left panel represent the best-fitting linear relations that describe the trend of increasing slope values as a function of wavelength for the three clusters. The coloured bands group the scatter points belonging to the same waveband, which are displaced for clarity. The left plot legend shows the slope values and their 1σ uncertainties. |
A steeper KR implies that the difference in the surface brightness between small and large ETGs is larger than that obtained with a shallower KR. This physically implies that smaller ETGs are more centrally concentrated than larger ETGs in the NIR regime with respect to the optical one. As different wavebands probe different stellar populations in the galaxy, the smooth increase in slope from optical to NIR also implies that smaller ETGs have stronger internal stellar population gradients than galaxies with larger effective radii. Additionally, this result points to the fact that the analysis of the KR at different redshifts should be conducted in the same rest-frame bands; otherwise, the wavelength evolution may impact the conclusions from the KR analysis.
We also split the samples of cluster members in apparent magnitude bins to replicate the conclusions in Nigoche-Netro et al. (2008) in regards to the KR slope dependence on the width of the magnitude range and the brightness of galaxies within the magnitude range. We were not able to assess whether this trend is also present in our data, given the small sample of spectroscopically confirmed members. The errors estimated via bootstrap are very high, because with small samples, removing an object changes the KR parameters dramatically. Therefore, any trend existing with magnitude is completely masked by the very large errors.
The trend of the intercepts shows an expected behaviour as a function of wavelength. The intercepts of the three clusters get brighter at larger wavelengths, because the sample of ETGs is expected to be constituted by a population of galaxies with passive spectral energy distributions. The trend as a function of redshift is also consistent with what we already found in Tortorelli et al. (2018), meaning that the intercepts become fainter at lower redshift due to the passive ageing of the ETG stellar populations. The scatter points of AS1063 and M0416 are almost consistent at all wavelengths, given their smaller difference in redshift with respect to M1149.
5. Conclusions
In this Letter, we present our investigation of how the KR parameters change as a function of the wavelength range probed. We performed this analysis using spectroscopically confirmed cluster members of the three FF clusters, Abell S1063 (z = 0.348), MACS J0416.1-240(z = 0.396), and MACS J1149.5+2223 (z = 0.542) in seven photometric wavebands from the observed B-band to the observed H-band.
We measured the galaxy structural parameters for the KR using the PYTHON package MORPHOFIT (Tortorelli & Mercurio 2023), following a refined version of the methodology of increasing image size already adopted in Tortorelli et al. (2018). We used the structural parameters to select ETGs as those with Sérsic indices, nF814W ≥ 2.5, and magnitude brighter than the completeness limit, mF814W ≤ 22.5 ABmag.
We built the KR across the whole range of available wavelengths, and find that the KR intercepts follow an expected trend, becoming fainter at lower redshift due to the passive ageing of the ETG stellar populations. We also find that the slopes of the KRs increase smoothly with wavelength for all three clusters.
This result extends the conclusions already found by La Barbera et al. (2010) at low redshift with SDSS to intermediate redshifts. The slope increase with wavelength implies that smaller ETGs are more centrally concentrated in the NIR than those with larger radii with respect to the optical regime. As different wavelengths probe different stellar populations, this also implies that smaller ETGs have stronger internal stellar population gradients than larger ETGs. Our investigation of the slope change with wavelength suggests that studies addressing the KR evolution should be conducted at similar rest-frame wavebands at different redshifts for a robust comparison.
Acknowledgments
We acknowledge financial contributions by PRIN-MIUR 2017WSCC32 “Zooming into dark matter and proto-galaxies with massive lensing clusters” (P.I.: P.Rosati), INAF “main-stream” 1.05.01.86.20: “Deep and wide view of galaxy clusters (P.I.: M. Nonino)” and INAF “main-stream” 1.05.01.86.31 “The deepest view of high-redshift galaxies and globular cluster precursors in the early Universe” (P.I.: E. Vanzella). The CLASH Multi-Cycle Treasury Program is based on observations made with the NASA/ESA Hubble Space Telescope. The Space Telescope Science Institute is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. Based on observations made with the European Southern Observatory Very Large Telescope (ESO/VLT) at Cerro Paranal, under programme IDs 60.A-9345(A), 095.A-0653(A), 294.A-5032(A) and 186.A-0798(A).
References
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [Google Scholar]
- Andreon, S., Dong, H., & Raichoor, A. 2016, A&A, 593, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Annunziatella, M., Bonamigo, M., Grillo, C., et al. 2017, ApJ, 851, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Balestra, I., Vanzella, E., Rosati, P., et al. 2018, A&A, 611, C2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bender, R., Burstein, D., & Faber, S. M. 1992, ApJ, 399, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Bergamini, P., Rosati, P., Mercurio, A., et al. 2019, A&A, 631, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2016, A&A, 587, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costantin, L., Corsini, E. M., Méndez-Abreu, J., et al. 2018, MNRAS, 481, 3623 [CrossRef] [Google Scholar]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [Google Scholar]
- D’Onofrio, M., & Chiosi, C. 2022, A&A, 661, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Onofrio, M., & Chiosi, C. 2023, A&A, in press https://doi.org/10.1051/0004-6361/202245057 [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [Google Scholar]
- Fagioli, M., Carollo, C. M., Renzini, A., et al. 2016, ApJ, 831, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A. 2009, MNRAS, 393, 1531 [Google Scholar]
- Gao, H., Ho, L. C., Barth, A. J., & Li, Z.-Y. 2020, ApJs, 247, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Granata, G., Mercurio, A., Grillo, C., et al. 2022, A&A, 659, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grillo, C., Karman, W., Suyu, S. H., et al. 2016, ApJ, 822, 78 [Google Scholar]
- Grillo, C., Rosati, P., Suyu, S. H., et al. 2018, ApJ, 860, 94 [Google Scholar]
- Grillo, C., Rosati, P., Suyu, S. H., et al. 2020, ApJ, 898, 87 [Google Scholar]
- Gruen, D., Brimioulle, F., Seitz, S., et al. 2013, MNRAS, 432, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Karman, W., Caputi, K. I., Grillo, C., et al. 2015, A&A, 574, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kormendy, J. 1977, ApJ, 218, 333 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Busarello, G., Merluzzi, P., Massarotti, M., & Capaccioli, M. 2003, ApJ, 595, 127 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., de La Rosa, I. G., & Lopes, P. A. A. 2010, MNRAS, 408, 1335 [CrossRef] [Google Scholar]
- Longhetti, M., Saracco, P., Severgnini, P., et al. 2007, MNRAS, 374, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Mercurio, A., Rosati, P., Biviano, A., et al. 2021, A&A, 656, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nigoche-Netro, A., Ruelas-Mayorga, A., & Franco-Balderas, A. 2008, A&A, 491, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H. W. 2011, Astrophysics Source Code Library [record ascl:1104.010] [Google Scholar]
- Rettura, A., Rosati, P., Nonino, M., et al. 2010, ApJ, 709, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Balestra, I., Grillo, C., et al. 2014, The Messenger, 158, 48 [NASA ADS] [Google Scholar]
- Saglia, R. P., Bender, R., & Dressler, A. 1993, A&A, 279, 75 [NASA ADS] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Saracco, P., Casati, A., Gargiulo, A., et al. 2014, A&A, 567, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saracco, P., Longhetti, M., & Gargiulo, A. 2010, MNRAS, 408, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sartoris, B., Biviano, A., Rosati, P., et al. 2020, A&A, 637, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tortorelli, L., & Mercurio, A. 2023, Front. Front. Astron. Space Sci., submitted, [arXiv:2302.07890] [Google Scholar]
- Tortorelli, L., Mercurio, A., Paolillo, M., et al. 2018, MNRAS, 477, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., De Barros, S., Cupani, G., et al. 2016, ApJ, 821, L27 [Google Scholar]
- Vanzella, E., Calura, F., Meneghetti, M., et al. 2019, MNRAS, 483, 3618 [Google Scholar]
- Ziegler, B. L., Saglia, R. P., Bender, R., et al. 1999, A&A, 346, 13 [NASA ADS] [Google Scholar]
Appendix A: Catalogues of structural parameters
The catalogues of structural parameters for the three clusters AS1063, M0416, and M1149 are provided as supplementary material to this letter. Catalogues are provided in the form of FITS tables. The table column names (in typewritten font) and their descriptions are as follows:
ID: ID in serial order.
RA: right ascension in degrees.
DEC: declination in degrees.
MAG_x: total magnitude in the x-band.
MAG_ERR_x: total magnitude error in the x-band.
RE_x: circularised effective radius in kpc in the x-band.
RE_ERR_x: circularised effective radius error in kpc in the x-band.
MU_x: average surface brightness within the effective radius in mag arcsec−2 in the x-band.
MU_ERR_x: average surface brightness within the effective radius error in mag arcsec−2 in the x-band.
N_x: Sérsic index in the x-band.
N_ERR_x: Sérsic index error in the x-band.
AR_x: axis ratio in the x-band.
AR_ERR_x: axis ratio error in the x-band.
PA_x: position angle in degrees in the x-band.
PA_ERR_x: position angle error in degrees in the x-band.
MAG_x, N_x, AR_x, PA_x and their respective errors are the final structural parameters obtained in Sect. 3 from the fit on the full images. The weighted-means re_x, MAG_x, AR_x and the errors re_ERR_x, MAG_ERR_x, AR_ERR_x of the effective radii in pixels, magnitudes and axis ratios in the x-band are used to compute the circularised effective radii in kpc,
the average surface brightnesses within that radius,
and their respective errors RE_ERR_x and MU_ERR_x.
All Tables
Best-fitting slopes, intercepts, observed scatters, and their 1σ errors obtained by fitting the KR to the ETG samples.
All Figures
 |
Fig. 1. Best-fitting KR slope β (left panel) and intercept α (right panel) evolution as a function of wavelength for AS1063, M0416, and M1149 (blue, green, and red points, respectively). The scatter points refer to the best-fitting KR slopes and intercepts obtained from the linear regression on the galaxy structural parameters measured with MORPHOFIT. The dashed lines in the left panel represent the best-fitting linear relations that describe the trend of increasing slope values as a function of wavelength for the three clusters. The coloured bands group the scatter points belonging to the same waveband, which are displaced for clarity. The left plot legend shows the slope values and their 1σ uncertainties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.