SsODNet: Solar system Open Database Network

J. Berthier; B. Carry; M. Mahlke; J. Normand

doi:10.1051/0004-6361/202244878

Home

All issues

Volume 671 (March 2023)

A&A, 671 (2023) A151

Full HTML

Open Access

Issue		A&A Volume 671, March 2023


Article Number		A151
Number of page(s)		27
Section		Catalogs and data
DOI		https://doi.org/10.1051/0004-6361/202244878
Published online		21 March 2023

A&A 671, A151 (2023)

SsODNet: Solar system Open Database Network

J. Berthier¹, B. Carry², M. Mahlke² and J. Normand¹

¹ IMCCE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ Paris 06, Univ. Lille, 75014 Paris, France
e-mail: jerome.berthier@obspm.fr; jonathan.normand@obspm.fr
² Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, CS 34229 06304 Nice Cedex 4, France
e-mail: benoit.carry@oca.eu; max.mahlke@oca.eu

Received: 3 September 2022
Accepted: 21 December 2022

Abstract

Context. The sample of Solar system objects has dramatically increased over the last decade. The number of measured properties (e.g., diameter, taxonomy, rotation period, thermal inertia, etc.) has expanded even more quickly. However, this wealth of information is spread over a myriad of studies, with different designations reported per object.

Aims. We provide a solution to the identification of Solar system objects based on any of their multiple names or designations. We also compile and rationalize their properties to provide an easy access to them. We aim to continuously update the database as new measurements become available.

Methods. We built a Web Service, SsODNet, which offers four access points, each corresponding to an identified necessity in the community: name resolution (quaero), compilation of a large corpus of properties (dataCloud), determination of the best estimate among compiled values (ssoCard), and a statistical description of the population (ssoBFT).

Results. The SsODNet interfaces are fully operational and freely accessible to everyone. The name resolver quaero translates any of the ~5.3 million designations of objects into their current and official designation. The dataCloud includes about 105 million parameters (osculating and proper elements, pair and family membership, diameter, albedo, mass, density, rotation period, spin coordinates, phase function parameters, colors, taxonomy, thermal inertia, and Yarkovsky drift) from over 3000 articles (updated continuously). For each of the known asteroids and dwarf planets (~1.2 million), a ssoCard that provides a single best-estimate for each parameter is available. The SsODNet service provides these resources in a fraction of second upon query. Finally, the extensive ssoBFT table compiles all the best estimates in a single table for population-wide studies.

Key words: astronomical databases: miscellaneous / catalogs / minor planets, asteroids: general

© The Authors 2023

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The first decade of the 2000s saw an order of magnitude increase in the sample of known Solar System objects (SSOs) from roughly 50 000 to 600 000. While this number has doubled since, the revolution of most recent decade has seen an even faster growth on the part of the measured properties of these bodies. About 2000 diameters and albedo had been determined from IRAS mid-infrared observations (Tedesco et al. 2002) and over 150 000 are available today (e.g., Mainzer et al. 2011; Masiero et al. 2011; Grav et al. 2011). Hundreds of detections of the Yarkovsky effect (Vokrouhlický et al. 2015) are available (e.g., Del Vigna et al. 2019; Greenberg et al. 2020) just 20 yr after the first-ever detection (Chesley et al. 2003).

This wealth of characterizations (e.g., colors, albedos, rotation periods, etc.) has allowed for multiple statistical studies on the forced orientation of family members by the Yarkovsky-O’Keefe-Radzievskii-Paddack (YORP) effect (Slivan 2002; Hanuš et al. 2016), the compositional distribution of the asteroid belt (DeMeo & Carry 2014), the size-frequency distribution of asteroid families (Parker et al. 2008; Masiero et al. 2013), the internal structure of minor bodies (Carry 2012; Scheeres et al. 2015), and the origins of near-Earth asteroids (Perna et al. 2018; Devogèle et al. 2019; Binzel et al. 2019), among many others.

The benefit of all these developments has not, however, come to full fruition. If some catalogs are publicly available in machine-readable formats on the Planetary Data System¹ (PDS), the Centre de Données astronomiques de Strasbourg² (CDS), or alternative repositories (with unfortunately an endless variety of formats), a significant fraction of results have only been tabulated within the relevant papers. Some journals offer machine-readable versions of these tables on their online versions, but only for recent articles. Furthermore, the designation of small bodies often evolves over time, going from several possible provisional designations to a single number and then ultimately establishing an official name. Hence, the same object can be referred to with different labels in different studies, making its cross-identification over several sources a complex task. Accessing to all the characteristics of a given body or population can thus prove tedious and even impractical.

Compiling estimates of SSO properties and deriving the best estimate for each is of high practical relevance for the computation of ephemerides in the Virtual Observatory (VO) Web services we maintain (Miriade, SkyBoT, Berthier et al. 2006, 2008). Dynamical properties (i.e., osculating elements) are required to compute the position of SSOs and physical properties are required to predict their apparent aspect as seen by an observer, such as (i) the apparent magnitude in V band, relying on the phase function (HG or HG₁G₂, Bowell et al. 1989; Muinonen et al. 2010), (ii) the apparent magnitude in any other band, requiring a color index derived from the spectral class (e.g., DeMeo & Carry 2013; Popescu et al. 2018), (iii) the flux at mid-infrared wavelengths, computed from the diameter and albedo through a thermal model (Harris & Davies 1999), (iv) the shape and orientation of a target on the plane of the sky (often referred to as physical ephemerides), based on its 3D shape model, rotation period, and spin-vector coordinates (e.g., Marciniak et al. 2012).

Beyond the ephemerides computation, an extensive and rationalized compilation of SSO properties has many applications, from detailed in-depth studies on specific targets to population-wide statistical description of parameters. Over the years, publicly available compilations of data have flourished, for instance, the Jet Propulsion Laboratory Small Bodies Database³, the Las Cumbres Observatory NEOExchange⁴ (Lister et al. 2021), the Lowell observatory Minor Planet Services⁵ (Moskovitz et al. 2021), the NEOROCKs physical properties database⁶ (Zinzi et al. 2021), the Observatoire de la Côte d’Azur Minor Planet Physical Properties Catalog⁷ (MP3C, Delbò et al. 2018), the Size, Mass and Density of Asteroids (SiMDA⁸, Kretlow 2020), and the SUPAERO ECOCEL⁹ (Kovalenko et al. 2022). While these services fulfill many of the community’s needs, most of them do not provide a fast machine-machine interface.

Thus, we have designed a fully scriptable Web Service named the Solar system Open Database Network (SsODNet) which is aimed at providing the best estimate of a variety of parameters for every SSO. Owing to the complexity of compiling SSO data as depicted hereinabove, SsODNet consists of a suite of chained steps: from the identification of objects to the massive compilation of data, ending with the selection of best estimates, and summarizing them in a table. As each of these steps represents a typical task relevant for the community, we propose a dedicated front-end (a Web service associated with an Application Programming Interface − API) for each.

In Sect. 2, we describe how quaero builds a unique identifier for each object, associating all its aliases and providing the identity of the SSO. In Sect. 3, we describe how dataCloud compiles the measurements and estimates of properties from many sources, providing the most-possible comprehensive data set of SSOs. In Sect. 4, we describe how ssoCard provides the best estimate of each SSO property, and lists them in a single organized identify card. In Sect. 5, we describe how ssoBFT summarizes the most-commonly requested of these parameters for all SSOs. We then describe how to query these services in Sect. 6 before discussing the future developments of SsODNet in Sect. 7.

2 Name resolver: `quaero`

The SsODNet.quaero name-resolution service is built to address the issue of identification of SSOs and, more generally, of all planetary and artificial objects gravitationally bound to a star. Upon the submission of any of the possible designations of a target, quaero returns its official or main designation, together with all its aliases. To be compliant with the spirit of the VO (“name resolver”) quaero can also return the equatorial coordinates of the object at a given epoch.

2.1 Context

The Solar System is populated by widely different types of celestial bodies: from planets and their satellites to minor planets (comets, asteroids, Centaurs, Kuiper-belt objects, etc.) and their satellites, and further on to artificial satellites, space probes, and space debris. Since the first exoplanet detection by Mayor & Queloz (1995), today we know of about 5000 planetary objects that orbit around other stars than the Sun. A few rogue planets (e.g., OTS 44 or Cha 110913-773444) and two interstellar objects (1I/’Oumuamua and 2I/Borisov) complete the picture of the planetary zoo.

The nomenclature of SSOs is entrusted to two groups under the auspices of the International Astronomical Union (IAU) Division F. The first is the Working Group for Planetary System Nomenclature (WG-PSN), which is in charge of naming features on planets, satellites, and asteroids. This group also names planets (although the IAU has not named a planet as of yet) and the natural satellites of major planets. The second is the Working Group for Small Bodies Nomenclature (WG-SBN), which is responsible for naming of all other small bodies (minor planets, satellites of minor planets, and comets). Both working groups share responsibility for naming dwarf planets (IAU 2020a).

As of today, there are no official name for exoplanets assigned by the IAU. The public names, assigned through a public naming process such as NameExoWorlds¹⁰ is distinguished from the official scientific designation, which follows the rules of the system used for designating multiple-star systems as adopted by the IAU (IAU 2020b).

Spacecraft, together with launchers, payloads, and space debris, are indexed for safety and cooperation purposes. They are usually named by their funders (space agencies, laboratories, or companies). They are also assigned an International Designator (COSPAR ID), under the responsibility of the Committee on Space Research (COSPAR) of the International Council for Science (ICSU), and a Satellite Catalog Number (NORAD ID) attributed by the United States Space Command (USSPACECOM).

Since the designation of the major bodies of the Solar System (the Sun, the Moon, the eight planets), more than 1.2 million objects have been inventoried, classified, and named. As of today, there are more than 5.3 million designations used to name them all. Objects can have multiple designations owing to the evolution of knowledge as well as changes in nomenclature over time¹¹. We illustrate this with the first asteroid discovered in 1801: Ceres. It is classified today as a dwarf planet. Its official designation is “(1) Ceres:” a number in parenthesis followed by a name. This official designation thus already contains two labels. However, Ceres was also named using provisional designations over the years, assigned to past astrometric observations that had not been immediately connected to its orbit: “1801 AA,” “1899 OF,” and “1943 XB,” and the corresponding packed names¹² “I01A00A,” “I99O00F,” and “J43X00B”. Thus Ceres can be known by eight different names. The all-time record is held by comets P/Halley (1P), with 59 designations, and P/Encke (2P), with 89 designations. We present in Fig. 1 the distribution of the number of designations by type of SSOs and we present a summary in Table 1.

Fig. 1

Histogram of the number of designations for each class of object.

Table 1

Statistics of the number of SSO designations by object class.

2.2 Quaero: /’k^waę.ro:/

This is the core of SsODNet. It ensures the reliability of the naming of SSOs and it allows us to cross-match identifications between their actual names and the designations used over time in the various data sets. In August 2022, we counted 1288 838 solar and extra-solar objects for 5 360208 designations (1:4 ratio).

Overall, SsODNet.quaero is designed to fulfill four main functionalities: (1) to identify a SSO from its designation; (2) to explore the naming of SSOs using wildcard, regular expression, or fuzziness; (3) to resolve the name of a SSO into sky coordinates; and (4) to provide an autocomplete feature that can be used to offer SSO name suggestions when a user types in an input field.

To achieve this goal, once a week we gather all the available planetary object designations from the Minor Planet Center (Marsden 1980) for asteroids and dwarf planets, the IMCCE’s CometPro Database (Rocher & Cavelier 1996) for comets, the Extrasolar Planets Encyclopaedia (Exoplanet-Team 2021) for exoplanets, and CelesTrak (Kelso 2021) for spacecrafts and debris. These designations are then stored and indexed in a dedicated database.

We use the NoSQL database Elasticsearch¹³ to manage the millions of designations. It is a full-text search engine based on the Apache Lucene library¹⁴. Each object is defined by a set of fields (document) defining its Id, name, aliases, parent, type, and so on. Documents are stored in an Elasticsearch index as JSON-format data. By default, Elasticsearch tries to guess the correct mapping for fields, but to meet the challenges of planetary object identification, we specified our own mapping.

If SSO designations are indexed as individual strings, then a user can only find whole names. To allow for the search of a name on a part of a designation, we decompose all the SSO designations into small chunks (tokens). However, at this step, each token is still matched literally. This means (among other things) that a search for a name with or without an accent or a special character, or one with mixed lowercase and uppercase characters, would possibly not result in a match with any name. To solve this issue, we defined the normalization rules to allow for the matching of tokens that are not exactly the same as the search names, but similar enough to still be relevant. For the full technical information, we refer to the documention¹⁵ of the SsODNet.quaero API.

3 Compilation of properties: `dataCloud`

The SsODNet.dataCloud service is designed to compile all published measurements and estimates of SSO properties. The dataCloud uses SsODNet.quaero to identify objects over their multiple designations. It also associates every estimate with a bibliographic reference and a method. Upon request, the dataCloud returns all the estimates of a given property or parameter for the requested SSO.

3.1 Context

Starting with the planetary motion (Newton 1760), the first studies of SSOs focused on their dynamics (Gauss 1809), which is required to compute their ephemerides. From the distribution of their orbital elements, Hirayama (1918) discovered the dynamical families. Time-series photometry has led to the determination of numerous rotation periods in the first half of the twentieth century (e.g., Bailey & Pickering 1913). The 1970s saw the advent of compositional and physical studies, with the first studies of diameter and albedo (e.g., Cruikshank & Morrison 1973), mass and, hence, the density (Schubart 1974), along with the spectrophotometry and taxonomy (e.g., Chapman et al. 1975). The handful of SSOs with spin-vector coordinates and triaxial dimensions of the 1980s (Drummond & Cocke 1989) grew to several hundreds in the 2000s thanks to the light-curve inversion technique (Kaasalainen & Torppa 2001). Similarly, estimates of thermal inertia and Yarkovsky drift are common nowadays (Hanuš et al. 2018; Greenberg et al. 2020), even though the first studies were completed only two decades ago (Lagerros 1996; Chesley et al. 2003).

Benefiting from these progresses is complex, however, as the fast-growing number of measured properties is spread over a myriad of articles. Machine-readable catalogs delivered by authors to the PDS or the CDS only represent the tip of the iceberg. Furthermore, there is a large heterogeneity in how SSOs are labeled (number, name, packed designation, etc.) and in how quantities are reported: masses, M, in terms of kg or solar masses (M_⊙) or as a GM product or the albedo in linear or logarithmic scale, for instance.

The sample size of individual articles may be small, but their sum is large. In particular, some size-limited sample may be extremely valuable, such as results on a single target obtained during a spacecraft rendezvous for example. Therefore, the goal of compiling every estimate should not be overlooked by the community.

SsODNet.dataCloud compiles in a single database as many estimates as possible for a variety of SSO properties. Such a centralization of data may appear anachronistic in the current landscape of connections to remote databases, such as what is regularly done in the VO (Bayo et al. 2008). It is, however, required here. First, the remote databases do not exist. Second, owing to the issue of SSO naming, on-the-fly cross-matches between resources would be slow upon query. We chose to place the workload on the server side, in an asynchronous process, to provide a fast service to users. Such a solution is already used for the ESA Gaia archive¹⁶, in which time-consuming crossmatches of Gaia catalog (Gaia Collaboration 2016, 2018, 2021) with other common large catalogs (e.g., SDSS DR9, 2MASS, allWISE, Ahn et al. 2012; Skrutskie et al. 2006; Wright et al. 2010; Cutri et al. 2013) are already computed and stored (see details in Marrese et al. 2017).

3.2 Method

The design of the dataCloud is very simple: the parameters are grouped by collection of properties in SQL tables, such as diameter and albedo (as they are seldom derived independently), mass, thermal inertia, taxonomy, astrometry (the MPCAT-OBS database, MPC 2021), and so on. There are a few exceptions to this general scheme. The osculating elements of asteroids from the Minor Planet Center (MPC, Marsden 1980) and the Lowell observatory (Bowell et al. 1994), as well as those of comets from the IMCCE (Rocher & Cavelier 1996), are stored in separated tables. The Appendix A provides the list of collections composing the dataCloud ecosystem.

Each entry of tables corresponds to a single determination of a parameter for a given target. Parameters are stored with their uncertainties, the method used to obtain them (see Appendix B), a selection flag (used to discriminate among estimates; see Sect. 4), and the bibliographic reference of the source of data. A given SSO, or bibliographic reference, may be repeated multiple times: some studies include many objects and the same SSO may have been analyzed in multiple studies. Figure 2 shows the distribution over time of the publications (currently 3007) used to build the dataCloud database. For convenience, a file compiling all the bibliographic references in bibtex format is available¹⁷.

A key aspect of the collections is the unique identifier assigned to each SSO, built upon their name and used to identify them across tables. At every update of the database, the name of each SSO (as published by authors) is tested with SsODNet.quaero and updated upon ingestion. Hence, all properties are linked together using the most up-to-date designation.

For each parameter, we started the compilation from scratch, individually adding each bibliographic reference. The only exceptions to this are the masses and the spins. For both, we first input a previous compilation of data, taken from Carry (2012) and Warner et al. (2021) respectively.

Fig. 2

Years of publication of bibliographic references used to populate SsODNet.dataCloud.

4 Selection of the best estimates: `ssoCard`

The SsODNet.ssoCard provides apractical solution to the question of finding the best estimate for a wide range of parameters of SSOs. From the dataCloud, it builds the resume of each SSO, named ssoCard. These ssoCard are small files that can be easily downloaded and read upon user request. The present first release of SsODNet.ssoCard proposes ssoCard for asteroids and dwarfplanets only. We plan to offerssoCard forothertypes of SSOs (comets, satellites) in subsequent releases (see Sect. 7).

4.1 Context

Among the hundreds of articles compiled in the dataCloud, a significant fraction report the same parameter for a given SSO. A question then arises about the most optimal way to choose a value. A simple statistical averaging cannot address the question: some methods are intrinsically more precise than others and some are direct measurements, while others are model-dependent. Moreover, uncertainties associated with values often do not account for possible biases, namely, forexternal errors. This implies that the choice of the best value cannot entirely rely on criteria that are based on the repeatability of the measurements.

The structure and format of data must also be addressed. The usual table format (i.e., rows and columns) is not very well adapted to these purposes. Some SSOs have estimates across a wide variety of parameters (osculating elements, proper elements, diameter, mass, density, colors across many filters, taxonomy, and so forth), while others have a few parameters only (e.g., osculating elements). Structuring the data in a flat 2D table implies that a vast majority of cells will be empty. With the current data in SsODNet, the filling factor of such a table would only be ~15% (see Sect. 5).

Furthermore, the association of data with meta-data (i.e., method, bibliographic reference, and units) is also an issue with regard to the table format. Considering that a human-readable bibliographic reference is composed of at least four fields (title, authors, year, bibcode), the number of columns will increase by a factor of four for each group of properties. In the current ecosystem of SsODNet.dataCloud, composed of 15 collections exposing 591 fields, it would imply a final table composed of 651 columns.

Considering all these elements, we chose to structure the parameters in a key-value data format allowing for nested objects and arrays. We chose the open standard file format JSON (Bray 2017). A XML-based format such as VOTable¹⁸ could have been suitable to include metadata, but given it is rather verbose in nature, it would significantly increase the volume of data to exchange.

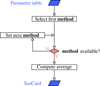Fig. 3

General workflow used to compute the best estimate of each parameter.

4.2 Method

The best estimate for each SSO property depends mainly on the method used to measure it: for example, a direct measurement from an in situ space mission can be considered to be more valuable than an indirect determination based on telescopic observations acquired from the Earth. Similarly, a modern measurement is often more accurate than an earlier measurement owing to technological advances. On the other hand, an old value remains useful because it increases the temporal validity of the measurement and can be unique. Finally, the accuracy (closeness to the true value) and precision (repeatability of the value) of measurements must be considered to choose a particular value among a data set or to compute a statistical average.

For each set of properties, we defined a decision tree that is schematized in Fig. 3. The methods are ordered in a preferential order. Among the ordered methods, the first available is chosen, and the weighted average μ is computed from Ν multiple estimates, x_i, by the least-squares estimator: 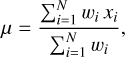$μ = \frac{Σ_{i = 1}^{N} w_{i} x_{i}}{Σ_{i = 1}^{N} w_{i}},$ $\mu = {{\Sigma _{i = 1}^N{w_i}{x_i}} \over {\Sigma _{i = 1}^N{w_i}}},$ (1)

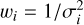where $w_{i} = 1 / σ_{i}^{2}$ ${w_i} = 1/\sigma _i^2$ and σ_i = (σ_+,i − σ_−,i)/2 is the arithmetic mean of the upper and lower uncertainties σ_+,i and σ_−,i.

Similarly, the upper and lower uncertainties on μ are computed as: 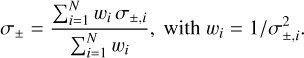$σ_{\pm} = \frac{Σ_{i = 1}^{N} w_{i} σ_{\pm,}_{i}}{Σ_{i = 1}^{N} w_{i}}, w i t h w_{i} = 1 / σ_{\pm, i}^{2} .$ ${\sigma _ \pm } = {{\Sigma _{i = 1}^N{w_i}{\sigma _{ \pm ,}}_i} \over {\Sigma _{i = 1}^N{w_i}}},\,\,with\,{w_i} = 1/\sigma _{ \pm ,i}^2.$ (2)

When the uncertainty of a value is unknown, we set it to 100% of the value to weight the mean. At this stage, the N estimates used to compute the average may be less than the total number of estimates available. Every single entry in SsODNet.dataCloud has a selection flag (see Sect. 3). Only three values are possible for this flag: −1, 0 (default), and 1. Any estimate with a selection flag of −1 is discarded from the computation of the best estimate. If an estimate is flagged with 1, it is considered to be the best estimate (we refrain from using it). The overwhelming majority of entries in dataCloud have a selection flag of 0.

We describe below how the preferential order is defined for each parameter and we provide the exhaustive order in Appendix C. Exceptions to this scheme of averaging include family membership, albedo, taxonomy, and the orbital elements of SSOs.

4.2.1 Osculating elements

We store in SsODNet.dataCloud the complete catalogs of osculating elements of asteroids and dwarf planets proposed by the MPC (mpcorb, Marsden 1980) and the Lowell Observatory (astorb, Bowell et al. 1994). Osculating elements are a consistent ensemble for each SSO. Thus, we do not select them individually, but as a group. As the primary source, we chose the astorb catalog for the ssoCard, completed with elements from mpcorb for SSOs that are not listed in astorb.

For each SSO, we used its osculating elements (semi-major axis, a, inclination, i, and eccentricity, e) to compute its Tisserand parameter (Tisserand 1889) with Jupiter (T_J) and report it in the ssoCard: 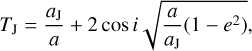$T_{J} = \frac{a_{J}}{a} + 2 \cos i \sqrt{\frac{a}{a_{J}} (1 - e^{2})},$ ${T_{\rm{J}}} = {{{a_{\rm{J}}}} \over a} + 2\cos \,i\sqrt {{a \over {{a_{\rm{J}}}}}\left( {1 - {e^2}} \right)} ,$ (3)

taking a_J = 5.203 363 01 au (mean J2000 orbital element).

4.2.2 Proper elements

Until recently, the only source of proper elements was the Asteroid-Dynamical Site¹⁹ (AstDyS, Knežević & Milani 2003, 2012). The computations used either the analytical or numerical methods by Milani & Knežević (1990, 1994), Knežević & Milani (2000), and Knežević et al. (2002). More recently, Vinogradova (2019) introduced the empirical approach.

The most recent and largest update on asteroid proper elements is provided by the Asteroid Families Portal²⁰ (Novakovic & Radovic 2019). It thus prevails over the others and we included it in SsODNet.dataCloud to report proper elements of SSOs in ssoCard. As Jupiter Trojans and KBOs are not reported in this catalog, we complemented it with the proper elements for these populations from AstDyS.

4.2.3 Families

The existence of asteroid families has been recognized over a century ago (Hirayama 1918). Many authors have been working on the subject over the last decades, using mainly the Hierarchical Clustering Method (HCM, Zappala et al. 1990). A new method has recently emerged, called V-shape (Bolin et al. 2017).

As families are groups of SSOs, the selection is family-based in contrast with other parameters that are SSO-based. We set as a reference the most-recent large-scale study (presently, Vinogradova 2019). All the families listed in the reference are considered valid and SSOs belonging to these families have a family item in their ssoCard describing their membership.

We then complete these families with those reported in the other studies listed in SsODNet.dataCloud. We distinguish two cases. For articles studying families in general (e.g., Milani et al. 2014), we add the families not reported in the reference data set. A complexity arises from the fact that different authors may label the same family under different names (such as Minerva and Gefion being two names pointing at the same family, Milani et al. 2014; Nesvorny 2015). We thus compute the fraction of common members between reported families. Whenever the overlap is smaller than 10%, the families are considered different. Alternatively, if one family is significantly smaller than the other (at most 20% in number of members), we include it to the list of families as it is likely a sub-family of the larger one.

For articles focusing on a single family (e.g., Tsirvoulis 2019), we consider that they supersede the reference data set. If the family they describe is present in the reference data set, we replace the family membership of all SSOs in the family. If not, we simply add the new family (e.g., Delbò et al. 2019). We illustrate the dynamical families of in the asteroid belt available in SsODNet in Fig. 4.

Fig. 4

Distribution of families (first panel), albedo (second), colors (third, using a color-scheme similar to Parker et al. 2008 based on a code by Ivezic et al. 2014), and taxonomy (fourth) against proper elements (semi-major axis and sine of inclination). The number of plotted objects is reported in each panel.

4.2.4 Pairs

Pairs of asteroids are objects on highly similar heliocentric orbits, first discovered by Vokrouhlický & Nesvorný (2008). They are similar to dynamical families with only two members and are thought to be formed by rotational fission (Scheeres 2007; Pravec et al. 2010). They are identified from the distance d between their orbits (in m.s⁻¹): 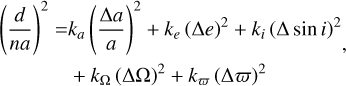$\begin{matrix} {(\frac{d}{n a})}^{2} = k_{a} {(\frac{Δ a}{a})}^{2} + k_{e} {(Δ e)}^{2} + k_{i} {(Δ \sin i)}^{2} \\ + k_{Ω} {(ΔΩ)}^{2} + k ϖ {(Δ ϖ)}^{2} \end{matrix},$ $\matrix{ {{{\left( {{d \over {na}}} \right)}^2} = {k_a}{{\left( {{{{\rm{\Delta }}a} \over a}} \right)}^2} + {k_e}{{\left( {{\rm{\Delta }}e} \right)}^2} + {k_i}{{\left( {{\rm{\Delta }}\sin \,i} \right)}^2}} \cr { + {k_{\rm{\Omega }}}{{\left( {{\rm{\Delta \Omega }}} \right)}^2} + k\varpi {{\left( {\Delta \varpi } \right)}^2}} \cr } ,$ (4)

with δa, δe, δ sin i, δω, and Δϖ as the difference in semimajor axis, eccentricity, sine of inclination, longitude of the ascending node, and argument of perihelion, respectively; n and a are the mean motion and semi-major axis of either component; and the numerical constants are k_a = 5/4, k_e = k_i = 2, and k_Ω = k_ϖ = 10⁻⁴ (Pravec et al. 2019). Backward integration has confirmed many of these pairs, with recent epochs in the past during which the two components were within their Hill sphere (see Žižka et al. 2016, for instance). These epochs are considered the ages of the pairs, the time at which the two components became gravitationnally unbound.

We consider all the pairs listed in the different sources compiled in the dataCloud. However, for the determination of the age, for the ssoCard we select the most recent determination over older studies.

4.2.5 Diameter

There are a number different methods available to estimate the diameter of a SSO. As a general scheme, we favor estimates obtained by a space mission (either via flyby or rendez-vous, such as Belton et al. 1992) over all the others. Diameter estimates based on full 3D shape modeling (including direct measurement such as radar echoes, disk-resolved imaging, or stellar occultation) are then considered the most reliable (e.g., Hudson & Ostro 1994; Carry et al. 2010; Viikinkoski et al. 2015; Bartczak & Dudziński 2018).

The next category of methods are convex shape models (generally obtained with the light-curve inversion method, Kaasalainen & Torppa 2001) scaled a posteriori using another measurement (stellar occultation or mid-infrared flux, Ďurech et al. 2011; Lagerros 1996) or tri-axial ellipsoid (e.g., Drummond & Cocke 1989; Drummond et al. 2014). These are followed by direct measurements limited to a single geometry, such as direct imaging (Marchis et al. 2006), stellar occultations (Dunham & Mallen 1979), interferometry (Delbò et al. 2009), and broadening of the instrument point-spread function (Brown & Trujillo 2004).

Then come the estimates from the analysis of mid-infrared fluxes with spherical models: STM (Lebofsky et al. 1986), FRM (Lebofsky & Spencer 1989), NEATM (Harris & Davies 1999), and NESTM (Wolters & Green 2009). The last ones chosen are the diameter estimates based on the absolute magnitude, H, and the albedo, p_V (Sect. 4.2.6) when the latter has been derived from the polarimetric phase curve of the SSO (e.g., Delbò et al. 2007). We present the complete list of methods and their order for computing the best diameter estimate in Table C.1.

4.2.6 Albedo

In most cases, the albedo is derived by combining a diameter estimate (D) with the absolute magnitude, H, at visible wavelengths (more specifically in the Johnson V band, hence, the p_V notation), using the canonical equation (Bowell et al. 1989): 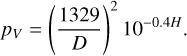$p_{V} = {(\frac{1329}{D})}^{2} 10^{- 0.4 H} .$ ${p_V} = {\left( {{{1329} \over D}} \right)^2}{10^{ - 0.4H}}.$ (5)

An albedo determination is thus closely linked with a diameter estimate and this is why both quantities are reported in a single table in SsODNet.dataCloud. Because the absolute magnitude is constantly refined with the new photometry associated with the astrometry reported to the MPC, we compute p_V using the latest available absolute magnitude, H, and the best estimate of the diameter (Sect. 4.2.5) using Eq. (5). The uncertainties are computed as: 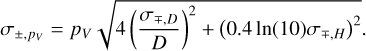$σ_{\pm, p_{V}} = p_{V} \sqrt{4 {(\frac{σ_{\mp, D}}{D})}^{2} + {(0.4 \ln (10) σ_{\mp, H})}^{2}} .$ ${\sigma _{ \pm ,{p_V}}} = {p_V}\sqrt {4{{\left( {{{{\sigma _{ \mp ,D}}} \over D}} \right)}^2} + {{\left( {0.4\ln \left( {10} \right){\sigma _{ \mp ,H}}} \right)}^2}} .$ (6)

Uncertainty on H is seldom provided, and we use a default value of 0.3. The only exceptions to this approach are albedo estimated by space missions or, alternatively, from polarimetric phase curves (see Table C.2), which are not recomputed. We present the albedo against proper orbital elements in Fig. 4.

4.2.7 Masses

The determination of the mass of an SSO relies on measuring the effect of its gravitational attraction on another celestial body: either a spacecraft or another(s) SSO(s). The only exception to this is the mass determination from the detection of Yarkovsky drift (Chesley et al. 2003).

The precision that can be achieved is strongly dependent on the type of interaction, whether that is with: a spacecraft, a satellite in orbit, or long-distance encounters (Carry 2012; Scheeres et al. 2015). We thus favor mass estimates achieved by radio science experiments during spacecraft encounters (Yeomans et al. 1997; Pätzold et al. 2011). Secondary estimates come from masses determined in binary systems by studying the orbits of their moons (Merline et al. 1999; Pravec et al. 2000; Ostro et al. 2006; Vachier et al. 2012; Pajuelo et al. 2018).

Masses determined from SSO-to-SSO long-distance interactions: close encounters (Standish & Hellings 1989; Siltala & Granvik 2020) and ephemerides (Baer & Chesley 2008; Fienga et al. 2008) follow. Finally, for an SSO with a detected Yarkovsky drift (Vokrouhlický et al. 2015), it is possible to determine its mass on the basis of a number of other parameters (diameter, albedo, obliquity, thermal inertia, etc., as per Chesley et al. 2014). We present the complete ordered list of methods for computing the best mass estimate in Table C.3.

4.2.8 Density

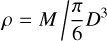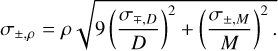For each SSO with both a mass M and a diameter D estimates, we compute its density ρ (kg m⁻³) and associated uncertainties as follows: $ρ = M / \frac{π}{6} D^{3}$ $\rho = {M \mathord{\left/ {\vphantom {M {{\pi \over 6}{D^3}}}} \right. \kern-\nulldelimiterspace} {{\pi \over 6}{D^3}}}$ (7) $σ_{\pm, ρ} = ρ \sqrt{9 {(\frac{σ_{\mp, D}}{D})}^{2} + {(\frac{σ_{\pm, M}}{M})}^{2} .}$ ${\sigma _{ \pm ,\rho }} = \rho \sqrt {9{{\left( {{{{\sigma _{ \mp ,D}}} \over D}} \right)}^2} + {{\left( {{{{\sigma _{ \pm ,M}}} \over M}} \right)}^2}.}$ (8)

In some cases, the density can be determined without knowledge of either the mass or the volume. This is often the case of small binary asteroid systems studied by optical light curves (Scheirich & Pravec 2009; Carry et al. 2015). A few binary systems imaged by radar are also included in this case (Ford et al. 2014). Last, the density can be derived from a detected Yarkovsky orbital drift (Rozitis & Green 2014). We did not set preference of a method over another and we chose to average these estimates together. The distribution of density for a few selected taxonomic classes is presented in Fig. 5.

Fig. 5

Kernel density estimate (KDE) of the density of the C, S, X, and B complexes. The bimodal distribution of X-types highlights the P and M sub-classes (average p_V of 0.044 and 0.129, below and above 2000 kg m⁻³, respectively). Similarly, Pallas is the sole contributor to high-density B-types.

4.2.9 Spin solutions

In most cases, the only available information on the spin of an SSO is its rotation period (often reported as synodic period). In some cases, however, the orientation of the spin axis has been determined, and we report its coordinates both in ECJ2000 (as reference time, longitude, and latitude; see Kaasalainen & Torppa 2001; Ďurech et al. 2010) and in EQJ2000 (as right ascension, declination, and the position of the prime meridian W₀ and Ẇ; see Archinal et al. 2018).

Spin-vector coordinates determined with the light-curve inversion method (Kaasalainen & Torppa 2001) are often degenerated with a mirror solution separated by 180° in ecliptic longitude. We use the selection flag (Sect. 3) to remove this ambiguity whenever one of the two spin solutions has been rejected a posteriori (from comparison with stellar occultation or disk-resolved imaging for instance, Marchis et al. 2006; Ďurech et al. 2011). For each SSO with spin-vector coordinates, we computed its obliquity using these coordinates and its osculating elements (Sect. 4.2.1). We present the distribution of rotation period and obliquity against diameter in Fig. 6.

Here, again, solutions obtained by spacecraft encounters are favored over any others. They are followed by spin solutions obtained by 3D shape modeling techniques that include direct disk-resolved measurements (stellar occultations, disk-resolved images, etc., e.g., Tanga et al. 2015; Vernazza et al. 2018; Shepard et al. 2018; Carry et al. 2019). These are followed by 3D shape models that are later scaled using complementary observations (mid-infrared fluxes, stellar occultations, disk-resolved images, etc., Hanuš et al. 2013b; Ďurech et al. 2011). Spin solutions associated with convex shape models, generally with a mirrored spin solution, were then chosen (Hanuš et al. 2013a; Marciniak et al. 2018), followed by solutions obtained from tri-axial ellipsoids (Drummond & Cocke 1989; Merline et al. 2013). Finally, there are the periods determined from light curves, with or without constraints on the spin coordinates (Lagerkvist 1978; Yeh et al. 2020). We refer to Table C.4 for a full listing of the order of preference.

The average spin coordinates are computed using Eq. (1). However, as several ambiguous spin solutions may co-exist for a given SSO, we identify which estimates correspond to which spin solution using K-Means clustering (Lloyd 1982), as provided by the scikit-learn²¹ python package (Pedregosa et al. 2011). We consider that up to four distinct spin solutions can be present, such as for (20) Massalia (Fig. 7). Spin coordinates must be within 30^° of the average to be include in a cluster. We set default uncertainties of 30^° on spin coordinates whenever they have not been specified by the respective authors. We used a similar approach, based on K-Means clustering, for the rotation periods. In this case, the threshold to belong to a solution was set to 0.2 h. The default uncertainty was set to 1 h.

Fig. 6

Rotation period (top) and obliquity (bottom) vs. diameter for 17 201 and 2596 SSOs, respectively. Darker shades of grey indicate higher density of points.

Fig. 7

Example of clustering of spin coordinates for (20) Massalia. Six solutions (blue) are possible (Kaasalainen et al. 2002; Hanuš et al. 2016; Cellino et al. 2019). The four separated spin coordinates (orange) of the four clusters are reported in the ssoCard.

4.2.10 Colors

Stricto sensu, the colors of SSOs are observable and not derived properties. Nevertheless, we compiled the colors of SSOs in SsODNet.dataCloud, with the same rationale as for derived properties: many colors are available but spread over many studies (e.g., Dandy et al. 2003; Snodgrass et al. 2010; Dumitru et al. 2018) and they are usually not in machine-readable format. Furthermore, colors can be used for taxonomic determination (Carvano et al. 2010; DeMeo & Carry 2013).

Several ancillary information for contextualization are recorded (Table A.3), such as the observing time, the source of measurement (plain English description and IAU Observatory code²² if available). The filters used to compute the colors are identified with the unique identifier of the SVO Filter Service²³ providing transmission curves and zero points (Rodrigo et al. 2012; Rodrigo & Solano 2020). Similarly, we record in which system the photometry is reported (Vega, AB, or ST).

The selection of best estimates is based on the time difference, Δ_t, between the observation of the two filters and how the color was computed. We favor (Table C.5) colors computed as a difference of absolute magnitudes from phase functions in each filter (Mahlke et al. 2021; Alvarez-Candal et al. 2022). In that case, we report the most-recent published value. Then we follow up with the colors computed as a difference of apparent magnitudes but corrected for light curve variations (Mommert et al. 2016; Erasmus et al. 2019). Last, we have the simple difference of apparent magnitudes (Popescu et al. 2018; Sergeyev & Carry 2021). Whenever several estimates of the same color with the two latter methods are reported, we computed their average as in Eq. (1), with the following weight to account for time difference: 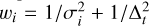$w_{i} = 1 / σ_{i}^{2} + 1 / Δ_{t}^{2}$ ${w_i} = 1/\sigma _i^2 + 1/{\rm{\Delta }}_t^2$ . Whenever the information on Δ_t is missing, we set it to 1 h.

Last but not least, filter transmissions are different in each facility. For a given color (e.g., g–i), the values from different observatories may differ (e.g., between the Sloan Digital Sky Survey and SkyMapper, see Fig. 9 in Sergeyev et al. 2022). We did not merge colors obtained with different filter sets, for instance, SLOAN/SDSS (g–i) vs. SkyMapper/SkyMapper (g–i), but instead we report the most precise results. An example of these colors is shown in Fig. 4.

Fig. 8

Decision tree for taxonomic classes. Classes based on spectroscopy are favored upon those based on broad-band photometry only. Similarly data sets covering the full VISNIR wavelength range are favored over NIR only, itself preferred to VIS only. Finally, for classification based on similar data sets, the Mahlke scheme is preferred over Bus-DeMeo, Bus, SMASS, and Tholen schemes.

4.2.11 Phase function

Phase functions describe the evolution of brightness with the phase angle (once it is corrected with respect to the Sun-target and target-observer distances). The absolute magnitude reported together with osculating elements (Sect. 4.2.1) is computed using the historical two-parameter HG phase function (Bowell et al. 1989), where G is generally assumed to be 0.15. This function has been shown to deviate from observed photometry at low and high phase angle, and a three-parameter HG₁G₂ function has been proposed (Muinonen et al. 2010). We collect these parameters in the dataCloud and report them in ssoCard. Because phase functions are wavelength-dependent (Sanchez et al. 2012; Mahlke et al. 2021), we associate these parameters with the filter in which they were derived, again using the unique identifier of the SVO Filter Service (Rodrigo et al. 2012; Rodrigo & Solano 2020).

A parameterized version of the phase function has been proposed for low-accuracy data (with two parameters, HG12, later refined as 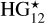${HG}_{12}^{⋆}$ ${\rm{HG}}_{12}^ \star$ , Penttilä et al. 2016). However, we stick to HG₁G₂ parameters only, as they have been shown to convey tax-onomic and albedo information (Shevchenko et al. 2016; Mahlke et al. 2021).

4.2.12 Taxonomy

Taxonomy is often used as a proxy for composition in statistical studies of populations (Parker et al. 2008; DeMeo & Carry 2014; Binzel et al. 2019; Hasegawa et al. 2021). The complexity of compiling taxonomic classes is manifold. First, several taxonomies (as classification schemes) have been developed and used by the community, such as Tedesco et al. (1989), Tholen (1989), Bus & Binzel (2002), DeMeo et al. (2009), and Mahlke et al. (2022). Second, there is a great diversity in the potential combinations of these schemes with observing techniques (multi-filter photometry and spectroscopy, Xu et al. 1995; Carry et al. 2016) and wavelength (visible only, near-infrared only, and both, Carvano et al. 2010; Popescu et al. 2018; Marsset et al. 2014).

We present in Fig. 8 the decision tree we applied to select the most relevant taxonomy for a given SSO. As a general rule, results from spectroscopy are favored over results from multifilter photometry. Within each observing technique, the results using both visible and near-infrared are favored, then those based on infrared only, and then finally those based on the visible only. Once the observing technique and wavelength range is selected, there may be several taxonomic schemes available, and we chose the Mahlke, Bus-DeMeo, SMASS, Bus, and Tholen taxonomies, respectively.

In an attempt to homogenize all the classes that have been reported for a given object, we also group similar classes under the term “complex,” following the associations listed in Table C.8. We give an example of the orbital distribution of these complexes in Fig. 4.

Fig. 9

All 1681 SSOs with a thermal inertia above 1 SI (gray), the 419 with a S/N above 3 (black), and a linear regression on the latter of equation log(Γ₀) = 2.5–0.29 log(D), a result that is similar to the recent work of Hung et al. (2022).

4.2.13 Thermal properties

Mid-infrared fluxes are often used to determine the diameter of an SSO (Sect. 4.2.5), from simple thermal models such as NE ATM (Harris & Davies 1999). More complex thermal models (referred to as thermophysical models, TPM, Lagerros 1996) can also be used, but require additional information on the object such as spin, 3D shape, and so on. One parameter used in TPM is the thermal inertia (in J s^−1/2 K⁻¹ m⁻²) controlling the resistance of the surface to changes of temperature.

The thermal inertia determination from spacecrafts are favored (Capria et al. 2014), followed by those determined from TPM using a priori knowledge on the spin and shape (Matter et al. 2013; O’Rourke et al. 2012), and, finally, the TPM applied to spheres (Müller et al. 2013), as listed in Table C.6. Thermal inertia (Γ) is a function of heliocentric distance (Vasavada et al. 1999; Rozitis et al. 2018). We thus report the thermal inertia at lau (Γ₀) from the Sun in the ssoCard, using the following relation: 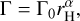$Γ = Γ_{0} r_{H}^{α},$ ${\rm{\Gamma }} = {{\rm{\Gamma }}_0}r_{\rm{H}}^\alpha ,$ (9)

where r_H is the heliocentric distance at the time of the observations and we take α =−3/4 following Delbò et al. (2015). We present the distribution of thermal inertia against diameter in Fig. 9.

4.2.14 Yarkovsky drift

While the orbital drift due to the delayed thermal emission by asteroid surface is extremely small (of the order of 10⁻⁴ au Myr⁻¹, Vokrouhlický et al. 2015), it was detected for the first time almost two decades ago (Chesley et al. 2003). We favor detections that include both optical and radar observations (Farnocchia et al. 2014, for instance) over those using optical only (e.g., Del Vigna et al. 2018). Finally, we consider those (Table C.7) estimated based on the age of dynamical families (Carruba et al. 2017).

Some authors have reported the semi-major axis drift, a (Nugent et al. 2012), while others have given the transverse acceleration, A₂ (Greenstreet et al. 2019), as in the case of cometary dynamical models (Marsden et al. 1973). We report both parameters in the ssoCard, using the following equation from Farnocchia et al. (2013) to convert between quantities: 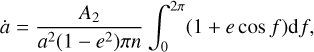$\dot{a} = \frac{A_{2}}{a^{2} (1 - e^{2}) π n} \int_{0}^{2 π} (1 + e \cos f) d f,$ $\dot a = {{{A_2}} \over {{a^2}\left( {1 - {e^2}} \right)\pi n}}\int_0^{2\pi } {\left( {1 + e\,\cos \,f} \right){\rm{d}}f} ,$ (10)

with a as the semi-major axis, e as the eccentricity, and n as the mean motion (Sect. 4.2.1).

5 Summary for all SSOs: `ssoBFT`

The ssoCard service described in previous section provides convenient access to the best estimates of many parameters, but limited to a single SSO. The last service composing SsODNet thus provides a broad and flat table (ssoBFT) that compiles all the parameters of the ssoCard for all SSOs. This table is very large (over 591 fields for 1223 984 SSOs, about 2.1 Gb). Yet, most fields are empty (i.e., there is no estimate of the given parameter for this SSO), resulting in only a 14.6% filling factor.

We propose the ssoBFT as an enhanced character separated values (eCSV²⁴) and an Apache parquet²⁵ files for users interested in the statistical properties of the asteroid population. These files can be downloaded at static urls (eCSV²⁶, parquet²⁷). We also provide this table to the CDS to ensure its fully VO-compliant access.

6 Accessing the services: `SsODNet` and rocks

We offer several access interfaces to the SsODNet service, described below.

6.1 REST interface

The quaero representational state transfer (REST) API is a low-level interface dedicated to developers. It is designed to offer an easy-to-use and fast solution to search for planetary objects (sso and search methods) to resolve their designations (resolver method) or to be used as an auto-completion mechanism for names (instant search method) into Web forms and applications connected to the Internet. In the framework of the Virtual Observatory, no standard protocol nor technical specification is quite capable of designing a fast-search engine. Thus, the core of SsODNet name resolver does not follow any current VO standard. Nevertheless, the underlying technology and the API we have chosen being intrinsically interoperable, the quaero service can easily be included in any VO ecosystem.

End-point:	https://api.ssodnet.imcce.fr/quaero/1/
Doc:	https://doc.ssodnet.imcce.fr/quaero.html

6.2 Web-service interface

We provide a Web-service interface, built upon XML and SOAP technology, that allows for a full interaction with SsODNet through several methods: (i) resolver: to identify SSO (high level API), (ii) dataCloud: to retrieve all known values of SSO properties, (iii) ssoCard: to retrieve the best estimates of SSO properties. The user can simply post a request to the method end-points to gather corresponding data, using a data transfer program such as wget or curl. More advanced users can implement the SOAP Web service to ensure an application-to-application communication between SsODNet and a software or a public Web page.

`SsODNet` server:	https://ssp.imcce.fr/webservices/ssodnet/ssodnet.php

Public interface:	https://ssp.imcce.fr/webservices/ssodnet/ssodnet.php7wsdl

Doc:	https://ssp.imcce.fr/webservices/ssodnet/

6.3 Web form interface

The easiest way to search for a SSO and to quickly consult its properties may be to use SsODNet dedicated Web form. The best estimates of the physical and dynamic properties (the ssoCard) are displayed in a comprehensive manner, together with bibliographic references. We also provide links to all values (i.e., dataCloud entry for each property of the SSO), and to the subset used to compute the best estimates (as defined by the decision trees, see Sect. 4).

Web form:	https://ssp.imcce.fr/forms/ssocard/
Doc:	https://ssp.imcce.fr/forms/ssocard/doc

6.4 Python interface: rocks

We provide a python interface to SsODNet named rocks. It offers a programmatic entry point both for data exploration and data processing. The interaction with the SsODNet repositories is asynchronous and results are cached on the user-side, providing a responsive user experience.

Data exploration is accessible via the command line interface of rocks in a straightforward, uniform syntax:

$ rocks [command|parameter] [asteroid_identifier]

Here, the parameter can be any key from the ssoCard or dataCloud catalogs, while the asteroid_identifier is any identifier that can be resolved by quaero. The result of the query is printed in the console. Commands such as id and info serve to identify an asteroid and to print the asteroid’s ssoCard.

$ rocks id “1975 XP”
(234) Barbara
$ rocks taxonomy Barbara
L
$ rocks diameter barbara
46.3 +− 5.0 km
$ rocks albedo 234
0.187 +− 0.2839

An overview of all compiled literature values is printed when requesting the plural of the parameters. This is possible for all parameters which have dataCloud entries, such as albedo, mass, taxonomy, etc.

$ rocks taxonomies ceres

Data processing is facilitated for python scripts using the rocks package. The main entry point is the rocks.Rock class, where each instance reflects a unique asteroid. The asteroid parameters are accessible as class attributes via the dot notation, which again leads to an intuitive syntax:

>>> import rocks
>>> vesta = rocks.Rock(4)
>>> vesta.albedo.value
0.38
>>> vesta.albedo.error.min_
−0.04
>>> vesta.albedo.error.max_
0.04
>>> vesta.albedo.description
‘Geometrical albedo in V band’

The asynchronous interaction with the locally cached data and the remote SsODNet repositories allow for a fast analysis process without the use of resource-intensive multiprocessing or multi-threading strategies. To provide an estimate of the execution times, we identified all asteroids in the SDSS Moving Object Catalog DR1²⁸ and retrieved their ssoCard. The catalog contains observations of 10,585 unique minor bodies, largely referred to by designations that are no longer the main identifier of the object. Using a combination of quaero queries and a local asteroid name-number-designation index, rocks identifies all objects within 2.5 s. The ssoCards are retrieved within 320 s from SsODNet, about 30 ms per asteroid. rocks then performs data validation and deserialization (i.e., converting the JSON server response into a python object) within 120 s, that is, about 11 ms per asteroid. A second execution of the analysis script would benefit from the locally cached ssoCards, rendering any request to SsODNet obsolete.

To install rocks, we can use the python package index (PyPI) under the package name space-rocks. The online doc-umentation²⁹ provides a guide on getting started and tutorials to achieve more advanced data processing results. We note that rocks is actively developed and maintained by the authors of this work.

Sources:	https://github.com/maxmahlke/rocks
Doc:	https://rocks.readthedocs.io

class	method	scheme	shortbib
G	Phot	Tholen	Tholen+1989
C	Spec	Bus	Bus&Binzel+2882
C	Spec	Bus	Lazzaro+2884
C	Spec	Tholen	Lazzaro+2884
C	Spec	Bus-DeMeo	DeMeo+2889
C	Spec	Bus	Fornasier+2814b
G	Spec	Tholen	Fornasier+2814b
C	Phot	Bus-DeMeo	Sergeyev+2822
C	Spec	Mahlke	Mahlke+2822

7 Future developments

We foresee several lines of development for the SsODNet service: data compilation and curation, expansion of the set of parameters and types of SSOs, and development of the interface.

Data compilation

First and foremost, we will continue to compile data into the dataCloud, aiming for completeness with respect to the listed parameters. Indeed, it is the building block of the ssoCard and the ssoBFT, which are automatically generated from the entries in the dataCloud. On the other hand, quaero has been working and been updated weekly for several years, following the growing list of SSOs listed by the MPC. Thus, a continuous scientific monitoring of publications is required for the service.

We welcome any feedback, especially on data sources that may be missing or erroneous entries. While we conducted multiple checks on the data included in SsODNet, some typographical errors may lurk in the unprecedented size of the data compilation. We will happily include sources that are not included in the current release of the service and correct entries.

Furthermore, SsODNet can be used by any group or researcher to publish regularly updated data. A simple file (VOTable, csv, …), with sufficient metadata at a static url can be used as a source, without requiring a server or a database with a web service.

Set of parameters

The set of parameters currently available in SsODNet is already broad, covering dynamical, surface, and physical properties (Table A.1). There are, however, other parameters of interest that will be added to the dataCloud (and, hence, ssoCard and ssoBFT), such as the source region probabilities for near-Earth objects (Granvik et al. 2017) and their minimal orbital intersection distance with planets (MOID, Marsden 1993), activity for asteroids and Centaurs (Hsieh & Jewitt 2006; Jewitt 2009), and radar albedos (Neeley et al. 2014). Additional computed parameters can also be added in ssoCard, such as surface gravity or escape velocity.

Types of SSOs

The present release of SsODNet focuses on asteroids because they are the prime targets of study of the authors. The service was nevertheless designed to cope with all classes of SSOs: comets, planets, satellites, and interstellar objects. For instance, quaero already deals with the designation of all these categories.

We thus welcome partnership with everyone willing to contribute to build this community database. Beside the collection and curation of data, a set of parameters relevant for these celestial bodies must be defined (e.g., non-gravitational acceleration for comets, libration amplitude and frequency for satellites), together with decision trees to estimate the best parameters. SsODNet has been envisioned as a service to the community and any contribution to it will expand its advantages.

User interface

SsODNet is mainly a machine-machine service, allowing for on-the-fly data retrieval. Both quaero and ssoCard are designed to cope with constant queries. The dataCloud entries for a given SSO can also be dumped easily, and the ssoBFT downloaded as a whole.

We plan to develop more advanced possibilities to query the data, both in dataCloud and ssoBFT. Users may be interested by searching entries from a given bibliographic reference, rather than for a specific SSO for instance. Similarly, users may be interested in a subset of the ssoBFT only (e.g., some specific parameters only for SSOs fulfilling certain conditions). While the latter is possible with TAP on the version of the ssoBFT hosted at the CDS, the former requires development on the server side of SsODNet.

8 Conclusions

We present a new Web Service, SsODNet, which provides a convenient solution to the issues of SSO identification and the compilation of properties. It consists of a suite of applications, each with its own programming interface: quaero for name resolution, dataCloud compiling SSO properties, ssoCard providing the set of best estimates for each SSO, and ssoBFT compiling the latter for all SSOS. These entry points deliver JSON as native outputs. We have released a python interface for these services: rocks, available in the python package index (PyPI). SsODNet is fully operational. The name resolver quaero is updated weekly to follow SSO discoveries. We plan on monthly updates for the others applications, following compilation of data from continuous monitoring of new publications. The future evolution of the service includes an extension of the suite of properties and classes of SSOs, along with an advanced query interface to retrieve large corpus of data.

Acknowledgements

This research has made use of the SVO Filter Profile Service supported from the Spanish MINECO through grant AYA2017-84089 (Rodrigo et al. 2012; Rodrigo & Solano 2020). This research has made use of the scikit-learn python package (Pedregosa et al. 2011). We did an extensive use of the VO TOPCAT software (Taylor 2005). Thanks to all the developers and maintainers. We would like to thank J. Masiero, F. E. DeMeo, and F. Spoto for discussions that led to the current decision trees used in SsODNet.

Appendix A Collections available in `SsODNet.dataCloud`

Table A.1

Description of the collections included in SsODNet.dataCloud.

For each collection we list the number of entries (N), number of SSOs (N_SSO), the reference to a table describing its fields (Desc.), and the number of included bibliographic references.

Table A.2

Description of the fields in the collection astorb of the dataCloud.

Fields follow the original ASTORB data (Bowell et al. 1994), and we refer to the online documentation for further details on each field (https://asteroid.lowell.edu/main/astorb/).

Table A.3

Description of the fields in the collection colors of the dataCloud.

Table A.4

Description of the fields in the collection cometpro of the dataCloud.

Fields follow the original COMETPRO data (Rocher & Cavelier 1996).

Table A.5

Description of the fields in the collection density of the dataCloud.

Table A.6

Description of the fields in the collection diamalbedo of the dataCloud.

Table A.7

Description of the fields in the collection family of the dataCloud.

Table A.8

Description of the fields in the collection masses of the dataCloud.

Table A.9

Description of the fields in the collection mpcatobs of the dataCloud.

MPC Web site: https://minorplanetcenter.net/iau/info/OpticalObs.html

Table A.10

Description of the fields in the collection mpcorb of the dataCloud.

Fields follows the original MPCORB data, see the online documentation https://www.minorplanetcenter.net/iau/infoMPOrbitFormat.html.

Table A.11

Description of the fields in the collection pairs of the dataCloud.

Table A.12

Description of the fields in the collection phase_function of the dataCloud.

Table A.13

Description of the fields in the collection proper_elements of the dataCloud.

Table A.14

Description of the fields in the collection spin of the dataCloud.

Table A.15

Description of the fields in the collection taxonomy of the dataCloud.

Table A.16

Description of the fields in the collection thermal_properties of the dataCloud.

Table A.17

Description of the fields in the collection yarkovsky of the dataCloud.

Appendix B Description of all the methods

Table B.1

Methods included in SsODNet.

Appendix C Method lists for best-estimate determination

Table C.1

Ranking of methods for diameter estimates (diamalbedo).

Table C.2

Selection order for albedo determinations (diamalbedo).

Table C.3

Selection order for mass determinations (masses).

Table C.4

Ranking of methods for spin properties (spin).

Table C.5

Selection order for colors (colors).

Table C.6

Ranking of methods for thermal properties (thermal_properties).

Table C.7

Selection order for Yarkovsky drift determinations (yarkovsky).

Table C.8

Class-complex connections for taxonomy.

References

Ahn, C.P., Alexandroff, R., Allende Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
Alvarez-Candal, A., Benavidez, P.G., Campo Bagatin, A., & Santana-Ros, T. 2022, A&A, 657, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Archinal, B.A., Acton, C.H., A’Hearn, M.F., et al. 2018, Celest. Mech. Dyn. Astron., 130, 22 [NASA ADS] [CrossRef] [Google Scholar]
Baer, J., & Chesley, S.R. 2008, Celest. Mech. Dyn. Astron., 100, 27 [NASA ADS] [CrossRef] [Google Scholar]
Bailey, S.I., & Pickering, E.C. 1913, Ann. Harvard Coll. Observ., 72, 165 [NASA ADS] [Google Scholar]
Bartczak, P., & Dudzinski, G. 2018, MNRAS, 473, 5050 [NASA ADS] [CrossRef] [Google Scholar]
Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bell, J.F., Owensby, P.D., Hawke, B.R., & Gaffey, M.J. 1988, in Lunar and Planetary Science Conference, 19, Lunar and Planetary Science Conference, 57 [NASA ADS] [Google Scholar]
Belskaya, I.N., & Shevchenko, V.G. 2000, Icarus, 147, 94 [NASA ADS] [CrossRef] [Google Scholar]
Belton, M.J.S., Veverka, J., Thomas, P., et al. 1992, Science, 257, 1647 [NASA ADS] [CrossRef] [Google Scholar]
Berthier, J., Vachier, F., Thuillot, W., et al. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, Astronomical Society of the Pacific Conference Series, 351, 367 [NASA ADS] [Google Scholar]
Berthier, J., Hestroffer, D., Carry, B., et al. 2008, LPI Contrib., 1405, 8374 [Google Scholar]
Binzel, R.P., Xu, S., Bus, S.J., et al. 1993, Science, 262, 1541 [NASA ADS] [CrossRef] [Google Scholar]
Binzel, R.P., DeMeo, F.E., Turtelboom, E.V., et al. 2019, Icarus, 324, 41 [NASA ADS] [CrossRef] [Google Scholar]
Bolin, B.T., Delbò, M., Morbidelli, A., & Walsh, K.J. 2017, Icarus, 282, 290 [CrossRef] [Google Scholar]
Bowell, E., Chapman, C.R., Gradie, J.C., Morrison, D., & Zellner, B. 1978, Icarus, 35, 313 [NASA ADS] [CrossRef] [Google Scholar]
Bowell, E., Hapke, B., Domingue, D., et al. 1989, Asteroids II, 524 [Google Scholar]
Bowell, E., Muinonen, K., & Wasserman, L.H. 1994, in Asteroids, Comets, Meteors 199, 160, eds. A. Milani, M. di Martino, & A. Cellino, 477 [Google Scholar]
Bray, T.E. 2017, The JavaScript Object Notation (JSON) Data Interchange Format, STD 90, RFC 8259, https://www.rfc- editor.org/info/rfc8259 [CrossRef] [Google Scholar]
Brown, M.E., & Trujillo, C.A. 2004, AJ, 127, 2413 [NASA ADS] [CrossRef] [Google Scholar]
Bus, S.J., & Binzel, R.P. 2002, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
Capria, M.T., Tosi, F., De Sanctis, M.C., et al. 2014, Geophys. Res. Lett., 41, 1438 [NASA ADS] [CrossRef] [Google Scholar]
Carruba, V., Vokrouhlickÿ, D., & Nesvornÿ, D. 2017, MNRAS, 469, 4400 [NASA ADS] [CrossRef] [Google Scholar]
Carry, B. 2012, Planet. Space Sci., 73, 98 [CrossRef] [Google Scholar]
Carry, B., Dumas, C., Kaasalainen, M., et al. 2010, Icarus, 205, 460 [NASA ADS] [CrossRef] [Google Scholar]
Carry, B., Matter, A., Scheirich, P., et al. 2015, Icarus, 248, 516 [NASA ADS] [CrossRef] [Google Scholar]
Carry, B., Solano, E., Eggl, S., & DeMeo, F.E. 2016, Icarus, 268, 340 [CrossRef] [Google Scholar]
Carry, B., Vachier, F., Berthier, J., et al. 2019, A&A, 623, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Carvano, J.M., Hasselmann, P.H., Lazzaro, D., & Mothé-Diniz, T. 2010, A&A, 510, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cellino, A., Hutton, R.G., Tedesco, E.F., Di Martino, M., & Brunini, A. 1999, Icarus, 138, 129 [CrossRef] [Google Scholar]
Cellino, A., Hestroffer, D., Lu, X.P., Muinonen, K., & Tanga, P. 2019, A&A, 631, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Chapman, C.R., Morrison, D., & Zellner, B. 1975, Icarus, 25, 104 [NASA ADS] [CrossRef] [Google Scholar]
Chesley, S.R., Ostro, S.J., Vokrouhlicky, D., et al. 2003, Science, 302, 1739 [NASA ADS] [CrossRef] [Google Scholar]
Chesley, S.R., Farnocchia, D., Nolan, M.C., et al. 2014, Icarus, 235, 5 [NASA ADS] [CrossRef] [Google Scholar]
Cruikshank, D.P., & Morrison, D. 1973, Icarus, 20, 477 [NASA ADS] [CrossRef] [Google Scholar]
Cutri, R.M., Wright, E.L., Conrow, T., et al. 2013, Explanatory Supplement to the AllWISE Data Release Products [Google Scholar]
Dandy, C.L., Fitzsimmons, A., & Collander-Brown, S.J. 2003, Icarus, 163, 363 [NASA ADS] [CrossRef] [Google Scholar]
Davidsson, B.J.R., Gutiérrez, P.J., & Rickman, H. 2007, Icarus, 187, 306 [NASA ADS] [CrossRef] [Google Scholar]
Del Vigna, A., Faggioli, L., Milani, A., et al. 2018, A&A, 617, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Del Vigna, A., Roa, J., Farnocchia, D., et al. 2019, A&A, 627, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Delbò, M., Cellino, A., & Tedesco, E.F. 2007, Icarus, 188, 266 [CrossRef] [Google Scholar]
Delbò, M., Ligori, S., Matter, A., Cellino, A., & Berthier, J. 2009, ApJ, 694, 1228 [CrossRef] [Google Scholar]
Delbò, M., Mueller, M., Emery, J.P., Rozitis, B., & Capria, M.T. 2015, Asteroid Thermophysical Modeling, 107 [Google Scholar]
Delbò, M., Tanga, P., Carry, B., Ordenovic, C., & Bottein, P. 2018, in Asteroids, Comets, and Meteors: ACM 2018 [Google Scholar]
Delbò, M., Avdellidou, C., & Morbidelli, A. 2019, A&A, 624, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
DeMeo, F.E., & Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
DeMeo, F.E., & Carry, B. 2014, Nature, 505, 629 [NASA ADS] [CrossRef] [Google Scholar]
DeMeo, F.E., Binzel, R.P., Slivan, S.M., & Bus, S.J. 2009, Icarus, 202, 160 [NASA ADS] [CrossRef] [Google Scholar]
Devogèle, M., Moskovitz, N., Thirouin, A., et al. 2019, AJ, 158, 196 [CrossRef] [Google Scholar]
Drummond, J.D. 2000, in NATO Advanced Study Institute (ASI) Series C, 551, Laser Guide Star Adaptive Optics for Astronomy, eds. N. Ageorges, & C. Dainty, 243 [CrossRef] [Google Scholar]
Drummond, J.D., & Cocke, W.J. 1989, Icarus, 78, 323 [NASA ADS] [CrossRef] [Google Scholar]
Drummond, J.D., Cocke, W.J., Hege, E.K., & Strittmatter, P.A. 1985, Icarus, 61, 132 [NASA ADS] [CrossRef] [Google Scholar]
Drummond, J.D., Carry, B., Merline, W.J., et al. 2014, Icarus, 236, 28 [NASA ADS] [CrossRef] [Google Scholar]
Dumitru, B.A., Birlan, M., Sonka, A., Colas, F., & Nedelcu, D.A. 2018, Astron. Nachr., 339, 198 [NASA ADS] [CrossRef] [Google Scholar]
Dunham, D.W., & Mallen, G. 1979, Rev. Mexicana Astron. Astrofis., 4, 205 [Google Scholar]
Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [Google Scholar]
Ďurech, J., Kaasalainen, M., Herald, D., et al. 2011, Icarus, 214, 652 [Google Scholar]
Ďurech, J., Delbò’, M., Carry, B., Hanuš, J., & Alí-Lagoa, V. 2017, A&A, 604, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Erasmus, N., McNeill, A., Mommert, M., et al. 2019, ApJS, 242, 15 [NASA ADS] [CrossRef] [Google Scholar]
Exoplanet-Team. 2021, The Extrasolar Planets Encyclopaedia, http://www.exoplanet.eu/ [Google Scholar]
Farnocchia, D., Chesley, S.R., Vokrouhlicky, D., et al. 2013, Icarus, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
Farnocchia, D., Chesley, S.R., Tholen, D.J., & Micheli, M. 2014, Celest. Mech. Dyn. Astron., 119, 301 [CrossRef] [Google Scholar]
Fenucci, M., Novakovic, B., Vokrouhlicky, D., & Weryk, R.J. 2021, A&A, 647, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2008, A&A, 477, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ford, T.F., Benner, L.A., Brozovic, M., et al. 2014, in AAS/Division for Planetary Sciences Meeting Abstracts, 46, AAS/Division for Planetary Sciences Meeting Abstracts #46, 213.15 [NASA ADS] [Google Scholar]
Gaia Collaboration (Brown, A.G.A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gaia Collaboration (Brown, A.G.A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gauss, K.F. 1809, Theoria motvs corporvm coelestivm in sectionibvs conicis solem ambientivm [Google Scholar]
Gehrels, T. 1956, ApJ, 123, 331 [NASA ADS] [CrossRef] [Google Scholar]
Gradie, J., & Tedesco, E. 1982, Science, 216, 1405 [NASA ADS] [CrossRef] [Google Scholar]
Granvik, M., Morbidelli, A., Vokrouhlicky, D., et al. 2017, A&A, 598, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Grav, T., Mainzer, A.K., Bauer, J., et al. 2011, ApJ, 742, 40 [NASA ADS] [CrossRef] [Google Scholar]
Greenberg, A.H., Margot, J.-L., Verma, A.K., Taylor, P.A., & Hodge, S.E. 2020, AJ, 159, 92 [NASA ADS] [CrossRef] [Google Scholar]
Greenstreet, S., Farnocchia, D., & Lister, T. 2019, Icarus, 321, 564 [NASA ADS] [CrossRef] [Google Scholar]
Hanuš, J., Broz, M., Ďurech, J., et al. 2013a, A&A, 559, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hanuš, J., Marchis, F., & Ďurech, J. 2013b, Icarus, 226, 1045 [CrossRef] [Google Scholar]
Hanuš, J., Delbò’, M., Ďurech, J., & Alí-Lagoa, V. 2015, Icarus, 256, 101 [CrossRef] [Google Scholar]
Hanuš, J., Ďurech, J., Oszkiewicz, D.A., et al. 2016, A&A, 586, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Hanuš, J., Delbò’, M., Ďurech, J., & Alí-Lagoa, V. 2018, Icarus, 309, 297 [CrossRef] [Google Scholar]
Hanuš, J., Pejcha, O., Shappee, B.J., et al. 2021, A&A, 654, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Harris, A.W., & Davies, J.K. 1999, Icarus, 142, 464 [NASA ADS] [CrossRef] [Google Scholar]
Hasegawa, S., Marsset, M., DeMeo, F.E., et al. 2021, ApJ, 916, L6 [NASA ADS] [CrossRef] [Google Scholar]
Hirayama, K. 1918, AJ, 31, 185 [Google Scholar]
Hsieh, H.H., & Jewitt, D. 2006, Science, 312, 561 [NASA ADS] [CrossRef] [Google Scholar]
Hudson, R.S., & Ostro, S.J. 1994, Science, 263, 940 [CrossRef] [Google Scholar]
Hudson, R.S., Ostro, S.J., & Harris, A.W. 1997, Icarus, 130, 165 [NASA ADS] [CrossRef] [Google Scholar]
Hung, D., Hanuš, J., Masiero, J.R., & Tholen, D.J. 2022, PSJ, 3, 56 [NASA ADS] [Google Scholar]
IAU 2020a, Naming of Astronomical Objects https://www.iau.org/public/themes/naming/ [Google Scholar]
IAU 2020b, Naming of Exoplanets https://www.iau.org/public/themes/naming_exoplanets/ [Google Scholar]
Ivezic, Z., Connolly, A., Vanderplas, J., & Gray, A. 2014, Statistics, Data Mining and Machine Learning in Astronomy (Princeton University Press) [CrossRef] [Google Scholar]
Jewitt, D. 2009, AJ, 137, 4296 [Google Scholar]
Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
Kaasalainen, M., Torppa, J., & Piironen, J. 2002, Icarus, 159, 369 [NASA ADS] [CrossRef] [Google Scholar]
Kelso, T. 2021, CelesTrak, https://celestrak.com/ [Google Scholar]
Knežević, Z., & Milani, A. 2000, Celest. Mech. Dyn. Astron., 78, 17 [Google Scholar]
Knežević, Z., & Milani, A. 2003, A&A, 403, 1165 [Google Scholar]
Knežević, Z. & Milani, A. 2012, in IAU Joint Discussion, IAU Joint Discussion, P18 [Google Scholar]
Knežević, Z., Lemaître, A., & Milani, A. 2002, The Determination of Asteroid Proper Elements, 603 [Google Scholar]
Kovalenko, I., Kempf, J., Popovichenko, O., Gateau, T., & Lizy-Destrez, S. 2022, Planet. Space Sci., 215, 105463 [NASA ADS] [CrossRef] [Google Scholar]
Kretlow, M. 2020, in European Planetary Science Congress, EPSC2020-690 [Google Scholar]
Lagerkvist, C.I. 1978, A&AS, 34, 203 [NASA ADS] [Google Scholar]
Lagerros, J.S.V. 1996, A&A, 310, 1011 [NASA ADS] [Google Scholar]
Lebofsky, L.A., & Spencer, J.R. 1989, in Asteroids II, eds. R.P. Binzel, T. Gehrels, & M.S. Matthews, 128 [Google Scholar]
Lebofsky, L.A., Sykes, M.V., Tedesco, E.F., et al. 1986, Icarus, 68, 239 [NASA ADS] [CrossRef] [Google Scholar]
Lister, T.A., Gomez, E., Chatelain, J., et al. 2021, Icarus, 364, 114387 [NASA ADS] [CrossRef] [Google Scholar]
Lloyd, S. 1982, IEEE Trans. Inform. Theory, 28, 129 [Google Scholar]
Mahlke, M., Carry, B., & Denneau, L. 2021, Icarus, 354, 114094 [Google Scholar]
Mahlke, M., Carry, B., & Mattei, P.-A. 2022, A&A, 665, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mainzer, A., Grav, T., Bauer, J., et al. 2011, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
Marchis, F., Kaasalainen, M., Hom, E.F.Y., et al. 2006, Icarus, 185, 39 [NASA ADS] [CrossRef] [Google Scholar]
Marciniak, A., Bartczak, P., Santana-Ros, T., et al. 2012, A&A, 545, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marciniak, A., Bartczak, P., Müller, T., et al. 2018, A&A, 610, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marrese, P.M., Marinoni, S., Fabrizio, M., & Giuffrida, G. 2017, A&A, 607, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Marsden, B.G. 1980, Celest. Mech., 22, 63 [CrossRef] [Google Scholar]
Marsden, B.G. 1993, in Near-Earth-Objects Interception Workshop, 36, Proceedings of the Near-Earth-Objects Interception Workshop, eds. G.H. Canavan, J.C. Solem, & J.D.G. Rather, 67 [Google Scholar]
Marsden, B.G., Sekanina, Z., & Yeomans, D.K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
Marsset, M., Vernazza, P., Gourgeot, F., et al. 2014, A&A, 568, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Masiero, J.R., Mainzer, A.K., Grav, T., et al. 2011, ApJ, 741, 68 [NASA ADS] [CrossRef] [Google Scholar]
Masiero, J.R., Mainzer, A.K., Bauer, J.M., et al. 2013, ApJ, 770, 7 [NASA ADS] [CrossRef] [Google Scholar]
Matter, A., Delbò, M., Carry, B., & Ligori, S. 2013, Icarus, 226, 419 [NASA ADS] [CrossRef] [Google Scholar]
Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
McCord, T.B., Adams, J.B., & Johnson, T.V. 1970, Science, 168, 1445 [NASA ADS] [CrossRef] [Google Scholar]
Merline, W.J., Close, L.M., Dumas, C., et al. 1999, Nature, 401, 565 [NASA ADS] [CrossRef] [Google Scholar]
Merline, W.J., Drummond, J.D., Carry, B., et al. 2013, Icarus, 225, 794 [NASA ADS] [CrossRef] [Google Scholar]
Milani, A., & Knežević, Z. 1990, Celest. Mech. Dyn. Astron., 49, 347 [NASA ADS] [CrossRef] [Google Scholar]
Milani, A., & Knežević, Z. 1994, Icarus, 107, 219 [NASA ADS] [CrossRef] [Google Scholar]
Milani, A., Cellino, A., Knežević, Z., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
Mommert, M., Trilling, D.E., Borth, D., et al. 2016, AJ, 151, 98 [NASA ADS] [CrossRef] [Google Scholar]
Moskovitz, N., Burt, B., Schottland, R., et al. 2021, in AAS/Division for Planetary Sciences Meeting Abstracts, 53, AAS/Division for Planetary Sciences Meeting Abstracts, 101.04 [NASA ADS] [Google Scholar]
MPC 2021, MPCAT-OBS: Observation Archive, https://minorplanetcenter.net/iau/ECS/MPCAT-OBS/MPCAT-OBS.html [Google Scholar]
Mueller, B.E.A., Tholen, D.J., Hartmann, W.K., & Cruikshank, D.P. 1992, Icarus, 97, 150 [NASA ADS] [CrossRef] [Google Scholar]
Muinonen, K., Belskaya, I.N., Cellino, A., et al. 2010, Icarus, 209, 542 [NASA ADS] [CrossRef] [Google Scholar]
Müller, T.G., Miyata, T., Kiss, C., et al. 2013, A&A, 558, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Neeley, J.R., Clark, B.E., Ockert-Bell, M.E., et al. 2014, Icarus, 238, 37 [NASA ADS] [CrossRef] [Google Scholar]
Nesvorny, D. 2015, NASA Planetary Data System, EAR [Google Scholar]
Newton, I. 1760, Philosophiae naturalis principia mathematica, vol. 1-4 [Google Scholar]
Novakovic, B., & Radovic, V. 2019, in EPSC-DPS Joint Meeting 2019, EPSC-DPS2019-1671 [Google Scholar]
Nugent, C.R., Margot, J.L., Chesley, S.R., & Vokrouhlicky, D. 2012, AJ, 144, 60 [NASA ADS] [CrossRef] [Google Scholar]
O’Rourke, L., Müller, T., Valtchanov, I., et al. 2012, Planet. Space Sci., 66, 192 [CrossRef] [Google Scholar]
Ostro, S.J., Margot, J.-L., Benner, L.A.M., et al. 2006, Science, 314, 1276 [NASA ADS] [CrossRef] [Google Scholar]
Oszkiewicz, D.A., Muinonen, K., Bowell, E., et al. 2011, J. Quant. Spec. Radiat. Transf., 112, 1919 [NASA ADS] [CrossRef] [Google Scholar]
Pajuelo, M., Carry, B., Vachier, F., et al. 2018, Icarus, 309, 134 [NASA ADS] [CrossRef] [Google Scholar]
Parker, A., Ivezic, Z., Juric, M., et al. 2008, Icarus, 198, 138 [NASA ADS] [CrossRef] [Google Scholar]
Pätzold, M., Andert, T.P., Asmar, S.W., et al. 2011, Science, 334, 491 [CrossRef] [Google Scholar]
Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
Penttilä, A., Shevchenko, V.G., Wilkman, O., & Muinonen, K. 2016, Planet. Space Sci., 123, 117 [CrossRef] [Google Scholar]
Perna, D., Barucci, M.A., Fulchignoni, M., et al. 2018, Planet. Space Sci., 157, 82 [CrossRef] [Google Scholar]
Popescu, M., Licandro, J., Carvano, J.M., et al. 2018, A&A, 617, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pravec, P., Sarounová, L., Rabinowitz, D.L., et al. 2000, Icarus, 146, 190 [NASA ADS] [CrossRef] [Google Scholar]
Pravec, P., Vokrouhlickÿ, D., Polishook, D., et al. 2010, Nature, 466, 1085 [NASA ADS] [CrossRef] [Google Scholar]
Pravec, P., Fatka, P., Vokrouhlickÿ, D., et al. 2019, Icarus, 333, 429 [NASA ADS] [CrossRef] [Google Scholar]
Rocher, P., & Cavelier, C. 1996, in Dynamics, Ephemerides, and Astrometry of the Solar System, 172, eds. S. Ferraz-Mello, B. Morando, & J.-E. Arlot, 357 [Google Scholar]
Rodrigo, C., & Solano, E. 2020, in XIV.0 Scientific Meeting (virtual) of the Spanish Astronomical Society, 182 [Google Scholar]
Rodrigo, C., Solano, E., & Bayo, A. 2012, SVO Filter Profile Service Version 1.0, IVOA Working Draft 15 October 2012 [Google Scholar]
Rozitis, B., & Green, S.F. 2014, A&A, 568, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rozitis, B., Green, S.F., MacLennan, E., & Emery, J.P. 2018, MNRAS, 477, 1782 [CrossRef] [Google Scholar]
Sanchez, J.A., Reddy, V., Nathues, A., et al. 2012, Icarus, 220, 36 [CrossRef] [Google Scholar]
Scheeres, D.J. 2007, Icarus, 189, 370 [NASA ADS] [CrossRef] [Google Scholar]
Scheeres, D.J., Britt, D., Carry, B., & Holsapple, K.A. 2015, Asteroid Interiors and Morphology, eds. P. Michel, F. DeMeo, & W.F. Bottke (Univ. Arizona Press), 745 [Google Scholar]
Scheirich, P., & Pravec, P. 2009, Icarus, 200, 531 [NASA ADS] [CrossRef] [Google Scholar]
Schubart, J. 1974, A&A, 30, 289 [NASA ADS] [Google Scholar]
Sergeyev, A.V., & Carry, B. 2021, A&A, 652, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sergeyev, A.V., Carry, B., Onken, C.A., et al. 2022, A&A, 658, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Shepard, M.K., Timerson, B., Scheeres, D.J., et al. 2018, Icarus, 311, 197 [NASA ADS] [CrossRef] [Google Scholar]
Shevchenko, V.G., Belskaya, I.N., Muinonen, K., et al. 2016, Planet. Space Sci., 123, 101 [NASA ADS] [CrossRef] [Google Scholar]
Siltala, L., & Granvik, M. 2020, A&A, 633, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Skrutskie, M.F., Cutri, R.M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
Slivan, S.M. 2002, Nature, 419, 49 [CrossRef] [Google Scholar]
Snodgrass, C., Carry, B., Dumas, C., & Hainaut, O. 2010, A&A, 511, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Solem, J.C. 1994, Nature, 370, 349 [NASA ADS] [CrossRef] [Google Scholar]
Standish, E.M., & Hellings, R.W. 1989, Icarus, 80, 326 [NASA ADS] [CrossRef] [Google Scholar]
Sykes, M.V., Cutri, R.M., Fowler, J.W., et al. 2000, Icarus, 146, 161 [NASA ADS] [CrossRef] [Google Scholar]
Tanga, P., Carry, B., Colas, F., et al. 2015, MNRAS, 448, 3382 [NASA ADS] [CrossRef] [Google Scholar]
Taylor, M.B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, Astronomical Society of the Pacific Conference Series, 347, 29 [NASA ADS] [Google Scholar]
Tedesco, E.F. 1989, in Asteroids II, eds. R.P. Binzel, T. Gehrels, & M.S. Matthews, 1090 [Google Scholar]
Tedesco, E.F., Williams, J.G., Matson, D.L., et al. 1989, in Asteroids II, eds. R.P. Binzel, T. Gehrels, & M.S. Matthews, 1151 [Google Scholar]
Tedesco, E.F., Noah, P.V., Noah, M., & Price, S.D. 2002, AJ, 123, 1056 [NASA ADS] [CrossRef] [Google Scholar]
Tholen, D.J. 1984, PhD thesis, University of Arizona [Google Scholar]
Tholen, D.J. 1989, in Asteroids II, eds. R.P. Binzel, T. Gehrels, & M.S. Matthews, 1139 [Google Scholar]
Tisserand, F. 1889, Bull. Astron. Serie I, 6, 241 [Google Scholar]
Tsirvoulis, G. 2019, MNRAS, 482, 2612 [NASA ADS] [CrossRef] [Google Scholar]
Vachier, F., Berthier, J., & Marchis, F. 2012, A&A, 543, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vasavada, A.R., Paige, D.A., & Wood, S.E. 1999, Icarus, 141, 179 [NASA ADS] [CrossRef] [Google Scholar]
Veeder, G.J., Matson, D.L., & Tedesco, E.F. 1983, Icarus, 55, 177 [NASA ADS] [CrossRef] [Google Scholar]
Vernazza, P., Broz, M., Drouard, A., et al. 2018, A&A, 618, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Viikinkoski, M., Kaasalainen, M., & Ďurech, J. 2015, A&A, 576, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vinogradova, T.A. 2019, MNRAS, 484, 3755 [Google Scholar]
Vokrouhlický, D. & Nesvornÿ, D. 2008, AJ, 136, 280 [CrossRef] [Google Scholar]
Vokrouhlickÿ, D., Bottke, W.F., Chesley, S.R., Scheeres, D.J., & Statler, T.S. 2015, The Yarkovsky and YORP Effects, eds. P. Michel, F. DeMeo, & W.F. Bottke, 509 [Google Scholar]
Warner, B.D., Harris, A.W., & Pravec, P. 2021, NASA Planetary Data System, 10 [Google Scholar]
Wolters, S.D., & Green, S.F. 2009, MNRAS, 400, 204 [NASA ADS] [CrossRef] [Google Scholar]
Wright, E.L., Eisenhardt, P.R.M., Mainzer, A.K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
Xu, S., Binzel, R.P., Burbine, T.H., & Bus, S.J. 1995, Icarus, 115, 1 [NASA ADS] [CrossRef] [Google Scholar]
Yeh, T.-S., Li, B., Chang, C.-K., et al. 2020, AJ, 160, 73 [NASA ADS] [CrossRef] [Google Scholar]
Yeomans, D.K., Barriot, J.P., Dunham, D.W., et al. 1997, Science, 278, 2106 [NASA ADS] [CrossRef] [Google Scholar]
Zappala, V., di Martino, M., Farinella, P., & Paolicchi, P. 1983, in Asteroids, Comets, and Meteors, 73 [Google Scholar]
Zappala, V., Cellino, A., Farinella, P., & Knežević, Z. 1990, AJ, 100, 2030 [CrossRef] [Google Scholar]
Zellner, B., & Bowell, E. 1977, in IAU Colloq. 39: Comets, Asteroids, Meteorites: Interrelations, Evolution and Origins, ed. A.H. Delsemme, 185 [Google Scholar]
Zellner, B., & Gradie, J. 1976, AJ, 81, 262 [Google Scholar]
Zessewitsch, W. 1932, Astron. Nachr., 246, 441 [NASA ADS] [CrossRef] [Google Scholar]
Zinzi, A., Giardino, M., Giunta, A., et al. 2021, in LPI Contributions, 2549, 5th Planetary Data Workshop & Planetary Science Informatics & Analytics, 7032 [Google Scholar]
Žižka, J., Galád, A., Vokrouhlickÿ, D., et al. 2016, A&A, 595, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

¹

https://pds.nasa.gov/

²

https://cdsweb.u-strasbg.fr/

³

https://ssd.jpl.nasa.gov/

⁴

https://neoexchange.lco.global/

⁵

https://asteroid.lowell.edu

⁶

https://neorocks.elecnor-deimos.com/web/guest/search-retrieval

⁷

https://mp3c.oca.eu

⁸

https://astro.kretlow.de/?SiMDA

⁹

http://www.ecocel-database.com

¹⁰

https://www.iau-100.org/name-exoworlds

¹¹

https://www.minorplanetcenter.net/iau/info/DesDoc.html

¹²

https://www.minorplanetcenter.net/iau/info/PackedDes.html

¹³

https://www.elastic.co/

¹⁴

https://lucene.apache.org/

¹⁵

https://doc.ssodnet.imcce.fr/quaero.html

¹⁶

https://gea.esac.esa.int/archive/

¹⁷

https://ssp.imcce.fr/data/ssodnet.bib

¹⁸

https://ivoa.net/documents/VOTable/

¹⁹

https://newton.spacedys.com/astdys/

²⁰

http://asteroids.matf.bg.ac.rs/fam/

²¹

https://scikit-learn.org

²²

https://minorplanetcenter.net/iau/lists/ObsCodesF.html

²³

http://svo2.cab.inta-csic.es/theory/fps/

²⁴

https://github.com/astropy/astropy-APEs/blob/main/APE6.rst

²⁵

https://parquet.apache.org/

²⁶

https://ssp.imcce.fr/data/ssoBFT-latest.ecsv.bz2

²⁷

https://ssp.imcce.fr/data/ssoBFT-latest.parquet

²⁸

http://faculty.washington.edu/ivezic/sdssmoc/sdssmoc.html

²⁹

https://rocks.readthedocs.io

All Tables

Table 1

Statistics of the number of SSO designations by object class.

	Fig. 1 Histogram of the number of designations for each class of object.
In the text

	Fig. 2 Years of publication of bibliographic references used to populate `SsODNet.dataCloud`.
In the text

	Fig. 3 General workflow used to compute the best estimate of each parameter.
In the text

	Fig. 4 Distribution of families (first panel), albedo (second), colors (third, using a color-scheme similar to Parker et al. 2008 based on a code by Ivezic et al. 2014), and taxonomy (fourth) against proper elements (semi-major axis and sine of inclination). The number of plotted objects is reported in each panel.
In the text

	Fig. 5 Kernel density estimate (KDE) of the density of the C, S, X, and B complexes. The bimodal distribution of X-types highlights the P and M sub-classes (average p_V of 0.044 and 0.129, below and above 2000 kg m⁻³, respectively). Similarly, Pallas is the sole contributor to high-density B-types.
In the text

	Fig. 6 Rotation period (top) and obliquity (bottom) vs. diameter for 17 201 and 2596 SSOs, respectively. Darker shades of grey indicate higher density of points.
In the text

	Fig. 7 Example of clustering of spin coordinates for (20) Massalia. Six solutions (blue) are possible (Kaasalainen et al. 2002; Hanuš et al. 2016; Cellino et al. 2019). The four separated spin coordinates (orange) of the four clusters are reported in the `ssoCard`.
In the text

	Fig. 8 Decision tree for taxonomic classes. Classes based on spectroscopy are favored upon those based on broad-band photometry only. Similarly data sets covering the full VISNIR wavelength range are favored over NIR only, itself preferred to VIS only. Finally, for classification based on similar data sets, the Mahlke scheme is preferred over Bus-DeMeo, Bus, SMASS, and Tholen schemes.
In the text

	Fig. 9 All 1681 SSOs with a thermal inertia above 1 SI (gray), the 419 with a S/N above 3 (black), and a linear regression on the latter of equation log(Γ₀) = 2.5–0.29 log(D), a result that is similar to the recent work of Hung et al. (2022).
In the text

SsODNet: Solar system Open Database Network

1 Introduction

2 Name resolver: quaero

2.1 Context

2.2 Quaero: /’kwaę.ro:/

3 Compilation of properties: dataCloud

3.1 Context

3.2 Method

4 Selection of the best estimates: ssoCard

4.1 Context

4.2 Method

4.2.1 Osculating elements

4.2.2 Proper elements

4.2.3 Families

4.2.4 Pairs

4.2.5 Diameter

4.2.6 Albedo

4.2.7 Masses

4.2.8 Density

4.2.9 Spin solutions

4.2.10 Colors

4.2.11 Phase function

4.2.12 Taxonomy

4.2.13 Thermal properties

4.2.14 Yarkovsky drift

5 Summary for all SSOs: ssoBFT

6 Accessing the services: SsODNet and rocks

6.1 REST interface

6.2 Web-service interface

6.3 Web form interface

6.4 Python interface: rocks

7 Future developments

Data compilation

Set of parameters

Types of SSOs

User interface

8 Conclusions

Acknowledgements

Appendix A Collections available in SsODNet.dataCloud

Appendix B Description of all the methods

Appendix C Method lists for best-estimate determination

References

All Tables

All Figures

2 Name resolver: `quaero`

2.2 Quaero: /’k^waę.ro:/

3 Compilation of properties: `dataCloud`

4 Selection of the best estimates: `ssoCard`

5 Summary for all SSOs: `ssoBFT`

6 Accessing the services: `SsODNet` and rocks

Appendix A Collections available in `SsODNet.dataCloud`