| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202244084 | |
| Published online | 01 February 2023 | |
Near-Earth object 2022 EB5: From atmospheric entry to physical properties and orbit
1
National Space Science Center CAS,
Nanertiao 17,
100190
Beijing, PR China
e-mail: bhzhou@nssc.ac.cn; limingtao@nssc.ac.cn
2
University of Chinese Academy of Sciences,
Yuquan Road 19A,
100049
Beijing, PR China
e-mail: gengshujuan18@mails.ucas.ac.cn
Received:
23
May
2022
Accepted:
6
December
2022
Context. The near-Earth object (NEO) 2022 EB5 is the fifth NEO found prior to entering the Earth's atmosphere. It fragmented over the Norway Sea on 2022 March 11 about two hours after being discovered by the astronomer Krisztián Sárneczky at Konkoly Observatory in Hungary. The Center for Near-Earth Object Studies (CNEOS) at NASA detected the visible radiation emitted at the time of its atmospheric entry. The Jet Propulsion Laboratory (JPL) and European Space Agency (ESA) derived its orbital elements based on observations of its pre-atmospheric orbit.
Aims. This paper aims to calculate the physical properties of this NEO, in particular, the bulk strength, type of the material, albedo, size, and mass, based on observations of its peak brightness at the time of its atmospheric entry. In addition, the heliocentric elements are computed from its interaction with Earth's atmosphere and compared with those derived from observations by JPL and ESA, respectively, to evaluate the accuracy of our method.
Methods. The flight equations of 2022 EB5 were inversely integrated from the peak brightness to the atmospheric boundary via the fourth-order Runge-Kutta method. A pancake model was utilized to simulate the fragmentation of the impactor. Parameters needed to complete the integration process that were unknown were set to be optimization variables and determined via a genetic algorithm.
Results. The results obtained show that 2022 EB5 was most likely a C-type asteroid with a maximal bulk strength of 2 MPa, diameter of 5–6 m, cometary density, and very low albedo that is no greater than 0.025. In addition, considering the effects of the atmosphere is helpful in getting a more accurate measurement for the semi-major axis, eccentricity, and inclination, although the accuracy of orbital elements strongly depends on the accuracy of USG sensors.
Key words: meteorites, meteors, meteoroids / Earth / minor planets, asteroids: individual: 2022 EB5
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
Small-sized near-Earth objects (NEOs) hit the Earth relatively frequently (Brown et al. 2002; Harris & D’Abramo 2015), with one meter-sized object making impact approximately every two weeks (Brown et al. 2016). However, their detections are more challenging given their small size and low albedo. In addition, their less severe impact hazard determines that they are not the main target of astronomical surveys. However, the famous Tunguska (Chyba et al. 1993; Jenniskens et al. 2019) and Chelyabinsk impact events (Brown et al. 2013; Popova et al. 2013) have proven that asteroids of decameters and even meters in length are capable of producing airbursts that may lead to severe casualties and economical losses. As a result, meter-sized objects are attracting more attention in the field.
On the evening of 2022 March 11 (UTC time), Hungarian astronomer Krisztián Sárneczky discovered a near-earth object in Konkoly Observatory and named it 2022 EB5. It was soon found that the probability of hitting the Earth of this newly-discovered object was 100%. And it did enter the Earth’s atmosphere about two hours after being discovered. The US government sensors (USG sensors) reporting to the Center for Near-Earth Objects Studies (CNEOS) website detected and recorded the velocity and location at the peak brightness of this impact as well as the intensity-time signature during its fragmentation, providing an estimate of the total impact energy based on the accumulated visible radiation. Teams at both the Jet Propulsion Laboratory (JPL) and European Space Agency (ESA) calculated its heliocentric orbit based on telescopic observations prior to the impact. There have been a total of six small bodies that have been detected prior to impact: 2008 TC3 (Jenniskens et al. 2009; Farnocchia et al. 2017), 2014 AA (Farnocchia et al. 2016), 2018 LA (Jenniskens et al. 2021), 2019 MO1, 2022 EB5, and 2022 WJ12. Two of these objects, 2008 TC3 and 2018 LA, fragmented over land and produced meteorites that were later recovered. The collection and analysis of meteorites suggest that both two objects were asteroids of the S-type (Farnocchia et al. 2017; Jenniskens et al. 2021). Nevertheless, 2022 EB5 broke up over the sea, leaving no chance of recovery of possible meteorites. Moreover, the trajectory of its bright flight was not caught by ground-based fireball networks, which makes it more difficult to determine its material and structure.
Generally, there are two methods applied for determining the type and the bulk strength of objects with the absence of meteorites (Brown et al. 2016). The first method is to use telescopic observations of the body prior to the atmospheric entry. Researchers can preliminarily estimate the size, cohesion strength, and material of an object on the basis of the relationship between the absolute magnitude, albedo, and size, the rotation speed as well as the near-infrared spectrum. However, obtaining observation data for small-sized objects is rare and errors increase as the diameter decreases due to the assumed albedo.
Another way to deduct the structure and material of an object is to observe and study its interaction with the atmosphere, its fragmentation behavior, deceleration, light curve, and the ablation process (Devillepoix et al. 2019). Fireball networks all around the world are able to record the trajectory of bright flights of meteoroids in their field of view. Analyzing the trajectory is helpful in learning about the variation of visible radiation and then the process of energy deposition. The greatest public resource for such observations is CNEOS, which records the location of peak brightness of meteoroids via sensors of satellites and the estimated total energy since 1988. Light curves of the vast majority of meteoroids can also be downloaded on the website of CNEOS as of 2022.
In most of the previous studies, the ram pressure of the mete-oroid at peak brightness is generally regarded as the upper limit of the bulk strength, while the actual strength remains unknown (Brown et al. 2016), and the pre-atmospheric mass can be calculated from the estimated original kinetic energy by assuming a fixed luminous efficiency and a constant velocity during atmospheric entry (Brown et al. 2016). With an assumed bulk density, the diameter can be estimated using a spherical assumption. The estimated bulk strength is usually greater than the real value as the height of fragmentation is higher than that of the peak brightness, which leads to the variance in ram pressure. Thus, it is necessary to simulate the atmospheric entry process to determine the effect on various physical variables of the atmosphere and to consequently to decide the bulk strength more accurately.
The most characteristic aspect during the atmospheric entry of an object is fragmentation (Artemieva & Shuvalov 2016). The process of energy release is recorded in the energy deposition curve, which illustrates the variation of the deposited energy per kilometer with the altitude or time. Several semi-analytical fragmentation models have been developed to achieve a quick simulation of the fragmentation process and reproduce the main feature of energy deposition. They are characterized by their treatment of the disintegration process.
The pancake model (Chyba et al. 1993; Hills & Goda 1993) takes the disrupted object as a single debris cloud composed of fragments and simulates the separation of fragments by the increase of the cloud’s wind-ward radius. The airburst occurs when the radius comes up to a specific extent, say, several times the original radius of the object. This moment generally coincides with the time when the energy deposition reaches its maximum and also corresponds with the peak brightness.
The separate fragmentation model (Baldwin & Sheaffer 1971; Mehta et al. 2015) treats fragmentation as a consecutive disintegration of the object into individual pieces that can then possibly be tracked down to the ground.
The fragment-cloud model (Wheeler et al. 2017, 2018) combines the two aforementioned models. The meteoroid breaks up into one debris cloud and several separate fragments every time it breaks up. The debris cloud follows the variation as it does in the pancake model, whilst the fragments will disrupt successively when their ram pressure exceeds the strength. The fragment-cloud model is also able to simulate the atmospheric entry of rubble piles and fractured meteoroids, instead of solely single monoliths by setting the model parameters (Wheeler et al. 2018).
All three types of models retain one aspect in common, namely, that fragmentation is triggered when the ram pressure exceeds the bulk strength of the object. In addition, they are all capable of reflecting the abrupt energy release at the peak brightness. The fragment-cloud model has a high level of accuracy due to its flexibility when the whole energy deposition curve is known, but the empirical parameters do increase the uncertainty, especially when the energy deposition process is not available. The pancake model, on the other hand, is able to invert rough physical properties of the body based on the point of peak brightness by using a small number of parameters (McMullan & Collins 2019), although it is not able to reflect all the details of the whole entry process.
The main challenge of calculating the variables of these models generally comes from the absence of initial conditions and the uncertainty in the model parameters. In cases where the initial conditions are well known, the manual trial-and-error method (Park & Brown 2012; Wheeler et al. 2018) is widely used. In this method, model parameters are manually adjusted until the observed and simulated energy deposition profiles match. However, as the number of unknown parameters increases, this method inevitably brings on higher labor costs, more repetitive work, and low efficiency, as well as the possibility of devising non-unique solutions.
To automate this process, numerical optimization can be used. The unknown variables can be taken as optimization variables and be automatically solved within the constraints of the fragmentation model or intrinsic physical relationship. Tárano et al. (2019) used a genetic algorithm and fragment-cloud model to solve the size, density, strength, and mass of the object involved the Chelyabinsk impact event. In that work, they also applied the method to the Lost City event (McCrosky et al. 1971) and the Benesov event (Borovicka et al. 1998). The inverted mass lies in the range measured and reported in other papers. However, the objective function in their method is a number of points on the energy deposition curve. This is only possible for those meteoroids whose bright flight stage was recorded by cameras. In their case, the number of constraints is smaller than the number of variables used in optimization, which can lead to non-unique solutions. The objective function is also so complex that it requires a large solution space and a considerable amount of time to solve the problem.
This paper is aimed at simulating the atmospheric entry of 2022 EB5 and determining its physical properties, mainly the bulk strength and the material of this object. The atmospheric process is calculated by using the pancake model and genetic algorithm on the basis of the observation data of its peak brightness. The physical variables at the atmospheric boundary are then converted to heliocentric orbital elements, which are compared with the observed orbital elements derived by JPL and ESA. Section 2 introduces the observation data of 2022 EB5. Section 3 explains the physical models and calculation methods. In Sect. 4, we present, analyze and discuss the results obtained. We present our conclusions in Sect. 5.
2 Observational data
2.1 Heliocentric orbital elements
The observations of 2022 EB5 primarily come from observatories or satellites such as the ESA Orbit Determination and Impact Monitoring system (ODIM) and the Minor Planet Center (MPC).
In particular, JPL3 and ESA4 calculated the osculating heliocentric orbital elements at a different time according to the observations severally. The heliocentric orbital elements and the 1-sigma error of the 2022 EB5 derived by JPL and ESA are listed in Tables 1 and 2, respectively. The symbol U denotes the U parameter, as a number between 0 and 9, reflecting the orbit uncertainty with 9 indicating a high uncertainty and 0 a low uncertainty5. According to its orbital elements, 2022 EB5 is an Apollo-type object.
There is a little discrepancy between the two sets of orbital solutions. The 1σ errors of the orbital elements provided by ESA are basically smaller compared with the solution given by JPL. This may result from the differences in calculation methods, the selection of observation sources, and the diversity in terms of time.
A statistical relation between the absolute magnitude, H, the albedo, pv, and the optic diameter, D (in m), is often used to estimate the diameter of NEOs (Bowell et al. 1989):
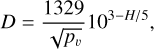 (1)
(1)
The nominal diameter of 2022 EB5 is 1.61 m if we assume the albedo is 0.147 which is the mean albedo (Morbidelli et al. 2020) used to convert absolute magnitude (31.66 in this case) into diameter. However, this estimated diameter could deviate relatively from the actual size of 2022 EB5 by a factor of two to three or even more considering it is a meter-scale impactor. Despite the lack of knowledge of its albedo, Eq. (1) still provides convenience in deciding its physical properties, which will be presented in Sect. 4.1.
Osculating orbital elements of 2022 EB5 at 23:58:50 on 2022 March 10 (UTC) derived by JPL using a total of 176 observations.
Orbital elements of 2022 EB5 at 00:00:00 on 2022 January 21 (UTC) derived by ESA.
Velocity and location at peak brightness and the estimated impact energy of 20222 EB5.
2.2 CNEOS data
The ground-based fireball networks did not catch the bright flight trajectory of 2022 EB5; however, the USG sensors of CNEOS6 recorded the velocity in Earth-Centered Earth-Fixed (ECEF hereafter) coordinate system and the location in World Geodetic System (WGS84) of the meteoroid at its peak brightness as well as the light curve during its fragmentation. The total impact energy, or (equally) the initial kinetic energy, was estimated via an empirical relationship between the total energy and the accumulated radiation energy (Brown et al. 2002). The data of CNEOS are listed in Table 3.
The CNEOS website reports the large fireballs detected by USG sensors all over the world. These sensors generally detect flashes of the fireball and measure the radiation energy of the meteoroids. They also record the location and the velocity vector of the fireball’s peak brightness for a small part of events. The light curves of a large number of meteoroids detected by USG sensors (including 2022 EB5) have also been available since 2022. The data of USG sensors have helped to calculate the mass, total impact energy (Brown et al. 2016) and even the pre-atmospheric orbit and strewn field (Carbognani 2021) of the impactor, especially when other observation data such as the observation of bright trajectory are absent. However, the accuracy of these data remains uncertain and varies greatly from parameter to parameter and event to event. Brown et al. (2016) found that the altitude of the peak brightness tended to be reasonably credible. The occasional discrepancy in the height often results from a multi-peak brightness recorded in the light curve. Devillepoix et al. (2019) compared the data of USG sensors with independent observations of ten events to discuss the reliability of USG sensors. They concluded that data from USG sensors are not recommended when determining the pre-entry orbit due to the possible large discrepancy in velocity and the variation in reliability in various events, but they can be used to estimate the strength as the height is generally accurate and the discrepancy in speed can hardly influence the order of magnitude of strength.
During the flight from the atmospheric boundary to the peak brightness of objects, there is no observable deceleration as these objects are so large that the drag component is negligible, which makes mass loss the main mechanism behind energy loss (Brown et al. 2016). Meanwhile, as the fragmentation condition is that the ram pressure exceeds the bulk strength of the object, there is a difference in the height of the beginning of fragmentation and the peak brightness. However, the altitude of fragmentation is generally unknown, so the ram pressure at peak brightness is token as a proxy of the bulk strength. In the case of 2022 EB5, these simplifications result in a pre-impact velocity of 17.24 km s−1, an initial mass of 112.65 t, which is calculated by the velocity and the estimated energy, and a bulk strength of 3.5 MPa with the atmospheric density calculated using a curve fit proposed by Wheeler et al. (2017) of the 1976 standard atmosphere model (U.S. Standard Atmosphere 1976). Nevertheless, even though the influence on the velocity of the atmospheric entry is slight, the strength deduced in this way may be quite inaccurate because of the sensitivity of the atmospheric density to the altitude, which may consequently affect the study of physical properties. Therefore, it is necessary to simulate the atmospheric entry process.
3 Models and methods
3.1 Flight equations and fragmentation
Due to the low atmospheric mass density at high altitudes – and thus, the negligible influence on ablation as a result – we assume that the atmospheric entry process started at an altitude of 100 km (Chyba et al. 1993), which is also regarded as the height of the atmospheric boundary in this paper. The flight of an object in Earth’s atmosphere is primarily dominated by gravity and atmospheric drag. The second-order differential flight equation of the object with respect to Earth is given by (Opik 2004):
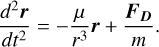 (2)
(2)
The vector r is the radius vector of the object in the Earth-centered inertial (ECI) coordinate system, whereas its norm is denoted as r. In addition, μ denotes the standard gravitational parameter of the Earth and m is the mass of the object. The symbol FD represents the atmospheric drag to the object and can be calculated via (Towner et al. 2022):
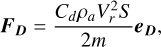 (3)
(3)
Here, Vr is the relative velocity of the object to the ground, also the norm of the velocity vector in the ECEF system, Vr. The unit vector eD defines the direction of the atmospheric drag force, namely, the opposite direction of the relative velocity, Vr. Then, Cd is the drag coefficient and equals 1; S is the area of the wind-ward cross-section; and ρa represents the atmospheric density. We use the curve fit proposed by Wheeler et al. (2017) of the 1976 standard atmosphere tables (U.S. Standard Atmosphere 1976):
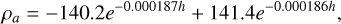 (4)
(4)
where h is the altitude.
Meanwhile, the mass of the object also reduces as the temperature of the object rises during the flight in the atmosphere. The loss of mass (i.e. ablation) follows as:
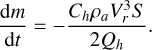 (5)
(5)
The symbol Ch denotes the heat transfer coefficient, usually set as 0.1, and Qh is the heat of ablation, a value that is related to the type of the object, explained further in Sect. 3.2.
As the object dives deeply into the atmosphere, the atmospheric density increases exponentially. Together with the hyper-velocity, this causes the ram pressure to reach megapascals, where the pressure is the ram pressure, 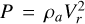 . And the object begins to break up at the moment when P exceeds its bulk strength, S0 (Chyba et al. 1993; Hills & Goda 1993; Wheeler et al. 2017). The pancake model proposed by Chyba et al. (1993) is utilized to simulate the fragmentation process (with the basic concept of the model depicted in Fig. 1).
. And the object begins to break up at the moment when P exceeds its bulk strength, S0 (Chyba et al. 1993; Hills & Goda 1993; Wheeler et al. 2017). The pancake model proposed by Chyba et al. (1993) is utilized to simulate the fragmentation process (with the basic concept of the model depicted in Fig. 1).
Once the fragmentation is triggered, the object starts to break up into plenty of smaller pieces. However, the fragments it generated do not disperse completely at the beginning but are still controlled by one common bow shock and behave as a debris cloud. Thus, they are considered as one single body until the gaps among each other are large enough. The separation of the fragments is described by the increase of the windward radius of the single body R, following:
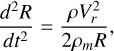 (6)
(6)
where ρm is the density of the object.
The rapid expansion of the radius suggests a significant increment in the contact area of the object and atmosphere, leading to an aggravation of deceleration and ablation and, hence, an enhancive deposition of energy. The energy release reaches its peak when the radius, R, expands to NR0. This peak is also considered as the occurrence of the drastic airburst and here it corresponds to the peak brightness; N is an empirical parameter that is equal to 2 when first proposed (Chyba et al. 1993), but is usually set to be 4–8 to obtain a good fit to the energy deposition curve derived from the light curve, as suggested by Collins et al. (2009).
The pancake model offers the advantages of quick computation and fewer empirical parameters when simulating the fragmentation process until the airburst occurs, which enables it to solve the physical variables via inverse integration. The initial conditions are the state vector, mass, radius, and radius variation rate at the peak brightness, while the target is the values of variables at the atmospheric boundary. The inverse integration is completed by the fourth-order Runge-Kutta method. The fragment-cloud model and the separate fragmentation model are not used here because of the absence of the energy deposition curve and their complexity, such as multi-fragmentation and complex empirical parameters, making it almost impossible to solve the equations inversely.
We note that the pancake model can only reflect the features of one fragmentation. For those objects that break up in the atmosphere more than once, as in the Chelyabinsk event, for example, the pancake model simulates one equivalent fragmentation and reproduces the abrupt energy deposition at the peak brightness. The height of the beginning of the equivalent fragmentation is physically not higher than that of the real first fragmentation. Therefore, the bulk strength (the ram pressure at the height of the beginning of the equivalent fragmentation) is not less than the real strength (the ram pressure at the peak brightness) or is the maximal value of the bulk strength.
 |
Fig. 1 Illustration of the pancake model presented by Chyba et al. (1993). The fragmentation starts when the ram pressure, P, exceeds the initial bulk strength, S0. And the airburst occurs, or the peak brightness is reached, at the very short moment when the windward radius of the object expands to N times the initial diameter of the object, R0. The height of fragmentation is the altitude where the fragmentation begins, which differs from the height of the airburst or, equivalently, the peak brightness. |
3.2 Solution of unknown variables
By comparing the known conditions in Sect. 2.2 and the equations in Sect. 3.1, it is apparent that seven variables are still unknown (needed to solve the equations by inverse integration): the density of the object, ρm; the heat of ablation, Qh; the bulk strength, S0; the mass at the peak brightness, mp; the radius at the peak brightness, Rp; the corresponding variation rate of radius, dRp; and the radius factor in the pancake model, N.
The radius factor, N, is an empirical parameter, so it is set to be 4 in this paper, and only 2 in a case where the former set leads to no solution. The density, ρm, and heat of ablation, Qh, are both relative to the material of the object. Since the material and type of the object remain unknown, we set four groups corresponding to four types of near-earth objects – comet, stony asteroid (S-type), carbonaceous asteroid (C-type), and iron asteroids (basically M-type). The density and heat of ablation of each group are artificially given according to their typical values in the literature (Chyba et al. 1993; Carry 2012), as Table 4 shows.
The other four unknown variables, S0, mp, Rp, and dRp, are optimization variables and can be solved with physical and model constraints via an optimization method. There are four independent constraints involved in this process: (1) the calculated variation rate of radius at the atmospheric boundary is zero, namely, dR0 = 0; (2) the calculated radius and mass at the atmospheric boundary should satisfy the mass calculation formula of a sphere, namely, R(m0) − R0 = 0. The radius R(m0) is computed from m0 based on the sphere assumption while R0 is the calculated radius at the atmospheric boundary via inverse integration, 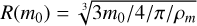 ; (3) the kinetic energy computed from the calculated velocity and mass at the atmospheric boundary should equal the energy estimated by CNEOS, namely, E(V0, m0) − E0 = 0; (4) the calculated radius R0 and the radius at peak brightness Rp should meet the relationship in the pancake model, namely, NR0 − Rp = 0. The subscript 0 represents the variables at the atmospheric boundary calculated by inverse integration, except for the initial kinetic energy.
; (3) the kinetic energy computed from the calculated velocity and mass at the atmospheric boundary should equal the energy estimated by CNEOS, namely, E(V0, m0) − E0 = 0; (4) the calculated radius R0 and the radius at peak brightness Rp should meet the relationship in the pancake model, namely, NR0 − Rp = 0. The subscript 0 represents the variables at the atmospheric boundary calculated by inverse integration, except for the initial kinetic energy.
It can be seen that the number of optimization variables is the same as that of the constraints, which guarantees the uniqueness of the solution.
The solving process is completed by a genetic algorithm (Gen et al. 2008). It is an optimization algorithm based on natural selection to solve minimum problems. The algorithm first selects a number of individuals from the ranges of optimization variables and evaluates their fitness by the objective function. Those with high fitness are able to generate more offspring in the next generation, while the less adaptable ones are much more likely to be eliminated. This process keeps happening until the manually set maximum number of generations is reached or the results satisfy the terminal conditions.
The range of four optimization variables S0, mp, Rp, and dRp are listed in Table 5.
The objective function, f, is the weighted sum of the four constraints among which the third constraint is adapted to fit the solving process better:
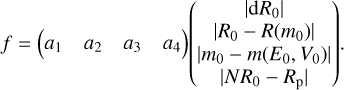 (7)
(7)
The parameters a1, a2, a3, and a4, are the weights of constraints and are initially set to be 10, 100, 0.01, and 50 to approximately balance the difference in magnitude of the constraints. They can be adjusted as the specific problem varies. Meanwhile, the standards of whether the solution is acceptable are |R0 − R(m0)|/R0 < 1%, |NR0 − Rp)|/Rp < 1%, |m0 − m(E0, V0)|/m0 < 0.1%, and |dR0| < 0.001.
We note that the constraints used in solving with the genetic algorithm are solely the four constraints listed in this section. It is obvious that the heliocentric orbital elements and the absolute magnitude derived from the observation are already known, but the elements are not considered constraints in solving unknown variables. There are mainly three reasons for this: first, the heliocentric orbital properties derived by JPL and ESA from observations show a discrepancy, indicating a possible error caused by the selection of orbital calculation method or observations. Thus, the derived orbital elements are more suitable for reference. Second, for most of the impact events that have occurred, the observed pre-atmospheric orbit is absent, while the data of atmospheric entry is more readily available. Solving on the basis of the physical relationship and model constraints during atmospheric entry is a more general way of dealing with impact events. Lastly, taking orbital elements and magnitude as constraints may lead to no solution. This is not only because the number of constraints will definitely exceed that of optimization variables, but because there tends to be a broad difference in terms of the accuracy of orbital observation and the precision of CNEOS sensors, which are not clearly defined.
Density and heat of ablation of four groups.
Range of optimization variables.
3.3 Orbital calculation and Tisserand’s parameter
The optimization and inverse integration of flight equation help to get the state vector in the ECI coordinate system at the atmospheric boundary which can then be converted to heliocentric orbital elements.
Then, another inverse integration of the governing equation of the two-body model (Earth-2022 EB5) is needed to calculate the state vector at Earth’s radius of the sphere of influence, RIOS = 922 790 km, to calculate the heliocentric orbital elements. Lunar gravity is neglected because the minimum possible close approach distance of 2022 EB5 to Moon is 0.00213 au7, much larger than Moon’s sphere of influence, which is approximately 0.00044 au (66 190 km) (Salazar et al. 2014).
For an NEO, once its heliocentric orbital elements are known, it is possible to approximately judge whether it is a comet or an asteroid by basically using Tisserand’s parameter, T, and the relationship between the perihelion distance, Q, the aphelion distance, q, and the semi-major axis of Jupiter (Tancredi 2014).
Tisserand’s parameter is a measure of orbital energy in restricted three-body problems. The larger Tisserand’s parameter, the lower the energy. Here, the three bodies are the sun, Jupiter and 2022 EB5. Tisserand’s parameter for 2022 EB5 is calculated as follows:
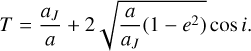 (8)
(8)
The symbol aJ is the semi-major axis of Jupiter; a and e are the best semi-major axis and eccentricity values for 2022 EB5; i is the angle between the orbital plane of 2022 EB5 and Jupiter. The criterion of approximately distinguishing asteroids and comets (Tancredi 2014) is summarized in Table 6.
Statistical criterion of distinguishing comets and asteroids.
3.4 Verification
The whole calculation process is illustrated in Fig. 2. Two impact events – the Košice event (Borovička et al. 2013b) and Chelyabinsk event (Brown et al. 2013) – are included to test the effectiveness of this method since both data from US government sensors and other observations of those events are available.
The Košice meteoroid impacted Earth’s atmosphere on February 28, 2010 over Slovakia (Borovička et al. 2013b). Its atmospheric trajectory was reconstructed from observations of three Hungarian surveillance video cameras. Several European Fireball Network (EN hereafter) camera radiometers recorded its light curve. A total of 218 meteorites were recovered and were classified as ordinary chondrites of type H5 (Gritsevich et al. 2014).
The physical properties and orbital elements of Košice mete-oroid we calculated are listed in Tables 7 and 8. Figure 3 shows the energy deposition rate at different altitudes of Košice mete-oroid. From Table 7, it can be seen that the strength is 1 MPa, which basically means that Košice meteoroid is an S-type or C-type asteroid. The dark solid line and the dotted lines in Fig. 3 derived by Wheeler et al. (2017) from its light curve respectively illustrate the energy deposition curve and the range of the energy deposition. There is more than one peak in this curve, implying that the Košice meteoroid fragmented at least twice, with the most drastic fragmentation occurring at an altitude of 36 km. The computed energy deposition curves of C-type and S-type groups are severally denoted by blue and red lines with each curve divided into two parts – the first part in solid line ends at the moment of airburst (also the moment of peak brightness), while the second part in dashed line illustrates the energy loss rate after the airburst. It can be seen that the second halves of the two energy deposition curves are less congruent with the one derived from the light curve. This is because the pancake model is developed mainly to simulate the fragmentation process instead of the following descent of the totally fragmented “pancake”. The large radius of the debris cloud tends to exaggerate the energy loss after the airburst, leading to a possible discrepancy between the calculated energy deposition curve and the profile derived from the light curve. Moreover, the calculated orbital elements of Košice event are mainly within the margin of error in the literature. However, we cannot further constrain the type of Košice meteoroid based solely on our results.
The other event is the Chelyabinsk event, which is one of the most studied meteoroid events and has been used for the validation of plenty of fragmentation models. However, the USG sensors detected height of peak brightness is 6 km lower than that derived from videos, which is due to the multi-peak in the light curve. Therefore, the energy deposition curve calculated using our method (dependent on the USG sensors) inevitably differs from that derived from videos, as Fig. 4 shows.
Even so, the discrepancy of both physical properties and orbital elements is not as large as the energy deposition curve. For the Chelyabinsk event, we only obtained the solution in the group labeled S-type (Tables 9 and 10), suggesting that other materials, as well as their corresponding parameter settings, cannot lead to a valid solution in the reasonable range of optimization variables. We note that the mass value derived by Popova et al. (2013) varies by a factor of two, while the mass from group Borovička et al. (2013a) is the best estimation, with a lower limit of 106 kg. Most parameters (both physical properties and orbital elements) are in the range or very close to the range derived in the literature, except the strength. The broad difference in strength is caused by the discrepancy in height of peak brightness, although it does not influence the judge of type in this case. The strength also implies that our method to a large extent depends on the accuracy of US G sensors.
These two events essentially verify that our method is valid in calculating or constraining the physical properties of the meteoroid. The Košice event can reflect the best accuracy of our method because the USG sensor-detected velocity, location, and height of peak brightness of this meteoroid are very close to those derived from observation of bright trajectory. The deviation of the physical properties and orbital elements of the Chelyabinsk event is higher than Košice event, but it is still within an acceptable range, although the height of peak brightness is 6 km lower than the height observed in videos. However, it should be noted that our method is highly dependent on the accuracy of USG sensors (uncertain in many cases), which means that data from other sources are often needed to validate the reliability of data from USG sensors.
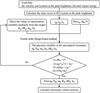 |
Fig. 2 Whole process of calculation. The velocity and position in the ECI system and the initial impact energy of 2022 EB5 are first computed based on the data at the peak brightness downloaded from CNEOS. The density and the heat of ablation are set according to Table 4. The genetic algorithm is then used to search for the solution to the optimization problem and generate the final values of optimization variables. After that, the physical variables at the atmospheric boundary and heliocentric orbital elements are derived accordingly. |
Physical properties and variables at atmospheric boundary of Košice meteoroid.
Calculated heliocentric orbital elements of the Košice meteoroid.
Physical properties and variables at the atmospheric boundary of Chelyabinsk meteoroid.
 |
Fig. 3 Energy deposition curve of Košice meteoroid. |
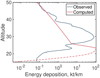 |
Fig. 4 Energy deposition curve of Chelyabinsk meteoroid. The computed group is the result of the S-type. The red solid line ends at the moment of the airburst while the dashed line illustrates the energy loss rate after the airburst. |
4 Results and discussion
4.1 Physical properties of 2022 EB5
This section discussed the inverted type, diameter, and bulk strength of this object. We first utilized the heliocentric orbital elements derived by JPL to calculate Tisserand’s parameter and a preliminarily look at the type according to the standards described in Sect. 3.3. The results show that for 2022 EB5, the Jupiter Tisserand invariant is T = 2.89. It is very likely to be a comet based on Tisserand’s parameter standard. However, the aphelion distance Q = 4.77 au is smaller than aJ, which suggests that it tends to be an asteroid. Therefore, the statistical standards based on orbit cannot lead to a clear answer here.
In Sect. 2.1, we present the relationship between the absolute magnitude, albedo, and diameter. This offers a way to estimate the diameter when the former two physical variables are known. The absolute magnitude of 2022 EB5 is 31.66, from which we get the variation of diameter with albedo, shown as Fig. 5. As we mention in Sect. 2, if we assume that the albedo is the average albedo of 0.147, then the diameter is 1.61 m. However, this estimate significantly depends on the accuracy of the albedo, as can be seen in Fig. 5. Thus, knowing the type of object is key. The NEOs of different types have albedos as follows: C types range between 0.03 and 0.11, S types range between 0.13 and 0.29, and M types between 0.1 and 0.3 (Usui et al. 2012).
A widely used empirical criterion to judge the type, as well as the strength and structure of a meteoroid, is the PE criterion (Ceplecha & McCrosky 1976; Brown et al. 2016). It is a one-dimensional criterion that includes the atmospheric density at the terminal height, the initial mass, velocity, and entry angle from the zenith of the meteoroid. However, it may not be convincing enough in the case of 2022 EB5, since the terminal height where the bright trajectory ends remains unknown and the calculation of terminal height can be very dependent on the fragmentation model chosen. A newly defined parameter, called the pressure resistance factor or pressure factor (PF) was proposed by Borovicka et al. (2022) to evaluate the structural strength on the basis of the maximal ram pressure. We chose the PF parameter to constrain the material strength of the object as the maximum ram pressure is more robust, easier to obtain and less dependent on observing circumstances than the terminal height. The PF parameter is given by:
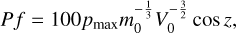 (9)
(9)
where pmax represents the maximum ram pressure in MPa, m0 denotes the initial mass in kg, V0 the initial velocity in km s−1, and z the entry angle from the zenith. Different ranges of PF values correspond to various strength groups (Ceplecha et al. 1998), as shown in Table 11. We note that the grouping in Table 11 is mainly for easier referencing – and it is not meant to suggest that each group corresponds to a specific type of NEOs as the PE factor does. A larger value implies a stronger structure of the meteoroid.
The dynamic pressure at the peak brightness is usually smaller than, but of the same order as the maximal pressure. Since the dynamic pressure at the peak brightness is hardly influenced by the pancake model, we calculated two columns of the PF parameter of various groups shown in Table 12, with the PF column computed on the maximal dynamic pressure, while the PFpeak column on the pressure at the peak brightness. All values of PF or PFpeak, except the PF value of the M-type group, suggest that 2022 EB5 is in strength group PF-III. Meteoroids in the PF-III strength group can be of type-II, type-IIIA, or type-IIIB in the PE system (see Borovicka et al. 2022, Fig. 3), which corresponds, respectively, to carbonaceous chondrite, short-period cometary, and weak cometary material (Ceplecha & McCrosky 1976; Brown et al. 2016). Therefore, 2022 EB5 is likely to be a C-type asteroid or a cometary object in accordance with the PF parameter. The PF parameter of the Chelyabinsk meteoroid based on both the maximal dynamic pressure and the pressure at peak brightness is also obtained for comparison. Both the PF and PFpeak values of the Chelyabinsk meteoroid are 0.21, larger than the PFpeak values and most of the PF values of 2022 EB5, suggesting a stronger structure than the object studied in this paper.
A further conclusion can be drawn with the atmospheric entry process taken into account. The obtained bulk strengths and the variables at the atmospheric boundary of four groups are listed in Table 12. It can be seen that the bulk strength of 2022 EB5 with the effects of the atmosphere taken into account is between 1.4 and 2.1 MPa, respectively, 40 and 60% less than the ram pressure at peak brightness 3.5 MPa, which is the general estimation value of bulk strength in the literature. This bulk strength is obviously too high for comets the strength of which is usually <0.01 MPa (Chyba et al. 1993; Trigo-Rodríguez & Llorca 2006) and too low for M-type asteroids usually with a strength larger than 10 MPa (Chyba et al. 1993). The range of diameter, 3-5.8 m, corresponds to a range of albedo of about 0.011-0.043, which (together with bulk strength) excludes the possibility of M-type asteroids and comets. The range of diameter then narrows to around 3.9–5.8, with the corresponding range of albedo between 0.011 and 0.025. Combining the range of albedo of various types of NEOs and the results of PF parameters, we suggest that there is a great possibility that 2022 EB5 is one asteroid of C-type with a very low albedo. We note that the diameter estimated from atmospheric entry is at least twice larger than the nominal diameter of 1.61 m.
There have been two carbonaceous asteroids that have been studied in situ, namely, the asteroid Ryugu (Watanabe et al. 2019) and Bennu (Chesley et al. 2014). Their densities are 1190 and 1260 kg m−3, respectively, lower than the assumed density of C-type in Table 4. Due to our evolving understanding of the NEO population, the densities of these two large C-type asteroids are similar to previously derived densities of meter-sized cometary objects. Thus, we added one group, that is, Ryugu/Bennu, where the density of 2022 EB5 is assumed to be equal to 1200 kg m3, close to the density of these two asteroids. The calculated results are shown in the second line in Table 12.
The position of group Ryugu/Bennu can further be justified by drawing the energy deposition curve of 2022 EB5. As is mentioned in Sect. 2.2, CNEOS published the light curve of most of the fireballs they detected since 2022, from which we can derive the energy deposition curve of those impact events. The radiation intensity per steradian of 2022 EB5 as a function of time can be downloaded on their website. We converted its light curve into an energy deposition curve using the empirical relationship between the luminous efficiency and the optic energy (see Brown et al. 2002).
Figure 6 shows the energy deposition rate as a function of the time of 2022 EB5. The bold gray line is the curve derived from the light curve while the dotted and dashed gray lines illustrate the ranges of estimation. There are approximately three main peaks in this curve with one sharp peak and two relatively gently peaks, suggesting that 2022 EB5 may experience three fragmentations, with the most drastic one occurring between 21:22:45 and 21:22:46. Figure 6 also compares the derived energy deposition curve with the three other calculated curves respectively drawn based on the data of the three most plausible groups – the C-type, Ryugu/Bennu, and S-type groups. It is obvious that the pancake model simulates one drastic equivalent fragmentation although the energy deposition after airburst is still exaggerated by the huge cross-sectional area as it is in the case of Košce meteoroid. The profile of the energy deposition curve of group Ryugu/Bennu is the most consistent one with that derived from the light curve, which suggests that 2022 EB5 is very likely to be a C-type asteroid with a cometary density.
Calculated heliocentric orbital elements of Chelyabinsk meteoroid.
 |
Fig. 5 The relationship between albedo and diameter of 2022 EB5. The dashed lines reflect the range of diameter for each albedo, taking account of the 1σ errors of magnitude observation. |
PF values and strength groups.
Physical properties and variables at the atmospheric boundary of 2022 EB5.
The calculated heliocentric orbital elements of 2022 EB5.
4.2 Orbital elements
Using the method mentioned in Sect. 3.3, the physical variables at the atmospheric boundary are converted to heliocentric orbital elements, as shown in Table 13.
To consider the accuracy more intuitively, we calculated the relative error of the calculated groups compared with the observed group. The corresponding errors are listed in Table 14.
It can be seen that the calculated ω and Ω of all groups are very close to the JPL and ESA solutions with the relative error all less than 0.6%. For other orbital elements, lower density results in higher accuracy, suggesting that the density of 2022 EB5 is very likely to be lower than the classical value of a C-type asteroid. However, the least relative error of the semi-major axis is 7.7% which is obviously much larger than the 1σ error of observation data. So as the cases of eccentricity and inclination. This possibly stems from the errors of both orbital observations and atmospheric observations of CNEOS.
In addition, the relative errors of a, e, and i of calculated groups are apparently smaller compared with the no-air group. Although the accuracy of ω and Ω of the no-air group is better than that of calculated groups, the differences are so little that they can be ignored. So, taking account of the atmospheric entry process can generally help to get more accurate orbital elements, but the effects of the atmosphere can be ignored when calculating the ω and Ω.
However, it should be noted that the accuracy of data from USG sensors, especially velocity, varies from event to event. The relatively high accuracy of 2022 EB5 cannot necessarily be extrapolated to other events.
 |
Fig. 6 Energy deposition curves of 2022 EB5. The energy deposition per second as a function of time instead of the energy loss per km varying as the altitude is shown in order to facilitate comparison. The time axis represents the second that passed 21:22 on March 11, 2022 UTC time. The maximum energy deposition rate occurs at 45.6 s, when the peak brightness as well as the so-called air burst takes place. The gray line represents the curve derived from the light curve reported by CNEOS, whereas the red dashed line, the yellow line, and the blue dot-dashed line illustrate the energy deposition curve of the C-type, Ryugu/Bennu, and S-type groups. |
Relative errors of calculated heliocentric orbital elements, given as a percent.
5 Conclusions
This paper applied a genetic algorithm and pancake model to solve the atmospheric entry process of the NEO 2022 EB5 based on the CNEOS data. During the atmospheric entry period from the boundary of the atmosphere to the peak brightness, the deceleration from the top of the atmosphere to the peak height is less than 1 km s−1 but the atmosphere deeply influences the solution of bulk strength by about 40 to 60%, which is important in deducing the structure and type of NEOs.
When it comes to the orbital calculation of 2022 EB5, converting orbital elements from the atmospheric trajectory computed from CNEOS data works well in terms of the argument of perihelion and ascending node, but it produces a relative error of several percent to over ten percent in other elements. The discrepancy in a, e, and i declines as the density decreases, while the relative errors of ω and Ω remain at a very similarly low level, the difference of which can be omitted. Besides, considering atmospheric entry increases the accuracy in calculating most orbital elements. Nonetheless, the case of 2022 EB5 cannot necessarily be extrapolated to other events in calculating orbit, since the accuracy of USG sensors remains uncertain for various events.
From our modeling, we conclude that the 2022 EB5 is very likely to be an asteroid of C-type with a diameter of 5–6 m, a bulk strength lower than 2 MPa, a very low density, and an albedo no larger than 0.025.
Acknowledgements
This work was supported by the Chinese State Administration of Science, Technology and Industry for National Defense (KJSP2020020303) and the Major Science and Technology Projects of Beijing (Z181100002918004).
References
- Artemieva, N. A., & Shuvalov, V. V. 2016, Ann. Rev. Earth Planet. Sci., 44, 37 [CrossRef] [Google Scholar]
- Baldwin, B., & Sheaffer, Y. 1971, J. Geophys. Res., 76, 4653 [NASA ADS] [CrossRef] [Google Scholar]
- Borovicka, J., Popova, O. P., Nemtchinov, I. V., Spurn’y, P., & Ceplecha, Z. 1998, A&A, 334, 713 [Google Scholar]
- Borovička, J., Spurnỳ, P., Brown, P., et al. 2013a, Nature, 503, 235 [CrossRef] [Google Scholar]
- Borovička, J., Tóth, J., Igaz, A., et al. 2013b, Meteorit. Planet. Sci., 48, 1757 [Google Scholar]
- Borovicka, J., Spurný, P., & Shrbený, L. 2022, A&A, 667, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowell, E., Hapke, B., Domingue, D., et al. 1989, Asteroids II (Tucson: University of Arizona press), 524 [Google Scholar]
- Brown, P., Spalding, R. E., ReVelle, D. O., Tagliaferri, E., & Worden, S. P. 2002, Nature, 420, 294 [Google Scholar]
- Brown, P. G., Assink, J. D., Astiz, L., et al. 2013, Nature, 503, 238 [NASA ADS] [Google Scholar]
- Brown, P., Wiegert, P., Clark, D., & Tagliaferri, E. 2016, Icarus, 266, 96 [CrossRef] [Google Scholar]
- Carbognani, A. 2021, EPJ Plus, 136, 616 [NASA ADS] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [CrossRef] [Google Scholar]
- Ceplecha, Z., & McCrosky, R. 1976, J. Geophys. Res., 81, 6257 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z., Borovička, J., Elford, W. G., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R., Farnocchia, D., Nolan, M. C., et al. 2014, Icarus, 235, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Chyba, C. F., Thomas, P. J., & Zahnle, K. J. 1993, Nature, 361, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, G., Melosh, H., & Marcus, R. 2009, AGU Fall Meeting Abstracts, 2009, NH31D–09 [Google Scholar]
- Devillepoix, H. A., Bland, P. A., Sansom, E. K., et al. 2019, MNRAS, 483, 5166 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Brown, P. G., & Chodas, P. W. 2016, Icarus, 274, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Jenniskens, P., Robertson, D. K., et al. 2017, Icarus, 294, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Gen, M., Cheng, R., & Lin, L. 2008, Network Models and Optimization: Multiobjective Genetic Algorithm Approach (Berlin: Springer Science & Business Media) [Google Scholar]
- Gritsevich, M., Vinnikov, V., Kohout, T., et al. 2014, Meteorit. Planet. Sci., 49, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & D’Abramo, G. 2015, Icarus, 257, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G., & Goda, M. P. 1993, AJ, 105, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P. A., Shaddad, M., Numan, D., et al. 2009, Nature, 458, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Popova, O. P., Glazachev, D. O., Podobnaya, E. D., & Kartashova, A. P. 2019, Icarus, 327, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Gabadirwe, M., Yin, Q.-Z., et al. 2021, Meteorit. Planet. Sci., 56, 844 [CrossRef] [Google Scholar]
- McCrosky, R. E., Posen, A., Schwartz, G., & Shao, C.-Y. 1971, J. Geophys. Res., 76, 4090 [Google Scholar]
- McMullan, S., & Collins, G. 2019, Icarus, 327, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Mehta, P., Minisci, E., & Vasile, M. 2015, in Proceeding of the 4th IAA Planetary Defense Conference, Frascati, Roma, 13 [Google Scholar]
- Morbidelli, A., Delbo, M., Granvik, M., et al. 2020, Icarus, 340, 113631 [NASA ADS] [CrossRef] [Google Scholar]
- Opik, E. J. 2004, Physics of Meteor Flight in the Atmosphere (USA: Courier Corporation) [Google Scholar]
- Park, C., & Brown, J. D. 2012, AJ, 144, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Popova, O. P., Jenniskens, P., Emel’yanenko, V., et al. 2013, Science, 342, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- Salazar, F., Macau, E., & Winter, O. 2014, Adv. Space Res., 53, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Tancredi, G. 2014, Icarus, 234, 66 [CrossRef] [Google Scholar]
- Tárano, A. M., Wheeler, L. F., Close, S., & Mathias, D. L. 2019, Icarus, 329, 270 [CrossRef] [Google Scholar]
- Towner, M., Jansen-Sturgeon, T., Cupak, M., et al. 2022, Planet. Sci. J., 3, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., & Llorca, J. 2006, MNRAS, 372, 655 [CrossRef] [Google Scholar]
- U.S. Standard Atmosphere 1976, U.S. Standard Atmosphere (USA: National Oceanic and Atmospheric Administration) [Google Scholar]
- Usui, F., Kasuga, T., Hasegawa, S., et al. 2012, ApJ, 762, 56 [Google Scholar]
- Watanabe, S., Hirabayashi, M., Hirata, N., et al. 2019, Science, 364, 268 [NASA ADS] [Google Scholar]
- Wheeler, L. F., Register, P. J., & Mathias, D. L. 2017, Icarus, 295, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, L. F., Mathias, D. L., Stokan, E., & Brown, P. G. 2018, Icarus, 315, 79 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Osculating orbital elements of 2022 EB5 at 23:58:50 on 2022 March 10 (UTC) derived by JPL using a total of 176 observations.
Orbital elements of 2022 EB5 at 00:00:00 on 2022 January 21 (UTC) derived by ESA.
Velocity and location at peak brightness and the estimated impact energy of 20222 EB5.
Physical properties and variables at the atmospheric boundary of Chelyabinsk meteoroid.
Relative errors of calculated heliocentric orbital elements, given as a percent.
All Figures
 |
Fig. 1 Illustration of the pancake model presented by Chyba et al. (1993). The fragmentation starts when the ram pressure, P, exceeds the initial bulk strength, S0. And the airburst occurs, or the peak brightness is reached, at the very short moment when the windward radius of the object expands to N times the initial diameter of the object, R0. The height of fragmentation is the altitude where the fragmentation begins, which differs from the height of the airburst or, equivalently, the peak brightness. |
| In the text | |
 |
Fig. 2 Whole process of calculation. The velocity and position in the ECI system and the initial impact energy of 2022 EB5 are first computed based on the data at the peak brightness downloaded from CNEOS. The density and the heat of ablation are set according to Table 4. The genetic algorithm is then used to search for the solution to the optimization problem and generate the final values of optimization variables. After that, the physical variables at the atmospheric boundary and heliocentric orbital elements are derived accordingly. |
| In the text | |
 |
Fig. 3 Energy deposition curve of Košice meteoroid. |
| In the text | |
 |
Fig. 4 Energy deposition curve of Chelyabinsk meteoroid. The computed group is the result of the S-type. The red solid line ends at the moment of the airburst while the dashed line illustrates the energy loss rate after the airburst. |
| In the text | |
 |
Fig. 5 The relationship between albedo and diameter of 2022 EB5. The dashed lines reflect the range of diameter for each albedo, taking account of the 1σ errors of magnitude observation. |
| In the text | |
 |
Fig. 6 Energy deposition curves of 2022 EB5. The energy deposition per second as a function of time instead of the energy loss per km varying as the altitude is shown in order to facilitate comparison. The time axis represents the second that passed 21:22 on March 11, 2022 UTC time. The maximum energy deposition rate occurs at 45.6 s, when the peak brightness as well as the so-called air burst takes place. The gray line represents the curve derived from the light curve reported by CNEOS, whereas the red dashed line, the yellow line, and the blue dot-dashed line illustrate the energy deposition curve of the C-type, Ryugu/Bennu, and S-type groups. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


