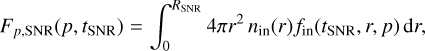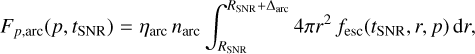| Issue |
A&A
Volume 670, February 2023
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202038748 | |
| Published online | 30 January 2023 | |
Study of the GeV to TeV morphology of the γ Cygni SNR (G 78.2+2.1) with MAGIC and Fermi-LAT
Evidence for cosmic ray escape
1
Inst. de Astrofísica de Canarias,
E-38200 La Laguna, and Universidad de La Laguna, Dpto. Astrofísica,
38206
La Laguna, Tenerife, Spain
2
Università di Udine, and INFN Trieste,
33100
Udine, Italy
3
National Institute for Astrophysics (INAF),
00136
Rome, Italy
4
ETH Zurich,
CH-8093
Zurich, Switzerland
5
Technische Universität Dortmund,
D-44221
Dortmund, Germany
6
Croatian Consortium: University of Rijeka, Department of Physics,
51000
Rijeka ;
University of Split – FESB,
21000
Split ;
University of Zagreb – FER,
10000
Zagreb ;
University of Osijek,
31000
Osijek ;
Rudjer Boskovic Institute,
10000
Zagreb, Croatia
7
Saha Institute of Nuclear Physics, HBNI,
1/AF Bidhannagar, Salt Lake, Sector-1,
Kolkata
700064, India
8
Centro Brasileiro de Pesquisas Físicas (CBPF),
22290-180
URCA, Rio de Janeiro (RJ), Brasil
9
IPARCOS Institute and EMFTEL Department, Universidad Complutense de Madrid,
28040
Madrid, Spain
10
University of Lodz, Faculty of Physics and Applied Informatics, Department of Astrophysics,
90-236
Lodz, Poland
11
Università di Siena and INFN Pisa,
53100
Siena, Italy
12
Deutsches Elektronen-Synchrotron (DESY),
15738
Zeuthen, Germany
13
Istituto Nazionale Fisica Nucleare (INFN),
00044
Frascati (Roma), Italy
14
Max-Planck-Institut für Physik,
80805
München, Germany
15
Institut de Física d’Altes Energies (IFAE), The Barcelona Institute of Science and Technology (BIST),
08193
Bellaterra (Barcelona), Spain
16
Università di Padova and INFN,
35131
Padova, Italy
17
Università di Pisa, and INFN Pisa,
56126
Pisa, Italy
18
Universitat de Barcelona, ICCUB, IEEC-UB,
08028
Barcelona, Spain
19
The Armenian Consortium: ICRANet-Armenia at NAS RA, A. Alikhanyan National Laboratory,
Republic of Armenia
20
Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas,
E-28040
Madrid, Spain
21
Universität Würzburg,
97074
Würzburg, Germany
22
Finnish MAGIC Consortium: Finnish Centre of Astronomy with ESO (FINCA), University of Turku,
20014
Turku ;
Astronomy Research Unit, University of Oulu,
90014
Oulu, Finland
23
Departament de Física, and CERES-IEEC, Universitat Autònoma de Barcelona,
08193
Bellaterra, Spain
24
Japanese MAGIC Consortium: ICRR, The University of Tokyo,
277-8582
Chiba ;
Department of Physics, Kyoto University,
606-8502
Kyoto ;
Tokai University,
259-1292
Kanagawa ;
RIKEN,
351-0198
Saitama, Japan
25
Inst. for Nucl. Research and Nucl. Energy, Bulgarian Academy of Sciences,
1784
Sofia, Bulgaria
26
Sapienza Università di Roma and INFN Roma,
00185
Rome, Italy
27
INAF, Osservatorio Astrofisico di Arcetri,
50125
Firenze, Italy
28
Institute for Astro- and Particle Physics, University of Innsbruck,
A-6020
Innsbruck, Austria
29
Port d’Informació Científica (PIC)
E-08193
Bellaterra (Barcelona), Spain
30
Dipartimento di Fisica, Università di Trieste,
34127
Trieste, Italy
31
INAF-Trieste and Dept. of Physics & Astronomy, University of Bologna,
Italy
Received:
25
June
2020
Accepted:
13
October
2020
Context. Diffusive shock acceleration (DSA) is the most promising mechanism that accelerates Galactic cosmic rays (CRs) in the shocks of supernova remnants (SNRs). It is based on particles scattering caused by turbulence ahead and behind the shock. The turbulence upstream is supposedly generated by the CRs, but this process is not well understood. The dominant mechanism may depend on the evolutionary state of the shock and can be studied via the CRs escaping upstream into the interstellar medium (ISM).
Aims. Previous observations of the γ Cygni SNR showed a difference in morphology between GeV and TeV energies. Since this SNR has the right age and is at the evolutionary stage for a significant fraction of CRs to escape, our aim is to understand γ-ray emission in the vicinity of the γ Cygni SNR.
Methods. We observed the region of the γ Cygni SNR with the MAGIC Imaging Atmospheric Cherenkov telescopes between 2015 May and 2017 September recording 87 h of good-quality data. Additionally, we analysed Fermi-LAT data to study the energy dependence of the morphology as well as the energy spectrum in the GeV to TeV range. The energy spectra and morphology were compared against theoretical predictions, which include a detailed derivation of the CR escape process and their γ-ray generation.
Results. The MAGIC and Fermi-LAT data allowed us to identify three emission regions that can be associated with the SNR and that dominate at different energies. Our hadronic emission model accounts well for the morphology and energy spectrum of all source components. It constrains the time-dependence of the maximum energy of the CRs at the shock, the time-dependence of the level of turbulence, and the diffusion coefficient immediately outside the SNR shock. While in agreement with the standard picture of DSA, the time-dependence of the maximum energy was found to be steeper than predicted, and the level of turbulence was found to change over the lifetime of the SNR.
Key words: acceleration of particles / cosmic rays / gamma rays: general / gamma rays: ISM / ISM: clouds / ISM: supernova remnants
© ESO 2023
1 Introduction
In the quest to identify the origin of Galactic cosmic rays (CRs), supernova remnants (SNRs) are the prime candidates. One main pillar of the so-called supernova paradigm is the mechanism of diffusive shock acceleration (DSA; see Blasi 2013; Gabici et al. 2019, for a review), which can efficiently transfer a fraction of the kinetic energy of the SNR shock wave to CRs. DSA predicts that CRs self-generate magnetic turbulence upstream of the shock that subsequently scatter them back downstream. For the most energetic CRs it is not clear whether such scattering centres are efficiently generated nor what the principal mechanism responsible for their production is. The answer probably depends on the evolutionary stage of the SNR. During the initial stage, when the shock speed is very high and the maximum energy of CRs is expected to increase, the non-resonant instability is thought to dominate (see Schure et al. 2012, for a review). At later times, when the shock speed starts decreasing and the maximum energy should also decrease, the amplification is probably dominated by the resonant streaming instability. During both stages at least a fraction of the highest energy CRs are expected to escape from the shock upstream (Ohira et al. 2010; Malkov et al. 2013; Celli et al. 2019a; Brose et al. 2020). The process of DSA is inevitably connected to the escape of CRs into the interstellar medium (ISM). In contrast to the acceleration process, the mechanism of CR escape from the accelerator is not well understood, also due to the lack of clear observational signatures. Evidence could be provided by γ rays produced from the interaction of escaping particles with the interstellar medium surrounding the SNR (Aharonian & Atoyan 1996; Gabici et al. 2009).
Because the number of CRs escaping is small, young SNRs are not expected to show clear signatures of CR–ISM interaction. Recently the H.E.S.S. Collaboration (2018) observed γ rays beyond the X-ray emission region in the SNR RX J1713.7-3946. However, the angular resolution of the γ-ray telescopes was insufficient to distinguish whether the γ-rays are generated by CRs escaping the SNR or if they are the signature of the shock precursor1.
During the adiabatic or Sedov–Taylor phase the shock velocity decreases significantly and large fractions of particles are released into the ISM. The interaction of such SNRs or their escaping CRs with dense molecular clouds was observed for a number of SNRs (W28, IC443, W44, W51C; see Slane et al. 2015, for a review). However, for such mature SNRs the shock has already encountered molecular clouds, and even low-energy CRs have escaped from the accelerator, so the escape process cannot be studied in isolation.
With an age of ~7 × 103 yr, the γ Cygni SNR is slightly older than RX J1713.7-3946, but younger than the middle-aged SNRs. Its circular radio shell suggests that, on a large scale, the hydrodynamic evolution has not yet been affected by density anisotropies, and X-ray observations confirm that the SNR is clearly in its adiabatic phase; it is therefore an interesting target to search for signatures of escaping CRs.
The γ Cygni SNR (also called G 78.2+2.1) is located in the heart of the Cygnus region close to the bright γ Cygni star, Sadr (mag=2.2, Hoffleit & Warren 1995). Since it hosts the pulsar PSR 2021+4026, which is likely associated with the SNR (Hui et al. 2015), it is believed to be the debris of a core collapse supernova.
At radio wavelengths the SNR shows a distinctively circular shell with a diameter of ~1° (Higgs et al. 1977; Wendker et al. 1991; Kothes et al. 2006). The emission is brighter towards the south-east and north-west of the shell than along the northeast–south-west axis. Further studies from Zhang et al. (1997) and Ladouceur & Pineault (2008) found that the flux spectral index αv varies between ~0.8 and ≲0.4 across the SNR. The softest index is found in the bright south-eastern part, while the spectrum is harder (~0.55) in the north-west and south-west (Ladouceur & Pineault 2008). Based on radio observations and using Σ-D relations, HI velocity measurements, and the association with the Wolf-Rayet binary V444 Cyg, the distance to γ Cygni was determined to be 1.5–2.6 kpc (see Table 1). It is unclear whether the SNR is surrounded by a larger HI shell. Gosachinskij (2001) reported a shell of 2°.0–2°.8 × 2°.5–3°.5 diameter centred approximately at the SNR, but noted that the HI structures are not necessarily at the same distance. Ladouceur & Pineault (2008) observed structures in emission bordering the SNR shell, but Leahy et al. (2013) claimed that those structures are absorption features by layers situated in front of the SNR. Given its position in an OB region, it is plausible that the SNR might be surrounded by a HI cavity blown by the wind of the progenitor’s stellar wind (Lozinskaya et al. 2000).
Observations of CO lines did not reveal any interaction of the SNR with molecular material (Higgs et al. 1983a) except for a hint at the south-eastern part (Fukui & Tatematsu 1988). The search for maser emission led to a negative result (Frail et al. 1996).
No optical counterpart of the SNR has been detected. Mavromatakis (2003) searched for optical emission lines ([NII], [SII], and [OIII]) and found patchy emission towards the south, south-east, and north-west of the SNR. In the south-east hints of shock-heated gas suggest that the low-density medium, in which the SNR evolves, contains clouds with pre-shock densities of ~20 cm−3 and a shock velocity of ~750 km s−1. The author further inferred that most of the hot dust and absorbing matter lies in the foreground of the SNR, which possibly obscures most of the optical emission.
In the X-ray band the emission is dominated by shock-heated gas, as expected for a Sedov–Taylor (ST) phase SNR, even in the case of efficient particle acceleration (Castro et al. 2011). The structure of the X-ray emission correlates with the radio band, except it is also bright in the south-west. The post-shock gas temperature indicates a shock speed of ~1000 km s−1 in all parts of the SNR (Higgs et al. 1983b; Lozinskaya et al. 2000; Uchiyama et al. 2002; Leahy et al. 2013). The gas temperature in the centre suggests that the reverse shock hit the centre about 1900 yr ago and thus the SNR is fully adiabatic (Hui et al. 2015). Towards the northern shell the X-ray emission extends beyond the SNR radio shell and may partially be produced by the stellar wind in the foreground (Leahy et al. 2013). Additionally, Uchiyama et al. (2002) found three clumps of hard X-ray emission in the north-west, of which two are likely of extragalactic origin (Leahy et al. 2013). One of these clumps (C2), however, may hint at bremsstrahlung clumps and a denser medium in that region.
At GeV energies the Fermi Large Area Telescope (Fermi-LAT) observed extended emission over all of the SNR radio shell (Lande et al. 2012). The source was modelled with a disc of 0°.63 ± 0°.05stat ± 0°.04sys radius centred on (α = 305°25, δ = 40°.52; J2000) and a power-law spectrum with index −2.42 ± 0.19. Later analyses of the SNR, however, found different extensions to better describe the data (Acero et al. 2016; Ackermann et al. 2017), and Fraija & Araya (2016) found the spectral index in the north-west of the shell to be harder compared to the other parts. Furthermore, the Fermi-LAT collaboration discovered the γ-ray bright pulsar PSR J2021+4026, the only variable γ-ray pulsar known to date. It has a spin-down power of 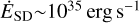 and a characteristic age of τC~77 kyr (Abdo et al. 2009). The pulsar spectrum follows a power law with exponential cut-off with a cut-off energy of Ec = 2.37 ± 0.06 GeV (Allafort et al. 2013).
and a characteristic age of τC~77 kyr (Abdo et al. 2009). The pulsar spectrum follows a power law with exponential cut-off with a cut-off energy of Ec = 2.37 ± 0.06 GeV (Allafort et al. 2013).
At TeV energies the VERITAS telescopes discovered extended emission at the north-west of the shell, which was modelled with a Gaussian source (VER J2019+407) centred at (α = 305°.02, δ = 40°.76; J2000; Aliu et al. 2013). The observation time was 21.4 h. The spectrum of the extended emission followed a power law (index of −2.37). In Abeysekara et al. (2018) VERITAS updated their findings with an increased exposure of ~40 h resulting in a softer spectral index (−2.79 ± 0.39stat ± 0.20sys). The source is also listed in the second HAWC catalogue as 2HWC J2020+403 (Abeysekara et al. 2017). Its centre is at (α = 305°.16, δ = 40°.37; J2000) and the spectral index of the measured power law is −2.95 ± 0.10. However, the angular resolution of the HAWC detector was not sufficient to determine the size or to detect substructures.
Table 1 summarises the properties of the γ Cygni SNR from the given references. In addition to the above-mentioned characteristics, it lists the age, the density inside the shell, and the explosion energy. The age is inferred from the size of the radio shell, the shock speed, and the particle density assuming a Sedov–Taylor model (see e.g. Eqs. (10) and (11)). Based on these measurements and estimates, in the following we assume a distance of 1.7 kpc, an age of 7000 yrs, an explosion energy of 1051 erg, and a shock speed of 103 km s−1. For the centre of the SNR radio shell we use (α = 305°.3, δ = 40°.43; J2000). As the ejecta mass is unknown, but the SNR likely resulted from a core-collapse supernova of an OB star, we use a canonical value of Mej = 5 M⊙ for type II supernovae (Chevalier 1977). It is important to note that the ranges given in Table 1 consider the optimal values from the listed publications excluding the uncertainties. The uncertainty ranges of all measurements are similar, and thus the average values are still a reasonable representation. The parameters are further correlated due to their connection via the Sedov–Taylor model. Combining all estimates considering their statistical uncertainties, systematic uncertainties of each instrument and method, and their correlation is beyond the scope of this work. Accordingly, when we use the extreme values from Table 1 in our estimations, the resulting ranges are suggestive rather than accurate uncertainty intervals.
Overall, the observed properties make the γ Cygni SNR a prime example of a Sedov–Taylor phase SNR, and perfect for studying the possible escape of CRs. The discrepancy between the morphology at GeV energies observed by Fermi-LAT and the concentrated emission at TeV energies reported by VERI-TAS indeed suggests an ongoing, energy-dependent process (see morphology described above, or compare Fig. 25 from Lande et al. 2012 and Fig. 1 from Aliu et al. 2013). We report on the observation of γ Cygni with the MAGIC telescopes and combine these observations with an analysis of Fermi-LAT data to explore the discrepancy in the GeV to TeV regime in greater detail.
Physical parameters of the γ Cygni SNR based on various measurements.
2 Observations and data analysis
2.1 MAGIC telescope observations and data analysis
The Major Atmospheric Gamma Imaging Cherenkov (MAGIC) telescopes are a system of two 17 m diameter imaging Cherenkov telescopes (IACTs) located at an altitude of 2200 m above sea level at the Observatorio del Roque de los Muchachos on La Palma, Canary Islands, Spain (28° 46′ N, 17° 53′ W). The telescopes detect γ-ray induced extensive air showers in the atmosphere via their Cherenkov light. The telescopes are operated in stereoscopic mode, where only showers triggering both telescopes are recorded. The telescopes cover the energy range from ~30 GeV to E > 100 TeV and have a field of view of 3°.5 diameter. At low zenith angles Zd < 30° and within 50 h, MAGIC can detect point sources above 200 GeV at a flux level of (0.66 ± 0.03)% of the Crab Nebula flux; at medium zenith angles 30° < Zd < 45° this level increases to (0.76 ± 0.04)% (Aleksić et al. 2016).
The observations for this work were performed over two periods between 2015 May and November and between 2017 April and September. The data of the latter period include dim and moderate moon data classified according to Ahnen et al. (2017), though the sensitivity is comparable to the period under dark conditions. The data cover a zenith range from 10° to 55°. The observations used two pointing positions in wobble mode with an offset of 0°.6 from the VERITAS source location.
Starlight increases the number of photoelectrons (ph.e.) in the pixels close to the position of Sadr in the camera. Hence, the pointing directions were chosen to have the same angular distance to Sadr, and thereby to reduce a systematic mismatch between the two pointings. Additionally, the position of Sadr was kept outside the trigger region of the camera (up to 1°.17 from the camera centre) so as not to increase the rate of spurious events. If the light yield in a camera pixel exceeds the safety threshold, it is switched off to save the photo-multiplier from ageing. This condition applied to 2–3 pixels at the position of Sadr neighboured by 12 pixels with higher light content. Artefacts from these features survived the analysis procedure at image sizes of size < 150 ph.e., where the additional star light or lost pixels significantly affected shower images arriving at the star’s position. We thus apply a size cut of size > 150 ph.e. to the MAGIC data implying an energy threshold of 250GeV. This limit was well above the energy threshold resulting from the general observational conditions (Moon conditions or zenith range). The MAGIC angular resolution, characterised by the point spread function (PSF), for this study was estimated to be 0°.08 (68% containment radius) at E > 250 GeV.
The MAGIC data were analysed using the MAGIC Analysis and Reconstruction Software (MARS; Zanin et al. 2013). The analysis involved quality selection, cleaning of the shower images from the night sky background, Hillas parametrisation, stereo reconstruction based on the disp method, and γ–hadron separation based on a random forest classifier. The data quality was controlled by monitoring the transparency of the atmosphere with a LIDAR system during observations (Fruck et al. 2014). In this analysis we only included data with an atmospheric transmission above 85% of the optimal transparency up to 12km above the telescopes. The cleaning levels were adapted depending on the night sky brightness following Ahnen et al. (2017). After quality cuts, the total dead-time corrected observation time amounted to 85 h.
We analysed the high-level data with the SkyPrism spatial likelihood analysis package (Vovk et al. 2018). SkyPrism contains routines for computing the event count map, the background map, and the instrument response functions (PSF, energy migration matrix, and exposure map). Based on these images, SkyPrism fits a user-defined source model to the measured event maps minimising the negative log-likelihood estimate. This way the package estimates detection flux normalisations and, if performed in several energy bins, extracts the source spectra for the considered model. Statistical inference in SkyPrism is based on a likelihood ratio test (LRT) defining the test statistic (TS)
where ℒ0 is the likelihood value of the null hypothesis and ℒ1 the likelihood of the hypothesis being tested. The TS value can be converted to statistical significance via Wilks’ theorem (Wilks 1938). If the null hypothesis is true, TS follows a χ2 distribution with n degrees of freedom, where n is the number of additional parameters in the hypothesis model. However, when testing the presence of source component (i.e. when the LRT is performed on the boundary of the parameter space with a single additional free parameter, the flux of the new source component), the TS is converted to Gaussian significances by 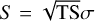 (Mattox et al. 1996; Protassov et al. 2002).
(Mattox et al. 1996; Protassov et al. 2002).
We used the exclusion map method to generate the background map, excluding a circular region of 0°.56 around the radio centre (α = 305°.3, δ = 40°.43; J2000) and around the VERITAS centre (α = 305°.02, δ = 40°.76; J2000). The considered MAGIC region of interest (RoI) used in this work had a size of 2°.5 × 2°.5 with a pixel size of 0°.02 × 0°.02. As the bins were smaller than the PSF, the spatial pixels were highly correlated, which is accounted for in the likelihood analysis. A description of the procedure used to estimat the systematic uncertainties on the source localisations and spectral parameters can be found in Appendix A.
2.2 Fermi-LAT data observations and data analysis
The Fermi-LAT is a γ-ray telescope on board the Fermi Gamma-ray Space Telescope (Atwood et al. 2009). It was designed to observe the energy range between 20 MeV and E > 300 GeV via the pair-conversion technique.
This study used data from ~9 yr of observation between 2008 Oct 27 and 2017 Sep 12 processed with the Pass 8 R2 reconstruction (Atwood et al. 2013) as provided by the Fermi Science Support Center (FSSC). The data were analysed using the Fermi Science Tools (version v11r5p32) in combination with the Fermipy package (version 0.17.3; Wood et al. 2017). We chose the ‘Source’ selection cuts and instruments responses (P8R2_SOURCE_V63) for a balance between precision and photon count statistics. Further, we split the data according to the four PSF classes and combined them in a joint likelihood function. As for MAGIC, the Fermi-LAT analysis uses the LRT of Eq. (1) for statistical inference. Accordingly, the TS approximates a χ2 distribution under the null hypothesis, except when testing the presence of a new component on the boundary, in which case 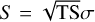 applies as well.
applies as well.
The zenith angle was limited to 105°, a time filter was applied (DATA_QUAL>0 && LAT_CONFIG==1), and the energy dispersion was considered for all sources except the Galactic and extragalactic diffuse emission. The interstellar emission model used was gll_iem_v06.fits, and the isotropic diffuse emission model was iso_P8R2_SOURCE_V6_PSF[0,1,2,3]_v06.txt for the corresponding PSF class.
Below ~ 10 GeV the emission from the pulsar (PSRJ2021+4026) dominates over the flux from the SNR. Using the off-pulse phase of the pulsar does not sufficiently suppress its contribution since the flux difference between the pulse peak and the off-pulse emission is only ~30% (Allafort et al. 2013). To reliably disentangle the two components, we limited the energy range of the Fermi-LAT data to 5–500 GeV. At E > 5 GeV the 95% containment radius of the Fermi-LAT PSF is smaller than the radius of the SNR. We chose the RoI to be 10° × 10° around the radio centre of the SNR, a spatial bin-size of 0°.05, and split the energy range in 18 bins (9/decade).
To model the contribution from background sources (including PSRJ2021+4026) in the RoI, we used the FL8Y source list4 as a starting point considering sources within 15° of the centre of the analysis. The source FL8Y J2021.0+4031e corresponding to the γ Cygni SNR was removed from the model. After running the optimisation procedure of the Fermipy package (‘gta.optimize’), we removed all sources with TS < 16 or those with no predicted counts. For the Cygnus Cocoon we used the spatial template of the extended source archive V18 provided online by the FSSC. A point source search in the RoI resulted in one significant, positive excess of > 5 σ over our model coinciding with a 2 FHL source (2FHL J2016.2+3713), which we added to our model. The remaining residuals stayed below <5 σ across the entire sky map. Sources related to the γ Cygni SNR system are discussed in Sect. 3.3. The treatment of the systematic uncertainties on the source localisations and spectral parameters are described in Appendix A.
 |
Fig. 1 Sky map in units of relative flux (excess over background) of the γ Cygni region as observed by MAGIC E > 250 GeV. Regions exceeding the 3σ (5σ) local, pre-trial TS significance for a point source are indicated by red (yellow) contours. The cyan line is the 400 K contour of the 408 MHz observation by the CGPS. The white diamond gives the position of the PSR 2021+4026, the green X the position of VER J2019+407, and the yellow star the position of Sadr (γ Cyg star; mag = 2.2). The inlay in the lower left corner shows the 39% and 68% containment contours of the MAGIC PSF. |
3 Analysis results
3.1 MAGIC morphological results
The image of the γ Cygni SNR obtained with the MAGIC telescopes above 250 GeV is displayed in Fig. 1 in terms of the relative flux. Relative flux is defined as the residual or excess events divided by the background events. The event count map and the background map were smoothed with a Gaussian kernel of σ = 0°.055, corresponding to the size of the PSF. Additionally, the background map was scaled to have the same median pixel values of the event count map for the area outside of the defined exclusion region (Sect. 2.1). Figure 1 also shows the 3 σ and 5 σ boundaries of the test statistic map, which for each pixel contains the deviation from a Gaussian distribution of the background-only hypothesis based on 500 random representations of the background map. This TSpoint value gives a hint of the local significance for a point source in each pixel5. The cyan lines are the 400 K contours of the 408 MHz observation by the Canadian Galactic Plane Survey (CGPS; Taylor et al. 2003). In the following we use this surface brightness level since it agrees best with published extension values in the radio band and is the level right above the brightness of the surroundings.
The emission observed by MAGIC is extended and patchy. The most prominent feature in the map is an extended region along the north-western rim of the radio shell. It seemingly consists of a bright roundish component centred on the rim and an adjunct arc-like appendix extending beyond the radio shell towards the west. The map shows faint emission areas inside the southern part of the radio shell; however, they are below the detection level for a point source.
Since the roundish emission in the north exhibits a higher surface brightness than the adjunct appendix, it seems implausible to account for both with just one source component. The former could be modelled well by a radially symmetric Gaussian with the position and the extension as free parameters. For the latter we used the sector of an annulus centred at the centre of the radio shell with the inner radius, the outer radius, the angular position of the centre (mathematically positive with respect to the decreasing RA axis), and the central angle as free parameters. However, it is difficult to determine the exact shape of the emission to the west of the SNR shell based on a visual inspection of the MAGIC skymap. Hence, we also applied a Gaussian to model this emission region. For the fit we assume a spectral power-law index of Γ = −2.8 in agreement with the value reported by Abeysekara et al. (2018).
Since the Gaussian source in the north of the SNR is better defined, we scanned its position and extension first. The scan resulted in a minimum at (α, δ; J 2000) = (304°.89 ± 0°.01stat, 40°.84 ± 0°.01stat) and an extension of σ = 0°.16 ± 0°.01stat. At this position we checked for a possible eccentricity, but the improvement over the radially symmetric Gaussian was not significant. The source was detected with a significance of 17.1 σ (in the absence of any other model component). In the following we refer to this source as MAGIC J2019+408.
Including MAGIC J2019+408 in the source model, we scanned the parameters of the arc-like source. When modelled with the annulus segment, it is detected at a significance of 10.3σ and the best-fit parameters are 0°.45 ± 0°.03stat for the inner radius, 0°.27 ± 0°.03stat for the extension (outer – inner radius), 5°.00 ± 0°.03stat for the positional angle, and 36°.58 ± 0°.03stat for the central angle.
When modelling the emission towards the west of the SNR with a second Gaussian instead of the arc model, the best-fit position was at (α, δ; J 2000) = (304°.51 ± 0°.02stat, 40°.51 ± 0°.02stat) with an extension of σ = 0°.12 ± 0°.01stat. The detection significance was 9.2σ. We address the question of model selection between these two alternatives in Sect. 3.4 after we examine the γ-ray emission over a wider energy range taking into account observations with Fermi-LAT. A search for point sources in addition to MAGIC J2019+408 and the arc or second Gaussian did not lead to any significant detections.
3.2 Energy-dependent morphology
Even though the observations with MAGIC provide a more precise image of the source at hundreds of GeV to TeV than previous observations, its morphology still differs from previously published Fermi-LAT skymaps. To study the evolution of the emission over the entire GeV to TeV range, we analysed the data set from the Fermi-LAT, which contained 1.5 times the observation time of the latest extended source catalogue (Ackermann et al. 2017). We split the Fermi-LAT and MAGIC data into two energy ranges each: 15–60 GeV and 60–250 GeV for the former and 250–500 GeV and 500–2.5 TeV for the latter.
The skymaps are shown in Fig. 2. The Fermi-LAT maps display the event counts (smoothed with a Gaussian kernel with σ = 0°.075) together with point source TS contours. The count images have the advantage of being free from any model dependency, but do not allow the exclusion of sources by including them in the background model. Thus, we chose a lower limit of 15 GeV to prevent the pulsar from dominating the image. TS contours are based on a point source search in addition to the background source model described in Sect. 2.2. The MAGIC skymaps are presented in terms of relative flux together with point source TS contours. In the 15–60 GeV range the emission predominantly comes from a region agreeing with the SNR radio shell. The intensity is nearly uniform across the shell and the 3 σ and 5 σ local significance contours seemingly agree with the radio contours. On the contrary, at 60 to 250 GeV the shell emission weakens, and a slightly extended emission at the northwestern rim stands out near MAGIC J2019+408. The position at which MAGIC observes the arc-like structure, however, does not show any significant emission.
MAGIC J2019+408 is the main component in the 250 to 500 GeV map measured by MAGIC. Emission at the arc position is becoming visible, but at a lower level compared to MAGIC J2019+408. The inside of the shell shows some faint emission. Finally, at 500 GeV to 2.5 TeV, the arc-like region brightens. The inside of the shell does not show any significant emission; instead, some emission towards the south of the shell becomes visible. Since this emission was not significant in the combined MAGIC data set and the TS contours are approximate Gaussian significances, it can only be considered a hint of emission.
 |
Fig. 2 Energy-dependent morphology of the γ Cygni SNR. Upper left: Fermi-LAT count map between 15 and 60 GeV smoothed with a Gaussian kernel (σ = 0°.75) and 3 σ and 5 σ contours of a point source search. The white line is the 400 K contour of the 408 MHz observation by the CGPS. The white diamond identifies the position of PSR 2021+4026. Upper right: same as upper left, but in the range from 60 to 250 GeV. Lower left: Relative flux map observed by MAGIC at 250–500 GeV together with 3 σ and 5 σ point source significance contours. The same radio contours as in upper panels are displayed in cyan. Lower right: same as lower left, but in the energy range from 500 GeV to 2.5 TeV. |
3.3 Fermi-LAT morphological results
To quantify the Fermi-LAT results from Sect. 3.2, the likelihood analysis presupposes a morphological template. To account for the extended uniform emission that is clearly visible in the 15 to 60 GeV skymap, previous analyses of the Fermi-LAT data used a radially symmetric disc model. When fitting the Fermi-LAT data E > 5 GeV we used a radial symmetric disc with the position and extension being free parameters and obtained (α, δ; J 2000) = (305°.24 ± 0°.02stat, 40°.49 ± 0°.02stat) and a radius of 0°.60 ± 0°.02. This result is consistent with the disc model reported in Ackermann et al. (2017). For the fit we used a spectral power-law index of Γ = 2, which is in the range of indices reported by the various Fermi-LAT catalogues.
As mentioned in Sect. 1, the estimated size of the disc varies between different Fermi-LAT studies (likely due to different energy ranges). All either partially or fully encompass MAGIC J2019+408. However, since it is visible in the Fermi-LAT data (E > 60GeV) and MAGIC data, it might be a distinct object from the disc. If it is not considered as such, photons might be misassigned to the disc pushing the fit towards a larger disc size. Assuming that the disc template is related to the SNR, and given the approximate agreement between the TS contours and the radio contours in the 15–60 GeV range, we consider it more plausible to base the disc model on the position and extension of the radio shell. The radially symmetric disc model is centred at (α, δ; J 2000) = (305°.30, 40°.43) with a radius of 0°.53. Fitting this model to the Fermi-LAT data resulted in remaining residual counts in the north-western region. Figure 3 displays the TS map for a point source search on top of the radio disc. The contours suggest the presence of a source of similar morphology to MAGIC-J 2019+408.
Assuming a point source, the source search resulted in the detection at a 6.1σ level (TS = 37) at (α, δ; J 2000) = (304°.92 ± 0°.02stat ± 0°.02sys, 40°.87 ± 0°.02stat ± 0°.02sys). Using the Fermipy routines we additionally fitted the extension of the source simultaneously with the position using a radially symmetric Gaussian source model. The best fit is obtained for (α, δ; J 2000) = (304°.98 ± 0°.03stat ± 0°.02sys, 40°.87 ± 0°.03stat ± 0°.02sys) and an extension of 0°.19 ± 0°.02stat ± 0°.01sys (68% containment; σ = 0°.13). The extension of the source is significant with a TS value of 28.4. These values agree within errors with the position and extension of the MAGIC-J 2019+408, so we associate the Fermi-LAT and MAGIC source. The fit was based on a spectral power-law index of Γ = 2.
The two sources, radio disc and MAGIC J2019+408, yield a log-likelihood value of ln (ℒ2src) = −160597, whereas the single extended disc model give ln(ℒ1disc) = −160621. However, both models are not nested, and thus the LRT cannot be used to gauge the significance of the ∆ ln (ℒ). Instead, we use the Akaike information criterion (AIC, Akaike 1974) to assess the relative quality of the two models. The AIC estimate of a model is defined as
where k is the number of degrees of freedom of the model and ℒ the likelihood value. The model with the smaller AIC value is preferred. Since the radio disc is fixed the former model has five free parameters (norm of the disc and 2D position, extension, and norm of the Gaussian) and the latter model has four (2D position, extension, and norm of the disc). Due to the ∆loglike = 24 improvement with only one additional parameter, the two-source model is preferred over the single larger disc.
 |
Fig. 3 Fermi-LAT TS map for a point source search on top of the background sources specified in Sect. 2.2 and including the radio-based disc model. Regions exceeding the 3σ (5σ) local, pre-trial TS significance for a point source are indicated by red (yellow) contours. The white line is the 400 K contour of the 408 MHz observation by the CGPS. The white diamond gives the position of PSRJ2021+4026. |
3.4 Common model and source spectra
To extract the spectra in the entire GeV to TeV range, we need to combine the findings in the previous section into a common source model. Particularly, based on the energy-dependent brightness ratio between different parts around the SNR described in Sect. 3.2, in the following we consider the γ-ray emission in the region to consist of three components: the interior of the SNR shell, MAGIC J2019+408, and emission west of the shell (arc or second Gaussian). The position and parameters of the models for each source are given in Table 2 and sketched in Fig. 4.
For the emission from the SNR shell, we kept the disc based on the radio observation. This disc partially overlaps with MAGIC J2019+408 and the arc region, thus we updated the parameters of the MAGIC analysis including the disc. For MAGIC J2019+408 it resulted in (α, δ; J 2000) = (304°.89 ± 0°.01stat ± 0°.04sys, 40°.88 ± 0°.01stat ± 0°.02sys) and σ = 0°.13 ± 0°.01stat ± 0°.02sys. To model MAGIC J2019+408 consistently for both instruments, we further averaged the MAGIC and Fermi-LAT location and extension of the Gaussian weighted with the inverse of their variances (statistical and systematic uncertainties added in quadrature): (α, δ; J 2000) = (304°.93, 40°.87) and σ = 0°.13.
For the annular sector template representing the arc we fixed the inner radius at the radius of the shell (0°.53 from the SNR centre) and rescanned the other parameters. The best-fit values were 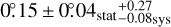 for extension,
for extension, 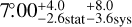 for the positional angle, and
for the positional angle, and 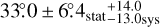 for the central angle. When supplying a second Gaussian as an alternative to the arc model. The best-fit was obtained for (α, δ; J 2000) = (304°.49 ± 0°.02stat ± 0°.05sys, 40°.56 ± 0°.02stat ± 0°.03sys) and σ = 0°.12 ± 0°.02stat ± 0°.04sys. Fitting these sources to the Fermi-LAT and MAGIC data results in the detection significances stated in Table 3.
for the central angle. When supplying a second Gaussian as an alternative to the arc model. The best-fit was obtained for (α, δ; J 2000) = (304°.49 ± 0°.02stat ± 0°.05sys, 40°.56 ± 0°.02stat ± 0°.03sys) and σ = 0°.12 ± 0°.02stat ± 0°.04sys. Fitting these sources to the Fermi-LAT and MAGIC data results in the detection significances stated in Table 3.
The model consisting of two Gaussians yields a slightly better log-likelihood value of ln (ℒ2gauss) = −36303 compared to the MAGICJ2019+408 and Arc model resulting in ln (ℒgauss+arc) = −36306. The two models are not nested, and we use the AIC (Eq. (2)) to access the relative model quality. Both models have the same number of free parameters: position (2D), extension, and the normalisation for the Gaussian and extension, positional angle, central angle, and flux normalisation for the Arc. The ∆ AIC = −6 can be converted to a probability estimate via exp(∆ AIC/2; see e.g. Burnham & Anderson 2004). Accordingly, the arc model is 6% as likely as the second Gaussian, which is <2σ in terms of Gaussian probability, and thus the arc model cannot be rejected based on this statistical test. Due to the same number of free parameters in both models and the small difference in the log-likelihood, other information-based model selection criteria (e.g. Bayesian information criterion) will give similar results. In the following we provide the spectra for both source models. However, in Sect. 4 we develop a theoretical model based on CRs escaping the SNR into a homogeneous medium. The annular sector is a better spatial representation for this model. Since both spatial templates are statistically equal, for the comparison against the theoretical model we employ the annular sector. Nonetheless, it is important to note that the Gaussian model does not alter the understanding of emission outside the SNR shell. The centre of the Gaussian is clearly situated outside of the SNR radio shell with the centre of the Gaussian being 0°.1 away from the edge of the SNR shell.
We extract the spectra of the source components from the MAGIC and Fermi-LAT data for the spatial components as defined in Table 2. For the Fermi-LAT data we used nine bins per decade over the range from 5 to 500 GeV, and the MAGIC data were binned into four bins per decade ranging from 250 GeV to 12.5 TeV. To consider the effect of the energy migration, the Fermi science tools and the SkyPrism analysis adjust an assumed spectral model via a forward folding procedure. As spectral model we used a power law of the form
with the photon index Γ, the normalisation constant N0, and the scaling energy (or pivot energy) E0. The best-fit results together with their uncertainties are summarised in Table 3. The choice of the spatial template for the arc region changes the spectra of the shell and MAGIC J2019+408 at a level below the statistical uncertainties. The contributions to the systematic uncertainties, estimated as described in Appendix A and listed in Table A.1, are added in quadrature. Since the spectral models are power laws, the systematic uncertainty on the energy scale is converted to an uncertainty on the flux normalisation and is added to it. We checked for a possible curvature of the spectrum of all sources by fitting a log-parabola spectrum (power-law exponent becomes Γ + ß log(E/E0) with the curvature factor ß). For none of the components and instruments was a significant curvature detected (improvement over power law based on a likelihood ratio test led to a significance < 3σ).
To better compare the data against theoretical model predictions, we additionally compute data points (flux in narrow energy bands). For the Fermi-LAT data we rebin the nine bins per decade to two bins between 5 and 13.9 GeV, two bins between 13.9 and 64.6 GeV, and two bins between 64.6 and 500 GeV. Thus, the energy bins are much wider (≳ 4 times) than the energy resolution (∆ E < 5%) and, even though the data points are not deconvolved, the correlation between the points can be considered negligible. Instead, for the MAGIC data the energy resolution (15–20%) is of the same order as the bin width, and the correlation between the data points needs to be taken into account. Hence, we used the forward folding technique for data points proposed in Vovk et al. (2018), in which the differential flux points are interpreted as the breaks of a broken power law with multiple energy breaks. The arc was not detected in the Fermi-LAT data and thus only spectral upper limits could be computed. The upper limits (ULs) of the Fermi-LAT data are 95% confidence UL using the semi-Bayesian method of the science tools following Helene (1983), and the MAGIC UL follow the method by Rolke et al. (2005). In Sect. 5.1, these data points are compared against a model curve.
Spatial models used for the MAGIC and Fermi-LAT likelihood analysis.
 |
Fig. 4 Left: sketch of the spatial model used in the likelihood of the Fermi-LAT and MAGIC data analysis. The blue circle indicates the position and extension of the disc modelling the SNR shell, the green circle gives the position and 68% containment radius of a Gaussian model of MAGIC J2019+408, and the orange annular sector was used for the arc region. The red radio contours and the position of PSR J2021+4026 (white diamond) are shown for reference. Right: same as left, but with the second Gaussian as spatial model for the arc region. |
3.5 Discussion of the observational results
Regarding the disc, given the agreement of the position and extension of the emission detected by Fermi-LAT with the radio shell, a random coincidence seems implausible. As explained above, fitting the Fermi-LAT data resulted in a slight offset from the radio position and extension, but the fit of the Fermi-LAT data might be affected by the presence of MAGIC J2019+408. Hence, a disc model agreeing with the radio shell seems reasonable. Our spectral results are in agreement with previously published results on this source by the Fermi-LAT collaboration considering the difference in the area of the disc models.
MAGIC J 2019+408 is present in the MAGIC and Fermi-LAT data. Its position is offset with respect to VER J2019+407 (0°.07 north of the latter), but still compatible (~2σ discrepancy considering combined errors). Aliu et al. (2013) did not observe the arc structure, and not considering it as a distinct source may explain the different positions. The fact that the extension of VER J2019+407 is significantly larger and the VERITAS collaboration claimed an asymmetric source when updating their results in Abeysekara et al. (2018) supports this assumption. To highlight the different location and morphology, we gave this source an identifier different from that of VERITAS. In the Fermi-LAT energy range the spectrum of MAGIC J2019+408 is slightly harder than that of the shell, consistent with the findings of Fraija & Araya (2016). The authors analysed Fermi-LAT data in a narrower energy range and performed a point source search on top of the larger disc model from the 3FGL (whereas we used a physically motivated radio-based model). Accordingly, they obtained a TS map different from ours (Fig. 3), associated the excess emission with VER J2019+407, and extracted the spectrum at the corresponding position. For MAGIC J2019+408 the possibility for an extended source unrelated to the SNR cannot be ruled out. However, X-ray and radio data do not show any hint of a possible Galactic counterpart such as a pulsar powering a wind. Additionally, the spectral agreement with the SNR interior, particularly in the energy range of Fermi-LAT, further supports the assumption of a connection with the SNR.
The arc-like region is detected by MAGIC alone, though the VERITAS skymaps in Weinstein (2015) and Abeysekara et al. (2018) show hints of an extended emission stretching out towards the west of the SNR. The differences in morphology can be understood as a result of the differences in the observation time (tMAGIC ~ 2 × tVERITAS) and the different methods for reconstructing the background emission: exclusion region for MAGIC versus ring background model for VERITAS. The ring background faces issues with extended sources (Berge et al. 2007). The exclusion region method is only insensitive to emission regions larger than twice the wobble distance (1°.2 for our MAGIC data). Thus, we cannot rule out that the arc-like structure is the residual of a much larger complex such as the Cygnus cocoon. However, given that the arc traces the rim of the SNR and its spectrum agrees with that of MAGIC J2019+408 at TeV energies, the association with the γ Cygni SNR is very plausible.
The PSF of the HAWC experiment does not resolve substructures in the γ Cygni region making a comparison with the MAGIC results difficult. HAWC determined the centre of the emission around the SNR close to the centre of the shell (Abeysekara et al. 2017), whereas from the MAGIC high-energy skymap one would expect it to be shifted towards the northwest. This suggests additional emission surrounding the SNR likely towards the south of the shell, a region not well covered by the MAGIC observations due to the presence of Sadr. Still the steep spectral index measured by HAWC is in agreement with a softening of the spectrum between the energy range covered by Fermi-LAT and MAGIC.
Results of the spectral analysis from the Fermi-LAT and MAGIC analysis for each source component.
4 Interpretation and modelling
4.1 Leptonic or hadronic emission
The radio emission proves the presence of high-energy electrons inside the shell, which can also be the origin of the γ-ray emission via inverse Compton scattering (IC) or bremsstrahlung radiation. Due to the low plasma density of 0.2 cm−3 inside the SNR shell (Table 1), the former emission will dominate over the latter even when only considering a CMB photon field. The high-energy spectrum from the shell of γ Cygni up to a few hundred GeV has a slope of ~E−2. In contrast, the average radio spectral index αR of 0.48–0.75 (Zhang et al. 1997; Gao et al. 2011; Kothes et al. 2006; Ladouceur & Pineault 2008) implies an electron spectrum between dN/dE ∝ E−1.96 and ∝ E−2.5, and thereby a harder inverse Compton (IC) spectrum in γ rays. Hence, a leptonic scenario requires an additional break in the spectrum in the keV to GeV range to bring both observations into agreement. Such a break can naturally arise from electron cooling. To obtain a synchrotron cooling time shorter than the lifetime of the SNR, the magnetic field inside the SNR needs to be B ≳ 20 µG.
If the emission outside the shell originates from IC as well, the morphology of the arc and MAGIC J2019+408 require either an enhancement of the radiation field in those regions or a specific guiding magnetic field creating an overdensity of electrons compared to other parts around the shell. Observations with the Infrared Astronomical Satellite (IRAS; Saken et al. 1992) indeed suggest a higher IR emission towards MAGIC J2019+408 at 25 µm and at 60 µm. However, the morphology of MAGIC J2019+408 does not agree with the IR structure and the peak of the former is offset with respect to the centre of the latter by ~0°.6. Additionally, the parallaxes of identified IR sources in the vicinity of MAGIC J2019+408 (Gaia Collaboration 2018) suggest that at least part of the IR emission is farther away than the γ Cygni system. The absence of non-thermal synchrotron radiation at MAGIC J2019+408 (skymaps in Ladouceur & Pineault 2008) also renders the magnetic field scenario unlikely. Finally, the arc region is dark in both IR and synchrotron which speaks against an IC scenario as well.
Accordingly, the most likely leptonic scenario for the arc and MAGIC J2019+408 is bremsstrahlung emission. Like a hadronic scenario, it requires a local enhancement of the target gas density and is independent from the constraints above. Nevertheless, in this case the power-law index of the electron spectrum needs to change from Γ ~ − 3 inside the shell to Γ ~ − 2 outside. Moreover, in order for bremsstrahlung to dominate over pion decay, the accelerated electron-to-proton ratio has to be ≫ 10−2, whereas the studies of multi-wavelength emission from several young SNRs point towards lower ratios of ≈10−3 or less (see e.g. Völk et al. 2005; Morlino & Caprioli 2012). Additionally, theoretical predictions based on particle-in-cell simulations of collisionless shocks hint at values of electron-to-proton ratios of ≲10−2 (Park et al. 2015).
In conclusion, even if a leptonic explanation cannot be completely ruled out, its realisation requires extreme conditions. Alternatively, the γ-ray emission can be explained in a hadronic scenario, which is not subject to these constraints. Hence, in the following we develop a hadronic model to explain the data and accordingly assume that the bulk of emission is due to hadronic interactions.
4.2 Escaping or precursor?
If the emission from the arc region is indeed connected to the SNR, the emission beyond the SNR shell can either be due to the CR precursor in front of the shock or produced by particles escaping from the shock. The former interpretation seems unlikely for two different reasons. Firstly, the spectrum from the arc region is softer (at most similar given the uncertainties) than the one detected from the SNR interior. Using the linear theory with a spatially constant diffusion coefficient in the precursor, the spectrum upstream of the shock is given by
where x is the distance upstream from the shock, p the particle’s momentum, ush the shock speed, and D1 the diffusion coefficient upstream (see e.g. Blasi 2013). If the spectrum at the shock is fsh ∝ p−α and the diffusion coefficient is D1(p) ∝ pβ (in general, ß > 0 and ß = 1 for Bohm diffusion), the spatially integrated spectrum upstream is
Hence, the spectrum from the arc region should be harder than the one inside the remnant unless the diffusion coefficient is constant in momentum, which would be difficult to explain from both observational and theoretical grounds.
The second argument comes from the comparison of the SNR age with the acceleration time. If the arc represents the shock precursor, the thickness of the arc ∆arc corresponds to the diffusion length λp of particles with momentum p upstream. Hence, we can estimate the diffusion coefficient at the central energy observed imposing λp = ∆arc ≃ D1(p)/ush. At a distance of 1.7 kpc, the extension of the arc is ∆arc ~ 5 pc for central energy of all MAGIC data of ~800 GeV, corresponding to parent protons of ~8 TeV, leading to a diffusion coefficient upstream of the shock equal to
Using the test particle approach and following Drury (1983), among others, from the diffusion coefficient we can estimate the acceleration time needed to produce particles at 8 TeV as
which is ~5 times the estimated SNR age (D2 is the diffusion coefficient downstream, u2 the velocity of the downstream plasma, and u1 the shock speed).
A major uncertainty regarding this interpretation results from the unknown 3D orientation of the γ-ray emission. The γ-ray data do not allow us to estimate the distance along the line of sight. Hence, for example, our analysis may misassign emission belonging to the arc region and situated outside of the SNR shell to our disc model if, in the 2D projection, it is mapped onto the SNR shell. Consequently, a possible misalignment can conceal spectral differences between the arc region and the shell. Accordingly, the precursor could not be excluded based on the spectral similarity. In that case, however, the extension of the arc would be underestimated by our model, strengthening the argument of the acceleration time. In summary, a precursor scenario for the arc region seems improbable and instead it is a region where particles escaping from γ Cygni interact with the ISM.
Using the observed extension of the arc we can put a lower limit to the external diffusion coefficient, Dout, assuming that particles located in the arc started escaping at the beginning of the ST phase. Considering the typical energy of 8 TeV for CR protons and reasonable values for the SNR parameters (see Table 1 and Mej = 5M⊙), we estimate the diffusion coefficient via the length (λdiff = (6Doutt)1/2; factor 6 assumes three dimensions):
Here RST = (Mej/ρ0)1/3 and 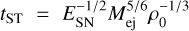 , while ∆arc = 0°.15 ≃ 5 pc. The estimated Dout is ~7 × 102 times smaller than the average Galactic diffusion coefficient at 8 TeV as obtained from direct CR measurements, i.e. DGal ≈ 6ß 1028(E/GeV)1/3cm2 s−1 (see e.g. Trottaet al. 2011; Yuan etal. 2017). Here and in the rest of the paper we assume a slope of 1/3 typical for Kolmogorov turbulence. If the turbulence were determined by other processes, the slope could be different. However, a different slope would not affect our main conclusions. Even when considering the large systematic uncertainty on the extension of the arc (∆arc would instead be 12 pc), Dout is still ~3 × 102 times smaller than the average DGal. We note that changing the SNR parameters in the range reported in Table 1 (always assuming that the estimated extension matches the real one), the ratio DGal/Dout ranges between ~8 × 101 and3 × 103. We note that the considerations in this section would apply equally to a leptonic scenario, with the only difference that the parameters would be tested at a parent particle energy of ~2 TeV instead of 8 TeV. Furthermore, the results would also hold when taking the offset between the SNR shell and the centre of the alternative Gaussian model for the arc region for ∆arc ~ 0°.1.
, while ∆arc = 0°.15 ≃ 5 pc. The estimated Dout is ~7 × 102 times smaller than the average Galactic diffusion coefficient at 8 TeV as obtained from direct CR measurements, i.e. DGal ≈ 6ß 1028(E/GeV)1/3cm2 s−1 (see e.g. Trottaet al. 2011; Yuan etal. 2017). Here and in the rest of the paper we assume a slope of 1/3 typical for Kolmogorov turbulence. If the turbulence were determined by other processes, the slope could be different. However, a different slope would not affect our main conclusions. Even when considering the large systematic uncertainty on the extension of the arc (∆arc would instead be 12 pc), Dout is still ~3 × 102 times smaller than the average DGal. We note that changing the SNR parameters in the range reported in Table 1 (always assuming that the estimated extension matches the real one), the ratio DGal/Dout ranges between ~8 × 101 and3 × 103. We note that the considerations in this section would apply equally to a leptonic scenario, with the only difference that the parameters would be tested at a parent particle energy of ~2 TeV instead of 8 TeV. Furthermore, the results would also hold when taking the offset between the SNR shell and the centre of the alternative Gaussian model for the arc region for ∆arc ~ 0°.1.
The result obtained in Eq. (8) represents an underestimation for two reasons. Firstly, we assume that the arc mainly extends orthogonally to the line of sight. If this is not true, ∆arc would be larger than 5 pc, resulting in a larger Dout. Secondly, the arc could represent an overdense region. If beyond this region the density drops to a lower value, γ rays could be undetectable even if CRs have diffused beyond ∆arc. A more thorough discussion on this point will be given in Sect. 5.3.
In the escape scenario, CRs are expected to escape radially symmetrically or, in case of a dominant main magnetic field, to escape mainly along the magnetic field direction. Emission beyond the shell should thus not be solely seen in the direction of the arc. A straightforward explanation could be that the arc has a higher density than the rest of the circumstellar medium (see discussion in Sect. 5.1). Additionally, a large-scale magnetic field oriented in the direction of the arc may cause a higher density of particles escaping into the arc region and can explain why emission is concentrated there (Nava & Gabici 2013). The radio emission indicates that the magnetic field is directed along the arc. The radio shell is not homogeneous, but presents two main lobes in the south-east and north-west, the latter roughly agreeing with the direction of the arc. Because the shock acceleration theory predicts a greater efficiency for the parallel shock configuration (i.e. B ‖ ush; Berezhko et al. 2002; Caprioli & Spitkovsky 2014), the two radio lobes could be interpreted as polar caps. In this situation another bright region can be expected on the opposite side of the SNR with respect to the arc, but again a low target gas density could impede its visibility.
Furthermore, the non-detection of emission on the opposite side of the SNR may partly result from the telescope pointing position chosen to avoid the influence of the bright star Sadr. The opposite site of the SNR is about ≳ 1° away from our pointing positions, where the acceptance of the MAGIC telescopes decreases to ≲ 1/2 of the full sensitivity. Nonetheless, MAGIC should have detected the emission if it had the same surface brightness within the covered energy range as the arc region, hence the emission in the south might be weaker, distributed over wider area, or have a different spectral energy distribution. The hints for emission at the south of the SNR shell visible in Fig. 2, and that HAWC determined the centre of the SNR to agree with the centre of the shell, still could be a sign of the existence of a counterpart to the arc around the southern shell.
4.3 Simplified approach for particle propagation
In this section we model the propagation of accelerated particles inside and outside the SNR in order to properly calculate the γ-ray emission. We follow the derivation proposed by Celli et al. (2019a; see that paper for further details). For simplicity we assume spherical symmetry inside and outside the remnant. The transport equation for accelerated protons in spherical coordinates is
where u is the advection velocity of the plasma and D the diffusion coefficient. The former is obtained from the SNR evolution. Because γ Cygni is clearly in the ST phase, we describe its evolution using the ST solution in the case of expansion inside uniform medium with density ρ0. The shock position Rsh and the shock speed as a function of time are
where ξ0 = 2.026 (for a monatomic gas with specific heat ratio γ = 5/3). The internal structure of the SNR is determined by adopting the linear velocity approximation (Ostriker & McKee 1988), in which the gas velocity profile for r < Rsh is given by
where σ is the compression factor at the shock. The radial profile of the gas density in the SNR interior (needed to calculate the γ-ray emission) is also given by the ST solution and can be closely approximated by the following polynomial with respect to the self-similar variable 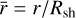 (t; Sedov 1959):
(t; Sedov 1959):
Here ρ0 the upstream density and the parameters αk and αk are obtained from a fitting procedure that gives a1 = 0.353, a2 = 0.204, a3 = 0.443, α1 = 4.536, α2 = 24.18, and α3 = 12.29 (Celli et al. 2019a).
In the following sections we solve the transport Eq. (9) using two different approximations, one for particles confined inside the remnant and one for the escaping particles.
4.4 CR distribution at the shock
Following Ptuskin & Zirakashvili (2005), we assume that the shock converts the bulk kinetic energy to relativistic particles with an efficiency ξCR, which is constant in time. The distribution function of CRs accelerated at the shock is determined by the DSA and is predicted to be a power law in momentum up to a maximum value, pmax‚0. In a simplified form we can write the spectrum at the shock as
where mp is the proton mass, Θ is the Heaviside function, and Λ(pmax‚0) is the function required to normalise the spectrum such that the CR pressure at the shock is 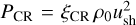 . We keep the power-law index α as a free parameter in order to fit the γ-ray data. We note, however that DSA predicts that α is equal or very close to 4.
. We keep the power-law index α as a free parameter in order to fit the γ-ray data. We note, however that DSA predicts that α is equal or very close to 4.
The maximum momentum at the shock is a function of time and its calculation requires a correct description of the evolution of the magnetic turbulence. However, this is a non-trivial task because the magnetic turbulence depends on the self-generation by the same particles and by damping effects and wave cascades. A comprehensive description of all these effects does not exist yet. Hence, here we use the general assumption, often used in the literature (see e.g. Gabici et al. 2009), that the maximum momentum increases linearly during the free expansion phase and decreases as a power law during the ST phase:
Here pM, the absolute maximum momentum reached at t = tST, and δ > 0 are treated as free parameters of the model.
Inverting Eq. (15) we can also define the escaping time, when particles with momentum p can no longer be confined and start escaping from the remnant,
It is also useful to define the escaping radius, namely the radius of the forward shock when particles with momentum p start escaping:
The particle distribution evolves in a different way before and after tesc(p), as we discuss below.
4.5 Distribution of confined particles
When t < tesc(p), particles with momentum p are confined inside the SNR and do not escape. A reasonable approximation for the distribution of these confined particles, which we call fc from here on, can be obtained from Eq. (9) neglecting the diffusion term. This approximation is accurate for p ≪ pmax,0(t), but we show below that in the test-particle case the diffusion inside the SNR does not play an important role. The simplified transport equation is
and the solution can be easily obtained using the method of characteristics, accounting for the plasma speed inside the SNR as approximated by Eq. (12). The solution can be written as (see also Ptuskin & Zirakashvili 2005)
where t′(t‚ r) is the time when the plasma layer located at the position r at time t has been shocked:
We simplify Eq. (19) using Eqs. (14) and (10) and neglecting the mild dependence of Λ(pmax) on t, and get
The function pmax(t, r) is the maximum momentum of particles at position r and time t, and it is equal to the maximum momentum of particles accelerated at time t′ diminished by adiabatic losses:
Here the last step uses Eq. (15). Interestingly, assuming test-particle DSA, where α = 3σ/(σ − 1), the distribution function of confined particles has only a mild dependence on r through the normalisation factor Λ(pmax). In this case, neglecting diffusion in the first approximation is justified because ∂rfc ≈ 0.
4.6 Distribution of escaping particles
When t > tesc(p), particles with momentum p cannot be confined any more and start escaping. In previous works, the escape is assumed to be instantaneous, meaning that particles with momentum p are immediately located outside the remnant at t > tesc(p). While this assumption can be a valid approximation for studying the final CR spectrum released into the Galaxy, it is invalid in the case of γ Cygni as we aim to describe the early phase of the escape process in a region close to the SNR.
An approximate solution for time t > tesc(p) can be obtained assuming that particles are completely decoupled from the SNR evolution and only diffuse. The evolution is therefore described by Eq. (9) dropping all terms including u:
This equation needs to be solved with the initial condition: fesc(tesc(p)‚ r‚ p) = fc(tesc(p), r, p) ≡ fc0(r, p) for r < Resc(p) and 0 elsewhere. The diffusion coefficient in the medium outside the SNR, Dout, is assumed to be spatially constant and is an unknown of the problem that we want to constrain from observations. Inside the SNR the diffusion coefficient, Din, is in general different from the one outside; nevertheless, for simplicity we assume Din = Dout (and that it is spatially constant). This approximation allows an analytic solution of Eq. (23) via the Laplace transform (see Celli et al. 2019a, for the full derivation). The final result is
where 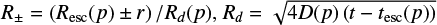 , and Erf is the error function. Examples of fesc are plotted in Figs. 5 and 6 for different times and different values of the diffusion coefficient. For all plots we assume a strong shock (σ = 4) and the test particle limit (α = 4).
, and Erf is the error function. Examples of fesc are plotted in Figs. 5 and 6 for different times and different values of the diffusion coefficient. For all plots we assume a strong shock (σ = 4) and the test particle limit (α = 4).
When Din ≠ Dout the leaking of particles from the remnant changes, but the profile of the distribution function outside of the remnant remains essentially the same, being determined mainly by Dout.
 |
Fig. 5 Distribution of escaping particles at one arbitrary fixed momentum, p* = 10 TeV, as a function of the radial coordinate normalised to Resc(p*) = 13 pc. Different lines refer to different times in units of tesc(p*) = 4000 yr, as labelled, and the vertical dashed lines correspond to the shock positions at those times. We assume Dout = DGal/100, δ = 2.2, and pM = 100 TeV. |
5 Gamma-ray spectra
5.1 Emission from the SNR interior and arc
Once the particle distribution is known at any position inside and outside the SNR, the calculation of γ-ray emissivity due to hadronic collisions is straightforward. The rate of emitted photons from a given region is
We parametrise the differential cross section following Kafexhiu et al. (2014). Jp(Ep, t) is the spatially integrated proton flux as a function of the kinetic energy Ep and observation time t. It is connected to the momentum distribution function as Jp(Ep)dEp = ßcFp(p)d3p, where Fp is the proton distribution in momentum convoluted with the target density in the region of interest. In particular, we distinguish two regions, the interior of the SNR and the fraction of the external spherical shell which include the arc. The corresponding distributions are
where the particle distribution inside the SNR is fin = fc for p < pmax,0(tSNR), and fin = fesc otherwise, with fc and fesc given by Eqs. (21) and (24), respectively. The gas distribution inside the remnant is given by Eq. (13), while in the arc we assume a constant density defined by narc. The additional factor ηarc accounts for the spherical shell fraction which includes the arc region.
Figure 7 shows our best fit to the observed γ-ray flux for both the SNR interior and the arc region. The parameters used to produce these curves are summarised in Table 4. Parameters related to the SNR evolution are fixed to the values from Table 1. All the other parameters are allowed to vary. The corresponding numbers in square brackets show the range of values resulting in curves, which are still in reasonable agreement with the data.
At first glance the large number of free parameters (six if we exclude the ones related to the SNR) suggest a strong degeneracy between them. Nevertheless, we can fix all the values with a reasonable small level of uncertainty because every parameter is connected to a specific feature of the spectrum.
First, the Fermi-LAT data from the remnant interior and the radio data fix the slope of the accelerated spectrum below TeV energies to be α ≃ 4.0. Secondly, the normalisation of the γ-ray flux fixes the acceleration efficiency to be ξCR ≃ 4%. In the energy range between 100 and 300 GeV the slope abruptly changes from ~E−2 to ~E−2.5. In our model this turning point defines the maximum energy of particles presently accelerated to be Emax(tSNR) ≃ 1–3 TeV. Noticeably, this energy is independently constrained by the Fermi-LAT upper limits on the flux from the arc region: to be compatible with the MAGIC data the γ-ray flux from this region needs to have a maximum in the range 100–300 GeV. This maximum corresponds to γ rays produced by the lowest energetic particles in the arc, which is very close to the maximum energy of particles accelerated now. Additional information is derived from the shape of the MAGIC spectrum that simultaneously determines EMAX (the maximum energy reached at the beginning of the ST phase), Dout and δ. Our model predicts that the shape of the γ-ray emission from the SNR and from the arc should be very similar in the MAGIC band. Considering the uncertainties in the data, this is compatible with observations.
Finally, the normalisation of the MAGIC data points of the arc spectrum sets the product of ηarc × narc. Because the observed geometry suggests a filling factor ηarc ~20% (with some uncertainties due to a possible line-of-sight effect; see Sect. 4.2) we also have an estimate of the target density in the arc region which has to be 1–2 cm−3. The targets inside the arc regions could be either the possible cavity wall reported by Ladouceur & Pineault (2008) or smaller clumps like that found inside the north-west shell by Uchiyama et al. (2002). The location of the cavity wall surrounding the SNR shell to the north claimed by Ladouceur & Pineault (2008) at velocities between −19 km s−1 and -11 km s−1 coincides with the arc region (see Fig. 8). Even in the optically thin case the column density in this range reaches 1 × 1021 cm−2, far exceeding the column density required by our model by one order of magnitude at least.
We also note that some level of uncertainty is introduced by the parametrisation of the differential cross section used in Eq. (25). We tried all four of the models considered in Kafexhiu et al. (2014; Geant 4.10, Pythia 8.18, SIBYLL 2.1, and QGSJET-1), but for sake of clarity we only show the results obtained with Pythia because for Eγ > 1 GeV it gives a γ-ray flux roughly between the maximum and minimum predictions (obtained with SIBYLL and Geant, respectively). At lower energies all the methods give essentially the same result. The uncertainty in the cross section mainly corresponds to a factor of ~2 difference in the target density of the arc or, equivalently, in the acceleration efficiency. This uncertainty is accounted for in the uncertainty interval shown in square brackets in Table 4.
 |
Fig. 6 Distribution of escaping particles at p* = 10 TeV/c and t = tSNR as a function of the radial coordinate normalised to Resc(p*) = 13 pc. Different lines refer to different values of the diffusion coefficient, as labelled. The vertical lines correspond to the shock position (dashed) and to the arc external edge (dot-dashed) as observed now. The remaining parameters are the same as in Fig. 5. |
 |
Fig. 7 Computed γ-ray flux due to π0 decay from the SNR interior (blue solid line) and from the arc region (orange dashed line) based on our model compared against data points from our Fermi-LAT (diamonds) and MAGIC (squares) analysis. |
 |
Fig. 8 HI emission at velocities between −19 km s−1 and −11 km s−1 measured by the CGPS. The red and yellow lines show the 3 σ and 5 σ significance contours of the γ-ray emission observed by MAGIC (Fig. 1). The cyan lines are the 400 K contours of the 408 MHz continuum emission from the CGPS. The white diamond gives the position of PSRJ2021+4026. |
5.2 Emission from MAGIC J2019+408
MAGIC J2019+408 has been detected by Fermi-LAT and by MAGIC. Remarkably the high-energy spectrum is very similar to the one detected from the arc region, whereas in the Fermi-LAT band the slope is slightly harder than the emission from the overall SNR but still compatible with the latter. This finding suggests that at least part of the emission from the hot spot should come from a region located inside the SNR where low-energy particles are also present. In the framework of the hadronic model proposed here, MAGIC J2019+408 can be understood as a combination of emission from the remnant interior plus a contribution from escaping particles located outside the SNR. In Fig. 9, we show a possible fit to the data by combining these two components and only adjusting the normalisation via the target density. Remarkably, this fit does not require any further tuning of the remaining parameters of the model and we keep the values reported in Table 4. Considering that the angular extension of the hot spot is ~0.1° and assuming a spherical geometry, the shown fit requires a density of ~45 cm−3 for the internal and for the external contributions. Hence, MAGIC 2019+408 could be due to an overdense cloud partially engulfed by the SNR shock and partially still outside of it. Alternatively, MAGIC J2019+408 could result from two (or more) clouds, spatially separated, one inside and one outside the SNR, but located along the same line of sight. It is worth mentioning that the estimated density of ~45 cm−3 is close to the value of ~20 cm−3 reported by Mavromatakis (2003) but in the east of the SNR.
Even though no direct interaction between the SNR and a cloud has been reported for the north of the SNR, CO emission is present at a velocity range of 2–10 km s−1 ‚ as shown by Ladouceur & Pineault (2008) based on CO J = 1 ← 0 observations by Leung & Thaddeus (1992). The left panel of Fig. 10 shows the SNR radio contours and MAGIC significance contours overplotted on this map. The right panel shows how the same contours compare against infrared emission at 100 µm indicating the location of dust. The CO emission borders the MAGIC contours and the dust emission is even located inside of them. However, both CO and dust trace the dense core of interstellar clouds. The density of our model for MAGIC 2019+408 of ~45 cm−3 is small compared to the critical density of CO (~1.1 × 103 cm−3), for example, and due to a typical dust-togas ratio of about 1:100 little emission from dust is expected. Hence, the absence of a direct morphological counterpart of MAGIC 2019+408. Nonetheless, the γ-ray emission may interact with the outer layers of a potential cloud. If the target material of MAGIC 2019+408 consists of HI entirely, the column density at the centre of a spherical cloud would be ~5 × 1020 cm−2. None of the velocity layers studied by Ladouceur & Pineault (2008) shows a structure coinciding with MAGIC 2019+408. Nonetheless, the two velocity ranges showing the CO emission (2 km s−1 < v < 10 km s−1) and the northern HI cavity wall (−19 km s−1 < v < −11 km s−1) show a sufficient HI column density at the position of MAGIC 2019+40 (a factor of 1.5 to 2 higher) even assuming an optically thin case. Regarding the different velocity ranges, Ladouceur & Pineault (2008) noted that the complex motion of the gas layers in this region complicates the assignment of a velocities. The search for a counterpart will thus require a dedicated study, though currently the observation suggest a sufficient amount of target material. It is important to note that the presence of a dense cloud engulfed by a shock could result in a harder hadronic spectrum due to magnetic field amplification around the cloud border, which prevents low-energy particles from penetrating the cloud. Nevertheless, this mechanism is only relevant when the density contrast between the cloud and the circumstellar medium is ≳103 (Celli et al. 2019b), otherwise the amplification of the magnetic field around the cloud is not strong enough. The density contrast in our case is below that threshold, hence the spectrum inside the cloud should be very similar to the one inside the SNR.
 |
Fig. 9 Computed γ-ray flux due to π0 decay from MAGIC J2019+408 based on our model compared against data points from our Fermi-LAT (diamonds) and the MAGIC (squares) analysis. The spectrum (green solid line) is modelled as the sum of emission from the remnant interior (blue dash-dotted line) and exterior (orange dashed line). |
 |
Fig. 10 Left: Average of CO J = 1 ← 0 emission between 2 km s−1 and 10 km s−1 based on data from Leung & Thaddeus (1992) interpolated on the coordinate grid of the MAGIC data. The cyan contours are the 400 K contour of the 408 MHz observation by the CGPS and the red and yellow contours are the 3 σ and 5 σ significance contours of the emission seen by MAGIC. The white diamond gives the position of the PSR J2021+4026. Right: 100 µm intensity map based on data from Schlegel et al. (1998) interpolated on the coordinate grid of the MAGIC data. Contours and symbol are the same as in the left panel. |
5.3 Implication for DSA
Our interpretation of the γ-ray spectra has interesting implications for the shock acceleration theory. First, the slope of accelerated particles is constrained to be close to 4, in agreement with the standard prediction of DSA. Even a value as steep as 4.2, required by direct CR observations (see e.g. Evoli et al. 2019), is still compatible with the data.6
In addition, we have shown that the maximum energy accelerated at the current SNR age is around a few TeV, while the maximum energy reached at the beginning of the ST phase is at most a few hundred TeV. Hence γ Cygni is not a PeVatron during the ST phase; nevertheless, we cannot exclude that higher energies could have been reached during the very early stage of its evolution. The fact that the maximum energy now is of the order of TeV immediately provides an estimate of the level of magnetic turbulence in the shock region. Using Eq. (8) we can estimate the diffusion coefficient upstream of the shock from the maximum energy and the remnant age. In quasi-linear theory, the diffusion coefficient D is expressed as a function of the turbulence level as D1(p) = DBohm/ℱ(kres), where DBohm = rLv/3, rL being the Larmor radius, and ℱ = (δB(kres)/B0)2 is calculated at the resonant scale kres = 1/rL(Emax). Hence, Emax(tSNR) = 1 TeV (obtained from the condition tacc = tSNR) inferred from the spectrum implies δB/B0 ≃ 0.25, where we assumed B0 = 3 µG. At first glance such a small value for the magnetic turbulence seems at odds with the common assumption that close to strong shocks the Bohm limit is reached. Nevertheless, two different arguments suggest that δB/B0 should be smaller than unity, as inferred here. First of all, the main mechanism often invoked to excite magnetic turbulence resonating with accelerated particles is the resonant streaming instability; however, it saturates at δB/B0 ≲ 1 (see Blasi 2013, Sect. 4.2). A higher level of turbulence requires other mechanisms like the non-resonant instability (NRI; Bell 2004), but such a mechanism is thought to be effective when the shock speed is ≫ 1000 km s−1 (Amato & Blasi 2009). Moreover, the NRI excites small-scale modes which, to efficiently scatter high-energy particles, requires an inverse cascade up to the larger scales that resonate with such particles. Hence, either the NRI is not efficiently excited or it is excited but the inverse cascade does not occur on the required timescale. CRs can amplify the magnetic field upstream, even though another mechanism that takes place when the medium is inhomogeneous (Drury & Downes 2012). Nevertheless, such a mechanism also requires high shock speeds in order to be effective. The exact condition is 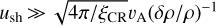 , where δρ is the typical level of density fluctuation in the upstream, while vA is the Alfvén speed. Using the parameter values adopted in this work, we easily obtain the condition ush ≫ 1000 km s−1. Furthermore, even if the amplification were efficient, the upstream plasma may be partially neutral and the ion-neutral friction could efficiently damp the magnetic turbulence resulting in δB/B0 ≪ 1 (see e.g. Nava et al. 2016).
, where δρ is the typical level of density fluctuation in the upstream, while vA is the Alfvén speed. Using the parameter values adopted in this work, we easily obtain the condition ush ≫ 1000 km s−1. Furthermore, even if the amplification were efficient, the upstream plasma may be partially neutral and the ion-neutral friction could efficiently damp the magnetic turbulence resulting in δB/B0 ≪ 1 (see e.g. Nava et al. 2016).
Another important piece of information inferred from the data is the time dependence of the maximum energy. As discussed in Celli et al. (2019b), an approximate way to infer the value of δ is by equating the acceleration time with the age of the remnant. Using Eq. (7), (i.e. 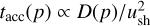 ) and writing the diffusion coefficient again in terms of the magnetic turbulence (D = DBohmℱ−1), we can write
) and writing the diffusion coefficient again in terms of the magnetic turbulence (D = DBohmℱ−1), we can write 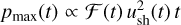 . In the absence of any magnetic field amplification and with a constant turbulence, the time dependence is only determined by the shock speed, which is ush ∝ t−3/5 in the ST phase, resulting in pmax(t) ∝ t−1/5. On the contrary, our inferred value of δ ≃ 2.55 requires that the magnetic turbulence should decrease in time as ℱ ∝ t−2.35 ∝ ush(t)3.9. Hence, even accounting for all the uncertainties, a constant value of magnetic turbulence in the shock precursor would be difficult to reconcile with our finding, which instead requires some level of magnetic amplification and/or damping. Interestingly, δ ≃ 2.55 is in good agreement with the phenomenological estimate of δ ≃ 2.48 by Gabici et al. (2009) derived from pmax ∝ t−δ and assuming pmax(t = 200 yr) = 5 PeV, and pmax(t = 5 × 104 yr) = 1 GeV.
. In the absence of any magnetic field amplification and with a constant turbulence, the time dependence is only determined by the shock speed, which is ush ∝ t−3/5 in the ST phase, resulting in pmax(t) ∝ t−1/5. On the contrary, our inferred value of δ ≃ 2.55 requires that the magnetic turbulence should decrease in time as ℱ ∝ t−2.35 ∝ ush(t)3.9. Hence, even accounting for all the uncertainties, a constant value of magnetic turbulence in the shock precursor would be difficult to reconcile with our finding, which instead requires some level of magnetic amplification and/or damping. Interestingly, δ ≃ 2.55 is in good agreement with the phenomenological estimate of δ ≃ 2.48 by Gabici et al. (2009) derived from pmax ∝ t−δ and assuming pmax(t = 200 yr) = 5 PeV, and pmax(t = 5 × 104 yr) = 1 GeV.
For the propagation of escaping particles, the highest energy points detected by MAGIC clearly require a diffusion coefficient ~ 10–35 times smaller than the average Galactic value. This ratio is a factor 2 to 3 × 102 lower than the prediction using Eq. (8). However, as already discussed in Sect. 4.2, Eq. (8) only provides a lower limit on Dout, and thus the two estimates can be considered compatible. Our finding that Dout ≪ DGal is not surprising given that DGal (obtained from the measurements of boron-to-carbon ratio in the local CR spectrum) represents an average over the large volume of the Galactic magnetic halo and could be completely different from the diffusion coefficient in the vicinity of γ Cygni.
In the first place, an effective smaller diffusion coefficient could result from the particle diffusion along magnetic flux tubes, hence 1D rather than isotropic 3D diffusion (Nava & Gabici 2013). A second possibility is stronger turbulence around the SNR, unsurprising owing to the complexity of the Cygnus region, which counts several potential sources of turbulence (SNRs and winds from massive stars and clusters). Alternatively, enhanced turbulence could be also naturally produced by the streaming instability of escaping CRs. This scenario has been investigated by several authors (Malkov et al. 2013; Nava et al. 2016; D’Angelo et al. 2016) who show that the diffusion can be easily suppressed by 1–3 orders of magnitude up to several parsecs from the SNR. The reduced Dout of our model compared to DGal is compatible with the diffusion coefficient derived for the vicinity of other SNRs such as W28 (Hanabata et al. 2014, and references therein) and W44 (Uchiyama et al. 2012). Distinguishing between these three possibilities (1D diffusion, larger external turbulence, or self-generated turbulence) is not easy but the last scenario has the advantage of being more predictive. If the escaping flux is known the diffusion coefficient can be calculated without adding any new free parameters. It should also be noted that we assumed for Dout the same Kolmogorov scaling inferred for DGal7. In the case of turbulence coming from external sources, the Kolmogorov scaling is indeed expected; instead, if the turbulence is self-generated the resulting scaling is usually different. Hence a self-consistent calculation is needed to provide a more detailed answer.
Clearly our model suffers from some limitations, mainly related to the assumptions of spherical geometry and homogeneity of the circumstellar medium. The γ-ray map shows a patchy structure suggesting the presence of a clumpy medium. Small dense clumps may significantly modify the hadronic γ-ray spectrum as a result of magnetic field amplification occurring in the shock-cloud interaction, which in turn modifies the propagation properties of the plasma (Gabici & Aharonian 2014; Inoue et al. 2011; Celli et al. 2019b). Nevertheless, this effect is mainly important at high shock speed and for a large density contrast between the clumps and the average circumstellar medium. It has been applied to SNR RX J1713, for example, whose shock has a speed of ~5000 km s−1 and where the estimated density contrast is above 103. In the case of γ Cygni both quantities are much smaller, it is hence probable that this effect plays a minor role.
Another possible issue is related to the contribution to the γ-ray spectrum coming from CR illuminated clouds located along the line of sight and erroneously attributed to the SNR interior. Even if such a scenario remains possible, the CO maps do not show any clear evidence of clouds along the same line of sight of the SNR disc (Leung & Thaddeus 1992), hence we are inclined to attribute all the emission from the disc region to the SNR interior.
6 Summary and future prospects
Combining MAGIC and Fermi-LAT data, we investigated the γ-ray emission in the vicinity of the γ Cygni SNR G 78.2+2.1, and identified three main source components: the SNR interior, an extended emission located immediately outside the SNR that we call the arc, and a Gaussian-shaped extended source MAGIC J2019+408 in the north-west of the remnant. The brightness ratio between the source components is energy dependent with the SNR shell dominating below ~60 GeV and the arc only being observed by MAGIC above 250 GeV. The morphologies and spectra of MAGIC J2019+408 and the arc suggest an association with the SNR. The indices for a power-law model for MAGIC J2019+408 and the shell are ~2 in the Fermi-LAT energy range and ~2.8 for the three components in the MAGIC energy range (similar within uncertainties, but explicitly 2.55 for the shell, 2.81 for the MAGIC J2019+408, and 3.02 for the arc).
We interpret the three components as the result of CRs escaping the shock of the SNR upstream into the ISM, while the shock is still capable of confining less energetic CRs. In this context, the differences between MAGIC J2019+408 and the arc can be understood by the presence of an over-dense cloud partially engulfed by the SNR. The observed extension of the arc does not agree with the predicted size of a shock precursor based on the characteristics of the SNR.
We further presented a theoretical model to interpret the data in the framework of DSA with the inclusion of time-dependent particle escape from the SNR interior. While a leptonic origin for the γ-ray emission cannot be ruled out, given the morphologies and spectra of the source components a hadronic scenario seems more plausible. Hadronic collisions can account for the γ-ray emission from all three regions (the SNR interior, the arc, and MAGIC J2019+408) provided the following criteria are met:
the spectrum of accelerated particles is ∝ p−4 and the acceleration efficiency is ≃3.8%;
the maximum energy of accelerated particles decreases in time as ∝ t−2.55 and, at the present moment, it is a few TeV while at the end of the free-expansion phase it reached an absolute maximum of about 100 TeV;
the level of magnetic turbulence in the shock region at the present moment is δB/B0 ≲ 1 and has to decrease in time, pointing towards the presence of self-exited magnetic waves from accelerated particles;
the diffusion coefficient in the region immediately outside the SNR has to be ~10–35 times smaller than the average Galactic value inferred from the boron-to-carbon ratio in the local CR spectrum;
the region around the SNR has to be patchy with extended clouds, with densities between 5 and 200 times higher than the average density of the circumstellar medium.
All these findings agree well with the standard DSA applied to a middle-aged SNR produced by a core-collapse explosion, except the quite steep time dependence of the maximum energy: the theory invoking resonant and non-resonant instabilities usually predicts flatter dependences. A way to explain the steep dependence is through some damping mechanism of the magnetic waves. We note, however, that the description of the particle escape is not completely understood yet, even when damping processes are neglected.
Another important point of our modelling is the fact that the high-energy emission from γ Cygni needs the contribution coming from particles that have formally escaped from the acceleration process but are still diffusing around and inside the SNR. This could be of general validity for middle-aged SNRs, especially if the diffusion coefficient around those objects is suppressed with respect to the Galactic value.
The understanding of the γ Cygni SNR could profit from future observation particularly of radio emission and the molecular material, the uncovered hard X-ray to sub-GeV energy range, and very high-energy γ rays. Deep radio observations like the one performed by Benaglia et al. (2021) could help to better understand the connection between the radio and the very high-energy emission from the region, and thus provide further information on the nature of the γ-ray emitter. Improved knowledge of the target material can reduce the uncertainty of our proposed model and determine the contribution from hadrons. Given that hard X-rays or MeV γ rays can resolve the SNR shell under the background from the pulsar, they may clarify the remaining uncertainties about a hadronic or leptonic origin by searching for possible bremsstrahlung, a cooling break in the spectrum of the SNR shell, or a pion cut-off. To validate our proposed model future γ-ray studies could test whether the extension of the arc region is energy-dependent. Hence, γ Cygni might be a prime target to study the particle escape process from SNRs particularly for deeper γ-ray observations with improved angular resolution.
Acknowledgements
We would like to thank the Instituto de Astrofísica de Canarias for the excellent working conditions at the Observatorio del Roque de los Muchachos in La Palma. The financial support of the German BMBF and MPG; the Italian INFN and INAF; the Swiss National Fund SNF; the ERDF under the Spanish MINECO (FPA2017-87859-P, FPA2017-85668-P, FPA2017-82729-C6-2-R, FPA2017-82729-C6-6-R, FPA2017-82729-C6-5-R, AYA2015-71042-P, AYA2016-76012-C3-1-P, ESP2017-87055-C2-2-P, FPA2017-90566-REDC); the Indian Department of Atomic Energy; the Japanese ICRR, the University of Tokyo, JSPS, and MEXT; the Bulgarian Ministry of Education and Science, National RI Roadmap Project DO1-268/16.12.2019 and the Academy of Finland grant no. 320045 is gratefully acknowledged. This work was also supported by the Spanish Centro de Excelencia “Severo Ochoa” SEV-2016-0588 and SEV-2015-0548, the Unidad de Excelencia “María de Maeztu” MDM-2014-0369 and the “la Caixa” F oundation (fellowship LCF/BQ/PI18/11630012), by the Croatian Science Foundation (HrZZ) Project IP-2016-06-9782 and the University of Rijeka Project 13.12.1.3.02, by the DFG Collaborative Research Centers SFB823/C4 and SFB876/C3, the Polish National Research Centre grant UMO-2016/22/M/ST9/00382 and by the Brazilian MCTIC, CNPq and FAPERJ. The Fermi LAT Collaboration acknowledges generous ongoing support from a
number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Energie Atomique and the Centre National de la Recherche Scientifique / Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K.A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This work performed in part under DOE Contract DE-AC02-76SF00515. This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
Appendix A Systematic Uncertainties
For both of the telescopes, MAGIC and Fermi-LAT, we consider two kinds of systematic uncertainties, those from the detector itself and those from the ingredients of the models supplied to the likelihood analysis.
For MAGIC Aleksic et al. (2016) studied the systematic uncertainties on the spectral parameters (flux normalisation, spectral index, and energy scale) resulting from the telescope performance8 for low and medium Zenith angles. Since the observations for this work were performed at the same elevations, we scaled those uncertainties with the signal-to-background ratio of each source component as described in Aleksic et al. (2016). Furthermore, the authors investigated the systematic uncertainty on the source position, which we considered for the localisation of MAGIC J2019+408. However, Aleksic et al. (2016) only examined point sources or slightly extended sources. Hence, we additionally studied the uncertainties arising from the imperfect knowledge of our 2D background and exposure shape, which are part of our SkyPrism model. To estimate their effect we ran the analysis using 50 random representations of the background model and exposure map. For the former we assumed that the content in each bin of the background acceptance model in camera coordinates follows the Poisson statistics with the original value as the mean value. According to the distribution in each bin we simulated random camera background models and proceeded in the same way as for the original model following (Vovk et al. 2018). For the exposure the random representations are based on the parameter uncertainties of the γ-ray acceptance model fitted to the Monte Carlo (MC) based acceptance described in Vovk et al. (2018).
Due to the wide energy range, the uncertainties affecting the spectral parameters are less of a concern for the morphological study. Thus, our estimates only include the uncertainties from the background and exposure model together with the effect of a possible underestimation of the MC based PSF model. Aleksic et al. (2016) and (Vovk et al. 2018) found that the MC based PSF might be 0°.02 smaller than the extension of point sources. For the spectra we considered the uncertainties from telescope performance and the uncertainties of the background and exposure model. Table A.1 contains the effect on each spectral parameter and source component for the various uncertainty origins. The uncertainties based on Aleksic et al. (2016) are listed under ‘instrument’ and the background and exposure model uncertainties as ‘bgr+exposure’.
For Fermi-LAT data we studied the uncertainty of the source localisation by fitting the localisation of all point sources in the RoI with associations at radio wavelength. We used the following catalogues: Manchester et al. (2005), Bennett et al. (1986), Douglas et al. (1996). For the sources in this sample, we estimated the additional systematic uncertainty in addition to the average statistical localisation uncertainty based on a Rayleigh distribution to accommodate the 68% offset from their catalogue position. For the estimation of the source extension we take into account the uncertainty of the PSF and the interstellar emission model (IEM). We evaluated the systematic uncertainty using the P8R2 version of the alternative IEMs from Acero et al. (2016) together with a ±5% scaling of the PSF. The uncertainties of the flux normalisation and spectral index result from the precision of the IEM and the effective area, so we computed it using the alternative IEMs and considering a ±5% uncertainty on the effective area (listed as instrumental uncertainty in Table A.1).9 The instrumental uncertainty on the energy scale is based on Ackermann et al. (2012). The effects on the spectral parameters are listed in Table A.1.
Systematic uncertainties for the spectral analysis of the Fermi-LAT and MAGIC data and each source component. The uncertainties are sorted according to their origin from either the IRFs of the detectors or the uncertainties on the shape of the background model and exposure for MAGIC and the IEMs for Fermi-LAT.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Science, 325, 840 [Google Scholar]
- Abeysekara, A. U., Albert, A., Alfaro, R., et al. 2017, ApJ, 843, 40 [Google Scholar]
- Abeysekara, A. U., Archer, A., Aune, T., et al. 2018, ApJ, 861, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 224, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2017, ApJ, 843, 139 [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [Google Scholar]
- Ahnen, M. L., Ansoldi, S., Antonelli, L. A., et al. 2017, Astropart. Phys., 94, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Akaike, H. 1974, IEEE Trans. Automatic Control, 19, 716 [CrossRef] [Google Scholar]
- Aleksic, J., Ansoldi, S., Antonelli, L. A., et al. 2016, Astropart. Phys., 72, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Aliu, E., Archambault, S., Arlen, T., et al. 2013, ApJ, 770, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Allafort, A., Baldini, L., Ballet, J., et al. 2013, ApJ, 777, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Amato, E., & Blasi, P. 2009, MNRAS, 392, 1591 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [CrossRef] [Google Scholar]
- Atwood, W. B., Albert, A., Baldini, L., et al. 2013, arXiv e-prints [arXiv:1303.3514] [Google Scholar]
- Bell, A. R. 2004, MNRAS, 353, 550 [Google Scholar]
- Benaglia, P., Ishwara-Chandra, C. H., Paredes, J. M., et al. 2021, ApJS, 252, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C., Lawrence, C., Burke, B., Hewitt, J. & J., M. 1986, VizieR Online Data Catalog: The MIT-Green Bank 5GHz Survey [Google Scholar]
- Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2002, A&A, 395, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [CrossRef] [EDP Sciences] [Google Scholar]
- Blasi, P. 2013, A&AR, 21, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P., Amato, E., & Serpico, P. D. 2012, Phys. Rev. Lett., 109, 061101 [Google Scholar]
- Brose, R., Pohl, M., Sushch, I., Petruk, O., & Kuzyo, T. 2020, A&A, 634, A59 [EDP Sciences] [Google Scholar]
- Burnham, K. P., & Anderson, D. R. 2004, Sociol. Methods Res., 33, 261 [Google Scholar]
- Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [CrossRef] [Google Scholar]
- Castro, D., Slane, P., Patnaude, D. J., & Ellison, D. C. 2011, ApJ, 734, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Celli, S., Morlino, G., Gabici, S., & Aharonian, F. A. 2019a, MNRAS, 490, 4317 [CrossRef] [Google Scholar]
- Celli, S., Morlino, G., Gabici, S., & Aharonian, F. A. 2019b, MNRAS, 487, 3199 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1977, ARA&A, 15, 175 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, M., Blasi, P., & Amato, E. 2016, Phys. Rev. D, 94, 083003 [CrossRef] [Google Scholar]
- Douglas, J. N., Bash, F. N., Bozyan, F. A., Torrence, G. W., & Wolfe, C. 1996, AJ, 111, 1945 [Google Scholar]
- Drury, L. O. 1983, Rep. Progr. Phys., 46, 973 [Google Scholar]
- Drury, L. O., & Downes, T. P. 2012, MNRAS, 427, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Evoli, C., Aloisio, R., & Blasi, P. 2019, Phys. Rev. D, 99, 103023 [CrossRef] [Google Scholar]
- Fraija, N., & Araya, M. 2016, ApJ, 826, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Goss, W. M., Reynoso, E. M., et al. 1996, AJ, 111, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Fruck, C., Gaug, M., Zanin, R., et al. 2014, in Proceedings, 33rd International Cosmic Ray Conference (ICRC2013): Rio de Janeiro, Brazil, July 2-9, 2013, 1054 [Google Scholar]
- Fukui, Y., & Tatematsu, K. 1988, in International Astronomical Union Colloquium, 101, 261 [CrossRef] [Google Scholar]
- Gabici, S., & Aharonian, F. A. 2014, MNRAS, 445, L70 [NASA ADS] [CrossRef] [Google Scholar]
- Gabici, S., Aharonian, F. A., & Casanova, S. 2009, MNRAS, 396, 1629 [Google Scholar]
- Gabici, S., Evoli, C., Gaggero, D., et al. 2019, Int. J. Mod. Phys. D, 28, 1930022 [CrossRef] [Google Scholar]
- Gaia Collaboration. 2018, VizieR Online Data Catalog: I/345 [Google Scholar]
- Gao, X. Y., Han, J. L., Reich, W., et al. 2011, A&A, 529, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gosachinskij, I. V. 2001, Astron. Lett., 27, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Hanabata, Y., Katagiri, H., Hewitt, J. W., et al. 2014, ApJ, 786, 145 [Google Scholar]
- Helene, O. 1983, Nucl. Instrum. Methods Phys. Res., 212, 319 [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Higgs, L. A., Landecker, T. L., & Roger, R. S. 1977, AJ, 82, 718 [Google Scholar]
- Higgs, L. A., Landecker, T. L., & Roger, R. S. 1983a, AJ, 88, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Higgs, L. A., Landecker, T. L., & Seward, F. D. 1983b, in Supernova Remnants and their X-ray Emission, 101, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffleit, D. & Warren, W. H., Jr., 1995, VizieR Online Data Catalog: V/50 [Google Scholar]
- Hui, C. Y., Seo, K. A., Lin, L. C. C., et al. 2015, ApJ, 799, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, T., Yamazaki, R., ichiro Inutsuka, S., & Fukui, Y. 2011, ApJ, 744, 71 [Google Scholar]
- Kafexhiu, E., Aharonian, F., Taylor, A. M., & Vila, G. S. 2014, Phys. Rev. D, 90, 123014 [Google Scholar]
- Kothes, R., Fedotov, K., Foster, T. J., & Uyanıker, B. 2006, A&A, 457, 1081 [CrossRef] [EDP Sciences] [Google Scholar]
- Ladouceur, Y., & Pineault, S. 2008, A&A, 490, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lande, J., Ackermann, M., Allafort, A., et al. 2012, ApJ, 756, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Landecker, T. L., Roger, R. S., & Higgs, L. A. 1980, A&AS, 39, 133 [Google Scholar]
- Leahy, D. A., Green, K., & Ranasinghe, S. 2013, MNRAS, 436, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, H. O., & Thaddeus, P. 1992, ApJS, 81, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Lozinskaya, T. A., Pravdikova, V. V., & Finoguenov, A. V. 2000, Astron. Lett., 26, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., Diamond, P. H., Sagdeev, R. Z., Aharonian, F. A., & Moskalenko, I. V. 2013, ApJ, 768, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [Google Scholar]
- Mavromatakis, F. 2003, A&A, 408, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morlino, G., & Caprioli, D. 2012, A&A, 538, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nava, L., & Gabici, S. 2013, MNRAS, 429, 1643 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Gabici, S., Marcowith, A., Morlino, G., & Ptuskin, V. S. 2016, MNRAS, 461, 3552 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., Murase, K., & Yamazaki, R. 2010, A&A, 513, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, J. P., & McKee, C. F. 1988, Rev. Mod. Phys., 60, 1 [Google Scholar]
- Park, J., Caprioli, D., & Spitkovsky, A. 2015, Phys. Rev. Lett., 114, 085003 [NASA ADS] [CrossRef] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2005, A&A, 429, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rolke, W. A., López, A. M., & Conrad, J. 2005, Nucl. Instrum. Methods Phys. Res. A, 551, 493 [Google Scholar]
- Saken, J. M., Fesen, R. A., & Shull, J. M. 1992, ApJS, 81, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [Google Scholar]
- Schure, K. M., Bell, A. R., O’C Drury, L., & Bykov, A. M. 2012, Space Sci. Rev., 173, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (Academic Press) [Google Scholar]
- Slane, P., Bykov, A., Ellison, D. C., Dubner, G., & Castro, D. 2015, Space Sci. Rev., 188, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Gibson, S. J., Peracaula, M., et al. 2003, AJ, 125, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R., Jóhannesson, G., Moskalenko, I. V., et al. 2011, ApJ, 729, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Takahashi, T., Aharonian, F. A., & Mattox, J. R. 2002, ApJ, 571, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Funk, S., Katagiri, H., et al. 2012, ApJ, 749, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Völk, H. J., Berezhko, E. G., & Ksenofontov, L. T. 2005, A&A, 433, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vovk, I., Strzys, M., & Fruck, C. 2018, A&A, 619, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weinstein, A. 2015, in European Physical Journal Web of Conferences, 105, 04005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wendker, H. J., Higgs, L. A., & Landecker, T. L. 1991, A&A, 241, 551 [Google Scholar]
- Wilks, S. S. 1938, Ann. Math. Stat., 9, 60 [Google Scholar]
- Wood, M., Caputo, R., Charles, E., et al. 2017, Int. Cosmic Ray Conf., 35, 824 [CrossRef] [Google Scholar]
- Yuan, Q., Lin, S.-J., Fang, K., & Bi, X.-J. 2017, Phys. Rev. D, 95, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Zanin, R., Carmona, E., Sitarek, J., Colin, P., & Frantzen, K. 2013, in Proc. of the 33st International Cosmic Ray Conference, Rio de Janeiro, Brasil [Google Scholar]
- Zhang, X., Zheng, Y., Landecker, T. L., & Higgs, L. A. 1997, A&A, 324, 641 [NASA ADS] [Google Scholar]
Not to be confused with the significance estimates based on likelihood ratios obtained with SkyPrism and listed in Table 3.
This is true for rigidities ≳200 GV, while at lower energies the CR spectrum suggests a different scaling (Blasi et al. 2012).
All Tables
Results of the spectral analysis from the Fermi-LAT and MAGIC analysis for each source component.
Systematic uncertainties for the spectral analysis of the Fermi-LAT and MAGIC data and each source component. The uncertainties are sorted according to their origin from either the IRFs of the detectors or the uncertainties on the shape of the background model and exposure for MAGIC and the IEMs for Fermi-LAT.
All Figures
 |
Fig. 1 Sky map in units of relative flux (excess over background) of the γ Cygni region as observed by MAGIC E > 250 GeV. Regions exceeding the 3σ (5σ) local, pre-trial TS significance for a point source are indicated by red (yellow) contours. The cyan line is the 400 K contour of the 408 MHz observation by the CGPS. The white diamond gives the position of the PSR 2021+4026, the green X the position of VER J2019+407, and the yellow star the position of Sadr (γ Cyg star; mag = 2.2). The inlay in the lower left corner shows the 39% and 68% containment contours of the MAGIC PSF. |
| In the text | |
 |
Fig. 2 Energy-dependent morphology of the γ Cygni SNR. Upper left: Fermi-LAT count map between 15 and 60 GeV smoothed with a Gaussian kernel (σ = 0°.75) and 3 σ and 5 σ contours of a point source search. The white line is the 400 K contour of the 408 MHz observation by the CGPS. The white diamond identifies the position of PSR 2021+4026. Upper right: same as upper left, but in the range from 60 to 250 GeV. Lower left: Relative flux map observed by MAGIC at 250–500 GeV together with 3 σ and 5 σ point source significance contours. The same radio contours as in upper panels are displayed in cyan. Lower right: same as lower left, but in the energy range from 500 GeV to 2.5 TeV. |
| In the text | |
 |
Fig. 3 Fermi-LAT TS map for a point source search on top of the background sources specified in Sect. 2.2 and including the radio-based disc model. Regions exceeding the 3σ (5σ) local, pre-trial TS significance for a point source are indicated by red (yellow) contours. The white line is the 400 K contour of the 408 MHz observation by the CGPS. The white diamond gives the position of PSRJ2021+4026. |
| In the text | |
 |
Fig. 4 Left: sketch of the spatial model used in the likelihood of the Fermi-LAT and MAGIC data analysis. The blue circle indicates the position and extension of the disc modelling the SNR shell, the green circle gives the position and 68% containment radius of a Gaussian model of MAGIC J2019+408, and the orange annular sector was used for the arc region. The red radio contours and the position of PSR J2021+4026 (white diamond) are shown for reference. Right: same as left, but with the second Gaussian as spatial model for the arc region. |
| In the text | |
 |
Fig. 5 Distribution of escaping particles at one arbitrary fixed momentum, p* = 10 TeV, as a function of the radial coordinate normalised to Resc(p*) = 13 pc. Different lines refer to different times in units of tesc(p*) = 4000 yr, as labelled, and the vertical dashed lines correspond to the shock positions at those times. We assume Dout = DGal/100, δ = 2.2, and pM = 100 TeV. |
| In the text | |
 |
Fig. 6 Distribution of escaping particles at p* = 10 TeV/c and t = tSNR as a function of the radial coordinate normalised to Resc(p*) = 13 pc. Different lines refer to different values of the diffusion coefficient, as labelled. The vertical lines correspond to the shock position (dashed) and to the arc external edge (dot-dashed) as observed now. The remaining parameters are the same as in Fig. 5. |
| In the text | |
 |
Fig. 7 Computed γ-ray flux due to π0 decay from the SNR interior (blue solid line) and from the arc region (orange dashed line) based on our model compared against data points from our Fermi-LAT (diamonds) and MAGIC (squares) analysis. |
| In the text | |
 |
Fig. 8 HI emission at velocities between −19 km s−1 and −11 km s−1 measured by the CGPS. The red and yellow lines show the 3 σ and 5 σ significance contours of the γ-ray emission observed by MAGIC (Fig. 1). The cyan lines are the 400 K contours of the 408 MHz continuum emission from the CGPS. The white diamond gives the position of PSRJ2021+4026. |
| In the text | |
 |
Fig. 9 Computed γ-ray flux due to π0 decay from MAGIC J2019+408 based on our model compared against data points from our Fermi-LAT (diamonds) and the MAGIC (squares) analysis. The spectrum (green solid line) is modelled as the sum of emission from the remnant interior (blue dash-dotted line) and exterior (orange dashed line). |
| In the text | |
 |
Fig. 10 Left: Average of CO J = 1 ← 0 emission between 2 km s−1 and 10 km s−1 based on data from Leung & Thaddeus (1992) interpolated on the coordinate grid of the MAGIC data. The cyan contours are the 400 K contour of the 408 MHz observation by the CGPS and the red and yellow contours are the 3 σ and 5 σ significance contours of the emission seen by MAGIC. The white diamond gives the position of the PSR J2021+4026. Right: 100 µm intensity map based on data from Schlegel et al. (1998) interpolated on the coordinate grid of the MAGIC data. Contours and symbol are the same as in the left panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![${\rm{TS = 2}}\left[ {{\rm{In}}\left( {{{\cal L}_1}} \right) - {\rm{In}}\left( {{{\cal L}_0}} \right)} \right],$](/articles/aa/full_html/2023/02/aa38748-20/aa38748-20-eq2.png)
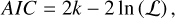
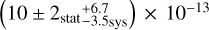

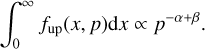
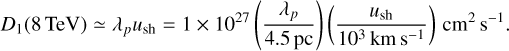
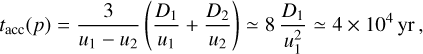
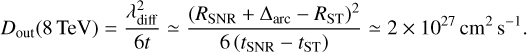
![${{\partial f} \over {\partial t}} + u{{\partial f} \over {\partial r}} = {1 \over {{r^2}}}{\partial \over {\partial r}}\left[ {{r^2}D{{\partial f} \over {\partial r}}} \right] + {1 \over {{r^2}}}{{\partial \left( {{r^2}u} \right)} \over {\partial r}}{{p\,\partial f} \over {3\,\partial p}},$](/articles/aa/full_html/2023/02/aa38748-20/aa38748-20-eq26.png)
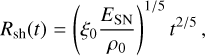
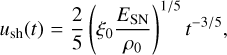
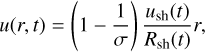
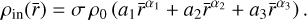
![${f_0}\left( {p,t} \right) = {{3{\xi _{{\rm{CR}}}}{u_{{\rm{sh}}}}{{\left( t \right)}^2}{\rho _0}} \over {4\pi c{{\left( {{m_p}c} \right)}^4} \wedge \left( {{p_{\max ,0}}\left( t \right)} \right)}}{\left( {{p \over {{m_p}c}}} \right)^{ - \alpha }}\Theta \left[ {{p_{\max ,0}}\left( t \right) - p} \right],$](/articles/aa/full_html/2023/02/aa38748-20/aa38748-20-eq32.png)
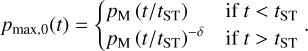
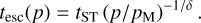
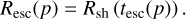
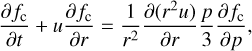
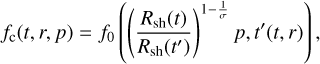
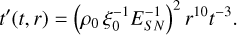
![$\matrix{{{f_c}\left( {t,r,p} \right) = {f_o}\left( {p,t} \right){{\left( {{{t'} \over t}} \right)}^{{{{{2\alpha \left( {\sigma - 1} \right)} \mathord{\left/{\vphantom {{2\alpha \left( {\sigma - 1} \right)} {5\sigma - 6}}} \right.\kern-\nulldelimiterspace} {5\sigma - 6}}} \mathord{\left/{\vphantom {{{{2\alpha \left( {\sigma - 1} \right)} \mathord{\left/{\vphantom {{2\alpha \left( {\sigma - 1} \right)} {5\sigma - 6}}} \right.\kern-\nulldelimiterspace} {5\sigma - 6}}} 5}} \right.\kern-\nulldelimiterspace} 5}}}} & {\Theta \left[ {{p_{\max }}\left( {t,r} \right) - p} \right].} \cr } $](/articles/aa/full_html/2023/02/aa38748-20/aa38748-20-eq40.png)
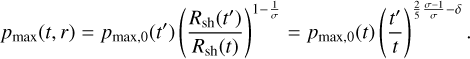
![${{\partial {f_{{\rm{esc}}}}} \over {\partial t}} = {1 \over {{r^2}}}{\partial \over {\partial r}}\left[ {{r^2}D{{\partial {f_{{\rm{esc}}}}} \over {\partial r}}} \right].$](/articles/aa/full_html/2023/02/aa38748-20/aa38748-20-eq42.png)
![$\matrix{{{f_{{\rm{esc}}}}\left( {t,r,p} \right) = {{{f_{c0}}\left( p \right)} \over 2}\Theta \left[ {t - {t_{{\rm{esc}}}}\left( p \right)} \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\{ {{{{R_d}} \over {\sqrt \pi r}}\left( {{e^{ - R_ + ^2}} - {e^{ - R_ - ^2}}} \right) + {\rm{Erf}}\left( {{R_ + }} \right) + {\rm{Erf}}\left( {{R_ - }} \right)} \right\},} \hfill \cr } $](/articles/aa/full_html/2023/02/aa38748-20/aa38748-20-eq43.png)