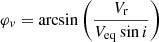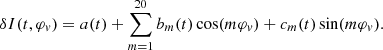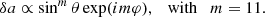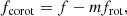| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202245017 | |
| Published online | 17 January 2023 | |
Spectroscopic detection of Altair’s non-radial pulsations⋆
1
IRAP, Université de Toulouse, CNRS, UPS, CNES, 14 avenue Édouard Belin, 31400 Toulouse, France
e-mail: michel.rieutord@irap.omp.eu
2
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris-Diderot, Sorbonne Paris-Cité, 5 place Jules Janssen, 92195 Meudon, France
3
Departamento de Física Teórica y del Cosmos, Universidad de Granada, Campus de Fuentenueva s/n, 18071 Granada, Spain
4
Université Côte-d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Bd de l’Observatoire, CS 34229, 06304 Nice Cedex 4, France
Received:
19
September
2022
Accepted:
26
October
2022
Context. Rapid rotation is a common feature of early-type stars but remains a challenge for models. Nevertheless, we need to understand its effect on stellar evolution in order to interpret the observed properties of numerous stars.
Aims. We wish to provide more observational constraints on the properties of fast rotating stars, especially their oscillation modes.
Methods. We focus on the nearby star Altair which is known to be a very rapidly rotating star with an equatorial velocity recently estimated at 313 km s−1. We observed this star with the high-resolution spectropolarimeter Neo-Narval over six nights, with one night of interruption, in September 2020.
Results. We detect significant line profile variations on the mean line profile of the spectra. Their time-frequency analysis shows that these variations are induced by gravito-inertial waves propagating at Altair’s surface with azimuthal wavenumbers of the order m = 10 − 15. With a preliminary computation of the eigenspectrum using the most recent concordance model of Altair we carried out a first modelling of the observed waves.
Conclusions. Altair was known as the brightest δ Scuti star. We now see that it is the brightest hybrid oscillating star with gravito-inertial waves and acoustic waves being excited. Clearly, more observations and more advanced models are needed to explain the observations in greater details.
Key words: stars: rotation / stars: early-type
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
At a distance of 5.13 pc, Altair (α Aql) is the closest early-type (A7V) fast rotating star to the Sun. As such, Altair has been intensively observed in interferometry (van Belle et al. 2001; Domiciano de Souza et al. 2005; Peterson et al. 2006; Monnier et al. 2007; Bouchaud et al. 2020; Spalding et al. 2022). An important result of interferometric observations is the determination of the inclination of Altair’s rotation axis on the line of sight. The most recent value is i = 50.7 ± 1.2° (Bouchaud et al. 2020). Since spectroscopy indicates that v sin i ≃ 227 ± 11 (Reiners & Royer 2004), 231 km s−1 (Takeda 2020) and 242 km s−1 (Bouchaud et al. 2020), it turns out that Altair’s equatorial velocity is likely over 300 km s−1. This means Altair is rotating at 74% of its critical angular velocity. As a consequence it is strongly flattened by the centrifugal force, making its equatorial radius 22% larger than the polar one. Hence, it is no surprise that such a star cannot be modelled with spherically symmetric models as shown by the fact that its age has not been determined by 1D models. Indeed, using such models Suárez et al. (2005) indicate a range of 225−775 Myr, while Domiciano de Souza et al. (2005) found another range of 1.2−1.4 Gyr. Thus, Altair is the star to be used for testing 2D models such as ESTER1 models (Espinosa Lara & Rieutord 2013; Rieutord et al. 2016). This test was the main objective of Bouchaud et al. (2020), who devised the first concordance model of Altair. Bouchaud et al. (2020) managed to match the interferometric, spectroscopic, and asteroseismic observations with a single 2D model. That model indicates that Altair is 100 Myr old and thus barely off the zero-age main sequence, as suspected by Peterson et al. (2006). In their 2D modelling, Bouchaud et al. (2020) show that asteroseismology was key to reducing some degeneracy on the mass of Altair. Altair is indeed a δ Scuti star, whose oscillations were first detected by Buzasi et al. (2005). Recently, Le Dizès et al. (2021) confirmed these δ Scuti oscillations and slightly increased the number of detected frequencies, thanks to the analysis of Microvariability and Oscillations of STars (MOST) satellite data (Walker et al. 2003). Le Dizès et al. (2021) also show the variability of the mode amplitudes and the probable coupling of the modes with thin convective layers not far below Altair’s surface.
In the present work we describe the first detection of non-radial pulsations of Altair with high-resolution spectroscopy using the 2-m Bernard Lyot Telescope at the Pic-du-Midi. In the past, similar detections have only been made on very few rotating stars, for example γ Bootis with v sin i ≃ 127 km s−1 (Ventura et al. 2007), or on spectroscopic binaries such as RS Chamaeleontis (Böhm et al. 2009). However, Altair is the star with the largest v sin i where such oscillations are detected. Compared to photometric observations, spectroscopic ones give an indication of the mode azimuthal wavenumber, which helps with mode identification and further constraining the fundamental parameters.
The paper is organised as follows: We first give a brief description of the data we use and their reduction (Sect. 2). This is followed by their analysis (Sect. 3) and a short discussion of the possible identification of modes (Sect. 4). We then revert to 2D models and discuss the comparison between data and model predictions (Sect. 5). Conclusions follow.
2. Observations and data reduction
Altair was observed over six nights between 2 September and 8 September 2020 at the Pic-du-Midi with the spectropolarimeter Neo-Narval (see López Ariste et al. 2022, for a presentation of the instrument) at the Cassegrain focus of the Bernard Lyot Telescope. The light of Altair was sampled approximatively every 3 min and a total of 643 spectra were obtained (see Table 1 for details). The duty cycle of these observations is, however, quite low at 0.21.
Observations dates and the average period of time sampling, ⟨δt⟩.
From the circular and linear spectropolarimetric data collected during this run, only the intensity signal was used. The data reduction was performed through the automated pipeline of the instrument, providing us with spectra covering the whole optical domain (380 to 1050 nm) at a resolving power of around 65 000. The peak signal-to-noise ratio, defined per unit of spectral resolution, is typically close to 1400. This latter value is reached at wavelengths close to 705 nm.
All observations were processed with the least-square deconvolution (LSD) method (Donati et al. 1997; Kochukhov et al. 2010) to extract a mean pseudo-line profile from every spectra. A list of around 6300 photospheric lines deeper than 1% of the continuum was extracted from the Vienna Atomic Line Database (VALD, see Kupka et al. 1999) without any selection of chemical species and assuming a surface temperature equal to 7500 K. According to Monnier et al. (2007), this temperature is representative of intermediate latitudes of this oblate star. The intensity signatures reported hereafter are qualitatively unchanged when other line masks with temperatures chosen to match lower or higher latitudes are adopted. The LSD profile example shown in Fig. 1 (top) is dominated by rotational broadening. Once an averaged profile (of all observations collected during the same night) is subtracted, bumps and dips become visible within line profiles (Fig. 1, bottom).
 |
Fig. 1. Upper panel: example of an LSD profile of Altair’s spectrum. Bottom panel: same LSD profile after subtraction of the average of all available profiles of the same night. |
3. Data analysis
Figure 2 illustrates the way we see the Doppler shift of Altair according to the Bouchaud et al. (2020) model. This model also gives an equatorial rotation frequency of 3.08 c/d (Le Dizès et al. 2021), which we adopted when moving from the observer’s frame to the co-rotating frame. Any feature moving in the line profile may or may not move in longitude in the co-rotating frame.
 |
Fig. 2. Rotational velocity field of Altair projected along the line of sight according to the Bouchaud et al. (2020) model. Velocities are in km s−1. The equator and north pole are marked. |
Relative amplitudes of the detected features are typically of the order of 10−3 in intensity (Fig. 1, bottom) and look like wave trains propagating in the prograde direction as shown in the left plots of Fig. 3 for each night. Typically, individual wave trains remain visible for roughly two hours.
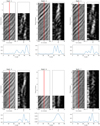 |
Fig. 3. Global view of the relative fluctuations in the mean line profile for each of the six nights of observation. For each night we show in the top left panel the signal as a function of time and radial velocity in km s−1. In the top-right panel we show the Lomb-Scargle periodogram of the line profile fluctuations in (virtual) longitude as a function of time and the azimuthal wavenumber m. The bottom plot shows a Lomb-Scargle periodogram of the time variations of the intensity in the eight pixels at the line centre that are marked by the red lines in the top-left panels. |
We assumed that these waves only propagate in longitude and that they are of the form I(θ)exp(imφ − iωt), where (θ, φ) are the spherical angles of a point at Altair’s surface. If perturbations are concentrated around Altair’s equator we can easily relate the radial velocity, Vr, at which the perturbation occurs and the longitude as
where Veq is the equatorial velocity and i is the angle between the line of sight and the rotation axis. Of course, Vr is corrected from the radial velocity of Altair. We call φv the virtual longitude to stress the fact that several longitudes actually contribute at a given radial velocity as is clear from the projected map shown in Fig. 2.
It is nevertheless interesting to see the azimuthal wavenumber, m, associated with the perturbations of the line if we replace the radial velocity coordinate by the virtual longitude. Hence, we get information on the apparent m values contained in the signal (e.g. Böhm et al. 2009). To this end, we computed a Lomb-Scargle periodogram of the line profile fluctuations (one is shown in Fig. 1, bottom) using the virtual longitude as the time analogue2. We chose the Lomb-Scargle periodogram instead of a simple Fourier transform since the data points are not regularly spaced in longitude (see below). This computation allows us to extract the azimuthal wavenumbers contained in the signal as a function of time, as shown in Fig. 3 (right plots). These plots clearly show that wavenumbers around m = 10 are conspicuously detected. We also note that wavenumbers change with time. This may be a consequence of beating waves or some non-linear evolution.
In addition to the foregoing azimuthal analysis of the line profile fluctuations, we can also compute a Lomb-Scargle periodogram at a given virtual longitude. We thus calculated this periodogram by selecting eight pixels around the line centre and thus exhibit a few frequencies for each night. The corresponding plots are shown in Fig. 3 (bottom) for each night. There we clearly see that all detected frequencies are between ∼20 and ∼50 cycles/day (c/d).
The next step was to relate the frequencies and the azimuthal wavenumbers, m. For that purpose we first fitted each line profile fluctuation with a limited Fourier series, namely
We then computed the Lomb-Scargle time periodogram of each coefficient, bm(t) and cm(t), for all the chosen wavenumbers. We thus derived the transforms 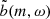 and
and 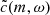 , from which we computed the spectral power
, from which we computed the spectral power 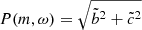 . As a result, we obtain an m − ω diagram analogous to the famous k − ω diagram of solar eigenmodes (e.g. Gonzalez Hernandez et al. 1998; Gizon et al. 2010). This diagram, which shows P(m, ω), is displayed for each night in Fig. 4.
. As a result, we obtain an m − ω diagram analogous to the famous k − ω diagram of solar eigenmodes (e.g. Gonzalez Hernandez et al. 1998; Gizon et al. 2010). This diagram, which shows P(m, ω), is displayed for each night in Fig. 4.
 |
Fig. 4. m − ω diagram for the six nights, showing the spectral power as a function of m and frequency in the observer’s frame. The solid blue line shows the time frequency of a standing wave in the co-rotating frame characterised by wavenumber m. Modes above that line are prograde, and modes below are retrograde. The two dashed blue lines delineate the inertial frequency band. |
As can be seen, spatial frequencies range from m = 5 to m ≃ 18 while time-frequencies stay in between 20 c/d and 50 c/d. Each diagram shows the frequency of a standing wave of azimuthal wavenumber m in the co-rotating frame, assuming a rotation period of 8 h deduced from the model of Altair by Bouchaud et al. (2020). We note that most of the modes are above this frequency, which shows that they are prograde modes in the co-rotating frame. Moreover, they are mostly in the inertial frequency band −2frot ≤ fcorot ≤ 2frot or slightly above; this indicates their nature, namely inertial or gravito-inertial modes (e.g. Rieutord & Valdettaro 1997; Dintrans et al. 1999; Dintrans & Rieutord 2000).
4. Mode detection and identification
The foregoing raw analysis shows that a set of waves are excited. To proceed towards their identification, we first tried to identify the azimuthal wavenumbers of their longitude dependence, namely their exp(imφ) dependence. In Fig. 5 (top), we show the spectral perturbation generated by a purely sectoral mode, propagating over the Bouchaud et al. (2020) model, which has a latitude-longitude amplitude fluctuation described by
 |
Fig. 5. Top: simulation of the line profile perturbation induced by a purely sectoral mode with m = 11 (amplitude is arbitrary). Bottom: fourier spectrum of the signal and the Lomb-Scargle periodogram. |
Figure 5 shows that the signal is neither periodic nor evenly sampled in longitude. Hence, the Fourier transform struggles to recover the right m. Figure 5 also shows that the Lomb-Scargle periodogram is more appropriate than the Fourier spectrum for recovering the actual m of the signal.
We then computed the Lomb-Scargle periodogram of bm(t) and cm(t), combining the data from each night. As expected from the m − ω diagram (Fig. 4), we detect the same frequency for several values of m, but with different amplitudes. Figure 6 summarises the results and shows the amplitude as a function of m for each given frequency. It is clear that the most prominent wave oscillates at 38.14 c/d and seems to be associated with an m = 11 wavenumber. In Table 2, we list the frequencies that have been unambiguously detected. We also give the amplitude of the signal in ppm and the most probable azimuthal wavenumber, m. As shown by Fig. 6, the association between frequency and wavenumber is not always clear.
 |
Fig. 6. Amplitude (in ppm) of the waves as a function of the azimuthal wavenumber used to do the projection of the Doppler signal. Waves are characterised by their frequency, f, given in c/d. |
Detected oscillation frequencies and their most probable azimuthal wavenumber (m).
Three of the detected frequencies (f1, f2, f5) are clearly in the inertial frequency band, since they verify fcorot ≤ 2frot, if we take frot = 3.08 c/d (see Sect. 3). The four other frequencies are also low frequencies only slightly above the inertial band. The modes associated with these frequencies are therefore gravito-inertial modes which may be either inertial modes (restored by the Coriolis force) perturbed by a stable stratification or reciprocally, gravity modes perturbed by rotation (see Dintrans et al. 1999, for canonical examples).
5. The word of models
5.1. Preliminary results
To gain further insight into the waves that are seen in the present spectroscopic data, we next focused on the concordance model of Altair derived by Bouchaud et al. (2020). We recall in Table 3 the fundamental parameters of this model that match the constraints derived from interferometric, spectroscopic and seismic data. The seismic data are frequencies obtained from WIRE photometry by Buzasi et al. (2005).
Fundamental parameters of an ESTER model that match the observational constraints on Altair derived by Bouchaud et al. (2020).
To further constrain the seismological properties of Altair, we computed some eigenmodes of the concordance model with the TOP code (Reese et al. 2021), which can handle ESTER 2D models. We naturally focused on the observed frequencies; more precisely, we scanned the frequency band f ± 0.05 c/d of each frequency listed in Table 2 for the three values of m around the most probable one. Hence, for the most prominent frequency, at 38.14 c/d, we investigated the frequency band [38.09, 38.19] c/d for azimuthal wavenumbers m = 10, 11, 12. We show in Fig. 7 a view of a mode that may give the signal observed at 38.14 c/d. Shifting this frequency in the co-rotating frame, namely
 |
Fig. 7. Surface amplitude (left) and meridional cut of the kinetic energy density (right) of a gravito-inertial mode that may give a signal at f = 38.14 c/d. The bottom-right plot is a zoomed-in view of the surface layers, and the dashed line shows the T = 50 000 K isotherm, around which the second ionisation of helium takes place. The depth is scaled by the polar radius of the model. |
with frot = 3.08 c/d, we find that it either belongs to the inertial frequency band, if m = 11 or 12, or is just above it if m = 10. As shown in Fig. 7, the amplitude of such a mode is only significant near the surface. The meridional map of the Brunt–Väisälä frequency (Fig. 8) shows that such modes actually propagate over two convectively unstable layers that sandwich a stable one. The deeper unstable layer is associated with the second ionisation of helium, which is the driver of the kappa mechanism in δ Scuti stars (Baglin et al. 1973; Balona et al. 2015). The 50 000 K isotherm, around which the second ionisation of helium takes place, is depicted in Fig. 7 (bottom right) and Fig. 8 (bottom), which show that this mode may be destabilised by the kappa mechanism.
 |
Fig. 8. Meridional section of the concordance model of Altair (e.g. Bouchaud et al. 2020) showing the Brunt–Väisälä frequency. Units on the colour bar are cycle/day. Negative values show the convectively unstable regions. The lower plot gives a zoomed-in view of the surface layers and the dashed line shows the T = 50 000 K isotherm around which the second ionisation of helium takes place. Depth is scaled by the polar radius of the model. |
This mode may be used to constrain the differential rotation of the star in the 1% depth surface layers. The knowledge of this differential rotation, close to the surface, will help in modelling a dynamo, which may be at the origin of Altair’s X-ray activity (Robrade & Schmitt 2009).
5.2. Discussion
The mode shown in Fig. 7 has been selected because of its (presumably) high visibility but we still do not know whether or not it is stable. Indeed, the foregoing computation neglected any non-adiabatic effect since preliminary non-adiabatic calculations showed inconclusive results for many reasons, which we discuss now.
Indeed, gravito-inertial modes form a dense spectrum in the adiabatic limit. Namely, any frequency below 2frot is as close as we wish to a mode frequency (e.g. Dintrans et al. 1999). Moreover, the modes contain singularities, which appear as shear layers in the eigenfunctions (e.g. Dintrans et al. 1999; Rieutord et al. 2001; Rieutord & Valdettaro 2018). This makes the computation of gravito-inertial modes in a stellar model quite difficult. In particular, we were unable to reliably compute the growth or the damping rates of the eigenmodes with frequencies in the range of the observed ones (e.g. Table 2).
Even if we ignore the stability question, there is still the issue of the density of frequencies in the spectrum. The observed frequencies listed in Table 2 have a limited precision of 0.05 c/d due to the short length of the time series. Our calculations show that in a frequency box of size 0.1 c/d, a dozen eigenmodes may be found if we only consider the least damped modes. Obviously, long time series will be needed to reduce this uncertainty.
On the theoretical side, the instability that drives the modes may not be of the usual nature, namely an exponential growth that is limited by a non-linear coupling with stable modes. Here, the spectral density of modes reveals the non-normality of the differential operator that governs the free oscillations. It allows the possibility of algebraic growth of perturbations (Schmid 2007; Rieutord 2015). In such a case the observed waves are not eigenmodes, but combinations of several eigenmodes.
The foregoing remarks underline the point that deciphering the wave frequencies at the surface of Altair, which we will attempt in future work, will be challenging.
On the observational side, it is clear that long time series are needed to narrow the error box on frequencies. They will thus be of great help in identifying the possible modes or quasi-modes that are observed.
6. Conclusions
In this paper we have presented the first spectroscopic detection of waves at the surface of Altair, a rapidly rotating star with an equatorial velocity likely over 300 km s−1. We have shown that the observed waves are in or near the frequency band [ − 2frot, 2frot] in the frame co-rotating with the star. They are thus identified as inertial or gravito-inertial waves. The difference between inertial waves and gravito-inertial ones comes from the influence of the stable stratification of the fluid. Pure inertial waves are restored only by the Coriolis force and, in stars, appear in their convection zone (e.g. the recent detection of these waves in the Sun by Gizon et al. 2021), while gravito-inertial waves are restored by both buoyancy and the Coriolis force. In Altair, thin convective layers exist close to the surface and may be the seat of pure inertial waves, which may drive a signature at the surface. An identification of observed waves with gravito-inertial waves is, however, more likely since convective layers are thin and separated by a radiative one. Finally, we note that the observed waves are characterised by rather high azimuthal wavenumbers, and propagate in the prograde direction. Their amplitude, in intensity, is of the order of 10−3.
Altair was known as the ‘brightest δ Scuti’ (Buzasi et al. 2005). We now see that its oscillation spectrum includes not only acoustic modes but also gravito-inertial waves. Low-frequency oscillations have actually already been detected by Buzasi et al. (2005) and Le Dizès et al. (2021) in photometric data; however, without constraints on the wavenumbers it has been difficult to assign them a definite category (gravito-inertial, pure inertial, or even acoustic) because of the high rotation frequency (∼3 c/d) and a possible non-axisymmetric nature. Hence, Altair now appears to be a hybrid oscillator, but its fast rotation still sets it apart from stars that show the hybrid state of δ Scuti and γ Doradus stars.
Our failure to more precisely identify the observed frequencies, using the best model of Altair (Bouchaud et al. 2020), shows that such an identification is difficult due to the spectral density of modes in or near the inertial frequency range. Dedicated work is therefore required to further progress in the interpretation of the observed frequencies, all the more that gravito-inertial modes are controlled by a non-normal differential operator in the adiabatic limit. This implies that the growth of the mode may be algebraic, as in shear instabilities, and may excite a wide or ever-changing oscillation spectrum (Schmid 2007).
On the observational side, what is needed is either longer time series, which will provide more precise frequency values, or more monitoring of the oscillations that have already been detected. Moreover, it will be very interesting to spectroscopically observe other fast rotators similar to Altair to see if such waves are also excited in stars with different fundamental parameters. The stars α Ophiuchi (Ras Alhague) and α Cephei (Alderamin) are very good targets for such investigations because of their brightness, but the recent work of Ma et al. (2022) shows that Altair may have numerous sisters.
ESTER (Evolution STEllaire en Rotation) is a project aimed at describing stellar evolution of rotating stars up to the breakup limit. It is based on the public code ESTER that presently computes the steady state of early-type rotating stars in two dimensions. The code is freely available at http://ester-project.github.io/ester/
Acknowledgments
M.R. would like to thank S. Charpinet for enlighting discussions on the analysis of the time series. He also acknowledges the support of the French Agence Nationale de la Recherche (ANR), under grant ESRR (ANR-16-CE31-0007-01). G.M.M. acknowledges support by “Contribution of the UGR to the PLATO2.0 space mission. Phases C/D-1”,1032 funded by MCNI/AEI/PID2019-107061GB-C64. Computations of Altair’s models and eigenfrequencies have been possible thanks to HPC resources from CALMIP supercomputing center (Grant 2022-P0107).
References
- Baglin, A., Breger, M., Chevalier, C., et al. 1973, A&A, 23, 221 [NASA ADS] [Google Scholar]
- Balona, L. A., Daszyńska-Daszkiewicz, J., & Pamyatnykh, A. A. 2015, MNRAS, 452, 3073 [Google Scholar]
- Böhm, T., Zima, W., Catala, C., et al. 2009, A&A, 497, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchaud, K., Domiciano de Souza, A., Rieutord, M., Reese, D. R., & Kervella, P. 2020, A&A, 633, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buzasi, D. L., Bruntt, H., Bedding, T. R., et al. 2005, ApJ, 619, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Dintrans, B., & Rieutord, M. 2000, A&A, 354, 86 [NASA ADS] [Google Scholar]
- Dintrans, B., Rieutord, M., & Valdettaro, L. 1999, J. Fluid Mech., 398, 271 [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2005, A&A, 442, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizon, L., Birch, A. C., & Spruit, H. C. 2010, ARA&A, 48, 289 [Google Scholar]
- Gizon, L., Cameron, R. H., Bekki, Y., et al. 2021, A&A, 652, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez Hernandez, I., Patron, J., Chou, D. Y., & TON Team 1998, ApJ, 501, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., Makaganiuk, V., & Piskunov, N. 2010, A&A, 524, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Dizès, C., Rieutord, M., & Charpinet, S. 2021, A&A, 653, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López Ariste, A., Georgiev, S., Mathias, P., et al. 2022, A&A, 661, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, S., Esamdin, A., García Hernández, A., et al. 2022, ApJ, 937, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J. D., Zhao, M., Pedretti, E., et al. 2007, Science, 317, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, D., Hummel, C., Pauls, T., et al. 2006, ApJ, 636, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Reese, D. R., Mirouh, G. M., Espinosa Lara, F., Rieutord, M., & Putigny, B. 2021, A&A, 645, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiners, A., & Royer, F. 2004, A&A, 428, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M. 2015, Fluid Dynamics: An Introduction (Springer), 508 [Google Scholar]
- Rieutord, M., & Valdettaro, L. 1997, J. Fluid Mech., 341, 77 [Google Scholar]
- Rieutord, M., & Valdettaro, L. 2018, J. Fluid Mech., 844, 597 [Google Scholar]
- Rieutord, M., Georgeot, B., & Valdettaro, L. 2001, J. Fluid Mech., 435, 103 [Google Scholar]
- Rieutord, M., Espinosa Lara, F., & Putigny, B. 2016, J. Comp. Phys., 318, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Robrade, J., & Schmitt, J. H. M. M. 2009, A&A, 497, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid, P. J. 2007, Annu. Rev. Fluid Mech., 39, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Spalding, E., Morzinski, K. M., Hinz, P., et al. 2022, AJ, 163, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez, J. C., Bruntt, H., & Buzasi, D. 2005, A&A, 438, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y. 2020, arXiv e-prints [arXiv:2012.15152] [Google Scholar]
- van Belle, G. T., Ciardi, D. R., Thompson, R. R., Akeson, R. L., & Lada, E. A. 2001, ApJ, 559, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, R., Catanzaro, G., Christensen-Dalsgaard, J., di Mauro, M. P., & Paternò, L. 2007, MNRAS, 381, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [Google Scholar]
All Tables
Detected oscillation frequencies and their most probable azimuthal wavenumber (m).
Fundamental parameters of an ESTER model that match the observational constraints on Altair derived by Bouchaud et al. (2020).
All Figures
 |
Fig. 1. Upper panel: example of an LSD profile of Altair’s spectrum. Bottom panel: same LSD profile after subtraction of the average of all available profiles of the same night. |
| In the text | |
 |
Fig. 2. Rotational velocity field of Altair projected along the line of sight according to the Bouchaud et al. (2020) model. Velocities are in km s−1. The equator and north pole are marked. |
| In the text | |
 |
Fig. 3. Global view of the relative fluctuations in the mean line profile for each of the six nights of observation. For each night we show in the top left panel the signal as a function of time and radial velocity in km s−1. In the top-right panel we show the Lomb-Scargle periodogram of the line profile fluctuations in (virtual) longitude as a function of time and the azimuthal wavenumber m. The bottom plot shows a Lomb-Scargle periodogram of the time variations of the intensity in the eight pixels at the line centre that are marked by the red lines in the top-left panels. |
| In the text | |
 |
Fig. 4. m − ω diagram for the six nights, showing the spectral power as a function of m and frequency in the observer’s frame. The solid blue line shows the time frequency of a standing wave in the co-rotating frame characterised by wavenumber m. Modes above that line are prograde, and modes below are retrograde. The two dashed blue lines delineate the inertial frequency band. |
| In the text | |
 |
Fig. 5. Top: simulation of the line profile perturbation induced by a purely sectoral mode with m = 11 (amplitude is arbitrary). Bottom: fourier spectrum of the signal and the Lomb-Scargle periodogram. |
| In the text | |
 |
Fig. 6. Amplitude (in ppm) of the waves as a function of the azimuthal wavenumber used to do the projection of the Doppler signal. Waves are characterised by their frequency, f, given in c/d. |
| In the text | |
 |
Fig. 7. Surface amplitude (left) and meridional cut of the kinetic energy density (right) of a gravito-inertial mode that may give a signal at f = 38.14 c/d. The bottom-right plot is a zoomed-in view of the surface layers, and the dashed line shows the T = 50 000 K isotherm, around which the second ionisation of helium takes place. The depth is scaled by the polar radius of the model. |
| In the text | |
 |
Fig. 8. Meridional section of the concordance model of Altair (e.g. Bouchaud et al. 2020) showing the Brunt–Väisälä frequency. Units on the colour bar are cycle/day. Negative values show the convectively unstable regions. The lower plot gives a zoomed-in view of the surface layers and the dashed line shows the T = 50 000 K isotherm around which the second ionisation of helium takes place. Depth is scaled by the polar radius of the model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.