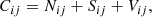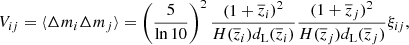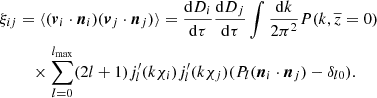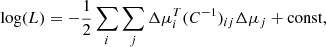| Issue |
A&A
Volume 668, December 2022
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202142640 | |
| Published online | 29 November 2022 | |
Inference of the cosmic rest-frame from supernovae Ia⋆
Fakultät für Physik, Universität Bielefeld, Postfach 100131, 33501 Bielefeld, Germany
e-mail: nhorstmann@physik.uni-bielefeld.de
Received:
11
November
2021
Accepted:
9
May
2022
We determine the proper motion of the Solar System from the Pantheon sample of type Ia supernovae (SNe). The posterior distribution of the Solar System proper velocity, its direction, and relevant cosmological parameters were obtained based on the observed distance moduli, heliocentric redshifts, and positions of SNe by means of a Markov chain Monte Carlo method. We accounted for the unknown peculiar motion of SNe by including their expected covariance from linear theory. We find that the Solar System moves with vo = 249 ± 51 km s−1 towards RA = 166 ± 16 deg, Dec = 10 ± 19 deg (J2000), (all at 68% C.L.). The direction of motion agrees with the direction of the dipole observed in the cosmic microwave background (CMB) (RA = 166 deg, Dec = −7 deg). The inferred velocity is 2.4σ lower than the value inferred from a purely kinematic interpretation of the CMB dipole (370 km s−1). Assuming a flat Λ cold dark matter model, we find no degeneracy of solar proper motion with other cosmological parameters. The dimensionless matter density, ΩM = 0.305 ± 0.022, is in excellent agreement with CMB measurements. We also find no degeneracy of the solar proper motion with the SN calibration nuisance parameter. Bulk flows might be able to explain why the solar motion appears to be slower than that of nearby SNe. We conclude that a larger sample of SNe, distributed over wide areas of the sky and a broad range in redshift, will allow an independent and robust test of the kinematic nature of the CMB dipole.
Key words: cosmological parameters / cosmology: observations / large-scale structure of Universe
SN data is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/668/A34
© N. Horstmann et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The existence of a cosmic rest-frame follows from the cosmological principle, which states that the Universe is spatially homogeneous and isotropic (at large enough scales or in a statistical sense). Any free-falling, non-rotating observer will asymptotically (for a Universe that exists forever) come to rest with respect to that frame, that is, all peculiar velocities become asymptotically small1. This is consistent with the observed smallness (i.e., v ≪ c) of the peculiar motions.
In this work, we use the Pantheon sample of type Ia SNe (Scolnic et al. 2018) to measure the peculiar motion of the Solar System with respect to a cosmic rest-frame defined by the SN sample itself and compare it with the peculiar motion inferred from observations of the cosmic microwave background (CMB; Planck Collaboration XXVII 2014; Saha et al. 2021). We use the measured heliocentric redshifts of the Pantheon SNe, which have been neatly compiled in a catalogue by Steinhardt et al. (2020).
Shortly after the discovery of the CMB, which is dominated by a thermal monopole at T0 = 2.7255 ± 0.0006 K (Fixsen 2009), the frame of this cosmic heat bath has been identified with the cosmic rest-frame (Stewart & Sciama 1967; Peebles & Wilkinson 1968). A peculiar motion of the Solar System gives rise the so-called solar dipole, which is modulated by the motion of Earth around the Sun, the so-called annual dipole. An observer moving with velocity v relative to a heat bath with a temperature 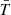 observes the temperature
observes the temperature
towards a direction given by the unit vector n, where cos θ = v ⋅ n/v, ![$ T_0 = \bar{T} + \mathcal{O}[(v/c)^2] $](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq3.gif) and
and ![$ T_1 = \bar{T} v/c + \mathcal{O}[(v/c)^3] $](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq4.gif) , with v denoting the speed of the observer and c the speed of light.
, with v denoting the speed of the observer and c the speed of light.
The CMB dipole, as measured with respect to the barycentre of the Solar System, was determined most precisely by Planck Collaboration I (2020), with a dipole amplitude of T1 = 3.36208 ± 0.00099 mK and pointing towards RA = (167.942 ± 0.007) deg, Dec = ( − 6.944 ± 0.007) deg (J2000). It is commonly assumed that the frame defined by the observed CMB dipole can be identified with the cosmic rest-frame, which implies that the Solar System moves at v/c = (1.23356 ± 0.00045) × 10−3, where the uncertainty is dominated by the uncertainty of T0.
However, the kinematic origin of the CMB dipole is a hypothesis that must be tested, and there are good reasons to believe that subdominant contributions to the CMB dipole are due to non-kinematic effects. If primordial fluctuations of space-time and matter are seeded via quantum fluctuations during cosmological inflation, we would expect contributions to the dipole from the Sachs–Wolfe effect, the proper motion of the last scattering surface, and an integrated Sachs–Wolfe effect in the early and late Universe. Extrapolating the Planck best fit to a cosmological constant and cold dark matter model (ΛCDM model), we expect the dipolar angular band power to be 𝒟1 ≈ (33 μK)2 2. This corresponds to a primordial contribution to the dipole amplitude T1 of the order of δT1 ≈ 0.05 mK. Recently, an upper limit on the intrinsic CMB dipole was presented in Ferreira (2021). It is possible to use higher multipole moments of the CMB to infer the solar motion (Challinor & van Leeuwen 2002), as it induces a coupling of neighbouring multipole moments due to Doppler boosting and aberration. In contrast to the direct measurement of the CMB dipole, the precision of that measurement is limited by the number of hot and cold spots of the CMB that can be resolved with a high signal-to-noise ratio. Planck Collaboration XXVII (2014), Planck Collaboration XVI (2016) showed that the kinematic dipole assumption is consistent with the anisotropies of the CMB at angular scales below one degree. Most recently, Saha et al. (2021) refined this analysis and found v/c = (0.996 ± 0.219) × 10−3 (about one σ smaller than the value inferred from the CMB dipole), with a large directional uncertainty of tens of degrees. Measuring the CMB at more frequency bands would in principle allow us to improve the accuracy, but this has to await the next CMB space mission.
While a comparison of the CMB dipole with the dipolar modulation of small-scale features of the CMB allows us, at least in principle, to disentangle a kinematic and a primordial intrinsic dipole, a measurement of the dipolar features of the Universe at different redshift would additionally allow us to test the question whether a cosmic (i.e., a universal) rest frame exists at all. This would also test the cosmological principle (Schwarz et al. 2015).
A simple method of measuring the rest frame in the late Universe is based on number counts of distant objects (Ellis & Baldwin 1984). It can be applied on radio surveys that cover large fractions of the sky, probe objects at high redshift, and are free from dust extinction. Several radio surveys from different instruments were analysed (Blake & Wall 2002; Singal 2011, 2019; Rubart & Schwarz 2013; Tiwari et al. 2015; Siewert et al. 2021), spanning a full decade in radio frequency. All radio source count dipoles agree within the errors with the direction of the CMB dipole, but they strongly disagree with the amplitude of the CMB dipole when the assumption is a kinematic origin of this matter dipole. The inferred solar velocity would be between a factor of four to ten larger than inferred from the CMB, increasing with decreasing radio survey frequency. If this is confirmed, a chromatic radio dipole excludes a simple kinematic interpretation (Siewert et al. 2021).
This excess matter dipole was confirmed by a similar analysis of quasars from infrared data (Secrest et al. 2021). Again, the quasar dipole points towards the CMB dipole direction, but shows a significant excess of the dipole amplitude. This is consistent with the findings at the higher radio frequencies, which also probe a similar sample of objects, that is, radio sources that are mostly active galactic nuclei.
These findings call for a closer investigation of the question of the cosmic rest-frame. This is assumed to be given by the solar dipole in almost all studies of observational cosmology, including the Hubble diagram.
The observed Hubble tension between global and local measurements of the Hubble rate, for instance, between Planck Collaboration VI (2020) and Riess et al. (2021), may even indicate a fundamental issue. This also raises the question of a direct test of the isotropy of the Hubble diagram (see e.g., McClure & Dyer 2007; Schwarz & Weinhorst 2007; Antoniou & Perivolaropoulos 2010; Kalus et al. 2013), which is also frame dependent. Recently, contradicting claims were raised in the literature on how anisotropic (Colin et al. 2019; Singal 2022; Krishnan et al. 2022) or isotropic (Hu et al. 2020; Rahman et al. 2022) the expansion is.
The discussion about large-scale bulk flows is also tightly related to this (see e.g., Colin et al. 2011; Feindt et al. 2013). To our knowledge, recent works in this context are based on the kinematic interpretation of the CMB dipole. To our surprise, only little effort has been invested to measure the solar motion by means of SNe out to large cosmological scales (Singal 2022). A crucial issue in this context are peculiar velocities of SNe and their host galaxies, as well as the consistent treatment of the SNe redshifts (see e.g., Davis et al. 2019; Peterson et al. 2022).
This work is structured as follows. In Sect. 2 we describe and summarize the effects of peculiar motion on the Hubble diagram. In addition to the Doppler effect on the redshift, the distance modulus is affected. While typically SN samples are published in the CMB frame with regard to the reported redshifts, the reported distance moduli are the heliocentric ones. The SN data used in this analysis are described in Sect. 3, with some additional details in Appendix A. Section 4 describes the Markov chain Monte Carlo (MCMC) method that we used to obtain the posterior distributions and a suite of consistency checks. More details about these checks are provided in Appendix B. Our results are presented in Sect. 5, and we conclude in Sect. 6.
2. Distance modulus and the observer’s motion
We start from an idealised measurement of the luminosity distance between a source and an observer, both being at rest with respect to a homogeneous and isotropic space-time, 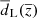 . We call this frame the cosmic rest-frame. We then introduce peculiar motions of the observer vo and emitter ve, following the discussion of Hui & Greene (2006). The dependence of the luminosity distance on relativistic Doppler shift and aberration was first studied in the seminal work of Sasaki (1987). In the following, overlined symbols denote quantities without peculiar motions.
. We call this frame the cosmic rest-frame. We then introduce peculiar motions of the observer vo and emitter ve, following the discussion of Hui & Greene (2006). The dependence of the luminosity distance on relativistic Doppler shift and aberration was first studied in the seminal work of Sasaki (1987). In the following, overlined symbols denote quantities without peculiar motions.
The (line-of-sight) comoving (with the cosmic rest-frame) distance is defined as
where the Hubble rate H(z) for the Λ cold dark matter model is given by
with ΩΛ = 1 − ΩM − ΩK, ΩΛ, ΩM, and ΩK denoting the dimensionless energy densities of cosmological constant, matter, and curvature, respectively, and H0 = H(0). The bolometric luminosity distance is
It is related to the angular diameter distance via the Etherington distance duality relation
which holds for arbitrary space-time geometries as long as light rays propagate in vacuum and as long as the limit of geometric optics applies (Etherington 1933; Schulze-Koops et al. 2017).
When we allow for peculiar motion, the first effect to take into account is the Doppler shift experienced by light due to the relative motion of source and observer. The redshift z measured in the heliocentric frame is connected to the redshift 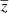 in the cosmic rest-frame, or comoving frame, via
in the cosmic rest-frame, or comoving frame, via
where γ = (1 − (ve − vo)2/c2)−1/2 is the Lorentz factor. Here, n is the unit vector pointing from the observer to the emitter. Expanding up to first-order in velocities, we obtain
ϕ and θ denote the observed angles between the line of sight and the peculiar motion of emitter and observer, respectively. 𝒪(v2) indicates second-order terms in ve and vo. Aberration of the angles can be ignored at linear order because the rest-frame angle 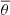 transforms as
transforms as 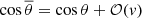 and thus, effects on the redshift are of order 𝒪(v2). The same holds true for
and thus, effects on the redshift are of order 𝒪(v2). The same holds true for 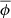 .
.
However, relativistic aberration gives rise to a first-order effect in the angular diameter distance
where δAe is the proper area of the emitter and δΩo is the solid angle at the observer, subtended by light rays from the emitter. When relative motion is considered, the latter will change. When Lorentz boosts are performed, the solid angle element transforms as
The angular diameter distance is then given by
Thereby, from Eq. (5), the luminosity distance can be written as
It remains to link the bolometric luminosity distance to the bolometric distance modulus,
which is inferred from the analysis of SN light curves, up to their absolute bolometric magnitude, which is treated as a nuisance parameter in the cosmological analysis (except when measuring H0). We must also express 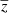 as a function of the measured redshift,
as a function of the measured redshift,
Then the fitting function, at linear order in peculiar velocities, reads
While we can hope to measure the velocity of the Solar System accurately, it is much harder to measure the peculiar motion of extragalactic objects. Their proper motion in particular can usually not be detected with current observational precision. Thus ve has to be inferred from incomplete and noisy data (e.g., see Carrick et al. 2015). An essential step in the reconstruction of peculiar velocities is that we must assume that the cosmic rest-frame is known.
In this work we wish to determine the cosmic rest-frame based on a sample of type Ia SNe. It would therefore be inconsistent to assume peculiar velocities that already make an assumption with respect to the quantities that we wish to measure. We therefore must refrain from applying peculiar velocity corrections for extragalactic objects, but rather take the corresponding uncertainties into account by including them in the covariance matrix in an appropriate way.
We did this by following Huterer et al. (2017). The covariance matrix can be written as (the indices denote individual SNe)
where Nij is the observational contribution to the covariance and includes uncertainties from photometry and light-curve fitting, while Sij represents the additional covariances between the different surveys within the complete data catalogue, as described for the Pantheon SN catalogue in Scolnic et al. (2018). Vij denotes the expected variances from peculiar motion and covariances from bulk flows, as predicted in linear perturbation theory. It reads
where
Above, P(k, z = 0) denotes the linear power spectrum today, Di is the linear growth factor, τ denotes conformal time, jl are spherical Bessel functions and the prime denotes a derivative with respect to their argument. Finally, Pl are Legendre polynomials.
It has been noted (Mohayaee et al. 2020) that this approach would not account for the fact that we observe the Universe from within a galaxy and that neither the Milky Way nor the Solar System are comoving with the cosmic rest-frame, while the derivation of the structure covariance in Eq. (16) assumes that the observer is comoving and sits at a random location in the Universe, that is, at a spot without a galaxy. This is certainly true, and this aspect could be improved by looking at constrained three-point correlations instead. However, we expect that the effect of this correction is small as we did not include very nearby SNe. The smallest SN distance in the considered sample is about 40 Mpc (z ∼ 0.01), and the majority of SNe lie at much larger distances. At distances above 40 Mpc, linear perturbation theory is a very reasonable approximation, and non-vanishing three-point correlations are not expected for Gaussian initial conditions in the linear regime.
3. Supernova sample
3.1. Pantheon catalogue
We used the Pantheon sample, which consists of 1048 type Ia SNe. It was originally compiled by Scolnic et al. (2018) from the surveys specified in Table 1. They are the Supernova Legacy Survey (SNLS; Guy et al. 2010), the Sloan Digital Sky Survey (SDSS; Smith et al. 2012; Sako et al. 2018), Pan-STARS1 (PS1; Scolnic et al. 2018), CfA1 – CfA4 (Riess et al. 1999; Jha et al. 2006; Hicken et al. 2009a,b, 2012), the Carnegie Supernova Project (CSP; Contreras et al. 2010), and various surveys using the Hubble Space Telescope (HST), namely CANDLES/CLASH (Rodney et al. 2014; Graur et al. 2014; Riess et al. 2018), GOODS (Riess et al. 2007), and SCP (Suzuki et al. 2012).
Surveys used for the Pantheon catalogue.
3.2. SN redshift
It has been pointed out by Davis et al. (2019) that the redshifts of SNe should be considered with great care. Commonly made mistakes in the handling of redshift estimates could lead to false cosmological conclusions. After Rameez (2019) noted several inconsistencies between redshifts quoted in the Pantheon (Scolnic et al. 2018) and JLA (Betoule et al. 2014) SN catalogues, Steinhardt et al. (2020) identified the cause of several of these inconsistencies regarding the redshift values quoted in the Pantheon catalogue and published an improved catalogue3. Here we make use of this improved catalogue after implementing additional corrections related to the positions of several SNe from the HST surveys as discussed in Appendix A. The improved Pantheon catalogue (Steinhardt et al. 2020) provides detailed information on each SN: the SN identifier, the original survey, the type of redshift measurement (SN, host, both), as well as values for zCMB, zhel, μ, RA, Dec, and the measurement uncertainties of zCMB and μ. The quoted redshift uncertainties are not fully self-consistent, as pointed out by Steinhardt et al. (2020). For example, some uncertainties are given as 0 because the original survey reported no uncertainties for them. For other surveys, only a general uncertainty is given and not an individual one for each SN. For this reason, we chose to neglect redshift uncertainties in our analysis.
As we wish to measure the proper motion of the Solar System, it is important to distinguish between the cosmological redshift, 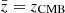 , and the observed heliocentric redshift, z = zhel, which includes effects of peculiar motion (here we ignore other effects, e.g., gravitational redshift). The connection is given by Eq. (13). One of the aspects pointed out by Steinhardt et al. (2020) in their Eq. (A.1) is the fact that Scolnic et al. (2018) omitted the term z(vo/c) cos θ, giving rise to errors for high redshifts.
, and the observed heliocentric redshift, z = zhel, which includes effects of peculiar motion (here we ignore other effects, e.g., gravitational redshift). The connection is given by Eq. (13). One of the aspects pointed out by Steinhardt et al. (2020) in their Eq. (A.1) is the fact that Scolnic et al. (2018) omitted the term z(vo/c) cos θ, giving rise to errors for high redshifts.
In a first step that just serves for illustrative purposes, we fit Eq. (14) to the full redshift-improved Pantheon sample. We did not include peculiar velocities of the emitters and did not take the full covariance matrix Cij into account (just the variances of μ as quoted in the catalogue). To illustrate the redshift distribution of the various subsamples of the Pantheon SN sample, we show the residuals to a fit to the Hubble diagram in Fig. 1. We varied H0 (treated as a nuisance parameter), ΩM, and vo for a flat ΛCDM model and fixed the direction of the peculiar of motion of the Solar System to the CMB dipole direction. The fit was obtained with the help of lmfit4 (Newville et al. 2014), and the corresponding figures are produced with matplotlib5 (Hunter 2007). We find a good quality of fit with χ2/d.o.f. = 1.0001 and best-fit values ΩM = 0.30 ± 0.01 and vo/c = 0.0008 ± 0.0001. Steinhardt et al. (2020) also provided the type of redshift measurement for each SN. The main distinction is between measurements that are inferred from the SN and redshifts inferred from the spectra of their respective host galaxy (hostz). Steinhardt et al. (2020) stated that the hostz values are more reliable and recommended using hostz measurements in future surveys. They also reported different fit results between the two methods for cosmological parameters. For this reason, we considered the hostz subset separately. We find that there is no substantial difference in the value of the inferred vo, just an increase in the uncertainty, consistent with the reduced number of data points (χ2/d.o.f. = 1.013). The corresponding residuals to the Hubble diagram are shown in Fig. 2. We therefore use the complete Pantheon sample for our analysis below, and use the subsample of SNe with known host galaxy redshifts for a consistency check.
 |
Fig. 1. Residual of the Hubble diagram as a function of the observed heliocentric redshift. The different colours indicate the redshift distributions of the individual SN surveys included in the Pantheon sample. |
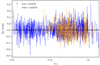 |
Fig. 2. Residual of the Hubble diagram as a function of the observed heliocentric redshift indicating SNe with host redshift measurements and with other redshift measurements. |
To estimate the peculiar velocities of SNe with zhel < 0.1, included in the inference of zCMB by Steinhardt et al. (2020), we used a tool published in conjunction with Carrick et al. (2015). This tool requires the cosmological parameters H0 and ΩM as well as for each SN zCMB, RA, and Dec as input parameters. For RA and Dec we directly used the values given by Steinhardt et al. (2020). zCMB was calculated from the heliocentric values given by Steinhardt et al. (2020) according to Eq. (13), without ve, using the solar velocity we obtained from our first analysis.
When assuming a velocity of vo/c = 0.00123 (Planck Collaboration I 2020), we recover the values of  given by Steinhardt et al. (2020) for z > 0.1 within a numerical uncertainty of about 10−6. For lower redshifts, the difference to the catalogued
given by Steinhardt et al. (2020) for z > 0.1 within a numerical uncertainty of about 10−6. For lower redshifts, the difference to the catalogued  is significantly larger when peculiar velocities are taken into account (as described above) and when they are omitted.
is significantly larger when peculiar velocities are taken into account (as described above) and when they are omitted.
However, reconstructing peculiar velocities from density fields requires knowing the cosmic rest-frame. Because the goal of our work is to determine this rest frame, peculiar velocities of the emitter are difficult to include in a consistent way. For this reason, we only included peculiar velocity corrections as a consistency check in our analysis, with the goal to obtain an estimate for their influence on our dipole values.
Steinhardt et al. (2020) adjusted the value of M in the distance moduli μ such that a fit yields a value of 70 km s−1 Mpc−1 for H0. We changed the absolute magnitude such that our fit agrees with H0 = 73.2 km s−1 Mpc−1, in line with Riess et al. (2021), when no peculiar motions of the sources are included and when the solar peculiar motion is fixed to the value inferred from the CMB (Planck Collaboration I 2020).
4. Parameter fitting and consistency
4.1. Method
We followed a Bayesian approach based on a MCMC method to compute the posterior probability for a set of five parameters (ΔH0, ΩM, vo, RA, and Dec), based on the redshift-corrected Pantheon data set described above. The quantity ΔH0 ≡ H0 − 73.2 km s−1 Mpc−1 was treated as a nuisance parameter, and we used flat priors for all parameters, allowing them to vary in broad ranges of −73.2 km s−1 Mpc−1 < ΔH0 < 46.8 km s−1 Mpc−1, 0 < ΩM < 1, 0 < vo < 0.002c, 0 deg < RA < 360 deg, −90 deg < Dec < 90 deg, and −0.3 < ΩK < 0.3.
We used emcee (Foreman-Mackey et al. 2013) as our implementation of the MCMC. Our likelihood function is, up to an irrelevant constant that also contains the determinant of the covariance matrix C, given by
where Δμi = μdata i − μmodel i is the distance modulus residual for SN with index i. The covariance matrix is C = N + S + V; see the text below Eq. (15). N is diagonal and contains the uncertainties in μdata i, and S describes correlations between the different surveys and SNe. Both are given by Scolnic et al. (2018). V accounts for correlations in peculiar velocities and is given by expression (16); see also Huterer et al. (2017). Strictly speaking, V depends on the cosmological parameters and should be recalculated in every iteration. Because this is computationally expensive, we fixed all required parameters to the best-fit values given by by the Planck 2018 results (Planck Collaboration I 2020; Planck Collaboration VI 2020), assuming the neglected effects to be small.
Figure 3 shows posterior distributions of the model parameters. The first distribution, ΔH0, is included to investigate potential degeneracy of this nuisance parameter with the cosmological parameters in question, but it is clear that we have fixed the absolute magnitude of SN Ia to an arbitrary value and thus ΔH0 must not be mistaken as a measurement of the Hubble rate. The second parameter is ΩM. The remaining three parameters provide the credibility regions for the peculiar velocity of the Solar System and its direction of motion in terms of RA and Dec.
 |
Fig. 3. Two-dimensional and one-dimensional posterior distributions for four model parameters and the nuisance parameter ΔH0 for the full redshift-corrected Pantheon sample. The contours show the 68% and 95% credibility levels. |
All contour plots in this work were created using the corner module for Python (Foreman-Mackey 2016) and show 68% and 95% credibility regions. The values labelled ‘Planck 2018’ indicate the Planck 2018 measurements and their 68% credibility intervals (Planck Collaboration I 2020; Planck Collaboration VI 2020). The values labelled ‘Riess et al. 2021’ are from Riess et al. (2021).
4.2. Consistency of subsamples
Before we discuss our main result, we analyse each SN survey of Table 1 and compare the results of these sub-samples to check for any inconsistencies between the different surveys. The corresponding posterior distributions and a more detailed discussion are presented in Appendix B.
Each individual SN sample from a single survey either agrees with the value ΩM found by Planck Collaboration VI (2020) within 1σ (PS1, SDSS, SNLS, and HST) or has no constraining power due to a lack of high redshift SNe in these surveys (CfA, CSP). We also ran our algorithm with different combinations of surveys. The entire catalogue agrees with its subsamples.
5. Results
We inspect Fig. 3 in more detail. It shows the 1D and 2D posterior distributions of the five free parameters of our base model using the whole Pantheon data set. We assume a flat ΛCDM model and account for peculiar motions by means of an additional contribution to the covariance matrix; see Eq. (16). The numerical results of the fit are provided in Table 2. The proper motion of the Solar System is specified by the three parameters (vo, RA, and Dec). The corresponding best-fit values inferred from the CMB are summarised from the literature in Table 3.
Best-fit values (median) and 68% credible intervals.
Planck best-fit values and credible intervals.
5.1. Nuisance parameter and matter density
The nuisance parameter ΔH0 shows some (expected) degeneracy with ΩM, but none with the inferred proper motion of the Solar System. Conversely, this also means that the value of the Hubble rate measured by means of calibrated SNe cannot be reduced by a significant amount by assuming a cosmic rest-frame that does not coincide with the CMB dipole frame. The effect of including the full covariance matrix and allowing for an arbitrary solar velocity in the analysis is an insignificant increase of ΔH0 = 0.23 km s−1 Mpc−1.
The best-fit matter density ΩM agrees very well with the CMB analysis (Planck Collaboration VI 2020).
5.2. Proper motion of the Solar System
The inferred direction of the Solar System proper motion is found to be consistent with the value inferred from Planck Collaboration I (2020) within 1σ. The velocity itself is found to be lower than that inferred from the CMB dipole (Planck Collaboration I 2020). The p-value for agreement with the CMB dipole is 0.0095. The median solar velocity is 2.4σ below the value inferred from the CMB dipole (Planck Collaboration I 2020). All subsamples of the Pantheon catalogue that are sensitive to vo show the same trend, and we find no parameter degeneracy with the other cosmological parameters. This means that low-redshift SNe (up to z ∼ 0.1), spread out over a wide area on the sky, are an excellent tool for inferring the cosmic rest-frame independently from the CMB. The precision of this inference is comparable with the precision of current radio surveys (Siewert et al. 2021).
5.3. Host galaxy redshifts
In order to test the robustness of our results, we also restricted our analysis to SNe with host galaxy redshifts. The results are shown in Fig. 4. We find significant differences in the matter density to the full Pantheon catalogue, as already reported by Steinhardt et al. (2020). ΩM is 2.1σ below the CMB estimate from Planck Collaboration VI (2020). However, the inferred value of vo is fully consistent with the full Pantheon sample and is 2.1σ lower than the value inferred from the CMB dipole of Planck Collaboration I (2020) with a p-value of 0.015.
 |
Fig. 4. Posterior distributions using only SNe with host galaxy redshifts. |
5.4. Curvature
Allowing for curvature and introducing ΩK as a sixth model parameter (see Fig. 5) leads to increased uncertainties for all varied parameters. Because ΩK = 0 is consistent with our analysis, we neglected curvature in the following analysis to save computation time and decrease the uncertainty. It is interesting to note that the best-fit value is slightly negative, as for the extended Planck analysis (Planck Collaboration VI 2020), but with much larger uncertainty and thus without any statistical significance. The inferred proper motion of the Solar System is not affected by the additional parameter.
 |
Fig. 5. Posterior distributions allowing for non-zero curvature. |
5.5. Minimum redshift
For further insight, we repeated the analysis omitting SNe with redshift zhel < zmin, in order to study the influence of nearby SNe. The dependence of the parameters ΔH0, ΩM, and vo on zmin is shown in Fig. 6. In this analysis, we allowed vo to vary in a wider range between 0 and 0.01c. The decreasing number of SNe leads to increasing uncertainties for high zmin, as expected. ΔH0 and ΩM both show a clear difference from the full data set at zmin > 0.1. For ΩM, the values decrease between zmin = 0.1 and zmin = 0.2 below the Planck value and subsequently increase above it at zmin > 0.3. ΔH0 shows a similar evolution, increasing between zmin = 0.1 and zmin = 0.2, decreasing afterwards. At zmin > 0.3, the uncertainties also grow quite large due to the decreasing number of SNe. Between zmin = 0.2 and zmin = 0.3, the number of SNe decreases from 637 to 421 SNe. The decrease in ΔH0 at higher redshifts is in line with the dependence of H0 on the probed SN redshifts described for example by Dainotti et al. (2021), who extrapolated this trend to the CMB measurements. The decrease is also seen in the analysis of time delays in gravitational lenses (Wong et al. 2020; Millon et al. 2020).
 |
Fig. 6. Best-fit parameters based on SNe with redshifts higher than zmin. All five parameters were varied (ΔH0, ΩM, vo, RA, and Dec). |
While the uncertainties in ΔH0 and ΩM start to increase significantly at zmin > 0.2, for vo, sizeable uncertainties make the analysis less conclusive at zmin > 0.05. Above zmin = 0.07, the inferred value of vo lies within one σ of the CMB inferred solar velocity. The increase in vo for zmin > 0.03 could be a reflection of a large bulk flows as reported in Carrick et al. (2015), when the solar velocity is inferred from the CMB dipole. This is further discussed in Sect. 5.7.
Our findings are also consistent with the analysis of Colgáin (2019), who measured the matter density for zCMB < zmax from the original Pantheon catalogue. A slight indication of a matter underdensity at zmax < 0.2 is reflected in our analysis by the increase in matter density above zmin = 0.2.
5.6. Peculiar velocities
We have used the structure covariance V so far to account for peculiar velocities of SNe. In order to test the effect of applying reconstructed peculiar velocities, we now use peculiar velocities from Carrick et al. (2015) for zhel < 0.1 instead. The resulting fits are shown in Fig. 7.
 |
Fig. 7. Posterior distribution using peculiar velocity corrections from Carrick et al. (2015). |
Correcting for peculiar velocities in this way changes the values by less than 1σ for all varied parameters. The largest change is found in vo, which increases by almost 1σ and therefore reduces the difference with the velocity inferred from the CMB dipole to 1.7σ and increases the p-value to 0.046.
We conclude that our estimate of the proper motion of the Solar System is also robust with respect to peculiar velocity corrections. However, these corrections should be considered with great care. Firstly, the inference of peculiar velocities from observed redshifts and the observed matter density distribution relies on an assumed cosmic rest-frame in the first place. Secondly, the uncertainties of the inferred peculiar velocities are hard to quantify. It is certainly inconsistent to apply corrections and to include the covariance matrix V. Thirdly, peculiar velocity corrections should be applied to host galaxy redshifts alone because the relative motion between an SN and its host cannot be known and can easily amount to a sizeable fraction of the peculiar velocity (see also the discussion in Peterson et al. 2022).
5.7. Bulk flows
We finally investigate whether the inferred solar motion might be partially attributed to a bulk flow of SNe at small cosmological distances. Previous works claimed the existence of such a bulk flow (Kashlinsky et al. 2008; Watkins et al. 2009; Dai et al. 2011; Feindt et al. 2013; Carrick et al. 2015). If the motion of the Local Group were aligned with the motion of other nearby structures, the Sun would be expected to move more slowly with respect to low-redshift SNe as compared to higher-redshift SNe. Qualitatively, this is indeed the case, as we show in Fig. 6. Excluding SNe at z < 0.04 leads to higher best-fit values for vo. However, if all assumptions we have made in this analysis were correct, then the effect of such a bulk motion should be included via the covariance matrix of Eq. (16). Apparently, the inferred uncertainty of the solar velocity when SNe are included in the range 0.01 < z < 0.04 is too small in order to conclude that this is an expected effect. There are two limitations to that argument, however. Firstly, it assumes that only effects of linear fluctuations are relevant, and secondly, it assumes that we use the correct cosmological model.
In order to test the bulk flow hypothesis, we modified our fit by assuming that all SNe at z < 0.03 (motivated by the analysis presented in Sect. 5.5) have the same value of ve = vbulk in the fixed direction RAbulk = 194 deg and Decbulk = −57 deg, as found by Carrick et al. (2015). Using a flat prior for the additional parameter vbulk does not allow us to break the degeneracy between vo and vbulk. In order to break this degeneracy, we added the Gaussian prior vbulk = 159 ± 23 km s−1, taken again from Carrick et al. (2015). The result of that fit is shown in Fig. 8 and Table 2. As expected, for vbulk, we essentially recover the prior, and we find the inferred solar motion to be consistent with the motion inferred from the CMB dipole. This is expected because Carrick et al. (2015) used the CMB dipole as an input to infer the bulk motion.
 |
Fig. 8. Posterior distribution assuming a constant bulk flow for all SNe with zhel < 0.03 in the fixed direction RAbulk = 194 deg, Decbulk = −57 deg with a Gaussian prior on the bulk velocity, vbulk = 159 ± 23 km s−1. Bulk direction and velocity prior are chosen according to Carrick et al. (2015). |
Thus, bulk flows as discussed in the current literature might cause the smaller inferred solar motion with respect to a sample of SNe at low redshifts.
6. Conclusions
Modern cosmology describes the Universe in the context of spatially homogeneous and isotropic space-time, the class of the Friedmann–Lemaître models. These models have in common that a cosmic rest-frame exists that is typically identified with the frame defined by the CMB dipole. The peculiar motion of the barycentre of the Solar System is consequently inferred from the CMB.
Here we have tested this hypothesis of a purely kinematic CMB dipole by means of SNe compiled in the Pantheon catalogue (Scolnic et al. 2018). The SN redshift–distance modulus relation, see Eq. (14), is sensitive to the radial peculiar motions of the SNe and the radially projected peculiar motion of the observer. While (for non-relativistic velocities) the SN redshift depends on (ve − vo)⋅n, the distance modulus depends on (2ve − vo)⋅n, as was first realised by Sasaki (1987). While inferring the peculiar velocities of the SN host galaxies needs additional observations and is limited to rather small redshifts (see e.g., Carrick et al. 2015), the effect of the Solar System motion is coherent and affects all SNe at all redshifts, which allows us to use a direction-dependent analysis of SN distance moduli to measure the Solar System proper motion.
It has been pointed out before that the Pantheon catalogue contains inconsistencies regarding the quoted values of heliocentric redshifts (Rameez 2019; Steinhardt et al. 2020). The Pantheon sample was not compiled with foresight of direction-dependent studies, which implies that there might be other issues that we were unable to identify in this study. We used an improved version of the Pantheon catalogue (see Steinhardt et al. 2020 and Appendix A) to measure the cosmic SN rest-frame and found that the direction of motion of the Solar System agrees well with the CMB dipole direction, but that the inferred Solar System velocity is well below the velocity inferred from the CMB dipole (see Table 2). Our findings are summarised in Fig. 9. The null hypothesis of a purely kinematic CMB dipole is found to have a p-value of 0.0095 when the unknown peculiar motion of SNe is accounted for by means of the covariance matrix from linear theory (Huterer et al. 2017). When we correct for peculiar motion (Carrick et al. 2015), which implies also that we must assume a cosmic rest-frame, the p-value increases to 0.046. We therefore conclude that it is premature to reject the hypothesis of a purely kinematic CMB dipole, but it is interesting to note that none of our tests produced a solar velocity exceeding the velocity from the CMB dipole.
 |
Fig. 9. Comparison of the posterior distribution for different measurements of the proper motion of the Sun. We show our own results taking the emitter peculiar velocities into account by using the covariance matrix in Eq. (16) and by means of corrections according to Carrick et al. (2015), respectively. For comparison, we also show the results from the analysis of high multipole moments of the CMB (Saha et al. 2021) and assuming that the CMB dipole is entirely explained by solar motion (Planck Collaboration I 2020). In the latter case, the uncertainties are too small to be displayed properly. We instead indicate the value by a vertical line. |
We tested the robustness of our findings with respect to the self-consistency of the Pantheon catalogue and the addition of further cosmological parameters. We confirmed that peculiar velocity corrections affect the final result, but move the median values by less than 1σ. As already pointed out by Steinhardt et al. (2020), using host galaxy redshifts does affect the inferred matter density, but leads to insignificant changes in the estimate of the Solar System proper motion.
We have also shown that bulk flows might explain why the solar motion appears to be slower than that of nearby SNe as compared to more distant SNe, but the inference of such a large-scale bulk flow strongly depends on the assumption that the cosmic rest-frame is defined by the CMB dipole. The task of this work is not to measure this bulk flow, but it is clear that more data are needed to be able to distinguish the effect of bulk flows and the solar motion. This might be possible in principle when it is traced over a range in redshift and a wide survey area because of the already mentioned (2ve − vo)⋅v dependence of the distance modulus (vo must not depend on redshift, while vbulk should).
It is also interesting to compare our findings with estimates of the matter dipole in Secrest et al. (2021) and Siewert et al. (2021), where an excess dipole was found in galaxy number counts that also points towards the CMB dipole. This excess might in principle be explained by a much larger motion of the observer. While the frequency dependence of the matter dipole excess found in Siewert et al. (2021) is certainly inconsistent with this explanation, the finding of this work is inconsistent as well, indicating that the search for systematic issues and an unexpectedly large contribution from a local clustering dipole must continue.
Another attempt to measure the solar proper motion from SN data was presented by Singal (2022) based on a different method. They used the JLA sample (Betoule et al. 2014) and the uncorrected Pantheon sample (Scolnic et al. 2018). Their estimate for the direction agrees with ours and shows a comparable but slightly larger uncertainty. In contrast to us, they inferred a solar velocity about four times higher than inferred from the CMB dipole. On the one hand, the factor of four would be in line with the findings on the matter dipole for quasars (Secrest et al. 2021). On the other hand, it is in stark disagreement with this work and with the higher CMB multipole moments (Saha et al. 2021). The reason for this strong disagreement is unclear. It might be related to inconsistent heliocentric redshifts as discussed in the appendix of Steinhardt et al. (2020).
The recently published Pantheon+ data set (Brownsberger et al. 2021; Peterson et al. 2022; Carr et al. 2022; Scolnic et al. 2022) will allow us to improve the analysis presented here. The new data set contains a total of 1800 SNe. The number of small-z SNe, which are of particular value for our analysis, is even tripled (585 with z < 0.08 compared to 194 in the Pantheon catalogue). The statistical power of such a larger sample should reduce the credible intervals obtained in this work by a factor of roughly 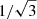 . When we assume that the best-fit values do not change with the new data, the larger statistics should be enough to test the kinematic dipole hypothesis on a statistically significant level. A recent analysis of this data set (Brout et al. 2022) indicates a dipole in the redshifts that is pointed roughly opposite to the CMB dipole. In contrast to our work, they did not attempt to infer the cosmic rest-frame from the SNe.
. When we assume that the best-fit values do not change with the new data, the larger statistics should be enough to test the kinematic dipole hypothesis on a statistically significant level. A recent analysis of this data set (Brout et al. 2022) indicates a dipole in the redshifts that is pointed roughly opposite to the CMB dipole. In contrast to our work, they did not attempt to infer the cosmic rest-frame from the SNe.
We conclude that SNe should be used to establish the cosmic rest-frame independently from the CMB and without making assumptions on the rest frame itself. It is probably best to start from the heliocentric redshifts and magnitudes and to account for all unknowns in the covariances. We have demonstrated that this approach preserves the statistical power to constrain the matter density and curvature6. We hope that we can encourage a greater emphasis on direction-dependent7 effects in observational studies of the expansion of the Universe.
See Barnes et al. (2006), for example, for a detailed discussion. Here we refer to their definition 3, which is equivalent to their definition 7 (the observer measures a vanishing CMB dipole) and implies their definition 1 (the change of comoving distance decays asymptotically).
We use the cosmological parameters of the best-fit flat ΛCDM model from Planck Collaboration VI (2020) and CAMB (Lewis et al. 2000) to obtain the expected primordial CMB dipole moment C1, which gives the angular band power 𝒟1 = C1/π.
Acknowledgments
The authors would like to thank Daniel M. Scolnic, Charles L. Steinhardt and Albert Sneppen for providing their data and giving insights into their work. We also thank Eoin Ó Colgáin for insightful comments and Gaurav Kumar for useful discussions regarding the data analysis. We also thank the anonymous referee for their excellent questions, suggestions, and comments. The results of this paper have been accomplished using NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), matplotlib (Hunter 2007), lmfit (Newville et al. 2014), emcee (Foreman-Mackey et al. 2013), corner (Foreman-Mackey 2016) and CAMB (Lewis et al. 2000). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
References
- Antoniou, I., & Perivolaropoulos, L. 2010, J. Cosmol. Astropart. Phys., 2010, 012 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, L. A., Francis, M. J., James, J. B., & Lewis, G. F. 2006, MNRAS, 373, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blake, C., & Wall, J. 2002, Nature, 416, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Brout, D., Scolnic, D., Popovic, B., et al. 2022, ApJ, 938, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Brownsberger, S., Brout, D., Scolnic, D., Stubbs, C. W., & Riess, A. G. 2021, ArXiv e-prints [arXiv:2110.03486] [Google Scholar]
- Carr, A., Davis, T. M., Scolnic, D., et al. 2022, Astronomical Society of Australia, 39, e046 [NASA ADS] [CrossRef] [Google Scholar]
- Carrick, J., Turnbull, S. J., Lavaux, G., & Hudson, M. J. 2015, MNRAS, 450, 317 [Google Scholar]
- Challinor, A., & van Leeuwen, F. 2002, Phys. Rev. D, 65, 103001 [Google Scholar]
- Colgáin, E. Ó. 2019, J. Cosmol. Astropart. Phys., 2019, 006 [CrossRef] [Google Scholar]
- Colin, J., Mohayaee, R., Sarkar, S., & Shafieloo, A. 2011, MNRAS, 414, 264 [Google Scholar]
- Colin, J., Mohayaee, R., Rameez, M., & Sarkar, S. 2019, A&A, 631, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contreras, C., Hamuy, M., Phillips, M. M., et al. 2010, AJ, 139, 519 [Google Scholar]
- Dai, D.-C., Kinney, W. H., & Stojkovic, D. 2011, J. Cosmol. Astropart. Phys., 2011, 015 [CrossRef] [Google Scholar]
- Dainotti, M. G., De Simone, B., Schiavone, T., et al. 2021, ApJ, 912, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. M., Hinton, S. R., Howlett, C., & Calcino, J. 2019, MNRAS, 490, 2948 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, G. F. R., & Baldwin, J. E. 1984, MNRAS, 206, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Etherington, I. M. H. 1933, Phil. Mag., 15, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Feindt, U., Kerschhaggl, M., Kowalski, M., et al. 2013, A&A, 560, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferreira, P. d. S., & Quartin, M., 2021, Phys. Rev. Lett., 127, 101301 [NASA ADS] [CrossRef] [Google Scholar]
- Fixsen, D. J. 2009, ApJ, 707, 916 [Google Scholar]
- Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Graur, O., Rodney, S. A., Maoz, D., et al. 2014, ApJ, 783, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Challis, P., Jha, S., et al. 2009a, ApJ, 700, 331 [Google Scholar]
- Hicken, M., Wood-Vasey, W. M., Blondin, S., et al. 2009b, ApJ, 700, 1097 [Google Scholar]
- Hicken, M., Challis, P., Kirshner, R. P., et al. 2012, ApJS, 200, 12 [Google Scholar]
- Hu, J. P., Wang, Y. Y., & Wang, F. Y. 2020, A&A, 643, A93 [EDP Sciences] [Google Scholar]
- Hui, L., & Greene, P. B. 2006, Phys. Rev. D, 73, 123526 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Huterer, D., Shafer, D. L., Scolnic, D. M., & Schmidt, F. 2017, J. Cosmol. Astropart. Phys., 2017, 015 [CrossRef] [Google Scholar]
- Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [Google Scholar]
- Kalus, B., Schwarz, D. J., Seikel, M., & Wiegand, A. 2013, A&A, 553, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Kocevski, D., & Ebeling, H. 2008, ApJ, 686, L49 [Google Scholar]
- Krishnan, C., Mohayaee, R., Colgáin, E. Ã., Sheikh-Jabbari, M. M., & Yin, L. 2022, Phys. Rev. D, 105, 063514 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- McClure, M. L., & Dyer, C. C. 2007, Nature, 12, 533 [Google Scholar]
- Millon, M., Galan, A., Courbin, F., et al. 2020, A&A, 639, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohayaee, R., Rameez, M., & Sarkar, S. 2020, ArXiv e-prints [arXiv:2003.10420] [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., & Ingargiola, A. 2014, https://doi.org/10.5281/zenodo.11813 [Google Scholar]
- Peebles, P. J., & Wilkinson, D. T. 1968, Phys. Rev., 174, 2168 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, E. R., Kenworthy, W. D., Scolnic, D., et al. 2022, ApJ, 938, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XXVII. 2014, A&A, 571, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2016, A&A, 594, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2020, A&A, 641, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahman, W., Trotta, R., Boruah, S. S., Hudson, M. J., & van Dyk, D. A. 2022, MNRAS, 514, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Rameez, M. 2019, ArXiv e-prints [arXiv:1905.00221] [Google Scholar]
- Riess, A. G., Kirshner, R. P., Schmidt, B. P., et al. 1999, AJ, 117, 707 [Google Scholar]
- Riess, A. G., Strolger, L.-G., Tonry, J., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Rodney, S. A., Scolnic, D. M., et al. 2018, ApJ, 853, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2021, ApJ, 908, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Rodney, S. A., Riess, A. G., Strolger, L.-G., et al. 2014, AJ, 148, 13 [Google Scholar]
- Rubart, M., & Schwarz, D. J. 2013, A&A, 555, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saha, S., Shaikh, S., Mukherjee, S., Souradeep, T., & Wandelt, B. D. 2021, J. Cosmol. Astropart. Phys., 2021, 072 [CrossRef] [Google Scholar]
- Sako, M., Bassett, B., Becker, A. C., et al. 2018, PASP, 130, 064002 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, M. 1987, MNRAS, 228, 653 [Google Scholar]
- Schulze-Koops, K., Perlick, V., & Schwarz, D. J. 2017, Class. Quant. Grav., 34, 215006 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, D. J., & Weinhorst, B. 2007, A&A, 474, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, D. J., Bacon, D., Chen, S., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 32 [Google Scholar]
- Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D., Brout, D., Carr, A., et al. 2022, ApJ, 938, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Secrest, N. J., von Hausegger, S., Rameez, M., et al. 2021, ApJ, 908, L51 [Google Scholar]
- Siewert, T. M., Schmidt-Rubart, M., & Schwarz, D. J. 2021, A&A, 653, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singal, A. K. 2011, ApJ, 742, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Singal, A. K. 2019, Phys. Rev. D, 100, 063501 [NASA ADS] [CrossRef] [Google Scholar]
- Singal, A. K. 2022, MNRAS, 515, 5969 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M., Nichol, R. C., Dilday, B., et al. 2012, ApJ, 755, 61 [Google Scholar]
- Steinhardt, C. L., Sneppen, A., & Sen, B. 2020, ApJ, 902, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, J. M., & Sciama, D. W. 1967, Nature, 216, 748 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, N., Rubin, D., Lidman, C., et al. 2012, ApJ, 746, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Tiwari, P., Kothari, R., Naskar, A., Nadkarni-Ghosh, S., & Jain, P. 2015, Astropart. Phys., 61, 1 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Watkins, R., Feldman, H. A., & Hudson, M. J. 2009, MNRAS, 392, 743 [Google Scholar]
- Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
Appendix A: SN positions
For 18 SNe from the GOODS and SCP surveys, we were unable to reproduce the redshift conversion between heliocentric and CMB frames given in Steinhardt et al. (2020). For two of the SNe in question, the declination given by Steinhardt et al. (2020) had a sign error, and for one SN, neither right ascension nor declination were given. The corrections are listed in Table A.1.
Corrected SNe positions.
Steinhardt et al. (2020) appear to have assumed the same value of cos θ for all 18 GOODS and SCP SNe, while the observations were taken in four different regions of the sky. We conclude that the values of zCMB reported by Steinhardt et al. (2020) should be updated in the improved catalogue, and correct SN positions should be applied. We did this in our analysis.
Appendix B: Sub-samples
Here we present 1D and 2D posterior distributions for the individual surveys included in the Pantheon data set (Figs. B.1 – B.2) and combinations of pairs of surveys (Figs. B.3 – B.4). The combination of two surveys tightens the constraints in all cases (as expected), and combinations that include the SNLS sample tend to prefer lower values of ΩM, but not at a statistically significant level and not when combined with the PS1 sample. Furthermore, we compared combinations that omit a single survey (Figs. B.5), which are also consistent with each other. However, we would like to point out that omission of the PS1 survey leads to a slightly lower value of ΩM as compared with the best fit from the CMB.
 |
Fig. B.1. Two-dimensional and one-dimensional posterior distributions for four cosmological parameters and the nuisance parameter ΔH0 using only data from CSP, SDSS, and CfA. The contours show the 68% and 95% credibility levels. |
 |
Fig. B.3. As Fig. B.1, but using data from the combinations SDSS and PS1, PS1 and CfA, and SDSS and CfA. |
 |
Fig. B.4. As Fig. B.1, but using data from the combinations SNLS and PS1, SNLS and SDSS, and SNLS and CfA. |
Further inspection of the posteriors of individual surveys reveals that surveys with a mean redshift above 0.3 have very little constraining power on the proper motion of the Solar System, but are good in constraining the matter density. Moreover, removing the CfA surveys leads to a significant increase in the uncertainty of the Solar System proper motion. In order to obtain meaningful constraints on vo, RA, Dec, at least two surveys must be combined. All combinations are consistent with the common fit. We therefore conclude that the combination of the various SN samples is at least self-consistent.
All Tables
All Figures
 |
Fig. 1. Residual of the Hubble diagram as a function of the observed heliocentric redshift. The different colours indicate the redshift distributions of the individual SN surveys included in the Pantheon sample. |
| In the text | |
 |
Fig. 2. Residual of the Hubble diagram as a function of the observed heliocentric redshift indicating SNe with host redshift measurements and with other redshift measurements. |
| In the text | |
 |
Fig. 3. Two-dimensional and one-dimensional posterior distributions for four model parameters and the nuisance parameter ΔH0 for the full redshift-corrected Pantheon sample. The contours show the 68% and 95% credibility levels. |
| In the text | |
 |
Fig. 4. Posterior distributions using only SNe with host galaxy redshifts. |
| In the text | |
 |
Fig. 5. Posterior distributions allowing for non-zero curvature. |
| In the text | |
 |
Fig. 6. Best-fit parameters based on SNe with redshifts higher than zmin. All five parameters were varied (ΔH0, ΩM, vo, RA, and Dec). |
| In the text | |
 |
Fig. 7. Posterior distribution using peculiar velocity corrections from Carrick et al. (2015). |
| In the text | |
 |
Fig. 8. Posterior distribution assuming a constant bulk flow for all SNe with zhel < 0.03 in the fixed direction RAbulk = 194 deg, Decbulk = −57 deg with a Gaussian prior on the bulk velocity, vbulk = 159 ± 23 km s−1. Bulk direction and velocity prior are chosen according to Carrick et al. (2015). |
| In the text | |
 |
Fig. 9. Comparison of the posterior distribution for different measurements of the proper motion of the Sun. We show our own results taking the emitter peculiar velocities into account by using the covariance matrix in Eq. (16) and by means of corrections according to Carrick et al. (2015), respectively. For comparison, we also show the results from the analysis of high multipole moments of the CMB (Saha et al. 2021) and assuming that the CMB dipole is entirely explained by solar motion (Planck Collaboration I 2020). In the latter case, the uncertainties are too small to be displayed properly. We instead indicate the value by a vertical line. |
| In the text | |
 |
Fig. B.1. Two-dimensional and one-dimensional posterior distributions for four cosmological parameters and the nuisance parameter ΔH0 using only data from CSP, SDSS, and CfA. The contours show the 68% and 95% credibility levels. |
| In the text | |
 |
Fig. B.2. As Fig. B.1, but using only data from SNLS and PS1. |
| In the text | |
 |
Fig. B.3. As Fig. B.1, but using data from the combinations SDSS and PS1, PS1 and CfA, and SDSS and CfA. |
| In the text | |
 |
Fig. B.4. As Fig. B.1, but using data from the combinations SNLS and PS1, SNLS and SDSS, and SNLS and CfA. |
| In the text | |
 |
Fig. B.5. As Fig. B.1, but using data from all surveys, excluding CfA, SDSS, PS1, and SNLS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} T(\boldsymbol{n}) = \bar{T} \frac{1 - \boldsymbol{v}^2/c^2}{1 - \boldsymbol{v}\cdot \boldsymbol{n}/c} = T_0 + T_1 \cos \theta + \mathcal{O} [(v/c)^2]\end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq2.gif)
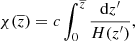
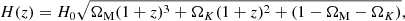
![$$ \begin{aligned} \overline{d}_{\rm L}(\overline{z})=\frac{(1+\overline{z})}{\sqrt{\Omega _K}} \frac{c}{H_0} \sinh {\left[ \sqrt{\Omega _K} (H_0/c) \chi (\overline{z})\right]}. \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq8.gif)
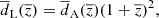
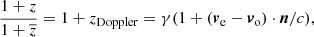
![$$ \begin{aligned} 1+z=(1+\overline{z})\left[1+ (v_{\rm e}/c) \cos \phi - (v_{\rm o}/c) \cos \theta \right]+\mathcal{O} (v^2) . \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq12.gif)
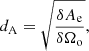
![$$ \begin{aligned} d\Omega = \overline{d\Omega } \frac{1-v_{\rm o}^2/c^2}{\left[1+ (v_{\rm o}/c) \cos \overline{\theta }\right]^2} = \overline{d\Omega } \left[1 - 2 (v_{\rm o}/c) \cos \theta \right] + \mathcal{O} (v^2). \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq17.gif)
![$$ \begin{aligned} d_{\rm A}(z)=\overline{d}_{\rm A}(\overline{z})\left[1+(v_{\rm o}/c) \cos \theta \right] +\mathcal{O} (v^2) . \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq18.gif)
![$$ \begin{aligned} d_{\rm L}(z)= \overline{d}_{\rm L}(\overline{z}) \left[1 + 2 (v_{\rm e}/c) \cos \phi - (v_{\rm o}/c) \cos \theta \right] +\mathcal{O} (v^2). \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq19.gif)
![$$ \begin{aligned} \mu = m_{\rm B} - M = 5 \log _{10}\left[ \frac{d_{\rm L}(z)}{\mathrm{Mpc} }\right]+25, \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq20.gif)
![$$ \begin{aligned} \overline{z}(z)=z + (1+z)\left[(v_{\rm o}/c) \cos \theta - (v_{\rm e}/c) \cos \phi \right] + \mathcal{O} (v^2). \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq22.gif)
![$$ \begin{aligned} \mu (z)&= 5 \log _{10}\left[ \frac{\overline{d}_{\rm L} \left(\overline{z}(z)\right)}{\mathrm{Mpc} }\right] + 25 \nonumber \\&\quad + 5 \log _{10}\left[1+2(v_{\rm e}/c) \cos \phi - (v_{\rm o}/c) \cos \theta \right]. \end{aligned} $$](/articles/aa/full_html/2022/12/aa42640-21/aa42640-21-eq23.gif)