| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 10 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202243377 | |
| Published online | 13 October 2022 | |
Trojan asteroids and the co-orbital dust ring of Venus
1
School of Astronomy and Space Science, Nanjing University,
163 Xianlin Avenue,
Nanjing
210023, PR China
e-mail: zhouly@nju.edu.cn
2
Key Laboratory of Modern Astronomy and Astrophysics in Ministry of Education, Nanjing University,
PR China
3
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz, Austria
4
Institute of Astronomy, National Central University,
Jhongli, Taoyuan City
32001, Taiwan
Received:
20
February
2022
Accepted:
13
June
2022
Context. Co-orbital asteroids have been thought to be the possible source of the zodiacal dust ring around the orbit of Venus, but the conclusions about the orbital stability and thus about the existence of Venus Trojans are inconsistent in the literature.
Aims. We present a systematic survey of the orbital stability of Venus Trojans that takes the dynamical influences from General Relativity and the Yarkovsky effect into account.
Methods. The orbits of thousands of fictitious Venus Trojans were simulated numerically. Using a frequency analysis, we describe their orbital stabilities and the dynamical mechanisms behind them. The influences of General Relativity and of the Yarkovsky effect, which were previously either neglected or oversimplified, were investigated in long-term numerical simulations.
Results. The stability maps on the (a0, i0) plane and (a0, e0) plane are depicted, and the most stable Venus Trojans are found to occupy low-inclination horseshoe orbits with low eccentricities. The resonances that carve the fine structures in the stability map are determined. General Relativity decreases the stability of orbits only little, but the Yarkovsky effect may drive nearly all Venus Trojans out of the Trojan region in a relatively short time.
Conclusions. The Venus Trojans have a poor orbital stability and cannot survive to the age of the Solar System. The zodiacal dust ring found around the orbit of Venus is more likely a sporadic phenomenon, as the result of a temporary capture into the 1:1 mean motion resonance of dust particles that were probably produced by passing comets or asteroids, but not by Venus Trojans.
Key words: celestial mechanics / minor planets, asteroids: general / planets and satellites: individual: Venus / methods: numerical
© Y.-B. Xu et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
In the circular restricted three-body problem (R3BP), the equilateral triangular Lagrange equilibrium points L4 and L5 are dynamically stable for all planets in the Solar System (see e.g. Érdi 1996b; Murray & Dermott 1999). For a long time, these solutions have been considered as only of theoretical interest, until Wolf (1907) discovered asteroid (588) Achilles, which librates around the L4 point of Jupiter. These asteroids were named by their discoverers after mythic characters in Greek legends about the Trojan War. From then on, it has become custom to call a celestial object librating around L4 or L5 of any planet a Trojan. Today, several thousand Trojans have been found orbiting around the orbit of Jupiter. A small number of Trojan asteroids have also been found around the Earth, Mars, Uranus, and Neptune.
Sharing the same orbit with a planet means that a Trojan asteroid has the same orbital period as the host planet, that is, they are in 1:1 mean motion resonance (MMR). The Trojan dynamics is always of special interest and has been studied theoretically and numerically for most of the planets in the Solar System. A comprehensive theoretical analysis in R3BP can be found for example in Szebehely (1967). A formal long-periodic solution for Trojans in R3BP was constructed by Garfinkel (1977, 1978). Based on the three-dimensional elliptic R3BP, an approximate analytical theory was developed by Érdi (1981, 1984, 1988), and the perturbations from other planets were taken into account by considering the Jupiter orbit as a secularly changing ellipse (Érdi 1996a).
Mikkola & Innanen (1992) explored the evolution of Trojantype asteroidal orbits with numerical simulations. With the advancement of computation ability, the numerical methods have been applied widely. Nearly a century after the discovery of Jupiter Trojans, the detection of the first Mars Trojan in 1990 (Bowell et al. 1990) caused many researches into the dynamical stability (Mikkola & Innanen 1994; Tabachnik & Evans 1999; Scholl et al. 2005a) and the origin of Mars Trojans (Christou 2013; Ćuk et al. 2015; Polishook et al. 2017). A decade later, the first Neptune Trojan was discovered (Pittichova et al. 2003). The origin and long-term stability of Neptune Trojans have been studied thoroughly (Dvorak et al. 2007; Zhou et al. 2009, 2011; Lykawka et al. 2009). Another decade later, the discovery and confirmation of the first Earth Trojan (Mainzer et al. 2011; Connors et al. 2011) elicited studies on the long-term stability of Earth Trojans (Dvorak et al. 2012; Marzari & Scholl 2013; Zhou et al. 2019). The first Uranus Trojan was discovered in 2011 (Alexandersen et al. 2013), before which their dynamical stabilities had been deeply studied (Nesvorný & Dones 2002; Marzari et al. 2003b), and Dvorak et al. (2010) postulated their existence at low and also high inclinations. This issue was recently thoroughly clarified by Zhou et al. (2020).
The observation of Venus Trojans (VTs for short) is challenging because of their close proximity to the Sun. A few searches in the Trojan region of Venus have so far reported no detection of stable VTs (Pokorný et al. 2020; Ye et al. 2020). However, there are a few studies on the dynamical stability and possibility of their existence. Tabachnik & Evans (2000) found stable VT orbits of both tadpole and horseshoe types over an integration timescale of 100 Myr and restricted the stable region to inclinations below 16°. Scholl et al. (2005b) presented a stability analysis of tadpole orbits over a gigayear timescale. They applied Laskar's frequency map analysis to derive dynamical maps, from the most stable region of which they integrated 30 chosen orbits to investigate the long-term stability. Under the purely gravitational model of the Solar System (consisting of the Sun and eight planets), all 30 test particles escaped after 1.2 Gyr. When a Yarkovsky effect of a certain strength was included, the lifespan decreased to 400 Myr. Thus the authors concluded that any population of primordial VTs on tadpole orbits would have disappeared by now. Using direct numerical integrations under the same gravitational model, Ćuk et al. (2012) found, however, that a substantial number of VTs of both tadpole and horseshoe orbits appear to be stable over 1 Gyr.
Recently, this controversy was taken up again by Pokorný & Kuchner (2019). Their main concern is the origin of the zodiacal dust ring of Venus rather than the long-term stability of VTs, but they reported that a group of hypothetical VTs may serve as the most essential source of the dust ring. They enlarged the number of test particles to 10 000 and included both tadpole and horseshoe orbits, and they extended the integration to the age of the Solar System (4.5 Gyr). Using the same purely gravitational model, they found that 8.2% of the test particles remained stable for the whole simulation, which they took to confirm the notion that primordial VTs could still exist today. However, the Yarkovsky effect was ignored in this research, although its importance had briefly been shown by Scholl et al. (2005b).
The first evidence for the presence of the dust ring associated with Venus is attributed to the measurements of the Venera 9 and 10 spacecraft (Krasnopolsky & Krysko 1979) and by measurements of the Helios mission (Leinert & Moster 2007), but conclusive measurements were finally obtained with STEREO (Jones et al. 2013, 2017) and by the Parker Solar Probe (Stenborg et al. 2021). The retention time of dust particles in the 1:1 MMR is shorter than 0.1–1 Myr before they are driven out by the drag induced by the so-called Poynting-Robertson effect (Klačka et al. 2014). If the dust ring is no temporary phenomenon, it must therefore be continuously filled with new particles either from the erosion of primordial VTs as Pokorný & Kuchner (2019) suggest, or from the zodiacal dust cloud. This needs to be examined carefully.
In one word, the dynamical structure in the Trojan region of Venus is not clearly known, and the mechanisms that produce and sustain the dust ring associated with Venus are still unclear. We also note that General Relativity (GR) has not been included in previous studies, although it could introduce considerable long-term influence to the motion of objects in the vicinity of the Sun. Both the stability of VTs and its implication on the existence of the dust ring around Venus deserve an investigation in greater detail.
Aiming at clarifying whether the primordial VTs serve as the main source of dust particles around the orbit of Venus, we present here an investigation of the dynamics of VTs with a frequency analysis method and numerical simulations. The rest of this paper is organised as follows. We introduce our model and methods in Sect. 2. The orbital stability of VTs is studied in Sect. 3. Then the effect of GR is examined in Sect. 4, followed by the investigation of the influence of the Yarkovsky effect. Finally, we conclude this paper in Sect. 5.
2 Model and Method
2.1 Dynamical Model
The dynamical model we adopted consists of the Sun, all planets in the Solar System, and massless fictitious VTs. We treated the Earth and the Moon as a whole in their barycentre. The initial planetary configuration at epoch of JD 245 7400.5 was taken from the JPL HORIZONS system1 (Giorgini et al. 1996). To explore the dynamical behaviour of VTs with different inclinations, we initialised the test particles with a grid on the (a0, i0) plane. The initial semi-major axis ranged from 0.71533 AU to 0.73133 AU with a step of 10−4 AU, and the inclination was sampled from 0° to 60° at intervals of 1°. Because there is no remarkable dynamical asymmetry between two triangular Lagrange points, we focused on the L4 point and initially placed VTs there with ω = ω2 + 60°, where co is the argument of per-ihelion2. For other angular elements including the longitude of the ascending node Ω and the mean anomaly M, we set the same values as for Venus. Hence the initial resonant angle
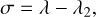 (1)
(1)
where λ = ω + Ω + M = ϖ + M is the mean longitude, is always 60° for all VTs. The initial eccentricity e was set to be the same value as for Venus e = e2 = 0.00675, as we did in our previous work (Zhou et al. 2009, 2019, 2020; Dvorak et al. 2012). This low eccentricity value is representative partly because the stable regions for Trojan asteroids around different planets are found to be located mainly at low eccentricities (e.g. Scholl et al. 2005a,b; Zhou et al. 2011). The dependence on eccentricity is further explored in Sect. 3.
2.2 Analysis Methods
The whole system was integrated up to ~ 10 Myr via a Lie-series integrator (Hanslmeier & Dvorak 1984) for the stability analysis. We used the same analysis method as we did in Zhou et al. (2009, 2011, 2019, 2020). An on-line low-pass digital filter was applied to the output of the integration to remove the short-period terms (Michtchenko & Ferraz-Mello 1995; Michtchenko et al. 2002), and then a fast Fourier transform (FFT) was applied to the filtered data to derive the frequency spectra.
The spectral number (SN) is defined as the number of peaks above a specific noise level in a power spectrum. The peaks are found under the criterion that their amplitudes are larger than the amplitudes of nearest four frequency points in the power spectrum. The critical amplitude was set to 1% of the highest peak, and the amplitudes below were considered the noise. The SN indicates the regularity of an orbit and generally reflects the long-term stability. The superiority and reliability of SN as the stability indicator for Trojans have been confirmed in Zhou et al. (2009, 2011, 2019, 2020).
To understand the structure seen in the dynamical map, we determined the locations of the resonances that dominate the orbital behaviour of VTs. For this purpose, the proper frequencies were precisely calculated via the method developed by Laskar (1990, 1993), which is basically an iterative scheme to search for the maximum of the amplitude of
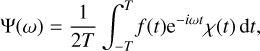 (2)
(2)
where f(t) is a quasi-periodic function obtained numerically over the time span [−T, T], ω is the target frequency, and the weight function χ(t) is the Hanning window χ(t) = 1 + cos(πt/T). A semi-analytical method was then used (see Sect. 3.2) to determine the location of resonances.
The integrator package Mercury6 (Chambers 1999), with some modifications to include GR and the Yarkovsky effect, was also adopted in our long-term numerical simulations of the VT motion to the age of the Solar System. The orbital stability of test particles was then examined by these simulations.
3 Dynamical Stability
3.1 Dynamical Map
Making use of the SN of cos σ, we constructed the dynamical maps. A step size of h = 0.01 yr was adopted to integrate the orbits, and after the low-pass filter, the outputs are given in every 213·h = 81.92 yr. We recorded 217 lines of outputs in total for the frequency analysis, so that the total integration time was T ≈ 1.07 × 107 yr. This time is longer than all the precession periods of planets (except for the nodal precession of Jupiter, see Table 1), thus these results can be used to reveal the involved secular mechanisms (for details of choosing the integration step size and output intervals, we refer to Zhou et al. 2009). The Nyquist frequency is thus 6.10 × 10−3 2π yr−1, and the resolution is 9.35 × 10−8 2π yr−1. In addition, results in a shorter time T/8 ≈ 1.34 × 106 yr were also used to obtain some details of the mechanisms of the short timescale.
The dynamical maps on the (a0, i0) plane for these two integration times are shown in Fig. 1. The blue orbits have the smallest SN, which means the greatest stability, and the red orbits are the opposite. On the maps we excluded the orbits that escaped from the co-orbital region of Venus3 within the integration time.
Overall, the dynamical maps are similar to the map for Earth Trojans (see Fig. 1 of Zhou et al. 2019). Symmetrically distributed around the libration centre at a = 0.72333 AU, the most regular orbits occupy the low-inclination region of i ≲ 10°, and the stable island extends up to i ≈ 20° and is interrupted by an unstable gap around i ≈ 24°. A much less regular region can be seen in between 28° ~ 40°. Compared to the Earth Trojans, the island at moderate inclinations (~30°) is much less stable, and it disappears in the longer integration (bottom panel of Fig. 1). Furthermore, the low-inclination stable island below i = 20° is solid, not like the dynamical maps for Earth Trojans, in which instability cavities exist at low inclinations.
A pair of instability strips stands vertically at 0.72333 ± 0.0018 AU. They are the separatrix of tadpole and horseshoe orbits and they could cause chaos. The edge of the stability region is defined by the Hill radius of Venus (~0.00676 AU), and on either side of the region lie the most stable VTs on horseshoe orbits. We conclude that some stability regions exist in which the stable VTs, especially those on horseshoe orbits, could reside, even for the age of the Solar System (see Sect. 3.3).
For a short integration time (1.34 × 106 yr), more details can be seen on the dynamical map for moderate- and high-inclined orbits. The instability gap around 24° is proven to be connected with the apsidal secular resonances with the Earth (ν34) and Mars (v4) (Brasser & Lehto 2002; Scholl et al. 2005b).
Eventually, some mechanisms on a longer timescale start to work, such as those related to the red belt around 15° on the dynamical map for 1.07 × 107 yr. We assume that the orbits over there should escape in the near future.
To calculate Fig. 1, the initial eccentricity was fixed at e0 = 0.00675, so it provides a representative collection of orbits in the low-eccentricity region in which the majority of stable orbits reside. To verify the dependence of the stability on the initial eccentricity, we calculated the SN on the (a0, e0) plane, this time with a fixed initial inclination at 5°. The dynamical map obtained from orbit integrations of 1.34 × 106 yr is shown in Fig. 2.
The stable regions are located at low eccentricities area, with the most stable orbits (in blue) occupying the region e0 ≲ 0.05. The dashed contour in Fig. 2 encloses orbits with SN < 102.06, with which the orbit will most probably survive 4.5Gyr in the pure-gravity model (see the discussion in Sect. 3.3). The vertical structures seen in Fig. 1, for instance the unstable strips corresponding to the separatrix between tadpole and horseshoe orbit, and the strips around a0 = 0.72053, 0.72613 AU are also shown in Fig. 2, implying that they arise due to mechanisms associated with the semi-major axis (mean motion).
In the low-eccentricity region in Fig. 2, we note that the feature of the dynamical map varies mainly along the semi-major axis (horizontally), but not along the eccentricity (vertically), that is, the dynamics does not sensitively depend on eccentricity in this low-eccentricity region. This phenomenon was also observed in Scholl et al. (2005b, Figs. 1 and 2 therein), who also reported by fitting polynomials for proper frequencies (g, s) that the eccentricity terms contribute much less than the inclination and the semi-major axis variation. A more evident dependence on eccentricity appears only in either high-inclination (≳20°) or high-eccentricity (≳0.17) regions (see Fig. 4 in Scholl et al. 2005b). These regions are for very unstable orbits however, and thus are not our concern in this paper. We therefore focus here on the dynamical maps on the (a0, i0) plane and set the initial eccentricity as e0 = 0.00675.
Proper frequencies of the planets in the Solar System.
 |
Fig. 1 Dynamical maps around the L4 point of Venus on the (α0, i0) plane for an integration time of 1.34 × 106 yr (top) and 1.07 × 107 yr (bottom). The colours indicate the base-10 logarithm of SN of cos σ for orbits surviving the integration time. |
 |
Fig. 2 Dynamical maps around the L4 point of Venus on the (a0, e0) plane for an integration time of 1.34 × 106 yr. The colours indicate the base-10 logarithm of SN of cos σ for orbits surviving the integration time. The dashed contour curve indicates log10 SN = 2.06 (see text for details). |
3.2 Frequency Analysis
The secular resonances carve the dynamical maps of Trojan asteroids of terrestrial planets (see e.g. Brasser & Lehto 2002; Zhou et al. 2019). To determine the secular resonances that cause the structures in the phase space, we conducted a frequency analysis method.
The proper frequencies of VTs are distinguishable from the forced frequencies because they are dependent on the orbital elements. Hence we can detect them in the frequency spectra. For details of determining the proper frequencies, we refer to Zhou et al. (2009). After obtaining the proper frequencies, we fit their dependences on the orbital elements of a0 and i0. Surely, the proper frequencies should also depend on the eccentricity e0. However, with fixed e0, we focus on the low-eccentricity region and do not analyse the eccentricity dependence in this paper.
We calculated and fitted the proper rates of the perihelion precession g = g(a0, i0) and of the ascending node precession s = s(a0, i0), which correspond to the proper frequencies of e cos ϖ and i cos Ω of VTs, respectively. Because the orbital behaviours of tadpole and horseshoe orbits are different from each other, their proper frequencies follow different dependences on the orbital elements. Piecewise quintic functions were adopted for the frequencies in these two regimes.
The secular resonances can be depicted by searching the integral domain for the combination of parameters (p, q, pj, qj) of the equation
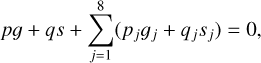 (3)
(3)
where gj and sj represent the precession rates of the perihelion and ascending node of the jth planet. The proper frequencies of the planets (see Table 1) andVTs were computedfromtheoutput of the 1.07 × 107 yr integration. The d’Alembert rule requires that 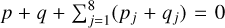 and
and 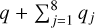 must be even. The value of
must be even. The value of 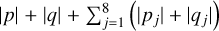 is defined as the degree of the secular resonance.
is defined as the degree of the secular resonance.
The main secular resonances we detected are shown in Fig. 3. The boundary between the tadpole and horseshoe orbits separates two regimes that are differently influenced by the secular resonances. Because the values of the proper frequencies of the horseshoe orbits are much higher than those of the tadpole orbits, Eq. (3), involving these frequencies, is less sensitive to different combinations of the proper frequencies of the planets. Therefore, the corresponding secular resonances are much closer to each other in the horseshoe regime, which means that the resonance overlap can take place more easily. It plays an important role in shaping the boundary of the stability region.
The apsidal secular resonances with the Earth (ν3) and Mars (ν4) clear the moderately inclined VTs, as we mentioned before. The locations are consistent with the result from Scholl et al. (2005b), although they depicted them on the plane of proper orbital elements. This type of apsidal resonances could increase the eccentricity of VTs to make them planet-crossing (see e.g. Murray & Dermott 1999). The orbits dominated by the ν3 and ν4 range from 17° to 35° (Brasser & Lehto 2002). The ν2 secular resonance, which is located in the high-inclination regime, could induce chaos, together with the ν11, which has also been determined by Brasser & Lehto (2002) and Scholl et al. (2005b). Orbits over 40° could also obtain a high eccentricity (Namouni 1999; Giuppone & Leiva 2016) via the von Zeipel-Lidov-Kozai mechanism (von Zeipel 1910; Lidov 1962; Kozai 1962; Ito & Ohtsuka 2019). The Tapsidal secular resonance with Saturn (ν6) lies in the low-inclination stability region. It seems to be weak because Saturn is too far away from the VTs. Nodal secular resonances such as ν13 and ν14 could control the variation in the inclination (see e.g. Murray & Dermott 1999). These two resonances could cause a variation in the inclination up to ~20°, while the inclinations of most of other orbits vary within 10°.
In addition to the linear secular resonances, we also searched for fourth-degree secular resonances. The resonances that only involve the apsidal (g) and nodal precession (s) are denoted by G- and S-type, respectively. The remainder are labelled C-type in the name of “combined”. We show the results in the right panel of Fig. 3, and the labels in the figure are explained as follows:
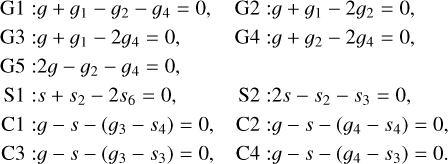 (4)
(4)
There are so many such resonances that we can only show some representatives of them. Many resonances could share the similar locations in the phase space, such as v2 and G2, and v6 and G4. These high-order secular resonances contribute to the fine structure of the dynamical maps. We note that C1–C4, four resonances of the same type g – s, gather around i0 = 15°. They clearly give rise to the instability strip there in the dynamical map, as we mentioned in Sect. 3.1. Involving both the apsidal and nodal precession, C1–C4 are thought to have remarkable influence on both the eccentricity and inclination. By inspecting the orbital evolution, we confirm the stronger variations in the eccentricity and inclination for orbits around 15°. We also note that the vertical strips along the inclination in the dynamical map are thought to be connected with the S-type resonances.
As is well known, the proper frequencies of the terrestrial planets change over time (Laskar 1989, 1990). The direct result of this frequency drift is that the related resonances could sweep a certain area in phase space, affecting more orbits and causing more resonance overlap. This is especially true for C1–C4 because they are close to each other and the frequency drift for the Earth and Mars is particularly remarkable (see Table 2). This is also true for G3 and S2. We note that the values of the frequency drift are calculated from our 1 Gyr integration of the Solar System and might certainly become higher for a longer integration time.
In addition to the frequency drift caused by the non-linear gravitational perturbation among planets, the GR also modifies the fundamental frequencies of the inner planets. For example, it produces an additional perihelion precession of 38 arcsec per century to Mercury. This change may then influence the effects of the resonances described above.
Adopting the first-order post-Newtonian expansion (e.g. Standish & Williams 2012), we included the GR effect from the Sun on the planets and VTs in our simulations. New locations of the resonances were obtained after GR was taken into account, as shown in Fig. 3. Because GR has the greatest influence on the apsidal precession of Mercury, the most obvious shift occurs in resonances involving g1, for example G1–G3. Fig. 3 still shows, however, that the effect of GR is only limited. In practice, GR can almost be ignored.
The secondary resonances could also play a role in Trojan dynamics (see e.g. Marzari et al. 2003a; Robutel & Gabern 2006; Zhou et al. 2009, Zhou et al. 2011, 2020). The 13:8 near-MMR (NMMR) between the Earth and Venus (Bazsó et al. 2010) might have a remarkable influence on the orbital behaviours of VTs. According to our calculation, the angle 13λ3 − 8λ2 circulates with a period about 238 yr, corresponding to a frequency of f13:8 = 4.193 × 10−3 2π yr−1. Secondary resonances take place when the frequency of the 13:8 NMMR (f13:8) intersects the libration frequency of the resonant angle cos σ of VTs (f). To determine the locations of secondary resonances on the (α0, i0) plane, we fixed one i0 and calculated the frequency f of the resonant angle for varying α0. Along this straight line of fixed i0 on the (α0, i0) plane, the frequency f changes with α0, and then we can determine whether f meets f13:8, where a secondary resonance occurs. We can also fix α0 and calculate the variation of f with respect to varying i0. Several examples are shown in Fig. 4.
The dynamical spectrum (Fig. 4) shows that for VTs with i0 = 17° (arbitrarily chosen as an example), f = f13:8 occurs around α0 = 0.72143 and 0.72523 AU (indicated by short arrows), which is very close to the separatrix between tadpole and horseshoe orbits (0.72153 and 0.72513 AU). Therefore, the overlap enhances the instability and causes a small extension of the instability strip away from the centre. The secondary resonance f = 2f13:8 appears around 0.72053 and 0.72613 AU (indicated by long arrows in Fig. 4), corresponding to the locations of two vertical strips in the dynamical map, and implying that this secondary resonance might be responsible for this unstable structure.
Moreover, for orbits with fixed semi-major axes, we find in Fig. 4 (open circles and diamonds) that the frequency f of the resonant angle changes only little as the inclination increases, implying that the structure caused by the secondary resonances appears as vertical strips in the dynamical map on the (a0, i0) plane. These vertical structures are clearly shown in Fig. 1, nearly parallel to the separatrix between the tadpole and horseshoe orbits. We also note that the overlap of these secondary resonances with the ν13 and ν14 secular resonances induces a growing instability along the initial inclination (Fig. 3).
Additionally, we inspected the frequency spectra of the eccentricity, and find that a small peak around f13:8 exists for VTs located in the aforementioned instability strip but not for VTs out of it, which also implies that this instability structure might be related with the 13:8 NMMR. However, considering the fact that the 13:8 resonance is of high order, its effect should be quite small, and we cannot completely exclude the possibility that other dynamical mechanisms contribute to the formation of these instability structures in the dynamical map and that the equality between frequencies mentioned above is just a coincidence.
 |
Fig. 3 Secular resonances over the short-time (1.34 × 106 yr) dynamical map on the (α0, i0) plane (see text for the explanations of the labels along the curves). The left panel depicts the linear secular resonances, and the right panel depicts the fourth-degree secular resonances. The tadpole and horseshoes orbits are separated by the vertical dark lines. Grey shadows delimit the coverage areas of the resonances considering the frequency drift of the inner planets. The distinguishable locations of secular resonances deduced from the model including GR effect are indicated by the dashed red lines (see text). |
Mean values 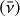 and amplitudes (max – min) of the proper frequencies of terrestrial planets.
and amplitudes (max – min) of the proper frequencies of terrestrial planets.
 |
Fig. 4 Libration frequency f of the 1:1 resonant angle for VTs (cos σ) vs initial semi-major axis (bottom abscissa) and initial inclination (top abscissa). Solid squares in orange indicate the orbits with varying semi-major axis but fixed initial inclination i0 = 17°; while open circles in blue and diamonds in green indicate the orbits with varying initial inclination but fixed semi-major axes a0 = 0.72053 and 0.72143 AU, respectively. The frequency of the 13:8 NMMR between the Earth and Venus f13:8 and its double value 2f13:8 are depicted by the dashed and solid lines, respectively. The arrows point to the intersections of f with these two lines. |
3.3 Long-term Stability
To confirm the long-term stability of VTs, we set those orbits that survived the 1.07 × 107 yr integration as the initial population (2271 orbits in total) and extended the integration to 4.5 Gyr using the Mercury6 (Chambers 1999) integrator package. Because these orbits are the survivors of the ~ 10 Myr evolution of the originally near circular orbits, they are reasonably expected to occupy the most stable region in the orbital elements space. Particularly, the instantaneous eccentricities of them may have formed the eccentricity distribution (Fig. 5) of long-termstability.
As shown in Fig. 5, the instantaneous eccentricities are distributed mainly in between e = 0.03 and 0.05, with sharp drops on both sides. This is consistent with the results in Pokorný & Kuchner (2019) where the most stable orbits surviving the Solar System age have initial eccentricities of about 0.04 (see Fig. 4a therein).
Integrated up to 4.5 Gyr, the lifespan of these orbits is shown in Fig. 6. About 39.5% of the orbits could survive to the age of the Solar System, and most of them are on horseshoe orbits. This agrees very well with the conclusion drawn from the dynamical map (Fig. 1).
For tadpole orbits, the long-time integrations confirm the results we obtained via the frequency analysis method (see Sect. 3.2). C1–C4 do destabilise the orbits around 15°, driving them out of the co-orbital region within 1 Gyr. Resonances including ν6, S2, G3, and G4 could also contribute to the escape of tadpole orbits, but are less effective than C1–C4. Certainly, VTs at the boundary of the stability region lose their stability in this long integration.
Overall, if we just consider a purely gravitational model of the Solar System, some primordial Venus companions exist, especially on horseshoe orbits. Scholl et al. (2005b) found no stable orbits that could survive 4.5 Gyr, probably owing to the small initial population (30). Pokorný & Kuchner (2019) obtained a survivor ratio of only 8.2% because there are too many high-eccentricity orbits in their initial population, while the eccentricity of the initial population in our simulation is almost concentrated around 0.04.
Because the SN is an indicator of orbital regularity, its value is correlated negatively with the lifespan of an orbit. We examined the SN values (calculated from the 1.34 × 106 yr integration) and lifespan of these orbits and find that 95% of orbits surviving 4.5 Gyr have log10 SN ≤ 2.06. Thus, we regard SN = 102.06 as the critical value for the most stable orbits, and mark the most stable areas in Fig. 2 by the contour curve. Apparently, the stable regions can hardly extend to e0 = 0.1, and most of them are in the low-eccentricity (e ≤ 0.05) region. Therefore, although the instantaneous eccentricities (0.00675 at time zero) of these initial population are very low, their distribution after ~107 yr evolution (Fig. 5) agrees basically with both the eccentricities of stable orbits found by Pokorný & Kuchner (2019) and our assumption that long-term stable orbits are mainly low-eccentricity ones. We conclude that the initial population adopted here to examine the long-term stability are representative. Even though some orbits with higher eccentricities (0.05−0.1) could survive 4.5 Gyr in this purely Newtonian gravitation model, the stability of all these orbits will finally be destroyed by the Yarkovsky effect, as we show below.
In addition to the Yarkovsky effect, GR, which may also change the orbital stabilities, is not included in the simulations so far. We determine the influence of GR in greater detail in the following section. The combined effects of GR and the Yarkovsky effect are then investigated subsequently.
 |
Fig. 5 Eccentricity distribution of the initial population for the 4.5 Gyr integration. The blue bins indicate the frequency of e, and the green curve is the cumulative frequency. An eccentricity lower than 0.02 or higher than 0.1 is not shown for clarity. |
 |
Fig. 6 Lifespan of VTs around the L4 point on the (a0, i0) plane. The colour indicates the lifespan in gigayears in logarithm. Only the orbits that survive the 1.07 × 107 yr integration are included, and orbits over 25° are omitted for clarity. |
4 General Relativity and the Yarkovsky Effect
4.1 General Relativity
The effect of GR was hardly ever mentioned in the research on the dynamical stability of objects in the Solar System because it was generally thought to be negligible unless in the very close vicinity of the Sun. VTs are on the orbit of Venus with a semimajor axis of about 0.7 AU, therefore their long-term stability could be affected at a non-negligible level both directly by GR and indirectly by its influence on the motion of planets.
To investigate how GR affects the long-term stability of VTs, we set the same initial population (2271 test particles surviving 1.07 × 107 yr) and integrated their orbits to 4.5 Gyr in a model including GR. During the integration, some orbits lost their stability and escaped from the Trojan region, and the survivor ratios of test particles during the whole time are illustrated in Fig. 7. For comparison, the survivor ratio in the model without GR is plotted in the same figure.
Without GR, 1365 test particles survive 1 Gyr and 898 survive 4.5 Gyr. With GR, these two numbers are 1264 and 810, respectively. The relative differences at 1 Gyr and at 4.5 Gyr are smaller than 10%, implying that GR does affect the stability of VTs, but not substantially so.
To further show the influence of GR on the orbital stability of VTs, we calculated the value of log10(T1/T2), where T1 is the lifetime of a test particle in the model without GR and T2 is this lifetime with GR. We plot the result in Fig. 8. As shown in Fig. 8, red and blue indicated the destabilising and stabilising effect of GR, respectively, which are mixed in the region. We still find that the red parts (destabilisation) are mainly located in the middle of the VT region, however, where the resonances involving the apsi-dal precession of inner planets and VTs gather (see Fig. 3). The stabilised parts (blue) are mainly located around the secondary resonance f = 2f13:8 at a = 0.72053 AU, 0.72613 AU, implying that the secondary resonance is almost destroyed due to GR.
 |
Fig. 7 Survivor ratio of test particles during 4.5 Gyr. The dashed line shows the model with GR, and the solid line shows the model without GR. |
 |
Fig. 8 Effect of GR in the VT region. The colour bar represents log10(T1/T2) (see text). Thus grey means that the lifetimes in both models are the same (4.5 Gyr), while red indicates that the corresponding orbit is destabilised to some extent by GR (T1 > T2), and blue is the opposite. |
4.2 Yarkovsky effect
The Yarkovsky effect produces a recoil force that arises from the absorption and anisotropic re-radiation of thermal energy, resulting in the long-term evolution of the semi-major axis for small objects orbiting the Sun (for a brief review see e.g. Bottke et al. 2006). Due to the rotation and revolution of the object, an asteroid may be subject to the diurnal Yarkovsky effect and the seasonal effect. Generally, the diurnal effect is much more remarkable than the seasonal effect unless the spin axis is parallel to the orbital plane. Therefore, it is reasonable to consider only the diurnal effect and neglect the seasonal one.
The Yarkovsky effect continuously increases the semi-major axis of an asteroid if it rotates prograde or decreases the semimajor axis if it is a retrograde rotator. The situation can be complicated when the asteroid is locked in an MMR. For Trojan asteroids, Wang & Hou (2017) showed that the libration amplitude of the semi-major axis undergoes remarkable variation when the Yarkovsky effect works together with the 1:1 MMR. The libration amplitude of the semi-major axis decreases with time for prograde rotating objects but increases for retrograde ones. This phenomenon has been observed in numerical simulations of the Earth Trojans (Zhou et al. 2019) and Jupiter Trojans (Hellmich et al. 2019). Due to this mechanism, Trojans are pushed either towards or away from the centre of libration, neither of which leads to a long-term stable region because the central part of tadpole orbits is less stable (see Figs. 1 and 6), just as in the case of the Earth Trojans (Zhou et al. 2019).
The Yarkovsky effect on an asteroid is determined in a complicated way by its distance to the Sun, its thermal parameters, the size, bulk density, surface density, spin rate, and the obliquity of its spin axis. Unfortunately, these parameters are generally poorly determined. Following Scholl et al. (2005b) and Brož & Morbidelli (2013), we may parametrise typical VTs with a bulk density of 2.5 g cm−3, a surface density of 1.5 g cm−3, a surface thermal conductivity of 0.001 Wm−1 K−1, a specific heat capacity of 680 J kg−1 K−1, an emissivity of 0.9, and a Bond albedo of 0.1. For typical rotators in the Solar System, as mentioned in Bottke et al. (2006), an object with a radius R = 1 km has a rotation period of 5000 s, and the rotation period is proportional to the radius. Based on these parameters, we simplified the formula of the semi-major axis drift rate for asteroids around the Venus orbit due to the diurnal Yarkovsky effect as (Vokrouhlický 1999; Xu et al. 2020)
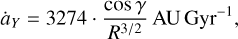 (5)
(5)
where γ represents the obliquity of the spin axis, and R is the asteroid radius given in metres.
4.3 Stability Under the Yarkovsky Effect
We performed numerical simulations of the motion of VTs in a model including the Yarkovsky effect that drives the semimajor axis of the Trojan to migrate following the rule in Eq. (5). We selected from previous simulations those 1365 test particles that survived 1 Gyr without GR and 1264 test particles that survived 1 Gyr with GR, and then integrated their orbits to 4.5 Gyr under Yarkovsky effects of different magnitudes. Several Yarkovsky drift rates ȧy = ±0.05, ±0.25, ±0.5 and ±2 AU Gyr−1 were adopted. When we assume that the spin axis is perpendicular to the orbital plane, that is, γ = 0° or 180°, the Yarkovsky drift rates chosen above can be translated into asteroid sizes with radii of 1600, 560, 350, and 140 m, respectively, according to Eq. (5).
The results of our simulations are summarised in Fig. 9, in which the survivor ratios of test Trojans at the end of each simulation are plotted.
The Yarkovsky effect apparently decreases the survivorratio. As the strength of the Yarkovsky effect increases, the survivor ratio drops down sharply. A similar relation has been observed for the Earth Trojans that are influenced by the Yarkovsky effect (Marzari & Scholl 2013; Zhou et al. 2019). Like for Earth Trojans, the asymmetry of the stability that the retrograde spinning Trojans (ȧY < 0) are less stable than the prograde spinning ones (ȧY > 0) with the same Yarkovsky effect (i.e. the same |ȧY|) is shown in Fig. 9 as well. For the same |ȧY| value, the survivor ratio of the inward-migrating retrograde rotators (γ = 180°) is lower than that of the outward-migrating prograde rotators (γ = 0°). This happens because of the different responses of the libration amplitude of the Trojans to the inward or outward semi-major axis drift (Wang & Hou 2017; Zhou et al. 2019; Hellmich et al. 2019), and also because of the different stability structures in the inner and outer regions of the dynamical map (Figs. 1 and 6).
Comparing the results that take the effect of GR (crosses) into account and the results without GR (open circles) in Fig. 9, we may find that the influence of GR becomes more prominent than that shown in Fig. 7, implying that the effect of GR on destabilising the Trojans’ motion is enhanced after cooperating with the Yarkovsky effect. The destabilisation of GR mainly occurs either in the inner central region or around the boundary of the stable island (red parts of Fig. 8), into which Trojans will always be pushed by the Yarkovsky effect within a given time. As a result, the Yarkovsky effect in a sense amplifies the effect of GR.
According to our experience that we obtained through studying the Earth Trojans (Zhou et al. 2019), the relation between the survivor ratio and the Yarkovsky drift rate shown in Fig. 9 can be numerically fitted by a piecewise Gaussian function for the positive and negative ȧY, separately. The fitting curves for test particles surviving 4.5 Gyr with GR are plotted in Fig. 9 (solid red lines), and they can be used to impose constraints on the sizes of primordial VTs that probably still exist today. If a survivor ratio of 1% is taken as the cut-off probability of existence (as in Zhou et al. 2019), which corresponds to ȧY = −0.50 AU Gyr−1 and +0.77 AU Gyr−1 on the fitting curves for retrograde and pro-grade spinning asteroids, respectively, we may infer from Eq. (5) that a primordial VT surviving the Yarkovsky effect for 4.5 Gyr cannot be smaller than 350 m in radius if it is a retrograde rotator (γ = 180°), and it should be larger than 260 m for a prograde rotator (γ = 0°).
Overall, due to the effect of GR and the Yarkovsky effect, the probability of the existence of primordial VTs that are not detected today is extremely low. This implies that the dust ring associated with Venus is replenished by some other sources.
 |
Fig. 9 Survivor ratio of VTs under the Yarkovsky effect. Black refers to the results of an integration to 1 Gyr, and red shows this for 4.5 Gyr. The crosses and open circles refer to the results with and without GR, respectively. The survivor ratio of 1.0 right at the centre shows the case ȧY = 0 (without the Yarkovsky effect). Solid lines are the fitting curves of the data for 4.5 Gyr with GR (red crosses, see text). |
5 Conclusion and Discussion
The orbital stability of VTs was thoroughly investigated via numerical simulations in this paper. In a fully gravitational model consisting of the Sun and eight planets, the motions of thousands of test particles in the region of 1:1 MMR with Venus were integrated to ~ 10 Myr. Based on these simulated orbits and using the spectral number as the indicator of orbital regularity, we plotted detailed dynamical maps on the (a0, i0) plane. Stable regions of low inclination (≲15°) for VTs mainly on horseshoe orbits were found (Fig. 1). Most of them are located in the region of low eccentricity (≲0.05) (Fig. 2).
Using the frequency analysis method, we determined the proper frequencies of VTs and then located the resonances that contribute to shaping the structures of the dynamical maps. We find that the instability of motion is mainly caused by the linear apsidal secular resonances v2, v3, v4, and v6, while the nodal secular resonances v13 and v14 may excite an inclination variation up to ~20° (Fig. 3). The secondary resonances related to the frequency of the quasi 13:8 MMR between the Earth and Venus are likely to cause the narrow vertical strips of instability on the (a0, i0) plane (Fig. 4). Some higher-order secular resonances involving apsidal and nodal precession of Trojans have been located as well, and they produce the fine structure in the dynamical maps. Their effects are further enhanced by the frequency drift (of planetary precession) in the inner Solar System, and they are partly responsible for the depletion of Trojans on tadpole orbits in the long term (Fig. 3). Compared to the effect of frequency drift, GR introduces only tiny changes in the stability (Fig. 7). In summary, in this purely gravitational model, either with or without GR, VTs of low inclination (≲15°) and small eccentricity (≲0.05) (Fig. 5), particularly those on horseshoe orbits, may survive to the Solar System age (Fig. 8).
However, the stability of asteroids in the Trojan region will be destroyed by the Yarkovsky effect (Fig. 9). As shown in our previous work (Zhou et al. 2019), the Yarkovsky effect has depleted practically all primordial Earth Trojans (if there were any) that are so small that they could avoid being detected by surveys such as OSIRIS-REx. Assuming that VTs have the same (typical) physical and thermal parameters as Earth Trojans, the Yarkovsky effect on VTs must be stronger than that on Earth Trojans because they are closer to the Sun. Taking a survivor ratio of 1% as the critical probability, our calculations show that a retrograde spinning VT surviving the Yarkovksy effect for 4.5 Gyr cannot be smaller than 350 m (or 260 m if it is spinning pro-grade). In other words, those asteroids smaller than 350 m (or 260 m) in radius have a probability of < 1% to survive to the Solar System age.
Recent surveys dedicated to searching for VTs placed upper limit on the sizes of these hypothetical objects. The null detection of VTs by the Zwicky Transient Facility (ZTF) twilight survey (Ye et al. 2020) with a limiting r-band magnitude of 19.5 suggests that there is no VT larger than 250–750 m (assuming albedos between 0.45 and 0.04). The Cerro-Tololo Inter-American Observatory (CTIO) twilight survey (Pokorný et al. 2020) with a limiting magnitude of 21 (corresponding to a radius ~200m for S-type and ~500 m for P-type asteroid) reported no detection of VTs either.
In one word, the Yarkovsky effect expels small VTs, and observational surveys deny the existence of large ones. Hence, we may conclude that undetected primordial VTs are very unlikely to exist today.
Our calculations suggest that the dust ring around the orbit of Venus cannot be the byproduct of erosion of primordial VTs. Still, a temporary capture of asteroids by the resonance may be possible and might be the source for co-orbital dust on smaller timescales. Five co-orbital objects of Venus are currently known, which are small asteroids on chaotic orbits. Their estimated lifetimes in the 1:1 MMR with Venus are rather short: object 2001 CK32 is currently in transition between a horseshoe and a quasi-satellite orbit with e ≃ 0.38, and numerical studies suggest that the resonant capture lasted for less than 10 000 years (Brasser et al. 2004). Asteroid 2002 VE68 currently stays on a fairly chaotic quasi-satellite orbit with e ≃ 0.41, and the temporary capture time is thousands of years (Mikkola et al. 2004). The three other co-orbital asteroids 2012 XE133, 2013 ND15, and 2015 WZ12 (de la Fuente Marcos & de la Fuente Marcos 2013, 2014, 2017) are much fainter and on eccentric thus less stable orbits. Because of their short lifetimes and short trajectory arcs in the vicinity of the Venus orbit, the contribution from these temporary co-orbital asteroids to the dust ring – if any – can only be seen as a temporary phenomenon.
An alternative mechanism for maintaining the dust ring is a continuous concentration and dispersion of dust particles in the 1:1 orbital resonance with Venus. Due to their small size, dust particles receive significant non-gravitational perturbations, such as radiation pressure, Poynting-Robertson drag, and solar wind drag (Burns et al. 1979). Driven by these perturbations, dust particles migrate toward the Sun from their birthplaces (main belt asteroids or Jupiter-family comets), and the orbital resonances with planets may trap or delay the travelling particles so that dust rings can form.
It is known that the capture of small objects into external resonances takes place, but it does not occur for internal resonances (Sicardy et al. 1993; Beauge & Ferraz-Mello 1994; Liou & Zook 1995). The co-orbital resonance, being neither an external nor an internal resonance, is special. Numerical studies already indicated the low capture probability of dust in the external and 1:1 MMRs with Venus (Jackson & Zook 1989; Dermott et al. 1994; Jeong & Ishiguro 2012). Recently, Sommer et al. (2020) studied the formation of resonant dust rings in the inner Solar System in great detail and reported that the neighbouring planet (Earth here) severely impairs the ability of the external resonances of Venus to trap dust particles. Consequently, circumsolar rings at the external and co-orbital resonances with Venus cannot be formed in this way.
Even when the dust particles have been captured, they may escape from the resonances with the aid of the non-gravitational perturbations. Zhou et al. (2021) reported that non-gravitational perturbations shift the location and size of the stability islands around the Lagrange points of Venus significantly, resulting in a short lifespan of the particles in the co-orbital region. After considering the interaction of charged dust grains with the interplanetary magnetic field, the authors determined that the Lorentz force further destabilises the orbits.
Therefore, neither primordial VTs, temporary co-orbital asteroids, nor migrating dust clouds are adequate to explain the dust ring around the orbit of Venus. Either there are some other sources that we do not know yet, or the dust ring itself is only a temporary phenomenon. The origin of the dust ring associated with Venus is still an open question.
Acknowledgements
We thank the anonymous referee for the insightful comments that help us to improve the manuscript. This work has been supported by the National Key R&D Program of China (2019YFA0706601) and National Natural Science Foundation of China (NSFC, Grants Nos. 11933001 & 12150009). We also acknowledge the science research grants from the China Manned Space Project with NO.CMS-CSST-2021-B08. C.L. was supported by the FWF national science fund with project number P-30542.
References
- Alexandersen, M., Kavelaars, J., Petit, J., & Gladman, B. 2013, Minor Planet Electronic Circulars, 2013-F19 [Google Scholar]
- Bazsó, Á., Dvorak, R., Pilat-Lohinger, E., Eybl, V., & Lhotka, C. 2010, Celest. Mech. Dyn. Astron., 107, 63 [CrossRef] [Google Scholar]
- Beauge, C., & Ferraz-Mello, S. 1994, Icarus, 110, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, William F. J., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Annu. Rev. Earth Planet. Sci., 34, 157 [CrossRef] [Google Scholar]
- Bowell, E., Holt, H. E., Levy, D. H., et al. 1990, BAAS, 22, 1357 [NASA ADS] [Google Scholar]
- Brasser, R., & Lehto, H. J. 2002, MNRAS, 334, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Brasser, R., Innanen, K. A., Connors, M., et al. 2004, Icarus, 171, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Brož, M., & Morbidelli, A. 2013, Icarus, 223, 844 [CrossRef] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [Google Scholar]
- Christou, A. A. 2013, Icarus, 224, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, M., Wiegert, P., & Veillet, C. 2011, Nature, 475, 481 [CrossRef] [Google Scholar]
- Ćuk, M., Hamilton, D. P., & Holman, M. J. 2012, MNRAS, 426, 3051 [CrossRef] [Google Scholar]
- Ćuk, M., Christou, A. A., & Hamilton, D. P. 2015, Icarus, 252, 339 [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2013, MNRAS, 432, 886 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2014, MNRAS, 439, 2970 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2017, RNAAS, 1, 3 [NASA ADS] [Google Scholar]
- Dermott, S. F., Jayaraman, S., Xu, Y. L., Gustafson, B. Å. S., & Liou, J. C. 1994, Nature, 369, 719 [CrossRef] [Google Scholar]
- Dvorak, R., Schwarz, R., Süli, Á., & Kotoulas, T. 2007, MNRAS, 382, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Dvorak, R., Bazsó, Á., & Zhou, L. Y. 2010, Celest. Mech. Dyn. Astron., 107, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Dvorak, R., Lhotka, C., & Zhou, L. 2012, A&A, 541, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Érdi, B. 1981, Celest. Mech., 24, 377 [CrossRef] [Google Scholar]
- Érdi, B. 1984, Celest. Mech., 34, 435 [CrossRef] [Google Scholar]
- Érdi, B. 1988, Celest. Mech., 43, 303 [Google Scholar]
- Érdi, B. 1996a, in Dynamics, Ephemerides, and Astrometry of the Solar System, eds. S. Ferraz-Mello, B. Morando, & J.-E. Arlot, IAU Symposium, 172, 171 [Google Scholar]
- Érdi, B. 1996b, Celest. Mech. Dyn. Astron., 65, 149 [Google Scholar]
- Garfinkel, B. 1977, AJ, 82, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Garfinkel, B. 1978, Celest. Mech., 18, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, in Bulletin of the American Astronomical Society, 28, AAS/Division for Planetary Sciences Meeting Abstracts #28, 1158 [Google Scholar]
- Giuppone, C. A., & Leiva, A. M. 2016, MNRAS, 460, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Hanslmeier, A., & Dvorak, R. 1984, A&A, 132, 203 [NASA ADS] [Google Scholar]
- Hellmich, S., Mottola, S., Hahn, G., Kührt, E., & de Niem, D. 2019, A&A, 630, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ito, T., & Ohtsuka, K. 2019, Monogr. Environ. Earth Planets, 7, 1 [Google Scholar]
- Jackson, A. A., & Zook, H. A. 1989, Nature, 337, 629 [CrossRef] [Google Scholar]
- Jeong, J. H., & Ishiguro, M. 2012, in Asteroids, Comets, Meteors 2012, 1667, 6201 [NASA ADS] [Google Scholar]
- Jones, M. H., Bewsher, D., & Brown, D. S. 2013, Science, 342, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, M. H., Bewsher, D., & Brown, D. S. 2017, Icarus, 288, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Klačka, J., Petržala, J., Pástor, P., & Kómar, L. 2014, Icarus, 232, 249 [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Krasnopolsky, V. A., & Krysko, A. A. 1979, Planet. Space Sci., 27, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1989, Nature, 338, 237 [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D Nonlinear Phenomena, 67, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., & Moster, B. 2007, A&A, 472, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [Google Scholar]
- Liou, J.-C., & Zook, H. A. 1995, Icarus, 113, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Lykawka, P. S., Horner, J., Jones, B. W., & Mukai, T. 2009, MNRAS, 398, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Bauer, J., Grav, T., et al. 2011, ApJ, 731, 53 [Google Scholar]
- Marzari, F., & Scholl, H. 2013, Celest. Mech. Dyn. Astron., 117, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Tricarico, P., & Scholl, H. 2003a, MNRAS, 345, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Tricarico, P., & Scholl, H. 2003b, A&A, 410, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michtchenko, T. A., & Ferraz-Mello, S. 1995, A&A, 303, 945 [NASA ADS] [Google Scholar]
- Michtchenko, T. A., Lazzaro, D., Ferraz-Mello, S., & Roig, F. 2002, Icarus, 158, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S., & Innanen, K. 1992, AJ, 104, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S., & Innanen, K. 1994, AJ, 107, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, S., Brasser, R., Wiegert, P., & Innanen, K. 2004, MNRAS, 351, L63 [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar system dynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Namouni, F. 1999, Icarus, 137, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Dones, L. 2002, Icarus, 160, 271 [CrossRef] [Google Scholar]
- Nobili, A. M., Milani, A., & Carpino, M. 1989, A&A, 210, 313 [NASA ADS] [Google Scholar]
- Pittichova, J. A., Meech, K. J., Wasserman, L. H., et al. 2003, Minor Planet Electronic Circulars, 2003-A55 [Google Scholar]
- Pokorný, P., & Kuchner, M. 2019, ApJ, 873, L16 [CrossRef] [Google Scholar]
- Pokorný, P., Kuchner, M. J., & Sheppard, S. S. 2020, PSJ, 1, 47 [Google Scholar]
- Polishook, D., Jacobson, S. A., Morbidelli, A., & Aharonson, O. 2017, Nat. Astron., 1, 0179 [NASA ADS] [CrossRef] [Google Scholar]
- Robutel, P., & Gabern, F. 2006, MNRAS, 372, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Scholl, H., Marzari, F., & Tricarico, P. 2005a, Icarus, 175, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Scholl, H., Marzari, F., & Tricarico, P. 2005b, AJ, 130, 2912 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Beauge, C., Ferraz-Mello, S., Lazzaro, D., & Roques, F. 1993, Celest. Mech. Dyn. Astron., 57, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Sommer, M., Yano, H., & Srama, R. 2020, A&A, 635, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Standish, M., & Williams, J. 2012, in Explanatory Supplement to the Astronomical Almanac, eds. P. K. Seidelmann, & S. E. Urban (California: University Science Books) [Google Scholar]
- Stenborg, G., Gallagher, B., Howard, R. A., Hess, P., & Raouafi, N. E. 2021, ApJ, 910, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Szebehely, V. 1967, Theory of orbits. The restricted problem of three bodies [Google Scholar]
- Tabachnik, S., & Evans, N. W. 1999, ApJ, 517, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Tabachnik, S. A., & Evans, N. W. 2000, MNRAS, 319, 63 [Google Scholar]
- Vokrouhlický, D. 1999, A&A, 344, 362 [NASA ADS] [Google Scholar]
- von Zeipel, H. 1910, Astron. Nachr., 183, 345 [Google Scholar]
- Wang, X., & Hou, X. 2017, MNRAS, 471, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M. 1907, Astron. Nachr., 174, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y.-B., Zhou, L.-Y., Lhotka, C., & Ip, W.-H. 2020, MNRAS, 493, 1447 [CrossRef] [Google Scholar]
- Ye, Q., Masci, F. J., Ip, W.-H., et al. 2020, AJ, 159, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L.-Y., Dvorak, R., & Sun, Y.-S. 2009, MNRAS, 398, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L.-Y., Dvorak, R., & Sun, Y.-S. 2011, MNRAS, 410, 1849 [NASA ADS] [Google Scholar]
- Zhou, L., Xu, Y.-B., Zhou, L.-Y., Dvorak, R., & Li, J. 2019, A&A, 622, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, L., Zhou, L.-Y., Dvorak, R., & Li, J. 2020, A&A, 633, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, L., Lhotka, C., Gales, C., Narita, Y., & Zhou, L.-Y. 2021, A&A, 645, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Mean values  and amplitudes (max – min) of the proper frequencies of terrestrial planets.
and amplitudes (max – min) of the proper frequencies of terrestrial planets.
All Figures
 |
Fig. 1 Dynamical maps around the L4 point of Venus on the (α0, i0) plane for an integration time of 1.34 × 106 yr (top) and 1.07 × 107 yr (bottom). The colours indicate the base-10 logarithm of SN of cos σ for orbits surviving the integration time. |
| In the text | |
 |
Fig. 2 Dynamical maps around the L4 point of Venus on the (a0, e0) plane for an integration time of 1.34 × 106 yr. The colours indicate the base-10 logarithm of SN of cos σ for orbits surviving the integration time. The dashed contour curve indicates log10 SN = 2.06 (see text for details). |
| In the text | |
 |
Fig. 3 Secular resonances over the short-time (1.34 × 106 yr) dynamical map on the (α0, i0) plane (see text for the explanations of the labels along the curves). The left panel depicts the linear secular resonances, and the right panel depicts the fourth-degree secular resonances. The tadpole and horseshoes orbits are separated by the vertical dark lines. Grey shadows delimit the coverage areas of the resonances considering the frequency drift of the inner planets. The distinguishable locations of secular resonances deduced from the model including GR effect are indicated by the dashed red lines (see text). |
| In the text | |
 |
Fig. 4 Libration frequency f of the 1:1 resonant angle for VTs (cos σ) vs initial semi-major axis (bottom abscissa) and initial inclination (top abscissa). Solid squares in orange indicate the orbits with varying semi-major axis but fixed initial inclination i0 = 17°; while open circles in blue and diamonds in green indicate the orbits with varying initial inclination but fixed semi-major axes a0 = 0.72053 and 0.72143 AU, respectively. The frequency of the 13:8 NMMR between the Earth and Venus f13:8 and its double value 2f13:8 are depicted by the dashed and solid lines, respectively. The arrows point to the intersections of f with these two lines. |
| In the text | |
 |
Fig. 5 Eccentricity distribution of the initial population for the 4.5 Gyr integration. The blue bins indicate the frequency of e, and the green curve is the cumulative frequency. An eccentricity lower than 0.02 or higher than 0.1 is not shown for clarity. |
| In the text | |
 |
Fig. 6 Lifespan of VTs around the L4 point on the (a0, i0) plane. The colour indicates the lifespan in gigayears in logarithm. Only the orbits that survive the 1.07 × 107 yr integration are included, and orbits over 25° are omitted for clarity. |
| In the text | |
 |
Fig. 7 Survivor ratio of test particles during 4.5 Gyr. The dashed line shows the model with GR, and the solid line shows the model without GR. |
| In the text | |
 |
Fig. 8 Effect of GR in the VT region. The colour bar represents log10(T1/T2) (see text). Thus grey means that the lifetimes in both models are the same (4.5 Gyr), while red indicates that the corresponding orbit is destabilised to some extent by GR (T1 > T2), and blue is the opposite. |
| In the text | |
 |
Fig. 9 Survivor ratio of VTs under the Yarkovsky effect. Black refers to the results of an integration to 1 Gyr, and red shows this for 4.5 Gyr. The crosses and open circles refer to the results with and without GR, respectively. The survivor ratio of 1.0 right at the centre shows the case ȧY = 0 (without the Yarkovsky effect). Solid lines are the fitting curves of the data for 4.5 Gyr with GR (red crosses, see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


