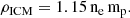EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 666 (October 2022) A&A, 666 (2022) A44 Full HTML
Open Access
Issue
A&A
Volume 666, October 2022
Article Number A44
Number of page(s) 16
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202243100
Published online 03 October 2022

© B. S. Kalita et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

The formation of massive galaxies (> 1011 M⊙) that happened within the first ∼3 Gyr after the Big Bang and was sustained by cold streams of gas (Birnboim & Dekel 2003; Kereš et al. 2005) is still not fully understood (Somerville & Davé 2015; Vogelsberger et al. 2020). Cold gas accretion, which includes smooth gas as well as clumpy material, is expected to be ubiquitous in high redshift dense environments (Dekel et al. 2009a). Encouraging observational evidence for cold streams was recently obtained for a sample of galaxy groups and clusters at 2.0 < z < 3.3 and for statistical samples of massive galaxies (Daddi et al. 2022a,b). Yet there remains a paucity of direct observations of how this critical process affects individual galaxies. In general, the need of gas accretion fueling the star formation in galaxies is abundantly clear and exemplified by the tight correlation between their star formation rates (SFRs) and the stellar mass at least up to z ∼ 4–6 (the star-forming main-sequence; Daddi et al. 2007; Elbaz et al. 2007; Whitaker et al. 2012; Speagle et al. 2014; Schreiber et al. 2015). Morphologically, this phase is expected to feature secularly growing disks (Daddi et al. 2010a; Tacconi et al. 2010; Dekel & Krumholz 2013; Feldmann & Mayer 2015).

Meanwhile, to accomodate for the existence of compact (∼1 kpc), spheroidal, quiescent galaxies (QGs) observed at z ∼ 2–4 (e.g., Valentino et al. 2020a; Lustig et al. 2021; D’Eugenio et al. 2021) in contrast to the relatively more extended star-forming disk galaxies (van der Wel et al. 2014), an intermediate population of compact star-forming galaxies (cSFGs) has been proposed and widely observed (Barro et al. 2013, 2014; van Dokkum et al. 2015; Puglisi et al. 2019, 2021). The feature at the heart of this hypothesis, quite literally, is the compact star-forming core that is expected to form the spheroidal bulge characteristic of the compact QGs. When gas is driven into the central compact region, the increase in the gas surface density results in a rise in star-formation that rapidly builds up the stellar mass of the bulge. However, the mode of formation of these cSFGs has been a matter of debate. On one hand, simulations predict that smooth-gas-accretion driven violent disk instabilities result in the gas being driven to the core of secularly evolving disk-like galaxies, once the galaxy mass reaches ∼109.5 M⊙ and thereby creating most of the stellar mass in a compact spheroidal structure (wet compaction; Dekel et al. 2013; Zolotov et al. 2015; Tacchella et al. 2016). Whereas observational studies of large statistical samples advocate the rapid effects of major mergers between galaxies leading to the formation of such objects (Cimatti et al. 2008; Ricciardelli et al. 2010; Fu et al. 2013; Ivison et al. 2013; Toft et al. 2014, 2017; Elbaz et al. 2018; Gómez-Guijarro et al. 2018). Both scenarios have its issues however. Wet compaction predicts the presence of high-gas fractions in cSFGs that is simply not observed (Puglisi et al. 2021; Gómez-Guijarro et al. 2022a,b). Whereas, a dominance of the merger-driven starbursts (pushing them a factor of 3–4 above the main sequence) would suggest that the galaxy simply transitions through the star-forming main-sequence on its way to becoming quiescent, making the tight correlation between the SFR and stellar masses difficult to reproduce. Although, Elbaz et al. (2018) does provide an tentative solution through a subpopulation of star-bursts hidden within the main-sequence.

The morphology of cSFGs could hold clues to disentangling the processes. Besides their characteristic submillimeter bright highly star-forming cores, the surrounding stellar regions can also provide valuable information, which is only possible through near-IR follow-ups of ALMA (submillimeter) detected cSFGs. In the wet compaction scenario, once the galaxy enters its peak compaction phase at ∼109.5 M⊙, the stellar disk (or a proto-disk) stays constant or shrinks while the core rapidly builds up mass (Tacchella et al. 2016). Whereas in case of major mergers between massive galaxies, clear signs of disturbed morphology, especially in the form of clumpy stellar structures (at least during the initial phases) is anticipated (Lotz et al. 2006; Bournaud et al. 2011; Rujopakarn et al. 2019; Calabrò et al. 2019) and extended tidal-tails (e.g., Bridge et al. 2010; Wen & Zheng 2016; Guo et al. 2016). Attempts at characterizing the stellar regions are already underway (e.g., Puglisi et al. 2021; Gómez-Guijarro et al. 2022a), with the narrative swaying in favour of mergers (Elbaz et al. 2018; Rujopakarn et al. 2019). Nevertheless, it is imperative to determine whether this is a universal trend, especially in regions where galaxies are expected to grow under the influence of high levels of accretion, which might be more conducive for the wet compaction scenario.

Therefore, to attempt a resolution, one will have to specifically investigate high-redshift massive dark-matter halos which are expected to allow the penetration and survival of cold-gas streams into a hot halo (Kereš et al. 2005; Dekel et al. 2009a). This is primarily driven by the expected evolution with halo mass (∝MDM) and redshift (∝(1 + z)α with α ≈ 2.25–2.50). Studying cSFG counterparts within such accretion-rich environments is our best bet at disentangling the effects of accretion and mergers. However, observationally establishing the presence of infalling cold-gas streams in halos has proved to be extremely challenging, with only a handful of convincing cases yet (using Ly-α emission as a tracer; Martin et al. 2015, 2019; Umehata et al. 2019; Daddi et al. 2021, 2022a,b). Following up on one of these cases, we investigate the galaxy-group RO-1001 at z = 2.91 presented in Daddi et al. (2021). The structure hosts three massive (> 1011 M⊙) star-forming galaxies in its inner core (along with an additional quiescent galaxy; Kalita et al. 2021a), at the center of its ∼4 × 1013 M⊙ dark-matter halo potential well. They are all < 70 kpc (9″) from the peak of the giant 300 kpc-wide Lyman-α halo centered on the group, and spectroscopically coincident with the intensity averaged Lyman-α emission within ±500 km s−1 (Fig. 1). Finally, the Lyman-α contours provide tentative identification of accretion-streams that are expected to feed the central halo and hence the three star-forming galaxies within.

thumbnail Fig. 1.

Location of the massive star-forming galaxies in the network of Lyman-α filaments. Left: color image composite of RO-1001, using observations in F160W, F125W and F606W. The ALMA data has been coadded to that in F606W since both trace star-formation, differing based on dust obscuration. The scaling of the ALMA data was done based on its flux to SFR ratio in comparison to the same for that in F606W. The white dashed contours trace the Lyman-α halo whereas the cyan arrows show the tentative directions of the three gas-accretion filaments converging onto the center of the group potential well (the correspondence to the galaxies is discussed in detail in Sect. 5.2). Right: zoom on the three star-forming galaxies (A, B and C) as seen in ALMA submillimeter dust-emission while the white contours trace the F160W flux tracing stellar light. The contours begin at 4σ with increments of 4σ. The arrows indicate the direction of the streams, which are shown in green if they are aligned with the major axis of the galactic disks (in dashed white lines), as discussed in Sect. 5.2. Those which are not, are in red. In case of Galaxy-A, we rather show the major axis of the ALMA contour with the white dashed line.

It needs to be noted that whenever we refer to accretion in this work, we are including both smooth gas as well as clumpy material. The latter is expected to make up ∼ one-third of the accreted matter (Dekel et al. 2009a) and its interaction with the galaxies could be observationally characterized as minor mergers of varying mass ratios. In this paper, we discuss the observational data in Sect. 2, followed by the analysis and results (Sect. 3). We then discuss galaxy morphology, star formation and their link to accretion in Sect. 4. Finally, we provide the conclusions in Sect. 8. Throughout, we adopt a concordance ΛCDM cosmology, characterized by Ωm = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1. We use a Chabrier initial mass function. Magnitudes and colors are on the AB scale. All uncertainties on measured parameters that have been quoted indicate the 90% confidence interval determined from the limits of Δχ2 = 2.71. All images are oriented such that north is up and east is left.

2. Observational data

To study the three star-forming galaxies (A, B and C) in RO-1001 (Fig. 1), we make use of HST-WFC3 imaging in 3 bands (F160W, F125W and F606W) over a total of 11 orbits during Cycle 27 (Proposal ID: 15190, PI: E. Daddi). The data reduction was executed using the pipeline grizli1. The 5σ point-source sensitivities reached are 26.25 (F160W), 26.47 (F125W) and 26.39 (F606W) with a pixel scale of 0.06″ and a half-power beam-width of 0.24″ for F160W. Public COSMOS F814W imaging (Scoville et al. 2007) was also incorporated into the analysis. Furthermore, we used the Ks-band image from data release 4 of Ultra-VISTA (McCracken et al. 2012). Finally, IRAC 3.6 μm and 4.5 μm images were taken from the Spitzer Matching Survey of the Ultra-VISTA Deep Stripes (SMUVS; Ashby et al. 2018), while those at 5.7 μm and 7.9 μm are obtained from the public COSMOS database (Laigle et al. 2016).

New Atacama Large Millimetre Array (ALMA) band 7 observations, taken in Cycle 7 (Project ID: 2019.1.00399.S, PI: R.M. Rich) provide the submillimeter information of our sources. The data reduction was carried out using the Common Astronomy Software Application (CASA) and a maximum sensitivity of 28 μJy beam−1 was reached, with a synthesized beam size of 0.49″ × 0.46″. Finally, we utilize NOrthern Extended Millimter Array (NOEMA) spectroscopy data to map the CO[3−2] transition in each of the three galaxies. The synthesized beam size at 88.3 GHz is 4.0″ × 1.8″. The spectra creation and analysis is carried out using a GILDAS-based pipeline2, and has been already discussed in a previous work (Daddi et al. 2021).

3. Analysis

We use the combination of the data listed above (Sect. 2) to derive the properties of the three star-forming galaxies in RO-1001. Each of them show extremely compact submillimeter bright rotating cores primarily centered on the much more extended (4–9×) near-IR detected stellar components (Fig. 1, right panel), with both being coplanar in at least two-thirds of the cases (Galaxies B and C). The stellar regions also show marked lopsidedness in their emission. We investigate in detail each of these aspects of the galaxies in this section. Given that Galaxy-B is the most extended and hence best resolved, we always begin with the description of its analysis for simplicity. We then proceed to Galaxies A and C, where the same prescription as that for Galaxy-B is used.

3.1. Near-IR surface brightness fitting

We investigate the distribution of rest-frame optical emission in Galaxy-B by model-fitting (Fig. 2) the intensity profiles using the software GALFIT (Peng et al. 2002, 2010). The H-band (F160W) image is used since it has the highest signal-to-noise among the available bands. We find that fitting and subtracting a double Sérsic profile (with indices ∼0.5) gives the best result, assessed by the maximum fluctuations in the residual image (found to be < 1σ). Care is taken to simultaneously subtract all nearby sources within ∼8″. We also fit the same profile, convolved with the appropriate point-source-functions (PSFs), to the images in all other observed wavelength windows to ascertain consistency. We find no > 1σ fluctuations in the respective residual images. We find that the two Sérsic profiles for Galaxy-B are clearly not spatially coincident with the submillimeter bright compact core (discussed below in Sect. 3.2), but rather fall ∼0.8″ on either side of it (and hence with a spatial separation of ∼0.16″ between the two Sérsic profile centers). We also find remarkable consistency of the axes ratio and position angles of the two Sérsic profiles, hence likely part of a continuous stellar structure. We repeat this procedure for Galaxies A and C. Galaxy-A is found to have a complex morphology which is fit with a double Sérsic in differing (almost orthogonal) orientations. Galaxy-C on the other hand is found to resemble Galaxy-B in terms of an accordance with two coaligned Sérsic profiles with low indices (< 1) on either side of submillimeter core. But in this case the separation is ∼0.2″, making it more compact than Galaxy-B.

thumbnail Fig. 2.

Morphological profile fitting of stellar emission. Left panel: HST F160W cutouts of Galaxies-A and B (top) and Galaxy-C (bottom) used for the morphological model fitting. Middle and right panels: GALFIT returned models and residuals of the same cutouts. In the latter, only the RO-1001 galaxy models have been subtracted. The rest of the sources, although used during the fit, have been left in the image.

To measure integrated effective radii (re) of each of the galaxies, we did an additional round of fitting using single Sérsic profiles. Besides using the generic version of the Sérsic profile, we also invoke the m = 1 Fourier component to account for the lopsidedness of the stellar components. This is due to quantify the emission asymmetry we observe in each of the cases which is later discussed in Sect. 5.1. We also measure growth curves using circular apertures with their centers fixed at the ALMA core of the galaxies to independently determine the effective radius. For Galaxy-A, we only use the northern component of its complex near-IR double emission, which we determine as the primary stellar region due to its proximity to the submillimeter emission. We use the average of all three methods that are consistent within 15–20%, to obtain the final measurements reported in Table 1: 3 ± 1 kpc, 9 ± 2 kpc and 4 ± 1 kpc for Galaxies-A, B and C respectively. It is noteworthy that for each galaxy, the single profiles are characterized by Sérsic indices < 1, indicating disk-like morphology (and hence we refer to them as disks throughout this work, a conclusion which will be reinforced in Sect. 4.2). The ellipticities measured for the three galaxies are 0.5 ± 0.1, 0.15 ± 0.05 and 0.5 ± 0.2 (A, B and C), indicating an almost edge-on orientation for Galaxy-B.

Table 1.

Properties of the star-forming massive galaxies in RO-1001.

3.2. Submillimeter emission analysis

The compact highly star-forming regions of the galaxies are detected thanks to their dust emission using ALMA at 870 μm. It is noteworthy that due to a well characterized PSF and high signal-to-noise, we have the ability to map structures much smaller than the integrated ALMA PSF (Rujopakarn et al. 2019). We begin with a detailed morphological analysis of the emission region in Galaxy-B. Due to the data being distributed over multiple partially overlapping pointings, we combine the ones with Galaxy-B within their primary beam. To do so, we follow the procedure outlined in Gómez-Guijarro et al. (2022a), for combination and stacking of individual pointings in ALMA. We phase shift each of them to set the source coordinates at their respective phase center. Finally, the pointings are combined into a single measurement set which provides the maximum sensitivity available with our data.

Since the Sérsic profile, commonly used to study galaxy morphologies, cannot be easily extended to the UV space due to its Fourier transform not being analytically expressible, we use a substitute. We exploit the Spergel profile (Spergel 2010), recently incorporated within the MAPPING procedure of GILDAS. This has been found to correlate well with the Sérsic profile allowing us to extract Sérsic parameters corresponding to the Spergel parameters we determine. To also determine the robustness of the fitting procedure (Fig. 3; Table 2), we perturb the initial parameters within a factor of 5 over a total of ∼200 times and repeat the fitting. We also artificially inject 1000 times the best fitting model of each galaxy at different empty locations (one at a time) and fit them individually to estimate reliable error for our measurements based on the a-posteriori dispersion of resulting parameters. This procedure also shows that there are no detectable systematic biases in the measured quantities.

thumbnail Fig. 3.

Top panel: ALMA 870 μm image of the core of RO-1001 with the three star-forming galaxies clearly visible. Each of them were fit with intensity profiles which were then subtracted to obtain the residual image displayed in the bottom panel. The ALMA PSF at 870 μm is shown in the inset on the top right.

Table 2.

Derived morphological Spergel parameters in submillimeter.

For Galaxy-B, we obtain an almost-perfect exponential profile characteristic of a disk of effective radius ∼1.1 kpc, with a Spergel index of 0.55 ± 0.12 (Sérsic index ∼1) and an ellipticity of 0.40 ± 0.01. From the model hence returned, we measure the 870 μm observed-frame flux. This is converted to a total-infrared luminosity (LIR; 8–1000 μm) using the integrated SED from the coadded photometry of RO-1001 (Daddi et al. 2021). This can then be converted to a SFR of 674 ± 106 M⊙ yr−1 using the widely adopted conversion relation (Kennicutt 1998; Daddi et al. 2010b):

SFR IR [ M ⊙ yr − 1 ] = 1.0 × 10 − 10 L IR [ L ⊙ ] . $$ \begin{aligned} \mathrm{SFR}_{\rm IR} [M_{\odot }\,\mathrm{yr}^{-1}] = 1.0 \times 10^{-10} \, L_{\rm IR} [L_{\odot }]. \end{aligned} $$(1)

The error for this measurement is determined from the 1σ dispersion in the dust-temperature dependent parameter ⟨U⟩, that is usually invoked during the conversion of the 870 μm flux to LIR. We use this to account for variations in dust temperature of individual galaxies with respect to the average value. This approach of evaluating SFR uncertainties is over-conservative, as it does not take into account that the integrated bolometric IR luminosity (hence SFR) of the 3 galaxies that is known to better than 10% accuracy, given the well sampled IR SED including Herschel (Daddi et al. 2021).

In Galaxy-A, we obtain a much different Spergel index (−0.61 ± 0.04) that translates to a Sérsic index ∼4. The situation is similar in Galaxy-C with a Spergel index of −0.48 ± 0.12, although it has an additional point source adjacent to it (at 0.14″). The sizes of these profiles are very compact with effective radii ∼0.7 kpc and 0.9 kpc. We measure the SFR using the same prescription as that for Galaxy-B, and estimate values of 345 ± 55 M⊙ yr−1 and 313 ± 50 M⊙ yr−1 for Galaxies A and C respectively.

3.3. Determining the quiescence of the stellar regions

Besides the measurements for the submillimeter bright compact cores, the high resolution 870 μm map (Sect. 2) also provides us with constraints on the levels of star formation in the surrounding regions. We are mainly interested in the estimates for the extended stellar regions detected in near-IR, that lack any submillimeter emission. Using the H-band models as fixed priors, we measure 3σ upper-limits for each of the galaxies by simultaneously fitting them along with the primary profiles for the cores in the ALMA data (uv plane). For Galaxy-B, we estimate a 3σ flux upper-limit of 0.25 mJy (corresponding to an SFR upper-limit of 19 M⊙ yr−1) for the stellar disk, while we obtain 0.77 mJy and 0.55 mJy (60 M⊙ yr−1 and 43 M⊙ yr−1) for Galaxies A and C respectively. This provides clear evidence of almost all star formation being concentrated at the core leaving the massive stellar disks devoid of it and well below the star-forming main-sequence (Fig. 4).

thumbnail Fig. 4.

Components of the three galaxies on the star-forming main-sequence: star-bursting bulges and quiescent disks. The SFR vs. stellar-mass values of the star-bursting core, the quiescent stellar disk and the combination of the two placed with respect to the star-forming main-sequence (Schreiber et al. 2015) at z = 3, shown as the black solid line. The shaded region demarcates the 0.3 dex uncertainty in the relation. We use the 3σ ALMA upper-limits as the value for SFR with the associated gray error-bars showing the range allowed by our SED model fitting. The latter have been artificially offset in the x-axis to emphasize the difference in the method of measurement.

We note that the estimation of the star formation upper limits in the stellar disks should be considered as overly conservative. This is because the conversion to SFR is done based on the average IR SED in the group which is driven by the coaddition of the emission from all three submillimeter bright galactic cores in RO-1001 that have a much higher SFR surface density (ΣSFR; for example see Fig. 5). Hence, the dust temperature in the disks would likely be lower due to a softer radiation field (based on the star-formation surface density vs. dust temperature relation, Valentino et al. 2020b, see also Magdis et al. 2012; Magnelli et al. 2014; Daddi et al. 2015), which would in turn drive our 3σ upper-limit even lower, probably at least by factors of 2−3.

thumbnail Fig. 5.

Spatial distribution of Galaxy-B stellar mass and star formation rates. Left: upper panel shows SFR distribution model of Galaxy-B, with the morphology determined by the F160W stellar emission in case of the disk, and the ALMA dust emission for the core. The amplitudes are determined by the SFR of the two components. Lower panel: is a 1D representation of the plot above, after a rotation the make the major axis horizontal. Middle: stellar mass distribution following the same procedure. Here the mass in the core is determined from the difference between the dynamical mass and gas-mass determined from the CO[3−2] emission line. Right: specific SFR provided by the ratio of the SFR and the stellar mass.

3.4. Star formation history modeling

We make use of the photometry obtained in observed frame optical and near-IR, to estimate a star formation history (SFH) and thereby the age of the stellar population as well as stellar masses. The measurements can primarily be attributed to the stellar disks since the prodigious submillimeter flux from the cores is by design at the expense of UV rest-frame flux. However, during our fitting procedure, we do fix an additional core component in each case using positional priors obtained in Sect. 3.2. Except in the IRAC bands, all others return fluxes < 5% of the total galaxy flux. However for IRAC, the PSF is a factor ∼10 larger than that of HST and a factor ∼5 compared to Ultra-VISTA. Hence in this case, the sources are unresolved and this leads to the photometry corresponding to the integration over the whole galaxy. Albeit, in each of the cases the stellar mass within the core is expected to be < 10% (based on estimates discussed in Sect. 3.5) that ensures a minimal contribution. Nevertheless, Fig. 6 does suggest progressively higher fluxes in the IRAC bands, leading to offsets from SED models. To limit the influence of the rapidly star-forming core, primarily in the IRAC bands with insufficient resolution to disentangle the core from the disk, we execute the SED fitting in three stages. The first is done using photometry up to the bands where the galaxies are well-resolved (2.1 μm). We then include the remaining 4 bands in pairs of two. We find that the results from the first two stages are almost identical within their errors and hence use the results of the second stage (up to the 4.5 μm band; due to better constraints). We show in Fig. 6 that the net photometry at the third stage is reproducible using the SED derived at stage-two and an additional highly obscured component for the core.

thumbnail Fig. 6.

Best-fit SED models in optical and near-IR for each of the three star-forming galaxies in RO-1001. The photometry with their respective errorbars are shown in red. The cyan contours show a modified SED with an addition of an example 0.1 Gyr old highly obscured (AV = 6.5–7.5) constant star-formation history SED in each case. In each case, the resulting stellar-masses are in agreement with our CO[3−2] estimates within 0.1 dex and are hence a representation of contributions of the star-bursting cores.

For a description of the SED model fitting, we refer the readers to Appendix A. The procedure for Galaxy-B returns the lowest reduced χ2 of 2.0 for the two declining SFH models used (composite-τ and delayed-τ). In case of a constant star-formation model this value is found to be 6.8 that translates to a Δχ2 = 38, making it highly unlikely. Hence, this indicates that the disk in Galaxy-B is undergoing a decline in star-formation, as already conclusively demonstrated by the ALMA upper limits. We also determine this decline to be significant by measuring the age vs. τ ratio from the delayed-τ models and it is found to be 7 ± 1. Given that the composite-τ models are relatively more robust, we use them to measure the look-back time of half-mass formation ( t 50 = 0 . 5 − 0.2 + 0.7 $ t_{50} = 0.5^{+0.7}_{-0.2} $ Gyr), that can be considered to be the approximate epoch at which the last major star formation episode had occurred. However, the results from delayed-τ models are also in agreement. Furthermore, we obtain a SFR estimate of 42 − 37 + 51 M ⊙ $ 42^{+51}_{-37}\,M_{\odot} $ yr−1, consistent with the ALMA 3σ upper-limit.

The picture is slightly less strict in Galaxy-C followed by Galaxy-A. In the former, the declining models still give the best fit (reduced-χ2 = 1.9) and a t 50 = 0 . 2 − 0.1 + 1.3 $ t_{50} = 0.2^{+1.3}_{-0.1} $ Gyr. But the constant star formation model is relatively less unlikely than for Galaxy-B, with a reduced-χ2 of 3.7. Galaxy-A on the other hand has values of 0.8 and 1.1 for almost equally plausible declining and constant star formation models, allowing for possible ongoing star formation in the disk. Nevertheless, the SFR in both these cases ( 94 − 94 + 66 M ⊙ $ 94^{+66}_{-94}\,M_{\odot} $ yr−1 for Galaxy-A and 66 − 49 + 446 M ⊙ $ 66^{+446}_{-49}\,M_{\odot} $ yr−1 for Galaxy-C) are still in general agreement with the much more stringent ALMA 3σ upper-limit.

We also derive UVJ colors (Fig. 7) not so much to ascertain quiescence that is already unambiguously demonstrated by ALMA, but rather to compare them to more classical examples of high redshift quiescent galaxies. Of special interest are the widely studied post-starburst (PSB) galaxies that have experienced quenching of star-formation over the last < 0.8 Gyr and generally show low dust attenuation (Gobat et al. 2012; Schreiber et al. 2018; Forrest et al. 2020; D’Eugenio et al. 2020; Valentino et al. 2020a). The PSB ages are potentially similar to the mass-weighted ages derived for our sample, while attenuation in our case is larger (Table 1). We find that the observed UVJ colors of our quiescent disks are much redder than those of known population of quiescent systems at z ∼ 3. Also, at least in two cases they are scattered just outside of the formal UVJ-passive boundary. However, when correcting for dust reddening the colors of the three galaxies in RO-1001 more closely resemble those of PSBs as well as of the massive quiescent galaxy with a mass-weighted age > 1 Gyr (Kalita et al. 2021a) within the same group (Fig. 7).

thumbnail Fig. 7.

UVJ colors of high-z QGs (z > 2.5) adapted from D’Eugenio et al. (2020). The post-star burst region is demarcated with the red box as specified in Belli et al. (2019). The marker sizes are proportional to the stellar mass. The red and blue stars are the dust uncorrected and corrected measurements of the quiescent stellar disks in the three star-forming galaxies within our sample. The final star in orange marks the location of Galaxy-D, a quiescent galaxy photometrically confirmed to be part of RO-1001 (Kalita et al. 2021a).

Finally for Galaxy-B, we pay special attention to the spatial decomposition of the stellar mass estimates (listed in Table 1) derived from the SED fitting procedure – by obtaining separate photometry of the northern and southern sections of its elongated disk. This is to quantify the lopsidedness in the stellar structure. We hence find the total stellar mass of 1.6 ± 0.4 × 1011 M⊙ for the complete stellar region is divided into 1.1 × 1011 M⊙ and 0.5 × 1011 M⊙ for the northern and southern segments. It is noteworthy that for this analysis, we only use observations up to the 2.1 μm band beyond which the resolution is too low to spatially disentangle the two parts.

3.5. Rotating gas traced by CO[3−2] transition

A direct spectroscopic tracer of the gas content of the galaxies is available in the form of NOEMA CO[3−2] transition observations. For Galaxy-B, we use its integrated luminosity ( log ( L CO ( 3 − 2 ) ′ / ( K km − 1 pc 2 ) ) = 10.46 $ \log(L^\prime_\mathrm{CO(3{-}2)}/(\mathrm{K\,km^{-1}\,pc^2})) = 10.46 $) to estimate a gas mass. This is calculated from the line flux (Daddi et al. 2021) using the relation prescribed in a recent work (Silverman et al. 2018). Using a standard R31 = 0.5 (Daddi et al. 2015; Valentino et al. 2020a,b), we hence derive log ( L CO ( 1 − 0 ) ′ ) = 10.76 $ \log(L^\prime_\mathrm{CO(1{-}0)}) = 10.76 $. 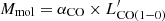The gas mass is finally computed as M mol = α CO × L CO ( 1 − 0 ) ′ $ M_{\mathrm{mol}} = \alpha_{\mathrm{CO}} \times L^\prime_\mathrm{CO(1{-}0)} $ by adopting a conversion factor αCO = 0.8 M⊙ (K km s−1 pc2)−1 as expected in starbursts (given location of the cores, with respect to the star-forming main-sequence in Fig. 4, and their very high SFR surface densities). This provides values of 4.6 × 1010 M⊙, 0.7 × 1010 M⊙, 4.2 × 1010 M⊙ for Galaxy-B, A and C respectively. Although, we do acknowledge that this estimate is dependent on our choice of conversion factors. Nevertheless, we can place a strict upper-limit on the gas mass using the dynamical mass estimates calculated below (that is, in the limiting case in which there was no stellar mass nor dark matter in the cores), which is less than 2× above the current values in each case. A Milky-Way-like αCO would have resulted in a factor of 5 higher gas-mass. Hence, these are in direct conflict with the dynamical mass values. Moreover, any increase in gas-mass would also indicate almost a negligible stellar mass, which in turn would place the galaxy-cores at a much higher offset from the star-forming main-sequence. This would suggest even more star-burst-like characteristics.

The width of the emission line in Galaxy-B is used to determine the dynamical mass within the dusty core where the gas is expected to be confined. Given the submillimeter emission profile of the core is found to resemble a disk, we measure the Mdyn, re within the effective radius re using the following relation (Daddi et al. 2010a):

M dyn , r e = 1.3 × r e × ( FWZV CO [ 3 − 2 ] / 2 ) 2 G sin 2 i ± 12.5 % . $$ \begin{aligned} M_{\mathrm{dyn},r_{\rm e}} = 1.3 \times \frac{r_{\rm e} \times \left(\mathrm{FWZV}_{\mathrm{CO}[3{-}2]}/2\right)^2}{G\,{\sin ^{2}}i} \pm 12.5\%. \end{aligned} $$(2)

The effective radius returned from the submillimeter emission profile is used in this equation. The width of the line, quantified by the parameter FWZVCO[3–2] is already reported in Table 1, while the inclination angle (i) is determined based on the ellipticity of the submillimeter profile. Subsequently, we measure the total dynamical mass, Mdyn, tot = 2 × Mdyn, re = 1.3 ± 0.1 × 1011 M⊙. The factor of 2 in invoked since only half of the mass is contained within re. We use the same procedure to obtain Mdyn, tot = 2.6 ± 0.3 × 1010 M⊙ and 1.7 ± 0.2 × 1011 M⊙ for Galaxies A and C. However, given their cores have morphology closer to a Sérsic index of 4, we re-estimate the Mdyn, tot using the following formula applicable to an elliptical galaxy dominated by random motion.

M dyn , r e ≈ 5.0 r e σ e 2 G · $$ \begin{aligned} M_{\mathrm{dyn},r_{\rm e}} \approx 5.0\, \frac{{r}_{\rm e}\,\sigma _{\rm e}^{2}}{G}\cdot \end{aligned} $$(3)

We measure the total dynamical masses of ∼2.2 × 1010 M⊙ and 2.4 × 1011 M⊙ for Galaxies A and C respectively, reasonably consistent with our earlier estimates. Although the relatively high discrepancy in case of Galaxy-C likely points to the rotational-dominance expected in a gas-rich structure. Nevertheless, we do not expect the structures to fully conform to such a dynamical arrangement due to the inherent dissipative nature of gas within them.

Finally, two separate continuum images are created for Galaxies B and C, by dividing the whole spectral range into two segments that are separated by the average location of the CO[3−2] emission of the whole galaxy. The offset between the peaks trace the plane of rotation, which are found to be in agreement with the major axes of the respective galaxies in both submillimeter and near-IR (Fig. 8). A similar analysis is not possible for Galaxy-A due to a low signal-to-noise of the CO[3−2] detection.

thumbnail Fig. 8.

Two panels showing the rotational properties in Galaxies B and C with three individual subimages: (top-left) the NOEMA CO[3−2] emission profiles for the blue and red-shifted sections with respect to the average galaxy profile shown as contours superimposed on the F160W image; (bottom-left) The NOEMA spectra with the CO[3−2] emission line in blue and the local Lyman-α profile in red; (right) The contours of the stellar disk (black; beginning at 8σ with increments of 4σ), the compact core (white; beginning at 100σ with increments of 50σ for Galaxy-B and at 50σ with increments of 25σ for Galaxy-C) and a representation of the blue and red-shifted CO[3−2] emission locations with the size of the compact core as seen in ALMA. The expected rotational axes have been also been provided for each component – disk in red, core in blue and CO[3−2] emission as black dashed lines. The NOEMA spin axes uncertainties are large enough to make the difference with the other component not statistically significant.

4. Results

4.1. Compact star-forming cores in extended quiescent stellar disks

The spatial decomposition of surface-brightness profiles of the galaxies reveals extremely compact submillimeter bright rotating cores and extended near-IR detected coplanar stellar disks showing varying levels of lopsidedness (Fig. 1, right panel). The size contrast is evident from the high near-IR to submillimeter radius ratios: ∼5–8 for Galaxy-B, while in case of Galaxy-A and C it is 4 ± 1 and 5 ± 1. Majority of the star formation is concentrated in the cores, with the IR-based SFR in the cores being a factor of 6–36× higher than the 3σ upper-limits in the disks. The mass concentrations also displays this dichotomy between the cores and the stellar components. Using the difference between the CO[3−2] derived dynamical masses and the gas masses, we obtain approximate stellar masses of the cores for each galaxy (≈2 × 1010 M⊙, 8 × 1010 M⊙ and 12 × 1010 M⊙). These are concentrated within the areas > 60× compact than the extended stellar regions that feature stellar masses of 3.2 ± 1.3 × 1011 M⊙, 1.6 ± 0.4 × 1011 M⊙ and 1.8 ± 0.5 × 1011 M⊙.

4.2. Morphological characterization

The single-peaked profiles point to these galaxies consisting of singular (albeit, lopsided) disks with central cores. This is corroborated by the single Sérsic profile fits (with indices ≲1; Sect. 3.1) to their near-IR surface-brightness profiles. About 10–40% of the stellar mass is concentrated in the cores occupying < 1% of the surface area of the whole galaxy. This is illustrated in Fig. 5 for Galaxy-B, the most extended of the three galaxies. We find comparable contrasts in the other two galaxies (based on their near-IR to submillimeter ratio, Table 1). Hence, the cores of these galaxies are likely forming the future stellar bulges. This is characterized by their nuclear location, masses, the extreme compactness similar to z ∼ 2–3 passive galaxies (Daddi et al. 2005), and their submillimeter surface brightness profiles with Sérsic index ∼4 for Galaxies-A and C, which is relatively unusual (Barro et al. 2016; Martig & Bournaud 2008, indicate that the indices should be closer to that for a disk). Galaxy-B although has an index ∼1, but the higher ellipticity of the core (0.40 ± 0.01) in comparison to the disk (0.15 ± 0.05) still supports the idea of bulge formation.

For Galaxies B and C, we do not expect their stellar disks to have been perturbed by major mergers involving equal-mass galaxies (with ratios 1:1 to ∼1:3), which have been studied in multiple simulations over the years (e.g., Bendo & Barnes 2000; Bournaud et al. 2005a; Nevin et al. 2019). Firstly, we conclude a lack of any visible disturbance in the disks from our well resolved and high signal-to-noise HST imaging (Fig. 1, right). Had these undergone major mergers, they would have had to consist of two perfectly aligned disks at a very early stage of collision (precoalescence), the probability of which is 0.1% and 0.4% for Galaxies B and C respectively based on the probability of the specific geometrical orientation (having uncertainties equal to the thickness of the disks). Coupled with the concurrence of both these galaxies are detected in the same exact scenario, the probability reduces to a negligible 0.04%. Moreover, the temporal aspect also makes such a scenario even more unlikely – given that both Galaxy-B and C are detected in the same situation within the observation window. Furthermore, had a major merger been the case, one would have detected a bimodality in the mass distribution associated with each participating galaxy rather than a centrally peaked profile, especially seen in Galaxy-B (Fig. 5).

An alternate scenario would have been the near-IR detected stellar disk and the submillimeter core are actually two separate galaxies. However, we also reject such a scenario due to the submillimeter bright segment being perfectly at the geometric center of the stellar emission region in not one but two separate cases within the same group. In Galaxy-A, with its disturbed stellar morphology however, the situation is different from its neighbors. As discussed earlier, the stellar emission can be decomposed into two almost perpendicular orientations. We observe that one of the two (the northern component) is better coinciding with the compact ALMA core, similar to that in Galaxies B and C. We therefore identify it as the primary stellar disk of Galaxy-A. The additional component is likely an in-falling equal-mass galaxy.

In at least two of the galaxies (B and C), the major axes of both the core and the disk are aligned within ∼3°, as well as with the major axis implied by the rotational patterns of the gas in the respective cores, determined from the CO[3−2] emission (Fig. 8). This is dependent on a reasonable assumption that the gas is confined within the same area as the dust. Hence, we conclude that these two galaxies have coplanar (and possibly corotating) stellar-disks and compact cores. The current data does not allow us to measure the major axis direction of the rotational pattern, or the severely lopsided stellar disk (by a factor > 3, toward the south) of Galaxy-A. For the latter, we are likely observing only the “heavier” part of the disk and hence the disk size and shape parameters cannot be satisfactorily determined. For Galaxy C, the ellipticities of the core and the stellar component are found to be in agreement (within 0.1). But in Galaxy-B, where the stellar component is observed edge-on (with an ellipticity of 0.15 ± 0.05), the core has a larger ellipticity (0.40 ± 0.01). However, it should be noted that all the three cores have values within 0.4–0.6.

4.3. Young cores within older disks

For the three cores, we find short gas-consumption timescales of 20 Myr, 70 Myr and 130 Myr and time taken to build the stellar masses, assuming constant rates of star-formation, ∼60 Myr, 120 Myr and 400 Myr. However, the short timescales ∼100 Myr for three such neighboring objects makes them statistically unlikely to be simultaneously observed. Hence we propose that the extreme star formation levels is rather the culmination of an increase over a larger period of time. The rate and the beginning of this increase cannot be ascertained. Nevertheless, these are still similar or smaller compared to the time scales characterizing the decline in star-formation of the stellar components, based on the goodness-of-fit from the best-fit SED composite τ-models (Schreiber et al. 2018): the look-back times to the epoch of half-mass formation (t50) are 1 . 7 − 0.7 + 0.3 $ 1.7^{+0.3}_{-0.7} $ Gyr, 0 . 5 − 0.2 + 0.7 $ 0.5^{+0.7}_{-0.2} $ Gyr and 0 . 2 − 0.1 + 1.3 $ 0.2_{-0.1}^{+1.3} $ Gyr for Galaxies A, B and C. Hence, the star-bursting cores only started getting built after the disks had already formed about half of their stellar mass and were past their last major episode of star-formation.

5. Discussion

In this section, we revisit the key observational results and discuss how their interplay leads to a coherent picture of the evolution of the three star-forming galaxies in RO-1001. Each of them feature extended stellar disks that are lopsided and quiescent, along with highly star-forming compact cores within them.

5.1. Lopsidedness and quiescence of the disks

We first begin with the severe lopsidedness of the stellar disks (Fig. 1, right panel). For Galaxy-B, the asymmetry in the stellar emission (of a factor of 2.0 in F160W-HST) manifests as a mass lopsidedness of 2.2 (Sect. 3.4) along the major-axis (Fig. 9). In Galaxy-C, the emission asymmetry, also along the major axis, is 1.6. The current data does not allow us to measure the major axis direction of the stellar disk of Galaxy-A, but only the lopsidedness upper limit (> 3) and direction (South), that is nearly perpendicular to the East-West ALMA core major axis (Fig. 9). Such asymmetries, not yet recognized at high redshifts, are in fact a common characteristic among spiral galaxies in the local Universe (Sancisi et al. 2008; Rix & Zaritsky 1995; Zaritsky & Rix 1997; Reichard et al. 2008), although relatively less pronounced. Since lopsidedness is usually contributed to tidal interactions and in-situ star-formation asymmetry (Sancisi et al. 2008), we attribute the strong lopsidedness in our sample to the accretion of material onto the galaxies, that is asymmetric gas-accretion (Bournaud et al. 2005b) (that is reflected by stellar-mass distribution hence created) or the tidal interaction (or minor mergers) with in-falling satellite subhalos (Zaritsky & Rix 1997; Kazantzidis et al. 2008, 2009), that may also include their assimilation into the primary galaxy halo. These less-severe interactions (with mass-ratios from 1:4 or lower) are expected to preserve the stellar disks (Bournaud et al. 2005b; Hopkins et al. 2009). Only in Galaxy-A, can we also associate the imminent major merger to also be playing a role.

thumbnail Fig. 9.

Additional stellar and dust components tracing the direction of accretion. The three panels showing the three residual F160W images of the galaxies after the subtraction of the primary disks (in green contours; starting at 4σ with increments of 4σ). The red solid contours show the ALMA 870 μm emission with the lines starting at 50σ with increments of 50σ. The red solid lines indicate the respective ALMA major axes. In case of Galaxies A and B, the dashed red contours starting at 3σ with steps of 0.5σ displays the ALMA residual emission after the subtraction of the primary emission regions. In case of Galaxy-C, the same contours show the additional point source adjacent to the core that was found during the fitting procedure. In this case, the contours are at 15, 25σ. Finally, the arrows indicate the likely directions of gas-accretion onto the galaxies based on the asymmetric distribution of all the aforementioned components, which also coincide with the direction in which the disks are lopsided.

Meanwhile, the quiescence of the stellar disks (albeit possibly not entirely passive), is the first indication of the presence of an apparent “outside-in” quenching mode in high-redshift massive galaxy populations, in contradiction to the classic “inside-out” configuration (Lang et al. 2014; Tacchella et al. 2015; Breda & Papaderos 2018). We consider various possible modes of quenching. Since we observe the galaxies to be undergoing an outside-in quenching, this could not have primarily occurred due to feedback from active galactic nuclei (AGN; Alatalo et al. 2015), known to quench galaxies inside-out (Tacchella et al. 2018). We also find no evidence of AGN activity from X-ray observations (Daddi et al. 2021), although a radio excess in Galaxy-C is indicative of weak past AGN activity in that galaxy. The process of morphological quenching (Martig et al. 2009), where the formation of a stellar bulge stabilizes the disk against further star-formation, is also improbable. The galaxies are far from being bulge-dominated, essential for this mode of quenching to be applicable, based on their stellar mass distributions. Also unlikely is cosmological starvation (Feldmann & Mayer 2015) since the availability of gas has already been established in RO-1001. Finally, ram-pressure stripping (RPS; Gunn & Gott 1972) could be regarded as a possible contributor as it is known to remove gas from external regions of galaxies (Bravo-Alfaro et al. 2000; Vollmer et al. 2001; Fumagalli et al. 2009; Boselli et al. 2014; Loni et al. 2021), therefore resulting in an apparent outside-in quenching (for a review, Boselli et al. 2022). It could also lead to compression of the gas in the galaxy which could result in the lopsidedness (although the stellar morphology would not be affected). However, as shown in Appendix B, a conservative lower-limit of the radius up to which RPS can remove gas from the sample in RO-1001 would be 10–15 kpc. This is more than an order of magnitude higher than the kpc-scale cores beyond which the galaxies have suppressed star-formation. Hence we do not expect RPS to be playing a major role.

The only possible scenarios capable of self-sufficiently explaining the observed suppression of star-formation are found to be connected to the aforementioned heavy lopsidedness in the disks. Introduction of such asymmetry, in a differentially rotating disk-like structure induces loss of angular momentum, causing mass to rapidly fall into the central regions (Combes & Gerin 1985). This process can be characterized as the triggering of the m = 2 Fourier component, denoting a bar, by the m  =  1 component that refers to the asymmetry or lopsidedness (Bournaud et al. 2005b), observed in our sample. Bars have already been found to efficiently suppress star-formation up to factors of ∼10 in the disk (Khoperskov et al. 2018), while driving gas into the core (Carles et al. 2016), albeit on less spectacular scales than what observed here. This could be a possible case of an early-phase bar-formation, which are usually scarce at high redshifts (e.g., Sheth et al. 2008). However, the resolution and sensitivity is not sufficient to confirm it. The accreted clumpy material driving the lopsidedness is also expected to feed the star-forming core, and in the process leading to a stabilization of the disk (Dekel et al. 2009b). Therefore the same outside-in quenching can be expected in all scenarios involving lopsidedness and compact star formation.

Moreover, the expected damping time of the lopsidedness is comparable to the Hubble time (Jog & Combes 2009), explaining their detection throughout our sample and allowing them to act as catalysts of bulge formation under the high redshift accretion conditions. This timescale is not however associated with the gas being funneled into the core, but rather the survival of the asymmetry that drives this process. We propose that accreted material is resulting in the compact star-forming cores within outside-in quenching disks, either directly (mergers) or indirectly (lopsidedness funneling gas to the core). The accretion may vary from smooth dust (hence presumably gas) components, to subhalo stellar clumps as in Galaxies B and C (while preserving the disks in the process), to additional massive stellar structures as observed in Galaxy-A.

5.2. Determining the direction of accretion

Due to the confluence of evidence for influence of accretion on the galaxies, we try to discuss possible tracers of this process. In an accreting galaxy, the lopsided part of the disks would be expected to mark the location of impact for the accreted material. Corroborative evidence can be found in our sample when the models of the primary disks in the F160W image and the submillimeter bright cores in the ALMA image are subtracted. Residual emission (stars in near-IR emission and dust in submillimeter) is clearly detected in each case (Fig. 9). In Galaxy-A, its F160W and the associated ALMA residuals demonstrate the presence of the similarly-massive companion merging into the disk. For Galaxies-B and C, their respective F160W residuals are much fainter (by ∼3 orders of magnitude) and are likely in-flowing small-mass clumps within or adjacent to the disks.

These are found to be preferentially located in the direction of the lopsidedness of the stellar-disks. We hence suggest that these indicators could be tracing the mass inflow into the core.

6. A generalized picture of accretion-driven galaxy evolution

In this section, we put forward a way to fit our work within the general framework of high-z massive galaxy evolution. Throughout, we suggest how our results indicating accretion onto galaxies is well suited to provide a general picture of galaxy mass-buildup at these redshifts.

6.1. Comparison to high-z compact star-forming galaxies

We start of by making a comparison with the widely studied cSFG population at similar redshifts (Cimatti et al. 2008; Ricciardelli et al. 2010; Fu et al. 2013; Ivison et al. 2013; Toft et al. 2014, 2017; Elbaz et al. 2018; Gómez-Guijarro et al. 2018, 2019; Puglisi et al. 2019, 2021). These cSFGs also feature compact kpc-scale submillimeter bright regions, as is observed in our sample. In fact, Puglisi et al. (2019) already suggested these regions (or cores) to be above the star-forming main sequence (as seen in our sample, Fig. 4). However, the surrounding disks being well below the star-forming main sequence as in our sample (Fig. 4), making galaxies appear to be quenching outside-in, have not yet been recognized. A similar scenario might hold for post-starbust galaxies (e.g., Baron et al. 2022). Another apparent difference is the average ratio of the near-infrared and submillimeter radii for cSFGs, that is ∼3 (Puglisi et al. 2021; Smercina et al. 2018; Lang et al. 2019). Although this is likely a lower limit due to many cSFGs remaining unresolved in large sample studies. It remains thus unclear if examples like the three galaxies in RO-1001 with ratios 4–9 could also present among cSFGs. Moreover, simply the size of Galaxy-B being a factor of 2.0–2.5 above the mass-size relation (van der Wel et al. 2014) for star-forming galaxies at z = 3, adds to the rarity of our sample, especially with regards to cSFGs. Another characteristic of cSFGs seemingly in conflict with our results is the expectation of major merger dominance within such samples (Elbaz et al. 2018). Both in galaxies B and C, the stellar disks appear to be well-preserved (Sect. 4.2).

We can however provide possible reasons behind these apparent discrepancies. Our high-resolution imaging capabilities in both near-IR and submillimeter for RO-1001 is usually not reached in larger statistical studies of cSFGs. Hence we might have simply been able to resolve the galaxies better to determine their properties. This allowed us to study the lopsidedness, the lack of dynamical perturbations (in Galaxies B and C) and the apparent outside-in quenching, based on which we draw the conclusions of our work. Although, we can also hypothesize a physical reasoning. Large statistical samples usually comprise of galaxies in the field which do not experience the high levels of accretion of gas and satellites expected within dense gas-rich environments like RO-1001 (accretion rate increases with halo mass; Dekel et al. 2009a). Hence the cSFGs in the regions with less accretion would be more likely to be results of major mergers driving gas into compact cores while destroying extended stellar disks. This is further exemplified by our direct visual investigation finding a complete lack of similarly massive galaxies with extended and continuous stellar morphology (like in Galaxy B) in the redshift window of 2.6 < z < 3.2 in both COSMOS and GOODS-South fields. If this is true, cSFGs with compact star-forming cores and very extended quiescent stellar disks (similar to our sample) might be more easily found in dense accretion-rich regions.

6.2. A link to the accretion filaments in RO-1001

Extending on our hypothesis of accretion onto the three star-forming galaxies in RO-1001, it is imperative to associate the discussed properties with the large-scale narrative of accretion for the galaxy-group (Daddi et al. 2021). Any ongoing accretion in RO-1001 would likely be coupled with the established Lyman-α-emitting filaments in RO-1001 (Daddi et al. 2021). Hydrodynamical simulations predict that massive galaxies evolving under the influence of nearby accretion-streams have their major axes aligned along the stream direction (Dubois et al. 2014; Codis et al. 2018). We observe a consistency with this prediction in our observations (Fig. 1, right panel). We quantify this by finding the probability for the chance alignment of the major axis of each galaxy with one of the three filaments. The range of allowed angles is approximated using the center of the galaxies and the edges of the −18.0 contour (corresponding to a surface brightness of 10−18 s−1 erg cm−2 arcsec−2) in Fig. 1, since it is the highest brightness level at which the Ly-α traced filaments are detected. We also ensure that the tentative direction of the filaments, qualitatively reported in Daddi et al. (2021), are within this subtended angle (<  ± 10°). We find total chance probabilities of 13%, 17% and 12%. Additionally, the probability of all three galaxies being aligned with one of the filaments (which is what we observe) is hence < 1%. This alignment, especially in case of disk-like galaxies, is attributable to the process of tidal torquing (Codis et al. 2015) by the massive accretion filaments. However, at the core of this lies the tidal interactions the galaxies experience due to infalling satellites (or minor mergers). Hence, the apparent alignments should be regarded as an indication of the galaxies accreting clumpy material, which has already been suggested in Sect. 5.1.

In each case however, we would still expect a level of bending of the accretion streams before the final impact on to the galaxies, revealed by offsets between the direction of accretion (Fig. 9) and the preferred filament (Fig. 1, right panel). We propose a scenario where the Galaxy-A, B and C are being fed by the southwestern, northern and southeastern filaments. The swap of the preferred filament for Galaxies A and C from those in their proximity has been made due to better alignment with the major-axis of the galaxies traced by near-IR and submillimeter emissions as well as the direction of accretion traced by the lopsidedness and residual emission (Fig. 9). Otherwise, for Galaxy-C the accretion direction would have been opposite to direction of approach of the filament. Moreover, there is an additional inconsistency of the line-of-sight velocities of the Lyman-α in the southeastern filament at the galaxy position (Daddi et al. 2021). For Galaxy-A, it has a large spatial displacement from the direction of the nearest southwestern filament. In each case hence, the actual streams of in-falling material would have needed to drastically bend before the final impact onto the galaxies. Nevertheless, even in our preferred scenario there is still a level of bending of the streams necessary as they approach the inner halos of the galaxies. For Galaxy-A, the major axis (measured here from ALMA) versus the lopsidedness and in-falling material direction are nearly orthogonal. Hence the bending is likely occurring in the line-of-sight. The same could also be true in Galaxy-B, where the northern filament with its reduced length likely has a major component along the line-of-sight. Hence, the in-falling stream would need to bend if it has to agree with the expected direction of accretion along the major-axis, on the plane of the sky (Fig. 9).

6.3. A unified picture of accretion-driven evolution

Based on the results of the three star-forming galaxies in RO-1001, we find evidence of massive disk-like galaxies expected to have secularly evolved featuring compact star-forming regions at their cores. We propose that the massive disks build up lopsidedness under the combined effects of gas and satellite accretion which in turn results in loss of angular momentum of the material. This drives the prodigous star-formation in the central regions. Such a scenario is likely being observed in Galaxies B and C. Although, gas can also be driven to the core by much more violent major mergers (Toft et al. 2017; Elbaz et al. 2018), but this leads to a destruction of the stellar disks which is only anticipated in Galaxy-C. However, we conclude that the “wet compaction” scenario proposed by simulations (Dekel et al. 2013; Zolotov et al. 2015; Tacchella et al. 2016), where compact stellar bulges get rapidly built up as a result of accretion-driven violent disk instabilities, is too extreme to reproduce the observations in RO-1001. Such a compaction simply does not allow for creation of extended and massive stellar disks (≳109.5 M⊙) while in our sample we are observing them with masses > 1011 M⊙.

Finally, the presence of massive stellar disks points to the need for a mode of destruction, since they are not usually observed in dense environments at lower redshifts (Bundy et al. 2010). Dynamical disturbances caused by mergers or galaxy harassment can easily be invoked for this (Toth & Ostriker 1992; Kazantzidis et al. 2006; Bullock et al. 2009; Purcell et al. 2009; Bournaud et al. 2011). We might already be observing such a scenario in action in Galaxy-A, with its signs of a forthcoming major merger. Finally, a possible end product may be the compact quiescent spheroidal galaxy (Kalita et al. 2021a) that has been photometrically confirmed to also be within the group, although it never grew beyond 1011 M⊙. It is curious however, that we have stumbled upon a galaxy-group with three massive galaxies close together with recent gas-rich star-bursting cores created within the last few 100 Myr. From each of their observed properties, they seem to have undergone a recent shift in evolution with a preference for the central region. A possible reason has recently been discussed in Noguchi (2022), where bulges get rapidly built-up in > 1011 M⊙ galaxies within dark-matter halo cores that are accessible to cold-gas filaments (Dekel et al. 2009a). This limit is related to the dependence of migration timescales of clumpy accreted material (already suggested in our sample by their lopsidedness, as discussed in Sect. 5.1) that feed the central star-forming region on the stellar mass of the galaxy. Hence, the galaxies in RO-1001, all of which are > 1011 M⊙, could simply be experiencing ideal conditions for a rapid buildup of bulges. It should be noted however that we refrain from estimating the timescale of migration of accreted clumps since such a calculation depends on the relative angular momentum of the inflowing material with respect to the disk. This can result in a range between a few tens to a few hundred Myrs, which is highly uncertain and heavily dependent on assumptions that we are not in a position make with the current data.

7. Caveats and future prospects

7.1. Further investigations

In our study, we are still lacking information about certain facets of the three galaxies in RO-1001. A spatially resolved spectroscopic study of the quiescent stellar regions would be extremely useful to constrain their star-formation histories. A lot of work in this direction has been done for massive QGs (e.g., Schreiber et al. 2018; Forrest et al. 2020; Valentino et al. 2020a), with signatures of rapid quenching of star-formation observed in their samples. Although we do determine rapid quenching of the stellar disks in our sample (Sect. 3.4), conclusive proof will only be available after obtaining spectroscopic data.

Furthermore, this will also allow the tracing of the metallicity of the stellar disks. It is hypthesized that accreted gas being metal-poor leads to a fall in the metallicity in the accreting galaxy (Lehner et al. 2013; Sánchez Almeida et al. 2013, 2014; Wotta et al. 2019). Hence, RO-1001 could be a test-bed for such theories. Finally, spectroscopy will also provide the kinematics of the stellar disk and determine the level of rotational dominance within the structure. This would be necessary to model the evolution of the galaxies as well as similar galaxies in the future featuring signs of accretion. This is especially of interest since we have suggested the possible prevalence of clumps migrating to the core of the galaxies, driving the high levels of star-formation. The timescales of in-flowing material is coupled with the rotation timescales of the respective disks (Dekel et al. 2009b).

7.2. Extending the search to other structures

Asymmetries in the stellar distribution as well as relative position of the submillimeter bright cores of cSFGs are rather common. However, they are mostly associated with galaxy-galaxy interactions (Elbaz et al. 2018; Cibinel et al. 2019; Puglisi et al. 2019). However, we demonstrate that if studied in higher resolution, they might reveal effects of accretion of gas and clumps especially in dark matter halos where cold-gas filaments are expected to survive in spite of the surrounding hot medium (Dekel et al. 2009a). Hence, deep observations of star-forming galaxies within dense-environments would be instrumental in establishing a generalized picture of massive galaxy evolution in dense environments. A few examples are in fact already available. CLJ1449+0856 (Gobat et al. 2011, 2013; Strazzullo et al. 2016; Coogan et al. 2018) has three highly star-forming galaxies that showcase clear offsets between their near-IR and submillimeter (or radio) contours, with one of them also featuring AGN activity (S7-N7 system; Kalita et al. 2021b). Using unresolved submillimeter data, they were regarded as mergers. However, reconsideration after obtaining high resolution data might reveal the asymmetries to be due to comparable features as those seen in RO-1001. Another such case is the highly star-forming galaxy, GN20, which is part of a proto-cluster at z = 4.05 (Daddi et al. 2009; Hodge et al. 2015). This too features a similar offset and is a confirmed member of a high-z dense environment. Additional sources of interest include galaxies within seven other high-z structures with Ly-α halos suggesting abundance of gas (Daddi et al. 2022a,b). Future well-resolved studies of these and additional structures hold much promise.

8. Summary and conclusions

Within a z = 2.91 galaxy-group of dark matter halo mass of ∼4  ×  1013 M⊙, we observe three massive (> 1011 M⊙ galaxies (Fig. 1). They have a combined star-formation rate of ∼1250 M⊙ yr−1, and are studied here with high resolution near-IR (HST) and submillimeter (ALMA) data. Each of the galaxies have extremely compact (effective radius ∼1 kpc) submillimeter bright cores where almost all of the star-formation and 10–40% of the stellar mass is confined. They will likely form the future bulges of their respective galaxies. These are embedded in coplanar stellar disk-like structures which are 4–8× more extended in radius.

The first key new result that emerge from our work is that all three galaxies show marked stellar disk lopsidedness of varying degrees (from 1.6 to > 3.0). The stellar morphology of two-thirds of galaxies (B and C) do not show signs of extreme dynamical disturbances however, hence limiting the role of major mergers. Although, the third (Galaxy A) is likely at an initial phase of collision with an equally massive counterpart. These are first, unique cases of high redshift galaxies in which lopsidedness has been recognized to play an important role.

Based on ALMA 3σ upper-limits, we also determine that star-formation is suppressed in the disks. They are found to be located > 1 dex below the star-forming main sequence (whose scatter is 0.3 dex), while the star-forming compact cores are mainly located above it (Fig. 4). These galaxies are among the first known cases of outside-in quenching observed in the distant Universe. Meanwhile, the cores could not have been forming stars beyond earlier than a few 100 Myr, which is the same epoch by which the disks had already formed about 50% of their stellar mass. This bimodality in star formation and stellar age coincides with the apparent outside-in quenching of the galaxies.

We conclude that the lopsidedness is intrinsically connected to gas being driven into the center of the potential well of the galaxies. The reason of this lopsidedness in at least Galaxies B and C is most likely the combined effect of accreted gas and clumps, the latter of which can be regarded as minor mergers. In case of Galaxy-A, the imminent major merger would also play a role.

Additionally, the importance of minor mergers due to accretion is exemplified by the alignment of the major axes of all three galaxies with one of the accretion streams established through Ly-α halo morphology in Daddi et al. (2021). This is expected to also result in the lopsidedness as well as any residual stellar and dust emission to converge onto the location of impact of the accretion-stream with the galaxies. We detect these signatures in each of the cases. Hence we make the first direct connection between accretion streams and the morphological transformation of galaxies driving compact star-formation in massive galaxies at high redshifts.

Finally, we show that in the presence of accretion, galaxies can build-up compact highly star-forming cores without the need of major mergers and therefore preserving their stellar disks. A key feature however is an asymmetry in the stellar distribution, which needs to be studied in high resolution to determine if it is driven by accretion of gas and clumps or by violent interactions like major mergers. Future studies of accretion-rich high-z dense environments would prove to be crucial.

Based on our results, we suggest an evolutionary pathway in which a secularly evolving disk within a dense environment with accretion (gas and clumps) grows substantial mass asymmetry and experiences the creation of a compact star-bursting core at the expense of the star-formation within the disk. This is inevitably followed by some form of disruptive event that leads to the destruction of the quiescent disk (Toft et al. 2017), leaving behind, and also possibly adding to (Elbaz et al. 2018; Puglisi et al. 2021), a stellar bulge. However, the ubiquity of such a scenario can only be revealed with more well-resolved observations of massive galaxies at the heart of well-studied high-redshift dense environments, which will likely become more accessible in the upcoming James Webb Telescope era.

Acknowledgments

First and foremost, we would like to express our gratitude to the anonymous referee for the valuable suggestions. We would also like to thank Gabriel Brammer for assistance with the use of grizli for the HST data reduction. R.M.R. acknowledges support from GO15910. V.S. acknowledges the support from the ERC-StG ClustersXCosmo grant agreement 716762. F.V. acknowledges support from the Carlsberg Foundation Research Grant CF18-0388 “Galaxies: Rise and Death” and from the Cosmic Dawn Center of Excellence funded by the Danish National Research Foundation under then Grant No. 140. This paper makes use of the following ALMA data: 2019.1.00399. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.

References

  1. Alatalo, K., Lacy, M., Lanz, L., et al. 2015, ApJ, 798, 31 [Google Scholar]
  2. Ashby, M. L. N., Caputi, K. I., Cowley, W., et al. 2018, ApJS, 237, 39 [CrossRef] [Google Scholar]
  3. Baron, D., Netzer, H., Lutz, D., Prochaska, J. X., & Davies, R. I. 2022, MNRAS, 509, 4457 [Google Scholar]
  4. Barro, G., Faber, S. M., Pérez-González, P. G., et al. 2013, ApJ, 765, 104 [Google Scholar]
  5. Barro, G., Trump, J. R., Koo, D. C., et al. 2014, ApJ, 795, 145 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barro, G., Kriek, M., Pérez-González, P. G., et al. 2016, ApJ, 827, L32 [NASA ADS] [CrossRef] [Google Scholar]
  7. Belli, S., Newman, A. B., & Ellis, R. S. 2019, ApJ, 874, 17 [Google Scholar]
  8. Bendo, G. J., & Barnes, J. E. 2000, MNRAS, 316, 315 [Google Scholar]
  9. Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [Google Scholar]
  10. Boselli, A., Cortese, L., Boquien, M., et al. 2014, A&A, 564, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Boselli, A., Fossati, M., & Sun, M. 2022, A&ARv, 30, 3 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bournaud, F., Jog, C. J., & Combes, F. 2005a, A&A, 437, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bournaud, F., Combes, F., Jog, C. J., & Puerari, I. 2005b, A&A, 438, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bournaud, F., Chapon, D., Teyssier, R., et al. 2011, ApJ, 730, 4 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bravo-Alfaro, H., Cayatte, V., van Gorkom, J. H., & Balkowski, C. 2000, AJ, 119, 580 [Google Scholar]
  16. Breda, I., & Papaderos, P. 2018, A&A, 614, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Bridge, C. R., Carlberg, R. G., & Sullivan, M. 2010, ApJ, 709, 1067 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bullock, J. S., Stewart, K. R., & Purcell, C. W. 2009, in The Galaxy Disk in Cosmological Context, eds. J. Andersen, B. M. Nordströara, & J. Bland-Hawthorn, 254, 85 [NASA ADS] [Google Scholar]
  20. Bundy, K., Scarlata, C., Carollo, C. M., et al. 2010, ApJ, 719, 1969 [NASA ADS] [CrossRef] [Google Scholar]
  21. Calabrò, A., Daddi, E., Fensch, J., et al. 2019, A&A, 632, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
  23. Carles, C., Martel, H., Ellison, S. L., & Kawata, D. 2016, MNRAS, 463, 1074 [NASA ADS] [CrossRef] [Google Scholar]
  24. Cibinel, A., Daddi, E., Sargent, M. T., et al. 2019, MNRAS, 485, 5631 [NASA ADS] [CrossRef] [Google Scholar]
  25. Cimatti, A., Cassata, P., Pozzetti, L., et al. 2008, A&A, 482, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Codis, S., Pichon, C., & Pogosyan, D. 2015, MNRAS, 452, 3369 [Google Scholar]
  27. Codis, S., Jindal, A., Chisari, N. E., et al. 2018, MNRAS, 481, 4753 [Google Scholar]
  28. Combes, F., & Gerin, M. 1985, A&A, 150, 327 [NASA ADS] [Google Scholar]
  29. Coogan, R. T., Daddi, E., Sargent, M. T., et al. 2018, MNRAS, 479, 703 [NASA ADS] [Google Scholar]
  30. Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
  31. Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
  32. Daddi, E., Dannerbauer, H., Stern, D., et al. 2009, ApJ, 694, 1517 [Google Scholar]
  33. Daddi, E., Bournaud, F., Walter, F., et al. 2010a, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
  34. Daddi, E., Elbaz, D., Walter, F., et al. 2010b, ApJ, 714, L118 [NASA ADS] [CrossRef] [Google Scholar]
  35. Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Daddi, E., Valentino, F., Rich, R. M., et al. 2021, A&A, 649, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Daddi, E., Delvecchio, I., Dimauro, P., et al. 2022a, A&A, 661, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Daddi, E., Rich, R. M., Valentino, F., et al. 2022b, ApJ, 926, L21 [NASA ADS] [CrossRef] [Google Scholar]
  39. Dekel, A., & Krumholz, M. R. 2013, MNRAS, 432, 455 [NASA ADS] [CrossRef] [Google Scholar]
  40. Dekel, A., Birnboim, Y., Engel, G., et al. 2009a, Nature, 457, 451 [Google Scholar]
  41. Dekel, A., Sari, R., & Ceverino, D. 2009b, ApJ, 703, 785 [Google Scholar]
  42. Dekel, A., Zolotov, A., Tweed, D., et al. 2013, MNRAS, 435, 999 [Google Scholar]
  43. D’Eugenio, C., Daddi, E., Gobat, R., et al. 2020, ApJ, 892, L2 [Google Scholar]
  44. D’Eugenio, C., Daddi, E., Gobat, R., et al. 2021, A&A, 653, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Domainko, W., Mair, M., Kapferer, W., et al. 2006, A&A, 452, 795 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Dubois, Y., Pichon, C., Welker, C., et al. 2014, MNRAS, 444, 1453 [Google Scholar]
  47. Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Elbaz, D., Leiton, R., Nagar, N., et al. 2018, A&A, 616, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Feldmann, R., & Mayer, L. 2015, MNRAS, 446, 1939 [Google Scholar]
  50. Forrest, B., Marsan, Z. C., Annunziatella, M., et al. 2020, ApJ, 903, 47 [NASA ADS] [CrossRef] [Google Scholar]
  51. Fu, H., Cooray, A., Feruglio, C., et al. 2013, Nature, 498, 338 [CrossRef] [Google Scholar]
  52. Fujita, Y. 2001, ApJ, 550, 612 [NASA ADS] [CrossRef] [Google Scholar]
  53. Fumagalli, M., Krumholz, M. R., Prochaska, J. X., Gavazzi, G., & Boselli, A. 2009, ApJ, 697, 1811 [NASA ADS] [CrossRef] [Google Scholar]
  54. Gobat, R., Daddi, E., Onodera, M., et al. 2011, A&A, 526, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Gobat, R., Strazzullo, V., Daddi, E., et al. 2012, ApJ, 759, L44 [Google Scholar]
  56. Gobat, R., Strazzullo, V., Daddi, E., et al. 2013, ApJ, 776, 9 [NASA ADS] [CrossRef] [Google Scholar]
  57. Gómez-Guijarro, C., Toft, S., Karim, A., et al. 2018, ApJ, 856, 121 [Google Scholar]
  58. Gómez-Guijarro, C., Magdis, G. E., Valentino, F., et al. 2019, ApJ, 886, 88 [Google Scholar]
  59. Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022a, A&A, 658, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Gómez-Guijarro, C., Elbaz, D., Xiao, M., et al. 2022b, A&A, 659, A196 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Gunn, J. E., & Gott, J. R., III 1972, ApJ, 176, 1 [Google Scholar]
  62. Guo, R., Hao, C.-N., Xia, X. Y., Mao, S., & Shi, Y. 2016, ApJ, 826, 30 [NASA ADS] [CrossRef] [Google Scholar]
  63. Hodge, J. A., Riechers, D., Decarli, R., et al. 2015, ApJ, 798, L18 [Google Scholar]
  64. Hopkins, P. F., Somerville, R. S., Cox, T. J., et al. 2009, MNRAS, 397, 802 [NASA ADS] [CrossRef] [Google Scholar]
  65. Ivison, R. J., Swinbank, A. M., Smail, I., et al. 2013, ApJ, 772, 137 [NASA ADS] [CrossRef] [Google Scholar]
  66. Jog, C. J., & Combes, F. 2009, Phys. Rep., 471, 75 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kalita, B. S., Daddi, E., D’Eugenio, C., et al. 2021a, ApJ, 917, L17 [NASA ADS] [CrossRef] [Google Scholar]
  68. Kalita, B. S., Daddi, E., Coogan, R. T., et al. 2021b, MNRAS, 503, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kazantzidis, S., Zentner, A. R., & Kravtsov, A. V. 2006, ApJ, 641, 647 [NASA ADS] [CrossRef] [Google Scholar]
  70. Kazantzidis, S., Bullock, J. S., Zentner, A. R., Kravtsov, A. V., & Moustakas, L. A. 2008, ApJ, 688, 254 [Google Scholar]
  71. Kazantzidis, S., Zentner, A. R., Kravtsov, A. V., Bullock, J. S., & Debattista, V. P. 2009, ApJ, 700, 1896 [NASA ADS] [CrossRef] [Google Scholar]
  72. Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [Google Scholar]
  73. Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [Google Scholar]
  74. Khoperskov, S., Haywood, M., Di Matteo, P., Lehnert, M. D., & Combes, F. 2018, A&A, 609, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
  76. Lang, P., Wuyts, S., Somerville, R. S., et al. 2014, ApJ, 788, 11 [NASA ADS] [CrossRef] [Google Scholar]
  77. Lang, P., Schinnerer, E., Smail, I., et al. 2019, ApJ, 879, 54 [Google Scholar]
  78. Lehner, N., Howk, J. C., Tripp, T. M., et al. 2013, ApJ, 770, 138 [NASA ADS] [CrossRef] [Google Scholar]
  79. Loni, A., Serra, P., Kleiner, D., et al. 2021, A&A, 648, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Lotz, J. M., Madau, P., Giavalisco, M., Primack, J., & Ferguson, H. C. 2006, ApJ, 636, 592 [NASA ADS] [CrossRef] [Google Scholar]
  81. Lustig, P., Strazzullo, V., D’Eugenio, C., et al. 2021, MNRAS, 501, 2659 [NASA ADS] [CrossRef] [Google Scholar]
  82. Magdis, G. E., Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
  83. Magnelli, B., Lutz, D., Saintonge, A., et al. 2014, A&A, 561, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Martig, M., & Bournaud, F. 2008, MNRAS, 385, L38 [NASA ADS] [Google Scholar]
  85. Martig, M., Bournaud, F., Teyssier, R., & Dekel, A. 2009, ApJ, 707, 250 [Google Scholar]
  86. Martin, D. C., Matuszewski, M., Morrissey, P., et al. 2015, Nature, 524, 192 [Google Scholar]
  87. Martin, D. C., O’Sullivan, D., Matuszewski, M., et al. 2019, Nat. Astron., 3, 822 [NASA ADS] [CrossRef] [Google Scholar]
  88. McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Nevin, R., Blecha, L., Comerford, J., & Greene, J. 2019, ApJ, 872, 76 [NASA ADS] [CrossRef] [Google Scholar]
  90. Noguchi, M. 2022, MNRAS, 510, 1772 [Google Scholar]
  91. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [Google Scholar]
  92. Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [Google Scholar]
  93. Pfeffer, J., Bekki, K., Couch, W. J., Koribalski, B. S., & Forbes, D. A. 2022, MNRAS, 511, 1072 [NASA ADS] [CrossRef] [Google Scholar]
  94. Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Puglisi, A., Daddi, E., Liu, D., et al. 2019, ApJ, 877, L23 [Google Scholar]
  96. Puglisi, A., Daddi, E., Valentino, F., et al. 2021, MNRAS, 508, 5217 [NASA ADS] [CrossRef] [Google Scholar]
  97. Purcell, C. W., Kazantzidis, S., & Bullock, J. S. 2009, ApJ, 694, L98 [NASA ADS] [CrossRef] [Google Scholar]
  98. Reichard, T. A., Heckman, T. M., Rudnick, G., Brinchmann, J., & Kauffmann, G. 2008, ApJ, 677, 186 [Google Scholar]
  99. Ricciardelli, E., Trujillo, I., Buitrago, F., & Conselice, C. J. 2010, MNRAS, 406, 230 [NASA ADS] [CrossRef] [Google Scholar]
  100. Rix, H.-W., & Zaritsky, D. 1995, ApJ, 447, 82 [Google Scholar]
  101. Rujopakarn, W., Daddi, E., Rieke, G. H., et al. 2019, ApJ, 882, 107 [NASA ADS] [CrossRef] [Google Scholar]
  102. Sánchez Almeida, J., Muñoz-Tuñón, C., Elmegreen, D. M., Elmegreen, B. G., & Méndez-Abreu, J. 2013, ApJ, 767, 74 [CrossRef] [Google Scholar]
  103. Sánchez Almeida, J., Morales-Luis, A. B., Muñoz-Tuñón, C., et al. 2014, ApJ, 783, 45 [Google Scholar]
  104. Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&ARv, 15, 189 [NASA ADS] [CrossRef] [Google Scholar]
  105. Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Schreiber, C., Labbé, I., Glazebrook, K., et al. 2018, A&A, 611, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [Google Scholar]
  108. Sheth, K., Elmegreen, D. M., Elmegreen, B. G., et al. 2008, ApJ, 675, 1141 [Google Scholar]
  109. Silverman, J. D., Rujopakarn, W., Daddi, E., et al. 2018, ApJ, 867, 92 [NASA ADS] [CrossRef] [Google Scholar]
  110. Smercina, A., Smith, J. D. T., Dale, D. A., et al. 2018, ApJ, 855, 51 [NASA ADS] [CrossRef] [Google Scholar]
  111. Somerville, R. S., & Davé, R. 2015, ARA&A, 53, 51 [Google Scholar]
  112. Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [Google Scholar]
  113. Spergel, D. N. 2010, ApJS, 191, 58 [NASA ADS] [CrossRef] [Google Scholar]
  114. Strazzullo, V., Daddi, E., Gobat, R., et al. 2016, ApJ, 833, L20 [NASA ADS] [CrossRef] [Google Scholar]
  115. Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
  116. Tacchella, S., Carollo, C. M., Renzini, A., et al. 2015, Science, 348, 314 [NASA ADS] [CrossRef] [Google Scholar]
  117. Tacchella, S., Dekel, A., Carollo, C. M., et al. 2016, MNRAS, 458, 242 [NASA ADS] [CrossRef] [Google Scholar]
  118. Tacchella, S., Carollo, C. M., Förster Schreiber, N. M., et al. 2018, ApJ, 859, 56 [Google Scholar]
  119. Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
  120. Toft, S., Smolčić, V., Magnelli, B., et al. 2014, ApJ, 782, 68 [Google Scholar]
  121. Toft, S., Zabl, J., Richard, J., et al. 2017, Nature, 546, 510 [NASA ADS] [CrossRef] [Google Scholar]
  122. Toth, G., & Ostriker, J. P. 1992, ApJ, 389, 5 [NASA ADS] [CrossRef] [Google Scholar]
  123. Umehata, H., Fumagalli, M., Smail, I., et al. 2019, Science, 366, 97 [Google Scholar]
  124. Valentino, F., Tanaka, M., Davidzon, I., et al. 2020a, ApJ, 889, 93 [Google Scholar]
  125. Valentino, F., Daddi, E., Puglisi, A., et al. 2020b, A&A, 641, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  126. van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [Google Scholar]
  127. van Dokkum, P. G., Nelson, E. J., Franx, M., et al. 2015, ApJ, 813, 23 [NASA ADS] [CrossRef] [Google Scholar]
  128. Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [Google Scholar]
  129. Vogelsberger, M., Marinacci, F., Torrey, P., & Puchwein, E. 2020, Nat. Rev. Phys., 2, 42 [Google Scholar]
  130. Vollmer, B., Cayatte, V., Balkowski, C., & Duschl, W. J. 2001, ApJ, 561, 708 [NASA ADS] [CrossRef] [Google Scholar]
  131. Wen, Z. Z., & Zheng, X. Z. 2016, ApJ, 832, 90 [NASA ADS] [CrossRef] [Google Scholar]
  132. Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [Google Scholar]
  133. Wotta, C. B., Lehner, N., Howk, J. C., et al. 2019, ApJ, 872, 81 [NASA ADS] [CrossRef] [Google Scholar]
  134. Zaritsky, D., & Rix, H.-W. 1997, ApJ, 477, 118 [Google Scholar]
  135. Zolotov, A., Dekel, A., Mandelker, N., et al. 2015, MNRAS, 450, 2327 [Google Scholar]

Appendix A: Spectral Energy Distribution Model Fitting

In order to fit SFH models to the galaxies, we use the results of the surface brightness distributions in F160W (which also provides the flux in the band) and then obtain the rest of the photometry using the best-fit models as priors in all other bands. We fit this photometry with BC03 stellar population models (Bruzual & Charlot 2003) to derive the properties of the three massive galaxies (Fig. 8). The redshift is fixed to the spectroscopic values previously published for the sources (Daddi et al. 2021). We use FAST++3 to determine the best fitting SED templates through a χ2 minimization procedure. We fix the metallicity to the solar value as is expected in massive galaxies and implement the Calzetti dust attenuation law (Calzetti et al. 2000), with a range of extinction values, AV = 0–5 in steps of 0.02. Finally, we use three different sets of SFH models.

Firstly, we use constant star formation models, characterized by no decline in star formation (it remains constant throughout) to check if a high attenuation star-forming scenario is formally consistent with the available photometry. We also use delayed τ-models. These feature an exponentially declining SFH that is characterized as ∝(t/τ2) e−t/τ with a peak of star formation at t = τ. The τ varies within [100 Myr, tobs] with steps of 0.1 dex, where tobs is the age of the universe at the redshift of the galaxy. Finally, we include the composite τ-models(Schreiber et al. 2018) which are similar to the τ-models, however with different timescales (τrise and τdecl) for the rising and declining phases separated by the epoch tburst.

SFR base ( t ) ∝ { e ( t burst − t ) / τ rise for t > t burst , e ( t − t burst ) / τ decl for t ≤ t burst . $$ \begin{aligned} \mathrm{SFR}_{\rm base} (t) \propto \left\{ \begin{array}{ll} e^{(t_{\rm burst} - t)/\tau _{\rm rise}}&\mathrm{for} t > t_{\rm burst}, \\ e^{(t - t_{\rm burst})/\tau _{\rm decl}}&\mathrm{for} t \le t_{\rm burst}. \\ \end{array}\right. \end{aligned} $$(A.1)

Both τrise and τdecl are varied within the range of [10 Myr, 3 Gyr], while for tburst a grid of [10 Myr, tobs] is used.

Appendix B: Prevalence of Ram Pressure Stripping

We investigate the effect RPS may have on the three star-forming galaxies in RO-1001. We use the following relation from Domainko et al. (2006) for the minimum radius up to which gas may be stripped from a galaxy (rstrip):

r strip = 0.5 r o × ln ( G M star M gas v gal 2 ρ ICM 2 π r o 2 ) . $$ \begin{aligned} \mathrm{r_{strip} = 0.5\,\mathrm{r_{o}} \times ln\left(\frac{G\,M_{star}\,M_{gas}}{v^{2}_{gal}\,\rho _{ICM}\,2\pi \, r_{o}^{2}}\right)}. \end{aligned} $$(B.1)

Here, the ro is the scale radius of the galaxies, while Mstar, Mgas corresponds to the gas and stellar mass of the galaxies. We note that vgal is the relative velocity between the galaxy and the ICM, for which we use the approximate virial velocity of the galaxies in RO-1001 (500 km s−1; Daddi et al. 2021). Finally, the density of the ICM (ρICM) is determined using (Boselli et al. 2022):

ρ ICM = 1.15 n e m p . $$ \begin{aligned} \mathrm{\rho _{ICM} = 1.15\,n_{e}\,m_{p}}. \end{aligned} $$(B.2)

We use the value of 10−3 cm−3 for the electron density (ne) as is expected in the core of clusters and groups (Vikhlinin et al. 2009; Sun et al. 2009; Pratt et al. 2010).

We hence get an rstrip = 10–15 kpc for the galaxies in RO-1001. However, this should be regarded as a conservative lower-limit since RPS efficiency is expected the steeply decrease at high-redshifts. This is primarily due to the contribution of non-gravitational heating which effectively reduces the ICM content (Fujita 2001). Moreover, the decreasing efficiency of RPS at high redshifts (z ≳ 2) is also suggested through simulations in (Pfeffer et al. 2022). Hence, in each of our sample galaxies, the rstrip is found to be a factor of ≳2 larger than the stellar disks.

All Tables

Table 1.

Properties of the star-forming massive galaxies in RO-1001.

In the text
Table 2.

Derived morphological Spergel parameters in submillimeter.

In the text

All Figures

thumbnail Fig. 1.

Location of the massive star-forming galaxies in the network of Lyman-α filaments. Left: color image composite of RO-1001, using observations in F160W, F125W and F606W. The ALMA data has been coadded to that in F606W since both trace star-formation, differing based on dust obscuration. The scaling of the ALMA data was done based on its flux to SFR ratio in comparison to the same for that in F606W. The white dashed contours trace the Lyman-α halo whereas the cyan arrows show the tentative directions of the three gas-accretion filaments converging onto the center of the group potential well (the correspondence to the galaxies is discussed in detail in Sect. 5.2). Right: zoom on the three star-forming galaxies (A, B and C) as seen in ALMA submillimeter dust-emission while the white contours trace the F160W flux tracing stellar light. The contours begin at 4σ with increments of 4σ. The arrows indicate the direction of the streams, which are shown in green if they are aligned with the major axis of the galactic disks (in dashed white lines), as discussed in Sect. 5.2. Those which are not, are in red. In case of Galaxy-A, we rather show the major axis of the ALMA contour with the white dashed line.
In the text
thumbnail Fig. 2.

Morphological profile fitting of stellar emission. Left panel: HST F160W cutouts of Galaxies-A and B (top) and Galaxy-C (bottom) used for the morphological model fitting. Middle and right panels: GALFIT returned models and residuals of the same cutouts. In the latter, only the RO-1001 galaxy models have been subtracted. The rest of the sources, although used during the fit, have been left in the image.
In the text
thumbnail Fig. 3.

Top panel: ALMA 870 μm image of the core of RO-1001 with the three star-forming galaxies clearly visible. Each of them were fit with intensity profiles which were then subtracted to obtain the residual image displayed in the bottom panel. The ALMA PSF at 870 μm is shown in the inset on the top right.
In the text
thumbnail Fig. 4.

Components of the three galaxies on the star-forming main-sequence: star-bursting bulges and quiescent disks. The SFR vs. stellar-mass values of the star-bursting core, the quiescent stellar disk and the combination of the two placed with respect to the star-forming main-sequence (Schreiber et al. 2015) at z = 3, shown as the black solid line. The shaded region demarcates the 0.3 dex uncertainty in the relation. We use the 3σ ALMA upper-limits as the value for SFR with the associated gray error-bars showing the range allowed by our SED model fitting. The latter have been artificially offset in the x-axis to emphasize the difference in the method of measurement.
In the text
thumbnail Fig. 5.

Spatial distribution of Galaxy-B stellar mass and star formation rates. Left: upper panel shows SFR distribution model of Galaxy-B, with the morphology determined by the F160W stellar emission in case of the disk, and the ALMA dust emission for the core. The amplitudes are determined by the SFR of the two components. Lower panel: is a 1D representation of the plot above, after a rotation the make the major axis horizontal. Middle: stellar mass distribution following the same procedure. Here the mass in the core is determined from the difference between the dynamical mass and gas-mass determined from the CO[3−2] emission line. Right: specific SFR provided by the ratio of the SFR and the stellar mass.
In the text
thumbnail Fig. 6.

Best-fit SED models in optical and near-IR for each of the three star-forming galaxies in RO-1001. The photometry with their respective errorbars are shown in red. The cyan contours show a modified SED with an addition of an example 0.1 Gyr old highly obscured (AV = 6.5–7.5) constant star-formation history SED in each case. In each case, the resulting stellar-masses are in agreement with our CO[3−2] estimates within 0.1 dex and are hence a representation of contributions of the star-bursting cores.
In the text
thumbnail Fig. 7.

UVJ colors of high-z QGs (z > 2.5) adapted from D’Eugenio et al. (2020). The post-star burst region is demarcated with the red box as specified in Belli et al. (2019). The marker sizes are proportional to the stellar mass. The red and blue stars are the dust uncorrected and corrected measurements of the quiescent stellar disks in the three star-forming galaxies within our sample. The final star in orange marks the location of Galaxy-D, a quiescent galaxy photometrically confirmed to be part of RO-1001 (Kalita et al. 2021a).
In the text
thumbnail Fig. 8.

Two panels showing the rotational properties in Galaxies B and C with three individual subimages: (top-left) the NOEMA CO[3−2] emission profiles for the blue and red-shifted sections with respect to the average galaxy profile shown as contours superimposed on the F160W image; (bottom-left) The NOEMA spectra with the CO[3−2] emission line in blue and the local Lyman-α profile in red; (right) The contours of the stellar disk (black; beginning at 8σ with increments of 4σ), the compact core (white; beginning at 100σ with increments of 50σ for Galaxy-B and at 50σ with increments of 25σ for Galaxy-C) and a representation of the blue and red-shifted CO[3−2] emission locations with the size of the compact core as seen in ALMA. The expected rotational axes have been also been provided for each component – disk in red, core in blue and CO[3−2] emission as black dashed lines. The NOEMA spin axes uncertainties are large enough to make the difference with the other component not statistically significant.
In the text
thumbnail Fig. 9.

Additional stellar and dust components tracing the direction of accretion. The three panels showing the three residual F160W images of the galaxies after the subtraction of the primary disks (in green contours; starting at 4σ with increments of 4σ). The red solid contours show the ALMA 870 μm emission with the lines starting at 50σ with increments of 50σ. The red solid lines indicate the respective ALMA major axes. In case of Galaxies A and B, the dashed red contours starting at 3σ with steps of 0.5σ displays the ALMA residual emission after the subtraction of the primary emission regions. In case of Galaxy-C, the same contours show the additional point source adjacent to the core that was found during the fitting procedure. In this case, the contours are at 15, 25σ. Finally, the arrows indicate the likely directions of gas-accretion onto the galaxies based on the asymmetric distribution of all the aforementioned components, which also coincide with the direction in which the disks are lopsided.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.