| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202243278 | |
| Published online | 09 August 2022 | |
Dark matter in galaxy clusters: Parametric strong-lensing approach⋆
1
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
e-mail: marceau.limousin@lam.fr
2
Institute of Physics, Laboratory of Astrophysics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
3
ESO, Alonso de Córdova 3107, Vitacura, Santiago, Chile
Received:
7
February 2022
Accepted:
10
June 2022
We present a parametric strong-lensing analysis of three massive galaxy clusters for which Hubble Space Telescope imaging is available, as well as spectroscopy of multiply imaged systems and galaxy cluster members. Our aim is to probe the inner shape of dark matter haloes, in particular the existence of a core. We adopted the following working hypothesis: any group- or cluster-scale dark matter clump introduced in the modelling should be associated with a luminous counterpart. We also adopted some additional well-motivated priors in the analysis, even when this degraded the quality of the fit, quantified using the root mean square between the observed and model-generated images. In particular, in order to alleviate the degeneracy between the smooth underlying component and the galaxy-scale perturbers, we used the results from previous spectroscopic campaigns, which allowed us to fix the mass of the galaxy-scale component. In the unimodal galaxy cluster AS 1063, a core mass model is favoured over a non-core mass model, and this is also the case in the multimodal cluster MACS J0416. In the unimodal cluster MACS J1206, we fail to reproduce the strong-lensing constraints using a parametric approach within the adopted working hypothesis. We then successfully added a mild perturbation in the form of a superposition of B-spline potentials, which allowed us to obtain a decent fit (root mean square = 0.5″), and finally find that a core mass model is favoured. Overall, our analysis suggest evidence for core cluster-scale dark matter haloes in these three clusters. These findings may be useful for the interpretation within alternative dark matter scenario, such as self-interacting dark matter. We propose a working hypothesis for parametric strong-lensing modelling in which the quest for the best-fit model is balanced by the quest for presenting a physically motivated mass model, in particular by imposing priors.
Key words: gravitational lensing: strong / dark matter / large-scale structure of Universe
© M. Limousin et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Dark matter (DM) is an elusive component that is thought to largely dominate the mass budget in astrophysical objects over a wide range of scales, in particular in galaxy clusters. However, more than 80 years after the first indirect evidence for DM in galaxy clusters (Zwicky 1937), we have no definitive clues about its existence, even though it is sometimes taken for granted. Evidence for DM is indirect only, and no well-understood and characterised particle detector has detected it so far, despite intense effort of the community (see e.g. Irastorza & Redondo 2018; Schumann 2019). As long as no such direct detection is reliably achieved, DM remains a hypothesis.
In this paper, we assume the DM hypothesis, and we focus on its distribution on cluster scales, using parametric strong-lensing techniques. Strong lensing (SL) is an essential probe of the DM distribution in the centre of galaxy clusters, where the mass density is so high that space time is locally deformed such that multiple images of background sources can form. This provides valuable constraints on the mass distribution.
Parametric SL mass modelling relies on the following working hypothesis, supported by N-body simulations: A galaxy cluster is an object composed of different mass clumps, each component of which is associated with a luminous counterpart and can (to some extent) be described parametrically. One advantage of parametric SL modelling is that the description of these mass clumps can be directly compared with theoretical expectations. However, a parametric description is sometimes not accurate nor adapted, emphasising the limit of parametric mass modelling and the need for more flexible approaches.
We usually have two types of mass clumps: cluster-scale DM clumps (whose typical projected mass within a 50″ aperture is about 1014 M⊙ at z ∼ 0.2) and galaxy-scale DM clumps associated with individual galaxies. Added to this description of the dominant DM component, the modelling mass components associated with the X-ray gas can also be considered (Paraficz et al. 2016; Bonamigo et al. 2018).
Parametric SL modelling displays interesting and puzzling features. We mention two of them that are addressed in this paper. First, it sometimes requires DM clumps whose position does not coincide with that of any luminous counterpart. This is the case in complicated merging clusters, for example MACS J0717 (Limousin et al. 2016) or Abell 370 (Lagattuta et al. 2019), where parametric mass modelling might not be the best modelling method. This also happens in apparently unimodal clusters (e.g. MACS J1206 studied in this work). These dark clumps are usually added in order to improve the fit significantly, but the physical interpretation of these clumps is not straightforward. Moreover, when they are taken for granted, their inclusion in the mass budget might be misleading. We might wonder whether we are really witnessing a dark clump. These dark clumps are more likely to express the limitations of parametric mass modelling in some clusters. In this case, the advantage of the parametric mass modelling mentioned above might lose its relevance.
Second, large core radii (sometimes larger than 100 kpc) are sometimes reported in parametric SL studies (e.g. Sand et al. 2004; Richard et al. 2010, 2021; Newman et al. 2013; Lagattuta et al. 2019). This has some implications for cosmological models (see the discussion by Limousin et al. 2016, L16 hereafter).
Finally, some mass models require a non-negligible external shear component (γext) in order to significantly improve the goodness of the reconstruction, but the physical origin of this external shear is not always clear, for example in Abell 370 (γext = 0.13, Lagattuta et al. 2019), in MACS J0329 and RX J1347 (γext = 0.07 and 0.10, respectively, Caminha et al. 2019), in MACS J1206 (γext = 0.12, Bergamini et al. 2019), in Abell 2744 (γext = 0.17, Mahler et al. 2017), and in SDSS 1029 (γext = 0.09, Acebron et al. 2022). This component can have either a physical origin or might be compensating for the limitations of the parametric modelling. In practice, the origin of this external shear can be missed because it can be due to substructures that are located far from the cluster core (Acebron et al. 2017) in regions that are not covered in narrowly targeted observations such as the one carried out with the Hubble Space Telescope.
Interestingly enough, some alternatives to the current cosmological Λ cold dark matter (ΛCDM) scenario allow for the formation of cores and offsets between luminous and dark components at the galaxy cluster scale as self-interacting dark matter (SIDM) models. For a recent review of the SIDM alternative, see Tulin & Yu (2018).
A thorough SIDM investigation of the size of the core radii in the galaxy cluster mass regime is still lacking, but we have some indications about its order of magnitude. With low statistics (50 haloes were resolved), Rocha et al. (2013) quantified halo core sizes in SIDM simulations with a cross section of 1 cm2 g−1 to be in the range 55−90 kpc. Their simulations with a cross section of 0.1 cm2 g−1 were not resolved enough to measure a core radius, but they predicted core radii to be in the range 10−12 kpc. Robertson et al. (2017) reported core radii smaller than 40 kpc. This upper bound was also found when self-interaction is frequent instead of rare (Fischer et al. 2021).
Studies of offsets between stellar and DM components in the SIDM scenario have shown that such offsets are probably small. In the case of the merging Bullet cluster, in which DM clumps positions are well constrained by SL, no such offset has been detected, providing an upper limit on the self-interacting cross section of the DM of 1.25 cm2 g−1 (Randall et al. 2008).
According to simulations by Kim et al. (2017), in merging clusters, a maximum galaxy DM offset of 20 kpc forms for a self-interaction of 1 cm2 g−1. The authors also reported that the maximum offset before the halo is completely disrupted is ∼100 kpc in an ideal case. Robertson et al. (2017) presented SIDM simulations with anisotropic scattering and reported DM-galaxy offsets smaller than 10 kpc. Fischer et al. (2021) claimed based on simulations of SIDM equal-mass mergers with frequent self-interactions that frequent self-interactions can cause much larger offsets than rare self-interactions. These offsets vary with time and are non-zero after the first pericentre passage. For a self-interaction of 1.0 cm2 g−1, they are found to be smaller than ∼100 kpc (versus 50 kpc for rare self-interactions of the same strength). Harvey et al. (2019) investigated the median BCG offset for different DM cross sections using the baryons and haloes of massive systems simulations (BAHAMAS; McCarthy et al. 2016) and found the median offset to be smaller than 10 kpc.
To conclude, within an SIDM scenario, core radii should be smaller than ∼100 kpc. In addition, any offset between stellar and DM components should be smaller than ∼100 kpc.
The main aim of this paper is to investigate the shape of DM at the galaxy cluster scale, in particular its central shape and the possible presence of a core, following the work presented by L16.
Constraints on DM properties, in particular its central shape, derived from SL have been hampered by the degeneracies inherent to this technique. Because SL is sensitive to the total projected mass, it can sometimes be difficult to obtain insights into the underlying central DM distribution, suggesting the need for robust and well-motivated priors in order to break these degeneracies.
One of the main degeneracies is between the smooth and the galaxy-scale DM components. L16 have shown that even in the Hubble Frontier Fields era, in which up to hundreds of multiple images can be detected, this degeneracy still exists and prevents us from obtaining insights on the DM distribution, in particular on its central shape and the presence of a core.
A promising avenue is to use priors on the galaxy-scale perturbers. Recent work by Bergamini et al. (2019, B19 hereafter) proposed to use kinematics of cluster members in order to alleviate this degeneracy by providing well-motivated priors on the mass of galaxy-scale perturbers that are used in the SL mass modelling.
In this paper, we revisit the mass models of three clusters for which B19 have derived reliable constraints on the galaxy-scale perturbers to be used as priors in the SL modelling. Our main aim is to investigate whether including these priors can effectively break the degeneracy described above and help in providing constraints on the inner shape of the underlying DM distribution. More precisely, following L16, we aim to determine whether we can distinguish between a core and a non-core mass model.
Other priors are also considered. They are aimed at presenting physically motivated mass models. In particular, we impose light and mass to coincide within a few arcseconds. At the redshift of the clusters considered in this work, this translates into a few dozen kiloparsec, that is, about what is allowed by SIDM scenarios.
We show that imposing priors sometimes leads to a decreased quality of the SL fit. This leads to the relevant (open) question about the balance between improving the fit and presenting a mass model that is physically relevant and reliable. We also provide some indications about a solution of this question.
2. Method
2.1. dPIE profile
Dark matter mass clumps are described using a dual pseudo-isothermal elliptical mass distribution (dPIE profile). We refer to Limousin et al. (2005) and Elíasdóttir et al. (2007) for a description of this mass profile. Here we give a brief overview. It is parametrised by a fiducial velocity dispersion σ, a core radius rcore, and a scale radius rs, sometimes referred to as the cut radius in other publications using this profile. We prefer using rs instead of rcut. It can be shown that this scale radius corresponds to the radius containing half the 3D mass (Elíasdóttir et al. 2007), hence rcut can be misleading. Between r = 0 and r = rcore, the mass density is constant. Then between r = rcore and r = rs, the mass density is isothermal, then it falls as r−4. For the large-scale DM clumps, we fixed the scale radius to an arbitrary high value.
2.2. Strong lensing
The mass models presented in this paper comprise large-scale DM haloes as well as perturbations associated with individual cluster galaxies, all being characterised using a dPIE profile. For the modelling of individual cluster galaxies, we used the results of B19 and refer to that paper for a full description.
The optimisation was performed in the image plane using the LENSTOOL software (Jullo et al. 2007). The goodness of fit was quantified using the rms between the predicted and the observed multiple images.
The positional uncertainty of the images is an important ingredient for the χ2 computation. It affects the derivation of errors in the sense that smaller positional uncertainties can result in smaller statistical uncertainties, which may be underestimated. Depending on the mass model explored, we set the positional uncertainty to a value of about the image plane rms in order to attain a reduced χ2 of order 1. In practice, a positional uncertainty of 1″ was set for all clusters. When investigating a mass model, the RATE parameter that controls the speed of convergence in the MCMC sampler (Jullo et al. 2007) is decreased until the results are stable in the sense that they do not depend on the RATE value, suggesting that the parameter space is well enough sampled.
2.3. Priors
Priors in parametric SL mass modelling are important and worth including when they are well motivated. The choice of priors can definitely lead to the best mass model that can be inferred from an SL analysis and therefore has to be taken with care and with caution. We considered the following priors that apply to all models presented in this work. Some additional priors are mentioned where relevant.
Large-scale DM clumps. We forced the positions of the large-scale DM clumps to coincide with a luminous counterpart. When a clear central dominant galaxy was present (e.g. in the centre of AS 1063), the position of the main DM clump was allowed to vary within the central light distribution (typically a few arcseconds from the centre of the light distribution). For mass clumps associated with a galaxy group (e.g. the north-east galaxy group in AS 1063), the position was allowed to vary within the light distribution of the galaxy group or of the dominant galaxy (drawn as a square in each figure). This also corresponds to a few arcseconds (∼20 kpc at z = 0.4). This is the order of magnitude of the offsets allowed by SIDM models.
The ellipticity was forced to be lower than 0.7, motivated by the results from numerical simulations (Despali et al. 2016), whereas it was allowed to reach 0.9 in the models by B19.
External shear. Any external shear taken into account in this work was forced to be smaller than 0.1 because there is no obvious massive neighbouring mass component that could account for such an external shear.
Galaxy-scale perturbers. We refer to B19 for the discussion of the photometric and spectroscopic data, in particular the observations used to measure the line-of-sight velocity dispersion of cluster members, whiched allow B19 to propose the prior on the mass of galaxy-scale perturbers that we use here. For MACS 0416, we refer to Bergamini et al. (2021), who presented more data than B19.
In short, B19 used VLT/MUSE integral-field spectroscopy in the cluster cores to measure the stellar velocity dispersion of 40-60 member galaxies per cluster. With these data, they determined the normalisation and slope of the galaxy Faber-Jackson relation between the luminosity and the velocity dispersion in each cluster. Then they used these parameters as a prior for the scaling relations of the sub-halo population in the SL modelling.
Moreover, the scale radius of an L* galaxy-scale perturber was forced to be in the range [5, 150 kpc] (instead of [0, 250 kpc] in B19), which is more in line with galaxy-galaxy lensing results (Monna et al. 2016; Limousin et al. 2007a; Natarajan et al. 2009).
X-ray gas. We explicitly took the gas component into account using the results by Bonamigo et al. (2018). In these three clusters, Bonamigo et al. (2018) analysed the X-ray gas and described its contribution to the mass budget by a superposition of dPIE profiles.
2.4. What is a “good” SL fit?
Strong-lensing studies typically quantify the goodness of fit using the rms between the observed and predicted positions of the multiple images. The lower this value, the better the SL fit. The border between a “good” and a “poor” fit is somehow subjective. Within the SL modelling community, we use to consider that an rms lower than 0.5″ constitutes a good fit and that an rms lower than 1″ is still acceptable. Considering recent parametric SL studies of massive clusters using space-based data and a spectroscopic confirmation of multiply imaged systems, rms between 0.15″ and 1.0″ are reported (see e.g. Cerny et al. 2018; Cibirka et al. 2018; Caminha et al. 2019; Mahler et al. 2019; Lagattuta et al. 2019; Rescigno et al. 2020; Acebron et al. 2020; Richard et al. 2021; Zitrin 2021). This consideration might also depend on the complexity of the cluster: a multimodal complex cluster is usually more difficult to model parametrically than a unimodal relaxed cluster.
Another related issue we were confronted with in our comparison of mass models is the question of the minimum rms between two models required in order to distinguish between them. Once again the answer to this question is subjective. In MACS J0717 (L16), the rms difference between a core and a non-core mass model was 0.5″ (in favour of the core model), and we argued that this difference was not large enough to distinguish between the two models. It is indeed comparable to or smaller than that due to an image misidentification (see e.g. the case of image 3.3 in Abell 2744 discussed in Jauzac et al. 2015), or to the difference caused by a structure along the line of sight that is unaccounted for (Host 2012). In this paper, we assume that a good fit is attained when the rms is lower than 1″, and that a difference of rms of 2″ is large enough in order to distinguish between two mass models with good confidence.
3. AS 1063
Abell AS 1063 (also known as RXJ 2248.7–4431), at a redshift 0.348, has been observed deeply as part of the CLASH (Postman et al. 2012) and Hubble Frontier Fields (HFF, Lotz et al. 2017) programs. It is the only HFF cluster that appears to be unimodal and is clearly dominated by a bright central galaxy.
If the dynamical state of the cluster has been debated, recent work combining X-ray and radio observations indicates a disturbed state. AS 1063 is in an early stage of merging (see Rahaman et al. 2021, and references therein).
3.1. Revisiting the Bergamini et al. (2019) model
Following B19, we considered 55 multiple images from 20 sources (all spectroscopically confirmed). We started by reproducing the B19 mass model, which includes an elliptical dPIE profile associated with the BCG, and a circular dPIE whose position was left free to vary in an area of 150″ × 120″ centred on the north-east region of the cluster, in which we can observe a galaxy group that generates additional SL features for which no spectroscopic information is available, hence it was not considered. This mass clump has a vanishing core radius and a scale radius fixed to an arbitrary high value.
We find the same parameters within the error bars and the same rms of 0.55″. This mass model is able to accurately reproduce the observational constraints. However, the location of the second clump does not coincide at all with the galaxy group in the north-east (separation of 40″), although it was introduced to be associated with it (see the cyan box in Fig. 1).
 |
Fig. 1. Core of AS 1063. Red circles represent the multiple images used in this work (see B19 for details). The boxes represent the location of the second mass clump associated with the north-east group. The size of the field is 150″ × 96″. North is up, east is left. |
We revisited the B19 mass model. As mentioned above, we considered that having a mass clump whose position is not associated with a light concentration is not satisfactory. We forced the position of this second mass clump to coincide with the light distribution of the most luminous galaxy of this group (red square in Fig. 1). We obtained an rms of 0.67″. If the rms increases by 0.12″, we prefer this mass model because each mass clump is associated with a luminous counterpart.
We then added an external shear component. This decreased the rms to 0.53″. The strength of this external shear is 0.03, and its position angle is 40°, pointing in the north-west direction. If it decreases the rms by 0.14″, we excluded it from the mass model we used to probe the underlying DM distribution. The main reason is that we do not observe any clear interpretation of this component (e.g. a mass concentration in the north-west), therefore including this external shear might compensate for the limitations of the parametric modelling and eventually dilute the conclusions of our study, which is to distinguish between a core and a non-core mass model. We test and discuss this further below.
Finally, we tried a model whose the underlying mass distribution was described by a single mass clump, and find an rms of 0.80″. We prefer a two-clump mass model (without external shear) because it has a physical interpretation. It constitutes the reference model with which we continue our investigations. Its parameters are given in Table 1. We note that the core radius is 89.5 ± 5.5 kpc, in agreement with previous studies.
AS 1063 results.
3.2. Non-core mass model: A peaky DM distribution?
Following L16, we investigate here if a non-core mass model for the main DM clump is also able to reproduce the observational constraints. We repeated the modelling and imposed that the core radius was smaller than 10 kpc. We obtained an rms of 3.83″. The parameters are given in Table 1. The difference of the rms between the reference core mass model and the non-core model is 3.16″, which we consider large enough to favour a core mass model. For this modelling, we placed a prior on the velocity dispersion of the second north-east mass clump. In the first attempts of testing a non-core mass model, we found that the velocity dispersion of the second mass clump reached values as high as 765 km s−1 (instead of 350 km s−1 for a core mass model), which is somewhat unrealistic given the optical richness and the absence of X-ray associated emission (Bonamigo et al. 2018). Therefore, we decided to limit the velocity dispersion of the second mass clump to 450 km s−1. As shown in Table 1, the value of this parameter remained at this upper bound of the prior in non-core models. The rms obtained without this prior is 2.56″; this would lead to a difference of the rms of 1.89″. This highlights the importance of physically motivated priors.
3.3. Cosmology
We assumed that the Universe is described by a flat Universe with wX = −1 and ΩM = 0.3.
We ran a core and a non-core mass model, letting wX and ΩM free. For each model, we compared the values of the optimised output cosmology with the values of the reference cosmology mentioned above. Our goal was to determine whether this test can help to distinguish between a core and a non-core mass model. For the core model, we obtain an rms of 0.62″ (instead of 0.67″ for the reference model) and the reference cosmology is retrieved. For the non-core model, we obtain an rms of 3.35″, and we do not retrieve the reference cosmology. In particular, ΩM remains at the lower allowed bound, that is, at 0. This test gives further credit to the non-core mass model. We did not aim to constrain the cosmology here, but to provide an additional test in order to distinguish between a core and a non-core mass model.
3.4. External shear
As mentioned above, an external shear component can compensate for the limitations of the parametric modelling and dilute the distinction between a core and a non-core mass model. The core mass model with an external shear gives an rms of 0.53″. For the non-core mass model, allowing an external shear component lowers the rms to 3.07″ (versus 3.75″ when no external shear is allowed).
When an external shear component is included, the rms difference is 2.54″. This is 0.5″ less distinguishing than the case without any external shear.
3.5. Degeneracies with the BCG
We removed the BCG from the galaxy catalogue and optimised it explicitly, in order to investigate any degeneracies between the main DM clump core radius and the BCG parameters. Its position was allowed to vary within ±4″ from its centre, and its core radius varied between 1 and 50 kpc. We used the values of B19 to place constraints on its velocity dispersion. B19 provided a Gaussian prior with a mean and a standard deviation. We considered the same mean and twice of their standard deviation in order to allow for more freedom. We obtained an rms of 0.64″. The optimised position is consistent with the centre of the light distribution. The ellipticity is unconstrained. Constraints on the core radius are very loose, the output PDF basically reproducing the prior, with a preference for the lower values. Therefore we see no degeneracies between the core radius of the BCG and the core radius of the main DM clump. The value of the main DM clump core radius is consistent with the reference model.
4. MACS 0416
At a redshift 0.396, MACS 0416 has been observed deeply as part of the HFF program.
4.1. Revisiting the Bergamini et al. (2019) model
Recently, B19 and Bergamini et al. (2021, B21 hereafter) presented two mass models for this cluster.
B19 reproduced 107 multiple images using a 3 DM mass clump model with 193 galaxy members in the modelling, reaching an rms of 0.61″. Each mass clump was associated with one of the three light concentrations of the cluster core (Fig. 2): one in the centre, associated with the BCG; one in the south-west, where a bright galaxy dominates; and one in the north-east, where three cluster members are located. They also optimised some parameters of two galaxies individually, which were found to have influence some multiple images. We kept them in the models explored here and refer to B19 for details.
 |
Fig. 2. Core of MACS 0416. Red circles represent the multiple images (see B19 for details). The locations of the mass clumps from different studies are shown by ellipses, whose sizes represent the 1σ error bar on the position. White boxes represent the priors on the position of each DM clump. North is up, east is left. The size of the field is 137″ × 105″. |
B21 reproduced 182 multiple images using a 4 DM mass clumps model with 212 galaxy members in the modelling, reaching an rms of 0.40″. This fourth mass component is located south-west of the cluster core (Fig. 2). This means that two mass clumps lie in this area, none of which are clearly associated with the brightest galaxy located in this area. As discussed above, we considered that DM clumps that are not associated with any luminous counterpart are not satisfactory, especially in this case, where it improves the fit by only ∼0.1″.
B21 also presented three mass models that reproduce the 182 multiple images fairly well (an rms between 0.45″ and 0.48″ instead of 0.40″), where the DM was described using only three mass clumps. Using three other figures of merit (matching of the internal kinematics of the cluster member galaxies as well as BIC and AIC criteria), they chose the four mass clump model as their reference model.
We also reproduced this mass model, where the 182 images are reproduced, by a three mass clump model with an rms of 0.49″. The location of each mass clump was allowed to vary by ±15″ from its luminous counterpart. We find each mass clump to coincide with its luminous counterpart even if this was not imposed. However, we note that the ellipticity of the two main DM clumps (the north-east clump is circular) is above 0.7 (0.84 and 0.73, respectively).
We then imposed the ellipticity of each mass clump to be lower than 0.7 and their positions to coincide with the light distribution (boxes on Fig. 2). For the central and south-west mass clumps, positions were allowed to vary within ±4″ from the centre of the associated bright galaxy. The position of the north-east mass clump was allowed to vary within ±3″ along the x-axis and within ±4″ along the y-axis from the centre of the associated luminous counterpart.
The rms is 0.63″. The core radii of each mass clump are 41.5 ± 2.7, 51.2 ± 3.7, and 60.4 ± 8.6 kpc. The ellipticities of the main and north-east mass distributions remained at 0.7. This model constitutes the reference model from which we continued our investigations. Its parameters are given in Table 2.
MACS 0416 results: cored model.
Similar three-clump mass models have also been proposed by Jauzac et al. (2014) and Richard et al. (2021). We show the positions of the mass clumps inferred in their analysis in Fig. 2.
4.2. Non-core mass model
We repeated the modelling by imposing the core radius of each mass clump to be smaller than 10 kpc.
We obtain an rms of 2.07″. This is 1.44″ lower than the core mass model, which is substantial. A core mass model is therefore clearly preferred, but this difference of the rms is not enough to distinguish between a core and a non-core model according to the (somewhat arbitrary) criteria proposed in Sect. 2.4. The ellipticities of the main and north-east mass distributions also remain at 0.7. The core radii of the three mass clumps remain at 10 kpc. All parameters are given in Table 3.
MACS 0416 results: non cored model.
4.3. Cosmology
We ran a core and a non-core mass model, letting wX and ΩM free. For each model, we compared the values of the optimised output cosmology with the values of the reference cosmology mentioned above.
For the core model, we obtain an rms = 0.51″ (instead of 0.63″ for the reference model), and the cosmology is different (ΩM = 0.16 ± 1.0, wX < 1.3). For the non-core model, we obtain an rms = 1.74″, and the cosmology is entirely different and basically unconstrained.
This test does not give further insights for distinguishing between a core and a non-core mass model.
5. MACS J1206
MACS J1206 is a unimodal cD dominated galaxy cluster located at a redshift 0.439. Although it is considered as dynamically relaxed (Sereno 2017), the smooth component (DM + hot gas) shows significant asymmetry.
5.1. Revisiting the Bergamini et al. (2019) model
B19 reproduced 82 multiple images using a mass distribution composed of three dark matter haloes, three dPIE clumps to model the X-ray surface brightness (Bonamigo et al. 2018), a strong external shear (γext = 0.12) of unknown origin, and 258 haloes describing the cluster members. This set of multiple images is well reproduced (rms = 0.46″).
The positions of the three DM clumps are illustrated in Fig. 3 (cyan ellipses). If one of these mass clumps is coincident with the cD galaxy, the others are not associated with any luminous counterpart. Their core radii are 37, 82, and 69 kpc (central, eastern, and western clump, respectively). B19 stated that these DM clumps are necessary to reproduce the apparently elongated asymmetry of the cluster. A similar mass model in terms of number and position of DM clumps was presented by Richard et al. (2021). The authors reached an equivalent rms.
 |
Fig. 3. Core of MACS J1206. Red circles represent the multiple images (see B19 for details). The locations of the three mass clumps proposed by B19 are shown by cyan ellipses, whose size represents the 1σ error bar on the position. Yellow boxes represent the prior on the position of the mass clumps included in the different mass model. North is up, east is left. The size of the field is 166″ × 110″. |
Such a three-clump mass model was previously proposed in the study by Caminha et al. (2017), who noted that these extra mass components should not be associated with extra DM haloes but do account for asymmetries that a single parametric profile cannot account for.
When we assume that the mass distribution is described by a single dPIE mass clump associated with the cD galaxy plus the galaxy component and the X-ray gas and perform the mass modelling, we obtain an rms of 2.24″. The mass clump parameters show that the ellipticity remains at the higher allowed bound (0.7) and that the core radius is constrained to 74 ± 3 kpc.
The rms difference between the former two models of 1.8″ favours a three mass clump model. We consider that this three clump model is not satisfactory, and we conclude that the SL constraints in MACS J1206 are not well reproduced by a single halo described parametrically. To present a physically motivated parametric mass model for MACS J1206, we pursued our investigations.
5.2. Two-clump mass model
We note that there is a bright galaxy east of the BCG (yellow box in Fig. 3) with which we associate a DM clump. We imposed the centre of this mass component to be within ±2″ from the centre of the associated luminous component, that is, within the yellow box in Fig. 3. We also allowed for an external shear component.
We obtained an rms of 1.45″. The main DM clump has a core radius of ∼35 kpc and has a high but reasonable ellipticity (∼0.6). On the other hand, the second DM clump is extremely flat, with a core radius reaching the higher bound of the prior of 230 kpc.
5.3. Three-clump mass model
North-west of the BCG is another bright galaxy (yellow box in Fig. 3) with which we associate a DM clump, investigating a three-clump mass model. We imposed the centre of this mass component to be within ±2″ from the centre of the associated luminous component and allowed for an external shear component.
The resulting rms is 1.38″. The parameters of the main DM clump are compatible with the parameters obtained in the case of the two-clump mass model, but the two other DM clumps display very flat mass profiles, with core radii of 190 and 230 kpc for the east and north-west clumps, respectively.
5.4. Four-clump mass model
South-west of the BCG is another bright galaxy (yellow box in Fig. 3) with which we associate a DM clump, investigating a four-clump mass model. We imposed the centre of this mass component to be within ±2″ from the centre of the associated luminous component and allowed for an external shear component.
The resulting rms is 1.19″. The parameters of the main DM clump are compatible with the parameters obtained in the case of the two-clump mass model. The other three DM clumps display very flat mass profiles, with core radii of 172, 200, and 145 kpc, respectively.
In all cases, we find that including an external shear allows decreasing the rms by ∼0.6″. Its value is ∼0.06.
We are able to lower the rms by adding clumps that we associate with some light concentrations. The higher the number of associations, the lower the rms. However, we are unable to obtain an rms lower than 1″. We also find that these additional mass clumps do require very large core radii. The radii lie between 145 and 230 kpc.
We conclude from this series of tests that MACS J1206 cannot be reliably described by a pure parametric model in which each mass component would be associated with a luminous counterpart.
6. Improving the parametric mass modelling with mild perturbations
In the case of MACS J1206, the parametric approach reaches its limit and does not allow us to provide a physically motivated parametric description of the mass distribution.
We added a (mild) perturbation to the parametric modelling to determine whether this might help to provide a decent fit. Our main concern is whether adding this perturbation might lose us the advantages of the parametric mass modelling, that is, we might obtain clump parameters that are biased by the perturbation. This would prevent us from performing cluster physics.
Recently, a similar option has been implemented in LENSTOOL (Beauchesne et al. 2021). This functionality consists of a surface of 2D B-spline functions that are added to the lensing potential. While it has been shown to provide enhancement to the reconstruction of a simulated cluster, this is the first time that it is applied to observational data. In comparison to the free-form approach developed in Jullo & Kneib (2009), this perturbative patch cannot reproduce a full mass distribution and has to be combined with other analytical potentials. Its total mass is always null, and it rather redistributes the mass from the other model components. If complex grids of B-spline functions are possible, the current implementation is limited to a squared regular mesh. As the perturbation should be small in comparison to the total mass model, the induced biases can be neglected, however. In addition, the grid does not need more knowledge than the size of the constrained area to be built, such as an existing mass model or the light distribution.
We first tested the inclusion of these perturbations on AS 1063, which is already well described by a parametric mass model. Then we used them on MACS J1206.
6.1. Test on AS 1063
We chose AS 1063 in order to test this approach and determine the response of the reference mass model presented in Sect. 3.1 to this perturbation.
We performed a mass model for AS 1063 as in Sect. 3, including the B-spline perturbation. We used the same scheme of priors as in Beauchesne et al. (2021) with a minimum lattice size of 105″ and a grid of 5 × 5 basis functions. However, we kept the previous uniform priors for the dPIE parameters. The resulting rms is 0.36″, which is an improvement by almost a factor of two when compared with the pure parametric mass model (0.67″).
We compared the parameters of the reference model (Table 1) with the parameters obtained when the perturbation was added. They agree within the 3σ error bars. This test suggests that the B-spline perturbation is able to improve the pure parametric fit (as shown in Beauchesne et al. 2021). In addition, this test also suggests that it is mild enough to avoid modifying the parameters of the associated parametric mass model significantly.
We also ran a non-core mass model in which we included the B-spline perturbation. The goal was to determine whether the perturbation is able to provide a decent non-core mass model. In other words, whether the perturbation able to compensate for the apparent need of a core in the centre.
We find an rms of 1.50″ instead of 3.83″ when the perturbation is not used. Comparing the outputs of these two models, we find that the main DM clump parameters agree with each other within the 3σ error bars. This suggests again that the perturbation is mild enough to modify the parameters of the parametric model only negligibly. In addition, given the value of the rms, we find that the perturbation is not able to compensate for the need of a core in the centre. In addition, the associated 2D mass map (Fig. 4, upper left panel) has an irregular shape. If the parameters of the associated parametric model are not significantly modified by the perturbation, we note that the resulting total mass map appears unphysical. Given the resulting shape of the mass map, we do not consider this mass model as physically relevant and did not use it for further investigations.
 |
Fig. 4. 2D mass maps (contours of 0.03, 0.04, 0.05, and 0.1 × 1012 M⊙ arcsec−2) for the different models explored here for AS 1063. The size of each panel is 140″ × 107″, centred on the cD galaxy. Top: 2D mass distribution corresponding to the main DM halo + the B-spline perturbation, when included. Bottom: main DM halo and perturbation plus individual galaxies. |
We show the 2D mass maps associated with each model in Fig. 4. The fit for the mass maps corresponding to the models with perturbation is good (rms = 0.36″) and the shapes of the mass contours are physically relevant, but they look unphysical when the fit is poor (rms = 1.50″).
We also tested this approach on MACS 0416 to investigate how the reference mass model presented in Sect. 4.1 responds to the perturbation. The resulting rms is 0.46″ (versus 0.63″ for the reference model). In addition, as for AS 1063, the parameters we obtained agree within the 3σ error bars with the parameters obtained without the B-spline perturbation.
The results from these tests are encouraging enough for us to apply the perturbation to MACS J1206.
6.2. Application to MACS J1206
6.2.1. Core mass model with perturbation
In addition to the single central DM clump, we considered a B-spline perturbation. No external shear was added. We obtained an rms of 0.53″ (instead of 2.24″ without perturbation or external shear, see Sect. 5.1).
Allowing for an external shear component does not improve the fit. The B-spline coefficients differ, suggesting that an external shear component can be described by the B-spline perturbation instead. Comparing the parameters of the main DM clump obtained with and without the perturbation, we find that they agree. Comparing the output PDFs for each parameter, we find that all parameters but one agree within the 3σ error bars. Only the position of the main clump along the x-axis disagrees between the two models. This disagreement is small, 5 kpc. We find that the perturbation is able to provide a decent fit without modifying the parametric part, allowing us to keep the advantages of the purely parametric mass modelling.
The parameters of the main DM clump (with perturbation) are given in Table 4. In particular, we find a core radius of 57.4 ± 1.7 kpc.
MACS J1206 results.
6.2.2. Non-core mass model
Keeping the perturbation in the modelling, we then imposed the core radius to be smaller than 10 kpc. The resulting rms is 7.39″. The parameters are given in Table 4. The difference in rms is substantial, 6.83″, which is large enough to favour a core mass model for MACS J1206. The associated mass map displays an unphysical shape (Fig. 5).
 |
Fig. 5. 2D mass maps for the different models explored here for MACS J1206. For clarity, we label these models only in the four top mass maps. The same labels apply in the four bottom maps. The size of each panel is 150″ × 105″, centred on the cD galaxy. Top: 2D mass distribution corresponding to the main DM halo + the B-spline perturbation, when included. Contours are 0.02, 0.03, 0.04, and 0.05 × 1012 M⊙ arcsec−2. Bottom: individual galaxies added to the main DM halo and the perturbation. Contours are 0.02, 0.03, 0.04, and 0.08 × 1012 M⊙ arcsec−2. |
 |
Fig. 6. Comparison between the integrated mass profile: The profile of B19 is shown in green, and the our mass profile is shown in yellow. The 3σ error bars are computed from the MCMC realisations. |
6.2.3. Additional tests
Keeping the core radius smaller than 10 kpc, we tested what happens without the B-spline perturbation. We obtain an rms of 11″.
Adding an external shear component lowers the rms to 9.4″. The value of this external shear remains at 0.1, which is the upper bound allowed by the prior (Sect. 2.3). Interestingly, when we allow this external shear to reach higher values, it is constrained to 0.26, a very unrealistic value because it is comparable to what would be experienced at 100″ from the centre of galaxy cluster Abell 1689 (Limousin et al. 2007b). In this case, the rms decreases to 2.4″. This once again highlights the importance of providing well-motivated priors in SL mass modelling.
In Fig. 5 we show the 2D mass maps corresponding to the different models of MACS J1206. The mass maps corresponding to the models with perturbation for AS 1063 show that for a good fit (rms = 0.53″), the shape of the mass contours are physically relevant, but they look unphysical when the fit is poor (rms = 7.39″).
6.3. Degeneracies with the BCG
We removed the BCG from the galaxy catalogue and optimised it explicitly, in order to investigate any degeneracies between the main DM clump core radius and the BCG parameters. The B-spline perturbation was considered in the modelling. The position of the BCG was allowed to vary within ±4″ from its centre and its core radius varied between 1 and 50 kpc. We used the values of B19 to place constraints on its velocity dispersion. B19 provided a Gaussian prior with a mean and a standard deviation. We considered the same mean and twice their standard deviation in order to allow for more freedom.
We obtain an rms of 0.50″. The optimised position of the BCG is consistent with the light distribution. Its ellipticity reaches the upper bound of the prior, and its core radius is constrained to be smaller than 5 kpc. The parameters of the main DM halo are consistent with the parameters obtained without optimising the BCG individually. Its core radius is found to be slightly larger in this case (14″ instead of 13″). We see no degeneracies between the core radius of the BCG and the core radius of the main DM clump.
6.4. Cosmology
We considered the core mass model presented in Table 4 and let the cosmology be free to vary. The rms is 0.53″ and the reference cosmology is retrieved (Fig. 8, left panel). When we repeated this exercise with the non-core mass model, the rms was 2.3″ (versus 7.39″). The resulting cosmology is different, with ΩM ∼ 0.
This test additionally supports the non-core mass model.
6.5. Comparison with B19
In Fig. 7 we compare the 2D total mass map we obtained for MACS J1206 with the map proposed by B19. They have similar shapes: the model presented here is very similar to the model proposed by B19 in terms of the 2D total mass map. This shows that the perturbation is able to reproduce the asymmetry given by the B19 three-clump mass model using only one single mass clump.
 |
Fig. 7. Comparison between our 2D mass map (upper right) and the mass map obtained by B19 (upper left) for MACS J1206. Lower panel: we overplot the mass contours corresponding to both studies. The size of each panel is 101″ × 77″, centred on the cD galaxy. Contours are 0.05, 0.06, 0.1, and 0.13 × 1012 M⊙ arcsec−2. Cyan ellipses represent the location of the three mass clumps proposed by B19, as in Fig. 3. |
We integrated the mass maps starting at the BCG centre in order to derive the 1D mass profile. The error bars were computed from the MCMC realisations. We present the mass profile in the radial range in which multiple images can be found, that is, up to ∼320 kpc from the centre. As expected, we find that they agree with each other (Fig. 6).
The two mass models fully agree in terms of total mass (the 2D maps and the 1D integrated profile), which is expected because the lensing constraints are sensitive to the total mass. However, we have two very different ways of constructing this total mass in terms of the underlying smooth DM component (the galaxy-scale perturbers were fixed to the same values as in the results of B19). While B19 proposed a three-clump mass model plus an external shear component, we propose a one-clump mass model with perturbation.
To further compare the two models, we let the cosmological parameters free during the optimisation. For the one-clump core mass model presented in this work, we considered the results obtained in Sect. 6.5, which show that the reference cosmology is retrieved. We considered the mass model published by B19 and let the cosmology free during the optimisation. To obtain stable results, we needed to lower the RATE value to 0.005. We obtain an rms of 0.43″, and the reference cosmology is not retrieved. The constraints in the (ΩM, wX) plane are compared in Fig. 8.
 |
Fig. 8. Comparison between the constraints obtained on the cosmological parameters using the reference model presented in Table 4 (left) and the model obtained with the B19 model (right). The cyan cross represents the reference cosmology. |
These two mass models are likely to provide different estimates of the magnification. Different mass distributions lead to different estimates of the magnification experienced by background sources. In MACS J0717, we found that the core and the non-core mass models lead to different magnification estimates, adding a systematic error that is in general larger than the statistical error derived from a given mass model. A thorough investigation of the difference of the magnification computed using the model presented here and the model by B19 is beyond the scope of this paper, but it should be taken into account when MACS J1206 is used as a gravitational telescope, as it might decrease the area of the image plane in which the magnification is well determined enough for reliable studies of the high-redshift Universe.
7. Discussion
We summarise our results in Table 5.
Summary of the results.
7.1. Physically motivated parametric mass modelling
We chose to present mass models that are physically motivated. In particular, we wished to avoid including large-scale DM clumps without luminous counterpart, even if this might degrade the SL fit. Therefore we imposed a strong prior on the position of the large-scale DM clumps. We prefer concluding that a parametric mass modelling is not suitable to describe a cluster instead of using ad hoc dark clumps, whose physical interpretation is misleading. In these cases, a non-parametric approach might be considered instead. We showed as a byproduct that using a mild perturbation in the form of B-splines is useful for obtaining a good fit while at the same time keeping the advantages of the purely parametric mass modelling.
Along this line, we have also considered other well-motivated priors, even though they sometimes degrade the quality of the fit. This is the case when the X-ray component is explicitly included in AS 1063. This is also the case when the strength of the external shear component in MACS J1206 is limited.
7.2. Inner shape and nature of DM
We have investigated the inner shape of the DM distribution in a sample of three massive galaxy clusters. In all cases, a core mass distribution is preferred over a non-core mass distribution. This is a potentially very exciting result because this might be a signature of SIDM. Prudently enough, we refrain from making any strong claims of evidence for SIDM. This would require performing this type of analysis on more galaxy clusters, performing rigorous tests with simulated data, and exploring other ways to improve the models within the standard CDM paradigm. In particular, interactions between baryons and DM that are not fully understood can lead to core formation.
In two cases, the rms difference is larger than 2″, which we consider large enough in order to disentangle between a core and a non-core mass distribution. It is even larger than 3″. In AS 1063, the rms difference is 3.16″ and the core radius is 89.5 ± 5.5 kpc. In MACS J1206, the rms difference is 6.83″ and the core radius is 57.4 ± 1.7 kpc. In MACS 0416, the rms difference is 1.44″ and the core radius of each clump is 41.5 ± 2.7 kpc, 51.2 ± 3.7 kpc, and 60.4 ± 8.6 kpc.
We did not try to model AS 1063 and MACS J1206, the two unimodal clusters studied here, using an NFW mass profile that is non-core by definition. The reason is that we did not observe multiple images at a radius that is large enough to constrain the typical size of the scale radius for a cluster-scale NFW halo. Ongoing BUFFALO observations (Steinhardt et al. 2020), in particular the weak-lensing data, might help to test whether an NFW mass profile is able to reproduce the weak- and strong-lensing data for AS 1063.
Our values are summarised in Table 5. We note that some of them are at the higher bound (AS 1063) of what seems to be allowed in an SIDM scenario. As discussed in the introduction, a thorough investigation of core radii within an SIDM scenario is still lacking.
An observable consequence of SIDM would be oscillations of the BCG around the centre of the halo after mergers, which could persist for several billion years (Kim et al. 2017). For the unimodal clusters studied here (AS 1063 and MACS J1206), we find that the offset between the BCG and the DM is smaller than ∼3 kpc, which is compatible with a CDM scenario without self-interactions (Harvey et al. 2019).
Andrade et al. (2021) recently presented a SL analysis of AS 1063 using a core NFW mass profile. It is not straightforward to compare the values of the core radius for this NFW profile and the core radius of a dPIE profile. However, Andrade et al. (2021) reported evidence for a core radius of 19.83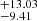 kpc. These authors studied a sample of eight regular galaxy clusters, three of which have a core strictly larger than 0.
kpc. These authors studied a sample of eight regular galaxy clusters, three of which have a core strictly larger than 0.
However, Sartoris et al. (2020) recently performed a joint fit to the velocity dispersion profile of the BCG and to the velocity distribution of cluster member galaxies over a radial range from 1 kpc to the virial radius and determined that the inner slope of AS 1063 is fully consistent with the NFW predictions.
7.3. Relaxing the B19 priors
The degeneracies between the smooth and the galaxy-scale components in MACS 0717 prevented us from distinguishing between a core and a non-core mass model. We have used priors on the galaxy-scale component from spectroscopic observations. For each cluster studied here, we relaxed the priors by B19 and used flat priors for the velocity dispersion and scale radius instead of the B19 results, as is usually done in SL modelling. The velocity dispersion was allowed to vary between 110 and 350 km s−1 and the scale radius varied between 5 and 150 kpc.
We present in Table 6 the results for each cluster for the core and the non-core mass models in terms of rms and parameters of the galaxy-scale perturbers.
Relaxing the B19 priors.
We found that the B19 priors are important for MACS 0717 and allow distinguishing between a core and a non-core mass model. It is unclear why these priors help in MACS J1206 but not in AS 1063 and MACS 0416. In the first two clusters, it is important to note that these priors are essential because they provide more realistic parameters for the galaxy-scale perturbers and therefore add more reliability to the results obtained on the inner shape of the DM distribution in these clusters as we are confident that they are not driven by the degeneracies between the smooth and the galaxy-scale components.
We stress that this study by B19 is a major step forward and enables more realistic SL mass modelling. With the development of spectrographs such as MUSE, we will have more and more clusters with spectroscopic data for galaxy-scale perturbers that can be included in SL modelling.
7.4. Including the X-ray gas component
For each cluster studied here, we investigated a model in which the X-ray gas component is not explicitly included in the modelling. For AS 1063, the rms is 0.60″ instead of 0.67″ for the reference model. The parameters of the two models agree within 1σ, except for the velocity dispersion of the main clump, which is about 100 km s−1 higher when the X-ray component is not included.
For MACS 0416, the rms is 0.57″ instead of 0.63″. The parameters of the two models for the different clumps agree within the 3σ error bars. The velocity dispersion of the north-east clump is found to be slightly higher when the X-ray component is not included (437 ± 34 versus 369 ± 22 km s−1).
For MACS 1206, the rms is 0.67″ instead of 0.53″. The parameters of the two models for the main clump agree within the 3σ error bars, except for the velocity dispersion, which is slightly higher to compensate (1158 km s−1 versus 1071 km s−1).
For AS 1063 and MACS 0416, the rms is slightly better when the X-ray gas component is excluded. Therefore, when the best possible rms is considered, a mass model might be favoured in which the X-ray component is excluded. However, we observe this component in the X-rays, therefore it is worth including it even if the description is not the best. This illustrates the question raised in the introduction of this paper about the balance between having the best possible fit and presenting a physically motivated mass model.
Ultimately, we might wish to fit the lensing constraints and the X-ray data simultaneously so that the rms becomes more representative of the inclusion of the X-ray component.
7.5. Choice of priors
During an optimisation process, LENSTOOL always provides an answer, that is, some best-fit parameters describing a mass distribution. LENSTOOL, like any other modelling algorithm, is agnostic about the physical relevance of the outputs, however. This is where expertise from the modeller must weigh in. In our experience, different modellers using the same set of data and the same modelling algorithm can obtain different answers (Meneghetti et al. 2017).
The parameter space is sometimes very large. It can therefore be relevant to limit it by imposing well-motivated priors. We always provide priors on each parameter, that is, a range within which they are allowed to vary. The tightness of this range depends on the availability of constraints obtained from other probes or from theory. For example, we here used the constraints obtained by B19 in order to place a prior on the galaxy-scale perturbers.
Different occasions have shown that the choice of priors changes the best model inferred from the analysis.
Related to the choice of priors is the quest for the best fit. The rms should be as low as possible, and definitely below a given threshold (assumed here to be 1″). However, we showed here that a mass model can sometimes provide a better fit but be unrealistic at the same time.
We propose a working hypothesis worth considering in parametric mass modelling: First, any large-scale mass clump should be associated with a light counterpart. Second, any well-motivated prior should be included.
Acknowledgments
We acknowledge P. Bergamini for sharing the results of the spectroscopic campaign which motivated us to revisit the mass models of these clusters. We acknowledge the referee for a careful and constructive report. M.L. acknowledges the Centre National de la Recherche Scientifique (CNRS) and the Centre National des Etudes Spatiale (CNES) for support. This research has made use of computing facilities operated by CeSAM (Centre de données Astrophysique de Marseille) data centre at LAM, France (https://www.lam.fr/service/cesam/).
References
- Acebron, A., Jullo, E., Limousin, M., et al. 2017, MNRAS, 470, 1809 [Google Scholar]
- Acebron, A., Zitrin, A., Coe, D., et al. 2020, ApJ, 898, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Acebron, A., Grillo, C., Bergamini, P., et al. 2022, ApJ, 926, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Andrade, K. E., Fuson, J., Gad-Nasr, S., et al. 2021, MNRAS, 510, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Beauchesne, B., Clément, B., Richard, J., & Kneib, J.-P. 2021, MNRAS, 506, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Bergamini, P., Rosati, P., Mercurio, A., et al. 2019, A&A, 631, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergamini, P., Rosati, P., Vanzella, E., et al. 2021, A&A, 645, A140 [EDP Sciences] [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2018, ApJ, 864, 98 [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017, A&A, 607, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Rosati, P., Grillo, C., et al. 2019, A&A, 632, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerny, C., Sharon, K., Andrade-Santos, F., et al. 2018, ApJ, 859, 159 [Google Scholar]
- Cibirka, N., Acebron, A., Zitrin, A., et al. 2018, ApJ, 863, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Despali, G., Giocoli, C., Bonamigo, M., Limousin, M., & Tormen, G. 2016, MNRAS, 466, 181 [Google Scholar]
- Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007, ArXiv e-prints [arXiv:0710.5636] [Google Scholar]
- Fischer, M. S., Brüggen, M., Schmidt-Hoberg, K., et al. 2021, MNRAS, 505, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, D., Robertson, A., Massey, R., & McCarthy, I. G. 2019, MNRAS, 488, 1572 [NASA ADS] [CrossRef] [Google Scholar]
- Host, O. 2012, MNRAS, 420, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Irastorza, I. G., & Redondo, J. 2018, Progr. Part. Nucl. Phys., 102, 89 [NASA ADS] [Google Scholar]
- Jauzac, M., Clément, B., Limousin, M., et al. 2014, MNRAS, 443, 1549 [Google Scholar]
- Jauzac, M., Richard, J., Jullo, E., et al. 2015, MNRAS, 452, 1437 [Google Scholar]
- Jullo, E., & Kneib, J. 2009, MNRAS, 395, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Kim, S. Y., Peter, A. H. G., & Wittman, D. 2017, MNRAS, 469, 1414 [NASA ADS] [CrossRef] [Google Scholar]
- Lagattuta, D. J., Richard, J., Bauer, F. E., et al. 2019, MNRAS, 485, 3738 [NASA ADS] [Google Scholar]
- Limousin, M., Kneib, J.-P., & Natarajan, P. 2005, MNRAS, 356, 309 [Google Scholar]
- Limousin, M., Kneib, J. P., Bardeau, S., et al. 2007a, A&A, 461, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Limousin, M., Richard, J., Jullo, E., et al. 2007b, ApJ, 668, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Limousin, M., Richard, J., Jullo, E., et al. 2016, A&A, 588, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Mahler, G., Richard, J., Clément, B., et al. 2017, MNRAS, 473, 663 [Google Scholar]
- Mahler, G., Sharon, K., Fox, C., et al. 2019, ApJ, 873, 96 [Google Scholar]
- McCarthy, I. G., Schaye, J., Bird, S., & Le Brun, A. M. C. 2016, MNRAS, 465, 2936 [Google Scholar]
- Meneghetti, M., Natarajan, P., Coe, D., et al. 2017, MNRAS, 472, 3177 [Google Scholar]
- Monna, A., Seitz, S., Geller, M. J., et al. 2016, MNRAS, 465, 4589 [Google Scholar]
- Natarajan, P., Kneib, J.-P., Smail, I., et al. 2009, ApJ, 693, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., & Sand, D. J. 2013, ApJ, 765, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Paraficz, D., Kneib, J.-P., Richard, J., et al. 2016, A&A, 594, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
- Rahaman, M., Raja, R., Datta, A., et al. 2021, MNRAS, 505, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, S. W., Markevitch, M., Clowe, D., et al. 2008, ApJ, 679, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Rescigno, U., Grillo, C., Lombardi, M., et al. 2020, A&A, 635, A98 [EDP Sciences] [Google Scholar]
- Richard, J., Smith, G. P., Kneib, J., et al. 2010, MNRAS, 404, 325 [NASA ADS] [Google Scholar]
- Richard, J., Claeyssens, A., Lagattuta, D., et al. 2021, A&A, 646, A83 [EDP Sciences] [Google Scholar]
- Robertson, A., Massey, R., & Eke, V. 2017, MNRAS, 467, 4719 [NASA ADS] [CrossRef] [Google Scholar]
- Rocha, M., Peter, A. H. G., Bullock, J. S., et al. 2013, MNRAS, 430, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Treu, T., Smith, G. P., & Ellis, R. S. 2004, ApJ, 604, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Sartoris, B., Biviano, A., Rosati, P., et al. 2020, A&A, 637, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schumann, M. 2019, J. Phys. G: Nucl. Part. Phys., 46, 103003 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhardt, C. L., Jauzac, M., Acebron, A., et al. 2020, ApJS, 247, 64 [Google Scholar]
- Tulin, S., & Yu, H.-B. 2018, Phys. Rep., 730, 1 [Google Scholar]
- Zitrin, A. 2021, ApJ, 919, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Core of AS 1063. Red circles represent the multiple images used in this work (see B19 for details). The boxes represent the location of the second mass clump associated with the north-east group. The size of the field is 150″ × 96″. North is up, east is left. |
| In the text | |
 |
Fig. 2. Core of MACS 0416. Red circles represent the multiple images (see B19 for details). The locations of the mass clumps from different studies are shown by ellipses, whose sizes represent the 1σ error bar on the position. White boxes represent the priors on the position of each DM clump. North is up, east is left. The size of the field is 137″ × 105″. |
| In the text | |
 |
Fig. 3. Core of MACS J1206. Red circles represent the multiple images (see B19 for details). The locations of the three mass clumps proposed by B19 are shown by cyan ellipses, whose size represents the 1σ error bar on the position. Yellow boxes represent the prior on the position of the mass clumps included in the different mass model. North is up, east is left. The size of the field is 166″ × 110″. |
| In the text | |
 |
Fig. 4. 2D mass maps (contours of 0.03, 0.04, 0.05, and 0.1 × 1012 M⊙ arcsec−2) for the different models explored here for AS 1063. The size of each panel is 140″ × 107″, centred on the cD galaxy. Top: 2D mass distribution corresponding to the main DM halo + the B-spline perturbation, when included. Bottom: main DM halo and perturbation plus individual galaxies. |
| In the text | |
 |
Fig. 5. 2D mass maps for the different models explored here for MACS J1206. For clarity, we label these models only in the four top mass maps. The same labels apply in the four bottom maps. The size of each panel is 150″ × 105″, centred on the cD galaxy. Top: 2D mass distribution corresponding to the main DM halo + the B-spline perturbation, when included. Contours are 0.02, 0.03, 0.04, and 0.05 × 1012 M⊙ arcsec−2. Bottom: individual galaxies added to the main DM halo and the perturbation. Contours are 0.02, 0.03, 0.04, and 0.08 × 1012 M⊙ arcsec−2. |
| In the text | |
 |
Fig. 6. Comparison between the integrated mass profile: The profile of B19 is shown in green, and the our mass profile is shown in yellow. The 3σ error bars are computed from the MCMC realisations. |
| In the text | |
 |
Fig. 7. Comparison between our 2D mass map (upper right) and the mass map obtained by B19 (upper left) for MACS J1206. Lower panel: we overplot the mass contours corresponding to both studies. The size of each panel is 101″ × 77″, centred on the cD galaxy. Contours are 0.05, 0.06, 0.1, and 0.13 × 1012 M⊙ arcsec−2. Cyan ellipses represent the location of the three mass clumps proposed by B19, as in Fig. 3. |
| In the text | |
 |
Fig. 8. Comparison between the constraints obtained on the cosmological parameters using the reference model presented in Table 4 (left) and the model obtained with the B19 model (right). The cyan cross represents the reference cosmology. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


