| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202142404 | |
| Published online | 12 August 2022 | |
ATLASGAL-selected massive clumps in the inner Galaxy
X. Observations of atomic carbon at 492 GHz
1
Korea Astronomy and Space Science Institute,
776 Daedeok-daero,
34055
Daejeon, Republic of Korea
e-mail: mlee@kasi.re.kr
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn, Germany
3
Department of Astronomy, University of Maryland,
College Park,
MD 20742
USA
Received:
10
October
2021
Accepted:
18
April
2022
Context. While high-mass stars are key drivers of the evolution of galaxies, how they form and interact with the surrounding gas is still not fully understood. To shed light on this overarching issue, we have been performing a multitelescope campaign to observe carbon species in ~100 massive clumps (“Top100”) identified by the APEX Telescope Large Area Survey of the Galaxy (ATLASGAL). Our targets constitute a representative sample of high-mass star-forming regions with a wide range of masses (~20−104 M⊙), bolometric luminosities (~60−106 L⊙), and evolutionary stages (70 µm weak, infrared weak, infrared bright, and H II region sources).
Aims. We aim to probe the physical conditions of [C I]-traced gas in the Top100 sample based on Atacama Pathfinder Experiment (APEX) [C I] 492 GHz observations. This is the first of a series of papers presenting results from our [C II] and [C I] campaign.
Methods. To determine physical properties such as the temperature, density, and column density, we combined the obtained [C I] 492 GHz spectra with APEX observations of [C I] 809 GHz and 13CO(2−1), as well as with other multiwavelength data, and employed both local thermodynamic equilibrium (LTE) and non-LTE methods.
Results. Our 98 sources are clearly detected in [C I] 492 GHz emission, and the observed integrated intensities and line widths tend to increase toward evolved stages of star formation. In addition to these “main” components that are associated with the Top100 sample, 41 emission and two absorption features are identified by their velocities toward 28 and two lines of sight, respectively, as “secondary” components. The secondary components have systematically smaller integrated intensities and line widths than the main components. We found that [C I] 492 GHz and 13CO(2–1) are well correlated with the 13CO(2–1)-to-[C I] 492 GHz integrated intensity ratio varying from 0.2 to 5.3. In addition, we derived the H2-to-[C I] conversion factor, X(C I), by dividing 870 µm-based H2 column densities by the observed [C I] 492 GHz integrated intensities and found that X(C I) (in units of cm−2 (K km s−1)−1) ranges from 2.3 × 1020 to 1.3 × 1022 with a median of 1.7 × 1021. In contrast to the strong correlation with 13CO(2–1), [C I] 492GHz has a scattered relation with the 870 µm-traced molecular gas. Finally, we performed LTE and non-LTE analyses of the [C I] 492 GHz and 809 GHz data for a subset of the Top100 sample and inferred that [C I] emission likely originates from warm (kinetic temperature ≳60 K), optically thin (opacity <0.5), and highly pressurized (thermal pressure ~(2–5000) × 105 K cm−3) regions.
Conclusions. Our [C I] 492 GHz survey demonstrates that [C I] 492 GHz is prevalent in the inner Galaxy and traces not only massive clumps, but also non-star-forming relatively diffuse gas. The strong correlation between [C I] 492 GHz and 13CO(2–1) indicates that they probe similar conditions, and the observed variations in the intensity ratio of the two transitions likely reflect local conditions of the interstellar medium. The scattered relation between [C I] 492 GHz and the 870 µm-based molecular gas, on the other hand, implies that [C I] 492 GHz and 13CO(2–1) probe warm molecular gas that surrounds denser and colder clumps traced by 870 µm emission.
Key words: ISM: general / submillimeter: ISM
© M.-Y. Lee et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
High-mass stars play a key role in the evolution of galaxies (e.g., Kennicutt & Evans 2012). For instance, massive stars inject a substantial amount of radiative and mechanical energy into the surrounding gas via ultraviolet (UV) radiation fields, stellar outflows and winds, and supernova explosions. This stellar feedback has been argued to be critical for regulating star formation in galaxies (e.g., Cox 1981; Silk 1997; Ostriker et al. 2010; Hopkins et al. 2014). In addition, high-mass stars enrich the interstellar medium with heavy elements throughout their lives, driving the chemical evolution of galaxies (e.g., Matteucci 2021).
Despite their importance, how high-mass stars form and interact with the surrounding gas is not yet fully understood (e.g., Motte et al. 2018). One of the primary challenges has been that massive star-forming regions tend to be widely separated and located far away from us due to the rarity of high-mass stars. Furthermore, high-mass stars reach the main sequence while deeply embedded in their parental molecular clouds, preventing us from probing the early stage of star formation with traditional optical and near-infrared (NIR) observations. To overcome these difficulties and provide a comprehensive census of high-mass star-forming regions, a number of Galactic plane surveys at far-infrared (FIR) and submillimeter wavelengths have been performed in recent years, including the APEX Telescope Large Area Survey of the Galaxy (ATLAS-GAL; Schuller et al. 2009). ATLASGAL is a 870 m survey of the inner Galaxy (covering |l| < 60 with |b| < 1.5 and 280 < l < 300 with −2 < b < 1) conducted with the Atacama Pathfinder Experiment (APEX) 12 m submillimeter telescope in Chile. This survey identified ~104 massive clumps (e.g., Contreras et al. 2013; Csengeri et al. 2014; Urquhart et al. 2014), and the brightest ~100 of them (Top100 hereafter) have been a subject of various follow-up studies, for example Giannetti et al. (2014) (investigating CO depletion and isotopic ratios), Csengeri et al. (2016) (probing SiO-traced shocked gas), Kim et al. (2017) (searching for H II regions), and König et al. (2017) (characterizing physical properties based on dust continuum emission). More specifically, König et al. (2017) constructed dust spectral energy distributions (SEDs) from 8 m to 870 m and measured dust temperatures and fluxes. Along with distance information, the authors then estimated clump masses, luminosities, and column densities on ~19〳 scales. These dust-based analyses showed that the Top100 sample could be divided into four groups, including 70 m weak sources (70w), mid-infrared (MIR) weak sources (IRw), MIR-bright sources (IRb), and MIR-bright sources associated with radio continuum emission (H II regions), and the dust temperature and bolometric luminosity increase along this sequence, implying that the Top100 sample represents different evolutionary stages of high-mass star formation.
We have been conducting a multitelescope campaign for observing carbon species in the Top100 clumps to address the following subjects: (1) Physical and chemical conditions of the interstellar medium leading to high-mass star formation; (2) Variations in the energetics of gas surrounding massive young stellar objects and protostellar objects as the sources evolve. Carbon is a critical ingredient in the evolution of the interstellar medium (e.g., Henning & Salama 1998). In its different forms (C+, C0, and CO), it is one of the primary coolants and provides a powerful diagnostic tool for examining the physical conditions and energetics of gas. For example, [C II], [C I], and low-J CO transitions (upper J − 4) can be used to probe the properties of photodissociation regions, while mid- and high-J CO lines can trace shock-heated gas (e.g., Pon et al. 2014; Lee et al. 2019). Among these carbon phases, atomic carbon has received relatively little attention, mainly because [C I] fine-structure transitions are typically fainter than low-J CO emission and are heavily affected by atmospheric absorption. Theoretically, atomic carbon is expected to be abundant at the surfaces of molecular clouds (e.g., Langer 1976), but subsequent observations have shown that [C I] emission is widespread throughout the clouds, invoking an interest in [C I] emission as a tracer of total gas mass (e.g., Frerking et al. 1989; Schilke et al. 1995; Kramer et al. 2008; Oka et al. 2001; Shimajiri et al. 2013).
This is the first of a series of papers presenting results from our [C II] and [C I] campaign for the Top100 sources. As a pilot study, we here focus on examining the physical conditions of [C I]-traced gas based on APEX [C I] 492 GHz single-pointing observations, and the two science subjects described above will be addressed with more data in forthcoming papers. The organization of this paper is as follows. In Sect. 2, we present APEX [C I] and 13CO(21) observations of the Top100 sources and describe the determination of line parameters (including central velocities and line widths) via Gaussian fitting. The observed properties of [C I] 492 GHz are probed across different evolutionary stages of high-mass star formation (Sect. 3) and are compared to molecular gas tracers (e.g., 13CO(2–1) and dust-based H2; Sect. 4). In addition, the [C I] 492 GHz and 809 GHz data for a small subset of the Top100 sources are analyzed to derive the physical conditions of [C I]-traced gas (Sect. 5). Finally, we discuss our results and summarize main findings in Sect. 6.
2 Observations and Data Reduction
2.1 [C I] 492 GHz
Single-Pointing Observations of the [C I] 3P1–3P0 transition at 492.16065 GHz were made toward 98 of the Top100 sources using the APEX FLASH+ (First Light APEX Submillimeter Heterodyne instrument; Klein et al. 2014) receiver in 2016 (project IDs: M0039-97 and M0013-98). Two different off positions were observed in the total power mode to avoid contamination, while additional observations were performed in the wobbler mode to accurately measure continuum levels. The characteristics of the observed sources, including locations, distances, and classifications, are summarized in Table A.1. The obtained spectra were processed with the GILDAS CLASS1 software and were converted into units of main-beam brightness temperature (TMB) using a forward efficiency (Feff) of 0.95 and a main-beam efficiency (Beff) of 0.46 based on Mars observations. The final spectra on 13′ scales were smoothed to a velocity resolution of 0.5 km s−1 and have a root-mean-square (rms) noise level of 0.10.6 K (median ~0.3 K).
2.2 [C I] 809 GHz
Nine of the Top100 sources were mapped in the [C I] 3P2–3P1 transition at 809.34197 GHz using the APEX CHAMP+ (Carbon Heterodyne Array of the MPIfR; Güsten et al. 2008) instrument in 2013 (project ID: M0010-92). The mapping was made in the On-The-Fly (OTF) mode with a coverage of 1.6′ 1.6′, and the observed sources are marked in Table A.1. The GILDAS CLASS software was employed for data reduction, and the processed data cubes were translated into the Tmb units by adopting Feff = 0.95 and Beff = 0.38 based on Mars observations. The final data on 8′ scales were smoothed to a velocity resolution of 0.7 km s−1 and have a median rms noise level of ~1 K.
2.3 13CO(21)
The 98 sources in our [C I] 492 GHz survey were also observed in the 13CO(21) transition at 220.39868 GHz (single-pointing) using the APEX PI230 receiver in 2016 (project ID: M0024-97). Unlike the [C I] 492 GHz observations, only one off position was observed for each source in the total power mode. The obtained 13CO(21) data were reduced using the GILDAS CLASS software and were converted into the TMB units by assuming Feff = 0.95 and Beff = 0.66 (Tang et al. 2018). The final science-ready spectra have a resolution of 30′ and a rms noise level of 0.040.14 K (median ~0.06 K) per 0.7 km s−1 channel.
2.4 Deriving Line Parameters
While the observed [C I] 809 GHz spectra can be approximated as single Gaussians, the [C I] 492 GHz and 13CO(21) spectra often show complex shapes with multiple components (Appendix B). For our analyses, we identified individual components by fitting Gaussian functions to the final spectra and estimated line parameters such as central velocities and full widths at half maximum (FWHMs). When two components are close to each other, we examined the difference between their central velocities and considered them as one component if the difference is smaller than the sum of their FWHMs. In addition, we calculated the integrated intensity (I([C I]) or I(13CO)) of each identified component by integrating the emission over a velocity range over which the component is clearly detected. For [C I] 809 GHz, we smoothed the cubes and used the spectra that were extracted at a resolution of 13′ to compare with the [C I] 492 GHz data (Sect. 5). The final [C I] 492 GHz and 13CO(21) spectra with the fitted Gaussians are shown in Fig. B.1, and the derived line parameters and integrated intensities are presented in Table A.2.
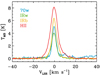 |
Fig. 1 Average [C I] 492 GHz spectra of the four evolutionary groups (70w, IRw, IRb, and H II region groups in blue, green, yellow, and red). To derive these spectra, sources with contaminated reference positions were excluded. |
3 Observational Results
In this section, we mainly discuss the observed properties of [C I] 492 GHz (integrated intensities and FWHMs) and how they vary in a diversity of environments.
3.1 [C I] 492 GHz Detection Rate
We regard components whose peak-to-rms ratios are equal to or higher than five as detections. With this threshold, we found that all 98 sources are detected in [C I] 492 GHz emission. The exact breakdown of the sources is as follows: 14, 31, 31, and 22 for the 70w, IRw, IRb, and H II region groups respectively. These different evolutionary groups have comparable median distances (~4kpc) and [C I] 492 GHz sensitivities (~0.3 K), making comparisons of the groups straightforward. In addition to the main components that are directly associated with the Top100 sources, secondary components are detected in both emission and absorption (Fig. B.1): 41 emission components toward 28 lines of sight and two absorption components toward two lines of sight. Throughout this paper, we refer to these components as “diffuse clouds”, since they likely trace colder and less dense gas than the main 98 components.
3.2 Average [C I] 492 GHz Spectra
To examine how [C I] 492 GHz changes across different environments, we first derived average spectra of the four evolutionary groups by shifting the observed spectra to a central velocity of 0 km s−1 based on the source velocities and stacking them (Fig. 1). For this, 94 sources with clean reference positions were considered (12, 30, 30, and 22 for the 70w, IRw, IRb, and H II region groups respectively).
Figure 1 shows that the characteristics of [C I] 492 GHz emission systematically change across the four evolutionary stages in terms of brightness and line width. Specifically, the peak temperature increases from 5.8 K to 7.8 K for the IRb and H II region groups, while the 70w spectrum has a slightly higher peak than the IRw spectrum (4.7 K versus 3.8 K). On the other hand, the FWHM increases toward more evolved stages: 4.3, 5.6, 5.9, and 8.4km s−1 for the 70w, IRw, IRb, and H II region groups. The peak temperature and FWHM values here were estimated from Gaussian fitting of the average spectra.
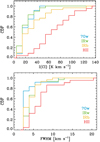 |
Fig. 2 CDFs of the [C I] 492GHz integrated intensity (top) and FWHM (bottom). For both plots, the 70w, IRw, IRb, and H II region groups are shown in blue, green, yellow, and red respectively. |
3.3 Integrated Intensities and Line Widths of the Main Components
Next we probed how statistically different [C I] 492 GHz properties are between the evolutionary stages by constructing cumulative distribution functions (CDFs) of the integrated intensity and FWHM for the main components (Fig. 2). Like in Sect. 3.2, we used the 94 sources with clean reference positions only.
The top panel of Fig. 2 suggests that the 70w, IRw, and IRb groups have comparable distributions of the integrated intensity, while the H II region group has systematically higher values (median I(C I) ~23, 21, 26, and 67 K km s−1 for the 70w, IRw, IRb, and H II region group respectively). This result is supported by two-sided Kolmogorov-Smirnov (KS) tests2 at a significance level of 5%, where only the H II region group is found to be statistically distinct from the rest. Similarly, we found that the 70w and H II region groups have the smallest and largest FWHMs, while the IRw and IRb groups have intermediate FWHMs (Fig. 2 bottom): median FWHM ~3.7, 4.6, 4.4, and 7.0 km s−1 for the 70w, IRw, IRb, and H II region group respectively. This conclusion again agrees with K-S tests where the 70w group is found to be statistically different from the IRw and H II region groups and the H II region group stands out against the rest.
 |
Fig. 3 Histograms of the [C I] 492 GHz integrated intensity (top) and FWHM (bottom). The distributions of the 94 main components and 38 diffuse cloud components are shown in black and gray respectively. |
3.4 Comparison Between the Main and Diffuse Cloud Components
As noted in Sect. 3.1, 41 components are detected along 28 lines of sight as secondary emission components. In comparison to the main components that are associated with the Top100 sources, these secondaries have systematically smaller values of the [C I] 492 GHz integrated intensity and line width (Fig. 3). For example, the median I(C I) is 29 K km s−1 and 4 K km s−1 for the main and diffuse cloud components respectively, while the median FWHM is 5 km s−1 and 2 km s−1. For these estimates and the histograms in Fig. 3, spectra with clean reference positions were used (94 and 38 for the main and diffuse cloud components respectively).
In summary, our APEX survey suggests that [C I] 492 GHz is ubiquitous and traces not only massive dense clumps, but also non-star-forming relatively diffuse gas. The observed integrated intensities and FWHMs systematically vary across different environments, which is likely driven by local conditions of the interstellar medium.
Types of [C I] 492 GHz and 13CO(21) detections.
4 Relation Between [C I] 492 GHz and Molecular Gas Tracers
From which part of a molecular cloud [C I] 492 GHz emission arises has long been a subject of debate. Considering the small difference between the ionization threshold of C0 (11.26 eV) and the dissociation threshold of CO (11.09 eV), C0 is expected to form a narrow layer between C+ and CO, limiting its usefulness as a tracer of total gas mass. However, a significant body of research has revealed that this expectation could be wrong and C0 could exist deep inside molecular clouds (e.g., Frerking et al. 1989; Schilke et al. 1995; Kramer et al. 2008). For example, the proportionality between the [C I] 492 GHz and low-J 13CO integrated intensities has often been interpreted as evidence of the widespread [C I] 492 GHz emission throughout molecular clouds (e.g., Keene et al. 1997; Oka et al. 2001; Shimajiri et al. 2013; Izumi et al. 2021). In this section, we try to shed light on the origin of [C I] 492 GHz emission by examining a relation between [C I] 492 GHz and molecular gas tracers (including 13CO(21) and 870 m-based H2).
4.1 [C I] 492 GHz and 13CO(21)
4.1.1 Classification of [C I] and 13CO Detections
We here probe the relation between [C I] 492 GHz and 13CO(21) in detail. First, we started our analysis by classifying the [C I] and 13CO data into three types: (1) Type 0 where [C I] 492 GHz and 13CO(21) are detected; (2) Type 1 where only 13CO(21) is detected; (3) Type 2 where only [C I] 492 GHz is detected. The breakdown of each type is summarized in Table 1.
Among 139 components that are seen in [C I] 492 GHz emission, 133 show clear 13CO(21) detections, implying a good correspondence between [C I] 492 GHz and 13CO(21) in general. On the other hand, 45 secondary components are newly detected in 13CO(21) only, which is in contrast to a handful number of components seen in [C I] 492 GHz only (5). This striking difference partially results from the higher sensitivity of the 13CO(21) data (Sect. 2).
 |
Fig. 4 Comparison between [C I] 492 GHz (black), 13CO(21) (black), H I (green), and 12CO(10) (orange) for five sources. For H I, the absorption spectrum from Brown et al. (2014) is shown for G337.920.48, while SGPS data are presented for the remaining sources. In addition, 12CO(10) spectra from the FUGIN (G14.490.14) and Mopra (G336.960.23 and G337.920.48) surveys are used. Over the [C I] 492 GHz and 13CO(21) spectra, the fitted Gaussians are overlaid in red. Finally, the source velocities and the secondary components that are seen in [C I] 492 GHz without corresponding 13CO(21) detections are indicated in blue and gray respectively. |
4.1.2 [C I] 492 GHz as a Tracer of “CO-Dark” Molecular Gas
The [C I] 492 GHz components without corresponding 13CO(21) detections are candidates for “CO-dark” molecular gas (referring to molecular gas that is not detected in 12CO(10) emission; e.g., Wolfire et al. 2010) and require an in-depth look. In Fig. 4, we compare [C I] 492 GHz, 13CO(21), H I, and 12CO(10) for the five sources toward which [C I] components without association with 13CO(21) emission are identified. For G08.710.41, G14.490.14, G336.960.23, and G351.57+0.77, H I is seen in emission, and 2′-scale spectra from the Southern Galactic Plane Survey (SGPS; McClure-Griffiths et al. 2005) are shown. On the contrary, absorption features are detected toward G337.920.48, and the H I absorption spectrum from Brown et al. (2014) is presented. Finally, for 12CO(1–0), 20′- and 36′-scale spectra from the FOREST Unbiased Galactic plane Imaging survey with the Nobeyama 45 m telescope (FUGIN; Umemoto et al. 2017) and the Mopra southern Galactic plane survey (Braiding et al. 2018) are used.
Figure 4 shows that G08.710.41 and G14.490.14 likely suffer from bad reference positions in 13CO(21) at the velocities of our interest (−9 km s−1 and 55 km s−1 respectively), which means that 13CO(21) could have been detected. On the other hand,13 CO(21) is simply too faint at the velocities of our interest for G336.960.23, G337.920.48, and G351.57+0.77 (−101 km s−1, −19 km s−1, and −16 km s−1 respectively), implying the I(13CO)-to-I([C I]) ratios lower than 0.7, 0.9, and 0.5 respectively. For these estimates, 13CO(21) 5− values for the velocity ranges where [C I] emission is integrated are considered. In general, Fig. 4 shows that H I is abundant toward the five sources. In particular, for G337.920.48, the [C I] component without association with 13CO(21) emission corresponds to the strongest absorption feature, implying a substantial contribution from the cold H I. On the contrary, 12CO(10) is not detected at the velocities of our interest for G336.960.23 and G337.920.48 (rms of ~12 K). These results suggest that the [C I] 492 GHz secondary components without corresponding13 CO(21) detections have a large amount of atomic gas and could trace CO-dark molecular gas. This conclusion, however, is drawn from a couple lines of sight and needs to be confirmed by extensive observations of [C I] 492 GHz, 13CO(21), and 12CO(10) with matching resolutions and sensitivities.
 |
Fig. 5 Comparison between the [C I] 492 GHz and 13CO(21) integrated intensities. All three types (Types 0, 1, and 2; Sect. 4.1.1) are used here, and the 70w, IRw, IRb, H II region groups, and diffuse cloud components are shown in different colors. For the Type 1, upper limits were calculated by N.C([C I]) [C I] 492 GHz 5− −v([C I]) where N.C([C I]) is the number of [C I] channels over which 13CO is detected and −v([C I]) is the velocity resolution of the [C I] spectra. A similar calculation was done for the Type 2, but using the number of 13CO channels over which [C I] is detected, 13CO 5−, and velocity resolution of the 13CO spectra instead. These derived upper limits are indicated as the arrows. Left: log scale. The measured minimum, median, and maxium I(13CO)-to-I([C I]) ratios (0.2, 1.8, and 5.3) are indicated as the dashed lines in different shades of gray color. Right: linear scale. A linear one-to-one relation is shown as the black dashed line. |
4.1.3 Correlation Between the [C I] and 13CO Integrated Intensities
In Fig. 5, we show a comparison between the [C I] 492 GHz and13 CO(21) integrated intensities for all three types. To provide different perspectives, both linear and log versions are presented. For this comparison, we excluded 41 detections that suffer from bad reference positions in [C I] 492 GHz or 13CO(21) and used arrows to mark upper limits for the Types 1 and 2.
In general, we found that the [C I] 492 GHz and 13CO(21) integrated intensities are well correlated. For instance, the Type 0 detections have a strong correlation between [C I] 492 GHz and 13CO(21) with a Spearman rank correlation coefficient of 0.95. This suggests that [C I] 492 GHz and 13CO(21) arise from similar regions of the interstellar medium, which could be supported by comparable line widths of the two transitions (Fig. 6): the median of the absolute difference between the [C I] 492 GHz and 13CO(21) line widths is 0.8 km s−1. Considering a factor of two larger resolution of the 13CO(21) data (13′ versus 30′), this difference in FWHM is surprisingly small. Finally, both [C I] 492 GHz and 13CO(21) are likely not too optically thick (Sect. 5.2; Urquhart et al. 2021), contributing to the good correlation between the two transitions.
4.1.4 Ratio of 13CO to [C I]
While [C I] 492 GHz and 13CO(21) are strongly correlated, the ratio of 13CO(21) to [C I] 492 GHz does vary, e.g., the I(13CO)-to-I([C I]) ratio ranges from 0.2 to 5.3 with a median of 1.8 (Fig. 5 left). These variations can be seen in Fig. 5 (right) as well, where the data points deviate from the linear one-to-one relation more significantly as the [C I] and 13CO integrated intensities increase beyond ~50 Kkm s−1. Considering that I([C I]) increases toward more evolved groups (Sect. 3.3), the systematic deviation from the linear one-to-one relation implies that the ratio of 13CO(21) to [C I] 492 GHz depends on the classification of the sources.
To examine how the ratio of 13CO(21) to [C I] 492 GHz depends on the classification of the sources, we constructed CDFs of I(13CO)/I([C I]) for the 70w, IRw, IRb, H II region, and diffuse cloud groups and found that the diffuse cloud and 70w groups have systematically lower ratios (Fig. 7). For example, the fraction of the sources with I(13CO)/I([C I]) < 2 are 87%, 80%, 48%, 57%, and 41% for the diffuse cloud, 70w, IRw, IRb, and H II region groups respectively. This conclusion is also supported by two-sided K-S tests, where the diffuse cloud and 70w groups are found to be drawn from the same distribution, while the null hypothesis is rejected at a significance level of 5% when the diffuse cloud components are compared against the IRw/IRb/H II region groups.
The observed variations in the 13CO(21)-to-[C I] 492 GHz integrated intensity ratio most likely result from local conditions of gas and implies that the Top100 sources are in different stages of carbon phase transition (C+-, C0-, or CO-dominated). The exact stages of carbon phase transition, as well as the underlying physical and energetic conditions, will be examined in forthcoming papers where observations of important cooling lines ([C II], [C I], [O I], and CO transitions) for the Top100 sources are analyzed using state-of-the-art models of photodissociation regions and shocks (e.g., Le Petit et al. 2006; Flower & Pineau des Forts 2015).
 |
Fig. 6 [C I] 492 GHz line width versus 13CO(21) line width. Only the Type 0 detections with simple spectra are shown here. |
 |
Fig. 7 CDFs of the I(13CO)-to-I([C I]) ratio. The 70w, IRw, IRb, H II region groups, and diffuse cloud components are shown in blue, green, yellow, red, and gray. For this plot, 97 Type 0 detections with clean off positions were considered. |
4.2 [C I] 492 GHz and 870 m-based H2
4.2.1 X(C I) Factor
In addition to 13CO(21), we examined a relation between [C I] 492 GHz and the total H2 column density by calculating the ratio of N(H2) to I([C I]) (X(C I) factor). For this calculation, we extracted the 870 m-based N(H2) estimates from König et al. (2017) for the 94 main components whose [C I] 492 GHz spectra have clean reference positions and scaled them by (13/19)2 to compensate the difference in resolution (13′ and 19′ for [C I] 492 GHz and H2 respectively; this scaling assumes that H2 uniformly fills the 19′ beam). The derived X(C I) ranges from 2.3 1020 to 1.3 1022 with a median of 1.7 1021 (in units of cm−2 (K km s−1)−1; Fig. 8 left), and this median value is consistent with recent observations of the massive star-forming region RCW 38 (1.4 1021; Izumi et al. 2021), as well as predictions from numerical simulations (~1021; Offner et al. 2014; Glover et al. 2015).
While showing a Gaussian distribution with the well-defined peak of 1.7 1021, X(C I) has large variations (a factor of 55). To examine if there is any trend in these variations, we constructed CDFs for the four evolutionary groups (Fig. 8 right). The constructed CDFs show that the H II region group has more sources with high X(C I) values. For example, sources with X(C I) >1.7 1021 constitute 77% of the H II region group, while accounting for 25%, 57%, and 33% of the 70w, IRw, and IRb groups. When examined at a significance level of 5% for two-sided KS tests, the H II region group was found to be statistically different from the 70w and IRb groups.
4.2.2 Dependence of X(C I) on N(H2)
Section 4.2.1 showed that N(H2) for a given I([C I]) is not constant and varies across the evolutionary groups. To better understand the origin of these variations, we examined how X(C I) changes with N(H2) (Fig. 9) and found that X(C I) has a weak dependence on N(H2) (Spearmans rank correlation coefficient of 0.7; we did not attempt to perform least-squares fitting, since proper fitting is impossible without uncertainties in the H2 column density). The same dependence of X(C I) on the H2 column density was also found by Offner et al. (2014) and Izumi et al. (2021). In particular, Offner et al. (2014) performed hydrodynamic simulations of Galactic molecular clouds with two different UV radiation fields (GUV = 1 and 10 Draine fields) and showed that X(C I) increases with N(H2) − 1022 cm−2 (gray lines in Fig. 9). This increase of X(C I) with N(H2) was interpreted as a result of [C I] 492 GHz becoming optically thick and less sensitive to high H2 column densities. In our case, however, [C I] 492 GHz is likely not too optically thick (Sect. 5). Our result could rather indicate the flattening of C0 abundance at high H2 column densities, which can be verified by a comprehensive excitation study based on extensive [C I] 492 GHz and 809 GHz observations.
4.2.3 Relation Between I([C I]) and N(H2)
The observed variations in X(C I) reflect a scattered relation between I([C I]) and N(H2) (Fig. 10), which is in sharp contrast to the tight correlation between I([C I]) and I(13CO) (Fig. 5 right). While bearing in mind possible sources for the scatter (e.g., variations in the assumed properties of dust and gas, such as the dust opacity at 870 m and dust-to-gas mass ratio), we take our result at face value and interpret it as a result of [C I] 492 GHz being a tracer of moderately dense molecular gas that is more closely associated with 13CO(21). Indeed, Duarte-Cabral et al. (2021) recently performed a cross-match between the ATLASGAL 870 m and SEDIGISM 13CO(21) surveys and found that 4824 ATLASGAL clumps are enveloped within 1709 SEDIGISM clouds, implying that 13CO(21) probes the molecular gas that surrounds denser and colder clumps traced by 870 m. Similarly, Plume et al. (2000) and Shimajiri et al. (2013) found that [C I] 492 GHz is poorly correlated with CS(10) and C18O(10) (dense molecular gas tracers) in Orion A. In general, our finding suggests that [C I] 492 GHz would not be a good tracer of total gas mass if the cloud mass is dominated by dense and cold molecular gas.
5 Physical Conditions Traced by [C I]
Two fine-structure transitions of [C I] at 492 GHz and 809 GHz are invaluable to constrain the physical properties of gas. For instance, in the optically thin regime, their flux ratio constrains the excitation temperature (Tex) as the integrated intensity is proportional to the upper state column density. In more general situations, including high optical depth cases, the physical properties of gas can be derived through escape probability radiative transfer models such as RADEX (van der Tak et al. 2007). In this section, we examine the physical conditions of [C I]-traced gas in a small subset of the Top100 sources by analyzing the [C I] 492 GHz and 809 GHz observations in the commonly adopted approximation of local thermodynamic equilibrium (LTE). Since it is not entirely clear what kind of the interstellar medium [C I] traces, we perform a non-LTE calculation as well to evaluate the impact of subcritical densities.
 |
Fig. 8 Distributions of the derived X(C I) values. Left: X(C I) histogram. The median value of 1.7 1021 cm−2 (K km s−1)−1 is indicated as the dashed line. Right: CDFs of the X(C I) factor (70w, IRw, IRb, and H II region sources in blue, green, yellow, and red respectively). |
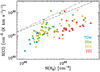 |
Fig. 9 X(C I) versus N(H2) (70w, IRw, IRb, and H II region sources in blue, green, yellow, and red). The predicted relations, X(C I) = 8.4 103 N(H2)0.79 (GUV = 1 Draine field) and X(C I) = 1.2 106 N(H2)0.69 (GUV = 10 Draine field), by Offner et al. (2014) are shown in gray. |
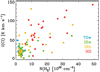 |
Fig. 10 I([C I]) versus N(H2) (70w, IRw, IRb, and H II region sources in blue, green, yellow, and red). |
5.1 LTE Calculation
As mentioned in Sect. 2.2, we observed nine sources in [C I] 809 GHz. To compare with the [C I] 492 GHz data, we smoothed the [C I] 809 GHz cubes and extracted spectra on 13′ scales from the pixels that correspond to the observed positions in our [C I] 492 GHz survey. The [C I] 809 GHz emission is detected in four sources, and the observed peak temperatures are summarized in Table 2.
Given that the observed sources are dense clumps, we could assume LTE conditions and derive physical conditions including the excitation temperature, opacities at 492 GHz and 809 GHz (−10 and −21), and atomic carbon column density (N(C)) (Appendix C). But before the LTE calculation, we first explored how the ratio of the 809 GHz to 492 GHz peak main-beam brightenss temperature (T21/T10) changes with the excitation temperature in two extreme cases: optically thin and thick regimes. When − − 1, Eqs. (C.1) and (C.5) suggest that T21/T10 can be written as
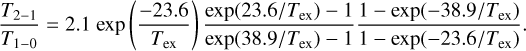 (1)
(1)
On the other hand, when − − 1, T21/T10 can be written as
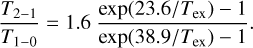 (2)
(2)
Eqs. (1) and (2) are plotted as a function of excitation temperature in Fig. 11.
Figure 11 shows interesting limiting behaviors. For example, the 809 GHz line would be twice as bright as the 492 GHz line (in temperature units) when the [C I]-emitting gas is warm (kBTex − hv2′1) and optically thin. On the other hand, the 809 GHz line would be about half as bright when the gas is cool (Tex~1020 K) and optically thick. The observed T2−1/T1−0 ranges from ~0.9 to ~1.7 (Table 2), suggesting that the [C I]-emitting gas is likely warm and optically thin.
To estimate Tex, −1−0, −2−1, N(C), and their associated 1′ uncertainties, we performed Monte Carlo (MC) simulations where the [C I] spectra are perturbed 1000 times based on the rms values (Gaussian errors are assumed). Each perturbed spectrum is fitted with a Gaussian function to measure the peak temperature, and Eqs. (C.2), (C.3), and (C.8) are applied to the measured temperatures to derive Tex, −1′0, −2′1, and N(C). For our calculation of N(C), −1−0 is used since it has a higher sensitivity than −2−1. Finally, the distribution of each parameter is examined to estimate a median value, as well as 34% boundaries from the median (so that the data points within the boundaries are 68% of the total number). These median values and 1− boundaries are provided in Table 2, and the normalized histograms of the derived parameters for G345.49+0.32 and G345.000.23 are shown in Fig. 12 to demonstrate our calculation. We note that G345.000.23 has asymmetric distributions, leading to a large uncertainty in Tex in particular. This is because the measured temperature ratio of 1.7 is on the asymptotic part of the T2−1/T1−0 versus Tex curve (Fig. 11) and therefore a small change in the ratio can result in a large variation in Tex. For the five sources where [C I] 809 GHz is not detected, lower and upper limits on the relevant parameters are provided in Table 2.
Zmuidzinas et al. (1988) observed Galactic star-forming regions (OMC 1, NGC 2024, S140, DR 21(OH), W3, M17, and W51) in [C I] 492 GHz and 809 GHz and performed similar excitation analyses. Compared to Zmuidzinas et al. (1988) results (3277 K), our excitation temperatures (49186 K) are slightly higher. In particular, we found a tendency of higher temperatures for more evolved sources (94 K and 186 K for the two H II region sources), though this needs to be verified by extensive [C I] 809 GHz observations in the future. Our optical depth values are, on the other hand, lower than Zmuidzinas et al. (1988) (e.g., −1−0 ~0.01−0.32 versus 0.22−1.25).
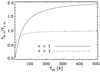 |
Fig. 11 Ratio of the 809 GHz to 492 GHz peak temperature (T21 /T10) as a function of excitation temperature (Tex). Optically thin and thick cases are shown in solid and dashed lines. |
 |
Fig. 12 Normalized histograms of the MC-based parameters (top: G345.49+0.32; bottom: G345.000.23). The median values and 1′ boundaries are indicated in red and blue. |
Properties of [CI] 492 GHz and 809 GHz.
 |
Fig. 13 Predicted 809 GHz-to-492 GHz temperature ratios for N(C) = 1016, 1017, and 1018 cm−2 (left, middle, and right, respectively). In each plot, the overlaied contours range from 10% to 90% of the peak temperature ratio with 20% steps. |
5.2 Non-LTE Consideration
While there is certainly a significant amount of dense gas in the observed massive clumps, whether the [C I] lines arise from this dense gas or from the lower density gas that surrounds the dense clumps is currently not clear. Since our previous calculations are based on the LTE assumption, it is therefore important to examine the impact of subcritical densities on the derived parameters.
To this end, we employed RADEX (van der Tak et al. 2007), where the radiative transfer equation for isothermal and homogeneous gas is solved based on the escape probability method to compute the intensities of atomic and molecular transitions. To cover a wide range of physical conditions, we created a RADEX model grid with the following parameters: kinetic temperature Tk = 10−500 K, H2 density n(H2)= 102106 cm−3, and C0 column density N(C) = 10161018 cm−2 (uniformly sampled in log space with ten, seventeen, and nine points). In addition to these key parameters, the line width of 5 kms−1 (median of the measured FWHM1−0; Table 2) and the background radiation of 2.73 K were assumed. To illustrate the RADEX modeling results, we present the predicted T2−1/T1−0 for N(C) = 1016, 1017, and 1018 cm−2 in Fig. 13.
Figure 13 illustrates a well-known degeneracy between the temperature and density: high density/low temperature and low density/high temperature combinations produce the same line ratio. To reproduce the observed T2−1/T1−0 of 0.91.7, Tk −60K and n(H2) −103 cm−3 are required, mostly ensuring LTE (densities lower than ~104 cm−3 mainly result in a difference between the kinetic and excitation temperatures). To explore the RADEX predictions more closely, we then selected the N(C) values that are closest to our LTE-based estimates and extracted the physical parameters that reproduce the observed line ratios within 1− uncertainties (Table 3). Our results show that the H2 density, kinetic temperature, and thermal pressure are poorly constrained, while the optical depths are relatively well constrained and not too different from our LTE values. The large variations in Tk and n(H2) are mostly driven by the density-temperature degeneracy and hinder us from inferring any systematic variation across the different evolutionary groups. On the other hand, the predicted brightness temperatures are comparable to the observed values. All these results imply that our LTE-based optical depths and C0 column densities are not heavily affected by subcriti-cal densities and [C I] emission arises from warm (Tk − 60 K), optically thin (− < 0.5), and highly pressurized regions (P/kB ~ (2−5000) 105 Kcm−3) in several of the Top100 sources.
6 Summary
In this paper, we present APEX observations of [C I] 492 GHz toward ATLASGAL-selected massive clumps in the inner Galaxy (Top100 sample). Our target sources have been extensively examined in dust continuum and spectral lines and constitute a representative sample of high-mass star-forming regions covering a significant range of masses (~20−104 M⊙), bolomet-ric luminosities (~60−106 L⊙), and evolutionary phases (70 µm weak, IR-weak, IR-bright, and H II regions). To examine the physical conditions of [C I]-traced gas in the Top100 sources, we combined our APEX [C I] 492 GHz spectra with multiwave-length observations of atomic and molecular gas and obtained the following results:
All 98 sources are detected in [C I] 492 GHz emission. In addition, 41 emission components and two absorption components are seentoward28 and two lines of sight respec-tively as secondary components. These results imply that [C I] 492 GHz is prevalent in the inner Galaxy and traces not only massive clumps, but also non-star-forming relatively diffuse gas;
The observed [C I] 492 GHz integrated intensities and line widths tend to increase toward evolved stages of star formation. In comparison to these main components that are associated with the Top100 sample, the secondary emission components have systematically lower [C I] 492 GHz intensities and FWHMs;
Among 139 components that are seen in [C I] 492 GHz emi-sison, 133 have clear 13CO(2−1) detections, implying a good correlation between [C I] 492 GHz and 13CO(2−1) in general (Spearman rank correlation coefficient of 0.95). The ratio of the13 CO(2−1) to [C I] 492 GHz integrated intensity changes from 0.2 to 5.3 though, likely driven by local conditions of the interstellar medium;
For the secondary components, 45 are detected in 13CO(2−1) emission only, while five are visible in [C I] 492 GHz emission only. This contrast in the detection statistics is partially due to the difference in sensitivity for the [C I] 492 GHz and 13CO(2−1) data. On the other hand, we found that the [C I] 492 GHz diffuse cloud components without corresponding 13CO(2−1) emission contain a significant amount of atomic gas and could trace CO-dark molecular gas. This conclusion, however, is based on few lines of sight and needs to be verified by sensitive [C I] 492 GHz, 13CO(2−1) and 12CO(1−0) observations in the future;
We derived the X(C I) factors by dividing the 870 µm-based H2 column densities by the [C I] 492 GHz integrated intensities and found that X(C I) (in units of cm−2 (Kkms−1)−1) ranges from 2.3 × 1020 to 1.3 × 1022 with a median of 1.7 × 1021. Our median value is in good agreement with recent observations of the massive star-forming region RCW 38 (1.4 × 1021), as well as predictions from numerical simulations of Galactic molecular clouds (~1021);
In contrast to the tight correlation with 13CO(2−1), [C I] 492 GHz shows a much more scattered relation with the 870 µm-traced molecular gas. We interpreted this as [C I] 492 GHz and 13CO(2−1) probing warm molecular gas that surrounds denser and colder clumps traced by 870 µm and cautioned not to use [C I] 492 GHz as a tracer of total gas mass if dense and cold molecular gas dominates the cloud mass;
Our LTE and non-LTE analyses showed that [C I] emission arises from warm (Tk ≳ 60 K), optically thin (τ < 0.5), and highly pressurized regions (P/kB ~ (2–5000) × 105 Kcm−3) in several of the Top100 sources.
Based on a large sample of sensitive [C I] 492 GHz spectra, this paper investigates the physical properties of [C I]-traced gas in a wide range of environments and sheds light on the origin of [C I] 492 GHz emission by probing the relation with molecular gas tracers. One of our key results is the systematic variation in the ratio of 13CO(2−1) to [C I] 492 GHz, which implies that the Top100 sources are in different stages of carbon phase transition (C+-, C0-, or CO-dominated). We will examine the exact stages of carbon phase transition and the underlying physical and energetic conditions in forthcoming papers where [C II], [C I], [O I], and CO observations from our multitelescope campaign are analyzed using state-of-the-art models of photodissociation regions and shocks (e.g., Le Petit et al. 2006; Flower & Pineau des Forêts 2015).
RADEX parameters for the individual sources.
Acknowledgements
We would like to thank the anonymous referee for constructive comments that improved this work. We also thank A. Gusdorf and M. Gerin for providing PRISMAS data and F. Le Petit for helpful comments. M.-Y.L. was partly supported by the Korea Astronomy and Space Science Institute grant funded by the Korea government (MSIT; project no. 2022-1-840-05) and the sub-project of A6 of the Collaborative Research Council 956 funded by the Deutsche Forschungsgemeinschaft (DFG).
Appendix A Tables
Characteristics of the observed Top100 sources.
Derived line parameters for [C I] 492 GHz and 13CO(2−1).
Appendix B Spectra
 |
Fig. B.1 APEX [C I] 492 GHz and 13CO(2−1) spectra (top and bottom for each panel). The fitted Gaussians are overlaid in red, and the source velocities are indicated as the gray dashed lines. Several spectra (in particular 13CO(2−1)) show absorption features, which most likely result from contaminated reference positions. On the other hand, [C I]-absorbing components toward G43.17+0.01 and G330.95−0.18 are labelled with the word “ABS”. |
Appendix C LTE Calculation
To calculate the physical properties of the [C I]-traced main components (Sect. 5.1), we combined the APEX [C I] 492 GHz and 809 GHz observations and followed the LTE-based procedure as below. First, we started with the following definition of optical depth:
![${\tau _\upsilon } = {{{c^3}} \over {8\pi {v^3}}}\left[ {\exp \left( {{{hv} \over {{k_B}{T_{{\rm{ex}}}}}}} \right) - 1} \right]{A_{{\rm{u1}}}}{\phi _\upsilon }{N_{\rm{u}}}$](/articles/aa/full_html/2022/08/aa42404-21/aa42404-21-eq26.png) (C.1)
(C.1)
where c is the speed of light, v is the frequency of the transition, h is the Planck constant, kB is the Boltzmann constant, Aul is Einstein’s spontaneous emission coefficient, ∅υ is the normalized spectral distribution of the transition as a function of velocity, and Nu is the column density of atoms in the upper transition state. With this definition for the optical depth, the τ2−1-to-τ1−0 ratio can be written as
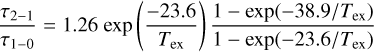 (C.2)
(C.2)
This equation assumes that [C I] 492 GHz and 809 GHz have the same excitation temperature and hence are in LTE. In addition, the atomic carbon column density can be estimated by
![$N\left( {\rm{C}} \right) = {{8\pi {v^3}} \over {{c^3}}}{Z \over {{A_{{\rm{ul}}gu}}}}\exp \left( {{{{E_{\rm{u}}}} \over {{k_B}{T_{{\rm{ex}}}}}}} \right)\,{\left[ {\exp \left( {{{hv} \over {{k_B}{T_{{\rm{ex}}}}}}} \right) - 1} \right]^{ - 1}}\mathop \smallint \nolimits^ {\tau _\upsilon }{\rm{\Delta }}\upsilon ,$](/articles/aa/full_html/2022/08/aa42404-21/aa42404-21-eq28.png) (C.3)
(C.3)
where ɡu and Eu are the statistical weight and energy of the upper transition state. The partition function Z is defined as
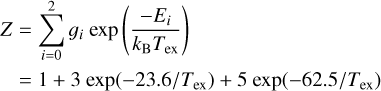 (C.4)
(C.4)
On the other hand, we considered the brightness temperature emitted from a region of uniform excitation temperature:
![${T_{\rm{B}}} = {{{{hv} \mathord{\left/ {\vphantom {{hv} {{k_{\rm{B}}}}}} \right. \kern-\nulldelimiterspace} {{k_{\rm{B}}}}}} \over {\exp \left( {{{hv} \mathord{\left/ {\vphantom {{hv} {{k_{\rm{B}}}{T_{{\rm{ex}}}}}}} \right. \kern-\nulldelimiterspace} {{k_{\rm{B}}}{T_{{\rm{ex}}}}}}} \right) - 1}}\left[ {1 - \exp \left( { - \tau } \right)} \right].$](/articles/aa/full_html/2022/08/aa42404-21/aa42404-21-eq30.png) (C.5)
(C.5)
For [C I] 492 GHz and 809 GHz, τ1−0 and τ2−1 can be written as
![${\tau _{1 - 0}} = \ln \,\left[ {1 - {T_{\rm{B}}}\left( {1 - 0} \right){{\exp \left( {23.6/{T_{{\rm{ex}}}}} \right) - 1} \over {23.6}}} \right]$](/articles/aa/full_html/2022/08/aa42404-21/aa42404-21-eq31.png) (C.6)
(C.6)
![${\tau _{2 - 1}} = \ln \,\left[ {1 - {T_{\rm{B}}}\left( {2 - 1} \right){{\exp \left( {38.9/{T_{{\rm{ex}}}}} \right) - 1} \over {38.9}}} \right].$](/articles/aa/full_html/2022/08/aa42404-21/aa42404-21-eq32.png) (C.7)
(C.7)
Therefore, the τ2−1-to-τ1−0 ratio is
![${{{\tau _{2 - 1}}} \over {{\tau _{1 - 0}}}} = {{ - \ln \,\left[ {1 - {T_{\rm{B}}}\left( {2 - 1} \right){{\exp \left( {{{38.9} \mathord{\left/ {\vphantom {{38.9} {{T_{{\rm{ex}}}}}}} \right. \kern-\nulldelimiterspace} {{T_{{\rm{ex}}}}}}} \right) - 1} \over {38.9}}} \right]} \over { - \ln \,\left[ {1 - {T_{\rm{B}}}\left( {1 - 0} \right){{\exp \left( {{{23.6} \mathord{\left/ {\vphantom {{23.6} {{T_{{\rm{ex}}}}}}} \right. \kern-\nulldelimiterspace} {{T_{{\rm{ex}}}}}}} \right) - 1} \over {23.6}}} \right]}}.$](/articles/aa/full_html/2022/08/aa42404-21/aa42404-21-eq33.png) (C.8)
(C.8)
Solving Eqs. (C.2) and (C.8) with the measured brightness temperatures numerically results in Tex, as well as τ1−0 and τ2−1.
References
- Braiding, C., Wong, G. F., Maxted, N. I., et al. 2018, PASA, 35, e029 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, C., Dickey, J. M., Dawson, J. R., & McClure-Griffiths, N. M. 2014, ApJS, 211, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, Y., Schuller, F., Urquhart, J. S., et al. 2013, A&A, 549, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, D. P. 1981, ApJ, 245, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csengeri, T., Leurini, S., Wyrowski, F., et al. 2016, A&A, 586, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duarte-Cabral, A., Colombo, D., Urquhart, J. S., et al. 2021, MNRAS, 500, 3027 [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2015, A&A, 578, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frerking, M. A., Keene, J., Blake, G. A., & Phillips, T. G. 1989, ApJ, 344, 311 [Google Scholar]
- Giannetti, A., Wyrowski, F., Brand, J., et al. 2014, A&A, 570, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glover, S. C. O., Clark, P. C., Micic, M., & Molina, F. 2015, MNRAS, 448, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Baryshev, A., Bell, A., et al. 2008, in SPIE Conf. Ser., 7020, 702010 [Google Scholar]
- Henning, T., & Salama, F. 1998, Science, 282, 2204 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Kereš, D., Oñorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Izumi, N., Fukui, Y., Tachihara, K., et al. 2021, PASJ, 73, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Keene, J., Lis, D. C., Phillips, T. G., & Schilke, P. 1997, IAU Symp., 178, 129 [NASA ADS] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W. J., Wyrowski, F., Urquhart, J. S., Menten, K. M., & Csengeri, T. 2017, A&A, 602, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, T., Ciechanowicz, M., Leinz, C., et al. 2014, IEEE Trans. Terahertz Sci. Technol., 4, 588 [CrossRef] [Google Scholar]
- König, C., Urquhart, J. S., Csengeri, T., et al. 2017, A&A, 599, A139 [Google Scholar]
- Kramer, C., Cubick, M., Röllig, M., et al. 2008, A&A, 477, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langer, W. 1976, ApJ, 206, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. Y., Madden, S. C., Le Petit, F., et al. 2019, A&A, 628, A113 [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 2021, A&ARv, 29, 5 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., et al. 2005, ApJS, 158, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., Bisbas, T. G., Bell, T. A., & Viti, S. 2014, MNRAS, 440, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T., Yamamoto, S., Iwata, M., et al. 2001, ApJ, 558, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C., McKee, C. F., & Leroy, A. K. 2010, ApJ, 721, 975 [CrossRef] [Google Scholar]
- Plume, R., Bensch, F., Howe, J. E., et al. 2000, ApJ, 539, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Pon, A., Johnstone, D., Kaufman, M. J., Caselli, P., & Plume, R. 2014, MNRAS, 445, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Keene, J., Le Bourlot, J., Pineau des Forets, G., & Roueff, E. 1995, A&A, 294, L17 [NASA ADS] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimajiri, Y., Sakai, T., Tsukagoshi, T., et al. 2013, ApJ, 774, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1997, ApJ, 481, 703 [CrossRef] [Google Scholar]
- Tang, X. D., Henkel, C., Wyrowski, F., et al. 2018, A&A, 611, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Umemoto, T., Minamidani, T., Kuno, N., et al. 2017, PASJ, 69, 78 [Google Scholar]
- Urquhart, J. S., Csengeri, T., Wyrowski, F., et al. 2014, A&A, 568, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, J. S., Figura, C., Cross, J. R., et al. 2021, MNRAS, 500, 3050 [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [Google Scholar]
- Zmuidzinas, J., Betz, A. L., Boreiko, R. T., & Goldhaber, D. M. 1988, ApJ, 335, 774 [NASA ADS] [CrossRef] [Google Scholar]
Throughout our analyses two-sided KS tests were done at a significance level of 5% when different distributions were compared. The null hypothesis that the compared two distributions are drawn from the same population is rejected if the D-statistics is larger than the critical D value 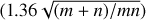 where m and n are the number of samples for the compared distributions) and the p-value is smaller than the significance level of 0.05.
where m and n are the number of samples for the compared distributions) and the p-value is smaller than the significance level of 0.05.
All Tables
All Figures
 |
Fig. 1 Average [C I] 492 GHz spectra of the four evolutionary groups (70w, IRw, IRb, and H II region groups in blue, green, yellow, and red). To derive these spectra, sources with contaminated reference positions were excluded. |
| In the text | |
 |
Fig. 2 CDFs of the [C I] 492GHz integrated intensity (top) and FWHM (bottom). For both plots, the 70w, IRw, IRb, and H II region groups are shown in blue, green, yellow, and red respectively. |
| In the text | |
 |
Fig. 3 Histograms of the [C I] 492 GHz integrated intensity (top) and FWHM (bottom). The distributions of the 94 main components and 38 diffuse cloud components are shown in black and gray respectively. |
| In the text | |
 |
Fig. 4 Comparison between [C I] 492 GHz (black), 13CO(21) (black), H I (green), and 12CO(10) (orange) for five sources. For H I, the absorption spectrum from Brown et al. (2014) is shown for G337.920.48, while SGPS data are presented for the remaining sources. In addition, 12CO(10) spectra from the FUGIN (G14.490.14) and Mopra (G336.960.23 and G337.920.48) surveys are used. Over the [C I] 492 GHz and 13CO(21) spectra, the fitted Gaussians are overlaid in red. Finally, the source velocities and the secondary components that are seen in [C I] 492 GHz without corresponding 13CO(21) detections are indicated in blue and gray respectively. |
| In the text | |
 |
Fig. 5 Comparison between the [C I] 492 GHz and 13CO(21) integrated intensities. All three types (Types 0, 1, and 2; Sect. 4.1.1) are used here, and the 70w, IRw, IRb, H II region groups, and diffuse cloud components are shown in different colors. For the Type 1, upper limits were calculated by N.C([C I]) [C I] 492 GHz 5− −v([C I]) where N.C([C I]) is the number of [C I] channels over which 13CO is detected and −v([C I]) is the velocity resolution of the [C I] spectra. A similar calculation was done for the Type 2, but using the number of 13CO channels over which [C I] is detected, 13CO 5−, and velocity resolution of the 13CO spectra instead. These derived upper limits are indicated as the arrows. Left: log scale. The measured minimum, median, and maxium I(13CO)-to-I([C I]) ratios (0.2, 1.8, and 5.3) are indicated as the dashed lines in different shades of gray color. Right: linear scale. A linear one-to-one relation is shown as the black dashed line. |
| In the text | |
 |
Fig. 6 [C I] 492 GHz line width versus 13CO(21) line width. Only the Type 0 detections with simple spectra are shown here. |
| In the text | |
 |
Fig. 7 CDFs of the I(13CO)-to-I([C I]) ratio. The 70w, IRw, IRb, H II region groups, and diffuse cloud components are shown in blue, green, yellow, red, and gray. For this plot, 97 Type 0 detections with clean off positions were considered. |
| In the text | |
 |
Fig. 8 Distributions of the derived X(C I) values. Left: X(C I) histogram. The median value of 1.7 1021 cm−2 (K km s−1)−1 is indicated as the dashed line. Right: CDFs of the X(C I) factor (70w, IRw, IRb, and H II region sources in blue, green, yellow, and red respectively). |
| In the text | |
 |
Fig. 9 X(C I) versus N(H2) (70w, IRw, IRb, and H II region sources in blue, green, yellow, and red). The predicted relations, X(C I) = 8.4 103 N(H2)0.79 (GUV = 1 Draine field) and X(C I) = 1.2 106 N(H2)0.69 (GUV = 10 Draine field), by Offner et al. (2014) are shown in gray. |
| In the text | |
 |
Fig. 10 I([C I]) versus N(H2) (70w, IRw, IRb, and H II region sources in blue, green, yellow, and red). |
| In the text | |
 |
Fig. 11 Ratio of the 809 GHz to 492 GHz peak temperature (T21 /T10) as a function of excitation temperature (Tex). Optically thin and thick cases are shown in solid and dashed lines. |
| In the text | |
 |
Fig. 12 Normalized histograms of the MC-based parameters (top: G345.49+0.32; bottom: G345.000.23). The median values and 1′ boundaries are indicated in red and blue. |
| In the text | |
 |
Fig. 13 Predicted 809 GHz-to-492 GHz temperature ratios for N(C) = 1016, 1017, and 1018 cm−2 (left, middle, and right, respectively). In each plot, the overlaied contours range from 10% to 90% of the peak temperature ratio with 20% steps. |
| In the text | |
 |
Fig. B.1 APEX [C I] 492 GHz and 13CO(2−1) spectra (top and bottom for each panel). The fitted Gaussians are overlaid in red, and the source velocities are indicated as the gray dashed lines. Several spectra (in particular 13CO(2−1)) show absorption features, which most likely result from contaminated reference positions. On the other hand, [C I]-absorbing components toward G43.17+0.01 and G330.95−0.18 are labelled with the word “ABS”. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


