| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 18 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141687 | |
| Published online | 04 February 2022 | |
Past and present dynamics of the circumbinary moons in the Pluto-Charon system
1
Universidad Nacional de Córdoba,
Observatorio Astronómico - IATE. Laprida 854,
5000
Córdoba,
Argentina
e-mail: cristian.giuppone@unc.edu.ar
2
Observatório do Valongo, Universidade Federal do Rio de Janeiro,
Ladeira do Pedro Antônio 43,
20080-090,
Rio de Janeiro,
Brazil
3
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, USP,
Rua do Matão 1226,
São Paulo,
SP
05508-090,
Brazil
Received:
30
June
2021
Accepted:
22
December
2021
Context. The Pluto-Charon (PC) pair is usually thought of as a binary in a dual synchronous state, which is the endpoint of its tidal evolution. The discovery of the small circumbinary moons, Styx, Nix, Kerberos, and Hydra, placed close to the mean motion resonances (MMRs) 3/1, 4/1, 5/1, and 6/1 with Charon, respectively, reveals a complex dynamical system architecture. Several formation mechanisms for the PC system have been proposed.
Aims. Assuming the hypothesis of an in situ formation of the moons, our goal is to analyse the past and current orbital dynamics of the satellite system. We plan to elucidate on in which scenario the small moons can survive a rapid tidal expansion of the PC binary.
Methods. We study the past and current dynamics of the PC system through a large set of numerical integrations of the exact equations of motion, accounting for the gravitational interactions of the PC binary with the small moons and the tidal evolution, modelled by the constant time lag approach. We construct stability maps in a pseudo-Jacobian coordinate system. In addition, considering a more realistic model that accounts for the zonal harmonic, J2, of Pluto’s oblateness and the ad hoc accreting mass of Charon, we investigate the tidal evolution of the whole system.
Results. Our results show that, in the chosen reference frame, the current orbits of all satellites are nearly circular, nearly planar, and nearly resonant with Charon, which can be seen as an indicator of the convergent dissipative migration experienced by the system in the past. We verify that, under the assumption that Charon completes its formation during the tidal expansion, the moons can safely cross the main MMRs without their motions being strongly excited and consequently ejected.
Conclusions. In the more realistic scenario proposed here, the small moons survive the tidal expansion of the PC binary without the hypothesis of resonant transport having to be invoked. Our results indicate that the possibility of finding additional small moons in the PC system cannot be ruled out.
Key words: celestial mechanics / planets and satellites: dynamical evolution and stability / planets and satellites: individual: Pluto / methods: numerical
© ESO 2022
1 Introduction
The Pluto-Charon (PC) binary has a mass ratio of ~0.122 and is currently found in a dual synchronous state, which is the typical endpoint of tidal evolution, over 1–10 Myr for this particular system (e.g. Farinella et al. 1979; Correia 2020). The orbit of Charon is almost circular, as confirmed by a 1σ upper limit of 7.5 × 10−5 (Buie et al. 2012). In the last 15 yr, the system has gained attention due to the discovery of its four small moons (Styx, Nix, Kerberos, and Hydra) and their complex circumbinary configurations. Several formation mechanisms for this satellite system have been proposed (Kenyon & Bromley 2021, and references therein). However, none of the proposed scenarios of the past evolution of the whole system has provided strong conclusions on whether the four small moons could survive the tidal expansion period of the PC binary.
The orbits of the small moons can be described with respect to the barycentre of the PC binary in the nearly circular and coplanar orbital geometry. Several works have studied the dynamical stability of the small moons, considering the possibility of the existence of putative satellites (e.g. Weaver et al. 2006; Kenyon & Bromley 2019c,a). Some have also considered the moons’ masses to be one order of magnitude larger than those determined by observational data (Tholen et al. 2008; Pires Dos Santos et al. 2011; Youdin et al. 2012). The orbital periods of the small moons place them very close to or even inside (depending on the uncertainties) the N/1 mean motion resonances (MMRs) with Charon, namely, 3/1, 4/1, 5/1, and 6/1 for Styx, Nix, Kerberos, and Hydra, respectively. For example, Brozović et al. (2015) obtained the period ratios of a satellite and Charon of 3.1565, 3.8913, 5.0363, and 5.9810 for Styx, Nix, Kerberos, and Hydra, respectively. While the double synchronous state of the PC binary is an indicator of the tidal evolution of the system, the positions of the moons with respect to the MMRs could be an indicator of a smooth migration process.
It is well accepted that Charon was formed as a result of a giant collision that most likely happened when the population of the Kuiper Belt was much denser than today (Canup 2005, 2011; Ward & Canup 2006; Asphaug et al. 2006; McKinnon et al. 2017; Walsh & Levison 2015). This giant impact could also have originated the very small circumbinary satellites Styx, Nix, Kerberos, and Hydra. There is evidence that the satellites are the same age as Pluto; indeed, the crater-counting data from New Horizons imply that the surface ages of Nix and Hydra are at least 4 billion years (Weaver et al. 2016).
Formation theories for the small moons in the PC system include an ‘intact capture scenario’ and a ‘planetesimal capture scenario’. In the scenario of intact capture (Canup 2005, 2011), a proto-Charon grows rapidly, in about 30 h after the collision event, within a massive debris swarm produced during the collision and extending from 4 RP to 25 RP (in units of Pluto’s radius). The commonly assumed initial position of Charon in the disc is around 4 RP (e.g. Cheng et al. 2014a,b; Woo & Lee 2018). Depending on the characteristics of the impact, the initial orbit of Charon varies its form, from circular to highly eccentric (eC ~ 0.50). The small moons belong to the debris swarm, and their initial positions are generally considered to be closer to Pluto than today.
To place the moons at their current locations, Ward & Canup (2006) proposed the mechanism of resonant transport. The main idea of the method is that, during the tidal expansion of the PC orbit, the small satellites can be captured into resonances with Charon and migrate outwards together with Charon. Several authors have tested this hypothesis and analysed the probability of capture in the MMRs of the kind N/1 (e.g. Lithwick & Wu 2008a; Cheng et al. 2014b; Woo & Lee 2018; Kenyon & Bromley 2021), which are considered to be strongest around binaries (e.g. Cuello & Giuppone 2019; Gallardo et al. 2021). However, Lithwick & Wu (2008b) found some difficulties in adjusting the values of Charon’s eccentricity, eC: in order to safely transport Nix to the 4/1 MMR, it should be eC < 0.024, while in order to transport Hydra to the 6/1 MMR, it should be eC >0.04. Cheng et al. (2014b) have found stable solutions (that is, without ejections from the system) for the test particles at the 5∕1, 6∕1, and 7∕1 MMRs but none at the 3∕1 and 4∕1 MMRs. Moreover, the orbits of the surviving particles were highly eccentric, in contrast with the currently nearly circular orbits of the small moons. In addition, the authors have found that, when the hydrostatic value of Pluto’s zonal harmonic, J2, was included in the model, there was no stable transport at the regions near the N/1 MMRs.
To overcome the problems of the resonant transport model, the scenario of planetesimal capture gained more attention. This scenario considers a ring of ejected material that ranges up to 60 RP, or even 200 RP; this value is even higher in the intact capture scenario (e.g. Pires dos Santos et al. 2012; Desch 2015; Walsh & Levison 2015; Kenyon & Bromley 2019b). Smullen & Kratter (2017) studied the evolution of a debris disc resulting from the Charon-forming impact, established regions of stability according to the tidal evolution of the PC binary, and characterised the collisions onto Charon’s surface that might leave visible craters. Woo & Lee (2018) studied several possibilities for survival of the test particles in the regions of the known moons during the tidal expansion of the PC binary (in situ formation scenario). Applying different tidal models, the authors found the most promising results when considered a constant-Δt tidal model with a large dissipation coefficient (A ~ 40) and an initially circular orbit for Charon (eC = 0.0); however, in their simulations they did not consider the impact of the zonal harmonic of Pluto’s oblateness.
The results obtained by either the tidal transport scenario or the in situ formation scenario are still inconclusive due to the poor knowledge of the precise orbital elements and masses of the small moons. The most precise orbital parameters of the PC system, reported in Brozović et al. (2015) and Showalter & Hamilton (2015) (see Table 1), present a dispersion of several orders of magnitude in the eccentricities and inclinations of the small moons. The solution from Showalter & Hamilton (2015) locked Pluto and Charon to the ephemerides of the Jet Propulsion Laboratory (JPL), PLU043. Our data are taken from JPL Horizons and correspond to the pre-computed solution PLU058/DE440, a fit to ground-based Hubble Space Telescope and New Horizons spacecraft encounter astrometry in the interval 1965–2018. To illustrate the uncertainties in orbital fits, we show in Table 1 the in-orbit errors (along the track) reported by Brozović et al. (2015) and also include the amplitude observed in the variation of orbital elements (see also Fig. A.1). The precise orbital dynamics of the small moons depends on the initial osculating orbital elements and the masses of the moons.
With this in mind, we introduce an additional mechanism that could provide a robust explanation for the existence of the four small circumbinary satellites at their current positions. For this, we first give a global view of the dynamics of the current Pluto system of small satellites in Sect. 2. In Sect. 3 we present the model, which describes the tidal interactions between Pluto and Charon, and discuss the choice of the parameter values adopted in this paper. In the next section we analyse how the tidal expansion of the PC binary, starting at different initial configurations, could affect the behaviour of the small moons located at their current positions (Sect. 4). In Sect. 5we analyse,in the frame of the in situ formation scenario, the effects of the tidal evolution of Charon’s orbit on a large grid of parameter values and initial conditions. In that section we also study the impact of the zonal harmonic of Pluto’s oblateness on the moons’ dynamics. To overcome the problem of survival of the moons during the passages through the low-order MMRs with Charon, we investigate the effects of a mass-accreting Charon on the moons’ behaviour in Sect. 6. Finally, we present our conclusions in Sect. 7.
2 Dynamical portrait of the current PC system
It is generally accepted that the current orbital configuration of the PC binary and the four small moons is a product of the evolutionaryhistory of the whole system during its lifetime, since the collision event that gave rise to Pluto’s satellites. In this context, a detailed analysis of the current relative positions of the Pluto system members may provide important constraints on the dynamical past of the whole system.
A representative picture of the PC system is shown in Fig. 1; it is calculated with data from the JPL Horizons site (see Table 1). To construct it, we used a modified Jacobi reference frame, in which orbital elements of the small moon are referred to the centre of mass of the PC system and the mutual interactions between the moons are neglected1. In this reference frame, the motion of a particle of Styx’s mass is simulated through the numerical integration over 200 yr (~3500 Styx orbital periods) and subsequently analysed using Δe or Δi indicators to better address the structure of the resonances. We calculate Δe as the amplitude of maximum variation in the orbital eccentricity of the satellites during the integrations, 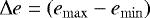 . Similarly,
. Similarly, 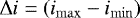 and
and 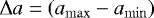 . Regions with higher Δe lead to chaotic motion, and Δe is a powerful indicator of secular and resonant dynamics that also serves to identify separatrices of MMRs (e.g. Dvorak et al. 2004; Ramos et al. 2015).
. Regions with higher Δe lead to chaotic motion, and Δe is a powerful indicator of secular and resonant dynamics that also serves to identify separatrices of MMRs (e.g. Dvorak et al. 2004; Ramos et al. 2015).
The instabilities in the motion of the particles are represented using a colour scale on the maps in Fig. 1, on the a–e plane (left panel) and a–I plane (right panel) of the initial conditions, where a, e, and I are the semi-major axis, the eccentricity, and the inclination of the particle, respectively. In the stability maps, the initial conditions for Charon are given in Table 1, whereas the initial values of the angular variables of the circumbinary moon are those given to Styx in Table 1. We note that all moons lie beyond the black continuous curve in the left panel, which delimits the domain of stable motion, according to the Holman–Wiegert criterion (HWC) derived in Holman & Wiegert (1999) for circumbinary configurations and also noticed by Smullen & Kratter (2017).
Figure 1 shows that the orbits of the moons are nearly circular, nearly planar, and nearly resonant. Although these features of the Pluto system have already been pointed out in previous studies, it is still worth analysing them in more detail. Indeed, as seen on the stability maps on the a–e and a–I planes, the small satellites are confined to the very small eccentricity and inclination regions of regular motion (blue colour). According to secular perturbation theories, very low eccentricities and inclinations are characteristic of the dynamical systems that have an angular momentum deficit (AMD) close to zero (Michtchenko & Rodríguez 2011). Regarding initially excited dynamical systems (in this case, due to the collisional origin of Charon), the low-AMD configurations are generally attained by the systems evolving under weak and slow dissipation.
The interpretation of the near resonant distribution of the small satellites requires the analysis of an additional dynamical mechanism, that is, a capture into MMRs. The stability maps in Fig. 1 show the MMRs produced by Charon as vertical strips of chaotic motion (red colour). The strong low-order MMRs, such as 3/2, 5/3, 2/1, 5/2, and 3/1, are located inside the domain of instability defined by the HWC (black curve in the left panel). In the low-eccentricity region, the 3/1 MMR can be regarded as an inferior limit of stability of the motion, and Styx is stuck to it. This moon lies so close to the 3/1 MMR that uncertainties in the determination of the angular variables of its orbit, such as the mean longitude and the longitude of the pericentre, might put it closer to the chaotic layer of the 3/1 MMR (e.g. in-orbit and radial errors reported in Brozović et al. 2015). The same is also true for Nix with respect to the 4/1 MMR (see the Styx and Nix panels in Fig. A.2) but is most noticeable for Kerberos and Hydra with respect to the 5/1 and 6/1 MMRs, respectively (see the bottom panels of Fig. A.2). This fact suggests that the small moons may have been involved in one of the MMRs at some period of their common history. Therefore, in this paper we analyse the interaction of the small moons with the main MMRs during the tidal expansion of Charon’s orbit.
It is worth emphasising that the uncertainties in the determination of the moons’ masses and the actual positions can provide a general view of the phase space of the PC system, but without specifying whether the objects are evolving near or inside the MMRs.
 |
Fig. 1 Dynamical maps on the a–e plane (left panel) and a–I plane (right panel) of the moon’s initial conditions calculated for the PC binary and a small moon of Styx’s mass with initial Styx orbital elements from JPL in Table 1. The current positions of the moons are shown by red crosses. The locations of the main MMRs are indicated, and the grey line in the right panel indicates the current inclination of Charon. The colour scale varies with Δe and Δi, increasing from blue (regular motion) to red (chaotic motion), as shown in the colour bars on the top of the figure. |
Orbital elements and masses of the Pluto satellites.
3 Tidal model
In this section we describe the tidal model, which we apply to investigate the orbital expansion of Charon and the implications for the orbital motion of the small moons. As described in the previous section, the orbital configuration of Pluto’s satellites is better represented in terms of the modified Jacobi elements. The initial Jacobi orbital elements are transformed to the Jacobi rectangular coordinates and velocities in a three-dimensional reference frame centred on Pluto. The equations of motion are solved using an N-body integrator with adaptable step size (for details, see Rodríguez et al. 2013). We considered the system consisting of Pluto, Charon, and an external small moon, where two large bodies undergo mutual tidal interaction but the external moon is not (directly) tidally affected, due to its small size and mass. We adopted a classical linear tidal model, in which the deformations of the bodies are delayed by a constant Δt, usually referred to as the tidal time lag (Mignard 1979). In this scenario, the PC tidal interaction is modelled following Cheng et al. (2014a)2, who assumed the collisional origin of Charon, when Charon emerges with a non-zero orbital eccentricity, eC, and an initial semi-major axis of aC = 4 RP (Ward & Canup 2006).
Both Pluto and Charon would be spinning after the collision, with the spin axes oriented in some directions with respect to the orbital plane of the binary. Due to the relatively small size and mass of Charon, in comparison with Pluto, the contribution of its spin to the total angular momentum is small, and it evolves quickly to the asymptotic tidal spin rate (in less than 10 yr). For the sake of simplicity, in this work we assume zero obliquity for both Pluto and Charon; the model of the PC binary, accounting for the arbitrary obliquities and the Sun’s perturbations, is studied in Correia (2020).
The total angular moment of the PC binary can be written, in the chosen reference frame and with the assumed approximations, as
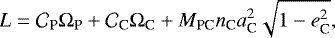 (1)
(1)
where MPC = mPmC∕(mP + mC) and nC are the reduced mass of the binary and the mean motion of Charon, respectively. According to classical theories, L is conserved during the tidal expansion of the PC binary. Hence, its amount for the PC system can be obtained knowing the masses of Pluto and Charon, mP and mC, and the current values of aC and nC. Indeed, at the dual synchronous state of the current PC binary, Charon’s orbit is circularised, that is, we can assume eC = 0 and ΩP = ΩC = nC.
Then, by substitution of these conditions into Eq. (1), the L value is obtained; in the following, this value is used to obtain the angular velocity of Pluto, ΩP, resolving Eq. (1) for given starting values of aC, eC, and ΩC, the angular velocity of Charon’s rotation.
Following Cheng et al. (2014a), we define the dissipation parameter, A, as
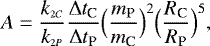 (2)
(2)
where (k2C, k2P) are the second-order Love numbers and (RP, RC) are the radii for Pluto and Charon, respectively. We note that, for the masses and the radii of Pluto and Charon (RC = 606 km),
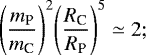 (3)
(3)
thus, the constant A can be closely understood as the ratio of time lags between Charon and Pluto. Cheng et al. (2014a) have also shown that, for an appropriate value of the ratio (A ~ 10), the eccentricity of Charon’s orbit, eC, remains roughly constant during most of the tidal evolution.
Our current knowledge of the physical properties of the PC system does not allow us to constrain the range of A values (see Eq. (2) and Lainey 2016; Quillen et al. 2017). However, it is easy to show through classical tidal theories that for A << 1 tidal forces on Pluto dominate the tidal evolution of the binary, whereas for A >> 1 the orbital expansion and circularisation are dictated by the tides on Charon. Previous works adopted different ranges for the possible values of A, namely, 1 < A < 18 (Cheng et al. 2014a,b); A = 10 or A = 40 (Woo & Lee 2018); and 1 < A < 16 (Correia 2020). In this work, we initially explored the wide range of 0.01 < A < 100; however, in order to place test moons at the current Styx position, we adopted the range 8 < A < 40.
Cheng et al. (2014a) show the tidal evolution of the PC system for different initial eccentricities of Charon. Here, we summarise the common features observed in the numerical integrations, which we refer to in our discussions below: (i) Independently of the initial values of Charon’s eccentricity, eC, it presents a peak at some moment during the PC expansion; (ii) the time evolution of ΩP ∕n is correlated with the peak of eC and can reach values of ~ 10; (iii) the semi-major axis of Charon attains its current value (16.5 RP) and the orbit is circularised, whereas both rotations synchronise with the orbital period after around 3 × 106 yr. It is worth emphasising that, according to tidal evolution theories, the double synchronous rotation is only attained when the orbit is completely circularised (see Cheng et al. 2014a). Also, at the end of the evolution, the angular momentum exchange between Pluto and Charon ceases and both orbital and rotational components attain their equilibrium configurations in the system.
4 Dynamics of the moons in a tidally evolving PC system
In this section we investigate the dynamics of the small moons located at their current positions during the tidal expansion of Charon’s orbit. For this, we use the same techniques described in Sect. 2. Considering that Charon’s orbital elements vary during the migration, we mapped the neighbourhood of each moon, applying the conservative model for different values of the semi-major axis, aC, and the eccentricity, eC, of Charon’s orbit and the fixed mass and initial conditions of the satellite (Table 1). In this way, we can visualise the dynamical behaviour of each moon at different configurations of the PC binary acquired in the past. Figure 2 shows the dynamical maps on the aC–eC planes, obtained for the current locations of Styx, Nix, Kerberos, and Hydra retrieved from JPL Horizons. The black curves show the positions of Charon on these planes as obtained through simulations of its tidal expansion in the past (described in the previous section). Three values were used for Charon’s eccentricity, namely 0.01, 0.1, and 0.2, while the other parameters were fixed at aC ∕RP = 4, ΩC ∕nC = 2, A =10, and ΔtP = 600 s. By construction, the three paths converge to the current position of Charon, at aC ≅ 16.5 RP and eC ≅ 0.
Now we can investigate the dynamical behaviour of each moon according to the position of Charon at any moment of its history. Indeed, for a chosen position of Charon in one of its paths on the aC–eC planes in Fig. 2, we can identify dynamical features that affect the behaviour of the moon at that instant. These features are mainly MMRs, which are identified by plotting the moon’s dynamics with the colour scale. In this way, we can distinguish between the stable (blue-white) and unstable (red) behaviour of satellites. The instabilities of the motion are clearly related to the MMRs, whose locations are indicated by the corresponding ratio in Fig. 2.
The strongest MMRs are of low order, 3/1 and 4/1, and we expect that the dynamical stability of the moons would be significantly affected by these resonances. Figure 2 shows that Charon’s paths (black curves) never cross the 3/1 MMR, and, consequently, none of the four small moons suffer the destabilising effects of this resonance. Currently, Styx stays close to this resonance (left-top panel), but its motion is still stable. It is worth noting here that the 3/1 MMR can be considered as an inferior limit of the stability of the circumbinary motion, as shown in Fig. 1.
According to Fig. 2, the actual position of Styx has been crossed by the 4/1 MMR at some moment in the past, as has that of Nix (right-top panel) at another period. Our simulations of the moons’ dynamics (described in the next section) show that the perturbations produced by this resonance increase with the increasing eccentricity of Charon. For Charon’s paths with eC = 0.1 and 0.2, Styx and Nix spend some time evolving in the 4/1 MMR, which might be sufficient to strongly excite their eccentricities and even eject them from their current positions. On the contrary, for Charon on a quasi-circular orbit (eC = 0.01), the passages of Styx and Nix through the 4/1 MMR may occur quickly and without significant excitation of their motions.
The width and, consequently, the dynamical effects of the higher-order MMRs, such as 5/1, 6/1, and, 7/1, rapidly decrease with decreasing order, as seen in Fig. 2. We expect that their passages through the current positions of the small moons would not produce perturbations to destabilise their motion, particularly for Charon evolving on a quasi-circular orbit during these passages. Thus, we conclude that, in order to ensure the simultaneous orbital stability of the four small moons during the orbital expansion of the PC binary, Charon’s eccentricity should be constrained to lower values. This fact points towards a dynamical scenario in which the adequate choice of Charon’s eccentricity at the beginning of the tidal expansion is essential in order to guarantee the orbital stability of the system of moons. In the next section we numerically simulate the impact of a migrating Charon on the orbital motions of Styx, Nix, Kerberos, and Hydra by taking simultaneous effects of the tidal evolution and gravitational perturbations into account.
5 Simulations of the moons’ behaviour under the tidal expansion of Charon’s orbit
In this section we analyse the behaviour of Styx, Nix, Kerberos, and Hydra during the orbital expansion of Charon’s orbit and their passages through the MMRs. Here, we assumed the in situ formation of the small moons, that is, our numerical simulations start with the satellites at their current positions. We worked in the modified Jacobi reference frame, where small moons are orbiting the barycentre of the PC binary. In this frame, we neglected the mutual perturbation between the moons, due to their small masses, which allowed us to solve their orbital motions in a separate way. We solved the exact equations of motion for each satellite according to the tidal model described in Sect. 3 and following Rodríguez et al. (2013). We considered coplanar configurations and the initial mean anomalies, and longitudes of pericentre were set to zero.
We performed a set of numerical simulations, varying the main parameters of the problem, namely, the initial semi-major axis and eccentricity of Charon’s orbit (aC, eC), the initial rotation velocities of Pluto and Charon (ΩC and ΩP), the time lag of Pluto, ΔtP, and the constant of dissipation, A (see Table 2). The initial orbital angles of Charon were set to zero. We fixed a fiducial set of parameters such that aC ∕RP = 4, eC = 0.001, ΩC ∕nC = 2, A =10, and ΔtP = 600s. Then, the simulations were done varying the parameters one by one, choosing the values listed in Table 2. It is worth noting that the initial value of ΩP is not a free parameter but is determined by the conservation of the angular momentum of the binary through Eq. (1).
The masses and current semi-major axes of the external moons were taken from Brozović et al. (2015) (see Table 1). The initial orbital eccentricities of the moons were assumed to be almost circular (e = 10−5). We note that in this section we work in the frame of the planar problem, when the small moon evolves on the orbital plane of the PC binary. Physical parameters, such as the masses and radii of Pluto and Charon, are the same as described in Sect. 3. Since the tidal evolution of the PC binary is not affected by the external small moon, we do not show the variations in their orbital and rotational components in this section (see Fig. 2 in Cheng et al. 2014a). In addition, we performed simulations for both ΔtP = 0.06 s and ΔtP = 0.6 s, but the results obtained were discarded since Charon did not reach its current semi-major axis after 100 Myr in these cases. We integrated the equations of motions over 100 Myr for ΔtP = 6 s and ΔtP = 60 s; for ΔtP = 600 s, we considered 10 Myr as the integration timescale.
In the following we summarise the results obtained for each of the four moons, emphasising the cases in which the final orbital configuration of the small moon is similar to its current one. We note that, despite the fact that the moons are currently in nearly resonant configurations, the uncertainties in their masses and orbital parameters could still place them inside the MMRs (see our discussion in Sect. 1 and Fig. A.2). In Table 3 we include the cases for which each of the moons reaches the end of the simulation in stable motion. Additionally, we identify the initial conditions for which the final eccentricity of the moon is smaller than 0.05, which is compatible with the current eccentricities of the moons (see our Fig. A.1).
 |
Fig. 2 Dynamical maps of Styx, Nix, Kerberos, and Hydra on the aC–eC plane of Charon’s initial conditions. On each map, black curves are Charon’s tidal trajectories, obtained for initial eC values of 0.01, 0.1, and 0.2; the initial conditions of the corresponding moon are fixed at those given in JPL from Table 1. The blue tones represent regular motions, while the brick tones correspond to increasing instabilities and chaotic motion; the colour bar on the top shows Δe. The locations of the main MMRs are indicated. |
Parameters adopted in the numerical simulations.
5.1 Styx
Styx is located at a mean distance of 42 650 km (≃35.9 RP) from the barycentre of the PC binary and is close to the 3/1 MMR with Charon (see Figs. 1 and A.2). Other initial conditions different from those shown in Table 3 tested forthis satellite lead to either ejection of the small moon from the system (Fig. 3, left panel) or a final orbit that is different from the current one (Fig. 3, right panel). In most cases, instabilities occur when Styx approaches the 4/1 or 5/1 MMRs, in this last case, only for a high initial eC.
Figure 4 illustrates Styx’s orbital evolution obtained for A = 100. We note that, despite an apparently slow increase, the semi-major axis of Styx remains close to the current value. The eccentricity acquires a mean value of 0.02, varying roughly between 0.007 and 0.04, which is also consistent with the oscillation of Styx’s current eccentricity. The final value of the mean-motion ratio is larger than the nominal location of the 3/1 MMR (see Fig. 1); the difference between the pericentre longitudes of Styx and Charon, Δϖ, oscillates around 180°, which is an indicator of the dissipative migration (see Sect. 4). We have verified that, for this particular simulation, all critical angles associated with the 3/1 MMR circulate.
The results obtained for Styx point out that the scenario with an initially quasi-circular orbit of Charon and a high dissipation ratio (large A) favours the stability of Styx’s motion during the orbital expansion of the PC binary. However, we note in Table 3 that only very specific combinations of the parameters allow Styx to remain on a stable orbit as the 4/1 MMR with Charon is crossed. For most of the explored initial conditions, Styx’s motion is strongly excited by the passage through this resonance, resulting in the escape from the system. In Sect. 6 we test the orbital stability of Styx (and the other small moons) assuming anon-time accretion of Charon’s mass.
Parameters and initial conditions under which the four small moons survive in the numerical simulations.
 |
Fig. 3 Two typical examples of the Styx orbital evolution resulting in either instability (left panel) or the final configuration, which is significantly different from its current orbit (right panel). Left panel: initial conditions used are aC ∕RP= 5, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 600 s. Styx is ultimately ejected from the system when the system crosses the 4/1 MMR between Charon and Styx (not shown), resulting in a strong increase in Styx’s eccentricity. Right panel: initial conditions used are aC ∕RP= 4, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 6 s. The orbital eccentricity is excited, due to the crossing of the 4/1 and 7/2 MMRs (not shown), to attain the mean value ≃ 0.1, which is substantially larger than the current Styx eccentricity. |
5.2 Nix
Nix lies at a mean distance of 48 690 km (≃41 RP) from the PCbarycentre and is currently close to the 4/1 MMR with Charon. The values of the initial conditions resulting in final configurations similar to the current orbit of Nix are shown in Table 3. Figure 5 shows examples of the orbital evolution obtained for aC∕RP = 3 and aC∕RP = 7. For aC ∕RP = 3 (orange curves), the resulting orbit clearly deviates from the current orbital configuration of Nix. In this case, the trapping into the 4/1 MMR excites Nix’s eccentricity, up to e = 0.16. The final semi-major axis is larger than the current value, with a difference of ≃ 2 RP. Moreover, the critical angle associated with the 4/1MMR, ϕ4∕1 = 4λ − λC − 3ϖC, librates around 180°, as do all other angles associated with the same MMR, while Δϖ oscillates around 0° (Fig. 5, bottom right). In this case, eC reaches ≃4 × 10−5 at 107 yr in one of the simulations due to perturbations from Nix (not shown here).
On the other hand, for aC∕RP = 7 (blue curves), the orbital evolution of Nix occurs with the eccentricity and semi-major axis close to their current values. All critical arguments associated with the 4/1 MMR circulate in the case aC ∕RP = 7, indicating that the moon is out of the resonance, although it is still very close to it. In this case, the mean-motion ratio oscillates around a mean value slightly smaller than the nominal position of the 4/1 MMR (Fig. 5, bottom left), in accordance with the current position of Nix given in Brozović et al. (2015) (see Figs. 1 and 2).
The results shown in Table 3 indicate that, in comparison with Styx, almost 40% of the tested initial conditions result in the final orbital configurations, which are similar to the current orbit of Nix.
 |
Fig. 4 Examples of initial conditions for Styx. Top row: time evolution of Styx’s semi-major axis (left) and eccentricity (right) during the tidal expansion of the PC binary. The initial conditions used in the simulations are aC ∕RP= 4, es C = 0.001, ΩC ∕nC = 2, A = 100, and ΔtP = 600 s. The final values of the orbital elements remain close to the current ones. Bottom row: time evolution of the mean-motion ratio (left) and Δϖ (right). We note that the mean value of nC∕n is larger than 3. The secular angle, Δϖ, oscillates around 180°. |
 |
Fig. 5 Examples of initial conditions for Nix. Top row: time variations in Nix’s semi-major axis (left) and eccentricity (right) for two different initial values of aC. The initial conditions are aC∕RP = 3 and aC ∕RP = 7, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 600 s. For aC ∕RP = 3, the eccentricity of Nix is excited to a mean value close to 0.16. Bottom row: time evolution of the mean-motion ratio (left) and two angles for Nix (right), namely, the secular angle, Δϖ, and the 4/1 MMR critical angle ϕ4∕1 = 4λ − λC − 3ϖC. The mean value of nC∕n is slightly smaller than 4 for aC∕RP = 7, whereas ϕ4∕1 and Δϖ librate around 180° and 0°, respectively, for aC∕RP = 3. |
5.3 Kerberos
Kerberos is the third small satellite orbiting the PC binary, at a mean distance of 48.6 RP, which places it close to the 5/1 MMR with Charon. Table 3 shows that all numerical simulations result in good agreement with the current orbit of this small moon.
Figure 6 shows the orbital evolution of Kerberos during the tidal expansion of the PC binary for two values of the initial Charon eccentricity, eC = 0.001 (grey curves) and eC = 0.1 (red curves). For both initial conditions, the output of the simulations satisfactory fits the current orbit of the moon. All critical angular combinations of the 5/1 MMR circulate, and the ratio nC ∕n oscillates around a mean value slightly larger than 5, which places the moon outside, but still close to, the 5/1 MMR (see Fig. 2). We show the angle ϕ5∕1 = 5λ − λC − ϖC − 3ϖ, obtained for eC = 0.001, in the bottom-right panel of Fig. 6. At around 5 × 106 yr, this angle changes its behaviour from circulation to libration around 0°.
 |
Fig. 6 Examples of initial conditions for Kerberos. Top row: orbital evolution of Kerberos for two initial conditions of eC, namely, 0.001 and 0.1. The other parameters are aC∕R = 4, ΩC ∕nC = 2, A = 10, and ΔtP = 600 s. These simulations are successful according to the adopted criteria (see Sect. 5). Bottom row: time variations in the mean-motion ratio (left) and ϕ5∕1 = 5λ − λC − ϖC − 3ϖ (right). We show the angle for the specific case of eC = 0.001. The mean value of nC∕n is larger than 5. |
5.4 Hydra
Hydra is the most distant known satellite of the PC binary, with a current barycentric semi-major axis of a ~ 54.5 RP. This small satellite is close to the 6/1 MMR with Charon. Most of the simulations reproduce the current orbit of Hydra, as shown in Table 3. Figure 7 shows the evolution for ΔtP = 6 s (brown curves) and ΔtP = 60 s (grey curves). We can note that, for ΔtP = 60 s, Hydra is trapped in the 6/1 MMR, with the critical angle ϕ6∕1 = 6λ − λC − ϖC − 4ϖ librating around 0°. Moreover, the ratio nC ∕n is slightly smaller than 6 for this specific trapping. In the case with ΔtP = 6 s, all critical angles of the 6∕1 MMR are circulating.
As in the case of Kerberos, all initial conditions result in a stable motion of the test moons, with e < 0.05, indicating good agreement with the current orbit of Hydra.
5.5 Discussion of the moons’ behaviour and proximity to MMRs
Analysing the parameter values in Table 3, we realise that it is unlikely that we can collect a specific set of parameters and initial conditions that would result in a final configuration of all four satellites that is consistent with the current one. This fact is mainly due to the difficulty of finding Styx in a stable configuration.
Since the determination of the satellite’s current orbits is affected by uncertainties, it is not clear whether they are captured or not in the MMRs. Thus, for the sake of completeness, we show in Table 4 the values of the parameters that provide the final orbits of the moons trapped in the nearest MMR with Charon with at least one of the associated critical angles librating. It is remarkable that the motion of Styx in the 3/1 MMR is always unstable, which confirms our suggestion that the 3/1 MMR delimits the domain of stable motion in the PC binary.
For the sake of completeness, we compare our results with those previously reported by Woo & Lee (2018). Their model considered A = 10 and A = 40 and an initial eC = 0 and eC = 0.2, in the case of tidal model of constant Δt. For a large A and an initial eC = 0, all test particles survive the entire simulation (see their Table 3, last row). Moreover, the particles near the MMRs with Charon have final eccentricity values larger than the current ones. On the other hand, for small and large A and initial eC = 0.2, the final orbits do not match the current ones. These results are in good agreement with ours; however, Woo & Lee (2018) only considered fixed values of Δt = 600 s and ΩP ∕n = 5.65 and an initial distance for Charon of aC = 4 RP, while our study presents a wider range of initial parameters and tidal dissipation.
 |
Fig. 7 Examples of initial conditions for Hydra. Top row: orbital variation in the semi-major axis (left) and eccentricity (right) of Hydra according to the adopted criteria. The initial conditions are aC ∕RP= 4, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 6 s. Bottom row:time variation in the mean-motion ratio (left) and ϕ6∕1 = 6λ − λC − ϖC − 4ϖ (right) for two values of ΔtP, namely, 6 s and 60 s. We note that, for ΔtP = 60 s, ϕ6∕1 librates witha large amplitude around 0°. For ΔtP = 6 s, all critical angles associated with the 6/1 MMR circulate. |
Parameters resulting in captures in the MMRs with Charon.
5.6 Survival time of the small moons under J2 evolution
In order to refine our model, we introduced an additional force due to the oblateness of Pluto. Pluto’s polar oblateness, parameterised by the zonal harmonic, J2, is modelled as (Cheng et al. 2014b)
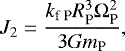 (4)
(4)
where kf P is the second-order fluid Love number of Pluto and ΩP is the angular rotation velocity of Pluto. Recently, Correia (2020) derived from the shape of Pluto a static value of J2 = 6 × 10−5. In this work, we use both formulations, adding them to the model described in Sect. 3.
We applied the model to study the behaviour of a ring composed of 300 particles, each with a very small mass of 1.49× 1015 kg (thus, we can neglect theirmutual perturbations and contributions in the total angular momentum of the system), at different positions chosen from the interval of 10 RP < a < 55 RP of the barycentric semi-major axis. We used the constant Δt model, A = 10, and the different initial values of Charon’s eccentricity, eC. It is worth noting that the value of eC constrains ΩP (and, equivalently, the initial rotation period of Charon). For example, starting at aC = 4RP, with eC = 0.001 and ΩC ∕nC=2 (i.e. PC = 0.38136 d) and using Eq. (1), we calculate the corresponding initial rotation period of Pluto as being P0 = 0.13858 d (P0 = 2π∕ΩP).
We worked with two kinds of disc particles: one is coplanar with the orbital plane of the PC binary, and the other is inclined, with the angle randomly chosen from the interval − 0.01° < i < 0.01°. In the coplanar disc, the particles start on nearly circular orbits, with eccentricities uniformly distributed in the interval 0.0 < e < 10−3. For Charon’s initial configuration, we considered aC = 4 RP and three values of the eccentricity, eC, namely, 0.001, 0.1, and 0.2. In the case of the inclined disc, the particles remain on nearly circular orbits, while aC = 4 RP and eC = 0.001. In both cases, we set random initial conditions for the angular variables of Charon’s and the particles’ orbits. The system composed of the PC binary and the ring of particles was integrated over 3 × 106 yr (approximately 150 × 106 periods of the binary)3.
The case of the initially inclined disc of particles was considered due to recently published results (Ćuk et al. 2020) that demonstrate that the tidal evolution of particles at low inclinations can induce resonant trapping and the excitation of the particles’ inclination, which is incompatible with the observed low inclinations of the moons in the PC system. The tests with an initially eccentric orbit for Charon were inspired by the results of the smooth particle hydrodynamic simulations reported in Canup (2005, 2011).
Figure 8 shows the survival times of the particles from the different discs. The results were obtained considering the zonal harmonic, J2, which evolves as the PC binary tidally expands, according to Eq. (4). We also investigated the behaviour of the disc considering the cases of J2 = 0 and J2 = 6 × 10−5, the latter value derived from Correia (2020); the results obtained are discussed in the appendix. We note in Fig. 8 that the particles can survive the tidal expansion of the PC binary (that is, remain in the PC system after 3 × 106 yr) only when Charon starts on a nearly circular orbit (eC = 0.001) and only in the region beyond Nix’s orbit. Also, there are no significant differences between the coplanar and low inclined discs (blue crosses and orange dots, respectively). Contrarily, in the case of an initially eccentric Charon orbit, all particles (green crosses and red dots) are ejected from the system in less than 103 yr due to capture in the MMRs and the subsequent excitation of the eccentricities, as described in Cheng et al. (2014a) and Kenyon & Bromley (2019b).
For the quasi-circular Charon orbit, the low-order 3/1 and 4/1 MMRs, at the positions of Styx andNix, respectively, are responsible for the rapid ejection of the particles (less than 104 yr). In this case, the survivors are observed only beyond Nix’s orbit. Moreover, even farther, in the regions around the current positions of Kerberos and Hydra (5/1 and 6/1 MMRs, respectively), most of the fictitious moons do not survive more than 105 yr. It is clear that these times are incompatible with the hypothesis of primordial moons after the system settled into its present configuration through an impact on Charon (Bromley & Kenyon 2020).
It is worth observing that, applying the simplified model, which considers the constant value of J2 (zero or J2 = 6 × 10−5), we obtain that the particles starting on nearly circular and nearly planar orbits at the current positions of Styx and Nix can survive the tidal expansion of the PC binary (for details, see the appendix). However, in the more realistic model, which accounts for the zonal harmonic, J2, evolving during the expansion, the additional perturbations destroy the stability of the particles in the range 10 RP < a < 55 RP. Moreover, no particles remain at the current positions of Styx and Nix. We repeated these experiments with a higher dissipation ratio, A = 20, and qualitatively obtain the same result.
 |
Fig. 8 Survival times of the small particles, for the different discs extending from 10 RP to 55 RP, during the tidal expansion of the PC binary, with the dissipation parameter A = 10, under the effect of the evolving zonal harmonic, J2. The colour symbols are used to identify the particles from the different discs (see text). |
6 Accreting Charon’s mass
In this section we introduce a scenario that considers the mass accretion of proto-Charon from the disc of debris left soon after the giant impact. The growth of Charon occurs simultaneously with the tidal expansion of its orbit around Pluto and could affect the behaviour of the small circumbinary moons described in the previous sections.
First, we analyse the evolution of the expanding binary with a growing Charon in Sect. 6.1. Then we introduce an additional small moon (either Styx or Nix) to assess the parameters of the tidal evolution in Sect. 6.2. Finally, we simulate the behaviour of the disc of particles in the PC system in Sect. 6.4. In this section we choose the plane of Charon’s orbit as a reference plane.
6.1 Tidal evolution of the PC binary with the accreting Charon mass
We started by considering the evolution of the PC pair described in Sect. 3, now including the accretion of Charon from the disc of debris. The duration of the accretion process was arbitrarily fixed at 104 yr after a giant impact, starting with Charon’s mass at 60% of its current value, which is in accordance with the results in Canup (2005) and Kokubo et al. (2000). Following Kokubo et al. (2000), we adopted a logarithmic law for the mass accretion, but we also considered an oligarchic growth defined as m ∝ t1∕3. The evolution of the increasing mass of Charon is shown in the left panel of Fig. 9 for both models. Assuming Charon to be a homogeneous sphere, we calculated its radius for a constant density of ρ = 1.70 g cm−3 and show its time evolution in the middle panel of Fig. 9. Finally, the right panel shows the time evolution of the zonal harmonic, J2, of Pluto’s oblateness during the tidal migration of a growing Charon. According to Eq. (4), J2 is a function of the orbital spin of Pluto ΩP, whose starting value was chosen as described below. For the chosen ΩP, J2 starts at ~ 0.17 and reaches 8 × 10−5 at the end of the migration, for both logarithmic and oligarchic laws of the mass accretion. We note that both models represent almost the same evolution of J2. We also show in the right panel of Fig. 9 the constant J2 of 6 × 10−5 derived in Correia (2020).
It is worth emphasising that, in the growing mass scenario, the total angular momentum of the PC binary given in Eq. (1) is no longer conserved. Thus, we need to obtain the initial value of Pluto’s spin, ΩP, and the dissipation ratio, A, in such a way that both can guarantee the current double synchronous configuration of the binary with orbital parameters compatible with those from Table 1.
Using a logarithmic law for Charon’s accretion and fixing A = 10 and eC = 0.001, we varied the initial rotation period of Pluto, P0 = 2π∕ΩP, in the range from 0.12 d to 0.21 d in order to determine the value that assures, at the end of the migration, the current configuration of the PC binary. We chose a low initial eccentricity for Charon due to constraints already described in Sect. 5.6. We simulated the tidal evolution of the PC binary and show the results in Fig. 10, where the time evolution of Charon’s semi-major axis, aC (in units of RP), is presented in panel (a). The horizontal dashed line, which shows the final state of the current system, corresponds to the initial value P0 = 0.149 d. Smaller initial values of P0 lead to wider PC binaries, while larger values of P0 lead to morecompact systems, more similar to the current PC configuration. The eccentricity of the binary is more efficiently damped for higher initial values of P0, as shown in panel b in Fig. 10. Panels c and d show the evolution of the angular velocities of Pluto and Charon, ΩP and ΩC (in units of the mean motion nC), respectively;it is clear that the system reaches the double synchronous rotation more rapidly for higher values of P0.
The time evolution of the accreting system for the different values of the dissipation parameter, A, is presented in Fig. 11. The values of A are chosen from the range [8 − 21], while the initial rotation period of Pluto and the initial Charon eccentricity are fixed at P0 = 0.149 d and eC = 0.001, respectively.Charon’s eccentricity, shown in the top panel of Fig. 11, is damped more efficiently as A increases. The evolution of ΩC (in units of the mean motion, nC) is shown in the bottom panel; we note that the synchronous state of Charon is more quickly attained for higher values of the dissipation parameter, A. The variations in the semi-major axis of Charon and the rotation of Pluto, ΩP, with the increasing A values are insignificant and are not shown in Fig. 11.
The tests described above allowed us to define the parameter values of P0 = 0.149 d and A for the interval [8 − 21], which are compatible with the current configuration of the PC binary. The tests, done with the oligarchic mass accretion, indicate an initial value of P0 = 0.157 d; however, the corresponding simulations have shown results that are qualitatively similar to those obtained with the logarithmic mass growth model.
 |
Fig. 9 Time evolution of Charon’s physical properties during the mass accretion: the mass, the radius, and the zonal harmonic, J2, from left to right. Colours represent the results obtained from the different accretion models. The dashed horizontal line (right panel) presents the constant J2 obtained in Correia (2020). |
 |
Fig. 10 Tidal evolution of the PC binary, for A = 10 and a logarithmic mass accretion of Charon during the first 104 yr, starting with the initial eccentricity eC = 0.001. Panels show the orbital semi-major axis, aC, in units of RP (panel a), the orbital eccentricity, eC (panel b), and the spin angular velocities of Pluto, ΩP (panel c) and Charon, ΩC (panel d) in units of the mean motion, nC. Each colour represents a different initial P0, in units of days. |
6.2 PC binary and a small moon
In this section the model is expanded with the additional of a small moon with the mass and orbital elements of either Styx or Nix. As described in the previous section, the behaviour of these two satellites is significantly affected by the passages through the strong 4/1 and 5/1 MMRs. We explored the parameter space of the problem defined by A and mi, where mi is the mass of the small moon. For the mass, we chose the extreme values of the masses of Styx and Nix, given by the uncertainties reported in Brozović et al. (2015) and Showalter & Hamilton (2015). We set the initial eccentricity of the small moon at e = 0.001, the semi-major axis at a = 44413 km (a ~ 37.4 RP) and a = 50690 km (a ~ 42.7 RP) for the Styx and Nyx clones, respectively, and the angular elements equal to zero. As shown below, these initial values of a were chosen to obtain the current positions of the small moons. All simulations in this section were done with the accretion time of 104 yr.
We started analysing the behaviour of the Styx clones during the tidal evolution of a growing Charon. We considered first a Styx mass of 1.49× 1015 kg, which corresponds to the 1σ estimate given in Brozović et al. (2015). Figure 12 shows the time evolution of the Styx orbital elements obtained for the values of the dissipation coefficient, A, ranging from 11 to 20; the elements are the semi-major axis (top panel) and the eccentricity (middle panel). We note that the test moon smoothly migrates inwards during the first ~ 104 yr, a period during which Charon’s mass is increasing. After the satellite reaches its current position (continuous horizontal line), it evolves with a nearly constant semi-major axis up to an encounter with some important MMRs with Charon.
The interaction of the moon with the MMRs is generally accompanied by the excitation of the moon’s eccentricity. We can observe this phenomenon in the middle panel of Fig. 12, which shows the time evolution of the moon’s eccentricity during the migration of a growing Charon. When Charon’s mass grows to 90% of its current value (in about 3 × 103 yr), the moon’s eccentricity is excited due to the approximation to the resonance domain, in this case, of the 9/1 MMR. From that event, the eccentricity can suffer consecutive excitations during the passages of the moon through the resonances, even being ejected from the system, depending on the value of A. The currentconfiguration of Styx is acquired for around 30% of the tested values of A, namely 16, 17, and 18. As observed in the bottom panel of Fig. 12, there are two ejections due to the 5/1 MMR and four due to the 4/1 MMR, and one is associated with the 7/2 MMR.
We repeated the simulations described above but this time analysing the behaviour of the Nix clones during the tidal expansion of an accreting Charon. We considered a value for Nix’s mass of 1.5 × 1016 kg, which is smaller than the mass range obtained in the orbital fits reported in Brozović et al. (2015) and Showalter & Hamilton (2015). The results obtained for Nix are shown in Fig. 13, which is similar to Fig. 12, but in this case we observe fewer ejections: one from the 6/1 MMR and another from the 4/1 MMR (see the bottom panel). We can observe in the middle panel of Fig. 13 that the particles experience consecutive eccentricity excitations during the passages through the MMRs, resulting in the higher dispersion of the final values when compared to the case of the Styx clones.
We redid the simulations described above for the Styx and Nix clones, considering now larger masses of 1.5 × 1016 kg and 4.5 × 1016 kg, respectively.We could not observe significant differences when comparing the new results to those obtained for the smaller masses of the test moons. Thus, we conclude that, in the range of values considered in this paper, the masses of the moons are not an important factor for achieving favourable configurations of the satellite system. On the other hand, the simulations conducted with the values of the dissipation coefficient, A, in the range 11− 20 did not allow definitive conclusions to be drawn regarding the influence of this parameter on the moon’s behaviour. In the next section we return to explore this issue.
 |
Fig. 11 Time evolution of the PC binary, eccentricity (top panel) and ΩC∕n (bottom panel), for the fixed initial P0 = 0.149 d and differentvalues of A, which are represented with different colours. |
 |
Fig. 12 Time evolution of the orbital elements of Styx, with the mass mS = 1.49 × 1015 kg, for the different dissipation values of A. The top panel shows Styx’s semi-major axis, the middle panel shows the eccentricity, and the bottom panel shows nC ∕n. The continuous horizontal line in the top panel indicates Styx’s current position, at a∕Rp = 35.7, while the dashed lines in the bottom panel identify the 3/1, 4/1, and 5/1 MMRs. |
6.3 Dependence on the accretion time
The accretion time of Charon, tacc, is an important parameter since it affects the time evolution of Charon’s orbital elements, particularly Charon’s eccentricity. As shown in Sect. 4, the ejection of a small circumbinary moon during the passage through one of the main MMRs is most likely for higher Charon eccentricity values. On the other hand, the rate of Charon’s mass accretion determines the damping rate of its eccentricity. Indeed, Fig. 14 shows the evolution of eC during the tidal expansion of Charon’s orbit. We use different colours to identify the tested values of the accretion time, namely 102, 103, 104, and 105 yr; the curve corresponding to the simulation with the ‘no-growing’ Charon, starting with its current mass, is also shown in Fig. 14. All simulations were performed with the initial value of eC = 0.001 and the A value fixed at 16. It is worth cautioning that the accretion rate determines the initial value of Pluto’s rotation period, P0; for the tested times of 102 yr, 103 yr, 104 yr, and 105 yr, we obtain optimal values of P0 = 0.1400 d, P0 = 0.1437 d, P0 = 0.149 d, and P0 = 0.1548 d, respectively (see Sect. 6.1 for details).
Figure 14 shows that the damping of Charon’s eccentricity is more efficient for an increasing tacc. Indeed, we can clearly observe that Charon’s eccentricity systematically increases with decreasing accretion time and reaches its maximum value in the case of the non-accreting process. The vertical dashed lines mark the main MMRs and allow us to evaluate eC when one of these MMRs crosses the current position of Styx. Hence, during the passages of the small moons through the MMRs, their motions will be more excited by Charon accreting the mass more rapidly. This fact would explain why we could not obtain successful results by simulating the evolution of the PC system without considering the accretion of Charon’s mass (see Sect. 5.6).
As shown in the previous sections, another important parameter of the problem is the dissipation coefficient, A. In order to link information on the dissipation parameter, A, to information on the accretion times, we prepared the parametric A–tacc plane, which is shown in Fig. 15. For a given point on the plane, we show the value of eC (in logarithmic scale) at the instant at which the 5/1 MMR, originated by a migrating Charon, crosses the current position of Styx. For this, we use the colour scale palette shown at the top of the figure. We note that the zero value on the y axis corresponds to the non-accreting Charon mass simulations. The red domains are associated with the highest eC values, while the dark blue domains are related to the lowest values. Observing the plane, we can conclude that the efficient damping of eC during the tidal expansion occurs for higher diffusion parameter values and the slower rate of accretion that favours the survival of the small satellites.
 |
Fig. 13 Same as Fig. 12 except for Nix, with the mass mN = 1.5 × 1016 kg at the position a∕Rp = 40.98 (continuous horizontal line). |
 |
Fig. 14 Eccentricity of a growing Charon during the tidal expansion of Charon’s orbit. Different colours are used to present the different values of the accretion time. The vertical dashed lines show the nominal locations of the main MMRs originated by a migrating Charon at Styx’s current position; each MMR is identified by the corresponding label. |
 |
Fig. 15 Parametric A–tacc plane showing, in colour scale, the values of Charon’s eccentricity, eC (in logarithmic scale) at the instant when the 5/1 MMR crosses Styx’s current location. |
6.4 Ring of particles in the accreting PC binary
In this section we consider the behaviour of the circumbinary thin disc of 500 particles during the tidal expansion of the accreting PC binary. Following Kenyon & Bromley (2019b), we first chose the disc, which is initially extended from 34 Rp to 60 Rp, with the eccentricities of the particles uniformly distributed between 0.5 × 10−3 and 1.5 × 10−3, no inclinations with respect to the orbital plane of the PC binary, and randomly chosen angular elements. We worked with particles with masses of either 1.49 × 1015 kg or 4.5 × 1016 kg; these values are still smaller than the mass of the PC binary; thus, the particles’ interactions can be neglected. Also, we selected random values of the dissipation parameter, A, in the interval [14−20] because these values favour the survival of the Styx and Nix clones, as described in the previous section. Finally, the time of the accretion of Charon’s mass is 104 yr.
Figure 16 shows the results obtained for the disc of particles with masses of 4.5 × 1016 kg as a function of the initial positions of the particles. The top panel shows the survival times of the test particles. In the regions beyond the Nix position, almost all particles survive the period of the tidal expansion of the accreting PC binary, while the region between Styx and Nix presents more instabilities (black dots in the top panel). In the middle panel of Fig. 16, we plot the final positions of the particles (orange) and Charon (blue). The final positions of the particles are generally closer to the binary than the initial conditions (the points lie slightly below the line ai = af, plotted as a continue blue line); this is a consequence of the increasing mass of the binary.
The bottom panel of Fig. 16 shows the final eccentricities of the PC binary (blue dots) and the particles (orange dots). For the particles with an initial a chosen in the range 34 Rp−45 Rp, the eccentricities are slightly higher than those from the range 45 Rp−60 Rp. The shaded region represents the extreme values of the eccentricities of the known moons, according to Table 1; the output of several simulations ends in this shaded region. The PC binary is almost circular, with eC ~ 10−5, which is compatible with its orbital fits (Brozović et al. 2015; Showalter & Hamilton 2015). We do not find any preference for A values in the range [14−20] in the region, which is interior to the Nix position; around 35% of particles survive in this region. We repeated the experiment choosing A values in the range [9−13] and found that 99% of the clones located inside the Nix’s orbit were ejected.
Several works have shown that the particles that start with low initial inclinations could be captured in a secular resonance, with a consequent excitation of their inclinations (e.g. Ćuk et al. 2020). We ran some experiments that considered a ring of particles similar to that described above but now inclined with an angle whose value was uniformly distributed in the range − 0.01° < i2 < 0.01°. We find no qualitative differences with the results presented in Fig. 16. Figure 17 shows the result obtained for the inclinations of the particles after 3 × 106 yr of the tidal evolution of the system. We observe some excitation of the inclination in the domain surrounding Styx and Nix, which is expected during the passages through the strong 4/1 MMR. These results are in agreement with the orbital fits reported in Showalter &Hamilton (2015).
The results obtained for the disc of the particles with a mass of 1.49× 1015 kg are similar to those described above. Thus, we can conclude that the simple model, which considers the accreting of Charon’s mass during the tidal expansion of the PC binary, is effective to explain the current locations of the small moons of Pluto without having to necessarily introduce the resonant transport mechanism.
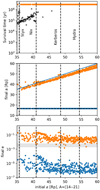 |
Fig. 16 Evolution of the ring of particles, each with a mass of 4.5 × 1016 kg, for an A in the range [14–21]. Top panel: survival times for particles. Middle panel: final semi-major axis of the small moons and Charon. Bottom panel: final eccentricity of Charon and the particles. The mass growth of Charon is set to 104 yr. Blue is used to indicate orbital parameters of Charon and orange for the particles. Orange dots represent survivors (the particles that remain close to initial configurations during the integration time of 3 × 106 yr). The black points in the top panel identify those particles that escape while the PC binary evolves. The shaded grey region indicates the range of values according to diverse authors (see Table 1). |
 |
Fig. 17 Distribution of inclination for the disc of particles after the dual synchronisation of the PC system with mass growth. Theorbits that do not survive the entire integration time are identified with black dots. The shaded grey region indicates the range of values according to diverse authors (see Table 1). |
7 Conclusions
We have analysed the stability and dynamical evolution of the small moons in the PC system, namely, Styx, Nix, Kerberos, and Hydra, during the tidal orbital expansion of Charon. We study the current architecture of the system and investigate how the tidal expansion of the PC binary system affects the orbital evolution of the small moons, extending previous studies.
The resonant structure around the PC binary exhibits N∕1 and N∕2 resonances, although most of them are weak in the low-eccentricity and low-inclination regimes. The 3/1 MMR is the strongest circumplanetary resonance, even for a low eccentricity and inclination of the moons (see Fig. 1). The current orbital configuration of the system does not show dynamical preferences of stable motion within the N/1 resonances despite the four small moons currently being located close to the 3/1, 4/1, 5/1, and 6/1 MMRs.
Using dynamical maps in the aC–eC plane, we reconstructed the tidal evolution of the PC system with a small moon initially placed at its current position (see Fig. 2). We adopted a tidal model parameterised by the constant time lag, Δt. When the PC system evolves assuming aninitial value of eC ~ 0.001, the resonances are weaker than when the PC system evolves from an initial value of eC ~ 0.1 or 0.2. Thus, the evolution from initially quasi-circular orbits avoids chaotic regions associated with N∕1 resonances, constraining the initial eccentricity of Charon. In addition, for small moons located near their current position, their semi-major axes do not secularly change unless they are captured in an MMR due to the tidal expansion of the PC binary.
The results of our numerical simulations indicate that it is possible to reproduce the current orbits of the four small moons of Pluto during the early tidal orbital expansion of Charon if we ignore the contribution of zonal harmonic, J2, and for a specific combination of initial conditions, such as Charon’s eccentricity, semi-major axis, and dissipation parameter, A. Hence, under the assumption of some specific values for the physical parameters and for the initial semi-major axis and eccentricity of Charon, these results point towards some specific scenarios (see Table 3). For example, for Styx and Nix, an initial almost circular orbit of Charon is needed in order to obtain a final stable orbit of the small satellites. In addition, a high dissipation in Pluto (ΔtP) allows for final orbital configurations of Styx that are in good agreement with their current orbits.
In the case of accreting Charon mass and considering an evolving J2 with dissipation coefficient A ≳ 14, we find that the small moons can survive the rapid evolution of the PC system and that the unlikely resonant transport of particles is no longer necessary. The ad hoc mass evolution of Charon might allow the moons to cross some resonances and not be trapped in specific positions of resonant motion. We also find that the eccentricity of Charon, eC, when Charon crosses the 5/1 MMR with the actual position of Styx might be used to estimate the accretion time or dissipation coefficient in order to obtain survival moons as the system tidally evolves. Our numerical simulations that consider a ring of particles between 34 RC and 60 RC show that a significant amount of particles remain in stable motion, with final orbits similar to the present small moons. Thus, the detection of additional small moons in future missions to the Pluto system should not be ruled out.
Further work is necessary to constrain the mass accretion in a more self-consistent scenario (e.g. Kokubo et al. 2000; Kokubo & Ida 1998). In addition, our model could be improved by considering mutual perturbations between the small moons(Showalter & Hamilton 2015; Lee & Peale 2006), by using a more realistic model for tidal dissipation within icy bodies (see Ferraz-Mello 2013; Folonier et al. 2018), or by considering the obliquity of Charon and perturbations from the Sun and Neptune (see e.g. Correia 2020).
Acknowledgements
N-body computations were performed at Mulatona Cluster from CCAD - UNC, which is part of SNCAD - MinCyT, Argentina. The constructionof the dynamical maps has made use of the facilities of the Laboratory of Astroinformatics (IAG/USP, NAT/Unicsul), whose purchase was made possible by FAPESP (grant 2009/54006-4) and the INCT-A. T.A.M. was supported by the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and São Paulo Research Foundation (FAPESP, grant 2016/13750-6). We acknowledge the program Professor Visitante do Exterior (PVE) from Pró-Reitoria de Pós-Graduação - Universidade de São Paulo. Edital PRPG 02/2019. The research done in this project made use of the Astroquery (Ginsburg et al. 2019), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018). The data presented in this paper are original from the authors, and are available upon reasonable request.
Appendix A Dynamical evolution of small moons
Here we provide complementary information to construct Table 1. In Fig. A.1 we show N-body integration of a three-body problem for a time span of 40 yr (grey lines), together with ephemerides taken from JPL Horizons. Amplitude oscillations of the orbital elements are resumed in Table 1 and agree with the colour scale presented in Fig 1. It is interesting to look first at the JPL ephemerides(blue lines in the figure). The left panels indicate the evolution of the semi-major axis, which presents amplitude of oscillations, from top to bottom, of 1761 km, 1086 km, 637 km, and 443 km (roughly Δa = 1.5RP, 0.9RP, 0.5RP, and 0.4RP) for Styx, Nix, Kerberos, and Hydra, respectively. We note that orbital elements are given with respect to the barycentre of the PC system. Osculating eccentricities present higher variations for closer moons and lower amplitudes for exterior moons (0.034, 0.025, 0.018, and 0.016, respectively). These variations are of the same order as the variations presented in Fig. 2 in Woo & Lee (2018) and Fig. 1 in Woo & Lee (2020), although the authors used the eccentricity for Charon from the JPL solution PLU043, which is older and an order of magnitude lower than the current determinations (solution PLU058). Finally, inclination evolution (right panels of Fig. A.1) shows oscillations around the midplane of the PC binary (denoted by an orange line, which is nearly coincident between N-body integrations and JPL query data). It is evident that the small moons can be either above or below the plane with different phases, and this inspired us in Sects. 5.6 and 6 to choose the PC orbit as reference plane, thus, for example, randomly defining inclinations around zero degrees.
Our N-body integrations (grey lines in Fig.A.1) show almost the same amplitudes as the JPL query (see also Table 1). However, there is an evident shift in the evolution of the semi-major axis of Nix and Hydra, although Δa is almost the same. We believe that the differences in the evolution of the semi-major axis in our simulations and JPL data could be due to the fact that the more sophisticated JPL model considers a significant number of perturbations, including the Sun and Neptune.
Figure A.2 shows four dynamical maps in the plane semi-major axis and mean anomaly, constructed using the mean exponential growth of nearby orbits (MEGNO) colour scale (e.g. MEGNO=⟨Y ⟩; Cincotta & Simó 2000, Y* = log10(⟨Y ⟩− 2)). MEGNO allows us to identify the separatrices of each resonance as chaotic (reddish colour of each panel). The MMR 3/1 is evidently more asymmetric than the 4/1, 5/1, and 6/1 MMRs because of its proximity to the PC binary. For example, for the Styx plane the separatrices show that the initial mean anomaly modifies the location of the resonance in ~1000 kms. Also, the MMRs 3/1 and 4/1 are wider than 5/1 and 6/1 MMRs because the moons experience greater excursions in eccentricity. These maps also help to understand that stability maps in planes a − e strongly depend on the chosen value of mean anomaly (in Fig. 1 these correspond to those from Styx, MS = 18.79°).
 |
Fig. A.1 Orbital evolution of Styx, Nix, Hydra, and Kerberos around the PC binary, from top to bottom, respectively. We show the evolution of the semi-major axis (left panels), eccentricity (middle panels), and inclination (right panels) for 40 yr. Blue lines correspond to data from JPL and grey lines to our N-body integrations. Orange lines correspond to the integrated inclination of Charon. |
 |
Fig. A.2 Stability maps on the a–M plane using the MEGNO colour scale for the four small moons. All other orbital parameters are set to the JPL values from Table 1. The current positions of the moons are shown by red crosses. The locations of the main MMRs are indicated. Small deviations from initial conditions within the estimated errors from PLU043 can place the moons inside the MMR regime. |
Appendix B Survival times of the disc described by simplified models
Here we present complementary information to that discussed in Sect. 5.6. Now we investigate the survival times of the disc of small moons, applying the model that uses fixed values of the zonal harmonic of Pluto’s oblateness, either J2 = 0 or J2 = 6 × 10−5 (the latter value was determined from the shape of Pluto in Correia 2020). We remember that our model consists of the tidally evolving PC binary and a disc of small moons extending from 10RP to 55RP (for more details, see Sect. 5.6).
Figure B.1 shows the case when the effect of the zonal harmonic is not considered (J2 = 0). For Charon starting on a nearly circular orbit, the survival times of the test moons on the planar orbits (blue crosses) monotonously increase (in log scale) with the increasing semi-major axis, reaching 103 yr for particles in the internal disc (10RP < a < 20RP). The particles at Styx’s position andbeyond it (a > 35RP) show survival times greater than 3 × 106 yr. Moreover, the numerical integrations of the individual orbits show that the moon’s motions are stable for more than 1 × 108 orbital periods of the PC binary.
When we consider a thin disc of small moons with inclinations uniformly distributed between − 0.01° and 0.01° (Fig. B.1, orange dots), we observe that survival times are similar to those obtained for a coplanar disc. A difference is observed essentially for the moons initially located at Charon’s position. We analyse the final inclinations of the particles in the thin disc in Fig. B.2 and observe that the orbits of the surviving moons around 20 RP reach inclinations of up to 25°. The inclinations of the particles located inside the limit given by the HWC are dispersed around the mean value of 5°. Also, some portion of the test particles near the Nix position is excited in inclination up to 5° but survive the time span of the simulations.
Figure B.1 also presents the survival times obtained for the coplanar disc, but with higher initial values of Charon eccentricities, namely, eC = 0.1 and eC = 0.2 (green crosses and red dots, respectively). These values put constraints on the initial rotational periods of Pluto, now P0 = 0.13791 d and P0 = 0.13593 d, respectively. For eC = 0.1, only particles beyond the Kerberos orbit survive for 106 yr. Setting the initial values of eC = 0.2 causes a faster depletion of the initial disc, < 105 yr. We do not find differences when we initially choose aligned or anti-aligned longitudes for the particle’s pericentre and the pericentre of Charon’s orbit.
Figure B.1 can be directly compared with Fig. 10 in Woo & Lee (2018), where almost all the particles in the range a > 30RP survive. However, their model was constructed for initial eC = 0, massless particles, and A = 40. We can observe in our simulations that moderate values (A = 10) allow the survival of particles. However, Woo & Lee (2018) explore neither cases with an almost initially circular Charon (eC ~ 0) nor cases with inclined particles.
The results obtained when setting a fixed value of J2 are presented in Fig. B.3. We remember that the static value of J2 = 6 × 10−5 was derived from the shape of Pluto in Correia (2020). We can observe that, for all initial eccentricities of Charon, the particles evolve almost in the same way as shown in Fig. B.1.
 |
Fig. B.1 Survival times of the test particles from different discs, all extending from 10RP < a < 55RP, for the dissipation parameter A = 10. We use different symbols and colours for initially coplanar and inclined discs as well as for different initial eccentricities of Charon’s orbit. We do not consider J2 effects, and the Charon mass is conserved during the integrations (see the text for more details). |
 |
Fig. B.2 Distribution of the final inclinations of the thin disc of particles shown in Fig. B.1. The particles ejected fromthe PC system are identified by black dots. |
 |
Fig. B.3 Same as in Fig. B.1, except considering the effect of a fixed zonal harmonic, J2 = 6 × 10−5. |
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Asphaug, E., Agnor, C. B., & Williams, Q. 2006, Nature, 439, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bromley, B. C., & Kenyon, S. J. 2020, AJ, 160, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Brozović, M., Showalter, M. R., Jacobson, R. A., & Buie, M. W. 2015, Icarus, 246, 317 [CrossRef] [Google Scholar]
- Buie, M. W., Tholen, D. J., & Grundy, W. M. 2012, AJ, 144, 15 [CrossRef] [Google Scholar]
- Canup, R. M. 2005, Science, 307, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2011, AJ, 141, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, W. H., Lee, M. H., & Peale, S. J. 2014a, Icarus, 233, 242 [CrossRef] [Google Scholar]
- Cheng, W. H., Peale, S. J., & Lee, M. H. 2014b, Icarus, 241, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M. 2020, A&A, 644, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuello, N., & Giuppone, C. A. 2019, A&A, 628, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ćuk, M., El Moutamid, M., & Tiscareno, M. S. 2020, Planet. Sci. J., 1, 22 [CrossRef] [Google Scholar]
- Desch, S. J. 2015, Icarus, 246, 37 [CrossRef] [Google Scholar]
- Dvorak, R., Pilat-Lohinger, E., Schwarz, R., & Freistetter, F. 2004, A&A, 426, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinella, P., Milani, A., Nobili, A. M., & Valsecchi, G. B. 1979, Moon Planets, 20, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S. 2013, Celest. Mech. Dyn. Astron., 116, 109 [Google Scholar]
- Folonier, H. A., Ferraz-Mello, S., & Andrade-Ines, E. 2018, Celest. Mech. Dyn. Astron., 130, 78 [Google Scholar]
- Gallardo, T., Beaugé, C., & Giuppone, C. A. 2021, A&A, 646, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Sipőcz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [Google Scholar]
- Holman, M. J., & Wiegert, P. A. 1999, AJ, 117, 621 [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2019a, AJ, 158, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2019b, AJ, 158, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2019c, AJ, 157, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2021, AJ, 161, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [Google Scholar]
- Kokubo, E., Ida, S., & Makino, J. 2000, Icarus, 148, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V. 2016, Celest. Mech. Dyn. Astron., 126, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2006, Icarus, 184, 573 [CrossRef] [Google Scholar]
- Lithwick, Y., & Wu, Y. 2008a, ArXiv e-prints [arXiv:0802.2951] [Google Scholar]
- Lithwick, Y., & Wu, Y. 2008b, ArXiv e-prints [arXiv:0802.2939] [Google Scholar]
- McKinnon, W. B., Stern, S. A., Weaver, H. A., et al. 2017, Icarus, 287, 2 [CrossRef] [Google Scholar]
- Michtchenko, T. A., & Rodríguez, A. 2011, MNRAS, 415, 2275 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1979, Moon Planets, 20, 301 [Google Scholar]
- Pires Dos Santos, P. M., Giuliatti Winter, S. M., & Sfair, R. 2011, MNRAS, 410, 273 [CrossRef] [Google Scholar]
- Pires Dos Santos, P. M., Morbidelli, A., & Nesvorný, D. 2012, Celest. Mech. Dyn. Astron., 114, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C., Nichols-Fleming, F., Chen, Y.-Y., & Noyelles, B. 2017, Icarus, 293, 94 [CrossRef] [Google Scholar]
- Ramos, X. S., Correa-Otto, J. A., & Beaugé, C. 2015, Celest. Mech. Dyn. Astron., 123, 453 [Google Scholar]
- Rodríguez, A., Giuppone, C. A., & Michtchenko, T. A. 2013, Celest. Mech. Dyn. Astron., 117, 59 [CrossRef] [Google Scholar]
- Showalter, M. R., & Hamilton, D. P. 2015, Nature, 522, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Smullen, R. A., & Kratter, K. M. 2017, MNRAS, 466, 4480 [Google Scholar]
- Tholen, D. J., Buie, M. W., Grundy, W. M., & Elliott, G. T. 2008, AJ, 135, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., & Levison, H. F. 2015, AJ, 150, 11 [CrossRef] [Google Scholar]
- Ward, W. R., & Canup, R. M. 2006, Science, 313, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, H. A., Stern, S. A., Mutchler, M. J., et al. 2006, Nature, 439, 943 [CrossRef] [Google Scholar]
- Weaver, H. A., Buie, M. W., Buratti, B. J., et al. 2016, Science, 351, aae0030 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J. M. Y., & Lee, M. H. 2018, AJ, 155, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J. M. Y., & Lee, M. H. 2020, AJ, 159, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., Kratter, K. M., & Kenyon, S. J. 2012, ApJ, 755, 17 [NASA ADS] [CrossRef] [Google Scholar]
Pires Dos Santos et al. (2011) reported gravitational effects due to Nix and Hydra on the test particles in the external region of the PC binary, but the masses of the moons used were one order larger than those reduced from the observations.
According to Cheng et al. (2014a) and Correia (2020), the PC binary acquires its current equilibrium position after (2−4) × 106 yr.
All Tables
Parameters and initial conditions under which the four small moons survive in the numerical simulations.
All Figures
 |
Fig. 1 Dynamical maps on the a–e plane (left panel) and a–I plane (right panel) of the moon’s initial conditions calculated for the PC binary and a small moon of Styx’s mass with initial Styx orbital elements from JPL in Table 1. The current positions of the moons are shown by red crosses. The locations of the main MMRs are indicated, and the grey line in the right panel indicates the current inclination of Charon. The colour scale varies with Δe and Δi, increasing from blue (regular motion) to red (chaotic motion), as shown in the colour bars on the top of the figure. |
| In the text | |
 |
Fig. 2 Dynamical maps of Styx, Nix, Kerberos, and Hydra on the aC–eC plane of Charon’s initial conditions. On each map, black curves are Charon’s tidal trajectories, obtained for initial eC values of 0.01, 0.1, and 0.2; the initial conditions of the corresponding moon are fixed at those given in JPL from Table 1. The blue tones represent regular motions, while the brick tones correspond to increasing instabilities and chaotic motion; the colour bar on the top shows Δe. The locations of the main MMRs are indicated. |
| In the text | |
 |
Fig. 3 Two typical examples of the Styx orbital evolution resulting in either instability (left panel) or the final configuration, which is significantly different from its current orbit (right panel). Left panel: initial conditions used are aC ∕RP= 5, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 600 s. Styx is ultimately ejected from the system when the system crosses the 4/1 MMR between Charon and Styx (not shown), resulting in a strong increase in Styx’s eccentricity. Right panel: initial conditions used are aC ∕RP= 4, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 6 s. The orbital eccentricity is excited, due to the crossing of the 4/1 and 7/2 MMRs (not shown), to attain the mean value ≃ 0.1, which is substantially larger than the current Styx eccentricity. |
| In the text | |
 |
Fig. 4 Examples of initial conditions for Styx. Top row: time evolution of Styx’s semi-major axis (left) and eccentricity (right) during the tidal expansion of the PC binary. The initial conditions used in the simulations are aC ∕RP= 4, es C = 0.001, ΩC ∕nC = 2, A = 100, and ΔtP = 600 s. The final values of the orbital elements remain close to the current ones. Bottom row: time evolution of the mean-motion ratio (left) and Δϖ (right). We note that the mean value of nC∕n is larger than 3. The secular angle, Δϖ, oscillates around 180°. |
| In the text | |
 |
Fig. 5 Examples of initial conditions for Nix. Top row: time variations in Nix’s semi-major axis (left) and eccentricity (right) for two different initial values of aC. The initial conditions are aC∕RP = 3 and aC ∕RP = 7, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 600 s. For aC ∕RP = 3, the eccentricity of Nix is excited to a mean value close to 0.16. Bottom row: time evolution of the mean-motion ratio (left) and two angles for Nix (right), namely, the secular angle, Δϖ, and the 4/1 MMR critical angle ϕ4∕1 = 4λ − λC − 3ϖC. The mean value of nC∕n is slightly smaller than 4 for aC∕RP = 7, whereas ϕ4∕1 and Δϖ librate around 180° and 0°, respectively, for aC∕RP = 3. |
| In the text | |
 |
Fig. 6 Examples of initial conditions for Kerberos. Top row: orbital evolution of Kerberos for two initial conditions of eC, namely, 0.001 and 0.1. The other parameters are aC∕R = 4, ΩC ∕nC = 2, A = 10, and ΔtP = 600 s. These simulations are successful according to the adopted criteria (see Sect. 5). Bottom row: time variations in the mean-motion ratio (left) and ϕ5∕1 = 5λ − λC − ϖC − 3ϖ (right). We show the angle for the specific case of eC = 0.001. The mean value of nC∕n is larger than 5. |
| In the text | |
 |
Fig. 7 Examples of initial conditions for Hydra. Top row: orbital variation in the semi-major axis (left) and eccentricity (right) of Hydra according to the adopted criteria. The initial conditions are aC ∕RP= 4, eC = 0.001, ΩC ∕nC = 2, A = 10, and ΔtP = 6 s. Bottom row:time variation in the mean-motion ratio (left) and ϕ6∕1 = 6λ − λC − ϖC − 4ϖ (right) for two values of ΔtP, namely, 6 s and 60 s. We note that, for ΔtP = 60 s, ϕ6∕1 librates witha large amplitude around 0°. For ΔtP = 6 s, all critical angles associated with the 6/1 MMR circulate. |
| In the text | |
 |
Fig. 8 Survival times of the small particles, for the different discs extending from 10 RP to 55 RP, during the tidal expansion of the PC binary, with the dissipation parameter A = 10, under the effect of the evolving zonal harmonic, J2. The colour symbols are used to identify the particles from the different discs (see text). |
| In the text | |
 |
Fig. 9 Time evolution of Charon’s physical properties during the mass accretion: the mass, the radius, and the zonal harmonic, J2, from left to right. Colours represent the results obtained from the different accretion models. The dashed horizontal line (right panel) presents the constant J2 obtained in Correia (2020). |
| In the text | |
 |
Fig. 10 Tidal evolution of the PC binary, for A = 10 and a logarithmic mass accretion of Charon during the first 104 yr, starting with the initial eccentricity eC = 0.001. Panels show the orbital semi-major axis, aC, in units of RP (panel a), the orbital eccentricity, eC (panel b), and the spin angular velocities of Pluto, ΩP (panel c) and Charon, ΩC (panel d) in units of the mean motion, nC. Each colour represents a different initial P0, in units of days. |
| In the text | |
 |
Fig. 11 Time evolution of the PC binary, eccentricity (top panel) and ΩC∕n (bottom panel), for the fixed initial P0 = 0.149 d and differentvalues of A, which are represented with different colours. |
| In the text | |
 |
Fig. 12 Time evolution of the orbital elements of Styx, with the mass mS = 1.49 × 1015 kg, for the different dissipation values of A. The top panel shows Styx’s semi-major axis, the middle panel shows the eccentricity, and the bottom panel shows nC ∕n. The continuous horizontal line in the top panel indicates Styx’s current position, at a∕Rp = 35.7, while the dashed lines in the bottom panel identify the 3/1, 4/1, and 5/1 MMRs. |
| In the text | |
 |
Fig. 13 Same as Fig. 12 except for Nix, with the mass mN = 1.5 × 1016 kg at the position a∕Rp = 40.98 (continuous horizontal line). |
| In the text | |
 |
Fig. 14 Eccentricity of a growing Charon during the tidal expansion of Charon’s orbit. Different colours are used to present the different values of the accretion time. The vertical dashed lines show the nominal locations of the main MMRs originated by a migrating Charon at Styx’s current position; each MMR is identified by the corresponding label. |
| In the text | |
 |
Fig. 15 Parametric A–tacc plane showing, in colour scale, the values of Charon’s eccentricity, eC (in logarithmic scale) at the instant when the 5/1 MMR crosses Styx’s current location. |
| In the text | |
 |
Fig. 16 Evolution of the ring of particles, each with a mass of 4.5 × 1016 kg, for an A in the range [14–21]. Top panel: survival times for particles. Middle panel: final semi-major axis of the small moons and Charon. Bottom panel: final eccentricity of Charon and the particles. The mass growth of Charon is set to 104 yr. Blue is used to indicate orbital parameters of Charon and orange for the particles. Orange dots represent survivors (the particles that remain close to initial configurations during the integration time of 3 × 106 yr). The black points in the top panel identify those particles that escape while the PC binary evolves. The shaded grey region indicates the range of values according to diverse authors (see Table 1). |
| In the text | |
 |
Fig. 17 Distribution of inclination for the disc of particles after the dual synchronisation of the PC system with mass growth. Theorbits that do not survive the entire integration time are identified with black dots. The shaded grey region indicates the range of values according to diverse authors (see Table 1). |
| In the text | |
 |
Fig. A.1 Orbital evolution of Styx, Nix, Hydra, and Kerberos around the PC binary, from top to bottom, respectively. We show the evolution of the semi-major axis (left panels), eccentricity (middle panels), and inclination (right panels) for 40 yr. Blue lines correspond to data from JPL and grey lines to our N-body integrations. Orange lines correspond to the integrated inclination of Charon. |
| In the text | |
 |
Fig. A.2 Stability maps on the a–M plane using the MEGNO colour scale for the four small moons. All other orbital parameters are set to the JPL values from Table 1. The current positions of the moons are shown by red crosses. The locations of the main MMRs are indicated. Small deviations from initial conditions within the estimated errors from PLU043 can place the moons inside the MMR regime. |
| In the text | |
 |
Fig. B.1 Survival times of the test particles from different discs, all extending from 10RP < a < 55RP, for the dissipation parameter A = 10. We use different symbols and colours for initially coplanar and inclined discs as well as for different initial eccentricities of Charon’s orbit. We do not consider J2 effects, and the Charon mass is conserved during the integrations (see the text for more details). |
| In the text | |
 |
Fig. B.2 Distribution of the final inclinations of the thin disc of particles shown in Fig. B.1. The particles ejected fromthe PC system are identified by black dots. |
| In the text | |
 |
Fig. B.3 Same as in Fig. B.1, except considering the effect of a fixed zonal harmonic, J2 = 6 × 10−5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


