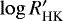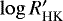© ESO 2022

1 Introduction

In many astronomical fields, one searches for periodicity in a time series of measurements. Due to observational constraints, the samples often are unevenly spaced, possibly with large gaps in the sampling. The search for periodicity is then typically done with periodograms, which can be defined in several ways. The different definitions can be viewed as a metric (most often the χ² difference) that compares two models: a base model and a model that includes this base model plus a periodic signal at a given frequency, for a grid of frequencies. Typically, periodic components are sinusoids, and the base model includes white, Gaussian noise (Lomb 1976; Scargle 1982). It can also include a constant (Ferraz-Mello 1981; Cumming et al. 1999; Reegen 2007; Zechmeister & Kürster 2009), general linear models Baluev (2008), non-sinusoidal functions Baluev (2013b, 2015), several periodic components Baluev (2013,a), or correlated noise (Delisle et al. 2020a). Once the periodogram is computed, detections are claimed if the false alarm probability (FAP) of the highest peak is below a certain threshold. The search for periodic signals can also be performed in a Bayesian framework. Periodograms can be defined as comparisons of marginal likelihoods of the two competing models, with or without a given frequency (Mortier et al. 2015; Feng et al. 2017). The analysis can also be done directly from the posterior distributions of orbital elements. In that case, to determine how many periodic components can be confidently detected, one computes the ratio of Bayesian evidences – or Bayes factors (Kass & Raftery 1995) – of models with n and n + 1 components. If the Bayes factor is above a certain threshold (usually 150), the addition of a periodic component is validated (e.g. Gregory 2007b,a; Tuomi 2012; Faria et al. 2016). Alternatively, one can use a detection criterion based on Bayesian model averaging (Hara et al. 2022).

A low FAP or high Bayes factor gives a measure of the confidence in a detection of a periodic component within a certain model of the data. If the model is inappropriate, there might be significant signals that do not correspond to strictly periodic signals. Certain noises are particularly likely to yield significant peaks: the ones that present a periodicity that is localised in time, similarly to wavelets. This situation is encountered in particular in the search for planets in radial velocity (RV) data. This type data consist of a time series of velocity projected along the line of sight (the RV) of a given star, measured thanks to the Doppler effect. If a planet orbits the star, then one expects periodic variation in the velocity. However, the surface of a star is not uniform: Spots and faculae break the flux balance between the approaching and receding limb of the star; furthermore, they inhibit convective blueshift. As a consequence, during their lifetime, stellar features introduce RV signals that might mimic planetary ones, in particular at the stellar rotation period or its harmonics (e.g. Saar & Donahue 1997; Boisse et al. 2011; Meunier et al. 2010; Dumusque et al. 2014), but also possibly at periods apparently unrelated to the stellar rotation (Nava et al. 2020).

One approach to this problem consists in trying to improve the data model and the detection metrics so that a significant detection has a meaning as close as possible to the detection of the signal of interest (here, a planet). In RV data analysis, stellar activity is typically modelled with a Gaussian process. This approach is taken in Haywood et al. (2014), Rajpaul et al. (2015), Jones et al. (2017), Gilbertson et al. (2020), and Hara et al. (2022). The stellar activity models are, however, imperfect, and another approach consists in being more agnostic to the form of stellar activity. For instance, Gregory (2016) suggests computing the Bayesian evidence of an apodised model, that is, a periodic planetary signal model multiplied by a function of the form ${\text{e}}^{-\frac{{(t-t_0)}^2}{{\tau }^2}}$, where τ and t₀ are free parameters. A signal is claimed to be of planetary origin if it is significant and if the posterior probability of the event τ ≥ T_obs, where T_obs is the total time span of observation, is greater than a given threshold. The rationale is that a planetary signal is a purely periodic signal and should therefore be identical from the beginning to the end of the dataset. In a periodogram setting, Schuster (1898); Mortier & Collier Cameron (2017) adopt a similar approach. They suggest computing the periodogram by adding one point at a time and determining whether the significance of a peak at a certain period grows steadily with the number of points.

One canenvision other diagnostics for determining if an apparently periodic signal presents signs of variability. In the present work we present tests to assess the timescale of a signal and to determine if its period, phase, and amplitude are constant. We suggest tests based on the periodogram and Bayesian formalisms.

The article is organised as follows. In Sect. 2, we define the diagnostics mentioned above. In Sect. 3, we show examples of applications to the solar HARPS-N data (Dumusque et al. 2021), HD 215152 (Delisle et al. 2018), HD 69830 (Lovis et al. 2006), and HD 13808 (Ahrer et al. 2021). We finally present our conclusions in Sect. 4.

2 Methods

2.1 Signal timescales

2.1.1 Apodised sinusoids periodograms

In this section, we define the apodised sinusoids periodogram (ASP) of a time series $y={(y(t_k))}_{k=1\dots N}$. Following the method of Baluev (2008) to define periodograms, we consider two alternative models of the time series y: a linear base model ${\mu }_{\mathcal{H}}$ of p parameters, and a model ${\mu }_{\mathcal{K}}$ that includes $\mathcal{H}$ plus an apodised sinusoidal component. The base model, as a vector with N components, is defined as $${\mu }_{\mathcal{H}}({\theta }_{\mathcal{H}})={\phi }_{\mathcal{H}}{\theta }_{\mathcal{H}},$$(1)

where ${\phi }_{\mathcal{H}}$ is an N × p matrix and ${\theta }_{\mathcal{H}}$ is the vector of p parameters to be fitted. For instance, the matrix ${\varphi }_{\mathcal{H}}$ can be simply taken as a column vector with all N entries equal to one, thus modelling an offset. If one assumes that the sinusoidal signal of frequency ω is in the data by default, ${\varphi }_{\mathcal{H}}$ can be defined as an N × 3 matrix with line i equal to [1, cos ωt_i, sin ωt_i]. The alternative model is defined as $${\mu }_{\mathcal{K}}({\theta }_{\mathcal{H}},\theta )={\phi }_{\mathcal{H}}{\theta }_{\mathcal{H}}+\mu (t,\theta ),$$(2)

where μ(t, θ) is an apodised periodic function. We compared the hypotheses $\mathcal{H}$: $y={\mu }_{\mathcal{H}}({\theta }_{\mathcal{H}})+ϵ$ for some ${\theta }_{\mathcal{H}}$ and $\mathcal{K}$: $y={\mu }_{\mathcal{K}}({\theta }_{\mathcal{K}})+ϵ$ for some ${\theta }_{\mathcal{K}}$, where ϵ is a Gaussian noise model (or random variable) of covariance matrix V.

In the present work, μ is specified as $$\mu (t,\omega ,\tau ,t_0,A,B)=w(\tau ,t_0)(A\cos \omega t+B\sin \omega t),$$(3)

where w(τ, t₀) is the apodisation function. Here we use Gaussian and box-shaped functions, that is, $$\begin{array}{ll}{w}_G(\tau ,t_0)\hfill & :={\text{e}}^{-\frac{{(t-t_0)}^2}{2{\tau }^2}}\hfill \\ w_B(\tau ,t_0)\hfill & :=1_{\left[t_0-\frac{\tau }{2},t_0+\frac{\tau }{2}\right]}(\tau ,t_0),\hfill \end{array}$$

where $1_X\left(x\right)$ is a function that is zero everywhere except when x ∈ X, but other choices are possible. One can envision further generalisations. Indeed, the periodic signal need not besinusoidal. It can be, for instance, Keplerian (Baluev 2015). Also, the base model $\mathcal{H}$ can be generalised to non-linear models.

Considering a model μ_i, $i=\mathcal{H}$ or $\mathcal{K}$ with parameters θ_i, and column vector residuals r = y −μ_i(θ_i), the χ² is defined as r^T V⁻¹r, where the suffix T denotes the matrix transpose. In the following equation, ${\chi }_{\mathcal{H}}^2$ is the χ² of the residuals after fitting the parameters ${\theta }_{\mathcal{H}}$ of model (1), and, for a set of fixed ω, t₀, and τ, the ${\chi }_{\mathcal{K}}^2(\omega ,t_0,\tau )$ is the χ² of the residuals after fitting the parameters ${\theta }_{\mathcal{H}},A,$ and B of model (2), on which the model depends linearly. We now define a periodogram-type counterpart to that of Gregory (2016): $$\begin{array}{ll}z(\omega ,t_0,\tau )\hfill & ={\chi }_{\mathcal{H}}^2-{\chi }_{\mathcal{K}}^2(\omega ,t_0,\tau ),\hfill \end{array}$$(6)

which represents the improvement of the fit gained by adding the μ component compared to the base model $\mathcal{H}$. In the following sections we use the following representation. For a given τ we represent the quantity $$\begin{array}{ll}{z}^{\prime }(\omega ,\tau )\hfill & ={\max }_{t_0}z(\omega ,t_0,\tau ).\hfill \end{array}$$(7)

The values of z′(ω, τ) are overplotted for different values of τ. In Fig. 1 we represent the values of z′ for four values of τ for the solarHARPS-N data (see Sect. 3.1 for more details). We call such a figure an apodised sinusoids periodogram (ASP).

Our definition of Eqs. (3) and (4) is similar to a continuous wavelet transform (Grossmann & Morlet 1984) applied to irregularly sampled time series (Foster 1996). Our choice of Eq. (4) is inspired by the Gabor wavelet, which minimises the product of time and Fourier domain variance (Daugman 1998). However, in the wavelet transform context the timescale, τ, and frequency, ω, are dependent on each other. Indeed, a family of wavelet ${({\psi }_{a,b})}_{a,b}$ is defined as the translation and dilation of a mother wavelet ψ, ${\psi }_{a,b}(x)=\psi ((x-b)/a)/\sqrt{a}$. In our case, the lifetime τ of a quasi-periodic feature is not unequivocally linked to its frequency, ω. As a consequence, even though having three free parameters instead of two introduces an extra computational load, we leave ω, τ, and t₀ as independent parameters.

2.1.2 Grid

Regular periodograms are usually computed on a grid of equispaced frequencies, ω_k = kΔω. The choice of Δω depends on the typical width of the periodogram peaks, which is approximately equal to 2π∕T_obs, where T_obs is the total time span of the observations. Then, Δω is chosen as 2π∕T_obs * 1∕N_ω, where N_ω is called the oversampling factor.

For the ASPs we need to construct a grid in three dimensions: ω, t₀, and T. The naive approach, consisting in having a fixed grid for each parameter and trying all the possible combinations, is unnecessarily computationally expensive. Indeed, for a given timescale, T, such that T < T_obs, the typical width of the peaks in ω is ≈ 2π∕T > 2π∕T_obs. To set the grid, the approach adopted here is to define the following quantities: (i) a maximum frequency, ω_max ; (ii) two oversampling factors, N_ω and N_t ; and (iii) a fixed number α < 1 and a number of timescales N_τ such that the grid of τ is defined as τ_k = α^k−1T_obs, k = 1…N_τ. We define two reference grids for ω and t₀ as ${\omega }^{\text{ref}}={({\omega }_k)}_{k=1\dots n_{\omega }}$ and $t_0^{\text{ref}}={(t_0{}_k)}_{k=1\dots n}$, where ω_k = kΔω, with Δω = 2π∕T_max∕N_ω and $t_0{}_k=k\Delta t_0$, with Δt₀ = τ_min∕N_t.

For eachτ_k, the waveletogram is computed on a sub-grid of ω^ref and $t_0^{\text{ref}}$, denoted by ω^τ and $t_0^{\tau }$. These are defined as ${\omega }_k^{\tau }={\omega }_{k{s}_{\omega }^{\tau }}^{\text{ref}}$ and $t_0^{\tau }{}_k=t_0^{\text{ref}}{}_{k{s}_t^{\tau }}$, where $s_{\omega }^{\tau }=\lfloor {\tau }_{\text{max}}/\tau \rfloor$ and $s_t^{\tau }=\lfloor \tau /{\tau }_{\text{min}}\rfloor$. The rationale behind these numbers is that, for a given τ, the grid spacing in ω is approximately 2π∕τ∕N_ω and the grid spacing in t₀ is τ∕N_t. Secondly, since the omega grid is not recomputed for every timescale, τ, one only has to compute the cos ωt and sin ωt terms once. Once this method is specified, one has to choose specific values for N_ω, N_t, ω_max, α, and n_T. The list of symbols and, when relevant, the default values we chose are reported in Table 1.

2.1.3 Statistics

In Gregory (2016), one computes the Bayesian evidence (or marginal likelihoods) of models containing k periodic components multiplied by an apodisation factor ${\text{e}}^{-\frac{{(t-t_0)}^2}{2{\tau }^2}}$. A planet detection is claimed if a signal is statistically significant (i.e. if the ratio of evidence of the model with it to the evidence without it is greater than a certain threshold) and if the posterior distribution of τ favours values greater than the total time span of the observations.

We here propose an alternative way to estimate the timescale on which the signal remains coherent, which can be computed very quickly from the periodogram. Denoting by t_τ,ω the value of t₀ and maximising the value of periodogram (6) for a given ω and τ, we computed the distribution of $D_z=z(\omega ,t_{\tau ,\omega },\tau )-z(\omega ,t_{{\tau }^{\prime },\omega },{\tau }^{\prime })$ with the hypothesis that model $\mathcal{K}(\omega ,t_{\tau ,\omega },\tau ,A^{\star },B^{\star })$ is correct, where the fitted cosine and sine amplitude A^⋆, B^⋆ are obtained by fitting model $\mathcal{K}$ 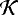to the data. The distribution of D_z can easily be expressedas a generalised χ² distribution, and its mean and variance is given by an analytical expression, which is given in Eqs. (A.9) and (A.10). This method does not take into account that ω is chosen as a maximum of the periodogram and could be refined in future work.

Secondly, one can define a FAP associated with Eq. (6), the same ways as done for a regular periodogram. In the remainder of the article, we do not use the FAP for ASPs; however, we use a FAP for regular periodograms (Baluev 2008; Delisle et al. 2020a). For the sake of conciseness, the method is described in Appendix B.

In general, assuming that the signal is in the form of the model $\mathcal{K}$ (Eq. (2)) will be an incorrect assumption. In particular, if aliasing cannot be neglected and the data contain several signal sources, not accounting for them might result in an inaccurate uncertainty on the timescale, τ, of the signal of interest. We suggest including all the periodic signals found to be significant in the base model (we give an example of this procedure in Sect. 3). Alternatively, at the price of a higher computational cost, one can search for several signals simultaneously, as shown in the next section.

2.1.4 Bayesian approach

In Gregory (2016), a detection is claimed if the posterior probability of the event τ > T_obs is greater than a certain threshold. However, such a criterion can be misleading. For instance, there might be datasets in which there are a few isolated measurements that are separated from the bulk of the measurements by a large time gap. In that case, most of the samples could correspond to τ < T_obs, though there is a possibility that the signal is consistent with a fully periodic signal. In addition to the posterior distribution of τ, we suggest considering a quantity f that quantifies the fraction of information captured by a certain window. We computed the posterior distribution of $$f=\frac{w{(\tau ,t_0)}^T{V}^{-1}w(\tau ,t_0)}{1^T{V}^{-1}1},$$(8)

conditioned on the frequency of the planet being within ± Δω of a given frequency of interest. In Eq. (8), 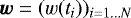$w={(w(t_i))}_{i=1\dots N}$ is the apodisation window (see Eq. (3)), V is the covariance matrix, and 1 is a vector of size N. The values of the vector w are between 0 and 1. If f is close to 1, then the apodised signal is close to a strictly periodic signal. On the contrary, a value of f close to 0 implies that the w has concentrated information in time. The definition of f is valid for any apodised signal – in particular, the planet model can be circular or Keplerian – and for all the signals in the data.

In Gregory (2016), the number of planets is determined by checking that the Bayes factor comparing the n + 1 and n planets model is greater than a certain threshold. The significance of the planet can also be established with the false inclusion probability (FIP; Hara et al. 2022), defined as follows. Considering a certain parameter space S (for instance, a period and eccentricity interval), the true inclusion probability (TIP) is the probability of having a planet with orbital elements in S marginalised over the number of planets in the system. The FIP is defined as 1−TIP. Instead of claiming a detection if the Bayes factor is above a certain threshold, we claim a detection if the probability of not having a signal with a period in [ω − Δω, ω + Δω] – marginalised on all parameters, including t₀ and τ – is below a certain threshold.

Fig. 1 ASPs computed iteratively on the solar data. Left column: ASPs corresponding to Eq. (7) for different values of τ. Middle column: zoomed-in view of the maximum peak of the ASP. Right: statistical test on the timescale described in Sect. 2.1.3. On the x axis we represent the ratio of τ to the total observation time assumed to be true. For each τi, i = 1…4 in abscissa, the position of the markers corresponding to τj, j = 1…4 is represented as the value of the periodogram peak for τi minus the expectancy of $D_z=z(\omega ,t_{\tau ,\omega },{\tau }_i)-z(\omega ,t_{{\tau }_j,\omega },{\tau }_j)$, and the error bar is the square root of the variance of Dz. Informally, the markers represent what the periodogram values at τj should be if τi in abscissa were the true timescale.

2.2 Amplitude and phase consistency

The second diagnostic we present in this work relies on computing the phase and amplitude of a signal at a given period with a moving time window. We consider, as in Sect. 2.1.1, the linear models $\mathcal{H}$ Eq. (1) and $\mathcal{K}$ Eq. (2). For the function μ, we adopt the definition of Eq. (3), where the window function w is box shaped. For each value of ω, t₀, and τ, one has estimates of parameters A and B (Eq. (3)). The uncertainties on A and B are obtained from the diagonal elements of the covariance matrix of the fit. From the estimates of A and B, we compute the local semi-amplitude K and phase ϕ $$\begin{array}{ll}K(\omega ,t_0,\tau )\hfill & =\sqrt{A^2+B^2}\hfill \\ \varphi (\omega ,t_0,\tau )\hfill & =\text{atan2}(-B,A),\hfill \end{array}$$

as well as the uncertainties on K and ϕ propagated from those on A and B with a simple Monte Carlo simulation. Alternatively, one can estimate the uncertainties on A, B, K, and ϕ with their posterior distributions, computed with a Monte Carlo Markov chain algorithm, which is more computationally expensive but propagates the uncertainties on the orbital elements more accurately.

For a given frequency ω and timescale τ, the quantities A,B, ϕ, and K and their uncertainties (computed from the least square fit or posterior distributions) can be used to check the consistency of the phase and amplitude of a signal at a given period. Assuming that the signal contains a pure sine at ω, the values of A and B or K and ϕ as a function of t₀ should be consistent with the hypothesis that A and B or K and ϕ are constant.

Besides a visual inspection of A and B or K and ϕ as a function of t₀, the hypothesis that the signal has a constant phase or amplitude can be checked with statistical tests. In particular, one can isolate values of A and B estimated in different windows. Here we denote estimates of A and B in disjoint windows with ${(A_i)}_{i=1\dots M}$ and ${(B_i)}_{i=1\dots M}$. If one neglects correlations that might happen between those estimates due to correlated noise, under the hypothesis that phase and amplitude are constant, then the statistics $$\begin{array}{ll}{\chi }_A^2\hfill & ={\displaystyle \sum _{i=1}^M\frac{{(A_i-{\mu }_A)}^2}{{\sigma }_{A_i}^2}}\hfill \\ {\chi }_B^2\hfill & ={\displaystyle \sum _{i=1}^M\frac{{(B_i-{\mu }_B)}^2}{{\sigma }_{B_i}^2}},\hfill \end{array}$$

where $${\mu }_X={\displaystyle \sum \frac{X_i}{{\sigma }_i^2}}/{\displaystyle \sum \frac{1}{{\sigma }_i^2}},$$(13)

with X = A or X = B, should follow a χ² distribution with M − 1 degrees of freedom. We can measure the quantiles of ${\chi }_A^2$ and ${\chi }_B^2$: If they are below a certain threshold, then the hypothesis that they are constant through time can be rejected. A χ² distribution with M − 1 degrees of freedom has mean M − 1 and standard deviation $\sqrt{2(M-1)}$. For a quick diagnostic, we suggest computing the quantity $$N{\sigma }_{{\chi }_i^2}=\frac{{\chi }_i^2-(M-1)}{\sqrt{2(M-1)}},i=A,B,$$(14)

which is the difference between the ${\chi }_i^2$ and its expected value divided by the standard deviation.

In the test suggested in this section, the time window w in Eq. (3) is assumed to be a box-shaped one. One could envision a more general one. However, for a consistent analysis, since the noise is also multiplied by the window, the covariance matrix of the noise would have to be modified according to the chosen window. If it is non-zero everywhere, then this comes down to doing the analysis of the data without any window, unless some numerical errors lead the covariance to be non-invertible. In that case, using a window comes down to a rectangular window. As a consequence, we here only consider box-shaped time windows (see Eq. (5)).

We stress that to evaluate the phase and amplitude consistency of a signal, one must have an accurate estimate of the period of the signal to analyse. If it is poorly estimated, then the phase will spuriously appear as a linear phase drift. As a consequence, we advise selecting the value of ω to be studied in depth from the regular periodogram containing all the data.

As mentioned in Sect. 2.1.3, in general, assuming that the signal is in the form of the model $\mathcal{K}$ (Eq. (2)) will be an incorrect assumption, and aliasing can be a problem. For instance, if the signal contains several sources that are strictly periodic, due to aliasing, the phase and amplitude of the signal under consideration might appear to vary significantly even though the signal is periodic. As a consequence, the fact that the quantities defined in Eq. (12) deviate from the mean is not always interpretable as a test of the hypothesis that the signal at frequency ω is constant in phase and amplitude. One of the assumptions in $\mathcal{K}$ is the noise model; however, it might not be known and needs to be adjusted to the data. We suggest including in the base model all the periodic signals found to be significant; this is elaborated on in Sect. 3.

In addition to testing for the consistency of the phase and amplitude of a signal, it might be interesting to study its relative phase and amplitude with another signal. For instance, one might want to see the evolution of the phase difference between the RV and $\log {R^{\prime }}_{\text{HK}}$ as a function of time to study the stellar activity. An example of such an analysis is given in Sect. 3.1.

2.3 Period consistency

Assuming a sinusoidal shape of the signal, the last parameter of an apparently periodic signal whose consistency in time can be evaluated is the period. A convenient representation is, for a given timescale τ, a colour map z(ω, t₀, τ) as defined in Eq. (6). For a given quasi-periodic signal, a local change in the χ² value mightbe due to a clustering or spacing of the observation time. A convenient representation for jointly evaluating period and amplitude consistency is the fitted semi-amplitude $K:=\sqrt{A^2+B^2}$ (see Eq. (3)) as a function of ω and t₀. To give meaningful diagnostics, it might be suitable to mask the values of K with an uncertainty above a certain threshold.

We suggest another test. Considering a frequency range [ω_l, ω_r] containing the frequency of a candidate periodic signal ω₀, for a given timescale τ, we plot $${\omega }^{\star }(t_0):=\arg {\max }_{\omega \in [{\omega }_l,{\omega }_r]}z(\omega ,t_0,\tau )$$(15)

as a function of t₀, where w_B is defined by Eqs. (3) and (5).

As in Sect. 2.2, one can test the hypothesis that approximately independent measurements of ω^⋆ stem from the same distribution. One can envision a further generalisation where one looks for shape variations in periodic signals. However, in the cases considered here, the signal-to-noise ratio would not allow conclusions to be drawn on this aspect. As a consequence, we do not consider it here.

We note that estimating the local phase, amplitude, and frequency of a signal is a problem also encountered in signal demodulation in the context of telecommunications (e.g. Madhow 2008). Phase consistency tests have been suggested in the context of discrete events, more specifically γ ray pulsars, to detect phase shifts relative to an expected position (de Jager 1994). Assessing whether period and amplitudes are constant with time has been done for Cepheids (Süveges & Anderson 2018b,a)

3 Applications

3.1 Solar data

3.1.1 Data analysis

In this section, we apply our methods to the HARPS-N solar data (Dumusque et al. 2021). This dataset contains the RV of the Sun measured with the HARPS-N solar telescope (Dumusque et al. 2015). This dataset spans three years, from BJD 2457222.1788 to 2458315.9982, and contains 34 550 measurements with a median interval between two samples of 5 min 38 s and a median nominal error of 0.22 m s⁻¹. The data are publicly available on the Data Analysis Center for Exoplanets (DACE) platform¹. We binned the data by half days, which means that data acquired between midnight and noon and between noon and midnight (local time at La Palmaobservatory) were averaged, weighted by their nominal uncertainties. We considered a Gaussian, uncorrelated noise model, with a 1 m s⁻¹ jitter added in quadrature to the nominal uncertainties.

We first performed an iterative search of signals using the ASPs defined in Sect. 2.1.1. We considered four timescales and computed Eq. (6) for τ∕T_obs = 10, 1/3, 1/9, and 1/27, where T_obs is the total time span of the observations. The grid in t₀ and ω is defined asin Sect. 2.1.2. We computed the ASP and then added to the base model the model corresponding to the maximum peak.

The left panel of Fig. 1a shows the first ASP, which presents a maximum at period ω⁽⁰⁾= 9000 days for τ⁽⁰⁾ = T_obs∕9 and $t_0^{(0)}$. We then added $w({\tau }^{(0)},t_0^{(0)})\cos {\omega }^{(0)}t$ and $w({\tau }^{(0)},t_0^{(0)})\sin {\omega }^{(0)}t$ to the base model and computed the ASP, obtaining Fig. 1b. The same operation was repeated, yielding Figs. 1c and d. In Figs. 2a–d, we represent the models that correspond to the highest peaks of Figs. 1a–d, respectively.

The middle panel of Fig. 1 presents a zoomed-in view of the maximum peak of the successive ASP. Horizontal dashed lines correspond to the values of z at the frequency where the maximum is attained. For instance, in (b) the maximum value is attained at period = 13.39 days. The blue, orange, red, and green horizontal lines represent the level of the periodogram peaks with τ∕T_obs = 10, 1/3, 1/9, and 1/27 at P⁽¹⁾ = 13.39 days. We found empirically that a downsizing factor of 1/3 for τ allows a reasonable compromise between resolution and grid size. Finally, the right panel represents the statistical test presented in Sect. 2.1.3. The four timescales corresponds to a value of τ, reported in abscissa. We now turn to Fig. 1b. For each timescale τ, we assumed that the data contain a signal at frequency P⁽¹⁾ and timescale τ. The points with error bars correspond to the expected value of the periodogram peak and its standard deviation, assuming τ is the correct timescale. For instance, in Fig. 1b, assuming τ = T_obs∕3 = 365 days would lead us to expect a z value with τ = T_obs over four sigmas away from the observed one. It then appears that the 13.39 day signal is consistently detected on the whole dataset. In comparison, signals at 9000 days, 158 days, and 26.9 days (Figs. 1a, c, and d) seem to be localised in time. The peaks at 26.9 and 13.39 days are compatible with the first and second harmonic of the solar rotation period. Low frequency structures are expected to come from correlated patterns stemming either from the star or the instrument.

The 13.39 day signal seems the most coherent of the four signals found. To further estimate if it is purely periodic, weapplied the methods of Sects. 2.2 and 2.3. As suggested in Sect. 2.3, we studied the consistency of the signal frequency by representing the values of z(ω, t₀, τ) (see Eq. (6)) and the amplitude K(ω, t₀, τ) for a given τ as a colour map. In Fig. 3 we represent z ((a) and (b)) and K ((c) and (d)) for τ = T_obs∕3 = 365 days ((a) and (c)) and τ = T_obs∕9 = 121 days ((b) and (d)). The base model is identical to the one used to compute Fig. 1b. It appears that the 13 day signal is present throughout the dataset. We notice that its apparent waning towards the edge of the dataset is due to the fact that when the t₀ reaches the beginning or end of the time series, the window includes half as many points compared to the middle of the time series. Signals at ~ 160 and ~ 25 days also seem tobe present but with more variability, which is consistent with the analysis of Fig. 1. In Fig. 3, we represent the quantity defined in Eq. (15), that is, the local maximum of z between certain frequencies as a function of t₀ for fixed τ (τ = T_obs∕3 = 365 days for (c) and τ = T_obs∕9 = 121 days for (d)). We chose a collection of frequencies, ω_k = kΔω, which are represented in grey in Figs. 3c and d. The maxima of z between 10 and 20 days consistently occurs at 13.39 days.

The 13 day signal seems to be consistently present in the data and to have a steady period. We further examined whether its phase, ϕ, and semi-amplitude, K, as defined in Eqs. (10) and (9) are constants of time. To avoid being polluted by other signals, we included a 26.9-day signal as well as a ninth-order polynomial in the base model, filtering out low frequency signals. In Figs. 4a and b, we represent the evolution of ϕ and K in red and green, respectively, as a function of t₀ for fixed τ (τ = T_obs∕3 = 365 days for (a) and τ = T_obs∕9 = 121 days for (b)); the uncertainties are represented with colour-shaded areas. Dashed red and green lines represent the mean values of ϕ and K. Dots corresponds to measurements done on disjoint box-shaped windows, which are thus approximately statistically independent, as shown in Appendix A.2. In Figs. 4c and d, we represent the values of A and B as defined in Eq. (3), with their uncertainties in blue (τ = T_obs∕3 = 365 days for (c) and τ = T_obs∕9 = 121 days for (d)). Points in orange correspond to the measurement times marked with dots in Figs. 4a and b, which yield approximately independent estimates of A and B. At the shortest timescale, it appears that 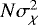$N{\sigma }_{\chi }^2$ as defined in Eq. (14) is greater than 5 (see Fig. 4d). In Fig. 4b the variation in amplitude does seem to significantly vary over time, with two peaks around BJD 2457400 and BJD 2458000, which is consistent with the behaviour seen in Fig. 3b. The statistical tests depend on the assumed noise model. To obtain more robust statistics, we performed the same analysis but adjusting an extra jitter term at each trial t₀ and propagated the uncertainty on K, ϕ, A, and B. The results are very similar and qualitatively unchanged. As a conclusion, it appears that the 13.39 day signal has a long timescale and a consistent period and phase, but its amplitude varies significantly with time.

Fig. 2 Models corresponding to the maximum of the ASPs in Fig. 1.

3.1.2 Discussion

From a phenomenological point of view, the presence of the 13.39-day signal, as well as the one at ~25 days, can be fully understood by the presence of active regions rotating with the solar surface, as those two periods corresponds to the second and P_rot term. By locally modifying the flux intensity of the solar surface (e.g. Saar & Donahue 1997) and by changing convection (e.g. Meunier & Lagrange 2013), the spot and the faculae on the surface of a solar-like star will impact RV data, with a semi-periodic signal that can be decomposed as a Fourier series, thus as a sum of periodic signals at the rotation period of the Sun and its first harmonics (Boisse et al. 2011).

It is often observed on solar-like stars that activity injects more power at P_rot∕2 than its rotation period P_rot (e.g. Boisse et al. 2011). This can be explained by the fact that not just one but several active regions perturb the RV measurement at the same time, but also because the Sun is seen equator-on; thus, active regions are seen only during half the rotation. On a star such as the Sun, the main contribution of the RV stellar activity signal comes from faculae (e.g. Meunier et al. 2010; Dumusque et al. 2014; Collier Cameron et al. 2019; Milbourne et al. 2019), which induce a strictly positive RV offset whatever their position on the solar disc, and the effect of an active region, in first approximation, can be viewed as a sinusoid truncated atzero (e.g. Meunier et al. 2010; Dumusque et al. 2014). This truncation alone cannot explain the predominance of the P_rot∕2 term, as the Fourier expansion of such a truncated sinusoid has a stronger P_rot term than P_rot∕2, where P_rot denotes the stellar rotation period. If spots are at different longitudes, the RV signal would resemble a sum of truncated sine signals with different phases, and random phase differences do not preferentially affect a given harmonic. However, a phase difference of two signals of 180° cancels out the first harmonic. As noted in Borgniet et al. (2015), there are generally two persistent active longitudes per hemisphere, shifted by 180° (Berdyugina & Usoskin 2003), and this might explain the second harmonic. We add that even if there are several such configurations of two diametrically opposed active longitudes at different phases, the sum of their contributions has a vanishing component at P_rot. The presence of active regions on the surface, not in opposite phase but randomly distributed, may introduce a signal at P_rot. We finally note that the RV effect of active regions is not only due to convective blueshift inhibition, but also to their difference in brightness relative to the surroundings, introducing an asymmetry in approaching and receding limbs. This signal of photometric origin resembles a sine function with period P_rot∕2 on [kP_rot∕2, (k + 1)P_rot∕2] for k even and equal to 0 for k odd (e.g. Dumusque et al. 2014). This truncated signal has a dominant power at P_rot∕2, which might partly explain the strong P_rot∕2 signal in Fig. 1b.

The change in amplitude and stability in phase can be explained by the presence of a few very large active regions that last for several months on the solar surface. The induced RV effect will be large and the signal consistent over a long period of time. The fact that the amplitude is large around BJD 2457400 can be explained by the Sun being active in 2015, with a lot of large active regions on its surface. The lower χ² closer to the beginning of the time series around BJD 2457217 is due to an edge effect. The sudden increase in amplitude around BJD 2458000 can be explained by the last large active region that appeared on the solar surface before the Sun reached the minimum of magnetic cycle 24 (clearly seen in the Log($R_{\text{HK}}^{\prime }$) time series in Fig. 6 of Dumusque et al. 2021).

Overall, our tentative explanation of the strength of the 13.39 day signal, its phase stability, and its amplitude variation is that stable magnetic regions diametrically opposed might have caused it. This speculative explanation requires further work to be properly accepted or rejected. We note that, thankfully, the amplitude of the solar 13.39 day harmonic is more variable than its phase, making it less likely that such a signal in stellar data could be mistaken for a planet.

Fig. 3 Consistency of the period of signals in the solar data. (a and b): value of the χ2 defined in Eq. (6) for the solar HARPS-N RV data as a function of t0 for τ = 365 (=Tobs ∕3) days (a) and τ = 121 (=Tobs ∕9) days (b). (c and d): value of the semi-amplitude as a function of t0 for τ = 365 (=Tobs ∕3) days (c) and τ = 121 (=Tobs ∕9) days (b). Grey areas correspond to 1 σ uncertainties greater than 30 cm s−1. (e and f): in blue, position of the mode of the ASP between frequencies represented in grey as a function of t0, as defined in Sect. 2.3. Computed for τ = 365 (=Tobs ∕3) days (c) and τ = 121 (=Tobs ∕9) days (d).

3.1.3 Radial velocity and log R$\text{'\_HK}$

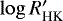We now compare the RV and $\log {R^{\prime }}_{\text{HK}}$ time series. We note that there is no apparent signal at 13-14 days in the $\log {R^{\prime }}_{\text{HK}}$ time series. In Fig. 5 we show the χ² map of the solar $\log {R^{\prime }}_{\text{HK}}$, binned with the same pattern as the RV. The base model is a second-order polynomial, and we added a jitter to the noise model equal to the standard deviation of the $\log {R^{\prime }}_{\text{HK}}$ time series divided by 2. In Fig. 5, there are low frequency signals at 200–400 days as well as signals close to the stellar rotation period, but none close to its first harmonic. As for the RV, we then performed an iterative search for signals (six iterations) and did not find signals at 13 days.

Furthermore, as suggested in Sect. 2.2, we studied the phase difference of RV and $\log {R^{\prime }}_{\text{HK}}$. In both time series, there is a signal at the solar rotation period. We fixed P = 26.25 days and computed the difference Δϕ RV phase - $\log {R^{\prime }}_{\text{HK}}$ as a function of t₀ for τ = 364 (=T_obs∕3) days, wherethe phases are defined in Eq. (10). The uncertainty on Δϕ is defined as the quadratic addition of the uncertainties on the RV and $\log {R^{\prime }}_{\text{HK}}$ phases. These were computed by fitting a free jitter error term for each choice of t₀. In Fig. 6, we represent the phase difference as a function of t₀ in purple, the shaded areas represent ± 1σ uncertainties, and the dots represent statistically independent phase measurements. The average difference of phase is 20 ± 6°, and this difference seems approximately constant throughout the observations. The RV 26 day signal is consistently in advance on the $\log {R^{\prime }}_{\text{HK}}$ by 1.5 ± 0.5 days.

Fig. 4 Phase and amplitude of the 13.39 day signal as a function of the time centre of the window t0 for the solar HARPS-N data, as described in Sect. 2.2 (solid red and green lines, respectively). Markers correspond to statistically independent estimates. Dashed red and green lines represent the average phase and amplitudes. The figures are all computed for a timescale of τ = 539 days, corresponding to τ∕Tobs = 1/9. Plots (a), (b), (c), and (d) are computed by adding iteratively the signals corresponding to the highest peaks to the base model.

Fig. 5 Value of the χ2 defined in Eq. (6) for the solar HARPS-N $\log {R^{\prime }}_{\text{HK}}$ as a functionof t0 for τ121 (=Tobs ∕9) days.

3.2 HD 215152

The star HD215152 was observed with the HARPS spectrograph over a 13 year period, from BJD 2452808 to 2457659. The data consist of 373 data points with mean error 0.73 m s⁻¹. The data are shown in Fig. 7. HARPS experienced an update of optical fibres in May 2015, which introduced a velocity offset. Data taken before and after the fibre update, labelled HARPS03 and HARPS15, are represented in blue and red, respectively.This system has been studied in Delisle et al. (2018), who claim the discovery of four super-Earths with orbital periods of 5.76, 7.28, 10.86, and 25.20 days. The analysis of Delisle et al. (2018) proceeds as follows. The data were modelled as a sum of Keplerian signals and two offsets: one corresponding to HARPS03 data and one to HARPS15 data. The $\log {R^{\prime }}_{\text{HK}}$ (Noyes 1984) was smoothed with a low-pass filter, and the resulting time series as well as the residuals (high-passed filter $\log {R^{\prime }}_{\text{HK}}$) were used as linear predictors. The data were analysed with a Gaussian noise model whose kernel is defined as the sum in quadrature of the nominal uncertainties, a free jitter, and a correlated component with a Gaussian auto-covariance (or kernel). The auto-covariance is ${\sigma }_R^2{\text{e}}^{-\Delta t^2/(2{\tau }_R^2)}$, where Δt is the time difference between measurements and ${\sigma }_R^2$ and τ_R are free parameters. The significance of the signals was established by computing periodograms where σ_J, σ_R, and τ_R are fitted at all trial frequencies. The periodogram was computed as the difference in the Bayesian information criterion (Schwarz 1978) of models $\mathcal{H}$ and $\mathcal{K}$. The rotation period of the star was estimated to be 43 days.

In this section, we present a re-analysis of the same data to assess the stability in amplitude, phase, and period of the detected signals. We have excluded the two points represented in black in Fig. 8 from the datasets on the ground that they deviate from the median of the HARPS15 data (blue points) by over four median absolute deviations.

To simplify the discussion, we assumed the same model as Delisle et al. (2018) and fixed the values of the noise parameters to their posterior medians, σ_J = 0.6 m s⁻¹ and σ_G = 1.2 m s⁻¹, and the timescale of the noise is τ_R = 2 days (we note that this is different from the apodisation timescale τ). In the base model (1), we also included the low-pass filtered $\log {R^{\prime }}_{\text{HK}}$ as well as the two offsets. We then computed the ASP (Eq. (6)) in four cases. In each one, we added to the base model six linear predictors, cos ω₁t, sin ω₁t, cos ω₂t, sin ω₂t, cos ω₃t, and sin ω₃t, where ω₁, ω₂, and ω₃ are the frequencies of three planets out of four. This comes down to assuming that three planets are securely detected and the consistency of the fourth is tested. The frequency grid goes from 0 to 0.8 cycles per day to avoid showing the aliases of the peaks.

When leaving out the 5.76, 7.28, and 10.86 day planets from the base model, we obtain respectively Figs. 8 a, b, and c. We see clearly that the maximum occurs for the longest coherence time (in blue) for planets at 5.76 days and 10.86 days. In the case of the 7.28 day signal, the maximum occurs at τ∕T_obs = 1∕3. However, as shown in the right panel, the τ∕T_obs = 10 hypothesis is not excluded. We note that the sampling of the HARPS data is very irregular, with a few samples between BJD 2453000 and 2454500 (see Fig. 8). When leaving out the 25 day planet, we obtain Fig. 8d. In that case, the highest peak corresponds to 46 days. If the τ = 10T_obs were true, the periodogram peak corresponding to τ = T_obs∕3 would be ~2 σ away from the highest peak (see the right panel of Fig. 8d). This is not surprising, as 46 days is close to the estimated rotation period of the star. When subtracting the 46 day signal with τ = T_obs∕3, we obtain Fig. 8e. The maximum peak is attained at 25 days and appears to be consistent with τ = 10T_obs, and thus a planet. We note, however, that the FAP obtained with a regular periodogram of the 25 day planet is 1%, so it might be suitable to acquire more points for a more significant detection.

We performed the test described in Sect. 2.2 for each of the four cases. Figure 9 shows the resulting plot. It appears that the phase and amplitude of the signals are compatible with the hypothesis that they are constant in all cases.

Fig. 6 Difference between the RV phase and $\log {R^{\prime }}_{\text{HK}}$ phase as a function of time for τ = Tobs ∕3.

Fig. 7 HD 215152 HARPS radial velocities. Data taken before and after the fibre update are represented in blue and red, respectively.

3.3 HD 69830

In this section, we illustrate the Bayesian method proposed in Sect. 2.1.4 with the HARPS03 data of HD 69830. This dataset contains 254 data points and spans 11.5 yr. The HD 69830 system is known to harbour three planets with minimum masses close to Neptune’s (Lovis et al. 2006) and periods of 8.667, 31.56, and 197 days.

As suggested in Sect. 2.1.4, we computed the joint posterior distribution of the orbital elements and the number of planets. The signal is represented as a sum of k Keplerian functions multiplied by an apodisation factor and a noise model (a random variable) $$y={\displaystyle \sum _{i=1}^k{\text{e}}^{-\frac{{(t-t_0)}^2}{2{\tau }^2}}}{\text{Kep}}_i(P,e,K,\omega ,M_0)+ϵ,$$(16)

where Kep(P, e, K, ω, M₀) is a Keplerian function (e.g. Perryman 2011) of period P, eccentricity e, semi-amplitude K, argument of periastron ω, and initial mean anomaly M₀. We used a Gaussian noise model for ϵ with a jitter term and an exponential decay, implemented with the spleaf software (Delisle et al. 2020b). The covariance matrix V has the form $$V_{ij}={\delta }_{ij}({\sigma }_i^2+{\sigma }_W^2)+{\sigma }_R^2{\text{e}}^{-\frac{{(t_i-t_j)}^2}{2T^2},}$$(17)

where δ_ij is the Kronecker symbol and σ_i is the nominal uncertainty on measurement i. The priors on the parameters are presented in Table 2. As in Hara et al. (2022), the posterior distributions were computed with POLYCHORD (Handley et al. 2015b,a).

In Fig. 10, we represent the posterior distribution of τ (defined in Eq. (16)) and f (defined in Eq. (8)) conditioned on the period P being such that |1∕P − 1∕P_i| < 1∕T_obs for i = 1, 2, 3 and P₁ = 8.66 days, P₂ = 31.56 days, and P₃ = 197 days. Here, T_obs is the total time span of the observations. The τ distribution for the P₃ = 197 day planets peaks below T_obs. In the f distribution (right) it is clear that all distributions peak at 1. In conclusion, all the three known planets are indeed consistently detected.

Fig. 8 ASPs computed on the HD 215152 HARPS data. All are computed with a base model that includes a linear activity model and offsets, as described in Sect. 3.2. They also include three of the four planets. Rows (a), (b), (c), and (d) correspond respectively to leaving out planets at 5.75, 7.28, 10.86, and 25.20 days. Left column: ASPs corresponding to Eq. (7) for different values of τ (blue, orange, green, and red correspond to τ∕Tobs = 10, 1/3, 1/9, and 1/27). Middle column: zoom-in on the maximum peak of the ASP. Right: statistical test on the timescale. When subtracting the 46 day signal with τ = Tobs∕3 (period at which the maximum of the ASP is attained in (d)), we obtain (e) (on the following page), where a coherent 25.2 d signal appears.

Fig. 9 Phase and amplitude as a function of the time centre of the window t0, as described in Sect. 2.2 (solid red and green lines, respectively). Markers correspond to statistically independent estimates. Dashed red and green lines represent the average phase and amplitudes. The figures are all computed for a timescale of τ = 539 days, corresponding to τ∕Tobs = 1∕9. Plots (a), (b), (c), and (d) correspond to base models that include offsets, linear activity indicators, and all the claimed planets except the 5, 7, 10, and 25 day planets, respectively.

Fig. 10 Diagnostics of the consistency of prensence of signals in the HD 69830 HARPS dataset. Left and right: posterior distribution of τ (defined in Eq. (16)) and f (defined in Eq. (8)) conditioned on the period P being such that |1∕P − 1∕Pi| = 1∕Tobs for i = 1, 2, 3 and P1 = 8.66 days, P2 = 31.56 days, and P3 = 197 days. The i = 1, 2, 3 correspondrespectively to the blue, orange, and green histograms. The black dotted line corresponds to τ = Tobs.

3.4 HD 13808

The HD 13808 system was observed with HARPS (Mayor et al. 2003) over a 10 year time span. The dataset contains 246 RV measurements and presents three candidate signals, at 14.1, 19, and 53.7 days. In Ahrer et al. (2021), the HARPS dataset was analysed with many different noise models based on the bisector span (Queloz et al. 2001) and the $\log {R^{\prime }}_{\text{HK}}$ (Noyes 1984). The stellar activity models were built upon the framework of Gaussian processes (Rajpaul et al. 2015) and the FF′ method (Aigrain et al. 2012). The models with different numbers of planets and different stellar activity models were compared through their Bayesian evidence. The authors conclude that the 14.1 and 53.7 day planets are securely detected and that the 19 day planet cannot be confidently claimed.

We next performed the same analysis as in Sect. 3.3. Following the method of Sect. 2.1.4, we computed the joint posterior distribution of ω, t₀, τ, and the number of planets. We used the same noise model (see Eq. (17)) and the same priors (see Table 2) as for HD 69830 as well as the same numerical method, POLYCHORD (Handley et al. 2015b,a).

First, to check that the signals are significant, as in Hara et al. (2022), we computed the FIP periodogram. It is definedas follows. We considered a grid of frequency intervals with a fixed length. The element k of the grid, I_k, is defined as [ω_k − Δω∕2, ω_k + Δω∕2], where Δω = 2π∕T_obs, T_obs is the total observation time span, and ω_k = kΔω∕N_oversampling. We took N_oversampling = 5. We then computed the probability of having at least one planet in I_k (the TIP) and the FIP = 1 - FIP. We then represented − log₁₀ FIP as a function of ω_k.

As suggested in Hara et al. (2022), we computed the FIP periodogram for different maximum numbers of planets. We found that the FIP periodograms obtained for three and four planets are almost identical and chose the three-planet models. To assess the computational uncertainties, we computed the FIP periodogram with three different runs of POLYCHORD. The resulting FIP periodogram is shown in Fig. 11; each run corresponds to an FIP periodogram of a different colour. It appears that the probability of not having a planet at 14.1 and 53.7 days is below 10⁻¹⁰ and 10⁻², respectively. The significance of the 18.9 day signal is much lower, with an FIP ~ 70%. We also did the same calculation with a white noise model, for which the 18.9 day signal is much more significant (FIP of 1%).

We then computed the posterior distribution of the apodisation timescale τ and the fraction of information captured by a window of given width f, as in Sect. 3.3. In Fig. 12 we represent the posterior distribution of τ (defined in Eq. (16)) and f (defined in Eq. (8)) conditioned on the period P being such that |1∕P − 1∕P_i| < 1∕T_obs for i = 1, 2, 3 and P₁ = 14.18 days, P₂ = 19 days, and P₃ = 53.8 days. We find that all signals have an f distribution peaking at 1.

In conclusion, in accordance with Ahrer et al. (2021), we find that the 14.1 and 53.7 day signals are statistically significant. The significance of the 19 day signal is too low to claim a detection. However, it appears that the signal is consistent in time, so a planetary origin cannot be excluded. However, this is not likely since, as shown in Ahrer et al. (2021), a 19 day signal is present in the ancillary indicators. We have seen in the case of the Sun (see Sect. 3.1) that the first harmonic of the rotation period exhibits a constant period and phase, but not a constant amplitude. Since the stellar rotation period is ~38 days, the 19 day signal could be another case of a first, stable harmonic of the rotation period.

Fig. 11 FIP periodogram of HD 13808: − log10 FIP (in blue) and log10 TIP (in yellow) of the presence of a planet in a centred frequency interval [ω − Δω, ω + Δω] as a functionof ω. Here, Δω = 2π∕Tobs, where Tobs is the total observation time span. Different colours correspond to independent computations with POLYCHORD. The plot inside the black box represents a zoom-in on the region close to 18.9 days.

Fig. 12 HD 13808 dataset. Left and right: posterior distribution of τ (defined in Eq. (16)) and f (defined in Eq. (8)) conditioned on the period P being such that |1∕P − 1∕Pi| < 1∕Tobs for i = 1, 2, 3 and P1 = 14.18 days, P2 = 19 days, and P3 = 53.8 days. The i = 1, 2, 3 correspondrespectively to the blue, orange, and green histograms. The black dotted line corresponds to τ = Tobs.

4 Discussion and conclusions

In the present work, our goal has been to assess whether an apparently periodic signal is strictly so, with a focus on the detection of planets in RV data. This can be done with models intended to capture all variations due to the planets and stellar activity (Haywood et al. 2014; Rajpaul et al. 2015; Jones et al. 2017; Hara et al. 2022). However, these models are not guaranteed to be trustworthy, which motivates the approach of the present work, whose methods offer a complementary outlook on the data.

Following Gregory (2016), we considered wavelet-like functions: periodic functions multiplied by an apodisation term. We suggested different representations and statistical tests to explore whether a signal is truly periodic, by constraining its timescale (see Sect. 2.1), its variation of phase and amplitude (see Sect. 2.2), and its frequency variation (see Sect. 2.3). We considered tests based on periodograms (see Sects. 2.1.1, 2.1.2, and 2.1.3) and on the Bayesian formalism (see Sect. 2.1.4). Periodograms provide interpretable figures and scan all the periods robustly and quickly, while their exploration might be difficult with random searches used for Bayesian inference. On the contrary, the latter method has the advantage of providing easily interpretable quantities. Depending on the objective and the size of the dataset, one of these two approaches might be more adapted.

The variability in the signal of interest can be assessed at different timescales with a typical Heisenberg uncertainty principle: the shorter the timescale of variation probed, the higher the uncertainty on the local estimates of phase, amplitude, and period. We recommend studying this variability on a grid of timescales chosen with an exponential decrease, as in wavelet decomposition (Mallat 1989).

Our tests were defined to assess the consistency with a certain data model. If other signals are present (trends, other periodic or quasi-periodic signals) or the shape of the signal examined is not sinusoidal – for instance, it corresponds to an eccentric planet – our indicators might present significant variations despite the signal being truly periodic. Asa consequence, for the results to be reliable it is crucial to model the signal of interest and other signals present simultaneously. The approach we suggest is either to model the data as a sum of apodised periodic components, as in Gregory (2016), or to assume that all periodic signals are truly periodic, except the one under consideration.

When assessing the phase and amplitude variability of a signal at frequency ω₀, it is crucial to use all the data to estimate ω₀ since the longest baseline gives the most precise estimate of ω₀. An inaccurate estimate of ω₀ might result in an apparent spurious linear phase shift with time.

We analysed the solar RV as measured by HARPS-N (Dumusque et al. 2021) as well as the HARPS data of HD 215152 (Delisle et al. 2018), HD 69830 (Lovis et al. 2006), and HD 13808 (Ahrer et al. 2021). The solar RV contains quasi-periodic signals at the first and second harmonic of the rotation period, the second harmonic having the larger amplitude of the two. The ~25–27 day region shows a varying period, phase, and amplitude. The second harmonic, appearing at 13.39 days, shows a period and phase constant within the uncertainties of statistical tests, showing that stellar activity signals can exhibit traits of purely periodic signals. Fortunately, the amplitude of the solar 13.39 day harmonic shows significant variations at the timescale of 121 days (total observation time span divided by nine). Such variability makes it less likely that such a stellar signal could be mistaken for a planet. These amplitude variations can be mapped to variations in the level of activity. This case shows that variations in amplitude, phase, and frequencies due to stellar activity can be very subtle and require a high signal-to-noise ratio to be statistically significant. These observations can speculatively be explained by the persistence of large active regions that are diametrically opposed, as suggested by Borgniet et al. (2015). A more rigorous testing of this hypothesis is left for future work.

In HD 13808, there is a potential low amplitude signal at 19 days, which also presents consistency in time. We therefore agree with the conclusion of Ahrer et al. (2021) that two planets can be confidently claimed. A planetary origin of the signal cannot, however, be excluded, which might motivate further observations.

The detection of four and three planets in HD 215152 and HD 69830 was claimed in Delisle et al. (2018) and Lovis et al. (2011), respectively. We find in both cases that all the planets exhibit constant phases and amplitudes, which strengthens these detection claims.

In the present work, we have suggested several methods to assess whether a signal is strictly periodic or not, but many others can be considered. The periodicity criteria and the techniques for simultaneous modelling of quasi-periodic signals, periodic signals, and noise and could both be explored in further detail. We leave this exploration and the comparison of the different criteria for future work.

Acknowledgements

The authors thank the anonymous referee for their very insightful comments, which helped to improve the paper. N.C.H thanks Michaël Cretigner for his input. N.C.H. and J.-B.D. acknowledge the financial support of the National Centre for Competence in Research PlanetS of the Swiss National Science Foundation (SNSF).

Appendix A Computations

A.1 Distribution of the difference of two χ² variables

We consider two models, $\mathcal{K}(\omega ,t_0,\tau )$ and $\mathcal{K}({\omega }^{\prime },t_{0^{\prime }},{\tau }^{\prime })$, which we denote by $$\begin{array}{l}\mathcal{K}(\omega ,t_0,\tau ):y=Ax+ϵ,ϵ~G(0,V)\\ \mathcal{K}({\omega }^{\prime },t_{0^{\prime }},{\tau }^{\prime }):y=Bx+ϵ,ϵ~G(0,V),\text{ }\end{array}$$

where G(0, V) is a multivariate Gaussian distribution of mean 0 and covariance V. Our aim is to compute the distribution of $z(\omega ,t_{\tau ,\omega },\tau )-z(\omega ,t_{{\tau }^{\prime },\omega },{\tau }^{\prime })$ under the hypothesis that $\mathcal{K}(\omega ,t_0,\tau )$ is correct. The data are supposed to follow the model v_A + ϵ, where v_A = Ax_t.

We further denote $P_M=M{(M^T{V}^{-1}M)}^{-1}{M}^T{V}^{-1}$ and H_M = V⁻¹P_M for a given matrix M. The residuals of the fit of models ${\mathcal{M}}_A$ and ${\mathcal{M}}_B$ are $$\begin{array}{ll}{r}_A=\hfill & (I-P_A)ϵ\hfill \\ r_B=\hfill & (I-P_B)(ϵ+v_A).\hfill \end{array}$$

We use the notations u_A := (I − P_B)v_A and V = LL^T, where L is the Cholesky decomposition of V, η := L⁻¹ϵ, and $$\begin{array}{ll}{\chi }_A^2\hfill & ={\eta }^T{L}^T(V^{-1}-H_A)L\eta \hfill \\ {\chi }_B^2\hfill & ={\eta }^T{L}^T(V^{-1}-H_B)L\eta +2u_A{V}^{-1}(I-P_B)L\eta +u_A^T{V}^{-1}{u}_A.\hfill \end{array}$$

Then, the difference of periodogram values is $$\begin{array}{ll}{D}_z\hfill & =z(\omega ,t_{\tau ,\omega },\tau )-z(\omega ,t_{{\tau }^{\prime },\omega },{\tau }^{\prime })={\chi }_A^2-{\chi }_B^2\hfill \\ \hfill & =-({\eta }^{T}D\eta +{\beta }^T\eta +\alpha ),\hfill \end{array}$$

where D = H_A − H_B, β = 2u_AV⁻¹(I − P_B)L, and $\alpha =u_A^T{V}^{-1}{u}_A$. Then, the expectancy and variance of D_z are $$\begin{array}{l}\text{nnmathbbm}E\left\{D_z\right\}=-{\sum }_i{D}_{ii}-\alpha \\ \text{nnmathbbm}V\left\{D_z\right\}={\sum }_{i,j}{D}_{ij}^2+{\sum }_i{\beta }_i^2.\end{array}$$

A.2 Independence of semi-amplitude and phase estimate

We supposed the data are $$y=y_0+ϵ,$$(A.11)

where y₀ is the model and ϵ is a random variable following a Gaussian distribution with null mean and covariance V. The two alternative linear models considered are: y = Mx + ϵ and y = M′x + ϵ. Thus, their corresponding least square estimates are $x_M:={(M^{T}WM)}^{-1}{M}^{T}Wy$ and $x_{M^{\prime }}:={({M^{\prime }}^{T}W{M}^{\prime })}^{-1}{M^{\prime }}^{T}Wy,$ where W := V⁻¹. Then, the covariance of x_M and $x_{M^{\prime }}$ is $$Cov(x_M,x_{M^{\prime }})={(M^{T}WM)}^{-1}{M}^{T}W{M}^{\prime }{({M^{\prime }}^{T}W{M}^{\prime })}^{-1}.$$(A.12)

We then address the case where M = [m, M₀] and M′ = [m′, M₀], where the brackets designate the concatenation of two matrices and m = [w(t − t₀)cos ωt, w(t − t₀)sin ωt], and $m^{\prime }=[w(t-t_{0^{\prime }})\cos \omega t,w(t-t_{0^{\prime }})\sin \omega t],$ where w is a box-shaped time window, zero everywhere except between t₀ − τ∕2 and t₀ + τ∕2, and $|t_0-t_{0^{\prime }}|>\tau$. That is, fitting M and M′ corresponds to fitting models of type $\mathcal{K}$ (see Eq. (2)) with different time centres t₀.

If the noise is uncorrelated, V is diagonal and so is W. Since $w(t-t_0)w(t-t_{0^{\prime }})=0,$ the coefficients of columns m and m′ from Eq. (A.12) are independent. If the noise is correlated, W is non-diagonal and $w{(t-t_0)}^{T}Ww(t-t_{0^{\prime }}),$ where w(t) is the column vector ${(w(t_i))}_{i=\mathrm{1..}N}.$

Appendix B FAP calculation

Here, we denote by the generic symbol Z(Y, θ) a function of the data Y that is either z, as defined in Eq. (6), or a fixed T, ω, t₀ → z(ω, t₀, T). The FAP is defined as $$\text{FAP}=\text{Pr}\{{\max }_{\theta }Z(Y,\theta )⩾Z_{\text{max}}|Y~\mathcal{H}\},$$(B.1)

where Z_max is the observed maximum of the periodogram on the data to be analysed and 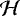$\mathcal{H}$ is defined in Eq. (1). The FAP can be computed using simulations that generate data following model $~\mathcal{H}$ and compute the empirical distribution of ${\max }_{\theta }Z(Y,\theta )$ or simulations that generate Y with random permutations of the input data. The value of ${\theta }_{\mathcal{H}}$ can be fixed to zero without loss of generality. This procedure can be very computationally heavy to reach low FAPs. The ASP is the special case of non-linear ‘Von Mises’ periodograms defined in Baluev (2013b), for which analytical approximations of the FAP can be derived. In that case, the specific form of the apodisation function must be specified. We here adopted the approach of Süveges (2014), which consists in generating data as in the simulation approach, but then fitting a generalised extreme distribution (GEV) to the generated samples. The analytical form of a GEV distribution is $$p(z;\mu ,\sigma ,\xi )=\frac{1}{\sigma }t{(z)}^{\xi +1}{\text{e}}^{-t(z)},$$(B.2)

where $$t(z)=\{\begin{array}{l}{\left(1+\xi \frac{z-\mu }{\sigma }\right)}^{-\frac{1}{\xi }}\text{ if }\xi \ne 0\hfill \\ {\text{e}}^{-\frac{z-\mu }{\sigma }}\text{ if }\xi =0\hfill \end{array}.$$(B.3)

The parameters μ, σ, and ξ can be estimated with a maximum likelihood estimate, and the uncertainties obtained from the inverse of the Fisher information matrix can be propagated to p(z;μ, σ, ξ) for a certain value of z to ensure that the computed FAP is sufficiently accurate.

This approach allows the number of simulations needed to estimate the low FAP levels to be drastically reduced. To illustrate this, we show in Fig. B.1 the histogram of 12,000 maxima of periodograms as well as the distribution (blue) and the fit of the 200 first simulations made with a Nelder-Mead algorithm (in orange). The simulation is made with the 70 first measurements of HD 85512 (Pepe et al. 2011).

Fig. B.1 Empirical distribution of the maximum of periodograms generated.

References

All Tables

All Figures

Fig. 1 ASPs computed iteratively on the solar data. Left column: ASPs corresponding to Eq. (7) for different values of τ. Middle column: zoomed-in view of the maximum peak of the ASP. Right: statistical test on the timescale described in Sect. 2.1.3. On the x axis we represent the ratio of τ to the total observation time assumed to be true. For each τi, i = 1…4 in abscissa, the position of the markers corresponding to τj, j = 1…4 is represented as the value of the periodogram peak for τi minus the expectancy of $D_z=z(\omega ,t_{\tau ,\omega },{\tau }_i)-z(\omega ,t_{{\tau }_j,\omega },{\tau }_j)$, and the error bar is the square root of the variance of Dz. Informally, the markers represent what the periodogram values at τj should be if τi in abscissa were the true timescale.

In the text

	Fig. 2 Models corresponding to the maximum of the ASPs in Fig. 1.
In the text

Fig. 3 Consistency of the period of signals in the solar data. (a and b): value of the χ2 defined in Eq. (6) for the solar HARPS-N RV data as a function of t0 for τ = 365 (=Tobs ∕3) days (a) and τ = 121 (=Tobs ∕9) days (b). (c and d): value of the semi-amplitude as a function of t0 for τ = 365 (=Tobs ∕3) days (c) and τ = 121 (=Tobs ∕9) days (b). Grey areas correspond to 1 σ uncertainties greater than 30 cm s−1. (e and f): in blue, position of the mode of the ASP between frequencies represented in grey as a function of t0, as defined in Sect. 2.3. Computed for τ = 365 (=Tobs ∕3) days (c) and τ = 121 (=Tobs ∕9) days (d).

In the text

Fig. 4 Phase and amplitude of the 13.39 day signal as a function of the time centre of the window t0 for the solar HARPS-N data, as described in Sect. 2.2 (solid red and green lines, respectively). Markers correspond to statistically independent estimates. Dashed red and green lines represent the average phase and amplitudes. The figures are all computed for a timescale of τ = 539 days, corresponding to τ∕Tobs = 1/9. Plots (a), (b), (c), and (d) are computed by adding iteratively the signals corresponding to the highest peaks to the base model.

In the text

	Fig. 5 Value of the χ2 defined in Eq. (6) for the solar HARPS-N $\log {R^{\prime }}_{\text{HK}}$ as a functionof t0 for τ121 (=Tobs ∕9) days.
In the text

	Fig. 6 Difference between the RV phase and $\log {R^{\prime }}_{\text{HK}}$ phase as a function of time for τ = Tobs ∕3.
In the text

	Fig. 7 HD 215152 HARPS radial velocities. Data taken before and after the fibre update are represented in blue and red, respectively.
In the text

Fig. 8 ASPs computed on the HD 215152 HARPS data. All are computed with a base model that includes a linear activity model and offsets, as described in Sect. 3.2. They also include three of the four planets. Rows (a), (b), (c), and (d) correspond respectively to leaving out planets at 5.75, 7.28, 10.86, and 25.20 days. Left column: ASPs corresponding to Eq. (7) for different values of τ (blue, orange, green, and red correspond to τ∕Tobs = 10, 1/3, 1/9, and 1/27). Middle column: zoom-in on the maximum peak of the ASP. Right: statistical test on the timescale. When subtracting the 46 day signal with τ = Tobs∕3 (period at which the maximum of the ASP is attained in (d)), we obtain (e) (on the following page), where a coherent 25.2 d signal appears.

In the text

Fig. 9 Phase and amplitude as a function of the time centre of the window t0, as described in Sect. 2.2 (solid red and green lines, respectively). Markers correspond to statistically independent estimates. Dashed red and green lines represent the average phase and amplitudes. The figures are all computed for a timescale of τ = 539 days, corresponding to τ∕Tobs = 1∕9. Plots (a), (b), (c), and (d) correspond to base models that include offsets, linear activity indicators, and all the claimed planets except the 5, 7, 10, and 25 day planets, respectively.

In the text

Fig. 10 Diagnostics of the consistency of prensence of signals in the HD 69830 HARPS dataset. Left and right: posterior distribution of τ (defined in Eq. (16)) and f (defined in Eq. (8)) conditioned on the period P being such that |1∕P − 1∕Pi| = 1∕Tobs for i = 1, 2, 3 and P1 = 8.66 days, P2 = 31.56 days, and P3 = 197 days. The i = 1, 2, 3 correspondrespectively to the blue, orange, and green histograms. The black dotted line corresponds to τ = Tobs.

In the text

Fig. 11 FIP periodogram of HD 13808: − log10 FIP (in blue) and log10 TIP (in yellow) of the presence of a planet in a centred frequency interval [ω − Δω, ω + Δω] as a functionof ω. Here, Δω = 2π∕Tobs, where Tobs is the total observation time span. Different colours correspond to independent computations with POLYCHORD. The plot inside the black box represents a zoom-in on the region close to 18.9 days.

In the text

	Fig. 12 HD 13808 dataset. Left and right: posterior distribution of τ (defined in Eq. (16)) and f (defined in Eq. (8)) conditioned on the period P being such that |1∕P − 1∕Pi| < 1∕Tobs for i = 1, 2, 3 and P1 = 14.18 days, P2 = 19 days, and P3 = 53.8 days. The i = 1, 2, 3 correspondrespectively to the blue, orange, and green histograms. The black dotted line corresponds to τ = Tobs.
In the text

	Fig. B.1 Empirical distribution of the maximum of periodograms generated.
In the text