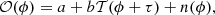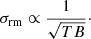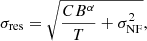EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 658 (February 2022) A&A, 658 (2022) A181 Full HTML
Free Access
Issue
A&A
Volume 658, February 2022
Article Number A181
Number of page(s) 11
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/202141121
Published online 21 February 2022

© ESO 2022

1. Introduction

Millisecond pulsars (MSPs, first discovered by Backer et al. 1982) are neutron stars that have been spun up or recycled to rotation periods shorter than ∼30 ms through accretion of matter from a binary companion star (Alpar et al. 1982; Bhattacharya & van den Heuvel 1991). Their extremely stable rotation periods make MSPs ideal laboratories for testing a diversity of extreme astrophysical phenomena that cannot be accessed on Earth. Their applications include investigating turbulence and structures of the interstellar medium (Keith et al. 2013; Lam et al. 2018; Donner et al. 2019), testing relativistic gravity (Taylor & Weisberg 1982; Archibald et al. 2018; Voisin et al. 2020), building a pulsar-based time standard (Hobbs et al. 2012, 2020), constraining masses in the Solar System (Champion et al. 2010; Caballero et al. 2018), measuring the magnetic field structure in the Galaxy (Han et al. 2018; Gentile et al. 2018), and detecting gravitational radiation (e.g. Shannon et al. 2015; Lentati et al. 2016; Arzoumanian et al. 2020).

Detecting nanohertz gravitational waves (GWs) using pulsar timing is one of the main foci in pulsar-timing research at present (see the recent reviews by Tiburzi 2018; Burke-Spolaor et al. 2019). It has been predicted (Jenet et al. 2005) that a detection can be achieved by monthly observations of 20 to 40 MSPs over five to ten years if these sources are characterised by white timing residuals with a root mean square (rms) of ∼100 ns. In order to achieve this, three major pulsar timing arrays (PTAs, see Foster & Backer 1990; Romani 1989) were constructed: the Parkes Pulsar Timing Array (PPTA, Manchester et al. 2013), the European Pulsar Timing Array (EPTA, Janssen et al. 2008; Desvignes et al. 2016), and the North-American Nanohertz Observatory for Gravitational waves (NANOGrav, Demorest et al. 2013). The three were subsequently combined in the International Pulsar Timing Array (IPTA, Verbiest et al. 2016; Perera et al. 2019). Even though substantial progress has been achieved in improving timing precision and sensitivity in subsequent data releases at the regional and global level, no detection has been achieved so far, primarily because of two limiting factors. Firstly, even the most recent and highest-quality data sets (e.g. the NANOGrav data set from Alam et al. 2021a,b) have too few pulsars with timing precisions below or at the 100-ns level. Secondly, there are a number of corrupting effects, whose impact on timing precision requires careful consideration (Shannon & Cordes 2012; Verbiest & Shaifullah 2018). One example of recent progress in this regard is the influence of the Solar System ephemerides, which was known to affect GW experiments (Tiburzi et al. 2016), but it was not properly taken into account until more recently (e.g. Arzoumanian et al. 2018a; Vallisneri et al. 2020). Beyond this, several fundamental aspects of pulsar-timing analyses were identified as potential targets for optimisation and harmonisation efforts during the first global PTA data combination (Verbiest et al. 2016). Three particular recommendations from this work are described below and are investigated in detail in this paper.

Firstly, all standard pulsar-timing analyses are based on matching a so-called template or standard profile to the observations. There are several different ways in which these template profiles can be constructed, however. As outlined by Lorimer & Kramer (2005), template profiles have traditionally been constructed by adding a large number of observations, which resulted in a pulse profile with a far higher signal-to-noise ratio (S/N) than any given observation. These templates have the advantage that by definition, they fully resemble the actual pulse shape, but the noise of the original observations is also contained in the template and hence may cause inaccurate correlations that are commonly referred to as self-standarding (Hotan et al. 2005). Three strategies have been devised to mitigate this issue: firstly, the template profile can be smoothed; secondly, the template can be restricted to contain only the single brightest observation (which is then removed from the subsequent timing analysis and only used as template profile); and thirdly, the template can be modelled with noise-free analytic functions (Lorimer & Kramer 2005). As was shown e.g. by Desvignes et al. (2016), Demorest et al. (2013), Kerr et al. (2020), several of these approaches are currently in use, but no comprehensive comparison of the various template-creation options has been published.

Secondly, after a template profile has been created, the time of arrival (TOA) of a given observation is derived from the cross-correlation between the observation and the template. Traditionally, this has been done in the Fourier domain by fitting the phase-gradient of the cross-power spectrum of the template and the observation (Taylor 1992), commonly referred to as the phase gradient scheme (PGS) cross-correlation algorithm (CCA). However, the standard implementation of this approach has often been found to report underestimated uncertainties. One suggested solution determines the TOAs in the same way, but derives the TOA uncertainties from a Monte Carlo analysis (referred to as the FDM method1). This solution has been suggested (Verbiest et al. 2016) to be superior. Furthermore, Hotan et al. (2005) proposed a Gaussian-interpolation (GIS) CCA in the time domain, which is supposedly better suited to low-S/N data sets. While recent pulsar-timing efforts have increasingly adopted the FDM method, usage of the PGS method is still widespread (Desvignes et al. 2016), in some cases (e.g. Arzoumanian et al. 2015) with lower bounds imposed on the pulse S/Ns in order to avoid underestimation of TOA uncertainties. A comprehensive, data-based (as opposed to simulation-based) comparative evaluation of the possible alternatives is so far lacking here as well.

Lastly, potential corruptions in the derived TOAs can arise from the usage of data-recording systems with large (⪆0.3) fractional bandwidths (Verbiest & Shaifullah 2018). This is particularly the case if the pulse-profile changes shape across the band and the scintillation bandwidth is of the same order as (or slightly smaller than) the observing bandwidth. Both of these conditions appear to be likely if the fractional bandwidth is large (Dai et al. 2015; Levin et al. 2016), causing the frequency-averaged profile shape to vary from one observation to the next. If the TOAs are derived from frequency-averaged observations and template, then the aforementioned variations will be reflected in the TOAs and in the TOA uncertainties, worsening the overall timing precision. One solution to this problem is to carry out two-dimensional template matching where the observation and template have a frequency resolution and where in addition to the phase offset (or TOA), a frequency drift (or dispersion measure) is determined (Liu et al. 2014; Pennucci et al. 2014). An alternative solution is to derive multiple TOAs across the bandwidth of the observation (Demorest et al. 2013; Arzoumanian et al. 2015), either against a frequency-averaged template or through matching each channel of the observation against the corresponding channel in the template. In all of this, it is an unsolved question which TOA bandwidth would be optimal: too narrow a bandwidth would leave little signal and create TOAs that have high levels of radiometer noise; too wide a bandwidth, and the scintillation effects risk becoming significant. The most useful TOA bandwidth is likely strongly pulsar dependent. To date, PTAs either fully frequency averaged their TOAs (Desvignes et al. 2016), used timing-model extensions to correct for profile-shape variations (Arzoumanian et al. 2015), or have carried out a mixed approach where both frequency-averaged and frequency-resolved TOAs have been derived (Kerr et al. 2020).

The three detailed aspects of TOA creation outlined above are investigated in this paper. Specifically, we introduce in Sect. 2 the data and pulsars we used to test and compare the aspects of timing on these data. In Sect. 3 we describe the various analysis methods that were compared: template creation is discussed in Sect. 3.1, template-matching methods in Sect. 3.2, and the most useful TOA bandwidth determination in Sect. 3.3. Before carrying out the actual analysis on the real data, we run some simulations to evaluate the reliability of the TOA uncertainties derived by the various TOA determination methods. These simulations are presented in Sect. 4. We discuss our findings on the three test pulsars in Sect. 5 and summarise our findings in Sect. 6.

2. Observations

Our analysis is based on data from the newest generation of data recorders at four of the radio telescopes that constitute the EPTA: the Effelsberg radio telescope (designated EFF), the Jodrell Bank Lovell radio telescope (JBO), the Nançay decimetric radio telescope (NRT), and the Westerbork synthesis radio telescope (WSRT). Details about the observing systems that are used at each of these observatories are given below. The pulsars we used for this initial investigation are PSRs J0218+4232, J1713+0747, and J2145−0750. These three pulsars were chosen because they represent a variety of characteristics. Specifically, PSR J1713+0747 is very bright, with a short duty cycle, and is one of the most precisely timed MSPs in PTAs. PSR J0218+4232 has a relatively high dispersion measure (DM), is fainter, and consequently not as well timed. PSR J2145−0750 is in between the other two in terms of brightness and timing precision, but has a significantly longer spin period and appears to have more significant stochastic wide-band impulse-modulated self-noise (or SWIMS, Osłowski et al. 2011, commonly also known as pulse-phase jitter).

Some basic properties for these three pulsars are given in Table 1. The observatory-specific details of the observations used are given in Table 2, and the number and date ranges of the observations are given in Table 3.

Table 1.

Basic parameters for the pulsars in our sample.

Table 2.

Description of the observational set-up for the data used in this paper.

Table 3.

Summary of the observations used in this paper.

In addition to the telescope-specific radio-frequency interference (RFI) mitigation strategies described below, all data were visually inspected through the software suite PSRCHIVE (Hotan et al. 2004; van Straten et al. 2012) before TOAs were derived as described in Sect. 3. Specifically, because the data near the edge of each sub-band are often corrupted by aliasing and spectral leakage problems, these channels were excised with the PAZ program.

2.1. Effelsberg radio telescope

The EFF is a homological Gregorian design with a 100 m paraboloidal primary reflector and a 6.5 m ellipsoidal secondary reflector. This makes EFF the world’s second-largest fully movable telescope. It operates at wavelengths from about 90 cm to 3.5 mm (i.e. observing frequencies from 300 MHz to 90 GHz).

The data from the EFF presented in this research were acquired with a typical cadence of 3−4 weeks between 2011 and 2019 with an integration time per source of about 30 min per observation. The data recorder (henceforth referred to as backend) used was the PSRIX pulsar-timing system (Lazarus et al. 2016), which is based on the reconfigurable open architecture computing hardware (ROACH) boards and carries out coherent dedispersion on central processing units (CPUs) using the DSPSR (van Straten & Bailes 2011) package. The observations were taken with the P-217 and P-200 receivers, centred at 1.3475 GHz in a frequency-multiplexing mode where eight 25 MHz wide sub-bands are independently dedispersed and written to disk. This results in observations with a total of 200 MHz of bandwidth, 128 frequency channels, 1024 phase bins, 10-s integrations, and full polarisation information.

These data were combined in time and frequency with the PSRADD command of the PSRCHIVE package (Hotan et al. 2004; van Straten et al. 2012). Subsequently, RFI was removed automatically with CLEAN.PY, the RFI excision script of the COASTGUARD package (Lazarus et al. 2016), using the “surgical” algorithm.

2.2. Lovell radio telescope

At Jodrell Bank Observatory, the 76-m Lovell telescope is used in a regular pulsar-monitoring programme. The observations used in this work were taken from that programme, have a centre frequency of 1.532 GHz, a time span of ∼7.5 years, a typical cadence of three weeks, and a typical integration time of 15 min. For PSR J1713+0747, the cadence was closer to one week. The backend used for these observations was a ROACH-based backend very similar to the one used at the EFF and described by Lazarus et al. (2016), and using the DSPSR package (van Straten & Bailes 2011) for real-time coherent dedispersion.

The JBO observations have a bandwidth of 400 MHz split over 25 16 MHz wide sub-bands, each channeled into 1 or 0.25 MHz wide frequency channels. The number of phase bins varies between 256 and 2048 depending on the pulsar observed. For the data set we used in this work, PSR J0218+4232 has the minimum 256 bins.

To remove the RFI, the spectral kurtosis method for real-time RFI removal (Nita et al. 2007) was applied during the DSPSR pre-processing, after which the data were run through some basic RFI-removal scripts. Finally, they were visually inspected to exclude the remaining RFI.

2.3. Nançay decimetric radio telescope

Built in 1965, the Nançay decimetric radio telescope (NRT) is a Kraus-type telescope with a collecting area of 6912 m2, equivalent to a 94 m parabolic dish. Since 2011, NRT observations of pulsars are made with the ROACH-based NUPPI backend (Cognard et al. 2013), a version of the Green Bank Ultimate Pulsar Processing Instrument (DuPlain et al. 2008) designed for Nançay. With a total bandwidth of 512 MHz, the NUPPI backend splits the full bandwidth into 128 channels, each channel with a bandwidth of 4 MHz. The observations used here were centred at 1484 MHz and were coherently dedispersed in real time on GPU units that are part of the NUPPI system.

The pulsars were observed with NUPPI since 2011 with a cadence that varied between five and ten days and with an integration time between 45 and 60 min per observation. Various automated RFI excision schemes were applied in post-processing offline.

2.4. Westerbork synthesis radio telescope

The WSRT, located in the Netherlands and operated by the Netherlands Institute for Radio Astronomy (ASTRON), is an east-west interferometric array with fourteen 25 m parabolic dishes. In terms of collecting area, this is equivalent to a 94 m single telescope.

Pulsar monitoring at the WSRT has been carried out at 350 MHz, 1.38 GHz, and 2.27 GHz with the Pulsar Machine II (PuMa-II) backend (Karuppusamy et al. 2008). Pulsar observations are recorded in eight 20 MHz wide sub-bands for a total observing bandwidth of 160 MHz with 512 (=8 × 64) frequency channels. Coherent dedispersion is performed offline with the DSPSR package.

The observations used in this paper were taken at a centre frequency of 1380 MHz and had a cadence of roughly one month and a total integration time of about 30 min. For PSRs J0218+4232 and J1713+0747, data with only 256 bins were used in this work.

3. Data processing techniques

In this section we describe the different algorithms and methods we used and compared. Specifically, the template creation methods are described in Sect. 3.1, the template-matching methods are outlined in Sect. 3.2, and the analysis in which we determined the most useful TOA bandwidth is described in Sect. 3.3. All of these algorithms and methods make use of the PSRCHIVE and TEMPO2 (Hobbs et al. 2006) software packages.

3.1. Template creation and comparison

The ideal template describes the pulse profile shape in perfect detail, without additive noise. A vital and complicating aspect in this regard is the fact that the achievable timing precision for a given profile shape is a strong function of the higher-frequency components present in the profile shape, that is, of sharp features in the profile (e.g. van Straten 2006). Consequently, depending on the pulsar in question, noise-mitigation methods such as smoothing or modelling of template profiles may require particular care in order to prevent negative impact on the timing potential of a given pulsar.

Common approaches towards template generation were already discussed in the introduction, thus here we summarise the four different methods we compare.

Single-brightest observation (henceforth “single”). Here we took the observation with the highest S/N for use as a template and removed it from the observations to be timed. This approach has the advantage that all true features of the pulse profile are present in the template, but the disadvantage that the templates tend to have higher noise levels than in alternative approaches and are more susceptible to negative impacts from effects such as scintillation, profile evolution, SWIMS, and man-made additional noise such as miscalibration or RFI. This approach is convenient for pulsars that have large variations in S/N because the noise present in the template for such pulsars may be negligible in comparison to the noise present in the typical observation. However, in the case that the data set is composed of a limited number of observations, it can be disadvantageous to exclude the most valuable (i.e. brightest) observation from the timing.

All observations added (henceforth “added”). The added template consists of all observations added together while aligning them using the timing ephemeris of the data. The RFI and misaligned integrations due to clock offsets, for instance, are then zapped out. The cleaned archives are then re-weighted with several methods (S/N, S/N2, and off-pulse rms) and the one with the highest resulting S/N is then chosen as the final added template. This approach also has the advantage that by definition, all true profile features are present in the template. In particular, for pulsars with stable S/Ns, the added template profile would have a much higher S/N than the single template. The main disadvantage is the risk of self-standarding (Hotan et al. 2005), which is due to the fact that noise in observations is correlated with their contributions in the template baseline. The impact of this effect is strongly dependent on the number of observations that is added to the template and on the S/N of the added observations (Hotan et al. 2005). Specifically, it has been found to be most relevant for pulsars in which the typical S/N is low (about ≲25) and in cases where fewer than several hundred observations are added together. The effect is also more problematic for strongly scintillating pulsars because the effective (i.e. S/N-weighted) number of added pulses tends to be smaller in this case.

Added with smoothing (henceforth “smoothed”). Here the added profile is taken as a basis and a smoothing filter is applied subsequently. Specifically, we used templates smoothed with the default wavelet-based smoothing algorithm of the PSRCHIVE/PSRSMOOTH routine (Demorest et al. 2013), that is, with an undecimated Daubechies wavelet with factor 8. The Daubechies wavelets are a family of orthogonal wavelets defining a discrete wavelet transform. The “undecimate” version of them is translation invariant, and the factor refers to the number of coefficients used (Daubechies 1992). Limited testing with variations in smoothing parameters and wavelets used indicated that these generally did not result in significantly different results for our analysis. The advantage of this approach is that the self-standarding issue should be removed as the noise in the template is largely suppressed, but this comes at the cost of a potential loss or suppression of sharp features in the pulse profile. An added complication is that smoothing algorithms can introduce artefacts in the template. The precise application of the smoothing algorithm could in itself be expanded to a far more extensive study, as results may also depend on the number of phase bins across a profile (i.e. the extent to which high-frequency profile features are resolved or not), but for the present work, we restrict ourselves to the most standard application of this method, in order to limit the dimensionality of our analysis.

Analytic profile (henceforth “analytic”). For this profile, von Mises functions (Jammalamadaka & Sengupta 2001; Evans et al. 2001) were fitted to the added profile. Because of the high S/N of the added profiles, dozens of components were typically required. Components were added and fitted interactively to avoid overfitting and to ensure as good a template profile as possible. This method has the clear advantage that the template profile is truly noise free, but often not all sharp features may be represented in the profile, either because they are misidentified as noise or because the analytic function cannot be indefinitely extended without affecting the stability and convergence of the least-squares fit. Consequently, self-standarding is of no concern, but timing precision may be compromised.

An illustration of how the different methods compare is included in Fig. 1, which shows the added templates derived from the NRT data for all three pulsars, as well as the profile differences comparing the added profile to the other three templates. As expected, the differences are mostly dominated by white noise, although the added-single difference does show coherent structure, in particular (although not exclusively) in the on-pulse phase range. This is likely caused by calibration issues, scintillation, or low-level RFI. The added-analytic difference is far better behaved, but here some non-white signals are visible as well, demonstrating the limitations of the von Mises functions in modelling pulse profile shapes. The added-smoothed difference is the closest to pure white noise for all three pulsars, indicating that the wavelet smoothing successfully removes noise and keeps structure. Nevertheless, even the smoothed template shows a minor deformation near the pulse peak of PSR J1713+0747. To which degree these discrepancies affect the timing of these pulsars is assessed in Sect. 5.1.

thumbnail Fig. 1.

Peak normalised added template profile and profile differences between the added and all other templates derived from NRT data. From top to bottom, shown are (a) PSRs J0218+4232, (b) J1713+0747, (c) J2145−0750.

We only used these templates in their frequency-averaged form, except for the analysis that focused on the most useful TOA bandwidth, which was based on an added template that was not frequency averaged. A comparative analysis of frequency-resolved analytic templates (as developed by Liu et al. 2014; Pennucci et al. 2014) is deferred to a separate study, given the inherent complexity and multi-dimensional analysis necessary for such work.

3.2. TOA determination methods

After creating a template profile, the TOA of a given observation can be determined by matching the observation to this template. Specifically, the observation 𝒪 can be related to the template 𝒯 as (Taylor 1992)

O ( ϕ ) = a + b T ( ϕ + τ ) + n ( ϕ ) , $$ \begin{aligned} \mathcal{O} (\phi ) = a+b\mathcal{T} (\phi +\tau )+n(\phi ), \end{aligned} $$

where ϕ is the rotational phase, a is an arbitrary offset, b is a scale factor, τ is the phase offset between observation and template, and n(ϕ) is a noise term. In order to solve for τ, a variety of possible approaches have been proposed. We compare three of the more commonly used methods, which are briefly described below.

Fourier phase gradient (PGS). The most common template-matching method used to date (and the default method used in the PSRCHIVE software package) is the so-called PGS method, described in detail by Taylor (1992). Based on the Fourier shift theorem, it matches the template to the observation by fitting for a slope in the Fourier space. A clear advantage of this approach is that the phase resolution does not impose a fundamental limit on the achievable measurement precision and therefore can result in significantly more precise measurements than time-domain cross-correlation methods (which, according to Taylor 1992, are limited to a precision about ten times lower than the data resolution). The main disadvantage of this method is that it underestimates the TOA uncertainty in the low-S/N regime because the TOA distribution no longer follows a Gaussian distribution (see the discussion in Arzoumanian et al. 2015, Appendix B).

Fourier domain with Markov chain Monte Carlo (FDM). One proposed solution to the underestimation of low-S/N TOA uncertainties is to probe the likelihood–phase shift dependence with a one-dimensional Markov chain Monte Carlo method, from which the TOA variance can be derived. This results in TOA values that are identical to those of the PGS method, but TOA uncertainties that are more realistic (i.e. larger), particularly for low-S/N observations.

Gaussian interpolation shift (GIS). This algorithm carries out a standard cross-correlation of the template and observation in the time domain and determines the phase offset by fitting a Gaussian to the cross-correlation function, whereby the centroid of the resulting Gaussian is defined as the TOA; the offset required to double the χ2 of the template-observation comparison is defined as the TOA uncertainty (Hotan et al. 2005). As mentioned above, this time-domain method has limited precision, but it was proposed as a more robust TOA determination method in the low-S/N regime. The application of a Gaussian in determining the peak position of the cross-correlation function should result in timing precision exceeding 10% of a phase bin, although this likely depends on the exact pulse shape.

3.3. TOA bandwidth and SWIMS

The most significant contribution to the TOA uncertainty is referred to as radiometer noise. For a certain telescope, according to the radiometer equation (for details, we refer to Appendix 1 of Lorimer & Kramer 2005), the radiometer noise, σrm, scales with bandwidth B, integration time T as

σ rm ∝ 1 TB · $$ \begin{aligned} \sigma _{\rm rm} \propto \frac{1}{\sqrt{TB}}\cdot \end{aligned} $$(1)

In general, the sensitivity of pulsar timing would increase with increasing observational bandwidth. However, as the TOA bandwidth increases, other noise sources become increasingly significant and the traditional approach of deriving TOAs from fully frequency-averaged observations can become increasingly complex, particularly if scintillation and profile evolution are significant.

At the other extreme, TOAs determined using native frequency resolution (referred to hereafter as fully frequency-resolved TOAs) significantly decreases the S/N, possibly leading to the low-S/N regime where some template-matching methods no longer provide reliable uncertainties; in addition, TOAs at native frequency resolution can substantially increase the data volume and hence the computational cost of timing analyses, particularly for wide-band systems. Consequently, there must be a most useful TOA bandwidth that maximises the TOA precision by limiting the deleterious effects of low S/N in fine frequency channels and those due to scintillation and profile evolution in frequency-averaged TOAs.

Here we have investigated such a most useful TOA bandwidth for a set of pulsar and backend combinations by quantifying the achievable timing precision as a function of the TOA bandwidth. To do this, we combined the best template-matching method with a frequency-resolved version of the optimal template profile and then carried out the timing of each pulsar and backend combination of our test dataset for a range of possible TOA bandwidths. This allowed us to investigate the improvement in the goodness of fit (of the timing model to the TOAs) via the reduced chi-squared of the linearised least-squares fit and the rms of the timing residuals, as well as the number of TOAs that remain after removing TOAs corresponding to total intensity profiles with S/N lower than 8, following Arzoumanian et al. (2015).

Radiometer noise is proportional to the square root of the TOA bandwidth, and jitter noise or SWIMS (Osłowski et al. 2011; Cordes & Downs 1985; Liu et al. 2012) behaves as a constant noise term, added in quadrature to the radiometer noise. The combined effect of profile evolution and scintillation strongly depends on the specific pulsar properties. Theoretically, this effect should become stronger with larger TOA bandwidths, but given the relatively narrow bandwidth of our data, it is likely to behave somewhat differently. In addition, a number of systematic effects (e.g. calibration errors or instrumental artefacts; see Verbiest & Shaifullah 2018, for a full review) are not expected to strongly depend on TOA bandwidth, although this would again be highly variable and dependent on the particular situation. In analysing the timing residual rms as a function of TOA bandwidth, we consequently do not expect the straightforward scaling of the radiometer noise (Eq. (1)), but expect a pulsar-dependent slope and likely some form of rms saturation at the widest bandwidths. We refer to the level of this rms saturation as the system-limited noise floor, or SLNF. Consequently, we quantify the residual rms as a function of TOA bandwidth as follows:

σ res = C B α T + σ NF 2 , $$ \begin{aligned} \sigma _{\mathrm{res} } = \sqrt{\frac{CB^{\alpha }}{T} + \sigma _{\mathrm{NF} }^2}, \end{aligned} $$(2)

where σres is the residual rms of the post-fit residuals, C is a constant, T is the integration time of the TOAs, B is the bandwidth of the TOAs, α is a scaling index that would be −1 in the case of pure radiometer noise, and σNF is the SLNF, that is, the part of the rms that does not scale with TOA bandwidth. This last term is mostly expected to quantify the impact of SWIMS2, but also comprises other effects as described above. An example of this dependence is shown in Fig. 2.

thumbnail Fig. 2.

A sketch of the dependence of σres on TOA bandwidth, for an idealised dataset. The black dots represent rms values, the blue dashed line indicates the median scintillation bandwidth and the red line is a fit of Eq. (2). The black line is for the case of pure radiometer noise, i.e. with no jitter or other corrupting noise sources (σNF = 0) and for standard scaling following the radiometer equation (α = −1).

While these considerations prevent a meaningful connection to the physical phenomenon of SWIMS, our analysis does allow a phenomenological determination of which TOA bandwidth optimally balances the various effects that impact the final timing rms.

4. Simulations

Because the analysis of real data is complex and multi-faceted, we first carried out some relatively straightforward simulations to gain information about a few key points of the subsequent analysis. Specifically, we used simulations to study how the TOA uncertainties from the various TOA determination methods scale with pulse S/N and to determine to which degree these results depend on the pulse shape. Furthermore, because these tests depend on the S/N that is used to place a cut-off to remove unreliable TOAs (in accordance with the advice of Arzoumanian et al. 2015), we also evaluated how well the standard S/N algorithm of the PSRCHIVE package can reproduce the simulated S/N.

These simulations were written in PYTHON using the NUMPY package and PSRCHIVE through its python interface. Specifically, noise-free templates were constructed with the PAAS routine of PSRCHIVE, after which white noise with varying intensity was added to these profiles. Here we tested five profile shapes as shown in the inset plots of Fig. 3: a simple Gaussian profile, a Gaussian profile with a sharp notch on its trailing edge, and finally, the analytic profiles derived for each of our three test pulsars, based on the NRT data described earlier.

thumbnail Fig. 3.

TOA uncertainty obtained from various noise-added profiles as a function of the simulated S/N. Top left panel: results for a simple Gaussian profile. Top right panel: results for a Gaussian profile with a notch. Bottom panels: results for the analytic templates of PSRs J0218+4232, J1713+0747, and J2145−0750, respectively, as derived from NRT data. CCAs are shown with different colours and markers, as indicated in the legend. The solid black line in each panel is a fit to high-S/N (> 10) FDM data and is extended to low-S/N data. At each S/N we plot, ten simulations were run, although they are typically indistinguishable at high S/N. The inset within each panel shows the profile. (a) Simple Gaussian profile. (b) Gaussian profile with a narrow notch. (c) PSR J0218+4232. (d) PSR J1713+0747. (e) PSR J2145−0750.

Ideally, according to the radiometer equation, the TOA uncertainty should follow an inverse relation with S/N in the form of 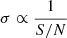σ ∝ 1 S / N $ \sigma \propto \frac{1}{S/N} $. Figure 3 shows that PGS and FDM are consistent with each other in most cases and follow this scaling in the high-S/N regime, although a minor deviation in the slope of the PGS curve can be identified for PSR J0218+4232. However, if the S/N is low, that is, lower than ∼10, the difference between FDM and PGS becomes more explicit, although the exact threshold S/N strongly depends on the pulse shape: for the complex profile shapes of PSRs J1713+0747 and J2145−0750, the curves coincide at lower S/Ns. For the simple Gaussian or Gaussian-with-notch profiles, the discrepancies are clearer even at S/N = 10. These results clearly show that PGS typically underestimates the TOA uncertainties in the low- to medium-S/N regime, although the degree of underestimation strongly depends on the profile shape. In contrast, FDM displays a tendency to overestimate the TOA uncertainties in the same S/N regime, primarily for pulse profiles with sharp features.

It is furthermore evident that GIS fails to determine the uncertainty correctly in the low-S/N and high-S/N regimes, except for a very narrow region. Similar to the results from Hotan et al. (2005), our simulations show that GIS works better in the low-S/N regime, and the range of good performance is wider for pulsars with a long duty cycle. Nevertheless, our simulations suggest that the uncertainties are consistently underestimated, even at low S/Ns. This difference may be partly related to the S/N of the template that was used, which we made unrealistically high to more clearly demonstrate the trends independen of template. However, the complexity of the pulse profile shape also clearly has a significant impact, as already anticipated by Hotan et al. (2005). For profiles with narrow features, our simulations for GIS show that the TOA uncertainty flattens off for S/Ns above a few tens, indicating a significant overestimation of the uncertainties for high-S/N observations.

Figure 4 shows the results of our consistency check on the S/N values returned by PSRCHIVE. Because the exact S/N depends on the precise definition that was used and on the pulse shape, no exact equivalence can be expected between the simulations and the measurements, but a linear relation should exist. Our results show that this linear relation does indeed describe most of the simulated S/N range, but this flattens off below an S/N of ∼10, where the S/N returned by PSRCHIVE is mostly unrelated to the actual simulated S/N. While the details of this figure and particularly the scaling at high-S/N differ between the various pulse profiles we tested, the flattening off below a S/N of ten is persistent.

thumbnail Fig. 4.

S/N determined with the standard implementation in PSRCHIVE as a function of simulated S/N. The blue points are the S/N of the individual simulations, and the red points indicate the median value of the simulations. The red error bars indicate the 25th and 75th percentiles at each real S/N. For this simulation, the analytic template based on NRT data of PSR J2145−0750 was used. Due to differences in the definition of the S/N, some inconsistencies between x and y values are expected, although the scaling should be linear, as is the case in the high-S/N regime. In the low S/N regime (S/N < 10), the S/Ns returned by PSRCHIVE are typically overestimated and have a significant random component. (The thick black lines indicate S/Ns of 8, which is used as an S/N cut-off value in this work, following Arzoumanian et al. 2015).

A consequence of this test lies in the interpretation of Fig. 3: while for some pulsars, the TOA uncertainties from FDM and PGS appear reliable down to an S/N of approximately five, in practice, it is not possible to reliably measure S/Ns below ten. Consequently, in order to reliably identify TOAs with reliable error bars, a cut-off at an S/N of about ten may be required in any case, which could cause any difference between PGS and FDM to become irrelevant for a wide range of pulse shapes. (In contrast, Fig. 3c indicates that for pulse shapes with particularly long duty cycles, the differences may persist even above a S/N of ten).

5. Results and discussion

To evaluate the timing precision as a function of the choice of template and CCA described in Sects. 3.1 and 3.2 and to study the most useful TOA bandwidth as described in Sect. 3.3, we analysed the TOAs with the timing models presented by Desvignes et al. (2016) and Chen et al. (2021). For PSR J1713+0747, we adopted the entire timing model of Chen et al. (2021), including DM and red noise models. For PSRs J0218+4232 and J2145−0750, we used the timing models from Desvignes et al. (2016), but did not include red noise or DM models. In the timing models of Desvignes et al. (2016), the planetary ephemerides were updated to DE438 and the reference clock was updated to TT(BIPM2019).

5.1. Template and CCA

For each combination of the templates and CCAs described in Sect. 3, we performed a TEMPO2 (Edwards et al. 2006; Hobbs et al. 2006) analysis, fitting only for the pulsar spin and its first derivative. For each fit, the reduced-χ2 and the residual rms value were recorded, along with the resulting timing residuals.

Figure 5 presents a pulsar and telescope-wise analysis of the timing performance. Here the poor performance of the GIS TOAs is clearly visible in all systems. Furthermore, it is evident that FDM and PGS results often cluster for the two stronger sources, with generally almost identical reduced-χ2 and rms values independent of the template creation method. This shows that the effect of template choice can be somewhat mitigated for these sources when these CCAs are used. Finally, when FDM and PGS do differ, FDM tends to outperform PGS, particularly in terms of the reduced-χ2 values obtained.

thumbnail Fig. 5.

Reduced-χ2 and residual rms for the three pulsars as a function of the selected CCA and template and the different telescopes. The dashed line indicates a reduced-χ2 of 1, and the red stars represent results from Desvignes et al. (2016).

Figure 5 also shows that for faint pulsars like PSR J0218+4232, the high noise levels in the single template severely compromise the results. In this case, even the added template shows poor results when combined with the PGS method, indicating that some level of self-standarding (as described by Hotan et al. 2005) may be at work. However, the FDM method appears to be far more robust to this phenomenon.

The timing residuals for each of the TOA sets were further assessed to determine unmodelled signals or persistent outlier TOAs. Using a two-tailed Kolmogorov-Smirnov test, we compared the power spectrum of these residuals against a power spectrum consisting of purely Gaussian or power-law signals, or a combination of both. We find that the power spectra of the timing residuals for all three pulsars are Gaussian or a Gaussian and power-law mixed distribution, suggesting that the updated timing models are sufficient given our data (i.e. the timing-model parameters that were not refitted model the TOAs sufficiently well for clear timing signatures to be absent from the data). Visual inspection of the timing residuals confirms that the timing residuals of PSRs J0218+4232 and J2145−0750 are essentially white. The timing residuals of PSR J1713+0747 still show some timing-noise signal that is not sufficiently modelled. This feature is mostly a consequence of a so-called “event”, which is known to be hard to model with standard red-noise models (Lam et al. 2018; Arzoumanian et al. 2020).

The remaining structure in the TOAs of PSR J1713+0747 results in some non-unity reduced-χ2 values, although the temporal nature of this feature causes different telescope sub-sets to be affected to different degrees. The significantly elevated reduced-χ2 values in the PSR J2145−0750 EFF and Nançcay data are likely due to a few highly precise TOAs that are affected by the solar wind (Tiburzi et al. 2021).

As a reference point for comparison, the reduced-χ2 and rms values obtained by Desvignes et al. (2016) are shown by a red star. Even though their analysis was based on a combined analysis of all four telescopes, spanned a different date range, used data from older observing systems, and fitted for all timing-model parameters, our results largely agree with this, although our timing precision tends to be slightly better, as expected.

5.2. TOA bandwidth

For each pulsar, the timing performance as a function of the TOA bandwidth was assessed using TOAs created with the ‘added’ template with the FDM CCA by splitting the archives into multiple channels. (In doing so, the template was split into the same number of channels, implying that each channel was timed against a template at its own frequency). The exact choice of the number of channels is specific to the telescope to accommodate the different bandwidths. At the EFF, the NRT, and the WSRT, the fully frequency-resolved archives were first averaged down to 32 channels and subsequently averaged down by factors of two. Because the native resolution at Jodrell Bank is different, the JBO data were first averaged down to 40 channels (or fewer) and were subsequently averaged down by factors of either 2.5 or 2.

Following the method described in Sect. 3.3, a standard TEMPO2 timing analysis was carried out for each choice of the number of channels, fitting for the same timing parameters as in Sect. 3 (i.e. pulse period and period derivative), along with DM and DM derivatives for frequency-resolved data. The resulting rms for each pulsar and telescope is plotted in Fig. 6.

thumbnail Fig. 6.

SLNF estimates for the three pulsars when the added template with the FDM CCA is used to generate the TOA with the available bandwidth at each telescope divided into the respective number of channels. The shaded regions along the fitted curves are the interquartile ranges for the fit, representing the error bounds on the estimated SLNF. The grey vertical bands show the expected scintillation bandwidth, estimated from the same data set as we present here (Liu et al. 2021). (a) SLNF estimates for PSR J0218+4232. (b) SLNF estimates for PSR J1713+0747. (c) SLNF estimates for PSR J2145−0750.

These plots show that the telescope-dependent rms that can be achieved decreases asymptotically as a function of the TOA bandwidth down to the SLNF, as shown by the fit lines in Fig. 6. A combination of factors influence this limit on the minimum rms.

For PSR J0218+4232, where the overall S/N of the profile continuously increases with greater channel bandwidth, the overall timing rms also continuously decreases. There does appear to be some sign of flattening, so that beyond ∼500 MHz, the rms may start to approach the SLNF.

Although PSR J0218+4232 is known to exhibit large amplitude pulses (Joshi et al. 2004), we do not find a significant influence of these pulses in our data because of the extended integration lengths, which imply averaging over several million pulses for each TOA.

For PSRs J1713+0747 and J2145−0750, we find clearer signs of flattening in the rms curves, indicating that fully averaging the TOAs across bandwidth may be unwise in these cases. Specifically, very little gain is made when averaging over more than ∼100 MHz TOA bandwidth.

As described in Sect. 3.3, these SLNFs include a variety of effects, including system and band noise as defined in Lentati et al. (2016), for example, and effects due to scintillation. Consequently, it might be considered that the most useful TOA bandwidth may depend on the scintillation bandwidth of the pulsar in question. However, this does not appear to be the case for our sample: PSR J0218+4232 has a scintillation bandwidth well below our finest resolution, while PSRs J1713+0747 and J2145−0750 have bandwidths that are probed by our analysis, but the behaviour of the curves does not significantly differ near the bandwidth range of the scintillation. A full investigation of the SLNF is beyond the scope of this paper, but would be in line with earlier analyses such as those by Lam et al. (2016) and Dolch et al. (2018).

6. Conclusions

We investigated the relative merits of three common TOA determination methods and four ways of generating timing templates by means of comparing their impact on the timing residuals and reduced-χ2 value for data sets from four different telescopes on three different pulsars. In addition, we checked how the timing rms reaches a plateau as TOA bandwidth is increased. This plateau or SLNF consists of a variety of factors, including SWIMS, instrumental noise, and timing noise. We also showed that it strongly depends on the telescope and pulsar in question.

With regard to the choice of the template generation scheme, we find that the single brightest observation leads to the worst timing performance. For the brighter pulsars, the added, smoothed and analytic templates lead to comparable minimum timing rms and red χ2, but for the lower S/N PSR J0218+4232, added templates can perform worse than the smoothed and analytical templates.

The analysis presented above also upholds the recommendation of Verbiest et al. (2016) that the CCA of choice for high-precision PTA work is the FDM method, although the PGS method is similarly reliable. In all pulsar, telescope, and backend combinations tested above, we find that FDM and PGS TOAs lead to the most reliable TOAs and TOA uncertainties, although in the low-S/N regime, both methods suffer systematic issues. Based on our finding that PGS TOAs may be as reliable as FDM-based ones, particularly for bright pulsars, a re-analysis of archival data for which PGS TOAs may already be available may well not be warranted. In some cases, particularly when noisy templates are used, FDM clearly outperforms PGS in terms of the reliability of TOA uncertainties.

In addition, we find that GIS-derived TOAs are not suitable for high-precision timing, leading to conservative timing models and a loss of model parameter sensitivity. Using the FDM CCA with added templates, we find that the most useful TOA bandwidth for minimising the achievable timing residual rms is mostly dependent on the pulsar brightness and instrumental sensitivity. For the sample studied here, fully frequency-averaged TOAs seem advantageous for the relatively faint PSR J0218+4232, whereas significantly narrower bandwidths seem optimal for the two brighter pulsars in our sample.

1

Whilst technically, it is accurate to refer to CCAs uniquely in terms of their TOA determination, throughout this paper we refer to cross-correlation methods in terms of their TOA and TOA uncertainty determination. This is in line with how these algorithms are used in practice and recognises the practical constraint that measurements and their uncertainties must be inextricably linked. Mathematically speaking, the pure TOA-determination algorithms of FDM and PGS are therefore identical, but the cross-correlation methods (which we consider to include the measurement uncertainty as well) will be considered different.

2

For the relatively limited fractional bandwidths considered in this work, the impact of SWIMS cannot be expected to depend on TOA bandwidth (Sallmen et al. 1999).

Acknowledgments

The EPTA is a multinational European collaboration, which consists ASTRON (NL), INAF/Osservatorio Astronomico di Cagliari (IT), Max-Planck-Institut für Radioastronomie (GER), Observatoire de Paris/Nançay(FRA), the University of Manchester (UK), the University of Birmingham (UK), the University of Cambridge (UK) and the University of Bielefeld (GER). J.W. acknowledges support from the China scholarship council. J.P.W.V. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG) through the Heisenberg programme (Project No. 433075039). Part of this work is based on observations obtained the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg. Pulsar research at the Jodrell Bank Centre for Astrophysics and the observations using the Lovell Telescope is supported by a consolidated grant from the STFC in the UK. The Nançay Radio Observatory is operated by the Paris Observatory, associated with the French Centre National de la Recherche Scientifique (CNRS). We acknowledge financial support from the Action Fédératrice PhyFOG funded by Paris Observatory and from the “Programme National Gravitation, Références, Astronomie, Métrologie” (PNGRAM) funded by CNRS/INSU and CNES, France. The Westerbork Synthesis Radio Telescope is operated by the Netherlands Institute for Radio Astronomy (ASTRON) with support from The Netherlands Foundation for Scientific Research NWO.

References

  1. Alam, M. F., Arzoumanian, Z., Baker, P. T., et al. 2021a, ApJS, 252, 4 [Google Scholar]
  2. Alam, M. F., Arzoumanian, Z., Baker, P. T., et al. 2021b, ApJS, 252, 5 [Google Scholar]
  3. Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
  4. Archibald, A. M., Gusinskaia, N. V., Hessels, J. W. T., et al. 2018, Nature, 559, 73 [Google Scholar]
  5. Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., et al. 2014, ApJ, 794, 141 [NASA ADS] [CrossRef] [Google Scholar]
  6. Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., et al. 2015, ApJ, 813, 65 [NASA ADS] [CrossRef] [Google Scholar]
  7. Arzoumanian, Z., Baker, P. T., Brazier, A., et al. 2018a, ApJ, 859, 47 [NASA ADS] [CrossRef] [Google Scholar]
  8. Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., et al. 2018b, ApJS, 235, 37 [CrossRef] [Google Scholar]
  9. Arzoumanian, Z., Baker, P. T., Blumer, H., et al. 2020, ApJ, 905, L34 [NASA ADS] [CrossRef] [Google Scholar]
  10. Backer, D. C., Kulkarni, S. R., Heiles, C., Davis, M. M., & Goss, W. M. 1982, Nature, 300, 615 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bailes, M., Harrison, P. A., Lorimer, D. R., et al. 1994, ApJ, 425, L41 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [Google Scholar]
  13. Burke-Spolaor, S., Taylor, S. R., Charisi, M., et al. 2019, A&ARv, 27, 5 [Google Scholar]
  14. Caballero, R. N., Guo, Y. J., Lee, K. J., et al. 2018, MNRAS, 481, 5501 [Google Scholar]
  15. Champion, D. J., Hobbs, G. B., Manchester, R. N., et al. 2010, ApJ, 720, L201 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chen, S., Caballero, R. N., Guo, Y. J., et al. 2021, MNRAS, 508, 4970 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cognard, I., Theureau, G., & Guillemot, L. 2013, SF2A-2013: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, 327 [Google Scholar]
  18. Cordes, J. M., & Downs, G. S. 1985, ApJS, 59, 343 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dai, S., Hobbs, G., Manchester, R. N., et al. 2015, MNRAS, 449, 3223 [NASA ADS] [CrossRef] [Google Scholar]
  20. Daubechies, I. 1992, Ten Lectures on Wavelets (Philadelphia: SIAM) [CrossRef] [Google Scholar]
  21. Demorest, P. B., Ferdman, R. D., Gonzalez, M. E., et al. 2013, ApJ, 762, 94 [Google Scholar]
  22. Desvignes, G., Caballero, R. N., Lentati, L., et al. 2016, MNRAS, 458, 3341 [Google Scholar]
  23. Dolch, T., NANOGrav Collaboration, Chatterjee, S., et al. 2018, J. Phys. Conf. Ser., 957, 012007 [NASA ADS] [CrossRef] [Google Scholar]
  24. Donner, J. Y., Verbiest, J. P. W., Tiburzi, C., et al. 2019, A&A, 624, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. DuPlain, R., Ransom, S., Demorest, P., et al. 2008, in Advanced Software and Control for Astronomy II, eds. A. Bridger, & N. M. Radziwill, SPIE Conf. Ser., 7019, 70191D [NASA ADS] [CrossRef] [Google Scholar]
  26. Edwards, R. T., Hobbs, G. B., & Manchester, R. N. 2006, MNRAS, 372, 1549 [Google Scholar]
  27. Evans, M., Hastings, N., & Peacock, B. 2001, Statistical Distributions (New York: Wiley) [Google Scholar]
  28. Foster, R. S., & Backer, D. C. 1990, ApJ, 361, 300 [NASA ADS] [CrossRef] [Google Scholar]
  29. Foster, R. S., Wolszczan, A., & Camilo, F. 1993, ApJ, 410, L91 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gentile, P. A., McLaughlin, M. A., Demorest, P. B., et al. 2018, ApJ, 862, 47 [NASA ADS] [CrossRef] [Google Scholar]
  31. Han, J. L., Manchester, R. N., van Straten, W., & Demorest, P. 2018, ApJS, 234, 11 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hobbs, G. B., Edwards, R. T., & Manchester, R. N. 2006, MNRAS, 369, 655 [Google Scholar]
  33. Hobbs, G., Coles, W., Manchester, R. N., et al. 2012, MNRAS, 427, 2780 [NASA ADS] [CrossRef] [Google Scholar]
  34. Hobbs, G., Guo, L., Caballero, R. N., et al. 2020, MNRAS, 491, 5951 [Google Scholar]
  35. Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [Google Scholar]
  36. Hotan, A. W., Bailes, M., & Ord, S. M. 2005, MNRAS, 362, 1267 [NASA ADS] [CrossRef] [Google Scholar]
  37. Jammalamadaka, S. R., & Sengupta, A. 2001, Topics in Circular Statistics (Singapore: World Scientific Publishing), 5 [CrossRef] [Google Scholar]
  38. Janssen, G. H., Stappers, B. W., Kramer, M., et al. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 633 [Google Scholar]
  39. Jenet, F. A., Hobbs, G. B., Lee, K. J., & Manchester, R. N. 2005, ApJ, 625, L123 [NASA ADS] [CrossRef] [Google Scholar]
  40. Joshi, B. C., Kramer, M., Lyne, A. G., McLaughlin, M. A., & Stairs, I. H. 2004, in IAU Symposium, eds. F. Camilo, & B. M. Gaensler, 319 [Google Scholar]
  41. Karuppusamy, R., Stappers, B., & van Straten, W. 2008, PASP, 120, 191 [NASA ADS] [CrossRef] [Google Scholar]
  42. Keith, M. J., Coles, W., Shannon, R. M., et al. 2013, MNRAS, 429, 2161 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kerr, M., Reardon, D. J., Hobbs, G., et al. 2020, PASA, 37, e020 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kramer, M., Xilouris, K. M., Lorimer, D. R., et al. 1998, ApJ, 501, 270 [Google Scholar]
  45. Lam, M. T., Cordes, J. M., Chatterjee, S., et al. 2016, ApJ, 819, 155 [Google Scholar]
  46. Lam, M. T., Ellis, J. A., Grillo, G., et al. 2018, ApJ, 861, 132 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lazarus, P., Karuppusamy, R., Graikou, E., et al. 2016, MNRAS, 458, 868 [Google Scholar]
  48. Lentati, L., Shannon, R. M., Coles, W. A., et al. 2016, MNRAS, 458, 2161 [Google Scholar]
  49. Levin, L., McLaughlin, M. A., Jones, G., et al. 2016, ApJ, 818, 166 [NASA ADS] [CrossRef] [Google Scholar]
  50. Liu, K., Keane, E. F., Lee, K. J., et al. 2012, MNRAS, 420, 361 [NASA ADS] [CrossRef] [Google Scholar]
  51. Liu, K., Desvignes, G., Cognard, I., et al. 2014, MNRAS, 443, 3752 [NASA ADS] [CrossRef] [Google Scholar]
  52. Liu, Y., Verbiest, J., Main, R., et al. 2021, A&A, submitted [Google Scholar]
  53. Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy (Cambridge: Cambridge University Press) [Google Scholar]
  54. Manchester, R. N., Hobbs, G., Bailes, M., et al. 2013, PASA, 30, 17 [CrossRef] [Google Scholar]
  55. Navarro, J., de Bruyn, G., Frail, D., Kulkarni, S. R., & Lyne, A. G. 1995, ApJ, 455, L55 [NASA ADS] [Google Scholar]
  56. Nita, G. M., Gary, D. E., Liu, Z., Hurford, G. J., & White, S. M. 2007, PASP, 119, 805 [Google Scholar]
  57. Osłowski, S., van Straten, W., Hobbs, G. B., Bailes, M., & Demorest, P. 2011, MNRAS, 418, 1258 [CrossRef] [Google Scholar]
  58. Pennucci, T. T., Demorest, P. B., & Ransom, S. M. 2014, ApJ, 790, 93 [NASA ADS] [CrossRef] [Google Scholar]
  59. Perera, B. B. P., DeCesar, M. E., Demorest, P. B., et al. 2019, MNRAS, 490, 4666 [Google Scholar]
  60. Romani, R. W. 1989, in Timing Neutron Stars, eds. H. Ögelman, & E. P. J. van den Heuvel (Dordrecht: Kluwer), 113 [CrossRef] [Google Scholar]
  61. Sallmen, S., Backer, D. C., Hankins, T. H., Moffett, D., & Lundgren, S. 1999, ApJ, 517, 460 [NASA ADS] [CrossRef] [Google Scholar]
  62. Shannon, R. M., & Cordes, J. M. 2012, ApJ, 761, 64 [NASA ADS] [CrossRef] [Google Scholar]
  63. Shannon, R. M., Ravi, V., Lentati, L. T., et al. 2015, Science, 349, 1522 [NASA ADS] [CrossRef] [Google Scholar]
  64. Stairs, I. H., Thorsett, S. E., & Camilo, F. 1999, ApJS, 123, 627 [NASA ADS] [CrossRef] [Google Scholar]
  65. Taylor, J. H. 1992, Phil. Trans. R. Soc. London A, 341, 117 [NASA ADS] [CrossRef] [Google Scholar]
  66. Taylor, J. H., & Weisberg, J. M. 1982, ApJ, 253, 908 [NASA ADS] [CrossRef] [Google Scholar]
  67. Tiburzi, C. 2018, PASA, 35, e013 [Google Scholar]
  68. Tiburzi, C., Hobbs, G., Kerr, M., et al. 2016, MNRAS, 455, 4339 [Google Scholar]
  69. Tiburzi, C., Shaifullah, G. M., Bassa, C. G., et al. 2021, A&A, 647, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Vallisneri, M., Taylor, S. R., Simon, J., et al. 2020, ApJ, 893, 112 [Google Scholar]
  71. van Straten, W. 2006, ApJ, 642, 1004 [NASA ADS] [CrossRef] [Google Scholar]
  72. van Straten, W., & Bailes, M. 2011, PASA, 28, 1 [Google Scholar]
  73. van Straten, W., Demorest, P., & Oslowski, S. 2012, Astron. Res. Technol., 9, 237 [NASA ADS] [Google Scholar]
  74. Verbiest, J. P. W., & Shaifullah, G. 2018, Classical Quantum Gravity, 35, 133001 [NASA ADS] [CrossRef] [Google Scholar]
  75. Verbiest, J. P. W., Lentati, L., Hobbs, G., et al. 2016, MNRAS, 458, 1267 [Google Scholar]
  76. Voisin, G., Cognard, I., Freire, P. C. C., et al. 2020, A&A, 638, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Basic parameters for the pulsars in our sample.

In the text
Table 2.

Description of the observational set-up for the data used in this paper.

In the text
Table 3.

Summary of the observations used in this paper.

In the text

All Figures

thumbnail Fig. 1.

Peak normalised added template profile and profile differences between the added and all other templates derived from NRT data. From top to bottom, shown are (a) PSRs J0218+4232, (b) J1713+0747, (c) J2145−0750.
In the text
thumbnail Fig. 2.

A sketch of the dependence of σres on TOA bandwidth, for an idealised dataset. The black dots represent rms values, the blue dashed line indicates the median scintillation bandwidth and the red line is a fit of Eq. (2). The black line is for the case of pure radiometer noise, i.e. with no jitter or other corrupting noise sources (σNF = 0) and for standard scaling following the radiometer equation (α = −1).
In the text
thumbnail Fig. 3.

TOA uncertainty obtained from various noise-added profiles as a function of the simulated S/N. Top left panel: results for a simple Gaussian profile. Top right panel: results for a Gaussian profile with a notch. Bottom panels: results for the analytic templates of PSRs J0218+4232, J1713+0747, and J2145−0750, respectively, as derived from NRT data. CCAs are shown with different colours and markers, as indicated in the legend. The solid black line in each panel is a fit to high-S/N (> 10) FDM data and is extended to low-S/N data. At each S/N we plot, ten simulations were run, although they are typically indistinguishable at high S/N. The inset within each panel shows the profile. (a) Simple Gaussian profile. (b) Gaussian profile with a narrow notch. (c) PSR J0218+4232. (d) PSR J1713+0747. (e) PSR J2145−0750.
In the text
thumbnail Fig. 4.

S/N determined with the standard implementation in PSRCHIVE as a function of simulated S/N. The blue points are the S/N of the individual simulations, and the red points indicate the median value of the simulations. The red error bars indicate the 25th and 75th percentiles at each real S/N. For this simulation, the analytic template based on NRT data of PSR J2145−0750 was used. Due to differences in the definition of the S/N, some inconsistencies between x and y values are expected, although the scaling should be linear, as is the case in the high-S/N regime. In the low S/N regime (S/N < 10), the S/Ns returned by PSRCHIVE are typically overestimated and have a significant random component. (The thick black lines indicate S/Ns of 8, which is used as an S/N cut-off value in this work, following Arzoumanian et al. 2015).
In the text
thumbnail Fig. 5.

Reduced-χ2 and residual rms for the three pulsars as a function of the selected CCA and template and the different telescopes. The dashed line indicates a reduced-χ2 of 1, and the red stars represent results from Desvignes et al. (2016).
In the text
thumbnail Fig. 6.

SLNF estimates for the three pulsars when the added template with the FDM CCA is used to generate the TOA with the available bandwidth at each telescope divided into the respective number of channels. The shaded regions along the fitted curves are the interquartile ranges for the fit, representing the error bounds on the estimated SLNF. The grey vertical bands show the expected scintillation bandwidth, estimated from the same data set as we present here (Liu et al. 2021). (a) SLNF estimates for PSR J0218+4232. (b) SLNF estimates for PSR J1713+0747. (c) SLNF estimates for PSR J2145−0750.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.