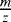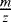EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 657 (January 2022) A&A, 657 (2022) A100 Full HTML
Free Access
Issue
A&A
Volume 657, January 2022
Article Number A100
Number of page(s) 12
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202141861
Published online 19 January 2022

© ESO 2022

1 Introduction

Sulfur is an important element for life as we know it, and its chemistry is particularly relevant for linking interstellar clouds to star-forming regions, to protoplanetary disks and stellar systems such as our own. S-bearing molecules are frequently used to trace the kinematics and the chemical evolution of star-forming (e.g., Zhou et al. 1993; Wakelam et al. 2004) and planet-forming (e.g., Dutrey et al. 1997; Le Gal et al. 2019) regions. Several S-bearing species have recently been detected in the coma of comet 67P (Calmonte et al. 2016). There is a big problem related to sulfur chemistry, however, which was first recognized in the early 1970s: it is not yet clear in which form most of the sulfur resides in molecular clouds. While cosmic abundances of ionized sulfur are found in diffuse clouds (Jenkins 2009), the abundance of CS, the most abundant S-bearing molecule in molecular clouds, cannot be reproduced by astrochemical models, unless the S abundance in the gas phase is reduced by several orders of magnitude (e.g., Penzias et al. 1971; Oppenheimer & Dalgarno 1974; Hasegawa et al. 1992; Bulut et al. 2021).

Several attempts have been made in the past to shed light on the missing sulfur problem in molecular clouds. Caselli et al. (1994) considered the possibility that most of the S in molecular clouds resides on the surface of dust grains; if this is the case, the rapid formation of H2S and the production of H2 from the H2S+H reaction in the ice create a sink of H atoms, which could also explain the very slow conversion of CO ice in CH3OH, which is indeed only observed in dense cores of molecular clouds and star-forming regions (e.g., Boogert et al. 2015; Goto et al. 2021). However, only upper limits have been measured for H2S in ice (e.g., Smith 1991; van der Tak et al. 2003; Jiménez-Escobar & Muñoz Caro 2011), thus excluding that the majority of solid S is in H2S form. Ruffle et al. (1999) proposed that most of the S depletion happens in translucent clouds, where S atoms are still mainly in atomic ionized form (see also Sternberg & Dalgarno 1995), while the dust grains are mainly negatively charged. In this scenario the Coulomb-enhanced freeze-out rate of S+ will rapidly deplete sulfur from the gas phase (see also Umebayashi & Nakano 1980, for generic cations). Vidal et al. (2017) compared their astrochemical modeling results to observations toward the TMC-1(CP) dark cloud and concluded that, depending on the cloud age, most of the sulfur could be either in the not observable atomic form or on HS and H2S in solid form. Laas & Caselli (2019) expanded the chemistry of sulfur by including S-bearing organic molecules and the Ruffle et al. (1999) freeze-out mechanism; they found a good agreement with observations in molecular clouds and concluded that the majority of S is trapped in organo-sulfur species in icy mantles of dust grains.

In laboratory experiments where H2S ice is irradiated either with UV photons or energetic particles (proxy for the interstellar cosmic rays), it has been found that a significant fraction of H2S can be transformed in allotropic forms of S, including the most stable form S8 (e.g., Jiménez-Escobar & Muñoz Caro 2011; Jiménez-Escobar et al. 2014). This has also been confirmed theoretically by Shingledecker et al. (2020) using astrochemical models inclusive of radiation chemistry; interestingly, these models predict that the impact of energetic particles in H2S-rich ices reduces the abundance of H2S, while enhancing SO2, OCS, and S8. The first interstellar molecule containing more than one S atom (S2H) was detected recently by Fuente et al. (2017) toward the Horsehead photodissociation region, suggesting an interesting interplay between gas-phase and surface chemistry. The GEMS large project (Rodríguez-Baras et al. 2021) at the IRAM 30 m telescope is also providing important observational constraints on sulfur chemistry in molecular clouds; for example, Navarro-Almaida et al. (2020) measured gas-phase H2S across several sources, finding good agreement with chemical models assuming non-depleted S abundances, but which highly overestimate the CS abundance. With the ROSINA instrument on board Rosetta, Calmonte et al. (2016) measured a variety of S-bearing molecules in comet 67P that appear to preserve pre-stellar ice (Altwegg et al. 2019; Drozdovskaya et al. 2019, 2021): the majority of S is in H2S ice (about 57%), followed by atomic S, SO2, SO, OCS, H2CS, CH3SH, CS2, S2, and other S-bearing organics.

Despite the many observations and chemical models available, there are still many open questions about sulfur chemistry in the interstellar medium: What happens to S atoms when adsorbed onto dust grains in translucent and molecular clouds? What is the chemistry of irradiated H2S ice? What fraction of sulfur atoms will form chains? Which S-bearing molecules should be observed to test the models? In this paper we focus our attention on detailed experimental work and its simulation with a Monte Carlo chemical model, with the aim of putting quantitative constraints on the S depletion and chemical processing in translucent and molecular clouds.

The paper is structured as follows. Section 2 describes the laboratory experiments and Sect. 3 presents the results of the experimental work. The Monte Carlo simulations are described in Sect. 4. Section 5 discusses photoprocesses of H2S ice in simulations and experimental work, while applications to interstellar molecular clouds and to Solar System conditions can be found in Sects. 6 and 7, respectively. Our conclusions are presented in Sect. 8.

2 Experiments: H2S irradiation with UV photons

The experimental results presented here were obtained using the InterStellar Astrochemistry Chamber (ISAC) at the Centro de Astrobiología (Muñoz Caro et al. 2010). ISAC is an ultra-high vacuum (UHV) chamber with a base pressure dominated by background H2 in the range P = 2.5−4.0 × 10−11 mbar, which corresponds to dense cloud interiors. H2S ice samples were grown by accretion of gas molecules onto the tip of a cold finger at 8 K, where a MgF2 infrared (IR) and ultraviolet (UV) transparent window served as the substrate for deposition. This temperature was achieved by means of a closed-cycle helium cryostat. The samples were then warmed up until complete sublimation was attained. A silicon diode temperature sensor and a LakeShore Model 331 temperature controller were used, reaching an accuracy of about 0.1 K.

The evolution of the solid sample was monitored by in situ transmittance Fourier transform infrared (FTIR) spectroscopy with a spectral resolution of2 cm−1. Column densities of each species in the ice were calculated from the IR spectra using the formula 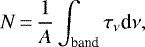(1)

where N is the column density in cm−2, τν the optical depth of the band, dν the wavenumber differential in cm−1, and A the band strength in cm molecule−1. The integrated absorbance is equal to 0.43 × τ, where τ is the integrated optical depth of the band. The adopted band strengths A derived from laboratory experiments are provided in Table 1.

The accretion rate measured by IR spectroscopy of the deposited ice was 1 ML s−1. Samples were UV irradiated using a microwave-discharge hydrogen-flow lamp (MDHL) that provides a flux of 2.5 ×1014 photons cm−2 s−1 at the sample position with an average photon energy of 8.6 eV. The MDHL spectrum is reported in Cruz-Diaz et al. (2014). The UV spectra were measured routinely in situ during the experiments with the use of a McPherson 0.2 m focal length VUV monochromator (Model 234/302) with a photomultiplier tube (PMT) detector equipped with a sodium salicylate window, optimized to operate in the range 100–500 nm (11.27–2.47 eV), with a spectral resolution of 0.4 nm. The UV absorption spectra of H2S ice samples served to monitor the detection of photoproducts generated upon UV irradiation at 8 K or later during warm-up. For more detailson the experimental protocol employed for VUV spectroscopy, see Cruz-Diaz et al. (2014).

Table 1

Photodissociation reactions with associated rates considered in the present study.

3 Experimental results

As reported by Jiménez-Escobar & Muñoz Caro (2011), thermal processing of H2S ice leads to crystallization at temperatures above 40 K. This process reduces the number of randomly oriented molecules and the vibration modes become narrower, see inset of Fig. 1, which agrees with Fig. 1 in Jiménez-Escobar & Muñoz Caro (2011). The antisymmetric and symmetric vibrations appear at 2553 and 2530 cm−1, respectively.The remaining amorphous domains are responsible for the IR band centered at 2538 cm−1.

thumbnail Fig. 1

Evolution of the H2S band strength as a function of temperature. Above 70 K thermal desorption becomes important, reducing H2S column density and preventing the quantification of the band strength.

3.1 Photoproduct formation in UV irradiated H2S ice

Ultraviolet irradiation of H2S ice samples produces HS⋅ radicals very readily, according to Reaction (2). HS⋅ radicals canalso react with hydrogen atoms in the backward reaction to reform the original H2S molecule. IR spectroscopy shows that H2S is dissociated during the first steps of UV irradiation when the recombination to form H2S is inhibited, which is a consequence of the low abundance of HS⋅ radicals. For larger irradiation periods, however, H2S recombination takes place, and reduces the overall H2S dissociation: 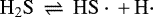(2)

The rapid formation of HS⋅ radicals favors Reaction (3), which produces H2S2 molecules and causes a second hydrogen elimination (Reaction (4)) forming S atoms. H2S2 molecules were detected at 8 K by IR spectroscopy through its H–S stretching mode centered at 2485 cm−1 (Isoniemi et al. 1999). On the other hand, S atoms can only be detected during the warm-up phase (see Sect. 3.2):

The rapid formation of H2S2 enables further reactions. H2S2 molecules can be dissociated by UV photons according to Reaction (5). H2S2 molecules can also recombine with HS⋅ radicals to produce H2S3 molecules (Reaction (6)):

Finally, H2S4 was also detected in our experiments. The presence of HS3 ⋅ radicals will produce H2S4 by reaction with the abundant HS⋅ radical (Reaction (7)). Secondly, two HS2 ⋅ radicals can react producing H2S4 molecules (Reaction (8)). The relatively low abundance of HS3 ⋅ radicals, and the low probability of 2 HS2⋅ radical-radical reactions in an environment dominated by HS⋅ radicals determine the low formation rate of H2S4 molecules. Nevertheless, H2S4 was detected during warm-up of the irradiated H2S ice by quadrupole mass spectrometry (QMS), as explained in Sect. 3.2:

Non-hydrogenated molecules can also be formed. The reaction between S atoms produces S2 molecules. Further S atom additions, as well as dehydrogenation of H2Sx species, can lead to larger Sx molecules. Some Sx species do not absorb in the IR and others display only very weak absorption bands. These products could not be detected by IR spectroscopy in our experiments, but they were measured by QMS during warm-up.

3.2 Warm-up of UV irradiated H2S ice

Some of the radical species made during UV irradiation of H2S ice react at low temperatures, such as HS⋅ radicals, while larger radical species may remain in the ice matrix until thermal energy during warm-up enables subsequent reactions. IR spectroscopy confirmed the production of H2S2 molecules at 8 K (Isoniemi et al. 1999). Overlapping of H–S IR stretching modes of H2S2 with those of larger H2Sx species, expected to present lower formation rates, hindered the estimation of their formation temperatures.

After the sublimation of amorphous and crystalline H2S molecules at 96 K, IR spectra show the crystallization of H2S2 (Fig. 2). From the IR band centered at about 2490 cm−1, two absorption features can be clearly distinguished at temperatures between 110 K and 150 K. These bands belong to the antisymmetric (2495 cm−1) and the symmetric (2482 cm−1) vibration modes of H2S2. Zengin & Giguère (1959) measured the IR spectrum of crystalline H2S2, reporting values in close agreement with our experiments and the work reported by Moore et al. (2007).

The band strength of the H2S2 IR band at 2490 cm−1 was estimated as follows. Martín-Doménech et al. (2015) provided a method to calculate the column density of a given species from the integrated QMS signal, after calibrating the QMS by using CO ice, by applying Eq. (9), where N(mol) is the column density of a given species in mol ⋅ cm−2, 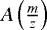is the integrated area taken from the QMS, kCO is the proportionality constant from the calibration of the QMS in a CO ice irradiation experiment leading to photodesorption of the CO molecules, σ+(mol) is the ionization cross section of each species ionized at a voltage of 70 eV in the QMS (data adopted from the National Institute of Standards and Technology), IF(z) is the ionization factor (which has been considered unity for all molecules), FF is the fragmentation factor (derived from the QMS spectrum of each species), and 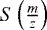is the sensitivity of the QMS (Martín-Doménech et al. 2015): 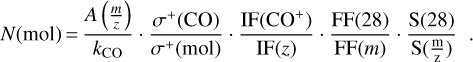(9)

Then, the ratio of column density of H2S to H2S2 () can be obtained from the QMS during thermal desorption of H2S and H2S2, using Eq. (10), and taking the area below the thermal desorption peak in the QMS: (10)

The band strength of the 2490 cm−1 IR feature of H2S2 can be obtained assuming that σ+(H2S2) = σ+ (H2S), as there is no reported value for σ+(H2S2), and calculating the column density of H2S from IR data before its thermal desorption: 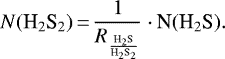(11)

Because the factor kCO cancels out and does not appear in Eq. (10), this method reduces the error due to (i) variation in the QMS sensitivity between the CO photodesorption experiment and the H2S irradiation experiment due to degradation of the QMS filament with time and (ii) different environmental conditions between those experiments since the measurement of the reference species, H2S, and that of the target molecule, H2S2, were made during the same experiment. Entering the estimated values of N(H2S2) and its corresponding integrated IR absorption in Eq. (1), an IR band strength value of A(H2S2) = 2.4 ± 0.5 × 10−17 cm mol−1 was obtained.

After thermal desorption of H2S2, a new IR feature becomes visible at 2481 cm−1 (Fig. 3). This IR band disappears gradually above 150 K during the thermal programmed desorption (TPD), suggesting that H–S stretching modes from species less volatile than H2S2 contribute to this vibration mode.

Figure 4 shows the thermal desorption of H2Sx molecules. Two peaks are clearly observed during H2S thermal desorption. A first desorption peak appearing at 88 K coincides with the disappearance of the 2538 cm−1 IR feature between 80 K and 90 K in Fig. 1, that is, thermal desorption of amorphous H2S molecules. More stable crystalline H2S molecules sublimate at slightly higher temperatures, producing a second peak at 96 K (see Fig. 4).

Furthermore, the QMS data in Fig. 4 shows evidence for H2S2 desorption, , with a maximum at 144 K, which coincides with the disappearance of the IR features at 2495 and 2482 cm−1 attributed to this species.

The better sensitivity of QMS compared to IR spectroscopy allowed the identification of larger species during ice warm-up. Figure 4 shows a maximum of 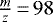at 184 K related to desorbing H2S3 molecules, and the peak of 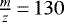at 204 K corresponds to thermally desorbed H2S4. The identification of H2S4 has been confirmed in several irradiation and warm-up experiments.

The fragmentation of desorbing H2Sx species when they impact the filament of the QMS can lead to S fragments that might be erroneously attributed to the desorption of Sx species formed in the ice. Nevertheless, this was not a problem since the 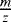values of Sx molecules were detected at temperatures that did not overlap significantly with those of H2Sx species. Figure 5 shows the thermal desorption of Sx species. The thermal desorption of S atoms reaches its maximum at 58 K, dragging some S2 molecules during this process. The main desorption of S2 molecules takes place at 113 K. If we assume that the molecular mass is the main factor determining the desorption temperature, S3 molecules are expected to desorb at approximately 180–200 K, but they were not detected in our experiments. The non-detection of S3 and the detection of S4, with a maximum of desorption at 283 K, suggests that a preferential formation scheme encompass the dimerization of S2 molecules, favoring the formation of Sx species witha pair number of S atoms.

thumbnail Fig. 2

IR spectra collected during warm-up of a previously UV irradiated H2S ice sample. After sublimation near 90 K of most H2S molecules, H2S2 molecules are allowed to interact forming a crystalline structure. Crystallization leads to narrowing of the antisymmetric and symmetric vibrations of H2S2 that appear at 2495 and 2482 cm−1, respectively.
thumbnail Fig. 3

IR spectra acquired during warm-up of previously irradiated H2S ice. This band is evidence of the presence of H2Sx molecules with x > 2 that were detected during desorption in the gas phase by QMS, H2S3, and H2S4 desorbing at temperatures below 225 K (see Fig. 4). Therefore, the small IR absorption that remains above 240 K is likely due to H2Sx species with x > 4 that are refractory at this temperature and could thus not be detected by the QMS.
thumbnail Fig. 4

Thermal programmed desorption of an irradiated H2S ice sample. Up to four different H2Sx species were detected with decreasing abundances. The most intense fragment forthe considered species is shown.

4 Monte Carlo simulations

We used a step-by-step Monte Carlo simulation to follow the deposition of H2S molecules on the surface as well as their photodissociation into other products. Our model is described in Cazaux et al. (2015, 2017). H2S molecules originating from the gas phase arrive at a random time and location on the substrate, which is represented as a grid, and follow a random walk. The arrival time depends on the rate at which gas species collide with the surface. The molecules arriving on the surface can be bound to the substrate and to other H2S, HS, or S species via van der Waals interactions. In the present study we use on-lattice kinetic Monte Carlo (KMC) simulations. Other types of simulations, such as the off-lattice KMC method, allow the distance of the species to be determined explicitly (Garrod 2013). In the present study, we consider the distance between two adsorption sites (and therefore the distance between two adjacent adsorbed species) to be equal for the entire grid, and concentrate on defining the reactions occurring within the chemical species that are deposited on the surface (H2S) or are produced by photodissociation reactions. Our model is meant to constrain the experimental results as accurately as possible, before being exported to interstellar medium conditions in Sects. 6 and 7.

The different mechanisms used in this model are accretion, diffusion, sublimation, chemical reaction, and photodissociation. These different mechanisms (accretion, diffusion, and sublimation) occur at rates that have been described ina previous work (Cazaux et al. 2018). The accretion rate given in number of molecules per second is (12)

where 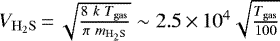cm s−1 is the thermal velocity of H2S, σ is the cross-section of the surface, Stick is the sticking coefficient, which we consider to be unity in this study. The distance between two sites is assumed to be 3 Å, which is consistent with the density of the number of sites typically assumed on surfaces 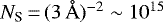cm−2. The cross-section scales with the size of the grid considered in our calculations (which is 40 × 40 sites) as cm2 = 1.4 × 10−12 cm2. The accretion rate of H2S molecules in the experiment is 1 ML s−1. In our calculations, the accretion rate in ML s−1 can be written as ML s−1. Therefore, we chose the density of H2S in our simulations to be about 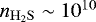cm−3 in order to reproduce experimental conditions.

The diffusion from one site to another is described in a previous work (Cazaux et al. 2017). In the present study, we consider an alpha coefficient (the ratio between diffusion barriers and thermal desorption barriers) of 0.9. Such slow diffusion was determined in a previous work (Cazaux et al. 2017) and is considered in the present study.

In the present work, we consider photodissociation reactions as well as the reactions between the photo-products. These mechanisms are described in the following subsections.

Table 2

Photodissociation reactions with associated rates considered in the present study.

4.1 Photodissociation reactions

Once a photon is absorbed by an H2S molecule, it will dissociate it into HS + H. The product of the reaction, HS, can also receive a photon and be dissociated further into S + H. For our model, the dissociation rates are taken from Shingledecker et al. (2020) and are reported in Table 2. As the photodissociation of H2S can produceS atoms, these S atoms can find each other and make chains, which increases their binding energies and lowers their photodissociation rates, as shown in Table 2. The rates are computed as 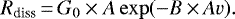(13)

In the experiments, each H2S molecule receives a photon every 10 s. The parameter G0 is the Habing radiation field (Habing 1968) which is the far-ultraviolet (FUV) radiation field (where 1 G0 equals a flux of 1.6 × 10−3 erg cm−2 s−1, which is equivalent to 2 × 107 cm−2 s−1). In order to have 0.1 photon per second, to mimic experimental conditions, we use G0 = 5 × 106. The dissociation rate of H2S molecules is therefore Rdiss = 0.015 s−1 for H2S and is 0.006 s−1 for HS.

thumbnail Fig. 5

Thermal programmed desorption of an irradiated H2S ice sample. A given m∕z value can correspond to the molecular ion of a species or to a fragment of a larger species. The desorption temperatures of Sx molecules are indicated by the solid vertical lines. Dashed lines indicate the desorption of H2Sx species. Apart from the molecular ion of each species, the values of the main fragments used to confirm the presence of these species are displayed.
Table 3

Reactions considered in the present study.

4.2 Chemical reactions

In the present simulations, we consider that species present in the solid phase (on the surface or in the ice) can react with each other. We consider a small solid-phase chemical network allowing five possible reactions, and report the associated pre-exponential factors and barriers in Table 3. These reactions have been selected in the chemical network from Shingledecker et al. (2019). In the present study, we do not consider chemical desorption.

4.3 Binding energies

The binding energies of S atoms, as well as H, H2, HS, H2S, and S chains are given in Table 4. The binding energies for the S chains are extrapolated by using the S chains observed in the experiments. S4 desorbs at 283 K (which implies a binding energy of ~8490 K), while S3 desorbs at approximately 200 K (binding energy of ~6000 K). These binding energies are reported in Table 4. This means that the difference in desorption peak in the TPD when S is added is approximately 80 K, which corresponds to an additional binding energy due to an additional S atom to the chain at approximately 2400 K. We take this value as an addition to the binding energy of the S chain when an extra S atom is added. We therefore reach a binding energy of 18 000 K for S8. It should be noted that this is a simple assumption, and the change in binding energy could decrease with the number of S atoms added, as is the case in clusters (Lin et al. 2005).

Table 4

Species considered in this study with their associated binding energies.

4.4 Results

4.4.1 TPD simulations of H2S

We performed Monte Carlo simulations for the deposition and irradiation of H2S in order to reproduce the experimental measurements. We first performed simulations without irradiation in order to reproduce a simple experimental TPD curve. Our results are reported in Fig. 6. In this figure, we reproduce the two peaks located at approximately 88 K and 96 K, as found in Fig. 4. To reproduce these two peaks we considered the binding energies of species in Table 4. In our calculations the strongest interaction between a species with a neighbor is considered. However, the width of the peaks seen in the experiments are of a few tens of K. This implies that the binding energy is not a single value but a distribution of values. To reproduce the width of the peak, we consider the strongest interaction of the species (from Table 4) and add the contribution of the neighbors around the considered species for 2%; this value was adopted as it reproduces the width the best. For example, an H2S molecule bound with two neighbors would have a binding energy of 2640 + 0.02 × 2640 = 2693 K. This takes into account the fact that the binding energy is increased if more neighbors are involved.

thumbnail Fig. 6

Thermal programmed desorption of H2S with MC simulations.

4.4.2 TPD simulations of irradiated H2S: Case without ice self-shielding

In these simulations, we deposit H2S on the surface and irradiate the molecules with UV photons in rates similar to experimental rates. The visualization of our Monte Carlo simulations for different surface temperatures is presented in Fig. 7. In this figure, we show the grid of 40 × 40 sites. Each cube shows one species, and the color identifies the species. The H2S molecules are presented in yellow, the HS molecules in green, and the S atoms in blue. The first panel represents the H2S after deposition, while the second, third, fourth, and fifth panels show the coverage of the surface during the TPD at 50, 100, 200, and 300 K, respectively. Our results show that after deposition, the H2S layers have not interacted much with the photons since most of the ice is yellow (and traces of green and blue). The deposition in our simulation takes about 8 s, and the molecules receive a photon every 10 s. This means that the number of products due to photodissociation are less important during the deposition than during the TPD (in our simulations). This is reflected by the composition of the surface at 8 K, showing that most H2S molecules are still present on the surface with a minority of HS and S species. The surface at 50 K, shown in the top middle panel of Fig. 7, illustrates a longer irradiation time since the time spent after deposition is 42 min. The photodissociation rate of H2S is Rdiss = 0.015 s−1 in our simulations, which implies that one H2S molecule would not survive such a long time since in 42 min it would have received about 40 photons, and the first photon would have already dissociated the molecule into HS + S. The surface coverage at 50 K is therefore mainly composed of S atoms, but also HS and a few H2S. The photo-products HS and S are dominant compared to the coverage at 8 K after deposition. In Fig. 7, top right panel, the surface temperature is 100 K. Most of the H2S and HS have desorbed from the surface, and mostly S atoms are present. The species are organized as chains, which allow them to have larger binding energies compared to individual species. These binding energies are reported in Table 4. For high temperatures only chains can still be present on the surface. The bottom left panel of Fig. 7 shows the surface at 150 K. Only chains with S atoms and sometimes an inclusion of HS or H2S can be observed. At 300 K, in the bottom middle panel, only a few chains remain on the surface and all other species have desorbed. These residues in our simulations under the form of chains cannot be seen experimentally in the TPD because their binding energies are too high. In our simulations the longest chain has seven S atoms, and few chains have six S atoms. The bottom right panel shows the same simulation and temperature as the bottom middle panel, but in this case the chains are highlighted by different colors, while in the previous figures the colors show which species make up the chain (S, HS, or H2S). We can clearly see that some chains can reach a maximum of six or seven S atoms in the present conditions.

In order to compare our results to the experimental measurements from Fig. 2, we present in Fig. 8 the simulated number of desorbed species during the TPD. Our results show different peaks that are attributed to S atoms, S chains, as well as HS, H2S, and H2S2. This TPD agrees very well with the experimental results, showing chains with up to four members. In the present simulations, we used a coverage of 3–5 ML (see top left panel of Fig. 7). This differs from the experimental conditions where thousands of monolayers were deposited on the surface. The ratios of the different peaks of the TPD would change significantly if the simulations were run for high H2S ice thickness. Our model, however, cannot compute such thick ice, but in the present study we can compare the temperature of the desorption peaks in the TPD and estimate the residuals remaining on the surface at high temperatures.

4.4.3 TPD simulations of irradiated H2S: case with self-shielding

In this section we perform similar simulations to those described in the previous section, but this time we assume that molecules shield themselves from the UV radiation. For simplicity, we consider that if a species is under another one, then it is shielded from radiation and will not receive photons. It is then expected that the layers under the surface will remain H2S as long as they are covered by other species, and will then be exposed only when the layers above sublimate. The results are presented inFig. 9. The surface coverage is shown from temperatures of 8 K (top left panel), 50 K (top middle panel), 100 K (top right panel), and 150 K (bottom left panel). These figures clearly show that there are many fewer chains on the surface than when shielding is not considered, as in Fig. 8, and that instead species such as H2S2 (two green boxes attached together) or H2S3 (one blue box surrounded by two green boxes) are formed on the surface. However, no chains longer than S3 are created, which is shown in Fig. 9 (bottom left panel), where chains are highlighted in different colors (for a surface temperature of 150 K). Therefore, there is no species on the surface after ~180 K as the binding energies of these chains are too low. This is reflected by the TPD in Fig. 10. This figure shows that S chains are present, but only contain two or three sulfur atoms. On the other hand, many hydrogenated sulfur species are present, desorbing attemperatures lower than 180 K.

thumbnail Fig. 7

H2S on the surface after deposition at 8 K (top left) and during TPD at 50 K (top middle), at 100 K, (top right), at 200 K (bottom left) and 300 K (bottom middle). The bottom right panel also shows the surface at 300 K but with the chains being highlighted by using one color per chain. In these simulations, the molecules in the ice do not shield each other and photons can therefore dissociate molecules from the top layers to the bottom layers. The deposition rate of H2S is 1 ML s−1, the heating ramp is 1 K min−1 and G0 = 5 × 106.
thumbnail Fig. 8

Thermal programmed desorption from Monte Carlo simulations of H2S. In these simulations shielding of molecules within the ice is not considered. The deposition rate of H2S is 1 ML s−1, the heating ramp is 1 K min−1, and G0 = 5 × 106.

5 Photoprocesses in H2S ice

In our simulations we considered at first that icy molecules do not shield each other from photons. As a result, we obtained a TPD dominated by atomic sulfur as well as S chains, showing the presence of S chains up to S4 and a small amount of hydrogenated sulfur species. Our results show that residues are present on the surface at the end of the TPD, and that these residues are under the form of chains containing up to six or seven sulfur atoms. This TPD is shown in Fig. 7. We also considered in a second step that icy species could shield each other from UV photons, and obtained a different TPD, dominated by hydrogenated sulfur species, as shown in Fig. 9. In this case the species on the surface desorb below 200 K and no residue is found after the TPD.

The experimental results reported in Fig. 5 show that the irradiation of H2S ice allows the formation of hydrogenated sulfur species which are dominating the TPD. The S chains are also present and desorb until very high temperatures. These results are reproduced by our simulations if icy species can shield each other (hydrogenated sulfur species dominate the TPD), but also if icy species do not shield each other (S chains up to four S atoms in the TPD, residue on the surface after the TPD). The experimental results showthat residues are still present on the surface after the TPD. Therefore, we can assume that H2S species have weak shielding properties so that hydrogenated species can survive under the present experimental conditions, and S chains can be formed.

It should be noted that we do not consider the effect of photodesorption or chemical desorption in this study. Photodesorption reduces the amount of solid H2S, meaning that less H2S is available for photodissociation to form HS, HS2, and H2S2 as well as chains. This implies that the total number of ice species could differ. However, the fraction of H2S versus other molecules should remain similar. Chemical desorption, on the other hand, would remove some formed species and send them into the gas phase (especially via H+HS → H2S; Oba et al. 2018; Shingledecker et al. 2020). This would reduce the amount of H2S species compared to other chemical species in the solid phase. The aim of the present study is to reproduce general experimental trends in the TPDs, so neglecting these processes will only slightly affect the abundances of the species in the ices which will not affect our conclusions.

thumbnail Fig. 9

H2S on the surface after deposition at 8 K (top left) and during TPD at 50 K (top middle), at 100 K (top right), and at 150 K (bottom left).The bottom right panel also shows the surface at 150 K, but the chains are highlighted with one color per chain. In these simulations the molecules in the ice do shield each other and photons cannot dissociate molecules if they are under another molecule. The deposition rate of H2S is 1 ML s−1; the heating ramp is 1 K min−1 and G0 = 5 × 106.
thumbnail Fig. 10

Thermal programmed desorption from Monte Carlo simulations of H2S. In these simulations, the molecules in the ice can shield each other. The deposition rate of H2S is 1 ML s−1; the heating ramp is 1 K min−1 and G0 = 5 × 106.

6 Application to molecular clouds: sulfur depletion

Only ~10% of the currently detected molecules contain sulfur atoms. This apparent lack of chemical diversity in sulfur-bearing species somewhat reflects a great problem in astrochemistry: while the observed gaseous sulfur accounts for its total cosmic abundance (S/H ~1.5 × 10−5) in diffuse clouds, there is an unexpected paucity of sulfur bearing molecules within molecular clouds. The sum of the observed gas-phase abundances of S-bearing molecules (mainly SO, SO2, H2S, and CS) constitute <1% of the cosmic abundance in cold and dense cores (n(H2) > 104 cm−3) (see, e.g., Agúndez & Wakelam 2013). One could think that most of the sulfur is locked on the icy grain mantles in these regions, but surprisingly the abundances of S-bearing species in the ice as measured by near-IR observations could only account for <5% of the total sulfur (Geballe et al. 1985; Palumbo et al. 1995; Boogert et al. 1997; Jiménez-Escobar & Muñoz Caro 2011). Fuente et al. (2019) investigated the sulfur content in the translucent part of TMC 1 where the freeze-out of molecules on the grain surfaces is expected to be negligible. These observations revealed that gas-phase sulfur is already one order of magnitude lower than the cosmic value in translucent gas; this means that 90% of S atoms are incorporated into the solid grains in the transition between the diffuse medium and the translucent cloud, corresponding to an abundance of S in the gas ~810−7 (Fuente et al. 2019). Sulfur atoms impinging in interstellar ice mantles are expected to preferentially form H2S. The understanding of H2S chemistry istherefore linked to the sulfur depletion problem. Chemical desorption of H2S upon formation from HS + H is significant (Oba et al. 2018). Navarro-Almaida et al. (2020) investigated the H2S abundance at the cloud edges, and concluded that chemical desorption of H2S from bare grains is needed to explain the high H2S abundance observed in the translucent gas (n(H2) < 104 cm−3) toward TMC 1 and Barnard 1b.

In the present study, we concentrate on the fraction of S atoms locked onto dust particles in the translucent phase, and therefore follow the fate of S atoms impinging the dust under these conditions. We can then address whether the high depletion of sulfur could be explained by our models, and more specifically whether they could be under the form of sulfur chains or HS or H2S. In translucent clouds sulfur is mainly under the form of S+ (Laas & Caselli 2019), and in dense photodissociation regions (PDRs) S+ can be present until extinction of ~4 (for PDRs with nH = 106 cm−3 and χ = 2 × 105, see Sternberg & Dalgarno 1995). The fact that sulfur is under cationic form influences its accretion rates, as discussed in Ruffle et al. (1999). We therefore adopt a correction factor of 1+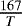 to account for the fact that the accretion rates are increased due to the charges of the sulfur, as mentioned in Ruffle et al. (1999). We performed simulations for translucent cloud conditions taking into account the fact that the accretion rate of S+ is higher due to the effect of the charge. The conditions we used in our simulations were taken from Laas & Caselli (2019) and Snow & McCall (2006), and are given in Table 5. In these simulations, reported in the left panel of Fig. 11, we show the coverage of S compared to HS and H2S as a function of time in translucent cloud conditions. The figure shows the increase in atomic sulfur under the form of S chains compared to H2S and HS. Sulfur preferentially forms chains more often than HS or H2S molecules, which comes from the fact that in the gas phase the ratio of atomic hydrogen to sulfur is 20 (see conditions in Table 5). However, because sulfur is under cationic form, its accretion rate is increased by 1 + 167∕T, which implies an accretion rate that is 7.5 times higher. This means that for each S+ accreting onthe dust, three H atoms accrete. At temperatures of 17 K the residence time of H atoms is very short, and therefore S atoms can make S chains. These chains are not due to diffusion, but to the fact that S+ arrives on an adsorbed S atom (or a S chain) and makes a chain (or a larger chain). In order to address whether the sulfur adsorbed on the dust surface could be responsible for the depletion of sulfur in the gas phase, we estimate how much gas-phase sulfur is needed to obtain the coverage obtained in our simulations. The surface area represented by carbon dust is nc × σc = 7.2 × 10−22 cm−1, by silicate dust is ns × σs = 4.4 × 10−21 cm−1, and by PAHs is nPAH × σPAH = 3.4 × 10−21 cm−1 (in Weingartner & Draine 2001 we consider the possibility that S chains form on PAHs). This corresponds to a total area of 8.5 × 10−21 cm−1. This total area is multiplied by the number of sites per area (1015 cm−2) to obtain the number density of sites per cm3 which is 8.5 × 10−6 cm−3. This implies that if the grains were covered by one monolayer of S (or HS or H2S), then 8.5 × 10−6 S atoms would be missing from the gas phase, and the gas-phase density of sulfur would drop to 1.4 × 10−6. The abundances of sulfur in translucent clouds have been reported to be ~ 8 × 10−7 (this is the most likely value taking into account the uncertainties 0.4–2.2 × 10−6; Fuente et al. 2019). Our results show that such a depletion of sulfur can occur in few times ~104 yr. We therefore suggest that the sulfur under the form of S+ in translucent clouds plays a significant role in setting the S depletion in denser regions as the timescale to reach such a depletion is quite short. The fact that sulfur atoms are creating chains on the surface allows layers to be built that can represent more than 100% surface coverage. The increase in S on the surface is due to the formation of S chains. The right panel of Fig. 11 shows the surface coverage at the end of the simulations; the blue boxes show the sulfur atoms and how they are organized on the surface. Our simulations suggest the creation of long S chains under translucent cloud conditions, which can explain the important depletion observed in the gas phase. As translucent clouds evolved further to molecular clouds and dense cores phases, and extinction increases, these S-rich grains will then be covered with ices. Some of these ices are composed of H2S which will adsorb on the icy grains during these phases as a fraction of sulfur is still in the gas phase. The sulfur chains from the translucent cloud phase, buried underneath the ice, cannot desorb in the hot core or hot corino phases sincethe temperature of the dust in these environments is too low to allow desorption (we observe up to S4 until 300 K). These buried chains could be ejected again in the gas phase upon shocks that would vaporize the ice, dust, and these chains. These chains could also be observed in our Solar System within interplanetary dust particles (IDPs), meteorites, and comets under a refractory form.

thumbnail Fig. 11

Sulfur coverage of S, HS, or H2S as a function of time for translucent cloud models with increase in accretion rate due to the charge (left panel). The compositionof the surface is visualized (right panel). In these simulations the temperature of the dust is 17 K, and G0 = 1.
Table 5

Parameters used in our simulations for translucent cloud conditions.

7 Application to Solar System conditions: origin of sulfur found in cometary material

In the present study we show that UV irradiation of H2S ice results in the formation of S chains. These chains are increasingly resistant to UV as their size increase. We show that H2S species in the ice can shield other sulfur bearing species to some extent. Our study therefore shows that photoprocesses of H2S ices can lead to the formation of S chains that either desorb (below 250 K for chains up to S4) or stay on the surface as residue for chains with more than four sulfur atoms.

Comets are known to be rich in H2S ice representing ~56% of the total sulfur budget, with some minor contribution from SO2, SO, and S2 (0.14%, Calmonte et al. 2016). The abundance of H2S in comets is up to 1.5% relative to H2O, as inferred from millimeter and submillimeter observations (Bockelée-Morvan et al. 2000; Boissier et al. 2007). In comet 67P, data analysis from the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA) showed the presence of S3 and S4. Calmonte et al. (2016) discussed whether they are real parent molecules or the products of even heavier Sn, fragmenting into S3 and S4. In the present study we show that large chains Sn do not desorb at temperatures below 300 K (experimental temperature range in the TPD), but stay as residue in the ice. We therefore suggest that the S3 and S4 chains measured in cometary material do not come from fragmentation from large Sn, but from UV processing of H2S-bearing ices leading to small sulfur chains.

The detection of S2, S3, and S4 makes radiolysis of H2S a very likely formation process, as already discussed by other authors (Grim & Greenberg 1987; Jiménez-Escobar et al. 2012; Woods et al. 2015) which could connect the cometary ice to the ISM. In particular, the S2 /H2S abundance ratio in comet 67P varied from less than 1% to about 3.4% (Calmonte et al. 2016); the latter value requires a substantial UV dose to convert H2S into S2 in the ice (Jiménez-Escobar et al. 2012). Other species, such as H2S2 and S2H, that are efficiently formed in H2S ice irradiation experiments (Jiménez-Escobar et al. 2012, this work), could not be detected in the coma of 67P; this was probably due to overlap with other species with similar mass-to-charge ratios (Calmonte et al. 2016). The present study suggests that small sulfur chains come either from UV photoprocesses of H2S or from S depletion in the cloud prior to the formation of the protosun. The different environments at which the formation of these S chains occurs are illustrated in Fig. 12. In the translucent stage, S chains are formed on bare grains due to the accretion of cationic S on grain surfaces, while in dense clouds S chains are formed via UV photoprocesses of H2S ice. In this case these chains are within the ices. Therefore, we cannot distinguish between the two possible formation scenarios by observation of small S chains alone. Large chains produced in the second scenario (translucent cloud phase) are present in the residues within and/or beneath ice mantles that do not desorb at temperatures typical of cometary conditions, and are therefore impossible to observe in the gas phase. Infrared bands are expected for the Sn species that would be very difficult to detect since they will be masked by the intense absorption features of ice species in the same spectral region. In particular, S8 displays a band near 465 cm−1 and other bands in the far-IR (Trofimov et al. 2009). These species could have been detected by the COSAC-Rosetta instrument on board the Philae lander, but the non-nominal landing on the 67P comet nucleus did not allow a sample to be extracted for analysis (Goesmann et al. 2015). Looking at the present experiments and simulations, UV photolysis of H2S ices produces a fraction of H2S/Sn (with n ≤ 3) on the order of 102 (from Fig. 5), while the Sn built in the translucent cloud conditions has mainly n > 4. The observations of S chains in comet 67P seem to be related with UV processes of H2S ice rather than S chains originating from the translucent cloud phase. This is in agreement with Calmonte et al. (2016) suggesting an ice origin of theS chains. Comparison of the different periods in the evolution of 67P show that at least in two periods the S follows more or less the H2S abundances,suggesting a common origin in the ice matrix.

thumbnail Fig. 12

Sketch summarizing the results for the formation of S chains via accretion in the translucent cloud phase, and via UV photoprocesses of H2S ices in molecular cloud phase. Adapted from Fuente et al. (2019).

8 Conclusions

In this study, laboratory experiments have been performed to study H2S irradiation with UV photons and have been compared to Monte Carlo simulations. We discussed the implications of our results for translucent clouds and comets. Our conclusions are the following:

  • 1.

    The 2538cm−1 band profile (H-S stretching) and integrated band strength of H2S ice change gradually up to about 60 K. Above this temperature the structure is dominated by the crystalline phase, as evidenced by the distinctive narrow features of antisymmetric and symmetric S-H modes (see Fig. 1);

  • 2.

    Upon H2S irradiation, the efficient formation of H2S2 molecules occurs already at 8 K, the lowest temperature in our experiments. Above 100 K, H2S ice sublimates and H2S2 molecules are allowed to form a crystalline ice structure (see Fig. 2). H2S2 desorbs at approximately 144 K;

  • 3.

    Molecules H2Sx with x > 2 are also observed in the IR (see Fig. 3). This is confirmed by the desorption of H2S3 during warm-up near 184 K, while H2S4 desorbs near 204 K (see Fig. 4);

  • 4.

    During warm-up of the previously irradiated H2S ice, the more volatile Sx species are detected. S desorbs near 58 K, S2 desorbs at approximately 113 K, and S4 desorbs at 283 K (see Fig. 5). Larger Sx species are more refractory and remain on the substrate at room temperature; S8 is by far the most abundant species in these residues (Muñoz Caro 2003);

  • 5.

    Monte Carlo simulations of the photodissociation of H2S ice shows that hydrogenated sulfur species observed in the experiments could be reproduced if species in the ice can shield each other. However, this shielding should be not too efficient to be able to reproduce the S chains observed in the experiments. We predict that the residues remaining after the TPD in the experiments are S chains with a length of up to six or seven S atoms;

  • 6.

    Applying our Monte Carlo simulations to translucent cloud conditions, we show that long S chains are created on a rather short timescales of a few 104 yr. The important depletion observed in these environments can therefore be explained by grains covered by Sn. These grains will be buried under ices in later stages as the cloud evolves;

  • 7.

    Small S chains observed in comets could in theory originate from processed H2S ices (during molecular cloud phases) or from S chains (during the translucent cloud phase). Since small chains are mainly produced by photoprocesses of H2S ice, we suggest that observations of S3 and S4 in 67P have an icy origin, and are not due to processes of long chains from the translucent cloud phase.

Acknowledgements

Part of this work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number Ts 17/2-1. H.C. was supported by PhD fellowship FPU-17/03172. A.F., P.R.M. and D.N.A. thank the Spanish MICINN for support under grant PID2019-106235GB-I100.

References

  1. Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
  2. Altwegg, K., Balsiger, H., & Fuselier, S. A. 2019, ARA&A, 57, 113 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bockelée-Morvan, D., Lis, D. C., Wink, J. E., et al. 2000, A&A, 353, 1101 [Google Scholar]
  4. Boissier, J., Bockelée-Morvan, D., Biver, N., et al. 2007, A&A, 475, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Boogert, A. C. A., Schutte, W. A., Helmich, F. P., Tielens, A. G. G. M., & Wooden, D. H. 1997, A&A, 317, 929 [NASA ADS] [Google Scholar]
  6. Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
  7. Bulut, N., Roncero, O., Aguado, A., et al. 2021, A&A, 646, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Calmonte, U., Altwegg, K., Balsiger, H., et al. 2016, MNRAS, 462, S253 [NASA ADS] [CrossRef] [Google Scholar]
  9. Caselli, P., Hasegawa, T. I., & Herbst, E. 1994, ApJ, 421, 206 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cazaux, S., & Spaans, M. 2009, A&A, 496, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cazaux, S., Bossa, J. B., Linnartz, H., & Tielens, A. G. G. M. 2015, A&A, 573, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Cazaux, S., Martín-Doménech, R., Chen, Y. J., Muñoz Caro, G. M., & González Díaz, C. 2017, ApJ, 849, 80 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cazaux, S., Bossa, J. B., Martin-Doménech, R., et al. 2018, Astrophys. Space Sci. Lib., 451, Monte Carlo Simulations of the Formation and Morphology of Interstellar Ices, eds. G. M. Muñoz Caro, & R. Escribano, 95 [Google Scholar]
  14. Cruz-Diaz, G. A., Muñoz Caro, G. M., Chen, Y.-J., & Yih, T.-S. 2014, A&A, 562, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Drozdovskaya,M. N., van Dishoeck, E. F., Rubin, M., Jørgensen, J. K., & Altwegg, K. 2019, MNRAS, 490, 50 [NASA ADS] [CrossRef] [Google Scholar]
  16. Drozdovskaya,M. N., Schroeder I, I. R. H. G., Rubin, M., et al. 2021, MNRAS, 500, 4901 [Google Scholar]
  17. Dulieu, F., Amiaud, L., Baouche, S., et al. 2005, Chem. Phys. Lett., 404, 187 [Google Scholar]
  18. Dutrey, A., Guilloteau, S., & Guelin, M. 1997, A&A, 317, L55 [NASA ADS] [Google Scholar]
  19. Fuente, A., Goicoechea, J. R., Pety, J., et al. 2017, ApJ, 851, L49 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fuente, A., Navarro, D. G., Caselli, P., et al. 2019, A&A, 624, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Garrod, R. T. 2013, ApJ, 778, 158 [NASA ADS] [CrossRef] [Google Scholar]
  22. Geballe, T. R., Baas, F., Greenberg, J. M., & Schutte, W. 1985, A&A, 146, L6 [NASA ADS] [Google Scholar]
  23. Goesmann, F., Hendrik Bredehöft, J., Cabane, M., et al. 2015, in EGU General Assembly Conference Abstracts, 8615 [Google Scholar]
  24. Goto, M., Vasyunin, A. I., Giuliano, B. M., et al. 2021, A&A, 651, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Grim, R. J. A., & Greenberg, J. M. 1987, A&A, 181, 155 [NASA ADS] [Google Scholar]
  26. Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
  27. Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [Google Scholar]
  28. Isoniemi, E., Khriachtchev, L., Pettersson, M., & Räsänen, M. 1999, Chem. Phys. Lett., 311, 47 [NASA ADS] [CrossRef] [Google Scholar]
  29. Jenkins, E. B. 2009, ApJ, 700, 1299 [Google Scholar]
  30. Jiménez-Escobar, A., & Muñoz Caro, G. M. 2011, A&A, 536, A91 [Google Scholar]
  31. Jiménez-Escobar, A., Muñoz Caro, G. M., Ciaravella, A., et al. 2012, ApJ, 751, L40 [Google Scholar]
  32. Jiménez-Escobar, A., Muñoz Caro, G. M., & Chen, Y. J. 2014, MNRAS, 443, 343 [Google Scholar]
  33. Laas, J. C., & Caselli, P. 2019, A&A, 624, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Le Gal, R., Öberg, K. I., Loomis, R. A., Pegues, J., & Bergner, J. B. 2019, ApJ, 876, 72 [Google Scholar]
  35. Lin, C. S., Zhang, R. Q., Lee, S. T., et al. 2005, J. Chem. Phys. B, 109, 14183 [NASA ADS] [CrossRef] [Google Scholar]
  36. Martín-Doménech, R., Manzano-Santamaría, J., Muñoz Caro, G. M., et al. 2015, A&A, 584, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Moore, M. H., Hudson, R. L., & Carlson, R. W. 2007, Icarus, 189, 409 [CrossRef] [Google Scholar]
  38. Muñoz Caro G. M., 2003, PhD thesis, Leiden University, The Netherlands [Google Scholar]
  39. Muñoz Caro, G. M., Jiménez-Escobar, A., Martín-Gago, J. Á., et al. 2010, A&A, 522, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Navarro-Almaida, D., Le Gal, R., Fuente, A., et al. 2020, A&A, 637, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Oba, Y., Tomaru, T., Lamberts, T., Kouchi, A., & Watanabe, N. 2018, Nat. Astron., 2, 228–32 [NASA ADS] [CrossRef] [Google Scholar]
  42. Oppenheimer, M., & Dalgarno, A. 1974, ApJ, 187, 231 [NASA ADS] [CrossRef] [Google Scholar]
  43. Palumbo, M. E., Tielens, A. G. G. M., & Tokunaga, A. T. 1995, ApJ, 449, 674 [Google Scholar]
  44. Penzias, A. A., Solomon, P. M., Wilson, R. W., & Jefferts, K. B. 1971, ApJ, 168, L53 [Google Scholar]
  45. Rodríguez-Baras, M., Fuente, A., Riviére-Marichalar, P., et al. 2021, A&A, 648, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Ruffle, D. P., Hartquist, T. W., Caselli, P., & Williams, D. A. 1999, MNRAS, 306, 691 [Google Scholar]
  47. Shingledecker, C. N., Vasyunin, A., Herbst, E., & Caselli, P. 2019, ApJ, 876, 140 [Google Scholar]
  48. Shingledecker, C. N., Lamberts, T., Laas, J. C., et al. 2020, ApJ, 888, 52 [Google Scholar]
  49. Smith, R. G. 1991, MNRAS, 249, 172 [NASA ADS] [CrossRef] [Google Scholar]
  50. Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [Google Scholar]
  51. Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
  52. Trofimov, B., Sinegovskaya, L., & Gusarova, N. 2009, J. Sulfur Chem., 30, 518 [Google Scholar]
  53. Umebayashi, T., & Nakano, T. 1980, PASJ, 32, 405 [NASA ADS] [Google Scholar]
  54. van der Tak, F. F. S., Boonman, A. M. S., Braakman, R., & van Dishoeck E. F., 2003, A&A, 412, 133 [Google Scholar]
  55. Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [Google Scholar]
  56. Wakelam, V., Caselli, P., Ceccarelli, C., Herbst, E., & Castets, A. 2004, A&A, 422, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Wakelam, V., Loison, J.-C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [Google Scholar]
  58. Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
  59. Woods, P. M., Occhiogrosso, A., Viti, S., et al. 2015, MNRAS, 450, 1256 [Google Scholar]
  60. Zengin, N., & Giguère, P. A. 1959, Can. J. Chem., 37 [Google Scholar]
  61. Zhou, S., Evans, Neal J., I., Koempe, C., & Walmsley, C. M. 1993, ApJ, 404, 232 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Photodissociation reactions with associated rates considered in the present study.

In the text
Table 2

Photodissociation reactions with associated rates considered in the present study.

In the text
Table 3

Reactions considered in the present study.

In the text
Table 4

Species considered in this study with their associated binding energies.

In the text
Table 5

Parameters used in our simulations for translucent cloud conditions.

In the text

All Figures

thumbnail Fig. 1

Evolution of the H2S band strength as a function of temperature. Above 70 K thermal desorption becomes important, reducing H2S column density and preventing the quantification of the band strength.
In the text
thumbnail Fig. 2

IR spectra collected during warm-up of a previously UV irradiated H2S ice sample. After sublimation near 90 K of most H2S molecules, H2S2 molecules are allowed to interact forming a crystalline structure. Crystallization leads to narrowing of the antisymmetric and symmetric vibrations of H2S2 that appear at 2495 and 2482 cm−1, respectively.
In the text
thumbnail Fig. 3

IR spectra acquired during warm-up of previously irradiated H2S ice. This band is evidence of the presence of H2Sx molecules with x > 2 that were detected during desorption in the gas phase by QMS, H2S3, and H2S4 desorbing at temperatures below 225 K (see Fig. 4). Therefore, the small IR absorption that remains above 240 K is likely due to H2Sx species with x > 4 that are refractory at this temperature and could thus not be detected by the QMS.
In the text
thumbnail Fig. 4

Thermal programmed desorption of an irradiated H2S ice sample. Up to four different H2Sx species were detected with decreasing abundances. The most intense fragment forthe considered species is shown.
In the text
thumbnail Fig. 5

Thermal programmed desorption of an irradiated H2S ice sample. A given m∕z value can correspond to the molecular ion of a species or to a fragment of a larger species. The desorption temperatures of Sx molecules are indicated by the solid vertical lines. Dashed lines indicate the desorption of H2Sx species. Apart from the molecular ion of each species, the values of the main fragments used to confirm the presence of these species are displayed.
In the text
thumbnail Fig. 6

Thermal programmed desorption of H2S with MC simulations.
In the text
thumbnail Fig. 7

H2S on the surface after deposition at 8 K (top left) and during TPD at 50 K (top middle), at 100 K, (top right), at 200 K (bottom left) and 300 K (bottom middle). The bottom right panel also shows the surface at 300 K but with the chains being highlighted by using one color per chain. In these simulations, the molecules in the ice do not shield each other and photons can therefore dissociate molecules from the top layers to the bottom layers. The deposition rate of H2S is 1 ML s−1, the heating ramp is 1 K min−1 and G0 = 5 × 106.
In the text
thumbnail Fig. 8

Thermal programmed desorption from Monte Carlo simulations of H2S. In these simulations shielding of molecules within the ice is not considered. The deposition rate of H2S is 1 ML s−1, the heating ramp is 1 K min−1, and G0 = 5 × 106.
In the text
thumbnail Fig. 9

H2S on the surface after deposition at 8 K (top left) and during TPD at 50 K (top middle), at 100 K (top right), and at 150 K (bottom left).The bottom right panel also shows the surface at 150 K, but the chains are highlighted with one color per chain. In these simulations the molecules in the ice do shield each other and photons cannot dissociate molecules if they are under another molecule. The deposition rate of H2S is 1 ML s−1; the heating ramp is 1 K min−1 and G0 = 5 × 106.
In the text
thumbnail Fig. 10

Thermal programmed desorption from Monte Carlo simulations of H2S. In these simulations, the molecules in the ice can shield each other. The deposition rate of H2S is 1 ML s−1; the heating ramp is 1 K min−1 and G0 = 5 × 106.
In the text
thumbnail Fig. 11

Sulfur coverage of S, HS, or H2S as a function of time for translucent cloud models with increase in accretion rate due to the charge (left panel). The compositionof the surface is visualized (right panel). In these simulations the temperature of the dust is 17 K, and G0 = 1.
In the text
thumbnail Fig. 12

Sketch summarizing the results for the formation of S chains via accretion in the translucent cloud phase, and via UV photoprocesses of H2S ices in molecular cloud phase. Adapted from Fuente et al. (2019).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.