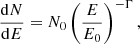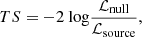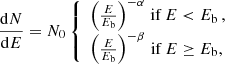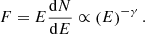| Issue |
A&A
Volume 657, January 2022
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202040039 | |
| Published online | 20 January 2022 | |
Searching for an additional high-energy component in Fermi-LAT GRB afterglows
1
School of Physics and Astronomy, Sun Yat-sen University, Zhuhai 519082, PR China
e-mail: tanbxuan@mail.sysu.edu.cn; zhangyong5@mail.sysu.edu.cn
2
School of Physics, Sun Yat-sen University, Guangzhou 510275, PR China
Received:
1
December
2020
Accepted:
6
September
2021
Context. The very high-energy (VHE; ≥100 GeV) component from at least two gamma-ray bursts (GRBs), that is, GRB 180720B and GRB 190114C, has been detected in the afterglow phase. It is widely discussed that the GeV to TeV emission originated from a synchrotron self-Compton (SSC) process. The VHE component may cause an upturn at the high-energy spectral ends in the Fermi-Large Area Telescope (Fermi-LAT) observing band.
Aims. We aim to find out whether an additional high-energy component commonly exists in the afterglows of Fermi-LAT GRBs. This study will help us to better understand how common it is for a GRB afterglow detected by Fermi-LAT to involve a VHE component.
Methods. First, we selected the GRBs that emit ≥10 GeV photons. The ≥10 GeV photons can be considered as a plausible proxy for a VHE component. We systematically analyzed 199 GRBs detected by Fermi-LAT from 2008–2019. If an additional high-energy component exists in the afterglows of Fermi-LAT GRBs, the best-fit spectral model could be a broken power law (BPL) model with an upturn above a break energy. We compared the afterglow spectra using power-law (PL) and BPL representations.
Results. Out of the 30 GRBs with ≥10 GeV photons that arrived after T90 (the time duration when 90% of the prompt emission was detected), 25 GRBs are tentatively or significantly detected at 0.1–200 GeV after 2 × T90. The spectrum of GRB 131231A shows an upturn above an energy break of 1.6 ± 0.8 GeV, supporting the BPL model. For GRB 131231A, we performed a modeling of its X-ray and γ-ray spectra and found that the SSC model can explain the upturn with acceptable parameter values. In the cases of GRB 190114C, GRB 171210A, GRB 150902A, GRB 130907A, GRB 130427A, and GRB 090902B, the improvement of the BPL fit compared to the PL fit is tentative or marginal.
Conclusions. There is no conclusive evidence that an additional higher energy component commonly exists in Fermi-LAT GRB afterglows, except for the group of Fermi-LAT GRBs mentioned above. Such an additional high-energy component may be explained by the SSC mechanism. Current and future VHE observations will provide important constraints on the issue.
Key words: gamma rays: stars / radiation mechanisms: non-thermal / relativistic processes / gamma-ray burst: general
© ESO 2022
1. Introduction
Gamma-ray bursts (GRBs) consist of short (tens of milliseconds to thousands of seconds) and bright prompt emission at ∼keV to MeV energies (e.g., Rees & Mészáros 1992; Mészáros & Rees 1997), followed by a longer (days to months) afterglow phase at the frequency range from radio to GeV γ-rays (e.g., Costa et al. 1997). Generally, the prompt emission is expected to be produced by some internal dissipation mechanisms such as a collisionless shock in the jet (Rees & Mészáros 1994), and the afterglow emission, from radio up to X-rays, can be described by synchrotron emission of external shock with surrounding medium (Mészáros & Rees 1997).
The Fermi Gamma-ray space Telescope1 (Ackermann et al. 2012), launched in 2008, plays an important role in the detection and spectral and timing characterisation of GRBs, with its two onboard instruments: the Large Area Telescope (LAT, 20 MeV to > 300 GeV) (Atwood et al. 2009) and Gamma-ray Burst Monitor (GBM, 8 keV to 40 MeV) (Meegan et al. 2009). At > 30 MeV, the Fermi-LAT can monitor GRBs in both the prompt and afterglow phases. It has detected 186 GRBs in the first decade at 100 MeV energies (see, e.g., Ajello et al. 2019); this corresponds to 8% of all GRBs that are detected with GBM. Photons of ≳10 GeV have been detected from GRBs 080916C (Abdo et al. 2009a), 090902B (Abdo et al. 2009b; Panaitescu 2017), 090328 (Panaitescu 2017), 090926A (Swenson et al. 2010; Ackermann et al. 2011; Yassine et al. 2017), 100414 (Panaitescu 2017), 110721 (Axelsson et al. 2012; Panaitescu 2017), 110731 (Ackermann et al. 2013b; Panaitescu 2017), 130427A (Tam et al. 2013; Ackermann et al. 2014), 130907A (Tang et al. 2014), 131231A (Liu et al. 2014), 140619B (Ruffini et al. 2015; Panaitescu 2017), and 160509A (Laskar et al. 2016; Tam et al. 2017).
Furthermore, Cherenkov telescope arrays MAGIC and H.E.S.S. have recently detected very high-energy (VHE; ≳100 GeV) emission from several GRBs, largely at the afterglow phase: GRB 180720B (Abdalla et al. 2019), GRB 190114C (MAGIC Collaboration 2019a), and GRB 190829A (H.E.S.S. Collaboration 2019). In the case of GRB 190114C, the highest observed photon energy reaches ∼1 TeV (MAGIC Collaboration 2019a).
Concerning the origin of the afterglow GeV emission, synchrotron emission from external shock electrons becomes the ‘standard’ radiation mechanism in the Fermi era, but a maximum synchrotron energy exists, typically ≲10 GeV (e.g., Kumar & Barniol Duran 2010; Piran & Nakar 2010). It is a great challenge for the traditional synchrotron mechanism to explain the ≳10 GeV emission, since the flux emitted by this mechanism above several GeV (the maximal cutoff energy) should be very small. The synchrotron self-Compton (SSC) component is expected to dominate in the GeV-TeV energy range (Mészáros & Rees 2000; Sari & Esin 2001; Zhang & Mészáros 2001), implying that the spectra of such GRBs should have two peaks in the broad-band spectral energy distribution (SED): one at the X-ray band, and the other at the TeV γ-ray band. Prompted by the recent VHE detections of GRBs, attempts to explain the VHE emission by the Compton processes have been performed (e.g., Wang et al. 2019; Fraija et al. 2019; Zhang et al. 2020).
Generally, the best-fit spectral model of LAT afterglow spectra is usually a power-law(PL) model (e.g., Ajello et al. 2019). Tam et al. (2013) were able to identify an additional hard component in the LAT afterglow in GRB 130427A. Following this, Panaitescu (2017) found a sample of LAT GRBs whose afterglow spectrum is better described by a broken power law (BPL) with a smaller high-energy photon index (β) than low-energy photon index (α), providing strong evidence of hardening spectrum above a few GeV. This indicates that an inverse Compton spectral component may exist in the GRB afterglow phase, and in particular in the Fermi-LAT energy band. It should be noted that the analysis by Panaitescu (2017) is based on aperture photometry, and is focused on the first 1000 s after the burst onsets.
Given the detection of VHE photons by Cherenkov telescope arrays from GRB afterglows up to a day, it is desirable to look for photons with the highest energies accessible to Fermi-LAT, e.g., 10–200 GeV, up to one day post-burst. Indeed, Fermi-LAT covers the spectral range between the two peaks (synchrotron and inverse-Compton) expected in the afterglow spectra and has likely been seen in GRB 190114C (MAGIC Collaboration 2019b). In this work, we expanded the above works to all LAT-detected GRBs, and up to one day after the burst, using maximum likelihood analysis.
2. Datasets and methods
2.1. Searching ≥10 GeV photons
From 2008 to 2020, Fermi-LAT detected more than 200 GRBs. The information about the Fermi-LAT GRBs can be obtained from the second Fermi-LAT GRB catalog (Ajello et al. 2019) and the Fermi website2. In June 2019, the Fermi-LAT team released the Second Fermi-LAT GRB Catalog (the first decade of GRBs detected by the Fermi-LAT), containing 186 LAT GRBs, from a search of a total of 2357 GRBs (Ajello et al. 2019). In order to enlarge the sample size of possible GRBs with high-energy photons as much as possible, we also considered GRBs listed on the web page of Fermi LAT GRBs3. It contains 146 GRBs (including some GRBs in the second Fermi-LAT GRB Catalog). GRB 190114C is the first GRB identified to emit ∼TeV emission, so it is also included. In the end, the GRB sample considered in this work contains a total of 199 GRBs.
Fermi-LAT data were downloaded from the Fermi-LAT database4, and the “extended”-class event files were downloaded and include all event classes (including the TRANSIENT class needed for GRB prompt emission analysis) and provide additional information for each event. Fermi Science Tools version 1.2.1 was used to reduce and analyze the 0.1–200 GeV data. For the event class, we chose “P8R3_Transient” if the time interval contains the prompt phase, while “P8R3_Source” was selected for the afterglow-only analysis. The zenith angle is constrained to be smaller than 100 degrees to exclude the gamma-ray emission from the Earth albedo.
In our analysis, the gtselect tool was used for selection cuts on the event data file. The photon class was selected with 16 for “transient” events and 128 for “source” events above 100 MeV. The search region has a radius of 10 degrees and is centered on the GRB location. The tool gtmktime was used to create good time intervals (GTIs) based on selections made using the spacecraft data file variables, and two tools were used to generate exposure maps: gtltcube, creating a livetime cube, and gtexpmap, generating an exposure map based on the event selection imposed on the photon file and the livetime cube. To suppress the background, the two diffuse emission components gll_iem_v07.fits5 (Galactic diffuse emission) and iso_P8R3_SOURCE_V2_v1.txt6 (isotropic diffuse component) were used in our analysis, and sources in the Fermi catalog (4FGL) were included as background sources. Finally, we performed the likelihood fit using the gtlike tool. All spectra were analyzed as such.
Generally, the best-fit spectral model of LAT afterglow spectra is a power law (see, e.g., Ajello et al. 2019):
where N0 is the normalisation factor, E0 is the pivot photon energy, and Γ is the photon index. The significance of a source can be measured by the test-statistic (TS) value (Ajello et al. 2019), which is defined as follows:
where ℒnull is the maximum of the likelihood function for the null hypothesis, and ℒsource is the maximum of the likelihood function for the alternative hypothesis. The detection significance of a source is around ∼(TS)1/2 standard deviation (or σ). The goodness of the different models can be estimated through ΔTS, which is defined as: ΔTSmodel1 − model2 = TSmodel1 − TSmodel2 = ( − 2log(ℒnull/ℒmodel1)) − ( − 2log(ℒnull/ℒmodel2)) = 2log(ℒmodel1/ℒmodel2), and the significance of improvements is calculated by ∼(ΔTS)1/2 standard deviation (or σ).
To search for ≥10 GeV photons, we analyzed all 199 GRBs with the time interval from the burst onset to 1 day thereafter with the steps described above7. Following that, we used the gtsrcprob8 tool to estimate the probability of each photon coming from a GRB, Psource. We checked all 199 GRBs to look for ≥10 GeV photons associated with a GRB, which are those with PGRB ≥ 97%. Finally, we obtain 67 photons above 10 GeV from 34 GRBs. The properties of these 67 photons and some properties of the 34 GRBs are given in Tables 1–3.
Highest energy events of Fermi-LAT GRBs for which ≥10 GeV photons arrive after T90 only.
Events with the highest energy of Fermi-LAT GRBs for which ≥10 GeV photons arrive in T90 only.
Events with the highest energy of Fermi-LAT GRBs for which ≥10 GeV photons arrive both within T90 and thereafter.
These 34 GRBs are potential GRBs associated with very high-energy photons. Our samples include the 29 GRBs discovered by the Fermi-LAT collaboration (Ajello et al. 2019) with > 10 GeV photons detected, so our results are consistent with the analysis of the Fermi-LAT collaboration (Ajello et al. 2019). Among the 34 GRBs, only one (GRB 090510A) is short duration, while the others are long duration. According to when the > 10 GeV photons arrived relative to the GRB trigger time, three categories can be seen: (1) for 27 GRBs, the ≥10 GeV photons arrived after T90 (T90 is the time duration when 90% of the prompt emission was detected, see Table 1); (2) for GRBs 160625B, 140619B, 110903A, and 080916C, their ≥10 GeV photons arrived in T90 (see Table 2); (3) for GRBs 160509A, 130427A, and 090902B, ≥10 GeV photons arrived in T90 and after T90 (see Table 3). All photons have energy below 100 GeV (in the observer’s frame), except for an interesting event – a 173 GeV photon arrived at 57071 s after trigger with about a 97% probability of being associated with GRB 131231A. The energy and arrival time of these photons in observer and source frames (when a measured redshift is available) are displayed in Fig. 1.
 |
Fig. 1. Energy and arrival time of photons with detected energy ≥10 GeV from Fermi-LAT GRBs from burst onset to one day thereafter. Red symbols represent photons that arrived within and after 2 × T90, shown in ⬧ and ⋆, respectively. Photon energy and arrival time in the source frame are also shown (in green) if measured redshift are available. Dashed arrows connect the same photons in the source frame and the observer’s frame. |
It is clear that most ≥10 GeV photons arrived in the afterglow phase, except for GRBs 160625B, 140619B, 110903A, and 080916C. It is rather nontrivial to explain late-time ≥10 GeV photons by synchrotron emission from external shock, as the maximum (cut-off) photon energy radiated by synchrotron is ∼5 GeV (Piran & Nakar 2010; Abdo et al. 2009a; Barniol Duran & Kumar 2011), while an additional component in afterglow phase could explain ≥10 GeV photons. It is therefore desirable to see if an additional high-energy spectral component can exist in the Fermi-LAT spectra, especially at the high energy end above 10 GeV. We now turn to the analysis of the 30 Fermi-LAT afterglow spectra.
2.2. Spectral analysis of significantly LAT-detected GRB afterglows with ≥10 GeV photons
To systematically analyze these 30 GRB afterglows, we adopted a unified end time (86.4 ks post-burst). The analysis time intervals start at 2 × T90 and end at ∼86.4 ks for every GRB, where 2 × T90 is adopted to minimize the contamination of the prompt emission at GeV energies. The reason to derive time-integrated spectra instead of time-resolved ones is twofold: (1) the number of photons for many of the LAT GRBs especially in the afterglow phase is small; (2) there is no strong indication of change of spectral index during the afterglow phase (Ackermann et al. 2013a).
Out of the 30 GRBs with ≥10 GeV photons arrived after T90, 25 GRBs are tentatively or significantly detected after 2 × T90 with TS ≥ 4, and this sample will form a basis to study the GeV afterglow spectra as a population.
We first used the PL model to describe the observed spectra. To compare the photon spectral indices between the 25 GRBs with the other 174 LAT GRBs, we plotted the index distribution in Fig. 2. The average spectral index of these 25 GRBs (Γ = 1.83 ± 0.53) is comparable to that of the typical Fermi-LAT GRBs (Γ = 1.69 ± 0.28). We found that the PL index distribution for the two populations is indeed similar, which indicates that there may not be an intrinsic difference between the GeV spectra of the two groups.
 |
Fig. 2. Distribution of spectral index from 174 typical GRB afterglows (black) and the 25 GRBs with ≥10 GeV photons detected (red), respectively. The spectra of afterglows from 2 × T90 to one day are fit with the PL model in 0.1–200 GeV. |
To search for an additional higher energy component in these 25 Fermi-LAT GRB afterglows, We utilized the BPL model to describe these GRBs, following Tam et al. (2013) and Panaitescu (2017). A BPL model may improve the fitting if an additional hard component exists in the spectrum. Subsequently, we considered the BPL model for the 25 GRBs:
where Eb is the break energy.
2.3. The possible additional higher energy components in the afterglow spectra
To identify the most probable GRBs in which an additional higher energy component may exist in the afterglow, we compared the afterglow spectra using PL and BPL, representations. There are 18 GRBs that can be well fit by the PL and BPL models. In Figs. 3 and 4, we plot the SEDs including the butterfly plots and spectral points. The PL and BPL parameters of the 18 GRBs are shown in Tables 4 and 5. In the cases of GRB 100213C, GRB 101014A, GRB 120916A, GRB 130502B, GRB 160422A, GRB 160521B, and GRB 160509A, small values of the break energy, Ebreak, do not allow the low-energy index (i.e., α) to be well constrained in the BPL fits.
 |
Fig. 3. 0.1–200 GeV PL and BPL spectra of the 7 GRBs in the E2dN/dE representation, using time range from the 2 × T90 to one day thereafter. Red and black lines show the PL model fits and BPL model fits, respectively. All ±1σ error contours are propagated from errors on the fit parameters. The vertical dashed lines indicate the energy of the most energetic photon detected. The spectra are extrapolated above the maximum photon energy to 200 GeV and are shown as dotted lines. The blue data points are fits with a power law in individual energy bands. The upper limits are calculated with assuming index = −3 (fixed). |
 |
Fig. 3. continued. |
 |
Fig. 4. 0.1–200 GeV PL and BPL spectra of the remaining 11 GRBs in the E2dN/dE representation, using a time range from the 2 × T90 to one day thereafter. Red and black lines show the PL model fits and BPL model fits, respectively. All the ±1σ error contours are propagated from errors on the fit parameters. The vertical dashed lines indicate the energy of the most energetic photon detected, and the spectra are extrapolated above the maximum photon energy to 200 GeV and are shown as dotted lines. The blue data points are fits with a power law in individual energy bands. The upper limits are calculated with assuming index = −3 (fixed). |
Fitting parameters of the PL and BPL model of seven GRBs that show a possible upturn in the afterglow spectra.
Fitting parameters of the PL and BPL model of 11 GRBs that do not show an upturn in the afterglow GeV spectra.
To search for candidates for which a BPL fits better than a PL, we impose a criterion on the 0.1–200 GeV GRB spectra. Based on the butterfly plots, the BPL model should show improvement compared to the PL model with ΔTSBPL − PL > 3. In the BPL model, the high-energy index (β) is harder than the low-energy index (α), and the spectral point SEDs also show the same behavior suggesting that a possible upturn exists in the higher energy. We outlined three different categories: (1) firstly, for GRB 131231A, ΔTSBPL − PL is 13.63 (∼3.7σ), and an upturn exists above the Ebreak. Therefore, the BPL model is significantly preferred over the PL model; (2) secondly, GRB 190114C, 171210A, 150902A, 130907A, 130427A, and 090902B all satisfy ΔTSBPL − PL > 3 and show a possible upturn above the Ebreak; therefore, the improvements should be tentative or marginal; (3) finally, for the GRBs with ΔTSBPL − PL < 3, there is no preference for any model. We also plot the spectra of the seven GRBs (ΔTSBPL − PL > 3) in Fig. 5, and the break energy Eb is around 1 GeV for many of these spectra.
 |
Fig. 5. Best-fit BPL photon spectra of the seven GRBs, which possibly reveal an upturn in the afterglow spectra and ΔTS = TSBPL − TSPL > 3. |
For the seven GRBs above with ΔTSBPL − PL > 3, if the additional high-energy component exists, it could originate from SSC. In this case, the index (β) of the high energy component should be harder than the index (α) of synchrotron emission at lower energies, the spectrum can be well fit by a BPL model with α − β = 0.5 (e.g., Panaitescu 2017). Therefore, we define a BPLα − β = 0.5 model with α − β fixed at 0.5 to describe the SSC spectrum. We find all seven GRBs could be fit by a BPLα − β = 0.5 model. It supports the notion that an SSC-like spectrum is acceptable for these seven cases. The fit results are presented in Table 4.
To summarize, we find that the BPL improvement for GRB 131231A is significant, with a maximum ΔTSBPL − PL = 13.63 (∼3.7σ) and an upturn above Ebreak = 1.6 ± 0.8 GeV. For GRB 190114C, GRB 171210A, GRB 150902A, GRB 130907A, GRB 130427A, and GRB 090902B, we regard the improvement of the BPL fit over the PL to be tentative or marginal, since these six GRBs show ΔTSBPL − PL > 3 and a possible upturn above Ebreak. The spectra of the other GRBs can be fit equally well by the two models.
2.4. The possible additional higher energy components in the prompt spectra
For these seven GRBs, we needed to see whether the additional high-energy component exists in prompt emission as well. To do so, we checked whether the spectrum exhibits an upturn during the prompt phase or shortly after. Therefore, we ran the unbinned analysis chain in T0 to T0 + 2 × T90 (where T0 is the GRB onset time) to obtain a power-per-decade spectrum F, defined as
Only GRB 090902B, GRB 130427A, and GRB 190114C show significant prompt emission. For these three GRBs, the high enough number of photons allow us to plot bin spectra. The power-per-decade spectra F of these three GRBs are shown in Fig. 6. We used the PL and BPL models to fit the data points with linear regression, and the χ2/d.o.f. values show that the BPL model gives a better fit for GRB 130427A than the PL model does. It is also apparent that an upturn exists in GRB 130427A during the prompt phase (i.e., T0 to T0 + 2 × T90), and the break energy is ∼2 GeV. In the prompt phase of GRB 190114C, the time-resolved spectrum shows that the spectrum evolves from a BPL to a PL over the course of the prompt phase (Ajello et al. 2020; Chand et al. 2020). In our analysis, we used time-integrated spectra over the whole prompt phase, and both models can describe the spectrum equally well.
 |
Fig. 6. Spectra F of GRB 090902B, GRB 130427A, and GRB 190114C in the time interval T0 to 2 × T90. The single power-law fits are made starting from 100 MeV and up to where measurements can be fit. Data (squares) without error bars are upper limits, which are calculated assuming Γ = −3 (fixed). The dash lines are the fits of the data points with a PL (red) or BPL (blue) model. The numbers next to the model fits are the index of the spectra F in each energy interval. |
3. Discussion
We found a group of GRB afterglows where an additional high-energy component above ∼1 GeV may exist (see Fig. 3). By comparing the TS values of these seven GRBs assuming either the PL or the BPL model, we find that the BPL model is the preferred model for GRB 131231A. In this case, ΔTSBPL − PL = 13.63 (∼3.7σ) is found, supported by an upturn above the Ebreak. We found tentative (or marginal) evidence that the BPL model could be superior to the PL model (3 < ΔTSBPL − PL < 9 and a possible upturn above Ebreak) for the cases GRB 190114C, GRB 171210A, GRB 150902A, GRB 130907A, GRB 130427A, and GRB 090902B. One should note that, as time evolves in the afterglow phase, the break energy could vary or even move outside of the instrument energy range, smoothing any sharp upturn when summing over spectra at different times. Therefore, evidence of such an upturn in time-integrated afterglow spectra could strengthen the existence of an upturn.
It is hard to explain the late-time ≥10 GeV photons by synchrotron emission (which is typically used to explain afterglow emission below ∼1 GeV), and the evidence of an upturn above a break energy of ∼1 GeV requires an additional spectral component at high energy. A leading explanation for this additional component is the SSC radiation in the external forward shock (see, e.g., MAGIC Collaboration 2019b, for the case of GRB 190114C). This radiation has been predicted over the past two decades (Panaitescu & Mészáros 1998; Wei & Lu 1998; Sari & Esin 2001; Zhang & Mészáros 2001; Mészáros et al. 2004; Fan & Piran 2008; Galli & Piro 2008; Nakar et al. 2009; Piran & Nakar 2010; Lemoine 2015), and the VHE afterglow emission detected in GRB 180720B and GRB 190114C provides strong evidence for such an SSC component origin (MAGIC Collaboration 2019b; Abdalla et al. 2019).
If the additional component is caused by SSC, in the synchrotron-SSC scenario, the Fermi-LAT spectrum below Eb representing the synchrotron emission would have a photon index larger than 2, while the SSC emission starts to dominate above a few GeV making the spectra “anomalously” turn up above the break energy. This is broadly consistent with the seven GRBs with an upturn at ∼1 GeV.
In order to investigate whether the SSC emission can explain the new component, we fit the observations of GRB 131231A whose spectrum upturn is the most significant in terms of ΔTSBPL − PL with a simple SSC model presented by Sari et al. (1998) and Sari & Esin (2001). This model gives an analytic approximation of synchrotron and SSC spectra ignoring the Klein-Nishina effects. This approximation is adequate given the limited photon statistics up to 200 GeV. The result of modeling to the Swift XRT and Fermi-LAT data of GRB 131231A, within the framework of the theory of afterglow emission from external forward shocks (Sari et al. 1998; Sari & Esin 2001), is shown in Fig. 7. The Swift-XRT data are analyzed by HEASOFTv6.25. The X-ray spectra are fit with an absorbed, redshifted PL model considering the column density of the Galactic hydrogen of nH = 0.028 × 1022 cm−2, that of the intrinsic hydrogen of nH = 0.24 × 1022 cm−2, and a redshift of z = 0.6429. The X-ray spectral index is obtained as 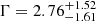 , which gives an unabsorbed 0.3–10.0 keV flux of (2.09 ± 0.9)×10−13 erg cm−2 s−1.
, which gives an unabsorbed 0.3–10.0 keV flux of (2.09 ± 0.9)×10−13 erg cm−2 s−1.
 |
Fig. 7. Modelling of broadband spectra of GRB 131231A in the time intervals 60 s-1day and 52 000–56 000 s. Thick black curves represent the theoretical spectra of synchrotron plus SSC corresponding to slow cooling in the external forward shock scenario. Dotted line and dashed line represent the synchrotron and SSC component, respectively. The adopted parameters are ϵe = 0.16, ϵB = 0.00001, p = 2.13, and n = 1 cm−3. |
We found that the SSC model can explain the upturn of the Fermi-LAT observed spectrum if the conditions at the source are the following. The energy of the spherical shock is roughly estimated to be E ≈ 9.2 × 1052 erg through the observed energy fluence (≈3.7 × 10−4 erg cm−2) from 100 MeV to 200 GeV and 60 s to one day after the burst onset. The relativistic shock propagates into a constant surrounding density n ≈ 1 cm−3, accelerating the electrons and forming a PL distribution of Lorentz factor γe with an index 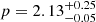 . A constant fraction
. A constant fraction 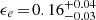 of the shock energy goes into the electrons and about 20% of the electron energy is radiated away via the synchrotron and SSC emission. A fraction
of the shock energy goes into the electrons and about 20% of the electron energy is radiated away via the synchrotron and SSC emission. A fraction 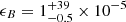 of the shock energy goes into amplifying the magnetic fields behind the shock. These three (n is fixed) free-parameter values of p, ϵe and ϵB resulted from an acceptable fit with the best goodness of fit χ2/d.o.f. = 4.23/(8–3), and their ranges correspond to one σ confidence interval.
of the shock energy goes into amplifying the magnetic fields behind the shock. These three (n is fixed) free-parameter values of p, ϵe and ϵB resulted from an acceptable fit with the best goodness of fit χ2/d.o.f. = 4.23/(8–3), and their ranges correspond to one σ confidence interval.
Corresponding to these values of fitting parameters and the observed time, the emitting relativistic electrons are in the regime of slow cooling. We note that ϵe ≫ ϵB, thus the necessary condition for efficient production of SSC radiation can be satisfied (Sari et al. 1998; Sari & Esin 2001). These results are consistent with a previous work by Liu et al. (2014) on the same GRB, who focused especially on the origin of the GeV afterglow before 1000 s post-burst.
Based on the spectra shown in Fig. 5, the spectra at high energies are harder than at low energies, if both components originate from the same shock, the low-energy component is synchrotron emission and higher energy components are possibly SSC emission. In this case, the synchrotron emission should be produced above the cooling break, and α = p/2. The SSC spectral index in the Fermi-LAT band should be β = (p − 1)/2, such that (α − β) = 1/2 (Panaitescu 2017). In our BPL results, we indeed found that (α − β)∼0.52 for GRB 130427A and (α − β)∼0.49 GRB 090902B, satisfying (α − β) = 1/2. We also found that the BPL model with α − β = 0.5 being fixed gives acceptable fits for the seven GRBs.
We compared the spectra of these seven GRBs above 20 GeV with the sensitivity of Cherenkov Telescope Array(CTA) and Major Atmospheric Gamma Imaging Cherenkov telescope(MAGIC) (Giuseppe 2019). We assumed z = 1 for GRB 171210A and GRB 150902A. We considered the EBL absorption (Franceschini & Rodighiero 2019) and performed an optimistic and extreme assumption that the spectrum extends with the same high-energy index (β) up to 10 TeV10, and the result is shown in Fig. 8. It can be seen that given favorable observing conditions, GRB 130427A, GRB 131231A, and GRB 190114C can likely be detected by CTA and MAGIC. The question as to whether the additional component commonly exists in Fermi-LAT GRBs can be ultimately tested by a large number of GRB observations using the LHAASO-WCDA detector (LHAASO Collaboration 2019), CTA array (CTA Consortium 2019), and the currently operating Cherenkov telescopes.
 |
Fig. 8. BPL energy spectra of the seven GRBs and the six-hour sensitivity of CTA and MAGIC. The time intervals of the seven GRBs are 2 × T90 to 24 h. We assume the high-energy index β of the intrinsic spectra extends up to 10 TeV. |
The photon index distribution of the 25 GRBs (with ≥10 GeV detected) is similar to other 174 Fermi-LAT GRBs, and both are indeed rather hard (Γ < 2) at the LAT band (see Fig. 2). This result lends support to the idea that these 25 GRBs do not form a distinctive class of their own, and their LAT afterglow spectra are not dissimilar to most other Fermi-LAT GRBs.
4. Conclusions
Based on the analysis of a large sample of Fermi-LAT afterglows, there is no conclusive evidence that an additional higher energy component commonly exists in Fermi-LAT GRB afterglows. On one hand, a group of GRBs, namely, GRB 190114C, GRB 171210A, GRB 150902A, GRB 131231A, GRB 130907A, GRB 130427A, and GRB 090902B, marginally or significantly supported by the plausible existence of an upturn above the break energy in the preferred BPL model, might require such a component at the high energy end. For GRB 130427A, the spectral upturn appears in both prompt and afterglow phases. On the other hand, the BPL model is not required in the large majority of cases as there is no improvement of the BPL fit compared to the PL fit for all other cases.
If the additional component really exists, it may have resulted from an SSC component. Besides this, we find that the SSC model can explain the upturn in GRB 131231A under acceptable typical parameter values of GRBs. Further evidence of the possible SSC component is provided by GRB 130427A and GRB 090902B, whose α − β (∼0.52 and ∼0.49, respectively) largely satisfy α − β = 0.5, and all seven GRBs could be satisfactorily fit by the BPLα − β = 0.5 model. These suggest that SSC emission exists in a group of GRBs (regardless of whether they are detected by ground-based VHE telescopes), and the SSC emission may last from the prompt to afterglow phases, as seen in GRB 130427A.
The possible additional high-energy component found in a group of Fermi-LAT GRBs is clearly in contradiction with a single component such as synchrotron emission for these afterglows, and SSC emission is a widely discussed mechanism to explain the additional high-energy component. Current and future VHE observations using CTA and LHAASO, and currently operating Cherenkov telescopes, will provide important constraints on whether SSC emission commonly exists among GRB afterglows.
https://fermi.gsfc.nasa.gov/ssc/observations/types/grbs/lat_grbs/table.php, retrieved on 2019 March 31.
This tool assigns a probability of each photon event that it belongs to a particular source; cf., https://raw.githubusercontent.com/fermi-lat/fermitools-fhelp/master/gtsrcprob.txt.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (NSFC) grants 11633007 and U1731136, Guangdong Major Project of Basic and Applied Basic Research (Grant No. 2019B030302001), and science research grant from the China Manned Space Project (No. CMS-CSST-2021-B09). Y.Z. thanks NSFC grant number 11973099 for financial support. This work made use of the LAT data and science tools available at the Fermi Science Support Center.
References
- Abdalla, H., Adam, R., Aharonian, F. A., et al. 2019, Nature, 575, 466 [Google Scholar]
- Abdo, A., Ackermann, M., Arimoto, M., et al. 2009a, Science, 323, 1688 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 706, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Asano, K., et al. 2011, ApJ, 729, 114 [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [Google Scholar]
- Ackermann, M., Ajello, M., Asano, K., et al. (Fermi/LAT collaboration) 2013a, ApJS, 209, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Asano, K., et al. 2013b, ApJ, 763, 71 [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Asano, K., et al. 2014, Science, 343, 6166 [Google Scholar]
- Ajello, M., Arimoto, M., Axelsson, M., et al. 2019, ApJ, 878, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Arimoto, M., Axelsson, M., et al. 2020, ApJ, 890, 9 [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Axelsson, M., Baldini, L., Barbiellini, G., et al. 2012, ApJ, 757, L31 [CrossRef] [Google Scholar]
- Barniol Duran, R., & Kumar, P. 2011, MNRAS, 412, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Chand, V., Pal, P. S., Banerjee, A., et al. 2020, ApJ, 903, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, E., Feroci, M., Piro, L., et al. 1997, IAU Circ., 6572, 1 [NASA ADS] [Google Scholar]
- CTA Consortium 2019, https://www.worldscientific.com/doi/pdf/10.1142/10986 [Google Scholar]
- Fan, Y. Z., & Piran, T. 2008, Front. Phys. China, 3, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Fraija, N., Barniol Duran, R., Dichiara, S., & Beniamini, P. 2019, ApJ, 883, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Franceschini, A., & Rodighiero, G. A&A, 603, A34 [Google Scholar]
- Galli, A., & Piro, L. 2008, A&A, 489, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giuseppe, D. S. 2019, EPJ Web Conf., 209, 01035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. collaboration. 2019, GCN Circ. #25566, https://gcn.gsfc.nasa.gov/gcn3/25566.gcn3 [Google Scholar]
- Klebesadel, R. W., Strong, I. B., & Olson, R. A. 1973, ApJ, 182, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Barniol Duran, R. 2010, MNRAS, 409, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, T., Alexander, K. D., Berger, E., et al. 2016, ApJ, 833, 88 [CrossRef] [Google Scholar]
- Lemoine, M. 2015, MNRAS, 453, 3772 [Google Scholar]
- LHAASO Collaboration (Bai, X., et al.) 2019, ArXiv e-prints [arXiv:1905.02773] [Google Scholar]
- Liu, B., Chen, W., & Liang, Y.-F. 2014, ApJ, 787, L6 [NASA ADS] [CrossRef] [Google Scholar]
- MAGIC Collaboration 2019a, Nature, 575, 455 [CrossRef] [Google Scholar]
- MAGIC Collaboration 2019b, Nature, 575, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Meegan, C. A., Paciesas, W. S., Pendleton, G. N., et al. 1998, AIP Conf. Proc., 428, 3 [NASA ADS] [Google Scholar]
- Meegan, C. A., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1997, ApJ, 476, 232 [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 2000, ApJ, 541, L5 [CrossRef] [Google Scholar]
- Mészáros, P., Razzaque, S., & Zhang, B. 2004, New Astron. Rev., 48, 445 [CrossRef] [Google Scholar]
- Nakar, E., Ando, S., & Sari, R. 2009, ApJ, 703, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A. 2017, ApJ, 837, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Mészáros, P. 1998, ApJ, 501, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T., & Nakar, E. 2010, ApJ, 718, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Mészáros, P. 1992, MNRAS, 258, 41 [Google Scholar]
- Rees, M. J., & Mészáros, P. 1994, ApJ, 430, L93 [Google Scholar]
- Ruffini, R., Muccino, M., & Kovacevic, M. 2015, ApJ, 808, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Esin, A. A. 2001, ApJ, 548, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [Google Scholar]
- Swenson, C., Maxham, A., Roming, P. W. A., et al. 2010, ApJ, 718, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Tam, P.-H. T., Tang, Q.-W., Hou, S.-J., et al. 2013, ApJ, 771, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Tam, P.-H. T., He, X. B., Tang, Q.-W., et al. 2017, ApJ, 844, L2 [Google Scholar]
- Tang, Q.-W., Tam, P.-H. T., & Wang, X. Y. 2014, ApJ, 788, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X. Y., Liu, R. Y., Zhang, H. M., et al. 2019, ApJ, 884, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, D. M., & Lu, T. 1998, ApJ, 505, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Yassine, M., Piron, F., Mochkovitch, R., et al. 2017, A&A, 606, 17 [Google Scholar]
- Zhang, B., & Mészáros, P. 2001, ApJ, 559, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H., Christie, I. M., Petropoulou, M., et al. 2020, MNRAS, 496, 974 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Highest energy events of Fermi-LAT GRBs for which ≥10 GeV photons arrive after T90 only.
Events with the highest energy of Fermi-LAT GRBs for which ≥10 GeV photons arrive in T90 only.
Events with the highest energy of Fermi-LAT GRBs for which ≥10 GeV photons arrive both within T90 and thereafter.
Fitting parameters of the PL and BPL model of seven GRBs that show a possible upturn in the afterglow spectra.
Fitting parameters of the PL and BPL model of 11 GRBs that do not show an upturn in the afterglow GeV spectra.
All Figures
 |
Fig. 1. Energy and arrival time of photons with detected energy ≥10 GeV from Fermi-LAT GRBs from burst onset to one day thereafter. Red symbols represent photons that arrived within and after 2 × T90, shown in ⬧ and ⋆, respectively. Photon energy and arrival time in the source frame are also shown (in green) if measured redshift are available. Dashed arrows connect the same photons in the source frame and the observer’s frame. |
| In the text | |
 |
Fig. 2. Distribution of spectral index from 174 typical GRB afterglows (black) and the 25 GRBs with ≥10 GeV photons detected (red), respectively. The spectra of afterglows from 2 × T90 to one day are fit with the PL model in 0.1–200 GeV. |
| In the text | |
 |
Fig. 3. 0.1–200 GeV PL and BPL spectra of the 7 GRBs in the E2dN/dE representation, using time range from the 2 × T90 to one day thereafter. Red and black lines show the PL model fits and BPL model fits, respectively. All ±1σ error contours are propagated from errors on the fit parameters. The vertical dashed lines indicate the energy of the most energetic photon detected. The spectra are extrapolated above the maximum photon energy to 200 GeV and are shown as dotted lines. The blue data points are fits with a power law in individual energy bands. The upper limits are calculated with assuming index = −3 (fixed). |
| In the text | |
 |
Fig. 3. continued. |
| In the text | |
 |
Fig. 4. 0.1–200 GeV PL and BPL spectra of the remaining 11 GRBs in the E2dN/dE representation, using a time range from the 2 × T90 to one day thereafter. Red and black lines show the PL model fits and BPL model fits, respectively. All the ±1σ error contours are propagated from errors on the fit parameters. The vertical dashed lines indicate the energy of the most energetic photon detected, and the spectra are extrapolated above the maximum photon energy to 200 GeV and are shown as dotted lines. The blue data points are fits with a power law in individual energy bands. The upper limits are calculated with assuming index = −3 (fixed). |
| In the text | |
 |
Fig. 5. Best-fit BPL photon spectra of the seven GRBs, which possibly reveal an upturn in the afterglow spectra and ΔTS = TSBPL − TSPL > 3. |
| In the text | |
 |
Fig. 6. Spectra F of GRB 090902B, GRB 130427A, and GRB 190114C in the time interval T0 to 2 × T90. The single power-law fits are made starting from 100 MeV and up to where measurements can be fit. Data (squares) without error bars are upper limits, which are calculated assuming Γ = −3 (fixed). The dash lines are the fits of the data points with a PL (red) or BPL (blue) model. The numbers next to the model fits are the index of the spectra F in each energy interval. |
| In the text | |
 |
Fig. 7. Modelling of broadband spectra of GRB 131231A in the time intervals 60 s-1day and 52 000–56 000 s. Thick black curves represent the theoretical spectra of synchrotron plus SSC corresponding to slow cooling in the external forward shock scenario. Dotted line and dashed line represent the synchrotron and SSC component, respectively. The adopted parameters are ϵe = 0.16, ϵB = 0.00001, p = 2.13, and n = 1 cm−3. |
| In the text | |
 |
Fig. 8. BPL energy spectra of the seven GRBs and the six-hour sensitivity of CTA and MAGIC. The time intervals of the seven GRBs are 2 × T90 to 24 h. We assume the high-energy index β of the intrinsic spectra extends up to 10 TeV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.