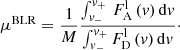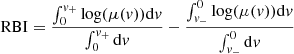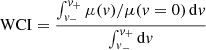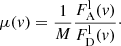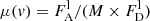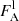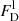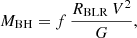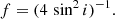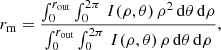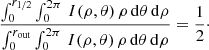EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A155 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A155
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202141820
Published online 26 October 2021

© ESO 2021

1. Introduction

The geometry and kinematics of the broad line region (BLR) in active galactic nuclei (AGNs) has been essentially investigated through reverberation mapping (Blandford & McKee 1982; Peterson 1993), a technique that takes advantage of the variability of the ionizing continuum to measure the response time of the emission lines, which is directly related to the size of the BLR. Time lags as a function of the velocity across the Hβ emission line profile have been measured in a dozen AGNs, providing information on the geometry and kinematics of the BLR. The geometry is generally a thick disk viewed close to face-on, while various kinematical signatures were found in the different objects, mostly virialized motions, inflows, or outflows (e.g., Bentz et al. 2009, 2010; Denney et al. 2010; Pancoast et al. 2014; Du et al. 2016a; Grier et al. 2017a; Xiao et al. 2018; Zhang et al. 2019). Recently, the advent of long-baseline near-infrared interferometry made it possible to spatially resolve the Pα and Brγ BLRs in two AGNs, revealing a thick disk dominated by Keplerian rotation (GRAVITY Collaboration 2018, 2021). These observations agree with the results from reverberation mapping.

Several studies have shown that line profile distortions are commonly observed in gravitationally lensed quasar spectra (Richards et al. 2004; Wayth et al. 2005; Sluse et al. 2007, 2011, 2012; O’Dowd et al. 2011; Guerras et al. 2013; Braibant et al. 2014, 2016; Motta et al. 2017; Fian et al. 2018; Popović et al. 2020). These line profile deformations are most often detected as red/blue or wings/core distortions (Sluse et al. 2012). Simulations have shown that reverberation is unable to reproduce the line deformations observed in most systems when the delay is shorter than 40 days. In these cases, the line deformations can be attributed to microlensing, that is, the differential magnification of spatially and kinematically separated subregions of the BLR. Microlensing-induced line profile distortions can thus provide independent constraints on the BLR structure.

Possible effects of microlensing on broad emission lines have been theoretically investigated by several authors (Nemiroff 1988; Schneider & Wambsganss 1990; Hutsemékers et al. 1994; Popović et al. 2001; Abajas et al. 2002, 2007; Lewis & Ibata 2004; O’Dowd et al. 2011; Garsden et al. 2011; Simić & Popović 2014). In particular, Braibant et al. (2017) have recently computed the effect of gravitational microlensing on quasar broad emission line profiles and their underlying continuum, considering representative BLR models and microlensing magnification maps. To analyze the large amount of simulated line profiles, the effects of microlensing have been summarized using four observables: μcont, the magnification of the continuum at the wavelength of the emission line, μBLR, the total magnification of the broad emission line, and two indices sensitive to red/blue and wings/core line profile distortions, denoted RBI and WCI, respectively. WCI, RBI diagrams that can serve as diagnostic diagrams to distinguish the different BLR models were then built. Furthermore, Hutsemékers et al. (2019) have developed a Bayesian probabilistic scheme to identify the models that best reproduce the observed line profile deformations. By comparing the microlensing-induced distortions of the Hα emission line observed in the lensed quasar HE0435−1223 with a large number of simulations, the authors concluded that BLR flattened geometries, such as a Keplerian disk or an equatorial wind, reproduce the observations best.

The quadruply lensed quasar Q2237+0305 at z = 1.695 (Huchra et al. 1985), also known as the Einstein cross, has been known for years to be a privileged laboratory for microlensing studies. The very short time delays of about one day (e.g., Vakulik et al. 2006) allow one to robustly interpret the spectral differences observed between the lensed images in terms of microlensing. Sluse et al. (2011) measured a size of the C IV emitting region that agrees with the radius-luminosity relation derived from reverberation mapping. These authors also found that the broadest components of the C IV and C III] lines are more strongly microlensed than the line cores, suggesting that the highest velocity parts of the profiles come from the most compact regions of the BLR. O’Dowd et al. (2011) found that the differential microlensing signature observed in the C III] emission line favors a gravitationally dominated BLR kinematics. Braibant et al. (2016) used a combination of optical and near-infrared spectra of the four images and reported the existence in image A of a large-amplitude microlensing effect that distorts the high-ionization C IVλ1549 Å line and the low-ionization Hα line in different ways. Making use of a dedicated disentangling method, they argued that the differential magnification of the blue and red wings of Hα favors a flattened, rotating, low-ionization region, whereas the roughly symmetric microlensing effect measured in C IV can be reproduced assuming that the high-ionization emission line is formed in a polar wind.

In order to place these results in a more quantitative framework, we now compare these observations with simulations for a set of simple but representative BLR models. We first characterize the microlensing effect in the C IV and Hα lines of Q2237+0305 by measuring the four indices μcont, μBLR, RBI, and WCI (Sect. 2). These indices are then compared with those obtained from the simulations, with the aim to constrain the BLR properties (Sect. 3). Conclusions form the last section.

2. Measurement of magnification and distortion indices

Quasi-simultaneous near-infrared and visible spectra of the four components of Q2237+0305 have been obtained in October 2005 (Eigenbrod et al. 2008a; Braibant et al. 2016). Observations, data reduction, and a first analysis focusing on microlensing are described in detail in Braibant et al. (2016). These spectra show that image A of Q2237+0305 is affected by a strong microlensing magnification effect that clearly distorts the C IVλ1549 Å and Hα line profiles. Long-term monitoring of the system between 2000 and 2008 (e.g., Mediavilla et al. 2015) shows that image D is most likely free of microlensing-induced variability. We then consider the spectrum of image D as the non-microlensed reference spectrum. The A/D macro-amplification ratio is M = 1.0 ± 0.1 (Agol et al. 2000). The microlensing-induced magnification factors of the continuum were estimated at the wavelengths of the C IV and the Hα emission lines in Braibant et al. (2016), after correcting image D for the differential extinction. These factors, denoted μcont, are reported in Table 1.

Table 1.

Measured magnification and distortion indices.

The μBLR, RBI, and WCI indices that quantify the effect of microlensing on the broad emission line profiles were estimated following Braibant et al. (2017) and Hutsemékers et al. (2019). The total microlensing-induced magnification of an emission line, μBLR, is obtained by integrating over the line profile the ratio between the emission line flux densities in images A and 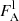D, and 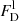respectively, after subtraction of the local continuum and correction for the A/D macro-amplification ratio, that is,

(1)

The red/blue RBI and wings/core WCI indices characterizing the line profile distortions are estimated using

(2)

and

(3)

where

(4)

RBI is sensitive to the asymmetry of the line profile deformations. It takes non-null values when the effect of microlensing on the blue and red parts of the line is asymmetric. WCI indicates whether the whole emission line is on average more or less affected by microlensing than its center. As they are defined, both RBI and WCI are independent of M.

The magnification profile μ(v) is plotted in Fig. 1 for the C IV and the Hα emission lines. Where the line flux is too low, μ(v) becomes unreliable. The indices are therefore computed over a restricted velocity range ([−5900,+5900] km s−1 for C IV and [−6450,+6450] km s−1 for Hα) that nevertheless encompasses most of the line profiles. The μBLR, WCI, and RBI indices are reported in Table 1. The errors on the indices are obtained by propagating the uncertainty of the line flux densities. This uncertainty is computed as the quadratic sum of the error on the total (line + continuum) flux density and the error on the continuum estimate, the latter being taken as the standard deviation of the continuum flux on each side of the emission lines. The exact value of the indices depends on several parameters such as the adopted underlying continuum, the velocity range, and the systemic redshift that defines the line center. The measured values are nevertheless stable within the quoted uncertainties for small variations of these parameters. They are also similar when using different smoothing values like those illustrated in Fig. 1.

thumbnail Fig. 1.

Flux density ratio , where M = 1, is illustrated as a function of the Doppler velocity for the C IVλ1549 Å and Hα emission lines observed in the lensed quasar Q2237+0305 (red lines). μ(v) is shown after smoothing the line profiles with a 220 km s−1 wide median filter and a 1500 km s−1 wide median filter (thin and thick red lines, respectively). Outside the displayed velocity range, μ(v) becomes unreliable due to the low line fluxes. The continuum-subtracted spectra of images A and D ( and , respectively) are superimposed for comparison (blue and black lines, in arbitrary units).

It is immediately clear from the shape of μ(v) and the values of the WCI and RBI indices that the C IV and the Hα emission lines are differently affected by the microlensing effect, as already noted in Braibant et al. (2016). The significantly positive value of RBI for Hα indicates that microlensing magnifies the receding velocities to a larger extent than the approaching ones. WCI larger than one in both lines indicates a significantly higher magnification of the line wings with respect to the line center.

3. Comparison with simulations

3.1. Microlensing simulations

We investigated the effect of gravitational microlensing on broad emission line profiles and the underlying continuum by convolving in the source plane the emission from representative BLR models with microlensing magnification maps. For the BLR models, we considered a rotating Keplerian disk (KD), as well as biconical polar (PW) and equatorial (EW) radially accelerated winds with inclinations with respect to the line of sight i = 22°, 34°, 44°, 62°. We investigated nine inner radius values for each BLR model: rin = 0.1, 0.125, 0.15, 0.175, 0.2, 0.25, 0.35, 0.5, and 0.75 rE, where rE is the microlensing Einstein radius. To compute the Einstein radius, we adopted a flat ΛCDM cosmology with H0 = 68 km s−1 Mpc−1 and Ωm = 0.31. The source and lens redshifts are zS = 1.695 and zL = 0.0394, respectively (Huchra et al. 1985), so that the Einstein radius is rE = 3.26 × 10−2 pc in the source plane for an average microlens mass of 0.3 M⊙. The outer radius was fixed to rout = 10 rin. This value largely encompasses the mean and half-light radii of the BLR models (Appendix A). The BLR models are assumed to have an emissivity ϵ = ϵ0 (rin/r)q that either sharply decreases with radius, that is, q = 3, or more slowly, that is, q = 1.5. Twenty BLR monochromatic images corresponding to twenty spectral bins in the line profile were produced using the radiative transfer code STOKES (Goosmann & Gaskell 2007; Marin et al. 2012; Goosmann et al. 2014). Each model also contains a continuum-emitting uniform disk seen under the same inclination as the BLR, and with an outer radius fixed at nine different values: rs = 0.1, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.6, and 0.7 rE. These values sample the range of continuum half-light radii r1/2 measured for Q2237+0305 and collected by Sluse et al. (2011), using rs ≃ 1.4 r1/2 for a uniform disk. Only models with rin ≥ rs were considered. For a full description of the models and additional details, we refer to Braibant et al. (2017).

The effect of microlensing on the BLR was modeled using a caustic network specific to image A of Q2237+0305. The magnification map was computed using the microlens ray-tracing code (Wambsganss 1999), considering a convergence κs = 0.394 for matter in compact objects and κc = 0 for continuously distributed matter, with an external shear γ = 0.395 (Kochanek 2004). The map extends over a 200 rE × 200 rE area of the source plane and is sampled by 20 000 × 20 000 pixels. To limit the impact of preferential alignment between the symmetry axes of the BLR models and the caustic network, the map was rotated by 0°, 30°, 45°, 60°, and 90°, and only the central 10 000 × 10 000 pixel parts of the rotated maps were finally used.

Distorted line profiles were obtained from the convolution of the monochromatic images of the BLR by the magnification maps, and were computed for each position of the BLR on the magnification maps, generating ∼108 simulated profiles per map and BLR model. Given the huge amount of simulated line profiles, we focused our analysis on the indices μcont, μBLR, RBI, and WCI that characterize the continuum and line profile magnification and distortions, and which can be directly compared with the observations.

3.2. WCI, RBI distributions

Figures 2 and 3 display for C IV and Hα the WCI, RBI distributions of the simulated microlensed line profiles that arise from the magnification of the different BLR models by the caustic network. Only simulations that match the μcont and μBLR values are represented. The BLR models are grouped according to their geometry/kinematics, inclination, and emissivity. The ranges of WCI and RBI values that correspond to the observed distortion of the line profiles (Table 1) are indicated by a small rectangle superimposed on the simulated WCI, RBI distributions.

thumbnail Fig. 2.

Two-dimensional histograms of simulated WCI, RBI for the C IV emission line. These indices were measured from simulated line profiles that arise from the BLR models KD, PW, and EW seen at inclinations 22°, 34°, 44°, and 62°. The BLR models with an emissivity ϵ0 (rin/r)q that sharply decreases with radius, i.e., q = 3, are illustrated in the left panel, while those that are characterized by a more slowly decreasing emissivity, i.e., q = 1.5, are illustrated in the right panel. Each model also contains a continuum-emitting disk seen under the same inclination. All continuum source radii and BLR sizes used in the simulations are considered, but only the models that reproduce the μcont and μBLR values measured for the C IV emission line are shown, i.e., 2.8 ≤ μcont ≤ 3.3 and 2.24 ≤ μBLR ≤ 2.78 (Table 1). The color map is logarithmic. The WCI and RBI values measured for C IV are plotted with their uncertainties as a small rectangle superimposed on the simulated WCI, RBI distributions.

thumbnail Fig. 3.

Two-dimensional histograms of simulated WCI, RBI for the Hα emission line. Same as Fig. 2, but only the models that reproduce the μcont and μBLR values measured for the Hα emission line are shown, i.e., 2.2 ≤ μcont ≤ 2.7 and 2.09 ≤ μBLR ≤ 2.35 (Table 1). The WCI and RBI values measured for Hα are plotted with their uncertainties as a small rectangle superimposed on the simulated WCI, RBI distributions.

We immediately see that a wide range of WCI, RBI values is generated. With the KD BLR model, high values of both WCI and RBI are generated. With the PW and EW models, either high WCI or high RBI values can be produced, respectively. Simulations performed with the q = 3 and q = 1.5 emissivity indices are very similar, as are the simulations performed for C IV and Hα, which only differ by the constraints on μcont and μBLR.

The KD model can reproduce the observed magnification and distortion indices regardless of the inclination and emissivity law. The EW model is rejected in all cases by the observations. The PW model can reproduce the C IV line deformation for the inclinations 34° and 44°, and the Hα line deformation for the inclinations 22° and 34° with the q = 1.5 emissivity law. The comparison of the observed indices with the simulations thus provide clear constraints on the geometry and kinematics of the BLR in Q2237+0305. The constraints are stronger than those derived for the lensed quasar HE0435−1223 (see Fig. 2 of Hutsemékers et al. 2019) due to a stronger microlensing effect (μBLR is significantly higher in Q2237+0305 than in HE0435−1223).

3.3. Probability of the different models

In order to identify the BLR models that best fit the observations, we computed the relative posterior probability that a given model (G, i) (where G = KD, PW, or EW, and i = 22°, 34°, 44°, or 62°) can more easily reproduce the four observables μcont, μBLR, RBI, and WCI. The method is described in detail in Hutsemékers et al. (2019). Practically, we computed the likelihood of the observables for each set of parameters characterizing the simulations. We then marginalized the likelihood over rs, rin, and q, as well as over the microlensing parameters. Because the different BLR models share the same parameters and associated priors, we can quantify their relative efficiency to reproduce the data by comparing their likelihoods, that is, by normalizing the marginalized likelihood by the sum of the likelihoods associated with each model G for each inclination i. This yields the relative probability of the different models, the values of which are given in Table 2 for the Hα and C IV BLRs independently.

Table 2.

Probability (in %) of the different BLR models for Hα and C IV.

We see that EW BLR models are totally rejected. The KD models are the most likely for both the Hα and C IV lines. PW models are also possible, especially for the high-ionization C IV BLR. In all cases, the most likely inclinations are 34° and 44°. Because the exact value of RBI for the C IV line could be affected by a global blueshift of the line, we also computed the model probabilities using RBI = 0, that is, a symmetric deformation of the C IV line. We find probabilities of 66% and 34% for the KD and PW (all i) models, respectively. These values do not strongly differ from the values given in Table 2 (75% and 26%, respectively), thus indicating that these results are robust.

Because the Hα and C IV BLRs are expected to share the same center and inclination, we also computed the probability of combinations of Hα and C IV BLR models that have the same position on the caustic map as well as identical inclinations. The EW models being rejected, we only considered the combinations of KD and PW models. Results are given in Table 3. The model combinations with KD for both the Hα and C IV BLRs are clearly favored. Other combinations involving PW for C IV are also possible. The most likely inclinations are 34° and 44°. We also added an independent constraint on the relative size of the continuum source at the wavelengths of Hα and C IV derived from microlensing-induced time variations. This constraint affects the BLR models through the condition rin ≥ rs. Between 1500 Å and 3000 Å restframe, the size of the continuum source was found to scale as λp, where p is between 0.8 and 1.3 (Eigenbrod et al. 2008b; Muñoz et al. 2016; Goicoechea et al. 2020). We could thus expect a factor 4 between the size of the continuum source at the wavelength of Hα and its size at the wavelength of C IV. However, because no measurement is available at the wavelength of Hα, we conservatively used rs(λHα) > 2 × rs(λC IV). As seen in Table 3, this additional constraint does not change the results.

Table 3.

Probability (in %) of [Hα/C IV] BLR model combinations.

In Fig. 4 we show two representative examples of model and map combinations that within the uncertainties reproduce the observables μcont, μBLR, RBI, and WCI measured for both Hα and C IV. In the left panel, the combination KD(Hα)/KD(C IV) with i = 34° is illustrated. Due to the dense caustic network, a small difference in BLR size is sufficient to have a roughly symmetric magnification for the C IV BLR and an asymmetric one for the Hα BLR, considering the same BLR model. The right panel shows a KD(Hα)/PW(C IV) combination at i = 34°. In this case, the BLR size is larger and more caustics are involved in a complex magnification pattern of the BLR. Multi-epoch data should allow us to disentangle these combinations. In these examples the Hα BLR appears larger than the C IV BLR, but it should be emphasized that we could not derive any significant information on their relative sizes on the basis of our data set (Sect. 3.4).

thumbnail Fig. 4.

Hα (in red) and C IV (in blue) BLR intensity maps superimposed on the magnification map with 0° rotation. These combinations of models and maps reproduce the measurements within the uncertainties. Left: Hα BLR model is characterized by the following parameters: KD, i = 34°, q = 3, rs = 0.15 rE, and rin = 0.175 rE, and the C IV BLR model is characterized by KD, i = 34°, q = 3, rs = 0.10 rE, and rin = 0.10 rE. The size of the map is 1.5 rE × 1.5 rE. Right: Hα BLR model is characterized by KD, i = 34°, q = 3, rs = 0.15 rE, and rin = 0.75 rE, and the C IV BLR model is characterized by PW, i = 34°, q = 1.5, rs = 0.10 rE, and rin = 0.25 rE. The size of the map is 5 rE × 5 rE.

3.4. Size of the BLR and black hole mass

By marginalizing over all parameters but rin, we can estimate the most likely BLR radius. However, rin does not properly represent the size of the BLR, which also depends on the light distribution. We therefore computed the mean and half-light radii for the different models as described in Appendix A, and estimated their relative probabilities in nine bins between the minimum and maximum values. The resulting probabilities are shown in Fig. 5. There is no significant difference between the sizes of the C IV and Hα BLRs. From the probability distributions, we estimate the mean radius of the BLR to be rm ≃ 1.4  ±  0.6 rE ≃ 54  ±  23 light-days, and the half-light radius to be r1/2 ≃ 1.2  ±  0.5 rE ≃ 47  ±  19 light-days. The latter value is in excellent agreement with the C IV BLR half-light radius derived from microlensing-induced time variability of the C IV line (Sluse et al. 2011).

thumbnail Fig. 5.

Relative probabilities (in percent) of the BLR mean radius rm and half-light radius r1/2 in rE units. Blue refers to the C IV BLR, and red to the Hα BLR.

Our estimate of the BLR radius may be compared to the radius–luminosity (R − L) relations derived from reverberation mapping. Using the relations given by Kaspi et al. (2021) for the C IV BLR, and the luminosity reported by Assef et al. (2011) (corrected for our cosmological parameters, and assuming λLλ(1350 Å) = λLλ(1450 Å) as in Vestergaard & Peterson 2006), we obtain R(C IV) ≃ 55 ± 30 light-days, which is in excellent agreement with our value. As shown by Grier et al. (2017b), the R − L relation for the Balmer line BLR is more complex: many measurements lie below the canonical relation of Bentz et al. (2013), thus possibly indicating selection effects or different BLR sizes in high-luminosity quasars. We translate our Hα BLR size measurement into an Hβ BLR size using the conversion r1/2(Hβ) ∼ 0.7 × r1/2(Hα) ∼ 33 light-days, which is derived visually from Fig. 10 of Grier et al. (2017b). This value is one order of magnitude lower than the size derived from the R − L relation of Bentz et al. (2013), which yields R(Hβ) ∼ 400 light-days using log[λLλ(5100 Å)] ≃ 46 (Assef et al. 2011). The microlensing estimate of the Hβ BLR radius thus lies much below the canonical relation, but it does agree with the deviation reported by Grier et al. (2017b) for high-luminosity objects. Because our measurements are not affected by the same selection effects as reverberation mapping, this might point to a real physical effect, possibly related to the accretion rate (Du et al. 2016b). Indeed, Q2237+0305 has a high dimensionless accretion rate 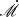= 370, computed using Eq. (3) of Du et al. (2016b).

Assuming virial motion, the mass of the black hole can be estimated using

(5)

where V is the velocity full width at half maximum (FWHM) of the broad emission line, f the virial factor and G the gravitational constant. For a thin Keplerian disk (our most likely model), Decarli et al. (2008) give

(6)

For the broad lines observed in the spectra of image D (unaffected by microlensing), we measure FWHM(C IV) = 3800 ± 400 km s−1 and FWHM(Hα) = 4000 ± 400 km s−1 by fitting a set of broad and narrow lines. For the narrow lines, we use FWHM ≃1070 km s−1 estimated from the [OIII] lines (Greene et al. 2010). The derived FWHMs of the C IV and Hα broad lines agree with those obtained by Assef et al. (2011) and Greene et al. (2010). According to Eq. (5), similar FWHMs of the C IV and Hα broad lines are expected if the BLRs have similar radii, as observed. Using i = 40 ± 5°, RBLR = 47 ± 19 light-days, and V = 3900 ± 500 km s−1, we finally obtain MBH = 9 ±5 × 107 M⊙.

4. Conclusions

We have compared quasi-simultaneous observations of the microlensing effect on the Hα and C IV broad emission lines in the quasar Q2237+0305 with simulations based on simple but representative BLR models and magnification maps. Our study shows that

  • the observed microlensing effect, characterized by a set of four indices, can be reproduced with some of the considered BLR models,

  • the equatorial wind model is rejected,

  • for both the Hα and the C IV BLRs the most likely model is the Keplerian disk; models with a polar wind for the high-ionization C IV BLR are possible, but less likely,

  • the most likely inclination of the system with respect to the line of sight is about 40°, as expected for a type 1 AGN and in agreement with the value derived from microlensing time series (Poindexter & Kochanek 2010),

  • the BLR half-light radius is ≃47 ± 19 light-days; the difference between the sizes the C IV and Hα BLRs cannot be estimated from our data set,

  • the C IV BLR radius agrees with the value obtained from microlensing time series and with the R − L relation derived from reverberation mapping, while the Balmer line BLR is one order of magnitude smaller than the value expected from the R − L relation of Bentz et al. (2013).

The different deformations of the Hα and C IV emission lines observed at the same epoch led Braibant et al. (2017) to suggest that the geometry and kinematics of the Hα and C IV BLRs were different. However, as illustrated in Fig. 4, small differences in BLR sizes are sufficient to produce different microlensing signatures with the same BLR model when the caustic network is dense. The most likely model we found for the Hα BLR in Q2237+305, the Keplerian disk, was also suggested in the lensed quasar HE0435−1223 using a similar analysis (Hutsemékers et al. 2019). This model does agree with the BLR models favored by reverberation mapping and near-infrared interferometry studies of other AGNs (Sect. 1). Microlensing clearly allows us to independently constrain the BLR geometry and kinematics in lensed quasars. While interferometry is currently limited to a few nearby AGNs, and reverberation mapping to low-luminosity low-redshift objects due to the very long response time in luminous and high-redshift objects, microlensing can explore the BLR in bright distant quasars as far as they are lensed and show strong line deformations. As shown in Figs. 2 and 3, high WCI values together with high RBI values can only be reproduced by the KD model. Single-epoch observations of strong, simultaneous, red/blue and wings/core distortions can thus be sufficient to discard the PW and EW models. Multi-epoch data would nevertheless be needed to catch the most sensitive line profile deformations (or place limits on them) and to test more sophisticated BLR models, in particular, by making use of the full μ(v) magnification profile.

1

Eq. A.1 corrects Eq. 8 given in Braibant et al. (2017).

Acknowledgments

We warmly thank Lorraine Braibant for her contribution to the earliest phases of this project. We also thank the referee for useful suggestions. This work was supported by the F.R.S.–FNRS under grants IISN 4.4503.19 and PDR T.0116.21.

References

  1. Abajas, C., Mediavilla, E., Muñoz, J. A., Popović, L. Č., & Oscoz, A. 2002, ApJ, 576, 640 [Google Scholar]
  2. Abajas, C., Mediavilla, E., Muñoz, J. A., Gómez-Álvarez, P., & Gil-Merino, R. 2007, ApJ, 658, 748 [CrossRef] [Google Scholar]
  3. Agol, E., Jones, B., & Blaes, O. 2000, ApJ, 545, 657 [CrossRef] [Google Scholar]
  4. Assef, R. J., Denney, K. D., Kochanek, C. S., et al. 2011, ApJ, 742, 93 [Google Scholar]
  5. Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2009, ApJ, 705, 199 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2010, ApJ, 716, 993 [Google Scholar]
  7. Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [Google Scholar]
  8. Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [Google Scholar]
  9. Braibant, L., Hutsemékers, D., Sluse, D., Anguita, T., & García-Vergara, C. J. 2014, A&A, 565, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Braibant, L., Hutsemékers, D., Sluse, D., & Anguita, T. 2016, A&A, 592, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Braibant, L., Hutsemékers, D., Sluse, D., & Goosmann, R. 2017, A&A, 607, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Decarli, R., Dotti, M., Fontana, M., & Haardt, F. 2008, MNRAS, 386, L15 [NASA ADS] [Google Scholar]
  13. Denney, K. D., Peterson, B. M., Pogge, R. W., et al. 2010, ApJ, 721, 715 [NASA ADS] [CrossRef] [Google Scholar]
  14. Du, P., Lu, K.-X., Hu, C., et al. 2016a, ApJ, 820, 27 [NASA ADS] [CrossRef] [Google Scholar]
  15. Du, P., Lu, K.-X., Zhang, Z.-X., et al. 2016b, ApJ, 825, 126 [CrossRef] [Google Scholar]
  16. Eigenbrod, A., Courbin, F., Sluse, D., Meylan, G., & Agol, E. 2008a, A&A, 480, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Eigenbrod, A., Courbin, F., Meylan, G., et al. 2008b, A&A, 490, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fian, C., Guerras, E., Mediavilla, E., et al. 2018, ApJ, 859, 50 [Google Scholar]
  19. Garsden, H., Bate, N. F., & Lewis, G. F. 2011, MNRAS, 418, 1012 [NASA ADS] [CrossRef] [Google Scholar]
  20. Goicoechea, L. J., Artamonov, B. P., Shalyapin, V. N., et al. 2020, A&A, 637, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Goosmann, R. W., & Gaskell, C. M. 2007, A&A, 465, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Goosmann, R. W., Gaskell, C. M., & Marin, F. 2014, Adv. Space Res., 54, 1341 [NASA ADS] [CrossRef] [Google Scholar]
  23. GRAVITY Collaboration (Sturm, E., et al.) 2018, Nature, 563, 657 [Google Scholar]
  24. GRAVITY Collaboration (Amorim, A., et al.) 2021, A&A, 648, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Greene, J. E., Peng, C. Y., & Ludwig, R. R. 2010, ApJ, 709, 937 [Google Scholar]
  26. Grier, C. J., Pancoast, A., Barth, A. J., et al. 2017a, ApJ, 849, 146 [NASA ADS] [CrossRef] [Google Scholar]
  27. Grier, C. J., Trump, J. R., Shen, Y., et al. 2017b, ApJ, 851, 21 [NASA ADS] [CrossRef] [Google Scholar]
  28. Guerras, E., Mediavilla, E., Jimenez-Vicente, J., et al. 2013, ApJ, 764, 160 [Google Scholar]
  29. Huchra, J., Gorenstein, M., Kent, S., et al. 1985, AJ, 90, 691 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hutsemékers, D., Surdej, J., & van Drom, E. 1994, Ap&SS, 216, 361 [CrossRef] [Google Scholar]
  31. Hutsemékers, D., Braibant, L., Sluse, D., & Goosmann, R. 2019, A&A, 629, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Kaspi, S., Brandt, W. N., Maoz, D., et al. 2021, ApJ, 915, 129 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kochanek, C. S. 2004, ApJ, 605, 58 [Google Scholar]
  34. Lewis, G. F., & Ibata, R. A. 2004, MNRAS, 348, 24 [NASA ADS] [CrossRef] [Google Scholar]
  35. Marin, F., Goosmann, R. W., Gaskell, C. M., Porquet, D., & Dovčiak, M. 2012, A&A, 548, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Mediavilla, E., Jimenez-Vicente, J., Muñoz, J. A., Mediavilla, T., & Ariza, O. 2015, ApJ, 798, 138 [Google Scholar]
  37. Motta, V., Mediavilla, E., Rojas, K., et al. 2017, ApJ, 835, 132 [NASA ADS] [CrossRef] [Google Scholar]
  38. Muñoz, J. A., Vives-Arias, H., Mosquera, A. M., et al. 2016, ApJ, 817, 155 [Google Scholar]
  39. Nemiroff, R. J. 1988, ApJ, 335, 593 [NASA ADS] [CrossRef] [Google Scholar]
  40. O’Dowd, M., Bate, N. F., Webster, R. L., Wayth, R., & Labrie, K. 2011, MNRAS, 415, 1985 [CrossRef] [Google Scholar]
  41. Pancoast, A., Brewer, B. J., Treu, T., et al. 2014, MNRAS, 445, 3073 [Google Scholar]
  42. Peterson, B. M. 1993, PASP, 105, 247 [NASA ADS] [CrossRef] [Google Scholar]
  43. Poindexter, S., & Kochanek, C. S. 2010, ApJ, 712, 668 [NASA ADS] [CrossRef] [Google Scholar]
  44. Popović, L. Č., Mediavilla, E. G., & Muñoz, J. A. 2001, A&A, 378, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Popović, L. Č., Afanasiev, V. L., Moiseev, A., et al. 2020, A&A, 634, A27 [EDP Sciences] [Google Scholar]
  46. Richards, G. T., Keeton, C. R., Pindor, B., et al. 2004, ApJ, 610, 679 [NASA ADS] [CrossRef] [Google Scholar]
  47. Schneider, P., & Wambsganss, J. 1990, A&A, 237, 42 [NASA ADS] [Google Scholar]
  48. Simić, S., & Popović, L. Č. 2014, Adv. Space Res., 54, 1439 [CrossRef] [Google Scholar]
  49. Sluse, D., Claeskens, J.-F., Hutsemékers, D., & Surdej, J. 2007, A&A, 468, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Sluse, D., Schmidt, R., Courbin, F., et al. 2011, A&A, 528, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Sluse, D., Hutsemékers, D., Courbin, F., Meylan, G., & Wambsganss, J. 2012, A&A, 544, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Vakulik, V., Schild, R., Dudinov, V., et al. 2006, A&A, 447, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
  54. Wambsganss, J. 1999, J. Comput. Appl. Math., 109, 353 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wayth, R. B., O’Dowd, M., & Webster, R. L. 2005, MNRAS, 359, 561 [NASA ADS] [CrossRef] [Google Scholar]
  56. Xiao, M., Du, P., Horne, K., et al. 2018, ApJ, 864, 109 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zhang, Z.-X., Du, P., Smith, P. S., et al. 2019, ApJ, 876, 49 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: BLR mean and half-light radii

The mean emission radius, rm, is defined as the radial distance weighted by the surface brightness of the BLR seen in projection onto the plane of the sky:

(A.1)

where (ρ, θ) are the polar coordinates in the plane of the sky, and I is the intensity of the emission from the BLR integrated over the spectral dimension1. The half-light radius r1/2 is defined by the equation

(A.2)

The values of rm and r1/2 are given in Table A.1 in units of the BLR inner radius rin for the different models.

Table A.1.

BLR mean and half-light radii for the different models.

All Tables

Table 1.

Measured magnification and distortion indices.

In the text
Table 2.

Probability (in %) of the different BLR models for Hα and C IV.

In the text
Table 3.

Probability (in %) of [Hα/C IV] BLR model combinations.

In the text
Table A.1.

BLR mean and half-light radii for the different models.

In the text

All Figures

thumbnail Fig. 1.

Flux density ratio , where M = 1, is illustrated as a function of the Doppler velocity for the C IVλ1549 Å and Hα emission lines observed in the lensed quasar Q2237+0305 (red lines). μ(v) is shown after smoothing the line profiles with a 220 km s−1 wide median filter and a 1500 km s−1 wide median filter (thin and thick red lines, respectively). Outside the displayed velocity range, μ(v) becomes unreliable due to the low line fluxes. The continuum-subtracted spectra of images A and D ( and , respectively) are superimposed for comparison (blue and black lines, in arbitrary units).
In the text
thumbnail Fig. 2.

Two-dimensional histograms of simulated WCI, RBI for the C IV emission line. These indices were measured from simulated line profiles that arise from the BLR models KD, PW, and EW seen at inclinations 22°, 34°, 44°, and 62°. The BLR models with an emissivity ϵ0 (rin/r)q that sharply decreases with radius, i.e., q = 3, are illustrated in the left panel, while those that are characterized by a more slowly decreasing emissivity, i.e., q = 1.5, are illustrated in the right panel. Each model also contains a continuum-emitting disk seen under the same inclination. All continuum source radii and BLR sizes used in the simulations are considered, but only the models that reproduce the μcont and μBLR values measured for the C IV emission line are shown, i.e., 2.8 ≤ μcont ≤ 3.3 and 2.24 ≤ μBLR ≤ 2.78 (Table 1). The color map is logarithmic. The WCI and RBI values measured for C IV are plotted with their uncertainties as a small rectangle superimposed on the simulated WCI, RBI distributions.
In the text
thumbnail Fig. 3.

Two-dimensional histograms of simulated WCI, RBI for the Hα emission line. Same as Fig. 2, but only the models that reproduce the μcont and μBLR values measured for the Hα emission line are shown, i.e., 2.2 ≤ μcont ≤ 2.7 and 2.09 ≤ μBLR ≤ 2.35 (Table 1). The WCI and RBI values measured for Hα are plotted with their uncertainties as a small rectangle superimposed on the simulated WCI, RBI distributions.
In the text
thumbnail Fig. 4.

Hα (in red) and C IV (in blue) BLR intensity maps superimposed on the magnification map with 0° rotation. These combinations of models and maps reproduce the measurements within the uncertainties. Left: Hα BLR model is characterized by the following parameters: KD, i = 34°, q = 3, rs = 0.15 rE, and rin = 0.175 rE, and the C IV BLR model is characterized by KD, i = 34°, q = 3, rs = 0.10 rE, and rin = 0.10 rE. The size of the map is 1.5 rE × 1.5 rE. Right: Hα BLR model is characterized by KD, i = 34°, q = 3, rs = 0.15 rE, and rin = 0.75 rE, and the C IV BLR model is characterized by PW, i = 34°, q = 1.5, rs = 0.10 rE, and rin = 0.25 rE. The size of the map is 5 rE × 5 rE.
In the text
thumbnail Fig. 5.

Relative probabilities (in percent) of the BLR mean radius rm and half-light radius r1/2 in rE units. Blue refers to the C IV BLR, and red to the Hα BLR.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.