| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202141691 | |
| Published online | 13 October 2021 | |
The young Hobson family: Possible binary parent body and low-velocity dispersal★
1
Institute of Astronomy, Charles University,
V Holešovičkách 2,
180 00
Prague 8,
Czech Republic
e-mail: vokrouhl@cesnet.cz, mira@sirrah.troja.mff.cuni.cz
2
Department of Astronomy, Faculty of Mathematics, University of Belgrade,
Studentski trg 16,
11000
Belgrade,
Serbia
3
Southwest Research Institute,
1050 Walnut St, Suite 300,
Boulder,
CO
80302,
USA
Received:
1
July
2021
Accepted:
3
August
2021
Context. Asteroid families with ages younger than 1 Myr offer an interesting possibility of studying the outcomes of asteroid disruptions that are little modified by subsequent evolutionary processes.
Aims. We analyze a very young asteroid family associated with (18777) Hobson in the central part of the main belt. We aim at (i) understanding its peculiar size distribution, and (ii) setting an upper limit on the characteristic dispersal velocity at subkilometer sizes corresponding to the smallest visible Hobson members.
Methods. We identified the Hobson family using an up-to-date asteroid catalog. A significant increase in the number of its known members allowed us to study their size distribution and compare it with computer simulations of catastrophic disruptions. Backward orbital integrations of the heliocentric orbits allowed us to confirm the previously suggested age of Hobson and helped to estimate limits of the ejection speed.
Results. The Hobson family has an unusual size distribution: two nearly equal-size bodies, followed by a population of smaller asteroids, whose distribution takes a characteristic power law. There are two possibilities to explain these data. Either a canonical impact onto a single parent body, requiring fine-tuned impact conditions that have not been studied so far, or an unconventional model for the parent object of the Hobson family, namely a binary with ≃7−9 km primary and a ≃2.5 km secondary. In the latter case, the primary was disrupted, leaving behind the largest remnant (18777) Hobson and a suite of subkilometer asteroids. The second largest asteroid, (57738) 2001 UZ160, is the nearly intact satellite of the parent binary. The excellent convergence of nominal orbits of Hobson members sets an upper limit of ≃(10−20) m s−1 for the initial dispersal velocity of the known members, which is consistent with both formation models. The Hobson family provides a so far rare opportunity of studying disruptions of small asteroids in a situation in which both the material strength and reaccumulation efficiency play an important role.
Key words: celestial mechanics / minor planets, asteroids: general
Movies associated to Figs. 8 and 9 are available at https://www.aanda.org
© ESO 2021
1 Introduction
Analyses of asteroid families, which consist of the dispersed pieces of a parent body that experienced a strong impact, belong to the fundamental tools that allow us to study asteroids in planetary science. By telescopic observations of the identified fragments, the families offer a look into a previously existing body and thereby allow us to constrain the degree of its thermal processing and geophysical differentiation. Studying the configuration of asteroids constituting a family, researchers may constrain the fragmentation process of the parent body. Statistics of families with parent bodies of different sizes in a given population (such as the main belt) may help constrain the general lines of its collisional evolution. The dynamical processes that may affect the configuration of fragments in a given family after it formed may provide information about its age. Some families may be suitably situated to instantly deliver large number of fragments to some of the principal resonant escape hatches to the planet-crossing population and therefore potentially affect the impactor flux onto terrestrial planets in the past. Kiyotsugu Hirayama would likely be surprised by the immense importance 1 of the asteroid families, about a century after he discovered the first three examples (Hirayama 1918).
The parameters of the size distribution and the velocity field with which the fragments were dispersed at the family-formation event are one of the data that researchers are trying to determine from the configuration of the fragments. This provides interesting information not only about the mechanics of the parent-body fragmentation, but may potentially provide important clues for the efficiency with which specific families were capable of directly delivering sizable fragments into resonances and thus set them on track to the planet-crossing populations. Hirayama himself considered this possibility (Hirayama 1928), see also Brouwer (1950, 1951), and obtained dispersal velocities of several hundreds of meters per second. These early works were able to grasp just the core of the families, consisting of their largest members, which means that the dispersal velocities of smaller members would likely be even higher. Modern versions of these efforts could have started only after (i) a much larger number of asteroids had been discovered, and (ii) tools for determining accurate values of the proper orbital elements were developed and became widely accessible. These two criteria are met since the early 1990s, and Zappalà et al. (1996) and Cellino et al. (1999) were among the first to apply techniques for estimating the dispersal velocity field from the observed families. However, these works only confirmed the earlier-noted problem that the determined velocities were systematically too high (e.g., Zappalà et al. 2002). At the same time, a solution of the discrepancy was at hand and consisted of the recognition of the dynamical processes that in the long term disturb the proper orbital elements that are used in the methods for determining velocity fields methods mentioned above. These processes primarily are of two types: (i) size-independent chaotic dynamics in diffusive mean-motion resonances (e.g., Nesvorný et al. 2002b), and (ii) size-dependent dispersion due to the Yarkovsky effect (e.g., Farinella & Vokrouhlický 1999; Bottke et al. 2001). In brief, the configuration of many asteroid families in the space of proper orbital elements is too inflated by the dynamical perturbations, such that the information about a much smaller initial state that is directly related to the dispersal velocity field is basically effaced. While some attempts to remove the dynamical component exist (e.g., Vokrouhlický et al. 2006), their accuracy becomes quite low as soon as the family age exceeds several tens or hundreds of million years.
The conditions required to overcome the dynamical evolution problem is apparent: the time to perturb the family configuration must have been short, or in other words, young families must be studied. While evident, the plan has its own difficulties. First, recent breakups would statistically imply smaller parent bodies, and thus also smaller sizes of the currently observed fragments. This again creates the need to extent reliable information about asteroid populations to smaller objects. Second, a chosen family needs to be confirmed to be young. An important step toward young asteroid family science occurred in 2002 with discovery of the Karin family (Nesvorný et al. 2002a). In addition to an increased number of known asteroids in the available catalogs, the key novelty of this work consisted of the idea that the origin of the family was dated by convergence of the secular angles, longitude of node Ω and perihelion ϖ, of the identified members. The families are by definition tight clusters in semimajor axis, eccentricity, and inclination values. This is how they are identified in the first place. However, the values of secular angles are generally randomized by differential precession. At their origin, even the Ω and ϖ values must have been clustered, however. Therefore, ideally, past simultaneous convergence of the secular angles of a significant number of members unambiguously signals the epoch of the family origin. Nesvorný et al. (2002a) studied 13 suitable Karin members and reported that this family is 5.8 ± 0.2 Myr old (the result may even be improved using the increasing number of recognized Karin members; e.g., Nesvorný & Bottke 2004; Carruba et al. 2016). More details about the Karin family, especially about what it can tell us about the initial dispersal velocities of its members, are given in Sect. 4.
Karin has started a new era of intense search for young asteroid families. Experience showed that the secular-angle convergence technique can be applied for families whose age is younger than ≃ (10−15) Myr (several examples are given in, e.g., Nesvorný et al. 2015). A new twist on the way to this goal was reached by the discovery of very young clusters with ages younger than ≃1 Myr. These extremely young structures possess an additional quality compared to the older families: their osculating (or mean) secular angles at the current epoch are still clustered because their differential precession did not have enough time to disperse them since the family origin. This property plays an important role in their identification (see also Sect. 2.2). These very young clusters therefore represent an even more pristine state that potentially allows us to characterize details of their formation event, including the velocity dispersal parameters. The first examples were discovered by Nesvorný et al. (2006b) and Nesvorný & Vokrouhlický (2006). While fascinating, many of the very young clusters are still poorly characterized because only few of their members are discovered so far. For only three cases are more than ~ 20 members known well enough to allow serious analysis 2: (i) the Datura family (e.g., Vokrouhlický et al. 2009, 2017a), (ii) the Schulhof family (e.g., Vokrouhlický & Nesvorný 2011; Vokrouhlický et al. 2016), and (iii) the Adelaide family (e.g., Vokrouhlický et al. 2021). The Datura and Adelaide families are examples of large cratering events, such that the largest observed fragment in the family gives us a good idea about the parent body. The Schulhof family is at the border between the cratering and catastrophic fragmentation of the parent object. None of the three cases of very young clusters with a wealth of fragments is the result of a highly energetic collision between a projectile and a parent body. This is expected because an impact by a small projectile is more likely than an impact by a large projectile, as is required for a super-catastrophic collision. This situation would be perhaps be the most interesting as far as the information about the velocity dispersal field is concerned, however. As a rule of thumb, the cratering events lift the escaping fragments with a characteristic velocity similar to the escape velocity from the parent object.
With this motivation in mind, we analyze the Hobson family. A tight cluster of four asteroids about the middle main belt object, (18777) Hobson was first reported by Pravec & Vokrouhlický (2009) as a side product of their search for asteroid pairs. These authors therefore did not pay much attention to its analysis other then noting the young age, younger than 0.5 Myr, based on the mutual convergence of their orbital secular angles. Rosaev and Plávalová then studied the Hobson cluster in a series of papers (see Rosaev & Plávalová 2016, 2017, 2018) with the following principal conclusions: (i) with more complete datasets of asteroids available, they completed the membership in this family up to nine members by 2018, (ii) they recognized the chaotic nature of the orbital evolution for most of the family members and pointed out a possible role of perturbations by the dwarf planet Ceres, and (iii) they used a simple model to constrain the Hobson family age, obtaining 365 ± 67 kyr. Finally, the Hobson cluster was briefly analyzed by Pravec et al. (2018), who added two more members (pushing the count to 11 asteroids) and confirmed the age to between 300 and 400 kyr with a different approach. They also concluded that the Hobson family is an outlier in their search for clusters possibly formed by a rotational fission of a parent asteroid. In all likelihood, it must have formed in a more traditional way, notably by catastrophic collision of two asteroids. Finally, they conducted valuable photometric observations of the two largest members, (18777) Hobson and (57738) 2001 UZ160 (Sect. 2.1).
Taking up this preliminary information, we revisit the Hobson family by noting a significant increase in the population of its fragments in the updated asteroid catalogs. Our count indicates a total of 45 members (Sect. 2.2). This relatively large sample allows us to improve the analysis and argue that the Hobson family probably is the result of a collision of a kilometer-sized projectile and a target that was about ten times larger (Sects. 2.3 and 3). Interestingly, the size distribution of the Hobson fragments presents nontrivial difficulties. It either requires a low-probability parametric combination that was not sampled in previous studies, or even a novel idea about is parent object: a typical small binary asteroid in the inner main belt population (Sects. 2.3 and 3). The analysis of the past convergence of the heliocentric orbits of the Hobson members provides information about the characteristic dispersal velocity at the origin (Sect. 2.4), and this appears to be in accord with both formation models. Theregime of kilometer-size parent objects colliding at high speed has not been probed yet in the available family data (Sect. 4). Our census of family members, together with their proper elements, is given in Appendix A. Some details related to our simulations of small-asteroid breakups are provided in Appendix B.
2 Hobson family
2.1 Largest fragments
The Hobson family is located in the middle part of the main belt and consists of small asteroids. As a result, we have only very little information about their physical properties. Fortunately, Pravec et al. (2018) conducted calibrated photometric observations of the two largest members in the season 2013/2014 with the following results:
The larger fragment, (18777) Hobson, had a synodic rotation period of 10.227 ± 0.004 h and a rather low light-curve amplitude of 0.21 magnitude. Observations at different filters provided a color index V − R = 0.477 ± 0.010 magnitude (using the Johnson-Cousins standard system) and an absolute magnitude H = 15.16 ± 0.05 at the middle of the light curve.
The smaller fragment, (57738) 2001 UZ160, had a synodic rotation period of 20.51 ± 0.01 hr and a larger light-curve amplitude of 0.65 magnitude. Observations at different filters provided a color index V − R = 0.46 ± 0.02 magnitude and an absolute magnitude H = 15.41 ± 0.05 at the middle of the light curve.
The slow rotation periods are notable, and the information about statistically compatible values of the color index V − R is important. They are consistent with S-type classification, which is not surprising in this zone of the asteroid main belt. We can thus extrapolate this result and consider that the Hobson family belongs to the S-type group. The geometric albedo value of S-type asteroids is pV = 0.20 ± 0.05 (e.g., Pravec et al. 2012), and this helps us to estimate that the sizes of (18777) Hobson and (57738) 2001 UZ160 are 2.82 ± 0.39 km and 2.52 ± 0.32 km (considering an uncorrelated uncertainty in absolute magnitude and geometric albedo for simplicity).
2.2 Family identification
In order to identify members in the Hobson family in current asteroid catalogs, we used the straightforward approach of Vokrouhlický et al. (2021). Following previous indications of its very young age, we assumed that the family must be clustered in a five-dimensional space of the osculating orbital elements: semimajor axis a, eccentricity e, inclination I, longitude of node Ω, and longitude of perihelion ϖ (alternatively, argument of perihelion ω). The higher dimensionality of this space, over just three dimensions of the proper orbital element space in which asteroid families are typicallyidentified (e.g., Nesvorný et al. 2015, and Appendix A), helps us to unambiguously discern the family members from background population of asteroids. We considered (18777) Hobson as a point of reference and constructed a box zone around it by letting the osculating orbital elements vary in some range: (i) semimajor axis ± 0.03 au, (ii) eccentricity ± 0.03, (iii) inclination ± 0.2°, (iv) longitude of node ± 25°, and (v) argument of perihelion ± 25°. The adopted range of values is an order of magnitude (or significantly more in secular angles) larger than the short-periodoscillations of the osculating orbital elements of asteroids in this zone. We used the catalog of asteroid orbital elements provided by Minor Planet Center (MPCORB.DAT) as of July 15, 2021, which contained about 1 100 000 entries, and we only discarded very poorly characterized single-opposition orbits with an observation arc shorter than a week.
Our search in this box zone resulted in 69 objects that are clearly divided into two populations: (i) 24 dispersed asteroids filling the whole zone roughly uniformly, these are the background population, and (ii) 45 objects (including Hobson) that are tightly clustered about the origin, which represent the Hobson family. Examples are shown in Figs. 1 and 2, where we show projections onto a plane of secular angles Ω versus ϖ and Ω versus I, respectively. The compactnessof the Hobson family in secular angles (Fig. 1) is impressive: if we were to statistically characterize their distribution, we would obtain 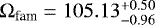 in degrees and
in degrees and 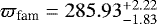 in degrees. Compare these values to the dispersion of nearly an order of magnitude larger in both angles of the 500 kyr old Datura family (see Fig. 12 in Vokrouhlický et al. 2017a) and to the basically nonclustered values of secular angles for ≤ 4.5 Myr old Nele family (see Fig. 5 in Carruba et al. 2018). There is hardly any doubt about the statistical significance of the Hobson family. Just taking the data from Fig. 1, we may interpret the 24 scattered background objects as evidence of a background population density of ~ 0.01 per degree square. In the 3° × 5° vicinity of (18777) Hobson, we have 45 asteroids, therefore the object density locally is ~3.0 per degree square. This argument does not even take into account the significant clustering in all other osculating elements of our initial search (Fig. 2). Additionally, we numerically integrated the nominal orbits of all 69 objects in the box zone of our search backward in time, reaching the 1 Myr epoch before the present. The orbits of all suggested Hobson members indicate a convergence of the secular angles to (18777) Hobson some 320 kyr ago (Sect. 2.4), while the orbits of the proposed 24 background asteroids do not converge at any moment during our test. The complete list of currently known Hobson members is provided in Table A.1.
in degrees. Compare these values to the dispersion of nearly an order of magnitude larger in both angles of the 500 kyr old Datura family (see Fig. 12 in Vokrouhlický et al. 2017a) and to the basically nonclustered values of secular angles for ≤ 4.5 Myr old Nele family (see Fig. 5 in Carruba et al. 2018). There is hardly any doubt about the statistical significance of the Hobson family. Just taking the data from Fig. 1, we may interpret the 24 scattered background objects as evidence of a background population density of ~ 0.01 per degree square. In the 3° × 5° vicinity of (18777) Hobson, we have 45 asteroids, therefore the object density locally is ~3.0 per degree square. This argument does not even take into account the significant clustering in all other osculating elements of our initial search (Fig. 2). Additionally, we numerically integrated the nominal orbits of all 69 objects in the box zone of our search backward in time, reaching the 1 Myr epoch before the present. The orbits of all suggested Hobson members indicate a convergence of the secular angles to (18777) Hobson some 320 kyr ago (Sect. 2.4), while the orbits of the proposed 24 background asteroids do not converge at any moment during our test. The complete list of currently known Hobson members is provided in Table A.1.
2.3 Size distribution
After we identified the currently known members of the Hobson family, we proceeded with further analyses. We started with the absolute magnitude H (or size D) distribution of the Hobson members. As mentioned in Sect. 2.1, accurate absolute magnitude values have been obtained from dedicated observations of the two largest fragments (18777) Hobson and (57738) 2001 UZ160. Unfortunately, no data of comparable accuracy are available for any of the other members. We therfore used absolute magnitudes from the MPCORB.DAT database. In addition to a random component in their uncertainty, Pravec et al. (2012) argued that these values may have a systematic offset of ≃ 0.25 magnitude for their respective H range (Fig. 1 in that reference). If we had to map the magnitude distribution to the size distribution, we may adopt the simplifying assumption of a pV = 0.2 geometric albedo based on S-type classification of the largest members in the family (Sect. 2.1).
Figure 3 shows our results. We start with the left panel, which provides the magnitude distribution of all members in the Hobson family. Starting from the third largest fragment at H ≃ 17.1 magnitude, the spectrum of magnitudes among the Hobson members steeply increases and may be approximated, at least in about 1 magnitude interval of H values, with a power law N(< H) ∝ 10γH with γ ≃ 0.95. Beyond magnitude 18, a strong incompleteness produces a bend in the distribution, which obviously brings the question which features hold and which are biased in our H(< H) knowledge. This is in principle a difficult question, and we answer it only approximately using information in Hendler & Malhotra (2020). These authors developed an empirical approach to characterize the completion limit Hlim of the main belt population of asteroids as a function of semimajor axis. At a ≃ 2.56 au, where the Hobson family is located, they obtained Hlim ≃ 17 magnitude (with about 0.2 magnitude uncertainty). This information suggests that (i) the population of Hobson members may be completely known at the large end, in particular, we may not be missing any fragment in the “gap” of the H(< H) distribution before the steep increase starts at about 17 magnitude, and (ii) the population beyond 17 magnitude becomes incomplete, with the implication that the true power-law exponent γ is steeper than the one we find here (Fig. 3). With this information, we return to the magnitude distribution of the Hobson members that should be known completely, namely the largest bodies. As we recalled in Sect. 2.1, this is represented by the pair of nearly equal-sized asteroids (18777) Hobson and (57738) 2001 UZ160. In the next two sections, we verify the mutual convergence of their orbits in the past and also confirm the convergence with other smaller members in the family. This excludes the possibility that either of them would be an interloper in the Hobson family. On the other hand, an arrangement of fragments in magnitude distribution as shown in the left panel of Fig. 3 is not seen in any of the known families 3, and it has yet to be reproduced in computer simulations of family-formation events. We consider, for instance, the most relevant set of such simulations in Ševeček et al. (2017). These authors conducted a large suite of simulations, in which a 10 km size parent asteroid was hit by projectiles of various sizes between ≃0.3 and 1.85 km, with various impact velocities between 3 and 7 km s−1, and at various impact angles. The situations covered basically all impact energy regimes, from subcatastrophic cratering events to supercatastrophic disruptions (see additional results of Ševeček et al. 2019, where effects of parent body rotation were studied). The mosaic of all possible resulting size (or equivalently, magnitude) distributions of fragments is shown in Fig. 1 of Ševeček et al. (2017) or Fig. 2 of Ševeček et al. (2019). None of them matches the observed distribution in the left panel of Fig. 3. Either (i) some assumptions in the Ševeček et al. (2017, 2019) studies were not applicable to the Hobson family parent object (possibly related to its internal structure or unsampled part of multidimensional parametric space of the reported disruption models), or (ii) something else must be taken into account.
If the first, we need to rerun simulations similar to Ševeček et al. (2017, 2019) with the emphasis on unsampled parametric combinations or so far unused assumptions about the internal mechanical properties of the target body. If the second, we need to seek a more unconventional solution. In this respect, we note the results from Pravec et al. (2016). These authors studied small binary asteroids in the near-Earth, Hungaria, and inner main-belt populations. For the inner main-belt group, Pravec et al. (2016) confirmed that about 15 ± 4% of D < 15 km asteroids are binary, at least half of which are systems with a close-by spin-orbit synchronized satellite on a nearly circular orbit. The typical size ratio of the satellite and primary in these binary systems is between 0.2 and 0.4, the typical satellite distance from the primary is between 2 and 3 (referred to as the primary size), and the typical orbital periods of the satellite are between 15 and 30 hr. Given their significant abundance in the population, it is conceivable that the parent objects of some small asteroid families in the inner main-belt would be binaries. Depending on the geometry of the impact, either primary or the satellite (or possibly both) may be involved in the collision and fragmentation. It is therefore possible, as an example, that the primary component in the binary collisionally disrupts and feeds the family with its fragments, leaving the former satellite largely intact.
Translated into the reality of the Hobson family, we might assume that (57738) 2001 UZ160 is the former satellite of the parent binary, for example. If the geometry of the family-forming impact allows it, this member may still record the properties of the satellite, including its size of ≃ 2.5 km and the synchronized rotation period of 20.5 h. These values are plausible, and they would imply an expected size of the broken primary in the 6 and 12 km range. The characteristic initial satellite orbit would have 15 and 30 km radius. Because the entire fragmentation process concerns the former primary in the binary system, the right panel of Fig. 3 would be relevant for comparison with computer simulations of small-asteroid disruptions such as in Ševeček et al. (2017, 2019). Asteroid (18777) Hobson would be the largest remnant, and the suite of kilometer-sized and smaller asteroids would be the small-size tail in the distribution. We note that the power-law approximation N(< H) ∝ 10γH of the tail population would have γ = 1.15 now. Observational limitations imply that the true (unbiased) distribution would have γ > 1.2 (say). The 2 magnitude gap between (18777) Hobson and the foot of the tail translates into a factor 10−0.4 ≃ 2.5 in size (independent of the surface albedo value). These are then the parameters to be matched by the results from computer simulations of asteroid disruptions (together with the proof that the secondary component in the parent binary remains intact).
In Sect. 3 we explore both possibilities using a smoothed-particle hydrodynamics (SPH) code for the fragmentation phase, followed with an N-body integrator for subsequent gravitational reaccumulation (thence the SPH/N-body numerical approach) based on the methods presented in Ševeček et al. (2017, 2019) (see also Appendix B). Since the works of Michel et al. (2001, 2003), this approach became the default tool for modeling the asteroid family formation. In particular, results form the SPH/N-body simulations allow us to compare the resulting size distribution of the synthetic Hobson family with the data shown above. We also obtain a prediction of the characteristic dispersal speeds of the fragments with respect to the largest remaining fragment, and these may be compared with results from our convergence experiments in Sects. 2.4 and 2.5.
 |
Fig. 1 Osculating values of the heliocentric secular angles in the ecliptic system in the target zone surrounding the Hobson family: the longitude of node Ω (abscissa) vs. the longitude of perihelion ϖ (ordinate). Left panel: total of 69 asteroids, clearly divided into (i) a random background population, and (ii) a strongly clustered family (symbols highlighted by the rectangle). Because the initial search used the argument of perihelion ω, the actively probed region around (18777) Hobson becomes tilted in Ω vs. ϖ axes, and the corner triangles in dark gray are excluded. Right panel: zoom on the Hobson family structure (range of the axes as in the gray rectangle in the left panel). The two largest asteroids, (18777) Hobson and (57738) 2001 UZ160, are highlighted in red and blue with diamonds. All smaller members are shown by filled circles: multi-opposition orbits in black, and the six single-opposition orbits in gray (asteroids 2014 JH120, 2014 OJ66, 2020 JM31, 2020 KP36, 2020 OY50, and 2021 MO5; Table A.1). The family is unusually compact in both Ω and ϖ, promising very young age. |
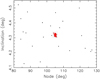 |
Fig. 2 Osculating values of the longitude of node Ω (abscissa) vs. the inclination I (ordinate) in the target zone surrounding the Hobson family. The limits of the axes depict our search zone. The members of the Hobson family (red symbols in the rectangle) are strongly clustered and can easily be distinguished from the dispersed background population of asteroids. |
 |
Fig. 3 Cumulative distribution N(< H) of the absolute magnitude H for known Hobson family members. Left panel: all members included: the red and blue diamonds denote the two largest remnants (18777) Hobson and (57738) 2001 UZ160, and filled circles show small members in the family. The gray line shows the power-law relation N(< H)∝ 10γH for γ = 0.95, which approximates the distribution of small members. Right panel: the second largest member, (57738) 2001 UZ160, is excluded from the distribution: the red diamond denotes (18777) Hobson, and the filled circles are smaller fragments in the family. The power-law relation N(< H)∝ 10γH has now γ = 1.15 (simply as an effect of removing the second largest body from the sample and linear-logarithmic scales on the axes). The upper abscissa in both panels provides an estimate of the size, assuming the geometric albedo pV = 0.2 (a plausible value for S-type asteroids). |
2.4 Nominal convergence of secular angles
We now return to the issue of a past orbital convergence of members in the Hobson family. As discussed in Sect. 1, in our context, we aim at shrinking the differences in the secular angles Ω and ϖ to near-zero values for as many orbits in the family as possible. The present-day ≃ 1° and ≃ 2° dispersion values in Ω and ϖ may already look very small, but in fact, they are not. Using the Gauss equations of the perturbation calculus (e.g., Nesvorný & Vokrouhlický 2006), it is easily clear that they still correspond to nearly 60 m s−1 dispersal in velocities (using Eq. (1) below). These values are expected in the largest families with > 100 km size parent objects, but far lower values are seen in tighter families (as an example, see Nesvorný et al. 2006a). This observation motivates a need of further convergence of secular angles in the past. Rosaev & Plávalová (2017, 2018) have already shown that this is possible for up to six members in the Hobson family. Here we take up their effort and extend it to all currently known members in the family (excluding only the poorly determined case of the six single-opposition members 2014 JH120, 2014 OJ66, 2020 JM31, 2020 KP36, 2020 OY50, and 2021 MO5; Table A.1).
While the behavior of the secular angles of all propagated orbits is the basis of the convergence test, Nesvorný & Vokrouhlický (2006) found it interesting to combine this multidimensional information into a single target parameter,
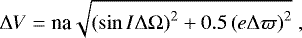 (1)
(1)
where na ≃ 18.6 km s−1 is the characteristic orbital velocity of the Hobson members, e and sin I are the orbital eccentricity and inclination (we may use the values of (18777) Hobson), and ΔΩ and Δϖ are dispersal values of longitude of node and perihelion. These quantities are defined as 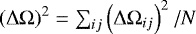 , where ΔΩij are simple differences in nodal longitudes of ith and jth objects, and N is the number of pair combinations between asteroids tested (and similarly for perihelia). In this way, the target function ΔV has a dimension of velocity and in a statistical sense, approximates the magnitude of the dispersal velocity among the orbits in the cluster. In spite of using only Ω and ϖ angles, ΔV depends on all three components of the velocity vectors and represents an average over the position in heliocentric orbit (true anomaly) in which different orbits are compared. Observing structure of the Gauss equations, Rosaev & Plávalová (2018) proposed analternative target function,
, where ΔΩij are simple differences in nodal longitudes of ith and jth objects, and N is the number of pair combinations between asteroids tested (and similarly for perihelia). In this way, the target function ΔV has a dimension of velocity and in a statistical sense, approximates the magnitude of the dispersal velocity among the orbits in the cluster. In spite of using only Ω and ϖ angles, ΔV depends on all three components of the velocity vectors and represents an average over the position in heliocentric orbit (true anomaly) in which different orbits are compared. Observing structure of the Gauss equations, Rosaev & Plávalová (2018) proposed analternative target function,
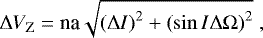 (2)
(2)
where 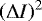 is now the dispersion of the inclination values among the propagated orbits. While ΔVZ again represents a statistical mean over the phase of the heliocentric motion, it provides information about the normal component VZ to the orbital plane, statistically averaged over the pair identification of orbits in the cluster. Therefore ΔVZ conveniently isolates the information about this normal velocity component, but does not tell us anything about the two in-orbit components. The diagnostic advantage of either ΔV or ΔVZ consists of their dependence on at least one of the secular angles. This is because these angles drift secularly, in contrast to the semimajor axis, eccentricity, or inclination values, which only oscillate with terms of various periods (both shorter and longer than the possible age of the family).
is now the dispersion of the inclination values among the propagated orbits. While ΔVZ again represents a statistical mean over the phase of the heliocentric motion, it provides information about the normal component VZ to the orbital plane, statistically averaged over the pair identification of orbits in the cluster. Therefore ΔVZ conveniently isolates the information about this normal velocity component, but does not tell us anything about the two in-orbit components. The diagnostic advantage of either ΔV or ΔVZ consists of their dependence on at least one of the secular angles. This is because these angles drift secularly, in contrast to the semimajor axis, eccentricity, or inclination values, which only oscillate with terms of various periods (both shorter and longer than the possible age of the family).
Ideally, ΔV or ΔVZ thus exhibit a clear minimum at the epoch of the family origin. In an ideal world, the result would be easy: one simulation would be enough to provide the exact epoch of the target function minimum (i.e., family origin), and its value would be the velocity dispersion. The real world is more complex because there are many more degrees of freedom to be considered. They have to do with our ability to reconstruct the orbital architecture of the family members in the past (typically hundreds of thousands of years for detected very young families). This is influenced by two aspects: (i) the initial orbital conditions of family-member asteroids are not known accurately even at the current epoch, and (ii) the mathematical model, which allows us to reconstruct the past states of the family orbits, may not be completely constrained or exhibit chaoticity. Both effects would require that every asteroid in the family is represented by a variety of clones for both (i) and(ii), and a huge number of possible clone mutual identifications would have to be considered. This is because each of these possible clone configurations would have its own time dependence on the target functions ΔV or ΔVZ in the past. Despite their global similarity, that is, most of them would reach a minimum at some epoch, they would not be identical. Shifts in (i) epochs of minima, and in (ii) minimum values would be inevitable. A statistical criterion would be needed to describe the results.
Starting with the works of Nesvorný et al. (2006b) and Nesvorný & Vokrouhlický (2006), researchers mostly used one possible variant. With a predefined tolerance value of ΔV magnitude, for instance, the estimated escape velocity from the parent objects of the family, they considered all possible ΔV functions, individual to clone configurations, that met the criterion and characterized them statistically. The goal of this approach was primarily the determination of the family age and its uncertainty, while the velocity dispersal at origin was only assumed. We did not follow this way. We are less interested in the age of the Hobson family, but we wish to learn something about the initial dispersal velocity of the observed fragments. We approached this goal using the simplest method, namely by using (i) just the nominal (best-fit) orbits of the family members, and (ii) the simplest force model for the orbital propagation. In (ii) we consider only the gravitational effects from the Sun, planets, and largest asteroids (Ceres, Pallas, and Vesta). We do not include the effects of thermal accelerations known as the Yarkovsky effect. This brings us back to the single, “ideal world” simulation mentioned above. However, the difference is in the interpretation of the results. We wish to determine the minimum of ΔV or ΔVZ that can be reached in the simulation, and we consider it to be the upper limit of the initial velocity dispersal of the family fragments. It is obvious that adding more degrees of freedom, represented by the clone variants of the objects (especially those related to the thermal accelerations), will allow us to decrease the minima of ΔV or ΔVZ. Quite likely, the true history of the family will be among these improved solutions. This is because it would appear strange that the hugely simplified base model would be better than truth.
We used a well tested swift_mvs orbit propagation package 4 for our runs. Planetary initial conditions were taken from the JPL ephemerides, and asteroid orbits (including Ceres, Pallas, and Vesta) were taken from the AstDyS site 5. All data were referred to the initial epoch MJD 59200.0, and orbital velocities were reversed to perform backward-in-time integration. We used a three-day time step and output the state vectors of all bodies every five years. The longest epoch reached in our simulation is 1 Myr. We performed two simulations: (i) the base model that only included planetary perturbations, and (ii) the extended model that also contained perturbations by Ceres, Pallas, and Vesta. This allowed us to estimate the role of the massive objects in the main belt on the Hobson family history. Before we report the results, we computed mean orbital elements of the Hobson members by eliminating short-period terms with peroids shorter than 500 yr. This is because our output is too sparse, and additionally, numerical integration is subject to effects of dynamical chaos, to resolve family formation conditions in the phase of motion about the Sun 6.
The upper panels in Fig. 4 show the behavior of the secular angles, the longitude of node (in red), and longitude of perihelion (in blue), referred to the value of (18777) Hobson in the base simulation. The left panels show the 12 largest members in the family with H ≤ 17.75 magnitude, and the right panels show all 39 multi-opposition members (see Table A.1). Presumably, the orbits of the additional set of small asteroids in the right panels are less constrained and potentially subject to stronger perturbations from the Yarkovsky effect. The bottom panels then summarize the data from the top panel into the numerical value of the ΔV target function from Eq. (1). We first discuss the results for 12 large asteroids at the left. We note an excellent degree of simultaneous convergence of both nodes and perihelia some 330 kyr ago. This agrees well with similar results of Rosaev & Plávalová (2017), but now for more than twice as many objects. In response, the ΔV target function has a sharp minimum at the same epoch, reaching 5.9 m s−1 at best. This value is impressively close to the estimated escape velocity from the parent body of the Hobson family (Sect. 3). When less accurate orbits of small fragments are included in the simulation, now a total of 39 orbits in right panels, the convergence becomes slightly defocused, and therefore the minimum ΔV value is slightly higher than 11.5 m s−1. This was expected, but the optimum ΔV values are still quite low. This witnesses the rather small dispersal velocity field down to fragments of ≃ 0.5 km. The minimum now corresponds to 307 kyr epoch, but the difference is well within the formal uncertainty value stated in Rosaev & Plávalová (2017).
The results do not change much when perturbations from Ceres, Pallas, and Vesta are included in the extended simulations. For instance, the minimum values of the ΔV target function are (i) 9.3 m s−1 when the 12 largest fragments are used (as in the left panels of Fig. 4), and (ii) 16.2 m s−1 when all 39 fragments are used. This is only slightly worse than in the base simulation. Unless very close encounters, the effects of the three most massive objects in the main belt (Ceres in particular) are moderate on the few hundred kyr timescale of interest.
Panels on Fig. 5 show the results we obtained using the ΔVZ target function (bottom) and the relevant angular differences with respect to the orbit of (18777) Hobson (see Eq. (2)): (i) inclination (in blue), and (ii) longitude of node multiplied with sine of inclination (in red). As expected, only the latter component shows a converging pattern, while the inclination oscillates. However, a sign of convergence for the inclination is expressed by a decrease in the oscillation amplitude. The convergence feature may look less impressive than in Fig. 4, but note the ordinate scale of both figures. The bottom panels show the behavior of the ΔVZ target function. Its minimum occurs consistently at about 320 kyr ago, and the minimum values are (i) 2.6 m s−1 when the 12 largest fragments are taken into account (left), and (ii) 6.4 m s−1 when all 38 fragments are taken into account (right). Interestingly, these values are not far from a factor 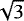 smaller than the corresponding minimum values of ΔV target function. This may indicate near isotropy of the ejection field of the Hobson fragments at origin.
smaller than the corresponding minimum values of ΔV target function. This may indicate near isotropy of the ejection field of the Hobson fragments at origin.
Finally, we recall that our definition of the target function ΔV in Eq. (1) contains root-mean-square ΔΩ and Δϖ values that were computed over all pair combinations of the orbits (definition introduced by Nesvorný & Vokrouhlický 2006, and similarly for ΔVZ in Eq. (2)). In this way, (i) there is no preferred orbit, but (ii) the ΔV and ΔVZ values may be conservatively high by an outlying contribution from distant orbits of small fragments in the family. Alternatively, a priori, a reference orbit in the family may be selected and a modified target function ΔV′ and 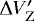 introduced, in which the ΔΩ and Δϖ are the root-mean-square values of the difference with respect to the reference orbit alone. If the reference orbit resides well within the center of the family, these values may be lower. For the sake of a test, we constructed these alternative options ΔV′ and
introduced, in which the ΔΩ and Δϖ are the root-mean-square values of the difference with respect to the reference orbit alone. If the reference orbit resides well within the center of the family, these values may be lower. For the sake of a test, we constructed these alternative options ΔV′ and 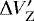 of the target function using two different reference orbits: (i) (18777) Hobson, and (ii) (57738) 2001 UZ160.
of the target function using two different reference orbits: (i) (18777) Hobson, and (ii) (57738) 2001 UZ160.
When the orbit of (18777) Hobson is chosen as a reference, ΔV′ reaches a minimum of about 4.4 m s−1 when orbits of H < 17.75 members are used, and 8.7 m s−1 when all members on multi-opposition orbits are used. These values are slightly lower than the minima in the bottom panels of Fig. 4, 5.9 and 11.5 m s−1, respectively. This confirms that the orbit of (18777) Hobson suitably lies in the center of the family. Interestingly, when the orbit of (57738) 2001 UZ160 is chosen as a reference, ΔV′ reaches a minimum of about 8.9 m s−1 when orbits of H < 17.75 members are used, and 12.2 m s−1 when all members on multi-opposition orbits are used. These values are higher, implying that the nominal orbit of (57738) 2001 UZ160 is slightly offset from the true center of the family. This may be an interesting indication in support of our model in which the parent object of the Hobson family is a binary (see discussion in Sect. 3). However, the differences are small and should not be overstated. A more thorough convergence analysis, in which geometrical and Yarkovsky clones of the family members are taken into account, could resolve this issue in the future.
 |
Fig. 4 Top: convergence of the mean values of secular angles, longitude of node in red and longitude of perihelion in blue, for Hobson family members in the base model with planetary perturbations alone. The time at abscissa extends to the past, and the ordinate shows the difference of the respective angle with respect to the orbit of (18777) Hobson. The reference frame is defined by the invariable plane of the Solar System. Bottom: value of target function ΔV from Eq. (1) computed for the orbits shown in the top panel. The gray horizontal line indicates 5 m s−1, the estimated escape velocity from the family parent asteroid (Sect. 3). Left panels: 12 members with H ≤ 17.75. Right panels: all Hobson members on multi-opposition orbits. The gray Gaussian curve in the top panels schematically indicates thesolution 365 ± 67 kyr for the age of the Hobson family from Rosaev & Plávalová (2017). |
 |
Fig. 5 Top: convergence of the mean values of inclination (blue curves) and longitude of node multiplied with a sine of inclination (red curves) for Hobson family members in the base model with planetary perturbations alone. The time at abscissa extends to the past, and the ordinate shows difference of the respective variable with respect to the orbit of (18777) Hobson. The reference frame is defined by the invariable plane of the Solar System. Bottom: value of the target function ΔVZ from Eq. (2) computed from the orbits shown in the top panel. The gray horizontal line indicates 5 m s−1, the estimated escape velocity from the family parent asteroid (Sect. 3). Left panels: 12 members with H ≤ 17.75. Right panels: all Hobson members on multi-opposition orbits. The gray Gaussian curve schematically indicates the solution 365 ± 67 kyr for the age of the Hobson family from Rosaev & Plávalová (2017). |
2.5 (18777) Hobson and (57738) 2001 UZ160 as a pair
In Sect. 2.3 we discussed the special status of the two largest members in the Hobson family, asteroids (18777) Hobson and (57738) 2001 UZ160. In our formation model from a parent binary, the former is the largest fragment from the family-forming event, while the latter is the surviving satellite of the proto-binary. In the previous section, we verified that the heliocentric secular angles of both asteroids tend to mutually converge at approximately the same epoch as all other orbits. Here we strengthen their relation by proving the possibility of a past convergence of their full Cartesian state vectors. This technique is only possible for two heliocentric orbits and was first used by Vokrouhlický & Nesvorný (2008) for an analysis of asteroid pairs.
We thus use numerical propagation of heliocentric orbits of (18777) Hobson and (57738) 2001 UZ160 backward in time to prove their close approach in physical space at a very low relative velocity. These conditions once occurred when the Hobson family was formed. In particular, the zone of family-formation in our model has a characteristic scale of the proto-binary, for instance, some 15–30 km. The expected relative velocity has a smaller contribution from the orbital motion of the binary components (some 2 m s−1 or less) and possibly larger component from the momentum imparted to the primary by the impactor (some 4 m s−1 or so). Ideally, these values set the quantitative measure of state-vectors proximity we would like to achieve. While actually possible in optimum cases (see, e.g., Vokrouhlický et al. 2017b, who analyzed the ≃ 16 kyr old pair of asteroids (6070) Rheinland and (54827) 2001 NQ8 on very stable orbits), these limits appear too ambitious for our target. This is because of their quite old age (between 300 and 400 kyr, Sect. 2.4) and much less dynamically stable orbits (see, e.g., Rosaev & Plávalová 2016, 2017, who reported the chaotic nature of the Hobson orbit, and our Appendix A). Additionally, the two sources of uncertainty in the reconstruction of the past asteroid state discussed in Sect. 2.4 still hold. These are due to the uncertainty in the initial conditions at the present epoch and to the incompleteness of the orbit-propagation model due to unknown parameters of the thermal accelerations. In the previous section, we did not take these effects into account. In contrast, we need to include both effects here by considering a multitude of statistically equivalent clone variants for each of the two asteroids. All these limiting aspects caused us to soften the convergence requirements in our simulations: we assumed (i) a 10000 km physical distance of the clones (about five times the Hill radius of the proto-binary of the Hobson family), and (ii) a 4 m s−1 relative velocity. When any two clones met these conditions, we considered them as a successful convergent situation. The best solutions weachieved bring the clones to a distance of several hundred kilometers and to a relative velocity lower than 1 m s−1, but given the limited number of the clones we can afford, there are only few such solutions. To have enough statistical information,we continued to assume the weaker convergence conditions.
The orbital uncertainty at the initial epoch of our simulation, MJD 59 200.0, was taken into account by representing each of the two asteroids by 5000 clones. These were generated using multidimensional Gaussian statistics in the space of the equinoctic orbital elements provided by the AstDyS website. The method takes into account all correlations of orbital elements, which are not severe (the largest occurs between the semimajor axis and the longitude in orbit), however. Additionally, each of the clones was assigned a random value of thermal accelerations (the Yarkovsky effect, e.g., Vokrouhlický et al. 2015). Because only the rotation period is known for (18777) Hobson and (57738) 2001 UZ160, we restricted ourselves to the simplest approach to model the thermal effects (see, e.g., Nesvorný & Vokrouhlický 2006; Vokrouhlický & Nesvorný 2008). We applied simulated transverse acceleration in the orbital dynamics of clones, which resulted in the secular semimajor axis drift d a∕dt predicted by the Yarkovsky effect. These values have a uniform distribution in the range 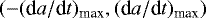 , where
, where 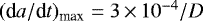 au Myr−1 (e.g., Vokrouhlický et al. 2015), with D the estimated asteroid size in kilometers. We took the values derived in Sect. 2.1. Our dynamical model contains perturbations from all planets, and we also took into account effects of the most massive objects in the asteroid belt: Ceres, Pallas, and Vesta. Perturbations of Ceres, in particular, have been found to be non-negligible in the Hobson zone by Rosaev & Plávalová (2016, 2017). We used a short integration time-step of 2 days and every 3 yr, which is slightly shorter than the orbital period of the asteroids in the Hobson family, and we evaluated the distance and relative velocity of all possible 50002 = 25 × 106 combinations of clones. A shorter frequency of the testing would clearly be better, but is more demanding in CPU time. The simulation was pursued until a million-year epoch in the past. As above, we used the swift_mvs software to carry out the simulations efficiently.
au Myr−1 (e.g., Vokrouhlický et al. 2015), with D the estimated asteroid size in kilometers. We took the values derived in Sect. 2.1. Our dynamical model contains perturbations from all planets, and we also took into account effects of the most massive objects in the asteroid belt: Ceres, Pallas, and Vesta. Perturbations of Ceres, in particular, have been found to be non-negligible in the Hobson zone by Rosaev & Plávalová (2016, 2017). We used a short integration time-step of 2 days and every 3 yr, which is slightly shorter than the orbital period of the asteroids in the Hobson family, and we evaluated the distance and relative velocity of all possible 50002 = 25 × 106 combinations of clones. A shorter frequency of the testing would clearly be better, but is more demanding in CPU time. The simulation was pursued until a million-year epoch in the past. As above, we used the swift_mvs software to carry out the simulations efficiently.
The results from our simulation are shown in Fig. 6, where we plot the statistical distribution of convergent clone combinations in the past. The histogram showing the differential distribution has 10 kyr bins (compare with Fig. 7a in Pravec et al. 2018, where similar results were obtained from fewer clonesand slightly different convergence criteria). Taken at a face value, the median, and 5–95% confidence limits of the cumulative distribution of the Hobson-2001 UZ160 age would be 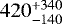 kyr. This is both (i) shifted in median and (ii) wider in spread than the nominal solution 365 ± 67 kyr from Rosaev & Plávalová (2017) (the median displacement is less of a problem because it is still within the formal uncertainty of the Rosaev & Plávalová 2017, solution). However, this is expected because our simulation is much more intensive. Rosaev & Plávalová (2017) only considered nominal orbits of a few Hobson members and disregarded the effect of the thermal accelerations in their dynamics. Especially the latter produce the long-age tail in our solution and allow a far wider range in the possible age of the Hobson-2001 UZ160 pair. As a result, the solution of Rosaev & Plávalová (2017) is a subset of our age solution from the pair of the two largest members in the Hobson family. On the other hand, the strength of the Rosaev & Plávalová (2017) age consists of taking more than two orbits into account (this is even far stronger in our Sect. 2.4). Unfortunately, it is not possible to apply our Cartesian-space convergence method to more than two orbits. However, it is obvious that considering more pairs of members in the Hobson family would delimit its age more strictly and to a narrower interval of values. This goal is beyond the scope of this paper, however. We are content here with a solid justification of both (18777) Hobson and (57738) 2001 UZ160 as true members in the family, and as explained above, setting the enveloping range for the Hobson family age suffices.
kyr. This is both (i) shifted in median and (ii) wider in spread than the nominal solution 365 ± 67 kyr from Rosaev & Plávalová (2017) (the median displacement is less of a problem because it is still within the formal uncertainty of the Rosaev & Plávalová 2017, solution). However, this is expected because our simulation is much more intensive. Rosaev & Plávalová (2017) only considered nominal orbits of a few Hobson members and disregarded the effect of the thermal accelerations in their dynamics. Especially the latter produce the long-age tail in our solution and allow a far wider range in the possible age of the Hobson-2001 UZ160 pair. As a result, the solution of Rosaev & Plávalová (2017) is a subset of our age solution from the pair of the two largest members in the Hobson family. On the other hand, the strength of the Rosaev & Plávalová (2017) age consists of taking more than two orbits into account (this is even far stronger in our Sect. 2.4). Unfortunately, it is not possible to apply our Cartesian-space convergence method to more than two orbits. However, it is obvious that considering more pairs of members in the Hobson family would delimit its age more strictly and to a narrower interval of values. This goal is beyond the scope of this paper, however. We are content here with a solid justification of both (18777) Hobson and (57738) 2001 UZ160 as true members in the family, and as explained above, setting the enveloping range for the Hobson family age suffices.
 |
Fig. 6 Distribution of convergent configurations for clones of (18777) Hobson and (57738) 2001 UZ160 in Cartesian space with the following criteria: (i) physical distance ≤ 10000 km, and (ii) relative velocity ≤4 m s−1. The gray histogram is a differential distribution using 10 kyr bins normalized to maximum convergent cases in a bin. The red line is a cumulative distribution. Time at abscissa extends to the past. Red vertical lines delimit median convergent time (solid), 5 and 95% levels of the cumulative distribution (dashed). |
3 Numerical model of the Hobson family formation
In order to understand formation of the Hobson family, we performed SPH/N-body simulations of single as well as binary asteroid breakups. Binarity is an important novel aspect compared to the previous models because the initial shock wave produced by the impactor in the target cannot propagate to the secondary, but its mass contributes to the total gravity (e.g., Rozehnal et al. 2016). If it survives intact, the secondary appears as one of large remnants in the newly formed family. Therefore the presence of a nearly preserved secondary may potentially help to explain the peculiar size-frequency distribution (SFD) of the Hobson family, which contains two similarly sized bodies (see also Sect. 2.3).
We used the Opensph code (Ševeček et al. 2019; Ševeček 2019) for all SPH and N-body simulations presented below. We substantially improved several aspects of our previous models or added entirely new features (compare with Ševeček et al. 2017). In particular, (i) the self-gravity effects were included already in the fragmentation phase, (ii) and this allowed us to prolong it up to 1000 s, until the fragments are well separated, (iii) we implemented a binary architecture of the target body, if needed, with the primary and the secondary components rotating synchronously, (iv) we abandoned perfect merging in the reaccumulation phase to avoid supercritical rotators, (v) we suppressed the merging efficiency to create similar spatial structures as in full SPH runs, and (vi) we implemented stochasticity testing by performing several simulations with almost the same initial conditions. Appendix B briefly summarizes the setup and parameters used in our simulations.
After trial and error, we found two possible solutions that match the SFD properties of the observed Hobson family (Fig. 3): (i) either a single parent asteroid breakup, which under special circumstances, results in a similarly sized pair of largest fragments, or (ii) a binary parent asteroid, with a breakup of the primary and the secondary (satellite) preserved as a pair component (the special situation of a contact binary is briefly discussed in Appendix C). Here we present the most characteristic examples of both, but we do not intend to accomplish a detailed scan of the vast parameter space of these simulations. This effort is postponed to future work.
 |
Fig. 7 Cumulative size-frequency distributions N(>D) of the fragments produced in the simulation where the parent object was a single asteroid (top) and a binary system (bottom). The observed Hobson-family data are shown with a blue line (assuming geometric albedo pV = 0.2 as in Fig. 3). A slight shift in the populations of kilometer-size and smaller fragments may be partly explained by the incompleteness of the observed family. |
Single parent body example
In the case of a single parent body model, we assumed a target size Dtar = 9 km, an impactor size Dimp = 1.3 km, an impact angle ϕ = 30°, and an impact velocity v = 5 km s−1. The resulting SFD of the synthetic family is shown and compared with the Hobson-family data in Fig. 7 (top panel). While still it slightly overestimates the population of small fragments, the simulation is a fairly acceptable match to the data. Most notably, it provides a pair of ≃2.5−2.7 km largest remnants, as seen in the Hobson family. We verified that the two largest remnants are not gravitationally bound and slowly diverge from each other. According to our tests, the resulting SFD shown in Fig. 7 requires fine-tuning of impact parameters. This is because the transient pair of the largest remnants most often merges into a single largest remnant accompanied by a suite of small fragments (very much like in the results shown by Ševeček et al. 2017, 2019). More insights into the underlying mechanism are provided by the sequence of plots showing the spatial distribution of SPH particles during the fragmentation phase (Fig. 8, top panels). The low impact angle corresponds to a near-to-head-on collision, fine-tuned to break the parent asteroid into two similarly sized fragments that diverge from each other just fast enough to prevent their reaccumulation (Fig. 8, bottom panels). We are currently not able to fully quantify the statistical likelihood of these special conditions of a breakup. This task would require an intense parameter space analysis. This is left for future work. We needed several dozen trials, but unsuccessful simulations to finally reach the solution described above. Thus the likelihood is at a few percent at most, but may be even lower 7.
 |
Fig. 8 Snapshots from an SPH/N-body simulation of a single parent body breakup. The basic parameters were a target size Dtar =9 km, an impactor size Dimp = 1.3 km, an impact angle ϕ = 30° (“near-to-head-on situation”), and an impact velocity v = 5 km s−1. The fragmentation phase is shown for the epochs t = 0, 10, 100, 103 s (top, a–d from left to right), and the reaccumulation phase for t = 0, 103, 104, 105 s (after handoff; bottom, e–h from left to right). The spatial distribution of SPH particles is plotted only within a limited range of the coordinate z ∈ (−1, 1) km to clearly show the interior structure of the parent body, its damage, and the clump formation zones. Colors correspond to the velocity v in m s−1 relative to the target body (scale shown using the bar). Individual panels can be described as follows: (a) the initial conditions, (b) high-speed ejecta formed at the impact site, (c) formation of a cavity with low relative speeds, (d) deformationof the target, (e) handoff phase, (f) streams of high speed, individual particles escaping from the system, (g) ongoing reaccumulation, and (h) formation of an unbound, nearly equal-size pair accompanied by the subkilometer fragments. (Animation is available online and at https://sirrah.troja.mff.cuni.cz/~mira/hobson/hobson.html). |
Binary parent body example
For a binary model, we assumed the following parameters: a primary size D1 = Dtar = 7.5 km, a secondary size D2 = 2.5 km, an impactor size Dimp = 1.4 km, an orbital and spin rate(s) ω = 17.55 d−1, an impact angle ϕ = 60°, an impact velocity v = 5 km s−1, a binary separation r = 10 km, and an orbital velocity vorb = 2 m s−1. We intentionally considered a more compact proto-binary than suggested in Sect. 2.3 (in particular, the secondary rotation period would only be ≃9 h), with the goal to test collisional fate of the secondary in the most severe regime. The resulting synthetic SFD is now shown in the bottom panel of Fig. 7. The second largest remnant in the synthetic population is the fully preserved, unbound secondary of the parent binary system. The remaining populations of bodies consist of the shattered primary, including the largest remnant. Again, the small number of tests we did at this stage does not permit a very detailed tuning in comparison with the data. For instance, in our simulation the largest remnant is slightly smaller than needed, at the expense of a more significant population of smaller fragments. Fine-tuning of the impact parameters would certainly allow an even better comparison between data and model. An intense effort in this direction would, however, only be successful when the observed population of Hobson members is corrected by the observational incompleteness. Here we only mention that we tried several simulations by slightly changing the impact velocity v = 4.96–5 km s−1 and the impact angle ϕ = 60–60.5°. Most often, the results were similar to what is shown in Fig. 7, but sometimes the primary was shattered too much (such that the largest fragment became even smaller than the secondary). We note that the results are insensitive to the initial separation r of the parent binary system, in particular, wider binaries with r = 20−30 km would provide still the same results. The secondary would become more easily unbounded and would certainly be preserved intact. Even in our compact variant with r = 10 km, the interior of the secondary never experiences damage or heating. In this respect, it is a singular member in the future family, but it is not clear what observation would allow us to determine this property.
Dispersal velocity of the largest fragments
In both models above, we also determined the final velocity dispersal with respect to the largest remnant (i.e., 18777 Hobson). Panels e and f in the bottom rows of Figs. 8 and 9 would suggest at first glance that the geometries of the velocity fields are very different. This is indeed true, but it concerns mostly the fast-escaping, resolution-level single particles in our simulations. The properties of the velocity fields for multi-particle clumps, representingreal fragments, are more similar to each other, especially when they are restricted to the set of the first few hundred largest fragments (this group overlaps with the sizes of the observed Hobson members; Fig. 7). For the sake of simplicity, we did not consider the directions of the relative velocity vectors with respect to the largest fragment, but only their magnitude. Figure 10 shows these results for both models, single asteroid and binary system parents. In both of them the velocities of the largest fragments (here with sizes ≥ 300 m) are in the range 0–4 m s−1, with a median of about 1.5 m s−1. A notable difference consists of the relative velocity of the second largest remnant, namely (57738) 2001 UZ160 (indicated by the arrow): this value is very low in the first model (≃0.5 m s−1), but much higher in the second model (≃3.2 m s−1; see also Fig. 9, bottom panels). However, all these velocities remain very low and satisfy the upper limits set by the backward convergence tests in Sect. 2.4 very well (although we recall a hint of the 57738 2001 UZ160 offset from other small members in the Hobson family reported at the end of that section). The escape velocity from the modeled parent systems is 5− 6 m s−1, which is slightly higher than the characteristic velocity dispersal of observable subkilometer fragments. The backward numerical integrations over hundreds of thousands of years are not deterministic enough to trace the tiny model difference in the relative velocity of the two largest remnants in the Hobson family when all sources of uncertainty are taken into account (Sect. 2.5). Unfortunately, the highest fragment velocities thus cannot distinguish between the two models for the parent system of the Hobson family. More detailed analyses are needed in the future.
 |
Fig. 9 Same as Fig. 8, but now for a binary parent object. The basic parameters were a primary size D1 = Dtar = 7.5 km, a secondary size D2 = 2.5 km, an impactor size Dimp = 1.4 km, an impact angle ϕ = 60°, an impact velocity v = 5 km s−1, and a separation r = 10 km. Individual panels can be described as follows: (a) the initial conditions with the binary architecture, (b) because of the near-to-grazing geometry of the impact, high-speed ejecta emanate from the impact site and surrounding surface zone, (c) ejecta reaching the secondary component in the binary, (d) the primary is preserved as the largest remnant in the family, (e) handoff phase with the preserved secondary component of the binary, (f) onset of reaccumulation of other fragments, (g) the secondary escaping from the system, (h) the reaccumulated primary (the secondary off-scale, not shown), which together form a distant pair, accompanied by smaller fragments. (Animation is available online and at https://sirrah.troja.mff.cuni.cz/~mira/hobson/hobson.html) |
4 Discussion and conclusions
It is interesting to compare our results with the much more detailed information about the Karin family, an archetype in the category of young families. Its quite larger known population of fragments allowed Nesvorný et al. (2006a) a detailed comparison of the family structure and size distribution with model predictions. Here we focus primarily on the conclusions related to the size distribution and velocity dispersal of the observed fragments.
Nesvorný et al. (2006a) found that the Karin family was formed by an impact of ≃ 5.8 km projectile onto an ≃33 km parent body with ≃6−7 km s−1 speed and ≃45° impact angle (average in the main belt). The largest created remnant, (832) Karin, is about 17 km, and the size distribution of the Karin fragments then follows from the second largest fragment of ≃ 5.5 km with a steep cumulative power law of ≃−5.3 exponent (which translates into a cumulative absolute magnitude exponent γKarin≃1.06, comparable with the Hobson population; Sect. 2.3). Modeling thus indicates that Karin resulted from a rather energetic collision with ≃(0.1−0.15) mass ratio between the largest remaining fragment and the parent body. It is interesting to note that the size distribution of fragments in the Karin and Hobson families are in many respects similar, but also have intriguing differences: (i) given the plausible observational incompleteness of the small Hobson members, it is possible that the power-law exponents of the size distribution section starting from the second and third largest fragments are similar (or even slightly steeper for Hobson), and (ii) the gap of ≃ (2−2.5) magnitude between the largest fragment(s) and the continuum section is also comparable in the two families. The Karin model thus fits our second, binary scenario for the Hobson family formation very well because the fragmentation properties of its primary compare well to what we see for Karin. The main difference clearly consists of the fact that the parent body of the Karin family was not binary, and thus the Karin family misses the second largest remnant of a comparable size to (832) Karin. As to the ejection velocities vej, Nesvorný et al. (2006a) found that Df ≃ 3 km fragments (typical for the steep leg in the size distribution) have mean barycentric ejection speeds of ≃ 12 m s−1 with the fastest (and smallest) launched at ≃30 m s−1. These values are comparable to or only slightly higher than the escape speed from the parent asteroid, namely ≃ 20 m s−1. This is again a similar ratio as in the simulations of the Hobson family.
Our findings indicate that many of the Karin family results may also hold for the Hobson family. Overall, the similarity of the size distributions has been mentioned above. The main characteristics of the dispersal velocity field of the observable fragments may also be similar if scaled by the estimated escape velocity from the parent body. The results in the Hobson caseare clearly much less accurate at this moment. They will hopefully significantly improve when the next decade of sky surveys will allow us to discover many more small fragments and even provide their physical characterization.
The significance of the Karin to Hobson comparison is especially highlighted by observing the difference in their estimated parent body size: (i) ≃33 km for the Karin family, and (ii) ≃7−9 km for the Hobson family. The quite larger size in the Karin case helps gravity to hold the fragments and moderate their typical dispersal velocities. Probing with Hobson a regime of much smaller parent objects is important because the gravity becomes much weaker in this case. We consider, for instance, that the specific energy for the disruption 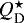 is more than an order of magnitude lower for the Hobson parent body (e.g., Benz & Asphaug 1999; Bottke et al. 2015).
is more than an order of magnitude lower for the Hobson parent body (e.g., Benz & Asphaug 1999; Bottke et al. 2015).
 |
Fig. 10 Distribution of the relative velocity of the 500 largest fragments (sizes approximately ≥300 m; Fig. 7) with respect to the largest remnant in our synthetic realizations of the Hobson family: (i) the case of a single parent body (top), and (ii) the case of binary parent system (bottom). The number of fragments in 0.2 m s−1 wide bins on the ordinate. The median value ≃1.5 m s−1 is shown by the dashed vertical line. The arrow indicates the velocity of the second largest remnant (57738) 2001 UZ160. |
Likelihood of the Hobson family formation from a parent binary
We next verified that our proposed formation of the Hobson family from the collisional disruption of a primary component of the main belt binary is justifiable in a statistical sense (plausibly assuming the same statistical properties of small binaries in its inner and middle parts). We first consulted the results shown in Fig. 15 of Bottke et al. (2005), where a characteristic timescale for the disruption of a main belt asteroid of a given size was determined. Their simulation considered the main belt as a whole and clearly did not resolve solitary and binary objects. The information is provided as a function of size only, which we associate with the ≃8 km size of the primary of our proposed binary object for the Hobson family. From this, we obtain a characteristic disruption timescale of ≃ (30−50) kyr. Taking into account that only every sixth to seventh is a binary (Pravec et al. 2016), the timescale becomes ≃ (180−350) kyr. From this point of view, the 300–400 kyr age of the Hobson family appears very plausible. The recent origin of the Hobson family from a binary does not need to be considered a statistical fluke.
As discussed in Sect. 3, an alternative possibility to our model of the binary parent body is a more traditional assumption of a single parent body. Because the required parent size is similar to the primary of the binary system discussed above, the Bottke et al. (2005) collisional model provides many such breakups in the past 500 kyr, for example. However, the formation of a pair of nearly equal-size largest remnants in the family needs special impact conditions (maybe with a probability of only 1%). This issue needs to be studied in more detail in future work.
Likelihood of a hypothetical Hobson-2001 UZ160 binary split
As discussed in Sect. 3, an alternative possibility to our model of a binary parent body is the more traditional assumption of a single parent body (requiring then special impact parameters). A pair of nearly equal-size largest remnants may be formed, but the question is whether these two objects more likely separate immediately into two asteroids on different heliocentric orbits, or create a bound binary that subsequently underwent instability. Here we show that the latter case is rather unlikely, and the immediate separation of (18777) Hobson and (57738) 2001 UZ160 is the preferred case.
First, we considered a scenario in which a putative binary disrupted due to a subcatastrophic impact onto one of the components. Assuming conservatively the orbital velocity of ≃ 0.5 m s−1, we used the formulas given in Nesvorný et al. (2011) and Nesvorný & Vokrouhlický (2019) to estimate that the required impactor size is ≃150 m. Already thisinformation appears to contradict the assumption of a nondisruptive event. This is because the critical impact specific energy for a ≃2.5 km target is low: 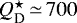 J kg−1 (e.g., Bottke et al. 2005, 2020). Therefore conventionally, when we assume a characteristic impact velocity of ≃ 5 km s−1, an impactor of ≃100 m would produce a catastrophic disruption of either component in the hypothetical binary. Even if we were generous and assumed a loose binary system prone to separation whose critical impact may be as small as ≃ 50 m, the idea would not hold. This is because the probability of such an impact in ≃ 400 kyr is very low. In order to show how large, we took the characteristic intrinsic collisional probability Pi ≃ 2.9 × 10−18 km−2 yr−1 of the objects in the main belt and considered that there are Nimp ≃ 108 such impactors (e.g., Bottke et al. 2005, 2020). In T ≃ 400 kyr (the estimated age of the Hobson family), we therefore expect ≃ NimpPiR2T ≃ 2 × 10−4 of such events to happen (R ≃ 1.25 km is the estimated characteristic size in the Hobson-2001 UZ160 binary). There is simply not enough time since the formation of the Hobson family for the hypothetical binary to split collisionally.
J kg−1 (e.g., Bottke et al. 2005, 2020). Therefore conventionally, when we assume a characteristic impact velocity of ≃ 5 km s−1, an impactor of ≃100 m would produce a catastrophic disruption of either component in the hypothetical binary. Even if we were generous and assumed a loose binary system prone to separation whose critical impact may be as small as ≃ 50 m, the idea would not hold. This is because the probability of such an impact in ≃ 400 kyr is very low. In order to show how large, we took the characteristic intrinsic collisional probability Pi ≃ 2.9 × 10−18 km−2 yr−1 of the objects in the main belt and considered that there are Nimp ≃ 108 such impactors (e.g., Bottke et al. 2005, 2020). In T ≃ 400 kyr (the estimated age of the Hobson family), we therefore expect ≃ NimpPiR2T ≃ 2 × 10−4 of such events to happen (R ≃ 1.25 km is the estimated characteristic size in the Hobson-2001 UZ160 binary). There is simply not enough time since the formation of the Hobson family for the hypothetical binary to split collisionally.
Another possibility is that the hypothetical Hobson-2001 UZ160 binary split dynamically. The most likely candidate process would be the binary Yarkovsky-O’Keefe-Radzievskii-Paddack (BYORP) radiative effect (e.g., Ćuk & Burns 2005). Here again the likelihood is very low, even taking the most aggressive scenario (e.g., assuming a permanent spin-orbital synchronous state without interruptions; see, e.g., Ćuk & Nesvorný 2010). In this case, the BYORP instability timescale would simply be the typical YORP timescale of a ≃ 2.5 km size asteroid at the heliocentric distance of the Hobson family, typically ≃ 10 Myr (e.g., Ćuk & Burns 2005). This is again much longer than the estimated age of the Hobson family.
Future prospects
The Hobson family will continue to be an interesting example of very young asteroid families. The experience from the past decade shows that its known population may easily double in the next few years, especially if powerful surveys such as the Vera C. Rubin Observatory will reach their expected operations. This will allow us not only to improve our analysis in this paper, but perhaps tackle other issues. Refining solution of the Hobson family age, guided by the synthetic model of the family formation, may be one of the most interesting projects. Eventually, this might help distinguishing among the two models of the parent system.
Movies
Movie 1 associated with Fig. 8 (hobson19_2_out) Access here
Movie 2 associated with Fig. 8 (hobson19_3_out) Access here
Movie 3 associated with Fig. 9 (hobson28_2_out) Access here
Movie 4 associated with Figs. 9 (hobson28_3_out) Access here
Acknowledgements
We thank the referee whose comments and suggestions helped to improve the submitted version of this paper. This research was supported by the Czech Science Foundation (D.V. and M.B.; grant 21-11058S). B.N. acknowledges the support of the Ministry of Education, Science and Technological Development of the Republic of Serbia, contract No. 451-03-68/2020-14/200104.
Appendix A Hobson family. Membership and proper elements
In this section, we provide a complete list of 45 Hobson family members determined in Sec. 2.2 and we represent the family using the traditional set of proper orbital elements: semimajor axis aP, eccentricity eP, and sine of the inclination sinIP. We use synthetic elements, determined by numerical integration (e.g., Knežević & Milani 2000, 2003). As mentioned in the appendix of Vokrouhlický et al. (2021), we cannot use data from the standard world storehouses of proper orbital elements, such as AstDyS8 or AFP9. This is because many of small Hobson members have been discovered only recently, and these databases have not been updated yet, or have rejected some orbits with too few observations at this moment. As a result, we computed the proper elements ourselves, using the methods described in the appendix of Vokrouhlický et al. (2021). Here we outline the principal steps.
The orbits of Hobson members were numerically integrated forward in time for 2 Myr using the base model, where only gravitational perturbation from planets and the attraction by the Sun were included. In order to enable a longer time step, we only discarded the innermost planet Mercury and performed the corresponding barycentric correction in the state vectors of planets. This has a negligible effect on the orbital zone of the main belt, where the Hobson family is located. We implemented an online digital filter to remove short-period terms (periods shorter than 300 yr), so that the simulation provided the mean orbital elements for each of the bodies. The postprocessing then represented the application of the Fourier analysis andthe removal of forced (planetary) terms, isolating thus the proper terms. Cartesian-like nonsingular elements were used for eP and sin IP. To assess the formal uncertainty of the proper elements, we used a simple running-box test. The nominal proper elements were computed for the whole 2 Myr long simulation. We then determined these elements also on eleven 1 Myr long windows shifted by 0.1 Myr, into which we segmented the original simulation. Their statistical standard deviation from the nominal values helped to characterize the formal uncertainty. We note that only nominal orbits of the asteroids were used in our simulation, disregarding thus the current orbital uncertainty from the observations. However, this is not a strong effect, except for the six single-opposition members in the Hobson family: 2014 JH120, 2014 OJ66, 2020 JM31, 2020 KP36, 2020 OY50, and 2021 MO5. In the worst case, namely 2014 OJ66 with the poorest astrometric set, the realistic semimajor axis uncertainty may be up to ≃ 8 × 10−4 au. Our results are summarized in Table A.1 and Fig. A.1.
 |
Fig. A.1 Hobson family represented by two possible plane projections of the proper orbital elements: (i) semimajor axis aP vs. sine of the inclination sinIP in the top panel, and (ii) semimajor axis aP vs. eccentricity eP in the bottom panel. The largest fragments (18777) Hobson (red) and (57738) 2001 UZ160 (blue) are shown by diamonds, and smaller family members are shown by filled circles (gray are the five single-opposition orbits). Vertical and horizontal bars are formal uncertainty values of the respective proper element from Table A.1. The uncertainty in eP is large due to perturbing effect of the g + g5 − 2g6 secular resonance. The gray dashed ellipses indicate proper element zones in which fragments may land if they are ejected isotropically from the barycenter of the family with 4 m s−1 velocity (assuming the true anomaly f = 50° and the argument of perihelion such that ω + f = 0°). The tilt in the bottom panel may be due to the perturbing effect of the g + g5 − 2g6 resonance, however. The particular dispersion of the family members in eP at aP ≃ 2.5636 au, with the noticeable uncertainty of the aP values, is due to the perturbation by the 9J-8S-2 three-body mean-motion resonance. |
As in Vokrouhlický et al. (2021), we purposely used a short time-span of 2 Myr in our method to determine the proper elements. This presumably conforms to the very young age of the family. However, there are drawbacks when longer-period terms perturb the orbital evolution. The forced terms due to the Uranus or Neptune nodal or pericenter precession are generally very small in the main belt. Some locations may be affected by nonlinear secular resonances that involve the Jupiter and Saturn node or perihelion precession frequencies, however (e.g., Milani & Knežević 1992, 1994). We find that the zone of the Hobson family is significantly perturbed by the g + g5 − 2g6 secular resonance that produces ≃ 1.2 Myr oscillations in the eccentricity vector and semimajor axis. The semimajor axis perturbation has a small amplitude, but the eccentricity effect is strong enough to cause a high value of δeP in our setup. Clearly, the values of eP are perturbed themselves. In the same time, their uncertainties δeP are not statistically random, but again are systematically affected by this resonance. Additionally, the Hobson family is crossed by the three-body mean motion resonance 9J-8S-2 near aP ≃ 2.5636 au (see, e.g., Gallardo 2014). This location is notable by (i) the observable uncertainty of the aP values and (ii) the anomalous dispersion of the eP from our 2 Myr-long integration. This effect is not apparent to this degree in the structure of the ≃ 330 kyr old Hobson family due to its youth, however. For these reasons, the bottom panel in Fig. A.1 is less useful for a discussion of the real Hobson family. However, the top panel with its projection onto the aP versus sin IP is valuable and helps appreciate the compactness of the family well within the limits of the 4 m s−1 isotropic ejection field, supporting the low dispersal field of the Hobson fragments studied in Sec. 2.4. The velocity limit in this projection may easily be tightened to ≃ 2 m s−1, with one or two outliers explained by an accumulated drift in proper semimajor axis by the Yarkovsky effect (up to ± (2 − 3) × 10−4 au in ≃ 350 kyr and subkilometer size body in the Hobson family).
The impractical structure of the Hobson family in the aP versus eP adds to the consideration the usefulness of traditional proper elements in the case of very young asteroid families. While a detailed analysis of this problem exceeds the topic of this work, we note that the structure of the family in mean or bital elements at the moment of convergence of secular angles (see Fig. 4) may be a more practical tool. In Sec. 2.4 we used information from mean inclination, longitude of node, and perihelion. However, we also confirmed that near the convergence epoch, the mean semimajor axis, eccentricity, and inclination may very well replace the proper elements in a representation similar to that shown in Fig. A.1. In particular, the position of the Hobson fragments again fit within the zone of 4 − 5 m s−1 isotropic ejection field. The long-period terms in these elements mean that the configuration of the family is not unique, however. Its compactness is not surprising at this moment because we noted that the nodal and perihelion dispersal values ΔΩ and Δϖ contribution to the target function (1) depend on all velocity components already.
Proper orbital elements and their formal uncertainty of the Hobson family members.
Appendix B Setup of the SPH/N-body simulations
The simulations presented in Sec. 3 were performed with the following numerical setup and material parameters (see also Ševeček 2019 for more details and definitions). The primary, the secondary, and the impactor were resolved using N = 105, 104, and 103 particles. We used the Diehl et al. (2012) random-yet-isotropic initial distribution.
All materials were similar to monolithic basalt, with the density ρ = 2700 kg m−3, the bulk modulus B = 2.67 × 1010 Pa, the shear modulus μ = 2.27 × 1010 Pa, the elastic modulus ϵ = 8 × 109 Pa, the Tillotson (1962) equation of state parameters a = 0.5, b = 1.5, B as above, α =5, β =5, an incipient vaporization energy Uiv = 4.72 × 106 J, a complete vaporizationenergy Ucv = 1.82 × 107 J, a sublimation energy Usub = 4.87 × 108 J, an initial scalardamage D = 0, a von Mises rheology, a von Mises limit Y = 3.5 × 109 Pa, a melting energy Umelt = 3.4 × 106 J, a Weibull coefficient k = 4 × 1035, and a Weibull exponent m = 9. We also performed tests with the Drucker-Prager rheology, but if the pressure-dependent limit Y (P) for a peak pressure P is similar to Y above, the outcome is similar. We did not analyse shapes of individual fragments.
The fragmentation phase duration was 103 s. The time step was controlled by the Courant number C = 0.2, the derivative factor 0.2, and the divergence factor 0.005. We used the asymmetric SPH solver, the standard SPH discretisation, the correction tensor for rotation, the predictor-corrector integrator, and we summed over undamaged particles. The artificial viscosity parameters were α = 1.5, β = 3. We also used the Barnes-Hut gravity solver, with the opening angle ϕ = 0.5, the multipole order ℓ = 3, and eventually, an equal-volume handoff.
The reaccumulation phase duration was 105 s, computed with the leap-frog integrator, a “merge-or-bounce” collisional handler, and a “repel-or-merge” overlap handler. The derivative factor was 0.005. For the normal restitution, we assumed a value 0.5, a tangential restitution 1, and a merge velocity limit αv = 0.25, where the condition for merging is
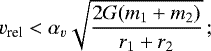 (B.1)
(B.1)
similarly, the merge rotation limit αω = 1.0. The final SFD was computed from masses. The model is still somewhat resolution dependent because the number of particles determines the smallest block size, and the SFD was built from these blocks.
Appendix C Contact binary model
For sake of completeness, we also considered an impact onto a contact (or close) binary, as opposed to the well-separated binary system discussed in Sec. 3. In particular, we used the same system and impact geometry parameters as in Sec. 3, but assumed a separation of the primary and secondary r = (D1 + D2)∕2, making them in contact. This is a different regime (compared to the wide binary system) because the singular neck in the system does not permit propagation of the impact-generated shock wave into the secondary. Nevertheless, the latter was now affected to a much higherdegree. This is because the secondary was slowly but efficiently pushed by the primary and squeezed along the perpendicular direction (see Fig. C.1). All these motions were highly subsonic. Eventually, most of the secondary mass was reaccreted because the mutual velocities are relatively low compared to direct ejecta from the primary. The reaccreted secondary must have a different internal structure, with damaged material and a fresh surface, than in the model of wide binary parent system. This is different from the case of a wide binary that we discussed in the main text.
 |
Fig. C.1 Simulation of a contact binary breakup. The spatial distribution of SPH particles is shown within a limited range of z ∈ (−1, 1) km and for t = 500 s. Colors correspond to the specific internal energy U in J kg−1. The primary was dispersed after a collision with the impactor (not shown). The secondary (on the right) was squeezed by a low-speed collision with the primary. In the reaccumulation phase, the primary and the secondary eventually provide the first andsecond largest remnants in the synthetic family. |
References
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Brož, M., Nesvorný, D., & Morbidelli, A. 2001, Science, 294, 1693 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bottke, W. F., Durda, D. D., Nesvorný, D., et al. 2005, Icarus, 179, 63 [Google Scholar]
- Bottke, W. F., Brož, M., O’Brien, D. P., et al. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 701 [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Ballouz, R. L., et al. 2020, AJ, 160, 14 [Google Scholar]
- Brouwer, D. 1950, AJ, 55, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Brouwer, D. 1951, AJ, 56, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. W. 1932, PASP, 44, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Nesvorný, D., & Vokrouhlický, D. 2016, AJ, 151, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Carruba, V., Vokrouhlický, D., Nesvorný, D., & Aljbaae, S. 2018, MNRAS, 477, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Michel, P., Tanga, P., et al. 1999, Icarus, 141, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Ćuk, M., & Burns, J. A. 2005, Icarus, 176, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Ćuk, M., & Nesvorný, D. 2010, Icarus, 207, 732 [Google Scholar]
- Diehl, S., Rockefeller, G., Fryer, C. L., Riethmiller, D., & Statler, T. S. 2012, ArXiv e-prints [arXiv:1211.0525] [Google Scholar]
- Farinella, P., & Vokrouhlický, D. 1999, Science, 283, 1507 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gallardo, T. 2014, Icarus, 231, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Hendler, N. P., & Malhotra, R. 2020, Planet. Sci. J., 1, 75 [Google Scholar]
- Hirayama, K. 1918, AJ, 31, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, K. 1928, Japanese J. Astron. Geophys., 5, 137 [NASA ADS] [Google Scholar]
- Knežević, Z., & Milani, A. 2000, Celest. Mech. Dyn. Astron., 78, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Knežević, Z., & Milani, A. 2003, A&A, 403, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel, P., Benz, W., Tanga, P., & Richardson, D. C. 2001, Science, 294, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Michel, P., Benz, W., & Richardson, D. C. 2003, Nature, 421, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Milani, A., & Knežević, Z. 1992, Icarus, 98, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., & Knežević, Z. 1994, Icarus, 107, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Bottke, W. F. 2004, Icarus, 170, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Vokrouhlický, D. 2006, AJ, 132, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Vokrouhlický, D. 2019, Icarus, 331, 49 [Google Scholar]
- Nesvorný, D., Bottke, W. F., Dones, L., & Levison, H. F. 2002a, Nature, 417, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Morbidelli, A., Vokrouhlický, D., Bottke, W. F., & Brož, M. 2002b, Icarus, 157, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Enke, B. L., Bottke, W. F., et al. 2006a, Icarus, 183, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., & Bottke, W. F. 2006b, Science, 312, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., Bottke, W. F., Noll, K., & Levison, H. F. 2011, AJ, 141, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Brož, M., & Carruba, V. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 297 [Google Scholar]
- Pravec, P., & Vokrouhlický, D. 2009, Icarus, 204, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., Kušnirák, P., Galád, A., & Hornoch, K. 2012, Icarus, 221, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Scheirich, P., Kušnirák, P., et al. 2016, Icarus, 267, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Fatka, P., Vokrouhlický, D., et al. 2018, Icarus, 304, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Rosaev, A., & Plávalová, E. 2016, ArXiv e-prints [arXiv:1612.04951] [Google Scholar]
- Rosaev, A., & Plávalová, E. 2017, Icarus, 282, 326 [CrossRef] [Google Scholar]
- Rosaev, A., & Plávalová, E. 2018, Icarus, 304, 135 [Google Scholar]
- Rozehnal, J., Brož, M., Nesvorný, D., et al. 2016, MNRAS, 462, 2319 [NASA ADS] [CrossRef] [Google Scholar]
- Ševeček, P. 2019, Astrophysics Source Code Library [record ascl:1911.003] [Google Scholar]
- Ševeček, P., Brož, M., Nesvorný, D., et al. 2017, Icarus, 296, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Ševeček, P., Brož, M., & Jutzi, M. 2019, A&A, 629, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tillotson, J. H. 1962, Metallic Equations of State For Hypervelocity Impact, General Atomic Report GA-3216. 1962. Technical Report [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2008, AJ, 136, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., & Nesvorný, D. 2011, AJ, 142, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Brož, M., Bottke, W. F., Nesvorný, D., & Morbidelli, A. 2006, Icarus, 182, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Ďurech, J., Michałowski, T., et al. 2009, A&A, 507, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 509 [Google Scholar]
- Vokrouhlický, D., Ďurech, J., Pravec, P., et al. 2016, AJ, 151, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Pravec, P., Ďurech, J., et al. 2017a, A&A, 598, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Pravec, P., Ďurech, J., et al. 2017b, AJ, 153, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Novaković, N., & Nesvorný, D. 2021, A&A, 649, A115 [Google Scholar]
- Zappalà, V., Cellino, A., Dell’oro, A., Migliorini, F., & Paolicchi, P. 1996, Icarus, 124, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Zappalà, V., Cellino, A., Dell’Oro, A., & Paolicchi, P. 2002, in Asteroids III, eds. W. F. Bottke, A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 619 [Google Scholar]
A conclusion against some early skeptical opinions, such as expressed by the late Ernest Brown: “Any hope of getting evidence from this source as to whether they [i.e. Hirayama families] were a result of an explosion or collision must be abandoned”. (Brown 1932).
This issue puzzled already Pravec & Vokrouhlický (2009) who wondered if (18777) Hobson belongs to their proposed cluster around (57738) 2001 UZ160 (their Table 6).
We also performed tests in which we used osculating elements and a very high temporal cadence of every time step of the integrator in evaluating the target functions (1) and (2). The resulting values of ΔV, for instance, exhibit high-frequency oscillations about the signal shown in the lower panels of Fig. 4, reaching slightly lower minimum values. Generally, our reported ΔV (t), and similarly ΔVZ(t), approximate the lower bound of these value rather well, however. A detailed study of the high-frequency signal patterns from our tests, with the goal of refining the Hobson family age, is not a goal of this study, however, and it is postponed to a future work.
The role of the parent body shape is one of the factors that have not been analyzed so far. We assumed a spherical shape, but possibly an impact onto a highly elongated body (such as the near-Earth asteroid 1620 Geographos) may more easily result in the formation of two nearly equal-size largest remnants.
All Tables
Proper orbital elements and their formal uncertainty of the Hobson family members.
All Figures
 |
Fig. 1 Osculating values of the heliocentric secular angles in the ecliptic system in the target zone surrounding the Hobson family: the longitude of node Ω (abscissa) vs. the longitude of perihelion ϖ (ordinate). Left panel: total of 69 asteroids, clearly divided into (i) a random background population, and (ii) a strongly clustered family (symbols highlighted by the rectangle). Because the initial search used the argument of perihelion ω, the actively probed region around (18777) Hobson becomes tilted in Ω vs. ϖ axes, and the corner triangles in dark gray are excluded. Right panel: zoom on the Hobson family structure (range of the axes as in the gray rectangle in the left panel). The two largest asteroids, (18777) Hobson and (57738) 2001 UZ160, are highlighted in red and blue with diamonds. All smaller members are shown by filled circles: multi-opposition orbits in black, and the six single-opposition orbits in gray (asteroids 2014 JH120, 2014 OJ66, 2020 JM31, 2020 KP36, 2020 OY50, and 2021 MO5; Table A.1). The family is unusually compact in both Ω and ϖ, promising very young age. |
| In the text | |
 |
Fig. 2 Osculating values of the longitude of node Ω (abscissa) vs. the inclination I (ordinate) in the target zone surrounding the Hobson family. The limits of the axes depict our search zone. The members of the Hobson family (red symbols in the rectangle) are strongly clustered and can easily be distinguished from the dispersed background population of asteroids. |
| In the text | |
 |
Fig. 3 Cumulative distribution N(< H) of the absolute magnitude H for known Hobson family members. Left panel: all members included: the red and blue diamonds denote the two largest remnants (18777) Hobson and (57738) 2001 UZ160, and filled circles show small members in the family. The gray line shows the power-law relation N(< H)∝ 10γH for γ = 0.95, which approximates the distribution of small members. Right panel: the second largest member, (57738) 2001 UZ160, is excluded from the distribution: the red diamond denotes (18777) Hobson, and the filled circles are smaller fragments in the family. The power-law relation N(< H)∝ 10γH has now γ = 1.15 (simply as an effect of removing the second largest body from the sample and linear-logarithmic scales on the axes). The upper abscissa in both panels provides an estimate of the size, assuming the geometric albedo pV = 0.2 (a plausible value for S-type asteroids). |
| In the text | |
 |
Fig. 4 Top: convergence of the mean values of secular angles, longitude of node in red and longitude of perihelion in blue, for Hobson family members in the base model with planetary perturbations alone. The time at abscissa extends to the past, and the ordinate shows the difference of the respective angle with respect to the orbit of (18777) Hobson. The reference frame is defined by the invariable plane of the Solar System. Bottom: value of target function ΔV from Eq. (1) computed for the orbits shown in the top panel. The gray horizontal line indicates 5 m s−1, the estimated escape velocity from the family parent asteroid (Sect. 3). Left panels: 12 members with H ≤ 17.75. Right panels: all Hobson members on multi-opposition orbits. The gray Gaussian curve in the top panels schematically indicates thesolution 365 ± 67 kyr for the age of the Hobson family from Rosaev & Plávalová (2017). |
| In the text | |
 |
Fig. 5 Top: convergence of the mean values of inclination (blue curves) and longitude of node multiplied with a sine of inclination (red curves) for Hobson family members in the base model with planetary perturbations alone. The time at abscissa extends to the past, and the ordinate shows difference of the respective variable with respect to the orbit of (18777) Hobson. The reference frame is defined by the invariable plane of the Solar System. Bottom: value of the target function ΔVZ from Eq. (2) computed from the orbits shown in the top panel. The gray horizontal line indicates 5 m s−1, the estimated escape velocity from the family parent asteroid (Sect. 3). Left panels: 12 members with H ≤ 17.75. Right panels: all Hobson members on multi-opposition orbits. The gray Gaussian curve schematically indicates the solution 365 ± 67 kyr for the age of the Hobson family from Rosaev & Plávalová (2017). |
| In the text | |
 |
Fig. 6 Distribution of convergent configurations for clones of (18777) Hobson and (57738) 2001 UZ160 in Cartesian space with the following criteria: (i) physical distance ≤ 10000 km, and (ii) relative velocity ≤4 m s−1. The gray histogram is a differential distribution using 10 kyr bins normalized to maximum convergent cases in a bin. The red line is a cumulative distribution. Time at abscissa extends to the past. Red vertical lines delimit median convergent time (solid), 5 and 95% levels of the cumulative distribution (dashed). |
| In the text | |
 |
Fig. 7 Cumulative size-frequency distributions N(>D) of the fragments produced in the simulation where the parent object was a single asteroid (top) and a binary system (bottom). The observed Hobson-family data are shown with a blue line (assuming geometric albedo pV = 0.2 as in Fig. 3). A slight shift in the populations of kilometer-size and smaller fragments may be partly explained by the incompleteness of the observed family. |
| In the text | |
 |
Fig. 8 Snapshots from an SPH/N-body simulation of a single parent body breakup. The basic parameters were a target size Dtar =9 km, an impactor size Dimp = 1.3 km, an impact angle ϕ = 30° (“near-to-head-on situation”), and an impact velocity v = 5 km s−1. The fragmentation phase is shown for the epochs t = 0, 10, 100, 103 s (top, a–d from left to right), and the reaccumulation phase for t = 0, 103, 104, 105 s (after handoff; bottom, e–h from left to right). The spatial distribution of SPH particles is plotted only within a limited range of the coordinate z ∈ (−1, 1) km to clearly show the interior structure of the parent body, its damage, and the clump formation zones. Colors correspond to the velocity v in m s−1 relative to the target body (scale shown using the bar). Individual panels can be described as follows: (a) the initial conditions, (b) high-speed ejecta formed at the impact site, (c) formation of a cavity with low relative speeds, (d) deformationof the target, (e) handoff phase, (f) streams of high speed, individual particles escaping from the system, (g) ongoing reaccumulation, and (h) formation of an unbound, nearly equal-size pair accompanied by the subkilometer fragments. (Animation is available online and at https://sirrah.troja.mff.cuni.cz/~mira/hobson/hobson.html). |
| In the text | |
 |
Fig. 9 Same as Fig. 8, but now for a binary parent object. The basic parameters were a primary size D1 = Dtar = 7.5 km, a secondary size D2 = 2.5 km, an impactor size Dimp = 1.4 km, an impact angle ϕ = 60°, an impact velocity v = 5 km s−1, and a separation r = 10 km. Individual panels can be described as follows: (a) the initial conditions with the binary architecture, (b) because of the near-to-grazing geometry of the impact, high-speed ejecta emanate from the impact site and surrounding surface zone, (c) ejecta reaching the secondary component in the binary, (d) the primary is preserved as the largest remnant in the family, (e) handoff phase with the preserved secondary component of the binary, (f) onset of reaccumulation of other fragments, (g) the secondary escaping from the system, (h) the reaccumulated primary (the secondary off-scale, not shown), which together form a distant pair, accompanied by smaller fragments. (Animation is available online and at https://sirrah.troja.mff.cuni.cz/~mira/hobson/hobson.html) |
| In the text | |
 |
Fig. 10 Distribution of the relative velocity of the 500 largest fragments (sizes approximately ≥300 m; Fig. 7) with respect to the largest remnant in our synthetic realizations of the Hobson family: (i) the case of a single parent body (top), and (ii) the case of binary parent system (bottom). The number of fragments in 0.2 m s−1 wide bins on the ordinate. The median value ≃1.5 m s−1 is shown by the dashed vertical line. The arrow indicates the velocity of the second largest remnant (57738) 2001 UZ160. |
| In the text | |
 |
Fig. A.1 Hobson family represented by two possible plane projections of the proper orbital elements: (i) semimajor axis aP vs. sine of the inclination sinIP in the top panel, and (ii) semimajor axis aP vs. eccentricity eP in the bottom panel. The largest fragments (18777) Hobson (red) and (57738) 2001 UZ160 (blue) are shown by diamonds, and smaller family members are shown by filled circles (gray are the five single-opposition orbits). Vertical and horizontal bars are formal uncertainty values of the respective proper element from Table A.1. The uncertainty in eP is large due to perturbing effect of the g + g5 − 2g6 secular resonance. The gray dashed ellipses indicate proper element zones in which fragments may land if they are ejected isotropically from the barycenter of the family with 4 m s−1 velocity (assuming the true anomaly f = 50° and the argument of perihelion such that ω + f = 0°). The tilt in the bottom panel may be due to the perturbing effect of the g + g5 − 2g6 resonance, however. The particular dispersion of the family members in eP at aP ≃ 2.5636 au, with the noticeable uncertainty of the aP values, is due to the perturbation by the 9J-8S-2 three-body mean-motion resonance. |
| In the text | |
 |
Fig. C.1 Simulation of a contact binary breakup. The spatial distribution of SPH particles is shown within a limited range of z ∈ (−1, 1) km and for t = 500 s. Colors correspond to the specific internal energy U in J kg−1. The primary was dispersed after a collision with the impactor (not shown). The secondary (on the right) was squeezed by a low-speed collision with the primary. In the reaccumulation phase, the primary and the secondary eventually provide the first andsecond largest remnants in the synthetic family. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


