EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A45 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A45
Number of page(s) 9
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202141491
Published online 07 October 2021

© ESO 2021

1 Introduction

Line surveys of molecular clouds at high spectral resolution are invaluable tools for carrying out molecular spectroscopy in space and for studying fundamental chemical processes. Since the discovery of HCO+, first assigned to an unidentified line (Buhl & Snyder 1970) based on ab initio calculations (Wahlgren et al. 1973) and subsequently confirmed in the laboratory (Woods et al. 1975), several molecular species have been detected in space prior to their characterization in the laboratory, in most cases aided by state-of-the-art ab initio calculations. Examples of this kind are HCS+ (Thaddeus et al. 1981), C4H (Guélin et al. 1978), C6H (Suzuki et al. 1986), and C3H+ (Pety et al. 2012), all of which were subsequently confirmed in the laboratory, as well as the cases of C5N− (Cernicharo et al. 2008), MgC3N and MgC4H (Cernicharo et al. 2019), and HC5NH+ (Marcelino et al. 2020), which have not been yet observed in the laboratory. If the source displays narrow lines and the spectral resolution ishigh enough, it is possible to resolve the hyperfine structure and derive very precise spectroscopic parameters (e.g., Cernicharo et al. 1987).

Here, we present a new case of molecular spectroscopy in space. Thanks to sensitive high-spectral resolution observations of the cold dark cloud L483 at mm wavelengths, we detected various groups of unidentified lines, revealing a complex hyperfine structure, which we confidently assign to H2NC. This speciesis the simplest member of the family of aminocarbyne ligands, well known in organometallic chemistry (Pombeiro et al. 2001). It is also a high-energy metastable isomer of the methylene amidogen radical (H2CN) and, as such, it has been largely ignored in many chemical and astrochemical studies. We however find that in the cold dark clouds L483 and B1-b, H2NC has the same abundance as H2CN itself. Theseresults illustrate nicely how the chemical composition of cold interstellar clouds is driven by chemical kinetics rather than by thermochemical considerations, contrary to the suggestion from Lattelais et al. (2009). In this work, we discuss which chemical reactions could be behind the formation of H2NC, which is a topic that has been overlooked in the literature.

2 Astronomical observations

We recently carried out a line survey of the cold dark cloud L483 in the 80–116 GHz frequency range with the IRAM 30 m telescope (Agúndez et al. 2019). Additional observations of L483 were carried out in December 2018 to cover the 72–80 GHz range. A group of lines spread over a frequency interval of 45 MHz around 72.2 GHz, close to the hyperfine components of the N = 1–0 transition of CCD, caught our attention when we found we could not assign them using the CDMS1 (Müller et al. 2005), JPL2 (Pickett et al. 1998), nor MADEX3 (Cernicharo 2012) catalogues. The spectral pattern is typical of a molecule with a complex fine and hyperfine structure. Since the hyperfine structure usually collapses for an increasing rotational quantum number, thelarge splitting observed suggests that the lines correspond to a rotational transition with a low rotational quantum number. Our first hypothesis was that the set of unidentified lines corresponds to the N = 1–0 rotational transition of a linear or quasi-linear species. The rotational constant B, or (B + C)/2, would then be 36.1 GHz, which implies that the species must contain two heavy atoms (C, N, O) and possibly oneor various H atoms. If the lines corresponded to a higher rotational transition, for instance, N = 2–1, the immediately higher transition, for instance, N = 3–2, would fall below 116 GHz, and we have no hint of it in our sensitive λ 3 mm data. Moreover, we are confident that the lines do not arise from a heavy isotopologue involving D, 13C, 15N, 17O, or 18O because thiswould imply a similar pattern of lines from the parent species at higher frequencies that are also significantly more intense (see the case of HDCCN; Cabezas et al. 2021), however, there is no feature in our λ 3 mm that would prove consistent with this possibility. The only species that fulfill these criteria, namely, HCN, C2H, and N2H+, have had the rotational spectrum of their minor isotopologues well characterized in the laboratory.

In order to confirm our hypothesis, we requested IRAM 30 m telescope time to search for the two immediately higher transitions. Observations were carried out in June 2019 and we detected unidentified lines at the expected positions of the N = 2–1 and N = 3–2 transitions, 144 and 216 GHz, respectively, thus confirming our initial hypothesis. Moreover, we also detected unidentified lines around 140 GHz, which were later assigned to the para species of H2NC. These observations, as well as the earlier ones, were done using the frequency-switching technique with a frequency throw of 7.2 MHz. To be sure that no line is missing due to the potential cancellation with negative artifacts, at ±7.2 MHz of each line, caused by this procedure, we carried out new observations around 72.2, 140, 144, and 216 GHz in November 2019, June 2020, and February and April 2021, using the wobbler-switching technique, with the secondary mirror nutating by 220″ at a rate of 0.5 Hz. All observations were done using the EMIR receivers connected to a fast Fourier transform spectrometer providing a spectral resolution of 50 kHz (Klein et al. 2012). Line intensities are expressed in terms of the antenna temperature, 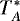, which can be converted to main beam brightness temperature, Tmb, by dividing by Beff/Feff. IRAM 30 mbeam efficiencies, forward efficiencies, and half power beam widths are given on the IRAM website4. Further details on the IRAM 30 m observations of L483 can be found in Agúndez et al. (2019) and Agúndez et al. (2021). The observed lines are shown in Fig. 1 and the frequencies and line parameters derived are given in Table 1.

We note that the frequencies of some of the hyperfine components of the N = 1–0 transition ofCCD observed in L483 differ significantly from those given in the CDMS catalogue (Müller et al. 2005). This was already noticed by Yoshida et al. (2019) in their observations of L1527. We therefore used the new frequencies to improve the spectroscopic parameters of CCD (see Appendix A).

We also make use of observations of the cold dark clouds B1-b and TMC-1, as well as of the z = 0.89 galaxy in front of the quasar PKS 1830−211. The observations of B1-b and TMC-1 were carried out with the IRAM 30 m telescope in the 72–74 GHz range in August 2018 and are part of a λ 3 mm line survey of these two sources (see Cernicharo et al. 2012 for more details), while those of PKS 1830−211 were done using the Yebes 40 m telescope in the Q band in a monitoring campaign of this source from April 2019 to July 2020 (see Tercero et al. 2020 for more details). Here, we added data taken during eight observing sessions from October 2019 to the data presented in Tercero et al. (2020). All the data were reduced using the program CLASS of the GILDAS software5.

thumbnail Fig. 1

Lines of H2NC observed in L483 (see parameters in Table 1). In red we show the computed synthetic spectra for a column density of H2NC of 1012 cm−2, ortho-to-para ratio of 3, rotational temperature of 4.0 K, full width at half maximum of 0.35 km s−1 (except for the 30,3–20,2 lines, in which case a value of 0.19 km s−1 was adopted), and an emission size that fills the IRAM 30 m main beam. Vertical blue lines indicate the position of CCD lines (see Appendix A).
Table 1

Line parameters of H2NC observed in L483.

3 Spectroscopic assignment to H2NC

Potential carriers of the unidentified lines observed in L483 are N2Hx, CNHx, COHx, NOHx, C2Hx, and O2Hx, including neutral or ionic forms. To obtain precise spectroscopic parameters that help in the assignment of the observed lines, we carried out high-level ab initio calculations for all plausible candidates. The geometry optimization calculations for all the candidates considered were done using the spin-restricted coupled cluster method with single, double, and perturbative triple excitations (RCCSD(T); Raghavachari et al. 1989), with all electrons (valence and core) correlated and the Dunning’s correlation consistent basis sets with polarized core-valence correlation quadruple-ζ (cc-pCVQZ; Woon & Dunning 1995). These calculations were carried out using the Molpro 2020.2 program (Werner et al. 2020). In addition to the rotational constants, we calculated the other parameters necessary for interpreting the rotational spectrum. At the optimized geometries of each species, we calculated the fine and hyperfine constants. They are the three spin-rotation coupling constants (εaa, εbb, and εcc), the magnetic hyperfine constants for the non zero nuclear spin nuclei (aF, Taa, and Tbb), and the nuclear electric quadrupole constants for the nitrogen nucleus (χaa and χbb) – if the molecule contains any. The spin-rotation coupling constants were calculated using the second order Møller-Plesset perturbation (MP2; Møller & Plesset 1934) with the aug-cc-pVQZ basis set. On the other hand, the other hyperfine constants were calculated at the quadratic configuration interaction with single and double excitations (QCISD; Pople et al. 1987) level of calculation with the aug-cc-pVQZ basis set. Harmonic frequencies were computed at UCCSD/aug-cc-pVQZ level of theory (Čížek 1969) to estimate the centrifugal distortion constants. These calculations were done using the Gaussian16 program (Frisch et al. 2016). Table 2 summarizes the results of these calculations.

Given the observed splitting of ~45 MHz, it is very unlikely that the carrier is a closed-shell species. Even if the molecule has two N nuclei, the hyperfine splitting would be of a few MHz and the number of lines would be smaller than the observed ones. Hence, the carrier should be an open-shell species containing at least two nuclei with a non zero nuclear spin, so that rotational transitions have fine and hyperfine structure. Taking this into account, closed-shell species such as cis-HNNH, H2NN, H2CN−, H2NC+, H2NO+, cis-HNOH+, and trans-HNOH+ were discarded. The value of (B+C)/2 derived from astronomical observations is 36.1 GHz, and thus the rotational constants calculated for NNH, HCN+, HCN−, H2CN+, cis-HCNH+, trans-HCNH+, and H2NC+ clearly exclude them as carriers. In the cases of NNH−, H2NN+, trans-HCNH, and cis-HCNH, the calculated (B+C)/2 are closer to the astronomical value, although the differences are larger than 2.5%. These four candidates can be discarded because the level of calculation used provides errors that are not larger than 1%. In addition, their predicted splitting does not agree with the observed one. For NNH−, H2NN+, and trans-HCNH, the hyperfine components of the 10,1 –00,0 transition span over 100–200 MHz, whereas for cis-HCNH, the splitting is very small at around 10 MHz. At this point, only three species show a (B+C)/2 value compatible with the observed one, 36.1 GHz. H2NC has the closest (B+C)/2 value, while cis-HCOH+ and trans-HCOH+ have values a bit larger, but also compatible taking into account the accuracy of the calculations. However, cis-HCOH+ and trans-HCOH+ have only two nuclei with non zero nuclear spin, and thus, the number of hyperfine components and their splitting pattern cannot explain all the unidentified lines observed in L483. In contrast, H2NC has three nuclei with non zero nuclear spin and its predicted splitting is consistent with the observed one. To obtain accurate spectroscopic parameters for our best candidate, H2NC, we scaled the calculated values using experimental to theoretical ratios derived for the isoelectronic species H2CN, for which experimental rotational parameters are known (Yamamoto & Saito 1992). This procedure has been found to provide rotational constants with an accuracy better than 0.1% (e.g., Cabezas et al. 2021). The theoretical rotational constants A, B, and C obtained bythis way are given in Table 3. It is seen that the calculated (B+C)/2, 36.092 GHz,is very similar to the observed value, which prompted us to consider H2NC as the starting point in our data analysis.

The observed frequencies (see Table 1) were analyzed with the SPFIT program (Pickett 1991) using an appropriate Hamiltonian for an asymmetric top with a doublet electronic state (2 B2) and C2v symmetry. The employed Hamiltonian has the following form: 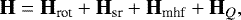(1)

where Hrot contains rotational and centrifugal distortion parameters, Hsr is the spin-rotation term, Hmhf represents the magnetic hyperfine coupling interaction term due to the N and H nuclei, and HQ represent the nuclear electric quadrupole interaction due to the N nucleus. The coupling scheme used is J = N + S, F1 = J + I1, and F = F1 + I2, where I1 = I(N) and I2 = I(H1) + I(H2). H2NC has two equivalent H nuclei and it is thus necessary to discern between the ortho and para species. The ortho levels are described by Ka + Kc even while the para levels by Ka + Kc odd. The hyperfine interaction term Hmhf is thus written explicitly as a two spin system: (2)

where 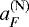and T(N) stand for the Fermi contact constant and the dipole-dipole interaction tensor for the N nucleus, respectively, and 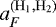and T(H1,H2) are averagesof the coupling constants for the two H nuclei. There is a term proportional to the difference of the coupling constants for the dipole-dipole interaction. However, the term connects levels only off-diagonal in Ka, and thus it can be ignored, treating the two H nuclei as if they are equivalent. In this manner, each energy level is denoted by six quantum numbers: N, Ka, Kc, J, F1, and F.

The results obtained from the fit are shown in Table 3. We experimentally determined the values for a total of thirteen molecular parameters, considering the two equivalent H nuclei. These parameters are the rotational constants B and C, the centrifugal distortion constant ΔN, the electron spin-rotation coupling constants εbb and εcc, the magnetic hyperfine constants for the nitrogen and hydrogen nuclei aF and Taa, and the nuclear electric quadrupole constant for the nitrogen nucleus χaa. Other constants were kept fixed to the theoretical values calculated in this work. The standard deviation of the fit is 15.2 kHz.

The results in Table 3 show an excellent agreement between the theoretical and astronomical values of the rotational constants B and C. The relative errors are 0.01 and0.06% for B and C, respectively.These errors are slightly larger if we compare with the unscaled theoretical values of B and C, 0.04 and 0.58%, respectively. The rotational constants provide information on the mass distribution of the molecular species and, thus, the good accordance between observed and calculated values could serve by itself to identify the spectral carrier. Moreover, the high resolution ofour survey allows us to completely scrutinize the fine and hyperfine structure of the rotational transitions. This structure depends strongly on the electronic environment of the molecular species, which is related to the number of nuclei with a non zero nuclear spin and their relative positions. Hence, the fine and hyperfine coupling constants determined are ideal fingerprints for the spectral carrier, providing key information for its identification. The results from our fit indicate that our carrier must have two equivalent hydrogen nuclei and one nitrogen nucleus, whose aF and Taa constants are in very good agreement with those predicted for H2NC. The aF and Taa values for the two H nuclei are comparable to those of H2CN, 233.152 MHz and 8.294 MHz, respectively (Yamamoto & Saito 1992), which is reasonable since their electronic environment is almost similar in both molecules. However, the aF and Taa for the N nucleus are very different in H2NC and H2CN. First, the Taa values for H2NC and H2CN are 3.413 MHz and −45.143 MHz, respectively, which indicates that the spin density on the N nucleus is much smaller in H2NC. Secondly, the Fermi constants aF have opposite signs, −22.8660 MHz for H2NC and 25.916 MHz for H2CN. This is explained by the different mechanisms for spin polarization due to the unpaired electron on both systems. Figure 2 shows the molecular orbital of the unpaired electron in the two species. In the case of H2NC, the orbital has a node at the location of the N atom, while for H2CN the N atom is completely covered by this orbital. The rest of parameters determined from our fit, ΔN, εbb, and εcc, agree reasonably well with the values calculated theoretically for H2NC. However, it should be mentioned that the accuracy of the prediction of the constants εaa, εbb, and εcc is usually much smaller than for the rotational or hyperfine constants. In the light of all these arguments we definitively conclude that the carrier of the unidentified lines observed in L483 is H2NC.

Table 2

Calculated molecular data for the candidates considered.

Table 3

Spectroscopic parameters of H2NC (all in MHz).

thumbnail Fig. 2

Geometries and molecular orbital for the unpaired electron in H2NC (left) and H2CN (right).

4 Discussion

4.1 H2NC/H2CN ratio in the interstellar medium

We computed synthetic spectra assuming local thermodynamic equilibrium to derive the column density of H2NC in L483. The relative intensities of the various rotational transitions observed constrain the rotational temperature to a low value, 4.0 ± 0.2 K, which is consistent with a highly polar carrier like H2NC. The calculated dipole moment of H2NC is 3.83 D (see Table 3). As full width at half maximum (FWHM) we adopted the average of the observed values, 0.19 km s−1 for the 30,3 –20,2 lines and 0.35 km s−1 for the rest (see Table 1). We derived a beam-averaged column density of (1.0 ± 0.2) × 1012 cm−2 for H2NC in L483 (see synthetic spectrum in Fig. 1). The ortho-to-para ratio is fully consistent with the statistical value of three.

H2NC is the highest energy member of the isomeric family composed of H2CN, trans-HCNH, cis-HCNH, and H2NC. Our calculations predict that H2CN is the most stable isomer, with trans-HCNH and cis-HCNH lying above by 7.9 kcal mol−1 and 12.8 kcal mol−1, respectively, while H2NC lies 29.9 kcal mol−1 higher in energy with respect to H2CN. These results are in agreement with those reported by Puzzarini (2010).

A further argument in support of the assignment to H2NC comes from astronomical observations that have indicated that the carrier is related to H2CN. This radical is also observed in L483 (see Agúndez et al. 2019 and Fig. 3). From the observed intensities of the 10,1 –00,0 and 20,2 –10,1 lines of H2CN in L483, wederived a rotational temperature of 4 K and a column density of (8 ± 2) ×1011 cm−2. This value is somewhat lower than that given by Agúndez et al. (2019) because at that time line strengths were incorrectly computed downward by a factor of three and now we also include the 20,2 –10,1 transition. The H2NC/H2CN abundance ratio in L483 is thus 1.25 ± 0.30. Our carrier, H2NC, is also observed in B1-b, where H2CN is detected as well. In B1-b we derive N(H2NC) = (1.0 ± 0.2) × 1012 cm−2 and N(H2CN) = (1.0 ± 0.2) × 1012 cm−2, which results in a H2NC/H2CN abundance ratio of 1.0 ± 0.3, similar to the value found in L483. Moreover, in the well known cold dark cloud TMC-1, which harbors a rich variety of molecules, neither H2NC nor H2CN are detected in our data. We derive 3σ upper limits to their column densities of 3.2 ×1011 cm−2 and 4.8 × 1011 cm−2, respectively. Ohishi et al. (1994) reported the discovery of H2CN in TMC-1. Although the column density derived by these authors, 1.5 × 1011 cm−2, is consistent with our 3σ upper limit, the identification of Ohishi et al. (1994) is questionable because the two lines detected are only marginally seen above their noise level and they should result in antenna temperatures above 20 mK at IRAM 30 m, which is not consistent with our data (see Fig. 3). Therefore, both our carrier and H2CN are seen in L483 and B1-b with a similar abundance ratio, while none of them are seen in TMC-1. This fact strengthens the idea that our carrier is related to H2CN.

The fact that the strongest hyperfine component of H2NC is 3–4 times more intense that the strongest one of H2CN in L483 and B1-b suggests that H2NC could be easily found in those sources where H2CN is detected. H2CN has been reported toward L1544 (Vastel et al. 2019) and the z = 0.89 galaxy in front of the quasar PKS 1830−211 (Tercero et al. 2020). We examined our Yebes 40 m data of PKS 1830−211 and we find significant absorption at the position of the strongest hyperfine components of H2NC 10,1 –00,0 (see Fig. 4). We computed synthetic spectra for H2NC and H2CN (red curves in Fig. 4) assuming the same physical parameters of the source reported by Tercero et al. (2020). We derive a H2NC/H2CN abundance ratio of 0.27 ± 0.08. The new data added to the PKS 1830−211 spectrum allow us to clearly distinguish an additional component for H2CN (blue curve; see Tercero et al. 2020. The fact that the H2NC/H2CN ratio is significantly lower than the values found in L483 and B1-b points to a chemical differentiation between this high-redshift galaxy and galactic cold interstellar clouds. In fact, the chemical composition in this lensing galaxy is more characteristic of diffuse ortranslucent clouds rather than of cold dense clouds, as indicated by the presence of ions such as C3H+ (Tercero et al. 2020). The case of H2NC and H2CN isomers reminds that of HNC and HCN. The HNC/HCN abundance ratio is ~1 in cold dense clouds (Hirota et al. 1998; Sarrasin et al. 2010) and <1 in diffuse clouds (Liszt & Lucas 2001). In the gravitational lens of PKS 1830−211 the abundance ratio HNC/HCN is 0.4 (Muller et al. 2006), in line with expectations if the source has a diffuse cloud character. Thus, similarly to the case of HNC and HCN, it is likely that in general cold dense clouds show H2NC/H2CN ratios around one and diffuse clouds H2NC/H2CN ratios below one. The presence of H2NC is therefore a further example of how chemical kinetics, rather than thermodynamics, regulate the chemical composition of interstellar clouds.

thumbnail Fig. 3

Strongest hyperfine components of H2NC and H2CN in L483, B1-b, and TMC-1. None of the two isomers were detected in TMC-1.
thumbnail Fig. 4

Absorption lines of H2NC and H2CN observed with the Yebes 40 m telescope towards PKS 1830−211. We assume aredshift of z = 0.885875 to compute the rest frequency. The y-axis is the intensity normalized to the total continuum level. The red lines are the synthetic spectra computed for one component, while in the H2CN spectrum, the blue line corresponds to an additional component and the green line to the sum of the two components. See more details in Tercero et al. (2020).

4.2 Chemistry of H2NC and H2CN

The isomer H2NC is missing in chemical kinetics databases used in astrochemistry, such as UMIST (McElroy et al. 2013) or KIDA (Wakelam et al. 2015). However, the more stable isomer H2CN is included and it is interesting to look at its main formation reactions. To this end, we ran a pseudo-time-dependent gas-phase chemical model with typical parameters of cold dark clouds (see, e.g., Agúndez & Wakelam 2013). We used the chemical network RATE12 from the UMIST database (McElroy et al. 2013), updated with reactions relevant for the chemistry of H2CN from Loison et al. (2015) and Hickson et al. (2015). According to our calculations, H2CN is formed with a peak abundance relative to H2 of ~10−10. The main formation reactions are C + NH3, N + CH3, and N + CH2CN, while it is mainly destroyed through reactions with neutral H, C, N, and O atoms. Taking into account that H2NC and H2CN are observed with similar abundances in L483 and B1-b, it is likely that both isomers share a common formation route.

The reaction between N and CH3 has been studied experimentally and theoretically. Experimental studies in the temperature range 200–423 K reveal a rate coefficient around 10−10 cm3 s−1, with a positive temperature dependence, and a branching ratio of 0.9 for production of H atoms (Marston et al. 1989a,b). Computational studies point to H2CN + H as main channel (Cimas & Largo 2006; Alves et al. 2008). The study of Alves et al. (2008) does not consider H2NC as product, but that of Cimas & Largo (2006) considers H2NC and trans-HCNH. Cimas & Largo (2006) show how the reactants N and CH3 approach via an attractive potential surface leading to an intermediate, H3CN, whose formation does not involve any barrier. This intermediate has two different possibilities for its further evolution. In the first place, elimination of a hydrogen atom would lead to H2CN + H, the most exothermic channel. This process involves a transition state which lies well below the reactants. A second possibility is isomerization into H2CNH, through hydrogen migration from carbon to nitrogen, which proceeds through a transition state also located well below the reactants. H2CNH may lead totrans-HCNH + H involving a lower barrier and a further isomerization into HCNH2 would produce the H2NC + H channel as final product. Although the three isomers, H2CN, trans-HCNH, and H2NC can be formed without any barrier (all the transition states are submerged below the reactants), the elimination of a hydrogen atom from the initially formed intermediate, H3CN, leading to H2CN + H, is the preferred reaction path. Cimas & Largo (2006) state that residual quantities of trans-HCNH can be formed, whereas for H2NC the branching ratio is negligible.

The reaction C + NH3 has been studied more recently and it has been found that it is rapid at 50 K, with a rate coefficient of 1.8 × 10−10 cm3 s−1 (Hickson et al. 2015). In a related study, Bourgalais et al. (2015) combined photoionization and LIF experiments supported by theoretical calculations and showed that the H2CN + H channel represents 100% of the product yield for this reaction. These authors rule out that trans-HCNH or cis-HCNH are formed, but do not discuss whether H2NC can be produced. The theoretical calculations reported by Bourgalais et al. (2015) show that the first step is the formation of a reaction intermediate, CNH3, in a process without any barrier. As in the case of the H3CN intermediatein the N + CH3 reaction discussed above, CNH3 can proceed through two different pathways. The first one, the elimination of a hydrogen atom, would lead to H2NC + H, through a transition state which lies below the reactants. This reaction path is illustrated in Fig. 5. On the other hand, the isomerization of the CNH3 intermediate through hydrogen migration from nitrogen to carbon can lead to HCNH2. This isomerization proceeds through a transition state also located below the reactants. HCNH2 can further evolve to form H2NC + H or trans-HNCH. A second hydrogen migration from nitrogen to carbon in HCNH2 produces H2CNH, which ultimately leads H2CN + H, that is the most exothermic channel. Although H2NC + H is not the most exothermic product channel, it could be the most favored channel if we consider the elimination of a hydrogen atom from CNH3 as the preferred reaction path, analogously to the N + CH3 results of Cimas & Largo (2006).

Another fact that reinforces the credibility of the previous statement is that the identification of H2CN as main product in the C + NH3 reaction by Bourgalais et al. (2015) is based exclusively in the agreement between their measured photoionization spectrum and that measured and attributed to H2CN by Nesbitt et al. (1991). However, as discussed by Holzmeier et al. (2013), the ionization energy measured by Nesbitt et al. (1991) is derived from an ion yield curve and it is therefore afflicted with a rather large uncertainty. In fact, Holzmeier et al. (2013) measured an excitation energy of 12.32 eV for H2CN, very different from the value derived by Nesbitt et al. (1991), 10.8 eV. This can be attributed to the fact that the method used by Nesbitt et al. (1991) contains less information than the threshold photoelectron spectra of Holzmeier et al. (2013), which precluded Nesbitt et al. (1991) from distinguishing between isomers. Since the experimental methods employed by Bourgalais et al. (2015) and Nesbitt et al. (1991) are quite similar, it is reasonable to think that both have the same limitations. Hence, if H2NC is formed in the experiment of Bourgalais et al. (2015), it could have escaped detection with their experimental setup.

The reaction between N and CH2CN was considered by Loison et al. (2015) to yield H2CN with a moderately high rate coefficient by analogy to the reaction N + CH3. However, no dedicated studies have been carried out on this particular reaction and thus it is uncertain whether H2CN or any of its metastable isomers are formed. Other plausible routes to H2CN and H2NC are the reactions between radicals NH + CH2 and NH2 + CH, although they are probably less efficient than N + CH3 and C + NH3 because the reactants are expected to have lower abundances. Formation routes involving ions are also possible, in particular those leading to the various possible isomers Hx CNH3−x+ (x = 0–3), which upon dissociative recombination with electrons can form H2CN and H2NC. A plausible such route could involve the reaction NH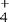 + C, although its rate coefficient and products are not known.

In summary, the two isomers H2CN and H2NC can be produced in a barrierless process in the reactions: N + CH3 and C + NH3, with H2NC being a more likely product of the latter reaction. In the light of our results, it would be interesting to revisit these two reactions and evaluate the yields of the different isomers: H2CN, trans- and cis-HCNH, and H2NC. Other routes are also possible, however the relevant theoretical or experimental information is missing.

thumbnail Fig. 5

Molecular structures of the species involved in the formation of H2NC in the C + NH3 reaction. TSstands for transition state.

5 Conclusions

We observed various sets of unidentified lines in the cold dark cloud L483, which we confidently assign to H2NC, a high-energy metastable isomer of H2CN. The astronomical lines are used to precisely characterize the rotational spectrum of H2NC. Both H2NC and H2CN are detected, in addition to L483, in the cold dark cloud B1-b and the high redshift lensing galaxy in front of the quasar PKS 1830−211. Neither H2NC nor H2CN are detected in the dark cloud TMC-1, which calls into question a previous claim of detection of H2CN in this source. We derived H2NC/H2CN abundance ratios ~1 in the cold dense clouds L483 and B1-b and 0.27 in the high-redshift galaxy. It appears that the H2NC/H2CN ratio behaves as the HNC/HCN ratio, with values around one in cold dense clouds and below one in diffuse and translucent media. The most obvious formation routes to H2CN and H2NC are the reactions N + CH3 and C + NH3. The latter is particularly favorable for production of H2NC. Further studies of these reactions able to constrain the yield of each isomer would allow us to improve our understanding of the chemistry behind H2NC and H2CN. This could open the door to the use of the H2NC/H2CN ratio as a proxy for the chemical or physical parameters of interstellar clouds.

Acknowledgements

We acknowledge funding support from Spanish Ministerio de Ciencia e Innovación through grants AYA2016-75066-C2-1-P, PID2019-106110GB-I00, and PID2019-107115GB-C21, and from the European Research Council (ERC Grant 610256: NANOCOSMOS). M.A. also acknowledges funding support from the Ramón y Cajal programme of Spanish Ministerio de Ciencia e Innovación (grant RyC-2014-16277). We thank Prof. Ingo Fischer for his comments on the photoionization spectrum of the methylene amidogen radical.

Appendix A New frequencies and spectroscopic parameters for CCD

Yoshida et al. (2019) pointed out that the frequencies of some of the hyperfine components of the N = 1-0 transition of CCD, as observed in L1527, are significantly different from those reported in the CDMS catalogue (Müller et al. 2005). The predictions from the CDMS catalogue are based in the experimental data reported by Bogey et al. (1985) and Vrtilek et al. (1985), who observed the N = 2-1, 3-2, 4-3, and 5-4 transitions, but only one hyperfine component of the N = 1-0 transition. Yoshida et al. (2019) reported observed frequencies in L1527 for seven hyperfine components of the N = 1-0 transition, with discrepancies with respect to the CDMS ones of up to 224 kHz. The inaccuracy of the N = 1-0 frequencies reported in the CDMS catalogue is due to the fact that they are calculated based on the laboratory measurements of higher N transitions with a limited spectral resolution, which makes it difficult to discern between close hyperfine components.

In the analysis of our IRAM 30m data of L483, we also noticed that the observed frequencies of the hyperfine components of the N = 1-0 and 2-1 transitions of CCD differ from those reported in the CDMS catalogue. In order to provide more accurate predictions of the rotational spectrum of CCD, we carried out a fit in which we only include the astronomical frequencies for the N = 1-0 and 2-1 transitions, along with another fit in which we also include the laboratory frequencies for the N = 3-2, 4-3, and 5-4 transitions. The spectroscopic parameters resulting from our fits are given in Table A.1, where they are compared with the original values reported by Bogey et al. (1985) and Vrtilek et al. (1985). The frequencies used in the fits are given in Table A.2.

The spectroscopic parameters derived in our two fits are very similar. The main difference is found in the distortion constant, D, which is affected by the inclusion of higher N transitions when moving from the astronomical fit to the astronomical + laboratory fit. There is a notable change in the new value of B derived in our fits compared to those derived by Bogey et al. (1985) and Vrtilek et al. (1985), whereas the value of D obtained in our combined fit agrees with those reported by Bogey et al. (1985) and Vrtilek et al. (1985). The new value for γ is determined more accurately and also agrees with what has been previously reported. The larger differences are found for the hyperfine constants bF and c, whose previous values also differ between the two laboratory studies. The high resolution of our measurements is reflected in a higher accuracy determination for these hyperfine constants. The nuclear quadrupole coupling constant eQq is also determined more precisely than before, but the previous values agree with the new one. We recommend the spectroscopic parameters derived in our combined astronomical + laboratory fit to predict the rotational spectrum of CCD.

Table A.1

Spectroscopic parameters of CCD (all in MHz).

Table A.2

Transition frequencies of CCD in MHz.

References

  1. Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
  2. Agúndez, M., Marcelino, N., Cernicharo, J., et al. 2019, A&A, 625, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Agúndez, M., Roueff, E., Cabezas, C., et al. 2021, A&A, 649, A171 [CrossRef] [EDP Sciences] [Google Scholar]
  4. Alves, T. V., de Oliveira Filho, A. G. S., & Ornellas, F. R. 2008, Chem. Phys. Lett., 457, 36 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bogey, M., Demuynck, C., & Destombes, J. L. 1985, A&A, 144, L15 [NASA ADS] [Google Scholar]
  6. Bourgalais, J., Capron, M., Kailasanathan, R. K. A., et al. 2015, ApJ, 812, 106 [CrossRef] [Google Scholar]
  7. Buhl, D., & Snyder, L. E. 1970, Nature, 228, 267 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cabezas, C., Endo, Y., Roueff, E., et al. 2021, A&A, 646, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Cernicharo, J. 2012, EAS Pub. Ser., 58, 251 [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cernicharo, J., Guélin, M., & Walmsley, C. M. 1987, A&A, 172, L5 [NASA ADS] [Google Scholar]
  11. Cernicharo, J., Guélin, M., Agúndez, M., et al. 2008, ApJ, 688, L83 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cernicharo, J., Cabezas, C., Pardo, J. R., et al. 2019, A&A, 630, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Cimas, A., & Largo, A. 2006, J. Phys. Chem. A, 110, 10912 [CrossRef] [Google Scholar]
  15. Čížek, J. 1969, Adv. Chem. Phys., 14, 35 [CrossRef] [Google Scholar]
  16. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision A.03 [Google Scholar]
  17. Guélin, M., Green, S., & Thaddeus, P. 1978, ApJ, 224, L27 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hickson, K. M., Loison, J.-C., Bourgalais, J., et al. 2015, ApJ, 812, 107 [CrossRef] [Google Scholar]
  19. Hirota, T., Yamamoto, S., Mikami, H., & Ohishi, M. 1998, ApJ, 503, 717 [NASA ADS] [CrossRef] [Google Scholar]
  20. Holzmeier, F., Lang, M., Hader, K., et al. 2013, J. Chem. Phys., 138, 214310 [NASA ADS] [CrossRef] [Google Scholar]
  21. Klein, B., Hochgürtel, S., Krämer, I., et al. 2012, A&A, 542, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Lattelais, M., Pauzat, F., Ellinger, Y., & Ceccarelli, C. 2009, ApJ, 696, L133 [Google Scholar]
  23. Liszt, H., & Lucas, R. 2001, A&A, 370, 576 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Loison, J. C., Hébrard, E., Dobrijevic, M., et al. 2015, Icarus, 247, 218 [NASA ADS] [CrossRef] [Google Scholar]
  25. Marcelino, N., Agúndez, M., Tercero, B., et al. 2020, A&A, 643, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Marston, G., Nesbitt, F. L., Nava, D. F., et al. 1989a, J. Phys. Chem., 93, 5769 [CrossRef] [Google Scholar]
  27. Marston, G., Nesbitt, F. L., & Stief, L. J. 1989b, J. Chem. Phys., 91, 3483 [NASA ADS] [CrossRef] [Google Scholar]
  28. McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [Google Scholar]
  30. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
  31. Muller, S., Guélin, M., Dumke, M., et al. 2006, A&A, 458, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Nesbitt, F. L., Marston, G., Stief, L. J., et al. 1991, J. Phys. Chem., 95, 7613 [CrossRef] [Google Scholar]
  33. Ohishi, M., McGonagle, D., Irvine, W. M., et al. 1994, ApJ, 427, L51 [NASA ADS] [CrossRef] [Google Scholar]
  34. Pety, J., Gratier, P., Guzmán, V., et al. 2012, A&A, 548, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [Google Scholar]
  36. Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [Google Scholar]
  37. Pombeiro, A. J. L., Fátima, M., & Guedes da Silva, C. 2001, J. Organomet. Chem., 617, 65 [CrossRef] [Google Scholar]
  38. Pople, J. A., Head-Gordon, M., & Raghavachari, K. 1987, J. Chem. Phys., 87, 5968 [NASA ADS] [CrossRef] [Google Scholar]
  39. Puzzarini, C. 2010, Int. J. Quant. Chem., 110, 2483 [Google Scholar]
  40. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [Google Scholar]
  41. Sarrasin, E., Ben Abdallah, D., Wernli, M., et al. 2010, MNRAS, 404, 518 [Google Scholar]
  42. Suzuki, H., Ohishi, M., Kaifu, N., et al. 1986, PASJ, 38, 911 [NASA ADS] [Google Scholar]
  43. Tercero, B., Cernicharo, J., Cuadrado, S., et al. 2020, A&A, 636, L7 [CrossRef] [EDP Sciences] [Google Scholar]
  44. Thaddeus, P., Guélin, M., & Linke, R. A. 1981, ApJ, 246, L41 [NASA ADS] [CrossRef] [Google Scholar]
  45. Vastel, C., Loison, J.-C., Wakelam, V., & Lefloch, B. 2019, A&A, 625, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Vrtilek, J. M., Gottlieb, C. A., Langer, W. D., et al. 1985, ApJ, 296, L35 [CrossRef] [Google Scholar]
  47. Wahlgren, U., Liu, B., Pearson, P. K., & Schaefer, H. F. 1973, Nat. Phys. Sci., 246, 4 [NASA ADS] [CrossRef] [Google Scholar]
  48. Wakelam, V., Loison, J.-C., Herbst, E., et al. 2015, ApJS, 217, 20 [Google Scholar]
  49. Werner, H.-J., Knowles, P. J., Knizia, G., et al. 2020, MOLPRO, version 2020.2 [Google Scholar]
  50. Woods, R. C., Dixon, T. A., Saykally, R. J., & Szanto, P. G. 1975, Phys. Rev. Lett., 35, 1269 [NASA ADS] [CrossRef] [Google Scholar]
  51. Woon, D. E., & Dunning, T. H., Jr. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
  52. Yamamoto, S., & Saito, S. 1992, J. Chem. Phys., 96, 4157 [NASA ADS] [CrossRef] [Google Scholar]
  53. Yoshida, K., Sakai, N., Nishimura, Y., et al. 2019, PASJ, 71, S18 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Line parameters of H2NC observed in L483.

In the text
Table 2

Calculated molecular data for the candidates considered.

In the text
Table 3

Spectroscopic parameters of H2NC (all in MHz).

In the text
Table A.1

Spectroscopic parameters of CCD (all in MHz).

In the text
Table A.2

Transition frequencies of CCD in MHz.

In the text

All Figures

thumbnail Fig. 1

Lines of H2NC observed in L483 (see parameters in Table 1). In red we show the computed synthetic spectra for a column density of H2NC of 1012 cm−2, ortho-to-para ratio of 3, rotational temperature of 4.0 K, full width at half maximum of 0.35 km s−1 (except for the 30,3–20,2 lines, in which case a value of 0.19 km s−1 was adopted), and an emission size that fills the IRAM 30 m main beam. Vertical blue lines indicate the position of CCD lines (see Appendix A).
In the text
thumbnail Fig. 2

Geometries and molecular orbital for the unpaired electron in H2NC (left) and H2CN (right).
In the text
thumbnail Fig. 3

Strongest hyperfine components of H2NC and H2CN in L483, B1-b, and TMC-1. None of the two isomers were detected in TMC-1.
In the text
thumbnail Fig. 4

Absorption lines of H2NC and H2CN observed with the Yebes 40 m telescope towards PKS 1830−211. We assume aredshift of z = 0.885875 to compute the rest frequency. The y-axis is the intensity normalized to the total continuum level. The red lines are the synthetic spectra computed for one component, while in the H2CN spectrum, the blue line corresponds to an additional component and the green line to the sum of the two components. See more details in Tercero et al. (2020).
In the text
thumbnail Fig. 5

Molecular structures of the species involved in the formation of H2NC in the C + NH3 reaction. TSstands for transition state.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.