| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201935010 | |
| Published online | 17 May 2019 | |
Isocyanogen formation in the cold interstellar medium
1
IRAP, Université de Toulouse, CNRS, UPS, CNES,
31400 Toulouse,
France
e-mail: cvastel@irap.omp.eu
2
Institut des Sciences Moléculaires (ISM), CNRS, Université de Bordeaux,
351 cours de la Libération,
33400 Talence, France
3
Laboratoire d’astrophysique de Bordeaux, Université de Bordeaux, CNRS, B18N, allée Geoffroy Saint-Hilaire,
33615
Pessac, France
4
CNRS, IPAG, Université Grenoble Alpes,
38000 Grenoble, France
Received:
3
January
2019
Accepted:
23
March
2019
Context. Cyanogen (NCCN) is the simplest member of the dicyanopolyynes group, and has been proposed as a major source of the CN radical observed in cometary atmospheres. Although not detected through its rotational spectrum in the cold interstellar medium, this very stable species is supposed to be very abundant.
Aims. The chemistry of cyanogen in the cold interstellar medium can be investigated through its metastable isomer, CNCN (isocyanogen). Its formation may provide a clue on the widely abundant CN radical observed in cometary atmospheres.
Methods. We performed an unbiased spectral survey of the L1544 proto-typical prestellar core, using the IRAM-30 m and have analysed, for this paper, the nitrogen chemistry that leads to the formation of isocyanogen. We report on the first detection of CNCN, NCCNH+, C3N, CH3CN, C2H3CN, and H2CN in L1544. We built a detailed chemical network for NCCN/CNCN/HC2N2+ involving all the nitrogen bearing species detected (CN, HCN, HNC, C3N, CNCN, CH3CN, CH2CN, HCCNC, HC3N, HNC3, H2CN, C2H3CN, HCNH+, HC3NH+) and the upper limits on C4N, C2N. The main cyanogen production pathways considered in the network are the CN + HNC and N + C3N reactions.
Results. The comparison between the observations of the nitrogen bearing species and the predictions from the chemical modelling shows a very good agreement, taking into account the new chemical network. The expected cyanogen abundance is greater than the isocyanogen abundance by a factor of 100. Although cyanogen cannot be detected through its rotational spectrum, the chemical modelling predicts that it should be abundant in the gas phase and hence might be traced through the detection of isocyanogen. It is however expected to have a very low abundance on the grain surfaces compared to HCN.
Key words: astrochemistry / molecular processes / line: identification / molecular data / radiative transfer
© C. Vastel et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Molecular complexity in the cold interstellar medium has been revealed to be extremely rich, due to the sensitivity and spectral resolution of modern instruments. Organic molecules have been detected, such as alcohols, aldehydes, acids, ethers, amines, and nitriles. The strong bond of the cyano group (–C ≡N) is present in many species such as cyanopolyynes (HCnN with n = 3,5,7, ...), and it has also been speculated that dicyanopolyynes might be abundant in interstellar clouds (Kolos & Grabowski 2000; Petrie et al. 2003). Dicyanopolyynes are very stable species formed by highly unsaturated linear chain of carbon atoms ended by a cyano group at each edge, such as N ≡C–(C ≡C)n–C ≡N. The simplest form of dicyanopolyynes is the non polar species, cyanogen (NCCN, also called C2N2), that cannot be observed through its rotational spectrum. Its metastable isomer, CNCN has however been detected recently towards L483, which harbours a Class 0 protostar, and tentatively in the cold dark cloud TMC-1 (Agúndez et al. 2018)by stacking of four transitions. The most plausible formation route in cold clouds is the reaction

The detection of protonated cyanogen (NCCNH+) in TMC-1 by Agúndez et al. (2015) is also a proof that cyanogen might be an abundant species in the interstellar medium, produced through the protonation of NCCN with H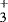 and HCO+:
and HCO+:
 (3)
(3)
with X=H2 and CO. NCCN, which has been detected in Titan atmosphere (Teanby et al. 2006) but not within cometary comae, has been proposed as a major source of the CN radical observed in cometary atmospheres (Bockelee-Morvan & Crovisier 1985; Bonev & Komitov 2000). Indeed, the photolysis of HCN, HC3 N, or NCCN could explain the CN origin. However the HC3N production rate is likely too low to reproduce CN density profile and the CN distribution in comets cannot be explained by the HCN photolysis only (Fray et al. 2005). The presence of NCCN in comets is therefore a reliable hypothesis to explain the CN origin. CNCN is a good probe to trace the presence of NCCN, since the two are supposed to be linked through reactions (1) and (2).
Some of the precursors of the molecules detected within comets are very likely formed within molecular clouds (see, for example, Geiss et al. 1999; Bockelée-Morvan et al. 2000; Ehrenfreund & Charnley 2000), and understanding of the formation of CNCN and NCCN under cold cloud conditions is a crucial step s the understanding of the molecular complexity in comets. As part of the IRAM-30 m Large Program ASAI1 (Lefloch et al. 2018), we carried out a highly sensitive, unbiased spectral survey of the molecular emission of the L1544 prestellar core with a high spectral resolution. In the present study we have examined the nitrogen chemistry in this core using the observations of isocyanogen, protonated cyanogen, and cyanoethynyl, used a radiative transfer modelling to determine the observed column densities and compared with the most up-to-date chemical modelling for cyanogen chemistry.
In Sect. 2 we present the observations from the ASAI spectral survey and the line identification for the cyanogen bearing species. Based on the detections and tentative detection, we compute in Sect. 3 the column densities of these species. In Sect. 4 we present a new chemical modelling and confront the results with the observations.
2 Observations
The observations for all transitions quoted in Table 1 were performed at the IRAM-30 m towards the dust peak emission of the L1544 pre-stellar core (α2000 = 05h04m17.21s, δ2000 = 25°10′42.8′′) in the framework of the ASAI Large Program. Observations at frequencies lower than 80 GHz have been performed in December 2015. All the details of these observations can be found in Vastel et al. (2014) and Quénard et al. (2017a) and line intensities are expressed in units of main-beam brightness temperature. The frequency range covered by the present spectral survey is 71.74–115.87 GHz. We selected transitions with an upper level energy lower than 30 K, and computed the rms over a range of 15 km s−1 with a spectral resolution of 50 kHz. Some transitions are labelled multiplet or triplet, meaning that the observations do not havethe spectral resolution necessary to resolve these transitions or that the hyperfine structure transitions have the same frequencies and slightly different Einstein coefficients. For example, the CNCN 8–7 transition can be decomposed in nine transitions (hyperfine structure due to the quadrupole of the two 14 N nuclei) at the same frequency of 82.784691 GHz: 87,8 –76,7, 89,10 –78,9, 88,8 –77,7, 89,9 –78,8, 89,8 –78,7, 88,7 –77,6, 87,7 –76,6, 88,9 –77,8, 87,6 –76,5. Another example is the 8 (J = 17/2)–7 (J = 15/2) transition of C3 N that can be decomposed in three hyperfine transitions: F = 19/2–17/2 at 79.1510059 GHz, F = 17/2–15/2 at 79.1509881 GHz and F = 15/2–13/2 at 79.1509863 GHz.
The line identification and analysis have been performed using the CASSIS2 software (Vastel et al. 2015a). The results from the line fitting take into account the statistical uncertainties accounting for the rms (estimated over a range of 15 km s−1 for a spectral resolution of 50 kHz).
We report the first detections of CNCN (isocyanogen), NCCNH+ (protonated cyanogen), C3N (cyanoethynyl), H2 CN (N-methaniminyl or methyleneamidogen), A- and E-CH3CN (methyl cyanide also known as acetonitrile or cyanomethane), and C2 H3CN (vinyl cyanide, also known as acrylonitrile or propenenitrile, H2 C=CH–C ≡N) in the L1544 prestellar core shown in Figs. 1–6 respectively. Some transitions of C2 N (cyanomethylidyne) and C4N (cyanopropynylidyne) are covered, although not detected, in this spectral survey.
Only the CNCN J = 8–7 and 10–9 transitions can be considered as detected (4.2 σ for the latter). We have superimposed in red our LTE best fitting solution (see Sect. 3) upon the observed transitions in Fig. 1. The agreement between the predicted intensities and the observations is satisfying except for the J = 9–8 transition. In order to improve the signal to noise ratio of our CNCN detection and the physical parameter determination, we have stacked the four transitions found in the spectral survey. The result is shown in the bottom panel of Fig. 1 (in black, sampled to the resolution of the 10–9 transition) and shows an emission line (in red) detected at a 7 σ confidence over 12 km s−1 (7.7 σ over 5 km s−1), with the following parameters for the Gaussian fit: T = 8 mK, FWHM = 0.48 km s−1, VLSR = 7.19 km s−1. The CNCN detected transitions (8–7 and 10–9) present different line widths quoted in Table. 1 (0.41 and 0.61 km s−1). These do, however, have high uncertainty on the VLSR of the 8–7 transition. A similar difference, if confirmed, has been observed for the detection of CNCN in the L483 dense cloud (line widths between 0.47 and 0.87 km s−1) (Agúndez et al. 2018).
A feature seems to be present in the spectrum of the 9–8 transition (Fig. 1) at about 12 km s−1. The unidentified (using the JPL and CDMS databases) transition is also seen in the spectrum of L483 (Agúndez et al. 2018) at ~5 km s−1 with respect to the 9–8 transition. The selection of the baseline around 5 km s−1 is therefore necessary to avoid this feature, hence a 7.7 σ detection for the stacking (see above).
We will compute, in the following section, the column densities for the detected species and some upper limits.
 |
Fig. 1 Observed transitions of isocyanogen (CNCN) in black with a LTE model (red) using Tex = 15 K and N = 6.5 × 1011 cm−2. Bottompanel: results (in black) from the stacking of the four observed transitions as well as the Gaussian fit (in red). |
3 Determination of the column densities
In this section we determine the column densities for the detected species (CNCN, NCCNH+, C3 N, A-CH3CN, E-CH3CN, H2 CN, C2 H3CN) and upper limits for C2N and C4N, taking into account the uncertainties based on the line fitting and also the absolute calibration accuracy, around 10% or better depending on the band considered. For that we used the CASSIS software, that interrogates the JPL and CDMS databases, and performs LTE and non LTE (when the collisions files are available) radiative transfer modelling. The number of detected transitions is not sufficient to explore a wide range of excitation temperatures.
For NCCNH+, we vary theexcitation temperature between 10 and 15 K, and compute a column density of (1.2–1.9) × 1010 cm−2. A lower value for the excitation temperature is not compatible with the upper limit on the 8–9 transition at 79.9 GHz. We note that the rms for both undetected transitions at 79.9 and 97.6 GHz is more than a factor two higher than for the detected transition at 88.8 GHz, therefore the expected intensities (less than 20 mK) are within the noise level.
For H2CN, we vary the excitation temperature between 5 and 15 K (a reasonable range for species detected in L1544), and compute a column density of (3–6) × 1011 cm−2. For isocyanogen (CNCN), the covered energy range is large enough to constrain the excitation temperature between 13 and 17 K, with a computed column density of [6.0–6.6] × 1011 cm−2.
For cyanoethynyl (C3N), the resulting excitation temperature is (7.2 ± 0.2) K and column density is (1.6 ± 0.1) × 1012 cm−2. For C2N and C4N, we can compute upper limits on the column densities of 2 × 1012 cm−2 and 1014 cm−2 respectively.
For methyl cyanide (CH3CN), we used the A and E forms provided in the CASSIS database3 and converged on an excitation temperature of 5 ± 0.5 K and a column density of (4.5 ) × 1011 cm−2 for the A form and (2.8
) × 1011 cm−2 for the A form and (2.8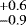 ) × 1011 cm−2 for the E form, with a A/E ratio of ~1.6, slightly higher than the ratio found by Minh et al. (1993) towards TMC-1 (~1.5). For C2 H3CN, we detected 10 transitions between 16 and 27 K, and used a rotational diagram analysis: Trot = (5.3 ± 0.3) K and N = (4.0 ± 0.5) × 1012 cm−2. We note that for all species, we carefully checked that the modelled transitions of the undetected lines are consistent with the noise level.
) × 1011 cm−2 for the E form, with a A/E ratio of ~1.6, slightly higher than the ratio found by Minh et al. (1993) towards TMC-1 (~1.5). For C2 H3CN, we detected 10 transitions between 16 and 27 K, and used a rotational diagram analysis: Trot = (5.3 ± 0.3) K and N = (4.0 ± 0.5) × 1012 cm−2. We note that for all species, we carefully checked that the modelled transitions of the undetected lines are consistent with the noise level.
We present in Table 2 a comparison between the observed column densities in the prototypical dark cloud TMC-1 and the values found in the L1544 prestellar core, at a later evolutionary stage. The latter values will be used in Sect. 4.2 for the chemical modelling of the core. The column densities are comparable for many species, such as CN, CNCN, H2 CN, HCN, HNC, HCNH+, despite the fact that TMC-1 is less evolved than L1544, which is showing signs of gravitational contraction in its centre (Caselli et al. 2012). For the other species, the column densities are higher in TMC-1, which can be explained by the fact that depletion is more pronounced in the prestellar core L1544.
Properties of the observed transitions for Eup lower than 30 K.
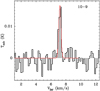 |
Fig. 2 Observed transition of protonated cyanogen (NCCNH+) with a LTE model (red) using Tex = 10 K, andN = 1.9 × 1010 cm−2. |
 |
Fig. 3 Observed transitions of cyanoethynyl (C3N) with an associated VLSR of 7.25 km s−1 (dashed lines) with a LTE model (red) using Tex = 7.2 K and N = 1.6 × 1012 cm−2. |
 |
Fig. 4 Observed transitions of methylene amidogen (H2CN) with a LTE model (red): Tex = 10 K, N = 3 × 1011 cm−2, ΔV = 0.35 km s−1. |
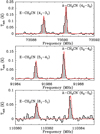 |
Fig. 5 Observed transitions of methyl cyanide (CH3CN) with a LTE model (red): Tex = 5K, N(A-form) = 4.5 × 1011 cm−2, N(E-form) = 2.8 × 1011 cm−2, ΔV = 0.45 km s−1. |
 |
Fig. 6 Observed transitions of C2H3CN with an associated VLSR of 7.25 km s−1 (dashed lines) with a LTE model (red): Tex = 5.3 K, N = 4.0 × 1012 cm−2, ΔV = 0.4 km s−1. |
4 Chemical modelling
4.1 Investigating the chemistry of dicyanopolyynes species in the interstellar medium
To build the chemical network for NCCN/CNCN/HC2N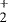 chemistry we start from the work of Agúndez et al. (2015, 2018) using a general methodology for the study of the chemistry described in details in Loison et al. (2014, 2017). The rate constants used in our study are presented inTable 3 and the details of the calculations are shown in the appendix. They were added to the chemical network of kida.uva.2014 (Wakelam et al. 2015) and additional updates from Wakelam et al. (2015); Loison et al. (2016); Hickson et al. (2016); Wakelam et al. (2017); Vidal et al. (2017); Loison et al. (2017).
chemistry we start from the work of Agúndez et al. (2015, 2018) using a general methodology for the study of the chemistry described in details in Loison et al. (2014, 2017). The rate constants used in our study are presented inTable 3 and the details of the calculations are shown in the appendix. They were added to the chemical network of kida.uva.2014 (Wakelam et al. 2015) and additional updates from Wakelam et al. (2015); Loison et al. (2016); Hickson et al. (2016); Wakelam et al. (2017); Vidal et al. (2017); Loison et al. (2017).
The main NCCN production pathways in our network are the CN + HNC and N + C3 N reactions. A minor reaction is the N + HCCN reaction which has been neglected in this study because HCCN is not supposed to be abundant in the interstellar medium. Indeed, HCCN has not been detected in TMC-1, with an upper limit on the fractional abundance (with respect to H2) of 2 × 10−10 (McGonagle & Irvine 1996), and it has not been included in our network. The CN + HNC reaction has been studied theoretically by Petrie & Osamura (2004) leading to a high rate constant at low temperature. The N + C3 N reaction was already in the KIDA network but producing only CN + CCN (Loison et al. 2014). For this study, we have performed an extensive theoretical calculations on the C3N2 triplet surface showing that N(4S) + C3 N(X2Σ+) is correlated not only to CN(X2Σ+) + CCN(X2Σ) but also to C(3P) + NCCN (X1Σ+) and to C(3P) + CNCN(X1Σ+) as shown on Table A.1 and Figs. A.1, B.1, and C.1. Considering the exoenergicities, the N + C3N → C + NCCN channel should be favoured.
Apart from the minor channel N + C3N → C + CNCN, the other CNCN production is through the electronic dissociation rate (DR) of HC2N , the latter being produced through NCCN + H
, the latter being produced through NCCN + H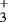 and NCCN + HCO+ reactions (see Eq. (3)). Other HC2N
and NCCN + HCO+ reactions (see Eq. (3)). Other HC2N production pathways show a barrier as CN + HCNH+ (see Table G.1). By comparison with similar DRs (Florescu-Mitchell & Mitchell 2006; Plessis et al. 2012; Reiter & Janev 2010), the H elimination seems to be an important pathway, assumed to be equal to 50% in this study. In that case, the NCCN production is highly exothermic and will carry a large internal energy, up to 668 kJ mol−1 (see Table 3). If the internal energy is above the dissociation limit, it will lead to dissociation producing H + CN + CN with a low branching ratio neglected here. On the contrary, if the internal energy is below the dissociation limit but above the isomerization barrier which is the most probable case as hydrogen atom and NCCN will cary some translational energy, it will lead to the production of NCCN and CNCN isomers as shown on Fig. D.1 and Table D.1. The branching ratio is assumed to be proportional to the ro-vibrational density of states of each isomer at the transition state (TS) energy (Herbst et al. 2000). As the DR of HC2N
production pathways show a barrier as CN + HCNH+ (see Table G.1). By comparison with similar DRs (Florescu-Mitchell & Mitchell 2006; Plessis et al. 2012; Reiter & Janev 2010), the H elimination seems to be an important pathway, assumed to be equal to 50% in this study. In that case, the NCCN production is highly exothermic and will carry a large internal energy, up to 668 kJ mol−1 (see Table 3). If the internal energy is above the dissociation limit, it will lead to dissociation producing H + CN + CN with a low branching ratio neglected here. On the contrary, if the internal energy is below the dissociation limit but above the isomerization barrier which is the most probable case as hydrogen atom and NCCN will cary some translational energy, it will lead to the production of NCCN and CNCN isomers as shown on Fig. D.1 and Table D.1. The branching ratio is assumed to be proportional to the ro-vibrational density of states of each isomer at the transition state (TS) energy (Herbst et al. 2000). As the DR of HC2N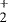 and CNCNH+ will lead to very similar products (NCCN, CNCN, HCN, HNC, and CN) with very similar branching ratios for our assumptions, we consider only one isomer for HC2N
and CNCNH+ will lead to very similar products (NCCN, CNCN, HCN, HNC, and CN) with very similar branching ratios for our assumptions, we consider only one isomer for HC2N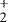 and CNCNH+.
and CNCNH+.
Ionic reactions are efficient NCCN and CNCN destruction pathways, either directly through reaction with He+ (Raksit & Bohme 1984) or through protonation as the DR of HC2N does not lead to 100% of NCCN and CNCN. Safrany & Jaster (1968a) have found some reactivity of NCCN with nitrogen atoms. However, it has been shown that, in this kind of experiment, the reactivity is due to the presence of metastable N
does not lead to 100% of NCCN and CNCN. Safrany & Jaster (1968a) have found some reactivity of NCCN with nitrogen atoms. However, it has been shown that, in this kind of experiment, the reactivity is due to the presence of metastable N (Michael 1980; Dutuit et al. 2013). We then performed DFT calculations, using the M06-2X/AVTZ method (this highly nonlocal functional developed by Zhao & Truhlar (2008) is well suited for structures and energetics of the transition states). Our calculations show that the N + NCCN and N + CNCN reactions have very large barriers in the entrance valley as shown on Tables E.1 and F.1 and are negligible at low temperatures.
(Michael 1980; Dutuit et al. 2013). We then performed DFT calculations, using the M06-2X/AVTZ method (this highly nonlocal functional developed by Zhao & Truhlar (2008) is well suited for structures and energetics of the transition states). Our calculations show that the N + NCCN and N + CNCN reactions have very large barriers in the entrance valley as shown on Tables E.1 and F.1 and are negligible at low temperatures.
We have also performed calculations on the N and O reactions with CNCN and the H, N, O reactions with NCCN, see Tables E.1 and F.1 showing in all cases large barrier in the entrance valley and then negligible rates at low temperatures. Safrany & Jaster (1968b) and Whyte & Phillips (1983) deduced from a complex experiment that carbon atoms quickly react with NCCN at room temperature, with a rate constant equal to 3 × 10−11 cm3 molecules−1 s−1. Their experiments are complex but are reliable on the fact that carbon atoms react with NCCN, leading directly or indirectly to CN radicals. However, the products assumed for this reaction, CN + CCN, are widely endothermic as shown of Fig. A.1. The only exothermic exit channel for this reaction, C3 + N2, is spin forbidden. Moreover, C3 and N2 cannot be the only products of the experiments since C3 and N2 have a very low reactivity towards nitrogen atoms contrary to the product obtained in the experiments. They cannot lead to CN which was identified as a product of the C + NCCN reaction in presence of N atoms.
An alternative explanation is the formation of NCCCN. In the experiment at few Torr, some, or most, NCCCN adduct will be stabilized through collisions and will react with the nitrogen atoms to produce CN and C3 N, as NCCCN has a triplet ground state and is reactive with atoms and radicals. In interstellar molecular clouds the pressure is too low for three-body reactions but radiative association may play a role.
Using a model developed in Hebrard et al. (2013), we calculated that 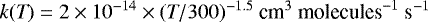 for the NCCCNproduction, leading to a low but non-negligible rate constant at 10 K. There is no experimental or theoretical data on the C + CNCN reaction but considering the very high reactivity of carbon atom with unsaturated hydrocarbons and HCN and HNC (Loison & Hickson 2015), which have similar –CN and –NC bonds than CNCN, there are very little doubt, if any, that this reaction does not show any barrier. Moreover we do not find any barrier at DFT level (M06-2X/AVTZ) for the C attack on CNCN leading in a first step to CCNCN, CNCCN, and CNCNC adducts. These adducts can evolve in different ways. First there is always the back dissociation into C + CNCN, these back dissociation being important only if other bimolecular exit channels involve high transition states, which is the case of CCNCN. In that case radiative association may also play a minor role neglected here. For CNCCN and CNCNC adducts, the back dissociation will not be the main process as there are pathways leading to C + NCCN channel. As not all the C + CNCN entrance channels lead efficiently (without high TS on the pathway) to bimolecular products, we consider a smaller rate constant that the one given by capture theory for the C+ CNCN → C + NCCN reaction.
for the NCCCNproduction, leading to a low but non-negligible rate constant at 10 K. There is no experimental or theoretical data on the C + CNCN reaction but considering the very high reactivity of carbon atom with unsaturated hydrocarbons and HCN and HNC (Loison & Hickson 2015), which have similar –CN and –NC bonds than CNCN, there are very little doubt, if any, that this reaction does not show any barrier. Moreover we do not find any barrier at DFT level (M06-2X/AVTZ) for the C attack on CNCN leading in a first step to CCNCN, CNCCN, and CNCNC adducts. These adducts can evolve in different ways. First there is always the back dissociation into C + CNCN, these back dissociation being important only if other bimolecular exit channels involve high transition states, which is the case of CCNCN. In that case radiative association may also play a minor role neglected here. For CNCCN and CNCNC adducts, the back dissociation will not be the main process as there are pathways leading to C + NCCN channel. As not all the C + CNCN entrance channels lead efficiently (without high TS on the pathway) to bimolecular products, we consider a smaller rate constant that the one given by capture theory for the C+ CNCN → C + NCCN reaction.
Comparison of the observed column densities (in cm−2) between the TMC-1 dark cloud and the L1544 prestellar core.
Summary of reactions review.
 |
Fig. 7 Radial distribution of the nitrogen bearing species abundances in L1544 for an age between 106 and 107 yr. |
Initial gas phase elemental abundances assumed relative to the total nuclear hydrogen density nH.
4.2 Chemistry in the L1544 prestellar core
We have applied the above chemistry to the prototypical prestellar source L1544. We used the gas-grain chemical code NAUTILUS (described in Ruaud et al. 2016) in its three-phase mode (gas-phase, grain-surface, and mantle chemistry) to predict the abundances of the simplest form of dicyanopolyynes species, CNCN, and its related species, CN, NCCNH+, C3 N, HCN, HNC, HCNH+, HC3NH+, HC3N, HNC3, HCCNC, H2 CN, CH3CN, CH2CN, C2 H3CN.
The methodology we have adopted here is similar to the studies already performed on L1544 (see for example Quénard et al. 2017a; Vastel et al. 2018a,b). A two step model has been used. The first phase represents the evolution of the chemistry in a diffuse or molecular cloud, with T = 20 K and several densities, ranging from 102 to 2 × 104 cm−3. We present in Table 4 the values of the initial gas phase elemental abundances, based on the results found by Quénard et al. (2017a) and Vastel et al. (2018b). We then used the resulting abundances at 106 yr in a second phase model, taking into account the density and temperature structure of the L1544 prestellar core that shows evidence for gravitational contraction (Caselli et al. 2012; Keto et al. 2014). In order to compare the results from the chemical modelling (abundances with respect to H) with the observations (column density) of the observed species presented in Sect. 2, we took into account the density profile across the core (see Jiménez-Serra et al. 2016; Quénard et al. 2017b; Vastel et al. 2018a,b) to determine the column density from the chemical modelling instead of the abundance at a specific radius. This methodology has been used for sources such as prestellar cores where molecular depletion at the centre, due to the low kinetic temperature and high H2 density, affects chemistry. Note that for cold dark clouds such as TMC-1, a single temperature and density have been assumed throughout the cloud, with a H2 column density of ~ 1022 cm−2 (Cernicharo & Guelin 1987; Fehér et al. 2016).
With the modifications of the chemical network presented in Sect. 4.1 we re-examine the chemistry of nitrogen species such as HCN, HNC (Quénard et al. 2017a), HC3N (Quénard et al. 2017a; Hily-Blant et al. 2018), HNC3 (Vastel et al. 2018a), HCCNC (Vastel et al. 2018a), HCNH+ (Quénard et al. 2017a), HC3NH+ (Quénard et al. 2017a), CH2CN Vastel et al. (2015b).
We present in Fig. 7 the variation of the modelled abundance as a function of radius for ages between 106 and 107 yr, for an initial gas density of 3 × 103 cm−3. We checked that varying the initial density from 102 to 2 × 104 cm−3 does not change much the results for an age between 106 and 107 yr. The abundances peak at a radius between [1–2] × 104 au, which can be explained by the carbon, oxygen, and sulphur depletion in the cold and dense central regions of prestellar cores. However, this peak is less pronounced compared to other species that do not contain Nitrogen (see for example Vastel et al. 2018b, for the study of Sulphur bearing species). This can be explained by the fact that nitrogen remains present in the gas phase at densities well above and temperature well below that at which CO depletes on to grains. The resulting molecular differentiation has been seen in many starless cores (e.g. Kuiper et al. 1996; Tafalla et al. 1998, 2006; Ohashi et al. 1999; Spezzano et al. 2016).
We present in Fig. 8 the variation of the modelled column density (in red) as a function of time from NAUTILUS and the comparison with the observed column densities (black horizontal lines) and upper limits (dashed horizontal lines) from Sect. 3. A variation by a factor of three on the modelled column density is shown. The thickness of the black lines corresponds to the uncertainty.
To compare the model results with observations, we used the method described in Wakelam et al. (2006) in which a distance of disagreement is computed as follows:
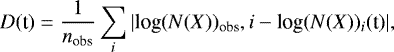 (4)
(4)
where N(X)obs,i is the observed column density, N(X)i(t) is the modelled column density at a specific age and nobs is the total number of observed species considered in this computation (14 in the case of nitrogen bearing species detected in L1544). We note that we did not take into account species where a lower limit has been derived from the observations (C2 N and C4 N).
Figure 9 shows its temporal variation, where a smaller value corresponds to a better agreement. Taking into account the present study, this distance is lower than unity for times higher than 6 × 105 and 3 × 106 yr. This time is of course model dependent and does not represent the “real” age of the source knowing that the chemical composition is constantly evolving in the interstellar medium. We then used the best-fit age ((1–3) × 106 yr) from the similar work performed for Sulphur chemistry in L1544 (Vastel et al. 2018b) and pinpoint a range between 3 × 106 and 6 × 106 yr for consistency between both studies.
We can see from Fig. 8 that all species are reproduced with the present chemical modelling. Using a higher elemental abundance for oxygen and/or carbon (higher by a factor of two, as observed in the diffuse medium, see for instance Jenkins 2009) will over-produce these species, leading to a much higher value for this distance of disagreement. NCCN reaches a calculated gas phase column density around 1014 cm−2 (and an abundance of ~ 10−8 at 104 au), similar to HCN. From our chemical modelling, the cyanogen/isocyanogen ratio is about a factor of 100. The predicted abundance of NCCN on the grain surfaces remains however low (≤10−12) to be compared to the high grain surface HCN abundance of ~5 × 10−7. It can be also noted that in our calculations C2N reaches a non negligible value, close to the upper limit which deserves to thorough investigation with more sensitive observations. The C2 H3CN calculated abundance is slightly under estimated which is likely due to the fact that C2 H4 is also under estimated in our modelling: C2 H3CN is produced through the CN + C2 H4 reaction and is a good proxy of C2 H4. Then, the gas phase and grain chemistry of C2 H4 deserve to be reviewed as C2 H4 is an important precursor of complex organic chemistry.
Our previous studies (Quénard et al. 2017a; Vastel et al. 2018a) tended to overestimate the production of HCN, HNC, HC3N, HNC3, HC3NH+. The inclusion of the new reactions, as well as the various KIDA updates revealed crucial to better understand the nitrogen chemistry, and nitriles in particular, in the cold and dense medium.
The study of the chemical evolution from the prestellar phase to the planetary disk is important to understand how the organics found in ourown solar system have been produced. The comparison between the prestellar core phase and the content of the comets studied so far is an important Ariane thread to understand this link. Our study predict a large quantity of NCCN, unfortunately invisible in the rotational transitions tracing the cold medium. This linear symmetric molecule, without permanent dipole moment, has been suggested a long time ago (Swings & Haser 1956) as a likely parent for the production of the CN radical observed in cometary atmospheres. Moreover, NCCN is likely the precursor of cyanomethanimine (HNCHCN), an HCN dimer proposed as precursor of adenine, recently detected by Rivilla et al. (2019) towards the Galactic Center quiescent molecular cloud G + 0.693. It is likely to have been formed on the surface of icy dust grains through the following reactions (Shivani & Tandon 2017):
 |
Fig. 9 Variation, in time, of the distance of disagreement. The grey box area represent a range between 6 × 105 and 3 × 106 yr (see text). |
 (5)
(5)
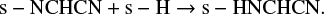 (6)
(6)
It therefore may be at the origin of a more complex cyanogen chemistry.
 |
Fig. 8 Variation of the modelled column density (in red) as a function of time and the comparison with the observed column density (black horizontal lines). The dashed line corresponds to an upper limit for the column density. The thickness of the black line corresponds to the errors on the column density given in Table 2. A variation by a factor of three on the modelled column density is shown in red. The grey vertical boxes highlight an area between 6 × 105 and 3 × 106 yr (see text). |
5 Conclusions
We investigated the formation of isocyanogen in the cold interstellar medium with the study of some nitrogen species in the prototypical prestellar core L1544. We report the detection of isocyanogen (CNCN), protonated cyanogen (NCCNH+), cyanoethynyl (C3N), methylene amidogen (H2CN), methyl cyanide (CH3CN) and acrylonitrile (C2H3CN). We then built a detailed chemical network for the NCCN/CNCN/HC2N chemistry to understand the isocyanogen formation in the cold interstellar medium. The main cyanogen production pathways considered in this new network are the CN + HNC and N + C3N reactions. The comparison between the observations of 14 detected nitrogen species in the L1544 prestellar core (CN, HCN, HNC, C3 N, CNCN, CH3CN, CH2CN, HCCNC, HC3N, HNC3, H2 CN, C2 H3CN, HCNH+, HC3NH+) as well as two upper limits (C4N, C2 N) and the predictions from the chemical modelling shows a very good agreement. Although NCCN cannot be detected through its rotational spectrum (due to a lack of a permanent electric dipole moment), we can trace this species through the detection of CNCN, since they are both produced through the same reaction. With this new chemical network, we predict a gas-phase column density of ~1014 cm−2 for the “invisible” NCCN, with an expected cyanogen abundance greater than the isocyanogen abundance by a factor of 100. However, itspredicted abundance on the grain surfaces remains low compared to the high grain surface HCN abundance. Unless NCCN is efficiently formed within protoplanetary disks, it is an unlikely major source of CN in cometary coma through its photolysis.
chemistry to understand the isocyanogen formation in the cold interstellar medium. The main cyanogen production pathways considered in this new network are the CN + HNC and N + C3N reactions. The comparison between the observations of 14 detected nitrogen species in the L1544 prestellar core (CN, HCN, HNC, C3 N, CNCN, CH3CN, CH2CN, HCCNC, HC3N, HNC3, H2 CN, C2 H3CN, HCNH+, HC3NH+) as well as two upper limits (C4N, C2 N) and the predictions from the chemical modelling shows a very good agreement. Although NCCN cannot be detected through its rotational spectrum (due to a lack of a permanent electric dipole moment), we can trace this species through the detection of CNCN, since they are both produced through the same reaction. With this new chemical network, we predict a gas-phase column density of ~1014 cm−2 for the “invisible” NCCN, with an expected cyanogen abundance greater than the isocyanogen abundance by a factor of 100. However, itspredicted abundance on the grain surfaces remains low compared to the high grain surface HCN abundance. Unless NCCN is efficiently formed within protoplanetary disks, it is an unlikely major source of CN in cometary coma through its photolysis.
Acknowledgements
We thank the CNRS program Physique et Chimie du Milieu Interstellaire (PCMI) co-funded by the Centre National d’Etudes Spatiales (CNES).
Appendix A: The C3N2 system
 |
Fig. A.1 Partial potential energy diagram for the C3N2 system on the triplet surface calculated at the M06-2X/AVTZ level including ZPE. The C3 + N2 exit channel in red is spin forbidden if C3 and N2 are in their singlet ground state. We cannot find the TS from NC-c.CC=N toward NC-c.C=NC at M06-2X/AVTZ level, both specieshaving very similar structure (two different cyclic isomers with slightly different geometries and energies). NC-c.CC=N is a local minimum but directly connected to NC-c.C=NC without barrier at semi-empirical AM1 level. So, this TS is very likely close in energy to NC-c.CC=N. |
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the C + NCCN energy, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various stationary points.
Appendix B: The NCCCN → TS1 → NC(C)CN isomerization
 |
Fig. B.1 Intrinsic reaction coordinate (minimum energy path) at M06-2X/cc-pVTZ for the NCCCN → TS1 → NC(C)CN isomerization. |
Appendix C: The CNCCN → NCCCN isomerization
 |
Fig. C.1 Intrinsic reaction coordinate (minimum energy path) at M06-2X/cc-pVTZ for the CNCCN → NCCCN isomerization. |
Appendix D: The NCCN → CNCN isomerization
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the NCCN energy, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various stationary points for the NCCN → CNCN isomerization.
 |
Fig. D.1 Intrinsic reaction coordinate pathway for the NCCN → CNCN isomerization calculated at M06-2X/AVTZ level. |
Appendix E: N, O + NCCN
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the N + NCCN and O + NCCN energies, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various transition states for N and O atoms additions on NCCN.
Appendix F: H, N, O + CNCN
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the H + CNCN, N + CNCN and O + CNCN energies, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various transition states for H, N, and O atoms additions on CNCN.
Appendix G: The CN + HCNH+ reaction
Relative energies at the M06-2X/AVTZ level (in kJ/ mol−1 at 0 K including ZPE) with respect to the CN + HCNH+ energy, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various stationary points for the CN + HCNH+ reaction.
References
- Agúndez, M., Cernicharo, J., de Vicente, P., et al. 2015, A&A, 579, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Marcelino, N., & Cernicharo, J. 2018, ApJ, 861, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Amano, T., & Scappini, F. 1991, J. Chem. Phys., 95, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- Anicich, V. G. 2003, JPL publication, 03-19 NASA [Google Scholar]
- Bockelee-Morvan, D., & Crovisier, J. 1985, A&A, 151, 90 [NASA ADS] [Google Scholar]
- Bockelée-Morvan, D., Lis, D. C., Wink, J. E., et al. 2000, A&A, 353, 1101 [Google Scholar]
- Bonev, B., & Komitov, B. 2000, BAAS, 32, 1072 [NASA ADS] [Google Scholar]
- Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
- Cazzoli, G., & Puzzarini, C. 2006, J. Mol. Spectr., 240, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., & Guelin, M. 1987, A&A, 176, 299 [NASA ADS] [Google Scholar]
- Crutcher, R. M., Churchwell, E., & Ziurys, L. M. 1984, ApJ, 283, 668 [CrossRef] [Google Scholar]
- Dutuit, O., Carrasco, N., Thissen, R., et al. 2013, ApJS, 204, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., & Charnley, S. B. 2000, ARA&A, 38, 427 [Google Scholar]
- Fehér, O., Tóth, L. V., Ward-Thompson, D., et al. 2016, A&A, 590, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Florescu-Mitchell, A. I., & Mitchell, J. B. A. 2006, Phys. Rep., 430, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Fray, N., Bénilan, Y., Cottin, H., Gazeau, M.-C., & Crovisier, J. 2005, Planet. Space Sci., 53, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Geiss, J., Altwegg, K., Balsiger, H., & Graf, S. 1999, Space Sci. Rev., 90, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, W. D., Ehlerding, A., Hellberg, F., et al. 2004, ApJ, 613, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Gerry, M. C. L., Stroh, F., & Winnewisser, M. 1990, J. Mol. Spectr., 140, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., Gottlieb, E. W., Thaddeus, P., & Kawamura, H. 1983, ApJ, 275, 916 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guélin, M., Neininger, N., & Cernicharo, J. 1998, A&A, 335, L1 [NASA ADS] [Google Scholar]
- Hebrard, E., Dobrijevic, M., Loison, J. C., et al. 2013, A&A, 552, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., Terzieva, R., & Talbi, D. 2000, MNRAS, 311, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickson, K. M., Loison, J.-C., & Wakelam, V. 2016, Chem. Phys. Lett., 659, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau Des Forêts, G., & Flower, D. 2008, A&A, 480, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Faure, A., Vastel, C., et al. 2018, MNRAS, 480, 1174 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Yamamoto, S., Mikami, H., & Ohishi, M. 1998, ApJ, 503, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., Friberg, P., Hjalmarson, A., et al. 1988, ApJ, 334, 107 [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Kawaguchi, K., Ohishi, M., Ishikawa, S.-I., & Kaifu, N. 1992a, ApJ, 386, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., Takano, S., Ohishi, M., et al. 1992b, ApJ, 396, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., Kasai, Y., Ishikawa, S.-I., et al. 1994, ApJ, 420, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., Rawlings, J., & Caselli, P. 2014, MNRAS, 440, 2616 [NASA ADS] [CrossRef] [Google Scholar]
- Kolos, R., & Grabowski, Z. 2000, Ap&SS, 271, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, T. B. H., Langer, W. D., & Velusamy, T. 1996, ApJ, 468, 761 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lefloch, B., Bachiller, R., Ceccarelli, C., et al. 2018, MNRAS, accepted [Google Scholar]
- Loison, J. C., & Hickson, K. M. 2015, Chem. Phys. Lett., 635, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., Wakelam, V., Hickson, K. M., Bergeat, A., & Mereau, R. 2014, MNRAS, 437, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]
- Loison, J.-C., Agúndez, M., Wakelam, V., et al. 2017, MNRAS, 470, 4075 [NASA ADS] [CrossRef] [Google Scholar]
- McGonagle, D., & Irvine, W. 1996, A&A, 310, 970 [NASA ADS] [Google Scholar]
- Michael, J. V. 1980, Chem. Phys. Lett., 96, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Minh, Y., Irvine, W., Ohishi, M., et al. 1993, A&A, 267, 229 [NASA ADS] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Spectr., 742, 215 [Google Scholar]
- Müller, H. S. P., Belloche, A., Menten, K. M., Comito, C., & Schilke, P. 2008, J. Mol. Spectr., 251, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Ohashi, N., Lee, S., Wilner, D., & Hayashi, M. 1999, ApJ, 518, 41 [Google Scholar]
- Ohishi, M., McGonagle, D., Irvine, William M., Yamamoto, S., & Saito, S. 1994, ApJ, 427, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Osamura, Y., Fukuzawa, K., Terzieva, R., & Herbst, E. 1999, ApJ, 519, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, S., & Osamura, Y. 2004, J. Phys. Chem. A, 108, 3623 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, S., Millar, T. J., & Markwick, A. J. 2003, MNRAS, 341, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Plessis, S., Carrasco, N., Dobrijevic, M., & Pernot, P. 2012, Icarus, 219, 254 [CrossRef] [Google Scholar]
- Quénard, D., Vastel, C., Ceccarelli, C., et al. 2017a, MNRAS, 470, 3194 [NASA ADS] [CrossRef] [Google Scholar]
- Quénard, D., Bottinelli, S., & Caux, E. 2017b, MNRAS, 468, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Raksit, A. B.,& Bohme, D. K. 1984, Can. J. Chem., 62, 2123 [CrossRef] [Google Scholar]
- Reiter, D., & Janev, R. K. 2010, Contrib. Plasm. Phys., 50, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Rivilla, V. M., Martín-Pintado, J., Jiménez-Serra, I., et al. 2019, MNRAS, 483, 114 [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [NASA ADS] [CrossRef] [Google Scholar]
- Safrany, D. R., & Jaster, W. 1968a, J. Chem. Phys., 72, 3318 [CrossRef] [Google Scholar]
- Safrany, D., & Jaster, W. 1968b, J. Chem. Phys., 72, 3305 [CrossRef] [Google Scholar]
- Safrany, D., & Jaster, W. 1968c, J. Phys. Chem. A, 72, 3305 [Google Scholar]
- Schilke, P., Walmsley, C. M., Henkel, C., & Millar, T. J. 1991, A&A, 247, 487 [NASA ADS] [Google Scholar]
- Shivani, M., & Tandon, P. 2017, Res. Astron. Astrophys., 17, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzano, S., Bizzocchi, L., Caselli, P., Harju, J., & Brünken, S. 2016, A&A, 592, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swings, P., & Haser, L. 1956, Institut d’Astrophysique, Liège [Google Scholar]
- Tafalla, M., Mardones, D., Myers, P. C., et al. 1998, ApJ, 504, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Santiago-García, J., Myers, P. C., et al. 2006, ApJ, 455, 577 [Google Scholar]
- Takano, S., Masuda, A., Hirahara, Y., et al. 1998, A&A, 329, 1156 [NASA ADS] [Google Scholar]
- Teanby, N. A., Irwin, P. G. J., de Kok, R., et al. 2006, Icarus, 181, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [Google Scholar]
- Vastel, C., Bottinelli, S., Caux, E., Glorian, J.-M., & Boiziot, M. 2015a, in SF2A-2015: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 313 [Google Scholar]
- Vastel, C., Yamamoto, S., Lefloch, B., & Bachiller, R. 2015b, A&A, 582, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Kawaguchi, K., Quénard, D., et al. 2018a, MNRAS, 474, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Quénard, D., Le Gal, R., et al. 2018b, MNRAS, 478, 5514 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Vigren, E., Semaniak, J., Hamberg, M., et al. 2012, Planet. Space Sci., 60, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., & Selsis, F. 2006, A&A, 451, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J.-C., Herbst, E., et al. 2015, ApJS, 217, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Loison, J.-C., Mereau, R., & Ruaud, M. 2017, Mol. Astrophys., 6, 22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whyte, A. R.,& Phillips, L. F. 1983, Chem. Phys. Lett., 98, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, S., & Saito, S. 1992, J. Chem. Phys., 96, 4157 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Y., & Truhlar, D. 2008, Theor. Chem. Acc., 120, 215 [CrossRef] [Google Scholar]
Astrochemical Surveys At Iram: http://www.oan.es/asai/
All Tables
Comparison of the observed column densities (in cm−2) between the TMC-1 dark cloud and the L1544 prestellar core.
Initial gas phase elemental abundances assumed relative to the total nuclear hydrogen density nH.
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the C + NCCN energy, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various stationary points.
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the NCCN energy, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various stationary points for the NCCN → CNCN isomerization.
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the N + NCCN and O + NCCN energies, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various transition states for N and O atoms additions on NCCN.
Relative energies at the M06-2X/AVTZ level (in kJ mol−1 at 0 K including ZPE) with respect to the H + CNCN, N + CNCN and O + CNCN energies, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various transition states for H, N, and O atoms additions on CNCN.
Relative energies at the M06-2X/AVTZ level (in kJ/ mol−1 at 0 K including ZPE) with respect to the CN + HCNH+ energy, geometries and frequencies (in cm−1, unscaled, calculated at the M06-2X/AVTZ level) of the various stationary points for the CN + HCNH+ reaction.
All Figures
 |
Fig. 1 Observed transitions of isocyanogen (CNCN) in black with a LTE model (red) using Tex = 15 K and N = 6.5 × 1011 cm−2. Bottompanel: results (in black) from the stacking of the four observed transitions as well as the Gaussian fit (in red). |
| In the text | |
 |
Fig. 2 Observed transition of protonated cyanogen (NCCNH+) with a LTE model (red) using Tex = 10 K, andN = 1.9 × 1010 cm−2. |
| In the text | |
 |
Fig. 3 Observed transitions of cyanoethynyl (C3N) with an associated VLSR of 7.25 km s−1 (dashed lines) with a LTE model (red) using Tex = 7.2 K and N = 1.6 × 1012 cm−2. |
| In the text | |
 |
Fig. 4 Observed transitions of methylene amidogen (H2CN) with a LTE model (red): Tex = 10 K, N = 3 × 1011 cm−2, ΔV = 0.35 km s−1. |
| In the text | |
 |
Fig. 5 Observed transitions of methyl cyanide (CH3CN) with a LTE model (red): Tex = 5K, N(A-form) = 4.5 × 1011 cm−2, N(E-form) = 2.8 × 1011 cm−2, ΔV = 0.45 km s−1. |
| In the text | |
 |
Fig. 6 Observed transitions of C2H3CN with an associated VLSR of 7.25 km s−1 (dashed lines) with a LTE model (red): Tex = 5.3 K, N = 4.0 × 1012 cm−2, ΔV = 0.4 km s−1. |
| In the text | |
 |
Fig. 7 Radial distribution of the nitrogen bearing species abundances in L1544 for an age between 106 and 107 yr. |
| In the text | |
 |
Fig. 8 Variation of the modelled column density (in red) as a function of time and the comparison with the observed column density (black horizontal lines). The dashed line corresponds to an upper limit for the column density. The thickness of the black line corresponds to the errors on the column density given in Table 2. A variation by a factor of three on the modelled column density is shown in red. The grey vertical boxes highlight an area between 6 × 105 and 3 × 106 yr (see text). |
| In the text | |
 |
Fig. 9 Variation, in time, of the distance of disagreement. The grey box area represent a range between 6 × 105 and 3 × 106 yr (see text). |
| In the text | |
 |
Fig. A.1 Partial potential energy diagram for the C3N2 system on the triplet surface calculated at the M06-2X/AVTZ level including ZPE. The C3 + N2 exit channel in red is spin forbidden if C3 and N2 are in their singlet ground state. We cannot find the TS from NC-c.CC=N toward NC-c.C=NC at M06-2X/AVTZ level, both specieshaving very similar structure (two different cyclic isomers with slightly different geometries and energies). NC-c.CC=N is a local minimum but directly connected to NC-c.C=NC without barrier at semi-empirical AM1 level. So, this TS is very likely close in energy to NC-c.CC=N. |
| In the text | |
 |
Fig. B.1 Intrinsic reaction coordinate (minimum energy path) at M06-2X/cc-pVTZ for the NCCCN → TS1 → NC(C)CN isomerization. |
| In the text | |
 |
Fig. C.1 Intrinsic reaction coordinate (minimum energy path) at M06-2X/cc-pVTZ for the CNCCN → NCCCN isomerization. |
| In the text | |
 |
Fig. D.1 Intrinsic reaction coordinate pathway for the NCCN → CNCN isomerization calculated at M06-2X/AVTZ level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


