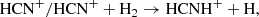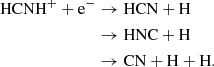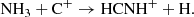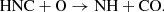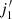EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 681 (January 2024) A&A, 681 (2024) L19 Full HTML
Open Access
Issue
A&A
Volume 681, January 2024
Article Number L19
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202348947
Published online 23 January 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Protonated hydrogen cyanide, also known as iminomethylium (HCNH+), is the simplest protonated nitrile. It has a dipole moment of ∼0.29 D (Botschwina 1986), large enough to allow its detection in radio astronomy. The first detection of this molecular cation in space took place toward Sgr B2, thanks to the observation of its three lowest rotational lines (Ziurys & Turner 1986). Since then, it has been observed in several cold star-forming regions such as the TMC-1 dark cloud (Schilke et al. 1991; Ziurys et al. 1992), the DR 21(OH) H II region (Hezareh et al. 2008), the L1544 pre-stellar core (Quénard et al. 2017), the L483 proto-star (Agúndez et al. 2022), and in 16 high-mass star-forming cores (Fontani et al. 2021). Recently, Gong et al. (2023) reported a comprehensive distribution analysis of HCNH+ within the Serpens filament and Serpens South, suggesting that this molecular cation is abundant in cold quiescent regions and deficient toward active star-forming regions. These observations present HCNH+ as a ubiquitous molecular cation in the cold interstellar medium (ISM) and reinforce the interest in understanding its chemistry.

HCNH+ is classified among the most important molecular ions in the ISM since it is the precursor of the widespread HCN and HNC. Ionic compounds play a crucial role in interstellar chemistry, serving as indispensable intermediates in ion-neutral reactions that govern gas-phase chemistry within cold cores (Agúndez & Wakelam 2013). Extensive research has been conducted to explore the chemistry of HCNH+ within dense, cold regions. This molecular cation is mostly formed in low temperature regions (Loison et al. 2014) through the following reactions:

(1)

and it undergoes destruction via a dissociative recombination with electrons (Loison et al. 2014; Semaniak et al. 2001):

(2)

Based on the reactions in Eqs. (1) and (2) for HCNH+ and similar reactions related to HC3NH+, the chemical model of Quénard et al. (2017) was unable to simultaneously reproduce the observed abundance of these protonated molecules toward the cold L1544 pre-stellar core. The authors pointed out that their model potentially underproduces HCNH+. Fontani et al. (2021) included, in addition to the previous reactions, Eq. (3) in their model as part of the dominant HCNH+ formation paths for cold high-mass star-forming cores:

(3)

They found that changing the initial conditions (the hydrogen column density) or key parameters (the cosmic ray ionization rate) of their chemical model does not lead to a better agreement with the observations. In both attempts, their prediction underestimates the observed HCNH+ abundance. In TMC-1, Agúndez et al. (2022) found that the [HCNH+]/([HCN]+[HNC]) abundance ratio is underestimated by the chemical model. This finding was seen as a general trend for protonated-to-neutral abundance ratios. More recently, Gong et al. (2023) investigated the impact of the hydrogen number density and the two energy barriers available in the literature for reaction (4), which plays an important role in the HCNH+ chemistry:

(4)

Although the authors successfully reproduced the observed abundance of HCNH+ in cold high-mass star-forming cores, it is worth noting the wide range of the reference data they used, [HCNH+]/[H2] = 3 × 10−11 − 10−9, which covers all the individual target sources. A selective comparison would suggest a chemical model that yields less HCNH+ than observed for five out of the nine studied sources.

The HCN and HNC molecules, which are two of the most important species found in star-forming regions, have been extensively studied both from a chemical perspective and in terms of rotational energy transfer. For example, the HCN and HNC abundance profiles derived by Daniel et al. (2013) through non-local thermodynamic equilibrium (non-LTE) analysis of observational spectra align well with the chemical predictions of Gérin et al. (2009). Part of this agreement between chemistry and observation can be attributed to the non-LTE modeling of observational spectra, which has been made possible by the availability of accurate HCN and HNC collisional rate coefficients (Ben Abdallah et al. 2012; Sarrasin et al. 2010). In the case of HCNH+, observed abundances have been determined using the LTE approximation, which can lead to discrepancies and consequently contribute to the disagreements with chemical models (Quénard et al. 2017; Fontani et al. 2021; Agúndez et al. 2022; Gong et al. 2023) discussed above. Therefore, it is of high interest to reevaluate the observed HCNH+ abundances employing a non-LTE approach, complemented with high accurate collisional rate coefficients.

In the frame of rotational energy transfer, the excitation of HCNH+ was first studied by Nkem et al. (2014). They used helium as a projectile and reported rate coefficients for temperatures up to 300 K, considering transitions among the 11 low-lying rotational energy levels. Recently, Bop & Lique (2023) extended the rotational basis considered in the previous work to the 16 first energy levels and also reported the HCNH+ scattering data due to collisions with H2, the most abundant species in the ISM. They demonstrated that both ortho-H2(j2 = 1) and para-H2(j2 = 0), where j2 represents the rotational quantum number of H2, result in remarkably similar cross sections. This finding supports the idea that only rate coefficients induced by collisions with para-H2(j2 = 0) are necessary for modeling the abundance of molecular cations in cold star-forming regions.

We revisit the excitation of this molecular cation by para-H2 taking into account the influence of the higher rotational energy level of the projectile (j2 = 2), as previously done by Hernández Vera et al. (2017) for HCN and HNC. Furthermore, we investigate the hyperfine splitting of the HCNH+ collisional rate coefficients resulting from the nonzero nuclear spin of nitrogen, as this effect is clearly resolved in the 1 → 0 observational line spectrum (Ziurys et al. 1992; Quénard et al. 2017).

The structure of this paper is as follows: Sect. 2 provides a concise overview of the scattering calculations. Section 3 is dedicated to the astrophysical modeling, while Sect. 4 presents the concluding remarks.

2. Collisional rate coefficients

Accurate potential energy surfaces (PESs; 4D PES for HCNH+-H2 and 2D PES for HCNH+-He), which are computed using the explicitly correlated coupled cluster method with single, double, and triple non-iterative excitation [CCSD(T)-F12] (Knowles et al. 1993, 2000) in conjunction with the augmented-correlation consistent-polarized valence triple zeta Gaussian best set (aug-cc-PVTZ) (Dunning 1989), are available in the literature (Bop & Lique 2023). These authors computed cross sections for the 16 low-lying rotational energy levels of HCNH+ due to collisions with both He and para-H2 (hereafter denoted as H2) using the “exact” close-coupling quantum mechanical approach (Arthurs & Dalgarno 1960), implemented in the MOLSCAT scattering code (Hutson & Green 1994).

The rotational energy levels were calculated using the spectroscopic constant of H2 [B0 = 59.322 cm−1 and D0 = 0.047 cm−1] and HCNH+ [B0 = 1.2360 cm−1 and D0 = 1.6075 × 10−6 cm−1] (Huber 2013; Amano et al. 2006). The calculations were performed from a total energy of 2.5 cm−1 to 800 cm−1, using a fine step size. To better treat the couplings between open and closed channels for convergence reasons, it was necessary to take into account the 31 low-lying rotational energy levels of HCNH+ (j1 = 0 − 30) in the calculations. The hybrid log derivative-airy propagator was used to solve the coupled equations (Alexander & Manolopoulos 1987). The integration limits were adjusted automatically for each total angular momentum (J), and the switching point from the log derivative to the airy integrator was set to 16 a0. The integration step was maintained below 0.2 a0 by adjusting the STEP parameter depending on the collision energy. Here, we address two important aspects of HCNH+–H2 collisions that have not been considered before: (i) the effect of the H2 rotational basis, specifically the inclusion of j2 = 2, and (ii) the HCNH+ hyperfine structure arising from the nonzero nuclear spin of nitrogen.

2.1. The impact of the H2 rotational basis

The excitation of HCNH+ by collisions with H2 has been investigated using only j2 = 0 (Bop & Lique 2023). The authors roughly estimated the mean deviation of the cross sections due to the inclusion of j2 = 2 in the calculations to ∼20%. Considering the huge anisotropy of the HCNH+−H2 potential energy surface and its deep global minimum of ∼1426.6 cm−1, revisiting the collisional excitation of HCNH+ by H2 with the most accurate level of precision becomes a necessary endeavor.

In Fig. 1, we evaluate the influence of the H2 rotational basis in the HCNH+ collisional cross sections for selected total energies. The incorporation of j2 = 0 − 2 into the H2 rotational basis results in deviations of up to a factor of three compared to the restriction to j2 = 0, while using an extended basis (j2 = 0 − 4) instead of j2 = 0 − 2 leads to moderate improvements, that is, deviations less than a factor of 1.5. For a total energy of 250 cm−1, the root mean square errors obtained when using j2 = 0 and j2 = 0 − 4 in comparison with the use of j2 = 0 − 2 are 65% and 9%, respectively. Therefore, restricting the H2 rotational basis to the ground level is insufficient to derive accurate collisional rate coefficients and the inclusion of j2 = 0 − 4 slightly improves the results obtained using j2 = 0 − 2, but the computational cost increases by a factor of approximately ten. Therefore, all calculations are performed including j2 = 0 − 2 in the H2 rotational basis.

thumbnail Fig. 1.

Comparison of the HCNH+ cross sections for selected total energies. We note that σJ = 0 − 5 is the sum of partial cross sections over total angular momenta up to J = 5. The stars depict the impact of including j2 = 0 − 2 in comparison to the constraint of the H2 rotational basis to j2 = 0, while the empty circles estimate the influence of a more exhaustive H2 rotational manifold (j2 = 0 − 4) with respect to j2 = 0 − 2. The dashed diagonal lines delimit an agreement region of a factor of 1.5.

2.2. Hyperfine resolved rate coefficients

Fully exploiting the information embedded within hyperfine resolved observational spectra requires an explicit description of the hyperfine splitting in the collisional rate coefficients. In this work, we only consider the coupling between the HCNH+ rotation and the nitrogen nuclear spin (I = 1). This coupling results in a slight splitting of each HCNH+ rotational level into three hyperfine components, with the exception of the ground energy level, which remains unsplit. The hyperfine components are identified by a quantum number F defined as |I − j1|≤F ≤ I + j1. We employed the nearly exact recoupling method (Alexander & Dagdigian 1985) in the scattering matrix, which produced the results presented in the previous section. In this manner, we computed hyperfine resolved rate coefficients for the HCNH+ 25 low-lying energy levels, (j1, F) ≤ (8, 9), at low temperatures (T = 5 − 30 K).

Figure 2 displays the HCNH+ hyperfine resolved rate coefficients obtained using both He and H2 as collision partners at 10 K, the typical temperature of cold star-forming regions. The magnitude of the H2-induced rates vary between ∼10−10 and ∼10−12 cm−3 s−1, whereas the He-rates drop drastically down to ∼10−14 cm−3 s−1. The hyperfine resolution does not alter the existing disparity between the He- and H2-rate coefficients, as discussed by Bop & Lique (2023), for the rotational transitions. The new insight into this plot is the unveiled propensity rule, Δj1 = ΔF, which applies to both projectiles. The data presented in this section are available in electronic supplementary material via the CDS and they will be accessible through databases such as Basecol, LAMDA, and EMAA.

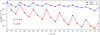thumbnail Fig. 2.

HCNH+ hyperfine resolved rate coefficients for the (8, 9) → (, F′) transitions at 10 K. The blue (red) line stands for collisional data obtained using H2 (He) as a projectile.

3. Modeling astronomical lines of HCNH+

The collisional rate coefficients calculated here can be applied to model the lines of HCNH+ in those astronomical sources where lines are narrow, so that the hyperfine structure can be resolved. In cold dense clouds, line widths are typically below 1 km s−1 (e.g., Agúndez et al. 2023), and thus if observed with a good enough spectral resolution, the hyperfine structure of the low-j1 lines of HCNH+ can be resolved.

Protonated HCN has been observed in different types of molecular clouds (e.g., Schilke et al. 1991). Here we focus on two cold dense clouds, TMC-1 and L483, where low-j1 lines of HCNH+ have been recently observed with a high spectral resolution. In the case of TMC-1, the j1 = 1 → 0 and j1 = 2 → 1 lines have been observed with the 30 m telescope of the Institut de Radio-Astronomie Millimétrique (IRAM) with a spectral resolution of 49 kHz. The observations of the j1 = 1 → 0 line at 74.1 GHz are part of a 3 mm line survey (Marcelino et al. 2007; Cernicharo et al. 2012), while those of the j1 = 2 → 1 line at 148.2 GHz are part of the Astrochemical Surveys At IRAM (ASAI) program (Lefloch et al. 2018). In the case of L483, the j1 = 1 → 0 line at 74.1 GHz was observed with the IRAM 30 m telescope with a spectral resolution of 49 kHz during a 3 mm line survey of this cloud (Agúndez et al. 2019, 2021). The observed lines are shown in Fig. 3.

thumbnail Fig. 3.

Lines of HCNH+ in TMC-1 (j1 = 1 → 0 and j1 = 2 → 1 in the left panels) and L483 (j1 = 1 → 0 in the right panel). Black histograms correspond to the observed line profiles, while the red lines correspond to the synthetic line profile calculated with the LVG model (see text).

To model the lines of HCNH+, we carried out excitation and radiative transfer calculations under the large velocity gradient (LVG) formalism (Goldreich & Kwan 1974). The code used is similar to MADEX (Cernicharo et al. 2012). We implemented the rate coefficients calculated here for inelastic collisions of HCNH+ with H2 and He, where the hyperfine structure of HCNH+ is taken into account. The adopted abundance of He relative to H2 is 0.17, based on the cosmic abundance of helium, which implies that collisional excitation is dominated by H2, with He playing a minor role. We adopted the physical conditions of TMC-1 and L483 from the study of Agúndez et al. (2023). For TMC-1 we adopted a gas kinetic temperature of 9 K and a volume density of H2 of 1.0 × 104 cm−3, while for L483 the adopted gas temperature is 12 K and the H2 volume density 5.6 × 104 cm−3. The adopted line width, 0.46 km s−1 for TMC-1 and 0.39 km s−1 for L483, was taken directly from the arithmetic mean of the values measured on the spectrum of the j1 = 1 → 0 line. We then varied the column density of HCNH+ until matching the velocity-integrated intensity of the observed lines. The calculated line profiles are compared to the observed ones in Fig. 3. The column densities derived for HCNH+ in TMC-1 and L483 are 4.2 × 1013 cm−2 and 2.4 × 1013 cm−2, respectively. Previous determinations of the column density based on LTE are 1.9 × 1013 cm−2 in TMC-1 (Schilke et al. 1991) and 2.7 × 1013 cm−2 in L483 (Agúndez et al. 2019). The values determined here differ with respect to the previous values by a factor of two for TMC-1 and by 10% for L483.

To understand the different improvements resulting from non-LTE modeling in comparison to the previous LTE-based abundances of HCNH+ obtained for TMC-1 and L483, we investigated the deviation of the brightness temperature (TB) with respect to LTE as a function of the gas density. Figure 4 shows that the use of He as a collision partner tends to delay the thermalization of the lines, whereas employing H2 as a projectile, which is the major gas component in cold dense clouds, suggests that LTE assumption is valid for densities larger than 2 × 104 cm−3. Furthermore, the j1 = 2 → 1 line from Schilke et al. (1991) is reported to have an intensity (in main beam temperature) of 0.48 K, which aligns well with our TB of 0.50 K obtained by correcting the 0.40 K antenna temperature with the beam efficiency of the IRAM 30 m telescope. We thus reinterpreted the observations of HCNH+ by employing the LTE assumption. As depicted in Table 1, using this approximation to determine the HCNH+ column density introduces an error of approximately 5% in both TMC-1 and L483. The factor of two observed in the case of TMC-1, when comparing the LVG-based column density with the data reported by Schilke et al. (1991), is likely to result from the assumptions incorporated in their analysis rather than an effect of the adopted LTE approximation.

thumbnail Fig. 4.

Density dependence of the HCNH+ brightness temperature ratio for the j1 = 1 → 0, 2 → 1, and 3 → 2 lines. Solid and dashed lines were obtained using the collisional rate coefficients of H2 and He, respectively. The dash-dotted line refers to thermalization. The line width was set to 1.0 km s−1. Thanks to the optically thin regime, these ratios are valid for column densities lower than 5 × 1013 cm−2.

Table 1.

Column density of HCNH+ (in 1013 cm−2) under the LTE assumption and the LVG formalism for TMC-1 and L483.

As discussed in the Introduction, the observed HCNH+ column densities are underestimated by predictions from chemical models. In the case of TMC-1, for example, Agúndez et al. (2022) found that their chemical model underestimates the [HCNH+]/([HCN]+[HNC]) abundance ratio by a factor of ten. Since we revealed that the observed HCNH+ column density in this region is actually twice as large, the protonated-to-neutral abundance ratio turns out to be a factor of 20 higher than predicted by the chemical model. Although this matter remains unresolved, we dispel any doubts that could implicate the observations, clearly identifying the chemical models as the sole factor. We suggest for future modelings using the new experimental rate constants of reactions in Eq. (1) measured for temperatures down to 17 K (Dohnal et al. 2023). Employing the latter results in the chemical models for cold dense clouds is more reasonable than the early reaction rates which were measured at room temperature (Wakelam et al. 2012).

4. Conclusion

We computed the first hyperfine resolved rate coefficients of HCNH+ induced by collisions with He and H2. We used the most accurate recoupling method based on nuclear spin-independent scattering matrices calculated by the mean of the close-coupling quantum mechanical approach. When employing H2 as the collision partner, we considered the coupling with the first excited rotational energy level of para-H2, thereby improving the previously available nuclear spin-free rotational rate coefficients.

Based on the new rate coefficients, we modeled HCNH+ emission lines observed toward TMC-1 and L483 using non-LTE radiative transfer calculations under the LVG formalism. With column densities of 4.2 × 1013 cm−2 and 2.4 × 1013 cm−2 for TMC-1 and L483, respectively, the synthetic spectra reproduced the observed ones quite well. The updated HCNH+ abundances differ by a factor of two and by 10% compared to the data previously available in the literature for TMC-1 and L483, respectively. It is worth noting that the large discrepancy observed in the case of TMC-1 is more likely due to an error in the early analysis of the observational spectra rather than an effect of the LTE assumption. The actual difference in the HCNH+ column density derived using LTE and LVG is approximately 5% for both TMC-1 and L483. Therefore, we confirm that the use of LTE to model the abundance of HCNH+ in cold, dense regions is reasonable. However, we strongly recommend employing the rate coefficients reported in this work for multiline analysis and for observations toward regions of moderate densities.

Acknowledgments

The authors acknowledge the European Research Council (ERC) for funding the COLLEXISM project No 811363, the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of Centre National de la Recherche Scientifique(CNRS)/Institut National des Sciences de l’Univers (INSU) with Institut de Chimie (INC)/Institut de Physique (INP) co-funded by Commissariat a l’Energie Atomique (CEA) and Centre National d’Etudes Spatiales (CNES). F.L. acknowledges the Institut Universitaire de France. M.A. and J.C. acknowledge funding support from Spanish Ministerio de Ciencia e Innovación through grants PID2019-107115GB-C21 and PID2019-106110GB-I00. This work made use of ASAI “Astrochemical Surveys At IRAM”.

References

  1. Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
  2. Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [Google Scholar]
  3. Agúndez, M., Roueff, E., Cabezas, C., Cernicharo, J., & Marcelino, N. 2021, A&A, 649, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Agúndez, M., Cabezas, C., Marcelino, N., et al. 2022, A&A, 659, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Agúndez, M., Marcelino, N., Tercero, B., Jiménez-Serra, I., & Cernicharo, J. 2023, A&A, 677, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Alexander, M. H., & Dagdigian, P. J. 1985, J. Chem. Phys., 83, 2191 [NASA ADS] [CrossRef] [Google Scholar]
  7. Alexander, M. H., & Manolopoulos, D. E. 1987, J. Chem. Phys., 86, 2044 [Google Scholar]
  8. Amano, T., Hashimoto, K., & Hirao, T. 2006, J. Mol. Struct., 795, 190 [Google Scholar]
  9. Arthurs, A. M., & Dalgarno, A. 1960, Proc. R. Soc. London. Ser. A. Math. Phys. Sci., 256, 540 [Google Scholar]
  10. Ben Abdallah, D., Najar, F., Jaidane, N., Dumouchel, F., & Lique, F. 2012, MNRAS, 419, 2441 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bop, C., & Lique, F. 2023, J. Chem. Phys., 158, 7 [CrossRef] [Google Scholar]
  12. Botschwina, P. 1986, Chem. Phys. Lett., 124, 382 [Google Scholar]
  13. Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
  14. Daniel, F., Gérin, M., Roueff, E., et al. 2013, A&A, 560, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dohnal, P., Jusko, P., Jiménez-Redondo, M., & Caselli, P. 2023, J. Chem. Phys., 158, 24 [Google Scholar]
  16. Dunning, T. H., Jr 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fontani, F., Colzi, L., Redaelli, E., Sipilä, O., & Caselli, P. 2021, A&A, 651, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [CrossRef] [Google Scholar]
  19. Gong, Y., Du, F., Henkel, C., et al. 2023, A&A, 679, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Gérin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Hernández Vera, M., Lique, F., Dumouchel, F., Hily-Blant, P., & Faure, A. 2017, MNRAS, 468, 1084 [Google Scholar]
  22. Hezareh, T., Houde, M., McCoey, C., Vastel, C., & Peng, R. 2008, ApJ, 684, 1221 [NASA ADS] [CrossRef] [Google Scholar]
  23. Huber, K. 2013, Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules (US: Springer) [Google Scholar]
  24. Hutson, J., & Green, S. 1994, Collaborative Computational Project [Google Scholar]
  25. Knowles, P. J., Hampel, C., & Werner, H.-J. 1993, J. Chem. Phys., 99, 5219 [NASA ADS] [CrossRef] [Google Scholar]
  26. Knowles, P. J., Hampel, C., & Werner, H.-J. 2000, J. Chem. Phys., 112, 3106 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lefloch, B., Bachiller, R., Ceccarelli, C., et al. 2018, MNRAS, 477, 4792 [Google Scholar]
  28. Loison, J.-C., Wakelam, V., & Hickson, K. M. 2014, MNRAS, 443, 398 [Google Scholar]
  29. Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [Google Scholar]
  30. Nkem, C., Hammami, K., Halalaw, I. Y., Owono Owono, L. C., & Jaidane, N.-E. 2014, Astrophys. Space Sci., 349, 171 [NASA ADS] [CrossRef] [Google Scholar]
  31. Quénard, D., Vastel, C., Ceccarelli, C., et al. 2017, MNRAS, 470, 3194 [Google Scholar]
  32. Sarrasin, E., Abdallah, D. B., Wernli, M., et al. 2010, MNRAS, 404, 518 [Google Scholar]
  33. Schilke, P., Walmsley, C., Millar, T., & Henkel, C. 1991, A&A, 247, 487 [NASA ADS] [Google Scholar]
  34. Semaniak, J., Minaev, B., Derkatch, A., et al. 2001, ApJS, 135, 275 [NASA ADS] [CrossRef] [Google Scholar]
  35. Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [Google Scholar]
  36. Ziurys, L., & Turner, B. 1986, ApJ, 302, L31 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ziurys, L., Apponi, A., & Yoder, J. 1992, ApJ, 397, L123 [CrossRef] [Google Scholar]

All Tables

Table 1.

Column density of HCNH+ (in 1013 cm−2) under the LTE assumption and the LVG formalism for TMC-1 and L483.

In the text

All Figures

thumbnail Fig. 1.

Comparison of the HCNH+ cross sections for selected total energies. We note that σJ = 0 − 5 is the sum of partial cross sections over total angular momenta up to J = 5. The stars depict the impact of including j2 = 0 − 2 in comparison to the constraint of the H2 rotational basis to j2 = 0, while the empty circles estimate the influence of a more exhaustive H2 rotational manifold (j2 = 0 − 4) with respect to j2 = 0 − 2. The dashed diagonal lines delimit an agreement region of a factor of 1.5.
In the text
thumbnail Fig. 2.

HCNH+ hyperfine resolved rate coefficients for the (8, 9) → (, F′) transitions at 10 K. The blue (red) line stands for collisional data obtained using H2 (He) as a projectile.
In the text
thumbnail Fig. 3.

Lines of HCNH+ in TMC-1 (j1 = 1 → 0 and j1 = 2 → 1 in the left panels) and L483 (j1 = 1 → 0 in the right panel). Black histograms correspond to the observed line profiles, while the red lines correspond to the synthetic line profile calculated with the LVG model (see text).
In the text
thumbnail Fig. 4.

Density dependence of the HCNH+ brightness temperature ratio for the j1 = 1 → 0, 2 → 1, and 3 → 2 lines. Solid and dashed lines were obtained using the collisional rate coefficients of H2 and He, respectively. The dash-dotted line refers to thermalization. The line width was set to 1.0 km s−1. Thanks to the optically thin regime, these ratios are valid for column densities lower than 5 × 1013 cm−2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.