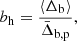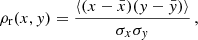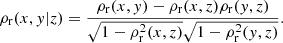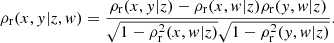EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A67 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A67
Number of page(s) 13
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202141077
Published online 12 October 2021

© ESO 2021

1. Introduction

Numerical N-body simulations have revealed that the clustering of dark matter halos depends not only on halo mass (e.g., Mo & White 1996; Sheth et al. 2001), but also on other halo properties, such as mass assembly history, as well as structural and dynamical properties (Gao et al. 2005; Wechsler et al. 2006; Wetzel et al. 2007; Jing et al. 2007; Bett et al. 2007; Gao & White 2007; Li et al. 2008; Faltenbacher & White 2010; Lacerna & Padilla 2011; Lazeyras et al. 2017; Xu & Zheng 2018; Salcedo et al. 2018; Mao et al. 2018; Chue et al. 2018). The dependence of the halo clustering on halo properties other than the halo mass is usually referred to as the halo assembly bias or the secondary bias. Understanding such a secondary bias with regard to the halo population is important not only for understanding the formation of dark matter halos in the cosmic density field, but also for understanding galaxy formation and evolution in dark matter halos (see e.g., Zhu et al. 2006; Yang et al. 2006; Zentner et al. 2014; Hearin et al. 2015; Wechsler & Tinker 2018; Wang et al. 2018; Salcedo et al. 2020).

It is well known that halo properties, such as assembly time, concentration, substructure, and spin, are correlated to one another in various ways (e.g., Jing & Suto 2002; Zhao et al. 2003; Gao et al. 2004; Allgood et al. 2006; Hahn et al. 2007; Wang et al. 2011; Mao et al. 2018). However, these properties exhibit complex trends in their secondary bias, sometimes in ways that differ from what would otherwise be expected from their mutual correlations. For instance, the dependence of the halo clustering on the assembly time is usually strong for low-mass halos, but weak at the massive end (see e.g., Gao et al. 2005; Jing et al. 2007; Li et al. 2008; Mao et al. 2018; Chue et al. 2018), while the secondary bias for the halo spin parameter increases with halo mass (e.g., Bett et al. 2007; Gao & White 2007; Faltenbacher & White 2010; Salcedo et al. 2018). Moreover, the dependence of the secondary bias on the two halo structural parameters, namely, halo concentration and subhalo abundance, changes sign at around the characteristic mass of collapse (Wechsler et al. 2006; Gao & White 2007; Salcedo et al. 2018).

These results imply that the secondary bias has multiple origins. This is supported by numerous investigations in the literature, most of which have focused on the secondary bias in the assembly time. For example, Wang et al. (2007) found that old small halos are usually located closer to massive structures than their younger counterparts (see also Hahn et al. 2009), a phenomenon referred to as the neighbour bias by Salcedo et al. (2018). Subsequent studies have shown that the secondary bias may also be related to the nearby cosmic web of halos (Yang et al. 2017; Paranjape et al. 2018; Ramakrishnan et al. 2019). Several processes related to the presence of massive neighbours have been proposed. For instance, the tidal field of the massive structure can accelerate the ambient matter and truncate the mass accretion onto small halos (Wang et al. 2007, 2011; Hahn et al. 2009; Shi et al. 2015; Paranjape et al. 2018; Mansfield & Kravtsov 2020). Splashback halos that have passed through massive host halos at any point may be severely stripped by the tidal force of the hosts (Ludlow et al. 2009; Wang et al. 2009). These halos, with close massive companions, are therefore expected to have an early assembly time because of the stripping and can contribute significantly to the secondary bias (Wang et al. 2009; Li et al. 2013; Mansfield & Kravtsov 2020; Tucci et al. 2021).

In addition to the truncation and stripping processes, Wang et al. (2011) found that dense environments can also enhance mass accretion by halos (see also Fakhouri & Ma 2009). This process is expected to yield a trend that is different from the measured secondary bias. These authors suggested that the halo-mass dependence of the secondary bias is partly caused by the competition between two categories of processes, the truncation by large-scale tidal field, and the availability of material to be accreted by halos (see also Chen et al. 2020). However, exactly how these processes contribute to the secondary bias is still unclear.

Suggestions have been made that the secondary bias in the halo concentration may share a common origin with the secondary bias in the assembly time (Han et al. 2019; Chen et al. 2020), although the two properties exhibit different trends as discussed above. Several studies (Salcedo et al. 2018; Han et al. 2019; Johnson et al. 2019; Tucci et al. 2021) pointed out that the secondary bias for the spin may have a different origin than both the assembly time and concentration. The correlation and alignment of the spin amplitude and direction with the local tidal field suggest that the tidal torques may play a key role in establishing the dependence of the halo bias on the spin parameter (Hahn et al. 2007; Shi et al. 2015; Chen et al. 2016; Wang & Kang 2018). Unfortunately, it is still unclear how the secondary bias for the concentration and spin is established and whether it is related to the halo assembly or produced by completely different processes.

Attempts have also been made to understand the origin of the secondary bias based on the initial conditions (e.g., Wang et al. 2007; Zentner 2007; Sandvik et al. 2007; Dalal et al. 2008; Desjacques 2008; Musso & Sheth 2012; Shi & Sheth 2018). For example, Wang et al. (2007) found that low-mass, older halos tend to be associated with perturbations of higher mass in the initial density field (the initial mass) that are expected to collapse into halos according to the spherical collapse model. They also found that the bias relation obtained from the initial masses in N-body simulations actually matches the secondary bias in the assembly time. Dalal et al. (2008) used the properties of density peaks in the initial conditions to infer the halo assembly time and concentration and found that the general trends in the secondary bias of these two halo properties can be reproduced in their model. For massive halos, they suggested that the secondary bias reflects the statistics of the random Gaussian field (see also Zentner 2007), while for low-mass halos, they reached conclusions that are similar to those in earlier studies (e.g., Wang et al. 2007, 2009). More recently, using the excursion set approach, Shi & Sheth (2018) suggested that the secondary bias possibly reflects the correlation of densities at different scales when the density at the halo-mass scale is fixed.

All these results provide valuable insight into the origin of the secondary bias. However, the correlations between peak properties and halo properties are ambiguous and the excursion set approach is not capable of modeling the effects of the tidal truncation.

Thus, the details of the secondary bias, in particular its mass-dependence, remain unresolved. It is still unclear whether or not the secondary bias for low- and high-mass halos share the same origin. It is also unclear why different halo properties exhibit different trends in their secondary bias, although they are correlated. Furthermore, since the secondary bias may already be present in the initial conditions, it is important to understand how it is connected to the secondary bias observed for the halo population in the evolved density field and whether it is the initial conditions or the subsequent evolution that plays the more important role in determining the secondary bias.

In this paper, we use both the evolved density field (at z = 0) and the linear density field to study the secondary bias of three halo properties: assembly time, concentration, and spin. We use various correlation analyses to disentangle the different effects. The paper is organized as follows. In Sect. 2, we describe the simulations, dark matter halo samples, the merger tree construction, and the quantities we use for our analyses. In Sect. 3, we study the correlation of halo properties with the evolved and linear density fields at a typical large scale at which halo bias can be measured. In Sect. 4, we study the correlation of halo properties with linear densities at various scales and present our findings of two types of correlations that can affect the secondary bias of halos. In Sect. 5, we use the two types of correlation to interpret the secondary bias for different halo properties and its dependence on halo mass. Finally, we summarize and discuss our results in Sect. 6.

2. Simulations and dark matter halos

2.1. Simulations, halos, and merger trees

In this paper, we use two simulations with different mass resolutions. The higher resolution one is the ELUCID simulation carried out by Wang et al. (2016) using the L-GADGET code, a memory-optimized version of GADGET-2 (Springel 2005). This simulation has 30723 dark matter particles, each with a mass of 3.08 × 108 h−1 M⊙, in a periodic cubic box of 500 comoving  h−1Mpc on a side. The other simulation has 20483 particles in a cubic box of 1 h−1 Gpc on a side, with a particle mass of 8.3 × 109 h−1 M⊙. This simulation is referred to as S1k in the following. The initial conditions of the two simulations are generated at redshift of 100 by using the Zel’dovich approximation (Zel’Dovich 1970). The cosmology parameters used in the simulations are both based on WMAP5 (Dunkley et al. 2009), namely: ΩΛ, 0 = 0.742, Ωm, 0 = 0.258, Ωb, 0 = 0.044, h = H0/100 km s−1 Mpc = 0.72, σ8 = 0.80, and ns = 0.96. The characteristic collapse mass, M*, defined as the characteristic mass scale at which the RMS of the linear density field is equal to 1.686 at the present time. For the present simulations, M* = 1012.5 h−1 M⊙ at z = 0. Outputs of the two simulations are made at 100 snapshots, from z = 18.4 to z = 0 equally spaced in the logarithm of the expansion factor.

Dark matter halos are identified using a friends-of-friends (FOF) group-finder with a linking length b = 0.2 (Davis et al. 1985). We used the SUBFIND algorithm (Springel et al. 2001) to identify gravitationally bound substructures (subhalos) within each FOF halo. This in turn makes it possible to build up halo merger trees to represent the detailed assembly histories of individual halos. Each member particle of a subhalo is assigned a weight that decreases with the absolute value of its binding energy. For a subhalo ‘A’ in a snapshot, its descendant is identified as the subhalo that is in the subsequent snapshot and contains the largest weighted number of particles belonging to ‘A’, and ‘A’ is considered as the progenitor of its descendant. In each FOF halo, the most massive subhalo is referred to as the main halo and the branch that traces the main progenitors of the main halo back in time is referred to as the main trunk of the merging tree.

Using halo merger trees, we can also identify splashback halos (e.g., Ludlow et al. 2009; Wang et al. 2009), which are the main halos at z = 0, but have been accreted by other massive halos in the past. As shown in Sect. 3, splashback halos mainly affect the secondary bias for small halos. These halos are expected to have experienced strong non-linear processes, in contrast to other normal halos. Since they are only a small fraction of the total halo population, we do not consider them in the majority of our analyses.

We selected three representative halo samples at z = 0 to show our main results. The first two, selected from ELUCID, contain 392 797 halos with 11.4 ≤ log Mh/h−1 M⊙ ≤ 11.6 (representing low-mass halos) and 49 968 halos with 12.4 ≤ log Mh/h−1 M⊙ ≤ 12.6 (representing M* halos), respectively. The other one contains 9085 halos with 13.9 ≤ log Mh/h−1 M⊙ ≤ 14.1 (representing massive halos) selected from the S1k simulation. The results for other halo mass bins are presented when necessary. We note that we only show results for halos that each contain more than 800 dark matter particles, corresponding to log(Mh/h−1 M⊙) > 11.4 in ELUCID and log(Mh/h−1 M⊙) > 12.9 in S1k. As shown below, our results using ELUCID and S1k, which have very different mass resolutions, are similar, suggesting that mass resolution does not affect our conclusions significantly.

2.2. Halo properties and overdensities

In this paper, we focus on the secondary bias of halo distribution using three halo properties: the assembly time, vmax/v200 and the spin. Here we list the definitions of these three properties together with the halo mass.

(1) Halo mass (Mh). It is defined as the mass contained in the spherical region of radius r200, centered on the most bound particle of the main halo, and within which the mean mass density is equal to 200 times the critical density.

(2) Halo assembly time (zf). It is the redshift at which Mh reaches half of its final mass at z = 0. It is determined by tracing the main trunk of the merger tree of the halo in question.

(3) Halo concentration (vmax/v200). It is characterized by vmax/v200 that is the ratio of the peak value of its circular velocity profile to the virial velocity (e.g., Gao & White 2007). The virial velocity is defined as the circular velocity at r200.

(4) Halo spin (λ). It is defined as 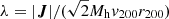, where J is the angular momentum measured by using particles within a sphere of r200.

As mentioned in the introduction, for a given halo mass, the halo bias depends significantly on the other three halo properties. To avoid ambiguity, we refer to the dependencies as the zf bias, the vmax/v200 bias and the λ bias, respectively. To understand their origin, we used over-densities measured on different scales from both the evolved and linear density fields. We thus need to know the positions of the proto-halos that correspond to the halos identified at z = 0. For each FOF halo at z = 0, the position of the proto-halo is defined as the average position of all particles that end up in the z = 0 halo. The following is the list of the over-densities used in our analyses.

(1) Δb. It is the overdensity measured within a large comoving radius range, Rb = [10−15] h−1Mpc, centered on each halo at z = 0. It is used to infer the halo bias factor at z = 0.

(2) δ(R). It is the linear overdensity at z = 18.4 at a series of comoving radius R, centered on the position of a proto-halo.

(3) δb. It is the linear overdensity at the comoving radius Rb at z = 18.4, centered on the position of a proto-halo. Note that δb is exactly δ(R) when R = Rb.

(4) δL. It is the linear overdensity at z = 18.4 within the halo Lagrangian radius, RL, centered on the position of its proto-halo. 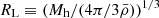, where Mh is the halo mass of the corresponding halo at z = 0 and 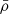is the mean comoving density of the universe. We note that δL is exactly δ(R) when R is chosen in the range of [0, RL].

(5) δe. It is the linear overdensity at z = 18.4 within [1, 1.2]RL for a proto-halo. It is exactly δ(R) when R = [RL, 1.2RL].

For clarity, we use δ to denote the overdensity measured at z = 18.4 and Δ to denote the present-day overdensity. As shown in Han et al. (2019), the bias factor at the scale from 5 to 20 h−1 Mpc is well consistent with the linear theory. We thus adopt Rb = [10, 15] h−1 Mpc to measure Δb. For any given halo sample, the halo bias is calculated as

(1)

where ⟨⋯⟩ denotes the average over all halos in the sample, and 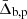is the mean overdensity measured at Rb centered on all particles in the density field at z = 0.

The linear densities used in this paper are measured from the snapshot at z = 18.4, rather than the initial condition at z = 100. At z = 100, the true overdensity is very small and the shot noise of particles is important, which can lead to systematic bias in the estimate of the true linear density fluctuation. On the other hand, the overdensities obtained at z = 18.4 are in good agreement with the prediction of the linear perturbation theory (see Appendix A). Finally, we note that the Lagrangian radii, RL, for the three representative halo samples are about 1.02, 2.19, and 6.94 h−1Mpc, respectively.

3. Halo secondary bias in evolved and linear density fields

Figure 1 shows the secondary bias for the three halo properties, zf (left), vmax/v200 (middle) and λ (right). In a given narrow mass range (0.2 dex), we select two sub-samples that consist of halos in the lower and upper 20 percent tails of the distribution of the halo property in question, respectively. We calculate the halo bias (bh) for each of the sub-samples and show it as a function of halo mass. The dashed and solid lines show the results including and excluding splashback halos, respectively. For the ELUCID simulation, we present the results for halos with −1 ≤ log(Mh/M*)≤1, while for the S1k simulation, results are shown for log(Mh/M*)≥0.5. Although the two simulations have very different mass resolutions, their results agree with each other well in the overlapping mass range, suggesting that our results are not significantly affected by numerical resolutions.

thumbnail Fig. 1.

Halo bias factor as a function of halo mass and other halo properties. In each panel the red (blue) lines show the results for halos in the upper (lower) 20% tails of the distribution of the halo property indicated in the panel. The dashed line shows the result for all halos, while the solid line shows the result excluding splashback halos. Results are shown for ELUCID and S1k halos in the mass ranges of log(Mh/M*) < 1 and log(Mh/M*) > 0.5, respectively. Error bars are the standard deviation calculated using 1000 bootstrap samples.

Figure 1 shows that splashback halos mainly affect results for low-mass halos, as expected from the fact that the fraction of the splashback population decreases with increasing halo mass (Wang et al. 2009). The exclusion of splashback halos decreases the bias for halos in the upper percentiles of the zf and vmax/v200 distributions, whereas the halo bias for the lower percentiles is not affected significantly. This is expected. At low zf, halo bias depends only weakly on zf (see e.g., Gao et al. 2005), while splashback halos on average have a higher value for zf (e.g., Wang et al. 2009). Different from zf and vmax/v200, the λ bias for the two subsamples are both significantly affected by the splashback halos. Splashback halos are expected to have experienced strong non-linear evolution, and consequently behave very differently from other halos in their relations to the linear density field. To reduce the uncertainties caused by splashback halos, we exclude them in our analyses.

All three parameters show strong secondary bias, but with very different halo-mass dependence (see also e.g., Faltenbacher & White 2010; Salcedo et al. 2018). Older halos are usually more strongly clustered than younger ones of the same mass. However, the zf bias becomes weaker as halo mass increases and is almost absent at log(Mh/M*) > 1. The vmax/v200 bias is significant over the whole mass range covered. More interestingly, it changes sign around Mh ∼ M*, above which less concentrated halos are actually more strongly biased. The λ bias is also strong in the whole mass range. Different from the other two parameters, its strength increases with the halo mass.

It is known that vmax/v200 increases with zf at given halo mass (e.g., Gao et al. 2004; Han et al. 2019), and so the zf bias and vmax/v200 bias may have a similar origin for low mass halos, as suggested by previous studies (e.g., Chen et al. 2020). However, for massive halos, the two secondary biases behave differently from the expectation of the correlation between the two parameters. Moreover, it is also known that older halos tend to have smaller spin over the whole mass range (e.g., Hahn et al. 2007; Wang et al. 2011), indicating that the zf bias and λ bias must be caused by different processes.

To understand the origin of the secondary bias and the complex mass dependence shown above, we investigate the correlations of the halo properties with the linear density field. Here, we first focus on δb, which is estimated at the same comoving scale as Δb. As shown in Fig. 2, δb and Δb are strongly correlated, albeit with considerable variance. It is thus interesting to investigate whether their correlations with halo properties are similar. We show the median of halo properties as functions of Δb and δb for the three representative halo samples in Figs. 3–5. To see which density indicator dominates the correlations, we split each of the representative halo samples into several equally sized sub-samples according to Δb or δb. We then show halo properties of individual subsamples of fixed δb as a function of Δb in the left panels (red lines), and those of fixed Δb as a function of δb in the right panels (blue lines). The numbers of the equally sized subsamples are 7, 5, and 5 for the low-mass, M* and cluster-sized halos, respectively.

thumbnail Fig. 2.

Correlations between the overdensities measured at z = 18.4 (δb) and at z = 0 (Δb) for three representative halo samples, as indicated in the panels. Both overdensities are measured within a large comoving radius range, Rb = [10−15] h−1 Mpc. The three contour lines in each panel enclose 67%, 95%, and 99% of halos, respectively.

thumbnail Fig. 3.

Median zf as a function of Δb (left panels) and δb (right panels) for three representative halo samples, as indicated in the panels. The red (blue) lines in left (right) panels show the results with δb (Δb) controlled (see the text for details). The error bars show the standard deviation calculated using 1000 bootstrap samples.

thumbnail Fig. 4.

Median vmax/v200 as a function of Δb (left panels) and δb (right panels) for three representative halo samples, as indicated in the panels. Details are the same as in Fig. 3.

thumbnail Fig. 5.

Median λ as a function of Δb (left panels) and δb (right panels) for three representative halo samples, as indicated in the panels. Details are the same as in Fig. 3.

For the halo assembly time, one can see clear dependence on both Δb and δb. The overall correlation strengths with the two densities are similar. The dependence weakens with increasing halo mass and disappears for cluster-sized halos, consistent with the results shown in Fig. 1. As one can see, for the two low mass bins, the dependence on Δb becomes very weak when δb is controlled. On the other hand, when Δb is controlled, the correlation of zf with δb for individual sub-samples follows the overall trend closely. For the most massive halos, no clear trend can be seen.

The results for vmax/v200 are also consistent with those shown in Fig. 1. We can see that the correlation shows opposite trends for low-mass and the most massive halos. The overall trends with Δb and δb are similar. However, as shown in Fig. 4, for both low and high mass halos, the dependence on Δb is absent when δb is controlled, but a clear correlation (positive for low-mass halos and negative for high-mass halos) is clearly seen with δb for fixed Δb. For halos with Mh ∼ M*, on the other hand, the trends of vmax/v200 with δb and Δb are both rather weak.

Finally, the overall correlation of λ with the two density parameters becomes stronger as the halo mass increases, consistent with the results shown in Fig. 1. If the samples are not controlled, the general trend in the λ–Δb correlation is similar to that in the λ–δb correlation. However, the results of the controlled samples clearly show that the linear density, δb, is the driving factor of the λ–Δb correlation for all the three halo samples.

The analyses presented above clearly demonstrate that the correlations of halo properties with Δb are driven by the correlations with δb in all cases where significant secondary bias is detected, through the correlation between Δb and δb. To demonstrate this in a more intuitive way, we divide halos in each mass bin into five subsamples of equal size according to δb. We then select halos in the upper and lower 20% of the distribution of a given halo property in each subsample and show the corresponding halo bias as a function of halo mass in Fig. 6. As we can see, when δb is controlled, the secondary bias for all the three halo properties disappears over the entire halo mass range probed, which is consistent with the results shown in Figs. 3–5. This demonstrates again that the secondary bias is more closely tied to the linear density field than to the halo properties. This also suggests that the origin of the secondary bias may be approached by investigating the correlations of halo properties with the linear density field, as we show below.

thumbnail Fig. 6.

Halo bias factor as a function of Mh, δb and halo properties (upper panels: zf, middle panels: vmax/v200, and lower panels: λ). For a given halo mass bin, we divide halos into five equally sized subsamples according to δb, as indicated in different columns. The red (blue) lines show the results for halos in the upper (lower) 20% of the distribution of a given halo property with δb controlled. The symbols, along with the color-coded and shaded region are the same as in Fig. 1.

4. Correlations of halo properties with linear densities on various scales

The results presented above show that halo properties are correlated with the linear over-density at a large comoving scale, Rb. Wang et al. (2007) found that the halo assembly time is also correlated with the linear over-density measured within the Lagrangian radius, δL. These two results suggest that halo properties are correlated with the linear density field on various scales. It is thus interesting to first investigate in more detail how the correlation varies with the scale. A convenient way to characterise the correlation strength of two variables, x and y, is to use their Pearson correlation coefficient, defined as

(2)

where 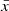(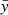) and σx (σy) are the mean and standard deviation of the variable x (y), respectively. As discussed in Han et al. (2019), the Pearson coefficient is a powerful tool for correlation analysis. If the two variables are roughly linearly correlated, the coefficient measures the steepness of the correlation between the corresponding normalized variables.

The Pearson coefficients, ρr, for the correlations of halo properties with δ(R) are shown in Fig. 7. We first look at the coefficients at the scale R = Rb (indicated by the vertical bands), namely, the correlations of halo properties with δ(Rb) = δb, and compare them with the results shown in the last section. The absolute values of the correlation coefficients of the three halo properties with δb range from 0 to 0.2, indicating that the secondary bias is in general a weak effect. The results show that δb is positively correlated with zf for the two low-mass samples, and that the coefficient is close to zero for the most massive halos. The coefficient for vmax/v200 changes its sign around M*, being positive and negative for halos of lower and higher masses, respectively. The correlation coefficient for λ is always positive and increases with halo mass. All of these are in good agreement with the results shown in the last section.

thumbnail Fig. 7.

Pearson correlation coefficients (ρr) between halo properties (left panel: zf; middle panel: vmax/v200; right panel: λ) and δ(R) as a function of R for three representative halo samples, as indicated. The vertical error bars (usually too small to be seen) indicate the uncertainties of the coefficients, calculated using 200 bootstrap samples. The results for δL and δe are marked with stars and open circles, respectively. Results on other scales are shown with solid circles. The vertical dotted lines indicate RL of the halos in question. The vertical shaded region indicates the range of Rb used to estimate the halo bias.

The scale dependence of these correlations is complex, although there are some interesting features. In the inner region of proto-halos, that is, R ≤ 0.6RL, the correlations are almost independent of the scale. As R increases, we see a rapid change in the correlation strength and even a change in the sign of the correlations around the Lagrangian radius, RL. At R = [1, 1.2]RL, the coefficients reach a (local) minimum for zf and vmax/v200, and a maximum for λ. At R > RL, the correlations show complex dependence on halo mass, which is different from the dependence on the overdensities within proto-halos. For example, for low-mass and M* samples, the coefficient for zf first increases with R and then decreases gradually to zero at large scales. For cluster-sized halos, on the other hand, the scale dependence appears monotonous.

These results suggest that the overdensities inside and outside the proto-halos may affect halo properties in different ways. In the following, we therefore consider the dependence on these two types of overdensities separately. Specifically, we use δL, the linear overdensity within the Lagrangian radius, to represent the inside overdensity of proto-halos, and use δe, measured at R = [1, 1.2]RL, to represent the outside overdensity (see Sect. 2.2 for the definition of the two quantities). We will also consider overdensities measured at larger scales when necessary.

Figure 8 shows the correlation coefficients between the three halo properties and δL as a function of halo mass. The three halo properties have different correlation strengths with δL, being the strongest for zf (ρr = 0.4 → 0.6) and the weakest for λ (ρr = −0.2 → −0.3). The strong and positive correlation with the halo assembly time is consistent with what was found in Wang et al. (2007). It is interesting that all the correlations show only a weak dependence on halo mass, which looks very different from the complex halo mass dependence of the secondary bias. We come back to this question in the next section. Since the two simulations with very different mass resolutions give similar coefficients in the overlapping mass range, it indicates again that numerical effects are not important for the halos used in our analyses.

thumbnail Fig. 8.

Pearson coefficients for the (partial) correlations of δL with halo properties, zf (left panel), vmax/v200 (middle panel), and λ (right panel), as a function of halo mass. As indicated in each panel, the red lines show the results of the correlations between δL and halo properties, the blue and green lines show the results with another property controlled, and the black lines show the results with δe controlled. The error bar shows the standard deviation calculated from 200 bootstrap samples.

In Fig. 9, we show the average of the halo properties in the (δL versus δe) space. As one can see, the three halo properties exhibit strong dependence on both overdensities in all the three mass bins. Consistently with the correlation coefficient results shown in Fig. 8, both zf and vmax/v200 have a strong positive correlation with δL, while λ has a negative correlation with δL. We also see a clear negative correlation of both zf and vmax/v200, and a clear positive correlation of λ, with δe for a given δL. These correlations are not always consistent with the results shown in Fig. 7. The discrepancy is produced by the fact that δL and δe are correlated, so that the correlation with δe depends on whether or not δL is controlled. Figure 10 shows the correlation coefficient between δL and δ(R) as a function of R. Clearly, δL is correlated with the over-density on different scales, including δe. The correlation coefficient decreases gradually with R, and depends only weakly on halo mass.

thumbnail Fig. 9.

Contours showing median zf (upper panels), vmax/v200 (middle panels), λ (lower panels) as a function of δe and δL for three representative halo samples as indicated in the panels. Only grids containing more than 100 halos are presented.

It is thus important to disentangle these correlations and we use a partial correlation coefficient to do so. The partial correlation coefficient measures the correlation coefficient between two quantities, x and y, with a third parameter, z, controlled, and is defined as (John et al. 1989):

(3)

A higher order partial coefficient can be computed from the lower order coefficient. For example, when two variables, z and w, are controlled, the coefficient can be written as:

(4)

The correlation coefficients between the three halo properties and δL, with δe controlled, are plotted in Fig. 8. With δe controlled, the correlations with δL become significantly stronger. This is expected, as the two densities are positively correlated (Fig. 10) but they have opposite correlations with the halo properties (Fig. 9). Again, we note that the halo mass dependence in these correlations are all weak.

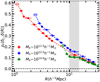thumbnail Fig. 10.

Pearson coefficients between δL and δ(R) as a function of R for three representative halo samples. The symbols, color-code, error bars, and shaded region are the same as in Fig. 7.

The correlation coefficients between the halo properties and δ(R), with δL controlled, are shown in Fig. 11. Here, the results are shown as a function of R/RL, instead of R. Controlling δL boosts the correlation strengths between δe and the halo properties, and makes the coefficients monotonous functions of R/RL at R/RL > 1. Among the three halo properties, vmax/v200 has the strongest (anti-) correlation with δe, and zf the weakest. Moreover, the positive correlation of λ with δ(R) extends to R > 5RL. In general, the correlations with δe and density at larger scales are the opposite to the correlations with δL, consistent with the results shown in Fig. 9. Remarkably, the correlations with δ(R) at R > RL depend on halo mass much weaker than seen in Fig. 7. To demonstrate this more clearly, we also show the results for other 12 mass bins, ranging from 1011.6 to 1014.4 h−1 M⊙ and with a bin width of 0.2 dex, as the gray lines. As can be seen here, the controlled correlations between halo properties and the over-density at R > RL indeed exhibit a weak dependence on halo mass.

thumbnail Fig. 11.

Partial correlation coefficients for correlations between halo properties and δ(R), with δL controlled (left panel), with δL and another halo property additionally controlled (middle and right panel), as a function of R/RL. The results in left panels are computed using Eq. (3) and those in the middle and right panels using Eq. (4). The symbols, the color code, and error bars are the same as Fig. 7. The gray lines show the results for other halo mass bins and the black lines show the mean results of these halo mass bins.

These results clearly suggest that two distinct types of processes may regulate the halo properties simultaneously. The first is related to the mean over-density within the proto-halos, namely, δL. According to the spherical collapse model, the mean linear over-density should be the same for all halos identified at the same time. The fact that δL is different for different halos indicates that the spherical collapse model is not accurate. As shown in Wang et al. (2007), some halos need a higher over-density to form, because local tidal fields may act to prevent the collapse of the outer parts of proto-halos. This may explain the positive correlations of δL with zf and vmax/v200, and the negative correlation with λ. The second is the negative correlation of the over-density at R > RL with both zf and vmax/v200, and the positive correlation with λ, when δL is controlled. As we see later in this work, these correlations are produced in part by the anti-correlation between the inner density of a proto-halo and the density exterior to RL. Both types of correlations have only weak dependence on halo mass, presumably because the linear density field is roughly scale-free over the scales concerned here. For convenience, we use internal correlations to refer to those related to δL, and external correlations to those related to δe and over-densities on larger scales.

Since the three halo properties are correlated with each other, it is important to check whether the internal and external correlations for a specific halo property are induced by the correlations for another halo property. In Fig. 8, we show the correlation coefficients between δL and one halo property with another property controlled. When zf is fixed, the correlations with both vmax/v200 and λ are largely reduced and close to zero. In contrast, the correlation with zf remains strong even when vmax/v200 or λ is fixed. This suggests that the zf–δL correlation is the dominant one, while the other two correlations are largely the secondary effects of the zf–δL correlation.

In Fig. 11, we show partial external correlation coefficients as functions of R, with zf or vmax/v200 or λ controlled in addition to δL. We see that the external correlation for vmax/v200 changes little when zf or λ is controlled. Similarly, vmax/v200 and zf have only little influence on the external correlation for λ. However, the external correlation for zf is strongly affected by the other two properties, in particular vmax/v200. When vmax/v200 is controlled, the external correlation efficiency of zf becomes close to zero over a large range of scales. These results suggest that the external correlation of zf is largely the secondary effect of the external correlation of vmax/v200, while the external correlation of λ has a different origin than that of both zf and vmax/v200.

To gain a greater understanding of the origin of the external correlations, we investigate the impact of the overdensity within [0.4−0.6]RL, denoted as δ(0.5RL). The partial correlation between δ(0.5RL) and δ(R) with δL controlled is shown in Fig. 12. It is similar to that of the external correlations of vmax/v200 and zf. At a given δL, δ(0.5RL) measures the density slope within the proto-halo. The anti-correlation between δ(0.5RL) and the linear density field immediately exterior to RL indicates that the density slope is coherent over a range of scales around RL. As suggested in Lu et al. (2006) and Dalal et al. (2008), the linear density profile of a proto-halo affects its accretion history and its final properties, such as zf and vmax/v200, which may explain, at least in part, the external correlations of vmax/v200 and zf. The density slope may also affect λ, not only because it is correlated with the moment of inertial tensor of the proto-halo, which couples the proto-halo with the tidal field, but also because of its correlation with the halo assembly time over which the external tidal field operates to generate the angular momentum.

thumbnail Fig. 12.

Partial correlation coefficient (Eq. (3)) between δ(0.5RL) and δ(R), with δL controlled, as a function of R/RL. Here, δ(0.5RL) is the average overdensity within [0.4−0.6]RL. The symbols, color-coding, and error bars are the same as in Fig. 11.

5. Exploring the origin of the secondary bias and its mass dependence

Using the results obtained above, we sought to understand the origin of the secondary bias and its mass dependence. From Eq. (3), we can write the Pearson coefficient between a halo property, p, and δb as:

(5)

where rb = Rb/RL, δ(rb) is exactly δb, and

(6)

Since ρr(p, δL) ranges from ∼ − 0.3 to ∼0.6 and ρr(δb, δL) is about 0.1, the value of α ranges from 0.8 to 1, with very weak dependence on halo mass. We thus can treat α as a constant close to unity.

Equation (5) shows that the correlation of halo properties with δb consists of two components, represented by the two terms on the right-hand side and related to the external and internal correlations, respectively. The secondary bias in the evolved density field, which is usually characterized by the p–Δb correlation, may thus be understood in terms of the p–δb correlation, as δb is tightly correlated with Δb and the correlation is quite independent of halo mass (Fig. 2). The external correlation can result in a negative correlation of δb with zf and vmax/v200 and a positive correlation with λ. The internal correlation affects the secondary bias via the δL–δb correlation, and can induce a positive correlation of of zf and vmax/v200 with δb, and a negative correlation between λ and δb. As shown in Figs. 8 and 11, both the external and internal components depend only weakly on halo mass. However, as we will show below, the two components combined can actually produce the mass dependence observed in the secondary bias.

Let us first look at the zf bias. For small halos with log(Mh/h−1 M⊙) = 11.5, the radius Rb corresponds to rb ≡ Rb/RL > 9.8. At such a large scaled radius, the external correlation is very weak, with ρr(zf, δ(rb)|δL) close to zero (Fig. 11). In this case, ρr(zf, δb)≃ρr(zf, δL)ρr(δb, δL), indicating that the positive correlation of zf with δb for these halos is mainly determined by the internal correlation. For M* halos, where rb = [4.56, 6.84], the contribution from the external correlation is still negligible, and so the dominant role is still played by the internal correlation. Moreover, since the zf–δL and δb–δL correlations for M* halos are similar to those for small halos (Figs. 7 and 10), the contribution of the internal correlation for the two halo mass samples are also similar. Indeed, as shown in Fig. 7, the correlation coefficients of zf with δb are very similar for the two halo samples. Finally, for massive cluster-sized halos, the scaled radius rb = [1.44, 2.16]. At such a scale, the external correlation becomes much stronger (Fig. 11), while the contribution of the internal correlation is only slightly stronger than that for the other two halo mass bins. Consequently, the external correlation is able to counterbalance the internal correlation, making the secondary bias for these halos very weak.

Similar analysis can be made for vmax/v200. The internal correlation of vmax/v200 is weaker, while the external correlation is stronger than that of zf, making the external correlation more important for the vmax/v200 bias. This also makes the mass-dependence of the vmax/v200 bias different from that of the zf bias. For small halos, the vmax/v200 bias is still dominated by the internal correlation, because their ρr(vmax/v200, δ(rb)|δL) is close to zero (Fig. 11). Thus, a positive vmax/v200–δb correlation is expected, consistent with the results shown in Figs. 1 and 4. For M* halos, the internal and external correlations become comparable, so that vmax/v200 is independent of δb. For massive cluster-sized halos, where rb becomes small, the external correlation becomes the dominant one, producing a negative correlation between vmax/v200 and δb. The change in the sign of the vmax/v200 bias is thus a result of the competition between the two correlations.

Finally for the spin, the internal correlation is even weaker and, thus, it plays only a minor role in producing the λ bias. As shown in Fig. 11, the external correlation for the spin decreases with R/RL slowly, and so the dominant effect for the λ bias is always the external correlation over the entire mass range. Since rb = Rb/RL decreases with increasing halo mass and the external correlation is stronger at smaller rb, an increasing trend with halo mass is produced, as shown in Figs. 1, 5, and 7.

The analyses above suggest that the secondary bias observed in the evolved density field is primarily produced by the internal and external correlations of halo properties with the linear density field, and that these correlations provide a transparent way to understand the origin of the secondary bias. We note that the results are not sensitive to the choice of Rb, on which the halo bias is estimated. Indeed, we reached very similar conclusions using other scales, although the details may be different. Other factors, which are not included in our analysis, may also contribute to or affect the secondary bias. For example, both the external and internal correlations show weak but complicated dependence on halo mass, indicating that the shape of the linear power spectrum may also play a role. In addition, the correlations of the halo properties with δb are not expected to be exactly the same as those with Δb, estimated at z = 0, although these two overdensities are correlated. As shown in Figs. 3–5, the non-linear evolution of the density field around halos weakens the strength of the secondary bias slightly, presumably because of the mixing of scales of the linear density field in the evolved field.

6. Summary and discussion

In this paper, we use two N-body simulations, ELUCID and S1k, to study the origin of the secondary bias for halo assembly time (zf), concentration (vmax/v200) and spin (λ), and its dependence on halo mass. Splashback halos, which have experienced strong non-linear processes, are excluded from our analyses. Our study is based on the correlations of these halo properties with linear densities at various scales. The main results can be summarized as follows.

  • We find that the correlations of halo properties with the density measured at Rb = [10, 15] h−1 Mpc are stronger in the linear density field than in the evolved density field at z = 0. The secondary bias in the evolved density field is the secondary effect of the correlations of halo properties with the linear density (Figs. 3–6) through the correlation of the two densities (Fig. 2).

  • The correlations of halo properties with the linear density field vary rapidly and even change signs around the halo Lagrangian radius and approach zero at larger scales (Fig. 7). This suggests that the linear densities inside and outside the proto-halos affect the final halo properties in different ways.

  • The three halo properties are strongly correlated with the average linear density within the Lagrangian radius, δL (Fig. 8). The zf and vmax/v200 of halos increase with δL, while λ exhibits a negative correlation with δL. The Pearson correlation coefficient shows that all the three correlations depend only weakly on the halo mass. Our results suggest that the internal correlations of vmax/v200 and λ are the secondary effects of the internal correlation of zf.

  • At a given δL, all the three halo properties are correlated with δ(R/RL) at R > RL in a way opposite to the internal correlation (Figs. 9 and 11). The conditional correlations, with δL fixed, show only weak dependence on halo mass for all the three halo properties. The external correlations for zf and vmax/v200 appear to share the same origin that may be partly related to the correlation of the inner slope of the proto-halos with the density field on large scales; the external correlation of λ may have a different origin.

  • The internal and external correlations are the main drivers of the secondary bias (Eq. (5)). For the zf bias, the internal correlation dominates for nearly the entire range of the halo mass, and the contributions of the two types of correlation are comparable for cluster-sized halos. For the vmax/v200 bias, the internal correlation dominates for low-mass halos and the external correlation dominates for cluster-sized halos, while the two correlations are comparable for M* halos. For the λ bias, the external correlation dominates over the whole mass range and the internal correlation only plays a minor role.

Our analysis offers a new perspective on the nature of the secondary bias. The results suggest that the combination of the internal and external correlations in the linear density field drives the secondary bias of the three halo properties considered here, and that the mass dependence of the secondary bias is the result of the competition of the two correlations and the mass dependence of the contribution of the external correlation. We therefore need to understand the mechanisms that produce the internal and external correlations in order to fully understand the origin of the secondary bias.

The internal correlation of zf was studied in Wang et al. (2007), who found that the proto-halo of a z = 0 halo with high zf is usually located in the vicinity of massive structures. These authors thus suggested that the large-scale tidal field associated with (neighbour halos or large scale structures) the high density can truncate the accretion of the material in the outskirt of the proto-halo (see also Salcedo et al. 2018). The stronger the tidal field is, the larger the truncation effect and the higher the assembly redshift. This can explain the zf–δL correlation. However, they suggested that this effect is only important for small halos (see also e.g., Dalal et al. 2008; Mansfield & Kravtsov 2020), which is not consistent with our finding that this effect is equally important for cluster-sized halos. This indicates that tidal truncation may also be important in the case of massive halos.

The external correlation can produce a secondary bias effect that is totally opposite to the internal correlation. The external correlation is complicated and more than one mechanism may be relevant. For example, previous studies (e.g., Fakhouri & Ma 2009; Wang et al. 2011) have suggested that dense environments can enhance the frequency of halo merging and mass accretion, producing an effect similar to that of the external correlation we observe here. The inner density profile within a proto-halo, which is found to correlate with large-scale density (Fig. 12), can also affect the assembly history and concentration of the halo (e.g., Lu et al. 2006; Dalal et al. 2008). A steeper initial profile, in general, produces an older and more concentrated final halo, leading to the external correlation. The external tidal field may not only truncate mass accretion onto a halo but can also accelerate the tangential velocity of the material around the halo and enhance the spin (e.g., Shi et al. 2015). This may explain the significant positive correlation between the spin and linear density at large scales. The steepness of the initial density profile, which is correlated with the large-scale density field, can also affect the spin through its correlation with the moment of the inertial tensor of the proto-halo and its correlation with the assembly time that the external tidal field operates over in order to generate the angular momentum.

Clearly, further investigations are still needed to understand the details of these mechanisms and how they affect the properties of halos. A detailed understanding of these mechanisms is essential not only for understanding the origin of the secondary bias, but also for constructing a comprehensive picture of halo formation in the cosmic density field. The results obtained here pave the way toward this goal.

Acknowledgments

We thank the anonymous referee for a useful report that significantly improves the paper. This work is supported by the National Key R&D Program of China (grant No. 2018YFA0404503), the National Natural Science Foundation of China (NSFC, Nos. 11733004, 11890693, and 11421303), and the Fundamental Research Funds for the Central Universities. We acknowledge the science research grants from the China Manned Space Project with No. CMS-CSST-2021-A03. The work is also supported by the Supercomputer Center of University of Science and Technology of China.

References

  1. Allgood, B., Flores, R. A., Primack, J. R., et al. 2006, MNRAS, 367, 1781 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bett, P., Eke, V., Frenk, C. S., et al. 2007, MNRAS, 376, 215 [NASA ADS] [CrossRef] [Google Scholar]
  3. Chen, S., Wang, H., Mo, H. J., & Shi, J. 2016, ApJ, 825, 49 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chen, Y., Mo, H. J., Li, C., et al. 2020, ApJ, 899, 81 [CrossRef] [Google Scholar]
  5. Chue, C. Y. R., Dalal, N., & White, M. 2018, JCAP, 2018, 012 [Google Scholar]
  6. Dalal, N., White, M., Bond, J. R., & Shirokov, A. 2008, ApJ, 687, 12 [NASA ADS] [CrossRef] [Google Scholar]
  7. Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
  8. Desjacques, V. 2008, MNRAS, 388, 638 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dunkley, J., Komatsu, E., Nolta, M. R., et al. 2009, ApJS, 180, 306 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fakhouri, O., & Ma, C.-P. 2009, MNRAS, 394, 1825 [NASA ADS] [CrossRef] [Google Scholar]
  11. Faltenbacher, A., & White, S. D. M. 2010, ApJ, 708, 469 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gao, L., & White, S. D. M. 2007, MNRAS, 377, L5 [NASA ADS] [CrossRef] [Google Scholar]
  13. Gao, L., White, S. D. M., Jenkins, A., Stoehr, F., & Springel, V. 2004, MNRAS, 355, 819 [Google Scholar]
  14. Gao, L., Springel, V., & White, S. D. M. 2005, MNRAS, 363, L66 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hahn, O., Porciani, C., Carollo, C. M., & Dekel, A. 2007, MNRAS, 375, 489 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hahn, O., Porciani, C., Dekel, A., & Carollo, C. M. 2009, MNRAS, 398, 1742 [NASA ADS] [CrossRef] [Google Scholar]
  17. Han, J., Li, Y., Jing, Y., et al. 2019, MNRAS, 482, 1900 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hearin, A. P., Watson, D. F., & van den Bosch, F. C. 2015, MNRAS, 452, 1958 [NASA ADS] [CrossRef] [Google Scholar]
  19. Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jing, Y. P., Suto, Y., & Mo, H. J. 2007, ApJ, 657, 664 [NASA ADS] [CrossRef] [Google Scholar]
  21. John, N., William, W., & Whitmore, G. A. 1989, Applied Statistics (3rd Edition) [Google Scholar]
  22. Johnson, J. W., Maller, A. H., Berlind, A. A., Sinha, M., & Holley-Bockelmann, J. K. 2019, MNRAS, 486, 1156 [CrossRef] [Google Scholar]
  23. Lacerna, I., & Padilla, N. 2011, MNRAS, 412, 1283 [NASA ADS] [Google Scholar]
  24. Lazeyras, T., Musso, M., & Schmidt, F. 2017, JCAP, 2017, 059 [Google Scholar]
  25. Li, Y., Mo, H. J., & Gao, L. 2008, MNRAS, 389, 1419 [NASA ADS] [CrossRef] [Google Scholar]
  26. Li, R., Gao, L., Xie, L., & Guo, Q. 2013, MNRAS, 435, 3592 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lu, Y., Mo, H. J., Katz, N., & Weinberg, M. D. 2006, MNRAS, 368, 1931 [NASA ADS] [CrossRef] [Google Scholar]
  28. Ludlow, A. D., Navarro, J. F., Springel, V., et al. 2009, ApJ, 692, 931 [NASA ADS] [CrossRef] [Google Scholar]
  29. Mansfield, P., & Kravtsov, A. V. 2020, MNRAS, 493, 4763 [NASA ADS] [CrossRef] [Google Scholar]
  30. Mao, Y.-Y., Zentner, A. R., & Wechsler, R. H. 2018, MNRAS, 474, 5143 [NASA ADS] [CrossRef] [Google Scholar]
  31. Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [Google Scholar]
  32. Musso, M., & Sheth, R. K. 2012, MNRAS, 423, L102 [NASA ADS] [CrossRef] [Google Scholar]
  33. Paranjape, A., Hahn, O., & Sheth, R. K. 2018, MNRAS, 476, 3631 [CrossRef] [Google Scholar]
  34. Ramakrishnan, S., Paranjape, A., Hahn, O., & Sheth, R. K. 2019, MNRAS, 489, 2977 [CrossRef] [Google Scholar]
  35. Salcedo, A. N., Maller, A. H., Berlind, A. A., et al. 2018, MNRAS, 475, 4411 [NASA ADS] [CrossRef] [Google Scholar]
  36. Salcedo, A. N., Zu, Y., Zhang, Y., et al. 2020, MNRAS, submitted [arXiv:2010.04176] [Google Scholar]
  37. Sandvik, H. B., Möller, O., Lee, J., & White, S. D. M. 2007, MNRAS, 377, 234 [NASA ADS] [CrossRef] [Google Scholar]
  38. Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
  39. Shi, J., & Sheth, R. K. 2018, MNRAS, 473, 2486 [NASA ADS] [CrossRef] [Google Scholar]
  40. Shi, J., Wang, H., & Mo, H. J. 2015, ApJ, 807, 37 [NASA ADS] [CrossRef] [Google Scholar]
  41. Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
  42. Springel, V., White, S. D. M., Tormen, G., & Kauffmann, G. 2001, MNRAS, 328, 726 [Google Scholar]
  43. Tucci, B., Montero-Dorta, A. D., Abramo, L. R., Sato-Polito, G., & Artale, M. C. 2021, MNRAS, 500, 2777 [Google Scholar]
  44. Wang, P., & Kang, X. 2018, MNRAS, 473, 1562 [CrossRef] [Google Scholar]
  45. Wang, H. Y., Mo, H. J., & Jing, Y. P. 2007, MNRAS, 375, 633 [NASA ADS] [CrossRef] [Google Scholar]
  46. Wang, H., Mo, H. J., & Jing, Y. P. 2009, MNRAS, 396, 2249 [NASA ADS] [CrossRef] [Google Scholar]
  47. Wang, H., Mo, H. J., Jing, Y. P., Yang, X., & Wang, Y. 2011, MNRAS, 413, 1973 [NASA ADS] [CrossRef] [Google Scholar]
  48. Wang, H., Mo, H. J., Yang, X., et al. 2016, ApJ, 831, 164 [Google Scholar]
  49. Wang, H., Mo, H. J., Chen, S., et al. 2018, ApJ, 852, 31 [Google Scholar]
  50. Wechsler, R. H., & Tinker, J. L. 2018, ARA&A, 56, 435 [NASA ADS] [CrossRef] [Google Scholar]
  51. Wechsler, R. H., Zentner, A. R., Bullock, J. S., Kravtsov, A. V., & Allgood, B. 2006, ApJ, 652, 71 [NASA ADS] [CrossRef] [Google Scholar]
  52. Wetzel, A. R., Cohn, J. D., White, M., Holz, D. E., & Warren, M. S. 2007, ApJ, 656, 139 [NASA ADS] [CrossRef] [Google Scholar]
  53. Xu, X., & Zheng, Z. 2018, MNRAS, 479, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  54. Yang, X., Mo, H. J., & van den Bosch, F. C. 2006, ApJ, 638, L55 [NASA ADS] [CrossRef] [Google Scholar]
  55. Yang, X., Zhang, Y., Lu, T., et al. 2017, ApJ, 848, 60 [NASA ADS] [CrossRef] [Google Scholar]
  56. Zel’Dovich, Y. B. 1970, A&A, 5, 84 [Google Scholar]
  57. Zentner, A. R. 2007, Int. J. Mod. Phys. D, 16, 763 [NASA ADS] [CrossRef] [Google Scholar]
  58. Zentner, A. R., Hearin, A. P., & van den Bosch, F. C. 2014, MNRAS, 443, 3044 [NASA ADS] [CrossRef] [Google Scholar]
  59. Zhao, D. H., Jing, Y. P., Mo, H. J., & Börner, G. 2003, ApJ, 597, L9 [NASA ADS] [CrossRef] [Google Scholar]
  60. Zhu, G., Zheng, Z., Lin, W. P., et al. 2006, ApJ, 639, L5 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Linear field at z = 18.4 and its relation to the initial condition

We used the simulation snapshots at z = 18.4, rather than the initial condition (at z = 100), to calculate the linear overdensities. Figure A.1 shows the comparison of the overdensities within the halo Lagrangian radius measured at z = 18.4 with the initial condition for the three representative halo samples, together with the prediction of the linear theory. Here, we use δL and 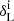to denote the overdensities at z = 18.4 and z = 100, respectively. We can see that the median values of the three correlations are consistent with the prediction of the linear perturbation theory, indicating that the density field at z = 18.4 is still in the linear regime. These results justify the use of the simulation data at z = 18.4 to estimate the linear densities.

When the mass resolution is not sufficiently high, there is a systematical problem in the initial condition due to shot noise. This problem is particularly severe for halos containing small number of particles. As we can see, for M* and cluster-sized halos that contain at least 8000 particles in each halo, the correlations are very tight, while for the low-mass halos, each of which has only about 800 particles, the correlation is much poorer. Thus, for halos with only about 800 particles, the overdensities measured from the initial condition are severely affected by the shot noise. To demonstrate this, we show the results for halos of log(Mh/M⊙)∼13 of both simulations in Fig. A.2. We choose this mass bin, because the S1k halos contain about 800 particles, similar to the low-mass halo sample. If shot noise were not important for these S1k halos, we would expect a similar correlation between the two simulations. However, the correlation is much weaker for S1k than for ELUCID. Clearly, shot noise can severely affect the measurements of the linear densities from the initial condition for halos containing less than 800 particles. We thus chose the snapshots at z = 18.4 to calculate the linear overdensities rather than the initial condition.

thumbnail Fig. A.1.

Contours show the correlation between and δL for three representative halo samples. The three contour lines in each panel enclose 67%, 95%, and 99% of halos. The blue solid line shows the median value and the blue dash lines show 1σ dispersion around the median relation. The red dashed lines show the prediction of the linear theory.

thumbnail Fig. A.2.

Similar to Fig. A.1 but for halos with log Mh = 13.0. The left and right panels show the results for S1k and ELUCID, respectively.

All Figures

thumbnail Fig. 1.

Halo bias factor as a function of halo mass and other halo properties. In each panel the red (blue) lines show the results for halos in the upper (lower) 20% tails of the distribution of the halo property indicated in the panel. The dashed line shows the result for all halos, while the solid line shows the result excluding splashback halos. Results are shown for ELUCID and S1k halos in the mass ranges of log(Mh/M*) < 1 and log(Mh/M*) > 0.5, respectively. Error bars are the standard deviation calculated using 1000 bootstrap samples.
In the text
thumbnail Fig. 2.

Correlations between the overdensities measured at z = 18.4 (δb) and at z = 0 (Δb) for three representative halo samples, as indicated in the panels. Both overdensities are measured within a large comoving radius range, Rb = [10−15] h−1 Mpc. The three contour lines in each panel enclose 67%, 95%, and 99% of halos, respectively.
In the text
thumbnail Fig. 3.

Median zf as a function of Δb (left panels) and δb (right panels) for three representative halo samples, as indicated in the panels. The red (blue) lines in left (right) panels show the results with δb (Δb) controlled (see the text for details). The error bars show the standard deviation calculated using 1000 bootstrap samples.
In the text
thumbnail Fig. 4.

Median vmax/v200 as a function of Δb (left panels) and δb (right panels) for three representative halo samples, as indicated in the panels. Details are the same as in Fig. 3.
In the text
thumbnail Fig. 5.

Median λ as a function of Δb (left panels) and δb (right panels) for three representative halo samples, as indicated in the panels. Details are the same as in Fig. 3.
In the text
thumbnail Fig. 6.

Halo bias factor as a function of Mh, δb and halo properties (upper panels: zf, middle panels: vmax/v200, and lower panels: λ). For a given halo mass bin, we divide halos into five equally sized subsamples according to δb, as indicated in different columns. The red (blue) lines show the results for halos in the upper (lower) 20% of the distribution of a given halo property with δb controlled. The symbols, along with the color-coded and shaded region are the same as in Fig. 1.
In the text
thumbnail Fig. 7.

Pearson correlation coefficients (ρr) between halo properties (left panel: zf; middle panel: vmax/v200; right panel: λ) and δ(R) as a function of R for three representative halo samples, as indicated. The vertical error bars (usually too small to be seen) indicate the uncertainties of the coefficients, calculated using 200 bootstrap samples. The results for δL and δe are marked with stars and open circles, respectively. Results on other scales are shown with solid circles. The vertical dotted lines indicate RL of the halos in question. The vertical shaded region indicates the range of Rb used to estimate the halo bias.
In the text
thumbnail Fig. 8.

Pearson coefficients for the (partial) correlations of δL with halo properties, zf (left panel), vmax/v200 (middle panel), and λ (right panel), as a function of halo mass. As indicated in each panel, the red lines show the results of the correlations between δL and halo properties, the blue and green lines show the results with another property controlled, and the black lines show the results with δe controlled. The error bar shows the standard deviation calculated from 200 bootstrap samples.
In the text
thumbnail Fig. 9.

Contours showing median zf (upper panels), vmax/v200 (middle panels), λ (lower panels) as a function of δe and δL for three representative halo samples as indicated in the panels. Only grids containing more than 100 halos are presented.
In the text
thumbnail Fig. 10.

Pearson coefficients between δL and δ(R) as a function of R for three representative halo samples. The symbols, color-code, error bars, and shaded region are the same as in Fig. 7.
In the text
thumbnail Fig. 11.

Partial correlation coefficients for correlations between halo properties and δ(R), with δL controlled (left panel), with δL and another halo property additionally controlled (middle and right panel), as a function of R/RL. The results in left panels are computed using Eq. (3) and those in the middle and right panels using Eq. (4). The symbols, the color code, and error bars are the same as Fig. 7. The gray lines show the results for other halo mass bins and the black lines show the mean results of these halo mass bins.
In the text
thumbnail Fig. 12.

Partial correlation coefficient (Eq. (3)) between δ(0.5RL) and δ(R), with δL controlled, as a function of R/RL. Here, δ(0.5RL) is the average overdensity within [0.4−0.6]RL. The symbols, color-coding, and error bars are the same as in Fig. 11.
In the text
thumbnail Fig. A.1.

Contours show the correlation between and δL for three representative halo samples. The three contour lines in each panel enclose 67%, 95%, and 99% of halos. The blue solid line shows the median value and the blue dash lines show 1σ dispersion around the median relation. The red dashed lines show the prediction of the linear theory.
In the text
thumbnail Fig. A.2.

Similar to Fig. A.1 but for halos with log Mh = 13.0. The left and right panels show the results for S1k and ELUCID, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.