| Issue |
A&A
Volume 514, May 2010
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200912636 | |
| Published online | 12 May 2010 | |
Mass function and bias of dark matter halos for non-Gaussian initial conditions
Institut de Physique Théorique, CEA Saclay, 91191 Gif-sur-Yvette,
France e-mail: patrick.valageas@cea.fr
Received:
4
June
2009
Accepted:
31
January
2010
Aims. We revisit the derivation of the mass function and the bias of dark matter halos for non-Gaussian initial conditions.
Methods. We use a steepest-descent approach to point out that exact results can be obtained for the high-mass tail of the halo mass function and the two-point correlation of massive halos. Focusing on primordial non-Gaussianity of the local type, we check that these results agree with numerical simulations.
Results. The high-mass cutoff of the halo mass function takes the same form as the one obtained from the Press-Schechter formalism, but with a linear threshold δL that depends on the definition of the halo (i.e. δL  1.59 for a nonlinear density contrast of 200). We show that a simple formula, which obeys this high-mass asymptotic and uses the fit obtained for Gaussian initial conditions, matches numerical simulations while keeping the mass function normalized to unity. Next, by deriving the real-space halo two-point correlation in the spirit of Kaiser (1984, ApJ, 284, L9) and taking a Fourier transform, we obtain good agreement with simulations for the correction to the halo bias, ΔbM(k,fNL), due to primordial non-Gaussianity. Therefore, neither the halo mass function nor the bias require an ad-hoc parameter q (such as δc
1.59 for a nonlinear density contrast of 200). We show that a simple formula, which obeys this high-mass asymptotic and uses the fit obtained for Gaussian initial conditions, matches numerical simulations while keeping the mass function normalized to unity. Next, by deriving the real-space halo two-point correlation in the spirit of Kaiser (1984, ApJ, 284, L9) and taking a Fourier transform, we obtain good agreement with simulations for the correction to the halo bias, ΔbM(k,fNL), due to primordial non-Gaussianity. Therefore, neither the halo mass function nor the bias require an ad-hoc parameter q (such as δc  δc
δc 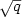 ), provided one uses the correct linear threshold δL and pays attention to halo displacements. The nonlinear real-space expression can be useful for checking that the “linearized” bias is a valid approximation. Moreover, it clearly shows how the
baryon acoustic oscillation at ~100 h-1 Mpc is amplified by the bias of massive halos and modified by primordial non-Gaussianity. On smaller scales, 30 < x < 90 h-1 Mpc, the correction to the real-space bias roughly scales as fNL bM(fNL = 0) x2. The low-k behavior of the halo bias does not imply a divergent real-space correlation, so that one does not need to introduce counterterms that depend on the survey size.
), provided one uses the correct linear threshold δL and pays attention to halo displacements. The nonlinear real-space expression can be useful for checking that the “linearized” bias is a valid approximation. Moreover, it clearly shows how the
baryon acoustic oscillation at ~100 h-1 Mpc is amplified by the bias of massive halos and modified by primordial non-Gaussianity. On smaller scales, 30 < x < 90 h-1 Mpc, the correction to the real-space bias roughly scales as fNL bM(fNL = 0) x2. The low-k behavior of the halo bias does not imply a divergent real-space correlation, so that one does not need to introduce counterterms that depend on the survey size.
Key words: gravitation / methods: analytical / large-scale structure of Universe
© ESO, 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


