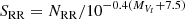EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A23 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A23
Number of page(s) 17
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/202141067
Published online 04 October 2021

© ESO 2021

1. Introduction

The main accepted galaxy formation paradigm predicts that galaxies grow hierarchically through mergers with other galaxies (e.g., Searle & Zinn 1978; White & Rees 1978), and thus the accretion of diffuse gas and dark matter occur especially into the halo. There are different types of mergers, but we can broadly distinguish major mergers from minor mergers, depending on the mass ratio of the two objects. In the first case, the masses of the two colliding galaxies are similar, while in the second case, a galaxy of lower mass is accreted onto a more massive galaxy. When a galaxy is observed, evidence of substructures and deviations from symmetry are clearly indicative of past or/and ongoing mergers. Clues can be detected within the galaxies themselves in different forms, such as streams, bridges, density waves, overdensities of stars, substructure in the galaxy gas, different globular cluster populations, and changes in kinematics. Proofs of merging events are found both in the Galaxy (Newberg et al. 2002; Belokurov et al. 2006; Martin et al. 2014) and in external galaxies (i.e., Einasto et al. 2012; Cohen et al. 2014; Abraham et al. 2018) such as the Andromeda galaxy (M31, Ibata et al. 2001). Therefore the history of our Milky Way (MW) is a history of accretion. At least seven past accretion events can be singled out: Kraken (Kruijssen et al. 2019, 2020), Sequoia, (Myeong et al. 2019), Sagittarius (Ibata et al. 1994), the Helmi stream (Helmi et al. 1999), and Gaia-Enceladus (Helmi et al. 2018), and both the Large and Small Magellanic Clouds (LMC and SMC) will infall toward the MW. We know that the Magellanic system is likely on its first passage around the MW (Kallivayalil et al. 2006, 2013; Besla et al. 2010).

The most representative example of a satellite galaxy that is accreted by our MW is the Sagittarius dwarf spheroidal galaxy (Sgr dSph). Discovered by Ibata et al. (1994), it is located behind the Galactic bulge at the heliocentric distance D ≈ 26.5 kpc (Monaco et al. 2004; Hamanowicz et al. 2016; Vasiliev & Belokurov 2020) and at about 6.5 kpc below the Galactic plane. The Sgr dSph represents an excellent laboratory because the tidal destruction process is still ongoing (Majewski et al. 2003; Law & Majewski 2010; Belokurov et al. 2014). The infall into the MW has been estimated to occur 8 ± 1.5 Gyr ago by Dierickx & Loeb (2017) and 9.3 ± 1.8 Gyr ago by Hughes et al. (2019). However, many questions about its formation and evolution before and after its accretion inside the Galactic halo still remain unanswered.

The mass of the Sgr progenitor and the present-day mass of the remnant are still topics of active discussion. The stellar mass of the main body is M* ∼ 2 × 107 M⊙ (Ibata et al. 2004) and the dynamical mass is Mdyn ∼ 2 × 108 M⊙ (Grcevich & Putman 2009). However, the subsequent census of its stellar content revealed that its total mass could be as high as 1011 M⊙ including its dark matter halo (Niederste-Ostholt et al. 2012; Laporte et al. 2018; Vasiliev & Belokurov 2020), indicating that this was a major merging process between our Galaxy and the Sgr dSph. Nevertheless, the accretion event of the progenitor of the Sgr dwarf was a minor merger with a mass ratio of 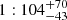. The accretion has occurred at z < 1, when the MW was already completely formed and its stellar mass was M > 1010 M⊙ (Kruijssen et al. 2020; see their Fig. 9).

Although this satellite appears to be quite elongated out to ∼100 kpc (Majewski et al. 2003; Law & Majewski 2010), its main body contains an overdensity of stars that is concentrated in its center, where the massive and metal-poor globular cluster NGC 6715 (M 54) is located. It is also coincident in position with the nucleus of the dwarf galaxy (e.g., Bassino & Muzzio 1995; Layden & Sarajedini 2000), although Bellazzini et al. (2008) have argued based on measurements of velocity dispersion profiles that M 54 is not the core of Sgr, but instead it may have formed independently and plunged to the core of Sagittarius as a result of dynamical friction. Although a large number of star clusters would be expected in these regions, only nine known and well-characterized GCs are associated with Sgr. In addition to NGC 6715, Arp 2, Terzan 7, and Terzan 8 are located in the main body, and Palomar 12, Whiting 1, NGC 2419, NGC 4147, and NGC 5634 are situated in the extended tidal streams (Bellazzini et al. 2020). We may expect that stars and globular clusters in the stream exhibit a different age-metallicity relation (AMR) to those formed in the central galaxy (Forbes & Bridges 2010; Leaman et al. 2013; Kruijssen et al. 2019). The stellar population appears to be divided into three groups. It is dominated by a metal-rich and intermediate-age ([Fe/H]= − 0.4 to −0.7 dex, t = 5 to 8 Gyr; e.g., Layden & Sarajedini 2000; Bellazzini et al. 2006) population in the central part of the galaxy. Additionally, indications of a young metal-rich population ([Fe/H]= − 0.4 and t = 2.5 Gyr) have been found that also includes stars of solar abundance (e.g., Monaco et al. 2005; Chou et al. 2007). On the other hand, an old and metal-poor (t = 10–13 Gyr, [Fe/H] ∼ − 2.2; Momany et al. 2005) counterpart also exists.

In addition, Mucciarelli et al. (2017) analyzed 235 giant stars and detected a metallicity gradient within the Sgr nucleus. They found two peaks of the metal-rich population, indicating that the stars in the metal-rich component formed outside in more than a few billion years with [Fe/H]= − 0.58 (38 ≤ R ≤ 70 kpc). Each subsequent generation of stars was more centrally concentrated, with [Fe/H]= − 0.38 (R ≤ 19 kpc). The authors also reported that some memory of its formation may still be detectable because the stellar population is not dynamically mixed. They also suggested that Sgr was affected by a strong gas loss that occurred 7.5 Gyr to 2.5 Gyr ago, presumably starting at the first peri-Galactic passage of the dwarf after its infall into the MW.

In all cases, it is crucial to complete the census of the GC systems in the Sgr dSph in order to set formation and evolution constrains. The first step was made by Minniti et al. (2021b), who identified 23 GC candidates that may belong to the Sgr dSph. They used the VISTA Variables in the Via Lactea Extended (VVVX) survey, and confirmed based on their further analysis that 12 of them are bona fide members. Additionally, Minniti et al. (2021a) later discovered 18 more GCs that might belong to the Sgr galaxy; 8 of them were confirmed as bona fide members. In both papers (hereafter M21, for simplicity), physical parameters such as reddening, extinction, and distance for each cluster were estimated. In this follow-up paper, we calculate other important parameters: metallicities and luminosities, and where possible, we give a rough estimate of the ages so that the AMR can be explored.

In Sect. 2 we briefly describe the observational data. In Sect. 3 we explain the methods we used to estimate the physical parameters and the resulting values for each Sgr GC. In Sect. 4 we focus on the RR Lyrae stars in the Sgr GC system. In Sect. 5 we show the metallicity distribution (MD) and luminosity function (LF) for all the GCs in the Sgr dSph, including the two new detections from M21 and previously known GCs, and we compare these distributions with the MD and LF of the MW, M31, and LMC. In Sect. 6 we provide a summary and conclusions.

2. Observational datasets: VVVX, 2MASS, and Gaia EDR3

We used the deep near-infrared (NIR) data from the VVV (Minniti et al. 2010; Saito et al. 2012) and VVVX (Minniti 2018) surveys, acquired with the VISTA InfraRed CAMera (VIRCAM) at the 4.1m wide-field Visible and Infrared Survey Telescope for Astronomy (VISTA; Emerson & Sutherland 2010) at the ESO Paranal Observatory. The VVV and VVVX data are reduced at the Cambridge Astronomical Survey Unit (CASU; Irwin et al. 2004), and further processing and archiving is performed with the VISTA Data Flow System (VDFS; Cross et al. 2012) by the Wide-Field Astronomy Unit and is made available at the VISTA Science Archive and ESO Archive. In our analysis, we used a preliminar version of the VVVX photometric catalog (Alonso-García et al., in prep.), which extracts the point-spread function (PSF) photometry from the VDFS-reduced images. To build this photometric catalog, an analysis similar to that described in Alonso-García et al. (2018) for the VVV original footprint was followed. In order to increase the dynamic range of our NIR photometry, we merged1 our deep VVVX photometry with the fainter catalogs from the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006). In this way, we are able to also provide accurate photometry for bright stars (Ks < 11 mag) that are saturated in the VVVX images. We also used the Ks-band photometry from McDonald et al. (2013) and McDonald et al. (2014) for Minni327 alone, which is located outside the VVVX area. On the other hand, we used the recent optical photometry from the Gaia Early Data Release 3 (EDR3; Gaia Collaboration 2021) in order to take advantage of the more precise astrometry and proper motions (PM), which were employed especially in the first part of the work (M21) to distinguish the nature of the candidates and the inclusion into the Sgr galaxy. By matching the Gaia EDR3 and VVVX datasets, we here construct optical and NIR color-magnitude diagrams (CMDs) in order to obtain the metallicity, age, and luminosity for each target.

3. Estimation of parameters for the new Sgr GCs

We focus on the 21 GCs that are recognized as confirmed Sgr members in M21. We list them and summarize their main physical properties in Table 1.

Table 1.

Position, metallicity, age, luminosity, mass-to-light ratio, mass, and specific frequency of RR Lyrae stars for all new Sgr GCs we analyzed.

Along the line of sight to the Sgr dwarf galaxy, high contamination from the nearby MW disk and from the more distant bulge field stars may represent an obstacle, but M21 applied a PM decontamination procedure that allows us to work on clean catalogs. To summarize, M21 performed two tests in order to estimate the statistical significance of the stellar overdensities in the Sgr main body. First, following the procedure of Koposov et al. (2007), they calculated the number of stars in excess with respect to the background field, whose random fluctuations were assumed to be Poissonian. After this, they compared that excess with the statistical error on the background number counts, and finally, they revealed the cluster detection when the significance exceeded 3σ. The second method concerns the variation of the background. In this case, M21 computed the number counts of sources included within several adjacent circles (r < 3′) around a wider area from each cluster center coordinate. Subsequently, they calculated the standard deviation of the distribution of these number counts to derive the signal-to-noise ratio and considered as significant all candidate GCs with detections higher than 3σ.

Our main goals are to derive reliable values of metallicity, age, and luminosity for an updated LF and a MD for this satellite galaxy. First, we built the optical and NIR CMDs for all the GCs in our sample (Fig. A.1), confirming that our targets are not bulge GCs, which should be ∼2.5 magnitudes brighter in the mean, as demonstrated by previous works (Minniti et al. 2010, 2017a,b, 2018; Palma et al. 2019; Garro et al. 2021). Additionally, we compared the Sgr GCs and bulge fields CMDs. To summarize, we first selected five bulge fields at the same latitude but ∼7° away from the Sgr main body. As done for our objects, we constructed the Gaia-VVVX catalogs, properly decontaminated by applying parallax and PM cuts. Figure 1 shows the comparison between these five bulge fields and Minni332 (taken as representative of the Sgr GCs) CMDs. This proves that the Sgr GCs shown in Fig. A.1 are not affected by the bulge population, and it clearly demonstrates that the Sgr GCs we investigated are not bulge GCs.

thumbnail Fig. 1.

Comparison between the Gaia EDR3 optical CMDs of Minni332, taken as representative of the Sgr GCs (Minniti et al. 2021a), and five bulge fields located at similar latitudes, but away from the Sgr main body.

Following the same strategy as Garro et al. (2020, 2021), we preferred the isochrone-fitting method in order to obtain robust results. We favored the PARSEC alpha-enriched isochrones (Bressan et al. 2012; Marigo et al. 2017), and adopted the reddening, extinction, and distance modulus values that were previously calculated by M21. Briefly, M21 derived appropriate reddening corrections using the maps of Schlafly & Finkbeiner (2011) and adopting the following relations for the extinctions and reddenings: AKs = 0.11 × AV, AKs = 0.72 × E(J − Ks), AG = 0.79 × AV and AG = 2.0 × E(BP − RP). M21 obtained a fairly uniform reddening. Additionally, M21 employed the RC absolute magnitudes and intrinsic color by Ruiz-Dern et al. (2018) in order to compute distances for each individual cluster. Thereafter, we fit in particular the position of RC, BHB, and brighter stars. The best-fitting age and metallicity were obtained by comparing our data with isochrones generated with different ages and metallicities and by selecting the best fit by eye. We first fixed the age and varied the metallicity. Then we fixed the metallicity and searched for the best-fitting age. The variations in age and metallicity have different effects in the evolutionary stages. Changing the metallicity affects the RGB and the RC particularly strongly, and conversely, changes in ages modify the position of the MS-TO regions. In this way, we assigned an error to age and metallicity by simultaneously changing the metallicity and age values until the fitting isochrones did not reproduce all evolutionary sequences in the optical and NIR CMDs.

We find 17 metal-rich GCs, specifically, 10 with [Fe/H]= − 0.3 to −0.5 dex and 7 with [Fe/H] between −0.6 and −0.9 dex. Another 4 GCs are metal poor with [Fe/H]= − 1.1 to −2.0 dex. Inspecting the luminosity function for each GC (Fig. A.2), we singled out the RC as a peak in the histogram. This confirms that the stellar population is metal rich. To provide some examples, we appreciate a clear excess in the histograms of Minni324, 330, 340, 342, and 344. Moreover, metal-poor clusters show blue horizontal branch stars (BHBs) as well as RR Lyrae variable stars (Sect. 4), for instance, Minni01, 147, and 335.

Using the same method, we tried to derive the age, but the absolute estimate of this parameter is a challenge when the magnitude of the main sequence turn-off (MSTO) is below the detection limit. However, a variety of works (e.g., Rosenberg et al. 1999; Gratton et al. 2003) have adopted a relative age determination (instead of absolute ages) from the observable CMDs, although this is less accurate. We can therefore obtain a solid lower limit for the age because the differences are ΔKs(HB-MSTO) > 1.80 mag and ΔG(HB-MSTO) > 3 mag, meaning that the clusters are not young, with an age ≳ 7 Gyr. This could be improved upon by measuring the extension of the giant branch because bright and red stars in an extended AGB are indicative of an intermediate-age system (e.g., Freedman et al. 2020, and references therein). Even so, it is hard to distinguish AGB stars from RGB stars in sparse CMDs like this. In addition, for the clusters containing RR Lyrae, a more stringent age limit can be derived from the typical ages of these variable stars, which are older than about 10 Gyr (see Sect 4).

Taking the lower limit found for the age and the RR Lyrae cluster membership into account, but also comparing our clusters with known Sgr GCs and their observable CMDs, we obtain more constrained ages for Minni 01, 146, 148, 147, 148, 311, 326, 330, 335, 338, and 343, and we find that all of them are old GCs. Additionally, we note that Minni 144, 145, 324, 325, 328, 329, 332, 340, 341, 342, and 344 are intermediate or old globular clusters with an age t > 8 Gyr. This shows that deeper observations are necessary to better constrain the ages of these GCs.

It is well known that the position and the morphology of the RGB in the CMD strongly depend on the metal content of the stellar population: the higher the metal content, the cooler the effective temperature Teff and the redder the RGB stars (e.g., Ferraro et al. 2000; Valenti et al. 2005). Therefore a series of empirical parameters (i.e., RGB colors at a fixed level of magnitude, RGB magnitude at a fixed color, and the RGB slope) can be used to derive a photometric estimate of the global metallicity of the considered stellar population. We preferred using the slopeRGB as another independent method to constrain our metallicity estimates. Specifically, we adopted the slopeRGB − [Fe/H] linear relation by Cohen et al. (2015) in the NIR passband. We derived the RGB slope as the line connecting two points along the RGB at the HB level and ∼2.5 mag brighter. The resulting values are listed in Table 1 (Cols. 9 and 10) and agree very well with those derived through isochrone-fitting.

Finally, we estimated the total luminosity MKs of all the GCs in our sample. Certainly, the total luminosity varies from GC to GC because it depends on several factors, such as the luminosity of the brightest stars, the distribution of members along the isochrones, and the presence or absence of red giants. We first measured the flux for each star and consequently the total flux for the target, and derived the absolute magnitude by converting the total flux. All resulting MKs are listed in Table 1. We also derived the equivalent absolute magnitude in V band, assuming that the mean (V − Ks) = 2.5 ± 0.5 mag for observed GCs in systems such as the MW and M31 (e.g., Barmby et al. 2000; Cohen et al. 2007; Conroy & Gunn 2010). Although this could be a rough approximation, studies (e.g., Pessev et al. 2008) have demonstrated that the smallest spread in intrinsic colors is found for clusters with ages ≳10 Gyr, whereas the larger spread in color is found for clusters in the age range 2 − 4 Gyr. On the other hand, comparing the intrinsic color with the M31 GC system, Wang et al. (2014) found a good correlation between (V − Ks) and metallicity (with a mean value ∼2.5), even if the relation shows a notable departure from linearity with a shallower slope toward the redder end ([Fe/H] ≳ − 0.1). Additionally, the V-band total luminosities should be trusted only to 1 − 1.5 mag, which is the scatter in this mean integrated color. A mean (V − Ks) = 2.5 therefore is an acceptable compromise for our targets.

These luminosities when calculated in this way are an underestimate of the total luminosity because the faintest stars are missing. However, Kharchenko et al. (2016) analyzed MW star clusters and noted that the cluster luminosity profiles show similar features, such as a relatively fast rise in the luminosity at small ΔKs2 owing to the dominant contribution of a few bright stars and a much slower increase when successively fainter stars were included. As a rule, the first 10–12 brighter members accumulate more than half of the integrated luminosity of a cluster; this no longer changes at ΔKs > 10.

Consequently, we derived the total luminosity in V-band (MVtot) by comparing our GC luminosities with other known GCs with similar metallicity in order to estimate the fraction of the luminosity that comes from low-mass stars. We explain the main steps we computed to estimate the total luminosity for each Sgr GCs in Appendix A.

We find that all new Sgr GCs are low-luminosity objects, at least ∼1.3 mag less luminous than the MW GC luminosity function peak (MV = ( − 7.4 ± 0.2) mag from Harris 1991; Ashman & Zepf 1998).

After we obtained the absolute magnitudes in Ks- and V-bands, we were able to estimate their masses. We first assumed a typical GC mass-to-light ratio M/LK ≈ 1, equivalent to M/LV ≈ 2 (Haghi et al. 2017; Baumgardt et al. 2020). Subsequently, because Haghi et al. (2017) reported the M/L−[Fe/H] relations (see their Fig. 2), we derived the M/L values, depending on our metallicity estimates, in order to obtain more rigorous results. In both cases, we find low-mass GCs with the same order of magnitude M ≈ 103 to 104 M⊙ (see Table 1). Additionally, we calculated the mass for each known Sgr GC listed in Table 2, finding a good agreement between our values and those listed in the Galactic Globular Cluster Database version 23 by Hilker et al. (2020). Clearly, the difference is due to the large scatter in the Haghi relations (Δ(M/LK)≈ ± 0.5 and Δ(M/LV)≈ ± 1.0).

Table 2.

Position, metallicity, age, luminosity and mass for the previously known Sgr GCs, used for comparison.

All these parameters are summarized in Table 1. We also mark with an asterisk all GCs that do not show well-populated RGBs because they could have less accurate parameters. However, we include them in our analysis because they have no effect on the final results.

4. RR Lyrae stars in the Sgr GC system

RR Lyrae stars are usually excellent tracers of metal-poor and old populations in the MW. M21 searched for these stars within 3′ and 10′ from the cluster centers. As expected, they found an excess of RR Lyrae in some metal-poor GCs, such as in Minni01 (N3′ = 1; N10′ = 3), Minni147 (N3′ = 1; N10′ = 6), and Minni335 (N3′ = 4; N10′ = 12). We assume that these variable stars are also present in GCs with intermediate metallicity, such as Minni144 (N3′ = 1; N10′ = 7), Minni145 (N3′ = 5; N10′ = 14), and Minni343 (N3′ = 3; N10′ = 13). Depending on the traditional stellar evolutionary theory, however, we do not expect many RR Lyrae stars in metal-rich GCs. However, a few metal-rich GCs in the Sgr dwarf show more RR Lyrae within 10′ from the cluster center: Minni148 (N3′ = 3; N10′ = 20), Minni324 (N3′ = 2; N10′ = 9), Minni326 (N3′ = 3; N10′ = 17), Minni328 (N3′ = 1; N10′ = 9), Minni330 (N3′ = 1; N10′ = 11), Minni332 (N3′ = 1; N10′ = 7), Minni340 (N3′ = 2; N10′ = 22), Minni341 (N3′ = 2; N10′ = 11), Minni342 (N3′ = 1; N10′ = 5), Minni343 (N3′ = 3; N10′ = 13), and Minni344 (N3′ = 1; N10′ = 15).

Even though this may appear to be an inconsistency, varied observational evidence has shown RR Lyrae stars also in some metal-rich GCs, such as NGC 6388 ([Fe/H]= − 0.44), NGC 6441 ([Fe/H]= − 0.46 – Pritzl et al. 2002; Clementini et al. 2005), NGC 6440 ([Fe/H]= − 0.36), and Patchick 99 ([Fe/H]= − 0.20 – Garro et al. 2021).

We also computed the specific frequency of RR Lyrae stars in the Sgr GCs. Suntzeff et al. (1991) defined the specific frequency of RR Lyrae stars SRR as the number of RR Lyrae stars NRR per unit luminosity, normalized to a typical Galactic globular cluster luminosity of MVt = −7.5 mag,

(1)

(following the notation of Harris 1996). Using the V-band total luminosities and considering the RR Lyrae stars within 3 arcmin, we find 4 ≲ SRR ≲ 87 for the Sgr GCs. They are also faint GCs and it is therefore expected that there are low number statistics. We note that SRR are lower limits because we did not include information about detection completeness or counted the candidate variable stars. On the other hand, in calculating SRR we normalized the NRR values to full cluster luminosities. Accounting for this effect is not trivial because we do not know the spatial distribution of RR Lyrae stars in any cluster, and because we imaged the center of each cluster, we expect the NRR to be 80–90% complete. This means that the SRR values may be 10–20% higher than quoted above. Therefore the determination of these quite reliable SRR allows us to give a lower age limit of age ∼ 10 Gyr for all clusters with SRR > 0. However, the absence of RR Lyrae stars does not necessary imply young ages because RR Lyrae are uncommon in metal-rich GCs, for example.

At this point, we compare the MW from the 2010 compilation of the Harris (1996) catalog. This catalog contains only 4 of the ∼150 Galactic GCs as having SRR > 60, and only 2 of these have SRR > 100. The highest value is reported for Palomar 13, SRR = 127.5. According to this and given our sample incompleteness, it is very likely that the Sgr dwarf galaxy has an SRR greater than this. It is certainly intriguing that only a tiny fraction of Galactic GCs have very high SRR as well as these Sgr GCs because we find only one GC with SRR > 60 (Minni145), and none with SRR > 100. This may suggest that Sgr GCs follow a similar trend as MW GCs.

5. Discussion

In the next sections, we highlight the main differences between the GCs within the Sgr dSph itself by comparing the resulting values for the newly discovered GCs (Table 1) and the well-known Sgr GCs (Table 2). However, we also wish to broaden the discussion by making the first comparison between the Sgr GC system and the GC system of neighboring galaxies: the MW, M31, and LMC.

5.1. Sagittarius globular cluster system

According to Bellazzini et al. (2020), at least nine GCs are associated with the Sgr stream: four clusters in the Sgr remnant, NGC 6715, Terzan 7, Terzan 8, Arp 2; two clusters in the trailing arm, Palomar 12 and Whiting 1; and three clusters that are likely associated with an old arm, NGC 2419, NGC 1447, and NGC 5634. Also Berkeley 29 an Saurer 1, two younger clusters that originally were associated with the Sgr tidal extension, have now been discarded using the improved Gaia EDR3 PMs (Gaia Collaboration 2021). M21 increased the number of GCs in the Sgr system. Hence, these discoveries pave the way to multiple studies on the understanding of Sgr dwarf itself, on the chemistry and dynamics of these systems, especially when compared with other GC systems, and they can also help to guide theoretical studies and simulations (e.g., Vasiliev et al. 2021; Vasiliev & Baumgardt 2021).

We find that the main body of the Sgr galaxy is mainly a metal-rich component, as shown in Fig. 2. Figure 3 shows the relation between the distance to the Sgr center and the metallicity of its GCs, which ranges from NGC 6715 (which coincides with the Sgr nucleus) to the most distant GC NGC 2419. We note that except for NGC 6715, which is metal poor, the metallicity is −0.3 > [Fe/H]>  − 0.9 in the innermost regions (R < 0.6 kpc), whereas between R ≈ 0.6 kpc and 40 kpc, there are both metal-rich (with the same metallicity range as the inner part) and metal-poor GCs, with −1.1 > [Fe/H]>  − 2.3. The spread in the MD of Sgr GCs appears to suggest that the Sgr dSph had an extended star formation history and therefore now contains high-metallicity clusters (Hughes et al. 2019). It appears that a metallicity gradient might be indicated because we do not find metal-poor GCs in the innermost regions, but we cannot conclude with high certainty that this occurs in the main body of Sgr dSph. The star cluster formation in the Sgr galaxy probably occurred in two different episodes. The AMR diagram (Fig. 4) shows that metal-poor GCs represent the old component with an average age ∼13 Gyr, while the metal-rich GCs span a wider range of ages from younger with t ∼ 7 − 8 Gyr to older with t ∼ 10 − 14 Gyr. This result also qualitatively agrees with the Sgr star formation history by Hasselquist et al. (in prep.), as they demonstrated that Sgr formed its metal-rich (−0.9 < [Fe/H]<  − 0.3) GCs some 6–8 Gyr ago. However, we can only speculate on the probable formation of these clusters because the epoch of accretion of the Sgr dwarf is largely uncertain and our GC ages are approximate: the older objects could be formed in situ within the Sgr progenitor and may consequently have been accreted onto the MW, whereas the younger ones can be the result of the merging event with the MW. This could be distorted because when a satellite galaxy infalls into the main galaxy halo, a subsequent gas stripping leads to a truncation of the GC formation in the smaller galaxy. However, there is evidence that some galaxies (i.e., LMC and SMC) continue to form clusters after they have entered the halo of the main galaxy. Additionally, Hughes et al. (2019) used the E-MOSAIC simulation and reported that more massive galaxies can continue to form GCs longer after entering the halo of the main galaxy. Many of the satellite galaxies in this population produce streams because the galaxies were accreted later, and so the streams survive until the present day. More massive streams host younger and more metal-rich GCs.

thumbnail Fig. 2.

Latitude vs. longitude map depicting the position of Sgr GCs in the main body. The colored points highlight the cluster metallicity. Red shows GCs with [Fe/H] ≥ − 0.5, orange shows GCs with −1.0 ≤ [Fe/H] ≤ − 0.6, and blue shows GCs with [Fe/H] ≤ − 1.1 for our convention. We included NGC 6715, Terzan 7, Terzan 8, and Arp 2 for comparison.

thumbnail Fig. 3.

Radial dependence of the metallicity for Sgr GCs. We consider the projected distance from the center of Sgr, adopting D = 26.5 kpc for this galaxy. The newly discovered Sgr GCs are marked with black points, and the known Sgr GCs are represented as red diamonds.

Although our age estimates are rough and we need deeper observations in order to reach the MSTO, Fig. 4 can help us to broadly reconstruct the formation history of the Sgr galaxy. We find similarities with the AMR shown in Massari et al. (2019) and Forbes (2020). Both these works assumed a leaky-box age-metallicity relation4. We reproduce in Fig. 4 the best-fit halo AMR found by Forbes (2020). We note that the Forbes fit follows the red diamonds, which represent the known Sgr GCs, whereas the newly discovered ones are located above that best fit. On the other hand, we also compared the Sgr AMR with those of the MW and LMC, as shown in Fig. 4. We appreciate that the Sgr AMR looks more like the MW (Leaman et al. 2013; Horta et al. 2021), whereas the halo AMR by Forbes (2020) shows a similar trend as the LMC AMR by Horta et al. (2021). It is important to note that when Horta et al. (2021) compared the AMR of massive clusters for the LMC sample, they argued that the AMR for the satellite galaxies is systematically higher than that for the MW, as expected from mass assembly bias. Investigating the origin of this bias, they found that the origin of the AMR trend in the stellar populations is a function of the galaxy mass. This means that higher-mass galaxies undergo more rapid enrichments because they retain the supernovae ejecta, and this consequently leads to a rapid enrichment of the interstellar medium (ISM). Instead, lower-mass galaxies grow more slowly over time because their potential wells are not deep enough and a large fraction of the SNe ejecta and stellar mass are lost, leading to a slower metal-enrichment process. Therefore this appears to indicate that the Sgr progenitor was not a small galaxy, on the contrary, it was massive enough to retain the stellar mass loss to quickly enrich its ISM.

thumbnail Fig. 4.

Age-metallicity relation for the Sgr GC system. The newly discovered Sgr GCs are marked with black points, and the known Sgr GCs are represented as red diamonds. In the top panel, the green line reproduces the AMR for the MW halo GCs shown in Forbes (2020, see their Fig. 3). In the bottom panel, the solid lines reproduce the median star cluster AMR relation for the LMC (orange) and Milky Way-mass (black) galaxies in the E-MOSAICS simulations by Horta et al. (2021, see their Fig. 3).

5.2. Metallicity distribution

The MD can provide important clues to the process and conditions relevant to galaxy formation. Therefore a comparison with other systems can open a wider view.

For these purposes, we built the MD for the Sgr GC system as shown in Fig. 5. We note two separate peaks, one metal-rich peak at dex, and a second metal-poor peak at dex. Additionally, we constructed the MD for the MW GC system based on the 2010 compilation of the McMaster Milky Way Globular Cluster catalog, Harris (1996), including 157 GCs. We also included the M31 GC system, which contains 504 GCs, by Fan et al. (2008). Finally, we also considered the LMC satellite galaxy, but in this case, we did not find a complete catalog, so we preferred to create it ourselves (by referring to Mackey & Gilmore 2004; McLaughlin & van der Marel 2005; Lyubenova et al. 2010; Colucci et al. 2011; Noël et al. 2013; Jeon et al. 2014; Wagner-Kaiser et al. 2017; Piatti & Koch 2018; Piatti et al. 2019; Horta et al. 2021). We selected 41 LMC GCs that are listed in Table 3. The table summarizes the cluster ID, observed V magnitude, reddening, metallicity, age, absolute magnitude in V-band, and references. Although many additional star clusters were cataloged by Palma et al. (2016), we did not consider them because most of these objects are very young and have a mean metallicity value of ∼ − 0.3 dex. Moreover, they have not been clearly categorized as open or globular clusters.

thumbnail Fig. 5.

Sagittarius metallicity distribution (top panel) and luminosity function (bottom panel), including the new and known GCs.

Table 3.

Properties of the LMC GCs used for comparison.

Figure 6 shows the MD for each sample, the Sgr, MW, M31, and the LMC. We find that each MD shows a Gaussian-like distribution. Especially a bimodal MD is shown for the Andromeda and MW galaxies, with the metal-poor peaks at dex and dex and metal-rich peaks at dex and dex, respectively. In contrast, we find a double-peaked distribution for the LMC with dex and dex. We expected a bimodal MD because this is a typical feature of all GC systems (e.g., Ashman & Zepf 1992).

thumbnail Fig. 6.

Metallicity distribution for Sgr (black histogram), MW (blue histogram), M31 (green histogram), and the LMC (magenta histogram) GC systems (in the left panel). We also show separately the Sgr and LMC metallicity distributions (in the right panel) as a zoomed plot of the left panel, and the middle panel highlights the Sgr MD. The histograms are constructed adopting a bin size of 0.2 dex.

The comparisons between these galaxies show differences. First, there are fewer metal-poor Sgr GCs than in the LMC, while the number is similar when only metal-rich populations are considered. On the other hand, the Sgr MD appears to follow both the MW and M31 MDs. In particular, the Sgr metal-rich GCs look more like the MW bulge GCs and also show a similarly wide age range. In contrast to the LMC, all the metal-rich GCs in the Sgr dwarf are therefore relatively old (age > 6 Gyr). This is consistent with the hypothesis that the Sgr GCs formed after infalling into the MW halo, and thus the progenitor satellite was gas rich, in accordance with what is shown in Fig. 4. Kruijssen et al. (2011) found based on numerical simulations of isolated and merging disk galaxies that the star clusters that survive the merger and populate the merger remnants are typically formed at the moments of the pericenter passage, namely slightly before the starbursts that occur during a galaxy merger. These clusters constitute a large fraction (30 − 60% per pericenter passage) of the survivors. They survived for two reasons: first, they are formed before the peak of the starbust, and second, the clusters that formed during the pericenter passage are ejected into the stellar halo, where the disruption rate is low and the survival chance is high. However, the clusters that are produced in the central regions during the peak of the starburst are short-lived and disrupt before they can migrate to the halo.

5.3. Luminosity function

The brightness distribution of the GCs, known as the globular cluster luminosity function (GCLF), is an important tool that can be used as a distance indicator as well as to constrain the theories on the formation and evolution of GCs (e.g., De Grijs et al. 2005; Nantais et al. 2006; Rejkuba 2012), and more precisely, to predict the dynamical processes that act in the destruction of GCs, especially when merging events between galaxies are involved. The main dynamical processes that can destroy GCs are (i) the mass loss due to the stellar evolution (i.e., supernova explosions, Lamers et al. 2010), (ii) dynamical friction (Alessandrini et al. 2014), (iii) tidal shock heating by passages through the bulge or disk (Gnedin & Ostriker 1997; Piatti & Carballo-Bello 2020), and (iv) evaporation due to two-body relaxation (Madrid et al. 2017). All of these processes, especially the last two, can change the luminosity distribution.

Many works (Rejkuba 2012, and references therein) have demonstrated that the GCLF is not a Gaussian distribution, nor there is a universal distribution in most galaxies (Huxor et al. 2014). Although the Gaussian fit is a useful parameterization (especially at the brighter end), its use has no physical motivation. The shape of the GCLF deviates from the Gaussian symmetric distribution for the MW as well as for the external galaxies because it shows a longer tail toward the faint end. This asymmetry is strongly related to the dynamical evolution of the initial cluster luminosity function, which is well approximated by power laws of the form dN(L)/dL ∝ Lα, with slopes in the range −2.4 ≲ α ≲ −2.0, as found by Larsen (2002), for example. Another reason that might explain why the GCLF deviates from the symmetry might also be the mass function because mass and luminosity are related parameters in GCs. It is therefore expected that as dynamic evolution modifies the GCLF, it also has an effect on the mass function (e.g., Fall & Zhang 2001). We suggest that many inconclusive objects, defined as such by M21 because they require additional data for confirmation or rejection (Minni02, 03, 04, 312, and 313, to name just a few), might be widespread or dissolute GCs.

Following the same line as for the MD, we compare the Sgr GCLF with the MW, M31, and LMC GCLFs.

We briefly describe the method we used to obtain reliable absolute magnitudes for the GCs in each sample. We derived the absolute magnitude in V-band for our Sgr GCs as explained in Sect. 3 and shown in Table 1, and we used the luminosities for the known Sgr GCs, shown in Table 2. Figure 5 depicts the final Sgr GCLF. This is a unimodal distribution, which exhibits a prominent peak at 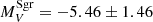mag and shows a tail toward the brighter end.

To build the MW GCLF, we adopted the MV values from the 2010 compilation of the Harris (1996) catalog. For the LMC GCLF, we again used our LMC catalog with 41 GCs (Table 3), for which we also recovered the V magnitudes and color excess E(B − V) in addition to the metallicities. We adopted the LMC distance modulus (m − M)0 = 18.56 mag from Di Benedetto (2008). For the M31 GCLF, we preferred a more complete catalog: the Revised Bologna Catalogue (RBC, V.5, August 2012 – Galleti et al. 2006, 2014) of M31 globular clusters and candidates. This catalog includes 2,060 objects, but we selected the 625 confirmed GCs (flag = 1) with optical photometry. For M31 we used a distance modulus (m − M)0 = 24.47 mag (McConnachie et al. 2005). At this point, we are able to calculate the absolute magnitude in V-band for the LMC and M31 GC system by applying the same method as for Sgr GCs (Sect. 3).

After we obtained the GC luminosities, we built the luminosity function for each sample, thus comparing these galaxies.

Figure 7 clearly shows a double-peaked M31 GCLF with the fainter peak at 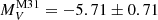mag and the brighter peak at 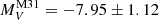mag. A less pronounced double-peaked is notable for the MW GCLF, which is shifted by ∼0.5 mag toward fainter luminosities with respect to that of M31 because the fainter peak is at 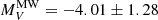mag and the brighter peak is at 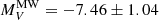mag. On the other hand, we find that the LMC GCLF is a unimodal distribution peaked at 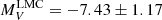mag, based on a sample with 38 GCs for which we recovered both V magnitudes and reddening values.

thumbnail Fig. 7.

Luminosity function for Sgr (black histogram), MW (blue histogram), M31 (green histogram), and the LMC (magenta histogram) GC systems (in the left panel). We also show separately the Sgr and LMC luminosity functions (in the right panel) as a zoomed plot of the left panel, and we use the middle panel to highlight the Sgr LF. The histograms are constructed considering a bin size of 0.5 mag.

A plausible reason for the observed double-peaked GCLFs in the MW and M31 might be that many GCs have been accreted by the Andromeda halo as well as by the MW halo (Peacock et al. 2010; Huxor et al. 2014). This scenario is additionally support when the Sgr GC system is included, for which the LF shows a fainter peak. More generally, Mackey & Van Den Bergh (2005) found a similar fainter peak in the GCLF of the young halo GCs of the MW, which they argued are most likely accreted objects. Therefore this appears to indicate that accreted Sgr GCs have survived disruption processes deriving from the merging event, and the GCs that we see today are the remnants of more massive objects or the final products of the accretion. However, we note that the faint Sgr clusters are relatively more numerous than their MW counterparts. Therefore this can indicate dynamical evolution, such as more efficient destruction in the larger galaxies, or incompleteness at the fainter peak, because we did not include many of the low-luminosity Galactic GCs that were recently discovered, nor did we consider that many more faint objects are still to be found.

Finally, the actual LMC LF may be more complex than the one we show in Fig. 7 because there is evidence for very complex and still ongoing star formation activity (Bruzual & Charlot 2003). However, based on our data, the LMC MV GCLF peak is brighter than the Sgr GCLF peak. This appears to suggest that the LMC forms more massive clusters or that the dynamical processes in the LMC are different than those undergone by the Sgr dwarf galaxy. However, this might also be because our results are incomplete, or because the LMC is generally younger than the Sgr dSph.

6. Summary and conclusions

We analyzed the new 21 GCs that were recently discovered by M21 in the main body of the Sgr dwarf galaxy. We built their optical Gaia EDR3 and NIR VVVX CMDs and proceeded to fit isochrone models in order to derive suitable values for their metallicities and ages. We confirmed our metallicity estimates using an independent method (slopeRGB − [Fe/H] relation by Cohen et al. 2015). Furthermore, we also calculated for each target the total luminosity in the Ks and V bands, finding all of them to be faint (MV > −6.2) clusters.

After the metallicities and luminosities were obtained, we were able to build the MD and the LF for the Sgr GC system (including the new GCs discovered by M21 and the previously known GCs associated with the Sgr dwarf) for the first time. We find that the main body of Sgr prevalently contains a metal-rich component. However, both metal-poor and metal-rich GCs are found, with very different ages: metal-poor GCs are old with t ∼ 13 Gyr, whereas metal-rich GCs show a wider age range from 7 − 8 Gyr up to 10 − 13 Gyr. Our age estimates are not very accurate because the MSTO for the GCs in our sample is below our detection limit, but we derived minimum ages assigning an age > 10 Gyr for the GCs with SRR > 0, and also a lower limit of ∼7 Gyr (derived from ΔKs(HB-MSTO) for all GCs with SRR = 0. We did not detect a metallicity gradient, but we find that the innermost regions (R < 0.6 kpc) show GCs with metallicities of ∼ − 0.5 dex, while between 0.6 and 40 kpc from the Sgr nucleus, we can find both metal-rich and metal-poor populations. We compared our results with the MD and GCLF of other galaxies: the MW, the Andromeda galaxy and the LMC, thus placing constraints on the formation and evolution of the Sgr dwarf galaxy. Based on this comparison, we suggest that the Sgr progenitor could have been a gas-rich galaxy, and that this gas was retained and subsequently converted into GCs during the infall into the MW halo. Many GCs survived the main dynamical processes (i.e., tidal shocks and two-body relaxation process), probably because they were formed before the main star formation burst and were pulled toward the halo, where these processes are less efficient. If this mechanism occurred, some of the inconclusive objects detected in the main body of Sgr by M21 might be dissolved GCs associated with the Sgr dwarf. Additionally, when we compare the GCLFs, since the Sgr distribution peaks at lower luminosities (MV ≈ −5.5 mag) than all other samples, we can conclude that the dynamical processes that destroy GCs are more efficient in larger galaxies than in smaller ones, or that many faint GCs are missed in our compilations.

1

To merge the catalogs, we first transformed the VVVX catalogs, which are in the VISTA magnitude system, into the 2MASS magnitude scale by applying the recipe from http://casu.ast.cam.ac.uk/surveys-projects/vista/technical/photometric-properties

2

Kharchenko et al. (2016) defined ΔKs as the magnitude difference between a given cluster member and the brightest cluster member.

4

The form of the age-metallicity relation used by Forbes (2020) is [Fe/H]= − p ln(t/tf), where p is the effective yield of the system, and tf is the lookback time when the system first formed from unenriched gas.

Acknowledgments

We gratefully acknowledge the use of data from the ESO Public Survey program IDs 179.B-2002 and 198.B-2004 taken with the VISTA telescope and data products from the Cambridge Astronomical Survey Unit. E.R.G. acknowledges support from an UNAB PhD scholarship and ANID PhD scholarship No. 21210330. D. M. acknowledges support by the BASAL Center for Astrophysics and Associated Technologies (CATA) through grant AFB 170002. J. A.-G. acknowledges support from Fondecyt Regular 1201490 and from ANID – Millennium Science Initiative Program – ICN12_009 awarded to the Millennium Institute of Astrophysics MAS.

References

  1. Abraham, R., Danieli, S., van Dokkum, P., et al. 2018, Res. Notes AAS, 2, 16 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alessandrini, E., Lanzoni, B., Miocchi, P., Ciotti, L., & Ferraro, F. R. 2014, ApJ, 795, 169 [NASA ADS] [CrossRef] [Google Scholar]
  3. Alonso-García, J., Saito, R. K., Hempel, M., et al. 2018, A&A, 619, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Ashman, K. M., & Zepf, S. E. 1992, ApJ, 384, 50 [NASA ADS] [CrossRef] [Google Scholar]
  5. Ashman, K. M., & Zepf, S. E. 1998, in Globular cluster system, (Cambridge: Cambridge Univ. Press), Cambridge Astrophys. Ser., 30 [Google Scholar]
  6. Barmby, P., Huchra, J. P., Brodie, J. P., et al. 2000, AJ, 119, 727 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barbuy, B., Bica, E., Ortolani, S., & Bonatto, C. 2006, A&A, 449, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Barbuy, B., Muniz, L., Ortolani, S., et al. 2018, A&A, 619, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bassino, L. P., & Muzzio, J. C. 1995, Observatory, 115, 256 [NASA ADS] [Google Scholar]
  10. Baumgardt, H., Sollima, A., & Hilker, M. 2020, PASA, 37 [CrossRef] [Google Scholar]
  11. Bellazzini, M., Correnti, M., Ferraro, F. R., Monaco, L., & Montegriffo, P. 2006, A&A, 446, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bellazzini, M., Ibata, R. A., Chapman, S. C., et al. 2008, AJ, 136, 1147 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bellazzini, M., Ibata, R., Malhan, K., et al. 2020, A&A, 636, A107 [CrossRef] [EDP Sciences] [Google Scholar]
  14. Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 642, L137 [Google Scholar]
  15. Belokurov, V., Koposov, S. E., Evans, N. W., et al. 2014, MNRAS, 437, 116 [NASA ADS] [CrossRef] [Google Scholar]
  16. Besla, G., Kallivayalil, N., Hernquist, L., et al. 2010, ApJ, 721, L97 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [Google Scholar]
  18. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  19. Chou, M.-Y., Majewski, S. R., Cunha, K., et al. 2007, ApJ, 670, 346 [NASA ADS] [CrossRef] [Google Scholar]
  20. Christian, C. A., & Friel, E. D. 1992, AJ, 103, 142 [NASA ADS] [CrossRef] [Google Scholar]
  21. Clementini, G., Gratton, R. G., Bragaglia, A., et al. 2005, ApJ, 630, L145 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cohen, J. G., Hsieh, S., Metchev, S., Djorgovski, S. G., & Malkan, M. 2007, AJ, 133, 99 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cohen, S. A., Hickox, R. C., Wegner, G. A., Einasto, M., & Vennik, J. 2014, ApJ, 783, 136 [NASA ADS] [CrossRef] [Google Scholar]
  24. Cohen, R. E., Hempel, M., Mauro, F., et al. 2015, AJ, 150, 176 [CrossRef] [Google Scholar]
  25. Colucci, J. E., Bernstein, R. A., Cameron, S. A., & McWilliam, A. 2011, ApJ, 735, 55 [NASA ADS] [CrossRef] [Google Scholar]
  26. Conroy, C., & Gunn, J. E. 2010, AJ, 712, 833 [NASA ADS] [CrossRef] [Google Scholar]
  27. Cross, N. J. G., Collins, R. S., Mann, R. G., et al. 2012, A&A, 548, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. De Grijs, R., Wilkinson, M. I., & Tadhunter, C. N. 2005, MNRAS, 361, 311 [NASA ADS] [CrossRef] [Google Scholar]
  29. Di Benedetto, G. P. 2008, MNRAS, 390, 1762 [NASA ADS] [Google Scholar]
  30. Dierickx, M. I. P., & Loeb, A. 2017, ApJ, 847, 42 [NASA ADS] [CrossRef] [Google Scholar]
  31. Einasto, M., Vennik, J., Nurmi, P., et al. 2012, A&A, 540, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Emerson, J., & Sutherland, W. 2010, Messenger, 139, 2 [Google Scholar]
  33. Fall, S. M., & Zhang, Q. 2001, AJ, 561, 751 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fan, Z., Ma, J., De Grijs, R., & Zhou, X. 2008, MNRAS, 385, 1973 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ferraro, F. R., Montegriffo, P., Origlia, L., & Pecci, F. F. 2000, AJ, 119, 1282 [NASA ADS] [CrossRef] [Google Scholar]
  36. Forbes, D. A. 2020, MNRAS, 493, 847 [NASA ADS] [CrossRef] [Google Scholar]
  37. Forbes, D. A., & Bridges, T. 2010, MNRAS, 404, 1203 [NASA ADS] [Google Scholar]
  38. Freedman, W. L., Madore, B. F., Hoyt, T., et al. 2020, ApJ, 891, 57 [Google Scholar]
  39. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Galleti, S., Federici, L., Bellazzini, M., Buzzoni, A., & Fusi Pecci, F. 2006, A&A, 456, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Galleti, S., Federici, L., Bellazzini, M., et al. 2014, VizieR Online Data Catalog, V/143 [Google Scholar]
  42. Garro, E. R., Minniti, D., Gómez, M., et al. 2020, A&A, 642, L19 [EDP Sciences] [Google Scholar]
  43. Garro, E. R., Minniti, D., Gómez, M., et al. 2021, A&A, 649, A86 [CrossRef] [EDP Sciences] [Google Scholar]
  44. Gnedin, O. Y., & Ostriker, J. P. 1997, ApJ, 474, 223 [NASA ADS] [CrossRef] [Google Scholar]
  45. Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2003, A&A, 408, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Grcevich, J., & Putman, M. E. 2009, ApJ, 696, 385 [NASA ADS] [CrossRef] [Google Scholar]
  47. Haghi, H., Khalaj, P., Hasani Zonoozi, A., & Kroupa, P. 2017, ApJ, 839, 60 [NASA ADS] [CrossRef] [Google Scholar]
  48. Hamanowicz, A., Pietrukowicz, P., Udalski, A., et al. 2016, Acta Astron., 66, 197 [NASA ADS] [Google Scholar]
  49. Harris, W. E. 1991, ARA&A, 29, 543 [NASA ADS] [CrossRef] [Google Scholar]
  50. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  51. Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [NASA ADS] [CrossRef] [Google Scholar]
  52. Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [NASA ADS] [CrossRef] [Google Scholar]
  53. Hilker, M., Baumgardt, H., Sollima, A., & Bellini, A. 2020, in Star Clusters: From the Milky Way to the Early Universe, eds. A. Bragaglia, M. Davies, A. Sills, & E. Vesperini, 351, 451 [NASA ADS] [Google Scholar]
  54. Hollyhead, K., Martocchia, S., Lardo, C., et al. 2019, MNRAS, 484, 4718 [NASA ADS] [CrossRef] [Google Scholar]
  55. Horta, D., Hughes, M. E., Pfeffer, J. L., et al. 2021, MNRAS, 500, 4768 [CrossRef] [Google Scholar]
  56. Hughes, M. E., Pfeffer, J., Martig, M., et al. 2019, MNRAS, 482, 2795 [Google Scholar]
  57. Huxor, A. P., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2165 [NASA ADS] [CrossRef] [Google Scholar]
  58. Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [Google Scholar]
  59. Ibata, R., Irwin, M., Lewis, G., Ferguson, A. M. N., & Tanvir, N. 2001, Nature, 412, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  60. Ibata, R., Chapman, S., Ferguson, A. M. N., et al. 2004, MNRAS, 351, 117 [NASA ADS] [CrossRef] [Google Scholar]
  61. Irwin, M. J., Lewis, J., Hodgkin, S., et al. 2004, in Optimizing Scientific Return for Astronomy through Information Technologies, eds. P. J. Quinn, A. Bridger, et al., SPIE Conf. Ser., 5493, 411 [Google Scholar]
  62. Jeon, Y.-B., Nemec, J. M., Walker, A. R., & Kunder, A. M. 2014, AJ, 147, 155 [NASA ADS] [CrossRef] [Google Scholar]
  63. Kallivayalil, N., van der Marel, R. P., & Alcock, C. 2006, ApJ, 652, 1213 [NASA ADS] [CrossRef] [Google Scholar]
  64. Kallivayalil, N., van der Marel, R. P., Besla, G., Anderson, J., & Alcock, C. 2013, ApJ, 764, 161 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kerber, L. O., Santiago, B. X., & Brocato, E. 2007, A&A, 462, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Kerber, L. O., Nardiello, D., Ortolani, S., et al. 2018, ApJ, 853, 15 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R. D. 2016, A&A, 585, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Koposov, S., de Jong, J. T. A., Belokurov, V., et al. 2007, ApJ, 669, 337 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kruijssen, J. M. D., Pelupessy, F. I., Lamers, H. J. G. L. M., Portegies Zwart, S. F., & Icke, V. 2011, MNRAS, 414, 1339 [NASA ADS] [CrossRef] [Google Scholar]
  70. Kruijssen, J. M. D., Pfeffer, J. L., Reina-Campos, M., Crain, R. A., & Bastian, N. 2019, MNRAS, 486, 3180 [Google Scholar]
  71. Kruijssen, J. M. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [CrossRef] [Google Scholar]
  72. Lamers, H. J. G. L. M., Baumgardt, H., & Gieles, M. 2010, MNRAS, 409, 305 [NASA ADS] [CrossRef] [Google Scholar]
  73. Laporte, C. F. P., Johnston, K. V., Gómez, F. A., Garavito-Camargo, N., & Besla, G. 2018, MNRAS, 481, 286 [Google Scholar]
  74. Larsen, S. S. 2002, AJ, 124, 1393 [NASA ADS] [CrossRef] [Google Scholar]
  75. Law, D. R., & Majewski, S. R. 2010, ApJ, 714, 229 [NASA ADS] [CrossRef] [Google Scholar]
  76. Layden, A. C., & Sarajedini, A. 2000, AJ, 119, 1760 [NASA ADS] [CrossRef] [Google Scholar]
  77. Leaman, R., VandenBerg, D. A., & Mendel, J. T. 2013, MNRAS, 436, 122 [NASA ADS] [CrossRef] [Google Scholar]
  78. Lyubenova, M., Kuntschner, H., Rejkuba, M., et al. 2010, A&A, 510, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Mackey, A. D., & Gilmore, G. F. 2004, MNRAS, 352, 153 [NASA ADS] [CrossRef] [Google Scholar]
  80. Mackey, A. D., & Van Den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef] [Google Scholar]
  81. Madrid, J. P., Leigh, N. W. C., Hurley, J. R., & Giersz, M. 2017, MNRAS, 470, 1729 [NASA ADS] [CrossRef] [Google Scholar]
  82. Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  83. Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
  84. Martin, N. F., Ibata, R. A., Rich, R. M., et al. 2014, ApJ, 787, 19 [Google Scholar]
  85. Martocchia, S., Dalessandro, E., Lardo, C., et al. 2019, MNRAS, 487, 5324 [NASA ADS] [CrossRef] [Google Scholar]
  86. Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. McConnachie, A. W., Irwin, M. J., Ferguson, A. M. N., et al. 2005, MNRAS, 356, 979 [NASA ADS] [CrossRef] [Google Scholar]
  88. McDonald, I., Zijlstra, A. A., Sloan, G. C., et al. 2013, MNRAS, 436, 413 [CrossRef] [Google Scholar]
  89. McDonald, I., Zijlstra, A. A., Sloan, G. C., et al. 2014, MNRAS, 439, 2618 [NASA ADS] [CrossRef] [Google Scholar]
  90. McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
  91. Minniti, D. 2018, in The Vatican Observatory, Castel Gandolfo: 80th Anniversary Celebration, eds. G. Gionti, & J. B. Kikwaya Eluo, 51, 63 [Google Scholar]
  92. Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New Astron., 15, 433 [Google Scholar]
  93. Minniti, D., Hempel, M., Toledo, I., et al. 2011, A&A, 527, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Minniti, D., Palma, T., Dékány, I., et al. 2017a, AJ, 838, L14 [NASA ADS] [CrossRef] [Google Scholar]
  95. Minniti, D., Geisler, D., Alonso-García, J., et al. 2017b, AJ, 849, L24 [CrossRef] [Google Scholar]
  96. Minniti, D., Schlafly, E. F., Palma, T., et al. 2018, AJ, 866, 12 [NASA ADS] [CrossRef] [Google Scholar]
  97. Minniti, D., Gómez, M., Alonso-García, J., Saito, R. K., & Garro, E. R. 2021a, A&A, 650, L21 [Google Scholar]
  98. Minniti, D., Ripepi, V., Fernández-Trincado, J. G., et al. 2021b, A&A, 647, L4 [CrossRef] [EDP Sciences] [Google Scholar]
  99. Momany, Y., Held, E. V., Saviane, I., et al. 2005, A&A, 439, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Monaco, L., Pancino, E., Ferraro, F. R., & Bellazzini, M. 2004, MNRAS, 349, 1278 [NASA ADS] [CrossRef] [Google Scholar]
  101. Monaco, L., Bellazzini, M., Bonifacio, P., et al. 2005, A&A, 441, 141 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  102. Mucciarelli, A., Carretta, E., Origlia, L., & Ferraro, F. R. 2008, AJ, 136, 375 [NASA ADS] [CrossRef] [Google Scholar]
  103. Mucciarelli, A., Origlia, L., Ferraro, F. R., Bellazzini, M., & Lanzoni, B. 2012, ApJ, 746, L19 [NASA ADS] [CrossRef] [Google Scholar]
  104. Mucciarelli, A., Dalessandro, E., Ferraro, F. R., Origlia, L., & Lanzoni, B. 2014, ApJ, 793, L6 [NASA ADS] [CrossRef] [Google Scholar]
  105. Mucciarelli, A., Bellazzini, M., Ibata, R., et al. 2017, A&A, 605, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
  107. Nantais, J. B., Huchra, J. P., Barmby, P., Olsen, K. A. G., & Jarrett, T. H. 2006, AJ, 131, 1416 [NASA ADS] [CrossRef] [Google Scholar]
  108. Newberg, H. J., Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [Google Scholar]
  109. Niederste-Ostholt, M., Belokurov, V., & Evans, N. W. 2012, MNRAS, 422, 207 [NASA ADS] [CrossRef] [Google Scholar]
  110. Noël, N. E. D., Greggio, L., Renzini, A., Carollo, C. M., & Maraston, C. 2013, AJ, 772, 58 [Google Scholar]
  111. Ortolani, S., Bica, E., & Barbuy, B. 1998, A&AS, 127, 471 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Ortolani, S., Bica, E., & Barbuy, B. 2006, ApJ, 646, L115 [NASA ADS] [CrossRef] [Google Scholar]
  113. Palma, T., Gramajo, L. V., Clariá, J. J., et al. 2016, A&A, 586, A41 [CrossRef] [EDP Sciences] [Google Scholar]
  114. Palma, T., Minniti, D., Alonso-García, J., et al. 2019, MNRAS, 487, 3140 [Google Scholar]
  115. Peacock, M. B., Maccarone, T. J., Knigge, C., et al. 2010, MNRAS, 402, 803 [NASA ADS] [CrossRef] [Google Scholar]
  116. Pessev, P. M., Goudfrooij, P., Puzia, T. H., & Chandar, R. 2008, MNRAS, 385, 1535 [NASA ADS] [CrossRef] [Google Scholar]
  117. Piatti, A. E., & Carballo-Bello, J. A. 2020, A&A, 637, L2 [CrossRef] [EDP Sciences] [Google Scholar]
  118. Piatti, A. E., & Koch, A. 2018, ApJ, 867, 8 [NASA ADS] [CrossRef] [Google Scholar]
  119. Piatti, A. E., Alfaro, E. J., & Cantat-Gaudin, T. 2019, MNRAS, 484, L19 [Google Scholar]
  120. Pritzl, B. J., Smith, H. A., Catelan, M., & Sweigart, A. V. 2002, AJ, 124, 949 [NASA ADS] [CrossRef] [Google Scholar]
  121. Rejkuba, M. 2012, Ap&SS, 341, 195 [NASA ADS] [CrossRef] [Google Scholar]
  122. Rosenberg, A., Saviane, I., Piotto, G., & Aparicio, A. 1999, AJ, 118, 2306 [NASA ADS] [CrossRef] [Google Scholar]
  123. Ruiz-Dern, L., Babusiaux, C., Arenou, F., Turon, C., & Lallement, R. 2018, A&A, 609, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Saito, R. K., Hempel, M., Minniti, D., et al. 2012, A&A, 537, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  125. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
  126. Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [Google Scholar]
  127. Siegel, M. H., Majewski, S. R., Law, D. R., et al. 2011, ApJ, 743, 20 [NASA ADS] [CrossRef] [Google Scholar]
  128. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  129. Suntzeff, N. B., Kinman, T. D., & Kraft, R. P. 1991, ApJ, 367, 528 [NASA ADS] [CrossRef] [Google Scholar]
  130. Valenti, E., Ferraro, F. R., & Origlia, L. 2004, MNRAS, 351, 1204 [NASA ADS] [CrossRef] [Google Scholar]
  131. Valenti, E., Origlia, L., & Ferraro, F. R. 2005, MNRAS, 361, 272 [NASA ADS] [CrossRef] [Google Scholar]
  132. Valenti, E., Ferraro, F. R., & Origlia, L. 2007, AJ, 133, 1287 [NASA ADS] [CrossRef] [Google Scholar]
  133. Valenti, E., Ferraro, F. R., & Origlia, L. 2010, MNRAS, 402, 1729 [NASA ADS] [CrossRef] [Google Scholar]
  134. Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
  135. Vasiliev, E., & Belokurov, V. 2020, MNRAS, 497, 4162 [Google Scholar]
  136. Vasiliev, E., Belokurov, V., & Erkal, D. 2021, MNRAS, 501, 2279 [NASA ADS] [CrossRef] [Google Scholar]
  137. Wagner-Kaiser, R., Mackey, D., Sarajedini, A., et al. 2017, MNRAS, 471, 3347 [Google Scholar]
  138. Wang, S., Ma, J., Wu, Z., & Zhou, X. 2014, AJ, 148, 4 [NASA ADS] [CrossRef] [Google Scholar]
  139. White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: LFs and CMDs for the new Sgr GCs

thumbnail Fig. A.1.

NIR and optical CMDs for all the Sgr GC in our sample. The Hess diagrams represent the VVVX (on the left) and Gaia EDR3 (on the right) datasets, the cyan points are the stars from the 2MASS catalog, and the dotted black lines are the PARSEC isochrones that best fit the evolutionary sequences.

thumbnail Fig. A.1.

continued.

thumbnail Fig. A.2.

Red and blue histograms depict the luminosity function for each Sgr GC in the NIR VVVX and in the optical Gaia EDR3 passbands, respectively. The histograms are constructed adopting a bin size of 0.1 mag because we wish to show the RC position as a clear excess.

thumbnail Fig. A.2.

continued.

Appendix B: Estimation of the total luminosity

As explained in Section 3, the integrated luminosities of the Sgr clusters, calculated in Ks−band, do not include the contribution from faint stars, undetected in our photometry, as we can appreciate in Fig. A.1. In order to better estimate the total luminosities of our clusters, we have therefore used the following approach.

The main goal of this approach is to quantify the fraction of luminosity that comes from the faintest stars. To do this, we compared the brightness of Sgr GCs with known and well-characterized GCs. We recovered for the GCs the reddening and distance modulus and list them in Table B.1. The main steps we adopted to achieve our results are listed below.

  1. We calculated the absolute magnitude MKs of known MW GCs (Table B.1), using the VVV/VVVX datasets. In this way, we were able to directly compare the luminosities found for Sgr GCs and known GCs in the same magnitude range (10.2 ≲ Ks ≲ 17.2, only for Terzan 8 we used 2MASS photometry 12.0 ≲ Ks ≲ 16.7).

  2. The obtained MKs was converted into the absolute magnitude in V−band (MV), using the typical GC color (V − Ks) = 2.5 mag (e.g., Barmby et al. 2000; Cohen et al. 2007; Conroy & Gunn 2010).

  3. We scaled the MV values to the absolute magnitude listed in the 2010 version of the Harris (1996) catalog (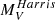). Consequently, we estimated the fraction of luminosity that comes from the faintest stars for each known GC, computing .

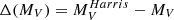  4. We grouped these GCs according to their metallicities, then we calculated the average of Δ(MV) fractions for each group.

  5. Finally, we added these averages to the Sgr luminosities. We considered at least two known GCs with the same metallicity range as the Sgr GCs (from −0.3 to −2.0).

We achieved an empirical correction to our cluster luminosities in this way, assuming similarity with other GCs. The resulting luminosities are listed in Table 1. We find that the missing luminosity was lower than 1.8 mag.

Table B.1.

Known and well-characterized GCs we used to derive the total luminosity for each Sgr GC.

All Tables

Table 1.

Position, metallicity, age, luminosity, mass-to-light ratio, mass, and specific frequency of RR Lyrae stars for all new Sgr GCs we analyzed.

In the text
Table 2.

Position, metallicity, age, luminosity and mass for the previously known Sgr GCs, used for comparison.

In the text
Table 3.

Properties of the LMC GCs used for comparison.

In the text
Table B.1.

Known and well-characterized GCs we used to derive the total luminosity for each Sgr GC.

In the text

All Figures

thumbnail Fig. 1.

Comparison between the Gaia EDR3 optical CMDs of Minni332, taken as representative of the Sgr GCs (Minniti et al. 2021a), and five bulge fields located at similar latitudes, but away from the Sgr main body.
In the text
thumbnail Fig. 2.

Latitude vs. longitude map depicting the position of Sgr GCs in the main body. The colored points highlight the cluster metallicity. Red shows GCs with [Fe/H] ≥ − 0.5, orange shows GCs with −1.0 ≤ [Fe/H] ≤ − 0.6, and blue shows GCs with [Fe/H] ≤ − 1.1 for our convention. We included NGC 6715, Terzan 7, Terzan 8, and Arp 2 for comparison.
In the text
thumbnail Fig. 3.

Radial dependence of the metallicity for Sgr GCs. We consider the projected distance from the center of Sgr, adopting D = 26.5 kpc for this galaxy. The newly discovered Sgr GCs are marked with black points, and the known Sgr GCs are represented as red diamonds.
In the text
thumbnail Fig. 4.

Age-metallicity relation for the Sgr GC system. The newly discovered Sgr GCs are marked with black points, and the known Sgr GCs are represented as red diamonds. In the top panel, the green line reproduces the AMR for the MW halo GCs shown in Forbes (2020, see their Fig. 3). In the bottom panel, the solid lines reproduce the median star cluster AMR relation for the LMC (orange) and Milky Way-mass (black) galaxies in the E-MOSAICS simulations by Horta et al. (2021, see their Fig. 3).
In the text
thumbnail Fig. 5.

Sagittarius metallicity distribution (top panel) and luminosity function (bottom panel), including the new and known GCs.
In the text
thumbnail Fig. 6.

Metallicity distribution for Sgr (black histogram), MW (blue histogram), M31 (green histogram), and the LMC (magenta histogram) GC systems (in the left panel). We also show separately the Sgr and LMC metallicity distributions (in the right panel) as a zoomed plot of the left panel, and the middle panel highlights the Sgr MD. The histograms are constructed adopting a bin size of 0.2 dex.
In the text
thumbnail Fig. 7.

Luminosity function for Sgr (black histogram), MW (blue histogram), M31 (green histogram), and the LMC (magenta histogram) GC systems (in the left panel). We also show separately the Sgr and LMC luminosity functions (in the right panel) as a zoomed plot of the left panel, and we use the middle panel to highlight the Sgr LF. The histograms are constructed considering a bin size of 0.5 mag.
In the text
thumbnail Fig. A.1.

NIR and optical CMDs for all the Sgr GC in our sample. The Hess diagrams represent the VVVX (on the left) and Gaia EDR3 (on the right) datasets, the cyan points are the stars from the 2MASS catalog, and the dotted black lines are the PARSEC isochrones that best fit the evolutionary sequences.
In the text
thumbnail Fig. A.1.

continued.
In the text
thumbnail Fig. A.2.

Red and blue histograms depict the luminosity function for each Sgr GC in the NIR VVVX and in the optical Gaia EDR3 passbands, respectively. The histograms are constructed adopting a bin size of 0.1 mag because we wish to show the RC position as a clear excess.
In the text
thumbnail Fig. A.2.

continued.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.