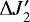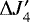EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A66 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A66
Number of page(s) 17
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/202140739
Published online 12 October 2021

© ESO 2021

1 Introduction

Neptune has two distinctive natural satellites in our Solar System: Triton, the only large satellite with a retrograde orbit, and Nereid, which has the most eccentric orbit. Causes of the distinctiveness are still inconclusive. A possible explanation is that Triton was once part of a binary planet orbiting around the Sun before a close encounter with Neptune (e.g., Agnor & Hamilton 2006); Nereid had been an inner regular satellite before this encounter. If this explanation is true, Nereid is probably the only survivor of the primordial regular satellite system formed before the capture of Triton (e.g., Brozović et al. 2020). Further dynamical studies are still necessary to clarify the origin of these two satellites (e.g., Rufu & Canup 2017; Li & Christou 2020; Li et al. 2020).

Triton and Nereid were the only two known Neptunian satellites before the space era. Triton was discovered in 1846 and Nereid in 1949. So far, they have only been visited by Voyager in 1989 and only 40% of Triton’s surface is clearly imaged. Future closeflybys of these satellites can be planed for their further physical studies. Some new space exploration missions to the Neptunian system (e.g., NASA’s Trident Mitchell et al. 2019; Prockter et al. 2019) have been proposed. To support these missions, as well as other physical studies of the Neptunian system, high-precision satellite ephemerides and relevant parameters are needed.

The pole orientation of Neptune is associated with gravitational effects due to the oblateness of Neptune. The latest published values and uncertainties of the pole orientation angles of Neptune are provided by NEP081 ephemerides (Jacobson 2009). Using these values, Tang et al. (2020) and Emelyanov & Arlot (2011) corrected the initial states of Triton and Nereid, respectively. Nevertheless, the present paper finds that the pole orientation of Neptune can also be refined with all the astrometric data available to us, and a revised pole model based on Boué & Laskar (2006), Fienga et al. (2008), and Manche (2011) is applied.

Generally speaking, new observations and new planetary and satellite ephemerides provide opportunities to improve the ephemeridesfor Triton and Nereid and the pole orientation of Neptune. On the one hand, the observations include a lot of new accurate Earth-based positions reduced with the Gaia astrometic catalogs (Lindegren et al. 2016, 2018) along with accurate positions obtained from Hubble Space Telescope (HST) (Showalter et al. 2019). The corrections of numerous old observations applied in OCNS2019 (Yuan et al. 2021), as well as new Triton and Nereid astrometric positions (presented in Sect. 2.3), are also included. Many observations are used for the first time for Triton and Nereid orbit determinations. On the other hand, the latest ephemerides for planets and all known regular satellites of Neptune, DE440 (Park et al. 2021) and NEP090 (Brozović et al. 2020), respectively, provide a new accurate background of the gravitational field. In particular, NEP090 provides reliable estimates of the masses of the regular satellites, allowing us to include their gravitational effects in the dynamical model. Besides, the dynamical model adopts new values of J2 (Brozović et al. 2020), rotation rate (Helled et al. 2010), and inertia factor (Podolak & Helled 2012) for Neptune.

The present paper is arranged as follows. Section 2 presents all the observations we use in the orbit determinations. Section 3 presents the numerical model of the dynamics of Triton and Nereid orbits and the pole orientation of Neptune. Section 4 presents our solution method and results, including comparisons with the Jacobson (2009) solution and accuracy estimations of our new orbit and pole solution. In Sect. 5, we give some discussions with geometric descriptions for the orbits and pole orientation. Conclusions are given in Sect. 6.

2 Observations

To determine the orbits of Triton and Nereid, we use all the available observations from 1847 to 2020. Tables A.1–A.5 summarize the observations we use in the orbit determination. These observations are as follows: Voyager imaging observations of the two satellites, Voyager B-plane coordinates and closest approach times at Triton and Neptune, HST astrometric observations of Triton, and Earth-based astrometric observations of the two satellites.

2.1 Voyager imaging data and B-plane data

The Voyager imaging data are pictures of the satellites against a stellar background that provides the pointing reference for the spacecraft camera. The data we use are the same as NEP081, that is, the camera pixel coordinates in the form of samples and lines1 (see Table A.1) rather than the FK4/B1950 coordinates reduced earlier in the astrographic form (Jacobson 1991). The latter were used by some orbit determinations of Triton (Emelyanov & Samorodov 2015; Tang et al. 2020) and Nereid (Emelyanov & Arlot 2011); however, the former were obtained using a more accurate reference star catalog, UCAC2 (Zacharias et al. 2004), and a newer Voyager trajectory, VGR2_NEP0812 (Jacobson 2008, 2009). And, when computing residuals with the former data, the theoretical positions should be converted from the International Celestial Reference System (ICRS) to the camera coordinate system rather than to the FK4/B1950 system. Formats and usage of the imaging data are provided by Jet Propulsion Laboratory (JPL)3. So far, the Voyager imaging data are still the most accurate data with an accuracy ranging from a few 100 km to ~ 5 km.

We also use the B-plane data provided in Jacobson (2008) to help fix the Triton position near the time of the spacecraft flyby. A B-plane isa key performance metric that is used by navigators for interplanetary missions to determine the accuracy of a spacecraft flyby trajectory. The B-plane is defined as a plane orthogonal to the hyperbolic trajectory plane, and described by three unit vectors 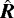, , 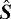and 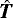, where 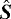is parallel to the hyperbolic excess velocity, 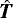lies in the ecliptic plane, and 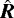completes the right-handed triad. The unit vectors 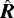and 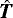are used as B-plane axes. The B-vector is defined to be the vector, B, from the origin (center of mass of the flyby target) to the spot where the incoming asymptote pierces the B-plane. B-plane data are the B-plane coordinates of B, 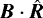, and 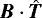, and the time of closest approach (TCA). We use the Voyager state vector at the reported TCA provided by VGR2_NEP081 to compute the theoretical B-plane data (see Table A.2). According to Jacobson (2008), these B-plane data can reflect, at the level of the reported uncertainties, the real Voyager encounter geometry at the closest approach.

2.2 Hubble Space Telescope astrometric data

Showalter et al. (2019) provide the HST astrometric observations of Triton along with the seven inner regular satellites. The satellite positions are measured relative to the center of Neptune in the tangent plane. Triton positions are obtained in 2004, 2005, 2011, and 2015, and have a reported accuracy of about 10 mas, which is about 210 km at the average distance of Neptune from Earth. So far, they are the most accurate relative positions obtained in the vicinity of the Earth, which have not been used in the previous Triton orbit determinations by Jacobson (2009), Emelyanov & Samorodov (2015), and Tang et al. (2020).

2.3 Earth-based astrometric data

The Earth-based astrometric data of Triton and Nereid include all those in OCNS20194 (Yuan et al. 2021) and one year of new CCD observations obtained from the Yaoan 0.8-m telescope (IAU code O49) in 2019–2020. These data, as well as the HST astrometry described in Sect. 2.2, are included in the updated version5 of OCNS2019. Absolute coordinates are corrected for star catalog biases with respect to Gaia-DR2 (Lindegren et al. 2018), which are applied by OCNS2019 to observations of Neptunian satellites for the first time.

The new observations are reduced in absolute coordinates with the Gaia-DR2 star catalog. The reduction procedure is the same as that of Yuan et al. (2021). These observations include 1492 new Earth-based observed coordinates (7% of the total available) obtained over 61 nights (2% of total observation nights) for Triton, and 378 (6%) over 28 nights (6%) for Nereid. In right ascension and declination, the standard deviations of the residuals with respect to DE440/NEP081 are about 0.′′ 03 for Triton and about 0.′′07 for Nereid.

There are seven main data sets not used in the previous orbit determinations of Triton (Jacobson 2009; Emelyanov & Samorodov 2015; Tang et al. 2020) and Nereid (Jacobson 2009; Emelyanov & Arlot 2011):

  • 1)

    Triton and Nereid CCD observations from the Lijiang 2.4 m telescope in 2013 and 2017 (Yuan et al. 2021).

  • 2)

    Triton and Nereid CCD observations from the Yaoan 0.8 m telescope in 2018–2020 (Yuan et al. 2021; the present paper).

  • 3)

    Triton photographic observations in the form of relative coordinates from Bordeaux Observatory in 1970 (Soulié et al. 1975).

  • 4)

    Triton meridian circle observations from Bordeaux Observatory in 2007–2013 (Dourneau et al. 2015).

  • 5)

    Re-reduced and new Nereid CCD observations from the Xinglong station of National Astronomical Observatory in 2006–2007 and 2012 (Yu et al. 2018, 2019), respectively.

  • 6)

    Nereid CCD observations from the Lijiang 2.4 m telescope in 2013, 2015, and 2017 (Yu et al. 2018).

  • 7)

    Nereid observations (2010–2018) that were reported by several observers to the Minor Planet Center at the Smithsonian Astrophysical Observatory (MPC 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018).

Table 1

Initial conditions and other parameters of Neptune and integrated satellites used in the dynamical modeling and relevant analysis.

Table 2

Parameters of the perturbing Sun, planets, and satellites used in the dynamical modeling and relevant analysis.

3 Dynamical modeling

In this section we present the numerical model of the dynamics of Triton and Nereid orbits and the pole orientation of Neptune. We neglected perturbations that have no observable effects. Table 1 summarizes the initial conditions and parameters of Neptune and integrated satellites used in our dynamical modeling and relevant analysis. Table 2 summarizes the dynamical parameters of the perturbing Sun, planets, and satellites. Positions of inner satellites are provided by NEP090 and those of the Sun and planets by DE440. For indices denoting these bodies, we use i = 0 for Neptune, i = 1, 2 for Triton and Nereid, respectively, i = 3…9 for the seven inner regular satellites of Neptune (Naiad, Thalassa, Despina, Galatea, Larissa, Proteus, and Hippocamp, respectively), and i = 10…13 for Sun, Jupiter, Saturn, and Uranus, respectively.

thumbnail Fig. 1

Differences in Triton and Nereid orbits between the model including complete perturbations from all the inner regular satellites of Neptune and other simplified models. The complete perturbations from inner regulars are calculated by using the positions provided by NEP090 ephemerides (Brozović et al. 2020). Parameters and are the corrections applied to the coefficients J2 and J4, respectively,for the simplification and speeding up of calculations of perturbations from inner regular satellites. The initial epoch is always 1989 September 1 TDB, near the time at which the most accurate data are obtained during Voyager’s encounter. The red area is the period spanned by Voyager encounter data (1988–1989) and the gray area without such data (1847–1987 and 1990–2020).

3.1 Numerical method

For modeling the dynamics of natural satellites, we developed an N-body code called FORCES (Find Orbits and Rotations, Construct Ephemerides, and Simulate; Yuan, in prep.) that enables (a) the simultaneous propagation of the orbits and rotations with a numerical integration of the equations of motion and (b) the generation of the partial derivatives needed to adjust the model parameters to fit the observations with a numerical integration of variational equations. The equations of orbital motion are represented in Cartesian coordinates with the planetary satellite system barycenter at the origin. Both orbits and orientations of bodies are defined as referred to the ICRS. In the present paper, we always set the initial epoch as 1989 September 1 TDB (Barycentric Dynamical Time), near the time at which the most accurate data are obtained during Voyager’s encounter (e.g., Brozović et al. 2020).

For necessary numerical integrations, we used a modified version of the IAS15 integrator (Rein & Spiegel 2015) developed in FORCES. The IAS15 integrator is developed based on the RA15 integrator (Everhart 1985), with additional implementation of a step-size control that can automatically choose an optimal time step. The RA15 is widely used in orbit determinations of natural satellites and asteroids (e.g., Lainey et al. 2004; Desmars et al. 2013, 2015). In this work, we modify IAS15 to enable simultaneous integration of a mixed-order system.

The predictor-corrector and step-size control parameters are set as 10−10 and 10−8, respectively.With this setting, the differences in satellite positions and the pole orientation of Neptune at integration epoch after integrating back and forth over one century are, respectively, at most a few meters and a few 10−6 mas. So, current settings of the control parameters can meet our accuracy requirements.

3.2 Gravitational interactions

In the dynamical model for Triton and Nereid orbits, NEP081 (Jacobson 2009) considers the point-mass gravitational effects of Neptune and Triton, the J2 and J4 zonal harmonics of Neptune’s gravitational potential, and the point-mass perturbations from the Sun, Jupiter, Saturn, Uranus, and the four inner planets. In order to improve the computational efficiency, NEP081 does not directly calculate the gravitational force of the inner planets, but adds their masses to the Sun. No other effects are considered in Emelyanov & Arlot (2011), Emelyanov & Samorodov (2015), and Tang et al. (2020). All the gravitational effects considered by NEP081 are included in our dynamical model.

In addition, we also tested whether the perturbations from the inner regular satellites of Neptune are negligible using the masses provided by NEP090 (Brozović et al. 2020). It should be noted that, given the initial epoch of integration, the ephemeris errors induced by a certain approximation in the dynamical model grow over time. We also have the requirement that these model induced errors must be smaller than the observation accuracy, which changes drastically with the data set. Therefore, we decided to use two periods, that is, the one spanned by Voyager encounter data (1988–1989) and the other without such data (1847–1987 and 1990–2020), in comparing the induced errors and the observation accuracies. In the former period, the best accuracy is ~ 5 km in positions; the latter, about 200 km (about 10 mas as seen from the Earth) in positions. It can be seen from the blue curves in Fig. 1 that the positional differences caused by the perturbations from inner regular satellites are larger than the accuracy in each period. Therefore, these perturbations are not neglected in our dynamical model. Subsequently, we used a method (e.g., Emelyanov & Kanter 2005) to improve the computational efficiency. To be specific, instead of using the positions provided by NEP090, the perturbations from some inner satellites can be considered by adding corrections to the J2 and J4 for Neptune as follows: 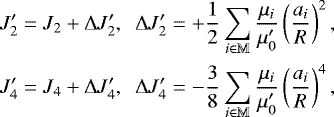(1)

where 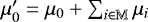, where 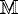is a set of considered satellites, μ denotes the gravitational parameter (GM), a the semimajor axis provided by Brozović et al. (2020), and R the reference radius for Neptune. As shown in Fig. 1, if applying Eq. (1) for all the inner satellites except for Proteus (), the introduced error is much smaller than the observation accuracies. So, in the present paper, we use the positions provided by NEP090 to compute the perturbations from Proteus and use Eq. (1) to compute those from other inner satellites.

thumbnail Fig. 2

Pole orientation of Neptune difference between the model including the perturbations from all inner regulars and that including the perturbations from only one inner regular, Proteus. All perturbations from inner regulars are calculated by using the positions provided by NEP090 ephemerides (Brozović et al. 2020). The initialepoch is 1989 September 1 TDB. The pole orientation difference is shown in the right ascension (αp) and declination (δp) referred to the ICRS.

3.3 Motion of the pole orientation of Neptune

The gravitational effects due to the oblateness of Neptune are associated with its pole orientation, 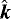. To ensure the self-consistency of the solutions and allow integration for a long time, we integrate the motion of the pole orientation of Neptune together with the two satellite orbits.

Neptune is a fast-rotating planet. The numerical integration of the full rotational motion of Neptune would require a very small time step. To avoid this problem, we apply the method proposed by Boué & Laskar (2006) and adopted for integrating the pole orientation motion of Earth (Fienga et al. 2008; Manche 2011). Let 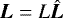denote the rotational angular momentum vector of Neptune, where L and 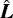are the magnitude and the unit vector in the direction of L, respectively. As the angle between 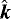and 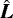, J, is small (≈ 2.6 × 10−6 ≈0.′′5 as estimated from the pole orientation parameters provided in Jacobson 2009), 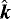can be replaced with 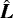, of which the motion equation up to order O(J2) (~ O(10−11)) can be written as 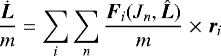(2)

which has all vectors expressed in the ICRS, where m is Neptune’s mass, Jn the n-th zonal harmonic of Neptune’s gravitational potential, ri the position vector from Neptune to the body i, and 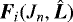the vector of the force acted on the body i due to Jn.

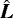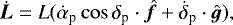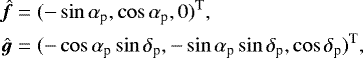As the torque caused by Jn is perpendicular to (e.g., Manche 2011), L is constant during the integration of Eq. (2). So, in practice, we only integrate the orientation angles of L, that is, pole right ascension αp and declination δp. To be specific, according to where (3)

the motion equation of (αp, δp) can be written as 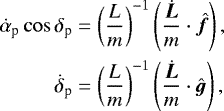(4)

where 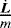is calculated by Eq. (2). The parameter 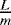is deduced from the latest inferred rotation rate and inertia factor of Neptune (Helled et al. 2010; Podolak & Helled 2012). However, we also note that, the difference between the new 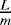value we use and that deduced from Jacobson (2009) is very small (0.075 σ) and the caused orbital difference is negligible. In our work, the inner satellites i = 3…7, 9 considered by Eq. (1) are neglected in Eqs. (2) and (4). As shown in Fig. 2, the caused difference in the pole orientation of Neptune is very small and thus negligible.

4 Solution method and results

4.1 Orbit determination and parameter estimation method

We determine the orbits by adjusting the parameters in our dynamical and observational models to fit the observations in a weighted least-squares (WLS) sense (e.g., Milani & Gronchi 2010). Using the WLS method, in addition to the nominal solution, the solution covariance matrix (CM) can also be obtained. The CM is a measure of the formal uncertainties in the adjusted model parameters; and the linear mapping of CM over time is a measure of the formal uncertainties in the propagations of the adjusted model parameters (e.g., Milani & Gronchi 2010).

However, these formal uncertainties are normally overly optimistic (e.g., Jacobson 2009; Desmars et al. 2009). The uncertainties introduced by accidental errors of observations are better assessed by performing bootstrap resampling of observations {ζk } (BR) with advantages of robustness (Desmars et al. 2009, 2013; Emelyanov 2010). Moreover, there are also uncertainties introduced by the errors in the nominal values of unadjusted model parameters {cℓ }. The effects of these errors on the distribution of possible solutions can be included by performing random sampling of {cℓ } (RS), which generates samples of {cℓ} from the Gaussian distributions, where means and variances are the nominal values 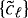and the squared uncertainties 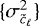of {cℓ }, respectively. These values 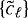and 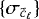are reported in Tables 1 and 2. Thus, to consider the effects of errors in {ζk } and 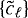, we use a method (BR-RS) performing both BR and RS:

  • 1)

    A new bootstrap sample of observations 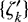is built as described in Desmars et al. (2009) and Emelyanov (2010).

  • 2)

    A new set of sampling values 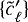of unadjusted parameters is generated from the Gaussian distributions .

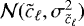  • 3)

    The model adopting 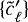is fitted to 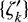and a new solution is obtained.

  • 4)

    The above steps are repeated as many times as desired, and a population of possible solutions is obtained.

The uncertainty of solution can be measured by the RMS of the differences between the possible solutions and the nominal solution. We call this uncertainty the BR-RS uncertainty.

4.2 Observational model parameters and the weighting scheme

Systematic errors in a data set are generally not known precisely enough. To cope with this problem, a constant bias is often introduced for each one-dimensional data set and, if necessary, is treated as an adjustable observational model parameter (e.g., Jacobson 2009). For Voyager imaging data, following Brozović et al. (2020), a single pair of sample and line biases is introduced. In addition to those biases of Earth-based astrometric data introduced and estimated in Jacobson (2009), biases for the new Triton meridian circle observations from Bordeaux Observatory (2007–2013) (Dourneau et al. 2015) and the Triton CCD observations of Wang et al. (2017) are also introduced. These additional biases are separately estimated for each observatory and each period of opposition.

For the weighting of the Voyager imaging data, as in previous work (e.g., Lainey et al. 2019), we use the uncertainties reported in Jacobson (2009) and rescale them by a scalar chosen to get 66% of astrometric residuals within 1σ level for each coordinate. For the Voyager B-plane data, the weights are evaluated with the uncertainties reported in Jacobson (2008). For the Earth-based and HST astrometric data, we assign the weights in accordance with the RMS of the post-fit residuals of each data group. The data are grouped according to data type, observatory, and period of opposition. Then, a 3σ rejection criteria is applied.

4.3 Adjusted dynamical parameters

Not all parameters (e.g., μs, μ1, μ2, J2, J4, and 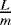) can be improved with the astrometry available to us. Some are well constrained with the Voyager radiometric tracking data (e.g., Jacobson 2008). For those parameters that cannot be improved, we keep them fixed in our orbit fitting process. The effects induced by their uncertainties on the adjusted parameters are assessed by the BR-RS method.

To prejudge whether the uncertainty of a parameter is possibly improvable, we analyzed the post-fit sensitivities of this parameter by a method analogous to that applied by for example, Beauvalet et al. (2012), Lainey (2016), and Dirkx et al. (2016). To be specific, by simulating ideal three-dimensional positions of satellites with the perturbation from a given parameter uncertainty turned on and then determining the satellite orbits with this perturbation turned off, we can see from the post-fit residuals how accurate the observations should be in order to improve this parameter. In this work, following Lainey (2016), we simulated data on a time span of 100 yr, roughly the time span of accurate observations. The only adjusted parameters of the orbit fitting simulations are the state vectors of Triton and Nereid at epoch.

For all the potentially adjustable parameters listed in Table 1, the pre- and post-fit residuals obtained from the abovementioned simulations are shown Table 3. The parameters and residuals in these tables show that the perturbations caused by the considered uncertainties can be absorbed in orbit fitting (e.g., Dirkx et al. 2016), especially for the GMs. Among the listed parameters, the pole orientation angles of Neptune at epoch are the most sensitive in the post-fit sense and can cause post-fit residuals up to a few tens of milliarcseconds as seen from Earth. Other parameters can only cause post-fit residuals at most a few milliarcseconds as seen from Earth, which, as mentioned in Lainey (2016), seems too small to be reliably detected from the astrometric data available to us. So, in our real orbit fitting process, in addition to the state vectors of Triton and Nereid at epoch, we also adjust the pole orientation angles of Neptune at epoch. We also tried to adjust other parameters in our real fitting process. However, as expected, these parameters are converged with formal uncertainties much larger than those listed in Table 1.

Our final solution is obtained by adjusting the state vectors of satellites at epoch, pole orientation angles of Neptune, and the observational model parameters mentioned in Sect. 4.2. The post-fit residual statistics are list in Tables A.1–A.5. The model we use can be fit to the observations with their estimated accuracies. The adjusted state vectors and pole orientation angles are summarized in Table 4. As shown in this table, the correlation between the two satellite state vectors, that between the two pole orientation angle, and that between each satellite state vector and each pole orientation angle are all weak. The pole orientation of Neptune is well constrained with a small formal 1σ uncertainty of 0.°012–0.°016. Triton has many observations and a long covered time interval that constrain its position at epoch down to a formal 1σ uncertainty of about 3 km. Nereid is much fainter than Triton and has fewer observations and a shorter covered time interval. This explains that its position at epoch is constrained with a little larger formal 1σ uncertainty of about 6–16 km. Also shown in Table 4 are the parameter value differences between our solution and NEP081 (Jacobson 2009). More details on the comparisons and reliable accuracy estimations for the orbit and pole solutions are provided in the following two sections.

The integrated ephemerides for Triton and Nereid are designated as FORCES-8-MAIN-2020. They are available online6 in SPICE format, covering years 1600–2650.

Table 3

Pre- and post-fit sensitivities of uncertainties of potentially adjustable dynamical parameters based on orbit fitting simulations over the 100-year period centered at the epoch t0.

Table 4

Summary of the dynamical parameter determinations.

thumbnail Fig. 3

Differences between our new ephemerides for Triton and Nereid and the previous JPL values, NEP081 (Jacobson 2009). These differences are shown in the orbit radial (R), transverse (T), and out-of-plane (N) directions defined by, for example, Jacobson (2009).

4.4 Comparisons and accuracies of Triton and Nereid orbits

Figure 3 compares the new orbits with NEP081. The differences are shown in the orbit radial (R), transverse (T), and out-of-plane (N) directions defined in, for example, Jacobson (2009). The big differences of Nereid orbit in R and T directions are directly related to the orbital mean motion difference, Δn, owing to the large orbital eccentricity. Jacobson (2009) formulated the relationship between the R and T changes of Nereid orbit using Δn. In this case, the relationship also closely matches the present Nereid orbit differences. The deduced Δn is +4.′′ 9 yr−1. Figure 4 presents the comparisons in distance.

We also compare the new orbits with the two most recent ephemerides available in MULTI-SAT7 (Emelyanov & Arlot 2008): the Emelyanov & Samorodov (2015) theory for Triton and the Emelyanov & Arlot (2011) theory for Nereid. These results are also presented in Fig. 4.

The formal orbital uncertainties derived by linear mapping of CM are shown in Fig. 5. However, to obtain more reliable accuracy estimations, it is necessary to consider the uncertainties in the observations and those in the unadjusted model parameters listed in Tables 1 and 2 with advantages of robustness. For this, we estimate the orbital uncertainties with the BR-RS method. The resulting BR-RS uncertainties are derived from 200 clones of the nominal orbits and shown in Fig. 6. The Jacobson (2009) formula relating the R and T changes of Nereid orbitalso closely match the present Nereid orbit uncertainties. The deduced BR-RS uncertainty in Nereid mean motion is σn ≈0.′′24 yr−1, that is, about 5% of Δn.

The orbits are well determined. Indeed, for the next 100 yr, the orbit uncertainties are expected to be within 200 km (about 10 mas as seen from the Earth) for Triton and 1000 km (50 mas) for Nereid as estimated by the BR-RS method.

thumbnail Fig. 4

Distances between the positions from our new ephemerides and those from NEP081 and MULTI-SAT (Emelyanov & Arlot 2008).The MULTI-SAT ephemerides are the Emelyanov & Samorodov (2015) theory for Triton and the Emelyanov & Arlot (2011) theory for Nereid. For the Emelyanov & Arlot (2011) theory, as MULTI-SAT only provides the ephemeris between 1920 and 2050, we only make the comparison in this time span.
thumbnail Fig. 5

Formal 1σ uncertainties in our Triton and Nereid orbits based on linear mapping of the covariance matrix. These uncertainties are represented in the orbit radial (R), transverse (T), and out-of-plane (N) directions.

4.5 Comparisons and accuracy of the pole orientation of Neptune

In addition to the orbital uncertainties, the CM and BR-RS methods used in the previous section also provide the formal and BR-RS uncertainties of the pole orientation of Neptune, respectively. Figure 7 shows the comparison with Jacobson (2009) solution and the formal and BR-RS uncertainties for the pole orientation angles at epoch, and Fig. 8 for the pole orientation motion. At the initial epoch, the pole solution is about three times both the formal and BR-RS 1σ uncertainties away from the Jacobson (2009) solution, but still matches that solution at about 1σ limits (also see Table 4). In 1800–2200, the pole orientation motion is well constrained with a BR-RS 1σ uncertainty of about 0.°01–0.°05, which is visibly smaller than that of the Jacobson (2009) solution.

The improvement of the uncertainty of the pole solution is mainly due to large numbers of accurate data accumulated after Jacobson (2009). If we only use the data available before 2009, the obtained formal uncertainty would be more than three times larger than the final solution provided in Table 4.

5 Discussion

5.1 Neptunian system angular momentum direction

Figure 9 shows the Neptunian system angular momentum direction based on our orbit and pole solution. This figure showsthat there is a visible linear drift in its motion. However, if we only consider the Neptune-Triton two-body system as assumed in the Jacobson (2009) model of the pole orientation of Neptune, the linear drift disappears.

thumbnail Fig. 6

BR-RS 1σ uncertainties in our Triton and Nereid orbits. These uncertainties are derived from 200 clones of nominal solution obtained by the BR-RS method. These values are shown in the orbit radial (R), transverse (T), and out-of-plane (N) directions.
thumbnail Fig. 7

Comparison with the Jacobson (2009) solution and the formal and BR-RS uncertainties for poleorientation angles of Neptune at the initial epoch 1989 September 1 TDB. Here, the BR-RS uncertainties are derived from 200 clones of the nominal pole orientation obtained by the BR-RS method. The differences and uncertainties are shown in the right ascension (αp) and declination (δp).

5.2 Mean orbital elements based on the precessing ellipse model

To permit a simple geometric description of the orbits, the mean orbital elements are provided in Table 5. In this table, following Jacobson (2009), the elements are derived by fitting a precessing ellipse to each integrated orbit over the 400-year time span from 1800 January 1 to 2200 January 1. For Triton, the ellipse represents a planetocentric orbit, and for the far more distant Nereid, an orbit with a focus located at Neptunian system barycenter.

As part of the model parameters, the Laplace plane pole directions also appear in Table 5. As expected, the Laplace plane pole of Triton matches the Neptunian system angular momentum direction (see Fig. 9).

5.3 Parameters of Triton’s motion based on Emelyanov & Samorodov (2015) model

For Triton, Emelyanov & Samorodov (2015) noted that the precessing ellipse model is only approximate as it does not consider the periodic perturbations in the orbital elements. Therefore, they developed a new analytical model by adding the corrections for these perturbations. In this work, we also add these corrections and then derive the parameters of the motion of Triton by fitting the analytical model to the integrated Triton orbit around Neptune over the 400-year time span from 1800 January 1 to 2200 January 1. The results are provided in Table 6.

Figure 10 compares both Triton positions calculated from the precessing ellipse model and those from the analytical model with the integrated orbit. This figure shows the residuals from the precessing ellipse model can reach 84 km, while the overall residuals from the analytic model do not exceed 14 km. Most of the time, the residuals from the precessing ellipse model exceed 20 km, but those from the analytical model are only several kilometers. The RMS of the analytic model is 6.5 km, much smaller than that of the precessing ellipse model. Generally speaking, the error of the analytical model is much smaller than that of the precessing ellipse model, and almost at the level of the best observation accuracy (~ 5 km). A more accurate model will probably be obtained with a redetermination of the abovementioned corrections for periodic perturbations based on DE440. This will be discussed in our future work.

As part of the model parameters, the pole direction of the orbital coordinate system defined by Emelyanov & Samorodov (2015) also appears in Table 6. This pole direction matches the Neptunian system angular momentum direction (see Fig. 9) within a few arcseconds and, as expected, much more closely than the Laplace plane pole.

thumbnail Fig. 8

Comparison with Jacobson (2009) solution and the formal and BR-RS 1σ uncertainties for the motion of the pole orientation of Neptune. The BR-RS uncertainties are derived from 200 clones of the nominal pole orientation obtained by the BR-RS method. The differences and uncertainties are shown in the right ascension (αp) and declination (δp).
thumbnail Fig. 9

Neptunian system angular momentum direction based on our orbit and pole solution. This direction is represented in terms of the right ascension (αr) and the declination (δr) referred to ICRS.

5.4 Rotational elements for the pole orientation of Neptune

To permit using the IAU standard on rotational elements (e.g., Archinal et al. 2018) to describe the geometry of the pole orientation of Neptune, an analytical representation is provided in Table 7. This representation is obtained by fitting trigonometric series to our integrated pole orientation from 1600 to 2650. Overall angular distance residuals are well constrained within about 0.′′08. As expected, the secular terms match the linear drift rates of the Neptunian system angular momentum direction (see Fig. 9).

6 Conclusions

The present paper reports on the new ephemerides for Triton and Nereid that are fitted to all available data through 2020. Many observations are used for the first time for Triton and Nereid orbit determinations. We also update the dynamical model for the present work. The new model makes use of the new ephemerides for planets and the inner satellites of Neptune, DE440 and NEP090, respectively. And, in addition to the gravitational effects considered by NEP081 (Jacobson 2009), this model also includes perturbations from inner satellites and a revised model for the motion of the pole orientation of Neptune. The model we use can be fit to the observations with their estimated accuracies.

The orbits are well determined with the orbit uncertainties expected to be within 200 km (about 10 mas as seen from the Earth) for Triton and 1000 km (50 mas) for Nereid for the next 100 yr as estimated from the BR-RS method. In particular, the correction in Nereid mean orbit motion from the NEP081 solution is +4.′′ 9 yr−1, with a BR-RS uncertainty of 0.′′ 24 yr−1. In the fitting process, we also determine the pole orientation of Neptune. At the initial epoch 1989 September 1 TDB, the right ascension and declination of the new pole orientation referred to the ICRS are αp = 299.°339 ± 0.°012 (formal)∕ ± 0.°014 (BR-RS) and δp = 42.°985 ± 0.°016 (formal)∕ ± 0.°045 (BR-RS), respectively. This pole orientation at epoch is about three times the formal and BR-RS 1σ uncertainties away from the JPL solution (Jacobson 2009), αp = 299.°38 ± 0.°12 and δp = 42.°95 ± 0.°03, but still matches them at about 1σ limits. In 1800–2200, the pole orientation motion is well constrained with a BR-RS uncertainty of about 0.°01–0.°05.

The new ephemerides for Triton and Nereid are designated as FORCES-8-MAIN-2020. These results are available online in SPICE format, covering years 1600–2650.

Geometric descriptions of the improved Triton and Nereid orbits and the pole orientation of Neptune are provided. Jacobson (2009) adopted a precessing ellipse model to describe the two satellite orbits, and we adopted this model as well. However, for Triton, Emelyanov & Samorodov (2015) noted that adding some necessary periodic terms to this model can describe the motion of Triton with much higher precision. By fitting the new model to our integrated Triton orbit, an improved analytical theory of the motion of Triton has been obtained. To describe the motion of the pole orientation of Neptune, we adopted the IAU standard. We find that the secular terms of rotational elements of the Neptune pole match the linear drift rate of the Neptunian system angular momentum direction.

Table 5

Mean orbital elements at epoch 2000 January 1.5 TDB referred to the local Laplace planes based on the precessing ellipse model fitted to the integrated orbit.

Table 6

Parameters of the motion of Triton at epoch 2000 January 1.5 TDB based on Emelyanov & Samorodov (2015) model fitted to the integrated orbit.

thumbnail Fig. 10

Residuals between Triton positions calculated from the precessing ellipse model (see Table 5) and the analytical model (see Table 6), respectively, with respect to the integrated orbit.
Table 7

Parameters of series for rotational elements of the pole orientation of Neptune at epoch 2000 January 1.5 TDB referred to the ICRS.

Acknowledgements

We thank the anonymous reviewer for helpful comments on an earlier draft of this paper. We acknowledge the science research grants from the China Manned Space Project with NO.CMS-CSST-2021-A12, CMS-CSST-2021-B10. This research is funded by the National Natural Science Foundation of China (NSFC) under grant Nos. 11178006, 11273066, 11533004, and 11673071. This research is also supported by the B-type Strategic Priority Program of the Chinese Academy of Sciences, Grant No. XDB41000000. This research has made use of data provided by the Lijiang 2.4-m Telescope at Yunnan Observatory and by the Yaoan High Precision Telescope at Purple Mountain Observatory, and the observational data extracted from the IAU Minor Planet Center (MPC), the Natural Satellite Data Center (NSDC), and the JPL Solar System Dynamics Website. This research has also made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Following tools have been essential to this research project: JPL Horizons On-Line Ephemeris System; NASA/JPL-generated SPICE data and the allied software.

Appendix A Additional tables

Table A.1

Voyager imaging data and the post-fit residual statistics.

Table A.2

Voyager B-plane data and the post-fit residual statistics.

Table A.3

Triton Earth-based and HST observations and the post-fit residual statistics (before 1901).

Table A.4

Triton Earth-based and HST observations and the post-fit residual statistics (after 1901).

Table A.5

Nereid Earth-based observations and the post-fit residual statistics.

References

  1. Agnor, C. B., & Hamilton, D. P. 2006, Nature, 441, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Aitken, R. G. 1899, Astron. Nachr., 149, 373 [CrossRef] [Google Scholar]
  3. Aitken, R. G. 1904, Lick Observ. Bull., 51, 157 [CrossRef] [Google Scholar]
  4. Albrecht, S., & Smitil, E. 1909, Lick Observ. Bull., 5, 109 [NASA ADS] [CrossRef] [Google Scholar]
  5. Alden, H. L. 1940, AJ, 49, 70 [CrossRef] [Google Scholar]
  6. Alden, H. L. 1943, AJ, 50, 110 [CrossRef] [Google Scholar]
  7. Archinal, B. A., Acton, C. H., A’Hearn, M. F., et al. 2018, Celest. Mech. Dyn. Astron., 130, 22 [Google Scholar]
  8. Balanovskiĭ, I. A. 1923, Mitteilungen der Nikolai-Hauptsternwarte zu Pulkowo, 9, 85 [Google Scholar]
  9. Barnard, E. E. 1893, AJ, 13, 10 [CrossRef] [Google Scholar]
  10. Barnard, E. E. 1894, AJ, 14, 9 [CrossRef] [Google Scholar]
  11. Barnard, E. E. 1895, AJ, 15, 41 [CrossRef] [Google Scholar]
  12. Barnard, E. E. 1898, AJ, 19, 25 [CrossRef] [Google Scholar]
  13. Barnard, E. E. 1899, AJ, 20, 41 [CrossRef] [Google Scholar]
  14. Barnard, E. E. 1901, AJ, 22, 27 [CrossRef] [Google Scholar]
  15. Barnard, E. E. 1903, AJ, 23, 105 [CrossRef] [Google Scholar]
  16. Barnard, E. E. 1906a, AJ, 25, 41 [CrossRef] [Google Scholar]
  17. Barnard, E. E. 1906b, AJ, 25, 100 [CrossRef] [Google Scholar]
  18. Barnard, E. E. 1907, AJ, 25, 164 [CrossRef] [Google Scholar]
  19. Barnard, E. E. 1909, Astron. Nachr., 181, 321 [CrossRef] [Google Scholar]
  20. Barnard, E. E. 1910, AJ, 26, 144 [Google Scholar]
  21. Barnard, E. E. 1912, AJ, 27, 111 [Google Scholar]
  22. Barnard, E. E. 1913, AJ, 28, 10 [Google Scholar]
  23. Barnard, E. E. 1915, AJ, 29, 39 [Google Scholar]
  24. Barnard, E. E. 1916, AJ, 30, 2 [Google Scholar]
  25. Barnard, E. E. 1917, AJ, 30, 214 [Google Scholar]
  26. Barnard, E. E. 1919, AJ, 32, 103 [Google Scholar]
  27. Barnard, E. E. 1927, AJ, 37, 127 [CrossRef] [Google Scholar]
  28. Beauvalet, L., Lainey, V., Arlot, J. E., & Binzel, R. P. 2012, A&A, 540, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Boué, G., & Laskar, J. 2006, Icarus, 185, 312 [NASA ADS] [CrossRef] [Google Scholar]
  30. Bower, E. C., & Hall, A. 1923, AJ, 35, 108 [Google Scholar]
  31. Brozović, M., Showalter, M. R., Jacobson, R. A., et al. 2020, Icarus, 338, 113462 [CrossRef] [Google Scholar]
  32. Burton, H. E. 1913, AJ, 28, 44 [Google Scholar]
  33. Burton, H. E., & Hall, A., J. 1919, AJ, 32, 113 [CrossRef] [Google Scholar]
  34. Christie, W. H. M. 1901, Greenwich Observations in Astronomy, Magnetism and Meteorology made at the Royal Observatory, Series 2 (USA: Rarebooksclub), 61, D240 [Google Scholar]
  35. Christie, W. H. M. 1904, Greenwich Observations in Astronomy, Magnetism and Meteorology made at the Royal Observatory, Series 2 (USA: Rarebooksclub), 64, G59 [Google Scholar]
  36. Christie, W. H. M. 1909, Greenwich Observations in Astronomy, Magnetism and Meteorology made at the Royal Observatory, Series 2 (USA: Rarebooksclub), 69, G207 [Google Scholar]
  37. Crawford, R. T. 1928, Lick Observ. Bull., 404, 8 [Google Scholar]
  38. Davis, C. H. 1874, MNRAS, 35, 49 [Google Scholar]
  39. Desmars, J., Arlot, S., Arlot, J. E., Lainey, V., & Vienne, A. 2009, A&A, 499, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Desmars, J., Li, S. N., Tajeddine, R., Peng, Q. Y., & Tang, Z. H. 2013, A&A, 553, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Desmars, J., Camargo, J. I. B., Braga-Ribas, F., et al. 2015, A&A, 584, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Dirkx, D., Lainey, V., Gurvits, L. I., & Visser, P. N. A. M. 2016, P&SS, 134, 82 [NASA ADS] [CrossRef] [Google Scholar]
  43. Dourneau, G., Le Campion, J. F., Rapaport, M., et al. 2007, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 89 [Google Scholar]
  44. Dourneau, G., Le Campion, J. F., Bontemps, S., et al. 2015, Notes Scientifiques et Techniques de l’Institut de Mecanique Celeste, 97 [Google Scholar]
  45. Drew, D. A. 1897, AJ, 17, 131 [Google Scholar]
  46. Drew, D. A. 1899, AJ, 20, 30 [Google Scholar]
  47. Emelyanov, N. 2010, Planet. Space Sci., 58, 411 [NASA ADS] [CrossRef] [Google Scholar]
  48. Emelyanov, N. V., & Arlot, J. E. 2008, A&A, 487, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Emelyanov, N. V., & Arlot, J. E. 2011, MNRAS, 417, 458 [CrossRef] [Google Scholar]
  50. Emelyanov, N. V., & Kanter, A. A. 2005, Sol. Syst. Res., 39, 112 [NASA ADS] [CrossRef] [Google Scholar]
  51. Emelyanov, N. V., & Samorodov, M. Y. 2015, MNRAS, 454, 2205 [Google Scholar]
  52. Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proceedings of IAU Colloq. 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, & G. B. Valsecchi. (Dordrecht: Reidel, Astrophysics and Space Science Library), 115 [Google Scholar]
  53. Fienga, A., Manche, H., Laskar, J., & Gastineau, M. 2008, A&A, 477, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Gomes-Júnior, A. R., Assafin, M., Vieira-Martins, R., et al. 2015, A&A, 580, A76 [CrossRef] [EDP Sciences] [Google Scholar]
  55. Hall, A. 1876, Astron. Nachr., 88, 131 [Google Scholar]
  56. Hall, A. 1877, Astron. Nachr., 90, 161 [Google Scholar]
  57. Hall, A. 1900, AJ, 20, 191 [Google Scholar]
  58. Hall, A. J. 1911, AJ, 26, 179 [CrossRef] [Google Scholar]
  59. Hall, A. J. 1920, AJ, 33, 62 [CrossRef] [Google Scholar]
  60. Hall, A. J. 1922, AJ, 34, 18 [CrossRef] [Google Scholar]
  61. Hall, A. J., & Burton, H. E. 1913, AJ, 28, 42 [CrossRef] [Google Scholar]
  62. Hammond, J. C. 1906, AJ, 25, 93 [Google Scholar]
  63. Hammond, J. C., & Rice, H. L. 1905, AJ, 24, 188 [Google Scholar]
  64. Harrington, R. S., & Walker, R. L. 1984, AJ, 89, 889 [Google Scholar]
  65. Harris, D., & van Biesbroeck, G. 1949, AJ, 54, 197 [CrossRef] [Google Scholar]
  66. Helled, R., Anderson, J. D., & Schubert, G. 2010, Icarus, 210, 446 [NASA ADS] [CrossRef] [Google Scholar]
  67. Henry, P. 1884a, Bull. Astron. Ser. I, 1, 89 [Google Scholar]
  68. Henry, P. 1884b, Bull. Astron. Ser. I, 1, 178 [Google Scholar]
  69. Henry, P., Boinot, A., & Sy, F. 1886, Bull. Astron. Ser. I, 3, 488 [Google Scholar]
  70. Hussey, W. J. 1899, AJ, 20, 71 [Google Scholar]
  71. Hussey, W. J. 1902, Lick Observ. Bull., 17, 139 [Google Scholar]
  72. Jacobson, R. A. 1991, A&AS, 90, 541 [Google Scholar]
  73. Jacobson, R. A. 2008, in AIAA/AAS Astrodynamics Specialist Conference and Exhibit (Pasadena, CA: Jet Propulsion Laboratory, National Aeronauticsand Space Administration), AIAA 2008-7372 [Google Scholar]
  74. Jacobson, R. A. 2009, AJ, 137, 4322 [Google Scholar]
  75. Kiseleva, T. P., Chanturiya, S. M., Vasil’eva, T. A., & Kalinichenko, O. A. 2012, Sol. Syst. Res., 46, 436 [CrossRef] [Google Scholar]
  76. Kiss, C., Pál,A., Farkas-Takács, A. I., et al. 2016, MNRAS, 457, 2908 [NASA ADS] [CrossRef] [Google Scholar]
  77. Kostinsky, S. 1900, Astron. Nachr., 152, 277 [Google Scholar]
  78. Kostinsky, S. 1902, Astron. Nachr., 157, 287 [Google Scholar]
  79. Kulyk, I., Izakevich, E. M., & Shatokhina, S. 2009, Private Communication to NSDC, http://nsdb.imcce.fr/obspos/OBS_COLL/N/nm0016.html [Google Scholar]
  80. Lainey, V. 2016, Celest. Mech. Dyn. Astron., 126, 145 [NASA ADS] [CrossRef] [Google Scholar]
  81. Lainey, V., Duriez, L., & Vienne, A. 2004, A&A, 420, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Lainey, V., Noyelles, B., Cooper, N., et al. 2019, Icarus, 326, 48 [Google Scholar]
  83. Landgraf, W. 1988, IAU Circ., 4542, 1 [Google Scholar]
  84. Lassell, W. 1849a, MNRAS, 9, 103 [Google Scholar]
  85. Lassell, W. 1849b, MNRAS, 10, 8 [Google Scholar]
  86. Lassell, W. 1850, MNRAS, 10, 132 [Google Scholar]
  87. Lassell, W. 1851, MNRAS, 11, 61 [Google Scholar]
  88. Lassell, W. 1852a, MNRAS, 13, 37 [Google Scholar]
  89. Lassell, W. 1852b, MNRAS, 12, 155 [Google Scholar]
  90. Lassell, W. 1857, MNRAS, 17, 70 [Google Scholar]
  91. Lassell, W. 1864, MNRAS, 24, 209 [Google Scholar]
  92. Li, D., & Christou, A. A. 2020, AJ, 159, 184 [CrossRef] [Google Scholar]
  93. Li, D., Johansen, A., Mustill, A. J., Davies, M. B., & Christou, A. A. 2020, A&A, 638, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Lohse, J. G. 1887, MNRAS, 47, 497 [Google Scholar]
  97. Manche, H. 2011, theses, Observatoire de Paris, France [Google Scholar]
  98. Milani, A., & Gronchi, G. F. 2010, Theory of Orbital Determination (Cambridge: Cambridge University Press) [Google Scholar]
  99. Mitchell, K. L., Prockter, L. M., Frazier, W. E., et al. 2019, Lunar Planet. Sci. Conf. Lunar Planet. Sci. Conf., 3200 [Google Scholar]
  100. MPC 1990, Minor Planet Center, Circular No. 40913 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  101. MPC 1999, Minor Planet Center, Circular No. 38967, 49878 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  102. MPC 2001, Minor Planet Center, Circular No. 43261, 44182, 47500, 47501, 49423 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  103. MPC 2002, Minor Planet Center, Circular No. 46216, 46508, 47500, 47501, 49423, 49767, 59029 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  104. MPC 2003, Minor Planet Center, Circular No. 49423, 49424, 49767 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  105. MPC 2004, Minor Planet Center, Circular No. 52312, 52313, 52492, 52493, 52887, 53171, 53948, 54697, 54698 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  106. MPC 2005, Minor Planet Center, Circular No. 54343, 54557, 54698, 54823, 54965, 55508 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  107. MPC 2006, Minor Planet Center, Circular No. 56794, 57110, 57416, 57417, 57573, 57574, 57792, 57793, 57947, 58097 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  108. MPC 2007, Minor Planet Center, Circular No. 59581, 59860, 60086, 60268, 60451, 60647, 60906, 61163 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  109. MPC 2008, Minor Planet Center, Circular No. 62864, 63123, 63363, 63584, 63806, 64093, (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  110. MPC 2009, Minor Planet Center, Circular No. 65920, 66450, 66686, 66905, 67130, 67668, 78327 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  111. MPC 2010, Minor Planet Center, Circular No. 70193, 71528, 72437, 80452 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  112. MPC 2011, Minor Planet Center, Circular No. 75593, 75849, 76329, 76732, 77162, 79140 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  113. MPC 2012, Minor Planet Center, Circular No. 79746, 79971, 80114, 80452 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  114. MPC 2013, Minor Planet Center, Circular No. 83713, 84214, 84512, 84739, 85079, 85502, 100688 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  115. MPC 2014, Minor Planet Center, Circular No. 89137, 89456, 90446, 90966, 100688, 100689 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  116. MPC 2015, Minor Planet Center, Circular No. 94830, 95374, 97001, 99414, 100689 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  117. MPC 2016, Minor Planet Center, Circular No. 101342 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  118. MPC 2017, Minor Planet Center, Circular No. 107170 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  119. MPC 2018, Minor Planet Center, Circular No. 110808, 115066, 115989 (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  120. Neuĭmin, G. N., & Pokrovskiĭ, K. D. 1926, Mitteilungen der Nikolai-Hauptsternwarte zu Pulkowo, 10, 418 [Google Scholar]
  121. Owen, W. M. 1999a, Private Communication to NSDC, http://nsdb.imcce.fr/obspos/OBS_COLL/N/nm0005.html [Google Scholar]
  122. Owen, W. M. 1999b, Private Communication to NSDC, http://nsdb.imcce.fr/obspos/OBS_COLL/N/nm0006.html [Google Scholar]
  123. Park, R. S., Folkner, W. M., Williams, J. G., & Boggs, D. H. 2021, AJ, 161, 105 [NASA ADS] [CrossRef] [Google Scholar]
  124. Parrish, N. M., & Stone, O. 1892, AJ, 12, 90 [Google Scholar]
  125. Perrine, C. D. 1903, Lick Observ. Bull., 39, 70 [Google Scholar]
  126. Perrotin, H. J. 1887, Bull. Astron. Ser. I, 4, 339 [Google Scholar]
  127. Podolak, M., & Helled, R. 2012, ApJ, 759, L32 [NASA ADS] [CrossRef] [Google Scholar]
  128. Prockter, L. M., Mitchell, K. L., Howett, C. J. A., et al. 2019, Lunar Planet. Sci. Conf., 3188 [Google Scholar]
  129. Qiao, R. C., Yan, Y. R., Shen, K. X., et al. 2007, MNRAS, 376, 1707 [Google Scholar]
  130. Qiao, R. C., Zhang, H. Y., Dourneau, G., et al. 2014, MNRAS, 440, 3749 [Google Scholar]
  131. Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [NASA ADS] [CrossRef] [Google Scholar]
  132. ROG 1899, MNRAS, 59, 501 [Google Scholar]
  133. ROG 1900, MNRAS, 61, 9 [Google Scholar]
  134. ROG 1903, MNRAS, 63, 503 [Google Scholar]
  135. ROG 1904, MNRAS, 64, 835 [Google Scholar]
  136. ROG 1905, MNRAS, 66, 10 [Google Scholar]
  137. ROG 1906, MNRAS, 67, 91 [Google Scholar]
  138. ROG 1907, MNRAS, 68, 33 [Google Scholar]
  139. ROG 1908, MNRAS, 68, 586 [Google Scholar]
  140. ROG 1913, MNRAS, 73, 155 [Google Scholar]
  141. Rose, L. E. 1974, AJ, 79, 489 [CrossRef] [Google Scholar]
  142. Rufu, R., & Canup, R. M. 2017, AJ, 154, 208 [CrossRef] [Google Scholar]
  143. Rümker, C. 1849, MNRAS, 9, 221 [Google Scholar]
  144. Schaeberle, J. M. 1895, AJ, 15, 25 [Google Scholar]
  145. Schaeberle, J. M. 1897, AJ, 17, 62 [Google Scholar]
  146. Schaeberle, J. M. 1898, AJ, 18, 168 [Google Scholar]
  147. Schaefer, M. W., & Schaefer, B. E. 1988, Nature, 333, 436 [CrossRef] [Google Scholar]
  148. Showalter, M. R., de Pater, I., Lissauer, J. J., & French, R. S. 2019, Nature, 566, 350 [NASA ADS] [CrossRef] [Google Scholar]
  149. Soulié, G., Dupouy, Teulet, Broqua, & Dulou. 1975, A&AS, 22, 49 [Google Scholar]
  150. Tang, K., Song, Y. Z., Shen, K. X., et al. 2020, A&A, 641, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  151. TMO 2014, CCD Astrometric Measurements from Table Mountain Observatory, https://ssd.jpl.nasa.gov/dat/planets/ccd_tmo.txt [Google Scholar]
  152. USNO 1881, Astronomical and Meteorological Observations made at the U.S. Naval Observatory, 17, 1 [Google Scholar]
  153. USNO 1911, Publications of the U.S. Naval Observatory Second Series, 6, A1 [Google Scholar]
  154. USNO 2013, CCD Astrometric Measurements from US Naval Observatory/Flagstaff Using the Flagstaff Astrometric Scanning Transit Telescope, https://ssd.jpl.nasa.gov/dat/planets/ccd1_nofs.txt [Google Scholar]
  155. USNO 2014, Flagstaff Astrometric Scanning Transit Telescope Planet and Planetary Satellite Observations, https://www.usno.navy.mil/USNO/astrometry/optical-IR-prod/solsys/fastt-plansat [Google Scholar]
  156. van Biesbroeck, G., Vesely, C. D., Aksnes, K., & Marsden, B. G. 1976, AJ, 81, 122 [NASA ADS] [CrossRef] [Google Scholar]
  157. Veiga, C. H., & Martins, R. V. 1998, A&AS, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  158. Veiga, C. H., & Vieira Martins, R. 1996, A&AS, 120, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Veiga, C. H., Vieira Martins, R., Le Guyader, C., & Assafin, M. 1996, A&AS, 115, 319 [Google Scholar]
  160. Veiga, C. H., Martins, R. V., & Le Guyader, C. 1999, A&AS, 136, 445 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  161. Veillet, C. 1982, A&A, 112, 277 [Google Scholar]
  162. Veillet, C., & Bois, E. 1988, A&A, 189, 303 [Google Scholar]
  163. Vieira Martins, R., Veiga, C. H., Bourget, P., Andrei, A. H., & Descamps, P. 2004, A&A, 425, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  164. Walker, R. L.,& Harrington, R. S. 1988, AJ, 95, 1562 [NASA ADS] [CrossRef] [Google Scholar]
  165. Walker, R. L., Christy, J. W., & Harrington, R. S. 1978, AJ, 83, 838 [Google Scholar]
  166. Wang, N., Peng, Q. Y., Peng, H. W., et al. 2017, MNRAS, 468, 1415 [Google Scholar]
  167. Winlock, J., & Pickering, E. C. 1888, Annals of Harvard College Observatory, 13, 86 [Google Scholar]
  168. Wirtz, C. W. 1905, Astron. Nachr., 169, 33 [Google Scholar]
  169. Yizhakevych, O. M., Andruk, V. M., & Pakuliak, L. K. 2016, Odessa Astron. Pub., 29, 155 [Google Scholar]
  170. Young, C. A. 1888, AJ, 8, 14 [Google Scholar]
  171. Yu, Y., Qiao, R. C., Yan, D., et al. 2018, Planet. Space Sci., 152, 82 [CrossRef] [Google Scholar]
  172. Yu, Y., Cheng, X., Qiao, R. C., et al. 2019, Planet. Space Sci., 165, 205 [CrossRef] [Google Scholar]
  173. Yuan, Y., Li, F., Fu, Y., & Ren, S. 2021, A&A, 645, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  174. Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
4

OCNS2019 is available at the National Astronomical Data Center of China (NADC) via https://nadc.china-vo.org/article/20200722160959?id=101047

5

The catalog OCANS-8-2020, which stands for the 2020 version of Observational Catalog of Astrometry for Natural Satellites of the 8th planet (Neptune), is available in http://paperdata.china-vo.org/yuanye/forces-8-main-2020.zip

All Tables

Table 1

Initial conditions and other parameters of Neptune and integrated satellites used in the dynamical modeling and relevant analysis.

In the text
Table 2

Parameters of the perturbing Sun, planets, and satellites used in the dynamical modeling and relevant analysis.

In the text
Table 3

Pre- and post-fit sensitivities of uncertainties of potentially adjustable dynamical parameters based on orbit fitting simulations over the 100-year period centered at the epoch t0.

In the text
Table 4

Summary of the dynamical parameter determinations.

In the text
Table 5

Mean orbital elements at epoch 2000 January 1.5 TDB referred to the local Laplace planes based on the precessing ellipse model fitted to the integrated orbit.

In the text
Table 6

Parameters of the motion of Triton at epoch 2000 January 1.5 TDB based on Emelyanov & Samorodov (2015) model fitted to the integrated orbit.

In the text
Table 7

Parameters of series for rotational elements of the pole orientation of Neptune at epoch 2000 January 1.5 TDB referred to the ICRS.

In the text
Table A.1

Voyager imaging data and the post-fit residual statistics.

In the text
Table A.2

Voyager B-plane data and the post-fit residual statistics.

In the text
Table A.3

Triton Earth-based and HST observations and the post-fit residual statistics (before 1901).

In the text
Table A.4

Triton Earth-based and HST observations and the post-fit residual statistics (after 1901).

In the text
Table A.5

Nereid Earth-based observations and the post-fit residual statistics.

In the text

All Figures

thumbnail Fig. 1

Differences in Triton and Nereid orbits between the model including complete perturbations from all the inner regular satellites of Neptune and other simplified models. The complete perturbations from inner regulars are calculated by using the positions provided by NEP090 ephemerides (Brozović et al. 2020). Parameters and are the corrections applied to the coefficients J2 and J4, respectively,for the simplification and speeding up of calculations of perturbations from inner regular satellites. The initial epoch is always 1989 September 1 TDB, near the time at which the most accurate data are obtained during Voyager’s encounter. The red area is the period spanned by Voyager encounter data (1988–1989) and the gray area without such data (1847–1987 and 1990–2020).
In the text
thumbnail Fig. 2

Pole orientation of Neptune difference between the model including the perturbations from all inner regulars and that including the perturbations from only one inner regular, Proteus. All perturbations from inner regulars are calculated by using the positions provided by NEP090 ephemerides (Brozović et al. 2020). The initialepoch is 1989 September 1 TDB. The pole orientation difference is shown in the right ascension (αp) and declination (δp) referred to the ICRS.
In the text
thumbnail Fig. 3

Differences between our new ephemerides for Triton and Nereid and the previous JPL values, NEP081 (Jacobson 2009). These differences are shown in the orbit radial (R), transverse (T), and out-of-plane (N) directions defined by, for example, Jacobson (2009).
In the text
thumbnail Fig. 4

Distances between the positions from our new ephemerides and those from NEP081 and MULTI-SAT (Emelyanov & Arlot 2008).The MULTI-SAT ephemerides are the Emelyanov & Samorodov (2015) theory for Triton and the Emelyanov & Arlot (2011) theory for Nereid. For the Emelyanov & Arlot (2011) theory, as MULTI-SAT only provides the ephemeris between 1920 and 2050, we only make the comparison in this time span.
In the text
thumbnail Fig. 5

Formal 1σ uncertainties in our Triton and Nereid orbits based on linear mapping of the covariance matrix. These uncertainties are represented in the orbit radial (R), transverse (T), and out-of-plane (N) directions.
In the text
thumbnail Fig. 6

BR-RS 1σ uncertainties in our Triton and Nereid orbits. These uncertainties are derived from 200 clones of nominal solution obtained by the BR-RS method. These values are shown in the orbit radial (R), transverse (T), and out-of-plane (N) directions.
In the text
thumbnail Fig. 7

Comparison with the Jacobson (2009) solution and the formal and BR-RS uncertainties for poleorientation angles of Neptune at the initial epoch 1989 September 1 TDB. Here, the BR-RS uncertainties are derived from 200 clones of the nominal pole orientation obtained by the BR-RS method. The differences and uncertainties are shown in the right ascension (αp) and declination (δp).
In the text
thumbnail Fig. 8

Comparison with Jacobson (2009) solution and the formal and BR-RS 1σ uncertainties for the motion of the pole orientation of Neptune. The BR-RS uncertainties are derived from 200 clones of the nominal pole orientation obtained by the BR-RS method. The differences and uncertainties are shown in the right ascension (αp) and declination (δp).
In the text
thumbnail Fig. 9

Neptunian system angular momentum direction based on our orbit and pole solution. This direction is represented in terms of the right ascension (αr) and the declination (δr) referred to ICRS.
In the text
thumbnail Fig. 10

Residuals between Triton positions calculated from the precessing ellipse model (see Table 5) and the analytical model (see Table 6), respectively, with respect to the integrated orbit.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.