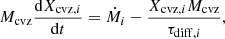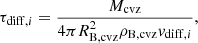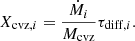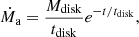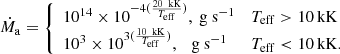EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A57 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A57
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202039692
Published online 11 October 2021

© ESO 2021

1. Introduction

It is well known that single stars with an initial mass between ∼1 and 8 M⊙ finally evolve into white dwarfs (WDs). Due to high gravitational fields (log g∼8 cm s−2), the heavy elements on WDs’ surfaces would diffuse downward during WD cooling. Usually, the timescale of diffusion (τdiff) at the photosphere is approximately several to 104 years (Koester 2009), which is much shorter than the cooling timescale (tcool ∼ 109 yr, e.g., Shapiro & Teukolsky 1983; Zhu et al. 2019; Lü et al. 2017, 2020). Therefore, cool WDs should have pure hydrogen (H) or helium (He) atmospheres. The former is referred to as a DA WD, while the latter is called a DB WD. However, Zuckerman et al. (2003) pointed out that more than 25% of WDs are polluted by metal elements such as Mg, Fe, and Na. WDs are referred to as DAZ or DBZ WDs if their spectra show H or He lines with heavy element lines. When only heavy elements lines are displayed in the spectra, WDs are categorized as DZ type. Three different ways are proposed as three possible sources for the surface heavy elements of the WDs, such as primordial or fallback stellar material, interstellar medium, or debris disk produced by WD tidally disrupting rocky objects (i.e. planets, e.g., Farihi 2016).

The pollution of WDs has been explained by ongoing accretion of planetary debris. A number of pieces of observational evidence show the infrared emission from debris disk around polluted WDs (Jura 2003; Farihi et al. 2009; Girven et al. 2012; Vanderburg et al. 2015), thus these polluted WDs become unique laboratories for studying the interior composition of exoplanets (Zuckerman et al. 2007; Koester et al. 2014; Jura & Young 2014). The chemical abundances detected on the surface of polluted WDs reflect the equilibrium between accretion for metal-rich material and diffusive sedimentation (Koester 2009; Bauer & Bildsten 2018).

Dupuis et al. (1992) initially explored the metal traces in WDs, and they also investigated the diffusion of metals accreted onto WDs (Dupuis et al. 1993a,b). Koester & Wilken (2006) calculated the diffusion timescales for some metals in DAZ WDs’ atmosphere, and they estimated the accretion rates for 38 DAZ WDs. Koester (2009) extended the above works to DAZ, DBZ, and DZ WDs. Considering diffusion and thermohaline mixing, Wachlin et al. (2017) and Bauer & Bildsten (2018) simulated the trace of metals for DAZ WDs. Bauer & Bildsten (2019) discuss the effects of the mixing processes, including convection, gravitational sedimentation, overshoot, and thermohaline instability on the diffusion. Using new WD envelope models and diffusion, Koester et al. (2020) investigated the atmospheres of carbon-rich WDs. In the theoretical models, the metal abundances of several polluted WDs can be explained well if suitable accretion rates are assumed (e.g., Koester 2009; Bauer & Bildsten 2018). They also predict that the metals would rapidly settle downward as soon as accretion stops. However, as is shown in Koester (2009) and Bauer & Bildsten (2018), the diffusion timescales of WDs increase when their effective temperature (Teff) decreases. For a WD with Teff < 10 kK, τdif is longer than about 106 yr. Therefore it is not sufficient to check long-timescale diffusion theory by only comparing theoretical results with several known cool WDs. A comparison involving a large observational sample of DB WDs with different Teff s becomes necessary.

Thanks to many large sky surveys, the number of observed WDs are dramatically increasing (e.g., Gaia Collaboration 2016, 2018; Chambers et al. 2016; Blouin et al. 2019). Up to now, there are more than 60000 WDs in The Montreal White Dwarf Database (Dufour et al. 2017), of which 1023 of them are DBZ or DZ WDs (Coutu et al. 2019). Observationally, Dufour et al. (2007) showed the spectroscopic and photometric data of 147 DZ WDs with Teff between about 6 kK and 12 kK. Based on SDSS DR10 and 12, Koester & Kepler (2015) analyzed the data of 1107 DBZ WDs whose effective temperatures are between about 50 kK and 11 kK. Hollands et al. (2017) identified 231 cool DZ WDs with Teff lower than 9 kK in SDSS DR12. They discuss the distribution of log[Ca/He] versus Teff for the three samples (see Fig. 11 of Hollands et al. 2017). At about Teff > 10 kK, Ca abundances rapidly decrease with Teff declining. Koester & Kepler (2015) suggest that this trend should be relative to the mass-accretion rates. However, Ca abundances of DZ WDs with Teff between 10 kK and 8 kK increase by about 100 times. Hollands et al. (2017) consider that this sharp increase might result from the decrease in the convective zone mass (Mcvz) or the increase in τdiff. The second downwards trend of a Ca abundance with Teff appears between 9 kK and 4 kK. Hollands et al. (2018) suggest that the trend is relative to Mcvz or τdiff.

Compared with DAZ WDs whose metal pollution is monotonically decreasing with Teff declining (Koester et al. 2014), DBZ WDs have more complicated progresses for metal pollution. The main reason is that DB WDs undergo different formation channels, and they have distinctive interior structures. In this work, employing the stellar evolution code, we investigated the physical mechanisms to explain the surface metal abundance of the polluted DB WD. The model descriptions are given in Sect. 2. DB WD’s properties and their accretion pollution are shown and discussed in Sects. 3 and 4. The paper ends with conclusions in Sect. 5.

2. Models

In the present paper, we used Modules for Experiments in Stellar Evolution (MESA, [rev. 12115]; Paxton et al. 2011, 2013, 2015, 2018, 2019) to create He-rich WDs without H, which are noted as DB WDs, and to simulate the element diffusion within them and metal-rich material accretion. There are many factors that can change the element abundances on a WD surface. Bauer & Bildsten (2019) discuss the effects of convection, thermohaline instability, gravitational diffusion, and rotation on the element mixing of WDs. Because the rotations velocities of most isolated WDs are low observationally (Berger et al. 2005; Kawaler 2015; Hermes et al. 2017), we did not consider the rotation. Convection directly determines the timescale of element diffusion (Koester 2009; Bauer & Bildsten 2018). In the present paper, we adopted the ML2 convection prescription (Bohm & Cassinelli 1971; Tassoul et al. 1990), and use Ledoux criterion for convection. The table named ‘DB_WD_tau_25′ in MESA, which is a helium dominated atmosphere table for DB WDs, is used to calculate the DB WD atmosphere boundary. The size of the convective zone depends on the mixing length parameter (αMLT). In order to discuss its effect, we consider αMLT to be 0.8 and 1.8 in different simulations.

Deal et al. (2013) and Wachlin et al. (2017) considered that thermohaline mixing can change the element abundances on the surfaces of polluted WDs. MESA adopts the method of Kippenhahn et al. (1980) to calculate the effects of thermohaline mixing, in which parameter αth is used to give the mixing efficiency. In our work, αth is considered to be 0, 1, and 1000 in different calculations in order to test its effects.

Schatzman (1945) suggested that the high gravitational fields in cool WDs should result in the downward diffusion of heavy elements. By resolving the Burgers equations which give multicomponent fluid’s evolutions (Burgers 1969), Thoul et al. (1994) investigated the element diffusion in the interior of the Sun. Using the approach in Thoul et al. (1994), MESA can calculate the chemical diffusion in the stellar interior (Paxton et al. 2015, 2018). The diffusion coefficients that originated from Paquette et al. (1986) and were updated by Stanton & Murillo (2016) are used in our models.

Similarly, metallicity (Z) can also affect stellar evolutions and WD properties. Here, Table 1 gives all cases in which different input parameters are considered.

Table 1.

All cases in the present paper are simulated.

3. Formation and structures of DB WDs

Many observations have shown that there are some H elements in the atmospheres of DBZ or DZ WDs (Voss et al. 2007; Koester & Kepler 2015; Coutu et al. 2019). However, the ratios of the H to He abundance estimated by these observations are lower than about 10−2. These H elements may be continuously accreted by DBZ or DZ WDs from the interstellar medium (Voss et al. 2007; Koester & Kepler 2015). Therefore, there might be no H elements left in the atmospheres of DB WDs when they form.

Usually, the range of DBZ or DZ WDs’ masses is between about 0.4 and 1.0 M⊙ and their mass distribution has a peak around 0.6 M⊙ (e.g., Han 1998; Han et al. 2000; Coutu et al. 2019). Taking 0.6 M⊙ DB WD created by the main sequence (MS) star under input parameters in case 1 as an example, we provide all steps involved to create DB WDs in the following.

Firstly, as is illustrated by the black line in the top left panel of Fig. 1, the 3.5 M⊙ MS star begins to evolve normally, that is, H starts to burn in the stellar core. The mass-loss rate (Ṁ) is calculated by the “Dutch” scheme (Paxton et al. 2011), in which Ṁ of hot and cool stars is provided by Nieuwenhuijzen & de Jager (1990), Nugis & Lamers (2000), Vink et al. (2001), Glebbeek et al. (2009), and Reimers (1975). The element mixing is mainly determined by convection and thermohaline instability. At this phase, in order to save CPU time, we did not consider gravitational diffusion.

thumbnail Fig. 1.

DB WD with a mass of 0.6 M⊙ produced by the main sequence star with an initial mass of 3.5 M⊙. The top left panel gives the evolution in the HR diagram for the star in case 1 (αMLT = 1.8, αth = 1 and Z = 0.02), in which the lines with different colors represent different evolutionary phases. The bottom left panel shows the evolutions in the HR diagram for stars with different input parameters which are given by different colors. The top right panel is similar to the top left panel, but for the evolution of H and He abundances on the stellar surface. The bottom right panel is similar to the bottom left panel, but for the evolution of the Ca abundance on stellar surfaces. Further details can be found in the text.

Secondly, as is shown by the red line in the top left panel of Fig. 1, we artificially enhanced the mass-loss rate up to 10−4 M⊙ yr−1 when the He-core mass was larger than 0.6 M⊙. The H-rich envelope is rapidly stripped, and the star evolves into a He star. As the red lines in the top right panel of Fig. 1 show, the H abundance (X(H)) on the stellar surface decreases from about 0.7 to roughly lower than 10−15, while X(He) increases up to about 0.98.

Thirdly, the WD cooling is involved, which is given by the green line. At this time, the H element almost is lost, and the He element is the lightest one, and it floats upward toward the stellar surface by gravitational settling. A DB WD is created.

The bottom left panel of Fig. 1 shows the evolution in the HR diagram for the star with different αMLT, αth, and Z. Obviously, the effects of input parameters on evolutionary tracks are negligible. The bottom right panel gives the change in X(Ca) on the stellar surface. The X(Ca) on the stellar surface starts to reduce because of gravitational sedimentation at the WD cooling phase.

Using a similar method, we also created DB WDs with 0.4 and 0.8 M⊙, which are shown in Fig. 2. The changes in X(H), X(He), and X(Ca) on these WD surfaces are given as well.

thumbnail Fig. 2.

Similar to Fig. 1, but for 0.4, 0.6, and 0.8 M⊙ DB WDs produced by MS stars in case 1 with initial masses of 2.5, 3.5, and 5 M⊙, which are represented by black, red, and green lines, respectively.

As the bottom left panel of Fig. 1 shows, the cooling tracks of DB WDs are hardly affected by the input parameters. Similarly, the effects of these input parameters on DB WD internal structures can be negligible.

In Fig. 3, we found that the profiles of the temperature, convective velocity (vcov), He abundance (X(He)), and the abundance ratio of Ca to He ([Ca/He]) for the 0.6 M⊙ DB WD at the same effective temperature are similar. Due to the strong gravitational diffusion of the WD, heavy elements sink down and light He element floats up. For example, X(Ca) on the DB WD’s surface has decreased to 10−15 from an initial 10−5, while a heavy He envelope with a mass of about 0.02 M⊙ forms around the WD surface. Figure 4 gives the profiles of 0.4 and 0.8 M⊙ DB WDs for case 1. Obviously, in our model, the He layer mass is affected by the WD’s mass. It changes from about 0.1 to 0.01 M⊙ when MWD increases from 0.4 to 0.8 M⊙.

thumbnail Fig. 3.

Structures of 0.6 M⊙ DB WDs in different effective temperatures (Teffs) for cases 1, 2, 4, and 5, respectively. The different Teffs are given by different lines. We note that T, vcov, X(He), and [Ca/He] represent the temperature, convective velocity, He abundance, and the abundance ratio of Ca to He, respectively.

thumbnail Fig. 4.

Similar to Fig. 3, but for 0.4 and 0.8 M⊙ DB WDs for case 1.

In Fig. 5, we provided the change in the convective-zone mass (Mcvz) around the WD surface with Teff. For the 0.6 M⊙ DB WD shown in the left panel of Fig. 5, the effects of input parameters on Mcvz can be negligible. The main reasons are as follows. Firstly, the mixing length parameter αMLT has a weak effect on Mcvz because a high density of WDs results in a small pressure scale height. For example, it is about 10 cm for a WD with Teff = 6 kK. Secondly, the thermohaline mixing hardly affects the convective zone of DB WDs, while it can significantly affect the Mcvz of DA WDs (Wachlin et al. 2017; Bauer & Bildsten 2018). Compared with the latter (10−15 − 10−11 M⊙ when Teff> 10 kK, Koester 2009; Wachlin et al. 2017), the Mcvz of DB is extremely massive, and between about 10−9 − 10−5 M⊙. A thick convective zone of DB WDs dilutes the effects of thermohaline mixing, which has been discussed by Bauer & Bildsten (2019). Bauer & Bildsten (2019) also mentioned that the mean molecular weight of a DB WD is more than two times that of a DA WD, which dilutes thermohaline mixing effects. Thirdly, metallicity has no effect on Mcvz because the heavy elements rapidly diffuse downward due to the strong gravitational field of WDs.

thumbnail Fig. 5.

Mass of convective zone (Mcvz) versus the WD’s effective temperature (Teff). The left panel is for the 0.6 M⊙ DB WD in different cases, while the right panel is for 0.4, 0.6, and 0.8 M⊙ DB WDs in case 1. Theoretical results from Benvenuto & Althaus (1997) and Koester (2009) are shown by different symbols. B97 and K09 refer to Benvenuto & Althaus (1997) and Koester (2009), respectively.

Compared with Mcvz of 0.6 M⊙ DB WD calculated by Benvenuto & Althaus (1997) and Koester (2009), the Mcvz in this work is similar to both of their results when Teff > ∼ 14 kK. We note that Mcvz in this work is between that in Benvenuto & Althaus (1997) and in Koester (2009) when Teff < ∼ 14 kK. The right panel of Fig. 5 shows Mcvz in the models of 0.4 and 0.8 M⊙ DB WDs. Compared with the results of Benvenuto & Althaus (1997), Mcvz is more massive in this work. The differences mainly result from the following possible aspects.

Firstly, in Benvenuto & Althaus (1997), the He layer mass of DB WDs is between about 10−2 and 10−6 M⊙. However, in our work, we considered the gravitational diffusion in DB WDs. The He layer mass is larger than 10−2 M⊙ and the heavy elements (such as Ca, Fe.) sink down. The different chemical profile around a WD surface can affect the convective zone.

Secondly, in Benvenuto & Althaus (1997) and Koester (2009), Mcvz is defined by the thermal time scale. However, Mcvz is defined by the Ledoux criterion in our results. As discussed in Koester (2009), Mcvz can differ by orders of magnitude because of different definitions.

4. Accreting pollution of DB WDs

The bottom right panels of Figs. 3 and 4 show that [Ca/He] on the surface of a DB WD decreases to about 10−15 due to gravitational settling when Teff > 20 kK. Chayer et al. (1995a) suggested that some element diffusion can be prevented by radiative levitation when the WD temperature is higher than 20 kK (Chayer et al. 1995b; Chayer 2014). In Fig. 6, we performed a test for the 0.6 M⊙ DB WD as follows: The gravitational settling is not included when the Teff of a cooling WD is higher than 20 kK, but it is included when Teff< 20 kK. We find that [Ca/He] rapidly decreases, and we can not explain the observations. Therefore, the heavy elements observed on the DB WD’s surfaces must originate from other sources. The rocky objects tidally disrupted by a DB WD are a possible source (Farihi 2016).

thumbnail Fig. 6.

Evolutions of log [Ca/He] during 0.6 M⊙ DB WD cooling, in which the gravitational diffusion is not involved when T > 20 kK. Black, red, and green dots represent observations from Koester & Kepler (2015), Dufour et al. (2007), and Hollands et al. (2017), respectively.

4.1. Metal-rich material accretion

In general, the element abundances on the surface of an accreting DB WD not only depend on the WD properties, but also on mass-accretion rates (Ṁa) and the chemical abundances of accreted material. In order to match the observed properties of G29–38 in Xu et al. (2014), Bauer & Bildsten (2018) assumed that the mass fractions of Fe, O, Mg, Si, and Ca were in accreted materials 0.307, 0.295, 0.199, 0.153, and 0.046, respectively. We adopted the above mass fractions.

By resolving the Burgers equations, MESA can calculate the chemical diffusion of an accreting WD. Figure 7 shows the evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD with a mass-accretion rate of 108 g s−1 when Teff = 20 kK. It takes about 104 yr to reach an accretion-diffusion equilibrium for the accreting DB WD. When the accretion stops, the Ca element diffuses downward within a diffusive timescale of about 106 yr, which is similar to what was found by Koester (2009). Obviously, input parameters (αMLT, αth and Z) have weak effects on the surface [Ca/He]. The main reasons are similar to those for Mcvz.

thumbnail Fig. 7.

Evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD with a mass-accretion rate of 108 g s−1 when Teff = 20 kK. Accretion ceases after 106 yr. The different lines represent different cases which are shown in the bottom left zone.

Figure 8 gives the evolution of [Ca/He] on the 0.6 M⊙ DB WD with different Ṁa at different Teffs. The timescale of reaching accretion-diffusion equilibrium is about 104 for all models. The mass-accretion rate and the effective temperature greatly affect the element abundances of an accreting DB WD. When Ṁa decreases from 1010 to 104 g s−1, [Ca/He] reduces from about 10−5 to 10−10. This means that the metal abundance of an accreting WD is approximately in proportion to the mass-accretion rate. In fact, Dupuis et al. (1992) and Koester (2009) assumed that the element abundances observed in polluted WDs should be accretion-diffusion equilibrium, and they suggested that the mass fraction of the ith element (Xcvz) in the convective zone is given by

(1)

thumbnail Fig. 8.

Evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD with different mass-accretion rates at different Teff s.

where Xcvz, i and Ṁi are the ith element abundance in the convective zone and the mass-accretion rate of ith element, respectively. Here, τdiff, i is the ith element diffusive timescale, which can be estimated by

(2)

where RB, cvz and ρB, cvz are the radius and the mass density at the bottom of the convective zone, respectively. Here, vdiff, i is the ith element velocity of downward sedimentation at bottom of the convective envelope. If τdiff is much shorter than the WD lifetime, Koester (2009) gave the relation between the mass-accretion rate and the element abundance by

(3)

Obviously, our result is consistent with Eq. (3).

However, the change in [Ca/He] with Teff is complex. When Teff decreases from 20 to 10 kK, [Ca/He] reduces by about three orders of magnitude. When it decreases from 10 to 8 kK, [Ca/He] slightly enhances. When it decreases from 8 to 6 kK, [Ca/He] reduces by about one order of magnitude again. This change can be explained by the relation of Teff and Mcvz(see Fig. 5).

Figure 9 gives the diffusion downward of the Ca element on the surface of 0.6 M⊙ DB WD after a lasting 106 yr accretion at different Teff. The evolution of [Ca/He] with Teff is similar to that in Fig. 8. In fact, Fig. 9 indicates the timescale of Ca element diffusion, that is τdiff, Ca. Obviously, it deeply depends on Teff. In our model, τdiff, Ca increases from about 105 to 109 yr when Teff decreases from 20 to 6 kK. However, τdiff, Ca in Koester (2009) increases from about 104 to 106 yr.

thumbnail Fig. 9.

Similar to Fig. 8, but for the evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD which just experiences lasting 106 yr accretion at different Teff. The mass-accretion rates are shown in the top middle region of every panel.

Based on Eq. (2), τdiff, Ca depends on Mcvz, RB, cvz, ρB, cvz, and vdiff, Ca. Figure 10 shows the profiles of X(Ca), vdiff, Ca, opacity(κ), and vconv around the surface of 0.6 M⊙ DB WDs with different Ṁa and Teff. Obviously, when comparing model of 108 with that of 106 g s−1, the mass-accretion rate can affect X(Ca), but it does not change the internal structure of the accreting DB WD, including the opacity, the mass density and the radius. The reason is that the matter accreted by a DB WD quickly diffuses the whole convective zone. The DB WD structure mainly depends on the cooling duration which is presented by the effective temperature. Due to the massive convective zone of DB WDs, compared with the He element, abundances of other heavy elements are very low. Therefore, the accreted matter cannot affect the internal structure of a DB WD, which depends on the cooling duration presented by Teff.

thumbnail Fig. 10.

Profiles of Ca abundance (X(Ca)), opacity (κ), Ca diffusive velocity (vdiff, Ca), convective velocity (vconv), mass density (ρ), and radius (R) around the surface of 0.6 M⊙ DB WDs with mass-accretion rates of 108 g s−1, but different effective temperatures which are represented by different lines.

Combining Figs. 5, 10, and 11, with DB WD cooling from Teff  =  20 kK to 6 kK, Mcvz increases from about 10−8 to 10−5 M⊙, ρB, cvz also increases from ∼1 to 103 g cm−3, vdiff, Ca at the base of the surface convection zone decreases from about 10−6 to 10−10 cm s−1, while RB, cvz keeps constant. Therefore, τdiff, Ca increases from about 105 to 109 yr. This means that, compared to tcool, τdiff, Ca cannot be neglected when Teff < 10 kK, that is, Eq. (3) is not suitable for cool polluted DB WDs. Of course, one should note, in our model, vdiff, Ca has irregular oscillations when Teff < 8 kK. Koester (2009) did not show vdiff, Ca. However, vdif, Ca may result in a great difference of τdiff, Ca between the present paper and Koester (2009).

thumbnail Fig. 11.

Similar to Fig. 10, but for Ṁ = 106 g s−1.

4.2. Accretion pollution with the power law

As Fig. 6 shows, the [Ca/He] of about 1500 DB WDs observed by Dufour et al. (2007), Koester & Kepler (2015), and Hollands et al. (2017) must be explained by accretion pollution. In the panels a, b, and c of Fig. 12, we gave the evolutional tracks of [Ca/He] with Teff for DB WDs with masses of 0.4, 0.6, and 0.8 M⊙ and constant mass-accretion rates of 1010, 108 and 106 g s−1, respectively. Obviously, the results hardly explain the observations.

thumbnail Fig. 12.

Effective temperature vs. log [Ca/He] for DB WDs. Panels (a), (b), and (c) represent models with different mass DB WDs and a constant accretion rate (106, 108 and 1010 g s−1), respectively. Panels (d) is for the mass-accretion rate given by Eq. (5). Black, red and green dots represent observations from Koester & Kepler (2015), Dufour et al. (2007) and Hollands et al. (2017), respectively.

In order to model the metal abundances in GD 362’s atmosphere, Jura et al. (2009) considered that Ṁa should decrease by the following power law:

(4)

where Mdisk is the mass of planet disrupted by a WD and tdisk is a characteristic timescale of the accretion disk. Jura et al. (2009) found that all of GD 362’s distinctive properties can be explained if Mdisk is between about 1025 and 1028 g, in which the range of tdisk is between about 2 × 105 and 109 yr.

However, based on Fig. 8 and panels a–c of Fig. 12, with DB WD cooling, a decreasing mass-accretion rate with a power law results in a continued decrease in [Ca/He]. Therefore, it can not explain the observations. According to our model, the mass-accretion rate should decrease when Teff> 10 kK, but it should increase when Teff< 10 kK. Considering that the Teff of WDs mainly depends on tcool and it can be compared with the observations, we assumed that Ṁa should change by the following power law:

(5)

Panel d of Fig. 12 gives the evolution of [Ca/He] with Teff for DB WDs with different MWD and a power-law Ṁa described by Eq. (5). Our results are consistent with the observations for DB WDs. The tdisk of an accretion disk composed purely of dust is higher than 109 yr (Farihi et al. 2008). Usually, the cooling timescale of a DB WD from 20 kK to 10 kK is about 108 − 109 yr, and it is about 109 yr from 10 kK to 5 kK. This means that a DB WD can accrete a disk, produced by itself, disrupting a planet during the whole cooling phase. The decrease in the mass-accretion rate when Teff > 10 kK results from the viscous dissipation of accretion disk (Jura et al. 2009). However, we did not find any model to explain its enhancement when Teff < 10 kK. If Eq. (5) basically represents the true trend of the mass-accretion rates, this indicates that the accretion disk produced by a WD disrupting a planet may have a complex structure.

5. Conclusions

In order to explain the evolutionary sequence of heavy element abundances observed among 1500 DB or DZ WDs, we used MESA to create DB WDs with masses of 0.4, 0.6, and 0.8 M⊙ by artificially stripping envelope once. The H-rich envelope was stripped when stars evolved into red giants. We investigated the effects of input parameters (αMLT, αth, and Z) on DB WD structures. Due to the small pressure scale height, thick convective zone, or mean molecular weight of DB WDs, these input parameters have a weak effect on DB WD structures, including interior temperatures, chemical profiles, and convective zones. Therefore, they hardly affect the evolution of heavy elements on the surface of DB WDs.

Due to high gravitational fields of DB WDs, the element diffusion in the theoretical model is too fast to explain the observations. Therefore, the heavy elements on the DB WDs’ surfaces may originate from the pollution by accreting the planet disrupted by these WDs. They mainly depend on the mass-accretion rates and the effective temperatures of DB WDs. In our model, a constant mass-accretion rate cannot explain the evolutionary sequence of a Ca element for about 1500 observed DB or DZ WDs. However, it is consistent well with the model in which the mass-accretion rate decreases by one power law when Teff > 10 kK and slightly increases by another power law when Teff < 10 kK. The observed DB WD evolutionary sequence of heavy element abundances originates from WD cooling and the change in the mass-accretion rate.

Acknowledgments

This work received the generous support of the National Natural Science Foundation of China, project Nos. 11763007, U2031204, and 11863005.

References

  1. Bahcall, J. N., & Loeb, A. 1990, ApJ, 360, 267 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bauer, E. B., & Bildsten, L. 2018, ApJ, 859, L19 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bauer, E. B., & Bildsten, L. 2019, ApJ, 872, 96 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benvenuto, O. G., & Althaus, L. G. 1997, MNRAS, 288, 1004 [NASA ADS] [CrossRef] [Google Scholar]
  5. Berger, L., Koester, D., Napiwotzki, R., et al. 2005, A&A, 444, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Blouin, S., Dufour, P., Thibeault, C., et al. 2019, ApJ, 878, 63 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bohm, K. H., & Cassinelli, J. 1971, A&A, 12, 21 [NASA ADS] [Google Scholar]
  8. Burgers, J. M. 1969, Flow Equations for Composite Gases (New York: Academic Press) [Google Scholar]
  9. Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
  10. Chayer, P. 2014, MNRAS, 437, L95 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chayer, P., Vennes, S., Pradhan, A. K., et al. 1995a, ApJ, 454, 429 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chayer, P., Fontaine, G., & Wesemael, F. 1995b, ApJS, 99, 189 [NASA ADS] [CrossRef] [Google Scholar]
  13. Coutu, S., Dufour, P., Bergeron, P., et al. 2019, ApJ, 885, 74 [NASA ADS] [CrossRef] [Google Scholar]
  14. Deal, M., Deheuvels, S., Vauclair, G., et al. 2013, A&A, 557, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Dufour, P., Bergeron, P., Liebert, J., et al. 2007, ApJ, 663, 1291 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dufour, P., Blouin, S., Coutu, S., et al. 2017, 20th European White Dwarf Workshop, 509, 3 [Google Scholar]
  17. Dupuis, J., Fontaine, G., Pelletier, C., et al. 1992, ApJS, 82, 505 [NASA ADS] [CrossRef] [Google Scholar]
  18. Dupuis, J., Fontaine, G., Pelletier, C., et al. 1993a, ApJS, 84, 73 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dupuis, J., Fontaine, G., & Wesemael, F. 1993b, ApJS, 87, 345 [NASA ADS] [CrossRef] [Google Scholar]
  20. Farihi, J. 2016, New Astron. Rev., 71, 9 [NASA ADS] [CrossRef] [Google Scholar]
  21. Farihi, J., Jura, M., & Zuckerman, B. 2009, ApJ, 694, 805 [NASA ADS] [CrossRef] [Google Scholar]
  22. Farihi, J., Becklin, E. E., & Zuckerman, B. 2008, ApJ, 681, 1470 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Girven, J., Brinkworth, C. S., Farihi, J., et al. 2012, ApJ, 749, 154 [NASA ADS] [CrossRef] [Google Scholar]
  26. Glebbeek, E., Gaburov, E., de Mink, S. E., et al. 2009, A&A, 497, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Han, Z. 1998, MNRAS, 296, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  28. Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
  29. Han, Z., Podsiadlowski, P., Maxted, P. F. L., et al. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
  30. Han, Z., Podsiadlowski, P., Maxted, P. F. L., et al. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hermes, J. J., Gänsicke, B. T., Kawaler, S. D., et al. 2017, ApJS, 232, 23 [Google Scholar]
  32. Hollands, M. A., Koester, D., Alekseev, V., et al. 2017, MNRAS, 467, 4970 [NASA ADS] [Google Scholar]
  33. Hollands, M. A., Gänsicke, B. T., & Koester, D. 2018, MNRAS, 477, 93 [NASA ADS] [CrossRef] [Google Scholar]
  34. Jura, M. 2003, ApJ, 584, L91 [Google Scholar]
  35. Jura, M., & Young, E. D. 2014, Ann. Rev. Earth and Planet. Sci., 42, 45 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jura, M., Muno, M. P., Farihi, J., et al. 2009, ApJ, 699, 1473 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kawaler, S. D. 2015, 19th European Workshop on White Dwarfs, 493, 65 [Google Scholar]
  38. Kippenhahn, R., Ruschenplatt, G., & Thomas, H.-C. 1980, A&A, 91, 175 [NASA ADS] [Google Scholar]
  39. Koester, D. 2009, A&A, 498, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Koester, D., & Kepler, S. O. 2015, A&A, 583, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Koester, D., & Wilken, D. 2006, A&A, 453, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Koester, D., Gänsicke, B. T., & Farihi, J. 2014, A&A, 566, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Koester, D., Kepler, S. O., & Irwin, A. W. 2020, A&A, 635, A103 [CrossRef] [EDP Sciences] [Google Scholar]
  44. Lü, G., Zhu, C., Wang, Z., et al. 2017, ApJ, 847, 62 [CrossRef] [Google Scholar]
  45. Lü, G., Zhu, C., Wang, Z., et al. 2020, ApJ, 890, 69 [CrossRef] [Google Scholar]
  46. Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
  47. Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
  48. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  49. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
  50. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  51. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  53. Paquette, C., Pelletier, C., Fontaine, G., et al. 1986, ApJS, 61, 177 [NASA ADS] [CrossRef] [Google Scholar]
  54. Reimers, D. 1975, Mem. Soc. Roy. Sci. Liege, 8, 369 [Google Scholar]
  55. Schatzman, E. 1945, Ann. Astrophys., 8, 143 [NASA ADS] [Google Scholar]
  56. Shapiro, S. L., & Teukolsky, S. A. 1983, A Wiley-Interscience Publication (New York: Wiley) [Google Scholar]
  57. Stanton, L. G., & Murillo, M. S. 2016, Phys. Rev. E, 93 [CrossRef] [Google Scholar]
  58. Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
  59. Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
  60. Vanderburg, A., Johnson, J. A., Rappaport, S., et al. 2015, Nature, 526, 546 [NASA ADS] [CrossRef] [Google Scholar]
  61. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Voss, B., Koester, D., Napiwotzki, R., et al. 2007, A&A, 470, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Wachlin, F. C., Vauclair, G., Vauclair, S., et al. 2017, A&A, 601, A13 [EDP Sciences] [Google Scholar]
  64. Xu, S., Jura, M., Koester, D., et al. 2014, ApJ, 783, 79 [NASA ADS] [CrossRef] [Google Scholar]
  65. Yu, J., Li, Z., Zhu, C., et al. 2019, ApJ, 885, 20 [NASA ADS] [CrossRef] [Google Scholar]
  66. Zhu, C., Liu, H., Lü, G., et al. 2019, MNRAS, 488, 525 [NASA ADS] [CrossRef] [Google Scholar]
  67. Zuckerman, B., Koester, D., Reid, I. N., et al. 2003, ApJ, 596, 477 [NASA ADS] [CrossRef] [Google Scholar]
  68. Zuckerman, B., Koester, D., Melis, C., et al. 2007, ApJ, 671, 872 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

All cases in the present paper are simulated.

In the text

All Figures

thumbnail Fig. 1.

DB WD with a mass of 0.6 M⊙ produced by the main sequence star with an initial mass of 3.5 M⊙. The top left panel gives the evolution in the HR diagram for the star in case 1 (αMLT = 1.8, αth = 1 and Z = 0.02), in which the lines with different colors represent different evolutionary phases. The bottom left panel shows the evolutions in the HR diagram for stars with different input parameters which are given by different colors. The top right panel is similar to the top left panel, but for the evolution of H and He abundances on the stellar surface. The bottom right panel is similar to the bottom left panel, but for the evolution of the Ca abundance on stellar surfaces. Further details can be found in the text.
In the text
thumbnail Fig. 2.

Similar to Fig. 1, but for 0.4, 0.6, and 0.8 M⊙ DB WDs produced by MS stars in case 1 with initial masses of 2.5, 3.5, and 5 M⊙, which are represented by black, red, and green lines, respectively.
In the text
thumbnail Fig. 3.

Structures of 0.6 M⊙ DB WDs in different effective temperatures (Teffs) for cases 1, 2, 4, and 5, respectively. The different Teffs are given by different lines. We note that T, vcov, X(He), and [Ca/He] represent the temperature, convective velocity, He abundance, and the abundance ratio of Ca to He, respectively.
In the text
thumbnail Fig. 4.

Similar to Fig. 3, but for 0.4 and 0.8 M⊙ DB WDs for case 1.
In the text
thumbnail Fig. 5.

Mass of convective zone (Mcvz) versus the WD’s effective temperature (Teff). The left panel is for the 0.6 M⊙ DB WD in different cases, while the right panel is for 0.4, 0.6, and 0.8 M⊙ DB WDs in case 1. Theoretical results from Benvenuto & Althaus (1997) and Koester (2009) are shown by different symbols. B97 and K09 refer to Benvenuto & Althaus (1997) and Koester (2009), respectively.
In the text
thumbnail Fig. 6.

Evolutions of log [Ca/He] during 0.6 M⊙ DB WD cooling, in which the gravitational diffusion is not involved when T > 20 kK. Black, red, and green dots represent observations from Koester & Kepler (2015), Dufour et al. (2007), and Hollands et al. (2017), respectively.
In the text
thumbnail Fig. 7.

Evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD with a mass-accretion rate of 108 g s−1 when Teff = 20 kK. Accretion ceases after 106 yr. The different lines represent different cases which are shown in the bottom left zone.
In the text
thumbnail Fig. 8.

Evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD with different mass-accretion rates at different Teff s.
In the text
thumbnail Fig. 9.

Similar to Fig. 8, but for the evolution of [Ca/He] on the surface of 0.6 M⊙ DB WD which just experiences lasting 106 yr accretion at different Teff. The mass-accretion rates are shown in the top middle region of every panel.
In the text
thumbnail Fig. 10.

Profiles of Ca abundance (X(Ca)), opacity (κ), Ca diffusive velocity (vdiff, Ca), convective velocity (vconv), mass density (ρ), and radius (R) around the surface of 0.6 M⊙ DB WDs with mass-accretion rates of 108 g s−1, but different effective temperatures which are represented by different lines.
In the text
thumbnail Fig. 11.

Similar to Fig. 10, but for Ṁ = 106 g s−1.
In the text
thumbnail Fig. 12.

Effective temperature vs. log [Ca/He] for DB WDs. Panels (a), (b), and (c) represent models with different mass DB WDs and a constant accretion rate (106, 108 and 1010 g s−1), respectively. Panels (d) is for the mass-accretion rate given by Eq. (5). Black, red and green dots represent observations from Koester & Kepler (2015), Dufour et al. (2007) and Hollands et al. (2017), respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.