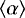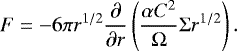| Issue |
A&A
Volume 652, August 2021
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 11 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202038797 | |
| Published online | 04 August 2021 | |
Forming pressure traps at the snow line to isolate isotopic reservoirs in the absence of a planet
1
Université de Paris, Institut de physique du globe de Paris, CNRS,
75005
Paris,
France
e-mail: charnoz@ipgp.fr
2
ISAS/JAXA,
Tokyo,
Japan
Received:
30
June
2020
Accepted:
26
April
2021
Context. Pressure maxima are regions in protoplanetary disks in which pebbles can be trapped because the regions have no local pressure gradient. These regions could be ideal places in which planetesimals might be formed or to isotopic reservoirs might be isolated. Observations of protoplanetary disks show that dusty ring structures are common, and pressure maxima are sometimes invoked as a possible explanation. In our Solar System, pressure bumps have been suggested as a possible mechanism for separating reservoirs with different nucleosynthetic compositions that are identified among chondrites and iron meteorites. In this paper, we detail a mechanism by which pressure maxima form just inward of the snow line in stratified disks (with a dead zone and an active layer). This mechanism does not require the presence of a planet.
Aims. We investigate the conditions for the formation of pressure maxima using a vertically averaged α viscosity model and release of water vapor at the snow line.
Methods. We considered a 1D α disk model. Using a combination of analytical and numerical investigations, we explored the range of conditions for a pressure maximum to form inside the dead zone and just inward of the snow line.
Results. When the vertically averaged α is a decreasing function of the surface density, then the release of water vapor at the snow line decreases the sound velocity, and a pressure bump appears in turn. This requires a constant inflow of icy pebbles with a ratio of the pebble influx to gas influx >0.6 for a power-law disk with a 1% ice-to-gas ratio, and >1.8 for a disk with an ice-to-gas ratio ~0.3%. If these conditions are met, then a pressure maximum appears just inward of the snow line due to a process that couples the dead and active layers at the evaporation front. The pressure bump survives as long as the icy pebble flux is high enough. The formation of the pressure bump is triggered by the decrease in sound velocity inward of the snow line through the release of water vapor.
Conclusions. This mechanism is promising for isolating early reservoirs carrying different isotopic signatures in the Solar System and for promoting dry planetesimal formation inward of the snow line, provided the vertically averaged description of a dead zone is valid.
Key words: protoplanetary disks
© S. Charnoz et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Formation of pressure maxima in protoplanetary disks is an active topic of research because these maxima are seen as ideal places in which pebbles might accumulate efficiently and subsequently form planetesimals through the so-called streaming instability process, for example (Johansen et al. 2007; Pinilla et al. 2012; Drążkowska & Dullemond 2014; Drążkowska & Alibert 2017; Charnoz et al. 2019). Pressure bumps might also act as dynamical barriers at which the radial drift of particles with a Stokes number (St) that deviates from zero would be slowed down, stopped, or even reversed because the disk becomes super-Keplerian for a positive pressure gradient. Dust and pebbles experience gas drag. Their drift velocity (relative to the gas) is (Weidenschilling 1977)
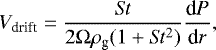 (1)
(1)
where Ω is the local Keplerian frequency, ρg is the gas density, and P the gas pressure. Because the direction of migration (relative to the gas) is dictated by ∂P∕∂r, a pressure bump is defined as a pressure maximum, so that on either side, drifting pebbles move toward the local pressure maximum. Conversely, for a pressure minimum, drifting pebbles will move away from the minimum.
For these reasons, a pressure maximum is also invoked as a possible dynamical barrier that could be at the origin of a major isotopic heterogeneity observed in Solar System meteorites: Meteorites can be divided into two broad groups because the variations in their stable isotopes do not depend on mass (Trinquier et al. 2008; Kruijer et al. 2017, 2020; Kleine et al. 2020). These are the carbonaceous chondrite (CC) group and the non-carbonaceous chondrite (NC) group. Based on their isotopic anomalies, iron meteorites can also be divided into the CC and NC groups. Accretion timescales modeled from Hf/W ages of metal silicate differentiation in parent bodies of iron meteorites belonging to the NC and CC groups show that NC bodies accreted earlier than CC bodies, but with an overlap at about ≃ 1.4 Myr after CAIs. The accretion ages of the parent bodies of chondrites and iron meteorites show that the NC and CC reservoirs were isolated very early in the disk (<0.4 Myr after CAIs for the NC group) and during nearly 2 Myr (Kruijer et al. 2017; Kleine et al. 2020).
Jupiter is often proposed (Kruijer et al. 2017; Kleine et al. 2020) as responsible for separating the two reservoirs, but it has recentlybeen argued that Jupiter may have formed too late for the isolation process to be efficient enough (Brasser & Mojzsis 2020). In the same study, it was proposed that the isolation may result from the presence of a pressure maximum that appeared in a few 100 Kyr after CAIs, but without detailing how this pressure bump could have formed. In addition, the very early model age for the accretion of the parent bodies of NC iron meteorites (<0.4 Myr after CAIs, Kruijer et al. 2017) shows that the separated NC and CC reservoirs probably existed in the disk before the formation of Jupiter.
Pressure maxima might also be interesting mechanisms explaining other observed disk features such as dusty ringed structures in transition disks (see, e.g., Pinilla et al. 2012; van der Marel et al. 2018) or as means to concentrate dust to form water-poor planetesimals if their formation occurred inward of the snow line (Ida & Guillot 2016; Ida et al. 2021; Charnoz et al. 2019; Hyodo et al. 2019, 2021a).
How a pressure bump might form in the absence of a planet is still unclear. Our study is an attempt to answer this question. Charnoz et al. (2019) reported the formation of a long-lasting pressure bump just inward of the snow-line and the subsequent runaway accumulation of dust at the bump when a stratified accretion disk with a dead zone is considered. However, the mechanism triggering this bump was not thoroughly investigated, but was clearly associated with the release of water vapor inward of the snow-line. Here we try to understand how a bump might form inward of a snow-line using the popular α disk description (which is not devoid of problems itself, see, e.g., Turner et al. 2014 for a critical review).
In Sect. 2, we introduce a simple parameterization of α to capture the effect of a dead zone in a protoplanetary disk. We detail with simple analytical arguments how the release of water vapor will trigger the formation of a pressure bump. In Sect. 3, we demonstrate the existence of this process with numerical simulations and investigate the space of free parameters. In Sect. 4, we investigate at which epoch a pressure bump might form during the disk evolution. Our results are discussed in Sect. 5 with a special emphasis on the separation of isotopic reservoirs as observed in our Solar System.
2 1D analytical study of a disk in which a α decreases with surface density
2.1 Vertically averaged α
Protoplanetary disks are thought to have a vertically stratified structure because of nonideal MHD (Magneto Hydro Dynamics) effects. The disk midplane may have a low turbulence and low accretion rate because of ohmic diffusion that prevents the onset of magnetorotational instability (Turner et al. 2014). This results in a quiet (i.e. non turbulent) ‘dead’ midplane with equivalent α (called αd) in the range 10−5 to 10−3 depending on local hydrodynamic turbulence (Bai & Stone 2013; Turner et al. 2014; Gressel et al. 2015; Kadam et al. 2019). It is topped by an active layer with a high accretion rate but low column density (Σa) in the range 100–1000 kg m−2 (Turner et al. 2014), and it may have a low level of turbulence (Béthune et al. 2017) despite the high accretion rate. In the active layer the effective value of α is designated by αa. The very upper layer may be occupied by disk winds, a region in which ambipolar diffusion is active that torques the two previous layers and where low-density winds breeze outward. The transition between the dead and active layers (in terms of column density) may be verysharp (Turner & Sano 2008; Bai & Stone 2013; Turner et al. 2014). In 1D models it is useful to introduce the vertically averaged α:
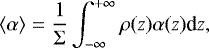 (2)
(2)
where ρ(z) and α(z) are the values of the gas density and α at altitude z, respectively.As the transition of the active to the dead layer is very sharp, it is possible to use a parameterization of 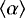 assuming that the disk is made of two layers: an active layer with constant column density Σa (100–1000 kg m−2, largely independent of the distance to the star (Turner & Sano 2008; Turner et al. 2014), and constant α = αa, and a dead midplane layer with surface density Σd = Σ − Σa and constant α = αd (see the appendix). Thus we obtain (Terquem 2008; Zhu et al. 2010; Bai & Stone 2013; Charnoz et al. 2019; Kadam et al. 2019)
assuming that the disk is made of two layers: an active layer with constant column density Σa (100–1000 kg m−2, largely independent of the distance to the star (Turner & Sano 2008; Turner et al. 2014), and constant α = αa, and a dead midplane layer with surface density Σd = Σ − Σa and constant α = αd (see the appendix). Thus we obtain (Terquem 2008; Zhu et al. 2010; Bai & Stone 2013; Charnoz et al. 2019; Kadam et al. 2019)
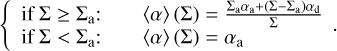 (3)
(3)
Following Kadam et al. (2019), we used αa = 10−2 and αd = 10−5. In the following, we use a simpler parameterization of 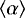 for clarity so that
for clarity so that 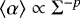 . It is therefore useful to introduce p, the exponent of the power law locally approximating
. It is therefore useful to introduce p, the exponent of the power law locally approximating 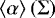 . It is
. It is
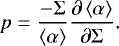 (4)
(4)
Inserting Eq. (3) into Eq. (4), we find that p ranges from 0 to (αa − αd)∕αa. Because αa ≫ αd, p can approach very closely 1. p is plotted in Fig. 1. For Σ < Σa, p = 0 because 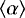 is a constant equal to αa. For Σ > Σa and Σ < Σaαa∕αd, p decreases from ~1 to 0. For Σ > Σaαa∕αd, p is almost equal to 0.
is a constant equal to αa. For Σ > Σa and Σ < Σaαa∕αd, p decreases from ~1 to 0. For Σ > Σaαa∕αd, p is almost equal to 0.
2.2 Small amplitude perturbation
For illustrative purposes, we start by considering the case of a small sound velocity perturbation to emphasize the strong effect it has on the disk pressure profile. The disk is described through the standard α disk formalism, in which the gas surface density Σ evolution obeys
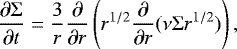 (5)
(5)
where ν and r are the local viscosity and distance to the star. Steady states are those solutions for which ∂Σ∕∂t = 0, implying νΣ = cst. Noting that the mass flux Ṁ = 3πνΣ, we obtain 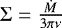 at steady state, which is well known. The effective viscosity is
at steady state, which is well known. The effective viscosity is 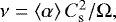 where Cs is the local sound velocity. We assume that
where Cs is the local sound velocity. We assume that 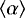 can be written as
can be written as
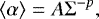 (6)
(6)
where A is a constant and p is a positive real number ≤1. For every value of Σ, there is a different value of p.
We replaced Eq. (6) into the expression of the steady-state surface density: Ṁ =3πνΣ. After solving for Σ, we obtained the surface density in the midplane at steady state Σss inside a dead zone and for a fixed value of p and Σ,
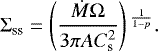 (7)
(7)
It is obvious from Eq. (7) that Σss has no steady-state solution for p = 1, and for p < 1, a minimum of sound velocity induces a maximum of surface density. In Eq. (7), p is fixed (given by Eq. (4)). For locally isothermal pressure 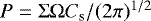 , we obtain for the local pressure at steady state Pss
, we obtain for the local pressure at steady state Pss
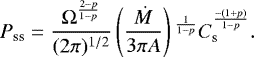 (8)
(8)
We now quantify the effect of a sound velocity perturbation (δCs) on the pressure profile at steady state. This sound velocity perturbation may result from a local variation of the gas mean molecular weight because water vapor is released at the snow-line. By calculating a first-order expansion of Pss as a function of Cs we obtain δPss, the pressure perturbation at steady state, as a function of the sound velocity perturbation δCs,
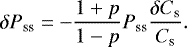 (9)
(9)
Again, the amplitude of the pressure perturbation diverges when p → 1, and δPss has a sign opposite to the sound-velocity perturbation. We now determine how strong δCs must be to induce a pressure bump by taking the derivative of Eq. (8) and setting that for a pressure bump ∂Pss ∕∂r ≥ 0. We write Ω = Br−3∕2 (with B a constant), and we obtain the condition for a pressure bump to appear by deriving Eq. (8) with respect to r,
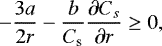 (10)
(10)
with a = (2 − p)∕(1 − p) and b = (1 + p)∕(1 − p) (two positive constants). Thus a pressure bump appears if the local derivative of Cs fulfills ∂Cs ∕∂r ≤−3a∕2br, which is a negative sound velocity perturbation.
Assuming that the disk is radiatively heated by the star, the unperturbed sound velocity profiles behave like Cr = Dr−1∕4, with D standing for a positive constant. We computed the amplitude of the sound velocity perturbation δC, above the unperturbed radiative profile, Cr, to trigger a pressure bump. We write Cs = Cr + δC and introduce it in Eq. (10). We derive the amplitude of the sound velocity perturbation to induce a pressure bump,
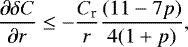 (11)
(11)
for p close tobut smaller than 1, we obtain 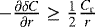 . This shows that the possibility of forming a pressure bump depends both on the amplitude of the sound perturbation (δC) and on its width (δr) by approximating
. This shows that the possibility of forming a pressure bump depends both on the amplitude of the sound perturbation (δC) and on its width (δr) by approximating 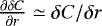 . We are interested here in sound–velocity perturbations induced by the release of water vapor just inward of the snow-line, which modify the mean molecular weight of the gas at constant temperature. As the isothermal sound velocity is
. We are interested here in sound–velocity perturbations induced by the release of water vapor just inward of the snow-line, which modify the mean molecular weight of the gas at constant temperature. As the isothermal sound velocity is 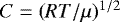 , we obtain δC = −1∕2Cδμ∕μ. Equation (11) is therefore rewritten as
, we obtain δC = −1∕2Cδμ∕μ. Equation (11) is therefore rewritten as
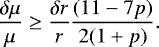 (12)
(12)
H2O has the molecular weight μH2O = 18 g mol−1, and the average gas of solar composition has μg = 2.3 g mol−1. The mean molecular weight is 1∕μ = f∕μH2O + (1 − f)∕μg (Schoonenberg & Ormel 2017). Noting f the water mass fraction, we obtain δμ∕μ = δfμ(1∕μg − 1∕μH2O) ≃ 0.87δf. The previous equation is accordingly rewritten in term of the water mass fraction,
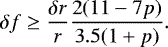 (13)
(13)
Here, δr is the radial spatial scale of the variation of the water-vapor content, typically the physical width of the snow-line controlled by the saturating vapor. δr is derived in Hyodo et al. (2021a), and δr is about ~0.2 au (their Eq. (54)) with the model settings used in Schoonenberg & Ormel (2017). δf is the amplitude of the variation of the water-vapor mass fraction. Before the inflow of water ice coming from beyond the snow-line f ≃0.01, this is the average water mass fraction in a disk of solar composition. Equation (13) provides a condition for the apparition of a pressure bump in the presence of increasing water vapor at the snow-lines. It states that a pressure bump will appear if δf ≥ 0.28 for p = 0.5 or δf ≥ 0.14 for p = 1. To test this criterion, we performed some simple tests with an α disk model solving Eq. (5) for gas and computing the viscosity using Eq. (6), so that p can be fixed. The initial water mass fraction, f, and δr, was set by hand using a Gaussian profile with standard deviation 0.1 au (Hyodo et al. 2021a). When Eq. (13) is satisfied, a pressure bump forms with this toy model. A pressure maximum appears for δf ≃ 0.2 in Fig. 2. The surface density profiles also changes slightly according to Eq. (7). For p close to 1, we therefore kept the criterion for pressure bump formation as δf > 0.2.
2.3 Large amplitude perturbation
We so far considered for illustrative purposes only a small perturbation of the sound velocity, and thus a small amount of water vapor. It has been found, however, that the sound velocity perturbation necessary to induce a bump is not so small (because 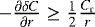 ). To continue our demonstration, we therefore abandoned our first-order development and returned to the original equations. We first computed the steady-state surface density by inserting Eq. (3) into the steady-state flux Ṁ = 3πνΣ. As it is common to parameterize the disk evolution using the accretion rate, Ṁ, we computed for different Ṁ the steady-state disk surface density assuming the dead-zone prescription for
). To continue our demonstration, we therefore abandoned our first-order development and returned to the original equations. We first computed the steady-state surface density by inserting Eq. (3) into the steady-state flux Ṁ = 3πνΣ. As it is common to parameterize the disk evolution using the accretion rate, Ṁ, we computed for different Ṁ the steady-state disk surface density assuming the dead-zone prescription for 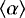 (Eq. (3)) combined with the steady-state relation Ṁ = 3πνΣ. After a little algebra, we obtained the steady-state surface density Σss :
(Eq. (3)) combined with the steady-state relation Ṁ = 3πνΣ. After a little algebra, we obtained the steady-state surface density Σss :
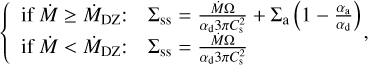 (14)
(14)
where ṀDZ is the critical accretion rate beyond which a region is embedded in a dead zone, 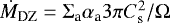 .
.
Assuming Ṁ > ṀDZ, the pressure in the dead zone at steady state is then
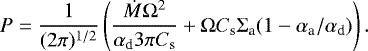 (15)
(15)
Then, we determined the condition for which ∂P∕∂r ≥ 0 in the DZ (Dead Zone). We obtain
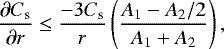 (16)
(16)
with the coefficients
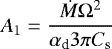 (17)
(17)
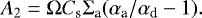 (18)
(18)
We now reformulate the above criterion in terms of water mass fraction enhancement at the snow-line. Because 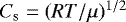 , then d Cs = 1∕2CsdT∕T − 1∕2Csdμ∕μ. In the region at the snow-line in which water vapor is released, we assume that d μ∕μ ≫dT∕T so d Cs ≃−1∕2dμ∕μ. Because δμ∕μ ≃ 0.87δf, the bump formation criterion (Eq. (16)) is rewritten in terms of water-vapor mass fraction (δf) is
, then d Cs = 1∕2CsdT∕T − 1∕2Csdμ∕μ. In the region at the snow-line in which water vapor is released, we assume that d μ∕μ ≫dT∕T so d Cs ≃−1∕2dμ∕μ. Because δμ∕μ ≃ 0.87δf, the bump formation criterion (Eq. (16)) is rewritten in terms of water-vapor mass fraction (δf) is
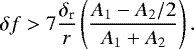 (19)
(19)
This equation gives a much better criterion for forming a pressure bump even in the case of strong sound velocity perturbation. The water-vapor enhancement necessary for forming a pressure bump δf as a function of Ṁ is plotted in Fig. 3 for δr∕r ≃ 0.1. At high surface densities and high accretion rate, δf ≃ 0.7 (equivalent to A2 ≪ A1 in Eq. (19)). A low accretion rate, δf ≃ 0.7, in agreement with estimates of the previous section. It is interesting that as the accretion rate decreases, it is increasingly easy for the disk to develop a pressure bump (as δf drops from 0.7 to 0.2). When the disk has lost most of its mass, and when the snow-line is no longer inside the dead zone, it is no longer possible to develop a pressure bump.
For the high accretion rates that are relevant for young disks, we keep for simplicity the criterion
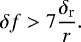 (20)
(20)
 |
Fig. 2 Pressure vs. distance in disks at steady states with different water-vapor mass fraction (f) enhancement at the snow-line (located at 3 au here). Here, Ṁ = 10−9M⊙ yr−1 and p = 0.1 (top), p= 0.5 (middle), and p = 0.9 (bottom). The width of the water-vapor-rich region is arbitrarily set to 0.1 au (numerically and analytically derived in Hyodo et al. 2021a). For the same mass fraction of water vapor, the pressure bump amplitude increases for larger p. |
2.4 Criterion in terms of the mass flux of icy pebbles
The criterion derived in Eq. (12) does not allow predicting the range of pebble and gas flux for which a pressure bump may form inside a dead zone. We therefore propose the following order of magnitude estimates: The vaporizationregion (the region around the snow-line in which icy pebbles evaporate) is located at a distance r and has a width δr. The water mass contained in this region is Mw. It is fed by the incoming flux of icy pebbles Fi = 2πrviΣi with an ice surface density Σi and an icy pebble velocity vi. Water vapor leaves this region with the same velocity as the gas vg, so that the water-vapor flux leaving the region is Fv = 2πrvgΣw. After a transient phase, the surface density of water vapor will reach a steady state, with a surface density at steady state Σw,ss = Σivi∕vg. For a pressure bump to appear, we must have Σw,ss∕Σ > δf. In this way, we define another (equivalent) condition for a pressure bump to form, as a function of gas velocity and ice surface density,
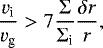 (21)
(21)
for δr ≃ 0.2 au (Hyodo et al. 2021a) and r ≃ 2 au, and for Σi∕Σ ≃ 0.01 (as typical values), we obtain vi∕vg > 70 for a pressure bump to appear. Equivalently, Eq. (21) can be formulated in terms of pebble-gas flux,
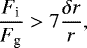 (22)
(22)
and with these values, we obtain Fi∕Fg > 0.7.
The conditions for a pressure bump to appear at the snow-line are summarized below:
The snow-line must be embedded within the dead zone (and not necessarily close to its edge);
The ice flux required for forming a pressure bump depends on the surface density at the snow-line. The higher the surface density (for young disks with high accretion rates), the higher the required flux. Conversely, as the surface density decreases, the accretion rate decreases also, and the lower the ice flux required for forming a pressure bump;
For a disk with a high surface density, which corresponds to a high accretion rate (> 10−7 M⊙ yr−1), assuming the Σi ∕Σ ≃ 0.01, a pressure bump will form at the snow-line if vi∕vg > 70, or equivalently, if Fi∕Fg > 0.7 for an ice-to-gas ratio of 1%. This corresponds to p close to 0. This shows that a high pebble flux is needed in dense disks to form a pressure bump;
For adisk with a low surface density (and an accretion rate in the range ≃ 10−9 M⊙ yr−1), assuming the Σi ∕Σ ≃ 0.01, a pressure bump will form at the snow-line if vi∕vg > 20, or equivalently, if Fi∕Fg > 0.2 for an ice-to-gas ratio of 1%. This corresponds to the case with p close to 1, so that it is easier in low surface density dead zones to form a pressure bump.
These above calculations assume that the surface density of the disk has reached a steady state (i.e., the accretion rate is constant everywhere). However, simulations of disks that include a dead zone (Zhu et al. 2010; Hasegawa & Takeuchi 2015; Charnoz et al. 2019) show that in general, no steady state is reached, and that the disk shows episodic phases of high and low accretion rates. In the next section, we therefore numerically study the formation of a pressure bump for a disk that is not in a steady state.
 |
Fig. 3 Water-vapor fraction at the snow-line that is required to induce a pressure bump as a function of the accretion rate (Ṁ), at 2 au. The solid red line shows δf for Σa = 100 kg m−2, and the solidblue line shows Σa = 1000 kg m−2. The dashed red and blue lines display ṀDZ, the accretion rate for which the 2 au region would be in a dead zone. |
3 Comparison with time-evolving simulations
We ran 12 disk evolution simulations in order to verify the validity of the criteria established in the previous section, which assume accretion at steady state so that the surface density follows Eq. (14). Here, we assumed a power-law surface density disk, so that is not at steady state, but corresponds to a more realistic case than in the previous section. We implemented a simple time-evolving alpha disk model very similar to the one described in Schoonenberg & Ormel (2017) and Hyodo et al. (2019) to treat gas, pebbles, and water vapor through diffusion and advection. The influx of icy pebbles was kept constant, as was the Stokes number of pebbles during their drift. The temperature profile was also constant and decreased like r−1∕2. Evaporation of water vapor was treated as in Schoonenberg & Ormel (2017) and resulted in a change of the local sound velocity that changed the effective viscosity ν through the relation 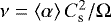 . The initial surface density of gas followed
. The initial surface density of gas followed 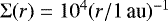 kg m−2, and the temperature profile was
kg m−2, and the temperature profile was 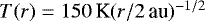 . The only difference to Schoonenberg & Ormel (2017) was the computation of α, for which we used the dead-zone prescription (Eq. (3)) with αd = 10−5 and αa = 10−2. From one simulation to the next, the Stokes number was varied from 0.01 to 0.1. The accretion rate was close to 10−7Ṁ⊙ yr−1, so that the theoretical criterion for forming a pressure bump was that the ice flux must be >0.6–0.7 times the gas flux. In the first set of simulations (Table 1), Σa was set to 100 kg m−2 so that the outer edge of the dead zone was located at 100 au, whereas the snow-line was initially located around 2 au. We present in Fig. 4 the case with S t = 0.1. In this configuration, the ratio vi∕vg = 822.1. A pressure bumps forms at about 6 Kyr (Table 1). The pressure bump never disappears and shifts inward by about 1 au as water vapor accumulates and increases the sublimation temperature. Like in Schoonenberg & Ormel (2017), the water-vapor mass fraction (f) does not evolve toward an asymptotic steady state in which the water-vapor mass fraction tends to decrease monotonically with distance. However, even after 1 Myr evolution, this steady state is still not reached here because the effective viscosity of the gas in the disk midplane is low. This represents a substantial fraction of the disk lifetime. Material tends to pile up at the snow-line with increasing efficiency as the viscosity drops with incoming water vapor, resulting in a sharper pressure bump with time.
. The only difference to Schoonenberg & Ormel (2017) was the computation of α, for which we used the dead-zone prescription (Eq. (3)) with αd = 10−5 and αa = 10−2. From one simulation to the next, the Stokes number was varied from 0.01 to 0.1. The accretion rate was close to 10−7Ṁ⊙ yr−1, so that the theoretical criterion for forming a pressure bump was that the ice flux must be >0.6–0.7 times the gas flux. In the first set of simulations (Table 1), Σa was set to 100 kg m−2 so that the outer edge of the dead zone was located at 100 au, whereas the snow-line was initially located around 2 au. We present in Fig. 4 the case with S t = 0.1. In this configuration, the ratio vi∕vg = 822.1. A pressure bumps forms at about 6 Kyr (Table 1). The pressure bump never disappears and shifts inward by about 1 au as water vapor accumulates and increases the sublimation temperature. Like in Schoonenberg & Ormel (2017), the water-vapor mass fraction (f) does not evolve toward an asymptotic steady state in which the water-vapor mass fraction tends to decrease monotonically with distance. However, even after 1 Myr evolution, this steady state is still not reached here because the effective viscosity of the gas in the disk midplane is low. This represents a substantial fraction of the disk lifetime. Material tends to pile up at the snow-line with increasing efficiency as the viscosity drops with incoming water vapor, resulting in a sharper pressure bump with time.
In all simulations we were able to perform for the case Σa = 100 kg m−2, a pressure bump forms because all our runs satisfy the criterion of Eq. (21), with vi ∕vg > 84 for a Stokes number as small as 0.01. Because of the expansive simulation time, we were unable to investigate lower values of vi ∕vg for this type of run. In a second set of runs, we set Σa = 1000 kg m−2, and a pressure bump formed down to a pebble Stokes number = 0.075 (Table 2) and vi ∕vg = 66.4 and Fi ∕Fg = 0.6. For lower values of the Stokes number and for vi∕vg < 66, no pressure bump formed up to 8.5 Myr evolution of the disk. The simple reasoning described above therefore gives a veryreasonable estimate of the threshold. In the remainder of our discussion, we therefore adopt vi ∕vg > 60 as the criterion for pressure bump formation for simplicity (and equivalently, Fi ∕Fg > 0.6, assuming a water-to-gasratio of 1%). We emphasize that in these simulations gas diffusion, which is included in the calculation, indeed acts againstthe piling up of gas to radially smooth the surface density peak. However, because α is a decreasing function of the surface density (Eq. (3)), diffusion is increasingly less efficient as the surface density increases. As a result, the surface density peaks are enhanced.
The simulations presented in Fig. 4 and in Tables 1 and 2 are useful because they are simple, with a constant Stokes number, temperature, gas, and pebble influx at the outer edge of the disk. They are useful to isolate the key mechanisms. However, in real disks, the influx of icy pebbles cannot be constant or last forever because the ice reservoir is finite and particles grow with time. It is therefore interesting to determine whether the pressure bump may form in a more realistic time-evolving disk including key processes such as viscous spreading, nonconstant pebbles flux, dust and gas transport, dust sublimation and condensation, dust growth, andradiative and viscous heating. We ran a time-dependent simulation similar to that of Drążkowska & Alibert (2017), which included the processes mentioned above (the code is described in Pignatale et al. 2018; Charnoz et al. 2019). We also used a temperature-dependent opacity table to compute the temperature in the midplane. The particle growth was computed with the model of Birnstiel et al. (2012). Additional details are given in Charnoz et al. (2019).
Our initial disk has a mass of 2% M⊙ and Σ(r) ∝ r−1. We used 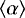 as defined in Eq. (3) with parameters Σa = 1000 kg m−2, αa = 10−2, and αd = 10−5. In this disk, the outer edge of the dead zone lies at about 10 au, which is well beyond the snow-line (at about 2 au). With these parameters, the gas accretion rate is about 10−8Ṁ yr−1. The results are displayed in Fig. 5 (it is essentially the same simulation as presented in Fig. 3 of Charnoz et al. 2019). At the snow-line (around 2 au), a surface density maximum forms in about 10 Kyr, when the sound velocity also decreases (dotted line in Fig. 5). At this time, the pebble Stokes number has grown to about 0.1–0.2 just beyond the snow-line (Fig. 3 of Charnoz et al. 2019). The gas surface density maximum is accompanied by silicate-rich dust accumulation just inward of the snow-line that is ice-free (red line). Just beyond the snow-line, ice-rich dustalso accumulates (solid blue line), promoted by water-vapor recondensation and a traffic-jam effect (as described inDrążkowska & Dullemond 2014; Schoonenberg & Ormel 2017; Drążkowska & Alibert 2017; Charnoz et al. 2019; Hyodo et al. 2019, 2021a). On timescales >100 Kyr, the pressure bump disappears because the icy material reservoir beyond the snow-line empties. When the icy pebble flux ends, the pressure bump disappears. The water-vapor surface density profile (dashed blue line) ends close to steady state and forms a plateau, which is consistent with Schoonenberg & Ormel (2017) and Hyodo et al. (2019). The wavy structures in the silicate dust density profiles inside 1 au are due to small opacity jumps between 300 K and 800 K in our opacity table (see Charnoz et al. 2019, Fig. 1) that change the midplane temperature, and thus the local viscosity. Because planetesimal formation is not considered in this simulation, nothing can save pebbles from ultimately being lost to the star when the bump disappears. If planetesimal formation were considered, they should form rapidly at the location of the bump because of the high surface density and high Stokes number. This will be investigated in a future study.
as defined in Eq. (3) with parameters Σa = 1000 kg m−2, αa = 10−2, and αd = 10−5. In this disk, the outer edge of the dead zone lies at about 10 au, which is well beyond the snow-line (at about 2 au). With these parameters, the gas accretion rate is about 10−8Ṁ yr−1. The results are displayed in Fig. 5 (it is essentially the same simulation as presented in Fig. 3 of Charnoz et al. 2019). At the snow-line (around 2 au), a surface density maximum forms in about 10 Kyr, when the sound velocity also decreases (dotted line in Fig. 5). At this time, the pebble Stokes number has grown to about 0.1–0.2 just beyond the snow-line (Fig. 3 of Charnoz et al. 2019). The gas surface density maximum is accompanied by silicate-rich dust accumulation just inward of the snow-line that is ice-free (red line). Just beyond the snow-line, ice-rich dustalso accumulates (solid blue line), promoted by water-vapor recondensation and a traffic-jam effect (as described inDrążkowska & Dullemond 2014; Schoonenberg & Ormel 2017; Drążkowska & Alibert 2017; Charnoz et al. 2019; Hyodo et al. 2019, 2021a). On timescales >100 Kyr, the pressure bump disappears because the icy material reservoir beyond the snow-line empties. When the icy pebble flux ends, the pressure bump disappears. The water-vapor surface density profile (dashed blue line) ends close to steady state and forms a plateau, which is consistent with Schoonenberg & Ormel (2017) and Hyodo et al. (2019). The wavy structures in the silicate dust density profiles inside 1 au are due to small opacity jumps between 300 K and 800 K in our opacity table (see Charnoz et al. 2019, Fig. 1) that change the midplane temperature, and thus the local viscosity. Because planetesimal formation is not considered in this simulation, nothing can save pebbles from ultimately being lost to the star when the bump disappears. If planetesimal formation were considered, they should form rapidly at the location of the bump because of the high surface density and high Stokes number. This will be investigated in a future study.
Summary of the results obtained for six simulations with Σa = 100 kg m−2.
Summary of the results obtained for six simulations with Σa = 1000 kg m−2.
 |
Fig. 4 Evolution of a disk with constant inflow of gas and pebbles. Here Σa = 100 kg m−2, and the pebble Stokes number is 0.1. (top) Pressures in the disk midplane vs. distance at different times, and (bottom) water-vapor mass fraction vs. distance for different times. See Table 1. |
 |
Fig. 5 Simulation of a full protoplanetary disk using |
4 Summary and discussion
4.1 Summary
We have detailed a process by which a pressure bump can form in a stratified protoplanetary disk, including a central layer that is dead to turbulence, and an actively accreting upper layer with a surface density Σa. Considering that the vertically averaged α is a decreasing function of surface density (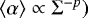 , we have shown that when the local sound velocity decreases (due to the release of vapor inward of the snow-line), a maximum in the local pressure appears whose magnitude increases with p. A physical explanation of this process, implying an interplay between the dead and active layer, is provided in Appendix A. This effect is especially efficient when p is close to 1, in other words, when the surface density at the snow-line is lower than ten times the active layer column density (which does not necessarily imply that the snow-line is located close to the outer edge of the dead zone). For a minimum mass solar nebula profile with
, we have shown that when the local sound velocity decreases (due to the release of vapor inward of the snow-line), a maximum in the local pressure appears whose magnitude increases with p. A physical explanation of this process, implying an interplay between the dead and active layer, is provided in Appendix A. This effect is especially efficient when p is close to 1, in other words, when the surface density at the snow-line is lower than ten times the active layer column density (which does not necessarily imply that the snow-line is located close to the outer edge of the dead zone). For a minimum mass solar nebula profile with 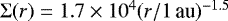 , we have p > 0.9 in the terrestrial planet region for Σa > 100 kg m−2 (check on Fig. 1), that is, already a very favorable situation for forming a pressure bump. The outer edge of the dead zone for the same nebula is located far beyond 10 au (when Σ =Σa).
, we have p > 0.9 in the terrestrial planet region for Σa > 100 kg m−2 (check on Fig. 1), that is, already a very favorable situation for forming a pressure bump. The outer edge of the dead zone for the same nebula is located far beyond 10 au (when Σ =Σa).
The conditions for the pressure-bump to form are summarized as follows. First the disk must be stratified, with a dead zone containing the snow-line. Second, the influx of icy pebbles must be high: for a young disk with Ṁ > 10−7M⊙ yr−1 the condition is Fi∕Fg > 0.6. For an old disk, Ṁ < 10−8M⊙ yr−1, we find Fi∕Fg > 0.2 is enough (where Fi and Fg are the icy-pebbles flux and gas-flux respectively). These numbers are for disk containing 1% of ice by mass. Note that, for our Solar System, 1% is approximately the mass fraction of all condensible material. The water mass fraction for our Solar System may instead be in the range ~0.3% (e.g., Bitsch & Johansen 2016), so the previous flux ratios must be multiplied by ~ 3. In this case, Fi ∕Fg > 1.8 is required (for Ṁ > 10−7 M⊕ yr−1). A flux as high is easily reached in a disk with Σa = 100 kg m−2 and containing pebbles with Stokes number > 0.03. Conversely, in a disk with Σa = 1000 kg m−2, a Stokes number >0.3 is required. The gas surface density at the snow line, Σ, must be in the range Σa < Σ < αa∕αd × Σa (i.e., a few 103 to a few 104 kg m−2) in order to create the pressure bump.
The mechanism described here has the following important properties:
The formation of a pressure bump just inward of the snow-line as long as the icy pebble flux is maintained and is high enough;
The accumulation of ice-free pebbles at the pressure bump, which may result in the formation of water-free planetesimals at the bump location;
Pebbles accumulating at the pressure bump are inherited from beyond the snow-line due to the inward drift of icy pebbles. They would not cross the bump, however, because the bump acts as a dynamical barrier and because they are progressively incorporated into larger planetesimals;
In addition to this process, beyond the snow-line, planetesimal formation can still occur at any time, following the processes described in Drążkowska & Alibert (2017) (e.g., the traffic-jam effect or recondensation of water vapor beyond the snow-line).
We emphasize again that this mechanism does not necessarily occur close to the outer edge of the dead zone. There is no need for a coincidence between the location of the snow-line and the outer edge of the dead zone (defined as Σ =Σa). For example, for p > 0.7 (a conditionvery favorable for the formation of the bump), the surface density at the snow-line must be higher than 1000Σa (Fig. 1). For a minimum mass solar nebula, with a snow-line at about 2 au, the outer edge of the dead zone would be at about >10 and >100 au for Σa = 1000 kg m−2 and Σa = 100 kg m−2, respectively.
The formation of the pressure bump may lead to a strong enhancement of the dust-to-gas ratio in the disk midplane, which is required to trigger the streaming-instability, and thus, planetesimal formation. In Fig. 5, which is our most realistic disk simulation of our paper, the ratio of dust to gas surface density at the bump increases to about Σd ∕Σd ≃ 0.1. At this place, the pebble Stokes number is about 0.3 (Charnoz et al. 2019). We can therefore estimate the dust-to-gas ratio of volumetric densities in the midplane. We assume that the pebbles are in a vertical steady state where turbulent diffusion acts against sedimentation, then the dust scale height 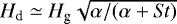 Drążkowska & Dullemond (2014), where α is αd here. The ratio of the volumetric densities of dust and gas in the midplane is also equal to ρd ∕ρg = (ΣdHg)∕(ΣgHd). We therefore obtain
Drążkowska & Dullemond (2014), where α is αd here. The ratio of the volumetric densities of dust and gas in the midplane is also equal to ρd ∕ρg = (ΣdHg)∕(ΣgHd). We therefore obtain 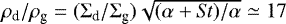 , which much larger that 1. It is very possible, accordingly, that planetesimals can form in the pressure bump that is visible in Fig. 5. However, we recall that other instabilities may develop that may or may not act against a concentration of dust. Hasegawa & Takeuchi (2015) investigated a viscous instability process using a new parameterization of α depending on the local magnetic field, and this is a generalization of the parameterization of α we use here. They showed that at the outer edge of the dead zone, the effective α may become negative, leading to a viscously unstable situation where density maxima can grow without bounds because of a negative effective diffusion coefficient. This instability may occur at the outer edge of the dead zone, when the surface density becomes comparable to Σa. This shows that the pressure bump formation process may occur in addition to the instability described in Hasegawa & Takeuchi (2015). However, we emphasize here that whereas the instability process of Hasegawa & Takeuchi (2015) occurs at the outer edge of the dead zone, the pressure bump formation process we describe here occurs well inside the dead zone, at the snow-line. Large-scale hydrodynamical instabilities are also known to develop, such as the Rossby wave instability, in the presence of a large viscosity gradient (that may occur at the outer edge of the dead zone) or in the presence of a strong pressure or density bump (as in our case) (Regály et al. 2012; Mohanty et al. 2013). This may imply that a large-scale vortex may potentially form at the pressure bump (this physics is not included in our simple 1D model) that might concentrate pebbles, and might lead to the formation of large planetesimals. In conclusion, the evolution of dust in such a bump, which might be subject to different types of hydrodynamical instabilities, should be investigated with 3D simulations in the future.
, which much larger that 1. It is very possible, accordingly, that planetesimals can form in the pressure bump that is visible in Fig. 5. However, we recall that other instabilities may develop that may or may not act against a concentration of dust. Hasegawa & Takeuchi (2015) investigated a viscous instability process using a new parameterization of α depending on the local magnetic field, and this is a generalization of the parameterization of α we use here. They showed that at the outer edge of the dead zone, the effective α may become negative, leading to a viscously unstable situation where density maxima can grow without bounds because of a negative effective diffusion coefficient. This instability may occur at the outer edge of the dead zone, when the surface density becomes comparable to Σa. This shows that the pressure bump formation process may occur in addition to the instability described in Hasegawa & Takeuchi (2015). However, we emphasize here that whereas the instability process of Hasegawa & Takeuchi (2015) occurs at the outer edge of the dead zone, the pressure bump formation process we describe here occurs well inside the dead zone, at the snow-line. Large-scale hydrodynamical instabilities are also known to develop, such as the Rossby wave instability, in the presence of a large viscosity gradient (that may occur at the outer edge of the dead zone) or in the presence of a strong pressure or density bump (as in our case) (Regály et al. 2012; Mohanty et al. 2013). This may imply that a large-scale vortex may potentially form at the pressure bump (this physics is not included in our simple 1D model) that might concentrate pebbles, and might lead to the formation of large planetesimals. In conclusion, the evolution of dust in such a bump, which might be subject to different types of hydrodynamical instabilities, should be investigated with 3D simulations in the future.
4.2 Implications
4.2.1 Isolation of isotopic reservoirs
Recent works (Kruijer et al. 2017; Nanne et al. 2019; Kleine et al. 2020) have proposed a qualitative time line for forming and isolating the NC and CC groups, invoking a first a phase of CAI formation close to the star, in a disk that is initially dominated by CC isotopic composition. It is proposed than within the first million years, the infalling cloud changes composition and feeds the terrestrial planet region of the disk. At about 1 Myr, the formation of Jupiter occurs at about 5 au and splits the disk into two reservoirs that follow isolated evolutions, where first the iron bodies and then the chondritic bodies are formed. The innermost reservoir, the NC, progressively stops its accretional evolution at about 1.5–2 Myr because no more material is accreted beyond the barrier that Jupiter forms. Finally, at about 5 Myr, Jupiter reaches its final mass and scatters the planetesimals inward, leading to a radial mixing of the two groups. This model was recently critically reviewed by Brasser & Mojzsis (2020), who argued that the formation of Jupiter as late as 1 Myr at 5 au would not prevent enough isolation of the CC and NC groups because pebbles would fast be delivered into the region of terrestrial planets. This delivery would lead to the isotopic contamination of the inner (NC) reservoir by material coming from the CC reservoir. It would also lead to a martian embryo that would be too large compared to its actual mass. The authors then suggested that the isolation of the reservoirs must have occurred before 1 Myr in order to achieve both well-separated isotopic groups and slow down the growth of Mars. In addition, recent work (Bitsch et al. 2015; Pirani et al. 2019; Öberg & Wordsworth 2019) suggested that Jupiter may have formed beyond 15 au and reached its final location only by the end of the disk lifetime, at around 3 Myr, well after the differentiation of the NC and CC iron bodies.
The pressure bump formation mechanism presented here may be an ideal alternative to the Jupiter hypothesis. The time line of events proposed in Kruijer et al. (2017), Nanne et al. (2019), and Kleine et al. (2020) might qualitatively be revisited as follows (see Fig. 6). First, at time = 0, the disk is dominated by CC isotopic composition and CAIs are formed and transported outward during the viscous expansion of the disk (Pignatale et al. 2018; Nanne et al. 2019). As the disk is still massive and pebbles are small (with stokes numbers < 0.01), the pressure bump cannot form. In the first few 100 Kyr, the material infalling from the cloud changes composition to NC and feeds the disk inner region inward of the snow-line. Before the pressure bump is established, pebbles can cross the snow-line. As the disk empties, the surface density at the snow-line then decreases < αa∕αd × Σa, which may occur in only a few 100 Kyr and leads to the spatial separation of the NC and CC groups. This situation lasts for a few million years as long as the pebble flux is maintained. During this period, NC and CC group bodies separately accrete inward and beyond the snow-line, respectively. Because the NC population is no longer fed with pebbles (which are blocked at the pressure bump), it may stop growing at about 2 Myr. At the end of the gas-disk life, when Σ <Σa at the snow-line, the pressure bump disappears, but planetesimals are already formed and do not migrate because of the gas drag. At approximately the same epoch, Jupiter should appear, migrating inward from the outer Solar System. It may scatter embryos and planetesimals, leading to substantial radial mixing of the two populations. Figure 6 shows the snow-line as fixed, but this is not mandatory. It is very possible that the snow-line may have migrated outward during the disk infall, and then inward during the disk evolution (Pignatale et al. 2018; Baillié et al. 2019).
 |
Fig. 6 Schematic of the disk and NC and CC populations evolution. Green shows the gas disk. The pressure bump is symbolized by a darker green zone, just inward of the snow-line. The dashed ellipse shows the dead zone. Blue and red arrows show the molecular cloud gas infall. Dots with a dark circle are the parent bodies of CC and NC bodies. Dots with a white circle show the iron and chondritic populations. This figure is inspired and modified from Kleine et al. (2020). |
4.2.2 Forming planetesimals
This mechanism might also explain how dust can accumulate efficiently inward of the snow-line and form water-free planetesimals. This has challenged models in recent years (Drążkowska & Dullemond 2014; Drążkowska & Alibert 2017; Ida & Guillot 2016; Hyodo et al. 2019, 2021a; Ida et al. 2021), showing that planetesimals may form rather beyond the snow-line (due to water-vapor recondensation, the traffic-jam effect, and dust-gas back-reaction) and so should always be mostly water rich, which is a problem when the petrology of ordinary chondrites is to be explained that only show little water alteration (Ida & Guillot 2016; Ida et al. 2021; Hyodo et al. 2021a).
We have neglected the effects of the back-reaction. We note that including the back-reaction with a dead-zone structure can develop the so-called no-drift runaway pile-up mode of pebbles at a certain heliocentric distance, forming planetesimals, before pebbles reach the snow-line (Hyodo et al. 2021b).
Forming planetesimals in dead zones at the snow-line is not in itself a new idea. It has been proposed in particular in Brauer et al. (2008). However, our work is different because Brauer et al. (2008) investigated the effect of ice accumulation beyond the snow-line and showed that the increase in dust-to-gas ratio may locally modify α and trigger a pressure maximum. The process investigated here does not rely on this effect, but rather on an accumulation of gas at locations of low sound velocities, for instance, just inward of the snow-line.
4.3 Making pressure traps at condensation fronts
The mechanism for forming a pressure bump detailed here might work at every condensation front, provided the flux of heavy evaporating species is strong enough and that an evaporating front is embedded in the dead zone. Observations of the TW-Hydra disk potentially reveal efficient trapping of CO or N2 dust >10 au at their evaporation front (Bosman & Banzatti 2019; McClure et al. 2020). However, we only focused on water evaporation. The viability of such a process at the CO or N2 condensation fronts must be quantified in a future study.
5 Limitations
Several limitations and uncertainties may limit the validity of our work. This simple model is based upon the assumption of an idealized α disk model with two layers (one dead, one active), the validity of which is still a matter of debate; see Turner et al. (2014) for a critical review. It should in the future be compared to nonideal MHD simulations, including dust, gas, and evaporation, for confirmation.
In addition, for the pressure bump to survive, it must be constantly replenished by incoming water vapor. However, the water-ice reservoir is limited, and its emptying timescale Te is short: it is about Te = mMd∕(ṀFi∕Fg), where m is the disk metallicity and Md is the disk mass. For Md = 0.02 M⊙, Fi ∕Fg = 0.6, Ṁ = 10−8M⊙ yr−1, and m = 0.01, we obtain Te ≃ 17 Kyr. Te is much shorter than the disk lifetime, and shorter than the accretion time of the CC chondrite group, but large uncertainties exist on all parameters: the disk mass, as well as Fi∕Fg and Ṁ, which evolve with time.
A speculative solution for the short timescale of water inflow may be the following: Manara et al. (2019) proposed that the disk may be continuously replenished during most of its lifetime by material infalling from the molecular cloud in order to explain the discrepancy between the measured dust content of disks in millimetric observations and the mass distribution of exoplanets. Feeding the disk with ISM material at the stellar ratio of the oxygen abundance would allow maintaining the inflow of icy pebbles, which in turn would allow the long-term existence of pressure maxima. This would be a major change in the paradigm of protoplanetary disk evolution, but it is still controversial. This is worth considering because simulations of star formation (starting from the molecular cloud) show that the infall phase could last up to a few million years (Padoan et al. 2014). While speculative, this possibility would be worth considering in future studies.
Acknowledgments
We wish to acknowledge the financial support of the Region Île-de-France through the DIM-ACAV + project: “HOC – Origine de l’eau et du carbone dans le Système Solaire”, the french “Programme National de Planetologie” (PNP), the program ANR-15-CE31-0004-1 (ANR CRADLE), the IdEx Université de Paris ANR-18-IDEX-0001, and program ANR-20-CE49-0006 (ANR DISKBUILD). R.H. was supported by JSPS Kakenhi JP17J01269 and 18K13600. R.H. also acknowledges JAXA’s International Top Young program. We warmly thank S. Ida, T. Guillot and R. Brasser for useful comments. We also thank our anonymous reviewer for a thoughtful review that helped us to largely improve the quality of the paper.
Appendix A Physical explanation for the viscous instability in a stratified disk
We give here a physical explanation for the origin of the pressure bump mechanism described in the paper. We emphasize the key role played by the layered accretion structure. We tracked the surface density Σ evolution of a stratified disk with two layers. The midplane layer (low turbulence) has a surface density Σd and α =αd, and the active layer (high turbulence) has a column density Σa and α = αa, with αa ≫ αd. The local total surface density is Σ = Σa + Σd. There are two key ingredients that cause the instability : first, The active layer has a fixed surface density Σa, second, there is a minimum of the sound velocity somewhere (e.g., at the snow-line due to the release of water vapor).
We assume that at location r0, there is a minimum of the sound velocity so that
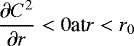 (A.1)
(A.1)
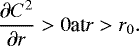 (A.2)
(A.2)
The question now is how the mass is transported in the disk at r0. The total mass flux F (i.e., the local accretion rate) can be split into two contributions: F = Fd + Fa (Fd is the mass flux in the DZ, and Fa is the mass flux in the active layer). It is useful to rewrite the surface density equation in terms of divergence of mass flux. The surface density evolution is
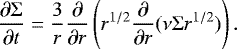 (A.3)
(A.3)
We introduce F as the local mass flux. Then the variation in density is always opposite to the divergence of the material flux,
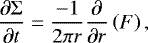 (A.4)
(A.4)
We write Ω = Br−3∕2. Considering the dead-zone and the active layers as two layers with constant α and developing the derivative, we have
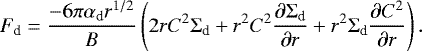 (A.6)
(A.6)
This is the flux in the DZ. When an overdensity of Σd in the dead zone (the second term) is strong enough, Fd is opposite to the density perturbation, and the viscous evolution will erase the density perturbation. This is
the classicalview of viscous diffusion where the material flux is opposite to density variations. When we repeat the same calculation for the active layer and recall that the surface density of the active layer is constant = Σa, we obtain for the radial flux in the active layer
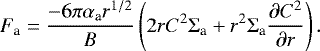 (A.7)
(A.7)
 |
Fig. A.1 Sketch of the two layers in the disk with their respective mass fluxes. |
If in the active layer ∂C2∕∂r is strong enough (in absolute value), the flux is always directed toward the minima of the sound velocity (Fa is positive when C2 decreases). This means that more material will be brought toward the sound velocity minima. Because no more than Σa of the column density can be in the active layer, the incoming material is transferred down to the dead zone (which can accept it without limit), so that Σd increases. Inother terms, the active layer will feed the dead zone with new material at places of low sound velocity (at r = r0 with our notations). The net result is that Σ increases at r0.
Equation (A.6) shows that when Σd is very high at r0, so the ∂Σd∕∂r term becomes very strong at some points and compensates for other terms, and eventually, Fd is directed away from the maxima of the surface density. This means that Σd cannot diverge to infinity. Rather, there is a transient phase with a strong increase in the surface density and a pressure bump is created, as described above.
This is a simplified two-layer model. The key idea is, however, that the column density of the active layer is almost constant it does not “feel” the density maxima in the DZ. As the gas accretes, the material is therefore transported and stored in the dead zone with low viscosity. In total, this creates a situation in which the vertically averaged diffusion coefficient ν decreases with increasing Σ, which is typical of a viscous instability process, which favors an enhancement of regions with high surface density.
References
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 767, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Baillié, K., Marques, J., & Piau, L. 2019, A&A, 624, A93 [CrossRef] [EDP Sciences] [Google Scholar]
- Béthune, W., Lesur, G., & Ferreira, J. 2017, A&A, 600, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Johansen, A. 2016, A&A, 590, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosman, A. D., & Banzatti, A. 2019, A&A, 632, L10 [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R., & Mojzsis, S. J. 2020, Nat. Astron., 8 [Google Scholar]
- Brauer, F., Henning, T., & Dullemond, C. P. 2008, A&A, 487, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnoz, S., Pignatale, F. C., Hyodo, R., et al. 2019, A&A, 627, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drążkowska, J., & Dullemond, C. P. 2014, A&A, 572, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drążkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gressel, O., Turner, N. J., Nelson, R. P., & McNally, C. P. 2015, ApJ, 801, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, Y., & Takeuchi, T. 2015, ApJ, 815, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Hyodo, R., Ida, S., & Charnoz, S. 2019, A&A, 629, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hyodo, R., Guillot, T., Ida, S., Okuzumi, S., & Youdin, A. N. 2021a, A&A, 646, A14 [EDP Sciences] [Google Scholar]
- Hyodo, R., Ida, S., & Guillot, T. 2021b, A&A, 645, L9 [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Guillot, T. 2016, A&A, 596, L3 [EDP Sciences] [Google Scholar]
- Ida, S., Guillot, T., Hyodo, R., Okuzumi, S., & Youdin, A. N. 2021, A&A, 646, A13 [EDP Sciences] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Kadam, K., Vorobyov, E., Regály, Z., Kóspál, Á., & Ábrahám, P. 2019, ApJ, 882, 96 [Google Scholar]
- Kleine, T., Budde, G., Burkhardt, C., et al. 2020, Space Sci. Rev., 216, 55 [CrossRef] [Google Scholar]
- Kruijer, T. S., Burkhardt, C., Budde, G., & Kleine, T. 2017, Proc. Natl. Acad. Sci. U.S.A., 114, 6712 [Google Scholar]
- Kruijer, T. S., Kleine, T., & Borg, L. E. 2020, Nat. Astron., 4, 32 [Google Scholar]
- Manara, C. F., Mordasini, C., Testi, L., et al. 2019, A&A, 631, L2 [CrossRef] [EDP Sciences] [Google Scholar]
- McClure, M. K., Dominik, C., & Kama, M. 2020, A&A 642, L15 [Google Scholar]
- Mohanty, S., Ercolano, B., & Turner, N. J. 2013, ApJ, 764, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Nanne, J. A. M., Nimmo, F., Cuzzi, J. N., & Kleine, T. 2019, Earth Planet. Sci. Lett., 511, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., & Wordsworth, R. 2019, AJ, 158, 194 [Google Scholar]
- Padoan, P., Haugbølle, T., & Nordlund, Å. 2014, ApJ, 797, 32 [Google Scholar]
- Pignatale, F. C., Charnoz, S., Chaussidon, M., & Jacquet, E. 2018, ApJ, 867, L23 [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pirani, S., Johansen, A., Bitsch, B., Mustill, A. J., & Turrini, D. 2019, A&A, 623, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2012, MNRAS, 419, 1701 [Google Scholar]
- Schoonenberg, D., & Ormel, C. W. 2017, A&A, 602, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terquem, C. E. J. M. L. J. 2008, ApJ, 689, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Trinquier, A., Birck, J. L., Allègre, C. J., Göpel, C., & Ulfbeck, D. 2008, Geochim. Cosmochim. Acta, 72, 5146 [Google Scholar]
- Turner, N. J., & Sano, T. 2008, ApJ, 679, L131 [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 411 [Google Scholar]
- van der Marel,N., Williams, J. P., & Bruderer, S. 2018, ApJ, 867, L14 [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
- Zhu, Z., Hartmann, L., Gammie, C. F., et al. 2010, ApJ, 713, 1134 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 p as a function of Σ for |
| In the text | |
 |
Fig. 2 Pressure vs. distance in disks at steady states with different water-vapor mass fraction (f) enhancement at the snow-line (located at 3 au here). Here, Ṁ = 10−9M⊙ yr−1 and p = 0.1 (top), p= 0.5 (middle), and p = 0.9 (bottom). The width of the water-vapor-rich region is arbitrarily set to 0.1 au (numerically and analytically derived in Hyodo et al. 2021a). For the same mass fraction of water vapor, the pressure bump amplitude increases for larger p. |
| In the text | |
 |
Fig. 3 Water-vapor fraction at the snow-line that is required to induce a pressure bump as a function of the accretion rate (Ṁ), at 2 au. The solid red line shows δf for Σa = 100 kg m−2, and the solidblue line shows Σa = 1000 kg m−2. The dashed red and blue lines display ṀDZ, the accretion rate for which the 2 au region would be in a dead zone. |
| In the text | |
 |
Fig. 4 Evolution of a disk with constant inflow of gas and pebbles. Here Σa = 100 kg m−2, and the pebble Stokes number is 0.1. (top) Pressures in the disk midplane vs. distance at different times, and (bottom) water-vapor mass fraction vs. distance for different times. See Table 1. |
| In the text | |
 |
Fig. 5 Simulation of a full protoplanetary disk using |
| In the text | |
 |
Fig. 6 Schematic of the disk and NC and CC populations evolution. Green shows the gas disk. The pressure bump is symbolized by a darker green zone, just inward of the snow-line. The dashed ellipse shows the dead zone. Blue and red arrows show the molecular cloud gas infall. Dots with a dark circle are the parent bodies of CC and NC bodies. Dots with a white circle show the iron and chondritic populations. This figure is inspired and modified from Kleine et al. (2020). |
| In the text | |
 |
Fig. A.1 Sketch of the two layers in the disk with their respective mass fluxes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.