EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 650 (June 2021) A&A, 650 (2021) A97 Full HTML
Open Access
Issue
A&A
Volume 650, June 2021
Article Number A97
Number of page(s) 10
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202140449
Published online 11 June 2021

© D. M. Malaspina et al. 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

Recent studies have demonstrated that solar wind particle distributions are highly unstable to the growth of plasma waves at distances from the Sun smaller than ∼55 solar radii (∼0.25 astronomical units). The plasma wave modes reported in this region of space include narrowband waves such as ion cyclotron waves (Bowen et al. 2020; Verniero et al. 2020), whistler-mode waves (Agapitov et al. 2020; Jagarlamudi et al. 2020; Cattell et al. 2021), Langmuir waves (Bale et al. 2019), ion acoustic waves (Mozer et al. 2020), and waves near the electron cyclotron frequency (Malaspina et al. 2020). Broadband waves have also been reported, including kinetic Alfvén waves (Chaston et al. 2020) and plasma turbulent fluctuations (Chen et al. 2020; Zhao et al. 2020; Zhu et al. 2020).

Plasma waves are important to the system-scale dynamics of the solar wind because they act to transfer energy from one part of solar wind particle distributions, the wave-unstable region, to other parts of the distribution where wave damping occurs. In this way, energy exchange mediated by plasma waves homogenizes mixed plasmas, smooths discontinuous distributions, relaxes particle beam distributions, and scatters particles in pitch angle.

This study focuses on plasma waves near the electron cyclotron frequency (fce) in the near-Sun solar wind. These waves, as reported in Malaspina et al. (2020), were found to preferentially occur in regions of extraordinarily low amplitude magnetic fluctuations (quiescent solar wind regions), where the solar wind magnetic field vector (B) remains within ∼5° of the theoretical Parker spiral direction. Additionally, the quiescent solar wind regions show distinctly different spectra of turbulent fluctuations, with 50 times higher frequency of the 1/f spectral break location compared to regions of the solar wind with switchbacks, consistent with less evolved solar wind in the quiescent regions (Dudok de Wit et al. 2020). Regions of high wave growth were found to coincide with a strong sunward drift of the electron core population, suggesting that the coincident electron strahl population was denser, focused more narrowly into a beam, or extended to higher energy compared to surrounding regions. The solar wind properties of low-amplitude ambient magnetic field fluctuations, Parker-spiral B vector, higher 1/f spectral break frequency, and strong sunward electron core drift, are consistent with the interpretation that these regions of high wave growth represent portions of the solar wind that are most directly magnetically connected to the solar corona. Therefore, these near-fce waves may therefore play an important role in the evolution of solar wind electrons early in their escape from the solar corona.

These near-fce waves were found to have two primary wave power peaks, one near fce and one near 0.7fce, and many higher harmonics of both frequencies. The waves were found to persist for time periods ranging from minutes to many hours. They were found to increase in occurrence and amplitude with decreasing distance to the Sun. The wave mode was not conclusively identified in Malaspina et al. (2020), although it was speculated that they might be electrostatic whistler-mode or electron Bernstein waves. In this analysis, the properties of the studied near-fce waves are found to be inconsistent with prior observations of whistler-mode waves in the solar wind (e.g., Zhang et al. 1998; Lacombe et al. 2014; Stansby et al. 2016; Tong et al. 2019)

Malaspina et al. (2020) used relatively low-cadence (∼0.87s), highly compressed survey spectral data from the Parker Solar Probe spacecraft to examine these waves. In the current study, the detailed properties of these waves are examined using captures of burst captures of high-cadence electric and magnetic field time series data. These data enable determination of a wealth of wave properties, which narrows the list of possible wave modes down and offers a new understanding of the instabilities that drive these waves. It also elucidates the impact that they have on the evolution of solar wind electron distribution functions.

The findings are surprising and demonstrate that (i) the near-fce waves consist of at least three separate but simultaneously occurring wave modes, one of which can be conclusively identified as electron Bernstein waves, and (ii) the portion of the electron distribution function that is unstable to wave growth is at exceptionally low energies, near the center of the electron core distribution. Furthermore, the data examined here constrain the wave polarization, wave vector direction, and magnitude, and suggest a possible geometry for the wave source regions.

2. Data

This analysis uses data from the Parker Solar Probe mission (Fox et al. 2016), primarily the FIELDS (Bale et al. 2016) and The Solar Wind Electrons Alphas and Protons (SWEAP; Kasper et al. 2016) instruments. The full Parker Solar Probe mission consists of 24 orbits of the Sun. Each close approach to the Sun (< 55 solar radii (RS)) is referred to as an encounter, and is numbered sequentially. At the time of writing, seven encounters have been completed.

This study uses data from the four FIELDS voltage sensors in the plane of the heat shield, which are operated as differential pairs (V12, V34), as well as magnetic field data from the Fluxgate Magnetometer (FGM) and Search Coil Magnetometer (SCM). Both survey and burst data products from the Digital Fields Board (DFB; Malaspina et al. 2016) are also used, including the AC-coupled survey power spectra (covering ∼140 Hz to 75 kHz at a cadence of ∼0.87 s) and triggered time-series bursts (150 kS s−1 for ∼3.5 s). Quasi-thermal noise measurements from the Radio Frequency Spectrometer (RFS; Pulupa et al. 2017) at a cadence of 16 s are used to determine the electron plasma density. This study uses data from SWEAP, primarily the proton velocity, as determined by the Faraday cup (Case et al. 2020).

FIELDS and SWEAP data are presented in the spacecraft coordinate system (and the spacecraft reference frame), where 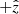points sunward, 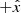points in the direction of motion of the spacecraft about the Sun (ram), and 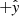completes the orthogonal set, pointing approximately to ecliptic south. To derive electric field amplitudes, the differential pair voltage data (V12, V34) are rotated into spacecraft coordinates and divided by an effective electrical length of 3.5 m (Mozer et al. 2020).

This study contains an analysis of one time-series burst, recorded near June 6, 2020, 12:09:54 UTC (encounter 5), but the results are generally applicable to similar bursts captured during any of the encounters examined thus far. Several hundred bursts of this type (150 kS s−1 for ∼3.5 s, six channels of time-series data) are captured per solar encounter. These bursts are selected by an on-board algorithm that seeks the highest-amplitude signals in V12 time-series data. During each of the first seven encounters, several tens of these bursts contain waves of the type explored here. The waves under study are frequently observed in the continuously recorded survey data (Malaspina et al. 2020).

3. Burst data analysis

Figure 1 shows the solar wind conditions for two minutes before and after the time-series burst of interest, which begins near June 6, 2020, 12:09:54 UTC. Figure 1a shows survey power spectra from ∼200 Hz to 75 kHz, with spectra produced once per ∼0.87 s. The power shown is the summed power from the two differential pair signals (V12 + V34). The electron cyclotron frequency (fce) is indicated by a white dashed line, and the time of burst capture is indicated by vertical dashed black lines. Figure 1b shows measurements from the FGM (sampled at ∼293 sample/s). Figure 1c shows the proton velocity vector as determined by SWEAP Faraday cup, and Fig. 1d shows the plasma density as determined by quasi-thermal noise fitting (Moncuquet et al. 2020). The velocities shown are in the frame of the spacecraft. Figure 1e shows the time-series waveforms under study (black shows Ex, and blue shows Ey), sampled at 150 000 samples s−1.

thumbnail Fig. 1.

Context plasma and magnetic field conditions for the studied interval of near-fce waves. Panel a: spectrogram of the differential voltage signals (V12 + V34). The dashed white line indicates the local electron cyclotron frequency. The dashed vertical black lines indicate the studied burst interval. Panels b,c: ambient magnetic field vector and plasma flow velocity in the spacecraft frame in spacecraft coordinates. Panel d: electron density determined by quasi-thermal noise measurements. Panel e: burst capture electric field time series in spacecraft coordinates.

Key features of the near-fce waves described in Malaspina et al. (2020) are observed, including steady wave power near 0.7 fce and fce, and extensive harmonic structure. The background magnetic field points close to the nominal Parker spiral direction for this radial distance from the Sun (∼28.85RS). The fluctuation amplitude of the magnetic field is low, such that (⟨δB⟩/⟨|B|⟩) ≈ 6.3 × 10−2, where 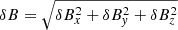and δBx = Bx − ⟨Bx⟩, and all averages are taken over the ∼200 s interval shown in Fig. 1b. The solar wind flow velocity is ∼250 km s−1 in the frame of the spacecraft, and the density is ∼600 cm−3. One significant difference from the observations reported in Malaspina et al. (2020) is that near-fce waves observed closer to the Sun than ∼35RS (close approaches of encounters 4, 5, and 6) often show broadband bursts of wave power in addition to prominent lines near ∼0.7fce and ∼1.0fce. The prominent lines become strong during the broadband bursts.

During this interval, the Debye length (λD) is ∼1.9 m, the electron gyroradius is ∼97 m, |B|≈152nT, Te ≈ 38 eV, and the electron thermal speed is ∼3700 km s−1. The electron gyrofrequency is fce ≈ 4200 Hz and the electron plasma frequency fpe ≈ 220 000 Hz, such that fpe/fce ≈ 52.

Figure 2 shows spectrograms (8192 samples per spectra) of the burst data in Fig. 1e. Here, the spectrogram frequencies are normalized to fce. Figure 2a shows the data between 0 and 10 fce, while Fig. 2b shows the spectral power, summed across the burst, at each frequency in Fig. 2a. Figures 2c and d show the same data, but only between 0 and 1.5 fce. The SCM burst data show no signal discernible from noise during this burst capture.

thumbnail Fig. 2.

Spectrograms of the high-cadence electric field data from Fig. 1e. Panel a: Fourier spectrogram of electric field data, with frequencies normalized to the local fce. Panel b: sum of the power spectral density at each frequency over the ∼3.5 s burst interval. Horizontal dashed lines show integer multiples of fce. Panels c,d: same data as panels a,b, but spanning a narrower frequency range.

Several wave modes can be identified in these data. In Figs. 2a, b, wave power between electron cyclotron harmonics up to at least the seventh harmonic are visible. The strongest wave power for this mode occurs at 1 fce < f < 2 fce, and successively higher frequencies have lower power. These signals do not appear at integer multiple frequencies of each other. Instead, they appear at variable frequencies between (N) fce < f < (N + 1) fce. These properties are consistent with electron Bernstein waves (Bernstein 1958). Electron Bernstein waves have been reported in the Earth’s magnetopause (Li et al. 2020), near an interplanetary shock (Wilson 2010), at the Earth’s bow shock (Breneman et al. 2013), and within the Earth’s magnetosphere (e.g., Christiansen et al. 1978). In the inner terrestrial magnetosphere, these waves are often referred to as electron cyclotron harmonic (ECH) waves (e.g., Zhou et al. 2017 and references therein). Electron Bernstein waves have been observed in the non-shocked solar wind before, but were associated with spacecraft charged-particle release (Baumgaertel & Sauer 1989). The presence of such waves in the open near-Sun solar wind is a novel observation. Through the rest of this publication, we refer to the electron Bernstein waves as type A waves. The type A wave power in the frequency range fce < f < 2fce has a center frequency of ∼5050 Hz, with a bandwidth of ∼1500 Hz, corresponding to a bandwidth (δf/f) of ∼31%.

Two other distinct wave modes are visible in Figs. 2c and 2d. The higher-frequency wave is designated type B and the lower frequency wave type C. Both are narrowband and show time-variable frequencies, leading to a summed power spread over a range of frequencies. When the wave power is averaged over significant fractions of a second (as in the survey power spectra), these are the waves producing the wave power peaks near ∼1.0fce (type B) and ∼0.7fce (type C) in the statistical results reported by Malaspina et al. (2020). The significant spread in frequencies reported in Malaspina et al. (2020) is consistent with time-variable frequencies of these waves. The properties of type B and C waves are explored below.

3.1. Type B: Extremely narrowband fce waves

The type B waves shown in Fig. 2c are extremely narrow, with a bandwidth of δf/f ≈ 3%. These waves vary in frequency with time throughout the burst, but do not exceed fce.

The wave frequency is observed to scale almost linearly with variation in the angle between the background magnetic field and the solar wind velocity (θB, Vsw). Figure 3a shows θB, Vsw throughout the burst event. Here, the magnetic field data from the FGM are down-sampled to one value per spectra (∼0.055 s). Proton velocity moments are determined at a much slower cadence than the fields data are sampled, so the closest (in time) proton velocity moment is used for the solar wind velocity. The proton velocity is steady during this interval (Fig. 1). Figure 3b reproduces the burst data electric field power spectra, but with a different color scheme to emphasize the type B and C wave-power peaks. The type B spectral peak for each of the 8192 sample spectra is indicated using asterisks, shifted down by ∼200 Hz so that both the narrow type B peak and the symbols can be shown. Gaps indicate times when the signal-to-noise ratio of the type B peak fell below 10. The symbols corresponding to different times are colored differently. Figure 3c plots the type B observed peak frequency (in radians/s, ωobs) as a function of cos(θB, Vsw). The colors match those in Fig. 3b, and at least three intervals with distinctly different slopes are visible.

thumbnail Fig. 3.

Initial Doppler analysis for burst data recorded near June 6, 2020, 12:09:54 UTC. Panel a: angle between the ambient magnetic field vector (B) and the proton flow vector (Vsw). Panel b: electric field spectrogram. The color scale is selected to highlight the type B wave power. Colored symbols indicate the peak type B frequency for each spectrum, plotted with an offset from the type B spectral line so that both are visible. Orange, red, and blue symbols correspond to three distinct slopes observed in panel c. The dashed black line indicates the local electron cyclotron frequency. Panel c: observed type B wave frequency (radians/s) as a function of the cosine of the angle shown in panel a.

Given the lack of significant magnetic field structure during this event (Figs. 1b, 3a), and the lack of observational evidence for a significant electron flow during the event under study, we conclude that any Doppler shift of wave frequencies must be due to a combination of solar wind flow speed and spacecraft motion. The wave frequency variation due to Doppler shift is given by ωobs = ωplasma + |k||Vsw|cos(θk, Vsw), where ωobs is the observed wave frequency, |k| is the magnitude of the wave vector, |Vsw| is the solar wind speed in the frame of the spacecraft, ωplasma is the proton-frame wave frequency, and θk, Vsw is the angle between the wave vector and the plasma flow in the frame of the spacecraft. When ωplasma, |k|, and |Vsw| are stable over the ∼3.5 s observation time, any change in ωobs should be due to variation in cos(θk, Vsw). Furthermore, if k is approximately fixed with respect to B over this burst interval, then ωplasma should vary linearly with θB, Vsw. That is, as the ambient magnetic field direction fluctuates, the wave frequency should also fluctuate. Furthermore, if the stated assumptions hold, then a linear fit to ωobs vs. cos(θk, Vsw) yields an offset corresponding to the plasma frame frequency (ωplasma) and a slope corresponding to |k||Vsw|. If the angle between k and B is known, a linear fit can be determined.

While the burst examined so far is consistent with a Doppler shift as the origin of the frequency variation, the second example shown in Fig. 4 demonstrates the effect more clearly. Figure 4 has a nearly identical format to Fig. 3 for an event recorded near January 29, 2020, 17:15:47 UTC. In Fig. 4b the symbols indicating the identified spectral peaks are shifted upward by 600 Hz so that the type B spectral line is visible. Type B spectral peaks cannot be clearly separated from other wave power near fce after ∼1.7 s into the event. At this time, a coherent low-frequency ion scale wave was present, causing perturbations in θB, Vsw. The corresponding frequency variation of ωobs is striking, and the fit to the data in ωobs − cos(θB, Vsw) space is linear.

thumbnail Fig. 4.

Same format as Fig. 3, but for a burst event recorded near January 29, 2020, 17:15:47 UTC. For this event, the frequency peak symbols are not color-coded, and they are offset upward in frequency for plotting.

3.1.1. Type B Doppler-shift fitting

Returning to the data shown in Fig. 3, estimates of |k| and ωplasma can be made using the frequencies indicated in Fig. 3a and the following procedure: B and Vsw vectors are used to construct an orthonormal coordinate basis defined by (B × Vsw)×B, B × Vsw, and B. In this coordinate basis, the magnetic field vector is B = [0, 0, 1] and the solar wind velocity vector is vsw = [0.31, 0, −0.95]. A range of possible unit vectors 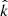are defined using the polar angle θ and azimuthal angle ϕ. Each angle pair (θ, ϕ) defines a direction of 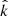with respect to B in each spectral window, such that k(BxVsw)xB = sin(θ)cos(ϕ), k(BxVsw) = sin(θ)sin(ϕ), and k(B) = cos(θ). With these angle definitions, the solar wind vector corresponds to [θ, ϕ] = [161.8° ,0° ]. These angles are defined such that θ = 0 (θ = 180) points parallel (antiparallel) to B, and ϕ = +90 points along +B × Vsw.

Given a 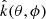and the measured Vsw, the quantity cos(θk, Vsw) can then be determined. The Doppler-shift equation (ωobs = ωplasma + |k||Vsw|cos(θk, Vsw)) can be written as a simple linear equation y = b + mx. Here, y is the type B ωobs in each spectral window. A least absolute deviation linear fit to the plot of y versus x yields a slope (m = |k||Vsw|) and an intercept (b = ωplasma). By sweeping through all possible directions of 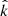, performing such a linear fit for each one, values of ωplasma and |k| can be determined throughout the (θ, ϕ) space.

Figure 5 shows the ranges of ωplasma and |k| that result from applying this procedure to the later part of the wave in Fig. 3a (indicated by blue symbols). In Fig. 5, regions of (θ, ϕ) space that yield ωplasma > ωce were removed from consideration. The fit output for fplasma/fce is shown in Fig. 5a and the fit output for |k| is shown in Fig. 5b.

thumbnail Fig. 5.

Doppler analysis output for the data points colored blue in Fig. 3. Panel a: wave frequency, normalized to fce, and panel b: wave number, in 1/m, both as a function of the angles θ and ϕ as defined in the text. Solutions with |f|> fce are not plotted.

Type B wave frequencies, in the spacecraft frame, are not observed to exceed the local fce in this wave event or any of the others examined thus far. If the plasma frame frequency is near fce, then this asymptotic behavior can be understood as indicating times when the Doppler shift becomes small. If the plasma frame frequency is much greater than fce, then the observed asymptotic behavior would require a Doppler-shift sign and magnitude that always produces f ≤ fce in the spacecraft frame. Given the natural variation of vsw and k between wave event observations, this is unlikely. Therefore we exclude solutions with f > fce.

Negative frequency solutions are also excluded. A negative plasma frame frequency corresponds to a polarization change between the spacecraft frame (positive frequency) and the plasma frame. However, the observed Doppler shifts are small relative to a wave with a plasma frame frequency near fce (considering again that the observed type B frequencies asymptote to f = fce). Such small Doppler shifts are inconsistent with reversal in polarization between the plasma frame and the spacecraft frame.

For the range of fplasma considered, the wave vector k is oblique, with 50° < θ < 130°. Given the Debye length (∼1.9 m) and electron gyroradius (∼97 m), lower values of |k| are more physically reasonable: |k| = 0.15(1/m) corresponds to a wavelength of λ ≈ 42 m. Requiring lower values of |k| place k within ∼30° of perpendicular to the plane defined by B and Vsw. If fplasma remains close to fce (small Doppler shift), then the wave is even more oblique (θ closer to 90°).

Figure 6 shows a similar fit output to Fig. 5, but for the earlier part of the wave in Fig. 3a (indicated by red symbols). For these data, the wave vector k is most oblique for fplasma far from fce, and slightly less oblique for fplasma near fce. The fit output values of |k| are similar to those determined in Fig. 5, but slightly higher. The fit outputs from Figs. 5 and 6 overlap in the region of (θ, ϕ) space where fplasma ≈ fce.

thumbnail Fig. 6.

Doppler analysis output for the red data points in Fig. 3. Same format as Fig. 5. Solutions with |f|> fce are not plotted.

We can now make another assumption: that the waves from the earlier and later parts of the burst have similar plasma-frame frequency (fplasma). If this is true, then the true 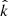is localized in the (θ, ϕ) region where Figs. 5 and 6 overlap, that is, along the dark blue region of Figs. 5a and 6a. Combined with the estimate that lower values of |k| are more physically reasonable, the following properties are now determined for the type B wave: (i) the wavelength is 21 < λ < 42 m, given 0.15 < |k|< 0.3 1/m, (ii) the wave vector is oblique, such that 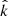is ∼70° from B, (iii) 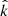is ∼60° from the plane defined by B and Vsw, and (iv) the plasma frame frequency (fplasma) is within ∼20% of the local fce. These are specific wave properties that can be useful to identify the wave mode.

3.1.2. Type B resonant velocities

The wave properties estimated above can be used to estimate the portion of the electron distribution function with which the type B waves resonate. In the case of Landau resonance, the resonant portion of the distribution can be determined using ωplasma = v ⋅ k. The component of the Landau resonance parallel to B satisfies v|| = ωplasma/( |k| cos(θk, B) ). The analysis in the prior section concluded that ωplasma ≈ ωce and 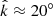from perpendicular to B, therefore cos(θk, B) ≈ cos (70° ) ≈ 0.17. Using these values and 0.15 < |k| < 0.3 (1/m) results in resonant velocities that correspond to electron energies (ℰ) of 0.19 eV < E|| < 0.75 eV. The component of the Landau resonance perpendicular to B satisfies v⊥ = ωplasma/( |k|sin(θk, B) ) and results in resonant energies of 0.025 eV < E⊥ < 0.10 eV. In either case, these resonant energies are low, near the center of the core electron velocity distribution function.

In the case of cyclotron resonance, the resonant portion of the distribution can be determined using ωplasma = v ⋅ k + Nωce, where N is a positive or negative integer and ωce = 2πfce. Cyclotron resonant velocities satisfy v|| = (ωplasma − Nωce)/(|k| cos(θk, B)). Because ωplasma ≈ ωce and the goal is to obtain approximate resonant energies, the assumption ωplasma = 0.98 ωce is used here, but is only important for the N = ±1 cyclotron resonances. Using all other assumptions from the Landau case, the N = 1 cyclotron resonance produces 0.00007 eV < E|| < 0.0003 eV, and N = −1 produces 0.74 eV < E|| < 3.0 eV. Extending to N = ±2 results in 0.2 eV < E|| < 0.8 eV and 1.7 eV < E|| < 6.7 eV for positive and negative cases, respectively. All resonant energies listed here are in the plasma frame.

The −N resonances correspond to electron energies further away from the center of the electron core distribution, which may be more realistic for these waves given the ∼38 eV electron core temperature. In this formulation, negative values of N correspond to the anomalous cyclotron resonance. With the anomalous cyclotron resonance, the resonant electron guiding center velocities are parallel to a component of the wave vector. For this case specifically, B points within ∼20° of sunward, and the Doppler shift is such that type B wave frequencies drop, so the type B wave vector generally points along B (sunward, against the solar wind flow). Therefore the resonant electrons guiding center velocities are likely sunward, implying that type B waves are resonant with a portion of the sunward core electron distribution.

3.2. Type C: Moderately narrowband fce/2 waves

The type C waves shown in Fig. 2c are moderately narrowband, with a bandwidth of δf/f ≈ 12%. These waves vary in frequency with time across the burst, but do not fall below fce/2. Similar to the type B waves, the type C frequency variation scales approximately linearly with variation in θB, Vsw. Strikingly, the frequency variation of type C waves mirrors that of type B waves (Fig. 2). Where type B waves decrease in frequency, type C increase, and vice versa. When type B waves asymptote to fce, type C waves simultaneously asymptote to fce/2. The mirrored Doppler shift suggests that the component of the wave vector along the solar wind direction for these two wave types is oppositely directed. The type B wave vector appears to have a component toward the Sun (Doppler frequency decrease), while the type C wave vector has a component away from the Sun (Doppler frequency increase). This mirrored Doppler shift behavior is consistently observed in all of the six burst data events examined in detail where both type B and C waves are distinct (other events are not shown here). A statistical study is required to explore this behavior more generally, but that is beyond the scope of the present work.

The same Doppler-shift fitting analysis that was applied to the type B waves can be applied to the type C waves, but with additional uncertainty in the results because the spectral peak frequency of the type C waves is not sufficiently distinct near the central region of this event, where the strongest variation in frequency occurs. Moreover, type C waves are not as narrowband as type B waves, producing additional frequency scatter that makes fits to the ωobs vs. cos(θk, Vsw) data more uncertain.

Figure 7 has the same format as Fig. 6, but shows results for type C frequency peaks from the second part of the burst event (after the most intense cyclotron power). Following similar reasoning to the type B analysis, the following properties are determined for the type C wave: (i) 0.08 < |k|< 0.15 1/m, (ii) a wave vector with 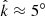from perpendicular to B, (iii) 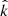less than ∼30° from perpendicular to the plane defined by B and Vsw, and (iv) a plasma frame frequency (fplasma) within ∼20% of fce/2.

thumbnail Fig. 7.

Doppler analysis output for the type C frequency peaks after the most intense cyclotron power. Same format as Fig. 5. Solutions outside the range 0.45fce < |f|< 0.8fce are not plotted.

Considering Landau resonance for type C waves, using cos(θk, B) ≈ cos (85° ) and 0.08 < |k| < 0.15 (1/m), we find that 3 eV < E|| < 10 eV and 0.02 eV < E⊥ < 0.08 eV. With cyclotron resonance, these values produce 0.80 eV < E|| < 2.9 eV for N = 1, and 6.5 eV < E|| < 23.0 eV for N = −1. For type C waves, as was determined for type B waves, all estimated resonant energies are low, near the center of the electron core distribution. Again, all resonant energies discussed are in the plasma frame.

3.3. Type B and C polarization

Polarization is another useful piece of information to help identify wave modes. Polarization determination in this case is somewhat hampered by having only two reliable electric field measurement directions (in the plane of the heat shield), but much can still be determined.

Figure 8a shows the wave power spectrogram of the burst under study. Horizontal dashed lines indicate fce and fce/2. The vertical solid lines indicate the central region in which the type A wave power maximizes. Figures 8b and c show the results of a cross-spectral analysis conducted on the two electric field signals shown in Fig. 1e. These signals are orthogonal because they are rotated into spacecraft coordinates. A filter was applied such that any cross-spectral result spectral bin with a wave power below 2 × 10−10 (V/m)2/Hz is not plotted. This was done to isolate the type A, B, and C waves. The cross-spectral analysis was conducted in the plane of the heat shield because only these two signals are well calibrated for this event.

thumbnail Fig. 8.

Type B and C cross-spectral analysis. Panel a: electric field spectrogram near fce. Dashed horizontal lines indicate fce and fce/2. Panel b: degree of polarization spectrum from cross-spectral analysis. Panel c: wave ellipticity spectrum from cross-spectral analysis. Vertical lines indicate the region of strongest type A wave power.

Figure 8b shows a spectrogram of degree of polarization. All three wave types show a high degree of polarization, indicating strong coherence between the two input signals. Figure 8c shows a spectrogram of the wave ellipticity, defined as the ratio of the minor axis to the major axis for the ellipse transcribed in the plane of the heat shield by the signal in each spectral bin. Red corresponds to right-handed polarization, and blue to left-handed polarization. The maximum magnitude of calculated polarization is ∼0.7, indicating elliptical polarization in the plane of the heat shield.

Figure 8c shows that type A waves are right-hand polarized, consistent with the interpretation that these are electron Bernstein waves. Outside the central region, the type A polarization is mixed and difficult to determine given the relatively low wave power in these signals. Type B waves are right-hand polarized outside the central region, and type C waves are left-hand polarized outside of the central region. Within the central region, type B and C signals become more ambiguous. Type B and C wave frequencies go to fce and fce/2, respectively, in the central region. The degree of polarization falls for type B waves, and the ellipticity becomes scattered, at times appearing left-hand polarized. This is difficult to interpret physically, as the type A and B signals become mixed during this interval. The type C polarization changes to right-handed within the central region, as the wave power becomes much more diffuse in frequency, and no distinct spectral peak is observed. This too is difficult to interpret physically, as the type C signals become mixed with other wave powers present during this interval near fce/2.

4. Discussion

From the above analysis, type B waves have the following properties: (i) a plasma-frame frequency near fce, (ii) right-hand elliptical polarization, (iii) a wave vector magnitude of 0.15 < |k|< 0.3 1/m, (iv) a wave vector direction ∼20° from perpendicular to B with a sunward component on either side of the central region, (v) resonance with low-energy electrons, close to the center of the electron core distribution, possibly anomalous cyclotron resonance, and (vi) a frequency variation (presumed due to Doppler shift) that mirrors that of the type C waves.

Type C waves have the following properties: (i) a plasma-frame frequency near fce/2, (ii) left-hand elliptical polarization, (iii) a wave vector magnitude of 0.08 < |k|< 0.15 1/m, (iv) a wave vector direction ∼5° from perpendicular to B with an anti-sunward component on either side of the central region, (v) resonance with low-energy electrons, close to the center of the electron core distribution, possibly anomalous cyclotron resonance, and (vi) a frequency variation (presumed due to Doppler shift) that mirrors that of the type B waves.

Given these properties as well as the amplitude variation of type A (electron Bernstein) waves throughout the burst event, we conclude that the central region is likely the source region for all three types of wave. This conclusion is based on the observation that type A (electron Bernstein) wave power maximizes in this region, and the observation that type B and C wave frequencies asymptote to ∼fce and ∼fce/2 in this region. If this is a source region, then waves will generally radiate away from it. We need to reconcile this concept with the observation that the Doppler shift for both type B and C waves has the same sense (down for type B, up for type C) on either side of the source region, however. The source region is assumed to be a cylinder. This assumption is based on the gyrotropic nature of electrons in the ambient solar wind, combined with the observed lack of magnetic field structure at the time when the type A wave power maximizes (less than 1 degree variation of the magnetic field vector, see Fig. 3a).

If the source region is cylindrical and elongated along B, then the combined solar wind and spacecraft velocity cause the structure to pass over the spacecraft at a small angle relative to the source region long axis. If the type B wave vectors are tilted everywhere along B (in a cone opening generally sunward), then the sign of the k ⋅ Vsw Doppler-shift term on either side of the source region would be negative, consistent with Fig. 2b. Similarly, if the type C wave vectors are tilted everywhere against B (in a cone opening generally anti-sunward), then the sign of the k ⋅ Vsw Doppler-shift term on either side of the source region would be positive, also consistent with Fig. 2b. Furthermore, if the type A (electron Bernstein) wave vectors were close to perpendicular with B, but radially outward from the cylindrical source region, then the type A frequency would be slightly higher at the start of the event and slightly lower at the end of the event. There is an indication of this behavior in Fig. 2b, comparing the frequencies of type A wave power near 0.5 s (∼1.3fce) and near 3 s (∼1.15fce). The schematic cartoon in Fig. 9 summarizes this source region concept. Here, the cones indicate the relative wave vector direction for each type of wave, but all types of wave are meant to originate from points along the full length of the source region cylinder.

thumbnail Fig. 9.

Cartoon schematic of the observed near-fce source region.

The estimated wavenumber ranges and orientations for type B and C waves allow estimates of plasma-frame wavelengths. For type B, 61 < λ|| < 122 m, and 22 < λ⊥ < 45 m. For type C, 480 < λ|| < 901 m, and 42 < λ⊥ < 79 m. All of these estimated wavelengths are one to two orders of magnitude longer than the Debye length (λD ∼ 1.9 m). The perpendicular wavelengths are similar to fractions of the electron gyroradius (ρe ∼ 97 m) such that for type B 1/4ρe < λ⊥ < 1/2ρe, and for type C 1/2ρe < λ⊥ < 1ρe.

Both type B and C parallel wavelengths are significantly smaller than the lower bound source region extent along B. This is a necessary condition for wave growth in this region. The source region is observed for ∼1 s. Assuming that it is embedded in the solar wind flow, it is moving ∼250 km s−1 radially away from the Sun in the frame of the spacecraft. Assuming that it extends along B and accounting for the 163° angle between B and Vsw, the lower bound source region extent along B is ∼260 km. This is much larger than the estimated parallel wavelengths.

A comparison of the observations and the source region picture presented above shows at least one unresolved discrepancy. If type B waves have a plasma frame frequency close to fce and they are resonant with electrons, then they should be right-hand polarized in the plasma frame. If type B waves have a sunward wave vector (consistent with anomalous cyclotron resonance, discussed in Sect. 3.1.2), then the Doppler shift will reduce their observed frequency by a small amount relative to their plasma frame frequency. With these properties (ωplasma ≈ ωfce, sunward 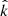, small Doppler shift), type B waves should be right-hand polarized in the spacecraft frame. This is consistent with the observed polarization in Fig. 8.

However, if type C waves have a plasma frame frequency close to fce/2 and they too are resonant with electrons, then they should also be right-hand polarized in the plasma frame. If type C waves have an anti-sunward wave vector, consistent with a Doppler shift up in frequency, by an amount smaller than their plasma frame frequency, then we expect that type C waves will also be right-hand polarized in the spacecraft frame. The observed polarization in Fig. 8 indicates left-hand, however. This discrepancy remains unresolved and likely requires a study that treats more than one burst event.

For both events presented here, the type B wave frequency in the spacecraft frame approaches the electron cyclotron frequency in the source region, where the wave emission is strongest. If our Doppler-shift interpretation of the wave frequency variation in time is correct, then why should the Doppler shift consistently minimize in the source region, where the k and vsw vectors presumably have an arbitrary orientation from event to event?

The physical quantities that produce Doppler shift are |vsw|, |k|, and cos(θk, vsw). Inside and outside the source region, we know that |vsw| is steady to our ability to measure it, and cos(θk, vsw) should be somewhat arbitrary from event to event. Although cos(θk, vsw) is not completely arbitrary, as the waves under study only appear when vsw is within ∼20° of parallel to radially outward from the Sun (Malaspina et al. 2020).

This leaves the possibility that |k| may be smaller inside the source region than outside. This could reduce the Doppler shift in the source region, and bring the wave frequency closer to its plasma frame value. There is some observational support for this. The blue points in Fig. 3c show a small cluster of points in the upper left corner, where the slope of the best-fit line would be shallower than the slope of the best-fit line to the majority of the blue points. This cluster of points exactly corresponds to the points in the center of the source region. A linear fit to these points alone for any value of θ, ϕ produces a slope, and therefore |k|, which is smaller by ∼40% than the |k| determined using the rest of the blue points. However, only this one event has been examined to this level of detail, and we do not yet know if a smaller |k| in the source region is a consistent property of these waves.

A second change in the wave spectra also occurs in the strong emission (source) regions: The wave bandwidth increases. This behavior can be seen in Fig. 2c near 1.3 s and is observed for type A, B, and C waves. The waves created in the region should produce a distribution of wave vectors within the source region that is more isotropic with respect to the background magnetic field direction compared to the distribution of wave vectors outside of the source region. The more isotropic the distribution of wave vectors, the broader the wave bandwidth should be because each wave vector produces a slightly different Doppler shift. This is consistent with the observations. A broader study is required to determine if these are general behaviors of the wave types studied here.

The instability or instabilities driving the observed waves are not definitively determined in this analysis, but we discuss some possibilities here. The first is the electron cyclotron drift instability (ECDI; e.g., Forslund et al. 1970, 1971, 1972). The free energy for the ECDI is a cross-field drift between electrons and ions, specifically, ions moving across the magnetic field. Waves radiated by this instability are observed as a coupling between electron Bernstein modes and Doppler-shifted ion acoustic waves. The ECDI is highly unlikely to cause the waves studied here because the magnetic field fluctuations are small. Without strong magnetic field gradients such as those at collisionless shocks, it is not clear how a sizeable ion beam moving across the magnetic field relative to the core ions and electrons moving with the solar wind might be created.

It is also possible to generate cyclotron harmonics with an electron beam drifting across the magnetic field. This instability requires that a fraction of the electrons drift with the E × B- and ∇ B-drifts at a magnetic field gradient (e.g., Gary & Sanderson 1970). Again, magnetic field fluctuations are small during the interval examined here, so this instability is not likely to be active.

Another possibility for generating the observed waves is through nonlinear wave-wave interactions. This class of processes usually requires a pump wave to amplify or couple to oscillations that mode-convert to other daughter modes. Harker & Crawford (1968) showed that a pump wave could generate two daughter waves in a form of a traveling wave parametric amplification, one of which would be cyclotron harmonic waves. The daughter waves were expected to have kVTe/Ωce ≲ 3, but our results suggest values > 10. This process requires a very uniform plasma and magnetic field, which is consistent with conditions of the solar wind reported during prior observations of the wave modes investigated here (Malaspina et al. 2020).

A more recent study found that an electromagnetic pump wave can decay into an ion acoustic wave and electrostatic electron Bernstein mode (e.g., Kumar & Tripathi 2006). This study also found that the converse can occur, that is, an electrostatic electron Bernstein wave in the presence of low-frequency, low-wavelength ion acoustic wave can generate electromagnetic electron cyclotron harmonics. The expected wave number for the electron Bernstein waves is kρce ∼ 2, while our observations suggest kρce > 10 for the type B waves and > 7 for type C waves.

Another possible candidate is a loss-cone instability (e.g., Ashour-Abdalla & Kennel 1978; Ashour-Abdalla et al. 1979). This instability is expected to grow for 3 ≲ kρce, h ≲ 15, where ρce, h is the thermal gyroradius of the hot electrons (sunward hot electrons in our work), and higher harmonics are expected at higher values of kρce, h. The suprathermal electron temperature is typically ∼2.5–5.0 times that of the core and total at both 1 AU and as close as 0.17 AU (e.g., Halekas et al. 2020; Wilson et al. 2019). Using this range, we find ρce, h ∼ 146–208 m, which gives us kρce, h ∼ 22–62 for type B and ∼11–31 for type C. These values are beyond the range of kρce, h where growth is expected. Finally, variations in the loss-cone instability have been performed using a stationary (in the plasma frame) perpendicular ring-beam combined with a core (e.g., Maxwellian) velocity distribution, but again, the expected wave numbers are kρce ≲ 3 (e.g., Hadi et al. 2015).

In the case studied here, a loss cone cannot form in the anti-sunward direction because the hot electrons in that direction form the strahl beam, which adiabatically narrows as these electrons escape the solar corona (e.g., Berčič et al. 2020 and references therein). However, at the studied radial distances from the sun, the strahl electron population has only just begun to scatter into the isotropic halo (Halekas et al. 2020). It is possible that a loss cone can form in the sense that the sunward portion of the halo may not yet be populated (via strahl scattering) at these radial distances. While the SPANe instrument does have an unobstructed field of view in the anti-sunward direction, the angular resolution in that direction is limited, which would not allow the detection of a loss cone if it was narrower than ∼20°. Furthermore, the analysis presented earlier indicates that the type B and C waves are resonant with electrons at much lower energies than those active in a loss-cone instability as discussed here.

Only some of the above possibilities can explain one of the more difficult issues pertaining to these observations, the polarizations. There are no known instabilities that would generate electron-scale fluctuations in this frequency range with a left-hand polarization. That is, none of the above instabilities could generate an intrinsically left-hand polarized oscillation with wavelengths at or below the electron gyroscale. The only potential mode is the ion acoustic wave in its electromagnetic form, but whether it can persist in this frequency range at these wavelengths while still being electromagnetic is not known. A possible source of ion acoustic modes is a nonlinear wave-wave interaction, as discussed above, but these specific processes should generate the electrostatic version of the wave. The expected wavelength of the ion acoustic mode is consistent with the estimates for the type C waves, however. When the wave normal angle of an ion acoustic wave is large, as estimated here for the type C waves, then the wave should be electromagnetic and not purely electrostatic.

Another complication is that of Doppler shifting. The left-hand polarization of the type C mode in the spacecraft frame is clear. The problem is that with our estimates for k ∼ 0.08–0.15 m−1 and the measurement of Vsw ∼ 250 km s−1, the maximum Doppler shift possible for the type C mode is only ∼3–6 kHz (i.e., assuming θkV ∼ 0°). However, our estimates of k were derived under constraints that suggested θkV could be as small as ∼50°. Then the Doppler-shift range for type C waves drops to ∼2.0–3.8 kHz. The type C waves are seen at ∼2.5–3.1 kHz in the spacecraft frame, so that their rest frame frequencies, were the polarization to be reversed, would need to be < 1 kHz. If the type C waves are intrinsically left-hand polarized, then they must be Doppler-shifted to higher frequencies in the spacecraft frame. However, this poses a problem as we are not aware of a left-hand polarized mode with kρce > 7, that is, a wavelength well below the thermal electron gyroradius.

5. Conclusions

This study examined high-cadence burst data captures of electric and magnetic fields of near-fce waves in the near-Sun solar wind. It was determined that these waves correspond to at least three separate, simultaneously occurring wave modes, referred to as types A, B, and C. Type A waves are identified as electron Bernstein waves given the frequency distribution of their prominent harmonics. The modes of the type B and C waves were not conclusively identified, but many of their properties were estimated, including their wave numbers (type B ∼0.23 m−1, type C ∼0.12 1/m), wave vector direction (type B ∼70°, type C ∼85°, from the ambient B-field direction), polarization (type B right-hand elliptically polarized, type C left-hand elliptically polarized, in the frame of the spacecraft), and frequency variation. The two wave types appear to be intimately connected, with opposing frequency variation in time, but with different magnitudes (df/f varies by ∼10% for type B waves and ∼30% for type C waves across the studied event). Resonant electron energies were estimated based on observed wave properties, indicating that these waves grow from an instability that is active near the center of the electron core population. By comparing the frequency and wave vector characteristics of all three waves, a source region geometry was suggested.

While only a single wave burst was examined in detail here, the prior statistical study (Malaspina et al. 2020) demonstrated that these near-fce waves can persist for minutes to hours, occurring on magnetic field lines close to the theoretical Parker spiral geometry with low fluctuation amplitudes. These near-fce waves are only observed in the near-Sun environment and become stronger and more frequently observed close to the Sun. They preferentially occur when the electron core shows a strong sunward drift.

These properties indicate that these waves grow along field lines that are most directly connected to the solar corona. They therefore contain electrons that have undergone the least evolution since escaping the corona. Therefore the waves studied here likely play an important role in the near-Sun evolution of the solar wind electron distribution function, particularly concerning the evolution of the cold core population as it interacts with the escaping strahl electrons.

Acknowledgments

The authors acknowledge helpful conversations with Rudolf Treumann concerning wave growth possibilities and helpful comments from Thierry Dudok de Wit. The authors thank the Parker Solar Probe, FIELDS and SWEAP teams. The FIELDS experiment on Parker Solar Probe was designed and developed under NASA contract NNN06AA01C. All data used here are publicly available on the FIELDS and SWEAP data archives: http://fields.ssl.berkeley.edu/data/, http://sweap.cfa.harvard.edu/pub/data/sci/sweap/.

References

  1. Agapitov, O. V., Dudok de Wit, T., Mozer, F. S., et al. 2020, ApJ, 891, L20 [Google Scholar]
  2. Ashour-Abdalla, M., & Kennel, C. F. 1978, J. Geophys. Res., 83, 1531 [CrossRef] [Google Scholar]
  3. Ashour-Abdalla, M., Kennel, C. F., & Livesey, W. 1979, J. Geophys. Res., 84, 6540 [CrossRef] [Google Scholar]
  4. Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
  5. Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 576, 237 [Google Scholar]
  6. Baumgaertel, K., & Sauer, K. 1989, J. Geophys. Res., 94, 11983 [CrossRef] [Google Scholar]
  7. Berčič, L., Larson, D., Whittlesey, P., et al. 2020, ApJ, 892, 88 [Google Scholar]
  8. Bernstein, I. B. 1958, Phys. Rev., 109, 10 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  9. Bowen, T. A., Mallet, A., Huang, J., et al. 2020, ApJS, 246, 66 [Google Scholar]
  10. Breneman, A. W., Cattell, C. A., Kersten, K., et al. 2013, J. Geophys. Res. (Space Phys.), 118, 7654 [CrossRef] [Google Scholar]
  11. Case, A. W., Kasper, J. C., Stevens, M. L., et al. 2020, ApJS, 246, 43 [Google Scholar]
  12. Cattell, C., Short, B., Breneman, A., et al. 2021, A&A, 650, A8 [CrossRef] [EDP Sciences] [Google Scholar]
  13. Chaston, C. C., Bonnell, J. W., Bale, S. D., et al. 2020, ApJS, 246, 71 [Google Scholar]
  14. Chen, C. H. K., Bale, S. D., Bonnell, J. W., et al. 2020, ApJS, 246, 53 [Google Scholar]
  15. Christiansen, P., Gough, P., Martelli, G., et al. 1978, Nature, 272, 682 [CrossRef] [Google Scholar]
  16. Dudok de Wit, T., Krasnoselskikh, V. V., Bale, S. D., et al. 2020, ApJS, 246, 3 [CrossRef] [Google Scholar]
  17. Forslund, D. W., Morse, R. L., & Nielson, C. W. 1970, Phys. Rev. Lett., 25, 1266 [CrossRef] [Google Scholar]
  18. Forslund, D. W., Morse, R. L., & Nielson, C. W. 1971, Phys. Rev. Lett., 27, 1424 [CrossRef] [Google Scholar]
  19. Forslund, D., Morse, R., Nielson, C., & Fu, J. 1972, Phys. Fluids, 15, 1303 [CrossRef] [Google Scholar]
  20. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gary, S. P., & Sanderson, J. J. 1970, J. Plasma Phys., 4, 739 [CrossRef] [Google Scholar]
  22. Hadi, F., Yoon, P. H., & Qamar, A. 2015, Phys. Plasmas, 22, 022112 [CrossRef] [Google Scholar]
  23. Halekas, J. S., Whittlesey, P., Larson, D. E., et al. 2020, ApJS, 246, 22 [Google Scholar]
  24. Harker, K. J., & Crawford, F. W. 1968, J. App. Phys., 39, 5959 [CrossRef] [Google Scholar]
  25. Jagarlamudi, V. K., Alexandrova, O., Berčič, L., et al. 2020, ApJ, 897, 118 [Google Scholar]
  26. Kasper, J. C., Abiad, R., Austin, G., et al. 2016, Space Sci. Rev., 204, 131 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kumar, A., & Tripathi, V. K. 2006, Phys. Plasmas, 13, 052302 [CrossRef] [Google Scholar]
  28. Lacombe, C., Alexandrova, O., Matteini, L., et al. 2014, ApJ, 796, 5 [Google Scholar]
  29. Li, W. Y., Graham, D. B., Khotyaintsev, Y. V., et al. 2020, Nat. Commun., 11, 141 [CrossRef] [Google Scholar]
  30. Malaspina, D. M., Ergun, R. E., Bolton, M., et al. 2016, J. Geophys. Res. (Space Phys.), 121, 5088 [CrossRef] [Google Scholar]
  31. Malaspina, D. M., Halekas, J., Bercic, L., et al. 2020, ApJS, 246, 21 [CrossRef] [Google Scholar]
  32. Moncuquet, M., Meyer-Vernet, N., Issautier, K., et al. 2020, ApJS, 246, 44 [Google Scholar]
  33. Mozer, F. S., Agapitov, O. V., Bale, S. D., et al. 2020, J. Geophys. Res. (Space Phys.), 125, e27980 [Google Scholar]
  34. Pulupa, M., Bale, S. D., Bonnell, J. W., et al. 2017, J. Geophys. Res. (Space Phys.), 122, 2836 [CrossRef] [Google Scholar]
  35. Stansby, D., Horbury, T. S., Chen, C. H. K., & Matteini, L. 2016, ApJ, 829, L16 [Google Scholar]
  36. Tong, Y., Vasko, I. Y., Artemyev, A. V., Bale, S. D., & Mozer, F. S. 2019, ApJ, 878, 41 [Google Scholar]
  37. Verniero, J. L., Larson, D. E., Livi, R., et al. 2020, ApJS, 248, 5 [Google Scholar]
  38. Wilson, L. B., I, Cattell, C. A., Kellogg, P. J., et al. 2010, J. Geophys. Res. (Space Phys.), 115, A12104 [Google Scholar]
  39. Wilson, L. B., III, Chen, L.-J., Wang, S., et al. 2019, ApJS, 245, 24 [CrossRef] [Google Scholar]
  40. Zhang, Y., Matsumoto, H., & Kojima, H. 1998, J. Geophys. Res., 103, 20529 [CrossRef] [Google Scholar]
  41. Zhao, L. L., Zank, G. P., Adhikari, L., et al. 2020, ApJ, 898, 113 [Google Scholar]
  42. Zhou, Q., Xiao, F., Yang, C., et al. 2017, Geophys. Res. Lett., 44, 5251 [CrossRef] [Google Scholar]
  43. Zhu, X., He, J., Verscharen, D., Duan, D., & Bale, S. D. 2020, ApJ, 901, L3 [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Context plasma and magnetic field conditions for the studied interval of near-fce waves. Panel a: spectrogram of the differential voltage signals (V12 + V34). The dashed white line indicates the local electron cyclotron frequency. The dashed vertical black lines indicate the studied burst interval. Panels b,c: ambient magnetic field vector and plasma flow velocity in the spacecraft frame in spacecraft coordinates. Panel d: electron density determined by quasi-thermal noise measurements. Panel e: burst capture electric field time series in spacecraft coordinates.
In the text
thumbnail Fig. 2.

Spectrograms of the high-cadence electric field data from Fig. 1e. Panel a: Fourier spectrogram of electric field data, with frequencies normalized to the local fce. Panel b: sum of the power spectral density at each frequency over the ∼3.5 s burst interval. Horizontal dashed lines show integer multiples of fce. Panels c,d: same data as panels a,b, but spanning a narrower frequency range.
In the text
thumbnail Fig. 3.

Initial Doppler analysis for burst data recorded near June 6, 2020, 12:09:54 UTC. Panel a: angle between the ambient magnetic field vector (B) and the proton flow vector (Vsw). Panel b: electric field spectrogram. The color scale is selected to highlight the type B wave power. Colored symbols indicate the peak type B frequency for each spectrum, plotted with an offset from the type B spectral line so that both are visible. Orange, red, and blue symbols correspond to three distinct slopes observed in panel c. The dashed black line indicates the local electron cyclotron frequency. Panel c: observed type B wave frequency (radians/s) as a function of the cosine of the angle shown in panel a.
In the text
thumbnail Fig. 4.

Same format as Fig. 3, but for a burst event recorded near January 29, 2020, 17:15:47 UTC. For this event, the frequency peak symbols are not color-coded, and they are offset upward in frequency for plotting.
In the text
thumbnail Fig. 5.

Doppler analysis output for the data points colored blue in Fig. 3. Panel a: wave frequency, normalized to fce, and panel b: wave number, in 1/m, both as a function of the angles θ and ϕ as defined in the text. Solutions with |f|> fce are not plotted.
In the text
thumbnail Fig. 6.

Doppler analysis output for the red data points in Fig. 3. Same format as Fig. 5. Solutions with |f|> fce are not plotted.
In the text
thumbnail Fig. 7.

Doppler analysis output for the type C frequency peaks after the most intense cyclotron power. Same format as Fig. 5. Solutions outside the range 0.45fce < |f|< 0.8fce are not plotted.
In the text
thumbnail Fig. 8.

Type B and C cross-spectral analysis. Panel a: electric field spectrogram near fce. Dashed horizontal lines indicate fce and fce/2. Panel b: degree of polarization spectrum from cross-spectral analysis. Panel c: wave ellipticity spectrum from cross-spectral analysis. Vertical lines indicate the region of strongest type A wave power.
In the text
thumbnail Fig. 9.

Cartoon schematic of the observed near-fce source region.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.