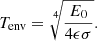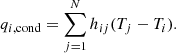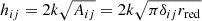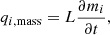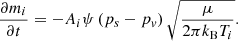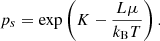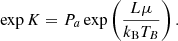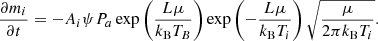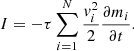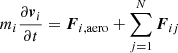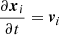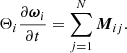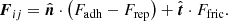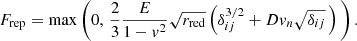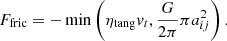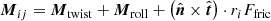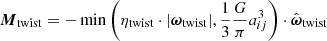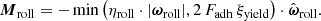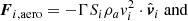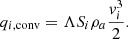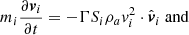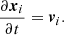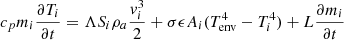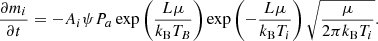| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202140305 | |
| Published online | 14 June 2021 | |
Three dimensional atmospheric entry simulation of a high altitude cometary dustball meteoroid
Institute of Fluid Dynamics, Swiss Federal Institute of Technology (ETH) in Zurich, Sonneggstrasse 3, 8092 Zürich, Switzerland
e-mail: lorenz.hulfeld@gmail.com
Received:
9
January
2021
Accepted:
7
April
2021
Aims. The break-up of a dustball meteoroid is investigated numerically based on fluid dynamics simulations of the meteoroid’s atmospheric entry flow. Both thermal and mechanical break-up mechanisms are implemented, in order to investigate dustball meteoroid disintegration.
Methods. A three dimensional model of a dustball meteoroid composed of thousands of small spherical grains was used in the atmospheric entry flow simulation, performed with the direct simulation Monte Carlo (DSMC) method. The dynamics of each meteoroid grain were calculated by means of the discrete element method (DEM), which models contact dynamics between grains. By coupling DEM with DSMC, the dynamics of a dustball meteoroid were calculated during atmospheric entry. In addition, thermal computations were also carried out taking into account the incoming atmospheric heat flux, thermal radiation, and grain ablation. Thus, this methodology is able to compute mechanical as well as thermal dustball meteoroid disintegration.
Results. To test this novel multi-physics simulation framework, a prototypical dustball meteoroid, namely a Draconid meteoroid, was simulated. Using typical material properties from the literature, the Draconid meteoroid was compressed due to aerodynamic forces to roughly half its size immediately after the start of the simulation at 200 km altitude. Later, aerodynamic-induced meteoroid rotation occured until the meteoroid disintegrated mechanically at 120 km altitude. The fact that the meteoroid disintegrated mechanically is directly related to the combination of material properties used in the simulation.
Key words: meteorites, meteors, meteoroids / methods: miscellaneous
© ESO 2021
1. Introduction
Jacchia (1955) concluded from Super-Schmidt photographic observations that fragmentation of small meteoroids during atmospheric entry is a common phenomenon. In accordance with Whipple’s cometary model (Whipple 1951), he concluded on the basis of these observations that meteoroids must be porous dustballs.
Hawkes & Jones (1975) developed the first quantitative dustball model and assumed that dustball meteoroids consist of stony or metallic grains embedded in a matrix of non-radiating volatile “glue”. They assumed that dustball meteoroids continuously release grains during atmospheric entry as the glue melts. They presumed that a dustball meteoroid has released all of its grains before the onset of ablation. Their model was able to fit light curves of different meteor types (Hawkes & Jones 1975; Fisher et al. 2000).
More recently, Campbell-Brown & Koschny (2004) developed a more qualitative dustball model. They adopted the assumption that dustball meteoroids are held together by a sort of glue and simulated heat conduction in the meteoroid and the release of grains where the glue reached the melting temperature. In contrast to Hawkes & Jones’s model, grain ablation was simulated on the basis of each grain’s temperature using the Clausius-Clapeyron equations, thus allowing for grain ablation before the dustball meteoroid which is fully disintegrated.
The most recent dustball model was proposed by Borovička et al. (2007). Their model does not presume a matrix of volatile glue. The grains are released based on thermal erosion, that is to say grains detach from the meteoroid surface after they receive a certain amount of thermal energy from the atmospheric flow.
The dustball models by Campbell-Brown & Koschny and Borovička et al. were recently compared against each other by fitting high resolution observations of several faint meteors (Campbell-Brown et al. 2013). The authors conclude that dustball models need to be improved significantly to fit the observations. Thus, rather than using simple analytical models, we decided to simulate the atmospheric entry flow about a three dimensional dustball meteoroid. As dustball meteoroids are mostly of cometary origin, the dustball model proposed in this paper was derived from the structure and formation of comets.
Comets formed early in the Solar System, about 4.6 G.y. ago, beyond the snow line and their composition has not evolved significantly since (Fernandez 2004; Mandt et al. 2015). Blum et al. (2014) found, based on the model by Skorov & Blum (2012), that comets must have formed from porous dust and ice aggregates by gravitational instabilities. Whenever a comet passes the inner Solar System, icy parts of the comet sublimate and the comet releases gas and dust. These dust aggregates (i.e., dustballs) remain approximately in the comet’s orbit and every time when Earth crosses a comets’ orbit, theses dustball meteoroids ablate during atmospheric entry, producing meteor showers (Greenberg 2000). Thus, by studying dustball meteoroids, we can gain knowledge about their parent comets and because comets have not evolved significantly since their formation, they provide a valuable record of the physical conditions in the early Solar System.
In the early Solar System, the gas surrounding the Sun (solar nebula) condensed into dust and ice particles, which led to the formation of the protoplanetary disk (PPD; Bouwman et al. 2008). These dust and ice grains subsequently formed small aggregates since they stuck together by adhesion after inelastic collisions (Weidenschilling & Cuzzi 1993). Experiments concerning the formation of protoplanetary dust aggregates were conducted in the last two decades by numerous researchers. Below, a few of these papers are summarized; a more complete review can be found in Blum & Wurm (2008).
Poppe et al. (2000a) performed collisions between micron-sized grains, corresponding to the first step of planetesimal and cometesimal formation in the solar nebula. They experimentally confirmed that due to Brownian motion collisions between micron-sized dust particles lead to sticking and subsequently to the formation of small fractal dust aggregates. Blum & Wurm (2000) investigated collisions between fractal dust aggregates in a micro gravity environment. They found that below a threshold velocity, the fractal dust aggregates stick together after a collision, forming bigger, very porous non-fractal dust aggregates. Blum et al. (2006) produced dust aggregates in the laboratory by random ballistic deposition. The resulting centimeter-sized aggregates showed good agreement of porosity and tensile strength with meteoroids of cometary origin.
Based on numerous laboratory experiments done in the last two decades, Güttler et al. (2010) and Zsom et al. (2010) showed that dust aggregates up to a centimeter in size can form in the PPD due to collisional growth. Thus, there is strong evidence that cometary meteoroids are aggregates of small dust grains. In addition to laboratory experiments about the formation of dust aggregates in the PPD, computational studies were done as well.
Dominik & Tielens (1997) modeled normal adhesive forces and rolling, sliding, and torsional friction between two interacting dust grains. On the basis of these contact laws, they developed a two dimensional discrete element method (DEM) code and applied it to the formation and collision of dust aggregates in the PPD. More recently, Wada et al. (2007, 2008) carried out similar two and three dimensional DEM computations of collisions between two dust aggregates. Ringl & Urbassek (2012) developed a simplified model of adhesion rolling, gliding, and torsional friction for grain-grain interactions. Their simplified code allows for faster simulations with more particles than the codes by the authors introduced above. Their code was applied in the PPD context (Gunkelmann et al. 2016, 2017). The use of DEM in astrophysical research has been established over the last two decades. Therefore, we decided to apply DEM to model a dustball meteoroid.
Due to the rarefied nature of the atmospheric entry flow about a dustball meteoroid, a particle-based simulation technique is best suited. Although very promising, particle-based flow simulations have very rarely been used in meteor science. The following publications are known to us.
Boyd (2000) used the direct simulation Monte Carlo (DSMC) method to compute the flow filed around a 1 cm-sized Leonid meteoroid during atmospheric entry. He performed a stationary DSMC computation of the ablating meteoroid at an altitude of 95 km. The wake behind the ablating meteoroid in the simulation was in quantitative agreement with measurements.
Vinković (2007) used DSMC to simulate high altitude Lenoids above 130 km. He used a model in which meteoroid particles were ejected from the surface to simulate sputtering of high altitude meteors. The results of his DSMC computations show good agreement with measured shapes and sizes of high altitude Leonids.
Stokan & Campbell-Brown (2015) used a particle-based method to simulate the ablation and deceleration of small non-fragmenting meteoroids. On the basis of collisions between particles, the light emission of meteors was simulated. They found good agreement between the width of simulated meteor wakes and observations. However, their simulated meteors showed less deceleration and shorter wakes than observed, which led to the conclusion that meteoroid fragmentation plays an important role in the observed small meteoroids.
Although rarely used until present, particle-based methods have shown very promising results and DEM has been established in the field of astrophysical research. By combining both methods, a simulation based on the physics of the atmospheric entry of a dustball meteoroid should be performed. The dynamics of each meteoroid grain is simulated with DEM and the atmospheric entry flow is computed by a highly flexible DSMC-Fokker-Planck algorithm (Küchlin & Jenny 2017). By coupling DEM to the atmospheric entry flow computation, the dynamics of a dustball meteoroid during its flight through the atmosphere can be investigated. Ablation of the meteoroid grains is calculated and compared to measurements of dustball meteoroids in order to validate the model.
2. Meteoroid model
As mentioned in the introduction, there is strong evidence that comets consist of loosely bound dust and ice aggregates and thus that cometary meteoroids are dust aggregates. Blum et al. (2006) showed that such dust aggregates have porosities and tensile strengths similar to cometary meteoroids. Therefore, the assumption was made that dustball meteoroids are loosely bound aggregates of their constituent grains and that they are held together by mechanical forces and not by some sort of nonradiating glue.
In the first step of planetesimal and cometesimal formation, fractal dust aggregates form in the PPD due to hit and stick collisions of dust grains, which subsequently collide with each other forming nonfractal, bigger, very porous dust aggregates (Poppe et al. 2000a; Blum & Wurm 2000). Therefore, the structure of a cometary dust ball meteoroid is modeled in this paper as a nonfractal porous agglomeration of grains. The meteoroid should be characterized by a certain porosity and is assumed to have a homogeneous structure throughout. Since the initial geometry of a meteoroid entering Earth’s atmosphere cannot be measured yet, the dustball meteoroid is assumed to have a nearly perfect spherical shape. Because of simplicity and to speed up the simulations presented in this paper, all grains were modeled as perfect spheres.
2.1. Grain bonds
We assume that the constituent grains are only held together by adhesive forces, although grains may also be held together by electromagnetism (Dominik & Nübold 2002). The adhesive force between two grains is modeled according to the DMT model (Derjaguin et al. 1975) as
where γ denotes the surface energy and rred is the reduced radius of the two grains, which is defined as
The repulsive force between two grains is modeled by the Hertzian theory (Hertz 1881) as
where E denotes the Young modulus and v is the Poisson ratio of the grains. The overlap σ of two grains is obtained as
where xi and xj denote the grains’ centroids. When two grains stick together, elastic deformation leads to the formation of a circular area between the grains. The radius of the contact area 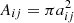 between two grains is given by Hertzian theory (Hertz 1881) as
between two grains is given by Hertzian theory (Hertz 1881) as
The equilibrium overlap of two grains in contact is obtained from FAdh = FHertz as
2.2. Grain masses
The grain masses and their distribution poses a central question in modeling a dustball meteoroid. A broad range of grain sizes as well as a power law and Gaussian distributions of grain masses were used by different authors to fit measurements using dustball models. We use a power law grain mass distribution according to
bounded by an upper and lower grain mass mu and ml (Borovička et al. 2007). All grains have the same density ρGrains and thus a grain’s radius is obtained as
2.3. Meteoroid building procedure
As stated at the beginning of this section, the meteoroid should have a homogeneous structure and a well defined porosity. To achieve this, the following meteoroid building procedure was introduced.
First the meteoroid’s mass mMet and porosity p must be defined. On the basis of these properties, the radius of the spherical meteoroid was calculated as
and the first meteoroid grain was placed randomly with a uniform probability density inside the meteoroid’s volume. Then, the other meteoroid grains were added by repeating the following steps until the meteoroid mass mMet was reached.
First, a random point was generated with a uniform probability density inside the meteoroid’s volume and the grain which lies nearest to this point was determined. Next, a new grain with mass mi according to Eq. (7) was generated. The new grain was attached to the previously determined grain in a random direction with equilibrium overlap according to Eq. (6). If the new grain overlapped with another grain, its position was calculated such that it had equilibrium overlap with both grains. After a new grain was attached to the meteoroid, the porosity of the meteoroid was calculated by summing up the volume of all present grains and dividing it by the volume of their convex hull. If the meteoroid’s porosity was too low, grains were removed until the desired porosity was reached. If the meteoroid did not remain in one piece after the removal of a grain, this grain must not have been removed.
2.4. Heat transfer
The temperature of each meteoroid grain was calculated as
where qi, conv, qi, rad, qi, cond, and qi, mass denote a grain’s convective, radiative, conductive, and mass loss dependent heat fluxes of a grain and cp, the specific heat capacity, which is equal for all grains.
2.4.1. Convective heat transfer
The convective heat transfer from the atmosphere to the meteoroid and within the meteoroid was obtained based on a simulation of the atmospheric entry flow around the meteoroid (see Sect. 3.1) through an atmospheric entry flow computation.
2.4.2. Radiative heat transfer
Radiative heat transfer inside the meteoroid was calculated using a view factor based radiation model. To calculate the view factors Fi → j from the ith grain to the jth grain, 105 rays were generated equally distributed on the surface of the ith grain with a random direction corresponding to diffusive radiation. The radiative heat flux was then obtained as
where σ is the Stefan-Boltzmann constant, ϵ is the emissivity of the grain material, and A is a grain’s surface area. The term in Eq. (11) with the environmental temperature Tenv accounts for the radiation from the environment, that is to say from the Sun or Earth. We note that Tenv is the temperature that a body in Earth’s orbit has when it is in thermal radiation equilibrium and is obtained as
Here E0 = 1.362 kW m−2 denotes the solar constant, which represents the Sun’s intensity at one astronomical unit.
2.4.3. Conductive heat transfer
Conductive heat transfer is modeled as
The heat transfer coefficient
is proportional to the conductivity k of the grain material and the contact area Aij between two grains (Kloss et al. 2012).
2.4.4. Heat loss due to mass loss
The heat consumed by meteoroid ablation is obtained as
where L denotes the heat of ablation (i.e., a combination of the heat of fusion and the heat of vaporization).
2.5. Mass loss
The mass loss of a meteoroid grain was modeled using the Knudsen-Langmuir and the Clausius-Clapeyron formalisms (Campbell-Brown & Koschny 2004). The Knudsen-Langmuir equation describes the mass loss of a grain in dependence of its temperature as
Here 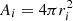 is the grain’s surface area, ψ is the condensation coefficient, which gives the probability that an evaporated meteoroid atom does not collide with the grain’s surface and condense, μ is the average mass of a meteoroid atom, and kB is the Boltzmann constant. The variable pv denotes the vapor pressure and ps is the saturated vapor pressure which is given at a certain temperature by the Clausius-Clapeyron equation as
is the grain’s surface area, ψ is the condensation coefficient, which gives the probability that an evaporated meteoroid atom does not collide with the grain’s surface and condense, μ is the average mass of a meteoroid atom, and kB is the Boltzmann constant. The variable pv denotes the vapor pressure and ps is the saturated vapor pressure which is given at a certain temperature by the Clausius-Clapeyron equation as
The constant K can be obtained by inserting a material’s boiling temperature TB at sea level pressure Pa into Eq. (17), which yields
By combining Eqs. (16), (17), and (18) and neglecting the vapor pressure pv for the high altitude meteors simulated in this paper, the mass loss of a meteoroid grain can be expressed as a function of its temperature as
2.6. Light production
The light production of the meteor was modeled according to the classical luminous equation (Bronshten 1983). The luminous intensity is proportional to the mass-loss rate and the kinetic energy of a meteoroid grain. The luminous intensity of the meteor was obtained by summing over all grains as
Here τ denotes the luminous efficiency. The magnitude was obtained from the luminous intensity as M = −2.5 log I (Borovička et al. 2007). In a future version of our code, the meteor light production could be computed directly from excited electrons of ablated meteoroid molecules in the context of a rarefied gas flow simulation.
3. Simulation procedure
3.1. Flow field
The degree of rarefaction of the atmospheric entry flow about a meteoroid can be characterized by the Knudsen number Kn = λ/L, where λ is the mean free path length in the atmosphere and L is a characteristic length scale of the meteoroid, for instance its diameter. Since a typical dustball meteoroid is in the free molecular flow regime during its entire atmospheric entry, a computational method must be used which is able to compute highly rarefied gas flows. In addition, a dustball meteoroid has a very complex geometry, and thus flow simulations must be able to handle such geometries. Thus, a recent parallel hybrid DSMC-Fokker-Planck implementation (Gorji & Jenny 2015; Küchlin & Jenny 2017), which is capable of simulating flows in the whole range of Knudsen numbers and possesses the computational efficiency to perform large-scale simulations involving complex geometries, was used for the flow field simulations around the dustball meteoroid.
3.1.1. DSMC method
The DSMC method pioneered by Bird (1994) uses computational particles to simulate a rarefied gas flow. Each computational particle represents a much larger number of atmospheric molecules. Computational particles were collected in computational cells with dimensions smaller than the local mean free path of atmospheric entry flow. A time step, which is smaller than the mean collision time, was used. Thus, the assumption is made that a computational particle can collide with any other particle inside the same cell regardless of its exact position. In addition, the assumption is made that only collisions between two particles occur. Thus, pairs of collision partners formed randomly in each cell and the probability of their collision was computed based on the relative velocity of the two particles and their physical properties. The macroscopic properties of the flow were obtained by ensemble averaging all particles in a computational cell. The collision between an atmospheric particle and a meteoroid grain was modeled purely diffusive for all DSMC computations used in this paper.
3.1.2. Atmospheric model
The molecular number density in the atmosphere was obtained using the NRLMSISE-00 model (Picone et al. 2002). Since the DSMC code (Küchlin & Jenny 2017) used to simulate the atmospheric entry flow around the meteoroid currently does not support multispecies gas mixtures, the atmosphere was modeled as pure N2 gas with a density according to NRLMSISE-00.
3.1.3. Meteoroid ablation
Since the Fokker-Planck-DSMC code (Küchlin & Jenny 2017) does not support multiple gas species, the ablated meteoroid material could not be simulated in the flow field around the meteoroid. The effect of meteoroid ablation on the flow field and the formation of a wake due to ablated meteoroid material should be studied in the future. When air species collide at very high velocities with ablated meteoroid material, dissociation and ionization reactions occur, forming an ion trail behind the meteoroid. Such ion trails are measured by radar observations. Thus, models of dissociation and ionization reactions could be included in the Fokker-Planck-DSMC code to simulate the formation of an ion trail and compare it to measured data.
In addition, a model of electron excitation could be included into the code to simulate the emitted light from excited particles. This would improve the physical modeling of light emission in comparison with the classical luminosity model (Bronshten 1983) used in this paper and would allow one to compute meteor spectra. These additions would result in better constraints of meteor modeling as the computed ion trails and meteor spectra could be compared to measurements. This would subsequently lead to a better understanding of the meteor phenomena and a better validation of meteor models.
3.2. Meteoroid dynamics
The main goal of this paper was to investigate disintegration- and drag-induced rotation of a dustball meteoroid during atmospheric entry. Thus, the simulation of the meteoroid’s dynamics during atmospheric entry must include deceleration, rotation, and break-up, which can be done by a single simulation technique, namely the discrete element method.
3.2.1. Discrete element method (DEM)
DEM pioneered by Cundall & Strack (1979) simulates the dynamics of each particle on the basis of external and inter-particle forces and moments. DEM is thus able to simulate the dynamics of a meteoroid grain due to external influences and interactions with neighboring grains. For spherical grains, the governing equations of DEM have the following form:
Here, Fi, aero denotes the aerodynamic force acting on th ith grain. The drag-induced aerodynamic moment was neglected. A grains inertia tensor is denoted by Θi and the inter-particle forces and moments by Fij and Mij, which are obtained based on the contact laws introduced below.
3.2.2. Contact laws
As mentioned in the introduction, the use of DEM in an astrophysical context has been established recently. Thus there are a number of contact laws proposed by different authors for the use of adhesive particles in DEM, for example, in work done by Luding (2008), Wada et al. (2007, 2008), and Dominik & Nübold (2002). However, their contact laws rely on very detailed implementations of the physics of grain-grain interaction, which makes them computationally expensive and restricts the number of computational particles. Recently, Ringl & Urbassek (2012) proposed a simplified, computationally faster version of the contact laws between adhesive particles, which nonetheless contains the essential physics of a grain-grain interaction. As the meteoroid’s dynamics shall be simulated during a significant part of its flight through Earth’s atmosphere, their contact laws were adopted here. The details of their method were published in Ringl & Urbassek (2012), but the calculation of the contact forces and moments is repeated here for convenience.
The contact force between two grains consists of an attractive (i.e., the adhesive force), a repulsive, and a frictional part, that is
Here, 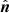 is the normal vector pointing from xi to xj and
is the normal vector pointing from xi to xj and 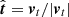 the normal vector of the tangential velocity between the grains. The repulsive force consisting of the Hertz force and its time derivative to account for a viscoelastic normal contact is calculated as
the normal vector of the tangential velocity between the grains. The repulsive force consisting of the Hertz force and its time derivative to account for a viscoelastic normal contact is calculated as
We note that D represents the dissipation constant, which is experimentally determined and vn is the relative velocity between two grains projected onto n. The sliding friction force between the grains is obtained as
Here, ηtang is the tangential damping constant and 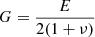 is the shear modulus.
is the shear modulus.
The contact moment between two grains has a twisting and a rolling friction part. The twisting moment points in the negative twisting direction. The twisting direction is the relative rotational velocity between two grains projected on their normal axis 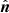 . The rolling velocity points in the direction of the relative rotational velocity minus the twisting velocity:
. The rolling velocity points in the direction of the relative rotational velocity minus the twisting velocity:
Here ηtwist and ηroll are damping coefficients analogous to ηtang used to mimic static friction. The critical rolling displacement is denoted by ξyield, and 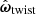 and
and 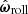 denote the unit vector of the twisting and rolling axes.
denote the unit vector of the twisting and rolling axes.
3.3. Flow-field-DEM coupling
Above, the computation of the flow field and the simulation of the meteoroid dynamics were introduced. These two methods were coupled, as explained below, in order to simulate the meteoroid along its trajectory. The steps listed below were repeated until the meteoroid was fully ablated or disintegrated.
The current meteoroid geometry and atmospheric density were used to perform a stationary simulation of the flow field around the meteoroid and obtain Fi, aero and qi, conv for each grain and to compute the view factors Fi → j between all meteoroid grains. On the basis of these stationary computations a transient simulation of the meteoroid was carried out. The dynamics of each grain initiated by the aerodynamic force Fi, aero were calculated by means of the DEM by solving Eqs. (21)–(23). Then the heat transfer was computed according to Eq. (10), using the stationary view factors Fi → j, and the mass loss of each grain was calculated according to Eq. (19). In addition, the meteoroid’s trajectory was also calculated. During the transient part of the simulation, the termination conditions introduced below were checked continuously to determine if new flow field and view factor computations are needed.
The displacement of each grain was tracked during the transient simulation as dxi = |xi − xi, 0|. Here, xi denotes a grain’s current position and xi, 0 is the grain’s position at the time the flow field and view factor computations were carried out. The following three termination conditions were introduced in order to guarantee that the flow field around the meteoroid and the view factors between the individual meteoroid grains did not change too much during a transient simulation step.
Firstly, the standard deviation of the grains’ displacements dx has exceeded its threshold value. Secondly, the atmospheric density as calculated by the NRLMSISE-00 model has changed by a certain amount. Thirdly, the meteoroid’s velocity (i.e., the velocity of the fastest grain) has changed by a certain amount. If one of these termination conditions was fulfilled, the current transient simulation step was terminated and new atmospheric entry flow and view factor computations were carried out.
3.4. Coordinate systems
During the transient simulation steps, two different coordinate systems were used. An Earth-fixed coordinate system was used to calculate the trajectory of the meteoroid and a meteoroid-fixed coordinate system was used to calculate the dynamics of the meteoroid. Both coordinate systems are sketched in Fig. 1.
 |
Fig. 1. Sketch of Earth-fixed coordinate system and moving system used during the simulation of a dustball meteoroid’s atmospheric entry. |
3.4.1. Earth-fixed system
The Earth-fixed system is defined such that its z-coordinate zE points away from the center of the Earth, that is to say the gravitational force acts in the negative z direction. Its x-axis xE is defined such that the trajectory of the meteoroid lies in the xz-plane of the Earth-fixed system. The origin of the Earth-fixed coordinate system is defined by the projection of the meteoroid’s position at the start of the simulation onto the Earth surface. At the start of the simulation, the meteoroid’s position is given in the Earth-fixed system as (0, 0, h0)E and its initial velocity by v0.
3.4.2. Moving system
The moving coordinate system was used to calculate the dynamics of each meteoroid grain with DEM and the atmospheric entry flow about the meteoroid. The free atmospheric entry stream flows in positive xM-direction. The origin of the moving system is initially located in the Earth-fixed system at (0, 0, h0)E. The moving system moves with a constant speed v0 and radiant zenith distance cos(zR) through Earth’s atmosphere, corresponding to a non-decelerated meteoroid. Thus, the moving system’s origin at time t is represented by (v0sin(zR)t, 0, h0 − v0cos(zR)t)E in the Earth-fixed system. The moving system’s orientation is such that its x-axis xM is opposed to v0.
3.4.3. Simulation domain
The simulation domain is defined by a cubic box in the moving coordinate system as sketched in Fig. 2. The simulation domain has a certain size L. The distance d between the meteoroid and the frond side of the simulation domain is chosen such that the inflow conditions are defined properly and a possible bow shock is located inside the simulation domain. All grains, which are currently located within the simulation domain, were simulated using the coupling procedure between DEM and Fokker-Planck-DSMC introduced above. Grains, which have left the simulation domain, can be simulated as described in Sect. 5. A grain which has left the simulation domain is not allowed to reenter again.
 |
Fig. 2. Sketch of the simulation domain. |
4. Simulating the atmospheric entry of a Draconid meteoroid
To test and validate the meteoroid model and the simulation procedure introduced above, a Draconid meteoroid was chosen. Firstly, Draconids were chosen since they represent some of the most fragile and porous meteoroids the Earth encounters. They are often used in the literature as prototype dustball meteoroids. Secondly, Draconid meteoroids enter Earth’s atmosphere at a relatively low speed of 24 km s−1. At such low speeds, sputtering of the meteoroids could be neglected and the mass loss can be modeled exclusively by thermal ablation (Popova et al. 2007) since our code is currently not able to simulate sputtering.
4.1. Modeling a Draconid meteoroid
The code used to simulate the flow field about the meteoroid (Küchlin & Jenny 2017) is currently not able to simulate ablated meteoroid material. Therefore, a meteoroid which stays in the free molecular flow regime during its entire flight through Earth’s atmosphere should be selected.
4.1.1. Reference Draconid
The Draconid meteor no. 96 measured by Borovička et al. (2007) was selected as a reference for the simulation presented here. The first reason to select this meteoroid is given by the fact that it is small enough to remain in the free molecular flow regime during its entire flight through the atmosphere. The mean free path length at 100 km, where this meteoroid disintegrates, is 14 cm and the Draconid’s diameter was measured to be 4.5 mm, which results in a Knudsen number of 31. However, the Knudsen number could be lower if meteoroid ablation was modeled.
Secondly, this meteoroid was selected because the number of grains proposed by Borovička et al. (2007) is small enough to enable a fast simulation. Simulations of larger meteoroids with hundreds of thousands of grains would be possible too, but that would lead to unacceptably high simulation times.
4.1.2. Material properties
Since no exact material parameters are known for Draconids, and since different Draconids may even have different material properties depending on their origin within the parent comet, certain Draconid material properties had to be assumed. The mechanical properties of SiO2 were used during the simulation, and black body radiation was assumed. The material parameters used in the simulation together with the sources where they were taken from are presented in Table 1.
Material properties employed to model a Draconid meteoroid.
4.1.3. Meteoroid geometry
To model the meteoroid, the procedure introduced in Sect. 2.3 was employed. Upper and lower grain masses of mu = 5.5 ⋅ 10−10 kg and ml = 2.8 ⋅ 10−10 kg, a power law index of s = 2.5, and an initial meteoroid mass of m0 = 1.35 ⋅ 10−5 kg were used. The Draconid’s porosity was assumed to be 90% (Borovička et al. 2007). The meteoroid’s initial geometry is presented in Fig. 3a. The meteoroid’s shape was assumed to be perfectly spherical.
 |
Fig. 3. Meteoroid before (a) and after (b) compression at about 200 km and a cut through the meteoroid at 135 km (c). The atmospheric entry flow is directed in the positive x-direction, while the meteoroid moves in the opposite direction. The radiant zenith distance of the meteoroid’s direction of flight is zR = 56.6°. |
4.2. Simulation parameters
The following parameters were used in the simulation of the Draconid’s atmospheric entry.
4.2.1. Initial conditions
It was found that for typical Draconid speeds around 24 km s−1, the forces and heat fluxes above 200 km are small enough not to lead to meteoroid disintegration shortly after the start of the simulation. Nevertheless, the forces at an altitude of 200 km were big enough to trigger meteoroid deformation right after the start of the simulation, as can be seen in Fig. 3. Since our simulation was computationally very expensive, we decided not to start the simulation at a higher altitude than h0 = 200 km.
The meteoroid’s initial velocity v0 at this altitude was obtained by extrapolating the measured velocity of meteor No. 96 (Borovička et al. 2007) to an altitude of 200 km. Thus, v0 = 23.73 km s−1 was obtained. The Draconid’s direction of travel, defined by its cosine of the radiant zenith distance (cos(zR) = 0.55), was adopted from the same source.
The assumption was made that the Draconid has no initial rotation, which is very unlikely as most celestial bodies are rotating. In addition, millimeter-sized meteoroids experience drag-induced rotation during ejection from their parent comet (Čapek 2014). The procedure introduced in Sect. 3 is able to simulate drag-induced meteoroid rotation during atmospheric entry. The meteoroid’s drag-induced rotation is presented in Sect. 4.3.2.
4.2.2. DSMC parameters
A parameter study of the flow field around the meteoroid was carried out to obtain the size of the simulation domain and the number of particles in the domain. Due to computational constraints, it was important for the purposes of this parameter study to find a minimal simulation domain and the smallest number of particles which still allow one to simulate the atmospheric entry flow. The goal of the parameter study was to obtain smooth heat fluxes and aerodynamic forces acting on the meteoroid grains.
It was found that the distance s between the meteoroid and the front side of the simulation domain should have a minimum size of 1 mm to properly resolve the inflow conditions and that a total number of 2 million particles is sufficient to obtain smooth enough forces and heat fluxes. The length of the simulation domain L was set to 10 cm. This ensures that a grain, which has left the simulation domain, has separated from the remaining meteoroid grains enough to justify the assumption of free flow about that grain.
4.2.3. DEM parameters
For the DEM part of the simulation, a time step size of dtDEM = 10−9 s was found to be small enough to accurately resolve the forces between meteoroid grains. On the basis of this time step, the damping coefficients were determined.
The dissipation coefficient A was determined such that two 50 μm grains stuck together after a normal collision with their critical sticking velocity vcrit = 0.17 m s−1 (Blum & Wurm 2000). This leads to A = 3 ⋅ 10−7 s. The damping coefficients ηtang, ηroll, and ηtwist depend on the time step size dtDEM. The tangential damping coefficient ηtang = 2.5 ⋅ 10−2 kg s−1 was determined in a test simulation. The other damping coefficients were chosen in agreement with Ringl & Urbassek (2012) as 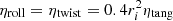 as a function of a grain’s radius ri.
as a function of a grain’s radius ri.
4.2.4. Coupling parameters
The following termination conditions were employed to couple the flow field and DEM computations throughout the Draconid’s atmospheric entry simulation. The changes in atmospheric density and meteoroid velocity were both set to 5%. A threshold value of 50 μm was used for the standard deviation of meteoroid grain displacements.
4.3. Results
The following section presents the results of the coupled simulation with the parameters introduced above. The deformation and motion of the meteoroid during its travel through Earth’s atmosphere is described until the meteoroid is fully disintegrated at about 120 km. Additionally, the meteoroid’s temperature distribution is presented below. The motion of the meteoroid grains after disintegration and the resulting meteor plots (i.e., light curve, deceleration curve, etc.) are presented in Sect. 5.
4.3.1. Meteoroid deformation
Figure 3a shows the initial meteoroid geometry at the start of the simulation at a 200 km altitude. The aerodynamic forces are small at this altitude, but they are able to deform the meteoroid within the first 0.17 s of the simulation. Meteoroid deformation occurs due to rolling between grains since rolling only requires small aerodynamic forces. During compression of the meteoroid, not a single bond between grains is broken, but many new grain bonds form due to collisions with subcritical velocities. The meteoroid geometry after compression at 0.17 s is shown in Fig. 3b. The meteoroid deformation depends on the rolling forces, which depend on the surface tension γ and the critical rolling displacement ξyield. If a higher value of ξyield was chosen, meteoroid compression might not have started at 200 km since the aerodynamic forces probably would have been too small. But most certainly the meteoroid would have been compressed, nevertheless, just at a lower altitude. In order to investigate whether meteoroid compression would happen if a higher critical rolling displacement was chosen, another simulation with a higher ξyield is required.
After compression, the meteoroid’s porosity decreases from 90% to about 80% since the meteoroid was compressed to roughly half its volume. The meteoroid’s structure is much stiffer now and there is no more deformation and rolling between meteoroid grains. This increased meteoroid stiffness results from a higher number of grain bonds, which makes it harder for grains to roll on each other. The simulation results show that after initial compression, the meteoroid keeps the same shape and orientation until an altitude of 155 km. At 155 km, the meteoroid begins to rotate due to slightly asymmetric aerodynamic forces. After compression and until disintegration of the meteoroid at 123 km, the meteoroid nearly behaves as a rigid body. Below 123 km, the aerodynamic forces grow big enough to trigger rolling between grains, which leads to further deformation of the compressed meteoroid. The subsequent disintegration of the meteoroid is discussed below.
4.3.2. Drag-induced meteoroid rotation
In Fig. 4, we can see the meteoroid’s rotational frequency from the start of the simulation until the beginning of meteoroid break-up. We can see that the meteoroid begins to rotate at about 155 km. Above this altitude, the aerodynamic forces acting on the grains were too small to induce meteoroid rotation. Below 155 km, the meteoroid begins to rotate faster and faster until it begins to break apart at about 123 km. Our simulation shows that even for a pretty symmetrical meteoroid drag-induced meteoroid, rotation occurs at a relatively high altitude of 155 km. Thus we can conclude that for a real nonsymmetrical meteoroid, drag-induced rotation plays an important role. Figure 3c shows the meteoroid at 135 km, and it can be seen that the meteoroid is rotating. In Fig. 5, we can see the meteoroid during disintegration between 123 and 120 km. We can see that the meteoroid still is rotating during disintegration, although it no longer behaves similar to a rigid body.
 |
Fig. 4. Meteoroid rotation frequency from the start of the simulation until the start of meteoroid disintegration. |
 |
Fig. 5. Meteoroid during disintegration. The radiant zenith distance of the meteoroid’s direction of flight (-x-axis) is zR = 56.6°. |
4.3.3. Meteoroid temperature
Figure 3c shows a cut through the middle of the meteoroid at 135 km. We can see that the meteoroid still has the same shape as at 197 km after compression and that it is rotating. The picture shows the temperature distribution of the meteoroid after 5 s of simulation time. We can see that only a small outer layer has reached a temperature of 550–450 K. Then there is a layer of grains between 450–350 K and the meteoroid’s core has only reached temperatures of 350–300 K. This is due to the fact that for most of the time, the front part of the meteoroid has been exposed to atmospheric entry flow and thus it received most of the thermal energy. We note that the dominant heat transfer mechanism inside the meteoroid is radiation. Conduction and convective heat transport between meteoroid grains are negligible since contact surfaces between grains and atmospheric density are very small. Figure 5 shows that after the disintegration of the meteoroid’s outer layer which had a temperature of about 600 K, the core of the meteoroid still had a temperature of only 350–400 K.
4.3.4. Meteoroid disintegration
In Fig. 5, we can see how the meteoroid disintegrates. We can also see meteoroid rotation during disintegration. At 123 km, aerodynamic forces are actually smaller than adhesive forces, but they are big enough to trigger significant rolling motion of grains in the compressed meteoroid. At 123 km, this leads to many grain collisions which are above the critical velocity. Super-critical collisions often lead to the separation of existing grain bonds. Separated grains may further collide with other meteoroid grains, which further triggers the break-up of grain bonds for super-critical collisions. On the other hand, subcritical collisions lead to the formation of new grain bonds. Due to super-critical collisions, grains continue to separate from the meteoroid. Figure 5 shows that the meteoroid continuously disintegrates from the outside in. The meteoroid disintegrates into small pieces of only a couple of grains. There is no such thing as a sudden break-up or fracturing of the meteoroid into a couple of big pieces. According to our simulation, the meteoroid is almost fully disintegrated at an altitude of 120 km. The break-up occurs over a 3 km altitude span due to super-critical grain collisions, which are triggered by aerodynamically-induced rolling motion.
The temperature of the grains is too low for significant ablation. Compared to the reference Draconid, which started to disintegrate at 102 km, the Draconid in our simulation started disintegrating 21 km earlier. Since break-up was initiated by the rolling motion between grains, a higher critical rolling displacement ξyield should be selected in order to correct for the mismatch in the disintegration height. In that case, however, ablation may become relevant since there is more time to heat up the grains. A more detailed discussion about dustball break up mechanisms, based on out simulation framework, can be found in Sect. 6.8.
In Fig. 5, one can see that grains around 600 K from the front of the meteoroid separated together with cold grains around 350 K from the back of the meteoroid. If thermal meteoroid disintegration occurs, only grains which have a high enough temperature would separate themselves from the meteoroid. This would probably lead to an increased disintegration duration. In addition, separated grains would instantaneously ablate, while the remaining meteoroid grains would need to heat up first before they separate. This results in a light curve which looks more like that of a typical dustball meteor (see Sect. 5.2).
4.3.5. Number density distribution
In Fig. 6, the grain number density distribution at the end of our simulation is presented. The coupled DEM-DSMC simulation was terminated at 119 km after almost every grain had separated from any other meteoroid grain. The figure shows that the meteoroid grains are not distributed symmetrically about the x-axis. This is due to meteoroid rotation occurring before and during disintegration.
 |
Fig. 6. Two dimensional number density distribution of the meteoroid grains after full disintegration at an altitude of 119 km. |
Grains which separated earlier have already been decelerated more than grains which separated later. Thus, a small physical wake of approximately 2.5 m length has formed. The meteoroid grains are distributed equally in space as a function of their mass since there was not enough time to separate them due to atmospheric deceleration.
5. Simulating grain ablation after meteoroid disintegration
After a grain has separated from the meteoroid by a sufficiently large distance, it can be simulated independently of all other meteoroid grains. Therefore the aerodynamic force and the incoming atmospheric heat flux acting on a separated meteoroid are obtained according to
Here, 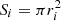 denotes the cross section of the grain, Λ is the heat transfer coefficient, Γ is the drag coefficient, ρa is the atmospheric density, vi is the grain’s absolute velocity, and
denotes the cross section of the grain, Λ is the heat transfer coefficient, Γ is the drag coefficient, ρa is the atmospheric density, vi is the grain’s absolute velocity, and 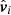 is the unit vector of the grain’s velocity.
is the unit vector of the grain’s velocity.
The dustball meteoroid which was used in the simulation was modeled on the basis of meteor no. 96 presented in Borovička et al. (2007). The biggest diameter of any grain in this meteoroid model is 70 μm. Borovička et al. (2007) reported that the corresponding meteoroid was fully ablated at an altitude of 93 km, where the mean free path in the atmosphere is 41 mm, which results in a Knudsen number of Kn = 585. Thus, even if grain ablation is taken into account, every separated meteoroid grain is clearly in the free molecular flow regime. Therefore, a heat transfer coefficient of Λ = 1 and a drag coefficient of Γ = 1 were used during the entire grain ablation simulation.
5.1. Ablation model
When a meteoroid grains have separated by a sufficiently large distance, the equations introduced above are used to calculate a grain’s aerodynamic force and heat flux.
Thus, the trajectory of a grain can be calculated according to
The ablation of a separated meteoroid grain was calculated similarly to grain ablation during the DEM-DSMC simulation, as presented in Sects. 2.4 and 2.5. By inserting Eq. (31) into Eq. (10) and neglecting radiative heat transfer with any other grain, the following equations were obtained:
We note that for separated meteoroid grains, these equations can be employed and neither DEM nor DSMC simulations should be performed any more. Thus calculating grain ablation after meteoroid disintegration was computationally very fast and thus allowed for us to optimize certain model parameters in order to better fit measurements of the reference Draconid from Borovička et al. (2007).
5.2. Light curve
Using the mass loss rate of each meteoroid grain according to Eq. (35), the meteor’s luminous intensity and its magnitude were calculated as explained in Sect. 2.6. The meteor’s magnitude was plotted to obtain its light curve. This fit, together with the measured light curve and the erosion model fit by Borovička et al. (2007), is presented in Fig. 7.
 |
Fig. 7. Resulting light curves based on the results of our DEM-DSMC simulation. Measurements and erosion fit of meteor No. 096 by Borovička et al. (2007) compared to our light curves, computed for three different values of heat of ablation. |
As one can see from Fig. 7, the resulting light curve, using the material properties from Table 1 (i.e., L = 3.5 ⋅ 106 J kg−1), does not match the reference from Borovička et al. (2007) very well. The meteoroid starts to ablate at 118 km, that is to say shortly after disintegration. First, the light curve looks like that off a dustball, but from 116 km on it has the shape of a classical single body light curve. This is due to the fact that after separation, there is no more shielding of meteoroid grains and every grain receives the full heat flux from the free atmospheric entry flow. At 116 km, nearly every grain is heated up to around 800 K. Since all meteoroid grains have the same temperature, they all ablate around the same time, thus producing a classical single body light curve below an altitude of 116 km. Further, using a specific heat of ablation of L = 3.5 ⋅ 106 J kg−1 caused the meteoroid to ablate too early.
Since thermal disintegration played no role, the simulation presented in Sect. 4.3 could also be carried out using a higher specific heat of ablation. The specific heat of ablation of L = 3.5 ⋅ 106 J kg−1 (Campbell-Brown & Koschny 2004) is one of the lowest values found in the literature; the highest one reported for Draconids is L = 25.0 ⋅ 106 J kg−1 (Borovička et al. 2007). Using this specific value results in the respective light curve presented in Fig. 7. One can see that the start of the light curve matches the measurements pretty well; there are significant discrepancies for the rest of the curve, however. The peak of the light curve is about 6 km lower and the magnitude is one order too small. The shape of the light curve looks like a typical symmetrical dustball light curve.
The lowest L-value leads to a light curve which occurs earlier than the measured one, and the highest L-value leads to a later onset. Thus, a value between the minimum and maximum heat of ablation values found in the literature should produce a better fit with observations. Therefore, a fitting procedure was performed to obtain the best match between the simulation and observations. The fitting procedure led to L = 13.7 ⋅ 106 J kg−1, and the resulting light curve is shown in Fig. 7. The start of the light curve is 6 km too high and from 108 to 102 km it does not match observations at all. Also the shape of this light curve looks more like a classical light curve rather than that of a dustball. However, from 102 km on, it fits measurements pretty well and, therefore, this heat of ablation value was adopted to produce the plots shown in the remainder of this section.
5.3. Deceleration curve
Using the luminous intensity of each grain, the deceleration of the meteoroid was calculated. The meteor’s deceleration was calculated as the height difference between the brightest meteoroid point (i.e., the highest magnitude grain) and the non-decelerated meteoroid (using the velocity of the brightest grain at 102 km altitude). This deceleration is plotted in Fig. 8 together with measurements of meteor no. 96 and the erosion fit by Borovička et al. (2007). We can see that our model agrees well with the measured deceleration below an altitude of 97 km.
 |
Fig. 8. Deceleration curve based on our simulation results, using a heat of ablation value of L = 13.7 ⋅ 106 J kg−1 compared to measurements and the erosion fit of meteor No. 096 by Borovička et al. (2007). |
5.4. Time height intensity scan
Based on the results presented in the previous section, a time height intensity scan was computed. We can see in Fig. 9 that the time height intensity scan is very thin in the beginning of the trajectory and gets bigger towards the end of the trajectory. Moreover, the end of the trajectory is blurred significantly. This artificial time height intensity scan compares very well with the Draconid time height intensity scans presented in Borovička et al. (2007). In the final part of the trajectory, one can also see the deceleration of the Draconid meteoroid since the time height intensity scan is no longer a straight line, but it bends upwards. For dustball meteoroids similar to Draconids, it is typical that one can see the deceleration in the time height intensity scan; this is in contrast to single body meteoroids, which produce a straight line.
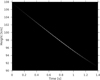 |
Fig. 9. Time height intensity scan computed from the results of the coupled simulation. |
5.5. Meteor trail intensity
The meteor’s trail intensity is shown in Fig. 10 at the following three different points along the trajectory: at the beginning, at the point of highest magnitude, and at the end of the trajectory. If one compares the computed trail intensity at the beginning of the meteor (107.5 km altitude) with measurements of dustball meteor trail intensities from Campbell-Brown et al. (2013) and Armitage & Campbell-Brown (2020), one can see good agreement. The trail intensity at an altitude of 107.5 km consists of a short peak ∼40 m in length. This agrees well with the measured trail intensities at the beginning of meteor light curves shown in Armitage & Campbell-Brown (2020).
 |
Fig. 10. Meteor trail intensity at three different points of the trajectory: at the beginning of the trajectory (Height = 107.5 km), at the point of highest magnitude (Height = 97.0 km), and at the end of the trajectory (Height = 90.5 km). |
The relative luminous intensity along the trail at peak magnitude is also plotted in Fig. 10. A comparison to measured trail intensities (Armitage & Campbell-Brown 2020; Campbell-Brown et al. 2013) shows bad agreement. The measured trail intensities peak at the beginning and decrease towards the end of the trail. The computed trail intensity at peak magnitude, however, increases constantly with an increasing trail distance. This effect is due to the fact that lighter particles decelerate faster than heavier particles and to the power law distribution of meteoroid grain masses, which ensures that the meteoroid consists of more lighter grains. Similar increasing trail intensities could also be observed in some of the modeled dustballs presented in Campbell-Brown et al. (2013), which used power law distributions. If another grain distribution (e.g., Gaussian) were chosen, other trail intensities would result. We can see that the trail at peak magnitude has a length around 200 m.
The trail intensity at the lowest computed height of 90.5 km can also be found in Fig. 10. We can see that it increases steeply at the beginning and is almost constant in the rest of the trail. The trail length is much bigger with over 800 m. This increase in trail length is due to the fact that grains lose mass during ablation and thus the remaining grains get even smaller, leading to larger separation due to higher atmospheric deceleration.
5.6. Wake length
The meteor’s wake length is shown in Fig. 11. One can see that the meteor produces a physical wake of up to 800 m near the end of its trajectory. The longest trail lengths for dustball meteors found in the literature (Armitage & Campbell-Brown 2020; Campbell-Brown et al. 2013) are around 450 m, which is somewhat shorter than what we predicted with our simulation. On the other hand, the wake lengths from Armitage & Campbell-Brown (2020) and Campbell-Brown et al. (2013) were taken at locations of higher magnitudes, where our simulation produces comparable wake lengths. In addition, it also must be noted that trail intensities and wake lengths are largely based on the grain size distribution, and not only on the disintegration details.
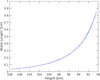 |
Fig. 11. Length of the meteor’s physical wake. |
6. Discussion
6.1. Coupling procedure
In the simulation presented in this paper, meteoroid and fluid dynamics were loosely coupled. In each time step, first a stationary DSMC computation about the meteoroid was carried out, and then the meteoroid dynamics was computed using constant aerodynamic forces acting on each grain. Future improvement of the simulation framework could include a tighter coupling between meteoroid and fluid dynamics, and maybe even direct coupling. Of course, there is a trade-off between computational efficiency and temporal accuracy. In the simulation presented in Sect. 4.3, a total of about 5’000 DSMC computations were carried out. The time step sizes between two consecutive DSMC computations varied greatly since they were largely determined by meteoroid deformation. Thus, much smaller time steps were used during meteoroid disintegration than at the point of the trajectory where the compressed meteoroid behaved like a rigid body.
6.2. Flow field
In the flow field simulations of this paper, a pure N2-atmosphere was considered. If a multispecies model was used, the composition of the atmospheric gas could be modeled more accurately, and ablated meteoroid material together with dissociation and recombination of molecules occurring at these high entrance velocities could be added to the flow simulations.
If the ionization of gas species was modeled in the flow simulations, ion trails could be computed and compared to measured radar echo data. Also electron excitation could be modeled, which would allow one to directly compute the light emission due to high energy collisions between ablated meteoroid material and atmospheric particles from the rarefied gas flow simulation. It would be interesting to study the meteoroid’s chemical wake based on such computations. Also, meteoroid spectra could be extracted from such a simulation. Light emissions based on ablated meteoroid particles were computed by Stokan & Campbell-Brown (2015) and Vinković (2007). Future work could include the aforementioned additions to the flow field computations and their application to the atmospheric entry of dustball meteoroids.
6.3. Grain bonds
The bonds between grains were modeled only by adhesive forces according to DMT (Derjaguin et al. 1975). Poppe et al. (2000b) experimentally investigated the electrical charging of protoplanetary grains as a result of collisions. They found that micron-sized grains are substantially charged after collisions with a plate (i.e., with a much bigger particle) at velocities of 10 m s−1. They concluded that electrical charging of micron-sized grains may play an important role in the formation of planetesimals and cometesimals in the solar nebula. Poppe & Schräpler (2005) performed collisions between micron-sized dust grains with velocities between 36 and 106 m s−1. They found a relatively high tribo-charging of the grains due to dissipation of the collision energy. They concluded that grain charging plays an important role in the sticking behavior between dust grains. Thus, grain bonds may be stronger than the adhesive force. In a future version of the code, an additional electromagnetic force could be introduced to model the interaction between electrically charged grains. Gunkelmann et al. (2017) performed DEM simulations of colliding condrules covered with dust shells using the granular mechanics code of Ringl & Urbassek (2012). They found that a dust shell increases the bouncing velocity by two orders of magnitude, that is from 2.4 mm s−1 to 0.75 m s−1. In their simulations, thicker and denser dust shells led to higher sticking velocities. Therefore, if meteoroid grains are covered by a thin dust shell, adhesive forces become stronger.
As shown in Sect. 4.3, the meteoroid disintegrates between an altitude of 123 km and 120 km, which is too high compared to the measurements of Borovička et al. (2007). If the meteoroid disintegrated at ∼102 km, according to the empirical data, the figures presented in Sect. 5 would be in much better agreement with the measurements of Draconid meteors. Since the meteoroid in our simulation disintegrates at an altitude which is ∼20 km too high, the separated grains have enough time to heat to the same temperature until ablation starts. If the meteoroid broke up at ∼102 km, the hotter grains from the meteoroid’s surface would start ablating before the colder ones from the interior. This would produce light curves closer to the ones expected for dustball meteoroids. The meteoroid breaks up at ∼120 km due to aerodynamic-induced rolling, which triggers collisions between grains leading to the break-up of grain bonds. In order for the meteoroid to break up at ∼102 km, grain bonds must be stronger so that they can withstand higher collision velocities, or the rolling friction between grains must be higher, such that aerodynamic forces no longer induce such high rolling and collision velocities. Grain bonds would be strengthened if an additional electromagnetic force was modeled, as mentioned above.
Heim et al. (1999) measured adhesion and rolling friction forces between micron-sized grains. They demonstrated that the adhesion force between micron-sized grains still has a linear dependence on their reduced radius. They found that the adhesive force between grains is ∼100 times stronger than the rolling force. In our simulation, the rolling friction was modeled by the adhesive force and the critical rolling displacement. In order to increase the rolling friction, one could either increase the adhesive force (i.e., increasing the surface tension) or the critical rolling displacement. We used a critical rolling displacement of ξyield = 3.2 nm (Heim et al. 1999). However, Heim et al. (1999) determined ξyield for micron-sized grains, while the grains in our simulation are one magnitude larger. The lower limit of ξyield = 0.2 nm is given by the mean distance between neighboring atoms and the maximum by the radius of the contact area aij (Heim et al. 1999). In future simulations a higher ξyield, lying between these limiting values, should be chosen in order to obtain a lower disintegration altitude. For example, the critical rolling displacement could be chosen such that the rolling friction would be 100 times lower than the adhesive force, corresponding to the experimental findings of Heim et al. (1999). A higher rolling friction would also result in a much smaller compression of the meteoroid at an altitude of 200 km and thus probably a more symmetrical meteoroid shape during the rest of the simulation.
Currently, the forces and moments between contacting grains are modeled independently of grain temperature. Future models could include grain interactions in dependence of their temperatures.
6.4. Grain sizes
The meteoroid used in our simulation was modeled using an exponential grain size distribution adapted from Borovička et al. (2007). This grain size distribution led to unrealistic meteor trail intensities presented in Sect. 5.5. Of course these trail intensities are also influenced by the disintegration of the meteoroid that is too early and the subsequent deceleration of the meteoroid grains. The trail intensities shown in Armitage & Campbell-Brown (2020) suggest that a constant or Gaussian grain distribution in combination with the meteoroid’s disintegration at the proper altitude might have produced more realistic meteor trail intensities.
Additionally, the grain sizes of 50–70 μm were adapted from Borovička et al. (2007) based on the results of their light and deceleration curve fits. It is possible that the referenced Draconid used in our simulation was built from differently sized grains. Bouwman et al. (2008) performed observations of seven protoplanetary disks in T Tauri systems with the Spitzer Space Telescope. On the basis of spectral analysis of their observations, they suggested grain sizes of up to 6 μm for amorphous silicates, 1 μm for enstatite grains, and 0.1 μm for forsterite grains. Comets are believed to be formed from unaltered protoplanetery disks. The stardust mission collected about 10’000 cometary particles ranging in size from 1 to 300 μm during its flyby of Comet 81P/Wild 2 (Brownlee et al. 2006). Thus, Draconids which are of cometary origin could be made of particles ranging from 0.1 to 300 μm in size. Future simulations could include meteoroids with different grain size ranges and grain size distributions.
6.5. Influence of material properties
The simulation presented in Sect. 4 only presents one single point in the whole material property space presented in Table 1. Since Draconid meteoroids ablate high in the atmosphere and do not produce meteorites, little is known about their material properties. Thus, for every parameter in Table 1, a whole range of values is possible. The material properties influence the meteoroid’s dynamics during atmospheric entry, its temperature, and ablation. With the right combination of these material properties, a good fit between simulation results and measurements can be expected. The influence of each parameter on the simulation results is discussed below.
The grain density influences inertia and the moment of inertia of each grain. A higher grain density would lead to less acceleration and rotational acceleration of each grain. A typical value for stony meteoroid grains is 3000 kg m−3, which was chosen here. However, also lower or higher grain densities would be possible. The Young modulus E and the Poisson ratio ν influence the repulsive force, sliding friction and twisting friction between grains. A higher E-value increases these values, while a higher ν lowers them. The surface tension γ is responsible for the adhesive force and thus also for the rolling friction. A higher surface tension increases both the adhesive force and rolling friction, thus leading to higher sticking forces between grains. As discussed in Sect. 6.3, a higher ξyield leads to higher rolling friction and subsequently to less deformation, as well as to disintegration at lower altitude. A lower heat capacity cp would lead to a faster increase in temperature. The conductivity k is responsible for the conductive heat transfer between grains, but conductive heat transfer is negligible due to the small contact areas between grains. Boiling temperature TB, condensation coefficient ψ, average atomic meteoroid mass μ, and specific heat of ablation L are responsible for the ablation of the meteoroid. The most influential one of them is L, which has been tuned in Sect. 5. The emissivity ϵ is responsible for the radiative heat transfer between grains. It also limits the maximum grain temperature for a given incoming atmospheric heat flux. A lower ϵ would lead to higher maximal grain temperatures, but less radiative heat transfer between grains.
6.6. Meteoroid structure
Apart from the various combinations of material properties, also the structure of the meteoroid plays a role. Only one simulation with a specific meteoroid geometry was carried out based on a grain size distribution adopted from Borovička et al. (2007). The structure was assumed to be homogeneous, the porosity was assumed to be 90%, and the shape was assumed to be spherical. Most probably, a real meteoroid does not have a perfect spherical shape. Pätzold et al. (2016) propose the mass, bulk density, porosity, and internal structure of comet 67P/Churyumov–Gerasimenko on the basis of its gravity field, measured by the Rosetta spacecraft. They found a bulk density of 533 kg m−3 and a porosity between 72–74%. They proposed a homogeneous structure of the comet with more dust than ice. They conclude that the porosity of the meteoroid results from the porosity of the comets material, rather than from its structure. Thus, there is evidence that cometary material is indeed pretty homogeneous, as is assumed in our simulation. On the other hand, Pätzold et al. (2016) suggest that the structure of cometary meteoroids might be much more compact than in our model and that the porosity of cometary material results from porous grains.
As different comets can also have different structures and material properties, it is possible that Draconids have a porosity around 90%. Trigo-Rodríguez & Llorca (2006) analyzed meteors of cometary origin. Based on their observations they found that the tensile strengths of cometary meteoroids are very similar for streams of a similar age. This supports the theory that cometary material gets compressed due to gas release. Thus, the structure of cometary material may change with time and meteoroids, even if they originate from the same parent comet, they can have different structures and porosities depending on the time of their release from the parent comet.
Future simulations could include different meteoroid structures. Homogeneous and inhomogeneous structures, along with different porosities and meteoroid shapes, could be considered, and their influence on the simulation results could be analyzed in order to make statements about the structure and shape of cometary meteoroids. Inhomogeneous and non-spherically shaped meteoroids would probably be subject to faster aerodynamically-induced rotation during atmospheric entry.
6.7. Initial meteoroid rotation
Čapek (2014) studied the rotation of cometary meteoroids due to gas drag during ejection from the parent comet under normal activity. It was found that millimeter-sized particles can be accelerated to a significant rotational speed, while particles bigger than 10 cm have negligible rotational speeds. The rotational speed of the meteoroid’s parent body was not taken into account, but it could lead to even higher rotational speeds. Thus, initial meteoroid rotation should be considered in future simulations. However, the DEM code is able to simulate drag-induced meteoroid rotation during the meteoroid’s atmospheric entry, which is presented in Sect. 4.3.2. Meteoroid rotation would lead to a more evenly distributed heat flux over the meteoroid’s surface.
6.8. Mechanical versus thermal disintegration
In our simulation, grain bonds can separate either due to mechanical forces or thermally if enough material ablates to trigger particle separation. In every dustball model found in the literature (Hawkes & Jones 1975; Campbell-Brown & Koschny 2004; Borovička et al. 2007; Armitage & Campbell-Brown 2020), meteoroid break-up is triggered thermally when the meteoroid has received a certain amount of thermal energy. Our simulation results suggest that a dustball meteoroid might break up mechanically before thermal effects become significant. According to our simulation, the dustball meteoroid broke up at an altitude where aerodynamic pressure is negligible compared to the tensile strengths of dustball meteoroids found in the literature. But our simulation showed that the mechanical break-up is triggered by the aerodynamically-induced rolling motion between grains and subsequent grain collisions producing enough force to break up grain bonds. Due to this effect, the simulated meteoroid was able to break up at an altitude where aerodynamic forces are much smaller than the adhesive forces holding the grains together.
It remains to be seen whether mechanical break-up of dustball meteoroids really exists, or if this is just a result of our simulation using this specific set of material properties. Comparison with measurements of Draconids show that probably a higher critical rolling displacement ξyield should have been chosen in order to obtain a higher rolling friction and to delay the break-up. If a higher rolling friction was chosen and mechanical break-up had started at a much lower altitude, it is possible that the meteoroid’s disintegration would have been triggered thermally due to the increased amount of ablated meteoroid material.
Simulations with more appropriate rolling friction between grains would show if meteoroid disintegration still gets triggered mechanically, or if thermal effects then play a more dominant role in the model. Further, as discussed in Sect. 5, also a higher specific heat of ablation should be chosen in order to better match measurements. Thus, its not clear whether according to our model thermal disintegration would really play a more significant role with more appropriate ablation parameters.
6.9. Applications to other meteoroid types
The coupled meteoroid model we have presented here can further be extended in order to be used with meteoroids other than dustballs. For more compact meteoroids, a DEM simulation which models cohesive forces between elements can be used to simulate meteoroid fragmentation. For single body meteoroids, which are not expected to fragment at high altitudes, the aerodynamic simulation is better coupled with a rigid body simulation in order to massively increase computational efficiency. This approach allows one to study the dynamics of a rigid body meteoroid during high altitude atmospheric entry.
In order for these extensions to justify their computational effort, an interesting three dimensional model of a meteoroid must be used. It makes little sense to use this simulation method with a spherical meteoroid geometry.
7. Conclusion
Until now, dustball models have been based on simple analytical equations, which did not take into account the three dimensional structure of a dustball meteoroid or the interaction between atmospheric flow and meteoroid grains. Campbell-Brown et al. (2013) applied the dustball models of Campbell-Brown & Koschny and Borovička et al. to ten faint meteors. Both models produced good fits of the wide filed measurements, but they failed to match the narrow field measurements. Thus, the authors concluded that dustball models need significant improvement.
We took a first step towards significantly improving dustball models by building an actual three dimensional dustball meteoroid and simulating it during atmospheric entry. On the basis of these atmospheric flow computations, temperature and mass loss of each meteoroid grain was computed, as well as the dynamic interaction between meteoroid grains. Our model is able to simulate thermal and mechanical meteoroid break-up based on the properties of adhering grains. Although our model needs to be improved, and many more simulations should be performed until good agreement between simulation results and measurements is achieved; this is a first step towards a more detailed, physical dustball model. To our knowledge, this is the first approach to simulate meteoroid disintegration based on a dynamic interaction between grains induced by aerodynamic forces.
Our simulation results indicate that meteoroid disintegration above ∼100 km might be triggered mechanically due to grain collisions. This contradicts the common belief that meteoroid disintegration at such high altitudes solely occurs due to thermal effects since the aerodynamic pressure is extremely small. It remains to be seen whether this is just a result of our simulation (with this specific set of material properties), or if mechanical meteoroid disintegration really occurs at high altitudes.
References
- Armitage, T., & Campbell-Brown, M. 2020, Planet. Space Sci., 186, 104915 [CrossRef] [Google Scholar]
- Bird, G. A. 1994, Clarendon, Oxford, 508, 128 [Google Scholar]
- Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [Google Scholar]
- Blum, J., Schräpler, R., Davidsson, B. J. R., & Trigo-Rodríguez, J. M. 2006, ApJ, 652, 1768 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., Gundlach, B., Mühle, S., & Trigo-Rodriguez, J. M. 2014, Icarus, 235, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J., Spurný, P., & Koten, P. 2007, A&A, 473, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Henning, T., Hillenbrand, L. A., et al. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Boyd, I. D. 2000, Leonid Storm Research (Dordrecht: Springer, Netherlands), 93 [CrossRef] [Google Scholar]
- Bronshten, V. A. 1983, Dordrecht (Holland) [Google Scholar]
- Brownlee, D., Tsou, P., Aléon, J., et al. 2006, Science, 314, 1711 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Čapek, D. 2014, A&A, 568, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 418, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell-Brown, M. D., Borovička, J., Brown, P. G., & Stokan, E. 2013, A&A, 557 [Google Scholar]
- Cundall, P. A., & Strack, O. D. L. 1979, Geotechnique, 29, 47 [Google Scholar]
- Derjaguin, B. V., Muller, V. M., & Toporov, Y. P. 1975, J. Colloid interface Sci., 53, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, C., & Nübold, H. 2002, Icarus, 157, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, Y. R. 2004, Comets, II, 223 [Google Scholar]
- Fisher, A. A., Hawkes, R. L., Murray, I. S., Campbell, M. D., & LeBlanc, A. G. 2000, Planet. Space Sci., 48, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Gorji, M. H., & Jenny, P. 2015, J. Comput. Phys., 287, 110 [CrossRef] [Google Scholar]
- Greenberg, J. M. 2000, Leonid Storm Research (Dordrecht: Springer, Netherlands), 313 [CrossRef] [Google Scholar]
- Güttler, C., Blum, J., Zsom, A., Ormel, C. W., & Dullemond, C. P. 2010, A&A, 513, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunkelmann, N., Ringl, C., & Urbassek, H. M. 2016, A&A, 589, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunkelmann, N., Kataoka, A., Dullemond, C. P., & Urbassek, H. M. 2017, A&A, 599, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawkes, R. L., & Jones, J. 1975, MNRAS, 173, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Heim, L.-O., Blum, J., Preuss, M., & Butt, H.-J. 1999, Phys. Rev. Lett., 83, 3328 [NASA ADS] [CrossRef] [Google Scholar]
- Hertz, H. 1881, J. Reine Angew. Math., 92, 110 [Google Scholar]
- Jacchia, L. G. 1955, ApJ, 121, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Küchlin, S., & Jenny, P. 2017, J. Comput. Phys., 328, 258 [CrossRef] [Google Scholar]
- Kloss, C., Goniva, C., Hager, A., Amberger, S., & Pirker, S. 2012, Prog. Comput. Fluid Dyn. Int. J., 12, 140 [CrossRef] [Google Scholar]
- Luding, S. 2008, Granular Matter, 10, 235 [Google Scholar]
- Mandt, K. E., Mousis, O., Marty, B., et al. 2015, Space Sci. Rev., 197, 297 [Google Scholar]
- Picone, J. M., Hedin, A. E., Drob, D. P., & Aikin, A. C. 2002, J. Geophys. Res.: Space Phys., 107, 1468 [NASA ADS] [CrossRef] [Google Scholar]
- Popova, O. P., Strelkov, A. S., & Sidneva, S. N. 2007, Adv. Space Res., 39, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Poppe, T., & Schräpler, R. 2005, A&A, 438, 1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poppe, T., Blum, J., & Henning, T. 2000a, ApJ, 533, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Poppe, T., Blum, J., & Henning, T. 2000b, ApJ, 533, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Pätzold, M., Andert, T., Hahn, M., et al. 2016, Nature, 530, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ringl, C., & Urbassek, H. M. 2012, Comput. Phys. Commun., 183, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Skorov, Y., & Blum, J. 2012, Icarus, 221, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stokan, E., & Campbell-Brown, M. D. 2015, MNRAS, 447, 1580 [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., & Llorca, J. 2006, MNRAS, 372, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Vinković, D. 2007, Advances in Space Research, 39, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2007, ApJ, 661, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2008, ApJ, 677, 1296 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Cuzzi, J. N. 1993, Protostars and Planets III, 1031 [Google Scholar]
- Whipple, F. L. 1951, ApJ, 113, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Sketch of Earth-fixed coordinate system and moving system used during the simulation of a dustball meteoroid’s atmospheric entry. |
| In the text | |
 |
Fig. 2. Sketch of the simulation domain. |
| In the text | |
 |
Fig. 3. Meteoroid before (a) and after (b) compression at about 200 km and a cut through the meteoroid at 135 km (c). The atmospheric entry flow is directed in the positive x-direction, while the meteoroid moves in the opposite direction. The radiant zenith distance of the meteoroid’s direction of flight is zR = 56.6°. |
| In the text | |
 |
Fig. 4. Meteoroid rotation frequency from the start of the simulation until the start of meteoroid disintegration. |
| In the text | |
 |
Fig. 5. Meteoroid during disintegration. The radiant zenith distance of the meteoroid’s direction of flight (-x-axis) is zR = 56.6°. |
| In the text | |
 |
Fig. 6. Two dimensional number density distribution of the meteoroid grains after full disintegration at an altitude of 119 km. |
| In the text | |
 |
Fig. 7. Resulting light curves based on the results of our DEM-DSMC simulation. Measurements and erosion fit of meteor No. 096 by Borovička et al. (2007) compared to our light curves, computed for three different values of heat of ablation. |
| In the text | |
 |
Fig. 8. Deceleration curve based on our simulation results, using a heat of ablation value of L = 13.7 ⋅ 106 J kg−1 compared to measurements and the erosion fit of meteor No. 096 by Borovička et al. (2007). |
| In the text | |
 |
Fig. 9. Time height intensity scan computed from the results of the coupled simulation. |
| In the text | |
 |
Fig. 10. Meteor trail intensity at three different points of the trajectory: at the beginning of the trajectory (Height = 107.5 km), at the point of highest magnitude (Height = 97.0 km), and at the end of the trajectory (Height = 90.5 km). |
| In the text | |
 |
Fig. 11. Length of the meteor’s physical wake. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



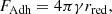
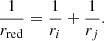
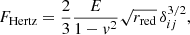
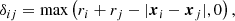
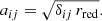
![$$ \begin{aligned} \delta _{\rm eq} = \left[ 6 \pi \, \frac{ \gamma }{E} \left( 1 - { v}^2 \right) \right]^{2/3} \root 3 \of {r_{\rm red} }. \end{aligned} $$](/articles/aa/full_html/2021/06/aa40305-21/aa40305-21-eq7.gif)
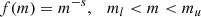
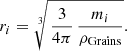
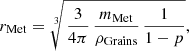
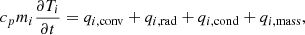
![$$ \begin{aligned} q_{i,\mathrm{rad}} = \sigma \epsilon \left[ \, \sum _{j=1}^N A_j F_{j \rightarrow i} T_j^4 + \left( 1 - \sum _{j=1}^N A_i F_{i \rightarrow j} \right) T_{\rm env}^4 - A_i T_i^4 \, \right], \end{aligned} $$](/articles/aa/full_html/2021/06/aa40305-21/aa40305-21-eq12.gif)