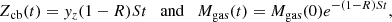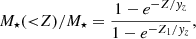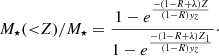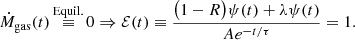| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202140836 | |
| Published online | 16 April 2021 | |
Letter to the Editor
The G-dwarf distribution in star-forming galaxies: A tug of war between infall and outflow
1
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: spitoni@phys.au.dk
2
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
Received:
19
March
2021
Accepted:
6
April
2021
In the past, the cumulative metallicity distribution function (CMDF) turned out to be a useful tool to constrain the accretion history of various components of the Milky Way. In this Letter, by means of analytical, leaky-box chemical evolution models (i.e. including both infall and galactic outflows), we study the CMDF of local star-forming galaxies that follow two fundamental empirical scaling relations, namely the mass-metallicity and main sequence relations. Our analysis shows that galactic winds, which are dominant mostly in low-mass systems, play a fundamental role in shaping this function and, in particular, in determining its steepness and curvature. We show that the CMDF of low-mass (M⋆/M⊙ ≤ 109.5) and high-mass (M⋆/M⊙ > 1010.5) galaxies substantially deviate from the results of a ‘closed-box’ model, as the evolution of the former (latter) systems is mostly dominated by outflows (infall). In the context of galactic downsizing, we show that downward-concave CMDFs (associated with systems with extremely small infall timescales and with very strong winds) are more frequent in low-mass galaxies, which include larger fractions of young systems and present more substantial deviations from equilibrium between gas accretion and reprocessing (either via star formation or winds).
Key words: galaxies: abundances / galaxies: evolution / galaxies: fundamental parameters / ISM: general
© ESO 2021
1. Introduction
In its original form, the G-dwarf problem consists in the fact that a ‘closed-box’ chemical evolution model1 predicts too many low-metallicity Galactic stars compared to the cumulative metallicity distribution function (CMDF) observed in the solar neighbourhood (van den Bergh 1962; Schmidt 1963). Various solutions have been proposed to fix this problem, including a time-varying stellar initial mass function (Schmidt 1963; Martinelli & Matteucci 2000) and an inhomogeneous star formation (Searle 1972); however, the most widely-accepted solution is perhaps the introduction of an ‘infall’ term in the standard chemical evolution equations, therefore, relaxing the assumption that the Galactic disc behaves as a closed box (e.g., Tinsley & Larson 1978; Tinsley 1980; Matteucci 1996, 2012). The main effect of considering slow gas accretion with a primordial composition in a chemical evolution model is the decrease in the fraction of low-metallicity stars compared to the predictions of the closed-box model. Following up on this idea, the adoption of an exponential infall of gas has become a fundamental assumption in several chemical evolution models of various components of our Galaxy (i.e. Matteucci & Francois 1989; Chiappini et al. 1997; Schönrich & Binney 2009; Romano et al. 2010; Matteucci et al. 2019; Grisoni et al. 2018; Spitoni et al. 2016, 2018, 2019a,b, 2020a, 2021).
The first extragalactic investigation of the G-dwarf problem in a large sample of spiral galaxies has been presented by Greener et al. (2021) recently in their analysis of the Mapping Nearby Galaxies at APO (MaNGA; Bundy et al. 2015) survey data, within the fourth SDSS data release. Thanks to new high-quality data, Greener et al. (2021) were able to construct the CMDFs from a stellar population fitting of the integrated light for a sizeable sample of galaxies as a function of stellar mass. Their results indicate that high-mass spirals (M⋆/M⊙ > 1010) generally show few low-metallicity stars, presenting a CMDF that is substantially different than the closed-box model, hence implying a history of gas accretion similar to the one of the Milky Way disc. By contrast, low-mass spirals (M⋆/M⊙ < 1010) present larger fractions of low-metallicity stars, showing, to a lesser extent, clear signs of a G-dwarf problem. In the light of these results, their interpretation is that low-mass galaxies present a metallicity distribution similar to the one expected if such systems that evolved as closed boxes.
One important ingredient which was ignored in such an interpretation is the effect of galactic winds on the CMDFs of the MaNGA galaxy sample. Mass and metal loss by means of galactic outflows is fundamental to explain the metallicity of the circumgalactic and intergalactic medium (e.g., Renzini & Andreon 2014), as well as some basic scaling relations observed both in local and distant galaxies. A recent work where galactic winds were found to play an important role is the theoretical study presented by Spitoni et al. (2020b, hereafter ES20) of the chemical evolution of local star-forming galaxies. The main assumption of this work is that local star-forming galaxies follow two fundamental, empirical scaling relations, namely the mass-metallicity relation (MZR) and the main sequence relation (MSR), namely the observed correlation between the star formation rate (SFR) and stellar mass. The study is based on analytical, ‘leaky-box’ chemical evolution models, where each galaxy originates by means of continuous accretion of primordial gas and can also experience outflows. The competition between these processes is fundamental for regulating the evolution of their metal content and their star formation history.
In using the models of ES20 in this Letter, we study, for the first time, the roles of infall and outflow in shaping the CDMF in galaxies as a function of their stellar mass. Our simple analytical formalism enables a straightforward interpretation of the CMDF and is useful to illustrate how the interplay between the flows of gas, of metals, and the star formation history of galaxies determine the most basic features of this particular function. In Sect. 2 we summarise the ES20 model, in Sect. 3 we present our study of the CDMF, and, finally, in Sect. 4 we draw our conclusions.
2. A summary of the ES20 model
Spitoni et al. (2017) present analytical solutions to the set of differential equations for the evolution of the total mass, gas mass, and metallicity in galaxies. In their most general form, the equation system includes the infall and outflow of gas, that is galaxies are allowed to evolve as leaky-box systems. The SFR is computed by means of the Schmidt (1959) law and can be expressed as ψ(t) = S ⋅ Mgas(t), where Mgas(t) is the gas mass at the time t and S is the star formation efficiency (SFE). For this quantity, we have assumed the scaling relation proposed by Boselli et al. (2014) between the typical galaxy gas depletion timescale and stellar content. The gas infall rate is expressed by the exponential law ℐ(t) = Ae−t/τ, where τ is the infall timescale. The quantity A is a constant, which is constrained by the total infall gas mass Minf (Spitoni et al. 2017). The outflow rate is proportional to the SFR of the galaxy (see Recchi et al. 2008) and is expressed as 𝒲(t) = λ ⋅ ψ(t), with λ being the wind parameter, which is also known as a loading factor with a dimensionless quantity. The analytical solution of Spitoni et al. (2017) for the evolution of the gas-phase metallicity Z, defined by the ratio between the mass of metals and the gas mass (i.e. Z = MZ/Mgas), is:
in which a primordial composition (i.e. metal-free) is assumed for the infalling gas, and the metallicity of the outflow is the same as the one of the interstellar medium (ISM), that is Zout = ZISM. In Eq. (1), parameter α is defined as α ≡ (1 + λ − R)S. The quantities yZ and R are the so-called yield per stellar generation and returned mass fraction. For both quantities yZ and R, we use the average values computed by Vincenzo et al. (2016) at various metallicities. Assuming a constant Salpeter (1955) stellar initial mass function (IMF) and the stellar yields of Romano et al. (2010), as metallicity-averaged values for the yield and for the return mass fraction, we use yZ = 0.0301 and R = 0.287, respectively. The other analytical expressions for the evolution of the total mass, gas mass, and stellar mass can be found in Spitoni et al. (2017).
In ES20, by adopting the aforementioned analytical solutions, model free parameters (i.e. the total infalling mass, the ‘loading factor’ or wind parameter λ, and the timescale of gas accretion τ) have been determined by imposing that the star-forming galaxies must follow the observed local MZR of Kewley & Ellison (2008) obtained with a calibration based on photoionisation models provided by Kewley & Dopita (2002) and the MSR of Peng et al. (2010). We refer the reader to Sect. 3 of Spitoni et al. (2020b) for further details about the methodology used to constrain the main parameters of our model.
In a 3D space formed by the SFR, oxygen abundances, and stellar mass, the ancestors of these galaxies lie on a hyper-surface, which is in good agreement with the fundamental metallicity relation of Mannucci et al. (2010). In order to obey the local scaling relations, in ES20 it was found that stronger winds (λ > 2) are needed in smaller stellar mass systems. As for the infall timescale parameter, low-mass and high-mass galaxies can have extended distributions, ranging from 0.1 to 10 Gyr, with slightly larger average values in the latter systems. By means of the same model used by ES20 to describe the backwards evolution of local systems, in Sect. 3 we show how the interplay between infall and galactic outflows is key for determining the shape of the CMDF in galaxies of different masses.
3. Model results and discussion
Using the analytical solutions presented in Spitoni et al. (2017), in Sect. 3.1 we analyse the main differences between the CMDF as predicted by means of closed-box and leaky-box models. In Sect. 3.2, we present the CMDF for the galaxies that follow the local MZR and MSR. Finally, in Sect. 3.3 we discuss further important implications of our results. In particular, we show at which stage ES20 galaxies can reach a state of equilibrium (defined by a balance between their infall, outflow, and star formation history) during their lifetimes and as a function of their mass, and if this stage can leave imprints on the CMDF distributions.
3.1. Closed-box versus leaky box CMDFs
In Fig. 1, we compare the CMDF and the age-metallicity relation predicted by a closed-box model with leaky-box systems, characterised by different values for the infall timescale τ and loading wind factor λ. In this case, the total infalling mass is fixed at the value of Minf = 1010 M⊙ and the adopted SFE is of S = 1 Gyr−1. However, the particular choice of these values does not affect the behaviour of the curves shown in the left panel of Fig. 1 nor their basic interpretation, as discussed in this section.
 |
Fig. 1. CMDFs (left panel) and temporal evolution of the gas phase metallicity Z (right panel) for models with different prescriptions for the infall and outflow. The grey shaded area in the left panel indicates the region reachable only by models with outflows and assuming a yield per stellar generation yz = 0.0301 (as in Spitoni et al. 2017). The solid light blue line shows the results of a closed-box model obtained assuming a lower value for the yield per stellar generation (yz ∼ 0.005), as in Fig. 1 of Greener et al. (2021). |
We consider the evolution of the closed-box model (solid black line), the outflow-only model (i.e. loading factor λ = 3.7 and no infall, black dotted line), and the pure-infall model (i.e. with infall parameter value τ = 8 Gyr and loading factor λ = 0, black dashed line) until they reach a metallicity of Z = 0.03, whereas their CMDFs are normalised to the total stellar mass value reached at Z = 0.03 (as in Fig. 1 of Greener et al. 2021). On the other hand, the other two leaky-box models with both infall and outflow reach the maximum metallicity at values smaller than Z = 0.03. We notice that only the three models with a non-zero wind parameter cross the shaded area in the left panel of Fig. 1. This basically implies that the inclusion of an outflow leads the models to reach maximal CMDF values at a lower metallicity than the pure-infall and closed-box models. One important feature of the curves shown in Fig. 1 concerns the curvature of the single tracks: A parabolic-like behaviour (namely an upward-concave curvature) is achieved only in models with a non-zero infall parameter.
Concerning the age-metallicity of the closed-box model, in Spitoni (2015) it is shown that in the presence of a Schmidt (1959) law for the SFR (ψ = S ⋅ Mgas), the temporal evolution of the metallicity Zcb and the gas mass can be expressed as follows:
respectively. These solutions can be retrieved by imposing A = 0 (no infall) and λ = 0 (no wind) in Eq. (1) and in Eq. (9) of Spitoni et al. (2017). The linear growth of the metallicity Zcb as a function of time is visible in the right panel of Fig. 1. From Eq. (2), we obtain the analytical expression for the CMDF, which can be expressed as follows:
where Z1 = 0.03 in our case. The shape of the CMDF is not dependant on the particular choice of the SFE. However, this is clearly not true for the evolution of the metallicity, as systems reach the Z1 value at different evolutionary times if different SFE values are adopted; in particular, the adoption of larger S values shortens the time to reach a high metallicity. Concerning the system with only wind (𝒲 = λ ⋅ ψ) and a Schmidt (1959) law for the SFR, the analytical solution for the CMDF can be expressed as follows:
From this expression, by imposing the no-wind condition (i.e. λ = 0), it is possible to retrieve the CMDF solution for the closed-box model of Eq. (3). Figure 1 shows that the age-metallicity for the closed-box and only outflow models are identical, which is in agreement with the findings of Spitoni (2015).
An important warning is in order when comparing the CMDF of the closed-box and outflow-only models. We note that in Fig. 1 of Greener et al. (2021), the closed-box solution is obtained assuming a ‘non-physically motivated’ (as stated by Greener et al. 2021) yield value of yz ∼ 0.005, roughly 6 times smaller than the one adopted in our analysis. In Matteucci (2012), it was underlined that for leaky-box models in presence of outflows, the ‘true yield’ (defined as ytrue = Z/ln[μ−1], where μ = Mgas/Mtot) is always lower than the ‘effective’ one obtained with closed-box models 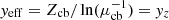 . This is basically the reason why, with a closed-box model (such as the one Greener et al. 2021), it is possible to achieve a CMDF with an identical shape to the one of our outflow-only model with λ = 3.7 (see Fig. 1). In conclusion, besides discussing the roles of infall and outflow in determining the particular shape of the CMDF, we have shown a particular case in which the CMDF of a leaky-box model can be the same as the one of a closed-box model with a reduced yield. This has to be beared in mind in the interpretation of this quantity.
. This is basically the reason why, with a closed-box model (such as the one Greener et al. 2021), it is possible to achieve a CMDF with an identical shape to the one of our outflow-only model with λ = 3.7 (see Fig. 1). In conclusion, besides discussing the roles of infall and outflow in determining the particular shape of the CMDF, we have shown a particular case in which the CMDF of a leaky-box model can be the same as the one of a closed-box model with a reduced yield. This has to be beared in mind in the interpretation of this quantity.
In a future work, it is our intention to take into account more sophisticated prescriptions for the gas infall and outflow rates, for instance, the presence of differential winds (Recchi et al. 2008), namely galactic winds in which metals are ejected out of the parent galaxy more efficiently than the other elements. What we expect in the case of a further depletion of metals is a saturation of the CMDF occurring at lower metallicities, that is to say a further increase in its steepness. Likewise, there is evidence that inflows at late times (Mitchell et al. 2020; van de Voort 2017) are chemically enriched (‘wind recycling’). An enriched gas infall in massive galaxies could help to alleviate the G-dwarf problem (Matteucci 2012).
3.2. CMDFs for star-forming galaxies of ES20
In Fig. 2, we present the CMDFs calculated with the models of ES20 in three different stellar mass bins, namely M⋆/M⊙ ≤ 109.5, 109.5 < M⋆/M⊙ ≤ 1010.5, and M⋆/M⊙ > 1010.5. In each panel of Fig. 2, the colour-coded tracks show the results obtained for each single galaxy, whereas the grey histogram shows the average CDMF computed in each bin. The results obtained by means of the ES20 model are compared to the tracks of the infall-only, outflow-only, and closed-box models described in Sect. 3.1.
 |
Fig. 2. CMDFs for star-forming galaxies which follow the local MZR and MSR (see ES20) computed in three different mass bins: M⋆/M⊙ ≤ 109.5 (left panel), 109.5 < M⋆/M⊙ ≤ 1010.5 (middle panel), and M⋆/M⊙ > 1010.5 (right panel). In each panel, the small solid circles that are connected by a thin grey line indicate the CMDFs of single galaxies, and they are colour coded according to the stellar mass at z ∼ 0.1. The thin magenta lines are used to indicate single galaxies with downward-concave CMDFs. The grey shaded histograms indicate the average values of the CMDFs computed in 14 different metallicity bins. The solid lines, dashed lines, and dotted lines represent the CMDF of the closed-box model, the only-infall model, and the only-outflow model, respectively, which were computed with the same parameters as indicated in Fig. 1. |
As is visible in the right panel of Fig. 2, in the largest stellar mass bin, the computed CMDFs significantly deviate from the predictions of the closed-box model. However, they are instead in good agreement with the infall-only model. Another noteworthy feature of the results obtained for the most massive galaxies is the complete lack of downward-concave curves, which are associated with systems with outflows but very short infall timescales (such as the dark blue line of Fig. 1, with τ = 0.2 Gyr).
The middle panel of Fig. 2 shows the CMDFs computed for galaxies with an intermediate stellar mass. The vast majority of galaxies in this mass bin still show upward-concave CMDFs, but in this case, we see the presence of a small fraction (∼2.1%) of models which show the opposite behaviour, that is downward-concave curves (as indicated by the magenta lines). As for the average CMDF, in general, it is in better agreement with the closed-box model than the one of the most massive bin.
To understand this result, one has to consider that the role of the galactic winds in the evolution of intermediate-mass galaxies is significantly stronger than for the most massive galaxies. The fact that our galaxies are forced to follow the local MZR implies final metallicity values which are lower than the ones of the galaxies in the most massive bin. In general, this implies a steeper increase in the average CMDF, which is qualitatively more similar to the one of the closed-box model than to the ones of leaky-box models.
An even more pronounced steepness is evident for most of the galaxies in the lower mass bin (left panel of Fig. 2). In this case, the presence of systems characterised by strong outflows and short timescales of gas accretion is 6.4%, hence larger than in the previous mass bin, as is visible from the more significant presence of downward-concave curves. The systems belonging to the lowest mass bin are characterised by the lowest final metallicity values (Z < 0.01), and they are therefore characterised by the steepest CMDFs of our sample. The average CMDF is in agreement with the prediction of our outflow-only model (with λ = 3.7), which is also equivalent to the closed-box model of Greener et al. (2021) with a reduced yield shown in Fig. 1.
In summary, the analysis of the CMDF described in this section confirms that the evolution of the most massive star-forming galaxies is dominated by infall, occurring on long timescales (> 1 Gyr). The systems whose evolution is more similar to the one of a closed-box, which in our picture can be envisaged as characterised by a controlled balance between infall and outflows, are intermediate-mass galaxies. Finally, the evolution of low-mass galaxies is dominated by outflows. Our analysis offers a novel point of view to confirm the well-known importance of outflows in regulating the properties of galaxies, which increases as their stellar mass decreases (e.g., Dekel & Silk 1986; Tremonti et al. 2004; Hirschmann et al. 2016; Lian et al. 2018).
3.3. Galactic downsizing and equilibrium condition
In this section, we discuss a few implications of our analysis which are mostly related to galactic downsizing. This is a well-known property consisting in substantial differences in the star formation history of low- and high-mass galaxies, with a higher star formation activity in the most massive galaxies at early epochs, followed by more intense SF in low-mass galaxies at more recent times (e.g., Cowie et al. 1996; Calura & Menci 2009; Calura et al. 2009; Mortlock et al. 2011).
In Fig. 3, it is useful for attention to be focussed on the roles of infall and outflow in regulating the evolution of star-forming galaxies and to show the allowed range of both parameters in galaxies of a different mass, as dictated by the local MZR and MSR. Here, with different colours, we show the regions occupied by galaxies of the same mass bins of Fig. 2 in the space described by λ and τ. The most massive galaxies (red shaded region in Fig. 3) occupy the bottom-right corner of the plot and are therefore characterised by the longest accretion timescales (> 1 Gyr) and by the smallest values of the wind parameter (λ < 0.7). On the other hand, the largest wind parameter values (λ > 2) characterise the evolution of the lowest mass galaxies (blue shaded region in Fig. 3), which are also characterised by the most extended range of infall parameters, spanning the interval 0.1 Gyr ≤ τ ≤ 10 Gyr.
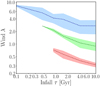 |
Fig. 3. Wind parameter λ versus infall time scale τ of the star-forming galaxies which follow the local MZR and MSR (ES20) and in the following three different stellar mass bins: M⋆/M⊙ ≤ 109.5 (blue line and region), 109.5 < M⋆/M⊙ ≤ 1010.5 (green), and M⋆/M⊙ > 1010.5 (red). The dashed lines represent the average values, whereas the shaded coloured regions represent the 1σ dispersion. |
The observed correlation between the galactic age and stellar mass relation is one main expression of galactic downsizing and, as shown by ES20, it directly stems from the local scaling relations of star-forming galaxies. In fact, at low redshift, these objects have to maintain a large reservoir of gas in order to be part of the local MSR. In this regard, weak winds and long infall timescales act together against a rapid gas consumption and cease star formation. In such conditions, a long lifetime is needed for them to be simultaneously metal-rich and still star-forming at present, which implies very old average ages and generally wide, upward-concave shapes for the CMDF.
On the other hand, lower mass systems are allowed to form continuously, and in all of them a low SFR and low metallicity, as required by the MZR and MSR, respectively, are both achieved by means of a wind parameter that is much stronger than more massive galaxies. Of these systems, those characterised by small (long) infall timescales show a downward- (upward-) concave CMDF.
The interplay between star formation, infall, and galactic winds regulates the gas content of galaxies and sets the timescale for them to reach a state of ‘equilibrium’, in which the amount of accreted matter is balanced by how much galactic material is processed, either via star formation or outflows (Peeples & Shankar 2011; Dayal et al. 2013; Lilly et al. 2013; Peng & Maiolino 2014). By means of our models, we assess at which stage of their life the star-forming galaxies of various masses can reach such equilibrium condition, which is defined by a null or very weak variation in the gas mass during their evolution (Maiolino & Mannucci 2019).
By imposing a null variation on the mass in the second equation of system (7) of Spitoni et al. (2017), we obtain:
In Fig. 4, we show the evolution of the ‘equilibrium’ parameter ℰ(t) defined above (i.e. ratio between reprocessed and accreted gas) in galaxies of three different mass bins as defined in Figs. 2 and 3. In this plot, values of ℰ(t) close to 1 are to be associated with systems in equilibrium. From Fig. 4, we can see that a well-defined relation between stellar mass and equilibrium timescale is in place, which is shown by the curvature of the average ℰ(t) computed in the three mass bins. The bulk of the galaxies in the highest mass bin have already started to behave as ‘gas-regulators’ (showing ℰ(t) ∼ 1) at redshift z ∼ 2.2, that is in the earliest phases of their life. This implies that these systems have spent almost their entire lifetime in equilibrium. On the other hand, on average, the objects with a stellar mass of M⋆/M⊙ ≤ 109.5 are characterised by the longest equilibrium timescales. In all three stellar mass bins of Fig. 4, several systems show a low-redshift upturn of ℰ. This is due to the late emergence of galaxies characterised by short timescales of accretion, which show stronger deviations from equilibrium in the lower mass bins as due to their stronger winds. The systems which cause the strongest deviations from the equilibrium are those that formed at the most recent times and the same systems characterised by downward-concave CMDF, with the smallest infall timescales and the strongest winds. As already discussed in Sect. 3.2, the importance of this population increases as we move towards a low stellar mass object, as is also visible from the average ℰ, which is significantly affected by the presence of these systems only in the stellar bin with M⋆/M⊙ ≤ 109.5.
 |
Fig. 4. Evolution of the quantity ℰ(t) introduced in Eq. (5) as a function of time for star-forming galaxies in the three stellar mass bins of Fig. 2. The single galaxy tracks (small solid circles connected by grey lines) are colour-coded according to their stellar mass at z ∼ 0.1, whereas the solid, thick black lines are the average values. The thick yellow line in the left panel represents the average ℰ(t), but it was computed excluding the two galaxies showing the largest values of the same quantity at redshift z = 0.1. In each panel, the magenta lines represent the galaxies characterised by downward-concave CMDFs. |
4. Concluding remarks
In this Letter, we have studied the CMDFs of star-forming galaxies as a function of their mass and by means of the ES20 model. We show how the shape of the CMDF in galaxies is determined by a ‘tug of war’ between infall and outflow. In agreement with the recent SDSS IV MaNGA data analysis of Greener et al. (2021), the CMDFs of the most massive objects (M⋆/M⊙ > 1010.5) substantially deviate from the closed-box model predictions and their evolution is dominated by infall, occurring on timescales typically of a few gigayears and is consistent with what was found in the earliest studies of the G-dwarf problem in the Milky Way (e.g., Tinsley & Larson 1978; Tinsley 1980). The evolution of intermediate-mass galaxies (109.5 < M⋆/M⊙ ≤ 1010.5) sees a controlled balance between infall and outflow and their CDMF is similar to the one obtained with an analytic closed-box model. Finally, in the evolution of low-mass (M⋆/M⊙ ≤ 109.5) galaxies, the outflows prevail and they present a much steeper average CDMF, more similar to the one achievable with a leaky-box analytic model with extremely short infall and a strong wind parameter. In individual galaxies, the stellar mass is a key parameter and it determines the timescale for reaching equilibrium between inflows and processed matter (both through winds and star formation). The strongest deviation from such equilibrium are presented by the youngest galaxies, whose frequency is larger in the lowest mass bin and which are characterised by a peculiar, downward-concave shape of the CMDF, which is only achievable with extremely small infall timescales and with a very strong wind parameter.
Acknowledgments
We thank the anonymous referee for constructive comments, which improved the quality of our work. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). E. Spitoni and V. Silva Aguirre acknowledge support from the Independent Research Fund Denmark (Research grant 7027-00096B). F. Calura acknowledges support from grant PRIN MIUR 2017 – 20173ML3WW_001 and from the INAF Main-Stream (1.05.01.86.31).
References
- Boselli, A., Cortese, L., Boquien, M., et al. 2014, A&A, 564, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., & Menci, N. 2009, MNRAS, 400, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Pipino, A., Chiappini, C., Matteucci, F., & Maiolino, R. 2009, A&A, 504, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Gratton, R. 1997, ApJ, 477, 765 [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Dayal, P., Ferrara, A., & Dunlop, J. S. 2013, MNRAS, 430, 2891 [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [Google Scholar]
- Greener, M. J., Merrifield, M., Aragón-Salamanca, A., et al. 2021, MNRAS, 502, L95 [Google Scholar]
- Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
- Hirschmann, M., De Lucia, G., & Fontanot, F. 2016, MNRAS, 461, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
- Lian, J., Thomas, D., & Maraston, C. 2018, MNRAS, 481, 4000 [Google Scholar]
- Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [Google Scholar]
- Martinelli, A., & Matteucci, F. 2000, A&A, 353, 269 [NASA ADS] [Google Scholar]
- Matteucci, F. 1996, Fund. Cosm. Phys., 17, 283 [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
- Matteucci, F., Grisoni, V., Spitoni, E., et al. 2019, MNRAS, 487, 5363 [Google Scholar]
- Mitchell, P. D., Schaye, J., & Bower, R. G. 2020, MNRAS, 497, 4495 [Google Scholar]
- Mortlock, A., Conselice, C. J., Bluck, A. F. L., et al. 2011, MNRAS, 413, 2845 [Google Scholar]
- Peeples, M. S., & Shankar, F. 2011, MNRAS, 417, 2962 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., & Maiolino, R. 2014, MNRAS, 443, 3643 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Spitoni, E., Matteucci, F., & Lanfranchi, G. A. 2008, A&A, 489, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A., & Andreon, S. 2014, MNRAS, 444, 3581 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [Google Scholar]
- Schmidt, M. 1963, ApJ, 137, 758 [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [Google Scholar]
- Searle, L. 1972, in IAU Colloq. 17: Age des Etoiles, eds. G. Cayrel de Strobel, & A. M. Delplace, 52 [Google Scholar]
- Spitoni, E. 2015, MNRAS, 451, 1090 [Google Scholar]
- Spitoni, E., Vincenzo, F., Matteucci, F., & Romano, D. 2016, MNRAS, 458, 2541 [Google Scholar]
- Spitoni, E., Vincenzo, F., & Matteucci, F. 2017, A&A, 599, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Matteucci, F., Jönsson, H., Ryde, N., & Romano, D. 2018, A&A, 612, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Cescutti, G., Minchev, I., et al. 2019a, A&A, 628, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Silva Aguirre, V., Matteucci, F., Calura, F., & Grisoni, V. 2019b, A&A, 623, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., & Calura, F. 2020a, A&A, 635, A58 [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Calura, F., Mignoli, M., et al. 2020b, A&A, 642, A113 [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021, A&A, 647, A73 [EDP Sciences] [Google Scholar]
- Tinsley, B. M. 1980, Fund. Cosm. Phys., 5, 287 [Google Scholar]
- Tinsley, B. M., & Larson, R. B. 1978, ApJ, 221, 554 [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1962, AJ, 67, 486 [Google Scholar]
- van de Voort, F. 2017, in The Effect of Galactic Feedback on Gas Accretion and Wind Recycling, eds. A. Fox, & R. Davé, 430, 301 [Google Scholar]
- Vincenzo, F., Matteucci, F., Belfiore, F., & Maiolino, R. 2016, MNRAS, 455, 4183 [Google Scholar]
All Figures
 |
Fig. 1. CMDFs (left panel) and temporal evolution of the gas phase metallicity Z (right panel) for models with different prescriptions for the infall and outflow. The grey shaded area in the left panel indicates the region reachable only by models with outflows and assuming a yield per stellar generation yz = 0.0301 (as in Spitoni et al. 2017). The solid light blue line shows the results of a closed-box model obtained assuming a lower value for the yield per stellar generation (yz ∼ 0.005), as in Fig. 1 of Greener et al. (2021). |
| In the text | |
 |
Fig. 2. CMDFs for star-forming galaxies which follow the local MZR and MSR (see ES20) computed in three different mass bins: M⋆/M⊙ ≤ 109.5 (left panel), 109.5 < M⋆/M⊙ ≤ 1010.5 (middle panel), and M⋆/M⊙ > 1010.5 (right panel). In each panel, the small solid circles that are connected by a thin grey line indicate the CMDFs of single galaxies, and they are colour coded according to the stellar mass at z ∼ 0.1. The thin magenta lines are used to indicate single galaxies with downward-concave CMDFs. The grey shaded histograms indicate the average values of the CMDFs computed in 14 different metallicity bins. The solid lines, dashed lines, and dotted lines represent the CMDF of the closed-box model, the only-infall model, and the only-outflow model, respectively, which were computed with the same parameters as indicated in Fig. 1. |
| In the text | |
 |
Fig. 3. Wind parameter λ versus infall time scale τ of the star-forming galaxies which follow the local MZR and MSR (ES20) and in the following three different stellar mass bins: M⋆/M⊙ ≤ 109.5 (blue line and region), 109.5 < M⋆/M⊙ ≤ 1010.5 (green), and M⋆/M⊙ > 1010.5 (red). The dashed lines represent the average values, whereas the shaded coloured regions represent the 1σ dispersion. |
| In the text | |
 |
Fig. 4. Evolution of the quantity ℰ(t) introduced in Eq. (5) as a function of time for star-forming galaxies in the three stellar mass bins of Fig. 2. The single galaxy tracks (small solid circles connected by grey lines) are colour-coded according to their stellar mass at z ∼ 0.1, whereas the solid, thick black lines are the average values. The thick yellow line in the left panel represents the average ℰ(t), but it was computed excluding the two galaxies showing the largest values of the same quantity at redshift z = 0.1. In each panel, the magenta lines represent the galaxies characterised by downward-concave CMDFs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} Z(t) = &\frac{{ y}_z \, S\big (1-R \big )}{\alpha \tau -1}\nonumber \\&\times \frac{M_{\rm gas}(0) \, t \, \big (\alpha \tau - 1 \big )^2+ A \tau \big [t - \tau (1 + \alpha t) + \tau e^{\alpha t -t/\tau } \big ]}{A \tau \big (e^{\alpha t -t/\tau } -1\big ) + M_{\rm gas}(0)\big (\alpha \tau -1\big )}, \end{aligned} $$](/articles/aa/full_html/2021/04/aa40836-21/aa40836-21-eq1.gif)