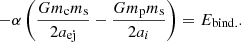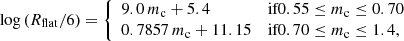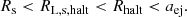| Issue |
A&A
Volume 648, April 2021
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202140442 | |
| Published online | 19 April 2021 | |
Letter to the Editor
The final orbital separation in common envelope evolution
Marquette University, Department of Physics, PO Box 1881, Milwaukee, Wisconsin 53201-1881, USA
e-mail: michael.politano@marquette.edu
Received:
28
January
2021
Accepted:
22
March
2021
In the majority of population synthesis calculations of close binary stars, the common envelope (CE) phase is modeled using a standard prescription based upon the conservation of energy, known as the alpha prescription. In this prescription, the orbital separation of the secondary and giant core at the end of the CE phase is taken to be the orbital separation when the envelope becomes unbound. However, recent observations of planetary nebulae with binary cores (BPNe), believed to be the immediate products of CE evolution, indicate orbital periods that are significantly shorter than predicted by population synthesis models using the alpha prescription. We argue that unbinding the envelope provides a necessary, but not sufficient, condition to escape a merger during CE evolution. The spiral-in of the secondary must also be halted. This requires the additional dynamical constraint that the frictional torque on the secondary be reduced to approximately zero. In this paper, we undertake a preliminary examination of the effect of adding this dynamical constraint in population synthesis calculations of BPNe. We assume that the frictional torque will be sufficiently reduced when the secondary enters a region within the giant where the mass-radius profile is flat. We crudely estimate the location of this region as a function of the core mass based upon existing stellar models of AGB stars between 1 and 7 M⊙. We calculate a theoretical orbital period distribution of BPNe using a population synthesis code that incorporates this dynamical constraint along with the alpha prescription.
Key words: binaries : close / stars: AGB and post-AGB / planetary nebulae: general
© ESO 2021
1. Introduction
The common envelope (CE) phase is believed to play a key role in the evolution of many close binary stars, yet a firm theoretical understanding of this phase remains elusive. In a typical CE scenario, the initially more massive star (the primary) is a giant and the less massive star (the secondary) is a low-mass main sequence star. Either as a result of tidal capture or unstable mass transfer due to Roche lobe overflow, the secondary star becomes engulfed in the envelope of the primary. The orbit of the secondary decays due to frictional drag and the secondary spirals in toward the core of the primary. There are two possible outcomes of such an evolution: Either a merger occurs or sufficient orbital energy is released on a short enough timescale to eject the envelope, leaving the embedded components intact but in a much closer orbit.
Detailed hydrodynamical calculations of CE evolution have been made by several researchers using both grid-based and SPH codes (e.g., Ivanova et al. 2013; Iaconi & De Marco 2019). In many of the grid-based calculations, the final outcome of the evolution was not able to be determined, primarily because of the large difference in spatial scales that need to be resolved (e.g., Sandquist et al. 1998). In some cases where the evolution was followed to completion, either the envelope was not able to be ejected or the final orbital separations were much larger than observed in post-CE systems, or both (e.g., Ricker & Taam 2012; Passy et al. 2012; Ohlmann et al. 2016; Sand et al. 2020). Nandez & Ivanova (2016) were able to unbind the envelope using recombination energy. Nevertheless, Iaconi & De Marco (2019), who conducted a detailed comparison of all 3-D simulations of the CE phase, conclude that the final orbital separations in all simulations must be considered upper limits due to a lack of spatial resolution or the size of the softening length applied to the gravitational potential of the particles. Further, the parameter space of post-CE binaries is not well covered by the simulations. Until these limitations are overcome, hydrodynamical calculations of the CE phase will not provide the necessary input for modeling populations of close binary stars using population synthesis techniques.
In order to make progress, a very simple model of the CE phase was proposed based upon the conservation of energy (Tutukov & Yungleson 1979). In this model, the envelope is assumed to be ejected (somehow) if sufficient orbital energy is released during the spiral-in to unbind it before a merger occurs. This so-called alpha prescription, shown in Eq. (1), was developed to estimate the orbital separation at which the envelope would become unbound.
In this prescription, mc, mp, Ebind, and ai are the core mass of the primary, the total mass of the primary, the binding energy of the primary’s envelope, and the orbital separation, respectively, all at the onset of the CE phase, ms is the mass of the secondary, aej is the orbital separation when the envelope becomes unbound, and α is the so-called CE efficiency parameter, which is an input parameter that represents the efficiency at which orbital energy is transferred to the envelope. Effectively, the many uncertainties in CE evolution have been encapsulated in the efficiency parameter, whose value is unknown. It is important to note that the alpha prescription assumes that any remaining envelope material interior to the orbit (after ejection) is small enough to have a negligible effect on the final orbital separation. Thus, in the alpha prescription, aej in Eq. (1) is considered to be the orbital separation at the end of the CE phase, which we shall denote as af.
Observations of post-CE binaries (PCEBs) have increased dramatically in the last ten years. Of particular importance are observations of planetary nebulae with binary cores (BPNe) since these systems are believed to have just exited the CE phase. Currently, there are ∼60 BPNe with known orbital periods1. A distribution of these periods is shown in Fig. 1. This distribution is sharply peaked near Porb = 1/3 day and contains few systems with orbital periods greater than 1 day.
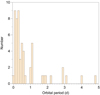 |
Fig. 1. Observed distribution of orbital periods in BPNe. |
Model populations of BPNe have been calculated independently by several researchers using population synthesis codes that employ the alpha prescription (deKool 1990; Yungleson et al. 2003; Han et al. 1995; Moe & De Marco 2006). For common input parameters (α = 1 and a flat initial mass ratio distribution), the orbital period distributions in these model populations are quite similar, but they do not match the observed distribution. Instead, the model orbital period distributions are broadly peaked, contain a large number of systems with periods greater than 1 day, and have a long-period tail.
The cause of the discrepancy between the theoretical period distributions and the observed orbital period distribution in BPNe remains unknown. Independent analyses conclude that the dearth of BPNe with orbital periods longer than 1 day is not likely a result of observational biases (De Marco et al. 2008; Rebassas-Mansergas et al. 2008; Miszalski et al. 2009; Davis et al. 2010; Jones & Boffin 2017). However, observational selection effects cannot be completely ruled out.
In this paper, we examine the effect of adding a dynamical constraint to determining the final orbital separation. Namely, we require that, in addition to unbinding the envelope, the frictional drag on the secondary must also be severely reduced in order to halt the spiral-in and avoid a merger. This dynamical constraint was proposed by Yorke et al. (1995) and Terman & Taam (1996), but it has never been incorporated into population synthesis calculations. Using data presented in Terman & Taam (1996), we have developed a very crude relationship between the orbital separation, at which spiral-in is halted, and the core mass of the giant primary. We have incorporated this relationship into our population synthesis code and calculated new theoretical orbital period distributions for BPNe. We find that these new distributions are in better agreement with the observed period distribution in BPNe.
In Sect. 2, we discuss the constraint in more detail and its incorporation into our code. In Sect. 3, we present the theoretical orbital period distributions in our model BPNe populations calculated with the dynamical constraint. We discuss these results and present our conclusions in Sect. 4.
2. Method
Yorke et al. (1995) and Terman & Taam (1996) argue that while the release of enough orbital energy to unbind the envelope is a necessary condition to avoid a merger, it is not a sufficient condition. The frictional torque on the secondary must also become sufficiently small, otherwise the orbital decay will not be halted and the secondary will continue to spiral in toward the core. The authors maintain that in order for this frictional torque to be reduced significantly, the envelope must contain a region where the mass-radius profile is flat (see Fig. 6 in Yorke et al. 1995). Terman & Taam (1996) estimated the outermost radial coordinate at which this flat region begins using the condition that V = −d ln p/d ln r is a minimum (see e.g., Schwarzschild 1958). In this expression, p is the pressure and r is the radial coordinate. Essentially, since V is proportional to M(r)/r, where M(r) is the mass contained within radius r, V will decrease outward in a region where the mass-radius profile is flat until M(r) begins to increase significantly. We denote this outermost radial coordinate as Rflat.
Yorke et al. (1995) and Terman & Taam (1996) note that the frictional torque will not immediately drop to zero at Rflat, since there is still sufficient material within the gravitational interaction region of the secondary. They estimated from their hydrodynamical calculations that the frictional torque will be reduced sufficiently to halt spiral-in at a radial coordinate between approximately Rflat/10 to Rflat/3, and they chose Rflat/6 as an estimate. Using stellar models of giant stars between 1 and 7 M⊙, Terman & Taam (1996) determined Rflat for giants at various points in their evolution. Choosing Rflat/6 as the radius at which the spiral-in is halted, they plotted this critical radius versus the core mass of the giant at various evolutionary stages and for various initial primary masses (Fig. 8 in Terman & Taam 1996).
We show in Fig. 2 a similar plot in which the data points for AGB stars are taken from Fig. 8 in Terman & Taam (1996) and the lines represent our crude linear fits to their data, which are expressed mathematically as follows:
 |
Fig. 2. Radius at which the spiral is halted versus the core mass of the giant at various evolutionary stages and for various initial masses. We note that Rhalt = Rflat/6. The data points are taken from Fig. 8 in Terman & Taam (1996) and the solid line is our linear fit to their data. The right scale on the y-axis is log Rhalt in R⊙. |
where Rflat is in centimeters and mc is in M⊙. We have neglected RGB stars in Fig. 2, since the data in Fig. 8 of Terman & Taam (1996) are much scarcer for RGB stars compared to AGB stars.
Yorke et al. (1995) and Terman & Taam (1996) further maintained that the envelope must be ejected before the orbital deceleration is significantly reduced. Once the orbital decay timescale increases significantly, even if enough orbital energy is available to unbind the envelope, it would be released on too long of a timescale to be effectively converted into mechanical energy and drive mass motion. Instead, it would be converted into thermal energy and radiated away, ultimately leading to a merger.
The population synthesis code used to calculate the model populations of BPNe has been described extensively in the literature (e.g., Politano et al. 2010). Since the only modification made to the code is the prescription for the CE phase, we refer the reader to the above paper for detailed information about the code. Here we focus on the incorporation of the dynamical constraint and we describe only the most salient features of the code.
In modeling the CE phase, we still used Eq. (1) to determine aej, which is the orbital separation at which the CE becomes unbound. The envelope binding energy was taken directly from the stellar models used in the population synthesis. We next determined Rflat from Eq. (2). The radius at which the spiral-in is halted is denoted by Rhalt. In our standard model, we assumed α = 1 and Rhalt = Rflat/6 (following Terman & Taam 1996), but we investigated other choices for these parameters. Finally, we determined the Roche lobe radius of the secondary at an orbital separation equal to Rhalt and compared it to the radius of the secondary, Rs. In order for the system to avoid a merger, we required that two criteria be met: (1) The envelope must have become unbound before the torque on the secondary was severely reduced and the orbital decay timescale became too long to drive ejection (i.e., aej > Rhalt); and (2) the Roche lobe radius of the secondary was greater than the radius of the secondary when the orbital separation equaled Rhalt (i.e., RL, s, halt > Rs). These criteria are nicely summarized by the following inequality,
We note that RL, s, halt = rL Rhalt, where rL is the dimensionless Roche lobe radius taken from Eggleton (1983).
If the inequality in Eq. (3) cannot be satisfied, a merger is assumed and the system is removed from the population. If the inequality can be satisfied, we assume that no further decay of the orbit occurs once the secondary reaches Rhalt and we set af = Rhalt.
In our calculations, we began with 109 zero-age main sequence binaries. We assumed a Miller-Scalo initial mass function (Miller & Scalo 1979) for the primary masses, an orbital period distribution that is flat in log P (Abt 1983), and an initial mass ratio distribution that is flat, g(q) dq = 1 dq (Duquennoy & Mayor 1991). We assumed a Galactic age of 1010 yrs, representative of a disk population, and assumed a constant star formation rate. We used full stellar models to follow the evolution of both stars and to determine the binding energy of the envelope at the onset of the CE phase. We only considered primaries on the AGB at the onset of the CE phase. Lastly, we assumed that the radius of the secondary remains unchanged during CE evolution.
3. Results
In Fig. 3, we show the BPNe orbital period distributions calculated using the CE prescription with the dynamical constraint for various values of Rhalt, ranging from Rflat/6 to Rflat, assuming α = 1. In Fig. 4, we show the model period distributions for various choices of α, assuming Rhalt = Rflat/2.
 |
Fig. 3. Model BPNe orbital period distributions for various values of Rhalt. The observed orbital period distribution in BPNe (histogram) and the orbital period distribution using the standard alpha prescription (red dashed line) are also shown for comparison. All distributions have been normalized to unity for the sake of comparison. |
 |
Fig. 4. Model BPNe orbital period distributions for various choices of α. In all cases, Rhalt = Rflat/2. All distributions have been normalized to unity for the sake of comparison. |
We find that the inclusion of the dynamical constraint as described in Sect. 2 has the following effects.
First, for all choices of Rhalt and α, the fraction of systems with orbital periods less than 1 day is significantly larger than the fraction found using the standard alpha prescription.
Second, for all choices of Rhalt and α, the distribution is peaked, in contrast to the broad distribution found using the standard alpha prescription. We find that the location and height of the peak in the Rhalt = Rflat/2 distribution best matches the observed distribution.
Third, the shape of the distribution is not very sensitive to the choice of α. Indeed, choosing a random value for α between 0 and 1 yields a nearly identical distribution to the distribution where alpha = 1. Only when α is globally very small is there any notable difference.
4. Discussion and conclusions
The alpha prescription was originally proposed as a way to crudely estimate the orbital separation at the end of the CE phase in lieu of a detailed model of CE evolution. However, it is unlikely that the many uncertainties in CE evolution can be distilled into a single global parameter whose value can be constrained by observations. Attempts to do so for PCEBs have succeeded only for very specialized choices of input parameters, for example, α ≲ 0.2−0.3 (Zorotovic et al. 2010).
One of the difficulties in modeling the CE phase is the wide range of timescales involved in the evolution. The rapid spiral-in phase occurs on a dynamical timescale and can only be properly modeled using a 3-D hydrodynamical code, while the slow spiral-in phase (also called the self-regulated phase) occurs on a thermal timescale and requires a 1-D stellar evolution code, which contains more detailed physics. In their comprehensive review of CE evolution, Ivanova et al. (2013) cite understanding the transition between the rapid and slow spiral-in phases as a high priority in advancing our understanding of CE evolution. An important step in that process is determining the orbital separation at which the orbital decay slows down. Once the secondary enters the flat mass-radius region of the envelope, the orbital decay time will begin to rise considerably (e.g., Terman & Taam 1996). We suggest that the transition between the two phases occurs somewhere within this region.
The improved agreement between the theoretical and observational orbital period distribution of BPNe suggests that inclusion of a dynamical constraint in population synthesis calculations may be an important consideration. However, the analysis we present here is very crude. In particular, a more detailed analysis of the relationship between Rflat, the core mass of the giant, and the total mass of the giant is needed (e.g., Lopez-Canelas & Politano 2015). We suggest a grid of Rflat for giants of various total mass and core mass needs to be calculated from detailed stellar models of both RGB and AGB stars. The question of whether there are a significant number of BPNe with RGB progenitors remains open (e.g., Hillwig et al. 2017; Jones et al. 2020). Nevertheless, they should be included in the population synthesis (e.g., Hall et al. 2013). Secondly, the frictional torque per unit volume, τ, is a function of the density, 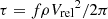 , where ρ is the local density, Vrel is the velocity of the secondary relative to the envelope, and f is a parameter related to the Mach number (Yorke et al. 1995). Once Rflat is reached, there is uncertainty as to the orbital separation at which the frictional torque becomes effectively zero. Terman & Taam (1996) assumed Rhalt = Rflat/6, but further investigation is needed to determine a more precise relationship.
, where ρ is the local density, Vrel is the velocity of the secondary relative to the envelope, and f is a parameter related to the Mach number (Yorke et al. 1995). Once Rflat is reached, there is uncertainty as to the orbital separation at which the frictional torque becomes effectively zero. Terman & Taam (1996) assumed Rhalt = Rflat/6, but further investigation is needed to determine a more precise relationship.
With the inclusion of the dynamical constraint, the final orbital separation primarily depends upon the evolutionary state of the giant star and is relatively independent of the secondary mass (as long as the envelope can become unbound). If the dependence on the total mass of the giant is weak, there should be a correlation between the distribution of core masses and the distribution of orbital periods in BPNe. Currently, there is an insufficient number of BPNe in which both the orbital period and the white dwarf mass are known. However, we expect that continued observations of BPNe will eventually allow this prediction to be tested.
See online catalog maintained by David Jones at drdjones.net/bcspn.
Acknowledgments
We gratefully acknowledge very useful conversations with A. Ruiter, T. Hillwig, and D. Jones. We also thank the anonymous referee for very helpful comments.
References
- Abt, H. A. 1983, ARA&A, 21, 343 [Google Scholar]
- Davis, P. J., Kolb, U., & Willems, B. 2010, MNRAS, 403, 179 [Google Scholar]
- deKool, M. 1990, ApJ, 358, 189 [Google Scholar]
- De Marco, O., Hillwig, T. C., & Smith, A. J. 2008, AJ, 136, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, P. D., Tout, C. A., Izzard, R. G., & Keller, D. 2013, MNRAS, 435, 2048 [Google Scholar]
- Han, Z., Podsiadlowski, Ph., & Eggleton, P. P. 1995, MNRAS, 272, 800 [Google Scholar]
- Hillwig, T., Jones, D., De Marco, O., et al. 2017, AJ, 153, 24 [Google Scholar]
- Iaconi, R., & De Marco, O. 2019, MNRAS, 490, 2550 [Google Scholar]
- Ivanova, N. 2011, ApJ, 730, 76 [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Jones, D., & Boffin, H. M. J. 2017, Nat. Astr., 1, 117 [Google Scholar]
- Jones, D., Boffin, H. M. J., Hibbert, J., et al. 2020, A&A, 642, 108 [Google Scholar]
- Lopez-Canelas, N., & Politano, M. 2015, IAU Gen. Assembly, 22, 55902 [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1979, ApJS, 41, 513 [Google Scholar]
- Miszalski, B., Acker, A., Moffat, A. F. J., Parker, Q. A., & Udalski, A. 2009, A&A, 496, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moe, M., & De Marco, O. 2006, ApJ, 650, 916 [Google Scholar]
- Nandez, J. L. A., & Ivanova, N. 2016, MNRAS, 460, 3992 [Google Scholar]
- Ohlmann, S. T., Ropke, F. K., Pakmor, R., & Springel, V. 2016, ApJ, 816, L9 [Google Scholar]
- Passy, J. C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [Google Scholar]
- Politano, M., van der Sluys, M., Taam, R. E., & Willems, B. 2010, ApJ, 720, 1752 [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [Google Scholar]
- Rebassas-Mansergas, A., Gãnsicke, B. T., Schreiber, M. R., et al. 2008, MNRAS, 390, 1635 [Google Scholar]
- Sand, C., Ohlmann, S. T., Schneider, F. R. N., et al. 2020, A&A, 644, A60 [CrossRef] [EDP Sciences] [Google Scholar]
- Sandquist, E. L., Taam, R. E., Burkert, A., et al. 1998, ApJ, 500, 909 [Google Scholar]
- Schwarzschild, M. 1958, Structure and Evolution of the Stars (New York: Dover) [Google Scholar]
- Terman, J. L., & Taam, R. E. 1996, ApJ, 458, 692 [Google Scholar]
- Tutukov, A. V., & Yungleson, L. R. 1979, in Mass Loss and Evolution of O-Type Stars, eds. P. S. Conti, & W. H. de Loore (Dordrecht: Reidel), 216 [Google Scholar]
- Yorke, H. W., Bodenheimer, P., & Taam, R. E. 1995, ApJ, 451, 308 [Google Scholar]
- Yungleson, L. R., Tutukov, A. V., & Livio, M. 2003, ApJ, 418, 794 [Google Scholar]
- Zorotovic, M., Scheiber, M. R., Gansicke, B. T., & Nebot Gomez-Moran, A. 2010, A&A, 520, 86 [Google Scholar]
All Figures
 |
Fig. 1. Observed distribution of orbital periods in BPNe. |
| In the text | |
 |
Fig. 2. Radius at which the spiral is halted versus the core mass of the giant at various evolutionary stages and for various initial masses. We note that Rhalt = Rflat/6. The data points are taken from Fig. 8 in Terman & Taam (1996) and the solid line is our linear fit to their data. The right scale on the y-axis is log Rhalt in R⊙. |
| In the text | |
 |
Fig. 3. Model BPNe orbital period distributions for various values of Rhalt. The observed orbital period distribution in BPNe (histogram) and the orbital period distribution using the standard alpha prescription (red dashed line) are also shown for comparison. All distributions have been normalized to unity for the sake of comparison. |
| In the text | |
 |
Fig. 4. Model BPNe orbital period distributions for various choices of α. In all cases, Rhalt = Rflat/2. All distributions have been normalized to unity for the sake of comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.